1 Introduction

Quantum correlations represent a crucial tool used to achieve various quantum tasks, including quantum secret sharing protocols, quantum teleportation, and quantum cryptography [1,2,3,4,5,6]. For a good while, entanglement accounted for all quantum correlations. Indeed, many works have been developed to detect and quantify entanglement [7,8,9,10,11,12]. But it  has been shown that unentangled mixed states may contain quantum correlations beyond entanglement that cannot be captured by entanglement quantifiers. Therefore, a new quantum measure, known as quantum discord was introduced in [13]. However, the minimization complexity presents a big obstacle during the computation of quantum discord for arbitrary quantum states. Hence, an alternative geometric approach to quantum discord by means of Schatten norms is explicitly derived [14, 15]. Recently, alternative measures were suggested to compute the amount of quantum correlations inherent in a mixed quantum state. Notably, local quantum uncertainty (LQU) was introduced by Girolami et al. [16]. The LQU based on the Wigner–Yanase Skew Information [17] quantifies the minimal quantum uncertainty in a quantum state due to the measurement of a given local observable. Furthermore, the Hellinger distance [18] provides a geometrical significance to the LQU. Interestingly enough, the LQU is quite easily calculable for all qubit–qudit system and has been broadly used in various works [19,20,21,22,23,24]. On the other side, a further quantifier of quantum correlations called local quantum Fisher information (LQFI) is noteworthy suggested [25]. It is a reliable discord-type quantifier and it is calculated via minimizing the quantum Fisher information (QFI) [26,27,28] over all local observables acting on one of the two subsystems.

An alluring candidate for a solid-state qubit is offered in semiconductor quantum dot systems [29, 30]. In particular, qubits based on spins of electrons confined in quantum dots present the advantages of being easy to integrate into existing electronics and having long coherence times, which can allow information in them to be processed [31]. Entanglement dynamics, quantum correlations, and quantum coherence in such systems have also been investigated [32, 33]. In addition, great attention has been devoted to spin–orbit interaction (SOI) in various quantum systems [34, 35]. In this regard, there are two types of spin–orbit interaction in solids. The first one is symmetry independent, appearing in all kinds of crystal and stems from SOI in atomic orbitals. The second type of SOI is symmetry dependent, which exists only in crystals without inversion symmetry. This latter includes the Dresselhaus interaction [36] which is a bulk-induced asymmetry, and the Bychkov–Rashba interaction [37, 38] which is a surface-induced asymmetry, produced either by the confining potential or an external electric field. In a quantum well with broken symmetry inversion along the growth z-axis, the Hamiltonian of the Rashba interaction is given by \(H_{R}=\alpha _{R}( \vec {z}\wedge \vec {p})\vec {\sigma }\), such that \(\alpha _{R}\) denotes the Rashba parameter. In contrast, \(\vec {p}\) and \(\vec {\sigma }\) reflect the momentum and the Pauli matrix vectors. The Rashba interaction is at the core of the expanding field of spintronics, which uses particles’ spins for information processing. Rashba coupling in quantum dots has already been investigated in [39,40,41].

The principal objective behind this manuscript is twofold. First, we shall study a system based on the interaction between a pair of quantum dots with a single electron located either in the left or the right dot based on Rashba coupling. The second part of this work is dedicated to examining the dynamics of thermal entanglement through Logarithmic negativity. Besides, a comparative study between entanglement and quantum correlations captured by LQFI and LQU in a double quantum dot system with Rashba interaction will be investigated. We shall illustrate the impact of the temperature, the Rashba spin–orbit coupling, the tunneling between the pair of quantum dots, and the Zeeman coupling on the quantum correlations of the considered system.

The outline of this paper is structured as follows: Sect. 2 contains some preliminaries about logarithmic negativity, local quantum uncertainty, and local quantum Fisher information. In Sect. 3, we give the Hamiltonian of the double quantum dot system with Rashba interaction and its thermal state. The behaviors of quantum correlations captured by logarithmic negativity, LQU, and LQFI in the considered system are explained and examined in Sect. 4. A summary of our outcomes appears in Sect. 5.

2 Quantum quantifiers

2.1 LN

Consider a bipartite system characterized by a two-qubit entangled mixed state \(\varrho\). One can use logarithmic negativity (LN) as an entanglement quantifier to measure the entanglement degree between two subsystems A and B [42] . It is established for a bipartite density matrix \(\varrho\) living in the Hilbert space \({{\mathcal {H}}}_{AB}={{\mathcal {H}}}_{A} \otimes {{\mathcal {H}}}_{B}\) as

$$\begin{aligned} {{\mathcal {L}}}N(\varrho )=\log _2\Vert \varrho ^{T_B}\Vert _1, \end{aligned}$$
(1)

\({\varrho ^{T_B}}\) is the partially transposed density matrix concerning the second subsystem of the two-qubit system. The norm \(\Vert \cdot \Vert _1\) refers to the trace norm (also known as Schatten-1 norm) of any operator \(\mathcal {O}\) and is typically expressed as

$$\begin{aligned} \Vert \mathcal {O}\Vert _1=tr\left( \sqrt{\mathcal {O}^{\dagger }\mathcal {O}}\right) . \end{aligned}$$
(2)

It is good to highlight that logarithmic negativity is an additive quantity and preserves entanglement monotonicity under deterministic local operations and classical communication (LOCC). From Eq.(1), the LN is calculated with the help of the eigenvalues \(\{\mu _i \}\) of the density operator \({\varrho }^{T_{B}}\) as

$$\begin{aligned} {{\mathcal {L}}}N(\varrho ) = \log _{2} \left( \sum _{i} |\mu _i| \right) . \end{aligned}$$
(3)

Moreover, LN is always nonnegative and goes to zero for product states, while it reaches its maximum value for maximally entangled states.

2.2 LQFI

Quantum Fisher information (QFI) is essential in quantum estimation theory. It defines the quantum counterpart of classical Fisher information. Indeed, QFI is a critical metric still widely used in the framework of quantum estimation theory to improve efficiency in parameter estimation situations (see, for instance, [43, 44]). It is important to note that the QFI is frequently associated with quantum correlations other than entanglement [45,46,47,48]. For an arbitrary quantum state \(\varrho _{\theta }\)  dependent on the variable θ, QFI is defined as [49, 50]

$$\begin{aligned} {\mathcal {F}}(\varrho _{\theta })=\frac{1}{4}\text {tr}[\varrho _{\theta } L_{\theta }^2], \end{aligned}$$

where \(L_{\theta }\) is a symmetric logarithmic derivative that solves the following equation:

$$\begin{aligned} \frac{d\varrho _{\theta }}{d\theta }=\frac{1}{2}( \varrho _{\theta } L_{\theta }+L_{\theta }\varrho _{\theta } ). \end{aligned}$$

The parameterized state \(\varrho _{\theta }\) is produced by acting a unitary operator U on the initial probe state \(\varrho\) (\(\varrho _{\theta } = U \varrho U^{\dagger }\)). The action U depends on the variable \(\theta\) and is constructed by a Hermitian operator H i.e., \(U = \textrm{e}^{-iH\theta }\). Consequently, \(\mathcal {F}(\varrho _{\theta })=\mathcal {F}(\varrho , H )\) is given by

$$\begin{aligned} {\mathcal {F}}(\varrho , H)=\frac{1}{2}\sum _{i,j, \kappa _i+\kappa _j>0}\frac{(\kappa _i-\kappa _j)^2}{\kappa _i+\kappa _j}|\langle \varphi _i|H | \varphi_j\rangle |^2. \end{aligned} $$
(4)

Here, we have employed the eigenbasis expansion of the density operator \(\varrho\), that is, \(\varrho = \sum \nolimits _{i = 1} {{\kappa _i}\left| {{\varphi _i}} \right\rangle \langle {\varphi _i}|}\) with \({\kappa _i} \ge 0\) and \(\sum \nolimits _{i = 1} {{\kappa _i}} = 1\). Now, let us consider a \(2 \otimes d\) bipartite quantum state \(\varrho\) belonging to the Hilbert space of the system (\({\mathcal {H}} = H_\textrm{A} \otimes H_\textrm{B}\)). By assuming that the dynamics of the first subsystem is governed by the phase shift operator \({e^{ - i\theta {H_A}}}\) which acts locally, where \({H_A} \equiv {H_a} \otimes {\mathbb {I}_B}\) is its corresponding local Hamiltonian. Hence, the next expression of the local quantum Fisher information (LQFI) can be derived [25]:

$$\begin{aligned} \mathcal {F}\left( {\varrho , {H_A}} \right) = \textrm{tr}\left( {\varrho {H}^2 _A} \right) - \sum \limits _{i,j, \kappa _i+\kappa _j>0} {\frac{{2{\kappa _i}{\kappa _j}}}{{{\kappa _i} + {\kappa _j}}}{{\left| {\left\langle {{\varphi _i}} \right| {H_A}\left| {{\varphi _j}} \right\rangle } \right| }^2}}. \end{aligned}$$
(5)

The quantity of quantum correlations quantified using local quantum Fisher information \(\mathcal {F}_L \left( \varrho \right)\) is defined as the minimum quantum Fisher information over all local Hamiltonians \({H_A}\) acting on a bipartite system’s subsystem A [25]:

$$\begin{aligned} \mathcal {F}_L (\varrho ) = {\text {min}}_{H_{A}}~\mathcal {F}(\varrho , H_A), \end{aligned}$$
(6)

where \(H_A=H_a \otimes I\). It should be emphasized that this measure is strictly positive and vanishes for zero discord bipartite states. It is also uniform under unitary local operations and gives the same output as the geometric discord for pure states. For the local operator \(H_a=\vec {\sigma }.\vec {r}\) when taking \(| \vec {r}|=1\) and \(\vec {\sigma }=(\sigma _x, \sigma _y, \sigma _z)\). One can verify that \(\textrm{tr}\left( {\varrho {H}^2 _A} \right) =1\) and that the sum term in Eq. (5) can be expressed as

$$\begin{aligned}&\sum \limits _{i,j, \kappa _i+\kappa _j>0} {\frac{{2{\kappa _i}{\kappa _j}}}{{{\kappa _i} + {\kappa _j}}}{{\left| {\langle {\varphi _i}|{H_A}\left| {{\varphi _j}} \right\rangle } \right| }^2}}\nonumber \\&\quad = \sum \limits _{i,j, \kappa _i+\kappa _j>0} {\sum \limits _{l,k=1}^3 {\frac{{2{\kappa _i}{\kappa _j}}}{{{\kappa _i} + {\kappa _j}}}} } \langle {\varphi _i}|{\sigma _l} \otimes \mathbb {I}_B\left| {{\varphi _j}} \right\rangle \langle {\varphi _j}|{\sigma _k} \otimes \mathbb {I}_B\left| {{\varphi _i}} \right\rangle \nonumber \\&\quad = {{\vec {r}}^{\dag } }.{{\mathcal {M}}}.{\vec {r}} \end{aligned}$$
(7)

where the (3 x3) symmetric matrix \({{\mathcal {M}}}\) entries are written as

$$\begin{aligned} {{{\mathcal {M}}}_{lk}} = \sum \limits _{i,j, \kappa _i+\kappa _j>0} {\frac{{2{\kappa _i}{\kappa _j}}}{{{\kappa _i} + {\kappa _j}}}\langle {\varphi _i}|{\sigma _l} \otimes \mathbb {I}_B\left| {{\varphi _j}} \right\rangle \langle {\varphi _j}|{\sigma _k} \otimes \mathbb {I}_B\left| {{\varphi _i}} \right\rangle }. \end{aligned}$$
(8)

It turns out that maximizing \({{\vec {r}}^\dag }.{{\mathcal {M}}}.{\vec {r}}\) over all unit vectors \({\vec r}\) is a required condition for minimizing Fisher information (\(\mathcal {F}\left( {\varrho ,{H_A}} \right)\)). The closed formula of LQFI is defined as

$$\begin{aligned} \mathcal {F}_L (\varrho )=1-\text {max}\{M_1,M_2,M_3 \}, \end{aligned}$$
(9)

where \(M_i\) (\(i=1,2,3\)) are the eigenvalues of the matrix \({\mathcal {M}}\).

2.3 LQU

The concept of local quantum uncertainty (LQU) is a valuable quantum correlation quantifier that will be applied in this study. Indeed, for a two-qubit state \(\varrho\), LQU is given as the minimum skew information achievable with single local measurements [51, 52]

$$\begin{aligned} \mathcal {U} (\varrho ) \equiv \min _{K_A} \mathcal {I}(\varrho , K_A \otimes \mathbb {I}_2), \end{aligned}$$
(10)

where \(K_A\) is the local Hermitian operator acting on qubit A, with a non-degenerate spectrum, and \(\mathbb {I}_2\) is the identity operator related to qubit B. Furthermore, the Wigner–Yanase skew information (WYSI) [17] is written as

$$\begin{aligned} \mathcal {I}(\varrho , K_A \otimes \mathbb {I}_2)=-\frac{1}{2}\textrm{tr}([\varrho ^{\frac{^1}{2}}, K_A \otimes \mathbb {I}_2]^{2}). \end{aligned}$$
(11)

The skew information (\(\mathcal {I}(\varrho , K_A \otimes \mathbb {I}_2)\)) is connected with the non-commutativity between the local operator \(K_A\) and \((\varrho )^{1/2}\). This approach was established to measure the unpredictability in mixed states [17]. Specifically, for bipartite systems, the LQU with regard to the first subsystem turns out to be [16]

$$\begin{aligned} {{\mathcal {U}}}\left( {{\varrho }} \right) = 1 - \max \left( {{\omega _{1}},{\omega _{2}},{\omega _{3}}} \right) \end{aligned}$$
(12)

where \(\omega _{i=1,2,3}\) is the spectrum of the (3-x-3) symmetric matrix \(\mathcal {W}_{AB}\) and the corresponding entries are provided by

$$\begin{aligned} \Big (\mathcal {W}_{AB}\Big )_{ij} \equiv \textrm{tr} \Bigg ( \varrho ^{1/2}\Big (\sigma _{Ai}\otimes {\mathbb {I}}_{B}\Big )\varrho ^{1/2} \Big (\sigma _{Aj}\otimes {\mathbb {I}}_{B} \Big )\Bigg ) \end{aligned}$$
(13)

where \(\sigma _{Ai} (i=1,2,3)\) are the standard Pauli operators acting on the subsystem A. Furthermore, the amount of LQU is related to LQFI, i.e., the LQU is majorized by LQFI using the following inequality [53, 54]:

$$\begin{aligned} {{\mathcal {U}}}\left( {{\varrho }} \right) \le \mathcal {I}(\varrho ,H)\le \mathcal {F}_L (\varrho ), \end{aligned}$$
(14)

where \({{\mathcal {U}}}\left( {{\varrho }} \right)\) and \(\mathcal {F}_L (\varrho )\) denote the LQU and LQFI introduced in Eqs.(12) and (9), respectively.  The quantity \(\mathcal {I} (\rho _{AB},H)\) stands for the skew information defined in Eq.(11).

3 Physical model

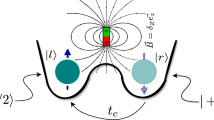
In this model, the system under consideration is double quantum dots with a single electron located in the left \(\big |L\rangle\) or right dot \(\big |R\rangle\), with Rashba interaction coupling (Fig. 1). The Hamiltonian model is given by

$$\begin{aligned} \begin{array}{ccc} H= & {} \frac{\Delta }{2}(\mathbb {I}\otimes \sigma _{z})+\eta (\tau _{x}\otimes \mathbb {I})-\alpha (\tau _{y}\otimes \sigma _{x}), \end{array} \end{aligned}$$
(15)

\(\tau _{x,y}\) are the Pauli matrices indicating the position of the electron \(\{\big |L\rangle , \big |R\rangle \}\), with \(\big |L\rangle \equiv \big |0\rangle\) and \(\big |R\rangle \equiv \big |1\rangle\). Moreover, \(\sigma _{x,z}\) denote the Pauli matrices describing the spin states of the electron \(\big |0\rangle\) and \(\big |1\rangle\). The Zeeman spin splitting \(\Delta\) is generated by a magnetic field B along the z-axis, \(\eta\) represents the tunneling coupling between the pair of quantum dots, and \(\alpha\) is the Rashba coupling. Therefore, the Hamiltonian matrix form is given in the basis \(\lbrace \vert 00 \rangle , \vert 01 \rangle , \vert 10 \rangle , \vert 11 \rangle \rbrace\) as follows:

$$\begin{aligned} H= \left( \begin{array}{cccc} \frac{\Delta }{2}&{}0&{}\eta &{}i\alpha \\ 0&{}-\frac{\Delta }{2} &{}i\alpha &{}\eta \\ \eta &{}-i\alpha &{}\frac{\Delta }{2}&{}0\\ -i\alpha &{}\eta &{}0&{}-\frac{\Delta }{2} \end{array} \right) . \end{aligned}$$
(16)

The eigenvectors and associated eigenvalues of the Hamiltonian (15) in the basis \(\left\{ \big |00\rangle ,\big |01\rangle ,\big |10\rangle ,\big |11\rangle \right\}\) are

$$\begin{aligned} E_1&= -\frac{1}{2}\sqrt{\Omega _{+}^{2}+4\alpha ^{2}}, \big |\varphi _{1}\rangle \nonumber \\&=\Lambda _{-}\left[ i\lambda _{-}\left( \big |00\rangle +\big |10\rangle \right) -\big |01\rangle +\big |11\rangle \right] , \end{aligned}$$
(17a)
$$\begin{aligned} E_2&= -\frac{1}{2}\sqrt{\Omega _{-}^{2}+4\alpha ^{2}}, \big |\varphi _{2}\rangle \nonumber \\&= \Xi _{-}\left[ i\xi _{-}\left( \big |00\rangle -\big |10\rangle \right) +\big |01\rangle +\big |11\rangle \right] , \end{aligned}$$
(17b)
$$\begin{aligned} E_3&= +\frac{1}{2}\sqrt{\Omega _{+}^{2}+4\alpha ^{2}}, \big |\varphi _{3}\rangle \nonumber \\&= \Lambda _{+}\left[ i\lambda _{+}\left( \big |00\rangle +\big |10\rangle \right) -\big |01\rangle +\big |11\rangle \right] , \end{aligned}$$
(17c)
$$\begin{aligned} E_4&= +\frac{1}{2}\sqrt{\Omega _{-}^{2}+4\alpha ^{2}}, \big |\varphi _{4}\rangle \nonumber \\&=\Xi _{+}\left[ i\xi _{+}\left( \big |00\rangle -\big |10\rangle \right) +\big |01\rangle +\big |11\rangle \right] , \end{aligned}$$
(17d)

where

$$\begin{aligned} \Lambda _{\pm }= & {} \frac{1}{\sqrt{2}\sqrt{\lambda _{\pm }^{2}+1}},\\ \lambda _{\pm }= & {} \frac{\Omega _{+}\pm \sqrt{\Omega _{+}^{2}+4\alpha ^{2}}}{2\alpha }, \Xi _{\pm }\\= & {} \frac{1}{\sqrt{2}\sqrt{\xi _{\pm }^{2}+1}},\\ \xi _{\pm }= & {} \frac{\Omega _{-}\pm \sqrt{\Omega _{-}^{2}+4\alpha ^{2}}}{2\alpha }, \Omega _{\pm }=\Delta \pm 2\eta . \end{aligned}$$

In such a setup, where the system is near a thermal bath, the Gibbs state gives a straightforward technique to expand the analysis to limited temperatures. When the system is in thermal equilibrium at temperature T with a thermal bath, the thermal density matrix can be obtained as

$$\begin{aligned} \varrho _T = \frac{1}{{{\mathcal {Z}}}} \exp ({\frac{-H}{k_B T}}), \end{aligned}$$
(18)

\({\mathcal {Z}}\) is the partition function provided as: \({{\mathcal {Z}}}= Tr[ \exp ({-H/k_B T})] = \sum ^{4}_{i=1} \exp ({-E_i/k_B T})\). It is worth mentioning that the basic approach of using Gibbs states enables us to explore thermal configurations such as the specific heat or magnetization without reference to the intricate relaxation dynamics. In the rest of this paper, we set Boltzmann’s constant to \(k_B =1\). In the standard basis, the Gibbs state \(\varrho _T\) of the double quantum dot system \(\varrho _T \equiv {\varrho }_{AB}\) can be written as

$$\begin{aligned} \varrho _T=\left( \begin{array}{llll} \varrho _{11} &{} \varrho _{12} &{} \varrho _{13} &{} \varrho _{14}\\ \varrho _{12}^{*} &{} \varrho _{22} &{} \varrho _{14} &{} \varrho _{24}\\ \varrho _{13} &{} \varrho _{14}^{*} &{} \varrho _{11} &{} -\varrho _{12}\\ \varrho _{14}^{*} &{} \varrho _{24} &{} -\varrho _{12}^{*} &{} \varrho _{22} \end{array}\right) , \end{aligned}$$
(19)
Fig. 1
figure 1

A scheme of the two coupled double quantum dots’ model

Full size image

The entries of the above thermal density matrix (19) are given by

$$\begin{aligned} \varrho _{11}= & {} \frac{1}{{\mathcal {Z}}}\Big (\Lambda _{+}^{2}\lambda _{+}^{2}e^{-\frac{E_{3}}{T}}+\Lambda _{-}^{2}\lambda _{-}^{2}e^{-\frac{E_{1}}{T}}\\{} & {} \quad +\Xi _{+}^{2}\xi _{+}^{2}e^{-\frac{E_{4}}{T}}+\Xi _{-}^{2}\xi _{-}^{2}e^{-\frac{E_{2}}{T}}\Big )\\ \varrho _{12}= & {} \frac{1}{{\mathcal {Z}}}\Big (i[-\Lambda _{+}^{2}\lambda _{+}e^{-\frac{E_{3}}{T}}-\Lambda _{-}^{2}\lambda _{-}e^{-\frac{E_{1}}{T}}\\{} & {} \quad +\Xi _{+}^{2}\xi _{+}e^{-\frac{E_{4}}{T}}+\Xi _{-}^{2}\xi _{-}e^{-\frac{E_{2}}{T}}]\Big )\\ \varrho _{13}= & {} \frac{1}{{\mathcal {Z}}}\Big (\Lambda _{+}^{2}\lambda _{+}^{2}e^{-\frac{E_{3}}{T}}+\Lambda _{-}^{2}\lambda _{-}^{2}e^{-\frac{E_{1}}{T}}\\{} & {} \quad -\Xi _{+}^{2}\xi _{+}^{2}e^{-\frac{E_{4}}{T}}-\Xi _{-}^{2}\xi _{-}^{2}e^{-\frac{E_{2}}{T}}\Big )\\ \varrho _{14}= & {} \frac{1}{{\mathcal {Z}}}\Big (i[\Lambda _{+}^{2}\lambda _{+}e^{-\frac{E_{3}}{T}}+\Lambda _{-}^{2}\lambda _{-}e^{-\frac{E_{1}}{T}}\\{} & {} \quad +\Xi _{+}^{2}\xi _{+}e^{-\frac{E_{4}}{T}}+\Xi _{-}^{2}\xi _{-}e^{-\frac{E_{2}}{T}}]\Big )\\ \varrho _{22}= & {} \frac{1}{{\mathcal {Z}}}\Big (\Lambda _{+}^{2}e^{-\frac{E_{3}}{T}}+\Lambda _{-}^{2}e^{-\frac{E_{1}}{T}}+\Xi _{+}^{2}e^{-\frac{E_{4}}{T}}\\{} & {} \quad +\Xi _{-}^{2}e^{-\frac{E_{2}}{T}}\Big )\\ \varrho _{24}= & {} \frac{1}{{\mathcal {Z}}}\Big (-\Lambda _{+}^{2}e^{-\frac{E_{3}}{T}}-\Lambda _{-}^{2}e^{-\frac{E_{1}}{T}}+\Xi _{+}^{2}e^{-\frac{E_{4}}{T}}\\{} & {} \quad +\Xi _{-}^{2}e^{-\frac{E_{2}}{T}}\Big ) \end{aligned}$$

where \({{\mathcal {Z}}}\) is the partition function obtained as \({{\mathcal {Z}}}=2[\cosh (\frac{\sqrt{\Omega _{+}^{2}+4\alpha ^{2}}}{2T})+\cosh (\frac{\sqrt{\Omega _{-}^{2}+4\alpha ^{2}}}{2T})]\).

The eigenvalues of the partial transposed density matrix \(({\varrho })^{T_{B}}\) used to obtain logarithmic negativity can be rendered explicitly as

$$\begin{aligned} \mu _{1,2}&= \frac{e^{-\frac{E_{3}+E_{4}}{T}}}{{\mathcal {Z}}}\times \Bigg [e^{\frac{E_{4}}{T}}\Big ((1+\lambda _{+}^{2})\Lambda _{+}^{2}+(1+\lambda _{-}^{2})\Lambda _{-}^{2}e^{\frac{2E_{3}}{T}}\Big )\nonumber \\&\quad {\mp } \bigg (4\xi _{+}^{2}\Xi _{+}^{4}e^{\frac{2E_{3}}{T}}+8\xi _{+}\Xi _{+}^{2}\xi _{-}\Xi _{-}^{2}e^{\frac{2(E_{3}+E_{4})}{T}}\nonumber \\&\quad +e^{\frac{2E_{4}}{T}}\Big (4\xi _{-}^{2}\Xi _{-}^{4}e^{\frac{2(E_{3}+E_{4})}{T}}\nonumber \\&\quad +((-1+\lambda _{+}^{2})\Lambda _{+}^{2}+(-1+\lambda _{-}^{2})\Lambda _{-}^{2}e^{\frac{2E_{3}}{T}})^{2}\Big )\bigg )^{\frac{1}{2}}\Bigg ],\end{aligned}$$
(20)
$$\begin{aligned} \mu _{3,4}&= \frac{e^{-\frac{E_{3}+E_{4}}{T}}}{{\mathcal {Z}}}\times \Bigg [e^{\frac{E_{3}}{T}}\Big ((1+\xi _{+}^{2})\Xi _{+}^{2}+(1+\xi _{-}^{2})\Xi _{-}^{2}e^{\frac{2E_{4}}{T}}\Big )\nonumber \\&\quad {\mp } \bigg ((-1+\xi _{+}^{2})^{2}\Xi _{+}^{4}e^{\frac{2E_{3}}{T}}+2(-1+\xi _{+}^{2})^{2}\Xi _{+}^{2}\nonumber \\&\qquad (-1+\xi _{-}^{2})^{2}\Xi _{-}^{2}e^{\frac{2(E_{3}+E_{4})}{T}} +e^{\frac{2E_{4}}{T}}\Big ((-1+\xi _{-}^{2})^{2}\Xi _{-}^{4}e^{\frac{2(E_{3}+E_{4})}{T}}\nonumber \\&\quad +4(\lambda _{+}\Lambda _{+}^{2}\lambda _{-}\Lambda _{-}^{2}e^{\frac{2E_{3}}{T}})^{2}\Big )\bigg )^{\frac{1}{2}}\Bigg ]. \end{aligned}$$
(21)

Moreover, the populations of the double quantum dots are given implicitly in terms of the energy spectrum of the system and the partition function as follows:

$$\begin{aligned} {\mathcal {P}}_{i} = \exp (-E_i/T)/\mathcal {Z}, \quad (i=1,...,4) \end{aligned}$$
(22)

where the condition: \(\sum _i ^4 \mathcal {P}_i = 1\), ensuring that trace unity should always hold.

4 Results and discussion

We dedicate this part to analyzing the findings from simulating the behavior of entanglement, skew information, and local quantum Fisher information for the double quantum dots. We address whether the parameters of the double quantum dots model soundly impact the quantification of quantum correlations. Indeed, in light of the above analytical results, we focus on comparing logarithmic negativity, LQU, and LQFI. On the other hand, we shall explain the dynamics and associated aspects of quantum entanglement and quantum correlations under Rashba coupling, thermal noise, and different system parameters settings.

To accomplish this, we plot the three proposed quantifiers, namely logarithmic negativity, LQU, and LQFI, against the temperature parameter and selected values of the Zeeman coupling parameter \(\Delta\) for \(\eta = \alpha = 1\).

Fig. 2
figure 2

Dynamics of LN textbfa), LQU (b) and LQFI (c) as functions of T for fixed values of \(\Delta\) when \(\eta =\alpha =1\). d The comparative dynamics between the three quantifiers for \(\Delta =3\)

Full size image

Figure 2 displays the evolution of entanglement utilizing logarithmic negativity, skew information correlations captured by LQU, and quantum correlations measured via LQFI against the temperature parameter T. Various physical parameters encoded in the double quantum dots system are considered. Indeed, in Fig. 2a, we plot the logarithmic negativity measure for different numbers of the Zeeman coupling parameter, namely \(\Delta\). All amounts of entanglement take their large amplitudes for \(T=0\) except for \(\Delta =0\), where the LN completely vanish \(\forall T\). As T increases, the logarithmic negativity decreases asymptotically until reaching a minimum value for large temperature values. Moreover, for the same initial settings, we show in Fig. 2b, c the evolution of LQU and LQFI, respectively. Both measures behave similarly where the state is correlated for small intervals of T. Again, the state becomes non-correlated at high values of temperature T. However, the LQU and LQFI provide the same information about the non-classical correlations  in the pair of dots system. We notice that skew information and LQFI behave in a similar way for \(\Delta = 0\). However, for \(\Delta >0\), LQFI shows more non-classical correlations, and the inequality \(\mathcal {U} (\rho _T) \le \mathcal {F}_L (\rho _T)\) always holds. Besides, Fig. 2d attempts to investigate a comparative study between logarithmic negativity, LQU and LQFI for \(\alpha =\eta =1\) and \(\Delta =3\). The bipartite quantum dot state is correlated for small values of T. At the same time, the sudden death phenomenon appears fast for entanglement (Fig. 2a) compared to the curves displayed for skew information and quantum correlations. In addition, the LQU and LQFI never vanish, even at robust temperatures. These findings are relevant as entanglement is more vulnerable to thermal noise and breaks down faster than the other non-classical correlations. It gives the supplementary information that even if the state is unentangled, there remain certain non-classical correlations, and therefore the system state is mixed. Despite the state having no entanglement, it could be desirable for some technological uses.

In the next step, we will investigate how the configuration of \(\eta\) affects the dynamics of entanglement, skew information, and local quantum information in the presence of thermal noise.

Fig. 3
figure 3

Dynamics of LN (a), LQU (b) and LQFI (c) in terms of T for selected values of \(\eta\) when \(\Delta =\alpha =1\). d The comparison between the three quantifiers for \(\eta =3\)

Full size image

The dynamics of entanglement, skew information, and quantum correlations versus T for various tunneling coupling strengths, namely \(\eta\), when \(\alpha =\Delta =1\), are depicted in Fig. 3 . First, we notice that in the case of \(\eta =0\), we can eliminate entanglement, skew information, and quantum correlation rates within the considered system. Moreover, for all the measures mentioned above, LN, LQU, and LQFI, the high temperatures T have a destructive effect on the entanglement within the considered system. We find that at low temperatures and when \(\eta\) is not null, quantum correlations increase in magnitude but decrease faster as T increases. Nevertheless, increasing values of \(\eta\) decreases their magnitude but tends to make them defy the harmful temperature rise. For illustration, for \((T=0.01, \eta =0.1\)) and \((T=0.01, \eta =0.2\)), logarithmic negativity (resp. LQFI) exposes the amount 0.893 (resp. 0.735) and 0.863 (resp. 0.671). Conversely, for \((T=0.5, \eta =0.1\)) and \((T=0.5, \eta =0.2\)), logarithmic negativity (resp. LQFI) displays the quantities 0.042 (resp. 0.013) and 0.100 (resp. 0.053). These results indicate that entanglement and quantum correlations may be tuned by controlling the parameter \(\eta\) depending on which purpose the quantum state is intended to be used. On the other hand, the amplitudes of LN, LQU, and LQFI are considerable compared to those depicted in Fig. (2).

To test the variation of logarithmic negativity, LQU, and LQFI against T and the Rashba interaction, we depict the three quantifiers for a variety of \(\alpha\)-strengths and \(\Delta =\eta =1\).

Fig. 4
figure 4

Dynamics of LN (a), LQU (b) and LQFI (c) in terms of temperature T for selected values of \(\alpha\) when \(\Delta =\eta =1\). d The comparative dynamics between the three quantifiers for \(\alpha =3\)

Full size image

A fascinating subject is considering the case when the Rashba interaction through spin-flip tunnel coupling \(\alpha\) exists in the system. Indeed, Fig. 4a displays the resulting LN as a function of the temperature T for various numbers of \(\alpha\). Obviously, for sufficiently low temperatures, LN reaches its maximum bounds. In particular, for \(\alpha =5\), the state is close to being maximally entangled at \(T\rightarrow 0\). Otherwise, the amount of LN decreases gradually and vanishes when the state becomes unentangled at high temperatures T. Furthermore, the quantities of LQU and LQFI presented in Fig. 4b, c show the same behavior as the entanglement's but with smaller amplitudes. Again, all proposed measures are less resistant to the increase  of the temperature T, and they vanish entirely for \(\alpha =0\). Besides, in Fig. 4d, we have plotted the amounts of LN, LQU, and LQFI in one plot. The entanglement rate inherent in the bipartite double quantum dots state follows the same behavior as LQU and LQFI. Interestingly enough, one can see that even if the state is separable, there will still always be quantum correlations beyond entanglement  in the double quantum dots system. A critical takeaway from the findings is that strong Rashba coupling can be used to build maximally entangled devices near zero conditions (\(T\approx 0\)), making the double QD system suitable for nonlocal tasks requiring higher entanglement degrees.

Next, we study the influence of the Zeeman coupling on the behavior of the system’s qualitative properties. We next also provide a comparison between entanglement, measured by LN, and quantum correlations evaluated by utilizing LQU and LQFI within the double quantum dot system.

Fig. 5
figure 5

Dynamics of LN (a), LQU (b) and LQFI (c) as functions of \(\Delta\) for selected values of \(\eta\) when \(T=\alpha =1\). d The comparative dynamics between the three quantifiers for \(\eta =2\)

Full size image

Figure 5a depicts the combined influence of the Zeeman coupling, namely \(\Delta\) and the tunneling coupling strength \(\eta\) on the entanglement. For \(\Delta =0\), the amount of LN vanishes. One may identify two regimes of logarithmic negativity. In the first regime, \(0<\Delta <5\), we witness the  phenomenon of sudden entanglement birth (ESB), for which entanglement rises until reaching a maximum peak around (\(\Delta \approx 5\)). The quantity of entanglement begins to deteriorate in the second regime (\(\Delta \ge 5\)) as the Zeeman coupling parameter increases. For large numbers of \(\Delta\), the LN tends towards a minimum value but never vanishes for large values of \(\eta\).  Skew information (LQU) and LQFI are presented in Fig. 5b, c, respectively. Both measures show the same behavior but with different upper bounds. It can be seen that increasing the tunneling coupling \(\eta\) has a destructive effect on the non-classical correlations. On the other hand, we exhibit in Fig. (5d) where we arbitrarily assumed that \(T=\alpha =1\) and \(\eta =2\). Again, LQU and LQFI fluctuate similarly between their maximum and minimum bounds, capturing the same information about the correlation of the pair of dots. For example, in the case when \(T=\alpha =1\), \(\Delta = 60\) and \(\eta =25\), LN exposes the amount \(2.59\times 10^{-2}\), whereas LQU and LQFI disclose the same amount \(3.30 \times 10^{-4}\). Entanglement is greater than non-classical correlations, implying that the Zeeman coupling influences more non-classical correlations. One may deduce that for constant low temperatures \(T\le 1\), steadily increasing the Zeeman coupling and the tunneling coupling strength convert the system’s state to be weakly correlated.

To acquire further insights into the system configuration, we will illustrate the combined influences of Zeeman coupling variation and spin–orbit coupling via the Rashba effect.

Fig. 6
figure 6

Dynamics of LN (a), LQU (b) and LQFI (c) as functions of \(\Delta\) for selected values of \(\alpha\) when \(T=\eta =1\). d The comparison between the three quantifiers for \(\alpha =4\)

Full size image

Figure 6 depicts the impact of changing the parameters \(\Delta\) and \(\alpha\) between the pair of quantum dots. We fix the other parameters T and \(\eta\) to unity. As shown, for \(\Delta =0\), LQU, and LQFI take a significant value when \(\alpha =0,3\) and gradually vanish for robust numbers of \(\Delta\). Otherwise, when \(\alpha =1;3;10\), the amounts of entanglement and non-classical correlations start to manifest a significant increase after a specific interval of \(\Delta\) and then decrease but never vanish even for strong values of the Zeeman coupling parameter generated by the external magnetic field. For any of the other values of \(\alpha =1;3;10\), a significant threshold in the Zeeman coupling has been identified, which is the critical point at which entanglement and non-classical correlations decline from their maximums to either zero or the lowest possible value. In other words, there are critical thresholds \(\Delta _c\) for each configuration (\(\alpha , \eta , T\)) where the spin of the electron points in the same direction as the magnetic field, leading the quantum state’s configuration to change as well. Consequently, there seems to be a critical value of \(\Delta\), which causes the population to degenerate and modify quantum correlations simultaneously. This \(\Delta\) has to be unique for each value of \(\alpha\) which justifies the observation of the identical pattern across all curves.

Fig. 7
figure 7

Dynamics of LN (a), LQU (b) and LQFI (c) as functions of \(\eta\) for selected values of \(\alpha\) when \(T=\Delta =1\). d The comparison between the three quantifiers for \(\alpha =2\)

Full size image

In Fig. 7, one can observe the same behavior as in Fig. 6. We see an abrupt birth of quantum correlations that attain a specific peak value and later drop as a function of increasing \(\eta\). For \(\alpha =3, 5, 10\), one notices the presence of a significant threshold of \(\eta\), at which point the three quantifiers start to decrease rapidly from their respective maximum values to their lowest values. The abrupt change of the entanglement and non-classical correlations arises from the existence of critical values of \(\eta\). Therefore, there appears to be a threshold of \(\eta\) that leads the system’s populations to degenerate, which also alters quantum correlations. The value of \(\eta\) must be unique for each value of \(\alpha\), further validating the discovery of the same trend in all cases. A relevant comparison here shows that increasing \(\eta\) beyond its critical value decreases the amounts of entanglement and non-classical correlations. Furthermore, one can observe that the system shows a lower amount of entanglement compared to non-classical correlations.

Fig. 8
figure 8

System’s energy levels versus Zeeman coupling (a), Tunneling strength (b) and Rashba coupling (c)

Full size image

From Fig. 8, one gains information about whether Rashba coupling, Zeeman coupling, and tunneling coupling induce energy level crossing or not. It is good to notice that a level crossing occurs if two eigenvalues are equal, which means that some two-qubit states have the same energy and thus same population, \(\mathcal {P}_i = \exp (-E_i / T)/\mathcal {Z}\), at a given T. In Fig. 8a, we observe that the Zeeman coupling does not induce level crossing between energy levels. However for the configuration \(\eta =\alpha =1\), we observe that at \(\Delta = 0\), the energy level \(E_1\) (resp. \(E_3\)) and \(E_2\) (resp. \(E_4\)) as well as the populations \(\mathcal {P}_1 = \mathcal {P}_2\) and \(\mathcal {P}_3 = \mathcal {P}_4\) are degenerate (crossed over), and the splitting (avoided crossing phenomenon) appears for raised Zeeman coupling. For example, for \(\alpha = \eta = \Delta = 1\) and \(T=4\), we find numerically that \(\mathcal {P}_1=0.148\), \(\mathcal {P}_2=0.176\), \(\mathcal {P}_3=0.308\) and \(\mathcal {P}_4=0.366\). It means that the Zeeman coupling induces the splitting of energy levels and populations rather than making them cross. On the other hand, one can see that the absolute value of the energies increases by increasing the Zeeman coupling. It should be noted that when \(\alpha = 0\) and for the condition \(\eta = \Delta = 1\), the energy level crossing is absent. However, the energy level crossing behavior appears as Rashba coupling strength increases (\(\alpha > 2.5\)). In Fig. 8b, we observe the same thing, that is \(E_1\) (resp. \(E_3\)) and \(E_2\) (resp. \(E_4\)) are degenerate (crossed over) only when the tunneling coupling is null. Interestingly, we also observe that even when \(\Delta \ne 0\) and when the tunneling coupling \(\eta\) is zero, the population becomes degenerated. Numerically, when \(\alpha = \Delta = 1\), \(\eta =0\) and \(T=4\), one finds that \(\mathcal {P}_1 = \mathcal {P}_2=0.181\) and \(\mathcal {P}_3=\mathcal {P}_4=0.318\). In Fig. 8c, one can notice that when \(\alpha = 0\) for the conditions \(\eta = \Delta = 1\), the energy level crossing is absent. However, as the Rashba coupling strength (\(\alpha > 2.5\)) increases, the energy level crossing behavior appears. One may conclude that Rashba coupling generates the quantum level crossing phenomenon even in the presence of splitting induced by Zeeman coupling and tunneling coupling.

From Figs. 2, 3, 4, 5, 6, 7 and 8, it is evident that in most of the above-cited proposed simulations, the entanglement amount, skew information, and quantum correlation behave in a quasi-similar way between their maximum and minimum upper bounds. Furthermore, the sudden birth phenomenon appears for small intervals of \(T, \Delta , \eta\), and \(\alpha\). At the same time, the phenomenon of sudden death  of entanglement happens when the system's parameters take larger values. Indeed, it is physically accurate that increasing the equilibrium temperature changes the population distribution of the system, indicating that transitions occur between the levels of each subsystem. These transitions increase the disorder within the system, leading to coherence decaying and destroying entanglement and quantum correlations. In general, the outcomes show that the frozen phenomenon appears mostly for LN and does not occur for LQU and LQFI, meaning that the state contains some correlation information about the system even when it is separable. The results discussed above show that the amount of LQFI is always more considerable than those displayed for LQU; it agrees with the results reported in Ref.[53, 54]. Based on these obtained results, one can also use the proposed measures, namely logarithmic negativity, LQU, and LQFI, as resources to perform a quantum teleportation scheme. Indeed, we have calculated the average fidelity using the pair quantum dot state as a quantum channel. Our results show that the average fidelity does not exceed the classical limit, namely 2/3, which reflects the extreme realizability for classical communication in our case.

5 Conclusion

In summary, we have investigated the dynamics of entanglement, skew information, and quantum Fisher information in double quantum dots system, which possess two charge configurations under Rashba spin coupling interaction. We have explored the implications of the different characteristics defining the system and environment, namely the Zeeman coupling parameter, the intensity of the tunnel coupling between the double quantum dots, the spin-flip tunnel coupling, and the Rashba coupling influence and equilibrium temperature effects. Consequently, these physical characteristics enabled us to examine the quantities revealed by LN, LQU, and LQFI versus each parameter. The obtained outcomes show that one can generate entanglement and non-classical correlations with custom amplitudes by tuning some parameters governing the physical model. On one hand, we have shown that small values of these parameters allow us to investigate the sudden birth phenomenon. Our results reveal that aside from thermal  interaction, increasing the Zeeman coupling and tunneling coupling strengths directs the double quantum system to lose its quantum advantages quickly. In contrast, our results demonstrated that Rashba interaction might be exploited to improve the quantum resources of the considered system.

These results can be employed analytically and experimentally in quantum theory, secure communication, and quantum estimation theory tasks. Future perspectives should highlight other systems to investigate the non-classical correlations under Rashba interaction. Besides, we can also generalize this work into higher dimensions.