1 Introduction

Among the different pollutants produced by combustion, soot is getting more and more attention from researchers, societal actors and industry. From environmental and health perspectives, it is important to characterize the emitted particulate matter, not only in terms of the total mass of the particles, but also of their surface [1, 2].

Unfortunately, the numerical prediction of soot particles’ morphology represents a difficult challenge since it has been shown that the biggest particles, namely aggregates, have fractal-like nature [3]. In specific, soot aggregates are constituted of small quasi-spherical particles, called primary particles. The aggregates surface is then classically retrieved once the number and the size of the primary particles are known. For this reason, it is essential to dispose of experimental [4,5,6,7,8,9,10] and numerical [11,12,13] tools allowing the characterization of the primary particle size distribution (PPSD).

Concerning the experimental determination of the primary particle size, the Transmission Electron Microscope (TEM) analysis of thermophoretically sampled soot has been extensively applied to determine the mean primary particle diameter \(d_{{\text {pp}}}\) and the primary particle size distribution [5,6,7,8,9]. When using the TEM technique, the \(d_{{\text {pp}}}\) is directly measured from pictures taken by microscope. Such technique brings information about the shape of the particles, such as the transition from spherical particles to aggregates. The TEM is one of the best techniques to visualize soot particles down to the size of \(\sim\)10 nm [8]. In addition to this technique, the Helium-Ion Microscopy (HIM) was developed for microscopy investigations at the nanoscales [14]. The retrieved information is similar to TEM, but HIM is classically used to characterize soot particles as small as 2 nm [15, 16]. Despite their relevant advantages, these techniques present some similar drawbacks. The measurements are performed intrusively and pointwise, limiting the analysis to few points in the flame. In addition, results depend on the algorithm and/or on the researcher criteria used to visually determine the number and the size of the primary particles in an aggregate.

Another option is the use of the Scanning Mobility Particle Sizer (SMPS), which provides information about the particle mobility diameter [17, 18]. In case of spherical particles, the primary particle size and the particle size coincide, so that this technique can be considered for the determination of the size of the primary particles. On the contrary, the extraction of \(d_{{\text {pp}}}\) from SMPS distributions remains very challenging for large aggregates.

Alternative to these aforementioned intrusive techniques, optical diagnostics represent a very accurate experimental approach suitable to perform investigations even in the harsh conditions of combustion. Among them, the Time-Resolved Laser-Induced Incandescence (TiRe-LII) is an in situ minimally invasive diagnostic technique that is more and more often used to retrieve information on \(d_{{\text {pp}}}\) and PPSD [10, 19,20,21]. In addition, the Planar Laser-Induced Incandescence can be used to obtain information on the spatial distribution of the PPSD in the whole laser plane.

Due to their advantageous properties, the TiRe-LII technique and laser diagnostics in general are powerful tools to investigate soot formation. However, when using laser diagnostics, the fundamental quantities of interest are usually not directly measured, but they are the results of a post-processing procedure applied to the detected signal (inverse method). Most of the time, such post-processing requires the quantification of various quantities simultaneously, leading to additional measurements, post-processing and/or assumptions. Unfortunately, each of them may be considered as a new source of uncertainty. Concerning the TiRe-LII approach, a long list of quantities are required to obtain the \(d_{{\text {pp}}}\) and the PPSD from the measured incandescence signal. Beside the LII signal decay, information on the gas phase, such as its temperature or pressure, and on the soot population, such as the number of particles per aggregate, are needed to correctly post-process the signal. Disposing of all these quantities simultaneously is more than challenging, since most of them are not even directly measured. This greatly complexifies the validation of the numerical models for the PPSD, which usually relies on comparing numerical results to experimental data.

On the contrary, recent numerical simulations can provide access to a wide range of information. For example, Salenbauch et al. [22] proposed to directly compare the numerical spatial evolution of the mass concentration of small and large particles to the spatial evolution of the Laser-induced Fluorescence and LII signals, respectively. Unfortunately, such comparison is not quantitative since it is not based on the same quantities (numerical particles concentration on the one side, experimental signals on the other size).

Alternatively, the numerical data can be utilized to reconstruct the experimental signal. A direct comparison between the numerically synthesized and the experimental signals can then be performed (forward method). Examples of a forward method for the validation of numerical simulations can be found in the literature [23,24,25]. However, to the author’s knowledge, no previous effort on comparison of synthesized and experimental TiRe-LII signals has been done in the literature for the validation of the numerical models in terms of PPSD.

The objective of this work is, therefore, to investigate the potential of a forward method for the validation of the numerically modeled PPSD, by comparing numerically synthesized signals to TiRe-LII experimental data. In this context, it is worth to be mentioned that the reconstruction of the PPSD from the experimental TiRe-LII signal is strongly affected by the post-processing and the experimental uncertainties. The aim of this paper is not to improve the quality of such reconstruction but to propose a new post-processing technique allowing for a consistent comparison of experimental and numerical results to strengthen the validation of the numerical modeling.

The structure of the paper is as follows. The uncertainties that are potentially introduced by the post-processing of the TiRe-LII signal to obtain the PPSD are quantified in Sect. 2 by reviewing results from the literature. Two indexes are suggested to characterize the LII signal in Sect. 3. An uncertainty evaluation on these quantities is carried out to a priori identify the possible advantages of the validation through synthesized TiRe-LII signals. Then, both the inverse and the forward validation methods are applied to a premixed ethylene flame in Sect. 4. The input numerical results are obtained from detailed simulations already validated in [26] and the experimental LII signals are extracted from [10]. Differences between measured and synthesized signals are highlighted and conclusions on the potential of the proposed approach for validating numerical models for the PPSD prediction are finally reported.

2 Literature overview on the current accuracy of \(d_{{\text {pp}}}\) determination by TiRe-LII

The TiRe-LII technique relies on the heating up of soot particles via a nanosecond laser pulse and the recording of the subsequent induced incandescence signal [27]. As large particles cool more slowly than small ones, the temporal evolution of the incandescence signal can be used to determine the primary particle size.

To obtain the PPSD from the signal decay, a post-processing inverse procedure is needed. The LII signal is reconstructed by solving the mass and the energy balance equations for theoretical PPSDs. Usually, the problem is recasted as a minimization problem, which allows to identify the distribution parameters minimizing the deviation between the measured signal and the theoretical one [10, 20, 28,29,30,31,32]. Such post-processing can be affected by two main sources of uncertainties. First, the reconstruction of the LII signal is known to be strongly dependent on the model and the parameters (such as soot density) selected for the mass and the energy balance equations as exhaustively discussed by Schulz et al. [33] and Michelsen et al. [34]. Second, most of the models rely on various input quantities, summarized in Table 1, which are not necessarily known. The role of each parameter in the signal modeling is not described here in details, but can be found in [33, 34]. Many of these variables are properties of the experimental equipments (“Equipment”), some of them are properties of the gaseous field around the investigated soot particles (“Ambient”) and numerous of them are characteristics of the soot particles themselves (“Soot”). The errors introduced by the parameters of the equipment are supposed to be limited by accurately designing the experimental setup and are not discussed here.Footnote 1 Some of the remaining variables can be measured (“M”), but this may possibly introduce additional errors and requires additional devices and/or post-processing. Some other parameters are generally assumed (“As”).

With the forward approach proposed in Sect. 3, uncertainties related to the LII model cannot still be avoided but some errors due to the input parameters can be reduced using the values available in the numerical simulations. The concerned parameters are marked by “N”.

Table 1 Main input parameters needed for the modeling of the temporal evolution of the TiRe-LII signal according to [35]
Full size table

Additionally to the five variables that are known from the numerical simulations (pressure p, temperature T, molecular weight of gas phase \(M_{\text {g}}\), PPSD shape and number of primary particles in the aggregate \(n_{\text {p}}\)), the thermal accommodation coefficient and the soot absorption function are today not well known but they are expected to depend on soot properties. Therefore, these two last quantities may be potentially recovered from numerical simulations, once the relations with other particles characteristics are identified. In the following, the effect of the uncertainties introduced by these parameters on \(d_{{\text {pp}}}\) is recalled from earlier studies.

2.1 Assumed or measured parameters

2.1.1 Soot absorption coefficient

Various values of the soot absorption function E(m), constant or wavelength dependent, can be found in literature [34, 36,37,38]. In particular, it has been found that E(m) varies between \(\sim\)0.2 and \(\sim\)0.4 even for a fixed laser wavelength of 1064 nm [10]. However, such high uncertainty does not greatly affect PPSD results since many of the LII models [30, 39] are insensitive to E(m) [28]. More specifically, it has been shown in [28] that a variation of ±0.1 from the reference value (\(E(m) = 0.3\)) did not lead to significant modifications of the PPSD, except when using the model of Lehre et al. [40].

2.1.2 Mass accommodation coefficient

The mass accommodation coefficient is a key parameter for the description of particle sublimation. In the literature, this quantity is characterized by a high uncertainty: its value varies between 0.5 and 1 [34]. To avoid the possible errors due to an inaccurate estimation of the mass accommodation coefficient, recent experimental studies suggest to work with a low laser fluence, so that the sublimation phenomenon is negligible compared to the other processes occurring after the interaction of the laser with the particles [10, 20, 27, 34, 39, 41]. Uncertainties on \(\beta\) can then be neglected.

2.1.3 Thermal accommodation coefficient

In the literature, the thermal accommodation coefficient \(\alpha _{\text {T}}\) is characterized by a large variability [42]. Values from 0.23 to 0.9 are classically used [34]. The wrong assumption can lead to significant inaccuracies in the estimation of \(d_{{\text {pp}}}\), since a variation of just ± 0.05 can result in significantly different PPSDs [28]. As long as the connection between \(\alpha _{\text {T}}\) and other soot properties is not established, the uncertainty related to this parameter is not avoidable. However, once the relation between \(\alpha _{\text {T}}\) and other particles characteristics will be known, the LII signal reconstruction from numerical results can potentially overcome this issue.

2.2 Numerically available parameters

2.2.1 Gas temperature

Several researches concern the impact of the uncertainty of the gas phase temperature \(T_{\text {g}}\) on the experimental estimation of \(d_{{\text {pp}}}\) from the Tire-LII signal. The exact deviation depends on the used models and only some examples are reported in the following.

Concerning a monodisperse distribution, Sun et al. [43] demonstrated that a variation of ± 200 K from 1700 K (± 12%) leads to errors in ± 3 nm for \(d_{{\text {pp}}}\) = 15 nm (± 20%) and ± 5 nm for \(d_{{\text {pp}}} = 40\hbox { nm}\) (± 13%). The significant impact of the flame temperature on the derived primary particle size was presented also by Will et al. [44]. For a variation of ± 180 K from 1800 K (±10%), the relative error of the diameter was about ±6 nm (±30%) and ±8 nm (±20%) for a particle of 20 and 40 nm, respectively. Cenker et al. [45] observed a deviation up to ±20% in the primary particle diameter for a temperature variation of ±15%.

Concerning lognormal distributions, Daun et al. [28] quantified the differences between two PPSDs derived from the same LII signal when perturbing the temperature around its exact value. The measure of difference was the Cramér-von Mises (CVM) goodness-of-fit parameter, which was defined as the area contained between the recovered and the exact particle size cumulative distribution functions, i.e., a zero CVM value means that the two PPSDs are identical. The CVM parameter for a temperature perturbation of \(\pm 30\hbox { K}\) from the nominal 1700 K varied between \(\sim\)0.1 and \(\sim 0.43\)Footnote 2, depending on the model used for the LII signal calculation [28].

Experimental uncertainties on temperature depend both on the used experimental technique as well as the investigated configuration with an error that can reach \(\pm \,\, 200\hbox { K}\) [20, 31, 46,47,48,49,50,51,52]. Even worse, the temperature value is often assumed when extracting PPSD information from TiRe-LII signal [31, 53, 54] greatly increasing the error bars on \(d_{{\text {pp}}}\). On the contrary, the numerical simulations provide the gas-phase temperature in the whole domain, so that the uncertainty on this quantity can be reduced by numerically reconstructing the LII signal and comparing it to the experimental one (supposing that the numerical model has been previously validated for the gaseous phase description).

2.2.2 PPSD shape

The presumed PPSD shape is one of the most relevant uncertainties. In many cases, a monodisperse distribution is assumed for the sake of simplicity [10, 19, 20]. However, the primary particle distribution is often observed to be a lognormal function [5, 20, 40], characterized by a geometric mean diameter \(d_{g}\) and standard deviation \(\sigma _{\text {g}}\):

$$\begin{aligned} f(d) = \frac{1}{\sqrt{2 \pi } d \ln \sigma _{\text {g}}} \exp \left[ - \frac{ (\ln d - \ln d_{\text {g}})^2 }{2 (\ln \sigma _{\text {g}})^2 } \right] . \end{aligned}$$
(1)

When assuming a monodisperse distribution, all particles have the same diameter \(d_{{\text {mono}}}\). In case of a lognormal distribution, the relation between a monodisperse equivalent mean particle diameter \(d_{{\text {mono}}}^{{\text {eq}}}\) (obtained by preserving the total volume and primary particle number but assuming a monodisperse distribution) and \(d_{\text {g}}\) is related to \(\sigma _{\text {g}}\), as depicted in Fig. 1. Depending on \(\sigma _{\text {g}}\), the ratio of the two characteristic diameters can vary significantly.

Fig. 1
figure 1

The relation between the monodisperse equivalent mean particle diameter \(d_{{\text {mono}}}^{{\text {eq}}}\) and the geometric mean diameter \(d_{\text {g}}\) for lognormal PPSD distribution as function of the standard deviation \(\sigma _{\text {g}}\)

Full size image

An exhaustive analysis was performed by Cenker et al. [45] on the possible \(d_{{\text {mono}}}\) values retrieved from LII signals constructed from a lognormal distribution with a wide range of {\(d_{\text {g}}\),\(\sigma _{\text {g}}\)} pairs (at 1750 K, 1 bar and \(n_{\text {p}}=1\)). In this work, the significant difference between \(d_{{\text {mono}}}\) and \(d_{\text {g}}\) extracted from the same signal was presented. As an example, for \(\{d_{\text {g}},\sigma _{\text {g}}\}=\{30\hbox { nm},1.4\hbox { nm}\}\) the resultant \(d_{{\text {mono}}}\) was 40 nm. A similar study was carried out by Chen et al. [21] with similar results. Sun et al. [43] also reevaluated a typical TiRe-LII signal with both monodisperse and lognormal distribution assumptions (at 1700 K, 1 bar and \(n_{\text {p}}=100\)). The retrieved characteristic diameters were \(d_{{\text {mono}}} = 19\hbox { nm}\) and \(d_{\text {g}} = 15\hbox { nm}\) with \(\sigma _{\text {g}} = 1.25\hbox { nm}\). However, it is important to mention that in both investigations [43, 45], the diameter \(d_{{\text {mono}}}\) derived by assuming monodispersity from the LII signal does not coincide with the monodisperse equivalent mean particle diameter, \(d_{{\text {mono}}}^{{\text {eq}}}\) of the lognormal distribution. Franzelli et al. [31] evaluated the measured LII signals of a series of co-flow laminar flames with both monodisperse and lognormal PPSD assumption. In this work, beside \(d_{{\text {mono}}}\), the arithmetic mean primary particle diameter defined as \(d_{{\text {amean}}}\) = exp (ln(\(d_{g}\)) + ( ln(\(\sigma _{\text {g}}\))\(^2\)) / 2 ) was presented. While \(d_{{\text {amean}}}\) varied in the range of 10–65 nm, \(d_{{\text {mono}}}\) reached up to \(\sim\) 90 nm, meaning a difference as high as 30% for the heavily sooting flame.

On the one side, all these works enlighten the fact that accounting for polydispersity may drastically change the reconstructed mean \(d_{{\text {pp}}}\) value and that a consistent definition between the experimental and the numerical mean \(d_{{\text {pp}}}\) diameter is necessary. On the other side, Daun et al. [28] showed that when the lognormal PPSD shape is valid, entirely different {\(d_{\text {g}}\),\(\sigma _{\text {g}}\)} pairs minimize the objective function of the iterative process. This means that various PPSDs can be considered as a good match to the experimental signal taking into account the experimental uncertainties, greatly weakening the validation of the numerical prediction in terms of the PPSD.

Finally, it has been shown that a lognormal PPSD shape cannot be considered as a generality [4, 5, 10, 45, 55, 56], so that no shape could be presumed with confidence even if it is necessary when post-processing TiRe-LII data.

By reconstructing the synthesized signal from the numerical results, uncertainties on the PPSD shape can be strongly limited improving the comparison accuracy.

2.2.3 Number of primary particles in the aggregate

In most of the cases, single spherical particles are assumed for the TiRe-LII signal evaluation [10, 19, 20, 31, 43], even if the cooling process strongly depends on the number of primary particles per aggregate (\(n_{\text {p}}\)) [21, 39, 42, 57]. Liu et al. [39, 41] studied the relation between \(n_{\text {p}}\) and the signal decay, providing a method to account for the shielding effect.Footnote 3

Accounting for \(n_{\text {p}}\) may have a strong impact on the results [58, 59]. As an example, the reevaluation of the measured TiRe-LII signal with \(n_{\text {p}}=100\) instead of \(n_{\text {p}}=1\) by Bladh et al. [10] led to the drop of the derived mean \(d_{{\text {pp}}}\) by 30%. The same exercise was performed by Sun et al. [43], where the difference between the two derived diameters is more than 30% (29 nm for \(n_{\text {p}}=1\) and 19 nm for \(n_{\text {p}} = 100\)).

Unfortunately, as long as the LII experiment is not accompanied by TEM measurements, the aggregate structure is unknown, leading to uncertainties on \(n_{\text {p}}\) and consequently on \(d_{{\text {pp}}}\). On the contrary, the numerical prediction provides information about the number of primary particles in the aggregate, so that the LII signal reconstruction can account for the phenomenon, allowing for a pertinent comparison of experiments and numerical predictions. The novel validation approach is then expected to reduce the \(n_{\text {p}}\) related experimental uncertainties.

2.2.4 Smallest detectable particle

Once the mean \(d_{{\text {pp}}}\) is obtained by post-processing the TiRe-LII signal, the comparison with the numerical results may be affected by an additional parameter: the smallest particle \(d_{{\text {det,min}}}\) that can emit a detectable LII signal. While earlier studies indicated that the smallest soot particles detected by TiRe-LII are in the range of 6–10 nm [60,61,62], a recent study of Betrancourt et al. [29] pointed out that soot particles as small as 2 nm can absorb laser energy and emit an LII signal. However, the lower detection limit may depend on the sensitivity of the system, as it was pointed out by Sirignano et al. [63]. Even if the value of \(d_{{\text {det,min}}}\) only slightly affects the soot volume fraction determination since the contribution of small particles is negligible [33], it can generally affect the value of \(d_{{\text {pp}}}\) calculated from the numerical PPSD [26]. Unfortunately, \(d_{{\text {det,min}}}\) is not available for all experiments, potentially affecting the accuracy of the inverse validation method. On the contrary, small particles do not influence significantly the LII signal so that the comparison of synthesized LII signals to experimental ones is expected to be less affected by \(d_{{\text {det,min}}}\).

3 The forward method and its potential improvement

In the forward method, the temporal evolution of the LII signal is first calculated for the numerically predicted PPSD extracting the quantities needed by the LII modeling from the numerical simulations. Then, the synthesized signal is compared with the experimental data. For this, different moments \(M_{\text {k}}\) of the LII signal \(I_{{\text {LII}}}(t)\) may be considered:

$$\begin{aligned} M_{\text {k}} = \int t^k I_{{\text {LII}}}(t) {\text {d}}t \end{aligned}$$
(2)

with t denoting the time starting from the peak of LII signal (\(t=0\) ns when \(I_{{\text {LII}}}\) is maximum). In the following, two indexes have been kept: the expected value

$$\begin{aligned} E=\frac{M_1}{M_0} \end{aligned}$$
(3)

and the non-dimensional standard deviation

$$\begin{aligned} \sigma ^{\star }=\frac{\sigma }{ E} \end{aligned}$$
(4)

with the standard deviation \(\sigma =\sqrt{ M_2 / M_0 - (M_1 / M_0)^2 }\). The skewness and the kurtosis indexes have also been considered but they did not provide a better description of the LII signal compared to E and \(\sigma ^{\star }\), so that they have not been used in the following analysis. The LII signal is reconstructed by an in-house code utilizing the signal modeling description provided by Hofmann et al. [35] and the conduction model developed by Liu et al. [39, 41].

3.1 Effect of exponential fitting of the signal

Cenker et al. [45] investigated the error introduced by approximating the LII signal by a single-exponential fit. They found that it can be considered as a good approximation in case of a monodisperse distribution, so that the characteristic decay time provides sufficient information to determine the diameter. However, as already said, the PPSD is rarely monodisperse and from the theoretical point of view, the decay rate is not a single-exponential function. For polydisperse distributions, the problem becomes more complex as the signal is the superposition of several quasi-single exponential signals with various decay times. To overcome this issue, Dankers and Leipertz [30] suggested to derive two characteristic LII signal decay times, \(\tau _1({\varDelta }t_1)\) and \(\tau _2({\varDelta }t_2)\) for two subsequent measurement time intervals (\({\varDelta }t_1\) and \({\varDelta }t_2\)), resulting in a double exponential function. They demonstrated that for a lognormal distribution, the correlation between {\(\tau _1\),\(\tau _2\)} and {\(d_{\text {g}},\sigma _{\text {g}}\)} is unambiguous when the signal noise is not considered. This approach has then been used in recent studies [21, 31, 45, 53].

However, both fits are approximations of the original signal and may lead to the loss of information. In the following, the effect of the approximation is discussed by comparing the E and \(\sigma ^{\star }\) indexes calculated from the original signal (subscript LII), the single- (subscript SExp) and the double- (subscript DExp) exponential fitted signals for both monodisperse and lognormal distributions. This discussion will also clarify how to interpret the E and \(\sigma ^{\star }\) indexes and will quantify the errors introduced by the fitting procedure.

3.1.1 Monodisperse distribution

Results for \(E_{{\text {LII}}}\), \(E_{{\text {SExp}}}\) and \(E_{{\text {DExp}}}\) for a monodisperse distribution are presented for different values of \(d_{{\text {mono}}}\) in Fig. 2. It can be observed that \(E_{{\text {LII}}}\) depends almost linearly on \(d_{{\text {mono}}}\), as shown by the dotted line in Fig. 2. Therefore, a single index is sufficient to characterize the signal in case of a monodisperse distribution. Supposing a perfectly exponential decay, \(E_{{\text {LII}}}\) is expected to be equal to the decay time \(\tau _{{\text {SExp}}}\) of the single-exponential fit, which is also shown in Fig. 2. It can be observed that the decay time \(\tau _{{\text {SExp}}}\) and the expected value \(E_{{\text {SExp}}}\) of the curve constructed from the single-exponential fit overlap, as expected. However, even for the monodisperse case, the single-exponentially fitted curve does not capture the expected value of the original curve \(E_{{\text {LII}}}\) for large diameters, showing the inaccuracy of the single-fit procedure. On the contrary, the expected value of the double-exponential fit \(E_{{\text {DExp}}}\) shows a good agreement with \(E_{{\text {LII}}}\) at least for a monodisperse distribution. For a monodisperse variation, a quasi-linear relation between \(E_{{\text {LII}}}\) and \(d_{{\text {mono}}}\) is observed meaning that an error observed on \(E_{{\text {LII}}}\) directly implies the same error on \(d_{{\text {mono}}}\). This provides a first indication to interpret the agreement between experimental and numerically synthesized signals. For example, assuming a monodispersed population, a disagreement of 20% on \(E_{{\text {LII}}}\) between the experimental and numerical signals implies an error of 20% on the predicted \(d_{{\text {mono}}}\). For a polydisperse population, this interpretation is more complex requiring the analysis at least of 2 indexes as discussed in the following.

Fig. 2
figure 2

Expected value E of the signal (LII) and the curves obtained by the single-exponential (SExp) and double-exponential (DExp) fit. The decay time \(\tau\) of the exponential fit is also provided

Full size image

3.1.2 Polydisperse distribution

In Fig. 3, \(E_{{\text {LII}}}\), \(E_{{\text {SExp}}}\), and \(E_{{\text {DExp}}}\) are presented for a lognormal PPSD with different {\(d_{g}\), \(\sigma _{\text {g}}\)} pairs. A similar behavior of E is observed for the three cases. First, it can be observed that a given value of E corresponds to multiple {\(d_{g}\), \(\sigma _{\text {g}}\)} couples so that a second index is needed to discriminate the PPSD, as expected. The recovered curves both from single- and double-exponential fits show a similar behavior. The double-exponential fit provides a good agreement for \(\sigma _{\text {g}} < 1.6\), the error remains below 5%. The error for the single-exponential fit varies between 10 and 30%, which confirms that for non-monodisperse distributions, the single-exponential fit cannot properly reproduce the LII signal.

In Fig. 3a–c, the time interval was chosen to avoid the effect of a limited detection time (18000 ns). However, in practical applications, the detection time is finite. To characterize the potential error, the evaluation was also performed by considering the signal only up to 800 ns, corresponding to the detection time of the experimental results [10] that will be used in Sect. 4. The resultant \(E_{{\text {LII}}}\) is presented in Fig. 3d. It can be observed that for large diameters, the values are significantly lower than at the full length of the signal, indicating that the choice of the detection time can affect the results. However, the numerical simulation can imitate the detection length and its temporal resolution, so that the validation is not affected by this deviation when using the forward approach.

Fig. 3
figure 3

Expected value E as function of {\(d_{g}\), \(\sigma _{\text {g}}\)} pairs. Results for a the original signal \(E_{{\text {LII}}}\), b the single-exponential fitted curve \(E_{{\text {SExp}}}\), c the double-exponential fitted curve \(E_{{\text {DExp}}}\) and d the original signal considering only up to 800 ns

Full size image
Fig. 4
figure 4

Non-dimensional standard deviation as function of {\(d_{g}\), \(\sigma _{\text {g}}\)} pairs. Results for a the original signal \(\sigma ^\star _{{\text {LII}}}\), b the double-exponential fitted curve \(\sigma ^\star _{{\text {DExp}}}\), c the original signal zoomed on small \(d_{\text {g}}\) values and d the original signal considering only up to 800 ns

Full size image

As the same \(E_{{\text {LII}}}\) may originate from various {\(d_{g}\), \(\sigma _{\text {g}}\)} pairs, a second index should be considered. In Fig. 4, \(\sigma ^\star\) is provided for the original signal and for the double-exponentially fitted curve \(\sigma ^\star _{{\text {DExp}}}\). For a single-exponentially fitted curve, the value is \(\sigma ^\star _{{\text {SExp}}}=1\) for all {\(d_{g}\), \(\sigma _{\text {g}}\)}. Results for the original signal show that \(\sigma ^\star _{{\text {LII}}}\) is almost insensitive to \(d_{\text {g}}\) for \(d_{\text {g}}>10 \,\hbox {nm}\), whereas it strongly varies with \(\sigma _{\text {g}}\). Therefore, the \(\sigma ^\star _{{\text {LII}}}\) value may be used in the inverse approach to identify the \(\sigma _{\text {g}}\) and, subsequently, detecting \(d_{\text {g}}\) from \(E_{{\text {LII}}}\). However, it should be reminded that such procedure is not valid for small \(d_{\text {g}}\) values (below 10 nm) since the \(\sigma ^\star _{{\text {LII}}}\) is also strongly \(d_{\text {g}}\) dependent (Fig. 4c). Such behavior is not affecting the accuracy of the forward validation procedure since \(\sigma ^\star _{{\text {LII}}}\) and \(E_{{\text {LII}}}\) from the synthesized and experimental signals can be directly compared without any need to retrieve \(d_{\text {g}}\) and \(\sigma _{\text {g}}\). In addition, it is important to point out that a limited detection time provides a significantly different \(\sigma ^\star _{{\text {LII}}}\) profile for large diameters, as observed in Fig. 4d. In particular, the dependence on \(\sigma _{\text {g}}\) is inverted since for increasing \(\sigma _{\text {g}}\) the \(\sigma ^\star _{{\text {LII}}}\) decreases. It is, therefore, clear that in most pratical situations, where a limited detection time is used for the experiments, it would not be possible to recover \(d_{\text {g}}\) and \(\sigma _{\text {g}}\) from \(E_{{\text {LII}}}\) and \(\sigma ^\star _{{\text {LII}}}\), proving once again the limits of the inverse approach. Alternatively, a longer detection time could be considered using multiple detectors as suggested by [64]. On the contrary, using the forward approach, it would be possible to compare the experimental and numerical synthesized signals to quantify the inaccuracy of the soot model. The double-exponential fit shows a similar behavior, but does not recover the same values of the original signal. In particular, for high \(\sigma _{\text {g}}\), it significantly under-predicts the index highlighting that the double-exponential fitting is not adequate for highly polydisperse distributions. Therefore, the \(d_{\text {g}}\) and \(\sigma _{\text {g}}\) values obtained in the inverse strategy may be affected by the double-exponential fitting procedure.

In conclusion, the use of a forward comparison of synthesized and experimental signals, characterized by their \(E_{{\text {LII}}}\) and \(\sigma ^\star _{{\text {LII}}}\), is expected to reduce the uncertainties on the validation procedure. Such post-processing approach can be applied to any PPSD shape and the signals can be reconstructed to meet the experimental resolution and detection time. In addition, it controls the errors related to the experimental fitting of the signals, even if additional indexes may be needed to improve the characterization of the signals. In this sense, the skewness and kurtosis indexes have also been tested but it was found that they were not of interest for the considered signals. In the following, the evolution of \(E_{{\text {LII}}}\) and \(\sigma ^\star _{{\text {LII}}}\) with variations of the numerically retrievable input parameters will be discussed to quantify a priori the additional potential improvements of the forward approach compared to an inverse comparison.

3.2 Sensitivity study

To quantify the potential errors avoided when using a forward procedure, the impact of the variations of the input parameters on the reconstruction of the LII signal is quantified here. For this, a reference signal is produced with a set of base parameters \(\bar{{\varPhi }}_0\):

$$\begin{aligned} \bar{{\varPhi }}_0 = (n_{p,0},T_0, M_{g,0}, p_0), \end{aligned}$$
(5)

for four different \(d_{{\text {pp}}}\) values (5, 15, 25 and 35 nm) with a monodisperse distribution (where not stated differently). The reference parameters are: \(n_{p,0}\) = 1, \(T_0\) = 1700 K, \(M_{g,0}\) = 28 kg/kmol, and \(p_0\) = 1 bar. Then, the parameters of \(\bar{{\varPhi }}=(n_{\text {p}}, T, M_{\text {g}}, p)\) are perturbed one-by-oneFootnote 4 and the change in the indexes is evaluated as:

$$\begin{aligned}\frac{{\varDelta }E_{{\text {LII}}}}{E_{LII,0}} = \frac{E_{{\text {LII}}}(\bar{{\varPhi }}) - E_{{\text {LII}}}(\bar{{\varPhi }}_0)}{E_{{\text {LII}}}(\bar{{\varPhi }}_0)} . \end{aligned}$$
(6)

The signals are calculated based on the physical model described by Hofmann et al. [35] and the conduction model by Liu et al. [39, 41]. The parameters not recoverable from the numerical simulation (\(\alpha _{\text {T}}\) and E(m)) were kept constant, with \(\alpha _{\text {T}}\) = 0.37 and E(m) = 0.32.

3.2.1 Temperature

The variation of \(E_{{\text {LII}}}\), introduced by a temperature perturbation, is shown in Fig. 5 along with the relative errors. The impact of the temperature modification is large. The relative error of \(E_{{\text {LII}}}\) is in the range of ±20% for the large particle diameters, and it is even larger for the 5-nm-diameter particle (almost 40%, when the temperature is modified by 10%). From results in Fig. 5, it can be observed that by underestimating/overestimating the gas temperature, significantly higher/lower diameter is derived. The use of a proper temperature is, therefore, essential to minimize errors on \(E_{{\text {LII}}}\). As discussed before, the inverse approach requires the experimental measurements of temperature. Alternatively, the forward approach allows the use of the numerical temperature to perform the validation of the numerical results. Of course, the accuracy of the numerically synthesized \(E_{{\text {LII}}}\) depends on the quality of the numerical prediction for both the gaseous and the solid phases. In this sense, the forward approach could be used to quantify the inaccuracy of the whole numerical strategy and not of the single soot phase modeling.

Fig. 5
figure 5

\(E_{{\text {LII}}}\) (triangles) and its relative error (circles) as a function of the temperature for four \(d_{{\text {pp}}}=5\), 15, 25 and 35 nm (red, green, blue and yellow)

Full size image

3.2.2 Pressure

A sensitivity analysis is performed by applying a perturbation of ±2.5% and ±5% with respect to 1 bar. In Fig. 6, \(E_{{\text {LII}}}\) and its relative error are shown for the pressure perturbation.

Fig. 6
figure 6

\(E_{{\text {LII}}}\) (triangles) and its relative error (circles) as a function of pressure for four \(d_{{\text {pp}}}=5\), 15, 25 and 35 nm (red, green, blue and yellow)

Full size image

It can be observed in Fig. 6 that \(E_{{\text {LII}}}\) does not vary significantly with the pressure for small \(d_{{\text {pp}}}\). On the contrary, for higher values of \(d_{{\text {pp}}}\), the \(E_{{\text {LII}}}\) becomes more sensitive to the pressure and the deviation is not negligible anymore. However, when looking at the relative error it can be deduced that the perturbation effect on \(E_{{\text {LII}}}\) is almost \(d_{{\text {pp}}}\) independent and reaches up to 5% for a pressure variation of 5%. Supposing that the dependence between \(E_{{\text {LII}}}\) and \(d_{{\text {mono}}}\) is linear, similarly to the results of Fig. 2, this means an error in the diameter up to 5%. Such error can be avoided with the novel forward approach, since information on pressure is classically available in the numerical simulations.

3.2.3 Molecular weight

To experimentally evaluate the gas-phase molecular weight \(M_{\text {g}}\), information on the local composition is required. Many species can be measured with high accuracy. However, extra experimental equipment and post-processing are needed to access these quantities. Even when using ethylene as fuel (whose molecular weight is similar to nitrogen), the gas-phase molecular weight can differ significantly from the one of air in the sooty region, since soot is accompanied not only by several high-molecular weight gas-phase species, like heavy PAHs, but also lighter species such as hydrogen, water vapor or acetylene. Therefore, the generally used approach, i.e., assuming air properties when retrieving the PPSD from the measured LII signal [10, 20, 31], is inaccurate. As an example, the \(M_{\text {g}}\) value has been extracted from the numerical simulations of different sooting flames at atmospheric pressure [26]. For a premixed ethylene laminar flame with an equivalence ratio of 2.1 and co-flow ethylene laminar flames with various ethylene content in the fuel stream (32%, 40%, 60% and 80 % volumetric ratio), the \(M_{\text {g}}\) value can vary between 25kg/mol and 30 kg/kmol in the sooty region; whereas, the general assumption is \(M_{\text {g}}\) = 28 kg/kmol.

Fig. 7
figure 7

\(E_{{\text {LII}}}\) (triangles) and its relative error (circles) as a function of the molecular weight for four \(d_{{\text {pp}}}\)=5, 15, 25 and 35 nm (red, green, blue and yellow)

Full size image

The sensitivity study presented in Fig. 7 reveals that, though other parameters (like \(n_{\text {p}}\) or temperature) cause higher variations in \(E_{{\text {LII}}}\), the error introduced by an inaccurate \(M_{\text {g}}\) estimation is not negligible. The error of \(E_{{\text {LII}}}\) for the variation of \(M_{\text {g}}\) with ±10% can reach up to ±5%. The relative error due to \(M_{\text {g}}\) perturbation does not show strong dependency on the \(d_{{\text {pp}}}\) in this range. Since the gas-phase molecular weight is one of the base variables of numerical simulations, the novel forward approach can remove the uncertainty related to \(M_{\text {g}}\) without any additional cost compared to the classical validation strategy.

3.2.4 Number of primary particles in the aggregate

As already discussed in Sect. 2.2, accounting for the morphology of the soot particles, i.e., the number of primary particles, drastically affects the \(d_{{\text {pp}}}\) value obtained from the experimental LII signal. To additionally quantify the sensitivity of \(E_{{\text {LII}}}\) to the number of primary particles in the aggregate, \(n_{\text {p}}\) was varied from 1 to 100 (1, 5, 30, 60 and 100). In Fig. 8, the \(E_{{\text {LII}}}\) and its relative error from the case with \(n_{\text {p}}\) = 1 are presented.

Fig. 8
figure 8

\(E_{{\text {LII}}}\) (triangles) and its relative error (circles) as a function of \(n_{\text {p}}\) for four \(d_{{\text {pp}}}\)=5, 15, 25 and 35 nm (red, green, blue and yellow)

Full size image

For all the considered diameters, \(E_{{\text {LII}}}\) drastically changes moving from a single particle assumption to an aggregate structure, even when it is characterized by a small number of primary particles. The relative error reaches 25% already at \(n_{\text {p}} = 10\). The difference in \(E_{{\text {LII}}}\) between \(n_{\text {p}} = 60\) and \(n_{\text {p}} = 100\) is not so relevant as the difference between \(n_{\text {p}} = 1\) and \(n_{\text {p}} = 10\). When the aggregate nature of the particle is not considered, a smaller \(E_{{\text {LII}}}\) is assigned to the same \(d_{{\text {pp}}}\), in agreement with the lower decay time observed for the similar tests performed by Liu et al. [41]. This implies an over-prediction of the \(d_{{\text {pp}}}\) value since for \(E_{{\text {LII}}}\) (for example \(E_{{\text {LII}}} = 160\hbox { ns}\)), a larger diameter (\(d_{{\text {pp}}}=35\hbox { nm}\)) is estimated for a spherical particle (\(n_{\text {p}} = 1\)) compared to big aggregates (for \(n_{\text {p}} = 100\), \(d_{{\text {pp}}} = 25\hbox { nm}\)).

This large source of errors can be avoided by reconstructing the LII signal from a numerical simulation that provides information about the aggregate nature of the particle, strengthening the validation of numerical modeling compared to the traditional inverse method.

3.2.5 PPSD shape

As mentioned before, the PPSD is not always lognormal. To see the effect on the indexes of a different PPSD shape, several tests are carried out. The first test corresponds to a ’bimodal’ distribution similar to the one experimentally observed by Abid et al. [7, 60]. It is imitated by a superposition of a first mode \(f_1\) with a large number of very small particles below 5 nm and a second “moving mode” \(f_2\) with a lognormal shape, characterized by a varying \(d_{\text {g}}^2={3 - 20}\hbox { nm}\) and a constant \(\sigma _{\text {g}}^2 = 1.25\hbox { nm}\). The first mode follows a Pareto distribution:

$$\begin{aligned} f_1(d) = \left\{ \begin{array}{lr} 0 &{} : d < d_{{\text {m}}}\\ {d_{{\text {m}}}^\alpha }{d^{-\alpha -1} } &{} : d \ge d_{{\text {m}}}, \end{array} \right. \end{aligned}$$
(7)

with \(\alpha =3\) and \(d_{{\text {m}}}=2.1\,\,\hbox {mm}\). The first mode and a few examples of the second mode are presented in Fig. 9. The distribution is split up to 0.5-nm-wide sections.

Fig. 9
figure 9

First mode \(f_1\) and examples of “moving mode” \(f_2\) with various \(d_{g}^2\) (indicated in the label)

Full size image

As discussed previously, two indexes are used to characterize the LII signal emitted by a polydisperse distribution. In Fig. 10, the \(E_{{\text {LII}}}\) and \(\sigma ^\star _{{\text {LII}}}\) are presented for the resultant bimodal distribution \(f_1+f_2\) and for the sole lognormal distribution \(f_2\). By comparing the two cases, the contribution of the first mode compared to a classical lognormal assumption can be evidenced. In both cases, the \(E_{{\text {LII}}}\) increases with \(d_{\text {g}}^2\), as expected from Fig. 3. The values related to the bimodal and the single lognormal PPSD are very similar, the deviance between the two values being below 1%. This means that the presence of a first mode in the PPSD only slightly affects the \(E_{{\text {LII}}}\) results compared to a classical lognormal assumption as observed in [45]. Concerning \(\sigma ^\star _{{\text {LII}}}\), it can be observed that it decreases for increasing \(d_{\text {g}}^2\) values in analogy with the results from Fig. 4. The difference between the two signals remains small, being below 1% for this second index, despite the very different PPSDs, indicating an almost negligible effect of the first mode on the LII signal, meaning that very similar LII signals are obtained with the two distributions \(f_2\) and \(f_1+f_2\). In Fig. 11, results of the mean \(d_{{\text {pp}}}\) for the bimodal and the lognormal distributions are presented. Since the LII signals are similar, it can be deduced that when investigating a bimodal distribution by assuming a lognormal shape, the \(d_{{\text {pp}}}\) value extracted from the LII signal overstimates the real \(d_{{\text {pp}}}\). On the contrary, when comparing the synthesized and the experimental signal, conclusions are not biased by the assumption of the PPSD shape.

Fig. 10
figure 10

\(E_{{\text {LII}}}\) and \(\sigma _{{\text {LII}}}^\star\) of the LII signal originating from the bimodal distributions \(f_1+f_2\) (black circle) and from the moving lognormal mode \(f_2\) only (white square). The moving mode has varying \(d_{\text {g}}^2\) and constant \(\sigma _{\text {g}}^2\)

Full size image
Fig. 11
figure 11

Primary particle diameter \(d_{{\text {pp}}}\) for the bimodal distributions \(f_1+f_2\) (circle) and for the moving lognormal mode \(f_2\) only (line) as function of \(d_{\text {g}}^2\)

Full size image

To investigate additionally the effect of the PPSD shape on the LII signal, a second test is performed. This time, the PPSD is obtained by superimposing two standard lognormal distributions: one (\(f_1\)) with fixed characteristics \(\{d^1_{g}, \sigma ^1_{\text {g}}\} = \{25\hbox { nm}, 1.2\hbox { nm}\}\) and another (\(f_2\)) with a fixed \(\sigma ^2_{\text {g}} = 1.2\) and a \(d^2_{g}\) varying from 10 to 60 nm (’moving mode’). Some examples of the distributions are presented in Fig. 12. Results on \(E_{{\text {LII}}}\) and \(\sigma ^\star _{{\text {LII}}}\) for the combined PPSD \(f_1+f_2\) and for the ’moving mode’ \(f_2\) are plotted in Fig. 13.

Fig. 12
figure 12

Examples of the PPSDs from two superimposed standard lognormal distributions \(f_1+f_2\) with various \(d_{g}^2\) (indicated in the label) of the moving mode \(f_2\)

Full size image

Concerning \(E_{{\text {LII}}}\), a quasi-linear behavior is observed with \(d_{\text {g}}^2\) when considering only the ’moving mode’ \(f_2\). When looking for the combined PPSD, it can be noticed that \(E_{{\text {LII}}}\) is initially constant until \(d_{\text {g}}^2<25\) nm. Therefore, the obtained value is equal to the \(E_{{\text {LII}}}\) value for a single lognormal function \(d_{\text {g}}\)=25 nm. This is because the fixed lognormal mode \(f_1\) has a constant \(d_{\text {g}}^1\)=25 nm and its contribution to the combined LII signal \(f_1+f_2\) is higher compared to the second moving mode \(f_2\) when \(d_{\text {g}}^2<d_{\text {g}}^1\).

Fig. 13
figure 13

\(E_{{\text {LII}}}\) and \(\sigma _{{\text {LII}}}^\star\) of the LII signal originating from two superimposed lognormal distributions \(f_1+f_2\) (solid line) and from the moving mode \(f_2\) only (dashed line). The moving mode has varying \(d_{\text {g}}^2\) and constant \(\sigma _{\text {g}}^2\)

Full size image

Once \(d_{\text {g}}^2>d_{\text {g}}^1\), it can be observed that \(E_{{\text {LII}}}\) for \(f_1+f_2\) is increasing with \(d_{\text {g}}^2\) and almost collapsing with the results for \(f_2\). Concerning \(\sigma _{{\text {LII}}}^\star\), the variations in Fig. 13 are so small that they can be considered as negligible. This is consistent with the fact that both \(\sigma _{\text {g}}^1\) and \(\sigma _{\text {g}}^2\) are kept constant in this test case. From \(E_{{\text {LII}}}\) and \(\sigma ^\star _{{\text {LII}}}\), it can be deduced that the LII signal is governed by the lognormal distribution with the higher \(d_{\text {g}}\) values and that the presence of a second mode with a smaller \(d_{\text {g}}\) cannot be easily identified from the LII signal.

Fig. 14
figure 14

\(E_{{\text {LII}}}\) and \(\sigma _{{\text {LII}}}^\star\) of the LII signal originating from two superimposed lognormal distributions \(f_1+f_2\) (solid line) and from the moving mode \(f_1\) only (dashed line). The moving mode has constant \(d_{\text {g}}^1\) and varying \(\sigma _{\text {g}}^1\)

Full size image

Finally, a PPSD is obtained by superimposing two standard lognormal distributions: one (\(f_1\)) with fixed characteristics ({\(d^1_{g}\), \(\sigma ^1_{\text {g}}\)} = {40 nm, 1.2 nm}) and another (\(f_2\)) with a fixed \(d^2_{g}=25\) nm and \(\sigma ^2_{\text {g}}\) varying from 1.05 to 1.6 nm (’moving mode’). Results are presented in Fig. 14. It can be observed that \(E_{{\text {LII}}}\) for \(f_1+f_2\) is almost constant for \(\sigma _2<1.45\) and higher than the result obtained when considering only \(f_2\). This proves that \(E_{{\text {LII}}}\) for a combined PPSD is mainly governed by the mode with the highest \(d_{\text {g}}\) (here \(f_1\)) for small \(\sigma _{\text {g}}^2\). Once \(\sigma _{\text {g}}^2>>\sigma _{\text {g}}^1\), the \(E_{{\text {LII}}}\) is also affected by the presence of the first mode. Similarly, \(\sigma ^\star\) for \(f_1+f_2\) is mainly governed by the mode with the highest \(d_{\text {g}}\), i.e., \(f_1\), except for \(\sigma _{\text {g}}^2>>\sigma _{\text {g}}^1.\)

In conclusion, the mode with the highest \(d_{\text {g}}\) mainly governs the LII signal at least as long as the other modes are not characterized by largely greater standard deviations, meaning by a large amount of big particles.

On the one side, this implies that it is extremely hard to correctly obtain the \(d_{{\text {pp}}}\) from the experimental LII signal unless the PPSD is known. Therefore, the accuracy of the validation of the numerical modeling based on \(d_{{\text {pp}}}\), i.e., the inverse method, is strongly affected by the assumption of the shape of the PPSD. With the forward method, information on the PPSD are extracted from the simulation. On the other side, it means that by applying the forward method, it is not possible to assess with certainty that the predicted PPSD agrees with the experimental ones, even if the synthesized and the experimental signals are in good agreement, since similar LII signals can be generated from different PPSDs. However, a disagreement on \(E_{{\text {LII}}}\) and \(\sigma ^\star _{{\text {LII}}}\) indicates that the predicted PPSD is not correct.

3.3 Discussion

All the above-discussed uncertainties decrease the quality of the traditional validation method of the numerical PPSD by TiRe-LII. Recent numerical simulations provide access to most of the needed parameters. Therefore, the LII signal can be synthesized with a reduced number of assumptions. While temperature, pressure and molecular weight are basic output quantities of CFD simulations, depending on the soot model, the “Soot” quantities in Table 1 are available on a different level. For detailed modeling, information on PPSD and \(n_{\text {p}}\) are classically available. Furthermore, once the relation of \(\alpha _{\text {T}}\) to other soot properties is known, this parameter can be also determined from the numerical calculation and related uncertainties can be avoided by the new approach. Utilizing these numerically derived quantities and the synthesized signal comparison approach, a more consistent validation of the whole modeling strategy can be performed. However, it has to be mentioned that as several PPSDs can lead to the same LII signal, the forward approach can not definitely confirm the validity of the PPSD, but it can be used to detect incorrect PPSDs and avoid the exclusion of a correct PPSD. Such issue is, however, intrinsic to TiRe-LII signal and affects the inverse method as well. In addition, general relations of \(\alpha _{\text {T}}\) and E(m) with other particles characteristics are today not available. Finally, it has to be reminded that the numerical synthesized reconstruction of the LII signal also depends of the quality of the gaseous phase description. However, also with the inverse technique, a correct prediction of the gas phase is a necessary step before validating the solid phase. In the following, the new validation approach is applied to the study of a premixed laminar sooting flame to prove the feasibility of the technique in the context of a real flame investigation.

4 Application to a premixed flame

In the following, both the traditional and the synthesized LII signal comparisons are performed for a target flame of the soot research community. The objective here is not the validation of the numerical model used for the simulation since it has been already discussed in [26] but to prove the feasibility of the forward approach. First, the mean diameters are calculated from the numerical PPSD obtained in [26] and compared to measurement results [10, 19, 20]. Then, the forward validation procedure is applied by reconstructing the synthesized LII signals from the numerical results at 4 different height above burners (HABs) and by comparing the \(E_{{\text {LII}}}\) and \(\sigma ^\star _{{\text {LII}}}\) indexes to the experimental data.

4.1 Flame configuration

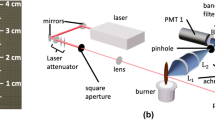
The third laminar premixed ethylene target flame from the 4th International Sooting Flame (ISF) Workshop [65] has been used here due to the availability of experimental LII signals in literature [10, 19, 20]. In these works, a so-called McKenna burner is used to produce a premixed flat ethylene/air flame with an equivalence ratio of \({\varPhi }= 2.1\). The total flow rate is 10 l/min (at 0 \(^\circ \hbox {C}\) and 1 atm) equivalent to 6.44 cm/s cold flow inlet velocity.

The LII measurements carried out by Bladh [10] were performed with a 1064-nm beam produced by a Q-switched Nd:YAG laser. The detection system was equipped with a bandpass filter at 575 nm with a 32-nm full width at half maximum (FWHM). The laser fluence was set to \(0.13\hbox { J/cm}^2\) and the temporal profile of the laser pulse had a FWHM of \(\sim 11\hbox { ns}\). This information, needed for the synthesization of the LII signal, has been extracted from [10].

4.2 Numerical setup and chemical mechanism

The associated numerical simulations have already been performed and validated in [26]. They were performed with the OpenSMOKE++ framework [66]. The kinetic mechanism includes 189 gaseous species and a chemical discrete sectional soot model (CDSM) with 20 sections (BINs), which are divided into subsections based on the H/C ratio. While heavy polycyclic aromatic hydrocarbons (PAHs) (from \(\hbox {BIN}_1\) to \(\hbox {BIN}_4\)) and small soot particles (from \(\hbox {BIN}_5\) to \(\hbox {BIN}_{{10}}\)) have 3 H/C subsections, large soot particles (\(\hbox {BIN}_{{11}}\) and \(\hbox {BIN}_{{12}}\)) and soot aggregates (from \(\hbox {BIN}_{{13}}\) to \(\hbox {BIN}_{{20}}\)) are divided into 2 H/C subsections. Information on the PPSD is obtained by transporting the equations for the primary particle number density of the sections with the method described in [26]. Due to the simplicity of the flame, the errors introduced by an improper modeling of the flow field of the flow-flame interaction are expected to be negligible.

The inlet velocity and the species mass fractions were prescribed according to the experimental setup. The temperature profile was imposed as suggested by the ISF Workshop [65] in the reference calculation. This temperature profile differs from the one experimentally obtained by Bladh et al. [10], so that a numerical simulation was also performed using the experimental gas temperature in the [0.7,1.8] cm region. No relevant difference in terms of PPSD has been evidenced between the two calculations (not shown) so that in the following, the validation is performed only with the results from the ISF temperature profile.

4.3 Classical inverse strategy: comparison of the mean primary particle diameter

The classical inverse validation of the model was performed by Bodor et al. [26]. Only the main results from [26] are summarized here to facilitate the reading. The LII measurements reported in Fig. 15 are based on an assumption of monodisperse population. Therefore, the monodisperse equivalent size recovered by Bladh et al. [10] is considered from the TEM measurements. For the same reason, the numerical PPSD results have been post-processed to obtain an equivalent mean diameter \(d_{{\text {mono}}}^{{\text {eq}}}\) [26]. The significant mismatch between the experimental results can be related to the different porous plug materials [67] used in the studies (a stainless steel porous plug was used in [19, 54]; a bronze plug was used in [10]).

In Fig. 15, the comparison of the numerical and the experimental results [10, 19, 54] is presented. Concerning the numerical results, \(d_{{\text {mono}}}^{{\text {eq}}}\) has been calculated with \(d_{{\text {det,min}}} = 2\ {\text {nm}}\) and \(d_{{\text {det,min}}} = 5\ {\text {nm}}\) (bottom and top blue dashed lines, respectively) providing a range of possible solutions (brown area) since the diameter of the smallest experimentally captured particle \(d_{{\text {det,min}}}\) is not indicated for all databases.

At low heights above burners (HABs), the numerical simulation tends to overpredict the \(d_{{\text {mono}}}\) and a slower diameter increase is obtained compared to all experimental data.

Fig. 15
figure 15

Experimentally [10, 19, 54] and numerically obtained primary particle diameter with monodisperse assumption. “\(n_{\text {p}}=100\)” marks the reevaluation performed at HAB = 1.7 cm by Bladh et al. [10] with aggregate structure assumption

Full size image

It can be noticed that depending on the used experimental database, it is possible to conclude that the numerical model overpredicts the mean \(d_{{\text {pp}}}\) in the early nucleating region or in the later surface growth region, leading then to different modifications of the model. The reevaluation with \(n_{\text {p}} = 100\) indicates that the difference may be also caused by the fact that the shielding effect was neglected when post-processing the experimental data. Depending on the smallest particle \(d_{{\text {det,min}}}\) considered when calculating the mean diameter from the numerical PPSD, the conclusions change again. Whereas with \(d_{{\text {det,min}}} = 2\) nm the model seems to be correct, the use of \(d_{{\text {det,min}}} = 5\) nm would mean that a slower growth of particles or a more intense nucleation is required.

In conclusion, the large error bars related to the uncertainty in the retrieved \(d_{{\text {pp}}}\) prevent from determining the strategy for the numerical model development. To draw further conclusions on the validation and/or to identify potential paths of improvements, a more reliable evaluation is needed. In particular, to identify the reactions that may need an update, it is crucial to accurately locate the region of the \(d_{{\text {pp}}}\) mismatch. Therefore, in the following section, the forward approach is tested on this configuration to understand if additional indications on the accuracy of the model can be obtained.

4.4 Novel forward strategy: comparison of TiRe-LII signals

In this section, the measured and the synthesized LII signals are compared in terms of \(E_{{\text {LII}}}\) and \(\sigma _{{\text {LII}}}^\star\) to reduce the uncertainties of the post-processing technique and potentially strengthen the validation procedure. By doing so, some potential weaknesses of the numerical model can be investigated additionally to the classical inverse strategy. Four HABs (7, 9, 13 and 17 mm) were selected for the LII signal reconstruction and to perform a comparison with the experimental data [10].

The LII signal was reconstructed by an in-house code using the model equations reported in [35, 39, 41]. The differential equation was solved with the fourth-order Runge–Kutta method using the characteristics of the laser in the measurements of Bladh et al. [20]: laser wavelength \(= 1064\hbox { nm}\), \(\hbox {fluence} = 0.13\hbox { J/}\hbox {cm}^2\), shot duration = 11 ns, bandpass filter \(= 575\pm 16\hbox { nm}\). Vaporization is neglected since a low fluence has been considered.

While in the first study of Bladh et al. [20] a varying \(\alpha _{\text {T}}\) (within the range of 0.5–0.61) has been used, the second study [10] was performed with a constant value of \(\alpha _{\text {T}}\) (0.37). Most of the works on TiRe-LII signal evaluations are based on a constant value of \(\alpha _{\text {T}}\) [27, 33], though \(\alpha _{\text {T}}\) was shown to depend on the soot particle characteristics [20, 68]. In the following, the constant value indicated by Bladh et al. [10] is used here since no reliable estimation of \(\alpha _{\text {T}}\) evolution along the flame was possible.

Fig. 16
figure 16

Comparison of synthesized and measured [10] LII signal indexes at four HABs (7, 9, 13 and 17 mm)

Full size image
Fig. 17
figure 17

Numerical PPSD for the premixed laminar flame experimentally investigated by [10]

Full size image

The indexes of the synthesized and experimental LII signals are compared in Fig. 16. The signal was reconstructed from the numerical PPSD considering \(d_{{\text {det,min}}} = 2\) nm and \(d_{{\text {det,min}}} = 5\) nm. The difference between the two cases is marginal, so that only \(d_{{\text {det,min}}} = 5\) nm is plotted. This confirms that the smallest particles only slightly contribute to the LII signal compared to the biggest ones. On the contrary, as deduced from Fig. 15, accounting (or not) for the smallest particles when calculating \(d_{{\text {pp}}}\) from a numerical PPSD can affect the results. Therefore, since the size of the smallest detectable particle \(d_{{\text {det,min}}}\) is not always clearly indicated in the experimental database, comparing synthesized and experimental LII signals is a more consistent approach to validate the numerical models.

For the interpretation of the results, it should be reminded that only the first 800 ns have been considered to calculate the indexes. Therefore, the tendencies should be interpreted by looking at Figs. 3d and 4d. Results on \(d_{{\text {mono}}}\) are also summarized in Table 2. The tendencies of the indexes are qualitatively similar between the experimental and the numerical results. The index \(E_{{\text {LII}}}\) increases up to 13 mm. This increase slows down for \(\hbox {HAB}>13\hbox { mm}\). Concerning \(\sigma _{{\text {LII}}}^\star\), it decreases with the HAB almost reaching a plateau for \(\hbox {HAB} \ge 13\hbox {mm}\). This behavior indicates that \(d_{\text {g}}\) and/or \(\sigma _{\text {g}}\) increase with the height above the burner. When compared to the experimental data, the numerical simulation over-predicts \(E_{{\text {LII}}}\) (and underestimates \(\sigma _{{\text {LII}}}^\star\)) for HAB=7 mm, whereas it under-predicts \(E_{{\text {LII}}}\) (and overestimates \(\sigma _{{\text {LII}}}^\star\)) for HAB=13 mm, with a quite good agreement for HAB=9 mm. This indicates that \(d_{\text {g}}\) and/or \(\sigma _{\text {g}}\) are initially overestimated by the simulation, whereas they are under-predicted downstream the flame. These results obtained with the forward approach confirm the results on \(d_{{\text {mono}}}\) obtained with the inverse technique in Table 2. Therefore, the forward analysis can be used to confirm the conclusions obtained with the inverse approach for \(d_{{\text {det,min}}}=2\hbox {nm}\).

Table 2 \(d_{{\text {mono}}}\) [nm] at different HABs derived from TiRe-LII by Bladh et al. [10] and from a numerical simulation with \(d_{pp,min} = 2\hbox { nm}\). The corresponding errors are indicated in the last columns
Full size table

However, an additional indication can be deduced by looking at the results with the forward approach. In Table 2, it can be observed that the error on \(d_{{\text {mono}}}\) is around \(\pm 30\)% for the different available points. On the contrary, when looking to \(\sigma _{{\text {LII}}}^\star\), a significant disagreement between the experimental and the numerical data is observed at HAB=7 mm. This indicates that the error on the PPSD prediction, presented in Fig. 17, is probably more significant at this height compared to the other positions. One possible scenario to explain the fact that the \(\sigma _{{\text {LII}}}^\star\) value is strongly underestimated is that \(\sigma _{\text {g}}\) is highly overestimated by the numerical results. This can possibly indicate that in the numerical PPSD of Fig. 17, the appearance of the second mode (composed of big particles largely contributing to the LII signal) is predicted too quickly. The forward procedure seems to indicate that the transition between unimodal to bimodal PPSD, often obtained as a results of collisional processes, is predicted too quickly. Therefore, a possible path of improvements of the model may consist in an accurate reduction of the collisional processes intensity, leading to a slower transition from a uni-modal to bi-modal PPSD, i.e., to higher \(\sigma _{\text {g}}\) values, and the verification of its effect on the synthesized LII signal. Additionally, it can be concluded that a longer detection time for experimental LII signals should be used to identify more easily if the discrepancies are related to \(d_{\text {g}}\) or \(\sigma _{\text {g}}\) misprediction using results from Figs. 3a and 4a.

5 Conclusions

In this work, a novel forward approach has been proposed to validate the numerical models for the primary particle size distribution prediction with experimental results obtained with the TiRe-LII technique. It is based on the numerical reconstruction of the temporal evolution of the LII signals from the simulation information. The difficulties of the traditional inverse strategy of validation were pointed out. They are mainly related to the uncertainties of the parameters governing the LII signal such as the gas temperature, the pressure, the molecular weight, the PPSD shape and the number of particles in the aggregate.

On the contrary, comparing directly the numerically synthesized and the experimental LII signals is very attractive since many of these quantities are generally available from detailed numerical simulations. To compare the experimental and the synthesized LII signals, two characteristic indexes have been suggested: the expected value \(E_{{\text {LII}}}\) and the non-dimensional standard deviation \(\sigma _{{\text {LII}}}^\star\). Thanks to these indexes, the error possibly introduced by the exponential fitting procedure frequently used for the TiRe-LII signal evaluations can be avoided.

The feasibility of the forward method was tested on a premixed ethylene ISF target flame [19] together with the inverse approach. The traditional inverse comparison is characterized by a significant experimental error bars and a strong effect of the definition of the experimental \(d_{{\text {det,min}}}\), so that no conclusion can be definitely assessed. On the contrary, the forward method showed that larger primary particles and/or a larger standard deviation of the PPSD should be predicted in the upper flame region. These conclusions are consistent with the results on \(d_{{\text {mono}}}\) obtained with the inverse method but they are less affected by the discussed uncertainties. Therefore, the novel forward approach can be considered as a consistent validation strategy complementary to the inverse method. Even if the forward strategy allows to reduce the uncertainties, it should be reminded that similar LII signal decay corresponds to various possible PPSDs, so that the agreement between synthesized and measured signal does not ensure the validity of the PPSD. This issue is not due to the post-processing validation strategy but it is intrinsic to TiRe-LII measurements. However, when a mismatch is observed in such a comparison, it can be used to state that the predicted PPSD is incorrect and add further indications for the modeling development. In addition, it has to be reminded that the numerical synthesized signal depends on the model’s accuracy for both the gas and the solid phases, allowing to investigate the quality of the whole numerical strategy and not only of the solid-phase simulation.

The potential improvement of the new approach is related to the thermal accommodation coefficient, which is one of the sources of uncertainty even in the novel approach. The dependency of \(\alpha _{\text {T}}\) on other soot properties is not clearly established yet. However, once the relation will be found, the reconstruction of the thermal accommodation coefficient could be done providing accurate predictions even in the presence of a nascent and mature soot particle mixture.