1 Introduction

In most combustion processes, carbonaceous nanoparticles called “primary particles” form from partially pyrolyzed fuel molecules. Due to their diffusive motion, these primary particles collide with each other, forming random shaped fractal-like aggregates consisting of up to a few hundred primary particles. The morphological parameters of fractal aggregates can be described by the fractal relationship [1, 2]:

$$\begin{aligned} N_\mathrm {p} = k_\mathrm {f} \left( \frac{2 R_\mathrm {g}}{d_\mathrm {p}}\right) ^{D_\mathrm {f}}, \end{aligned}$$
(1)

where \(N_\mathrm {p}\) is the number of primary particles per aggregate, \(R_\mathrm {g}\) is the aggregate radius of gyration representing its size, \(d_\mathrm {p}\) is the diameter of the primary particles, and \(D_\mathrm {f}\) and \(k_\mathrm {f}\) are the fractal dimension and prefactor, respectively [3]. Due to the random process of aggregation the aggregate sizes follow a broad, self-preserving, size distribution, which can adequately be described by a log-normal distribution [4]. The probability density for a specific size z is then given by

$$\begin{aligned} p \left( z,\mu ,\sigma _\mathrm {g}\right) =\frac{1}{z \ln \sigma _\mathrm {g} \sqrt{2 \pi }} \cdot \exp ^{-\frac{\left( \ln z - \ln \mu \right) ^2}{2 \left( \ln \sigma _\mathrm {g}\right) ^2}}, \end{aligned}$$
(2)

where \(\mu\) is the median and \(\sigma _\mathrm {g}\) the geometric standard deviation of the distribution. Transmission electron microscopy (TEM) of soot samples reveals that a double log-normal distribution of \(N_\mathrm {p}\) may even be a better descriptor for some samples [5, 6]; however, in this work, we will use the common single log-normal distribution in \(R_\mathrm {g}\).

Primary particle diameters are also polydisperse, although less so than the aggregate sizes. Kiss et al. [7] showed that the residence time considering drift and diffusion mechanisms in nanoparticle growth processes lead to a self-preserving log-normal size distribution. One possibility to measure the primary particle size distribution (PPSD) and the aggregate morphology is TEM, but it is a very time-consuming procedure [8]. Moreover, intrusive sampling affects the flow field of the combustion process and results in distinct perturbations and sampling bias towards hotter regions of the process [9]. Further uncertainties arise from the imaging process and the interpretation of 3D objects from 2D projection data [10].

For this reason non-invasive optical measurement techniques with a high spatial and temporal resolution are beneficial. Elastic light scattering (ELS), as an example, allows for the determination of the aggregate size and morphology in terms of \(R_\mathrm {g}\) and \(D_\mathrm {f}\) [11]. Most often, the angle-dependent scattering intensity is measured by either a single rotatable detector [12, 13], or by simultaneous acquisition of scattering signals with multiple detectors at different positions [14]. While most techniques suffer from a limited set of detection angles, the wide-angle light-scattering (WALS) approach, first introduced by Tsutsui et al. [15] and further developed by Oltmann et al. [16] and Huber et al. [17], acquires quasi-continuous scattering data over a wide angular range with high signal-to-noise ratios. While this approach is mainly used to infer the ensemble averaged aggregate sizes, the appearance of \(d_\mathrm {p}\) in Eq. (1) suggests that it also offers the possibility for determining the size distribution parameters. However, the primary particle size is, except for very large \(d_\mathrm {p}\), not accessible with ELS.

Time-resolved laser-induced incandescence (TiRe-LII) has developed into a powerful tool for measuring the particle volume fraction [18] as well as the primary particle size in various applications [4, 19, 20]. Particle size determination with TiRe-LII is based on the principle of measuring the decay rate of the incandescence signal produced by an ensemble of laser-heated soot particles as they thermally equilibrate with their surroundings. Most often, the spectral incandescence is measured at multiple wavelengths and used to define a pyrometric temperature. Small particles with a high surface-to-volume ratio cool rapidly, while the larger particles cool more slowly. Quantitative estimates of primary particle size distribution parameters are found by regressing simulated temperature decay curves generated using a heat transfer model to ones derived from experimental TiRe-LII traces. Over the years, cooling models have become progressively more detailed and elaborate, as summarized in Ref. [21]. While TiRe-LII is mainly used to make pointwise measurements of particle concentrations and sizes, using suitable optics and detectors it can also be extended to determine an average primary particle diameter over a plane, as shown by Will et al. [22]. It is well known that qualitative estimates of polydispersity can be inferred from the cooling curve, e.g., by the departure of the pyrometric temperature from an exponential decay at longer cooling times [23]. Following the work of Vander Wal et al. suggesting that LII can be used for the prediction of primary particle sizes [24], this paper is dedicated to the question of whether reliable quantitative estimates of particle size distributions can be determined from TiRe-LII data.

The influence of polydisperse primary particle sizes (as defined by the primary particle size distribution, PPSD) on the incandescence signal has long been known. While predicting the signal for a known particle size distribution is straightforward (i.e., the forward problem), Roth et al. [25] showed that the inverse problem of inferring the particle size from the spectral incandescence decay involves deconvolving a Fredholm integral equation of the first-kind [26], which is mathematically ill-posed. At the same time, much work has been performed aiming at the determination the PPSD in the literature. Lehre et al. [27, 28] used direct non-linear regression to investigate the correlation between the flame temperature and the primary particle size distribution prospecting for a detailed uncertainty analysis of LII. Further work was done by Dankers et al. [29], who split the signal decay curve into two time regions based on the fact that small particles do not contribute significantly to the signal after several tens of nanoseconds. Kuhlmann et al. [30] obtained the primary particle size distribution parameters of a polydisperse aerosol by assuming a log-normal distribution and applying a fitting procedure based on the method of cumulants. Liu et al. [23] presented a simple approach for the multi variable optimization to determine the size distribution parameters and further revealed that the temperature decay in the first nanoseconds after the laser pulse is related to the Sauter mean diameter for low-fluence experiments. All these approaches were reviewed by Daun et al. [31], who highlighted the ill-posedness of the problem due to the fact that some parameters in the LII model (e.g., the thermal accommodation coefficient) suffer from uncertainties [32] and cannot be considered as deterministic.

Most of the above works do not consider how the aggregate structure may influence TiRe-LII derived primary particle sizes. This occurs mainly through the “shielding” effect in which primary particles near the center of the aggregate are screened from incident gas molecules by primary particles on the aggregate periphery [33,34,35,36]. Liu et al. [37] accounted for this effect using an equivalent diameter for the heat conduction term, which was a function of the aggregate parameters. They further state that temperature decay curves from LII within the flame environment are less affected by the aggregate structure, compared to cold aerosol cases [38]. Daun et al. [39] showed how directional scattering may influence heat transfer, while Johnsson et al. [35] emphasized the influence of “bridging” of primary particles on the LII signal. Singh et al. [40] recently highlighted how changed optical properties can influence the size determination. The aggregate structure can also influence the spectroscopic model, due to shortcomings in the Rayleigh–Debye–Gans polyfractal aggregate (RDG-PFA) theory that is almost exclusively employed to model the spectral emission cross sections of soot aggregates [41, 42]. Though, most of these findings are mainly neglected in this work, they will introduce additional uncertainties to the results and emphasize the meaning of aggregation on LII.

The aim of this work is to critically assess the possibility of inferring the PPSD with TiRe-LII by considering the aggregate structure and their size distribution through a shielding approach for a hot gas and a cold gas case. Bayesian inference is used to quantify the uncertainty induced by measurement noise and uncertainties about the aggregate size distribution. A more detailed analysis follows in which the uncertainty of model parameters is also considered, following Refs. [43,44,45,46,47]. These include the thermal accommodation coefficient \(\alpha\), the bath gas temperature, \(T_\mathrm {g}\), and, of course, the aggregate size distribution and morphology. The results show that in the absence of any prior information about the aggregate size distribution, the uncertainty in the inferred PPSD is large. With increasing knowledge about the aggregation state of the aerosol, the uncertainties in the primary particle size distribution parameters narrow, especially for the aerosol case. Nevertheless, since the uncertainties associated with many of the model parameters are large, especially for soot, determination of the PPSD with TiRe-LII becomes challenging.

2 Derivation of the measurement model

According to RDG-PFA theory [48], incandescence from a soot aggregate can be approximated as the superposition of incandescence from the constituent primary particles. In reality, due to various effects that include aggregate shielding (discussed below), the primary particle temperatures within an aggregate are unlikely to be uniform at any instant, but instead obey a distribution having a finite width, which complicates calculation of the spectral emission from the aggregate. Moreover, these approaches neglect transition-regime effects that would be important for larger aggregates [37].

Instead, to make the problem computationally tractable, we invoke the following assumptions from Liu et al. [37]:

  1. 1.

    The primary soot particles are in point contact (no bridging).

  2. 2.

    The primary soot particle diameters are uniform within an aggregate of size \(N_\mathrm {p}\) (containing \(N_\mathrm {p}\) primary soot particles), but are allowed to vary from aggregate to aggregate, i.e., primary particles are only polydisperse within the particle ensemble, but monodisperse within a single aggregate.

  3. 3.

    There is no correlation between \(d_\mathrm {p}\) and \(N_\mathrm {p}\), i.e., both \(d_\mathrm {p}\) and \(N_\mathrm {p}\) can vary independently. Consequently, the distributions of the primary particle diameter and the aggregate size are independent and both are assumed to be log-normal.

  4. 4.

    The potentially non-uniform temperature distributions among primary soot particles within an aggregate are neglected.

These assumptions are widely used and we assume the errors introduced by the approximations are mostly uncritical. In the result section, we could confirm the results of Johnsson et al. [35] concerning the effects of bridging on heat conduction. However, due to the lack of models including bridging for all heat transfer mechanisms, the major part of this work is based on assumption 1. Following the assumptions, primary particle temperatures within each aggregate are modeled as uniform at any instant, but the instantaneous temperatures will vary between aggregates. The incandescence signal is thus given by

$$\begin{aligned} \begin{aligned} S_{\uplambda }(t)&=C \int _{d_\mathrm {p}=0}^{\infty } \int _{R_\mathrm {g}=0}^{\infty } C^\mathrm {agg}_{\mathrm {abs,}\uplambda }(d_\mathrm {p},R_\mathrm {g}) \cdot I_{\mathrm {b},\uplambda } \left[ T_\mathrm {}(d_\mathrm {p},R_\mathrm {g})\right] \\&\quad \cdot p(d_\mathrm {p}) \cdot p(R_\mathrm {g}) \; \mathrm {d}d_\mathrm {p} \; \mathrm {d}R_\mathrm {g}, \end{aligned} \end{aligned}$$
(3)

where \(I_{\mathrm {b},\uplambda }\) is the blackbody spectral intensity, \(p(d_\mathrm {p})\) and \(p(R_\mathrm {g})\) are probability densities for the primary particle diameter and aggregate radius of gyration, \(C^\mathrm {agg}_{\mathrm {abs,}\uplambda }(d_\mathrm {p},R_\mathrm {g})\) is the absorption cross section of an aggregate containing primary particles of diameter \(d_\mathrm {p}\) and radius of gyration, \(R_\mathrm {g}\), and C is a calibration constant that accounts for factors that include the particle volume fraction, beam width, and detection solid angle. According to RDG-PFA [48]

$$\begin{aligned} \begin{aligned} C^\mathrm {agg}_{\mathrm {abs,}\uplambda }(d_\mathrm {p},R_\mathrm {g})&=N_\mathrm {p}(R_\mathrm {g},d_\mathrm {p},k_\mathrm {f},D_\mathrm {f}) \cdot C^\mathrm {pp}_{\mathrm {abs,}\uplambda }(d_\mathrm {p}) \\&= N_\mathrm {p}(R_\mathrm {g},d_\mathrm {p},k_\mathrm {f},D_\mathrm {f}) \cdot \frac{\pi ^2 d_\mathrm {p}^3 }{\uplambda } E({\tilde{m}}), \end{aligned} \end{aligned}$$
(4)

where \(E({\tilde{m}})\) is the absorption function of soot, here assumed as 0.3 [43] and independent of wavelength, while \(N_\mathrm {p}\) is given by Eq. (1).

In the case of low-fluence TiRe-LII, the instantaneous effective temperature of an aggregate containing primary particles of diameter \(d_\mathrm {p}\) and having radius of gyration \(R_\mathrm {g}\) is obtained from an energy balance on the aggregate:

$$\begin{aligned} \rho \cdot c_\mathrm {p} \cdot N_\mathrm {p}(R_\mathrm {g},d_\mathrm {p},k_\mathrm {f},D_\mathrm {f}) \cdot \frac{\pi d_\mathrm {p}^3}{6} \frac{\mathrm {d}T_\mathrm {p}}{\mathrm {d}t}={\dot{Q}}_\mathrm {abs}+{\dot{Q}}_\mathrm {cond}+{\dot{Q}}_\mathrm {subl}, \end{aligned}$$
(5)

where \({\dot{Q}}_\mathrm {abs}\) is the rate at which energy is absorbed by the aggregate, \({\dot{Q}}_\mathrm {cond}\) is the rate at which heat is conducted from the aggregate, and \({\dot{Q}}_\mathrm {subl}\) models the heat loss due to sublimation. In this work additional heat transfer mechanisms in the energy balance, e.g., thermal radiation, are neglected as they do not show significant contribution [4]. The absorption term is given by

$$\begin{aligned} {\dot{Q}}_\mathrm {abs} = H \cdot g(t) \cdot C^\mathrm {agg}_{\mathrm {abs,}\uplambda }(d_\mathrm {p},R_\mathrm {g}), \end{aligned}$$
(6)

where H is the fluence (here \(0.09\,\hbox {J/cm}^2\)), g(t) is the temporal variation function, taken to be a Gaussian distribution of width \(\sigma _\mathrm {Laser}=3.3\,\hbox {ns}\), and \(C^\mathrm {agg}_{\mathrm {abs,}\uplambda }\) is the absorption cross section evaluated at the excitation wavelength of 532 nm.

In cases where the aerosol is composed of isolated nanospheres having diameters smaller than the molecular mean free path in the gas \(\varLambda\), gas molecules travel ballistically between the nanoparticle surface at \(T_\mathrm {p}\), and a region of the gas at \(T_\mathrm {g}\), which acts as a thermal reservoir. In this case, the rate of heat conduction can be calculated from the average energy transferred when a gas molecule scatters from the nanoparticle surface. This average energy can be calculated from the maximum energy transferred weighted by the thermal accommodation coefficient \(\alpha\) [49, 50]. The maximum energy transfer mainly depends on the temperature difference \((T_\mathrm {p} - T_\mathrm {g})\) and the active degrees of freedom of the gas molecules [50, 51]. In many LII models, the number of accessible degrees of freedom is assumed to correspond to that of an equilibrium gas. These allow to calculate the specific heat ratio \(\gamma\) and the heat conduction of a primary particle in the free-molecular regime is given by [49]

$$\begin{aligned} {\dot{Q}}_\mathrm {cond,FMR}^{\mathrm {pp}}= -\frac{\alpha \pi d_\mathrm {p}^2}{4} p_\mathrm {g} \sqrt{\frac{2k_\mathrm {b}T_\mathrm {g}}{\pi m_\mathrm {g}}}\left( \frac{\gamma +1}{\gamma -1}\right) \left( \frac{T_\mathrm {p}}{T_\mathrm {g}}-1\right) , \end{aligned}$$
(7)

where \(m_\mathrm {g}\) is the average mass of gas molecules, \(p_\mathrm {g}\) is the gas pressure and \(k_\mathrm {b}\) Boltzmann’s constant. Filippov and Rosner [52] further advocate calculating a modified specific heat ratio according to

$$\begin{aligned} \frac{1}{\gamma ^*-1}=\frac{1}{T_\mathrm {p}-T_\mathrm {g}}\int _{T_\mathrm {g}}^{T_\mathrm {p}} \frac{\mathrm {d}T}{\gamma (T)-1}, \end{aligned}$$
(8)

which accounts for the temperature dependence of the vibrational energy models. Here, one should keep in mind that these modes are likely inaccessible during the gas-surface scattering underlying free-molecular heat conduction. Thus, although widely used for the modeling of LII, using Eq. (8) could lead to model errors as discussed in detail by Daun et al. [50]. These errors are assumed to be small as long as the thermal accommodation coefficient is calculated in a consistent way.

While this approach works for isolated nanospheres, it cannot be applied directly to soot aggregates due to the aggregate shielding effect. Filippov et al. showed that this effect can cause the heat conduction rates from primary particles within a single aggregate to differ by as much as an order of magnitude, depending on the size, fractal structure, thermal accommodation coefficient, and the current flow regime [33]. To account for aggregate shielding, several authors [33, 37] suggest representing the aggregate using a hypothetical equivalent sphere of diameter \(d_\mathrm {eff}\), having an area \(\pi d_\mathrm {eff}^2\) that produces the same heat transfer rate in the free-molecular regime, as one would expect due to due to aggregate shielding. The temperature calculated using this area should, in principle, correspond to an average of the primary particle temperatures at any instant. Liu et al. [37] propose a fractal-like relationship:

$$\begin{aligned} d_\mathrm {eff} = \left( \frac{N_\mathrm {p}}{k_\mathrm {h}}\right) ^{1/D_\mathrm {h}} \cdot d_\mathrm {p}, \end{aligned}$$
(9)

where the parameters

$$\begin{aligned} k_\mathrm {h}=1.04476 + 0.22329 \cdot \alpha + 7.14286\cdot 10^{-3} \cdot \alpha ^2 \end{aligned}$$
(10)

and

$$\begin{aligned} D_\mathrm {h}=1.99345 + 0.30224 \cdot \alpha - 0.11276 \cdot \alpha ^2 \end{aligned}$$
(11)

are found from a quadratic fit to numerical results obtained by tracing the trajectories of gas molecules interacting with randomly generated fractal aggregates that correspond to \(k_\mathrm {f}=2.3\), \(D_\mathrm {f}=1.78\), and a range of values for \(\alpha\) and \(N_\mathrm {p}\). Due to the expense of performing further direct simulation Monte Carlo (DSMC) calculations, the dependency of the shielding parameters on the accommodation coefficient is extended for further aggregate parameters, assuming that Eqs. (10) and (11) are independent of \(k_\mathrm {f}\) and \(D_\mathrm {f}\). The shielding effect is most pronounced for larger values of \(\alpha\) (i.e., the greatest reduction in heat transfer area), since in this scenario, the outermost aggregates “perfectly accommodate” all incident gas molecules, whereas at lower values of \(\alpha\), it is more probable that low-energy gas molecules can access the interior primary particles via nearly adiabatic primary and secondary scattering events with primary particles on the aggregate periphery.

The above analysis assumes that heat transfer occurs within the free-molecular regime, in which gas molecules travel ballistically between the soot aggregate and the equilibrium gas at \(T_\mathrm {g}\). The situation is more complex when the aggregate gyration radius is comparable to \(\varLambda\), in which case heat conduction takes place within the transition regime. In this scenario, the gas molecules undergo intermolecular collisions in the vicinity of the aggregate, thereby reducing the effectiveness of heat transfer for a given \(p_\mathrm {g}\) and \(T_\mathrm {g}\). Even in the simplest case of an isolated sphere, the Boltzmann equation governing transition-regime conduction is analytically intractable, while numerical solutions (typically DSMC [49]) are time-consuming to carry out. Instead, a range of interpolation schemes are used that estimate the transition-regime solution from the continuum and free-molecular regime rates based on the Knudsen number \(Kn=\varLambda /d_\mathrm {p}\). Of these, the Fuchs boundary sphere method [49, 53] has been shown to be most suitable for LII calculations, since it can account for the temperature dependence of gas transport properties between the nanoparticle surface and the surrounding gas. In this approach, the gas is envisioned as a free-molecular spherical shell (the “boundary sphere”) that envelops the particle, in turn surrounded by a continuum gas. The boundary sphere thickness, \(\delta\), is typically set equal to the mean free-molecular path at the unknown boundary sphere temperature, \(\varLambda (T_\delta )=\varLambda _\delta\). The boundary sphere temperature, in turn, is solved for by setting the free-molecular heat transfer rate \({\dot{Q}}_\mathrm {cond,FMR}^{\mathrm {pp}}\) between \(T_\mathrm {p}\) and \(T_\delta\) (given by Eq. (7) with \(T_\delta\) substituted for \(T_\mathrm {g}\)) equal to the continuum heat transfer rate \({\dot{Q}}_\mathrm {cond,c}^\mathrm {pp}\) between \(T_\delta\) and \(T_\mathrm {g}\), with

$$\begin{aligned} \begin{aligned} {\dot{Q}}_\mathrm {cond,c}^\mathrm {pp}&= -2 \pi \left( d_\mathrm {p}+2\delta \right) \int _{T_\mathrm {g}}^{T_\delta } k(T) \mathrm {d}T \\&= -2 \pi \left( d_\mathrm {p}+2\delta \right) {\bar{k}} (T_\delta -T_\mathrm {g}), \end{aligned} \end{aligned}$$
(12)

where \({\bar{k}}\) is the temperature-dependent heat conduction coefficient of the surrounding gas.

In the case of soot aggregates, Liu et al. [37] suggest that the equivalent sphere diameter derived from free-molecular calculations, Eqs. (9)–(11), be substituted for \(d_\mathrm {p}\) in Eqs. (7) and (12). It should be noted, however, that to the best of the authors’ knowledge, this assumption has not been tested and the physical connection between this diameter and the fractal-like geometry of soot aggregates is not obvious. Nevertheless, in lieu of any alternative, this approach is adopted here to account for both shielding and transition-regime effects from soot aggregates.

The sublimation term of the aggregate is modeled as \({\dot{Q}}_\mathrm {subl,FMR}^{\mathrm {agg}}=N_\mathrm {p} \cdot {\dot{Q}}_\mathrm {subl,FMR}^{\mathrm {pp}}\) with

$$\begin{aligned} {\dot{Q}}_\mathrm {subl,FMR}^{\mathrm {pp}}= -\pi d_\mathrm {p}^2 \beta \frac{\varDelta H_\mathrm {v}}{M_\mathrm {v}} \varPhi _\mathrm {v}, \end{aligned}$$
(13)

where \(\varPhi _\mathrm {v}=p_\mathrm {v}\sqrt{(2\pi R_\mathrm {s} T_\mathrm {p})^{-1}}\) is the mass flux of the sublimed gas crossing a unit area towards one side, \(R_\mathrm {s}\) is the specific gas constant, \(p_\mathrm {v}\) the vapor pressure of evaporated carbon clusters above the phase interface, \(M_\mathrm {v}\) is the mean molecular weight of the sublimed species, and \(\varDelta H_\mathrm {v}\) is the energy required to liberate one cluster from the condensed phase. In this work, \(\varDelta H_\mathrm {v}\), \(p_\mathrm {v}\), and \(M_\mathrm {v}\) are found following the procedure of Smallwood et al. [54], who also describe some of the uncertainties associated with this calculation. Furthermore, the evaporation coefficient is assumed \(\beta =1\). Moreover, Eq. (13) neglects the shielding and transition-regime effects described above, which should apply to both incident gas molecules for heat conduction and evaporated carbon clusters during sublimation. For hot bath gases or high fluence measurements, \(T_\mathrm {p}(t)\) could reach the sublimation temperature. Completely neglecting sublimation in the energy balance, Eq. (5), would lead to a relative error of approximately 10% in \(T_\mathrm {p}(t)\). For those cases, one should keep possible model errors in mind. However, for cold bath gas temperatures and the low fluence assumed in this work, sublimation has no significant effect on the particle temperature (relative deviation for \(T_\mathrm {p}(t)\) below 0.1%). Then, the influence of model uncertainties introduced by these approximations should also be negligible.

3 Methods

3.1 Bayesian inference

With the model described in the previous section and a presumed log-normal distribution for the primary particle diameter as well as for the radius of gyration a straightforward calculation of a signal decay curve is possible. In this work, \({\mathcal {N}}(\mu ,\varvec{\Gamma } )\) denotes a normal distribution with mean \(\mu\) and covariance \(\varvec{\Gamma }\). The signal is a vector of n discrete time steps:

$$\begin{aligned} \mathbf{b }=\left[ S_{\uplambda }(t_1),S_{\uplambda }(t_2), \ldots ,S_{\uplambda }(t_n)\right] ^\mathrm {T}. \end{aligned}$$
(14)

Recovering the primary particle size distribution from measured data requires a multivariate analysis for all quantities of interest (QoI) \(\mathbf{x }=(\mu _{d_\mathrm {p}},\sigma _{d_\mathrm {p}})\) commonly solved by a least-square minimization [55]. This leads to the maximum likelihood estimate (\(\mathbf{x }_\mathrm {MLE}\)) for those parameters. However, besides the QoI, further, so-called nuisance parameters have to be incorporated into the evaluation, as they cannot be considered deterministic. Adding these parameters to the vector \(\mathbf{x }\) increases the ill-posedness of the problem and the least-square method may fail to find a proper solution.

Using Bayes inference presents several advantages. First, it is possible to add prior information about certain parameters like the nuisance parameters with appropriate weights. This is very useful, as usually some knowledge about a certain parameter is available, although the exact value might be not known. Furthermore, one obtains information about the uncertainty of each QoI and nuisance parameters [45]. Bayesian inference is built on Bayes’ theorem [56]:

$$\begin{aligned} p(\mathbf{x }\vert \mathbf{b })=\frac{p(\mathbf{b } \vert \mathbf{x }) \cdot p_\mathrm {pr}(\mathbf{x })}{p(\mathbf{b })} , \end{aligned}$$
(15)

where \(p(\mathbf{b }\vert \mathbf{x })\) is the likelihood of observing the data b conditional a given x, \(p_\mathrm {pr}(\mathbf{x })\) is the prior probability for the parameters x and \(p(\mathbf{b })\) is the marginal likelihood serving as a normalization to fulfill the Law of Total Probability. The posterior \(p(\mathbf{x }\vert \mathbf{b })\) is the probability density for the (unknown and stochastic) parameters \(\mathbf{x }\) given the measured data \(\mathbf{b }\). It increases when the deviation between measured and modeled signals as well as all prior information are minimized. In the case of no prior information, mathematically expressed by uniform priors, \(p(\mathbf{x }\vert \mathbf{b }) \propto p(\mathbf{b }\vert \mathbf{x })\) follows from Eq. (15).

In general, the (simulated) measurement signal \(\mathbf{b }\) can be obtained by corrupting the unperturbed modeled data \(\mathbf{b }_\mathrm {mod}\) with measurement noise \(\mathbf{e }_\mathrm {noise}\) and model error \(\mathbf{e }_\mathrm {mod}\), so that

$$\begin{aligned} \mathbf{b }_\mathrm {} = \mathbf{b }_\mathrm {mod} + \mathbf{e }_\mathrm {noise}+\mathbf{e }_\mathrm {mod}. \end{aligned}$$
(16)

As stated above, in this work, model errors are neglected for further evaluation; thus, the obtained results represent a best case scenario.

In the case of normally distributed measurement noise

$$\begin{aligned} \mathbf{e }_\mathrm {noise} \propto {\mathcal {N}}(0,{{\varvec{\Gamma }}_{\mathbf{b}}}) \end{aligned}$$
(17)

the simulated signal is obtained from \(\mathbf{b }_\mathrm {} = \mathbf{b }_\mathrm {mod} + \mathbf{e }_\mathrm {noise}\). Then, the probability \(p(\mathbf{b }\vert \mathbf{x })\) for observing the data \(\mathbf{b }\) given \(\mathbf{x }\) can be calculated by [56]

$$\begin{aligned} \begin{aligned} p(\mathbf{b }\vert \mathbf{x })&= \frac{1}{\sqrt{(2 \pi )^{n} \cdot \det {{\varvec{\Gamma }}_{\mathbf{b }}}}} \cdot \\&\quad \cdot \exp \left( -\frac{1}{2}\left( \mathbf{b }_\mathrm {}-\mathbf{b }_\mathrm {mod} (\mathbf{x })\right) ^\mathrm {T} {\varvec{\Gamma }}_\mathbf{b }^{-1} \left( \mathbf{b }_\mathrm {}-\mathbf{b }_\mathrm {mod}(\mathbf{x })\right) \right) . \end{aligned} \end{aligned}$$
(18)

Assuming independent measurement noise with a diagonal covariance matrices \({{\varvec{\Gamma }}_\mathbf{b }} = \mathrm {diag}(\sigma _1^2,\sigma _2^2,\ldots ,\sigma _n^2)\) maximizing the likelihood \(p(\mathbf{b } \vert \mathbf{x })\) leads to a weighted least-square minimization of the residual function, with the weighing factors \(\sigma _\mathrm {b,j}^{-1}\). Including normally distributed prior knowledge with mean \(\mu _{\mathrm {pr}}\) and standard deviation \(\sigma _{\mathrm {pr}}\) the maximum a posteriori (MAP) estimate for all quantities of interest \(\mathbf{x }_\mathrm {MAP}\) is calculated by a weighted least-square minimization of the residual function [43]:

$$\begin{aligned} \begin{aligned} \mathbf{x }_\mathrm {MAP}&\hat{=}\arg \!\min \left[ \left( \sum _{\mathrm {j}=1}^{n}\frac{\left( b_\mathrm {j}-b_{\mathrm {j,mod}}(\mathbf{x })\right) ^2}{\sigma _\mathrm {b,j}^2}\right) \right. \\&\quad \left. +\left( \sum _{\mathrm {k}=1}^{n_\mathrm {pr}}\frac{\left( \mu _\mathrm {pr,k}-x_{\mathrm {k,mod}}\right) ^2}{\sigma _\mathrm {pr,k}^2} \right) \right] . \end{aligned} \end{aligned}$$
(19)

In addition to the \(\mathbf{x }_\mathrm {MAP}\), Bayesian inference can also be used to derive a probability density for each QoI through marginalization. From the posterior probability density \(p(\mathbf{x }\vert \mathbf{b })\), one can calculate the probability density for a specific quantity of interest \(x_i\) contained within \(\mathbf{x }\) by integration [56]:

$$\begin{aligned} p(x_i \vert \mathbf{b }) = \int \cdots \int \! p(x_j \vert \mathbf{b }) \prod _{j \ne i}^{} \mathrm {d}x_j . \end{aligned}$$
(20)

The marginalized probability density for one QoI, containing information about the uncertainty, is derived from multiple integration over all other variables of the vector \(\mathbf{x }\) [57]. The marginalized probability density can be further summarized in terms of credibility intervals for each QoI, e.g., with 90% credibility the variable \(x_i\) lies within \(\left[ x_i^-, x_i^+\right]\). For high-dimensional problems with many QoI, the integration needed for marginalization is often complex and time-consuming. For this reason, \(p(\mathbf{x }\vert \mathbf{b })\) is often approximated by a normal distribution around the \(\mathbf{x }_\mathrm {MAP}\) [57], corresponding to a locally approximated linear measurement model. From the Jacobian \(\mathbf{J }\) evaluated at \(\mathbf{x }_\mathrm {MAP}\), one can estimate the covariance matrix of \(\mathbf{x }\) by [58]:

$$\begin{aligned} {\varvec{\Gamma }}_{\mathbf{x }} = \left[ \mathbf{J }(\mathbf{x }_\mathrm {MAP})^{\mathrm {T}} \cdot {\varvec{\Gamma }}_{\mathbf{b }}^{-1} \cdot \mathbf{J }(\mathbf{x }_\mathrm {MAP}) +{\varvec{\Gamma }}_\mathrm {pr}^{-1}\right] ^{-1}. \end{aligned}$$
(21)

The variances of the normally distributed posterior densities for each quantity of interest, therefore, correspond to the diagonal elements of \({\varvec{\Gamma }}_{\mathbf{x }}\). For verification of the uncertainties derived from the approximated normal shape of \(p(\mathbf{x }\vert \mathbf{b })\), a Markov Chain Monte Carlo (MCMC) algorithm can be applied on the probability \(p(\mathbf{x }\vert \mathbf{b })\) [56]. Starting from an initial point \(\mathbf{x }_0\), each further step with random direction in \(\mathbf{x }\) leads, via the Metropolis–Hastings criterion, to a series of samples in \(\mathbf{x }\) that become ergodic to the posterior probability density function [43, 57]. From the density of sampled points in \(\mathbf{x }\), the probability density and credibility intervals can be estimated.

For a better visualization of dependencies of certain QoI on each other, the dimensionless correlation matrix based on the correlation coefficients can be computed as [58]

$$\begin{aligned} \rho _{\mathrm {cor},ij} = \frac{{\varvec{\Gamma }}_{\mathbf{x },ij}}{\sigma _{x_{i}} \cdot \sigma _{x_{j}}}. \end{aligned}$$
(22)

These coefficients are bounded by \(-1 \le \rho _{\mathrm {cor},ij} \le 1\), where all the diagonal entries \(\rho _{\mathrm {cor},ii}\) are exactly 1. A negative value for the coefficient of correlation shows that an increase of one parameter \(x_i\) leads to a decrease of the other \(x_j\), whereas a positive sign indicates that the correlation between both quantities is unidirectional. A value of \(\rho _{\mathrm {cor}}(x_i,x_j)\) close to zero indicates no significant correlation between the parameters.

3.2 Noise model

One of the key aspects of the evaluation process is to determine the measurement uncertainty of the LII signal \(\sigma _\mathrm {b}\) for use in Eq. (19). To obtain an appropriate noise model LII-measurement data are analyzed. To that end, 50 averaged LII-data from 100 single shots (5000 single shots in total) were recorded during measurements on soot particles from a soot generator as used by Huber et al. [17] based on a premixed ethene/air flame at an equivalence ratio \(\varPhi =2.2\,\). Each of those 50 averaged data sets was background-corrected and normalized to the overall maximum value of the 50 averaged signals. From these 50 averaged signal curves at each time step t after the signal peak a mean value \(\mu _\mathrm {b}\) and a standard deviation \(\sigma _\mathrm {b}\) were determined, assuming independent and normally distributed noise. The results are depicted in Fig. 1.

Fig. 1
figure 1

Standard deviation of the signal over the mean signal magnitude for 50 normalized and background-corrected signal decay curves, each averaged over 100 single shots (circles), a linear (red, coefficient of determination \(R^2=0.89\)) and a square root fitting curve (blue, \(R^2=0.84\)). The inset shows an averaged signal in comparison to a modeled one corrupted with the linear noise model

Full size image

As one can see, the standard deviation increases nearly linearly with an offset. Sipkens et al. [59] presented a general error model for laser-induced incandescence focusing on the different types of noise. For single-shot signals, the noise follows a Poisson–Gaussian probability density function. Pure shot noise would result in a square root behavior (blue line in Fig. 1) arising from the discrete nature of photon counting, which does not describe the measurement trend well. Thermal and electrical noise contribute to the Gaussian distribution of the single-shot noise model and lead to the offset. At the same time LII signals are typically averaged over multiple single shots. Sipkens et al. note that shot-to-shot variations result in a linear trend between \(\mu _\mathrm {b}\) and \(\sigma _\mathrm {b}\) depicted in the red line of Fig. 1. Therefore, the linear behavior indicates that the present system is limited by fluctuations of the laser intensity or variations in the soot concentration caused by the combustion process in the soot generator. The coefficient of determination \(R^2\) underlines these findings. For a linear fit, \(R^2\) is 0.89, while for an exponent of 0.5, corresponding to pure shot noise, \(R^2\) is only 0.84. Therefore, with the reasonable assumption of a linear noise model, a simulated signal curve can be corrupted with noise to recreate a theoretical measurement signal, as depicted in the inset of Fig. 1. Signals from a flat flame ethene/air burner at \(\varPhi =2.3\) showed similar trends. Accordingly, the same noise model is used for both the flame and the aerosol case.

4 Results and discussion

In the upcoming section, three different scenarios are presented. The level of uncertainty associated with certain parameters is increased from a simple 2D example to higher dimensional scenarios representing real measurement situations.

4.1 2D scenario

First, a 2D example with two unknown parameters is considered to demonstrate the principle of the evaluation technique. For this case, the distribution parameters \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) shall be recovered from a simulated LII signal, corrupted with artificial noise, but known and presumed deterministic parameters for \(\mu _{R_\mathrm {g}}\), \(\sigma _{R_\mathrm {g}}\), C, \(T_\mathrm {g}\), \(\alpha\), \(E({\tilde{m}})\), \(D_\mathrm {f}\), \(k_\mathrm {f}\) and \(\rho\) for a hot surrounding gas scenario with \(T_\mathrm {g}\) = 1600 K. In this 2D case, the vector \(\mathbf{x }\) only contains the quantities of interest \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\). The aggregates’ structural parameters in Table 1 are based on TEM data (laminar premixed ethyne/air flame, equivalence ratio \(\varPhi =2.3\), sampled at 17 mm above the burner surface, Mc-Kenna type burner). The other parameters represent typical mean values from the literature and measurement situations (as well as standard deviations for the discussion in upcoming sections). While these parameters correspond to one special case, a somewhat different choice of these parameters, e.g., for \(D_\mathrm {f}\), will not alter the overall conclusion regarding the effects of shielding on the uncertainties obtained when determining the PPSD. The decision to build up to a 11D scenario in the upcoming sections is based on some of the most important parameters. Of course, the addition of further quantities to the vector \(\mathbf{x }\) would lead to increasing uncertainties in the QoI. The evaluation time is \(\approx 500\) ns starting 10 ns after the signal peak using 1 ns steps. The integration limits in Eq. (3) are 25 nm and 1025 nm in \(R_\mathrm {g}\) and 5 nm and 80 nm in \(d_\mathrm {p}\) with enough refinement, so the integration error is negligible in comparison to the measurement noise. After its generation, the modeled signal for \(\mu _{d_\mathrm {p}}=20\,\hbox {nm}\) and \(\sigma _{d_\mathrm {p}}=1.2\) is superimposed with measurement noise from the linear noise model resulting in a theoretical measurement signal \(\mathbf{b }_\mathrm {}\). Then, for the 2D case without prior knowledge, Eq. (19) simplifies to a weighted least-square minimization with

$$\begin{aligned} \mathbf{x }_\mathrm {MLE}\hat{=}\arg \!\min \left\| \left( \frac{\left[ \mathbf{b }_\mathrm {} - \mathbf{b }_\mathrm {mod}(\mathbf{x })\right] ^2}{\sigma _\mathrm {b}^2}\right) \right\| . \end{aligned}$$
(23)
Table 1 Input values for modeling a theoretical measurement signal \(\mathbf{b }\) based on TEM analysis
Full size table
Fig. 2
figure 2

Likelihood \(p(\mathbf{b } \vert \mathbf{x })\) (contours in logarithmic scale) for different geometric mean and geometric standard deviation values of the primary particle size distribution for a 2D scenario. The red dashed lines mark the exact input values for signal generation, while the black-dashed lines depict the \(\mathbf{x }_\mathrm {MLE}\) values. The black ellipse depicts the 95% credibility interval for the normal approximation of the probability around the \(\mathbf{x }_\mathrm {MLE}\) deriving from the Jacobian. The filled gray circles are results of 4500 accepted steps of a MCMC simulation resulting in the marginalized histograms on top and aside for both QoI. The marginalized probability densities for each QoI, obtained by integration and from the normal approximation of the probability density are depicted as green and black curves, respectively

Full size image
Fig. 3
figure 3

Log-normal distributions of the primary particle diameter derived from 50 random samples of the 4500 MCMC steps in Fig. 2 together with the \(\mathbf{x }_\mathrm {exact}\) in red and \(\mathbf{x }_\mathrm {MLE}\) in black

Full size image

Figure 2 summarizes the results of the least-square minimization. The resulting \(\mathbf{x }_\mathrm {MLE}\) with \(\mu _{d_\mathrm {p}}=19.8\,\hbox {nm}\) and \(\sigma _{d_\mathrm {p}}=1.22\) (black diamond and black-dashed lines) is close to the input values (red diamond and red dashed lines) for the simulation. To visualize the probability density a straightforward evaluation of \(p(\mathbf{x }\vert \mathbf{b }) \propto p(\mathbf{b }\vert \mathbf{x })\) at several grid points around the \(\mathbf{x }_\mathrm {MLE}\) value is applied and plotted in Fig. 2 (contours in log scale). As one can see, the problem is slightly ill-posed as there is a valley of possible solutions with the probability density decreasing towards the edges of the valley. For example, a primary particle size distribution with an underestimated \(\mu _{d_\mathrm {p}}\) but overestimated \(\sigma _{d_\mathrm {p}}\) can explain the measured LII-data equally well within the measurement noise. In this case, the integration for the marginalization of the probability density for \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) from Eq. (20) can be approximated by a summation over all grid points in both directions. The marginalized probability densities are plotted as green lines in the upper and right graph of Fig. 2. As one can see each of the two probability densities can be approximated by the normal shape around the \(\mathbf{x }_\mathrm {MLE}\) depicted as black curves, corresponding to a local linear approximation of the measurement model around the MLE. The resulting 95% credibility interval from this approximation is also depicted as ellipse in the contour plot of Fig. 2. As the computational effort for the multi-dimensional integration increases with increasing number of unknown variables, the probability density for each QoI based on Eq. (21) is approximated as normally distributed for the following considerations. To verify the uncertainties in \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\), an MCMC simulation with 4500 steps is carried out. The results are plotted onto the contour (filled gray circles) confirming the shape of the valley of possible solutions. All steps are marginalized and binned and the resulting histograms for both QoI are plotted above and beside of the contour plot (gray bars). The histograms are in good agreement with the normally distributed probability density function as well as with those derived from marginalization of \(p(\mathbf{b }\vert \mathbf{x })\). The 95% credibility intervals are comparably narrow for the 2D case with \(\mu _{d_\mathrm {p}}\in [19.14\mathrm {\,nm}; 20.54\mathrm {\,nm}]\) and \(\sigma _{d_\mathrm {p}}\in [1.16; 1.28]\). In Fig. 3, the resulting recovered log-normal primary particle size distributions of 50 random samples from the MCMC (blue circles in Fig. 2) are plotted together with the distributions deriving from \(\mathbf{x }_\mathrm {exact}\) and \(\mathbf{x }_\mathrm {MLE}\) in red and black, respectively. Although the credibility intervals seem narrow, the influence on the recovered PPSD is clearly visible in Fig. 3. However, for this 2D scenario, all other parameters are considered to be deterministic and known exactly, which is unrealistic.

4.2 4D scenarios

For practical applications \(\mu _{R_\mathrm {g}}\) and \(\sigma _{R_\mathrm {g}}\) cannot be determined exactly but are limited by the accuracy of their corresponding measurement technique, e.g., TEM analysis or ELS. Here, it is important to assess how uncertainties in the aggregate size distribution propagate into uncertainties in \(\mu _{d_\mathrm {p}}\) and \(N_\mathrm {p}\). The desired vector \(\mathbf{x }\) now consists of the four variables under investigation (\(\mu _{d_\mathrm {p}},\sigma _{d_\mathrm {p}},\mu _{R_\mathrm {g}},\sigma _{R_\mathrm {g}}\)) and an additional nuisance parameter C, not actually under investigation, but necessary as a constant for scaling the normalized signal. All other parameters, e.g., \(T_\mathrm {g}\), \(\alpha\), \(E({\tilde{m}})\), \(D_\mathrm {f}\), \(k_\mathrm {f}\), \(\rho\) are still assumed to be perfectly known.

First, a case without any prior information about \(\mu _{R_\mathrm {g}}\) and \(\sigma _{R_\mathrm {g}}\) (4D no priors) reveals the impact of the aggregate size distribution on heat conduction through shielding. The shielding effect should be more pronounced for large aggregates due to the higher number of primary particles deriving from the fractal approach in Eq. (3) [33]. Knowledge about the aggregate size distribution is then incorporated into the inference via Eq. (19).

One way to measure the aggregate size is using elastic light-scattering techniques as for example WALS [57] or multi-angle light scattering (MALS) [62]. As the probe volume always contains a polydisperse distribution of aggregates following \(p(R_\mathrm {g})\), the resulting effective structure factor:

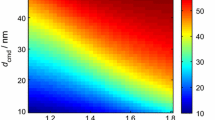
$$\begin{aligned} S_{\mathrm {eff}}(q,R_\mathrm {g},D_\mathrm {f})=\frac{{\int p(R_\mathrm {g}) \cdot N_\mathrm {p}^2 \cdot S(q,R_\mathrm {g},D_\mathrm {f}) \, \mathrm {d}R_\mathrm {g}}}{{\int p(R_\mathrm {g}) \cdot N_\mathrm {p}^2 \, \mathrm {d}R_\mathrm {g}}}, \end{aligned}$$
(24)

is based on the structure factor \(S(q,R_\mathrm {g},D_\mathrm {f})\) for each aggregate size \(R_\mathrm {g}\). For scattering in the Guinier regime, it can be approximated by \(S_{\mathrm {eff}}(q,R_\mathrm {g},D_\mathrm {f})\approx 1-1/3 \cdot q^2 \cdot R_\mathrm {g,eff}^2\), from which an effective radius of gyration \(R_\mathrm {g,eff}\) of the ensemble can be determined [11]. However, its value is shifted towards larger aggregate sizes, as their scattering intensity is scaled by an exponent of \(2 \cdot D_\mathrm {f}\), deriving from substituting \(N_\mathrm {p}^2\) in Eq. (24) with the fractal approach from Eq. (1). Figure 4 shows the link between the aggregate size distribution parameters \(\mu _{R_\mathrm {g}}\), \(\sigma _{R_\mathrm {g}}\) and \(R_\mathrm {g,eff}\) for an assumed log-normal aggregate size distribution in a contour plot. For example, an aggregate distribution of \(\mu _{R_\mathrm {g}}=80\,\hbox {nm}\) and \(\sigma _{R_\mathrm {g}}=1.7\) leads to an effective radius of gyration of \(R_\mathrm {g,eff}=238\,\hbox {nm}\).

Therefore, the second case uses prior knowledge about the effective radius of gyration (4D \(R_\mathrm {g,eff}\)), usually obtained from light-scattering experiments, to evaluate the posterior probability density of \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\). The Gaussian distributed prior probability density of \(R_\mathrm {g,eff}=(238 \pm 10)\,\hbox {nm}\) is based on typical results from light-scattering measurements with an angular resolution of 1\(^\circ\) [17]. The orange band in Fig. 4 marks all \((\mu _{R_\mathrm {g}}, \sigma _{R_\mathrm {g}})\) within the \(1-\sigma _{R_\mathrm {g,eff}}\) credibility interval of the prior probability density. Obviously, a variety of different aggregate size distributions lead to the same effective radius of gyration, which makes the problem ill-posed in itself. This was discussed in detail by Huber et al. [57], where Bayesian inference was used to deconvolve the actual aggregate size distribution parameters from scattering measurements.

Fig. 4
figure 4

Correlation between the aggregate size distribution parameters \(\mu _{R_\mathrm {g}}\), \(\sigma _{R_\mathrm {g}}\) and the effective radius of gyration \(R_\mathrm {g,eff}\). The orange band marks the 68% credibility interval of the \(R_\mathrm {g,eff}\) prior probability density \((238 \pm 10)\) nm, while the white ellipse tags the 68% credibility interval for prior knowledge about \(\mu _{R_\mathrm {g}}=(80 \pm 11)\) nm and \(\sigma _{R_\mathrm {g}}=1.7 \pm 0.06\). The red ellipse refers to prior knowledge of the covariance matrix from the WALS analysis

Full size image

Therefore, in a third case, Gaussian distributed priors for \(\mu _{R_\mathrm {g}}\) and \(\sigma _{R_\mathrm {g}}\) are added (4D \(\mu _{R_\mathrm {g}}, \sigma _{R_\mathrm {g}}\)). Table 1 lists the assumed values for both parameters, with their mean values based on TEM measurements from a premixed ethyne/air flat flame at \(\varPhi =2.3\). The width of the probability densities of both priors is expected to be \((80 \pm 11)\) nm and \(1.7 \pm 0.06\) based on the width of the credibility intervals around the MLE obtained from light-scattering measurements as reported by Huber et al. [57] for this range of aggregate sizes. This is a rather conservative assumption of the prior knowledge, as the Bayesian analysis of WALS data also provide the covariance of \(\mu _{R_\mathrm {g}}\) and \(\sigma _{R_\mathrm {g}}\). In Fig. 4, the white ellipse marks the 68% region for both \(\mu _{R_\mathrm {g}}\) and \(\sigma _{R_\mathrm {g}}\) highlighting the difference between the prior knowledge about the aggregate distribution parameters and the effective radius off gyration.

In a fourth case (4D \(R_\mathrm {g}\) WALS), the correlation between \(\mu _{R_\mathrm {g}}\) and \(\sigma _{R_\mathrm {g}}\) from the covariance matrix of the WALS analysis is taken into account, resulting in the red ellipsoid that obviously provides the most detailed information about the aggregate size distribution. A Cholesky decomposition [63] of the inverse covariance matrix from WALS measurements \({\varvec{\Gamma }}^{-1}_{\mathrm {WALS}}\) is used to get the weighing matrix according to \(\mathbf{W } = \mathrm {chol} \left( {\varvec{\Gamma }}^{-1}_{\mathrm {WALS}} \right)\) with \({\varvec{\Gamma }}^{-1}_{\mathrm {WALS}}=\mathbf{W }^T \mathbf{W }\). It can be used to find the \(\mathbf{x }_\mathrm {MAP}\) by replacing the second term of Eq. (19) with

$$\begin{aligned} \left( \sum _{\mathrm {k}=1}^{n_\mathrm {pr}}\left( \mathbf{W } \cdot \left( \mu _\mathrm {pr,k}-x_{\mathrm {k,mod}}\right) \right) ^2 \right) . \end{aligned}$$

For all four 4D scenarios, a flame case surrounding with \(T_\mathrm {g}=1600\,\hbox {K}\) as well as an aerosol case with \(T_\mathrm {g}=300\,\hbox {K}\) are analyzed. The resulting uncertainties of \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) and the corresponding width of the 68% credibility interval are listed in Table 2 together with the related normal distributions in Fig. 5 for both the hot (left) and the cold gas case (right). In Fig. 5, the 4D scenarios are presented as red curves with solid lines for the “4D no priors”, dot–dashed lines for the “4D \(R_\mathrm {g,eff}\)”, dashed lines for the “4D \(\mu _{R_\mathrm {g}}, \sigma _{R_\mathrm {g}}\)” and dotted lines for the “4D \(R_\mathrm {g}\) WALS” case. The 2D case presented in Sect. 4.1 is depicted in blue lines to refer to a “best case” scenario, where all aggregate parameters are deterministic.

Table 2 Results for \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) for different scenarios presented for a hot and cold surrounding gas case
Full size table
Fig. 5
figure 5

Uncertainties of both QoI (\(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\)) deriving from the values in Table 2, both quantities assumed as normally distributed. Left: hot case with a surrounding gas temperature of 1600 K, right: cold case with 300 K. The different colors refer to different scenarios: blue for 2D, red for 4D and green for 11D

Full size image

For both ambient gas temperature cases, the uncertainties of \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) are large when no prior information is assumed about the aggregate size distribution. It should be mentioned that the uncertainties presented in Table 2 may exceed the expectation values and thus do not present the real state of knowledge (e.g., negative values for \(\mu _{d_\mathrm {p}}\) within the uncertainty). This is a result of the normal approximation of the probability density. In those cases, the uncertainties rather highlight that the outcome is uninformative, indicating a flat shaped probability density. Adding information about the effective radius of gyration (dotted–dashed lines) does not significantly improve the uncertainties in \(\mu _{d_\mathrm {p}}\), although the uncertainties of \(\sigma _{d_\mathrm {p}}\) narrow with the \(R_\mathrm {g,eff}\) prior, especially for the 1600 K case. With knowledge about the aggregate size distribution the uncertainties narrow. Especially, for the cases “4D \(\mu _{R_\mathrm {g}}, \sigma _{R_\mathrm {g}}\)” (dashed lines) and “4D \(R_\mathrm {g}\) WALS” (dotted lines), the uncertainties of the distribution width approach the probability densities obtained from the 2D case. A general trend can be seen in Fig. 5, which is most pronounced for the cold aerosol case: as soon as some information about the aggregate distribution is provided, the width \(\sigma _{d_\mathrm {p}}\) of the PPSD can be determined with a relatively low uncertainty. This can be explained by the effects of large primary particles that would still incandesce even at late times of the LII signal. As the signal has almost decayed completely at those late times, however, the presence of large primary particles can be excluded. For the cold aerosol case, beside the high-temperature gradient between the particle and the surrounding gas also the prior uncertainty associated to \(T_{\mathrm {g}}\) must be taken into account. Here, we assume that temperature measurements in the cold gas are more precise than those at elevated flame temperatures. The effect is discussed in more detail in the following 11D case. As the simulations show, the effect of aggregate shielding is much more pronounced in the cold ambient surrounding scenario. Without any prior on \(\mu _{R_\mathrm {g}}\) and \(\sigma _{R_\mathrm {g}}\) as well as for the case “4D \(R_\mathrm {g,eff}\)”, almost no relevant information about the PPSD can be retrieved. This result is in agreement with the findings of Liu et al. [38], who stated that the primary particle diameter as well as the distribution of the aggregate size impact the particle temperature for low ambient gas temperatures. By adding more prior knowledge about both aggregate distribution parameters, however, the uncertainties narrow to an acceptable level.

In essence, the 4D simulations show that, although thermal shielding of aggregates influences the LII process significantly, it is possible to determine the PPSD with reasonable uncertainties. To that end, however, specific information about the aggregation state of the system must be available, particularly when performing LII measurements on cold soot aerosols.

4.3 11D scenario

In reality, many of the LII model parameters are subject to considerable uncertainty. For example, the measurements of the ambient gas temperature \(T_\mathrm {g}\) within a flame are always affected by certain error [64]. The thermal accommodation coefficient \(\alpha\) and absorption function \(E({\tilde{m}})\) are also subject to considerable uncertainty due to the techniques used to measure these parameters as well as variations in the composition and structure of soot. It is, therefore, unreasonable to model these parameters as “perfectly known”, which is reflected in the increasing trend to include these, and other model parameters, as nuisance parameters in Bayesian inference studies [56]. Therefore, additional nuisance parameters are added to the vector \(\mathbf{x }=(\mu _{d_\mathrm {p}},\sigma _{d_\mathrm {p}},\mu _{R_\mathrm {g}},\sigma _{R_\mathrm {g}},C,T_\mathrm {g},\) \(\alpha ,E({\tilde{m}}),D_\mathrm {f},k_\mathrm {f},\rho )\) leading to a 11D inference problem. Once again, the underlying prior probability densities are assumed to be Gaussian and are listed in Table 1. For the aggregate parameters, the same priors are used as presented for the “4D \(\mu _{R_\mathrm {g}}, \sigma _{R_\mathrm {g}}\)” case. The resulting uncertainties of \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) are plotted as green lines in Fig. 5 with the underlying values listed in Table 2. It is not surprising that due to the additional uncertainties of all the nuisance parameters, the uncertainties in \(\mu _{d_\mathrm {p}}\) increase to a significant level with a relative uncertainty of \(\approx 17\%\). No noticeable difference between the hot and cold gas case is observable, as the uncertainties of the QoI are dominated by the uncertainties of the nuisance parameters exceeding the influence of the aggregate size distribution. The posterior probability density of \(\sigma _{d_\mathrm {p}}\) is still narrow, especially for the cold ambient surrounding gas case and compared to the probability density of \(\mu _{d_\mathrm {p}}\). As the median value \(\mu _{d_\mathrm {p}}\) is mainly dependent on the decay rate of the LII signal, it is strongly influenced by parameters affecting the decay rate of each specific primary particle size, such as the thermal accommodation coefficient. High uncertainties in those parameters thus lead to a very high uncertainty of \(\mu _{d_\mathrm {p}}\). However, the distribution width \(\sigma _{d_\mathrm {p}}\) describes the relative weight of each particle size in the distribution (and the corresponding decay rate) and is thus less affected by those parameters and uncertainties, as they mainly enter \(\mu _{d_\mathrm {p}}\). In our case, wide size distributions with a high number of large primary particles (relative to the median \(\mu _{d_\mathrm {p}}\)) are very unlikely due to the behavior of their LII signal. Those large particles cool significantly slower than small ones. Assuming a broad PPSD, the high number of small- and medium-sized particles would be responsible for the strong signal within the first few hundred nanoseconds. For later times, their signal has almost completely decayed, and only the large particles would generate visible signal with a slow decay curve. As the simulated narrow PPSD contains no large primary particles, no signal at late times is present, excluding the possibility of large particles. Thus the measurement time has a great effect on the possibility for PPSD determination, especially for cold bath gas cases, as shown in Fig. 6. By shortening the evaluation time by a factor of three the uncertainties in \(\sigma _{d_\mathrm {p}}\) almost double from ± 0.018 to ± 0.028, while the uncertainties in \(\mu _{d_\mathrm {p}}\) are almost unaffected. As an interim conclusion we want to emphasize that especially for the determination of the width of the PPSD it is essential to measure the LII signal until its decay to the noise level. At the same time, the probability of monodispersely distributed primary particles (\(\sigma _{d_\mathrm {p}}=1\)) for all hot gas cases is very unlikely, even without prior knowledge. For cold aerosol cases, profound knowledge of the shielding effects is required. Probability densities \(p(\sigma _{d_\mathrm {p}})>\)0 for \(\sigma _{d_\mathrm {p}}<\)1 arise from the approximation of normally distributed probability densities around the \(\mathbf{x }_\mathrm {MAP}\) and, of course, do not represent a physical case.

Fig. 6
figure 6

Normally distributed uncertainties of both QoI (\(\mu _{d_\mathrm {p}}\) on top and \(\sigma _{d_\mathrm {p}}\) below) for different lengths of measurement time for a bath gas temperature of 300 K. The results for the 11D case are presented as green lines, while the red lines depict the 4D \(\mu _{R_\mathrm {g}}, \sigma _{R_\mathrm {g}}\) case

Full size image

Summarizing the results for the 11D scenario, the possibility of determining the PPSD with LII by itself for soot samples seems doubtful as many uncertainties from physical and optical properties as well as from the consideration of the aggregate structure in the shielding approach lead to a variety of possible solutions. On the other hand, determining the PPSD with LII appears feasible provided that some information is available about the aggregate structure and size distribution.

For the 11D scenario only the most important parameters of LII are included as stochastic variables. However, further models and their parameters could be included, e.g., to assess the validity of the assumptions made in the theory section. As an example, adopting the approach presented by Johnsson et al. [35] to account for the bridging effect showed only minor influence on the resulting uncertainties of the size distribution parameters. Assuming an overlap factor \(C_\mathrm {ov}=0.25\pm 0.05\) as an additional nuisance parameter lead to an estimate of \(\mu _{d_\mathrm {p}}=18.6\,\hbox {nm}\), while \(\sigma _{d_\mathrm {p}}\) is almost unaffected. This is in agreement with the findings of Johnsson et al. [35] reporting an overestimation of the particle size by 9% if bridging is neglected. However, as bridging does not show significant influence on the uncertainties (below 2.5%) and cannot be included into all models comprehensively, the upcoming discussion is further based on the 11D scenario.

It is important to ascertain which of the nuisance parameters are most responsible for the uncertainty in the QoI. To this end, a MCMC with 15,000 steps was carried out for the 11D case with hot surrounding. Figure 7 shows the marginalized histograms of the eleven quantities along the graphs on the diagonal, which reasonably match the normal distributions expected from the locally linear model approximation. For some variables, e.g., the density \(\rho\), the MCMC histograms do not match the prior probability densities, which are in each case wider compared to the sampled histograms. This indicates too few steps of the MCMC. Applying more MCMC steps, the accordance with the least-square minimization should further be improved. However, due to the double integral in Eq. (3) the computation time is quite high, typically about 200 s for each accepted step, limiting the size of the Markov chain. Moreover, from Fig. 7 the correlations between the different quantities can be seen in the corresponding off-diagonal graphs, where each green circle depicts an accepted MCMC step. As an example, there is a high correlation between the density \(\rho\) (column 11) and \(E({\tilde{m}})\) (row 8) or between \(\mu _{d_\mathrm {p}}\) (row 1) and \(\alpha\) (column 7). A more detailed discussion on the correlation between the different parameters is given in the next section.

Fig. 7
figure 7

Results of a MCMC with 15,000 steps for the 11D case with hot surrounding gas temperature. The diagonal axes represent the marginalized histograms for each QoI with the \(\mathbf{x }_\mathrm {MAP}\) (red), the \(\mathbf{x }_\mathrm {exact}\) (black-dashed) and the Gaussian shaped probabilities (black). The green filled circles represent each accepted step, where each combination of two quantities is presented in the according row and column combination. This allows to identify the degree of correlation between the parameters

Full size image

4.4 Discussion of the correlation matrices

To analyze the impact of each nuisance parameter on the quantities of interest the correlation matrices for the different scenarios for the hot gas case are presented in Fig. 8. As introduced in Sect. 3, the correlation matrix, as the standardized covariance matrix, visualizes the link between the different parameters. According to Eq. (22), all the diagonal entries are 1 and the matrix is symmetric. The correlation coefficient of two parameters is defined in the entry of the corresponding row and column of the matrix. For the 2D case, the \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) are highly correlated, as a change in one quantity can only be countervailed by a change in the other. The negative value \(\rho _{\mathrm {cor},12}=\rho _{\mathrm {cor},21}=-0.99\) indicates that a larger median primary particle size leads to a smaller \(\sigma _{d_\mathrm {p}}\) (and the other way around), which is also obvious from Fig. 2. The 4D case with prior knowledge of the aggregate size distribution parameters shows that the correlation between \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) is reduced as the aggregate size distribution parameters exert a competing influence. Furthermore, \(\sigma _{d_\mathrm {p}}\) is less correlated with the aggregate distribution parameters than \(\mu _{d_\mathrm {p}}\). This is a confirmation that the uncertainties in \(\sigma _{d_\mathrm {p}}\) are not as sensitive to the introduction of different aggregate size distribution parameters as the uncertainties in the median of \({d_\mathrm {p}}\). By introducing further nuisance parameters, the correlation coefficient between both QoI is close to zero. In addition, the aggregate distribution parameters do not show a strong influence on either \(\mu _{d_\mathrm {p}}\) or \(\sigma _{d_\mathrm {p}}\), whereas parameters like \(\alpha\), \(\rho\), or \(E({\tilde{m}})\) are highly correlated with the median of the primary particle diameter. To give an example, a certain signal decay curve may be explained by a certain \(\mu _{d_\mathrm {p}}\) at a certain surrounding gas temperature. By assuming a higher value for \(T_{\mathrm {g}}\), the cooling rate would theoretically be decreased. On the basis of the initial signal decay curve, only a reduction of the median primary particle size can countervail the overestimation of \(T_{\mathrm {g}}\). This leads to the negative value of the correlation coefficient \(\rho _{\mathrm {cor}}(\mu _{d_\mathrm {p}},T_{\mathrm {g}})\). On the other hand, an increase in the thermal accommodation coefficient \(\alpha\) would theoretically increase the cooling rate. This effect can only be compensated by assuming bigger particles and, therefore, results in a positive correlation coefficient \(\rho _{\mathrm {cor}}(\mu _{d_\mathrm {p}},\alpha )\). Furthermore, the link between certain nuisance parameters itself can be analyzed. As already mentioned in the discussion of Fig. 7, the density \(\rho\) and \(E({\tilde{m}})\) are highly correlated. In Eqs. (4)–(6), it becomes obvious that an increase in the density once again is positively correlated with the \(E({\tilde{m}})\) value. The fractal prefactor \(k_{\mathrm {f}}\) has a high correlation coefficient with \(\mu _{d_\mathrm {p}}\), as it acts as a kind of scaling factor in the fractal approach and in Eq. (3). As the probability density of the prior knowledge about this factor is very wide (Table 1), it has a strong influence on the determined PPSD. Comparing the correlation matrix of the 11D case with the MCMC of Fig. 7 similarities in certain parameters are observable. The high correlation between \(E({\tilde{m}})\) and \(\rho\) is especially prominent in the MCMC. Furthermore, the slope of the MCMC is in agreement with the sign of the correlation coefficient, e.g., the positive value for \(\rho _{\mathrm {cor}}(\mu _{d_\mathrm {p}},\alpha )\) or the negative one for \(\rho _{\mathrm {cor}}(\mu _{d_\mathrm {p}},k_{\mathrm {f}})\). Some other correlations, highlighted by the correlation matrix, are not present in the MCMC graphs. For example, the dependence between \(\mu _{d_\mathrm {p}}\) and \(\rho\) is not obvious in the MCMC, which might be due to the limited amount of MCMC steps. Here, the computationally efficient least-square minimization shows a great advantage over the time-consuming MCMC simulation in detecting correlations.

Fig. 8
figure 8

Correlation matrices for hot surrounding gas: 2D no priors (a), 4D \(\mu _{R_\mathrm {g}}, \sigma _{R_\mathrm {g}}\) (b), and 11D all priors (c) cases

Full size image

5 Conclusions

While TiRe-LII has evolved as a routine technique for the determination of primary particle sizes, the question under which circumstances their distribution can be obtained, has been mostly neglected so far. Although there have been many approaches for the determination of this distribution, the distribution of aggregate sizes, which influence heat conduction via shielding and transition-regime effects, has been widely neglected. The aim of this paper was to analyze this effect for two typical situations encountered in LII, namely, a flame and a cold soot aerosol case.

Regarding the main question addressed in the title of this work: can soot primary particle size distributions be determined using laser-induced incandescence? The answer is yes—for specific conditions. It highly depends on the prior knowledge of certain parameters as well as information about the aggregation state of the system. The measurement noise is amplified into uncertainties in the inferred primary particle size distribution parameters \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) by the ill-posedness of the problem. If one had exact knowledge of all other parameters of the system, robust estimates for \(\mu _{d_\mathrm {p}}\) and \(\sigma _{d_\mathrm {p}}\) could be found with little uncertainty. However, the ill-posedness and the uncertainties increase under the influence of aggregation through thermal shielding and uncertainties in model parameters. As various parameters influence the LII signal and signal decay, our major conclusion is: especially when including uncertainties in model parameters in the evaluation, the determination of the PPSD from LII-data is highly uncertain without profound knowledge of the aggregate size distribution, of which the measurement is thus indispensable.

The second conclusion implies that the median and the width of the PPSD are affected differently: the uncertainty of the median strongly depends on prior knowledge on the aggregate size distribution and other parameters. Yet, in many cases, the uncertainty of the width of the PPSD is less dependent on prior knowledge. In most measurement situations, it is, therefore, more difficult to determine the size of the primary particles, compared to the polydispersity.

Finally, we want to emphasize the importance of performing sophisticated uncertainty analysis for the determination of the PPSD and the correct interpretation of the outcome.