Estimation of soot absorption function via the two separated pulses laser-induced incandescence technique

Abstract

An original in situ experimental approach is proposed to estimate the absorption function of soot particles in flames: the two separated pulses laser-induced incandescence technique (SP-LII). The SP-LII technique is based on measuring the peak temperature of soot particles heated by laser pulses at two different fluences. From these two temperature measurements, the absorption function is estimated by solving the energy equation applied to soot particles during laser energy absorption once the product of soot density and specific heat is known. In order to solve the energy equation, two methods are considered here. The first method, called the “absorption model” (AM), solves the energy equation when all loss terms are neglected during absorption. The second method uses a look-up table (LUT) generated with an LII code in which the main loss terms are modelled. Both methods also provide information on the gas temperature $T_0$, assuming that gas and solid phases are at equilibrium. First, the SP-LII technique’s accuracy and limits are theoretically explored using peak temperatures from simulations done with an LII code. Overall, the AM method is efficient but is restricted to soot primary particles diameter $> \sim 10$ nm and low fluences. By contrast, the LUT method has an extended operational range, but it requires more information than the AM method, and its accuracy depends on the validity of the power loss models used to generate the look-up table. It is then concluded that the AM method represents the best compromise between the complexity of the methods and the expected accuracy of the results. Then, the feasibility of the SP-LII technique is proven by performing measurements in a laminar diffusion methane/air sooting flame and post-processing them with the AM method. Results for the absolute value and for the spatial evolution of ${E(m_{\lambda} )}$ are coherent with the literature. Finally, a possible extension of the SP-LII technique to turbulent flames is discussed.

1 Introduction

Extensive efforts are still needed to reduce soot emissions from combustion systems due to their harmful impact on health [1] and their global negative effect on the climate [2]. In this context, experiments on laboratory flames are performed to understand the complex processes behind soot formation, to provide databases for numerical validation and to characterise the soot particles’ physical and optical properties.

Soot optical properties are quantities characterising the particles’ interactions with light: absorption, emission, or scattering. Specifically, the absorption function ${E(m_{\lambda} )}$ represents soot emission and absorption. It is defined from the refractive index $m_\lambda = n -ik$: ${E(m_{\lambda} )} = - \text {Im} \left( \frac{m_\lambda ^2 -1}{m_\lambda ^2 +2} \right)$. The refractive index is itself dependent on the wavelength $\lambda$. The precise characterisation of ${E(m_{\lambda} )}$ is important for many reasons:

• 1. It is a key property when performing laser-induced incandescence (LII) as its absolute value is required for the estimation of the soot volume fraction $f_v$ by auto-compensating LII (AC-LII) [3] or when using extinction techniques to calibrate LII signals [4,5,6].

• 2. The ratio of ${E(m_{\lambda} )}$ at two wavelengths is required to determine the soot temperature by two-colour LII pyrometry [7].

• 3. The absorption function is also linked to the maturity level of the soot particles, which gives information on soot ageing. Specifically, Michelsen et al. [8] define the maturity level as a way to describe the progress of soot from inception to fully mature soot, where mature soot is a graphite-like particle that has fully evolved at high temperature.

Evidence in the literature indicates that the absorption function value increases with maturity. For example, Snelling et al. [9] developed a technique to determine ${E(m_{\lambda} )}$, which was applied by Bladh et al. [10], Bejaoui et al. [11], Maffi et al. [12], and Eremin et al. [13] on a flat premixed flame stabilised on a McKenna burner. They all observed an increase of ${E(m_{\lambda} )}$ with the height above the burner (HAB). By monitoring elastic light scattering before and after an LII pulse on a McKenna burner, Olofsson et al. [14] found that the sublimation fluence threshold decreases when increasing HAB. The authors indicate that these results could be explained by lower ${E(m_{\lambda} )}$ values for the youngest soot particles found in the lower part of the flame. Lopez et al. [15] investigated ethylene/air diffusion laminar flame on Santoro and Gulder burners. They observed differences between the fluences curves obtained in the flame axis and the flame edge. They suggested that an increase of the absorption cross-section (which is proportional to ${E(m_{\lambda} )}$) with maturity could explain these differences. Yon et al. [16] presented a 2D map of the distribution $E(m_{\lambda })$ (for three values of $\lambda$) in a diffusion flame. They observed that the highest values of the absorption function are located on the outer edge of the flame wings and at the tip of the flame, while lower values are in the inner lower part of the flame.

As it is generally admitted that the absorption function depends on the soot maturity [17], the absorption function is a good tracer for soot maturity. Several techniques have been developed to estimate soot particles’ optical properties. Here, the most common approaches to determine the absolute value of ${E(m_{\lambda} )}$ are quickly reminded and are separated into two categories: ex situ and in situ techniques.

Ex situ techniques require extracting soot from the flame. The sampling is intrusive and may introduce uncertainties on ${E(m_{\lambda} )}$ that are difficult to be quantified. Among them, the reflectometry [18, 19] allows access to the soot refractive index from measurements of plane-polarised reflected intensities from a polished compressed soot sample. To this end, soot particles are collected in a flame and compressed at very high pressure ($\approx 400$ bars) to form a $\sim 1$ gram pellet before being polished. This intrusive technique may significantly change soot properties during the extraction, compression or polishing phase.

More recently, Yon, Bescond et al. [20, 21] estimated ${E(m_{\lambda} )}$ of soot sampled in a flame (ex situ), with a technique based on extinction spectra analysis and accounted for Rayleigh–Debye–Gans (RDG) theory for fractal aggregate.

Unlike ex situ techniques, in situ ones allow the estimation of soot properties directly in the flame and do not require soot extraction, so they are generally less intrusive. One of the most used in situ techniques to determine ${E(m_{\lambda} )}$ in a flame is the one developed by Snelling et al. [9]. It relies on the comparison of the experimental and numerical maximum effective temperatures reached by the heated soot particles. It requires the knowledge of the product of the soot specific heat with density $\rho c$, the peak soot temperature, the initial soot temperature (supposed to be equal to the local gas temperature) and the primary particle diameter. The absorption function is retrieved by adjusting its value as input of an LII numerical model by minimising the difference between the numerical effective soot temperature and the experimental one.

By neglecting the loss terms during the laser absorption phase, the dependency of the primary particle diameter disappears. Thus, ${E(m_{\lambda} )}$ can be estimated without the need for an LII code, but still from the measurements of the peak temperature and the gas temperature once $\rho c$ is known [4, 9, 22, 23]. Hagen et al. [22] recently developed a technique based on the consecutive heating of the same soot particle by two laser pulses at two different wavelengths. It allows estimating the ${E(m_{\lambda} )}$ ratio at the two laser wavelengths in transient but slowly varying flow. In addition, provided that the soot peak temperatures and the gas temperature are known, the absolute value of ${E(m_{\lambda} )}$ can be obtained using the method presented in [9].

Other works [24, 25] use the relation existing between the extinction coefficient $K_\textrm{ext}$, the volume fraction $f_v$, the ratio of the scattering to the absorption coefficient $\rho _{sa}$ and the absorption function:

$$\begin{aligned} K_\textrm{ext} = \frac{6\pi (1+\rho _{sa}) f_v {E(m_{\lambda} )}}{\lambda }. \end{aligned}$$

(1)

The extinction coefficient is obtained from extinction measurements, $\rho _{sa}$ is computed with the RDG theory, $f_v$ is determined using gravimetric analysis [25] (an ex situ technique) or by modulated LII [24]. Then, ${E(m_{\lambda} )}$ can be computed from Eq. (1).

More recently, Mannazhi et al. [26] have determined ${E(m_{\lambda} )}$ by comparing experimental fluence curves to fluence curves generated with an LII code. To avoid the high-temperature phenomena, they compared only the low fluence part of the experimental curves to multiple numerical curves generated using different values of ${E(m_{\lambda} )}$. The closest numerical curve to the experimental one gives an estimation of the absorption function. This method still requires measuring or assuming the gas temperature as an LII code is used.

Yon et al. [16] have recently presented a new technique to characterise soot maturity. It uses line-of-sight-attenuation (LOSA) and flame emission measurements at multiple wavelengths. Flame temperature is obtained with two-colour pyrometry or from absorption/emission measurements. Flame temperature and emission measurements permit computing the ratio of ${E(m_{\lambda} )}$ for two $\lambda$ values. A maturity coefficient $\beta _m$ is introduced and obtained by fitting the ratios of ${E(m_{\lambda} )}$ considering a power law: ${E(m_{\lambda} )} = \lambda ^{-\beta _m}$. $\beta _m=0$ corresponds to totally mature soot (no spectral dependence of ${E(m_{\lambda} )}$), while higher $\beta _m$ values are obtained for less mature soot particles that show a spectral dependency for ${E(m_{\lambda} )}$. Then, if soot particles are supposed to be composed of organic and graphite carbon only, results of a previous work of Bescond et al. [21] are used to directly link the determined value of $\beta _m$ to the organic content of the soot and to the absolute value of ${E(m_{\lambda} )}$ at a given wavelength.

In line with these works, a new in situ approach for the estimation of ${E(m_{\lambda} )}$ is proposed: the separated pulse LII technique (SP-LII). This approach proposes to retrieve the ratio $\frac{{E(m_{\lambda} )}}{\rho c}$ and the gas temperature $T_0$ from two consecutive single shots experiments. By assuming $\rho c$, it is then possible to retrieve the absolute value of ${E(m_{\lambda} )}$. These quantities are computed from the measurements of two peak temperatures of soot particles that are heated by laser pulses at two different fluences. The advantages of this approach are multiple. First, it is directly applicable in flames; thus, it can be seen as in situ. Then, it is theoretically applicable to turbulent flames. In addition, it does not require any prior estimation or assumption for the gas temperature; thus, it relies only on LII experiments. This is especially important in turbulent flames as the gas temperature may see important variations in time for a specific spatial location. Also, as it is an LII-based technique, soot volume fraction can be estimated with calibrated LII or AC-LII. In addition, if measurements are time-resolved, soot primary particle diameter can be estimated by fitting the decay of the LII signals [27]. Finally, it has the potential to be applied to 2D visualisation of the spatial evolution of ${E(m_{\lambda} )}$ in flames.

The SP-LII technique is of great interest as the spatially resolved determination of ${E(m_{\lambda} )}$ would improve the spatial estimations of the soot volume fraction while providing complementary information on soot maturity.

This paper is structured as follows. First, Sect. 2 presents the LII numerical code used. The experimental setup used for the proof-of-concept of the SP-LII technique applied to laminar flame is then presented in Sect. 3. The theoretical framework for the technique and two methods to retrieve ${E(m_{\lambda} )}$ and $T_0$ from LII signals are presented in Sect. 4. A theoretical evaluation of the technique is presented in Sect. 5, where the technique’s performance and robustness are quantified by relying on numerical synthesised signals from the LII code. The feasibility of the SP-LII is proven by considering a laminar diffusion methane/air flame in Sect. 6. Finally, Sect. 7 focuses on the theoretical extension of the technique to turbulent flame.

2 LII modelling

The laser-induced incandescence (LII) diagnostic tool consists of heating soot particles to high temperatures ($\sim$2500–4500 K) using a pulsed laser. The laser-heated particles emit considerably more radiative energy than the non-laser-heated ones, making LII suitable for studying soot particles in flames. The interest of LII is that multiple information can be gained by looking at the peak and temporal evolution of the intensity radiated by the soot particles. Numerous models to describe the LII process exist in the literature [28]. In the following, the models retained in this work are quickly summarised.

2.1 Description of the LII code

The energy equation

The LII code used in this work reproduces the heating by a laser pulse of a monodisperse population of non-aggregated spherical soot particles. It solves the energy conservation equation for the internal energy U, where only the most commonly accepted loss terms (radiation, conduction and sublimation) are considered:

$$\begin{aligned} \frac{\textrm{d} U}{\textrm{d} t}=\dot{Q}_\textrm{abs}-\dot{Q}_{ \textrm{cond }}-\dot{Q}_{ \textrm{rad }}-\dot{Q}_{ \textrm{sub }}, \end{aligned}$$

(2)

where $\dot{Q}_\textrm{abs}$ is the thermal power absorbed by the soot particles, $\dot{Q}_\textrm{cond}$, $\dot{Q}_{sub}$ and $\dot{Q}_\textrm{rad}$ are the power lost by the soot particles by conduction, sublimation and radiation, respectively. The internal energy of the particle U can be expressed as $U=\frac{\pi d_p^3}{6} \rho cT_p$ for a spherical particle of diameter $d_p$, density $\rho$, specific heat c and at temperature $T_p$. The density is one of the input parameters of the LII code and is constant while the specific heat is temperature dependent. Its expression comes from [29].

Absorption term

The absorbed power is given by:

$$\begin{aligned} \dot{Q}_\textrm{abs}=\sigma _\textrm{abs} \cdot \dot{Q}_\textrm{laser}(t), \end{aligned}$$

(3)

where $\sigma _\textrm{abs}$ is the absorption cross-section and $\dot{Q}_\textrm{laser}(t)$ is the instantaneous surface power of the laser pulse verifying: $\int _{t_0}^{t_0 + \Delta t_{pulse}} \dot{Q}_\textrm{laser}(t)\textrm{d}t = F$, F being the laser fluence, $t_0$ is the beginning of the laser pulse and $\Delta t_{pulse}$ is the pulse’s duration.

For a laser wavelength $\lambda _\textrm{laser}$ of 1064 nm, and for typical soot primary particle diameter of 10–50 nm, the size parameter is $x = \frac{\pi d_p}{\lambda _\textrm{laser}}<<1$. Thus, the absorption behaviour can be described by the Rayleigh approximation. For a spherical particle of geometric cross-section $A_p = \frac{\pi d_p^{2}}{4}$, the Rayleigh approximation gives an emissivity $\epsilon = \frac{4\pi d_p E(m_{\lambda })}{\lambda _\textrm{laser}}$. The absorption cross-section is given by:

$$\begin{aligned} \sigma _{a b s}=\epsilon A_{p}=\frac{\pi ^{2} d_{p}^{3} E(m_{\lambda })}{\lambda _{ {laser }}}. \end{aligned}$$

(4)

Thus, Eq. (3) can be rewritten as:

$$\begin{aligned} \dot{Q}_{a b s}=\frac{\pi ^{2} d_{p}^{3} E(m_{\lambda })}{\lambda _{ {laser }}} \cdot \dot{Q}_{ {laser }}(t). \end{aligned}$$

(5)

It should be noted that in the Rayleigh regime, the absorption of the soot particles is volumetric and not proportional to the surface area. Also, as in this paper $E(m_{\lambda })$ always refers to the absorption function at the laser wavelength, $E(m_{\lambda _\textrm{laser}})$ is replaced by ${E(m_{\lambda} )}$ to have a more compact notation.

Conduction term

A free molecular regime is assumed to describe the conduction term:

$$\begin{aligned} \dot{Q}_{ {cond }}=\frac{\alpha \pi d_{p}^{2} P}{8} \sqrt{\frac{8 R T_{0}}{\pi W_{g a s}}} \frac{\gamma ^{*}+1}{\gamma ^{*}-1}\left( \frac{T_{p}}{T_{0}}-1\right) , \end{aligned}$$

(6)

where the thermal accommodation coefficient $\alpha$ is an input parameter of the LII code. R is the universal gas constant, P is the ambient gas pressure, $W_\textrm{gas}$ is the average gas molar mass, and $\gamma ^*$ represents an averaged value of the gas specific heat ratio $\gamma$ between the temperature of the gas $T_0$ and of the particle $T_p$. The gas is supposed to have the properties of nitrogen. The soot temperature before the laser pulse is supposed to be equal to the gas temperature $T_0$.

Radiative term

The expression of the radiation losses is the same as in [30] and is given by:

$$\begin{aligned} \dot{Q}_\textrm{rad} = 8 \pi ^{3} d_{p}^{3} E(m_{\lambda }) \frac{(k_B T_p)^5}{h^4 c_\textrm{light}^3} \int _{0}^{\infty } \frac{t^{4}}{e^{t}-1} \textrm{d} t, \end{aligned}$$

(7)

where $k_B$ is the Boltzmann constant, $c_\textrm{light}$ is the light velocity and $\int _{0}^{\infty } \frac{t^{4}}{e^{t}-1} \textrm{d}t = 24.886$.

Sublimation term

The sublimation term is given by:

$$\begin{aligned} \begin{array}{l} \dot{Q}_\textrm{sub}=\frac{\Delta H_\textrm{vs}}{W_\textrm{vs}} J_\textrm{sub} \\ J_\textrm{sub}=\frac{\textrm{d} M}{\textrm{d} t}=\frac{\pi d_{p}^{2} W_\textrm{vs}}{N_\textrm{Av}} \frac{1}{\frac{1}{N_{C}}+\frac{1}{N_\textrm{FM}}}, \end{array} \end{aligned}$$

(8)

where the continuum flux term is $N_{C}=\frac{2 P_\textrm{vs} a_{d i f f}}{k_{B} T_{p} d_{p}}$, with $a_{d i f f}=\frac{f k_{B} T_{p}}{4 \sigma (W_\textrm{vs}) P} \sqrt{\frac{R T_{p}}{\pi W_\textrm{vs}}}$, $f=\frac{9 \gamma -5}{4}$, and the free molecular flux term is: $N_{F M}=\frac{\beta P_\textrm{vs}}{k_{B} T_{p}} \sqrt{\frac{R T_{p}}{2 \pi M_\textrm{vs}}}$. $\Delta H_\textrm{vs}$, $W_\textrm{vs}$, and $P_\textrm{vs}$ are, respectively, the average enthalpy of formation, the molar mass and the partial pressure of sublimed carbon clusters. $\sigma$ is an average molecular cross-section for subliming species that depends on $W_\textrm{vs}$. The mass accommodation coefficient $\beta$ is an input parameter of the LII code.

2.2 Reference input parameters

The LII code requires several input parameters: ${E(m_{\lambda} )}$, $T_0$, F, $\rho$, $d_p$, $\alpha$, and $\beta$. These parameters represent either experimental inputs (F), unknown quantities to be determined by the SP-LII technique (${E(m_{\lambda} )}$, $T_0$), soot properties ($\rho$, $d_p$) or modelling parameters ($\alpha$, $\beta$). The selected reference values for these parameters are gathered in Table 1. Two reference fluences $F_1$ and $F_2$ are given as the SP-LII requires two pulses at different fluences. The reference peak temperatures are also given in Table 1. They correspond to the peak temperatures $T_{M_1}$ and $T_{M_2}$ obtained with the LII code with the reference inputs. To simplify notation, in the following, the mathematical set $\Omega _\textrm{ref}$ will refer to ${\Omega _\textrm{ref} = \left\{ F_{1_\textrm{ref}}, F_{2_\textrm{ref}}, \rho _\textrm{ref}, d_{p_\textrm{ref}}, \alpha _\textrm{ref}, \beta _\textrm{ref} \right\} }$.

Commonly used values for $\alpha$ and $\beta$ are retained: 0.3 and 1, respectively [28]. It has to be noted that $\beta$ is set to the maximum possible value. This is likely to overestimate the sublimation level, representing a worst case scenario. The reference fluences are selected to limit sublimation as classically done for LII measurements for the estimation of ${E(m_{\lambda} )}$. The other reference parameters are selected to be representative of soot particles in flames in standard conditions. They are chosen not to be on the construction point of the look-up table presented in Sect. 4.3.

Table 1 Reference input parameters for the LII code and reference peak temperatures extracted from the simulations done with the reference input parameters

2.3 Utilisation of the LII code

The role of the LII code introduced in this section is triple:

• 1. Introduce theoretical behaviours to illustrate the principle of the SP-LII technique (Sect. 4.1).

• 2. Construct a look-up table that can be used to determine ${E(m_{\lambda} )}$ and $T_0$ from experimental data (Sect. 4.3).

• 3. Evaluate a priori the performance and robustness of the SP-LII technique (Sect. 5).

3 Experimental method

3.1 Experimental setup

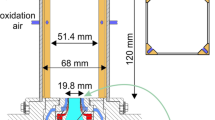
The configuration considered to prove the feasibility of the SP-LII technique is a Yale diffusion co-flow burner [31] mounted on a 3-axis translation stage. The methane is injected through the central fuel injector of $\sim$3.9 mm inner diameter. The flame is stabilised with an air co-flow flowing through a porous surface of 4.8 mm inner diameter and 49.5 mm outer diameter surrounding the injector. Mass flow controllers impose methane and air mass flow rates to 0.20 and 30 ln.min$^{-1}$ (0$^\circ$ C and 1 atm), respectively. The obtained flame is a stabilised $\sim$4 cm laminar diffusion flame (Fig. 1a). The experimental setup is presented in Fig. 1b. The laser source is a Powerlite Continuum laser, operating at 1064 nm, with an FWHM duration of $\sim$8 ns. A laser attenuator composed of a half-wave plate and two polarisers allows varying the laser beam’s fluence. A 1 mm square aperture selects the most uniform part of the laser beam. A lens (f = 300 mm) relays the image of this aperture to form a nearly top-hat laser beam above the burner in the flame, visualised in Fig. 2. The laser pulse’s energy is measured with an energy measurer (Gentec-EO QE25LP-S-MB-D0). The LII signal is collected at 90$^\circ$ from the laser beam. The achromatic lenses $\text {L}_1$ and $\text {L}_2$ of the collection system have a focal length of, respectively, $f_1$ = 150 mm and $f_2$ = 200 mm. The signal is focused on a 500 $\mu$m diameter pinhole, resulting in a spatial resolution of 375 $\mu$m. A dichroic mirror (Semrock FF605-Di02-25x36) with a cutoff wavelength of 605 nm separates the radiations according to their wavelength. Wavelengths below 605 nm go through the bandpass filter $\text {B}_1$, centred on 578 nm (Edmund optics 87766) before being collected by one of the two HAMAMATSU R2257 photomultiplier tubes (PMT). Higher wavelengths go through the bandpass filter $\text {B}_2$, centred on 716 nm (Edmund optics 67053) and are collected by the second PMT. After crossing the flame, the laser beam is collected by a photodetector (DET10A2) to monitor the laser energy stability and to trigger the signal acquisition with an 8-bit Lecroy WS434 oscilloscope. As the flame is laminar and steady, the samples are averaged over 700 single shots to ensure a good signal-to-noise ratio (SNR). The flame background is subtracted from the LII signal. The system is calibrated using a calibrated integrating sphere (OL-455-2) placed at the flame’s location.

Fig. 1

(a) Image of the CH4/air flame stabilised on the Yale diffusion burner. (b) Scheme of the LII experimental bench

Fig. 2

Top left: top-hat profile averaged over 50 laser shots, colourised by counts on the CMOS sensor of the beam profiler (Gentec-EO BEAMAGE-4 M). Top right: horizontal summation of the CMOS counts. Bottom left: vertical summation of the CMOS counts. Bottom right: occurrences of the counts in the top hat

3.2 2C-LII pyrometry

The soot particles’ peak temperature is computed by 2C-LII pyrometry [3, 10, 12] via:

$$\begin{aligned} T_M = \frac{h c_\textrm{light}}{k_B} \left( \frac{1}{\lambda _2} - \frac{1}{\lambda _1} \right) \frac{1}{\ln \left( \frac{S_{{LII}_{\lambda _1}}}{S_{LII_{\lambda _2}}} \frac{1}{R_{12}} {\left( \frac{\lambda _1}{\lambda _2} \right) }^6 \frac{\Delta \lambda _2}{\Delta \lambda _1} C_\textrm{calib}\right) }, \end{aligned}$$

(9)

where h and $k_B$ are the constants of Planck and Boltzmann, respectively. $\lambda _1$ = 578 nm and $\lambda _2$ = 716 nm are the two central collection wavelengths of the collection system, $\Delta \lambda _1$ and $\Delta \lambda _2$ are the widths of the collection windows. $\frac{S_{{LII}_{\lambda _1}}}{S_{LII_{\lambda _2}}}$ is the ratio of the maximum of the LII signals detected at wavelengths $\lambda _1$ and $\lambda _2$, and $R_{12} = \frac{E(m_{\lambda _1})}{E(m_{\lambda _2})}$ is the ratio of the absorption function at $\lambda _1$ and $\lambda _2$. $C_\textrm{calib}$ is a calibration constant that depends on the collection system.

In this work, the ratio $R_{12}$ is assumed to be unity. This assumption is expected not to significantly affect the conclusion obtained on this work.

Using the technique developed by Therssen et al. [32], multiple authors studied this ratio at 1064 and 532 nm in different flames and at different heights above the burner (HAB) [13, 15, 32,33,34]. Except for [34], which studied a low-pressure flame, they all found values close to 1 with a maximum of 15% difference from this value, and with a weak evolution along the HAB traducing a weak spectral evolution of ${E(m_{\lambda} )}$ with maturity. By studying multiple flame locations in a laminar diffusion flame, Snelling et al. [35] bounded the spectral dependency of ${E(m_{\lambda} )}$ by a maximum of a 20% variation between 500 and 945 nm. Finally, one of the conclusions of the reviewing work of Liu et al. [17] is that for mature soot, the absorption function shows negligible spectral dependence in the visible and near-infrared. In regard to these results, the spectral variation of the absorption function between 578 and 716 nm should be minimal, even for less mature ones. Despite this, other values for the ratio $R_{12}$ are considered for the quantification of uncertainties presented in Sect. 6.3. To explore more broadly the potential effect of a spectral dependence of ${E(m_{\lambda} )}$ on this wavelength range, the authors provide the experimental database of the displayed results as supplementary material.

4 The separated pulses laser-induced incandescence technique

4.1 Principle of the SP-LII technique

The peak (or maximum) temperature $T_M$ reached by the soot particles after a laser pulse depends on the energy quantity available (i.e. the laser pulse’s fluence), but also on the particles’ capacity to absorb it, i.e. its absorption function. This fact is illustrated by Fig. 3a in which the soot peak temperature is calculated with the LII code with parameters $\left\{ \ {T_0}_\textrm{ref}, \ {d_p}_\textrm{ref}, \ \rho _\textrm{ref}, \ \alpha _\textrm{ref}, \ \beta _\textrm{ref} \right\}$ and with various values of laser fluences and for three values of ${E(m_{\lambda} )}$. $T_M$ appears to be linearly proportional to F for low fluences values. This linear behaviour is lost for fluences high enough to induce sublimation. In the specific conditions of these simulations, the temperature for which sublimation starts to play a role is $\sim$ 3500 K. Looking at Fig. 3a, it is clear that the slope of the linear part of the peak temperature curves depends on ${E(m_{\lambda} )}$.

Figure 3b represents the laser fluence dependence of $T_M$ for four sizes of soot primary particle diameter with input parameters $\left\{ {E(m_{\lambda} )}_\textrm{ref},\ {T_0}_\textrm{ref}, \ \rho _\textrm{ref}, \ \alpha _\textrm{ref}, \ \beta _\textrm{ref} \right\}$ and with various values of laser fluences. The curves are almost superimposed for diameters larger than 10 nm, meaning that the peak temperature is mostly independent of the soot primary particle diameter. However, this is not true anymore for the smallest particles as the curve for $d_p=1$ nm is clearly detached from the others. This is due to the fact that small particles are characterised by a larger surface-to-volume ratio compared to big particles, inducing more significant conduction losses during laser heating.

Fig. 3

(a) Peak temperature of the soot particles as a function of laser fluence for three different values of the absorption function: ${E(m_{\lambda} )}$ = 0.2 (green), 0.3 (blue) and 0.4 (red). The dashed lines represent the initial slope of the curves. The horizontal black line represents the separation between the linear and sublimation regimes. (b) Peak temperature of the soot particles as a function of laser fluence for four different values of soot primary particle diameter: $d_p$ = 1 (green), 10 (blue), 20 (red) and 50 nm (black)

The SP-LII technique is based on the observation that once the soot density and specific heat are given, the peak temperature is mainly governed by ${E(m_{\lambda} )}$ while being relatively independent of other soot properties such as the primary particle diameter at least for $d_p>\sim 10$ nm. Therefore, taking advantage of the linear evolution of $T_M$ with fluence at a fixed ${E(m_{\lambda} )}$, the SP-LII technique proposes to retrieve the absorption function ${E(m_{\lambda} )}$ and the gas temperature $T_0$ from two measurements of the peak temperature $(T_{M_1}$, $T_{M_2})$, corresponding to two different laser fluences $F_1$ and $F_2$.

Two methods to compute ${E(m_{\lambda} )}$ and $T_0$ from $T_{M_1}$ and $T_{M_2}$ are presented and compared in this work. The first approach, called the “absorption model” (AM), is based on the resolution of Eq. (2) when all loss terms are neglected. The second strategy uses a look-up table (LUT) in which are stored values of $T_M$ obtained by solving the entire energy equation with the LII code for multiple values of the input parameters.

4.2 The absorption model

Derivation of the equations

For laser fluences low enough to avoid sublimation, the thermal losses occurring during the laser pulse due to radiation and conduction are expected to be small. Thus, the radiation, conduction and sublimation terms in Eq. (2) can be neglected. The only terms remaining are the variation of the internal energy and the absorbed power. The integration over the pulse duration of this reduced energy equation gives:

$$\begin{aligned} \int _{T_0}^{T_M} \frac{\pi d_{p}^{3}}{6} \rho c d T_p = \int _{t_{0}}^{t_{0}+\Delta t_{p u l s e}} \pi ^{2} d_{p}^{3} \frac{E(m_{\lambda })}{\lambda _\textrm{laser}} \dot{Q}_\textrm{laser}(t) \textrm{d}t, \end{aligned}$$

(10)

which reduces to:

$$\begin{aligned} \frac{E(m_{\lambda })}{\overline{\rho c}}=\frac{\lambda _{ {laser }}}{6 \pi } \frac{T_{M}-T_{0}}{F}, \end{aligned}$$

(11)

where $\overline{\rho c}=\frac{1}{T_{M}-T_{0}} \int _{T_{0}}^{T_{M}} \rho c\ dT$ accounts for the temperature dependency of the product of density and specific heat.

Equation 11 links $T_0$, $T_M$ and F to $E(m_{\lambda })$. Thus, considering two laser pulses at different fluences $F_1 \ne F_2$, it is possible to derive the following system of two equations:

$$\begin{aligned} \begin{array}{c} E(m_{\lambda })=\frac{\lambda _{ {laser }}}{6 \pi }(T_{M_2}-T_{M_1})(\frac{F_{2}}{\overline{\rho c_{2}}}-\frac{F_{1}}{\overline{\rho c_{1}}})^{-1}\\ \\ T_{0}=(\frac{F_{2}}{\overline{\rho c_{2}}} T_{M_1}-\frac{F_{1}}{\overline{\rho c_{1}}} T_{M_2})(\frac{F_{2}}{\overline{\rho c_{2}}}-\frac{F_{1}}{\overline{\rho c_{1}}})^{-1}. \end{array} \end{aligned}$$

(12)

Using Eq. (12), $E(m_{\lambda })$ at the laser wavelength and $T_0$ can be computed from the experimental data $([F_1, T_{M_1}], [F_2, T_{M_2}])$ once the soot particles’ density and specific heat are known. Equation 12 does not depend on $d_p$ because the two remaining terms in the energy equation are volumetric, leading $d_p^3$ to cancel out. Thus, there is no need to determine values for $d_p$, reducing the need for experimental processes. The effect of the absence of sensitivity to $d_p$ for the smaller particles will be investigated later in Sect. 5.2.

Validity of the assumption neglecting the losses

${E(m_{\lambda} )}$ and $T_0$ are computed with the AM method neglecting the radiation, conduction and sublimation processes. To quantify the impact of this simplification, simulations have been run by deactivating each loss term in the LII code one by one and using $\Omega _\textrm{ref} / \left\{ {F_2}_\textrm{ref} \right\}$. The peak temperatures are extracted from these simulations. For a given $F_2$ value, ${E(m_{\lambda} )}$ and $T_0$ are computed with the AM method from the obtained value for $T_{M_1}$ and $T_{M_2}$ and are compared to ${E(m_{\lambda} )}_\textrm{ref}$ and ${T_0}_\textrm{ref}$. Different values of $F_2$ are investigated, and the deviations from the reference quantities are presented in Fig. 4. When the simulations are run without the loss terms, the values of ${E(m_{\lambda} )}_\textrm{ref}$ and ${T_0}_\textrm{ref}$ are exactly recovered, ensuring that the AM is not biased. When only radiation is considered, no significant deviation from the reference ${E(m_{\lambda} )}_\textrm{ref}$ and ${T_0}_\textrm{ref}$ is seen ($<1\%$), confirming that radiation has only a low impact on the results. The addition of the conduction terms in the energy equation solved by the LII code brings a small deviation from the ${E(m_{\lambda} )}_\textrm{ref}$ ($\approx 2 \%$ for this case), and no visible deviation for ${T_0}_\textrm{ref}$. It has been verified that a higher value of $\alpha$ would have increased the deviation from ${E(m_{\lambda} )}_\textrm{ref}$ but stays of a few per cent. Finally, when sublimation is considered in the LII code, no visible deviation is added for laser fluences below 100 mJ/cm$^2$. Above this value, the deviations of both ${E(m_{\lambda} )}$ and $T_0$ largely increase with fluence. The $\beta$ value, deliberately selected high, explains why sublimation has such a strong effect even for moderate fluences.

Fig. 4

Estimations with the AM method of deviations of ${E(m_{\lambda} )}$ (left, in blue) and $T_0$ (right, in pink) as a function of $F_2$ when different loss terms are considered in Eq. (2): no losses ($\diamond$), radiation ($\times$), radiation and conduction ($\bullet$), and radiation, conduction and sublimation (solid lines)

In conclusion, these results confirm the legitimacy of neglecting the radiation term. It also points out that the neglected conduction term introduces a small deviation from the reference values, independently of the value of the laser fluence. More importantly, it shows that the AM method is expected to perform well only for laser fluences that do not induce strong sublimation of the soot particles. In the following, the simulations are run with all loss terms activated in the LII code.

4.3 The look-up table

The absorption model neglects losses. Therefore, its accuracy is reduced when losses become significant. Thus, a second way to determine ${E(m_{\lambda} )}$ and $T_0$ from two peak temperatures at two fluences is proposed here: the look-up table (LUT) method. The LUT method is based on a multi-entry table storing $T_M$ values. This LUT has to be generated only once using an LII code before exploiting any experimental results. Each entry of the LUT corresponds to an input parameter of the LII code: ${E(m_{\lambda} )}$, $T_0$, F, $d_p$, $\rho$, $\alpha$, and $\beta$ (the LUT is a table of dimension 7). The values of the parameters used in this work are gathered in Table 2. The LUT is generated by extracting $T_M$ from simulations obtained with the LII code for each possible combination of the input parameters.

Table 2 Values of the input parameters of the LII code used to create the look-up table

Once the LUT is generated, ${E(m_{\lambda} )}$ and $T_0$ can be retrieved with the following protocol:

• $d_p$, $\rho$, $\alpha$, and $\beta$ have to be set (using experimental measurements, literature reviews or best guess).

• Two couples of fluence and peak temperature have to be experimentally determined: a first experiment gives $[F_1, {T_{M_1}}]$ and a second one gives $[F_2, {T_{M_2}}]$.

• The knowledge of $d_p$, $\rho$, $\alpha$, $\beta$, and $F_1$ permits the extraction from the LUT of a sub-table of dimension two in which are stored $T_M$ values. The dimensions of the sub-table correspond to the entries of the LUT that are not set: ${E(m_{\lambda} )}$ and $T_0$. A second sub-table of $T_M$ can be extracted using $F_2$ instead of $F_1$. These two sub-tables are called $\Psi _1$ and $\Psi _2$.

• For each element in $\Psi _1$ and $\Psi _2$, the table $\Xi$ of dimension two is computed:

$$\begin{aligned} \Xi ({E{(m_\lambda )}_{}, T_{0_{}}} )= \vert \Psi _1({{E(m_{\lambda} )}_{}, T_{0_{}}} )- {T_{M_1}} \vert + \vert \Psi _2({{E(m_{\lambda} )}_{}, T_{0_{}}}) - {T_{M_2}} \vert . \end{aligned}$$

(13)

• The most probable couple ${E(m_{\lambda} )}$ and $T_0$ is obtained by choosing the values of ${E(m_{\lambda} )}$ and $T_0$ that minimise $\Xi$.

Consistency of the LUT method

The LUT method selects ${E(m_{\lambda} )}$ and $T_0$ as the one minimising Eq. (13). One can ask if the selected values are really representative of the true values for the absorption function and the gas temperature. In order to verify the consistency of the LUT method, the reference input parameters $\Omega _\textrm{ref}$ with $T_{{M_1}_\textrm{ref}}$ and $T_{{M_2}_\textrm{ref}}$ are retained here. The expected values for the absorption function and the gas temperature are ${E(m_{\lambda} )}_\textrm{ref}$ and $T_{0_\textrm{ref}}$. It has to be noted that, for the reference case, all entries of the LUT but, the fluences, $\alpha _\textrm{ref}$ and $\beta _\textrm{ref}$ are off-grid: i.e. the parameters of $\Omega _\textrm{ref}$ are not parameters used for the generation of the LUT. This has been done to test the robustness of the LUT method.

Fig. 5 shows the computed inverse of $\Xi$ (high values means low errors) versus ${E(m_{\lambda} )}$ and $T_0$. The region of lower error is narrow, and the global minimum is found for ${E(m_{\lambda} )}_\textrm{ref}$ and $T_{0_\textrm{ref}}$, proving the validity of the LUT method (it has been tested in multiples other conditions). It can be seen that the low error region corresponds to the crossing of two diagonals represented by the white dashed lines. The diagonals correspond to the minimum error for each pulse considered alone, and their slope depends on the pulse’s fluence. The region of low errors narrows when the difference in fluence pulse increases and widens when $F_1$ approaches $F_2$. Thus, to increase the accuracy of the LUT method pulse, $F_1$ and $F_2$ should be as spread as possible.

Fig. 5

Inverse of $\Xi$ (define by Eq. (13)) versus ${E(m_{\lambda} )}$ and $T_0$. The white dashed lines help to visualise the low error regions for the two pulses considered alone

5 Theoretical evaluation of the SP-LII technique

5.1 Procedure for the theoretical study of the SP-LII technique

In this section, the SP-LII was tested with numerically synthesised signals. Thus, the peak temperatures $T_{M_1}$ and $T_{M_2}$ were not experimentally determined temperatures but come from simulations. Owing to this, the performance of the SP-LII could be analysed, and an uncertainty analysis of the AM and LUT methods could be performed as the output of the methods should be the ones given as input of the LII code: ${E(m_{\lambda} )}_\textrm{ref}$ and $T_{0_\textrm{ref}}$.

The protocol used in this section is schematically represented in Fig. 6. To compact notations, the $\Omega$ sets contain: $\Omega = \left\{ F_1, F_2, \rho , d_p, \alpha , \beta \right\}$. The quantities ${E(m_{\lambda} )}_\textrm{ref}$, $T_{0_\textrm{ref}}$ and $\Omega ^\textrm{SIM}$ constitute the inputs of the LII code. $T_{M_1}$ and $T_{M_2}$ are extracted from the simulations, and are considered as inputs for the AM and LUT methods along with the set $\Omega ^{PP}$ to obtain ${E(m_{\lambda} )}_\textrm{post}$ and ${T_0}_\textrm{post}$ where $_\textrm{post}$ is the post-processing method, either AM or LUT. These values are compared to the reference ${E(m_{\lambda} )}_\textrm{ref}$ and ${T_0}_\textrm{ref}$ values. The superscript $^\textrm{SIM}$ refers to the parameters used as input of the LII code, and $^{PP}$ refers to the input parameters of the post-processing of the AM and LUT methods.

The performance of the SP-LII technique coupled with AM or LUT post-processing methods will be first evaluated in Sect. 5.2 as a function of the laser fluence or of the soot properties assuming that all parameters are well-known, i.e. $\Omega ^{PP} = \Omega ^\textrm{SIM}$. Then, in Sect. 5.3, the parameters used for the post-processing are taken to be different from those of the simulations (i.e. $\Omega ^\textrm{SIM} \ne \Omega ^{PP}$) in order to quantify the impact of uncertainties in these parameters on the performance of the methods. Numerous works [36,37,38,39,40] numerically treat the quantification of uncertainties of LII-based techniques by combining multiple sources of errors. In this work, a “one parameter at a time” procedure is used to quantify the errors on both ${E(m_{\lambda} )}$ and $T_0$ associated with uncertainties on multiple LII parameters and to erroneous estimations of the soot peak temperature. The advantage of this approach is that it gives a precise knowledge about the direct impact: amplitude of overestimation/underestimation of ${E(m_{\lambda} )}$ and $T_0$ for each of the parameters over their studied range.

Fig. 6

Scheme describing the procedure for the SP-LII theoretical analysis. The $\Omega$ sets contain: $\Omega = \left\{ F_1, F_2, \rho , d_p, \alpha , \beta \right\}$

5.2 Performance of the technique

The performance of the AM and LUT methods are evaluated in this section by considering $\Omega ^\textrm{SIM} = \Omega ^{PP}$: the same inputs used for the generation of $T_{M_1}$ and $T_{M_2}$ are used for the AM and LUT post-processing.

In the following, the performance will be evaluated as a function of $F_2$ and $d_p$.

$\mathbf {2\textrm{nd}}$ pulse fluence: $\mathbf {F_2}$

Simulations are run for $\Omega ^\textrm{SIM} / \left\{ {F_1}^\textrm{SIM},\ {F_2}^\textrm{SIM} \right\} = \Omega _\textrm{ref} / \left\{ {F_1}_\textrm{ref},\ {F_2}_\textrm{ref} \right\}$. $F_1^\textrm{SIM} = F_1$ is set to either 50, 100 or 150 mJ/cm$^2$, $F_2^\textrm{SIM} = F_2$ is varied from 25 to 225 mJ/cm$^2$. Here, $\Omega ^\textrm{SIM} = \Omega ^{PP}$. Figures 7a and 7b express the deviations of ${E(m_{\lambda} )}_\textrm{post}$ and ${T_0}_\textrm{post}$ from ${E(m_{\lambda} )}_\textrm{ref}$ and ${T_0}_\textrm{ref}$ for both the AM and LUT methods. The breaks in the curves correspond to the case $F_1 = F_2$ for which the SP-LII technique cannot work.

As discussed in Sect. 4.2, the losses cause the AM method to underestimate ${E(m_{\lambda} )}$ and to overestimate $T_0$. Sublimation starts to have a visible impact for laser fluences higher than 100 mJ/cm$^2$. When the laser fluence of at least one of the pulses approaches 150 mJ/cm$^2$, the deviations of the AM method exceed $20\%$ and $8\%$ for ${E(m_{\lambda} )}$ and $T_0$, respectively, and continue to increase rapidly for higher fluences. It is reminded that sublimation has a strong effect on the AM method even at moderate fluences since the worst case ($\beta _\textrm{ref}=1$) has been retained here.

With the LUT method, the deviations stay near $5 \%$. These low errors are mostly due to interpolation errors that may be reduced by refining the LUT database. It has to be pointed out that such good results are obtained because the same sublimation model and mass accommodation coefficient are used for both the data generation ($T_{M_1}$ and $T_{M_2}$), and the LUT generation, i.e. no uncertainties on the model are considered.

Fig. 7

Deviations of ${E(m_{\lambda} )}$ (figure a) and $T_0$ (figure b) obtained with the AM (solid lines) and the LUT method (dotted line) as a function of $F_2$. The symbols and colours correspond to different $F_1$: 50 (green $\times$), 100 (blue $\star$) and 150 mJ/cm$^2$ (red +)

Overall, sublimation significantly impacts the AM method and imposes an upper fluence limit. In practice, this upper limit can be experimentally determined from the break of linearity in the temperature fluence curves (see Fig. 3a). By contrast, the LUT method performs well for all fluence.

Soot primary particle diameter: $\mathbf {d_p}$

Here, simulations are run for $\Omega ^\textrm{SIM} / \left\{ {d_p}^\textrm{SIM} \right\} =\Omega _\textrm{ref} / \left\{ {d_p}_\textrm{ref} \right\}$ for $d_p$ values ranging from 1 to 41 nm, and $\Omega ^\textrm{SIM} = \Omega ^{PP}$. Figure 8 represents the deviation of ${E(m_{\lambda} )}$ and $T_0$ as a function of $d_p$ obtained with the AM and LUT methods. Estimation with the AM method worsens when $d_p$ decreases as already discussed in Fig. 3b. Thus, one should expect larger deviations when applying the AM method to small soot particles. Concerning the LUT, it has to be precise that the results of Fig. 8 for $d_p$ $\le$ 11 nm comes from a refined table with a 1 nm step, as the initial discretisation of 10 nm (see Table 2) was to rough for the smallest particle sizes and produced deviations exceeding 20% for ${E(m_{\lambda} )}$. This discretisation problem explains the $\sim$ 3% deviation in ${E(m_{\lambda} )}$ around $d_p$ = 15 nm. Apart from that, above $d_p$ = 20 nm, the deviations for both ${E(m_{\lambda} )}$ and $T_0$ are null. Thus, to minimise the deviations, the LUT table should be refined for small particles, while a rough discretisation is enough for larger particles. Concerning $T_0$, the deviation is always under 2.5%, both for the AM and the LUT methods, indicating that the gas temperature estimation is not really sensitive to the particle diameter.

Fig. 8

Deviations of ${E(m_{\lambda} )}$ (left axis, in blue) and $T_0$ (right axis, in pink) obtained with the AM (solid lines) and the LUT methods (dotted line) as a function of $d_p$

5.3 Uncertainty analysis

The uncertainty analysis aims to investigate the sensitivity of the SP-LII technique to the parameters contained in $\Omega$, as in practice, not all of them are known. For that, the parameters selected as input of the LII code are different from the ones used as inputs for the AM and LUT post-processing, i.e. $\Omega ^\textrm{SIM} \ne \Omega ^{PP}$ (see Fig. 6). The analysis is performed for $\rho$ for both the AM and LUT methods and for $d_p$, $\alpha$ and $\beta$ solely for the LUT method (as the AM is independent of these parameters).

Density

Here, $\Omega ^\textrm{SIM} = \Omega _\textrm{ref}$, ${E(m_{\lambda} )}$ and $T_0$ are computed using ${T_{M_1}}_\textrm{ref}$ and ${T_{M_2}}_\textrm{ref}$ and the reference parameters without $\rho _\textrm{ref}$: $\Omega ^{PP} / \left\{ \rho ^{PP} \right\} = \Omega _\textrm{ref} / \left\{ \rho _\textrm{ref} \right\}$. Instead, $\rho$ is varied from 1200 to 2100 kg/m$^3$, i.e. an error is intentionally introduced in the input of the post-processing). The resulting deviations from ${{E(m_{\lambda} )}}_\textrm{ref}$ and $T_{0_\textrm{ref}}$ are plotted in Fig. 9a.

With the AM method, the deviation of ${E(m_{\lambda} )}$ is linear with $\rho$ while the deviation on $T_0$ is independent of $\rho$. This can be explained by the weak temperature dependence of c in the LII code. Indeed, neglecting its temperature dependence allows rewriting Eq. (12) as

$$\begin{aligned} \begin{array}{c} \frac{{E(m_{\lambda} )}}{\rho c} = \frac{\lambda _\textrm{laser}}{6 \pi } \frac{T_{M_2} - T_{M_1}}{F_2 - F_1}\\ \\ T_{0}=\frac{F_2 T_{M_1}-F_1 T_{M_2}}{F_{2} - F_{1}}. \end{array} \end{aligned}$$

(14)

These new equations illustrate the fact that if $\rho c$ is temperature independent, the SP-LII technique retrieves the ratio $\frac{{E(m_{\lambda} )}}{\rho c}$ and not directly ${E(m_{\lambda} )}$, while $T_0$ becomes independent of $\rho$ and c. Thus, with the AM method, an error done on $\rho c$ of X% brings an error on ${E(m_{\lambda} )}$ of the same amount, while it does not directly impact $T_0$.

For the LUT post-processing, the deviation of ${E(m_{\lambda} )}$ still has a linear behaviour with the same slope as for the AM but with a different offset leading to better estimations. The oscillations seen for $T_0$ come from interpolation errors between the points of the look-up table. The vertical black dashed line in Fig. 9a represents the reference density $\rho _\textrm{ref} = 1950$ kg/m$^3$, a value for which no deviation should be seen. The not null deviations for this value for the AM come from the neglected losses (mainly conduction).

Soot primary particle diameter: $d_p$

The same procedure as for the density is applied here with $\Omega ^{PP} / \left\{ {d_p}^{PP} \right\} = \Omega _\textrm{ref} / \left\{ {d_p}_\textrm{ref} \right\}$ with $d_p$ varying from 1 to 41 nm. Figure 9b represents the deviation of ${E(m_{\lambda} )}_\textrm{LUT}$ and ${T_0}_\textrm{LUT}$ from ${E(m_{\lambda} )}_\textrm{ref}$ and ${T_0}_\textrm{ref}$. For comparison purposes, the solid lines give the deviations obtained with the AM post-processing, which is not sensitive to $d_p$. For the LUT, similarly to what has been done for Fig. 8, the refined table (with a 1 nm step) is used for $d_p \le$ 11 nm. The deviations of the LUT method on the range $d_p = 10-41$ nm are below 5% for ${E(m_{\lambda} )}$ and below 2% for $T_0$. For lower diameters, the deviation for ${E(m_{\lambda} )}$ increases with decreasing $d_p$ and reaches $\sim$ 35% for $d_p$ = 1 nm. This shows that with an incorrect assumption on $d_p$ ($d_p<10$ nm instead of 26 nm), the estimation of ${E(m_{\lambda} )}$ with the LUT method is worse than the one of the AM method. These results indicate that the experimental determination of $d_p$ is not mandatory in flame regions containing mainly soot particles of relatively large $d_p$, as a coarse estimation would be accurate enough ($\approx 10-40$ nm). On the contrary, in flame regions where smaller soot particles may be encountered (incipient or oxidised soot particles), a wrong assumption on $d_p$ would produce non-negligible errors (up to 35% in this example) in the estimation of ${E(m_{\lambda} )}$. The vertical black dashed line represents the reference diameter ${d_p}_\textrm{ref} = 26$ nm, a value for which no deviation should be seen. The not null deviations for this value for the AM come from the neglected losses.

Fig. 9

Deviations of ${E(m_{\lambda} )}$ (left axis, in blue) and $T_0$ (right axis, in pink) as a function of (a): the density and (b) the primary particle diameter used for the post-processing. Results obtained with the AM and LUT method are plotted with solid and dotted lines, respectively. The vertical black dashed lines represent the reference density (figure a) and reference primary particle diameter (figure b)

Thermal accommodation coefficient:

$\alpha$ In LII codes, conduction losses are governed by the thermal accommodation coefficient $\alpha$. In the literature, multiple values of $\alpha$ range from 0.23 to 0.9 [28] with values in general near 0.3 and almost always below 0.5. Thus, verifying the influence of an uncertainty of $\alpha$ on the SP-LII technique can be interesting. The same procedure as for $\rho$ and $d_p$ is now used for $\alpha$, the only difference being that the procedure is repeated for three different values of $d_p$ as it is expected that conclusions may differ regarding the soot primary particle diameters.

Here, $\Omega ^\textrm{SIM} / \left\{ {d_p}^\textrm{SIM} \right\} = \Omega _\textrm{ref} / \left\{ {d_p}_\textrm{ref} \right\}$, ${d_p}^\textrm{SIM}$ will take the values 1, 26 and 41 nm leading each time to different ${T_{M_1}}$ and ${T_{M_2}}$. $\Omega ^{PP} / \left\{ \alpha ^{PP} \right\} = \Omega _\textrm{ref} / \left\{ \alpha _\textrm{ref} \right\}$, and, $\alpha ^{PP}$ is varied from 0.2 to 0.5. The resulting deviations of ${E(m_{\lambda} )}_\textrm{LUT}$ and ${T_0}_\textrm{LUT}$ from ${{E(m_{\lambda} )}}_\textrm{ref}$ and ${T_0}_\textrm{ref}$ are plotted in Fig. 10. To limit confusion, the superscript $^\textrm{SIM}$ and $^{PP}$ are specified.

Whatever the thermal accommodation coefficient used for the post-processing, there is no notable difference in the deviations (below 4% and 2% for ${E(m_{\lambda} )}$ and $T_0$, respectively) for the two largest particles size considered here. Whereas assuming 0.2 or 0.5 for this coefficient induces up to 25% difference in the deviation of ${E(m_{\lambda} )}$ for the smallest particles’ size considered here. However, the determination of $T_0$ does not suffer much from uncertainties on $\alpha$ even for the smallest soot particles.

Fig. 10

Deviations of ${E(m_{\lambda} )}$ (left axis, in blue) and $T_0$ (right axis, in pink). The X-axis represents $\alpha ^{PP}$, the thermal accommodation coefficient used for the post-processing of the LUT method. The symbols differentiate the value of the soot primary particle diameter used for the data generation: $d_p^\textrm{SIM}$: 1 ($\diamond$), 26 ($\star$) and 41 nm ($\times$). The vertical black dashed line represents the reference thermal accommodation coefficient $\alpha _\textrm{ref} = 0.3$

Overall, the estimation of $T_0$ is not significantly affected by the uncertainty existing on $\alpha$. The same can be said for ${E(m_{\lambda} )}$ as long as the soot size is more than a few nanometres. Thus, in practice, it is not essential to precisely know $\alpha$ for the SP-LII technique.

Mass accommodation coefficient:

$\beta$ In the literature, uncertainties on $\beta$ are even higher than the ones encountered for $\alpha$. Values ranging from 0 to 1 can be found [28, 41]. This high spreading of $\beta$ values may indicate that the sublimation model does not represent well the actual physical processes. Leaving this last remark aside, the impact of uncertainty on $\beta$ is presented here.

The high uncertainty on the value of $\beta$ and its expected non-linear impact on ${E(m_{\lambda} )}_\textrm{LUT}$ and ${T_0}_\textrm{LUT}$ brings the necessity to adapt the previous procedure for the study of $\beta$. The set considered is $\Omega ^\textrm{SIM} / \left\{ \beta ^\textrm{SIM}, F_2^\textrm{SIM} \right\} = \Omega _\textrm{ref} / \left\{ {\beta }_\textrm{ref}, {F_2}_\textrm{ref} \right\}$, multiples values are considered for ${\beta }^\textrm{SIM}$ between 0 and 1.

$\Omega ^{PP} / \left\{ \beta ^{PP}, {F_2}^{PP} \right\} = \Omega _\textrm{ref} / \left\{ \beta _\textrm{ref}, {F_2}_\textrm{ref} \right\}$, and $\beta ^{PP}$ will take the values 0, 0.25, 0.5 and 1. The reference fluence $, {F_2}_\textrm{ref}$ is increased to ${F_2}_\textrm{ref}$ = 140 mJ/cm$^2$ = $F_2^\textrm{SIM}$ = $F_2^{PP}$ in order to have significant sublimation (see Fig. 7). The deviations are plotted in Fig. 11a and Fig. 11b as a function of $\beta ^\textrm{SIM}$ and for the four values of $\beta ^{PP}$ considered. To limit confusion, the superscript $^\textrm{SIM}$ and $^{PP}$ are specified. For comparison purposes, the solid black line represents the results obtained when using the AM method.

As expected, for $\beta ^{PP}=0$, the deviations obtained with the LUT and the AM methods are close because in this case, they both neglect sublimation. The remaining differences are explained by the conduction losses that are accounted for by the LUT method and its interpolation errors. It appears that when the pulses have low to moderate laser fluence ($F_1 = 50$ and $F_2 = 140$ mJ/cm$^2$), the lack of knowledge of $\beta$ can bring deviations as much as 20% for ${E(m_{\lambda} )}$ and 10% for $T_0$. Thus, an unfortunate hypothesis of $\beta$ can bring a worse estimation of ${E(m_{\lambda} )}$ and $T_0$ than simply using the AM method.

By comparing Fig. 11a with Fig. 11b, it can be seen that the deviations of $T_0$ are about half as large as those on ${E(m_{\lambda} )}$.

Fig. 11

Deviations of ${E(m_{\lambda} )}$ (figure a) and $T_0$ (figure b) as a function of $\beta ^\textrm{SIM}$: the mass accommodation coefficient used for the data generation. The deviations are represented for the AM and LUT methods in solid and dotted lines, respectively. The symbols differentiate the results of the LUT method obtained with the different assumptions on the value of $\beta ^{PP}$: 0 (black), 0.25 (red $\times$), 0.5 (green $\star$) and 1 (blue $\diamond$)

When working with laser fluences where little sublimation is to be expected, assuming $\beta \sim 0.2$ rather than higher values seems to limit the maximum error done on ${E(m_{\lambda} )}$ to ± 10% and ± 5% for $T_0$. In practice, the potential of the LUT method is limited by the lack of knowledge of $\beta$ and/or by the incorrect representation of the sublimation processes. This encourages working at laser fluences that do not trigger sublimation.

5.4 Error on peak temperatures estimation

The experimental determination of the soot temperature by two-colour LII pyrometry or by any other experimental technique is subjected to bias causing errors in the determination of $T_{M_1}$ and $T_{M_2}$. Two kinds of errors are investigated here: an overestimation of $T_{M_1}$ of 10%, and an overestimation of both $T_{M_1}$ and $T_{M_2}$ by 10%.

Looking at Eq. (14) for the AM method, and regarding what has been said in Sect. 4.3 about the uniqueness of solution for the LUT method, it is to be expected that the difference of fluence between the two pulses plays a role in the computed deviations of both ${E(m_{\lambda} )}$ and $T_0$. Thus, the procedure retained here is the following: simulations are performed with $\Omega ^\textrm{SIM} / \left\{ {F_2}^\textrm{SIM} \right\} = \Omega ^{PP}= \Omega _\textrm{ref} / \left\{ {F_2}_\textrm{ref} \right\}$, where $F_2^\textrm{SIM} = F_2$ is varied from 25 to 225 mJ/cm$^2$. The peak temperatures $T_{M_1}$ and $T_{M_2}$ are extracted from the simulations, and a 10% error is added on at least one of them to obtain $\widetilde{T_{M_1}}$ and $\widetilde{T_{M_2}}$. Finally, ${E(m_{\lambda} )}_\textrm{post}$ and ${T_0}_\textrm{post}$ are computed with both methods with these modified peak temperature $\widetilde{T_M}$ and with parameters $\Omega ^{PP} = \Omega ^\textrm{SIM}$. The procedure is illustrated in Fig. 12.

Fig. 12

Scheme describing the procedure for the analysis of the impact of peak temperature errors on the estimation of ${E(m_{\lambda} )}$ and $T_0$ with the SP-LII method. The sets $\Omega$ contain: $\Omega = \left\{ F_1, F_2, \rho , d_p, \alpha , \beta \right\}$

Figure 13a represents the deviation of ${E(m_{\lambda} )}$ and $T_0$ from ${E(m_{\lambda} )}_\textrm{ref}$ and ${T_0}_\textrm{ref}$ as a function of $F_2$ for $\widetilde{T_{M_1}}= 1.1\cdot T_{M_1}$ and $\widetilde{T_{M_2}}= T_{M_2}$. The deviations of ${E(m_{\lambda} )}$ and $T_0$ are significantly more important than the ones for uncertainties on $\rho$, $d_p$, $\alpha$ and $\beta$. With the AM method, when $F_2$ is approaching $F_1$, the deviation from the true value skyrockets because the denominators of Eq. (12) is low, so an error on $T_{M_1}$ has a larger importance than for higher fluence differences. The deviation is quite high for the highest laser fluences, mainly because of sublimation. For ${F_1}=50$ mJ/cm$^2$, the optimum laser fluence for $F_2$ is near 125 mJ/cm$^2$. Deviations with the LUT method are lower for all laser fluences than with the AM method. However, between 60 mJ/cm$^2$ and 190 mJ/cm$^2$, the 19% deviation for ${T_0}_\textrm{LUT}$ from ${T_0}_\textrm{ref}$ corresponds to the upper limit of the LUT in terms of $T_0$: 2200 K (see Table 2). The estimation of ${E(m_{\lambda} )}$ also degrades when approaching 50 mJ/cm$^2$, as discussed in Sect. 4.3. This is due to the wider region in the error map when both laser pulses have similar fluence values, increasing the chance of selecting an incorrect couple (${E(m_{\lambda} )}_\textrm{LUT}$, ${T_0}_\textrm{LUT}$).

It was verified, but not shown here, that if the 10% error is set on $T_{M_2}$ instead of $T_{M_1}$, it leads to the same conclusion: the pulses fluences should be as spread as possible but with an upper limit given by the sublimation process.

Figure 13b considers the case of a systematic error in the estimation of temperature, i.e. $\widetilde{T_{M_1}}= 1.1\cdot T_{M_1}$ and $\widetilde{T_{M_2}}= 1.1\cdot T_{M_2}$. In this case, with the AM method and at low laser fluences, the 10% error made on $T_M$ is directly transmitted to ${E(m_{\lambda} )}$ and $T_0$: i.e. an X% overestimation on the peak temperature induces X% overestimation of both ${E(m_{\lambda} )}$ and $T_0$ (see Eq. (14)).

Concerning the LUT method, for laser fluences above 125 mJ/cm$^2$, the look-up table saturates (reaches its upper limit for ${E(m_{\lambda} )}$) and globally performs worse than the AM method.

Fig. 13

Deviations of ${E(m_{\lambda} )}$ (left axis, in blue) and $T_0$ (right axis, in pink) obtained using the AM method (solid lines) and the LUT method (dotted line) as a function of $F_2$ when (a) only $T_{M_1}$ is overestimated by 10%, and (b) both $T_{M_1}$ and $T_{M_2}$ are overestimated by 10%

Overall, both the AM and LUT methods are quite sensitive to errors in the estimation of the peak temperatures.

The accuracy of the LUT method is strongly affected by the uncertainties in the model’s parameters, such as $\beta$ and on the models themselves. Thus, in the following, the experimental feasibility of the SP-LII technique is proven only by considering the simplest approach, i.e. the AM method.

6 Experimental application of the SP-LII technique

In order to prove its feasibility, the SP-LII technique is applied to a laminar diffusion methane/air flame to measure the spatial evolution of ${E(m_{\lambda} )}$ at the laser wavelength (1064 nm). The steady behaviour of a laminar flame improves the signal-to-noise ratio (SNR) of the LII signal and makes it possible to measure the peak temperatures at the two fluences at different instants, simplifying the experimental setup.

6.1 Laser fluence selection

As deduced from the previous theoretical analysis, the selection of laser fluences is crucial. Thus, to select the best fluence couple for the study of the whole flame, measurements of the soot particles’ peak temperature are done via 2C-LII pyrometry for various laser fluences and at five different axial locations. These locations correspond to different soot populations with possibly different optical properties.

The linear behaviour predicted by the LII code (see Fig. 3a) is seen for the five curves of Fig. 14 up to a limit of $\sim$4000 K. Above this value, high-temperature phenomena are responsible for the loss of linearity, so the measurements fall outside the assumptions of the SP-LII technique. A lower limit of 2600 K is introduced to guarantee that the flame emission has a negligible weight compared to the LII emission of the probed soot particles, avoiding then erroneous peak temperature estimations. The optimal laser fluences must be selected:

• low enough to limit the occurrence of high-temperature phenomena that go beyond the limits of the technique,

• high enough to ensure a good SNR,

• with $\Delta F = F_2 -F_1$ high enough to limit the technique’s sensitivity to errors on peak temperature estimations, as previously discussed in Fig. 13a.

The blue zone in Fig. 14 identifies the fluence range allowing to compute ${E(m_{\lambda} )}$ for the five flame locations studied here. According to Fig. 14, the couple 64/106 mJ/cm$^2$ can probe all HABs from 29 to 36 mm and is best suited for the soot particles found above HAB = 30 mm as the higher peak temperature reached induces a better SNR. The couple 106/149 mJ/cm$^2$ is more adapted to the younger soot particles that absorb less, which are found at HAB $\le$ 29 mm. It should be noted that these fluences are not necessarily the most adequate for all flames. An analysis of the peak soot temperature as a function of the laser’s fluence shall be systematically performed.

Fig. 14

Particles’ peak temperature as a function of laser fluence for five different HABs along the flame centerline: 29 mm (blue o), 30 mm (red $\times$), 32 mm (black $*$), 34 mm (cyan $\square$) and 36 mm (magenta $\diamondsuit$). The horizontal dashed lines represent the temperature limits of 2600 K and 4000 K. The oblique dashed lines represent linear regressions of the temperature curves in the linear regime. The blue zone represents the fluences compatible with the SP-LII technique for the five HABs

6.2 Application of the SP-LII

Section 5.3 shows that the uncertainties characterising the parameters needed by the LUT method might be quite high, especially because the mass accommodation coefficient is unknown. In addition, the LUT method requires information on the primary particle diameter, i.e. additional ex situ and/or in situ measurements that are out of the scope of this work. Thus, ${E(m_{\lambda} )}$ and $T_0$ are computed here with only the simpler AM method. Nevertheless, the results using the LUT method are available in Appendix A. Here, a uniform, temperature-independent product $\rho c$ equal to 4.6$\cdot 10^6$ J/K/m$^3$ is assumed [42]. In this case, Eq. (12) reduces to Eq. (14). To calculate peak temperature values via Eq. 9, the absorption function is assumed constant as a function of the wavelength, i.e. $R_{12}$ = 1. The experimental data that correspond to the right side in Eq. (14) are provided in the supplementary material to allow the readers to explore the potential evolution of $\rho c$ with soot maturity.

The computed values of ${E(m_{\lambda} )}$ for the couples: 64/106, 106/149, and 64/149 mJ/cm$^2$ as a function of HAB are displayed in Fig. 15a, on the flame centreline. Values of ${E(m_{\lambda} )}$ were discarded when one of the two peak temperatures was outside the temperature limits of Fig. 14. The estimation of ${E(m_{\lambda} )}$ and $T_0$ for various axial and radial positions are gathered in partial 2D maps in Fig. 15b. When multiples estimations of ${E(m_{\lambda} )}$ are available for one flame position (for instance, for 29 $\le$ HAB $\le$ 30.5 mm in Fig. 15a), the averaged value is retained in Fig. 15b. The coloured discs in Fig. 15b represent the collection surface of 375 $\mu$m diameter of the collection system.

On the flame axis, ${E(m_{\lambda} )}$ rapidly increases from 0.1 at HAB = 28 mm to 0.39 at HAB = 31 mm, followed by a stagnation up to the detection limit at 36 mm. While the couple 64/106 mJ/cm$^2$ allows probing HABs from 29 to 36 mm, the couple 106/149 only adds a few points below 29 mm, but it enables catching the rapid growth of ${E(m_{\lambda} )}$ at the lower HABs. Higher fluences would be necessary to probe lower HABs. ${E(m_{\lambda} )}$ increases rapidly with the radial position for the three lower HABs and stays constant and equal to $\approx$ 0.39 for HAB = 31 and 35 mm. A smaller probe volume would be necessary to properly catch the rapid radial evolution of ${E(m_{\lambda} )}$. Globally, the inner and lower parts of the flame contain soot particles with low values of ${E(m_{\lambda} )}$ corresponding to young soot. The higher and outer parts of the flame contain more mature soot characterised by higher values for ${E(m_{\lambda} )}$. A direct comparison of the values of ${E(m_{\lambda} )}$ with data from the literature is not possible as this flame is not a reference flame, but values and trends can be compared. Multiple works have estimated the axial evolution of ${E(m_{\lambda} )}$ in the premixed flame of a McKenna burner with the technique described in [9]. Maffi et al. [12] found values near 0.3 for HAB $\ge$ 10 mm. Eremin et al. [13] saw an increase from $\sim$0.3 at HAB = 10 mm up to $\sim$0.42 at HAB = 20 mm. Bladh et al. [10] and Bejaoui et al. [11] found an increase from $\sim$0.2 and $\sim$0.22, respectively, at HAB = 7 mm to $\sim$0.45 and $\sim$0.37, respectively, at HAB = 15 mm. Yon et al. [16] presented a 2D map of $E(m_{\lambda = 810 \text {nm}})$ for an ethylene/air laminar diffusion flame stabilised on a Gülder burner. Their results are consistent with the present work. They found ${E(m_{\lambda} )}$ values ranging from 0.1 to 0.4, with the highest values for ${E(m_{\lambda} )}$ at the outer part of the flame, while the lower values are found in the lower and inner regions of the flame. One significant difference with the present work is that they found a rapid increase of the absolute value of ${E(m_{\lambda} )}$ at the flame’s tip; such behaviour is not seen in Fig. 15b.

The right part of Fig. 15b gives the gas temperature estimated by the SP-LII. $T_0$ ranges from 2000 to 2400 K, which is high for an atmospheric methane/air flame. This high estimation of $T_0$ may be explained by fluences high enough to start sublimation: the limit of 4000 K may be too high (linearity is in fact lost before 4000 K, see Fig. 14). This tends to overestimate $T_0$ and underestimate ${E(m_{\lambda} )}$, as shown in Fig. 4. However, reducing the laser fluences while keeping a constant difference between them is difficult as the SNR limit is rapidly reached due to the low soot load in this flame.

Overall, trends in the spatial evolution of ${E(m_{\lambda} )}$ agree with the literature for premixed flame and for the diffusion flame studied in [16]. The absolute values of ${E(m_{\lambda} )}$ found in this work are also in line with the ones of the literature. The uncertainties in the presented experimental results are discussed in the following.

Fig. 15

a ${E(m_{\lambda} )}$ as a function of HAB for three couple of laser fluences: 64/106 mJ/cm$^2$ (blue $\circ$), 64/149 mJ/cm$^2$ (red $\times$) and 106/149 mJ/cm2 (black $*$). b Left: distribution of absolute value of ${E(m_{\lambda} )}$. Right: distribution of $T_0$

6.3 Uncertainties of the SP-LII approach

The assumptions of the SP-LII approach induce uncertainties on the computed values for both ${E(m_{\lambda} )}$ and $T_0$. The uncertainties are here quantified along the flame’s axis for the AM method.

First, as the SP-LII technique allows access to $\frac{{E(m_{\lambda} )}}{\rho c}$, the estimated value of ${E(m_{\lambda} )}$ depends on the product $\rho c$. As previously discussed in section 5.3, an error of X% on $\rho c$ brings the same error on ${E(m_{\lambda} )}$. Unfortunately, very little data about this product are available in the literature. Thus, it is difficult to realistically quantify the existing uncertainty on $\rho c$. Consequently, uncertainties coming from a potential error on $\rho c$ cannot be provided.

Second, with the AM method, the conduction losses are neglected. This brings an error depending on the soot size. Figure 8 shows that using the AM method brings an underestimation of ${E(m_{\lambda} )}$ that can go as high as 15% for soot particles of 2.5 nm (roughly the minimum soot size detectable by LII [41]). A 15% underestimation of the absorption function is then retained. The corresponding uncertainty region for ${E(m_{\lambda} )}$ along the flame’s axis is plotted in Fig. 16a.

Finally, the uncertainty attributed to the assumption of unity $R_{12} = \frac{E(m_{\lambda _1=578\ \text {nm}})}{E(m_{\lambda _2 = 716 \ \text {nm}})}$, i.e. a constant absorption function with wavelength when calculating $T_M$ with Eq. 9, must be quantified. For that, the soot peak temperatures are recomputed, changing the value of $R_{12}$ in Eq. 9. In [21], Bescond et al. studied the wavelength dependence of the absorption function of soot from diverse sources. The highest value for the ratio $R_{12}$ is 1.3. It corresponds to soot particles with a high organic content generated by a miniCAST soot generator. Inversely, using the formula in [9], which links the absorption function and the wavelength, one finds $R_{12} = 0.94$. Figure 16b shows the evolution of ${E(m_{\lambda} )}$ along the flame’s axis for the three considered values of $R_{12}$: 0.94, 1 and 1.3. The uncertainty zone due to the assumption of unity $R_{12}$ corresponds to the area in between the estimations of ${E(m_{\lambda} )}$ considering $R_{12}$ = 0.94 and $R_{12}$ = 1.3. The assumptions $R_{12}$ = 0.94 results in a 5 to 11% increase of the absolute value of ${E(m_{\lambda} )}$ depending on the HAB, while $R_{12}$ = 1.3 results in a 27 to 31% decrease of ${E(m_{\lambda} )}$. Assuming a higher value for $R_{12}$ results in lower estimations of ${E(m_{\lambda} )}$. This is an important observation. It means that when assuming $R_{12}$ = 1, the SP-LII technique would overestimate the true value of ${E(m_{\lambda} )}$ for the young soot particles that usually show stronger absorption at lower wavelengths ($R_{12} > 1$). In other words, a low value of ${E(m_{\lambda} )}$ cannot originate from the uncertainty on $R_{12}$, but results from the presence of lowly absorbing soot particles. The area of uncertainty due to $R_{12}$ represented by the blue-shaded region in Fig. 16b indicates the extreme limits that ${E(m_{\lambda} )}$ can take. Indeed, it seems unlikely that $R_{12}$ significantly deviates from 1, especially in the region HAB > 31 mm, where ${E(m_{\lambda} )}$ (with $R_{12}$ = 1) corresponds to the values for mature soot commonly encountered in the literature [17].

Fig. 16

a ${E(m_{\lambda} )}$ as a function of HAB for $R_{12}$ = 1 (red $\circ$). The red-shaded region represents the additional +15% uncertainties due to the effect of $d_p$ on the conduction losses. b ${E(m_{\lambda} )}$ as a function of HAB considering three different values of $R_{12}$: 0.94 (blue dotted line), 1 (red $\circ$) and 1.3 (black dashed line). The blue-shaded region between the dotted and dashed lines represents the uncertainty region of ${E(m_{\lambda} )}$ due to the uncertainty on $R_{12}$

Overall, the assumptions of neglected conduction losses and $R_{12}$ = 1 induce approximately a ± 30% uncertainty on the absorption function. However, one must remember that this does not include the hardly quantifiable error done on $\rho c$, which is directly transferred to ${E(m_{\lambda} )}$. In addition, other sources of errors not inherent to the SP-LII technique, like measurements and calibration errors, are not included.

7 Theoretical extension of the SP-LII technique to turbulent flames

The SP-LII technique is easily applicable to stationary flames, where the soot distribution is supposed to be stationary. In this case, the characteristics of the particles in the collection volume are expected not to vary with time. Thus, various acquisitions at different laser fluences can be performed in sequence. However, for turbulent flames in which the soot distribution constantly varies, the time decorrelation of the pulse is not possible, and single shots measurements must be exploited. In principle, two laser heads are required to heat the same soot particles consecutively. A first laser pulse of fluence $F_1$ heats the soot particles, initially at $T_0$, to a temperature $T_{M_1}$. Then, the soot particles cool down to the gas temperature $T_0$. After a predetermined short delay, a second laser pulse at fluence $F_2$ heats the same group of soot particles to a temperature $T_{M_2}$. Figure 17 illustrates the principle of the SP-LII technique applied to turbulent flames. It represents the power absorbed by the soot for two laser pulses shot at 100 and 3100 ns (i.e. with a pulse delay of 3 $\mu$s), and the corresponding temporal evolution of the soot particles’ temperature. For the specific conditions selected for this simulation, the 3 $\mu$s pulse delay is enough to let the soot particles cool back to the gas temperature. In the following, some of the key parameters for the application of the SP-LII technique to turbulent flames will be discussed.

Fig. 17

Temporal evolution of the soot particle temperature (left axis, solid blue line), and the power absorbed by the soot particle (right axis, dashed red line) after being heated by two laser pulses separated by 3 $\mu$s

7.1 LII pulse delay

The delay between the pulses is fundamental in the turbulent version of the SP-LII technique. If the delay is too short, the soot particles’ temperatures before the first and the second laser pulse would not be equal, introducing a bias in the estimation of both ${E(m_{\lambda} )}$ and $T_0$. A too long delay makes the soot particles probed by the first laser pulse to leave the collection volume. In that case, the pulses would probe different populations of soot particles (with possibly different properties), leading to erroneous results. Thus, it is necessary to properly define the delay between the pulses by accounting for the soot particles’ cooling time and the displacement of the group of soot.

Cooling time

For atmospheric flames, the cooling time is dominated by the conductive exchange term via Eq. (8), which depends on several parameters, but especially on $d_p$ and $\alpha$. In order to quantify the cooling time, simulations are run with $\Omega _\textrm{ref} / \left\{ {d_p}_\textrm{ref}, \alpha _\textrm{ref} \right\}$. The cooling time is represented in Fig. 18 as a function of $d_p$ for five values of $\alpha$. The cooling time is defined as the time elapsed between $T_p = T_M$ and $T_p = T{_0}_\textrm{ref} + 10$ K = 1870 K.

It is reminded that in the retained LII code assumes monodispersed and non-aggregated soot particles. The shielding effect is not considered in these results. Thus, the cooling time would probably be more important for large aggregates.

Figure 18 shows the same conclusion as one can find by analytically solving the soot particles’ cooling considering only conduction (Eq. (2)): the cooling time is proportional to $d_p$ and inversely proportional to $\alpha$. Setting the cooling time to $\Delta t = 10 \ \mu$s would be enough for all soot primary particle size if $\alpha \ge 0.3$, while only the particles bigger than 20 nm would not be in thermal equilibrium with the gas if $\alpha$ = 0.1.

Fig. 18

Cooling time as a function of $d_p$ for $\alpha$ = 0.1 ($\star$), 0.3 ($\times$), 0.5 (dotted line), 0.7 (dashed line) and 0.9 (solid line). The cooling time is defined as the time elapsed between $T_p = T_M$ and $T_p = T{_0}_\textrm{ref} + 10$ K = 1870 K

A precise knowledge of $\alpha$ would allow a better estimation of the cooling time required, allowing to lower the delay between the two laser pulses and extending the domain of application of the SP-LII technique.

Soot displacement

Concerning the soot displacement, here, it is assumed that the second pulse should also heat at least 75% of the soot particles heated by the first pulse to have results representative of the probed soot population. Assuming a uniform soot displacement in a collection volume of characteristic size of $L^*=1$ mm, and a pulses delay of 10 $\mu$s, the maximum allowable velocity could be estimated by: $\frac{L^*}{4\Delta t} = 25$ m/s. This limit may still be exceeded in case of highly turbulent flames.

7.2 Gas heating

In [43], Snelling et al. observed anomalies in the cooling rate of laser-heated soot particles that can be explained by an increasing bath gas temperature originating from the energy liberated by the cooling of the soot particles. The bath gas temperature increases with the laser fluence as more energy is transferred to the soot particles. The excess in gas temperature was found to $\sim$ 400 K for a laser fluence of 169 mJ/cm$^2$ at a laser  wavelength of 532 nm, for an operating point charged with $\sim$ 4 ppm of soot. Other works [44, 45] have studied the same experimental point for laser fluences between 125 and 150 mJ/cm$^2$ at 1064 nm. Nordström et al. [44] used coherent anti-Stokes Raman spectroscopy to determine the gas temperature before and during LII. They found a $\sim$100 K increase of the bath gas temperature 2 $\mu$s after the LII pulse. Mansmann et al. [45] compared 2C pyrometry with and without the occurrence of LII pulse and found an 80 K increase in the gas temperature 7 $\mu$s after the LII pulse.

Cenker et al. [46] used a rapid camera to investigate the gas heating by LII at various laser fluences in a laminar diffusion flame. They showed that the gas heating last for up to several milliseconds.

These results encourage once again the usage of low fluences to limit as much as possible the heating of the gas after the first pulse to have a similar gas temperature before both LII pulses. In addition, the SP-LII is expected to perform worse in zones with high soot volume fraction as the soot will transfer energy to the gas proportionality to the soot volume fraction. However, this effect is expected to only slightly impact the results of the SP-LII technique in most of its applications as in a very highly sooted region $\sim$ 4 ppm, and using fluences of $\sim$ 150 mJ/cm$^2$ (which is the order of magnitude of fluences to be used with the SP-LII technique), produces only a $\sim$ 100 K difference in gas temperature [44], resulting in a 100 K difference in initial soot temperature with the assumption of thermal equilibrium.

7.3 Alteration of the soot properties after the first pulse

Applying the SP-LII technique in a turbulent flame requires that the same soot particles are heated twice by the laser pulses. Thus, the first laser pulse must not significantly modify the soot properties. According to Fig. 7a, using a weaker laser pulse followed by a stronger one is identical to the opposite, meaning that the order of the pulses seems not to modify much the determined values of ${E(m_{\lambda} )}$ and $T_0$. However, the high-temperature effects, such as annealing, are not accounted for. In several works [47,48,49], soot particles were heated by two consecutive laser pulses. The results have shown that depending on the laser fluence, the laser heating of the soot particle cause annealing that tends to enhance the soot’s optical properties. Vander Wal et al. [47] found that annealing enhances the soot optical properties for fluences as low as 100 mJ/cm$^2$ at a laser wavelength of 1064 nm. Cenker et al. [48] found a significant increase of soot absorption for laser fluences (at 1064 nm) above 170 mJ/cm$^2$ corresponding to $\sim$ 4000 K. Török et al. [49] studied three operation points of a miniCAST burner corresponding to different soot. Different combinations of first and second laser pulses were explored. They showed that pre-heating soot with a first laser pulse affects the soot properties differently depending on their maturity. By analysing the extinction coefficient of soot that was extracted from two laminar diffusion flames and irradiated by a laser source at 1064 nm, Migliorini et al. [50] found no variation of the optical properties for a fluence of 100 mJ/cm$^2$, while for 270 mJ/cm$^2$, a noticeable difference in the spectral dependence of $K_\textrm{ext}$ was observed. The spread of the fluence limit observed in these works and the work [49] indicates that the modification of soot properties through laser heating depend on the soot maturity. Thus, in order to reduce errors coming from sublimation, annealing and other high fluences phenomena, it is desirable to use laser fluences as low as possible, and it is advised that the ${1\textrm{st}}$ laser pulse is the lowest one to limit the alteration of the soot particles’ properties before the $2\textrm{nd}$ laser pulse.

8 Conclusion

The separated pulse LII technique allows estimating the ratio $\frac{{E(m_{\lambda} )}}{\rho c}$. Then, the knowledge of the product $\rho c$ allows accessing ${E(m_{\lambda} )}$. The SP-LII approach consists of measuring the soot particles’ peak temperature at two different laser fluences. This technique does not require prior knowledge of the local gas temperature and provides an estimate for it. This technique also has the potential to be applied in turbulent flames.

Two methods to compute ${E(m_{\lambda} )}$ and $T_0$ have been theoretically compared using numerically synthesised LII signals obtained from an LII code. The first method called the “absorption model” (AM) consists of neglecting the loss terms in the energy equation and solves it analytically. It directly calculates ${E(m_{\lambda} )}$ and $T_0$ from two equations. It is a simple and efficient way to compute ${E(m_{\lambda} )}$ and $T_0$ but deviates when sublimation appears or when soot particles have a primary particle diameter below $\sim 10$ nm.

The second method (LUT) used to retrieve ${E(m_{\lambda} )}$ and $T_0$ is through a look-up table built with an LII code. It has proven to be accurate even when sublimation occurs and for all primary particle sizes, as long as the look-up table has enough data points.

An uncertainty analysis pointed out that the error made on ${E(m_{\lambda} )}$ is linear with the error made on the assumed value for the soot density, while $T_0$ is not impacted much. Knowledge of the soot primary particle diameter and the thermal accommodation coefficient seems not to be of prior importance if particles with a diameter above $\sim 10$ nm are investigated. In addition, for the LUT method, in the absence of knowledge of the mass accommodation coefficient, a value below 0.2 might limit the deviation obtained using the look-up table method for low to moderate laser fluences. The peak temperatures have to be estimated as accurately as possible as this information has an important impact on the estimation of ${E(m_{\lambda} )}$ and $T_0$.

Globally, the LUT method performs slightly better than the AM. However, it requires more inputs that are mostly unknown, for example, the soot primary particle diameter and the thermal and mass accommodation coefficients. Moreover, it relies on the validity of the models describing the loss terms in the soot energy equation considered for the generation of the table. Therefore, the LUT method has to be used with caution.

Particular attention is required when using moderate to high laser fluences, as in this case, the difficult-to-model sublimation term (but also other high-temperature phenomena such as annealing) plays an important role which can lead to larger errors.

The authors recommend using adapted laser fluences to avoid these phenomena. Consequently, the LUT method interest is reduced only to account for soot particle size differences at the cost of higher complexity. In most applications, the simpler AM method should be sufficient to estimate ${E(m_{\lambda} )}$.

In order to prove its feasibility, the SP-LII technique has been applied to a laminar diffusion methane/air flame on averaged LII signals. The estimation of ${E(m_{\lambda} )}$ with the AM method was found to be coherent with the literature. The uncertainty on the absorption function ratio that is required to compute the soot peak temperatures, and the uncertainties inherent to the AM method (neglected conduction losses) result in a ± 30% uncertainty on the determined values of the absorption function.

Finally, the extension of the method to turbulent flames was theoretically discussed. In that case, the delay between the two laser pulses must be carefully selected so that it is long enough to allow the soot particles to cool down to the gas temperature, but short enough to ensure that the two laser pulses heat the same group of soot particles.

The recommendations for the experimental application of the separated pulse LII technique are the following:

• Avoid heating soot to temperatures inducing high-temperature phenomena that break the linear relation between peak temperature and laser fluence. The laser fluence limit can be obtained by looking at the fluence curves, and it will depend on soot maturity.

• The lower laser pulse should have the lowest laser fluence allowed by the signal-to-noise ratio.

• The laser fluence of the two pulses should be selected as spread as possible to limit the impact of the error made on the estimation of the peak temperatures.

• When applied to turbulent flames:

  • The delay between the two laser pulses should be estimated considering the soot residence time in the collection volume and the soot cooling time.

  • The laser fluence of the first pulse should be lower than the second one to reduce the potential change of soot properties, which may be caused by the interaction of the high-energy laser beam with the soot particles and to reduce the bath gas heating.

The experimental application of the SP-LII technique to turbulent flames will be investigated in future works.

A Estimation of \({E(m_{\lambda} )}\) along the flame’s axis with the LUT method

In order to test the LUT method with the experimental data of the $CH_4$/air flame, a new look-up table adapted to the test case and with refinement in the fluence direction was created. The parameters $d_p$, $\rho$, $\alpha$ and $\beta$ are selected as follows:

• $d_p$ is set to 10 nm.

• With the AM method, $\rho c$ = 4.6e6 J/K/m$^3$ was selected. However, the LII code used for the look-up table generation does not allow the change of the specific heat, which is hardcoded as a temperature-dependent function. Thus, To be consistent with the value selected with the AM method, it was decided to set the density to $\rho$ = $\frac{4.6e6}{c(T=3300K)}$ = 2067 kg/m$^{3}$.

• $\alpha$ is set to 0.3.

• For $\beta$, three cases were considered. The first one is $\beta$ = 0. It allows confronting the AM and the LUT methods with the same assumptions regarding the sublimation losses. The second case is $\beta = 0.2$. This case was considered to verify if the LUT allows exploiting the data where the soot peak temperature exceeds the limit of 4000 K. The value $\beta$ = 0.2 was selected following the conclusion about the mass accommodation coefficient of Sect. 5.3. The last case is $\beta$ = 0.13, the value for which the best agreement in ${E(m_{\lambda} )}$ estimations is seen for the three couples of laser fluences.

Figure 19a compares the estimation of ${E(m_{\lambda} )}$ of the AM and LUT methods when sublimation is neglected ($\beta = 0$). The LUT estimations are almost always above the ones of the AM, with a maximum of + 14%. This difference can be explained by the conduction losses that are accounted for with the LUT.

Figure 19b is identical to Fig. 19a, but with $\beta$ = 0.2 instead of $\beta$ = 0. In this case, the estimations of ${E(m_{\lambda} )}$ are plotted even when the peak temperature exceeds the limit of 4000 K. For the couple 64/106 mJ/cm$^2$, ${E(m_{\lambda} )}$ is 3 to 20% higher than the ones for $\beta$ = 0 up to HAB = 35 mm. Above that, ${E(m_{\lambda} )}$ reaches the table limit (0.6) at HAB = 37 mm. For the two other couples, ${E(m_{\lambda} )}$ reaches the table’s upper limit at HAB = 33 and 34 mm for 64/149 mJ/cm$^2$ and 106/149 mJ/cm$^2$, respectively. Such high values for ${E(m_{\lambda} )}$ show that the sublimation process is over-predicted.

The HABs for which the estimations of the LUT are close to the one of the AM method correspond to the ones for which the peak temperatures are the lowest ($< \sim$3500 K).

The best agreement for the three couples of laser fluence is found for $\beta$ = 0.13. This case is plotted in Fig. 19c. In this case, estimations of ${E(m_{\lambda} )}$ with the LUT method are close to the AM method for HAB < 31 mm. Above that, differences slightly increase, and ${E(m_{\lambda} )}$ reaches $\sim$0.5 at HAB = 36 mm before sharply increasing at the flame’s extremity. The results of Fig. 19c should be interpreted with care and do not legitimise the usage of high fluences for the SP-LII if one sets $\beta$ = 0.13. The authors believe that the strong variations in the estimation of ${E(m_{\lambda} )}$ with the hypothesis made on $\beta$ confirm the necessity to avoid high laser fluences even when using the LUT method.

Fig. 19

Evolution of ${E(m_{\lambda} )}$ as a function of HAB for three couple of laser fluences: 64/106 mJ/cm$^2$ (blue $\circ$), 64/149 mJ/cm$^2$ (red $\times$) and 106/149 mJ/cm$^2$ (black $*$). The solid lines represent the estimations obtained using the AM method, while the dotted lines are for the LUT method for a $\beta$ = 0, b $\beta$ = 0.2, and c $\beta$ = 0.13