1 Introduction

The two-dimensional positively curved three-body problem has been studied for several authors, for instance (Borisov et al. 2016, 2004; Diacu 2012; Diacu et al. 2012a, b; Diacu and Pérez-Chavela 2011; Pérez-Chavela and Reyes-Victoria 2012; Pérez-Chavela and Sánchez-Cerritos 2018; Martínez and Simó 2013; Tibboel 2013; Zhu 2014; Diacu and Zhu 2020). In all these papers, the masses are moving under the influence of the cotangent potential, which is the natural extension of the planar Newtonian problem to the sphere.

Consider a point q on \({\mathbb {S}}^2\), \(|q|^2=1\). In the spherical coordinates, q is represented by \(q=(\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta )\in {\mathbb {R}}^3\). The Lagrangian for the three-body problem on \({\mathbb {S}}^2\) is given by

$$\begin{aligned} L = K - V, \end{aligned}$$
(1)

where the kinetic energy K and the cotangent potential V are

$$\begin{aligned} K=\sum \nolimits _k\frac{m_k}{2} \left( {\dot{\theta }}_k^2+\sin ^2(\theta _k){\dot{\phi }}_k^2\right) , \quad V= - \sum \nolimits _{i<j} \frac{m_i m_j\cos \sigma _{ij}}{\sqrt{1-\cos ^2(\sigma _{ij})}}. \end{aligned}$$

Dot on symbols represents the time derivative, the indexes i, j, k run for 1, 2, 3, and \(m_k\) are the masses. The arc angle \(\sigma _{ij}\) is the angle between the two points \(q_i\) and \(q_j\) as seen from the center of \({\mathbb {S}}^2\). In order to avoid the singularities (Diacu et al. 2012b), the range of \(\sigma _{ij}\) is restricted to \(0< \sigma _{ij}< \pi \,\, \text{ for } \text{ all } \,\, i\ne j.\) Then \(\cos \sigma _{ij}\) is given by the inner product of \(q_i\) and \(q_j\), namely

$$\begin{aligned} \cos \sigma _{ij} =\cos \theta _i\cos \theta _j+\sin \theta _i\sin \theta _j\cos (\phi _i-\phi _j). \end{aligned}$$

The equations of motion derived from Lagrangian (1) are

$$\begin{aligned} \begin{aligned}&\frac{\textrm{d}}{\textrm{d}t}\left( m_i {{\dot{\theta }}}_i\right) =m_i \sin \theta _i\cos \theta _i {{\dot{\phi }}}_i^2- \frac{\partial V}{\partial \theta _i},\\&\quad \frac{\textrm{d}}{\textrm{d}t}\left( m_i\sin ^2(\theta _i){{\dot{\phi }}}_i\right) =- \frac{\partial V}{\partial \phi _i}. \end{aligned} \end{aligned}$$
(2)

Definition 1

A relative equilibrium (RE in short) on \({\mathbb {S}}^2\) is a solution of the equations of motion with \({{\dot{\theta }}}_i=0\) and \({{\dot{\phi }}}_i=\omega =\) constant.

Then, the equations for a relative equilibrium are reduced to

$$\begin{aligned} \begin{aligned} \omega ^2 m_i \sin \theta _i\cos \theta _i =\sum _{j\ne i}\frac{m_i m_j}{\sin ^3(\sigma _{ij})} \Big ( \sin \theta _i\cos \theta _j-\cos \theta _i\sin \theta _j\cos (\phi _i-\phi _j) \Big ) \end{aligned} \end{aligned}$$
(3)

and

$$\begin{aligned} \begin{aligned}&m_1 m_2\sin \theta _1 \sin \theta _2 \sin (\phi _1-\phi _2)/\sin ^3(\sigma _{12})\\&\quad =m_2 m_3\sin \theta _2 \sin \theta _3 \sin (\phi _2-\phi _3)/\sin ^3(\sigma _{23})\\&\quad =m_3 m_1\sin \theta _3 \sin \theta _1 \sin (\phi _3-\phi _1)/\sin ^3(\sigma _{31}). \end{aligned} \end{aligned}$$
(4)

We call them as “equations of relative equilibria” in the following.

Definition 2

(Euler and Lagrange RE) An Euler RE (ERE) is an RE where three bodies are on the same geodesic. If this is not the case, we call it Lagrange RE (LRE).

In Fujiwara and Pérez-Chavela (2023), we showed that there are two cases of ERE: three bodies are on a rotating meridian, or they are on the equator. Obviously for ERE the rotation axis is the z-axis.

Definition 3

(Shape and configuration) A shape is the figure on the sphere formed by the three arc angles, which are, up to permutation, the angles \(\sigma _{12},\sigma _{23}\), and \(\sigma _{31}\). A configuration is the placement on the sphere, of the elements \(\theta _1, \theta _2, \theta _3\) and \(\phi _1 - \phi _2, \phi _2 - \phi _3, \phi _3 - \phi _1\).

In the following, we simply write \(\{\sigma _{ij}\}\) for the representation of a shape, and \(\{\theta _k, \phi _i-\phi _j\}\) for a representation of a configuration. Similarly, we write \(\{m_k\}\) for \(\{m_1,m_2,m_3\}\).

In 1772 Lagrange (1772), J.L. Lagrange published an amazing result for the Newtonian problem of the three bodies: Any three arbitrary masses located at the vertices of an equilateral triangle, generates a relative equilibria. In other words, if we put any three different masses, as for instance the Sun, Jupiter and a small stone, at the vertices of an equilateral triangle, then there exists an angular velocity \(\omega \) such that the three masses rotate uniformly around their center of mass, the motion is like a rigid body. This is that we call mass-independent shape for RE. In a natural way, we extend this concept to the sphere, and we raise the question: Are there mass-independent RE shape for the three-body problem on \({\mathbb {S}}^2\)?

For the 2-body problem on the sphere, the RE have been classified in Theorem 4.1 of Borisov et al. (2018) for arbitrary attractive potentials. From this classification it follows that, independently of the specific form of the potential, all shapes \(\sigma _{12}\in (0,\pi )\) except for \(\sigma =\pi /2\) are mass-independent shapes for RE. Ahead in this paper we give a simple proof of this statement for the cotangent potential by considering the limit \( m_3\rightarrow 0\) in our setting (see Proposition 3).

In Diacu et al. (2012a), Diacu et al. showed that in order to generate a RE for three masses located at the vertices of an equilateral triangle parallel to the equator, the masses should be equal. In Zhu (2014), Zhu proved that for the cotangent potential, any three masses placed on the equilateral triangle on a rotating meridian generate a RE. Some years later in Fujiwara and Pérez-Chavela (2023), we extended this result for general potentials which only depends of mutual distances among the masses.

One might be interested in RE with \(\theta _1=\theta _2=\theta _3\). The three bodies move along the same circle, which is parallel to the equator. This group of RE must be the simplest RE. In the corresponding Newtonian problem, RE with \(r_1=r_2=r_3\) are realized only when \(m_1=m_2=m_3\) (and the shape is equilateral), they form a “choreography”. However, Diacu and Zhu showed that besides the equilateral RE with \(m_1=m_2=m_3\) (which form a “choreography”), a non trivial group of isosceles RE exist on \({\mathbb {S}}^2\): for \(m_2=m_3\) and \(m_1=\nu m_3\) with \(\nu \in (0,2)\) (Diacu and Zhu 2020). The latter solution is not “choreography,” because “choreography” requires “equal time spacing on the orbit” between the bodies. The latter solutions have different time spacing if \(\nu \ne 1\). This is an interesting example for motions along a same orbit with different time spacing between bodies. Examples of non-circular choreographies on \({\mathbb {S}}^2\) were studied by Montanelli Montanelli and Gushterov (2016).

The goal of this paper is to show that, for the cotangent potential, besides to the equilateral triangle, we have one additional isosceles triangle shape on a rotating meridian, which is independent of the choice of the masses. We believe that this work will open a door for the search of new RE on curved spaces and the stability of them, as well as its possible applications.

In Definition 3, we emphasized the difference between shape and configuration. In order to be more accurate, we close this section by giving the precise definitions of the concepts that we will use in this article.

Definition 4

A RE shape for the two-dimensional constant positively curved threebody problem, is a shape which can form a RE. In particular we call Lagrange RE shape (Lagrange shape in short) and Euler RE shape (Euler shape in short) to the shapes which can form LRE and ERE, respectively.

Definition 5

(Mass-independent shape for RE) A mass-independent RE shape is a shape \(\{\sigma _{ij}\}\) that can form an RE for any masses \(\{m_k\}\).

After the introduction, where we define the concepts that we will study here, the paper is organized as follows: in Sect. 2, we state the equations used to generate LRE and ERE. We prove that there are no mass-independent Lagrange shapes, and there are no mass-independent Euler shapes on the equator. In Sect. 3, we prove the main result of this article: the existence of mass-independent Euler shape on a rotating meridian. Since the rotation axis depends on masses, the configuration made from the mass-independent shape depends on masses (see (Fujiwara and Pérez-Chavela 2023) for details). At the end of this section we briefly discuss the case of the restricted - problem on the sphere.

In Sect. 4, we show the configurations for different choice of the masses. In Sect. 5, we look for continuations of RE shape from mass-independent Euler shapes. We show that each one of them can be continued as a RE shape which is mass dependent. We finish the paper with an Appendix to describe the properties of some special shapes.

2 Preliminaries

In paper (Fujiwara and Pérez-Chavela 2023), we proved that, for the positively curved three-body problem, the necessary and sufficient condition for a shape to generate a LRE is \(\lambda _1=\lambda _2=\lambda _3\). Where the \(\lambda _i\)’s are

$$\begin{aligned} \begin{aligned} \lambda _1&=\frac{(m_2+m_3)\sin ^3(\sigma _{23}) -m_2\cos (\sigma _{12})\sin ^3(\sigma _{31}) -m_3\cos (\sigma _{31})\sin ^3(\sigma _{12})}{\sin ^3(\sigma _{23})},\\ \lambda _2&=\frac{(m_3+m_1)\sin ^3(\sigma _{31}) -m_3\cos (\sigma _{23})\sin ^3(\sigma _{12}) -m_1\cos (\sigma _{12})\sin ^3(\sigma _{23})}{\sin ^3(\sigma _{31})},\\ \lambda _3&=\frac{(m_1+m_2)\sin ^3(\sigma _{12}) -m_1\cos (\sigma _{31})\sin ^3(\sigma _{23}) -m_2\cos (\sigma _{23})\sin ^3(\sigma _{31})}{\sin ^3(\sigma _{12})}. \end{aligned} \end{aligned}$$

Proposition 1

There are no mass-independent Lagrange shapes.

Proof

The equation \(\lambda _1-\lambda _2=\lambda _2-\lambda _3=0\) has the form

$$\begin{aligned} \left( \begin{array}{ccc} S_{11} &{} S_{12} &{} S_{13} \\ S_{21} &{} S_{22} &{} S_{23} \end{array}\right) \left( \begin{array}{c}m_1 \\ m_2 \\ m_3\end{array}\right) = \left( \begin{array}{c}0 \\ 0 \end{array}\right) . \end{aligned}$$

Where, each \(S_{ij}\) is a function of \(\{\sigma _{ij}\}\). To satisfy the above equation for any \(\{m_k\}\), all the elements \(S_{ij}\) must be 0. But, \(S_{11}=S_{12}=0\) yields

$$\begin{aligned} \cos \sigma _{12}\,\frac{\sin ^3(\sigma _{23})}{\sin ^3(\sigma _{31})} =\cos \sigma _{12}\,\frac{\sin ^3(\sigma _{31})}{\sin ^3(\sigma _{23})} =1. \end{aligned}$$

Which does not have solution for \(\sigma _{ij}\in (0,\pi )\).

Therefore, there are no mass-independent shapes for LRE. \(\square \)

2.1 ERE on the Equator

When three bodies are on the equator, \(\theta _i=\pi /2\), and \(\sin \sigma _{ij}=|\sin (\phi _i-\phi _j)|\). Therefore the equations for relative equilibria (3) are automatically satisfied, and (4) takes the form

$$\begin{aligned} \frac{m_1m_2\sin (\phi _1-\phi _2)}{|\sin (\phi _1-\phi _2)|^3} =\frac{m_2m_3\sin (\phi _2-\phi _3)}{|\sin (\phi _2-\phi _3)|^3} =\frac{m_3m_1\sin (\phi _3-\phi _1)}{|\sin (\phi _3-\phi _1)|^3}. \end{aligned}$$

Proposition 2

There are no mass-independent Euler shapes on the equator.

Proof

Obviously, there are no mass-independent solution of \(\{\phi _i-\phi _j\}\). \(\square \)

2.2 ERE on a Rotating Meridian

For ERE on a rotating meridian, it is convenient to extend the range of \(\theta _i\) to \(-\pi \le \theta _i\le \pi \) and \(\phi _i=0\). Then \(\sin \sigma _{ij}=|\sin (\theta _i-\theta _j)|\), and the equations of relative equilibria (3) are

$$\begin{aligned} \omega ^2 m_i \sin \theta _i\cos \theta _i =\sum _{j\ne i}\frac{m_i m_j\sin (\theta _i-\theta _j)}{|\sin (\theta _i-\theta _j)|^3}, \quad i=1,2,3. \end{aligned}$$
(5)

The equations of relative equilibria (4) are automatically satisfied.

We have proved in Fujiwara and Pérez-Chavela (2023) that if A defined by

$$\begin{aligned} A=\left( \sum _\ell m_\ell ^2+2\sum _{i<j}m_im_j\cos (2(\theta _i-\theta _j)) \right) ^{1/2} \end{aligned}$$
(6)

is not zero, then the necessary and sufficient condition for the shape \(\{\theta _i-\theta _j\}\) to be an Euler shape on a rotating meridian is

$$\begin{aligned} \begin{aligned}&m_1m_2\left( \frac{s\omega ^2}{2A}\sin \Big (2(\theta _1-\theta _2)\Big ) - \frac{\sin (\theta _1-\theta _2)}{|\sin (\theta _1-\theta _2)|^3} \right) \\&\quad =m_2m_3\left( \frac{s\omega ^2}{2A}\sin \Big (2(\theta _2-\theta _3)\Big ) - \frac{\sin (\theta _2-\theta _3)}{|\sin (\theta _2-\theta _3)|^3} \right) \\&\quad =m_3m_1\left( \frac{s\omega ^2}{2A}\sin \Big (2(\theta _3-\theta _1)\Big ) - \frac{\sin (\theta _3-\theta _1)}{|\sin (\theta _3-\theta _1)|^3} \right) , \end{aligned} \end{aligned}$$
(7)

for \(s=1\) or \(-1\).

Remark 1

The parameter \(s=\pm 1\) comes from the fact that, when we study RE on a rotating meridian, it is convenient to enlarge the range angle \(\theta _k\) to \(- \pi< \theta _k < \pi \), with \(\phi _k=0\). When we study a particular configuration, the equations of relative equilibria (3) and (4) determine the sign of s (see (Fujiwara and Pérez-Chavela 2023) for more details).

The configuration \(\{\theta _k\}\) is given by

$$\begin{aligned} \begin{aligned} \cos (2\theta _1)&=s A^{-1}\left( m_1+m_2\cos \Big (2(\theta _1-\theta _2)\Big ) +m_3\cos \Big (2(\theta _1-\theta _3)\Big ) \right) ,\\ \sin (2\theta _1)&=s A^{-1}\left( m_2\sin \Big (2(\theta _1-\theta _2)\Big ) +m_3\sin \Big (2(\theta _1-\theta _3)\Big ) \right) . \end{aligned} \end{aligned}$$
(8)

The other angles \(\theta _k\) are determined by \(\theta _k=\theta _1+(\theta _k-\theta _1)\).

For the special shapes with \(A=0\), the map from the shape to configuration, \(\{\theta _i-\theta _j\}\rightarrow \{\theta _k\}\), is not determined uniquely. Therefore, we have to check whether each of such shapes can satisfy the equations for relative equilibria (3) or not. See Appendix.

In the next section, we will show the existence of a non-equilateral mass-independent Euler shape on a rotating meridian.

3 Mass-Independent Shapes for ERE on a Rotating Meridian

To get a mass-independent shape, any term in the parentheses of Eq. (7) must be zero, namely,

$$\begin{aligned} \frac{s\omega ^2}{2A}\sin \Big (2(\theta _i-\theta _j)\Big ) =\frac{\sin (\theta _i-\theta _j)}{|\sin (\theta _i-\theta _j)|^3} \end{aligned}$$
(9)

for \((i,j)=(1,2), (2,3), (3,1)\).

From now on, in order to facilitate the reading of the manuscript we introduce the new variables \(\tau _k=\theta _i-\theta _j\) for \((i,j,k)=(1,2,3), (2,3,1)\), and (3, 1, 2). The range of \(\tau _k\) is \((-\pi ,\pi )\). The relation between \(\sigma _{ij}\) and \(\tau _k\) is \(\sigma _{ij}=|\tau _k|\) and \(\sin \sigma _{ij}=|\sin \tau _k|\). Equation (9) in \(\tau _k\) variables is,

$$\begin{aligned} \frac{s\omega ^2}{2A}\sin (2\tau _k) =\frac{\sin \tau _k}{|\sin \tau _k|^3}, \quad k=1,2,3. \end{aligned}$$
(10)

Since \(\tau _3=\theta _1-\theta _2=-(\tau _1+\tau _2)\), we can take \(\tau _1\) and \(\tau _2\) as the independent variable to give a shape. To avoid the singularity, \(\sin \tau _k\ne 0\). We can restrict the range of \(\tau _2\in (0,\pi )\), because we can rotate the system by \(\pi \) around the north pole if \(\tau _2<0\). Therefore, the non-singular shapes \(\{\sigma _{ij}\}\) and the ordered set \((\tau _1,\tau _2)\) are in correspondence one to one in the set

$$\begin{aligned} U_\text {phys} =\{(\tau _1,\tau _2)| \tau _1\in (-\pi ,\pi ), \tau _2\in (0,\pi ), \sin (\tau _1)\sin (\tau _2)\sin (\tau _1+\tau _2)\ne 0\}. \end{aligned}$$

This is the shape space for RE on a rotating meridian.

Since \(\sin \tau _k\ne 0\), the Eq. (10) are equivalent to

$$\begin{aligned} \frac{s\omega ^2}{A}\cos \tau _k =\frac{1}{|\sin \tau _k|^3}. \end{aligned}$$

Given that \(\cos \tau _k=0\) cannot satisfy this equation, we assume \(\cos \tau _k\ne 0\). So, the above conditions are

$$\begin{aligned} \frac{s\omega ^2}{A} =\frac{1}{\cos (\tau _k)|\sin \tau _k|^3}. \end{aligned}$$
(11)

The equations for \(\tau _k\) are

$$\begin{aligned} \cos (\tau _1)|\sin \tau _1|^3 =\cos (\tau _2)|\sin \tau _2|^3 =\cos (\tau _3)|\sin \tau _3|^3, \end{aligned}$$
(12)

or in variables \(\tau _1,\tau _2\)

$$\begin{aligned} \cos (\tau _1)|\sin (\tau _1)|^3 =\cos (\tau _2)|\sin (\tau _2)|^3 =\cos (\tau _1+\tau _2)|\sin (\tau _1+\tau _2)|^3. \end{aligned}$$
(13)

In order to graphically illustrate the content of our main theorem, we consider the functions \(f_1\) and \(f_2\) of \((\tau _1, \tau _2)\) given below and illustrate the curves \(f_1(\tau _1, \tau _2)=0, f_2(\tau _1, \tau _2)=0\) in the domain \((0,\pi ) \times (0,\pi )\) (see Fig. 1).

$$\begin{aligned} f_1(\tau _1, \tau _2)= & {} \cos (\tau _1)|\sin (\tau _1)|^3 - \cos (\tau _2)|\sin (\tau _2)|^3,\\ f_2(\tau _1, \tau _2)= & {} \cos (\tau _1)|\sin (\tau _1)|^3 - \cos (\tau _1+\tau _2)|\sin (\tau _1+\tau _2)|^3. \end{aligned}$$
Fig. 1
figure 1

The solid curves and the dashed curves represent \(f_1(\tau _1, \tau _2)=0\) and \(f_2(\tau _1, \tau _2)=0\), respectively, the intersection points of these curves give us the possible mass-independent shapes for ERE

Full size image

Now, we are in conditions to state and prove the main result of this article.

Theorem 1

In the two-dimensional constant positively curved three-body problem, there are exactly two RE shapes which are independent of the masses, both of them are on a rotating meridian (Euler shapes), one isosceles triangle with equal arc \(\tau _0=2^{-1}\arccos ((\sqrt{2}-1)/2)\) and one equilateral triangle with the same arc \(\tau _\text {e}=2\pi /3\).

Proof

In the previous section we showed the no existence of mass-independent Lagrange shapes nor Euler shapes on the equator. Then, it is only necessary to analyze the Euler shapes on a rotating meridian.

For an isosceles triangle on a rotating meridian, we consider the case \(\tau =\tau _1=\tau _2 \in (0,\pi )\setminus \{\pi /2\}\). Then, Eq. (13) takes the form

$$\begin{aligned} \cos (\tau )|\sin \tau |^3 =\cos (2\tau )|\sin (2\tau )|^3. \end{aligned}$$
(14)

Therefore, \(\cos \tau \) and \(\cos (2\tau )\) must have the same sign. Namely, \(0<\tau <\pi /4\) (both are positive) or \(\pi /2<\tau <3\pi /4\) (both are negative).

We divide the proof in three steps depending of the different shape of the triangle, isosceles, equilateral or scalene.

\(hfill\square \)

3.1 Step 1: For \(0<\tau <\pi /4\) We Obtain an Isosceles Euler Shape

Proof

For the case \(0<\tau <\pi /4\), \(\sin \tau \) and \(\sin (2\tau )\) are positive. Then, the equation for \(2\tau \) is

$$\begin{aligned} 4\cos (2\tau )(\cos (2\tau )+1)=1, \end{aligned}$$

a second order polynomial in \(\cos (2\tau )\) whose solution is \(\cos (2\tau _0)=(\sqrt{2}-1)/2\) corresponding to \(\tau _0=2^{-1}\arccos ((\sqrt{2}-1)/2)=0.6810...<\pi /4\).

For this solution,

$$\begin{aligned} A^2 =(m_1-m_2)^2+\left( 3-2\sqrt{2}\right) m_1m_2 +m_3^2+\left( \sqrt{2}-1\right) (m_2m_3+m_3m_1) >0. \end{aligned}$$

Therefore, we get one isosceles solution. \(\square \)

Observe that we didn’t use any special properties for \(\{m_k\}\) in this calculation. Any mass \(m_k\) can be located in middle of the other two masses \(m_i\) and \(m_j\).

In variables \((\tau _1,\tau _2)\), the three shapes for the isosceles RE (which we are counting just as one) are \((\tau _0,\tau _0)\), \((-2\tau _0,\tau _0)\), and \((-\tau _0,2\tau _0)\).

3.1.1 Step 2: For \(\pi /2<\tau <3\pi /4\) We Obtain a Unique Equilateral Euler Shape

Proof

In this case, the sign of \(\sin \tau \) and \(\sin (2\tau )\) are opposite. Therefore the equation for \(\cos (2\tau )\) is reduced to

$$\begin{aligned} 4\cos (2\tau )(\cos (2\tau )+1)=-1. \end{aligned}$$

The solution in \(\pi /2<\tau <3\pi /4\) is \(\cos (2\tau )=-1/2\) corresponding to \(\tau =2\pi /3\). Therefore, \(\tau =\theta _2-\theta _3=\theta _3-\theta _1=2\pi /3\), and \(\theta _1-\theta _2=-2\tau =-4\pi /3 \equiv 2\pi /3 \mod 2\pi \). Namely, this is an equilateral triangle.

For this solution,

$$\begin{aligned} A^2=\sum _{i<j}(m_i-m_j)^2. \end{aligned}$$

Therefore, \(A=0\) for equal masses case. But, obviously \(\theta _1-\theta _2=\theta _2-\theta _3=\theta _3-\theta _1=2\pi /3\) and \(\omega ^2=0\) satisfies (5) for equal masses case. For not equal masses we have \(A\ne 0\). \(\square \)

To finish the proof of Theorem 1 we only have to prove the non-existence of mass-independent scalene Euler shape. We will do it in the next step.

3.1.2 Step 3: There Are No Mass-Independent Scalene Euler Shape on a Rotating Meridian

Proof

The Eq. (13) in terms of \(a=\tau _1\), \(b=\tau _2\) is

$$\begin{aligned} \cos (a)|\sin (a)|^3 =\cos (b)|\sin (b)|^3 =\cos (a+b)|\sin (a+b)|^3. \end{aligned}$$
(15)

The use of a and b is for later convenience. Obviously, \(\cos (a)\), \(\cos (b)\), and \(\cos (a+b)\) must have the same sign. Therefore, there are four possible regions.

  1. I:

    \(\pi /2<a<\pi ,\pi /2<b<\pi \), and \(\pi<a+b<3\pi /2\)

  2. II:

    a, b and \(0<a+b<\pi /2\)

  3. III:

    \(-\pi /2<a<0\), \(0<b<\pi /2\) and \(0<a+b<\pi /2\)

  4. IV:

    \(-\pi /2<a<0\), \(0<b<\pi /2\) and \(-\pi /2<a+b<0\)

3.1.3 Region I: \(\pi /2<a<\pi ,\pi /2<b<\pi \), \(\pi<a+b<3\pi /2\)

For this region, the Eq. (15) are equivalent to

$$\begin{aligned} \cos (a)\sin ^3(a)&=\cos (b)\sin ^3(b),\end{aligned}$$
(16)
$$\begin{aligned} 2^{-1}\big (\cos (a)\sin ^3(a)+\cos (b)\sin ^3(b)\big )&=-\cos (a+b)\sin ^3(a+b). \end{aligned}$$
(17)

Equation (16) yields

$$\begin{aligned} \begin{aligned} 0=&\cos (a)\sin ^3(a)-\cos (b)\sin ^3(b)\\ =&2^{-1}\sin (a-b) \Big (\cos (a+b)-\cos (2(a+b))\cos (a-b)\Big ). \end{aligned} \end{aligned}$$
(18)

Obviously, \(a=b\) is a solution, and this yields \(a=b=2\pi /3\) as above. Here we assume \(a\ne b\) to look for other solutions.

Then Eq. (18) reduces to

$$\begin{aligned} \cos (a+b) =\cos (2(a+b))\cos (a-b). \end{aligned}$$

If \(\cos (2(a+b))=0\), then \(a+b=5\pi /4\). But \(\cos (a+b)=\cos (5\pi /4)\ne 0\). Therefore \(\cos (2(a+b))\ne 0\). Then

$$\begin{aligned} \cos (a-b) =\frac{\cos (a+b)}{\cos (2(a+b))}\ne 1. \end{aligned}$$
(19)

(\(=1\) is excluded, because we are assuming \(a\ne b\)). The region for the absolute value of the right-hand side is smaller than 1, if \(4\pi /3< a+b<3\pi /2\).

On the other hand, using

$$\begin{aligned} \begin{aligned}&\cos (a)\sin ^3(a)+\cos (b)\sin ^3(b)\\&\quad =2^{-1}\sin (a+b)\Big ( \cos (a-b) -\cos (2(a-b))\cos (a+b) \Big ), \end{aligned} \end{aligned}$$

the Eq. (17) yields

$$\begin{aligned} \cos (a-b) -\cos (2(a-b))\cos (a+b) =-4\cos (a+b)\sin ^2(a+b). \end{aligned}$$
(20)

Substituting (19) in this equation, we get the equation for \(a+b\),

$$\begin{aligned} \frac{\cos (a+b)\sin ^4(a+b)}{\cos ^2(2(a+b))} \Big (2\cos (2(a+b))+1\Big )=0. \end{aligned}$$
(21)

But there are no solutions for \(a+b\in (4\pi /3,3\pi /2)\).

Thus, in this region the unique solution is the equilateral triangle shape \(a=b=2\pi /3\).

3.1.4 Region II: \(a,b,a+b\in (0,\pi /2)\)

For this region, the equations are

$$\begin{aligned} \cos (a)\sin ^3(a)&=\cos (b)\sin ^3(b),\end{aligned}$$
(22)
$$\begin{aligned} 2^{-1}\big (\cos (a)\sin ^3(a)+\cos (b)\sin ^3(b)\big )&=\cos (a+b)\sin ^3(a+b). \end{aligned}$$
(23)

By the same procedure, Eq. (22) yields, \(a=b\) or the same relation in (19).

For \(a=b\), we get \(a=b=2^{-1}\arccos ((\sqrt{2}-1)/2)\) as in the previous subsection.

For \(a\ne b\), we use the relation (19). In the region \(a+b\in (0,\pi /2)\), the range of the solution is \(a+b\in (\pi /3,\pi /2)\).

Now, the Eq. (23) yields

$$\begin{aligned} \cos (a-b)-\cos (2(a-b))\cos (a+b) =4\cos (a+b)\sin ^2(a+b). \end{aligned}$$

Substituting \(\cos (a-b)\) in (19) in this equation, we get

$$\begin{aligned} \frac{\cos (a+b)\sin ^2(a+b)}{\cos ^2(2(a+b))} \Big (2\cos ^2(2(a+b))+\cos (2(a+b))+1\Big )=0. \end{aligned}$$

But this equation has no solution.

Thus, in this region, the solution is only the isosceles triangle shape \(\theta _2-\theta _3=\theta _3-\theta _1=2^{-1}\arccos ((\sqrt{2}-1)/2).\) Here the mass \(m_3\) is placed in middle of the other two masses.

3.1.5 Region III: \(-\pi /2<a<0\), \(0<b<\pi /2\) and \(0<a+b<\pi /2\)

By the definition of a and b, the region in terms of the coordinates \(\theta _i\) is given by \(\theta _3-\theta _2,\theta _2-\theta _1,\theta _3-\theta _1 \in (0,\pi /2)\). Now, we redefine \(a=\theta _3-\theta _2\), \(b=\theta _2-\theta _1\), then \(a+b=\theta _3-\theta _1\) with \(a,b,a+b\in (0,\pi /2)\).

By this redefinition, Eq. (15) are invariant, and the region for the variables a, b is the same as for the Region II. Therefore, the solution is only the isosceles triangle shape \(\theta _3-\theta _2=\theta _2-\theta _1 =2^{-1}\arccos ((\sqrt{2}-1)/2)\). Here the mass \(m_2\) is placed in middle of the other two masses.

3.1.6 Region IV: \(-\pi /2<a<0\), \(0<b<\pi /2\) and \(-\pi /2<a+b<0\)

Using a similar argument for \(a=\theta _3-\theta _1\), \(b=\theta _1-\theta _2\) we obtain that the solution is only the isosceles solution \(\theta _3-\theta _1=\theta _1-\theta _2=2^{-1}\arccos ((\sqrt{2}-1)/2)\). Here the mass \(m_1\) is placed in middle of the other two masses.

This finishes the proof of the step 3. \(\square \)

With all the above, we have proved Theorem 1. \(\square \)

3.2 Mass-Independent Shapes for Relative Equilibria in the Two-Body Problem and the Restricted Three-Body Problem on the Sphere

The arguments given in the previous section are correct, even for the case when one of the masses \(m_k>0\) is really small. The next question is: What happen in the limit case when one of the mass, let’s say \(m_3 \rightarrow 0.\) There are two physically interesting problems to consider in this limit. One is the two-body problem, just considering the two masses \(m_1\) and \(m_2\) and neglecting the existence of the third mass. Another one is “the restricted three-body problem on the sphere.” where the position of \(m_3\) is concerned. This last case has been examined in Kilin (1999); Martínez and Simó (2017). We will show that our results are still true in the two- and the three-body problem.

We start from the equations in (7). For \(m_3\rightarrow 0\), we obtain two equations

$$\begin{aligned} m_1m_2\left( \frac{s\omega ^2}{2A}\sin \Big (2(\theta _1-\theta _2)\Big ) - \frac{\sin (\theta _1-\theta _2)}{|\sin (\theta _1-\theta _2)|^3} \right) =0, \end{aligned}$$
(24)

and

$$\begin{aligned} \begin{aligned}&m_2\left( \frac{s\omega ^2}{2A}\sin \Big (2(\theta _2-\theta _3)\Big ) - \frac{\sin (\theta _2-\theta _3)}{|\sin (\theta _2-\theta _3)|^3} \right) \\ =&m_1\left( \frac{s\omega ^2}{2A}\sin \Big (2(\theta _3-\theta _1)\Big ) - \frac{\sin (\theta _3-\theta _1)}{|\sin (\theta _3-\theta _1)|^3} \right) . \end{aligned} \end{aligned}$$
(25)

Note that the last equation does not contain the term \(m_3\).

We have the following propositions.

Proposition 3

For the two-body problem on a rotating meridian, any shape \(|\theta _1-\theta _2|\in (0,\pi )\) except \(\pi /2\) is a mass-independent shape.

Proof

For the two-body problem, the condition of ERE on a rotating meridian is only the Eq. (24). Obviously, \(|\theta _1-\theta _2|\in (0,\pi )\) except \(\pi /2\) satisfies this condition by choosing \(s\omega ^2\) properly. \(\square \)

Proposition 4

The mass-independent shapes in the restricted three-body problem on a rotating meridian are the same as in the three-body problem on the sphere with finite masses.

Proof

The conditions for this problem are (24) and (25). The last one determines the position of \(m_3\). Therefore, a mass-independent shape must make all terms inside of the parentheses zero. That is, the conditions are the same as for the three-body problem with finite masses. \(\square \)

4 Configuration of Mass-Independent Shape for Several Masses

Even for a mass-independent shape \(\{\sigma _{ij}\}\), the configuration \(\{\theta _k, \phi _i-\phi _j\}\) depends on the masses \(\{m_k\}\), because of the mass dependence of the rotation axis (z-axis) given by the inertia tensor (Fujiwara and Pérez-Chavela 2023).

4.1 Configurations of Equilateral Solution

If at least two masses are distinct, the equilateral solution has \(A>0\). Then, by Eq. (11), \(s=-1\) and \(\omega ^2=8A/(3\sqrt{3})\). The configuration is given by Eq. (8),

$$\begin{aligned} \begin{aligned} \cos (2\theta _1)&=\frac{1}{A}\left( \frac{m_2+m_3}{2}-m_1\right) ,\\ \sin (2\theta _1)&=\frac{\sqrt{3}}{2A}(m_2-m_3). \end{aligned} \end{aligned}$$
(26)

In Fig. 2, we show the configurations for several masses. The configuration is uniquely determined by Eq. (26).

On the other hand, for equal masses case, the configuration is indefinite. Namely, any configurations with \(\theta _i-\theta _j=2\pi /3\), \((i,j)=(1,2)\), (2, 3), (3, 1) satisfy the equation for relative equilibria (3) with \(\omega =0\). (See Step 2, in the proof of Theorem 1.)

Fig. 2
figure 2

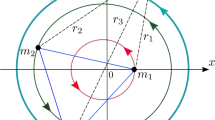
Configurations for several masses, from top to bottom, \((m_1,m_2,m_3)=(0.1,0.5,1)\), (0.4, 0.5, 1), (0.8, 0.9, 1), and (1, 1, 1). The vertical and horizontal axes represent the axis of rotation (z-axis) and the equator, respectively. The masses \(m_1\), \(m_2\), and \(m_3\) are indicated by the ball, square, and star, respectively. Columns from left to right, the equilateral configuration (left column), the isosceles whose center is \(m_3\) (the second column), \(m_1\) (the third column), and \(m_2\) (the right). The configuration for equilateral of equal masses (the bottom left corner) is indefinite, any configuration for equilateral shape is RE. See Sect. 4.1 for detail

Full size image

4.2 Configurations of Isosceles Solution

For the isosceles shape, \(A>0\), \(s=1\) and \(\omega ^2=16A/\sqrt{16\sqrt{2}-12}\). Let \(\tau _0=2^{-1}\arccos ((\sqrt{2}-1)/2)\) be the arc angle of equal arcs.

For \(\theta _2-\theta _3=\theta _3-\theta _1=\tau _0\),

$$\begin{aligned} A^2=\sum _\ell m_\ell ^2 -m_1m_2\left( 2\sqrt{2}-1\right) +(m_1+m_2)m_3\left( \sqrt{2}-1\right) , \end{aligned}$$

for \(\theta _3-\theta _1=\theta _1-\theta _2=\tau _0\),

$$\begin{aligned} A^2=\sum _\ell m_\ell ^2 -m_2m_3\left( 2\sqrt{2}-1\right) +(m_2+m_3)m_1\left( \sqrt{2}-1\right) , \end{aligned}$$

and for \(\theta _3-\theta _2=\theta _2-\theta _1=\tau _0\),

$$\begin{aligned} A^2=\sum _\ell m_\ell ^2 -m_3m_1\left( 2\sqrt{2}-1\right) +(m_3+m_1)m_2\left( \sqrt{2}-1\right) . \end{aligned}$$

In Fig. 2, we show the configurations for several masses.

5 Continuation of RE Shape from Mass-Independent Euler Shape

In the previous sections, we were concentrated on the mass-independent shapes. In this section, we search the continuations of RE shape near the mass-independent Euler shapes. We will show that every one of them can be continued to mass-dependent Euler shapes.

5.1 Condition for Euler Shapes on a Rotating Meridian

In this subsection, we review the condition for Euler shapes on a rotating meridian.

We have seen that Eq. (7) is a necessary and sufficient condition for Euler shape. Let \(F_{ij}\) and \(G_{ij}\) be

$$\begin{aligned} \begin{aligned} F_{ij}&=m_im_j\frac{\sin \tau _k}{|\sin \tau _k|^3} =\frac{m_im_j}{f(\tau _k)},\\ G_{ij}&=m_im_j\sin (2\tau _k), \end{aligned} \end{aligned}$$

for \((i,j,k)=(1,2,3),(2,3,1)\), and (3, 1, 2), where \(f(x)=\sin (x)|\sin (x)|\). Then, the condition (7) for the shape \(\{\tau _k\}\) is equivalent to (see (Fujiwara and Pérez-Chavela 2023) for details)

$$\begin{aligned} d =\left| \begin{array}{cc} G_{12}-G_{23} &{} G_{31}-G_{12} \\ F_{12}-F_{23} &{} F_{31}-F_{12} \end{array}\right| =0 \end{aligned}$$

for \(A\ne 0\). The explicit expression for d is

$$\begin{aligned} d=\frac{-m_1m_2m_3 \,g}{f(\tau _1)f(\tau _2)f(\tau _3)}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} g&=m_1f(\tau _1)\Big ( f(\tau _2)\sin (2\tau _2)-f(\tau _3)\sin (2\tau _3)\Big )\\&+m_2f(\tau _2)\Big ( f(\tau _3)\sin (2\tau _3)-f(\tau _1)\sin (2\tau _1)\Big )\\&+m_3f(\tau _3)\Big ( f(\tau _1)\sin (2\tau _1)-f(\tau _2)\sin (2\tau _2)\Big ). \end{aligned} \end{aligned}$$

Any solution of \(g=0\) in \((\tau _1,\tau _2)\in U_\text {phys}\) with \(A\ne 0\) is an Euler shape. Therefore, the condition \(g=0\) defines one-dimensional continuation of Euler shape in the shape space \(U_\text {phys}\).

5.2 Euler Shapes Near the Equilateral Euler Shape

For Euler shapes near the equilateral solution \(p_\text {I}=(2\pi /3,2\pi /3)\), it is sufficient to consider the region \(U=\{(\tau _1,\tau _2)| \sin (\tau _1)>0, \sin (\tau _2)>0, \sin (\tau _1+\tau _2)<0\}\cap U_\text {phys}\).

It is easy to verify that \(A^2=\sum _{i<j}(m_i-m_j)^2\) at \(p_\text {I}\).

Proposition 5

For not equal masses, two continuations of mass-dependent Euler shape pass through the equilateral Euler shape.

Proof

For not equal masses case, since at least one mass is different from the other, \(A^2>0\) at \(p_\text {I}\). Since A is a continuous function of p, we can take a region in U around \(p_\text {I}\), where \(A\ne 0\), and thus any solution of \(g=0\) in this region gives Euler shape.

At \(p_\text {I}\), \(g=\partial g/\partial \tau _1=\partial g/\partial \tau _2=0\). And the Hessian at this point is

$$\begin{aligned} H =\left( \begin{array}{cc} \partial ^2 g/\partial \tau _1^2 &{}\partial ^2 g/(\partial \tau _1\partial \tau _2) \\ \partial ^2 g/(\partial \tau _2\partial \tau _1) &{} \partial ^2 g/\partial \tau _2^2 \end{array}\right) =\frac{9\sqrt{3}}{4} \left( \begin{array}{cc} m_3-m_1 &{} m_2-m_1 \\ m_2-m_1 &{} m_2-m_3 \end{array}\right) . \end{aligned}$$

The determinant is given by

$$\begin{aligned} \det H=-\frac{243}{32}\sum _{i<j} (m_i-m_j)^2. \end{aligned}$$

By the assumption that at least two masses are different, \(\det H<0\). Therefore the point \(p_\text {I}\) is a saddle point. So, two \(g=0\) contours will pass through this point. \(\square \)

Proposition 6

For equal masses case, three continuations of Euler shape pass through the equilateral Euler shape.

Proof

For equal masses case \(m_k=m\), \(A=0\) has just one solution in U, given by \(p_\text {I}\). See Corollary 2 in Appendix 6 for a proof. As shown above, \(p_\text {I}\) gives Euler shape. Therefore, any solution of \(g=0\) in U gives Euler shape. Fortunately for equal mass in U, the function g has the following simple form

$$\begin{aligned} \begin{aligned} g&=\frac{m}{2} \Big (3-\cos \tau _1-\cos \tau _2-\cos (\tau _1+\tau _2)\Big )\\&\sin (\tau _1-\tau _2) \sin (2\tau _1+\tau _2) \sin (\tau _1+2\tau _2). \end{aligned} \end{aligned}$$

Since the first term is positive in U, the solution of \(g=0\) in U are \(\tau _1=\tau _2\), \(2\tau _1+\tau _2=2\pi \), or \(\tau _1+2\tau _2=2\pi \). Thus, on the \((\tau _1,\tau _2)\) plane, the three above straight lines pass through the point \(p_\text {I}=(2\pi /3, 2\pi /3)\), that is, the equilateral triangle Euler shape is not isolated. \(\square \)

5.3 Euler Shape Near the Isosceles Mass-Independent Euler Shape

In this subsection we will show that the isosceles mass-independent Euler shapes is not isolated, it has a continuation of mass-dependent Euler shapes.

Proposition 7

The mass-independent isosceles Euler shape has one continuation of mass-dependent Euler shape.

Proof

It is enough to show a proof for the mass-independent isosceles Euler shape given by \(p_\text {II}=(\tau _0,\tau _0)\), with \(\tau _0=2^{-1}\arccos ((\sqrt{2}-1)/2)\). The proof for the isosceles Euler shapes when the middle mass is different, that is for the shapes \(p_\text {III}=(-2\tau _0,\tau _0)\) and \(p_\text {IV}=(-\tau _0,2\tau _0)\) follows in a similar way using the same redefinition of coordinates as in Region III and Region IV, in the previous section.

We consider the region \(U=\{(\tau _1,\tau _2)| \sin (\tau _1)>0, \sin (\tau _2)>0, \sin (\tau _1+\tau _2)>0\}\cap U_\text {phys}\) near the point \(p_\text {II}=(\tau _0,\tau _0)\).

Since at this point \(A>0\), we can find a small region in U where \(A>0\) and therefore any solution of \(g=0\) gives an Euler shape.

Now, at \(p_\text {II}\), \(g=0\) and

$$\begin{aligned} \begin{aligned} g_1&=\frac{\partial g}{\partial \tau _1} =\frac{1}{8}\left( \left( 22-12\sqrt{2}\right) m_1 -\left( 10-\sqrt{2}\right) (m_2+m_3) \right) ,\\ g_2&=\frac{\partial g}{\partial \tau _2} =\frac{1}{8}\left( \left( 10-\sqrt{2}\right) (m_1+m_3) -\left( 22-12\sqrt{2}\right) m_2 \right) . \end{aligned} \end{aligned}$$

So, \(g_1=g_2=0\) is impossible, because, the unique solution for \(g_1=g_2=0\) is \(m_1=m_2=-(1+\sqrt{2})m_3<0\). Therefore, at least one of \(g_1\) or \(g_2\) is different from zero; and by the implicit function theorem, there is a continuation of \(g=0\) that passes through \(p_\text {II}\). \(\square \)

5.4 Numerical Calculations for Continuation of Euler Shapes

Fig. 3
figure 3

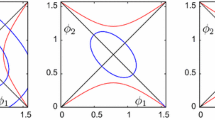
Continuations of \(g(\tau _1,\tau _2)=0\) in the shape space \(U_\text {phys}\) for \((m_1,m_2,m_3)=(0.1,0.5,1)\) (upper left), (0.4, 0.5, 1) (upper right), (0.8, 0.9, 1) (lower left), and (1, 1, 1) (lower right). The horizontal and vertical axes are \(\tau _1=\theta _2-\theta _3\) and \(\tau _2=\theta _3-\theta _1\), respectively. In each picture, the four black circles represent the mass-independent shapes, and three hollow circles represent the excluded shapes (singular points)

Full size image

In Fig. 3, we show continuations of Euler shapes for several masses that are represented by \(g=0\). As you can see, the continuation curve changes as the masses are changed. However, as we proved in Sect. 4 and shown in Fig. 3, the continuation curve passes through the (not moved) mass-independent Euler shape.

6 Appendix A: Solutions for the Equation \(A=0\)

In this section, the solutions of \(A=0\) in \(U_\text {phys}\) are described, where A and \(U_\text {phys}\) are defined by (6) and (3), the \(\tau _k\) are unknowns and the masses \(m_k\) are parameters.

In the following result, we assume that the masses must satisfy the triangle inequality \(m_i+m_j>m_k\) for all choices of (i, j, k), otherwise there are no solutions.

Proposition 8

The solutions of \(A=0\) in \(U_\text {phys}\) are given by,

$$\begin{aligned} \begin{aligned} \cos (2\tau _k)&=\frac{m_k^2-m_i^2-m_j^2}{2m_im_j},\\ \frac{\sin (2\tau _3)}{m_3}&=\frac{\sin (2\tau _1)}{m_1} =\frac{\sin (2\tau _2)}{m_2}, \end{aligned} \end{aligned}$$
(27)

where \(\tau _k=\theta _i-\theta _j\), \((i,j,k)=(1,2,3),(2,3,1)\), and (3, 1, 2).

Proof

Since, \(A^2=\left| \sum _\ell m_\ell e_\ell \right| ^2\) with \(e_\ell = (\cos (2\theta _\ell ),\sin (2\theta _\ell ))\in {\mathbb {R}}^2\), \(A=0\) is equivalent to \(\sum _\ell m_\ell e_\ell =0\). This means that the three vectors \(m_\ell e_\ell \) form a triangle with sides of length \(m_\ell \). That is the masses \(\{m_k\}\) satisfy the triangle inequality. The equality is excluded, because otherwise at least one of the equations should satisfy \(2\tau _k\equiv 0 \mod 2\pi \) (namely \(\tau _k \equiv 0 \mod \pi \)) which is excluded in \(U_\text {phys}\).

Using \(m_k e_k =-(m_i e_i+m_j e_j)\), \(m_k^2=\left| m_i e_i + m_j e_j\right| ^2\) and \(0=(m_i e_i+m_j e_j)\times e_k\) we obtain the equations in (27). \(\square \)

Corollary 1

The number of solutions for the equation \(A=0\) in \(U_\text {phys}\) for given masses \(\{m_k\}\) could be 0 or 4.

Proof

If the masses do not satisfy the triangle inequality, the number of solutions is zero.

For the masses that satisfy the triangle inequality, by the first equation of (27),

$$\begin{aligned} \cos \tau _k =\pm \sqrt{\frac{m_k^2-(m_i-m_j)^2}{4m_im_j}} \,\ne 0. \end{aligned}$$
(28)

Now, let

$$\begin{aligned} \alpha _k=\arccos \sqrt{\frac{m_k^2-(m_i-m_j)^2}{4m_im_j}} \in (0,\pi /2) \text{ for } k=1,2, \end{aligned}$$

be one of the solution of (28). Then the solutions of this equation are

$$\begin{aligned} \begin{aligned} \tau _1&= -\pi +\alpha _1,\quad -\alpha _1, \quad \alpha _1, \quad \pi -\alpha _1 \in (-\pi ,\pi ),\\ \tau _2&=\alpha _2, \quad \pi -\alpha _2 \in (0,\pi ). \end{aligned} \end{aligned}$$

By the second line of (27), \(\sin (2\tau _1)\) and \(\sin (2\tau _2)\) must have the same sign, therefore, the solutions of (27) are the following four,

$$\begin{aligned} (\tau _1,\tau _2) = (-\pi +\alpha _1,\alpha _2), \quad (-\alpha _1,\pi -\alpha _2), \quad (\alpha _1,\alpha _2), \quad (\pi -\alpha _1,\pi -\alpha _2). \end{aligned}$$

\(\square \)

Corollary 2

For the equal masses case, the four solutions of \(A=0\) in \(U_\text {phys}\) are \((\tau _1,\tau _2)=(-2\pi /3,\pi /3)\),    \((-\pi /3,2\pi /3)\),    \((\pi /3,\pi /3)\),    \((2\pi /3,2\pi /3)\).

Proof

For the equal masses case, \(\cos \tau _k=\pm 1/2\), therefore \(\alpha _1=\alpha _2=\pi /3\). Then, the solutions are obviously the four given above. \(\square \)

Corollary 3

The shape corresponding to the solution of the equation \(A=0\) when \(\tau _i=\tau _j\) in \(U_\text {phys}\) is realized only when \(m_i=m_j\).

Proof

It is obvious from the Eq. (27). \(\square \)