Relative equilibria of the restricted three-body problem in curved spaces

Abstract

We use a formulation of the N-body problem in spaces of constant Gaussian curvature, ${\kappa }\in \mathbb {R}$, as widely used by A. Borisov, F. Diacu and their coworkers. We consider the restricted three-body problem in $\mathbb {S}^2$ with arbitrary ${\kappa }>0$ (resp. $\mathbb {H}^2$ with arbitrary ${\kappa }<0$) in a formulation also valid for the case ${\kappa }=0$. For concreteness when ${\kappa }>0$ we restrict the study to the case of the three bodies at the upper hemisphere, to be denoted as $\mathbb {S}^2_+$. The main goal is to obtain the totality of relative equilibria as depending on the parameters ${\kappa }$ and the mass ratio $\mu$. Several general results concerning relative equilibria and its stability properties are proved analytically. The study is completed numerically using continuation from the ${\kappa }=0$ case and from other limit cases. In particular both bifurcations and spectral stability are also studied. The $\mathbb {H}^2$ case is similar, in some sense, to the planar one, but in the $\mathbb {S}^2_+$ case many differences have been found. Some surprising phenomena, like the coexistence of many triangular-like solutions for some values $({\kappa },\mu )$ and many stability changes will be discussed.

1 Introduction

The gravitational N-body problem is usually studied in flat spaces, $\mathbb {R}^2$ or $\mathbb {R}^3$. However it is already a classical problem to study the effect of the space curvature. See, e.g., Borisov et al. (2004), Diacu (2012), Diacu to appear in CJM, and references therein for detailed accounts on historical facts. The interest of the study is also stressed in problem 13 of the nice series of problems in Kozlov (1995). One can consider spaces of constant Gaussian curvature ${\kappa }\ne 0$ like 3-spheres (resp. 2-spheres) of radius $R={\kappa }^{-1/2}$ embedded in $\mathbb {R}^4$ (resp. in $\mathbb {R}^3$) for ${\kappa }>0$, and on hyperbolic 3-spheres (resp. 2-spheres) of imaginary radius $iR={\kappa }^{-1/2}$ embedded in the Minkowski space $\mathbb {R}^{3,1}$ (resp. in $\mathbb {R}^{2,1}$) for ${\kappa }<0$.

Properties of the solutions can allow to test assumptions on the curvature or, based on experimental data, to put bounds on the admissible value of ${\kappa }$. To this end one has to extend the classical Newtonian force function to the curved space. See Diacu to appear in CJM for details and context.

We are interested in how the relative equilibria of the flat case change due to curvature. For concreteness we shall reduce to 2-dimensional problems, the spherical case $\mathbb {S}^2_+$ and the hyperbolic case $\mathbb {H}^2$. Furthermore it is very convenient to consider a unified formulation allowing to pass from the flat case $\mathbb {R}^2$ when ${\kappa }=0$ to $\mathbb {S}^2_+$ for ${\kappa }>0$ and to $\mathbb {H}^2$ for ${\kappa }<0$. While a point in $\mathbb {R}^2$ is identified by coordinates (x, y), looking at the surfaces $\mathbb {S}^2$ and $\mathbb {H}^2$ in the form

$$\begin{aligned} \mathbb {S}^2_{{\kappa }}= & {} \{(x,y,z)|{\kappa }(x^2+y^2)+({\kappa }^{1/2}z+1)^2=1\}, \\ \mathbb {H}^2_{{\kappa }}= & {} \{(x,y,z)|{\kappa }(x^2+y^2)+(|{\kappa }|^{1/2}z+1)^2=1, z\!\ge \! 0\}, \end{aligned}$$

it is clear that they are revolution surfaces tangent to $z=0$ at $x=y=0$. $\mathbb {S}^2$ has the equator located on $z=-1/\sqrt{{\kappa }}$. In the case of $\mathbb {H}^2$ one can put z as a function of $x,y,{\kappa }$. The same is true for ${\kappa }>0$ if we restrict ourselves to consider points in $\mathbb {S}^2_+$, i.e., on the upper hemisphere.

Further studies can consider the problem in $\mathbb {S}^3$ and $\mathbb {H}^3$. Then, for small ${\kappa }$ one can look at the practical domain of stability around the triangular points, to be compared with the real observations of Jupiter Trojan asteroids (a total of 6457 on August 20, 2016, according to the Minor Planet Center). Beyond the local behavior around the points this domain is bounded by several large invariant manifolds, see Simó et al. (2013) and references therein for details. At least for this physical application it seems reasonable to consider only the upper hemisphere.

Based on results in Diacu to appear in CJM, F. Diacu has presented in arXiv:1508.06043 the following unified equations for the N-body problem with masses $m_i,i=1, \ldots ,N$

$$\begin{aligned} {\ddot{x}}_i= & {} \sum _{j=1}^N\frac{m_j\left[ x_j-\left( 1-\frac{{\kappa }r_{ij}^2}{2}\right) x_i\right] }{r_{ij}^3\left( 1-\frac{{\kappa }r_{ij}^2}{4}\right) ^{3/2}}- {\kappa }{\dot{r}}_i^2 x_i, \qquad \nonumber \\ {\ddot{y}}_i= & {} \sum _{j=1}^N\frac{m_j\left[ y_j-\left( 1-\frac{{\kappa }r_{ij}^2}{2}\right) y_i\right] }{r_{ij}^3\left( 1-\frac{{\kappa }r_{ij}^2}{4}\right) ^{3/2}}- {\kappa }{\dot{r}}_i^2 y_i, \end{aligned}$$

(1)

where $r_{ij}^2=(x_i-x_j)^2+(y_i-y_j)^2+\sigma (z_i-z_j)^2$ and ${\dot{r}}_i^2={\dot{x}}_i^2+{\dot{y}}_i^2+\sigma {\dot{z}}_i^2$, being $\sigma =1$ if ${\kappa }\ge 0$ and $\sigma =-1$ if ${\kappa }<0$.

The study of relative equilibria of the N-body problem in the flat case has a long history. In particular, for the three body problem it is well known, since Euler and Lagrange, the existence of 3 collinear and 2 triangular relative equilibria for any values of the masses, see. e.g., Siegel and Moser (1971) and Szebehely (1967). The stability for these equilibria for arbitrary positive masses and for the related homographic solutions with any value of the eccentricity has been studied by different authors. See for instance Martínez et al. (2006) and references therein for this problem which depends on two essential parameters.

A study of Kepler’s problem in manifolds of constant curvature can be found in Kozlov and Harin (1992) and Chernoïvan and Mamaev (1999). Several papers, like García-Naranjo et al. (2016), Diacu and Pérez-Chavela (2011), Diacu (2012, 2014) and Zhu (2014), study the existence of relative equilibria of the curved problem for 3 or more bodies. In Martínez and Simó (2013) a related problem was studied, looking at the general three-body problem with equal masses in $\mathbb {S}^2$ and considering homographic solutions and its stability. In Diacu et al. (2013) four bodies are considered, also in $\mathbb {S}^2$, one of them of mass $m_1=1$ located at the north pole ($x=y=z=0$ in the present variables) and the other three of equal mass at the vertices of an equilateral triangle located on a parallel ($z=$ constant) and looking for stability. In both cases there are few parameters in the problem.

In Borisov et al. (2004) and Chernoïvan and Mamaev (1999), the study of the two body and Kepler problems, respectively, in $\mathbb {S}^2$ is completed with periodic orbits and the existence of chaotic dynamics is shown for some masses. An interesting question could be the existence of invariant tori and the fractions of the phase space which have regular/chaotic dynamics and how this depends on the mass ratio and the energy.

Our goal in this paper is to study the full set of relative equilibrium solutions in the case of the restricted three-body problem and its stability properties. That is, we consider two massive bodies of masses $m_1$ and $m_2$. One can scale the unit of mass in such a way that $m_1+m_2=1$ and use simply the mass ratio $\mu =m_2$ to specify the masses. First we look for solutions of this two-body problem such that they are at rest in a system which rotates with angular velocity $\alpha$ around the z axis. Then we consider the possible location of a massless body such that the three bodies are in a relative equilibrium.

In this way the problem depends on parameters $\mu ,\alpha$ and ${\kappa }$. However, after a suitable normalization, one can reduce to consider 2 parameters, $\mu$ and ${\kappa }$ (taking $\alpha =1$) or $\mu$ and $\alpha$ (taking ${\kappa }=1$ or ${\kappa }=-1$). We shall choose the most convenient normalization to simplify the proofs and the numerical computations. As done in Martínez and Simó (2013), the use of 2 parameters allows for a rich set of solutions.

For the restricted problem there are important differences between the cases ${\kappa }\!>\!0$ and ${\kappa }\!<\!0$. While in the case of $\mathbb {H}^2$, ${\kappa }<0$, the relative equilibria appear to be the classical 3 Eulerian and 2 Lagrangian solutions, like in the planar case, in the case of $\mathbb {S}^2_+$, ${\kappa }>0$, several bifurcations appear, changing the number of equilibria. The most relevant facts in $\mathbb {S}^2_+$ are the following:

• 1. The number of collinear solutions, with the three bodies on the same meridian in the rotating system, ranges between 1 and 5,

• 2. The number of triangular solutions, the three bodies being not located on a maximal circle, ranges between 0 and 8,

• 3. Collinear and triangular equilibria of the planar case, ${\kappa }=0$, can be continued numerically to ${\kappa }\ne 0$. In particular, starting at one of the classical Lagrangian solutions, $L_5$, the continuation path to ${\kappa }>0$ passes through a collinear solution and reaches the other Lagrangian solution $L_4$ when ${\kappa }$ returns to zero.

In Sect. 2 the equations of motion are written in a suitable rotating frame and the conditions for relative equilibrium are obtained. The two-body problem is studied completely in Sect. 3. If ${\kappa }< 0$, for any $\mu \in (0,1)$ and $\alpha \ne 0$, there is a unique equilibrium. However, if ${\kappa }>0$, for any fixed $\mu \in (0,1)$ the number of equilibria changes depending on $\alpha$. The spectral stability is also determined in both cases. See Kilin (1999) for related numerical results.

Section 4 is devoted to obtain existence results for the restricted problem, considering the collinear and triangular cases in Sects. 4.1 and 4.2, respectively. The case $\mathbb {H}^2$ is completely described in Propositions 4.1 and 4.2. In the case $\mathbb {S}^2_+$, analytic results are provided for $\mu =1/2$ and for some limit cases, both for collinear and triangular equilibria. It is also proved that for any admissible fixed $\mu$ and $\alpha$ the number of triangular relative equilibria is at most 8. Moreover there are triangular equilibria that can not be obtained by continuation of the planar case. Furthermore, some bifurcation curves are obtained analytically.

Section 5 is devoted to complete numerically the results obtained in Sect. 4. A complete picture is given for the full range of parameters, both in the collinear and triangular cases. The bifurcation curves are completely described. In the triangular case, we found a tiny region in the parameter domain where there are exactly 8 relative equilibria. The numerical continuation of the solution from the planar case shows the connections between the Lagrangian solutions $L_4$ and $L_5$ as mentioned above in point 3. Moreover, the domain where there exist triangular equilibria not connected with the ones in the planar case, is numerically described.

Section 6 is devoted to the spectral stability of the relative equilibria, including both theoretical and numerical results.

2 Equations of motion

It will be convenient to rewrite Eqs. (1) in the case of three bodies in an equivalent form which introduces several auxiliary functions to be widely used in what follows

$$\begin{aligned} {\ddot{\mathbf{q}}}_i= & {} \sum _{j=1, j \ne i}^3 \frac{m_j}{d_{ij}^3} [ \mathbf{q}_j - f_{ij} \mathbf{q}_i ] - {\kappa }v_i \mathbf{q}_i, \qquad i=1,2,3, \end{aligned}$$

(2)

where $\mathbf{q}_i =(x_i,y_i)$ and

$$\begin{aligned} v_i= & {} | {\dot{\mathbf{q}}}_i|^2 + {\kappa }\frac{( \mathbf{q}_i, {\dot{\mathbf{q}}}_i)^2}{E_i^2}, \quad E_i = {\sqrt{1-{\kappa }{A}_i}}, \quad A_i = x_i^2 + y_i^2, \nonumber \\ \rho _{ij}^2= & {} (x_i-x_j)^2 + (y_i-y_j)^2\! +\! {\kappa }\frac{(A_i\! -\!A_j)^2}{(E_i+E_j)^2}, \quad f_{ij}= 1\!- \!\frac{{\kappa }}{2} \rho _{ij}^2, \quad \nonumber \\ d_{ij}= & {} \rho _{ij} \left( 1 - \frac{{\kappa }}{4} \rho _{ij}^2 \right) ^{1/2}. \end{aligned}$$

(3)

Let us denote by $\mathbf{U}_i = (\xi _i, \eta _i)^T,\; i=1,2,3$ the coordinates of the masses $m_1, m_2, m_3$ in a frame which rotates with angular velocity $\alpha$, that is,

$$\begin{aligned} \mathbf{q}_i = {{\mathcal {R}}}(\theta ) \mathbf{U}_i, \qquad {{\mathcal {R}}}(\theta ) = \left( \begin{array}{cr} \cos \theta &{} - \sin \theta \\ \sin \theta &{} \cos \theta \\ \end{array} \right) , \end{aligned}$$

where $\alpha ={\dot{\theta }}(t)$. In the rotating frame the equations of motion are

$$\begin{aligned} {\ddot{\mathbf{U}}}_i - 2 \alpha J {\dot{\mathbf{U}}}_i - \alpha ^2 \mathbf{U}_i = \sum _{j \ne i} m_j g_{ij} [ \mathbf{U}_j - f_{ij} \mathbf{U}_i] - {\kappa }v_i \mathbf{U}_i, \qquad i=1,2,3, \end{aligned}$$

(4)

where

(5)

and $f_{ij},d_{ij}$ are defined as in (3). We note that for ${\kappa }> 0$, $E_i$ is defined if $\xi _i^2 + \eta _i^2 < 1/\sqrt{{\kappa }}$. However, in the case ${\kappa }< 0$, there is no restriction on $(\xi _i, \eta _i).$ Reduced expressions for these functions are given in the “Appendix”.

The restricted three body problem is obtained when $m_3 =0$. Then (4) reduce to

$$\begin{aligned}&{\ddot{\mathbf{U}}}_1 - 2 \alpha J {\dot{\mathbf{U}}}_1 - \alpha ^2 \mathbf{U}_1 = m_2 g_{12} [ \mathbf{U}_2 - f_{12} \mathbf{U}_1] - {\kappa }v_1 \mathbf{U}_1, \nonumber \\&{\ddot{\mathbf{U}}}_2 - 2 \alpha J {\dot{\mathbf{U}}}_2 - \alpha ^2 \mathbf{U}_2 = m_1 g_{21} [ \mathbf{U}_1 - f_{21} \mathbf{U}_2] - {\kappa }v_2 \mathbf{U}_2,\\&{\ddot{\mathbf{U}}}_3 - 2 \alpha J {\dot{\mathbf{U}}}_3 - \alpha ^2 \mathbf{U}_3 = \sum _{j =1,2} m_j g_{3j} [ \mathbf{U}_j - f_{3j} \mathbf{U}_3] - {\kappa }v_3 \mathbf{U}_3.\nonumber \end{aligned}$$

(6)

The equations for an equilibrium are

$$\begin{aligned}&\alpha ^2 (1 - {\kappa }(\xi _1^2 + \eta _1^2)) \mathbf{U}_1 + m_2 g_{12} ( \mathbf{U}_2 - f_{12} \mathbf{U}_1) = 0, \end{aligned}$$

(7)

$$\begin{aligned}&\alpha ^2 (1 - {\kappa }(\xi _2^2 + \eta _2^2)) \mathbf{U}_2 + m_1 g_{12} ( \mathbf{U}_1 - f_{21} \mathbf{U}_2) = 0, \nonumber \\&-m_1 g_{13} \mathbf{U}_1 - m_2 g_{23} \mathbf{U}_2 +[m_1 g_{13} f_{13} + m_2 g_{23} f_{23} - \alpha ^2 (1-{\kappa }(\xi _3^2 + \eta _3^2))] \mathbf{U}_3 = 0.\nonumber \\ \end{aligned}$$

(8)

We shall assume $\eta _1 = \eta _2 =0$ at the equilibrium. In fact, by the rotational symmetry we can take $\eta _1 =0$. Then (7) implies $\eta _2 =0$. Therefore the equations for an equilibrium of the two body problem reduce to

$$\begin{aligned}&\alpha ^2 (1-{\kappa }( \xi _1^2 + \eta _1^2) ) \xi _1 = - m_2 g_{12} (\xi _2 - \xi _1 f_{12}), \end{aligned}$$

(9)

$$\begin{aligned}&\alpha ^2 (1-{\kappa }( \xi _2^2 + \eta _2^2) ) \xi _2 = - m_1 g_{12} (\xi _1 - \xi _2 f_{21}). \end{aligned}$$

(10)

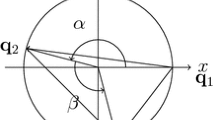
However, if $\eta _1=\eta _2=0$ from (50) we have $f_{12}\!= \!{\kappa }\xi _1 \xi _2 + E_1 E_2$ and then $\xi _2 - \xi _1 f_{12} = E_1 (\xi _2 E_1 - \xi _1 E_2)$ and $\xi _1\! -\! \xi _2 f_{21}\! =\! - E_2 (\xi _2 E_1\! -\! \xi _1 E_2)$. Hence, in order to satisfy (9) and (10), $\xi _1$ and $\xi _2$ must have opposite sign. So, from now on we shall assume that the bodies of masses $m_1,m_2$ are located at $\mathbf{U}_1=(r_1,0)^T$, $\mathbf{U}_2=(-r_2,0)^T$, respectively, where $r_1\!>\!0, r_2\!>\!0$ satisfy the equilibrium equations

$$\begin{aligned}&\alpha ^2 r_1 (1-{\kappa }r_1^2) = m_2 g_{12} E_1(r_2 E_1+r_1 E_2),\end{aligned}$$

(11)

$$\begin{aligned}&\alpha ^2 r_2 (1-{\kappa }r_2^2) = m_1 g_{12} E_2(r_2 E_1+r_1 E_2). \end{aligned}$$

(12)

First we shall study the existence of solutions of (11), (12) and consider the corresponding equilibria $(r_1,0)^T,\; (-r_2,0)^T$ for the primaries. Then we shall study the stability of these equilibria.

Once $r_1>0,r_2>0$ are fixed we shall look for the equilibria, $\mathbf{U}_3=(a,b),$ of $m_3$. We shall distinguish mainly two cases: collinear and triangular.

For collinear solutions, that is $b=0$, (8) reduces to

$$\begin{aligned} {[}m_1 g_{13} f_{13} + m_2 g_{23} f_{23} - \alpha ^2 (1-{\kappa }a^2) ] a - m_1 g_{13} r_1 + m_2 g_{23} r_2 =0. \end{aligned}$$

(13)

The corresponding equations for non collinear solutions, that is $b\ne 0$, are

$$\begin{aligned}&m_1 g_{13} r_1 - m_2 g_{23} r_2 = 0, \end{aligned}$$

(14)

$$\begin{aligned}&m_1 g_{13} f_{13} + m_2 g_{23} f_{23} - \alpha ^2 (1-{\kappa }(a^2+ b^2)) = 0. \end{aligned}$$

(15)

Remark 2.1

For ${\kappa }\ne 0$ the Eqs. (2) can be reduced to the case ${\kappa }=1$ if ${\kappa }$ is positive and to ${\kappa }=-1$ if ${\kappa }$ is negative. This is achieved by introducing new variables $\mathbf{Q}_i=\mathbf{q}_i|{\kappa }|^{1/2},$ $i=1,2,3,$ and a new time $\tau$, defined by $d\tau =|{\kappa }|^{3/4} dt$. This scaling will be useful to simplify some analytic and numerical computations. However we shall keep the dependence on ${\kappa }$ to study the continuation of solutions from the planar case ${\kappa }=0$ to the curved space ${\kappa }\ne 0$. We note that for the equilibria Eqs. (11) to (15) the scaling is achieved by introducing $\rho _i = r_i |{\kappa }|^{1/2},$ $i=1,2$, $A=a|{\kappa }|^{1/2},$ $B=b|{\kappa }|^{1/2}$ and ${\hat{\alpha }}= \alpha |{\kappa }|^{-3/4}$. In a similar way one can keep ${\kappa }$ without any normalization and set $\alpha =1$.

3 The two body problem in $\mathbb {S}^2_+$ and $\mathbb {H}^2$

First we consider the Eqs. (11) and (12) for the primaries. They can be written as

$$\begin{aligned} \mu = F(r_1,r_2), \qquad \alpha ^2 = G(r_1,r_2), \end{aligned}$$

(16)

where

$$\begin{aligned} F(r_1,r_2) = \frac{r_1 E_1}{r_1 E_1 + r_2 E_2}, \quad G(r_1,r_2) = \frac{1}{(r_1 E_2 + r_2 E_1)^2 (r_1 E_1+r_2 E_2)} \end{aligned}$$

(17)

and we have used (51) and (52). See also (23).

Given some values of $\mu$ and $\alpha ^2$, we are interested in the number of solutions $(r_1,r_2)$ of (16) with $(r_1,r_2)\!\in \!Q\!:=\!(0,1/ \sqrt{{\kappa }})\! \times \! (0,1/\sqrt{{\kappa }})$ if ${\kappa }\!>\!0$, and $(r_1,r_2) \!\in \! (0,\infty )\! \times \! (0,\infty )$ if ${\kappa }\! <\! 0$.

We work in $\mathbb {S}^2_+$ for ${\kappa }>0$. See Borisov et al. (2004), Chernoïvan and Mamaev (1999) and Kilin (1999), for results in the lower hemisphere.

Proposition 3.1

Assume ${\kappa }\!>\!0$. For any $\mu \!\in \!(0,1)\!\setminus \!\{1/2\}$, there exists $\alpha _c(\mu )^2\! >\! {\kappa }^{3/2}$, such that

• 1. If $0<\alpha ^2<\alpha _c^2$ then (16) has no solutions for $r_1,r_2$ in Q,

• 2. If $\alpha ^2 = \alpha _c^2$, (16) has exactly two solutions in Q,

• 3. If $\alpha ^2 > \alpha _c^2$, (16) has exactly four solutions in Q.

If $\mu =1/2$ then (16) has no solutions for $0<\alpha ^2< {\kappa }^{3/2}$, four solutions for $\alpha ^2> {\kappa }^{3/2}$, and exactly one solution $(r_1,r_2) =(1/\sqrt{2{\kappa }},1/\sqrt{2{\kappa }})$ if $\alpha = {\kappa }^{3/2}$.

Proof

In order to simplify computations we shall take ${\kappa }=1$ (see Remark 2.1) and we keep the same notation $r_1, r_2, \alpha$ for the scaled variables. Given some values of $\mu$ and $\alpha$ we look for the number of intersections of the level curves of F and G corresponding to values $\mu$ and $\alpha$ respectively.

The level curves of F can be obtained explicitly. In particular, if $\mu =1/2$ they have two components: $r_2=r_1$ and $r_1^2+r_2^2=1$ which intersect at the point $P_*=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$. In fact, $P_*$ is the unique critical point of the functions $F(r_1,r_2)$ and $G(r_1,r_2)$ in the square $Q=(0,1)\!\times \!(0,1)$, and $F(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})=1/2$ and $G(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})=1$. So, $P_*$ is a solution of (16) for $\mu =1/2$ and $\alpha ^2=1$.

To emphasize the symmetries we introduce a change of variables

$$\begin{aligned} (r_1,r_2)\in Q\mapsto (u,v)\in {{\mathcal {Q}}}=\{(u,v)\in \mathbb {R}^2\,|\,-\pi /2<u\pm v< \pi /2 \}, \end{aligned}$$

where $u=\phi _1+\phi _2-\pi /2,\,\, v=\phi _1-\phi _2$ being $\phi _1,\phi _2$ in $(0,\pi /2)$ such that $r_i=\sin (\phi _i)$, $i=1,2$. In the new variables the Eq. (16) become

$$\begin{aligned} \mu= & {} {\hat{F}}(u,v):=\frac{1}{2}(1-\tan u \tan v ),\qquad (u,v)\in {{\mathcal {Q}}},\end{aligned}$$

(18)

$$\begin{aligned} \alpha ^2= & {} {\hat{G}}(u,v):=\frac{1}{\cos ^3 u \cos v}, \qquad (u,v) \in {{\mathcal {Q}}}. \end{aligned}$$

(19)

From (19) it is clear that there are no solutions if $\alpha ^2<1$ (that is, $\alpha ^2<k^{3/2}$ for the non scaled $\alpha$). If $\alpha ^2=1$ then $u=v= 0$, and $\mu ={\hat{F}}(0,0)=1/2$. Then $P_*$ is the unique solution in this case. From now on we shall consider $\alpha ^2>1$.

The following equalities hold

$$\begin{aligned} {\hat{F}}(u,v)={\hat{F}}(-u,-v),\qquad {\hat{G}}(u,v)={\hat{G}}(-u,v)={\hat{G}}(u,-v) = {\hat{G}}(-u,-v). \end{aligned}$$

Moreover, (18) is equivalent to $1-2\mu =\tan u\tan v$. Then, it is sufficient to consider $0<\mu <1/2$. In this case (18) has two symmetrical branches in the first and third quadrants, respectively. Notice that ${\hat{F}}(u,v)=1/2$ reduces to the axes. Therefore it is sufficient to consider $0<\mu <1/2$, and $(u,v)\in \hat{{{\mathcal {Q}}}}:=\{(u,v)\in {{\mathcal {Q}}}\,|\,u>0,v>0\}.$

In $\hat{{{\mathcal {Q}}}}$, (18) and (19) are, respectively, the graphs of the following functions

$$\begin{aligned} v = f(u):=\arctan \left( \frac{1-2 \mu }{\tan u} \right) , \qquad v = g(u):=\arccos \left( \frac{1}{\alpha ^2 \cos ^3 u} \right) . \end{aligned}$$

For $(u,v)\in \hat{{{\mathcal {Q}}}}$ an elementary computation gives $f^\prime (u)<0,\, f^{\prime \prime }(u)>0,\,g^\prime (u)<0,\, g^{\prime \prime }(u)<0$. Therefore, given $\mu \in (0,1/2)$ and $\alpha ^2>1$, the graphs of f and g in $\hat{{{\mathcal {Q}}}}$ can intersect in 0, 1 or 2 points. The number of solutions changes when a tangency is achieved. It is easy to check that tangencies occur along the bifurcation curve

$$\begin{aligned} v = \arcsin ( \sqrt{3} \sin u), \end{aligned}$$

(20)

which is an increasing function from the origin to the point $(u,v)=(\pi /6, \pi /3)$. Given a value of $\mu ,$ $0<\mu <1/2$, let $(u_\mu ,v_\mu )\in \hat{{{\mathcal {Q}}}}$ be the point of the bifurcation curve (20) such that ${\hat{F}}(u_\mu ,v_\mu )=\mu$. Then we define $\alpha _c(\mu )^2={\hat{G}} (u_\mu ,v_\mu )\!>\!1$ and the Lemma follows. $\square$

Figure 1 shows level curves of F and G, as functions of the angles $\phi _1$ and $\phi _2$, for different values of $\mu$ and $\alpha$, displaying also the symmetry lines $\phi _2=\phi _1$ and $\phi _1+\phi _2=\pi /2$. In the left plot we show two different values of $\alpha ^2$, both giving rise to solutions. For $\alpha ^2=\alpha _c^2(0)$ the G level curve is tangent to the boundaries of the domain and it has four components for $\alpha ^2> \alpha _c^2(0)$. Note that increasing $\alpha ^2$ for ${\kappa }$ fixed is equivalent to fix $\alpha ^2$ and let ${\kappa }$ tend to 0.

Fig. 1

Some level curves of F (in red) and G (in blue), as functions of $(\phi _1,\phi _2)$, for $\mu =0.4,\;\alpha ^2=1.5$ and $\alpha ^2=4$ (left), $\mu =0.6,\; \alpha ^2=1.2<\alpha _c^2(\mu )$ (middle), $\mu =0.6,\;\alpha ^2=1.5>\alpha _c^2(\mu )$ (right)

Figure 2 shows the two branches of the bifurcation curve in magenta, using the angles $\phi _1,$ $\phi _2$. Also tangent level curves of F and G have been plotted. As additional information we display the critical scaled function $\alpha _c^2$ as a function of $\mu \in (0,1/2)$. It is immediate to check that $\alpha _c(\mu )^2$ is decreasing, with limit values $\alpha _c(0)=16/\sqrt{27},\alpha _c(1/2)=1$. One also has $\alpha _c^2(\mu )=\alpha _c^2(1-\mu )$.

Fig. 2

Bifurcation curves in magenta and some level curves of F and G with the bifurcation curve, represented in the $(\phi _1,\phi _2)$ variables. Left $\mu =0.3701431592, \; \alpha ^2 =1.480380414$. Middle $\mu =0.5474073109, \; \alpha ^2 = 1.168557976$. The right plot shows $\alpha _c^2$ as a function of $\mu$

Proposition 3.2

Assume ${\kappa }< 0$. For any fixed $\mu \in (0,1)$ and $\alpha ^2 \ne 0$, there is a unique solution of (16) with $r_1 >0,$ $r_2 >0$.

Proof

According to Remark 2.1 we can take ${\kappa }=-1$. Similar to what was done for Proposition 3.1 let us introduce $\gamma _1,\gamma _2$ such that $r_i=\sinh (\gamma _i),\,i=1,2$ and then $E_i=\sqrt{1+r_i^2}=\cosh (\gamma _i)$. The level curves of F and G satisfy

$$\begin{aligned} \sinh (2\gamma _2)= & {} \frac{1-\mu }{\mu }\sinh (2\gamma _1)\!\quad \! {\text{ and }}\nonumber \\ G^*(\gamma _1,\gamma _2):= & {} \sinh ^2(\gamma _1+\gamma _2) (\sinh (2\gamma _1) +\sinh (2\gamma _2))=\frac{2}{\alpha ^2}, \end{aligned}$$

(21)

respectively. From the first Eq. in (21) one has $\gamma _2$ strictly increasing wrt $\gamma _1$ (and, hence, $r_2$ wrt $r_1$) for fixed $\mu$. From the second one, and using $\partial G^*/\partial \gamma _i>0,\,i=1,2$, one has $\gamma _2$ strictly decreasing wrt $\gamma _1$ (and, hence, $r_2$ wrt $r_1$) for fixed $\alpha$. The level curves of F pass through (0, 0) and the ones of G through $(0,r_2^*)$ and $(r_1^*,0)$ where the related $\gamma _i^*$ satisfy $\sinh ^2(\gamma _i^*)\sinh (2\gamma _i^*)=2/\alpha ^2$. This proves the existence of a unique intersection point. $\square$

Proposition 3.3

Assume that $\mu$, $\alpha ^2$ and ${\kappa }\ne 0$ are fixed. Let $r_1>0, r_2>0$ satisfy the equilibrium Eqs. (11) and (12). Then the relative equilibrium of the two body problem is spectrally stable if ${\kappa }^2 r_1^2 r_2^2 < 1/4$ and, it is unstable if ${\kappa }^2 r_1^2 r_2^2 > 1/4$.

Proof

We introduce new variables $x_i=\xi _i, \; y_i= \eta _i, \; X_i = {\dot{\xi }}_i, \; Y_i = {\dot{\eta }}_i,$ $i=1,2$ to write (6) as a first order system

$$\begin{aligned}&{\dot{x}}_i=X_i,\quad {\dot{y}}_i=Y_i,\quad {\dot{X}}_i=2\alpha Y_i+\alpha ^2x_i-{\kappa }x_iv_i+F_i,\quad \\&{\dot{Y}}_i=-2\alpha X_i+\alpha ^2y_i-{\kappa }y_iv_i+G_i, \quad i=1,2, \end{aligned}$$

where

$$\begin{aligned} F_1= & {} \frac{m_2}{d_{12}^3} (x_2 - x_1 f_{12}),\quad F_2=\frac{m_1}{d_{12}^3} (x_1 - x_2 f_{12}), \nonumber \\ G_1= & {} \frac{m_2}{d_{12}^3} (y_2 - y_1 f_{12}), \quad G_2 = \frac{m_1}{d_{12}^3} (y_1 - y_2 f_{12}),\\ f_{12}= & {} {\kappa }(x_1 x_2 + y_1 y_2) + E_1 E_2, \\ v_i= & {} \alpha ^2 (x_i^2 + y_i^2) + X_i^2 +Y_i^2 + 2 \alpha ( x_i Y_i - y_i X_i) + \frac{{\kappa }}{E_i^2} (x_i X_i + y_i Y_i)^2, \quad i=1,2, \end{aligned}$$

and $d_{12}^{-3} = \Delta _{12}^{-3/2}$ where

$$\begin{aligned} \Delta _{12}= & {} x_1^2 + y_1^2 + x_2^2 +y_2^2 - {\kappa }(x_1^2 + y_1^2)(x_2^2 +y_2^2) - {\kappa }(x_1 x_2 + y_1 y_2)^2 \\&- 2(x_1 x_2 + y_1 y_2) E_1 E_2. \end{aligned}$$

Let ${{\mathcal {M}}}$ be the differential matrix associated to the system above at the equilibrium

$$\begin{aligned} (x_1,x_2,y_1,y_2,X_1,X_2,Y_1,Y_2)=(r_1,-r_2,0,0,0,0,0,0). \end{aligned}$$

Then

$$\begin{aligned} {{\mathcal {M}}}= & {} \left( \begin{array}{cc}0&{}I_4\\ {{\mathcal {A}}}&{}{{\mathcal {B}}}\\ \end{array}\right) , \quad {{\mathcal {A}}} = \left( \begin{array}{cc} \alpha ^2 {{\mathcal {A}}}_1 + {{\mathcal {F}}} &{} 0 \\ 0 &{} \alpha ^2 {{\mathcal {A}}}_2+{{\mathcal {G}}} \\ \end{array}\right) , \qquad {{\mathcal {B}}}=2\alpha \left( \begin{array}{cc} 0 &{} {{\mathcal {A}}}_2 \\ -I_2 &{} 0 \\ \end{array}\right) , \\ {{\mathcal {A}}}_1= & {} diag (E_1^2 - 2 {\kappa }x_1^2, E_2^2 - 2 {\kappa }x_2^2), \quad {{\mathcal {A}}}_2 = diag (E_1^2, E_2^2). \end{aligned}$$

${{\mathcal {F}}}$ (${{\mathcal {G}}}$) stands for the $2\times 2$ differential matrix of $(F_1,F_2)$ ($(G_1,G_2)$) with respect to $x_1,x_2$ ($y_1,y_2$) at the equilibrium, and $I_k$ stands for the identity of order k.

The characteristic polynomial of ${{\mathcal {M}}}$ reduces to

$$\begin{aligned} p(\lambda )=det(-\lambda ^2 I_4+\lambda {{\mathcal {B}}} + {{\mathcal {A}}} ) =0. \end{aligned}$$

(22)

Using the special structure of the matrix above, the Eq. (22) can be written as

$$\begin{aligned} det ( (-\lambda ^2 I_2 + \alpha ^2 {{\mathcal {A}}}_1 + {{\mathcal {F}}} ) (-\lambda ^2 I_2+\alpha ^2{{\mathcal {A}}}_2+{{\mathcal {G}}})+4\alpha ^2\lambda ^2{{\mathcal {A}}}_2)=0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} det (\lambda ^4 I_2 + \lambda ^2 {{\mathcal {C}}} + {{\mathcal {D}}}) = 0, \end{aligned}$$

where

$$\begin{aligned} {{\mathcal {C}}}=3\alpha ^2{{\mathcal {A}}}_2-\alpha ^2 {{\mathcal {A}}}_1- {{\mathcal {F}}} - {{\mathcal {G}}}, \quad {{\mathcal {D}}} = (\alpha ^2 {{\mathcal {A}}}_1 + {{\mathcal {F}}}) (\alpha ^2 {{\mathcal {A}}}_2 + {{\mathcal {G}}}). \end{aligned}$$

Then

$$\begin{aligned} p(\lambda )= & {} \lambda ^8 + (c_{11}+ c_{22}) \lambda ^6 +\left( det ({{\mathcal {C}}} ) + d_{11}+ d_{22} \right) \lambda ^4 \\&+(c_{11} d_{22} + c_{22} d_{11}-c_{12} d_{21}-c_{21} d_{12}) \lambda ^2 + det ({{\mathcal {D}}}), \end{aligned}$$

where $c_{ij},d_{ij}$ are the elements of the matrices ${{\mathcal {C}}}$ and ${{\mathcal {D}}}$, respectively.

To compute these matrices it is useful to take into account the expression for $d_{12}^{-3}$ given above in terms of $\Delta _{12}$. Furthermore, if we denote by $\Delta$ the function $\Delta _{12}$ at the equilibrium, it turns out that

$$\begin{aligned} \Delta = L^2, \qquad L= x_1 E_2 - x_2 E_1 = r_1 E_2 + r_2 E_1. \end{aligned}$$

(23)

Then the matrices ${{\mathcal {F}}}$ and ${{\mathcal {G}}}$ are easily computed as

$$\begin{aligned} {{\mathcal {F}}}\! =\! \Delta ^{-3/2}\! \left( \!\! \begin{array}{cc} m_2\left( 2 f_{12}+{\kappa }r_1\frac{L}{E_1}\right) &{}\!-2m_2 f_{12} \frac{E_1}{E_2} \\ - 2m_1 f_{12}\frac{E_2}{E_1}&{}\!m_1\left( 2f_{12}+{\kappa }r_2 \frac{L}{E_2}\right) \end{array}\!\! \right) , \quad {{\mathcal {G}}}\! =\! \Delta ^{-3/2}\! \left( \!\! \begin{array}{cc} -m_2 f_{12} &{}\!m_2 \\ m_1 &{} \!- m_1 f_{12} \\ \end{array}\!\! \right) . \end{aligned}$$

Using (16), (17) we obtain

$$\begin{aligned} {{\mathcal {F}}} = \alpha ^2 \left( \begin{array}{cc} {\kappa }r_1^2 + \frac{2 r_1 E_1 f_{12}}{L} &{} -\frac{2 r_1 E_1^2 f_{12}}{E_2 L} \\ \frac{-2 r_2 E_2^2 f_{12}}{E_1 L} &{} {\kappa }r_2^2 + \frac{2 r_2 E_2 f_{12}}{L}\\ \end{array}\right) , \qquad {{\mathcal {G}}} = \frac{\alpha ^2}{L} \left( \begin{array}{cc} - r_1 E_1 f_{12} &{} r_1 E_1 \\ r_2 E_2 &{} - r_2 E_2 f_{12} \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} \alpha ^2 {{\mathcal {A}}}_2 + {{\mathcal {G}}} = \frac{\alpha ^2}{L} \left( \begin{array}{cc} r_2 E_1 &{} r_1 E_1 \\ r_2 E_2 &{} r_1 E_2 \\ \end{array}\right) . \end{aligned}$$

It is clear that $det (\alpha ^2 {{\mathcal {A}}}_2 + {{\mathcal {G}}}) = 0$. Hence $\lambda =0$ is a double zero of $p(\lambda )$ as it would be expected.

In a similar way we compute the matrices ${{\mathcal {C}}}$ and ${{\mathcal {D}}}$ as

$$\begin{aligned} {{\mathcal {C}}}= & {} \frac{\alpha ^2}{L} \left( \begin{array}{cc} 2 r_2 E_1 + r_1 E_2 &{} \frac{r_1 E_1}{E_2 } (2 E_1 f_{12} - E_2) \\ \frac{r_2 E_2}{E_1 } (2 E_2 f_{12} - E_1) &{} r_2 E_1 + 2 r_1 E_2 \\ \end{array} \right) , \\ \mathcal{D}= & {} \frac{\alpha ^2}{L} \left( \begin{array}{cc} r_2 (1-2 {\kappa }r_1^2) E_1 &{} r_1 (1-2 {\kappa }r_1^2) E_1 \\ r_2 (1-2 {\kappa }r_2^2) E_2 &{} r_1 (1-2 {\kappa }r_2^2) E_2 \\ \end{array} \right) . \end{aligned}$$

Moreover it is easy to compute

$$\begin{aligned}&c_{11} + c_{22} = 3 \alpha ^2, \quad d_{11} + d_{22} + det ({{\mathcal {C}}}) = (3 - 4 {\kappa }^2 r_1^2 r_2^2) \alpha ^4,\\&c_{11}d_{22}+c_{22}d_{11}-c_{12}d_{21}-c_{21} d_{12}=(1-4{\kappa }^2 r_1^2r_2^2) \alpha ^6 . \end{aligned}$$

So, the characteristic polynomial becomes

$$\begin{aligned} p(\lambda )&=\lambda ^8+3\alpha ^2\lambda ^6+(3-4{\kappa }^2 r_1^2 r_2^2) \alpha ^4 \lambda ^4 + (1 - 4 {\kappa }^2 r_1^2 r_2^2) \alpha ^6 \lambda ^2 \\&=\lambda ^2 (\lambda ^2+\alpha ^2) (\lambda ^4 + 2 \alpha ^2 \lambda ^2 + (1 - 4 {\kappa }^2 r_1^2 r_2^2) \alpha ^4 ). \end{aligned}$$

Let us introduce $\nu = \lambda ^2 / \alpha ^2$. The polynomial $q(\nu ):=\nu ^2 + 2 \nu + 1-4 {\kappa }^2 r_1^2 r_2^2$ has a minimum at $\nu =-1$ and $q(-1) = - 4 {\kappa }^2 r_1^2 r_2^2 <0$. Then if $1-4{\kappa }^2 r_1^2 r_2^2 > 0$ the zeroes of $q(\nu )$ are negative and they give imaginary values of $\lambda$. In this case the equilibrium is spectrally stable. If $1 - 4 {\kappa }^2 r_1^2 r_2^2 < 0$, $q(\nu )$ has a positive zero giving rise to one eigenvalue $\lambda > 0$, so the equilibrium is unstable. $\square$

Remark 3.1

Once $r_1$ and $r_2$ are given, the values of $\mu$ and $\alpha ^2$ are determined using (16). Then one can look for collinear relative equilibria (a, 0),  with a satisfying (13) and triangular equilibria (a, b), being (a, b) a solution of (14), (15). So, we can consider the Eqs. (11) to (15) depending on $r_1,r_2,a$ and b. These equations are invariant under the symmetry $(r_1,r_2,a,b) \rightarrow (r_2,r_1,-a,b)$. Therefore it is sufficient to consider $r_1 \le r_2$.

Some results about stability, in a different sense, for the $\mathbb {H}^2$ case can be found in García-Naranjo et al. (2016).

4 Relative equilibria for the restricted problem

4.1 Collinear relative equilibria

Assume $r_1, r_2, \mu ,$ and $\alpha$ fixed satisfying (16). We consider the Eq. (13) for a

$$\begin{aligned} \alpha ^2 a(1-{\kappa }a^2)=(1-\mu )g_{13}(f_{13}a-r_1)+\mu g_{23}(f_{23}a+r_2). \end{aligned}$$

(24)

Using (55) and (57) (see the “Appendix”) for $(x,y)=(a,0)$ the Eq. (24) can be written as

$$\begin{aligned} (1-\mu ) \frac{S_1}{|S_1|^3} + \mu \frac{S_2}{|S_2|^3} - \alpha ^2 a E_3 =0, \end{aligned}$$

(25)

where $E_3 = \sqrt{ 1 - {\kappa }a^2}$, $S_1 = a E_1 - r_1 E_3,$ $S_2 = a E_2 + r_2 E_3$.

One has to distinguish three cases according to the position of $m_3$: $r_1 < a$ ($S_1> 0, \; S_2 >0$), $- r_2< a < r_1$ ($S_1 < 0, \; S_2 >0$), $a < - r_2$ ($S_1< 0, \; S_2 <0$). However, the third case reduces to the first one by exchanging $r_1$ and $r_2$ and changing the sign of a.

To study the solutions of (25) it will be useful to write it as $h_L(a) = h_R(a)$ where

$$\begin{aligned} h_L(a)= (1-\mu ) \frac{S_1}{|S_1|^3} + \mu \frac{S_2}{|S_2|^3},\qquad h_R(a) = \alpha ^2 a E_3. \end{aligned}$$

4.1.1 The collinear relative equilibria in $\mathbb {H}^2$

Proposition 4.1

Assume ${\kappa }<0$. For any fixed $\mu \in (0,1),$ $\alpha \ne 0$, there are 3 collinear relative equilibria.

Proof

We shall prove that there is exactly one solution of (25) at each interval $a > r_1,$ $- r_2< a < r_1$, and $a < - r_2$.

Notice that $h_R(a)=\alpha ^2 a\sqrt{1+|{\kappa }|a^2}$ is a function of a increasing without bound and $h_R(0)=0$.

Assume $a > r_1$. Then $S_1 > 0 ,$ $S_2 > 0$ and $h_L(a) = \frac{1-\mu }{S_1^2} + \frac{\mu }{S_2^2}.$ Using (58) and Lemma 7.1

$$\begin{aligned} \frac{d h_L(a)}{d a } = - (1-\mu ) \frac{2 f_{13}}{E_3 S_1^3} - \mu \frac{2 f_{23}}{E_3 S_2^3} < 0. \end{aligned}$$

Then $h_R(a)$ and $h_L(a)$ intersect at a unique point $a>r_1$ which is a solution of (25).

If $- r_2< a < r_1$, then $S_1 < 0,$ $S_2 > 0$ and $h_L(a) = -\frac{1-\mu }{S_1^2} + \frac{\mu }{S_2^2}.$ As before, $h_L(a)$ is a decreasing function of a and then there is a unique solution of (25) in that interval. The third case follows by symmetry. $\square$

4.1.2 The collinear relative equilibria in $\mathbb {S}^2_+$

Let us consider ${\kappa }> 0$. In this case, for $0< a < 1/\sqrt{{\kappa }}$, $h_R(a) = \alpha ^2 a \sqrt{1-{\kappa }a^2}$ is a concave function which has a maximum at $a = 1/\sqrt{2 {\kappa }}$ and $h_R(0) = h_R(1/\sqrt{{\kappa }}) =0.$ So, we can expect more than three solutions of (25) depending on the values of $r_1, r_2$.

First we consider the case $r_1 = r_2$. In this case $\mu =1/2$ and $\alpha ^2=1/(8 r_1^3 E_1^3).$

Proposition 4.2

Assume ${\kappa }> 0$ and $r_1=r_2$ fixed. Then there is a value $r^*= 0.337849954\ldots$, zero of a polynomial given in the proof, such that

• 1. If $\sqrt{{\kappa }}\,r_1<r^*$ then there are 5 collinear relative equilibria one of them between the primaries, and two additional ones at each side of the primaries.

• 2. If $\sqrt{{\kappa }}\,r_1 > r^*$ then there is a unique collinear equilibrium between the primaries.

• 3. If $\sqrt{{\kappa }}\, r_1=r^*$ then there are three collinear equilibria, one of them between the primaries and one at each side of the primaries.

In any case, $a=0$ for the equilibria between the primaries.

Proof

To simplify the computations we shall take ${\kappa }= 1$ (see Remark 2.1). In the case $- r_1< a < r_1$ the Eq. (25) can be written as

$$\begin{aligned} -16 r_1^4 E_1^4 \frac{a}{(a^2- r_1^2)^2} = a \end{aligned}$$

and it has a unique solution $a=0$. Therefore for any value of $r_1$ there is a unique collinear relative equilibrium with negligible mass between the two primaries.

Let us consider a collinear equilibrium with $a>r_1$. In this case $S_1 >0,$ $S_2 > 0$ and $h_L(a) = \frac{1}{2} \left( \frac{1}{S_1^2} + \frac{1}{S_2^2} \right)$. We compute

$$\begin{aligned} \frac{d }{da} h_L(a)= & {} -\frac{2a}{(a^2-r_1^2)^3}(a^2 P+Q),\qquad \\ \frac{d^2}{da^2}h_L(a)= & {} \frac{2}{(a^2-r_1^2)^4}(3Pa^4+(3r_1^2P+5Q)a^2+Q r_1^2), \end{aligned}$$

where $P=1- 2 r_1^2,$ $Q=r_1^2 (3-2 r_1^2).$

We claim that $h_L(a)$ is a decreasing convex function for $0< r_1< a < 1$.

This is trivial if $0<r_1\le 1/\sqrt{2}$. Let us assume that $1/\sqrt{2}<r_1<1$. Using that $a^2 < 1$ and $P < 0$ we obtain

$$\begin{aligned} a^2 P + Q> (1+ r_1^2 - 2 r_1^4) >0. \end{aligned}$$

Then $\frac{d }{da} h_L(a) <0$ for $r_1< a < 1$. Let be

$$\begin{aligned} {\hat{N}}(a^2) = 3 P a^4 + (3 r_1^2 P + 5 Q) a^2 + Q r_1^2. \end{aligned}$$

It is easy to check that ${\hat{N}}(0) >0$ and

$$\begin{aligned} {\hat{N}}(1) = (3 + 12 r_1^2 -13 r_1^4 - 2 r_1^6 ) > 0. \end{aligned}$$

Therefore ${\hat{N}}(a^2) >0$ and $\frac{d^2 }{da^2} h_L(a) >0$ for any $r_1< a < 1$. So, the claim is proved.

Using that $h_R(a)$ is a concave function if $a>0$, we conclude that the number of solutions of $h_L(a)=h_R(a)$ with $r_1<a<1$ is less than or equal to two.

Now we shall look for tangencies between $h_L(a)$ and $h_R(a)$.

After eliminating square roots, the equation $h_L(a)=h_R(a)$ for collinear equilibria with $a > r_1$, is reduced to

$$\begin{aligned}&a^{12}-(1+4 r_1^2)a^{10}+2 r_1^2(2+3 r_1^2)a^8-2 r_1^4(3+2 r_1^2) a^6 \\&\quad + r_1^6 (- 256 E_1^8 r_1^2 + 64 E_1^6-E_1^2 + 5 ) a^4 + r_1^8(256 E_1^8-128 E_1^6 -1) a ^2 + 64 r_1^{10} E_1^6 =0. \end{aligned}$$

So, we obtain a polynomial equation of degree 6 in $A:=a^2$. To look for bifurcation points we compute the resultant of the polynomial above and its derivative with respect to A. Besides a constant factor the resultant is $t^{20}(t-1)^{20}R$, where $t=r_1^2$ and R is an even polynomial in $T=t-1/2$

$$\begin{aligned} R = T^{12}-\frac{3}{4}T^{10}+\frac{45}{256}T^8+\frac{11}{256}T^6- \frac{2421}{65536}T^4+\frac{2319}{262144}T^2-\frac{11449}{16777216}. \end{aligned}$$

It is easy to prove that R has exactly two real zeroes $0<t_1<1/2<t_2<1$. However, only the value $t_1$ gives a bifurcation point with $a>r_1$ ($t_2$ gives rise to a value of $a,\,a<r_1$). So, we conclude that if $r_1=r_2$ there is a unique bifurcation point such that the number of collinear equilibria with $a>r_1$ passes from two to zero as $r_1$ increases. The numerical values are $t_1=0.1141425915\ldots ,\, r^*=\sqrt{t_1}=0.3378499541\ldots$ and then $a=0.8939525657\ldots$. $\square$

Limit cases

Two limit cases can be easily studied: $r_1=0$ and $r_2=1/\sqrt{{\kappa }}$ (i.e., the second mass is at the equator). In any case the solutions of (25), will be called limit collinear relative equilibria (LCRE). In the first case one has $\mu =0$ and the equations reduce to $r_2^3E_2= |a|^3E_3$ for $|a|<1/\sqrt{{\kappa }}$. Using the function $f_1(x):=x^3\sqrt{1-{\kappa }x^2}$, it is easy to prove the following Proposition

Proposition 4.3

Assume $r_1=0$ and $0\!<\!r_2\!<\!1/\sqrt{{\kappa }}$. Then for any $r_2$ there is a LCRE with $a=r_2$. If $r_2\!\ne \!\sqrt{3}/(2\sqrt{{\kappa }})$, there exist two additional LCRE symmetrical wrt the origin.

If $r_2=1/\sqrt{{\kappa }}$ and $0<r_1<1/\sqrt{{\kappa }}$ we have $\mu =1$ and we obtain the equation $r_1E_1^3=a E_3^3$ for $a>0$. As before the following Proposition holds.

Proposition 4.4

Assume $r_2 =1/\sqrt{{\kappa }}$ and $0< r_1 < 1/\sqrt{{\kappa }}$. Then

• 1. If $r_1\ne r_2/2$, there is one LCRE with $a>r_1$ if $r_1<r_2/2$, and $0<a<r_1$ if $r_1>r_2/2$.

• 2. If $r_1 = r_2/2$ there are no LCRE.

4.2 Triangular relative equilibria

Assume $r_1, r_2, \mu ,$ and $\alpha$ fixed satisfying (16). One has to solve (14), (15) for a, b.

Using (14), (50) and (17) we can eliminate $g_{13}$ in (15) to obtain the equivalent system

$$\begin{aligned} \sigma _1\Delta _{23}=\Delta _{13},\qquad (r_1E_2+r_2E_1)^3E_1=E_3\Delta _{23}^{3/2}, \end{aligned}$$

(26)

where $\sigma _1:=(E_2/E_1)^{2/3}$ and $\Delta _{13},$ $\Delta _{23}$ are given in (55) with $x=a, y=b$. This suggests to introduce new variables $U:=\Delta _{13}>0$ and $V:=\Delta _{23} >0$, that is (see 55)

$$\begin{aligned} U= b^2 + S_1^2, \quad V=b^2 + S_2^2, \qquad S_1 = a E_1 - r_1 E_3, \quad S_2 = a E_2 + r_2 E_3. \end{aligned}$$

To write $E_3$ in terms of the new variables, we note that using (54) with $x=a, y=b$, we obtain

$$\begin{aligned} E_3 = \frac{r_2 f_{13} + r_1 f_{23}}{r_1 E_2+ r_2 E_1}, \qquad a = \frac{(E_2 f_{13}-E_1 f_{23})}{ {\kappa }(r_1 E_2+ r_2 E_1)}. \end{aligned}$$

(27)

Moreover, from (50) one has $f_{13}^2=1-{\kappa }U$ and $f_{23}^2=1-{\kappa }V$. That is, once U, V are fixed, $f_{13}$ and $f_{23}$ are determined except by a sign. Therefore

$$\begin{aligned} E_3^2=\frac{r_2^2(1-{\kappa }U)+r_1^2(1-{\kappa }V)\pm 2r_1r_2\sqrt{1-{\kappa }U}\sqrt{1-{\kappa }V}}{(r_1 E_2+ r_2 E_1 )^2}, \end{aligned}$$

(28)

where we shall take the sign $+ (-)$ if $f_{13} f_{23} >0$ $(<0)$. Using U, V (26) becomes

$$\begin{aligned} \sigma _1 V=U,\qquad (r_1 E_2+ r_2 E_1 )^6 E_1^2 = E_3^2 V^3, \end{aligned}$$

(29)

where $E_3^2$ is given by (28). Therefore (29) reduces to

$$\begin{aligned} P_\pm (V):=V^3(r_2\sqrt{1-{\kappa }\sigma _1 V} \pm r_1 \sqrt{1-{\kappa }V})^2-\sigma _2 =0, \end{aligned}$$

(30)

where $\sigma _2=(r_1 E_2+r_2 E_1)^8E_1^2$. We recall that it is sufficient to consider $r_1\le r_2$ (see Remark 3.1). In this case if ${\kappa }>0$, one has $\sigma _1<1$ and then $P_{\pm }(V)$ are defined for $V\in [0,1/{\kappa }]$. If ${\kappa }<0$, then $f_{13}>0$ and $f_{23}>0$ for any a, b (see (3)). So in this case we only need to consider the function $P_+(V)$ which is defined for any $V\ge 0$.

Let us see now how to recover a and b from the zeroes of $P_{+}(V)$ in the general case ${\kappa }\ne 0$. Assume that $V_0$ satisfies $P_+(V_0)=0$ and let be $U_0=\sigma _1 V_0$. In this case $f_{13}$ and $f_{23}$ have the same sign that we take positive in order to have $E_3>0$. So $f_{13}=\sqrt{1-{\kappa }U_0}$ and $f_{23}=\sqrt{1-{\kappa }V_0}$. Using (27) we compute $E_3$ and a. Finally, if $(1-{\kappa }a^2-E_3^2)/{\kappa }>0$, we get two equilibria with

$$\begin{aligned} b=\pm \sqrt{(1-{\kappa }a^2-E_3^2)/{\kappa }}\,. \end{aligned}$$

(31)

For ${\kappa }>0$, if $V_0\in (0,1/{\kappa })$ is a solution of $P_-(V_0)=0$ and $U_0=\sigma _1 V$, one has to take $f_{13}$ and $f_{23}$ with opposite sign such that $E_3>0$ in (27). Then the equilibria are determined as before.

4.2.1 Triangular relative equilibria in $\mathbb {H}^2$

Proposition 4.5

Assume ${\kappa }<0$. For any fixed $\mu \in (0,1)$ and $\alpha ^2 > 0$, there are exactly two symmetric triangular relative equilibria $(a, \pm b)$ with $b \ne 0$. Moreover, if $r_1 =r_2$ then $a=0$.

Proof

First we assume $r_1=r_2$. In this case $\sigma _1\! =\!1$ and $U= V$. Then $|S_1| = |S_2|$. This implies $a=0$ and so, $E_3^2=1-{\kappa }b^2$ and $V\! =\! b^2 + r_2^2 E_3^2\! =\! r_1^2\! +\! b^2 E_1^2$. The second equation of (29) becomes

$$\begin{aligned} 2^6 r_1^6 E_1^8 = E_3^2 (r_1^2 + b^2 E_1^2)^3. \end{aligned}$$

(32)

The right hand side of the equation above is an increasing function of $b^2$ equal to $r_1^6$ for $b=0$. Using that $2^6 E_1^8>1$ we conclude that for any $r_1>0$, (32) has a unique solution $b^2 \ne 0$ giving rise to two triangular equilibria $(0, \pm b)$.

Now we shall prove that in the general case, that is, $r_1$ different of $r_2$, the triangular equilibria do not degenerate to collinear, that is, $b\ne 0$. To do this we assume that (a, 0) is a solution of (29). Then $U=S_1^2$, $V=S_2^2$ with $E_3=\sqrt{1-{\kappa }a^2}$ and (29) reduces to

$$\begin{aligned} E_1 |S_1|^3=E_2 |S_2|^3, \qquad E_1 (r_1 E_2+r_2 E_1)^3 = E_3 |S_2|^3, \end{aligned}$$

which is equivalent to

$$\begin{aligned}&h_1(a) := E_3 |S_1|^3 - E_2 (r_1 E_2+r_2 E_1)^3 =0,\nonumber \\&h_2(a) := E_3 |S_2|^3 - E_1 (r_1 E_2+r_2 E_1)^3 =0. \end{aligned}$$

(33)

Using $d(E_3 |S_1|^3)/da$ it is easy to check that $h_1(a)$ has exactly two zeroes: $a=-r_2,$ $a=a_1\!>\!r_1$, and $h_1(a)\!<\!0$ if and only if $-r_2\!<\!a\!<\!a_1$. In a similar way, $h_2(a)$ has exactly two zeroes: $a=-a_2\!<\!-r_2,\,a= r_1$. Therefore (33) has not real solutions and there are no triangular equilibria with $b=0$.

Going to the general case we know that it is sufficient to look for the zeroes of

$$\begin{aligned} P_+(V):= V^3 (g(V))^2 - \sigma _2 =0, \end{aligned}$$

(34)

where

$$\begin{aligned} g(V)= r_1 \sqrt{1- {\kappa }V} + r_2 \sqrt{1- {\kappa }\sigma _1 V}, \qquad \sigma _2 = E_1^2 (r_1 E_2 + r_2 E_1)^8. \end{aligned}$$

We note that for $V\!>\!0$, $P_+(V)$ is a monotonically increasing function with $P_+(0)\!<\!0$ and going to infinity as V goes to infinity. Therefore there is a unique $V_0\! >\! 0$ such that $P_+(V_0) =0$.

Assume that $V_0$ is a solution of (34). To obtain a relative equilibrium we proceed as explained before. First we compute $E_3$ using (27) and (34) as

$$\begin{aligned} E_3=\frac{g(V_0)}{r_1E_2+r_2E_1}=\frac{E_1(r_1E_2+r_2 E_1)^3}{V_0^{3/2}}. \end{aligned}$$

Then

$$\begin{aligned} a = \frac{ r_1^2 - r_2^2 + V_0(E_1^2 - \sigma _1 E_2^2)}{ (r_1 E_2 + r_2 E_1) (E_1 \sqrt{1- {\kappa }V_0} + E_2 \sqrt{1-{\kappa }\sigma _1 V_0})} \end{aligned}$$

and $b^2 = V_0-(a E_2 + r_2 E_3)^2$. To finish the proof it remains to prove that $V_0-(a E_2 + r_2 E_3)^2 > 0$.

Assume that for some $r_1={\hat{r}}_1>0$, $r_2={\hat{r}}_2>0$, the expression above is negative. Using the symmetry we can assume also that ${\hat{r}}_1<{\hat{r}}_2$. Let us consider the segment $\gamma =\{(r_1,r_2)\,|\,r_1={\hat{r}}_1,\,{\hat{r}}_1 \le r_2\le {\hat{r}}_2\}$. We know that for $(r_1,r_2)=({\hat{r}}_1,{\hat{r}}_1)$ there are two equilibria $(0,\pm b)$ with $b\ne 0$. The continuity with respect to $r_2$ implies that there is some ${\hat{r}}_1\le \rho \le {\hat{r}}_2$ such that $V_0-(aE_2+r_2E_3)^2=0$. In this case, we should obtain a triangular/collinear relative equilibrium, which is not possible. This ends the proof. $\square$

4.2.2 Triangular relative equilibria in $\mathbb {S}^2_+$

The case ${\kappa }>0$ is more rich that the case ${\kappa }< 0$. After Lemma 7.1 we know that if ${\kappa }> 0$, the functions $f_{13}$ and $f_{23}$ do not have constant sign. So we have to study the zeroes of the two functions $P_{\pm }(V)$.

First we shall study the existence of triangular relative equilibria in the case $r_1=r_2$.

The case $r_1=r_2$

If $r_1=r_2$ from (16) and (17) $\mu =1/2$ and $\alpha ^2=1/(8 r_1^3 E_1^3)$.

Proposition 4.6

Assume $r_1=r_2$. Then one has $a=0$ and there exist three values $0\!<\!\beta _1\!<\!\beta _2\!<\beta _3=\!1- 2^{-3/2}$ such that

• 1. If $\;0<{\kappa }r_1^2 <\beta _1 \;$ or $\;\beta _2<{\kappa }r_1^2 < \beta _3$ there are exactly 4 triangular configurations.

• 2. If $\;\beta _3\!<\!{\kappa }r_1^2<1$ there are exactly 2 triangular configurations.

• 3. If $\;\beta _1<{\kappa }r_1^2<\beta _2$ there are no triangular configurations.

• 4. If $\; {\kappa }r_1^2=\beta _1\;$ or $\; {\kappa }r_1^2=\beta _2$ there are exactly 2 triangular configurations $(a,b)=(0,\pm \sqrt{(3-4{\kappa }r_1^2)/(4(1-{\kappa }r_1^2))})$.

• 5. If $\; {\kappa }r_1^2 = \beta _3$ there are 2 triangular configurations and another configuration $(a,b)=(0,0)$ which is in fact collinear.

Proof

In order to simplify the computations we shall take ${\kappa }=1$ (see Remark 2.1). If $r_1=r_2$, then $E_1=E_2$, $\sigma _1=1$ and $U=V$. In this case $P_-(V)=-\sigma _2<0$ constant, so we only need to consider the function $P_+(V)$.

Let $V_0$ be a solution of $P_+(V)=0$. Then $f_{13}= f_{23} = \sqrt{1- V}$ and using (27) we obtain

$$\begin{aligned} E_3 = \frac{f_{13}}{E_1} = \frac{\sqrt{1- V_0}}{E_1}, \qquad a=0. \end{aligned}$$

Therefore

$$\begin{aligned} b^2 = 1 - E_3^2 = \frac{V_0 - r_1^2}{E_1^2}. \end{aligned}$$

So, if $V_0 > r_1^2$ is a solution of $P_+(V)=0$ we obtain two triangular equilibria

$$\begin{aligned} (a,b) = \left( 0,\pm \sqrt{\frac{V_0 - r_1^2}{E_1^2}}\right) . \end{aligned}$$

If $V_0=r_1^2$ there is a unique configuration $(a,b)=(0,0)$ which in fact is collinear.

We are interested in the number of zeroes of $P_+(V)$ which satisfy $r_1^2<V<1$. We call them admissible zeroes of $P_+(V)$, each one giving rise to two triangular configurations.

In this case $P_+(V)$ becomes

$$\begin{aligned} P_+(V) = 4 r_1^2 ( V^3 (1- V) -2^6 r_1^6 E_1^{10}). \end{aligned}$$

It is obvious that $P_+(0) < 0$ and $P_+(1) < 0$.

This function has a unique maximum in the interval (0, 1) located at $V=3/4$ and

$$\begin{aligned} P_+( 3/4) = r_1^2 \left( \frac{27}{4^3} - 2^8 r_1^6 E_1^{10} \right) . \end{aligned}$$

Bifurcations can appear when $P_+(3/4)=0$ that is, if we introduce $\beta :=r_1^2$, when

$$\begin{aligned} 27 = 2^{14} \beta ^3 (1- \beta )^5 \end{aligned}$$

holds. This equation has exactly two solutions in the interval (0, 1) , $\beta _1 = 0.1570186981\ldots ,$ and $\beta _2 = 0.6357277816\ldots$. Therefore $P_+(V)$ has no zeroes if $\beta _1<r_1^2< \beta _2,$ it has exactly one zero if $r_1^2=\beta _1$ or $r_1^2 = \beta _2$, and two zeroes otherwise.

On the other hand $P_+(r_1^2)=4r_1^8 E_1^2(1-2^6 E_1^8)$ and $P_+(r_1^2)=0$ if $r_1^2=\beta _3$. Then, if $r_1^2>\beta _3$, $P_+(r_1^2)>0$ and so, $P_+(V)$ has two zeros $V_1,V_2$ with $0<V_1<r_1^2<V_2<1.$ The solution $V_1$ is not admissible and from $V_2$ we obtain two triangular equilibria. When $r_1^2=\beta _3$, $P_+(V)$ has two zeros, $0<V_1=r_1^2<V_2<1$. From $V_2$ we obtain two equilibria and from $V_1$ we get $b=0$, that is, a collinear equilibrium. For $r_1^2<\beta _3$ the two zeros, which exist for $r_1^2\in (0,\beta _1)\cup (\beta _2,\beta _3)$, are admissible. The Fig. 3 summarizes the solutions displaying $b^2$ as a function of $r_1^2$. $\square$

Fig. 3

Plot of the triangular solutions for $r_1=r_2$. The horizontal (vertical) variable is $r_1^2$ ($b^2$). The vertical lines correspond to $r_1^2=\beta _1$ and $r_1^2=\beta _2$. $(\beta _3,0)$ is the lower end point of the right curve located on $b^2=0$. On the right a magnification around $[\beta _2,\beta _3]$. This Figure is an equivalent version of Figure 11 in Kilin (1999)

General case

Let us consider now the general case, $r_1 \ne r_2$. As usual we can restrict to $r_1<r_2$.

Theorem 4.1

Assume ${\kappa }>0$, $r_1,r_2,\mu ,\alpha ^2$ fixed satisfying (16), (17). The number of triangular relative equilibria is at most equal to 8. Moreover, if ${\kappa }(r_1^2+r_2^2)=1,$ there are no triangular relative equilibria.

Proof

As usual we can take ${\kappa }=1$ and it is enough to consider $r_1<r_2$ and, hence, $\sigma _1<1$.

For the functions $P_{\pm }(V)$, as defined in (30), it is clear that $P_{\pm }(0) = - {\sigma }_2 < 0$ and $P_+( 1) = P_-( 1)$. Moreover $P_-(V)<P_+(V)$ for any $V\in (0,1)$ (see Fig. 4).

Fig. 4

Plots of $P_{\pm }(V)$ for $r_2=0.4$ and a $r_1=0.05$, b $r_1=0.16$, c $r_1=0.2$, d $r_1=0.38$

Let us consider $P_+(V)$ and let be

$$\begin{aligned} g_+(V):= r_2 \sqrt{1-\sigma _1 V} + r_1 \sqrt{1-V}. \end{aligned}$$

Then $g_+(0)=r_1 + r_2 > 0$ and $d g_+/d V < 0$. Moreover $d P_+(V)/d V = 0$ implies that

$$\begin{aligned} 3 g_+(V) = - 2 V \,d g_+(V)/d V. \end{aligned}$$

This equation has a unique solution $V_*\in [0,1]$ (notice that the right hand side is an increasing function of V and $g_+(V)$ is decreasing) which is a maximum of $P_+(V)$. Therefore, depending on the values of $r_1,r_2$, $P_+(V)$ can have 0, 1 or 2 zeroes.

We note that $\displaystyle {\frac{d P_+(V)}{dV}\rightarrow -\infty }$ and $\displaystyle { \frac{d P_-(V)}{dV}\rightarrow +\infty }$ as $V\rightarrow 1^-$.

We claim that $P_-(V)$ has at most two critical points in the interval (0, 1).

Then the maximum number of zeroes of $P_-(V)$ in (0, 1) is three. However, as $P_+(1)=P_-(1)$ we conclude that the total number of zeroes of $P_{\pm }(V)$ is at most equal to four. Using that for any zero of $P_{\pm }(V)$ we can obtain at most two (symmetrical) relative equilibria, the maximum number of triangular relative equilibria is eight.

To prove the claim we compute

$$\begin{aligned} \frac{dP_-(V)}{dV}=V^2 g_-(V)\left( 3 g_-(V)+2V\frac{dg_-(V)}{dV}\right) , \end{aligned}$$

(35)

where

$$\begin{aligned} g_-(V)= r_2 \sqrt{1- \sigma _1 V} - r_1 \sqrt{1-V}. \end{aligned}$$

If $g_-(V)=0$ we obtain $V= (r_2^2 - r_1^2)/(r_2^2 \sigma _1 - r_1^2)$. However we are assuming $r_1 < r_2$ and $\sigma _1 < 1$, which would give $V>1.$ Therefore, the positive critical points of $P_-(V)$ must satisfy

$$\begin{aligned} 3 g_-(V) + 2 V \frac{d g_-(V)}{d V} =0, \end{aligned}$$

or, equivalently,

$$\begin{aligned} r_2 (3-4\sigma _1 V) \sqrt{1-V} = r_1 (3-4 V) \sqrt{1- \sigma _1 V}. \end{aligned}$$

(36)

For further use we note that if in (35) we use $P_+$ we shall obtain

$$\begin{aligned} r_2 (3-4\sigma _1 V) \sqrt{1-V}=-r_1 (3-4 V)\sqrt{1-\sigma _1 V}. \end{aligned}$$

(37)

Eliminating the square roots we obtain, both for (36) and (37)

$$\begin{aligned} \begin{array}{rl} Q(V):=&{}16\sigma _1(r_2^2\sigma _1-r_1^2)V^3+8(-3(\sigma _1+1)(r_2^2\sigma _1-r_1^2) + r_2^2 \sigma _1^2 - r_1^2 ) V^2 \\ &{} + 3(8(r_2^2\sigma _1-r_1^2)+3(r_2^2-\sigma _1r_1^2))V+9(r_1^2 - r_2^2) =0. \end{array} \end{aligned}$$

(38)

A simple computation shows that

$$\begin{aligned}&Q(0)< 0,\quad Q\left( \frac{3}{4}\right) =-\frac{9}{4}r_2^2 (\sigma _1-1)^2<0,\quad Q\left( \frac{3}{4\sigma _1}\right) =\frac{9}{4 \sigma _1^2}r_1^2(\sigma _1-1)^2>0,\\&Q(1)=r_1^2 (1-\sigma _1) \!>\!0. \end{aligned}$$

Then, for any $r_1\!<\!r_2$, Q has at least one zero in the interval $(3/4,3/(4\sigma _1))$ and so, it has at most two zeroes outside this interval. However, if $3/4\!<\!V\!<\!3/(4\sigma _1)$ then $(3-4\sigma _1 V)(3-4V)$ $<0$ and so, it is not a solution of (36). We conclude that (36) has at most two solutions in (0, 1) which are critical points of $P_-(V)$ and the claim is proved.

Assume now $r_1^2+r_2^2=1$ and, hence, $E_1=r_2,E_2=r_1,\sigma _2=r_2^2$. We shall prove that $P_+(V)$ has no zeroes in this case. Because of the symmetry and that the case $r_1=r_2$ is proved in Proposition 4.6 item 3., it is enough to consider $0<r_1<r_2$. Furthermore, as for $r_1=r_2$ there are no solutions with $r_1=1/\sqrt{2}$, it is enough to see that no zeros appear in the range $0<r_1<r_2$.

Let $t:=\sqrt{\sigma _1}=(E_2/E_1)^{1/3}$. Then the equation $P_+(V)=0$ can be written as

$$\begin{aligned} V^3(1-t^2V+t^6(1-V))-1=-2V^3t^3\sqrt{1-t^2 V}\sqrt{1-V}. \end{aligned}$$

(39)

Let Q(T, V) be the polynomial obtained by taking squares in (39) and setting $T=t^2$. The domain of interest is $(T,V)\in (0,1)^2$. We compute the resultant of Q and $\partial Q/\partial V$ to look for the existence of critical points of Q wrt V which are zeros of Q and divide it by $2^{16}T^{19}(T-1)^8(T+1)^6$. One obtains the symmetrical polynomial R(T) given by

$$\begin{aligned} \begin{array}{rcl} R(T)&{}=&{}729(T^{12}+1)+1458(T^{11}+T)+1944(T^{10}+T^2)-15363(T^9+T^3) \\ &{} &{}-33102(T^8+T^4)+51309(T^7+T^5)+137602T^6. \end{array} \end{aligned}$$

If R(T) has a zero $T_1\in (0,1)$, it should also have a zero $1/T_1>1$. It is immediate to check that all the derivatives are positive at $T=9/8$. Hence there are no zeros with $T>9/8$. The expansion around $T=1$ in the variable $\tau =T-1$, ${\hat{R}}(\tau )=R(1+\tau )=\sum _{k=0}^{12}c_k \tau ^k$ has all $c_k\!>\!0$ except $c_5=-94188$. But $c_4=1080645$. This ensures that no zeros occur for $T\in (1,9/8)$. Summarizing R has no zeros in (0, 1) and, therefore, no zeros of $P_+(V)$ appear in the range. $\square$

Remark 4.1

From Theorem 4.1 it follows that the lack of connection between the domains of existence of triangular relative equilibria already seen in Proposition 4.6 for $r_1=r_2$ is general. That is, there are disconnected domains of existence of these solutions.

Limit cases

To simplify the formulas we shall take ${\kappa }=1$ in all this subsection.

Our purpose is to study the solutions of (29) in two limit cases: $r_1=0$, excluding $r_2=0$, and $r_2=1$, excluding $r_1=1$. In any case we refer to these solutions as “limit triangular relative equilibria” (LTRE).

First we consider $r_1 =0$. In this case, $P_+$ and $P_-$ coincide and they are equal to

$$\begin{aligned} P(V) := r_2^2 [\, V^3 (1- \sigma _1 V ) - r_2^6 \,]. \end{aligned}$$

Proposition 4.7

Assume $r_1\! =\!0$, $r_2\! >\!0$. There exists a value ${\hat{r}}_2\! =\! 0.8260313577\ldots$ such that

• 1. If $0 < r_2 \le {\hat{r}}_2$ then there are two LTRE with

  $$\begin{aligned} a = \frac{1}{r_2} \left( 1 - r_2^2 - \sqrt{1-{\hat{V}}} \right) , \quad b = \pm \sqrt{ r_2^2 - a^2}, \quad {\hat{V}}=r_2^2(1-r_2^2)^{-1/3}. \end{aligned}$$

  (40)

• 2. If ${\hat{r}}_2< r_2 < 1$ there are no LTRE.

Moreover for $\sqrt{1 - 2^{-3/2}}< r_2 < {\hat{r}}_2,$ two additional LTRE are obtained with

$$\begin{aligned} a = \frac{1}{r_2} ( 1 - r_2^2 + \sqrt{1-{\hat{V}}} ), \quad b = \pm \sqrt{ r_2^2 - a^2}. \end{aligned}$$

(41)

If $r_2 = \sqrt{1 - 2^{-3/2}}$, then (41) becomes collinear. For $r_2 = {\hat{r}}_2,$ (40) and (41) coincide.

Proof

If $r_1 =0$, $P_+=P_-$ and they are equal to

$$\begin{aligned} P(V)=r_2^2(V^3(1-sV)-r_2^6)=r_2^2(sV-r_2^2)(-V^3+s^2V^2+r_2^2sV+r_2^4 ), \end{aligned}$$

where $s = (1-r_2^2)^{1/3}$. P has a unique extremum, which is a maximum, located at $V_m=3/(4s)$. The value of $V_m$ is less than 1 if $r_2<\sqrt{37}/8 =0.760345\ldots$. Moreover

$$\begin{aligned} P (1)= r_2^2 [1- r_2^6 -(1-r_2^2)^{1/3} ], \end{aligned}$$

which is positive if $0< r_2 < \hat{r_2} =0.8260313577\ldots$ and negative if $\hat{r_2}< r_2 < 1$.

Then if $0 < r_2 \le {\hat{r}}_2$, P(V) has a unique zero ${\hat{V}} = r_2^2 (1- r_2^2)^{-1/3}$ in the interval [0, 1], and for ${\hat{r}}_2< r_2 < 1$, P(V) has no zeroes in the interval [0, 1] .

Assume $0\le r_2\le {\hat{r}}_2$. From (27) we obtain $E_3=f_{13}$, so $f_{13}=\sqrt{1-s{\hat{V}}}=\sqrt{1-r_2^2}=E_2$ and $f_{23}=\pm \sqrt{1-{\hat{V}}}$. If $f_{23} = \sqrt{1-{\hat{V}}}$, then $a = (E_2^2 - \sqrt{1-{\hat{V}}})/r_2$.

Using that $E_3=E_2$ in this case, the condition $1-a^2-E_3^2\ge 0$ to have a LTRE reduces to $r_2^2 \ge a^2$, that is,

$$\begin{aligned} - r_2^2 \le E_2^2 - \sqrt{1-{\hat{V}}} \le r_2^2 \qquad {\text{ or }}\qquad 1 - 2 r_2^2 \le \sqrt{1-{\hat{V}}} \le 1\,. \end{aligned}$$

It is clear that the right hand side inequality is satisfied. For the one on the left we assume $1-2r_2^2\ge 0$, otherwise the inequality is trivially satisfied. Then, the inequality is equivalent to $4(1-r_2^2)^{4/3}\ge 1$, and this is satisfied, in particular, if $r_2^2 \le 1/2$. So, we obtain a LTRE.

Now assume $f_{23}=-\sqrt{1-{\hat{V}}}$ and then $a=(E_2^2+\sqrt{1-{\hat{V}}})/r_2$. As before, the condition to have a LTRE is $r_2^2 \ge a^2$ which reduces to

$$\begin{aligned} \sqrt{1-{\hat{V}}} \le -1 + 2 r_2^2. \end{aligned}$$

This inequality is satisfied if $r_2\ge \sqrt{1-2^{-3/2}}\approx 0.80401903.$ Then for a small range of values of $r_2$, $\sqrt{1-2^{-3/2}}\le r_2\le {\hat{r}}_2$ there are two additional LTRE given in (41).

We note that if $r_2={\hat{r}}_2$, then ${\hat{V}}=1$ and (40) and (41) coincide. Furthermore, in $r_2=\sqrt{1-2^{-3/2}}$ the value of b in (41) is zero, so in fact the LTRE is collinear. $\square$

The second limit case corresponds to $r_2 = 1$ and then

$$\begin{aligned} P_{\pm } (V) = V^3 [1 \pm r_1 \sqrt{1-V} ]^2 - (1-r_1^2)^5. \end{aligned}$$

Proposition 4.8

Assume $r_2 = 1$, $0< r_1 < 1$. For any $r_1 \in (0,1)$, there are exactly two solutions of $P_{\pm }(V)=0$, $0< {\hat{V}}_+< {\hat{V}}_- = 1- r_1^2 < 1$ , such that $P_+({\hat{V}}_+) =0,$ $P_-({\hat{V}}_-) =0.$

Moreover, there is a unique solution $(a,b) = (r_1,0)$ which corresponds to a collision.

Proof

In this case, $P_{\pm }(0)=-(1-r_1^2)^4<0$ and $P_{\pm }(1)=1-(1-r_1^2)^5>0$ for any $0<r_1\le 1$. Moreover $P_+(V)$ has a unique extremum in (0, 1) which turns out to be a maximum located at $V_m=3(8r_1^2-3+\sqrt{9+16r_1^2}) /(32r_1^2).$ $P_-(V)$ is an increasing function of V in this interval which has a unique zero $V=1-r_1^2$. Therefore for any $r_1\in (0,1)$ there are exactly two solutions of $P_{\pm } (V) =0$.

Let us consider ${\hat{V}}_-=1-r_1^2$. Then $f_{13}=1,$ $f_{23}= -r_1$ and using (27) $E_3=\sqrt{1-r_1^2},$ $a=r_1$ and then $b=0$. Notice that this corresponds to a collision of the negligible mass with $m_1$.

If we take ${\hat{V}}_+$, then $f_{13}=1,$ $f_{23}=\sqrt{1- {\hat{V}}_+}$, and

$$\begin{aligned} E_3 = \frac{1 + r_1 \sqrt{1- {\hat{V}}_+}}{\sqrt{1- r_1^2}}, \qquad a = - \sqrt{1- {\hat{V}}_+}\, . \end{aligned}$$

It is easy to check that $1-a^2-E_3^2\!<\!0$ if $0< r_1 < 1$ and so, there is no LTRE in this case. $\square$

Triangular/Collinear relative equilibria

In this section we study the existence of solutions of the Eqs. (14), (15) with $b=0$. We note that these solutions satisfy also (13) and so they are collinear. In this sense we call them triangular/collinear relative equilibria (T/CRE).

We assume $0< r_1 < 1$.

Let us take $b=0$. Then the system (26), in the form (29) reduces to

$$\begin{aligned} t | a E_2 + r_2 E_3 | = |a E_1 - r_1 E_3|\,,\quad (r_1E_2+r_2E_1)^3 E_1 = E_3 | a E_2 + r_2 E_3 |^3, \end{aligned}$$

where $t=\sigma _1^{1/2}=(E_2/E_1)^{1/3}$ and now $E_3=\sqrt{1-a^2}$.

Three cases must be considered

• 1. $a E_2 + r_2 E_3 > 0,$ $a E_1 - r_1 E_3 > 0$ with the negligible mass at the right hand side of $m_1$.

• 2. $a E_2 + r_2 E_3 > 0,$ $a E_1 - r_1 E_3 < 0$ with the negligible mass between $m_1$ and $m_2$.

• 3. $a E_2 + r_2 E_3 < 0,$ $a E_1 - r_1 E_3 < 0$ with the negligible at the left hand side of $m_2$.

Once the signs of $aE_2+r_2E_3$ and $aE_1-r_1E_3$ are fixed, the variable a can be eliminated from the system above to derive an implicit equation for $r_1$ and $r_2$. The results are summarized in the following Proposition

Proposition 4.9

Let $t=(E_2/E_1)^{1/3}$. Then

• 1. If $r_1, r_2$ satisfy

  $$\begin{aligned} 1 - t^4 = [ 1 + t^2 + 2 t ( r_1 r_2 - E_1 E_2) ]^2, \end{aligned}$$

  (42)

  then there exists a T/CRE, (a, 0) being $a=\displaystyle {\frac{(r_1 +t r_2)}{ \sqrt{ (E_1 -t E_2)^2 + (r_1 +t r_2)^2} }}$, with the negligible mass at the right hand side of $m_1$.

• 2. If $r_1, r_2$ satisfy

  $$\begin{aligned} 1 + t^4 = [ 1 + t^2 - 2 t (r_1 r_2 - E_1 E_2) ]^2, \end{aligned}$$

  (43)

  then there exists a T/CRE, (a, 0) being $a^2=\displaystyle {\frac{(r_1-tr_2)^2}{(E_1+tE_2)^2+(r_1-tr_2)^2}}$, with the negligible mass between $m_1$ and $m_2$. The sign of a must be the one of $r_1-tr_2$.

• 3. If $r_1, r_2$ satisfy

  $$\begin{aligned} t^4 -1 = [ 1 + t^2 + 2 t ( r_1 r_2 - E_1 E_2) ]^2, \end{aligned}$$

  (44)

  then there exists a T/CRE, (a, 0) being $a=\displaystyle {- \frac{(r_1 +t r_2)}{ \sqrt{ (E_1 -t E_2)^2 + (r_1 +t r_2)^2} }}$, with the negligible mass at the left hand side of $m_2$.

The behavior of the curves mentioned in Proposition 4.9 is shown in Fig. 5.

Fig. 5

Using the variables $(r_1,r_2)$ we display in red the T/CRE curves corresponding to (42), going from (0, 0) to $(0,r^{**})$ with $r^{**}=\sqrt{1-2^{-3/2}}$, to (43), going from (0, 1) to (1, 0) and to (44), going from (0, 0) to $(r^{**},0)$. For reference we show in black level curves of $\mu$ for $\mu =j/10,j=2,\ldots ,8$ and also for $\mu =0.48, 0.52$

Remark 4.2

We note that in case 1. the curve (42) reaches $r_1=0$ at $r_2=r^{**}= \sqrt{1-2^{-3/2}}$, in agreement with the result in Proposition 4.7. A symmetrical behavior appears in the case 3 (which also follows from 1. by replacing t by 1 / t). Furthermore in case 2. the curve (43) intersects $r_1=r_2$ at $r_1=r^{**}$, which agrees with item 5. of Proposition 4.6.

From Fig. 5 one can see that two curves are tangent to $r_1=r_2$ at (0, 0) and one has horizontal (resp. vertical) tangent at (0, 1) (resp. at (1, 0)). It can be interesting to see the order of tangency. Because of the symmetry it is enough to consider what happens near $r_1=0$ with $r_2>r_1$. This is the contents of the following Proposition

Proposition 4.10

• 1. The curve corresponding to (42) behaves as $r_2=r_1+12r_1^3+ {\mathcal {O}}(r_1^5)$ around $r_1=0$.

• 2. The curve corresponding to (43) behaves as $r_2=1-32r_1^6+ {\mathcal {O}}(r_1^8)$ around $r_1=0$.

Proof

For simplicity we rename $r_1=\varepsilon ,r_2=\delta$. Then the local expression of t, expanded in powers of $(\varepsilon ,\delta )$, is

$$\begin{aligned} t=1+(\varepsilon ^2-\delta ^2)/6+(7\varepsilon ^4-2\varepsilon ^2\delta ^2-5\delta ^4)/72+{\mathcal {O}}_6, \end{aligned}$$

where ${\mathcal {O}}_6$ denote terms of total degree $\ge 6$ wrt $\varepsilon ,\delta$. The square roots due to $E_1,E_2$ in (42) are eliminated by suitable transfer of terms and taking squares. Up to order 4 the terms on the related equation are

$$\begin{aligned} \frac{8}{3}\varepsilon ^2-\frac{8}{3}\delta ^2+5\varepsilon ^4+\frac{56}{3}\varepsilon ^3\delta + 22\varepsilon ^2\delta ^2+\frac{40}{3}\varepsilon \delta ^3+5\delta ^4=0. \end{aligned}$$

The usual Newton polygon arguments produce the desired answer. Note that in the quadratic part one has to take the positive root.

The case of (43) is slightly different. As in t it appears $(1-r_2^2)^{1/6}$, it is convenient to look for $r_2$ of the form $1-\delta ^6/2$ while we put again $r_1=\varepsilon$. Proceeding as before one obtains

$$\begin{aligned} 4\varepsilon ^2-4\varepsilon \delta +\delta ^2-8\varepsilon ^3\delta +12\varepsilon ^2\delta ^2-4\varepsilon \delta ^3+ {\mathcal {O}}_6, \end{aligned}$$

which gives $\delta =2\varepsilon +{\mathcal {O}}(\varepsilon ^3)$. The result follows. $\square$

As already said, the present paper restricts to $\mathbb {S}^2_+$. For some results including the lower hemisphere, see Kilin (1999).

5 The restricted 3-body problem in $\mathbb {S}^2_+$: A numerical study

We have proved that in the symmetrical case, $\mu =1/2$, the number of collinear relative equilibria in $\mathbb {S}^2_+$ are 1, 3 or 5 (see Proposition 4.2), and the number of triangular (and non collinear) equilibria are 0, 2 or 4 (see Proposition 4.6). Moreover, in Theorem 4.1 we have proved that in the general case $\mu \in (0,1)$, the number of triangular equilibria is at most 8.

In this section we complete the study of the number of equilibria in $\mathbb {S}^2_+$ for any $\mu \in (0,1)$ using numerical methods.

To compute the relative equilibria for the restricted 3-body problem in $\mathbb {S}^2_+$, given $r_1$ and $r_2$, we should solve Eq. (13) for the collinear case and Eqs. (14–15) in the triangular one, together with Eqs. (11–12) for the position of the primaries.

In order to get a complete picture of the solutions we do the following:

• 1. We consider a grid of values of $(r_1,r_2) \in Q=(0,1)\times (0,1)$ with a small step size, assuming ${\kappa }=1$. Then,

  • (a) We compute the values of a for a collinear equilibrium and the values of (a, b) for a triangular one, for every value of $(r_1,r_2)$ in the grid. The results are shown in Figs. 6 and 10. Different colors correspond to different number of equilibria.

  • (b) In order to refine the curves in the $(r_1,r_2)$ square which separate regions with a different number of equilibria, we describe the evolution of the $(r_1,r_2,a,b)$ variables (with $b=0$ in the collinear case) and detect bifurcations.

• 2. We start at the planar case ${\kappa }=0$, with $(r_1,r_2,a,b,k)$ as variables (keeping $b=0$ for the collinear case). Carrying out arc-length parameter continuation for fixed values of the mass ratio $\mu$, we describe the evolution of the planar equilibria in $\mathbb {S}^2_+$. The arc-length parameter will be denoted as s. See, e.g., Simó (1990) for details on continuation in general problems. To do the representation in the normalized sphere with ${\kappa }=1$, one should plot $(r_1 \sqrt{{\kappa }}, r_2 \sqrt{{\kappa }})$ and, hence, the planar case leaves from the origin. Along the continuation we detect and refine turning points and bifurcations. As mentioned at the end of Remark 2.1 one can normalize $\alpha$. The value $\alpha =1$ has been used along the continuation in all cases.

  We remark that the possibility of passage from ${\kappa }=0$ to ${\kappa }\ne 0$, for $|{\kappa }|$ small, follows immediately from the implicit function theorem, because of the stability properties in the planar case: no one of the non-trivial eigenvalues is equal to zero.

  The same continuation method is used to describe the evolution of equilibria which start at other limit cases.

Note that if ${\kappa }<0$ we can proceed in a similar way, using $\sqrt{-{\kappa }}$ to normalize.

In Fig. 6 left we recover lines of constant $\mu$ in the $(r_1,r_2)$ variables. For $\mu =1/2$ one has the lines $r_1=r_2$ and $r_1^2+r_2^2=1$, meeting at the point $(\sqrt{1/2},\sqrt{1/2})$, to be denoted as C. Curves to the left/right of C correspond to $\mu <1/2$ and the ones in the upper/lower part to $\mu >1/2$. The values used for $\mu$ are 0.1, 0.2, 0.3, 0.4, 0.45 and 0.49 and its complements to 1, that is, the values $1-\mu$. On the line $\mu =0.2$ one can see two points of coordinates $P_1\approx (0.121712,0.609584)$ and $P_3\approx (0.115614,0.550032)$. The role of these points will be discussed later. Points with the same role appear on the other $\mu =$ constant lines.

Fig. 6

Left Curves of constant value of $\mu$ in Q. Right Number of solutions of the collinear problem as a function of $(r_1,r_2)$. Blue, green and red correspond to $5,\,3$ and 1 solutions

5.1 The collinear case: global results

Collinear solutions are computed scanning $(r_1,r_2)$ as explained. The results are shown in Fig. 6 right. Some lines of constant value of $\mu$, leaving from the origin, are shown.

For the planar case, ${\kappa }=0$, using the initial (non scaled) variables there are three Euler solutions with $-r_2< r_1 < a,$ $-r_2< a < r_1$ and $a< -r_2 < r_1$. They are located at the origin in the closure of Q.

Using continuation the values of $r_1,r_2$ start to increase, moving up along a line of constant $\mu$, but the behavior is different in the three cases.

(1) The solution with $r_1 < a$ has a turning point at $P_1$ (see line $\mu =0.2$ in Fig. 6 left) at the boundary of the green and red domains shown in the figure. Then it goes back to the origin in Q while a tends to 1. We recall that for a variable going to $\pm 1$ means that the related body is going to the equator of $\mathbb {S}^2_+$. See Fig. 7 for the evolution of $r_2$ and a (in red).

(2) For the case $-r_2< a < r_1$ the solution continues up to the point $(r_1,r_2)=(0,1)$, i.e., along the full line of constant $\mu$. Concerning a it starts decreasing and then it increases, tending to $0^-$ when $r_1$ tends to $0^+$ (blue lines in Fig. 7). No turning point shows up for this branch.

(3) In the case $a <$-$r_2$, there is again a turning point like $P_3$ at the boundary between blue and green regions. From that point on, both $r_1$ and $r_2$ tend to $0^+$. Concerning a it is always decreasing, tending to −1 (magenta lines in Fig. 7).

Hence, it follows that for given values of $(r_1,r_2)$ along a $\mu$ constant line, the continuation gives 5 collinear solutions up to the point $P_3$, then 3 solutions between $P_3$ and $P_1$ and, finally, one solution between $P_1$ and the point (0, 1) in Fig. 6.

Fig. 7

Left Evolution of the values of $r_2$ along the continuation, as a function of $\arctan (s)$ for $\mu =0.2$. The red (resp. blue, resp. magenta) line corresponds to case 1) (resp. 2) and 3)). Right A similar plot for the evolution of a, with the same color convention. The maximal value of the red (resp. magenta) curve in the left plot corresponds to $P_1$ (resp. to $P_3$)

On Fig. 6 right we see that there are other collinear solutions which can not be obtained from the planar case. Some of them, for $\mu <1/2$, appear in the region bounded by $r_1=1,r_1=r_2$ and $r_1^2+r_2^2=1$. In that region, for every point $(r_1,r_2)$ near (1, 1), there is a unique collinear equilibrium with $-r_2<a< r_1$ that can be continued along the full line of constant $\mu$ up to (1, 0). Figure 8 left shows $a,r_1$ and $r_2$ as functions of s, where $s=0$ is taken at $a=0$.

There are other solutions emerging from (0, 1) (and symmetrically from (1, 0)), not connecting to (0, 0). They lie on the left top green part of Fig. 6 right. In that region there are three collinear solutions, one of them with $-r_2<a<r_1$ has been obtained by continuation from the planar case. The other two satisfy $a>r_1$. Using continuation one has a turning point at the green-red boundary of that domain. The values of $r_1$ ($r_2$) go from 0 (1) to the turning point and again to 0 (1). The value of a tends to 1 from one side (say, when $s\rightarrow -\infty$) and to 0 from the other side (see Fig. 8).

Fig. 8

A couple of examples of solutions not emerging from $r_1=r_2=0$ for $\mu =0.3$. Left emerging from (1, 0) and going to (1, 1). Right emerging from (0, 1) and returning to it. In both plots the red, magenta and blue lines correspond to the locations of $r_1,-r_2$ and a, respectively. The horizontal variable is the continuation parameter s in a moderate range

Fig. 9

The locations of $r_1$ and $-r_2$ are shown in blue. The red lines show the values of a for the collinear solutions. Left $r_2=0.7,r_1\in (0,0.1]$. Right $r_1=0.05,r_2\in [0.95,1)$

It is also interesting to look at the behavior of solutions near limit cases. In Fig. 9 left we plot the solutions near $r_1=0$ with constant $r_2<\sqrt{3}/2$. We found 5, 3 and 1 solutions (blue, green and red domains in Fig. 6 right). Moreover we see that solutions which come from the planar problem in cases (2) and (3) tend to the location of $-r_2$ when $r_1\rightarrow 0^+$. So, skipping these solutions leading to collision, only 3 solutions remain in the limit case as predicted by Proposition 4.3. In Fig. 9 right we fix $r_1=0.05$ and $r_2$ in the interval [0.95, 1). One passes from 1 to 3 solutions at the turning point related to the red-green boundary. Solutions in cases (1) and (2) tend to the location of $r_1$ when $r_2 \rightarrow 1^-$. Again skipping the solutions leading to collision, only 1 solution remains in the limit case as predicted by Proposition 4.4.

5.2 The triangular case: global results

Figure 10 shows the number of triangular solutions as a function of $(r_1,r_2)$. As proved in Proposition 4.6 for $r_1=r_2$, there is a range of values for which no triangular solutions exist. This has also been found to occur when scanning the $(r_1,r_2)$ plane, for a large set of values (domain in green) including $r_1^2+r_2^2=1$, see last part of Theorem 4.1. This domain separates two regions, see Remark 4.1: one accessible from (0, 0) by continuation, the other not.

Fig. 10

Number of solutions with $b\!>\!0$ in the triangular case, as a function of $(r_1,r_2)$. In the green, red, magenta and blue domains there are, respectively, 0, 1, 2 and 3 solutions. Similar for $b\!<\!0$. The boundaries between green-magenta and red-blue domains correspond to turning points. The black curves between magenta-red ($r_1+r_2\!>\!1$) and magenta-blue ($r_1\!+ \!r_2\!<\!1$) domains correspond to passages through collinear. We plot in black the case $r_1=r_2$, discussed theoretically, and a line for $\mu =0.172$. Close to that line other phenomena, to be described, occur in a tiny domain. Note that the blue domains and the upper magenta domain (magnified on the right) are very narrow

To perform the continuation from ${\kappa }=0$, we start at $(r_1,r_2,a,b)= (\mu ,1-\mu ,\mu -1/2,\sqrt{3}/2)$, i.e., at $L_5$. The continuation starting at $L_5$ for ${\kappa }=0$ is similar for a big range of values of $\mu$, but there is a tiny domain, not visible in Fig. 10, where it is different.

As an example of the first case we consider $\mu =0.499$. Figure 11 shows the evolution of the different variables. Leaving from (0, 0) the value of $r_1$ increases up to a maximum, $M_1$, then it decreases up to a minimum m (see the magnification in the second plot) and then it reaches a new maximum, $M_2$. After that point the behavior is symmetrical, ending in the $L_4$ planar solution. The points $M_1$ and m correspond to turning points located at the magenta-green boundary and the blue-red boundary respectively. The point $M_2$ belongs to the other boundary of the blue domain. At that point the solution is degenerated in the sense that $b=0$ and so, the triangular solution becomes collinear as found in Proposition 4.9. This collinear solution is nothing else that the one obtained for that $\mu$ in the region $r_1<a$ (case 1)) after leaving from the planar case, reaching the turning point of the type $P_1$ and going back. In a figure like Fig. 7 left it would be located in the red curve in the part which goes down. In the third part of Fig. 11 we plot the evolution of (a, b) along the continuation. Initially a is almost constant, moving first a little to the left, then to the right, until b is close to 1. After this the (a, b) point is close to the equator.

Fig. 11

Evolution of the solution leaving from $L_5$ in the planar case for $\mu =0.499$. From left to right the value of $r_1$ as a function of s; magnification in the $r_1$ direction of the flat part in the left plot; behavior of (a, b) along the continuation; the distance to the equator as a function of s shown as $\log _{10}(1-\sqrt{a^2+b^2})$

Fig. 12

Some results for $\mu =0.172$. Left $r_1$ as a function of s. Middle a detail of the central part of the left plot. The central minimum corresponds to collinear, but before it one can see two extrema in the plot, in contrast with the second plot in Fig. 11. Right evolution of (a, b)

A different evolution is obtained for $\mu =0.172.$ In Fig. 12 we display curves similar to the ones in Fig. 11. Comparing the two figures we see that the passage through collinear ($b=0$) corresponds to a maximum of $r_1$ for $\mu =0.499$ and a minimum for $\mu =0.172$. The inspection for a slightly smaller value of $\mu$ like $\mu =0.15$ shows that the two leftmost extrema in the middle plot of Fig. 12 have disappeared, and after the first turning point, $r_1$ reaches the minimum corresponding to the collinear passage. This suggests the existence of two critical values of $\mu$, with $\mu _{c_1}<0.172<\mu _{c_2}$, such that the following holds:

• (a) For $\mu =\mu _{c_1}$ there exists a value $s_{c_1}$ such that $\frac{dr_1}{ds}(s_{c_1})=\frac{d^2r_1}{ds^2}(s_{c_1})=0, \frac{d^3r_1}{ds^3}(s_{c_1})<0$. The value of $r_1$ at the collinear solution is below $r_1(s_{c_1})$. Hence, for $\mu >\mu _{c_1}$ two new turning points are created. This leads to a domain with 4 triangular solutions with $b>0$, as shown by Fig. 12 middle. The new lines of turning points meet at a cusp.

• (b) For $\mu =\mu _{c_2}$ there exists a value $s_{c_2}$ such that $\frac{dr_1}{ds}(s_{c_2})=\frac{d^2r_1}{ds^2}(s_{c_2})=\frac{d^3r_1}{ds^3} (s_{c_2})=0$, while $\frac{d^4r_1}{ds^4}(s_{c_2})\!<\!0$ and for $s=s_{c_2}$ the solution has $b=0$. In other words, the three extrema in Fig. 12 middle, two maxima for $b\!>\!0,b\!<\!0$ and a minimum for $b=0$, coincide for $s=s_{c_2}$. The value $\mu _{c_2}$ gives the end of the domain having 4 triangular solutions with $b>0$.

Figure 13 gives a full evidence of the above suggestion. We consider only solutions with $b\!>\!0$. The same number of solutions appears with $b\!<\!0$. To the left of $\mu _{c_1}$, near the leftmost black vertical curve ($\mu =0.1654$) there is one solution below the blue curve (hence red color in Fig. 10) and two on top of it (magenta domain). To the right of the $\mu _{c_2}$, near the rightmost black vertical curve ($\mu =0.1794$) there is one solution below the red curve (red domain in Fig. 10), three between the red and the blue curves (blue domain) and two on top of the blue curve (magenta domain).

Fig. 13

A magnification of a tiny domain crossed by the $\mu =0.172$ black line shown in Fig. 10. To make the visualization easier, the variables plotted are $(r_1,r_2+2.53r_1)$. The red curves correspond to turning points, while the blue one to passage through collinear solution. The black lines show part of the continuation data for $\mu \!= \!0.1654,\mu =0.172$ and $\mu \!=0.1794$, from left to right. The value $\mu =0.1654$ is close to $\mu _{c_1}$, as introduced in item (a) above, and $\mu =0.1794$ is close to $\mu _{c_2}$, as introduced in item (b)

Finally, for intermediate values $\mu _{c_1}<\mu <\mu _{c_2}$, like the central black line in Fig. 13, there is one solution below the lower red curve (red domain), three between that curve and the blue one (blue domain), four solutions between the blue curve and the upper red one (a tiny size domain not seen in Fig. 10) and two on top of the upper red curve (magenta domain). This implies that the blue domain in Fig. 10, with $\mu <1/2$ and when $r_2$ goes up, is not ending at $r_1=0$ but at the cusp shown in Fig. 13. Compare with Fig. 20 in next Section.

Remark 5.1

After Theorem 4.1 we knew that the number of triangular relative equilibria is at most equal to 8. Numerically a small domain where there are exactly 8 has been found.

Next we shortly comment on the triangular solutions which emerge from the (1, 1) point in Fig. 10. Assume we start with a solution with $b>0$. Following a line with constant value of $\mu$, see Fig. 6 left, for instance on the upper part, $r_2$ close to 1 and hence $\mu >1/2$, that line goes from (1, 1) to (0, 1). But before reaching (0, 1) the triangular solution meets the green-magenta boundary in Fig. 10 where a turning point appears. When going back along constant $\mu$ we meet the black curve of solutions with $b=0$ and enter the zone $b<0$. This is exemplified in Fig. 14 for $\mu =0.5603$.

Bifurcation curves

In Fig. 10 we have identified the 3 curves T/CRE (triangular solutions with $b=0$) given in Proposition 4.9, as the boundary of magenta-red domain in the upper part (42), and the boundaries of magenta-blue domain (43), (44).

Fig. 14

Example of the behavior of the triangular solutions emerging from (and tending to) the point (1, 1) for $\mu =0.5603$. Left Plot of $r_1$ as a function of s showing a maximum M between two nearby minima. Right A plot displaying (a, b) showing the location of M on $b=0$

The other bifurcation curves correspond to double zeros of functions $P_\pm$ defined in (30). From (30) and (38), and taking squares in a suitable way, one can compute the resultant wrt V giving rise to several curves in Q. Besides some spurious curves we obtain two which correspond to the boundaries between green and magenta domains in Fig. 10. The lower one goes from $(0,{{\hat{r}}}_2)$ to $({{\hat{r}}}_2,0)$ as given in Proposition 4.7. Two more curves appear in the domain $r_1<r_2$ (and the symmetrical ones in $r_2<r_1$) and are shown as thick red curves in Fig. 15 left. They start at (0, 0) and end at the cusp point labeled as C. In the same figure we plot as a blue thin line the curve corresponding to T/CRE which goes from (0, 0) to $(0,r^{**})$ with $r^{**}=\sqrt{1-2^{-3/2}}$, in agreement with Proposition 4.9 and Remark 4.2 (see Fig. 5). The red curves in Fig. 15 left correspond to double zeros of $P_+$ (the closer one to $r_1=0$) and of $P_-$. The blue curve is tangent to the second red curve at T, see Fig. 15 right. Following the upper red curve between C and T the radicand in (31) is positive, giving rise to two values of b. But from T till the origin the radicand is negative. So, no real triangular solutions appear. Comparing Fig. 15 with Fig. 13 we see the agreement between continuation and the theoretical approach.

Fig. 15

Two branches, in thick red lines, giving double zeros of $P_\pm$ and a thin blue curve of T/CRE. Right a magnification using $(r_1,r_2+2.53r_1)$ around the cusp point C and showing also the tangent point T

To summarize we show in Fig. 16 left the curves involved in the main bifurcations for the triangular (in red) and collinear (in blue) solutions. Skipping the values of $(r_1,r_2)$ located at the bifurcations curves, in the collinear case one has $1,\,3$ or 5 solutions. In the triangular one, and counting both the solutions with $b>0$ and $b<0$, one has $0,\,2,\,4,\, 6$ or 8 solutions. However, 8 solutions appear in a tiny domain (see Fig. 13) located near $r_1=0.10,\,r_2=0.61$. This domain is contained between the two blue curves, in a region with 3 collinear solutions. This gives a total of 11 relative equilibria. The same number can be found in other domains. On the other hand, in the domain containing the point $r_1=r_2= 1/\sqrt{2}$ only one solution exists: the collinear relative equilibrium with $-r_2<a<r_1$. So we can conjecture that:

The number of relative equilibria (collinear $+$ triangular) ranges between 1 and 11 in $\mathbb {S}^2_+$.

In Fig. 16 left values near $r_2=1$ are not properly seen, because of their small width. To this end we magnify the vertical scale in Fig. 16 right. The red curves are tangent to $r_2=1$ at $r_1=0$ and the blue one is tangent to $r_2=1$ at $r_1=1/2$, according to the results in Sect. 4.

Fig. 16

Left Bifurcation curves for the triangular (in red) and collinear (in blue) solutions. Together they bound different open sets where the number of relative equilibria is constant. Right A magnification

6 Stability analysis

In this section we assume that the two primaries are in a relative equilibrium, that is, $\mathbf{U}_1=(r_1,0),$ $\mathbf{U}_2 = (-r_2,0)$ with $r_1, r_2$ satisfying (11), (12) and $\mu , \alpha$ given by (17). We shall write $\mathbf{U}_3 = (x,y)$ and ${\dot{\mathbf{U}}}_3 = (X,Y)$. From (4) with $i=3$ we obtain the equations for the third body, that we write as

$$\begin{aligned} {\dot{x}}=X,\quad {\dot{y}}=Y,\quad {\dot{X}}=2\alpha Y+\alpha ^2 x-{\kappa }v_3 x+{\hat{F}}, \quad {\dot{Y}}=-2\alpha X+\alpha ^2 y-{\kappa }v_3 y+{\hat{G}}, \end{aligned}$$

having (a, b, 0, 0) as equilibrium point, with $b=0$ in the collinear case. Proceeding in an analogous way to the proof of Proposition 3.3, with the help of (54), (55), it turns out that the characteristic polynomial is of the form

$$\begin{aligned} p(\lambda ) = \lambda ^4+\beta _2 \lambda ^2 + \beta _0. \end{aligned}$$

(45)

According to the signs of $\beta _0$, $\beta _2$ in (45) and the discriminant $D=\beta _2^2-4\beta _0$ we can have the following possibilities: (1) Complex-Saddle (CS) if $D<0$; (2) Elliptic-Hyperbolic (EH) if $\beta _0 < 0$; (3) Elliptic-Elliptic (EE) if $D >0$, $\beta _0 >0$ and $\beta _2 >0$; (4) Hyperbolic-Hyperbolic (HH) if $D >0$, $\beta _0 >0$ and $\beta _2 < 0$.

6.1 The collinear case

Let us consider a collinear equilibrium, that is $(x,y)=(a,0)$ with a satisfying (13). For convenience we shall write (13) as done in (24)

$$\begin{aligned} m_1 g_{13}(f_{13}a-r_1)+ m_2 g_{23} (f_{23} a + r_2) = \alpha ^2 a E_3^2. \end{aligned}$$

Using (57) the equation above is equivalent to

$$\begin{aligned} m_1 g_{13} S_1 + m_ 2 g_{23} S_2 = \alpha ^2 a E_3. \end{aligned}$$

(46)

First we shall derive simple expressions for $\beta _0$ and $\beta _2$. By taking $x=a, y=0$ in (59) we obtain

$$\begin{aligned} {\hat{G}}_y:= {\hat{G}}_y (a,0) = - [m_1 f_{13} g_{13} + m_2 f_{23} g_{23} ] \end{aligned}$$

and using (57)

$$\begin{aligned} {\hat{F}}_x:= & {} {\hat{F}}_x (a,0)= 3\left[ m_1 f_{13}S_1^2\Delta _{13}^{-5/2}\!+m_2 f_{23}S_2^2\Delta _{23}^{-5/2} \right] -\left[ m_1 f_{13}g_{13}\!+m_2f_{23}g_{23}\right] \\&+\frac{{\kappa }a}{E_3}\left[ m_1S_1 g_{13}\!+m_2 S_2 g_{23}\right] . \end{aligned}$$

However, $S_1^2 \Delta _{13}^{-5/2} = g_{13}$ and $S_2^2 \Delta _{23}^{-5/2} = g_{23}.$ Moreover using (46) we obtain

$$\begin{aligned} {\hat{F}}_x (a,0) = 2 [ m_1 f_{13} g_{13} + m_2 f_{23} g_{23} ] + \alpha ^2 {\kappa }a^2 = - 2 {\hat{G}}_y + \alpha ^2 {\kappa }a^2. \end{aligned}$$

(47)

Furthermore, if $y=0$, ${\hat{F}}_y (x,0)= {\hat{G}}_x (x,0)=0$ and using (47) the coefficients of $p(\lambda )$ in (45) are

$$\begin{aligned} \beta _2 = \alpha ^2 (2 - {\kappa }a^2) + {\hat{G}}_y, \qquad \beta _0 = (\alpha ^2 E_3^2 + {\hat{G}}_y)(\alpha ^2 (1-2 {\kappa }a^2) - 2 {\hat{G}}_y). \end{aligned}$$

(48)

Proposition 6.1

For any $\mu \in (0,1)$ and $\alpha ^2$, a collinear relative equilibrium in $\mathbb {S}^2_+$ can not be of type HH. In $\mathbb {H}^2$ they are of EH type.

Proof

A collinear equilibrium is of type HH if the following inequalities hold $\beta _2^2 - 4 \beta _0 >0,$ $\beta _0 >0$ and $\beta _2 < 0$. It is well known that the collinear equilibria are EH if ${\kappa }=0$.

Assume ${\kappa }>0$. We recall that in the $\mathbb {S}^2_+$ case, ${\kappa }a^2 < 1$.

Let (a, 0) be an equilibrium such that $\beta _2<0$. Then from (48)

$$\begin{aligned} {\hat{G}}_y< - \alpha ^2 (2-{\kappa }a^2)< - \alpha ^2 < 0 \end{aligned}$$

and $\alpha ^2 + 2 {\hat{G}}_y< \alpha ^2 (-3 + 2 {\kappa }a^2) < 0$. Furthermore we can write

$$\begin{aligned} \beta _0=\alpha ^4 E_3^2 (1-2{\kappa }a^2) - {\hat{G}}_y (\alpha ^2 + 2 {\hat{G}}_y). \end{aligned}$$

If $1 - 2 {\kappa }a^2 \le 0$ it is clear that $\beta _0 < 0$ and then the equilibrium should be of type EH. Assume that $1 - 2 {\kappa }a^2 > 0$ then

$$\begin{aligned}&\beta _0\!<- {\hat{G}}_y \alpha ^2 E_3^2 (1\!- \!2 {\kappa }a^2)\! -\! {\hat{G}}_y (\alpha ^2+2{\hat{G}}_y)\!<-{\hat{G}}_y\alpha ^2(E_3^2(1-2{\kappa }a^2)-1) \\&\quad = -\! {\hat{G}}_y \alpha ^2 {\kappa }a^2 (-3\! +\! {\kappa }a^2)\! <\! 0. \end{aligned}$$

As before the equilibrium should be of type EH.

Now we pass to prove that the collinear solutions in $\mathbb {H}^2$ are EH. As ${\kappa }<0$ and ${\hat{G}}_y<0$ in this case, according to (48) it is enough to prove $\alpha ^2 E_3^2+{\hat{G}}_y<0$. But according to (24) we can write $a{\hat{G}}_y=-a[m_1f_{13}g_{13}+m_2f_{23}g_{23}]=-\alpha ^2 aE_3^2-m_1g_{13}r_1+ m_2g_{23}r_2,$ where $g_{13},\,g_{23},\,S_1,\,S_2$ are given in (55, 56). Therefore $a(\alpha ^2 E_3^2+{\hat{G}}_y)= -m_1g_{13}r_1+m_2g_{23}r_2:=R$ and if $a>r_1>0$ it is enough to prove $R<0$. From (16, 24), one has that $m_1$ and $m_2$ are proportional to $r_2E_2$ and $r_1E_1$, respectively, with a factor $>0$.

Replacing in the previous expression, taking $r_1r_2(S_1S_2)^{-3}$ as a factor we obtain $h(r_1,r_2,a):=-E_2(aE_2+r_2E_3)^3+E_1(aE_1-r_1E_3)^3$, negative if $\mu \le 1/2$ because $r_2\ge r_1$. In particular this holds for the value of a which gives a relative equilibrium with $a>r_1>0$ for any $r_2\ge r_1$.

Consider now $\mu >1/2$ (i.e., $r_2<r_1$). For a fixed a the absolute value of the first term in h increases if $r_2$ increases. The worst case appears for $r_2=0$ and it reduces to $-a^3$. Let $a=\sinh (\psi _3),r_1=\sinh (\psi _1)$. For any given $\psi _3>\psi _1>0$ one has to check that $h_1(\psi _1):=-(\sinh (\psi _3))^3+\cosh (\psi _1)(\sinh (\psi _3-\psi _1))^3<0$, and we note $h_1(0)=0$. But the derivative $dh_1(\psi _1)/d\psi _1$, skipping a positive factor, becomes $\tanh (\psi _1)\tanh (\psi _3-\psi _1)-3$ obviously $<0$.

This proves the case $a>r_1$ for any $\mu \in (0,1)$ and, by symmetry, the case $a<-r_2$. For $-r_2<a<r_1$ consider $a\ge 0$ (i.e., $r_1\ge r_2$, $\mu \ge 1/2$), the case $a\le 0$ following by symmetry.

Given $r_1\ge r_2$ one can find $a^*$ such that $h(r_1,r_2,a^*)=0$. Similar to the previous case one checks $dh(r_1,r_2,a)/da<0$ and, hence, $h(r_1,r_2,a)<0$ for $a>a^*$. This value of $a^*(r_1,r_2)$ can be substituted in the equilibrium equation which, removing nonzero factors, can be written as

$$\begin{aligned} L(r_1,r_2,a):=\frac{r_2E_2}{(r_1E_3-aE_1)^2}-\frac{r_1E_1}{(r_2E_3+aE_2)^2}+ \frac{aE_3}{(r_1E-2+r_2E_1)^2}. \end{aligned}$$

It is easy to check $L(r_1,r_2,a)\le 0$ for $a=a^*(r_1,r_2)$ if $r_1\ge r_2$. Then, the value of a for which $L=0$ is less than the one of the equilibrium. So, $h(r_1,r_2,a)<0$ for the equilibrium and $\beta _0<0$. $\square$

6.2 The triangular case

The following lemma gives simplified expressions for the coefficients of the characteristic polynomial in the triangular case.

Lemma 6.1

Let (a, b) be a triangular equilibrium. Then the characteristic polynomial is

$$\begin{aligned} p(\lambda ) = \lambda ^4 + \alpha ^2 \lambda ^2 + \beta _0, \end{aligned}$$

where

$$\begin{aligned} \beta _0= & {} b^2 \left( 9 m_1 m_2 f_{13} f_{23} L^2 \Delta _{31}^{-5/2} \Delta _{32}^{-5/2} - 3 {\kappa }\alpha ^2 \left[ m_1 f_{13} r_1^2 \Delta _{31}^{-5/2} + m_2 f_{23} r_2^2 \Delta _{32}^{-5/2}\right] \right) , \nonumber \\ \end{aligned}$$

(49)

being $L = r_2 E_1 + r_1 E_2$.

Proof

We assume that (a, b) is a solution of the Eqs. (14), (15). Using (54) the Eq. (15) becomes

$$\begin{aligned} {\kappa }x [m_1 r_1 g_{13} - m_2 r_2 g_{23}] + E_3 [m_1 E_1 g_{13} + m_2 E_2 g_{23}] - \alpha ^2 E_3^2 =0. \ \end{aligned}$$

The equilibrium satisfies (14), so, the equation above reduces to $m_1 E_1 g_{13} + m_2 E_2 g_{23} = \alpha ^2 E_3$.

However using (60) for $\beta _2$ in (45) we obtain $\beta _2 = 2 \alpha ^2 - \frac{1}{E_3} [m_1 E_1 g_{13} + m_2 E_2 g_{23} ].$ Therefore at the equilibrium $\beta _2 = \alpha ^2$. A long but simple computation, using the formulas provided at the Appendix, gives the value of $\beta _0$ given in the statement. $\square$

Proposition 6.2

If ${\kappa }< 0$ there are no triangular relative equilibria of type HH nor EH.

Proof

As $\beta _2 > 0$, the case HH is not possible. Moreover $\beta _0 >0$ as far as $f_{13}, f_{23}$ are positive. Then the case EH is not possible. $\square$

Assume ${\kappa }>0$. For the triangular/collinear equilibrium, $\beta _0=0$ and the characteristic equation becomes

$$\begin{aligned} \lambda ^4 + \alpha ^2 \lambda ^2 =0 \implies \lambda = 0 \;\; (\text{ double }), \quad \pm |\alpha | i. \end{aligned}$$

In the general case, that is $b \ne 0$, the stability is determined by the coefficient $\beta _0$ as follows:

• 1. If $0< \beta _0 < \alpha ^4/4$, then the equilibrium is spectrally stable (elliptic-elliptic case, EE).

• 2. If $\beta _0 < 0$, then the equilibrium is unstable (elliptic-hyperbolic case, EH).

• 3. If $\beta _0 > \alpha ^4/4$ , then the equilibrium is in the complex-saddle case (CS).

In the next section we shall see numerically that the three cases are realizable.

Several results about qualitative stability properties can be found in Kilin (1999).

6.3 Numerical study of the stability

In this section we study numerically the linear stability properties of the different relative equilibria using the results of the continuation procedure. The stability changes are compared to the folds detected along the continuation, as described in Sects. 5.1 and 5.2 and with the previous theoretical results.

6.3.1 Numerical studies for the collinear case

Let us consider first the solutions obtained by continuation of the planar case in $\mathbb {S}^2_+$. To obtain a complete picture we perform the computations of stability parameters for different values of $\mu$ in (0, 1). All these solutions leave from the planar case as EH, as known for ${\kappa }=0$.

The solution with $r_1<a$ reaches the green-red boundary in Fig. 6 if $\mu < 1/2$ and the blue-green one if $\mu >1/2$. At these boundaries a fold bifurcation is produced giving rise to an elliptic-hyperbolic bifurcation and the solution becomes EE at the fold (see Fig. 17). Then, for small $\mu$, when going back approaching to $(r_1,r_2)=(0,0)$ (but not the planar case) there is an inverse bifurcation returning to EH. This is produced quite soon if $\mu \in (0,\mu _c)$ for some critical value $\mu _c = 0.081...$ The computations suggest that there is no interval of EE type for $\mu = \mu _c$ (see also Fig.  18). Then, increasing $\mu$ the EE range increases, reaching the full arc approaching (0, 0) for $\mu \ge 1/2$.

The results for the solution with $a<-r_2$ are obtained from the previous one by changing the roles of $\mu$ and $1-\mu$ (see Fig. 17 right). The solution with $-r_2<a<r_1$ is of EH type.

Fig. 17

Stability properties of the collinear solutions leaving from ${\kappa }=0$ as a function of a normalized parameter s. Left case $r_1<a$. Right case $a<-r_2$. The red lines denote relative equilibria of EH type, and the green points denote EE equilibria. The different curves, from top to bottom, correspond to values of $\mu$ from 0.1 to 0.9 with step 0.1. For $\mu =0.2$ the points $P_1,P_3$ of Fig. 6 left, are shown

Fig. 18

Domain of EE relative equilibria in Q after the passage through the fold line. On top of the diagonal for $\mu <1/2$. The point marked as C corresponds to the critical value $\mu _c$

Figure 18 shows the values of $(r_1,r_2)$ for which one has some collinear relative equilibrium with $r_1<a$ of EE type. We note that for the solution with $a < -r_2$, one obtains a figure symmetrical with respect the diagonal.

Summarizing, the numerical computations show that

The collinear solutions obtained by continuation from the planar case are of EH or EE type. Only the solutions with $r_1<a$ or $a<-r_2$ can be of EE type after the fold according to Fig. 18 and the symmetrical one.

Now we analyze the solutions not connected with the planar case. The solution leaving from (0, 1) and returning to it (Fig. 8, right) changes stability at the fold when it reaches the red-green domain in Fig. 6. It passes from EH to EE according to Fig. 19, left.

Fig. 19

Left changes in stability for the branch leaving from and returning to (0, 1). Right changes in stability for the branch leaving from (1, 1) and going to (1, 0). Color code: red, green and blue for EH, EE and CS. The black parts mean that the two-body problem is unstable. On the left (resp. right) part the values of $\mu$ are 0.05 and 0.3 (resp. 0.1, 0.2, 0.3, 0.4, 0.45 and 0.49)

Let us consider now the solutions starting at (1, 0) and going to (1, 1). Initially they are of EH type, then they change to EE and finally to CS (Fig. 19, right). But to have stability one must require also stability of the two body problem, that is, $2\sqrt{{\kappa }}r_1r_2<1$. In Fig. 19 black lines correspond to instability of the two body problem.

6.3.2 Numerical studies for the triangular case

In Sect. 5.2, for any $\mu$, the triangular solutions for ${\kappa }=0$ are continued to ${\kappa }>0$. Then they pass through a triangular-collinear configuration in the middle of the range and return to ${\kappa }=0$ in a symmetrical way. In between, they have several folds depending on the values of $\mu$ where stability changes. We summarize the results in Fig. 20, where we plot $r_2$ as a function of the normalized arc-length parameter s.

First we note that solutions leave the planar case as EE type for small $\mu$, but as $\mu$ increases they leave from ${\kappa }=0$ being of CS type. As it is well known the transition occurs at the Routh critical value $\mu _R=(1-\sqrt{23/27})/2$. This change can be seen in the two left upper plots in Fig. 20 for $\mu =0.030$ and $\mu =0.050$, respectively.

Fig. 20

Evolution of the stability along the continuation as a function of a normalized arc-length parameter. In the vertical variable the value of $r_2$ is plotted. The color code is red, green and blue for EH, EE and CS, respectively. From left to right the values of $\mu$ are 0.030, 0.050, 0.165 and 0.166 on the top line and 0.179, 0.180, 0.300 and 0.490 in the bottom one. The behavior for $\mu >1/2$ is the same as for $1-\mu$

By increasing $\mu$, $(r_1, r_2)$ enter to the small domain in Fig. 13. The evolution of stability in this domain is shown in Fig. 20 for $\mu =0.166$ and $\mu = 0.179$. We can see that two small intervals of EE type appear in the central region which become larger until they intersect giving rise to a unique EE interval in the central part as in the case $\mu =0.180$. The evolution of stability for $\mu =0.180$ is maintained for large values of $\mu$ up to 0.5.

Note that in the two top right and the two bottom left plots in Fig. 20, it is hard to distinguish the minima and maxima in the central part. This is due to the narrow width of the blue zone in Fig. 10. See, for instance Fig. 12 for $\mu =0.172$ where the central zone has been magnified. In that figure the vertical variable is $r_1$, but the behavior for $r_2$ is the same.

Remark 6.1

In the blue domain of Fig. 10 there are four triangular solutions of EE type.

If we look at the left plot in Fig. 14, the stability range (assuming $r_1r_2<1/2$) corresponds to the domain between the two symmetric minima that appear in the figure.

Fig. 21

In the top left, top right and bottom left the values of $(r_1.r_2)$ for which at least one of the solutions obtained by continuation from ${\kappa }=0$ to ${\kappa }>0$ is of EE, EH or CS type, respectively. The bottom right plot shows the results for ${\kappa }\!<\!0$ (until a moderate value ${\kappa }=-10$; going to values ${\kappa }\!<\!-10$ the blue zone, of CS type, increases). Only a tiny domain of EE type is found for $\mu$ or $1-\mu$ small

A summary of the stability character is shown in Fig. 21. For given values $(r_1,r_2)$ (and, hence, for the related value of $\mu$) several different solutions can exist. So, we plot in green, red and blue the domains for which at least one of the solutions is EE, EH or CS type, respectively. Note that the different regions are not disjoint. Their boundaries coincide with the ones which separate different regions in Fig. 10, except for the EE $\rightarrow$ CS transition.

Triangular solutions leaving from the (1,1) point are EH type until they reach the magenta-green boundary in the right upper part of Fig. 10, when they turn to EE. Then they have the passage through collinear (magenta-red boundary) and return to magenta-green boundary, where they recover the EH character. If we look at the stability of the full three bodies, one has to recall that $2\sqrt{{\kappa }}r_1r_2<1$ is a necessary condition for the stability of the primaries.

Fig. 22

Stability properties EE, EH, CS, with the usual color code, for the solutions as seen in the (a, b) variables. In the EE case (green) it can happen that the same point corresponds to different solutions, i.e., different values of $(r_1,r_2,\mu )$

At the right bottom plot in Fig. 21 we show the results for ${\kappa }<0$ up to ${\kappa }=-10$. Only tiny domains are of EE type (in green), close to the axes. Most of the solutions are of CS type. If ${\kappa }<-10$ the blue region increases without bound.

We can also consider what happens to the stability properties of the solutions in $\mathbb {S}^2$ leaving from the planar case when seen in the (a, b) variables. This is shown, globally, in Fig. 22. Only the upper part, $b\ge 0$, is shown, because of the symmetry. This corresponds to the solutions going from $L_5$ for ${\kappa }=0$ to collinear. The color code is as usual. In EH and CS domains (red and blue in Fig. 22) every point (a, b) corresponds to one triangular solution. However, in the EE domain (green) a point (a, b) can correspond to triangular solutions for different values of $\mu$.

Appendix

In this Appendix we give reduced formulas for the functions which appear in the equations of the restricted problem.

Let us consider the functions $\rho _{ij}, f_{ij}, g_{ij}$ defined in (5). It is easy to check that they can be written as

$$\begin{aligned}&{\kappa }\rho _{ij}^2 = 2 [1- {\kappa }(\xi _i \xi _j + \eta _i \eta _j) - E_i E_j], \nonumber \\&f_{ij} = {\kappa }(\xi _i \xi _j + \eta _i \eta _j) + E_i E_j, \qquad 1- f_{ij}^2 = {\kappa }\Delta _{ij}, \end{aligned}$$

(50)

$$\begin{aligned}&\Delta _{ij} \!= \!\xi _i^2 \!+\! \eta _i^2 \!+ \!\xi _j^2\! +\! \eta _j^2\! -\! {\kappa }( \xi _i^2\! +\! \eta _i^2)(\xi _j^2 \!+\! \eta _j^2)- {\kappa }(\xi _i\xi _j\!+\!\eta _i\eta _j)^2-2(\xi _i\xi _j+\eta _i\eta _j ) E_i E_j, \nonumber \\ \end{aligned}$$

(51)

$$\begin{aligned}&g_{ij}:= \frac{1}{d_{ij}^3} = \left( \frac{{\kappa }}{1-f_{ij}^2} \right) ^{3/2} = \frac{1}{\Delta _{ij}^{3/2}}, \end{aligned}$$

(52)

where $E_i=\sqrt{1- {\kappa }(\xi _i^2 + \eta _i^2)}.$

If $\mathbf{U}_1=(\xi _1,\eta _1)^T=(r_1,0)^T,$ $\mathbf{U}_2=(\xi _2,\eta _2)^T=(-r_2,0)^T,$ $\mathbf{U}_3= (\xi _3,\eta _3)^T = (x,y)^T,$ then

$$\begin{aligned}&{\kappa }\rho _{13}^2 = 2 (1 - {\kappa }r_1 x - E_1 E_3), \quad {\kappa }\rho _{23}^2 = 2 (1 + {\kappa }r_2 x - E_2 E_3), \end{aligned}$$

(53)

$$\begin{aligned}&f_{13} = {\kappa }r_1 x + E_1 E_3, \quad f_{23} = - {\kappa }r_2 x + E_2 E_3, \end{aligned}$$

(54)

$$\begin{aligned}&g_{13} = \Delta _{13}^{-3/2}, \quad g_{23} = \Delta _{23}^{-3/2}, \quad \Delta _{13}= y^2 + S_1^2, \quad \Delta _{23} = y^2 + S_2^2, \end{aligned}$$

(55)

$$\begin{aligned}&S_1 = x E_1 - r_1 E_3, \quad S_2 = x E_2 + r_2 E_3, \end{aligned}$$

(56)

where $E_j= \sqrt{1-{\kappa }r_j^2},$ $j=1,2$, $E_3 = \sqrt{1-{\kappa }(x^2 + y^2)}$. Then one has

$$\begin{aligned} f_{13} x - r_1 = - {\kappa }r_1 y^2+ S_1 E_3, \qquad f_{23} x + r_2 = {\kappa }r_2 y^2 + S_2 E_3 \end{aligned}$$

(57)

and, furthermore

$$\begin{aligned} \frac{\partial f_{13}}{\partial x } = - \frac{{\kappa }S_1}{E_3}, \qquad \frac{\partial f_{23}}{\partial x } = - \frac{{\kappa }S_2}{E_3}, \qquad \frac{\partial S_1}{\partial x } = \frac{f_{13}}{E_3}, \qquad \frac{\partial S_2}{\partial x } = \frac{f_{23}}{E_3}. \end{aligned}$$

(58)

Lemma 7.1

Assume ${\kappa }>0$ and $r_1,r_2$ fixed. Then $f_{13}$ and $f_{23}$ are convex functions in $C_{{\kappa }}:=\{ (x,y)\in \mathbb {R}^2 \,|\,{\kappa }(x^2+y^2) < 1 \}$, such that for any $(x,y) \in C_{{\kappa }}$

$$\begin{aligned} - \sqrt{{\kappa }} r_1< f_{13} \le 1, \qquad - \sqrt{{\kappa }} r_2 < f_{23} \le 1.\end{aligned}$$

Moreover $f_{13}=0$ along the curve $\gamma _{13} = \{ (x,y) | x \le 0, {\kappa }(x^2 + E_1^2 y^2 ) = E_1^2 \}$, and $f_{23}=0$ on the curve $\gamma _{23} = \{ (x,y) | x \ge 0, {\kappa }(x^2 + E_2^2 y^2 ) = E_2^2 \}$.

If ${\kappa }<0$, then $f_{13}>0$ and $f_{23}>0$ at any point.

Proof

Using

$$\begin{aligned} \frac{\partial ^2 f_{13}}{\partial x^2} = - \frac{{\kappa }E_1}{E_3^3} (1-{\kappa }y^2)< 0, \quad \frac{\partial ^2 f_{13}}{\partial y \partial x} = - {\kappa }^2 x y \frac{E_1}{E_3^3}, \quad \frac{\partial ^2 f_{13}}{\partial y^2} = - \frac{{\kappa }E_1}{E_3^3} (1-{\kappa }x^2) <0, \end{aligned}$$

it follows that the Hessian of $f_{13}$ is negative definite in $C_{{\kappa }}$. Similar formulas hold for $f_{23}$ by replacing $E_1$ by $E_2$. The maximum for $f_{13}$ is equal to 1 and it is attained at the point $(x,y)=(r_1,0)$ and the minimum is achieved at the point $(x,y)= (-1/\sqrt{{\kappa }},0).$ Similar for $f_{23}$. The case ${\kappa }<0$ is obvious from (3). $\square$

Let us consider the functions ${\hat{F}}$, ${\hat{G}}$ introduced in Sect. 6. We compute the partial derivatives

$$\begin{aligned} {\hat{F}}_x= & {} \frac{1}{E_3} \left\{ - 3 m_1 (r_1 - x f_{13} ) f_{13} S_1 \Delta _{13}^{-5/2} + 3 m_2 (r_2 + x f_{23} ) f_{23} S_2 \Delta _{23}^{-5/2} \right. \nonumber \\&\left. -E_3 [ m_1 f_{13} g_{13} + m_2 f_{23} g_{23} ] + {\kappa }x [ m_1 S_1 g_{13} + m_2 S_2 g_{23} ] \right\} , \nonumber \\ {\hat{F}}_y= & {} \frac{y}{E_3} \left\{ - 3 m_1 (r_1 - x f_{13} ) E_1 f_{13} \Delta _{13}^{-5/2} + 3 m_2 (r_2 + x f_{23} ) E_2 f_{23} \Delta _{23}^{-5/2} \right. \nonumber \\&\left. + {\kappa }x \, [ m_1 E_1 g_{13} + m_2 E_2 g_{23} ] \right\} , \nonumber \\ {\hat{G}}_x= & {} \frac{y}{E_3} \left\{ 3 m_1 S_1 f_{13}^2 \Delta _{13}^{-5/2} + 3 m_2 S_2 f_{23}^2 \Delta _{23}^{-5/2} + {\kappa }\, [m_1 S_1 g_{13} + m_2 S_2 g_{23} \,] \right\} , \nonumber \\ {\hat{G}}_y= & {} -\left[ m_1 f_{13} g_{13} + m_2 f_{23} g_{23} \right] \nonumber \\&+ \frac{y^2}{E_3} \left\{ 3 m_1 f_{13}^2 E_1 \Delta _{13}^{-5/2} + 3 m_2 f_{23}^2 E_2 \Delta _{23}^{-5/2} + {\kappa }\,[ \, m_1 E_1 g_{13} + m_2 E_2 g_{23} \,]\right\} .\nonumber \\ \end{aligned}$$

(59)

Lemma 7.2

For any real ${\kappa }$, the following identity holds

$$\begin{aligned} {\hat{F}}_x+{\hat{G}}_y = \frac{1}{E_3} [m_1 E_1 g_{13} + m_2 E_2 g_{23} ]. \end{aligned}$$

(60)

Proof

From (59) it follows

$$\begin{aligned} {\hat{F}}_x+{\hat{G}}_y= & {} -2 \left[ m_1 f_{13} g_{13} + m_2 f_{23} g_{23} \right] + \frac{{\kappa }x}{E_3} \left[ m_1 S_1 g_{13} + m_2 S_2 g_{23}\right] \\&+ \frac{{\kappa }y^2}{E_3}\left[ \, m_1 E_1 g_{13} + m_2 E_2 g_{23} \,\right] \\&+\frac{3 m_1 f_{13}}{E_3} \Delta _{13}^{-5/2} \left[ (r_1 - x f_{13}) S_1 + y^2 f_{13} E_1 \right] \\&+ \frac{3 m_2 f_{23}}{E_3} \Delta _{23}^{-5/2} \left[ (r_2 + x f_{23}) S_2 + y^2 f_{23} E_2 \right] . \end{aligned}$$

Using (57) and (54)

$$\begin{aligned} (r_1 - x f_{13}) S_1 + y^2 f_{13} E_1 = E_3 (y^2 + S_1^2), \quad (r_2 + x f_{23}) S_2 + y^2 f_{23} E_2 = E_3 (y^2 + S_2^2). \end{aligned}$$

Note that from (55), $\Delta _{13}^{-5/2} (y^2 + S_1^2) = \Delta _{13}^{-3/2}= g_{13}$ and $\Delta _{23}^{-5/2} (y^2 + S_2^2) = g_{23}$. Using (56) to write

$$\begin{aligned} m_1 S_1 g_{13} + m_2 S_2 g_{23} = x \left[ \, m_1 E_1 g_{13} + m_2 E_2 g_{23} \,\right] + E_3 \left[ - m_1 r_1 g_{13} + m_2 r_2 g_{23} \right] , \end{aligned}$$

one can easily obtain (60) after some cancellations. $\square$