Introduction

Nanoindentation is often used to test the mechanical properties of materials. The plastic response of materials can be characterized by indentation hardness [1]. The Oliver–Pharr analytical method [2] is generally used to calculate the elastic modulus and indentation hardness of materials in the nanoindentation test. Due to the lots of assumptions including homogeneous, linearly elastic, isotropic, incompressible, etc., the method is limited with regard to determining the mechanical properties of the heterogeneous and multiscale structural materials. Although the different hardness techniques commonly used vary in test setup, indenter geometry, test methodology, etc., techniques mentioned above essentially involve applying a known amount of load and determining the volume of the plastic zone beneath the indenter [3].

Indeed, the strain field under the indenter is very heterogeneous and complex. One significant problem in the indentation modeling of the elastic–plastic materials is to determine the volume of the plastic zone, due to the coupling of elastic and plastic deformation beneath the indenter. In most studies of indentation, the contact radius between the indenter and the specimen is assumed to be the plastic zone radius [4]. However, Durst et al. deem that the radius of the plastic zone is bigger than the contact radius for most materials [5]. In the study by Durst et al., they did not give detailed research results about the radius of the plastic zone. The relation between the indentation depth and the radius of the plastic zone needs to be determined by finite element (FE) simulation because the deformation process under the indenter cannot be observed during the nanoindentation experiment.

At present, the FE approach has become essential for investigating the mechanical properties of materials. The constitutive models are the bases of describing the mechanical behavior of materials, and the FE simulation of complex problems [6]. In the phenomenological theory of plasticity, the constitutive model of materials is described by a yield surface and an associated flow rule [7]. For the associated flow rule, the plastic potential function is equal to yield function. The yield function did dual role-playing, in associated plasticity flow, it not only models the yielding of materials, but also acts as the plastic potential function. Therefore, the yield criterion lies at the core of the phenomenological description of the plastic deformation for materials [8].

A number of yield surface development are already visible in recent researches [9,10,11], to mention just a few representative approaches that have led to further developments. It is widely accepted that metal deformation occurs with zero or negligible plastic dilatancy, i.e., permanent volume change after plastic deformation [12]. However, for many engineering materials such as polymer, amorphous materials, cellular materials, and rock-like materials, their yield behavior exhibits a dependence on hydrostatic pressure, and this type of material is called pressure-sensitive materials [13, 14]. In addition, these materials also exhibit a difference in flow stress between tension and compression. This phenomenon is referred to as the strength asymmetrical effect. For example, the uniaxial compression strength is much higher than the uniaxial tensile strength for concrete, rocks, and ceramics. A number of studies have been devoted to the description of deformation and strength of various materials with a tension-compression asymmetry [15].

In this work, an elasto-plastic constitutive model considering the strength asymmetrical effect between compression and tension of pressure-sensitive materials has been proposed, and it is applied into the FE Method software ABAQUS by a reasonably designed UMAT subroutine. Through the FE analysis of the indentation, the plastic zone under the indentation is visualized, and the radius of the plastic zone under the indentation is obtained. The plastic zone radius plays an important role when analyzing the indentation size effect of materials [16]. The relationship between the plastic zone radius and indentation depth will help to calculate accurately the strain below the indenter, and provides data support for the study of nanoindentation. In addition, the significance of this research could provide a method to investigate the nanoindentation behavior by the macroscopic constitutive relation and numerical simulation.

Constitutive model based on ellipse yield criterion

The average normal stress (\(\sigma_{{\text{m}}}\)) and equivalent stress (\(\sigma_{{\text{e}}}\)) are the main variables for describing the mechanical response of pressure-sensitive materials. The average normal stress is calculated from the components of the diagonal of the Cauchy stress tensor (\({\varvec{\sigma}}\)): \(\sigma_{{\text{m}}} = (\sigma_{1} + \sigma_{3} + \sigma_{3} )/3\), \(\sigma_{i}\) are the principal normal stress. Similarly, equivalent stress can be calculated by second invariant of deviatoric stress tensor (\( \varvec{s} = \varvec{\sigma } - \sigma _{{\text{m}}} \varvec{I},\, \varvec{I} \) is the identity matrix) [17]. So, the equivalent stress can be expressed by the principal normal stress as well:

$$ \sigma_{e} = \sqrt {\left( {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{1} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{2} } \right)^{2} } \right)/2} $$
(1)

To account for the strength asymmetry between compression and tension of pressure-sensitive materials, the elliptic criterion similar to the one used by Kermouche et al. [18] to discuss the plastic behavior of amorphous silica is modified. For the pressure-sensitive materials, the strength differential effects are usually considered to be caused by normal stress [19]. Thus, an ellipse yield function for pressure-sensitive materials is proposed as follows:

$$ \left( {\frac{{\sigma_{e} }}{a}} \right)^{2} + \left( {\frac{{\sigma_{m} + b}}{c}} \right)^{2} = 1 $$
(2)

where a, b and c are material parameters. Thereinto, the parameter a is related to equivalent stress, i.e., the second invariant of the deviatoric stress, and the parameter c represented the contribution of hydrostatic pressure to the yield behavior of materials. The physical significance of the constant b is describing the strength differential effects of material, and based on the relationship between compression yield stress \(\sigma_{{{\text{cy}}}}^{{}}\) and tension yield stress \(\sigma_{{{\text{ty}}}}^{{}}\), it can be written as:

$$ b = \sqrt[2]{{\sigma_{{{\text{cy}}}}^{2} - \sigma_{{{\text{ty}}}}^{2} }} $$
(3)

The assumption is made that the hardening behavior of material is isotropic hardening, because no loading path effect is involved in this study. The yield function is the isosurface of the hardening parameter and can be determined by the evolution of the parameter c. Hence, the yield function can be expressed as:

$$ F = \left( {\frac{{\sqrt {\left( {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{1} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{2} } \right)^{2} } \right)/2} }}{a}} \right)^{2} + \left( {\frac{{\frac{{(\sigma_{1} + \sigma_{3} + \sigma_{3} )}}{3} + \sqrt[2]{{\sigma_{{{\text{cy}}}}^{{2}} - \sigma_{{{\text{ty}}}}^{{2}} }}}}{{f(\varepsilon_{e}^{p} )}}} \right)^{2} - 1 $$
(4)

where f is the hardening function and is related to material property. \(\varepsilon_{e}^{p}\) is equivalence plastic strain, and it can be obtained by the plastic work equivalence principle (i.e., \(\sigma_{ij} :\varepsilon_{ij} = \sigma_{e} \varepsilon_{e}^{p}\)).

According to the plastic theory, the total strain increment can be split into the elastic strain increment and the plastic strain increment, i.e., \({\text{d}}\varepsilon_{ij} = {\text{d}}\varepsilon_{ij}^{e} + {\text{d}}\varepsilon_{ij}^{p}\). The generalized plastic potential theory can mathematically be formulated as the following general form [20]:

$$ {\text{d}}\varepsilon_{ij}^{p} = {\text{d}}\lambda \frac{\partial G}{{\partial \sigma_{ij} }} $$
(5)

where G is the plastic potential function and dλ is called the “consistency parameter.” According to the associated flow rule, G should be equal to F. The consistency parameter can be evaluated by applying the consistency condition (\(\dot{F} = 0\)) on the introduced yield function:

$$ \dot{F} = \frac{\partial F}{{\partial \sigma_{ij} }}:{\text{d}}\sigma_{ij} + \frac{\partial F}{{\partial f}}\frac{\partial f}{{\partial \varepsilon_{e}^{p} }}{\text{d}}\varepsilon_{e}^{p} = 0 $$
(6)

Based on the classical plastic theory [21], the stress–strain relationship is expressed as follows:

$$ {\text{d}}\sigma_{ij} = \left[ {C_{{\text{e}}} } \right]{\text{d}}\varepsilon_{ij}^{e} = \left[ {C_{{\text{e}}} } \right]\left( {{\text{d}}\varepsilon_{ij}^{{}} - {\text{d}}\varepsilon_{ij}^{p} } \right) $$
(7)

where [Ce] is the usual matrix of elastic constants.

Then, by substituting the plastic strain tensor rate from Eq. (5) into Eq. (7), it reads:

$$ {\text{d}}\sigma_{ij} = \left[ {C_{{\text{e}}} } \right]{\text{d}}\varepsilon_{ij}^{e} = \left[ {C_{{\text{e}}} } \right]\left( {{\text{d}}\varepsilon_{ij}^{{}} - {\text{d}}\lambda \frac{{\partial {\text{F}}}}{{\partial \sigma_{ij} }}} \right) $$
(8)

In view of Eqs. (6) and (8), the following expressions can be obtained:

$$ {\text{d}}\lambda = \frac{{\frac{\partial F}{{\partial \sigma_{ij} }}:C_{e} :{\text{d}}\varepsilon_{ij}^{{}} }}{{\frac{\partial F}{{\partial \sigma_{ij} }}:C_{e} :\frac{\partial F}{{\partial \sigma_{ij} }} - \frac{\partial F}{{\partial f}}\frac{\partial f}{{\partial \varepsilon_{e}^{p} }}}} $$
(9)

By incorporating the consistency parameter from Eq. (9) into Eq. (8) such as follows:

$$ {\text{d}}\sigma_{ij} = \left[ {C_{{\text{e}}} } \right]d\varepsilon_{ij}^{e} = C_{{\text{e}}} :\left( {{\text{d}}\varepsilon_{ij}^{{}} - \frac{{\frac{\partial F}{{\partial \sigma_{ij} }}:C_{{\text{e}}} :{\text{d}}\varepsilon_{ij}^{{}} }}{{\frac{\partial F}{{\partial \sigma_{ij} }}:C_{{\text{e}}} :\frac{\partial F}{{\partial \sigma_{ij} }} - \frac{\partial F}{{\partial f}}\frac{\partial f}{{\partial \varepsilon_{e}^{p} }}}}\frac{\partial F}{{\partial \sigma_{ij} }}} \right) $$
(10)

By reordering Eq. (10), the elasto-plastic continuum tangent is therefore:

$$ C_{ep} = C_{e} - \frac{{C_{e} :\frac{\partial F}{{\partial \sigma_{ij} }} \otimes \frac{\partial F}{{\partial \sigma_{ij} }}:C_{e} }}{{\frac{\partial F}{{\partial \sigma_{ij} }}:C_{e} :\frac{\partial F}{{\partial \sigma_{ij} }} - \frac{\partial F}{{\partial f}}\frac{\partial f}{{\partial \varepsilon_{e}^{p} }}}}. $$
(11)

In this section, an elliptic model is modified based on theoretical analysis. The generalized elasto–plasticity model is established, and obtaining the theoretical Jacobian matrix. The generalized elasto–plasticity constitutive equation, especially, serves for the numerical solution and makes the implementation more convenient.

Calibration of proposed constitutive model for PMMA

Poly(methyl methacrylate) (PMMA) is a widely used pressure-sensitive material in the field of aircraft and automotive industries due to its excellent properties such as transparency, low density, and high impact resistance [22, 23]. The mechanical properties of PMMA have been reported by a lot of researches. Qiu et al. [24] and Lin et al. [25] conducted a series of quasi-static uniaxial compression and combined shear-compression tests. The compression stress–strain relationship of PMMA can be characterized well by the linear hardening function, as shown in Eq. (12),

$$ f\left( {\varepsilon_{e}^{p} } \right) = d + e\varepsilon_{e}^{p} $$
(12)

where e is the strain hardening coefficient, and d is the initial yield stress. The symbol f and \(\varepsilon_{e}^{p}\) represent hardening function and equivalent plastic strain. Based on the results of Qiu et al. and Lin et al., the material parameters can be obtained, and the detailed results are shown in Table 1 [24, 25]. In addition, the physical meanings of parameters a and b in Table 1 are given in Eq. (2).

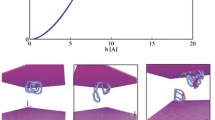
Table 1 The values of material parameters [24, 25]
Full size table

The experimental yield data (Qiu et al. and Lin et al.) [24, 25] and theory yield surfaces are summarized in principal stress space, as shown in Fig. 1. Obviously, this modified yield criterion can be successfully applied to describe the yield behavior of PMMA.

Fig. 1
figure 1

The experimental yield loci (Qiu et al. and Lin et al.) and theoretical yield surfaces [24, 25]

Full size image

Application to nanoindentation FE analysis of PMMA

In this study, the software ABAQUS is used to simulate the nanoindentation of PMMA. The axisymmetric geometrical model is shown in Fig. 2, and it comprises two components, conical indenter and tested sample. The angle θ between the surface of the conical indenter and the plane of the surface is 19.68 degrees, and it can ensure that the conical indenter is equivalent to the Berkovich indenter [26]. Thereinto, the sample is set to a cylinder with the diameter of 50 μm and height 30 μm, and it can ensure that the plasticity affected region does not exceed the boundary of the geometrical model, when the indentation depth (h) reaches 2000 nm.

Fig. 2
figure 2

Axisymmetric FE model for the nanoindentation

Full size image

In the nanoindentation experiment, the indenter is made of diamond, and its elastic modulus is 1141 GPa [26], which is much larger than the elastic modulus of the test material. Therefore, the conical indenter is set as a rigid body in this FE model. The displacement is applied in the -y direction, and the x direction is a fixed boundary, so that it does not move in the transverse direction. The contact type between the indenter surface and the sample surface is face-to-face contact, and the friction is ignored, because the load–displacement relationship and the simulated stress–strain field are not affected by the friction conditions [27]. The FE mesh of the conical indenter and tested sample is shown in Fig. 2. In order to ensure the convergence of numerical results, the minimum size of the element in the contact region is about 100 nm. The number of elements and nodes for the sample is 3767 and 3831, respectively. The convergence of mesh is verified, that is, further refinement of mesh size would not improve the accuracy of simulation results.

The proposed constitutive model is inputted via “User-Defined Material” in ABAQUS, and it is numerically implemented by static implicit algorithm UMAT. In the constitutive model, the elastic modulus and Poisson's ratio of PMMA were, respectively, set as 4.40 GPa and 0.38, respectively [28]. Then, according to the calibrated constitutive relation and the established FE model, the indentation deformation of PMMA was analyzed by FE method. Figure 3 shows the Mises stress field in the deformed region. It is noticed that the deformation area below the indenter is hemispherical, and Mises stress is distributed gradient along the depth direction. The maximum stress is about 140 MPa.

Fig. 3
figure 3

Distribution of the Mises stress (unit in MPa) for the nanoindentation of PMMA

Full size image

The comparison of the depth–load obtained by experimental (dots) [25] and simulation models (lines) is given in Fig. 4. These two kinds of results are very close, and the maximum difference is approximately 9.93% for the indentation depth reaching 1370 nm. This comparison result proves the rationality of constitutive model and FE model.

Fig. 4
figure 4

Comparison of the loading force-indentation depth relation between the experimental data (dots) [25] and simulated results (lines) for PMMA

Full size image

In order to further analyze the plastic deformation under the indenter, Fig. 5 shows the graphical results of the plastic strain distribution for sample. Assume that it is plastic deformation zone when the strain reaches 0.2%. \(\rho_{1}\) and \(\rho_{2}\) represent the distance from the indenter tip in the y direction and x direction, respectively. Hence, the plastic zone radius (R) can be expressed as:

$$ R = \frac{{\rho_{1}^{2} + \rho_{2}^{2} }}{{2\rho_{1}^{{}} }}. $$
(13)
Fig. 5
figure 5

Distribution of plastic strain for the nanoindentation of PMMA

Full size image

To calculate the plastic zone radius of different indentation depths, Fig. 6a and b shows the relationship \(\rho_{1}\), \(\rho_{2}\) with the indentation depth. It can be seen that the strain decreases nonlinearly with the increase in \(\rho_{1}\) and \(\rho_{2}\). In addition, when the deformation reaches the same strain level, \(\rho_{1}\) is larger than \(\rho_{2}\) at all indentation depths.

Fig. 6
figure 6

a \(\rho_{1}\)–strain curves of different indentation depths and b \(\rho_{2}\)–strain curves of different indentation depths

Full size image

According to Fig. 6 and Eq. 13, when indentation depth reaches 420, 840, 1260, 1280, and 2100 nm, the plastic zone radius is 1901, 4249, 6484, 7834, and 10131 nm, respectively, as shown in Fig. 7. It can be seen that the radius of plastic zone changes linearly with the increase in indentation depth. The plastic zone radius is about 4.84 times of the maximum indentation depth based on the fitting result.

Fig. 7
figure 7

Relation of plastic zone radius and indentation depth

Full size image

As is known to all, the plastic zone radius plays an important role when analyzing the indentation size effect of materials [4]. The contact radius of indenter is frequently used to replace the radius of the plastic zone in many studies [29, 30], because the plastic zone radius cannot be measured by experiment. However, based on the above analysis results, it can be seen that the radius of the plastic zone is much greater than contact radius of the indenter. Although the direct relationship between the plastic zone radius and the indentation depth cannot be verified by experiment, the high consistency of load-displacement curves between numerical simulation and experiment in Fig. 4 can indirectly prove the rationality and accuracy of the research results.

Conclusions

In this paper, a generalized elasto–plasticity constitutive equation is developed by the modified elliptic yield criterion. This criterion can be used to describe the strength asymmetry between compression and tension of pressure-sensitive materials. This constitutive equation is used to study the nanoindentation behavior of PMMA via numerical simulation. It shows that FE simulations using the developed constitutive model reproduce the experimentally measured indentation load–displacement curves with reasonable accuracy. Then, the plastic deformation of indentation is discussed in detail, and the relation between the plastic zone radius and the maximum indentation depth is obtained. This relationship will help to accurately calculate the strain below the indenter and provides data support for the study of nanoindentation.