Indentation of PU at different scales and computational modeling: identification of viscoelasticity and quantification of adhesion effects

Abstract

In the present study, nanoindentation and macroindentation tests are performed on a soft polymer: polyurethane (PU). Strong viscoelasticity is represented by the force-displacement data on both scales. A finite element method based on an inverse procedure is employed to identify the nonlinear viscoelasticity of PU. An appropriate viscoelastic model is chosen, and the corresponding parameters are identified by matching the experimental responses with the predictions of the computational model. At the very beginning, the uniaxial tensile test, which has a homogeneous deformation, is used to prove the isotropic properties and incompressibility of PU and to identify the viscoelasticity as a reference and verification source. The comparison between the identified results from nanoindentation and macroindentation allows to quantifying the adhesion effects in nanoindentation. The quantification is treated with a traction–separation relationship incorporated into the numerical adhesive contact model. Comparable strain rates in the macro-, nanoindentation and uniaxial tensile tests are considered to identify the viscoelasticity.

1 Introduction

Rapid development in nanotechnology has led to a wide range of emerging applications of thin films or coatings recently. For instance, not only metallic but also polymeric thin films have been widely used to protect nanodevices or to improve mechanical properties of such devices, e.g., microelectromechanical systems (MEMS) or nanoelectromechanical systems (NEMS). Hence, the mechanical behavior of thin film/substrate systems is of great importance. Nanoindentation technique has emerged as a successfu tool to measure properties of materials at sub-microscales [11, 31–33]. However, some problems still need to be resolved in order to make a wide adaption of nanoindentation in polymer thin films or coatings.

First of all, most of the polymeric materials show highly elastic and viscous material behavior at the same time, called viscoelasticity. In the past decades, investigations of viscoelastic effects of polymer materials using experimental testing, constitutive modeling and numerical computation have been published in e.g., [18, 28]. Therefore, an analysis method to evaluate the viscoelasticity of polymers from the nanoindentation force-displacement data is required. However, the Oliver and Pharr method [31, 32], which is applied in the automatic analysis procedure of most indentation instruments, is only able to determine hardness and elastic modulus. This analysis method assumes that the material behaves in an elastic–plastic manner and does not exhibit any time-dependent behavior or load rate dependence. Hence, it is not applicable to a viscoelastic polymer. In order to identify the viscoelastic behavior of polymers by nanoindentation, two ways have been documented in literature instead of the Oliver and Pharr method. The first method is based on analytical or semi-analytical solutions. These solutions are based on parameters of the respective viscoelastic model and represent the relationship between indentation force and displacement. The model parameters are obtained by fitting the experimental force-displacement data with the analytical functions. Since the linear viscoelastic contact solutions are derived from the Hertz elastic contact theory by the correspondence principle, this method is restricted by yielding accurate identification only for specific linear viscoelastic models for small deformation under fixed experimental processes. Furthermore, effects like nonlinear friction, adhesion and surface roughness in nanoindentation experiments are not taken into account in the analytical solutions. The second method, the so-called inverse method, is performed by combining finite element method (FEM) modeling and numerical optimization. In this method, the objective function, which is the difference between experimental and numerical data, is minimized with respect to the model parameters using the numerical optimization. The parameters of the constitutive models are identified as the optimized solution. Huber et al. [20, 21, 23, 40] have been the first to apply this method in indentation. They used neural networks to identify the material parameters from indentation experiments on metals. However, the inverse method is still a new topic regarding nanoindentation problems of polymer materials. Hartmann [16] identified the viscoplastic model parameters with uniaxial tests and validated them using indentation tests. Rauchs [34, 35] employed a gradient-based numerical optimization method to identify viscous hyperelastic and elasto-viscoplastic material parameters. Guessasma [14] determined viscoelastic properties of biopolymer composite materials using the finite element calculation and nanoindentation experiments. Liu [27] characterized the soft viscoelastic gels via indentation and optimization-based finite element analysis. Similarly, Wang [42] identified the mechanical properties of viscoelastic/plastic materials from nanoindentation data with a procedure combining numerical optimization with a finite element indentation model. Saux et al. [25] identified the constitutive model for rubber-like elasticity from microindentation tests. As the inverse method permits us to handle any material model with nonlinear properties and to include additional effects in the numerical model, it is a useful new method to deal with the problems of identifying rate-dependent material properties from nanoindentation. Therefore, the finite element-based inverse method has been used in our previous work to identify the hyperelastic and viscoelastic properties from indentation data and to quantify additional effects such as adhesion or surface roughness effects [5, 7, 8].

Secondly, as mentioned at the beginning, nanoindentation has a considerable advantage to determine local properties from continuously measured force-displacement data with high resolution. Unfortunately, there are various problems that influence the actual material response during indentation, e.g., friction, adhesion, surface roughness and further indentation process-associated factors. These problems result in a systematic error between the numerical and the experimental results that often leads to even larger errors in the parameter identification [3, 30, 34, 41]. In this case, results of the characterization from nanoindentation need to ensure that their approximations are appropriate for answering questions about the real behavior of thin polymer films. In essence, a verification process is required to assure that the chosen material model together with the identified parameters from nanoindentation is able to predict the real responses in engineered systems. Hence, in the present study, the verification is performed not only by comparing the numerical prediction with the experimental data in nanoindentation. In addition, taking into account data from uniaxial tension tests and from multiaxial compressive loading as applied during indentation allows for a deep insight into the material’s behavior. Furthermore, indentation tests will be performed on different scales, i.e., macro- and nanoindentation tests, leading to a quantification of the surface interaction effects related to adhesion forces. The comparison of these different deformation situations allows a validation of the proposed material model and the corresponding identified parameters, respectively.

In this paper, a soft polymer: polyurethane (PU), which behaves nonlinearly elastic as well as intermediate viscoelastic (the Deborah number De$\cong$1), is chosen to be investigated. At the very beginning, the uniaxial tensile test, which has a homogeneous deformation, is used to prove the isotropic properties and incompressibility of PU and to identify the viscoelasticity as a reference and verification source. Both nanoindentation and macroindentation tests are performed. A FEM-based inverse procedure is employed to identify the nonlinear viscoelasticity of PU. An appropriate viscoelastic model is chosen, and the corresponding parameters are identified by matching the experimental responses with the predictions of the computational modeling. The comparison between the identified results from nanoindentation and macroindentation allows the quantification of the adhesion effects in nanoindentation. The quantification is treated with a traction–separation relationship incorporated into the numerical adhesive contact model. The strain rate in the macro-, nanoindentation and uniaxial tensile tests are considered to identify the nonlinear viscoelasticity. This article is organized as following: The sample preparation, the experimental setup and the experimental data are described in Sect. 2. The numerical treatment including the FEM-based inverse method, the considered viscoelastic model and the adhesive contact model are presented in Sect. 3, while Sect. 4 discusses and explains the results of the characterization and comparison. Finally, the conclusions are given in Sect. 5.

2 Samples and experiments

2.1 Preparation of the samples

The investigated polyurethane (PU)¹ is synthesized from three commercial monomers provided by Bayer MaterialScience AG, Germany. Desmodur$^{\tiny \textregistered }$CD is an aromatic isocyanate hardener and consists of methylene diphenyl diisocyanate, shortly termed as MDI (54 % diphenylmethane-4,4-diisocyanate, 45 % diphenylmethane-2,4-diisocyanate and 1 % diphenylmethane-2,2-diisocyanate). Desmophen$^{\textregistered }$2060 BD, which is shortly called diol, is a linear polypropylene ether diol. Desmophen$^{\textregistered }$1380 BT, shortly called as triol, is a branched polypropylene ether triol. The chemical reaction of Desmophen$^{\textregistered }$2060 BD with MDI generates linear chains, while Desmophen$^{\textregistered }$1380 BT contributes cross-links due to its trifunctionality. Therefore, the mechanical behavior of the PU depends on the mixing ratio of triol and diol. In this study, the investigated PU is mixed with a hydroxyl group ratio of OH$_\mathrm{{triol}}$ : OH$_\mathrm{{diol}}$ = 80$:$20 and stoichiometrically with MDI. The monomers are stored and mixed in desiccated air at room temperature within a glove box to avoid parasitic reactions of the isocyanate with water. For the preparation of the dogbone specimens and the specimens for indentation tests, the reacting monomer mixture is cast on a leveled PTFE surface with thickness of 2 mm and cylindrical molds. The mixture is cross-linked at room temperature for 72 h and then fully cured in dried air at 90 $^\circ \mathrm C$ for another 4 h. This synthesized PU has a glass transition temperature about $-5\,^\circ \mathrm C$ as measured by differential scanning calorimetry (DSC) tests. Hence, this PU is an entropy elastomer polymer in the viscoelastic state at room temperature.

The dogbone specimens for the tensile tests, which have a length of 75 mm, a width of 4 mm in the center of the dogbone and a thickness of about 2 mm, are die-cut from the PU film. The cylindrical specimens for macroindentation and nanoindentation have a diameter of approximately 30 and 20 mm, a height of about 18 and 4.5 mm, respectively. All the three kinds of specimens are shown in Fig. 1.

Fig. 1

Sketches of specimens: dogbone specimen for tensile test (left), cylindrical specimens for macro- and nanoindentation tests (right)

2.2 Experimental setup

The uniaxial tensile tests are performed with a homemade device. Detailed description of the technique and the testing method is given in [24]. The macroindentation experiments are performed using a custom-made device, which was originally designed to perform uniaxial tensile tests for polymers. The actuator Linos LT 50 ST$^{\textregistered }$ is able to apply the tensile as well as the compression forces; thus, it produces the compression effect required for indentation. The upper clamp in the tensile device, shown in Fig. 2, is replaced by a cylindrical metal rod, to which the tip of the indentation is glued. The metal rod is screwed into a central hole in the S-bracket force sensor from ME-Messsysteme$^{\textregistered }$. The spherical indenter tip consists of a hardened bearing ball with a diameter of 5 mm. The flexibility of this indentation device can be neglected with respect to the compliance of the soft polymers. The displacement of the indenter is controlled and measured through the linear stage in a closed loop control of the stepper motor. The position is supplied via the integrated encoder by the number of steps of the stage. Loosing steps yields an error message of the device. The maximum displacement of 150 mm can be measured with a resolution of 1 $\upmu$m. In the meantime, the reaction force is measured via a sensor KD24s of ME-Messsysteme$^{\textregistered }$ in the range of 20 N and a linear accuracy of 0.1 %. With a computer control, realized by LabVIEW$^{\textregistered }$, both the values of the force sensor and the displacement signal of the linear stage can be collected simultaneously. The experimental results are compared with the data obtained in the Leibniz Institute for New Materials (INM), Saarland University, using a commercial macroindenter universal testing instrument Z 1446 produced by Zwick GmbH, Germany. The maximum difference of the compared force values obtained by both indentation devices with the same displacement history is about 6.9 %. This difference is comparable with the divergence of the repeated experiments performed by both macroindentation devices, and hence, it is acceptable.

Fig. 2

Construction of custom-made tensile tester (left) and developed macroindentation device (right)

The nanoindentation experiments² have been performed on a TI 900 TriboIndenter$^{\textregistered }$ of Hysitron Inc., MN, USA. The Hysitron TriboIndenter$^{\textregistered }$ provides quantitative testing capabilities with both normal and lateral force loading configurations. The transducer used in the TriboIndenter$^{\textregistered }$ is based on three-plate capacitor technology providing simultaneous actuation and measurement of force and displacement with a sub-nN and sub-nm resolution, respectively. The device uses a drift correction procedure that is very important for precise measurements at the nanoscale. In the quasi-static mode, the TriboIndenter$^{\textregistered }$ has a force noise floor better than 100 nN and a displacement noise floor less than 0.2 nm. A three-sided pyramidal diamond tip, known as standard Berkovich geometry, is used in all nanoindentation experiments.

2.3 Comparable deformation rate

It is well known that the hyperelastic and viscoelastic property of PU to be identified is related to the strain level and stress state [9, 35]. Therefore, it is necessary to make sure that the deformation levels and its rates used in the three kinds of tests are comparable. The deformation rate to evaluate here is chosen to be the rate of the Green-Lagrange strain tensor $\mathbf{E}$, which is often used in the large deformation in the continuum field. The deformation rate can then be determined by $\dot{\mathbf{E}}={\mathrm{d}\mathbf{E}}/\mathrm{d}t$, where $t$ is the loading time. Since a homogeneous deformation state is involved in the uniaxial tensile test, it is simple to determine its Lagrange strain once the stretch is directly measured during the test. However, it is not the case for both macro- and nanoindentation tests, since indentation has a locally inhomogeneously compressive deformation. In this study, we will evaluate the deformation rate of the indentation tests with the strain distribution plots obtained from numerical simulations and with the traditional representative strain concept in contact mechanics. Figure 3 displays the distribution of the Green-Lagrange strain in the indentation direction in macro- and nanoindentation obtained from the numerical model. In both indentation cases, the strains are maximized at the contact range just under the tip and radially diminish to zero with increasing distance from the contact center. The circular strain zones with the various values shown in the color bar validate that the deformation in indentation is mainly multiaxial and locally compressive (${E}_{11}<0$) by nature. Only slight tensile effects (${ E}_{11}>0$) exist outside the contact zone.

Fig. 3

Distribution of the Green-Lagrange strain at the indentation direction ${E}_{11}$: macroindentation with a maximum displacement of 0.5 mm (left) and nanoindentation with a maximum displacement of 3 $\upmu$m (right)

The “indentation strain” is a concept obtained from indentation stress–strain relationship in the classical contact mechanics. For instance, the mean contact pressure $p_\mathrm{{m}}$, which has an actual physical significance as stress, is given by [17]

$$\begin{aligned} {p_\mathrm{{m}}}=\frac{{F }}{\pi a^2}=\left( \frac{4E^*}{3\pi }\right) \,\frac{a}{R}, \end{aligned}$$

(1)

$E^*$ is the reduced modulus, and $a$ and $R$ are the radii of the contact area and spherical indenter tip, respectively. Therefore, the second term in Eq. (1) is defined as an indentation stress–strain relationship similar to that is commonly obtained from conventional uniaxial tension and compression tests. The mean contact pressure $p_\mathrm{{m}}$ is often considered to be the “indentation stress,” and the quantity $a/\mathrm {R}$ is termed the “indentation strain.” According to this concept and the contact solution in [39],

$$\begin{aligned} {p_\mathrm{{m}}}=\frac{E^*}{2}\,\mathrm {cot}\alpha , \end{aligned}$$

(2)

where $\alpha$ is the half-angle of the conical tip, the “indentation strain” in conical indentation is $\mathrm {cot}\alpha$. Hence, indentation using a conical or an effective pyramidal tip is also defined as constant-strain indentation. The Green-Lagrange strain value ${E}_{11}$ and representative strain $\varepsilon$ of the three tests are listed in Table 1. The maximum strain values of uniaxial tensile tests are larger than the indentation tests. Both the ${E}_{11}$ and $\varepsilon$ strain value of macro- and nanoindentation are comparable with the values in tensile tests if the tensile displacement is 10 mm. Therefore, it is possible to keep the strain levels and the deformation rates in the three different tests being comparable considering the rate dependency of polymers. It should keep in mind that the expression “nanoindentation” in this paper is due to the used Triboindenter that has a resolution of nanometer and nanonewton. The maximum deformations in all nanoindentation are actuality in the micrometer range in order to avoid the influence of substrate and to have a comparable strain and strain rate with macroindentation and tensile tests.

Table 1 The Green-Lagrange strain value ${E}_{11}$ and representative strain $\varepsilon$

2.4 Experimental results

In this study, on the one hand, experiments with different deformation forms at different scales such as uniaxial tensile test, macro- and nanoindentation tests are taken into account. The comparison of these different experiments allows a validation of the proposed material model and supplies a deeper insight into the material’s behavior. On the other hand, both viscoelastic phenomenons that are stress relaxation and strain creep are able to display in nanoindentation. It is interesting to validate the identified material parameters from relaxation test with creep behavior, and vice versa.

2.4.1 Tensile tests

As a first step, the uniaxial tensile tests are used to prove the assumption of isotropic and incompressible properties of PU. The custom-made device for the tensile test is able to measure the three-dimensional deformations that are elongation and transverse stretches $\lambda _1$, $\lambda _2$ and $\lambda _3$, respectively. The ratio of the two transverse deformations $\lambda _2/\lambda _3$ is used to verify the isotropic property. As shown in Fig. 4 (left), the average value of $\lambda _2/\lambda _3$ is close to 1, which guarantees that the tested PU is isotropic. The volume strain in terms of the Jacobian $J$, which can be computed by $J=\mathrm{{det}}\mathbf{F}=\lambda _1\,\lambda _2$ $\lambda _3$, is used to prove the incompressibility. Similarly, the values of $J$ at different displacements for three individual tensile tests of new samples are shown in Fig. 4 (right). On average, the assumption of incompressibility $\mathrm{{det}}\mathbf{F}=1$ is fulfilled quite well. As a second step, relaxation tensile tests are performed with two kinds of deformation rates during the loading state, as shown in Fig. 5. After loading, the specimens are hold at different levels of deformation. The intention of the tests is to show the rate dependency of PU at various levels of deformations, which will be used to verify the characterized results from the indentation tests.

Fig. 4

Verification of isotropic property (left) and incompressibility (right)

Fig. 5

Relaxation testing: with a Lagrange strain rate of 0.366 s$^{-1}$ (left) and 0.733 s$^{-1}$ (right)

2.4.2 Macroindentation

In macroindentation, a monotonic test combined with multi-cyclic loading is performed to evaluate the basic elasticity, as shown in Fig. 6. A maximum displacement of 0.5 mm is achieved monotonically with five steps, each step contains five cycles of loading and unloading with an amplitude of 0.05 mm. In the force-displacement curve, the average of the loading and unloading loops is approximated as the basic elastic response. Secondly, the rate-dependent property is investigated in macroindentation by single cyclic testing with three different deformation rates. The maximum displacement of 0.5 mm is linearly reached in three loading times of 10, 50 and 100 s, and the followed unloading is treated with the same velocity. The hysteresis loops in Fig. 7 (left) are dependent on the loading time. The hysteresis loops of a loading time of 50 and 100 s are so small and close to the approximated basic elastic response as obtained in Fig. 6 (right). In the relaxation test, the same maximum displacement of 0.5 mm is linearly reached within four loading times 1, 10, 50 and 100 s, and this displacement is hold for 200 s. Figure 7 (right) displays the relaxation of force in macroindentation using four kinds of loading rates. The deformation rate-dependent effects in the relaxation behavior are obvious. The approximated basic elastic behavior is able to predict the equilibrium responses in both cyclic and relaxation tests. It is worth to note that the behavior of the loading time of 50 and 100 s in both two tests is similar and close to the basic elastic behavior. As expected, no adhesion effects can be observed in macroindentation tests since no negative forces are involved in the force-displacement curves in Fig. 7.

Fig. 6

Stepwise testing with five cycles of loading at each step to investigate the basic elasticity: displacement controlled loading history and the force-time response (left), the force-displacement loop and evaluated basic elasticity (right)

Fig. 7

Force-displacement loop of cyclic testing with various loading rate (left) and force relaxation with different loading time (right), both are compared with the approximated basic elasticity

2.4.3 Nanoindentation

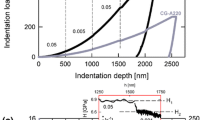
The nanoindentation experiments are performed with both open-loop load and displacement control in an automatic way. The indentations can be automatically performed by the control computer including the saving of the experimental data once the indentation patterns are set. As shown in Fig. 8 (left), an indentation pattern used in this study is a 3 $\times$ 3 matrix with an interval of 15 $\upmu$m. The directions of the arrows display the indentation path. The intervals should be large enough in order to avoid the influence from the neighboring indentations. Figure 8 (right) shows the individual curves of the indentations excluding the data with large discretization from the average. The good reproducibility of the curves in indentation results in a further verification of the homogeneous behavior in microscale of PU. Furthermore, creep tests are performed using a consistent rate of 5 $\upmu$N/s with a series of maximum forces ranging from 50 to 100 $\upmu$N, which can be seen in Fig. 9 (left). As shown in Fig. 9, the viscoelasticity is obviously represented by the creep responses of the indentation depth. The residual displacements [see Fig. 9 (right)] after withdrawing the indenter may be due to the possibilities of viscous hysteresis, adhesion effects between the indenter and specimen or plastic deformation. In the displacement controlled tests, cyclic tests are firstly performed with a maximum displacement of 3000 nm under a spectrum of loading times ${T}=1$, 10, 50 s. The force-displacement curves shown in Fig. 10 (left) display the obviously rate-dependent viscous hysteresis. The prominent measured negative forces after withdrawing the indenter are classical indication of adhesion measurements, which are termed pull-off force. In the relaxation tests, the indenter is hold at the maximum indentation depth in the cyclic test for 500 s. It can be seen from Fig. 10 (right) that the force relaxes fast in the first 75 s and then slowly reaches the equilibrium state. Similar to the cyclic test, a comparable negative force is also obtained in the relaxation test during pull off.

Fig. 8

Indentation pattern in automatic way (left), individual displacement creep curve (right)

Fig. 9

Nanoindentation with Berkovich indenter under load control with a series of maximum loads: displacement creep responses (left), force-displacement data (right)

Fig. 10

Nanoindentation with Berkovich indenter under displacement control with maximum displacement of 3000 nm: cyclic force-displacement data with various rates (left), force relaxation data (right)

As conclusion from the experimental results of the tests, PU shows obviously rate-dependent viscous hysteresis. No indication can be found in these results to support the possibility of plastic deformation. A viscoelastic model for isotropic and incompressible material with a spectrum of relaxation times is necessary to be taken into account. According to the comparison of the indentation force-displacement data at macroscale and nanoscale, adhesion effects have to be quantified in order to identify the viscoelasticity from nanoindentation force-displacement data accurately.

3 Numerical treatment

3.1 FEM-based inverse method

The inverse method is a general framework that is used to convert observed measurements into information about a physical object or system of interest. The finite element (FE)-based inverse method is popular because it allows for specimens with arbitrary shapes and physical processes with arbitrary loading conditions. This method is especially powerful if the material or structure properties are complex, e.g., nonlinear, heterogeneous and anisotropic. Since the indentation process on polymers involves strongly nonlinear contact mechanics as well as nonlinear time-dependent material properties and some further influential quantities, the FE-based inverse method is chosen to develop a robust analysis procedure in this study.

Figure 11 represents the flowchart of the developed analysis procedure using the FE-based inverse method, which is a mixed experimental and numerical optimization problem. First of all, the force-displacement data obtained from the nanoindentation experiments are used as reference source and are imported into an optimization procedure. The error contributions such as adhesion effects, surface roughness and other process-associated factors are involved in the experimental data. The optimization procedure is developed combining the FEM code ABAQUS$^\circledR$ with a mathematics tool Matlab$^\circledR$. In the optimization procedure, the boundary value problem of nanoindentation is simulated in ABAQUS$^\circledR$ taking into account the real geometry and real boundary conditions as same as in the experiments. In the numerical model, it is important to choose a suitable contact model between the tip and the surface, a material model for the specimen and further models predicting other affecting responses. It is the goal to determine the corresponding parameters of these models by this procedure. The principle of the method is to compare experimental force-displacement data with the computed results from the finite element model. Starting with guessed initial values, the models’ parameters are iteratively updated by an optimization algorithm. The identification can then be formulated as an optimization problem where the objective function $f(x)$ to be minimized is an error function of the least squares type that expresses the difference between the experimental measurements and the numerical predictions.

Fig. 11

Flowchart of the developed analysis procedure using FE-based inverse method

The choice of the optimization-based method for minimizing an objective function is a topic of interest. It is generally advised to use globally convergent optimization algorithms whenever possible. These algorithms are simulated annealing or genetic algorithms, such as evolutionary algorithms, or deterministic algorithms like the simplex method. The gradient-based algorithm is full of troublesome gradient calculation and the further drawback of local convergence. Genetic or evolutionary algorithms are globally convergent and are the only useful choice in a multi-objective optimization. Therefore, in our study, the genetic algorithm in the Matlab$^\circledR$ Optimtool is used to connect with the FEM computation in ABAQUS$^\circledR$/Standard in the parameter identification process. The details of the genetic algorithm and the explanation of the optimization procedure can be found in our previous studies [6, 7]. In this study, the used FEM models with the boundary value problems of indentation are the same as the model applied in [8] for nanoindentation and in [9] for macroindentation, respectively. The real tip geometry, which has been studied in [8], is also considered here since the same Berkovich indenter is used in the experiments on PU.

3.2 Viscoelastic model

In order to construct a phenomenological 3D viscoelastic model, a one-dimensional rheological model is introduced, as illustrated in Fig. 12. An extra spring is connected in parallel with $n$ Maxwell elements. It is a useful model to represent quantitatively the mechanical behavior of real viscoelastic materials. As the extra spring represents the elasticity in the relaxed state, the Maxwell elements display the viscous material response considering a number of discrete relaxation times $r_j\in (0,\infty ),j=1,...,n$. The finite viscoelasticity is characterized explicitly by means of an internal variable model following the concept of Simo [38] and Holzapfel [19]. These internal variables can be assumed to be the strains or stresses of the Maxwell elements, like the stresses $\mathbf{Q}_j$ as shown in Fig. 12. A three-dimensional viscoelastic model suitable for finite strains and small perturbations away from the equilibrium state is postulated on the theory of compressible hyperelasticity within the isothermal regime. The Helmholtz free-energy function $\psi$ uses the multiplicative decomposition of the deformation gradient into a so-called volumetric part and an isochoric part. Such a type of formulation is preferred for numerical realization using the finite element method considering the nearly incompressibility of the rubber-like materials. ABAQUS$^{\textregistered }$ modifies the viscoelastic damage model proposed by Simo [38] to describe three-dimensional finite-strain viscoelasticity. The model implemented in ABAQUS$^{\textregistered }$ is a time domain generalization of either hyperelastic or hyperfoam constitutive model using the volumetric/deviatoric-split hereditary integral in the reference configuration for large strain materials and a standard push-forward operator [1, 38]. This viscoelastic model will be shortly described in the following.

Fig. 12

Rheological model of the viscoelasticity with $j=1,...,n$ Maxwell elements

First, the change of the free energy $\psi$ within an isothermal viscoelastic process from the reference to the current configuration is given as

$$\begin{aligned} {\psi }(\mathbf{C},\mathbf{\Gamma _1}...\mathbf{\Gamma _n})={ \psi }^\infty _\mathrm{vol}(J)+{\psi }^\infty _\mathrm{iso}({\bar{\mathbf{C}}})+\displaystyle \sum \limits _{j=1}^{n}\Upsilon _j({\bar{\mathbf{C}}},\mathbf{\Gamma }_j), \end{aligned}$$

(3)

in which the first two terms are strain-energy stalled in the extra spring and the third term is responsible for the viscoelastic contribution. The corresponding constitutive equations describing the isothermal viscoelastic behavior at finite strains can be obtained by using the second law of the thermodynamics in the form of the Clausius-Planck inequality. The physical expression for the second Piola–Kirchhoff stress S is in the form of

$$\begin{aligned} \mathbf{S} = 2\frac{\partial \psi (\mathbf{C},\mathbf{\Gamma _1}...\mathbf{\Gamma _n})}{\partial \mathbf{C}}=\mathbf{S}^\infty _{\mathrm{vol}}+\mathbf{S}^\infty _{\mathrm{iso}}+\displaystyle \sum \limits _{j=1}^{n}\mathbf{Q}_j, \end{aligned}$$

(4)

and the nonnegative internal dissipation $\mathcal {D}_\mathrm{int}$ is

$$\begin{aligned} \mathcal {D}_\mathrm{int} = -\displaystyle \sum \limits _{j=1}^{n}2\frac{\partial \Upsilon _j({\bar{\mathbf{C}}},\mathbf{\Gamma }_j)}{\partial \mathbf{\Gamma }_j}:\frac{1}{2}\dot{\mathbf{\Gamma }}_j\ge 0. \end{aligned}$$

(5)

The stress is split into the volumetric part $\mathbf{S}^\infty _\mathrm{vol}$, isochoric pure elastic part $\mathbf{S}^\infty _\mathrm{iso}$ and the viscoelastic part $\displaystyle \sum \limits _{j=1}^{n}\mathbf{Q}_j$, with the definitions

$$\begin{aligned} \mathbf{S}^\infty _\mathrm{vol} = J\frac{\mathrm{d }\psi (J)}{\mathrm{d} J}\mathbf{C}^{-1}, \mathbf{S}^\infty _{\mathrm{iso}} = J^{-2/3}\mathbb {P}:2\frac{\mathrm{d \psi }({\bar{\mathbf{C}}})}{\mathrm{d} {\bar{\mathbf{C}}}}, \end{aligned}$$

(6)

herein, the fourth-order projection tensor $\mathbb {P}=\mathbb {I}-\frac{1}{3}\mathbf{C}^{-1}\otimes \mathbf{C}$ is the deviatoric operator in the reference configuration. In Eq. (4), the additional internal tensor variables $\mathbf{Q}_j, j=1,...,n$ are introduced, which may be interpreted as non-equilibrium stresses characterized by the viscoelastic response. By the analogy with the second term of Eq. (6) and with the linear viscoelasticity, one can define the internal constitutive equations (for details, please see [18], chapter 6)

$$\begin{aligned} \mathbf{Q}_j = J^{-2/3}\mathbb {P}:2\frac{\partial \Upsilon _j({\bar{\mathbf{C}}},\mathbf{\Gamma }_j)}{\partial {\bar{\mathbf{C}}}}=-2\frac{\partial \Upsilon _j({\bar{\mathbf{C}}},\mathbf{\Gamma }_j)}{\partial \mathbf{\Gamma }_j},\qquad j=1,...,n. \end{aligned}$$

(7)

The evolution equations which govern the internal variables $\mathbf{Q}_j,$ $j=1,...,n$ should be specified in a suitable way so that the viscous dissipation $\mathcal {D}_\mathrm{int}$, i.e., the inequality Eq. (5), is satisfied. Considering efficient time integration algorithms suitable for the finite element procedure, we choose linear evolution equations for each of the internal variables according to [19, 38]

$$\begin{aligned} \dot{\mathbf{Q}}_j + \frac{\mathbf{Q}_j}{r_j}=\dot{\mathbf{S}}_{\mathrm{iso}\,j},\qquad j=1,...,n, \end{aligned}$$

(8)

herein, the tensors $\mathbf{S}_\mathrm{isoj}$ characterize the isochoric second Piola–Kirchhoff stresses corresponding to the strain energy ${\psi }_\mathrm{isoj}({\bar{\mathbf{C}}})$ which is responsible for the $j$th relaxation process with relaxation time $r_j$, $j=1,...,n$. According to Govindjee and Simo [13], if a viscoelastic medium such as a thermoplastic elastomer is composed of identical polymer chains, e.g., silicone rubber, we can assume that $\mathrm{\psi }_\mathrm{isoj}$ is replaceable by $\mathrm{\psi }_\mathrm{iso}^\infty$

$$\begin{aligned} {\psi }_\mathrm{isoj}({\bar{\mathbf{C}}})=\beta _j^\infty \mathrm{\psi }_\mathrm{iso}^{\infty }({\bar{\mathbf{C}}}),\qquad j=1,...,n, \end{aligned}$$

(9)

where $\beta _j^\infty \in [0,\infty )$ are given as non-dimensional strain-energy factors associated with the relaxation times $r_j$, $j=1,...,n$. Finally, the stresses $\mathbf{S}_{\mathrm{iso}j}$ can be replaced by $\mathbf{S}_\mathrm{iso}^\infty$ as

$$\begin{aligned} \mathbf{S}_{\mathrm{iso}j}=J^{-2/3}\mathbb {P}:2\beta _j^\infty \frac{{\partial \psi }({\bar{\mathbf{C}}})}{\partial {\bar{\mathbf{C}}}}=\beta _j^\infty \mathbf{S}_{\mathrm{iso}}^\infty ({\bar{\mathbf{C}}}),\qquad j=1,...,n. \end{aligned}$$

(10)

The free energy of the Mooney–Rivlin form involves parameters associated with both strain invariants and provides a relatively simple mathematical and reliable constitutive model for the nonlinear deformation behavior of isotropic rubber-like materials. It is physically founded and includes typical effects known from nonlinear elasticity at moderate finite strain [29, 36]. In this study, according to the strain invariant plane in [9] (Fig. 18), the indentation deformation state relates to both strain invariants of incompressible material. Another advantage of the Mooney–Rivlin model can be found in the fact that it has the same form of the neo-Hooke model if the parameter associated with the second strain invariant is set to zero. Hence, the Mooney–Rivlin model is also suitable for the uniaxial tensile test in which the elastic behavior related to the second invariant is negligible [22]. In this study, the finite elastic response of the considered PU is assumed to be characterized by using the Mooney–Rivlin model. In particular, the free energy of the extra spring in Fig. 12, which is responsible for the equilibrium elastic behavior, can be expressed as

$$\begin{aligned} {\psi }(\mathbf{C})={\psi }^{\infty }_\mathrm{vol}(J)+{\psi }^{\infty }_\mathrm{iso} ({\bar{\mathbf{C}}})=\frac{1}{{D}_{1}}(J-1)^2+{C}_{10} ({\bar{I}}_1-3)+{C}_{01}({\bar{I}}_2-3). \end{aligned}$$

(11)

The compressibility parameter $D_1$ can be interpreted as a penalty parameter that enforces incompressibility if small values are chosen.

3.3 Quantify adhesion effects

As shown in the force-displacement data of nanoindentation test, the negative forces or residual displacements in displacement controlled or force controlled experiments, respectively, display the adhesion effects. Hence, it is required to quantify such effects in order to characterize the viscoelastic behavior of PU from the force-displacement data. The main idea in our work to quantify adhesion effects is similar to identification of viscoelasticity using the inverse method, as explained in Sect. 3.1. The adhesion effects will be numerically described by mathematical formulations in the adhesive contact model, and the parameters in the formulations can then be identified by comparing the numerical computational results with the experimental measurements.

Concerning the numerical treatment of the contact problem, a contact pair is formed with the tip of the indenter as the master surface and the polymer layer as the slave surface. In this study, because the ratio of the indentation depth to the layer thickness is smaller than 1 %, the friction is negligible according to numerical results of our previous work [4]. Hence, here we only focus on the normal contact. The default contact pressure–clearance relationship used in ABAQUS$^{\textregistered }$/Standard is referred as the “hard” contact model. In this case, the formulation of the normal contact is used as a constraint for non-penetration, which treats the normal contact as an unilateral constraint problem. It only transmits pressure once the surfaces are in contact within a contact zone $c$, as shown in Fig. 13 (left). However, this interaction model is not sufficient to simulate the real experimental behavior as adhesion is not taken into account. As a result, an adhesion zone is added to the contact zone forming an interaction area of radius $c+a$. The adhesive behavior is implemented as an interaction of the contact pair. It is defined as a surface-based cohesive behavior in ABAQUS$^{\textregistered }$ with a traction–separation relationship as shown in Fig. 13 (right), which assumes initially linear elastic behavior followed by the initiation and the evolution of damage. The elastic behavior is written in terms of an adhesive stiffness $\mathbf{K}=[K_\mathrm{nn},K_\mathrm{ss},K_\mathrm{tt}]^T$ that relates the stresses to the separation at the damage initiation ${\varvec{\delta }}^0=[\delta _\mathrm{nn}^0,\delta _\mathrm{ss}^0,\delta _\mathrm{tt}^0]^T$ across the interface. The process of degradation begins when the contact separation satisfies a certain damage initiation criterion related to $\varvec{\delta }^0$. An exponential damage evolution law describes the nonlinear rate at which the adhesive stiffness $\mathbf K$ is degraded once the corresponding initiation criterion is reached. The evolution laws are defined with a separation at the complete failure $\delta _\mathrm{nn}^t$ and the non-dimensional exponential parameter $\alpha ^E$.

Fig. 13

Adhesive contact geometry (left), traction–separation relationship with a linear or exponential damage evolution law in adhesive contacts (right)

4 Characterization results and discussion

The parameters of the considered viscoelastic model in Sect. 3.2 are identified using the FEM-based inverse procedure developed in Sect. 3.1. The relaxation experimental data, Fig. 5 (left, B $_{11}=3.93$), Fig. 7 (right, ${T}=10$ s) and Fig. 10 (right) for tensile, macro- and nanoindentation tests, are used as referent data to be compared with the numerical simulations, respectively.

4.1 Identified results

As shown in the experimental data Figs. 7 and 10 (left), the tests with various process times ${T}$ $=$ 1, 10, 50, 100 s have three different hysteresis loops and maximum forces. The test results of ${T}$ $=$ 50 and ${T}=100$ s have almost the same results. It is proven in [37] that the maximum hysteresis loop depends on the ratio of the process time $T$ to the relaxation time $\mathrm r$. It is expected that in this time period about several hundreds seconds, PU has three different relaxations. Hence, three Maxwell elements will be considered to express the relaxation spectrum of PU. The algorithm requires bounds and initial values for each parameter. The computational cost can be reduced if narrow bounds are chosen. Also the choice of the starting values has influence on the convergence speed to the optimal results. In general, the choice of the bounds depends on the problem and the experience of the user. In this study, firstly, the basic elasticity of PU is identified from the approximated elastic behavior in macroindentation as shown in Fig. 6, which is used as the reference source to set the bounds and initial values of $C_{10}$ and $C_{01}$. The finally identified parameters with the chosen bounds and initial values of the material parameters are shown in Table 2.

Table 2 The identified parameters of material and adhesive contact model with an exponential evolution law

Now the identified results will be verified by comparing the numerical simulations with the corresponding experimental measurements. Firstly, it is worth to note that $C_{01}$ is identified with a very small value relative to $C_{10}$. The reason which has been explained in [9, 22] is that the contribution to the uniaxial tensile behavior due to the second invariant is negligible according to the strain invariant plane in [9] (Fig. 18). It is shown in Fig. 14 (left) that the numerical simulation fits the corresponding experimental data that is called reference curve ($B_{11}$=3.93) best. However, if the simulations are compared with other experimental data that are not chosen in parameter identification, the deviation becomes larger (relaxation data at smaller deformations, cf. the experimental curves of $B_{11}$=3.02, $B_{11}$=2.22, $B_{11}$=1.59). It’s worth noting that the fast relaxation processes cannot be captured with identified relaxation times of the chosen viscoelastic model at the maximum deformation of $B_{11}$=1.59. One physical explanation could be that the relaxation times of the three Maxwell chains should be a function of the deformation rather than a simple constant. It is the versa case in Fig. 14 (right) that a larger deviation is found in the fitness of deformation $B_{11}$=3.93. In this case with a higher deformation rate compared to the reference experimental data, the fast relaxation processes cannot be captured with this material model. A similar reason could be that the relaxation times should also be a function of deformation rate. Hence, although the deviations in this study are acceptable, it seems that the identification of hyperelastic and viscoelastic properties is dependent on the strain level and the deformation rate. A more complicate material model, in which the relaxation time is a function of strain as well as strain rate, is expected to more accurately describe the viscoelastic behaviors.

Fig. 14

Comparison of experimental data and numerical simulations: relaxation testing with a Lagrange strain rate of 0.1465 s$^{-1}$ (left) and 0.293 s$^{-1}$ (right) during loading

For macroindentation, it can be seen in Fig. 15 that the Mooney–Rivlin model with the identified results can be exactly described the approximated basic elasticity from the stepwise cyclic test. The match between the numerical prediction and experimental data of the single cyclic tests with process times of ${T}=$ 10, 100 s is acceptable with reasonable differences. In the relaxation behavior, the numerical simulation curves overlap the experimental data of ${T}=$ 10 and 100 s. In the case of fast loading, the maximum force obtained from the experiment is about 10 % higher than the numerical result, which is the same in the investigation of re-identification of viscoelasticity from nanoindentation in our previous work [7]. But for both the relaxation process and equilibrium state, the numerical simulations are exactly the same as the experimental response. Therefore, the deviation of 10 % may arise due to the inaccurately identified parameters of the elastic part in the Maxwell elements.

Fig. 15

Comparison of experimental data and numerical simulations: relaxation testing with a Lagrange strain rate of 0.1465 s$^{-1}$ (left) and 0.293 s$^{-1}$ (right)

The identification of nanoindentation contains two cases that in one case, the adhesive contact model is used in the numerical model, and in the other case, the adhesion effects are not taken into account. The identified parameters are listed in Table 2, and the term “Nanoindentation” refers to the identification without adhesion effects. It is shown that except $C_{10}$, $r_2$ and $\beta _3^\infty$, all the other parameters have approximately consistent values for these two cases. Firstly, the differences of the numerical simulation using parameters identified from the numerical model with and without adhesion effects are shown in Fig. 17 (left) by comparing with the experimental creep data. The numerical creep curve with adhesion effects exactly fits the experimental response. For the numerical data obtained without adhesion effects, a deviation from the experimental measurement in the creep process and in the residual displacement is observed. By this point of view, the adhesion effects in nanoindentation have some influence on the force-displacement data during the holding and unloading stages. In Fig. 17 (right), the numerical simulation with the adhesion effects is able to predict the nanoindentation relaxation behavior of PU very well. Furthermore, the considered viscoelastic model and the adhesive contact model with the identified parameters are verified by comparing with experimental force-displacement data in cyclic tests using load and displacement control, as shown in the left and right side of Fig. 16, respectively. In both of the figures, deviations are displayed in the loading part of the force-displacement curves. But the matches in the unloading part are perfect, these results coincide with the conclusion of our previous work [8]. A potential reason for the deviation in the loading part may lie in the larger thermal drift in nanoindentation, which is not able to be fully excluded by the drift correction procedure of the device.

Fig. 16

Comparison of experimental data and numerical simulations: relaxation testing with a Lagrange strain rate of 0.1465 s$^{-1}$ (left) and 0.293 s$^{-1}$ (right)

Fig. 17

Investigation of correlation of the three tests in nanoindentation: creep test (left) and relaxation test (right)

4.2 Comparison and discussion

The characterization of PU from the three kind of tests will be compared and discussed in this section. It can be seen from Table 2 that the identified parameters of the three Maxwell elements are almost the same except some of the parameters in the case of nanoindentation without adhesion. The individual difference of the identified $C_{10}$ and $C_{01}$ between tensile and indentation tests is large, but the total difference of the sum $C_{10} + C_{01}$ is negligible. The reason is that the accurate identification of $C_{10}$ and $C_{01}$ is dependent on the deformation state and strain level [2, 10, 22] and on the noise level of the experimental data [6]. Comparing the results obtained from indentation tests, all parameters of the viscoelastic model are approximately consistent of the nanoindentation with adhesion and of the macroindentation. That means if the adhesion effects are considered in the numerical model, the identified viscoelasticity of PU is the same from macro- and nanoindentation. Such a result dovetails nicely with the theoretical expectation that the adhesion effect, which is sensitive in nanoscale surface interaction, is negligible in macroindentation. The prominent differences of the identified values between the macroindentation and nanoindentation without adhesion effects further support this conclusion.

Furthermore, the correlation of the characterization results of tensile test, macro- and nanoindentation is investigated by predicting the experimental data of one test with the parameters obtained from the other two tests. Firstly, as shown in Fig. 17, the creep and relaxation process in nanoindentation can be exactly predicted by the viscoelastic model with the parameters identified from tensile and macroindentation tests. However, the residual displacement and the negative force in the unloading part cannot be reproduced in the simulation using a numerical model in which the adhesion effect is not taken into account. Secondly, as shown in Fig. 18 (left), the relaxation together with loading and unloading behaviors in macroindentation is perfectly predicted with simulation using the parameters obtained from tensile test and nanoindentation with adhesion effects. An acceptable deviation about 5 % between the experimental maximum force and the numerical value appears if the parameters obtained from nanoindentation excluding the adhesion effects are used. Hence, comparing with the characterization results from macroindentation, it can be concluded that the viscoelasticity of the unfilled homogeneous PU in this study is able to be accurately evaluated from nanoindentation without consideration of the adhesion effects. This conclusion leads to the valuable result that it is possible to measure the adhesion force as well as the viscoelasticity of adhesive polymers from nanoindentation using the presented FEM-based inverse procedure and the proposed adhesive contact model. The result is not contradictory to the results in some articles, e.g., [15, 26, 43], in which the strong influence of adhesion effects in nanoindentation measurements of plastic material is presented, because the adhesion has strong influence on the residual displacement and the contact area, which leads to error contributions of the measured elastic modulus and the identified plasticity. It should be kept in mind that the precondition for the same characterization of viscoelasticity from macro- and nanoindentation is that deformation rates in both indentation tests are comparable as shown in Table 1.

Fig. 18

Investigation of correlation of the three tests in macroindentation (left) and tensile test (right)

Figure 18 (right) represents the results of numerically predicting the tensile relaxation behavior at different deformations using the parameters obtained from indentation. If a relatively small deformation ${B}_{11}=1.59$ is present, the simulation results using parameters from indentation match the experimental data better than in the prediction using the parameters from the tensile test itself. However, in the case of large deformation ${B}_{11}=3.93$, a large deviation is observed between the experimental response and the predictions using the parameters from indentation. Similarly, a conclusion stated in [12, 34] that the constitutive parameters obtained from microindentation measurement of filled rubber-like elastomers were usually not suitable to describe the macroscopic tensile tests. Saux et al. argued that the reasons in [12, 34] could be the stiffening effect at large strain for the filled rubber and the numerous error contributions in the nano- or microindentation experiments [25]. These two aspects are avoided in our study since the considered PU is an unfilled material and the nanoindentation results are proved by macroindentation. Therefore, the different deformation states and strain levels, which are well known to be of primary influence, could be the potential reason. As we have discussed in [9], the correlation between the indentation and the uniaxial tensile test depends on the strain level. For the tensile test at a deformation of ${B}_{11}=1.59$, and macro- and nanoindentation, which have a relative small strain compared to deformation ${B}_{11}=1.59$, the same material model has approximately the same behavior if the parameters identified from the tensile and macro- or nanoindentation tests are chosen. However, the parameters identified in indentation are not able to reproduce the tensile behavior at large strain ${{B}}_{11}=3.93$. This result may stem from the fact that the stiffening at large strains in tensile test is not properly captured by the responses in indentation test, which is mainly compressive by nature, and the strain level in indentation test is not large enough to trigger the increase in stiffness.

5 Conclusions

In this study, identification of the nonlinear viscoelasticity of a soft polymer PU from indentation at different scales and the quantification of the adhesion effects in nanoindentation is investigated. As far as we known, it is the first time that the strain level and the deformation rates of macroscale tensile and macro- to nanoindentation tests have been compared in this study. The deformation rate is chosen to be comparable in the three kind of tests in order to compare the identification results of viscoelasticity. Based on this precondition, the rate- or time-dependent behavior of PU in macroindentation and nanoindentation is able to be perfectly described with each of the identified viscoelastic parameter sets from all of the three kind of tests. Just the adhesion effects in nanoindentation, which is prominent in the unloading curve, an adhesive contact model is required to be taken into account in the numerical computation. If we compare the identified viscoelasticity from macro- and nanoindentation, one can conclude that in this study, the viscoelasticity of PU can be identified with an acceptable accuracy whether the adhesion effects in the unloading part is included or not. These results lead to a valuable conclusion that it is possible to simultaneously measure the adhesion force and viscoelasticity of adhesive polymer thin films from nanoindentation using the presented FEM-based inverse procedure and the proposed adhesive contact model. The correlation between the indentation and the uniaxial tensile test depends on the strain level. The identified viscoelastic model from macro- and nanoindentation can accurately describe the uniaxial tensile behavior at small deformation, but it is not able to reproduce the tensile behavior at large strain. Up to now, the results obtained in this study are applicable for the unfilled polymer which has been proven to be isotropic and homogeneous. The applicability in anisotropic and inhomogeneous polymeric materials is still need to be proven and will be considered in our further work. The comparison of characterization of viscoelasticity in this study will be further investigated in biaxial tensile test in which the contribution due to the second term in the Mooney–Rivlin model is larger.