1 Introduction

To explain or predict the course of evolution in the past or in future has been one of the most intriguing and ambitious subjects in the modern science. In the end, the evolution is the outcome of interaction between random alteration of DNA sequences, i.e. mutation, and the environment surrounding the living organism of interest.

Among numerous attempts to understand the evolution, theoretical approaches using game theory and dynamical system have been developed for almost half century. Namely, evolutionary game theory was initiated by Maynard Smith and Price’s celebrated work in (1973). Much progress has been made in this direction by Taylor and Jonker (1978), Taylor (1979) and Smith (1982) for example. Eventually approaches to the dynamical stability of strategies have arisen by using the theory of (continuous-time and discrete-time) dynamical system and have created the notion of evolutionary stable strategy. See Hofbauer and Sigmund (1998), Taylor (1989), Eshel (1983) and Takada and Kigami (1991) for example. In these works, however, the authors mainly discussed dynamical systems whose phase spaces are the collection of (vector-valued) strategies, i.e. trait values of competitors. Consequently little attention had been paid to the variation of populations of groups having different trait values although it is a substantial part of the process of evolution.

To take dynamics of population into account, the theory of adaptive dynamics was brought forth by the works due to Metz et al. (1996), Geritz et al. (1998) and Dieckmann and Law (1996), to name but a few. In this framework, the fitness function, which is the reproduction rate of an individual, depends on both populations and trait values of competitors. Combining the dynamical system of populations describing competition and the random process corresponding to sporadic occurrence of mutation, adaptive dynamics tries to unravel the course of gradual change of phenotypic trait value.

More precisely, the adaptive dynamics consists of the following two parts:

  • (COM) Competition: Deterministic dynamical system which describes the competition between groups possessing different trait values.

  • (MUT) Mutation: Stochastic process which describes the occurrence of mutants.

To begin with, we assume that the population is dominated by a group, called residents, with a single trait value. And then once a mutation governed by (MUT) happens, another group, called mutants, with a new trait value emerges. Then we use (COM) to determine the new dominant group, residents or mutants. Assuming that the average time of the occurrence of mutation in (MUT) is much longer than the relaxation time, i.e. the time needed to reach a new equilibrium, in (COM), one can iterate (COM) and (MUT) alternately to investigate the course of the evolution.

In this paper our main interest is the deterministic dynamical system in (COM) described as ODEs. More precisely, we are going to investigate how the outcome of the competition is determined, in other words, the global behavior of the dynamical system (COM). A typical scenario is that out of two equilibriums dominated by residents and mutants respectively, one of them is globally stable and the other is unstable.

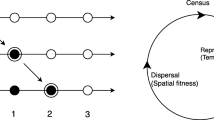
Geritz et al. (2002) have dealt with a discrete time model of a monomorphic population having multiple attractors. In this model, there exists a pair of a resident dominant state and a mutant dominant state corresponding to each attractor of the monomorphic population. Making use of their own “tube theorem”, which corresponds to a discrete version of Lemma A.2 in this paper, they have shown that if a shift between a resident dominant state and a mutant dominant state occurs, then those states constitute one of the pairs mentioned above corresponding to a single attractor of the monomorphic population. As for continuous time models, i.e. ODE models, Geritz have gotten an analogue of the tube theorem for a special class of model in (2005), where he have shown “invasion implies fixation theorem”, which is a counterpart of the ”invasion implies substitution principle” mentioned below. Note that there exists a generating function in the sense of Brown and Vincent (1987) and Vincent and Brown (2005) for Geritz’s model and that the global stability is determined by invasion fitness, which is also called invasion exponent, and often denoted by \(s_x(y)\) in literatures as Geritz et al. (1998), Diekmann (2004) and Brännström et al. (2013).

In this direction, a remarkable achievement is the establishment of the “invasion implies substitution” principle, IIS principle for short, by Dercole and Rinaldi (2008). More precisely, they have shown that the sign of the local gradient of invasion fitness determines which group survives, residents or mutants under the assumption of the existence of generating function. Note that their framework includes Geritz’s one in (2005). In this paper, we use \(\theta \) to denote the invasion fitness. See (2.9) for the explicit definition. Mathematically, the local gradient of the invasion fitness is an index of the local stability of the equilibrium dominated by residents. Therefore, the invasion implies substitution principle means that the local stability determines the global stability. In general, such an immediate coincidence of the local and the global stabilities is not at all obvious. So what does cause such a coincidence? More generally, what is the secret of success of the global stability analysis using the invasion fitness? Our answer will be the existence of an associated generating function in the sense of Brown and Vincent (1987) and Vincent and Brown (2005). Note that there exists an associated generating function in both frameworks of Geritz (2005) and Dercole and Rinaldi (2008). Then, the subsequent natural question is what happens without such a strong constraint as the existence of an associated generating function. In this respect, our goal is to obtain a criterion of the global stability for a class of models which are out of the scope of the invasion fitness and still reasonable as a model of competition of residents and mutants. For this purpose, we are going to introduce the notion of raw invasion fitness \(\Theta \) as a natural extension of invasion fitness and show the results including:

  • Theorem 3.2: The shift of global stability between resident dominant state and mutant dominant state is caused by uniform positivity (and negativity as well) of the local gradients of raw invasion fitness on the line segment between the two states.

  • Theorem 3.9: There exists a generating function associated with a dimorphic system if and only if the local gradients of raw invasion fitness only depends on the total population of two competing groups having different trait-values.

Another reason to seek a theory beyond the scope of the invasion fitness is the question on the stability of global behavior under perturbations of an original system. For example, let us consider the following system:

$$\begin{aligned} \begin{aligned} \frac{dn_1}{dt}&= n_1\big (1 - (n_1 + n_2) + (x_2 - x_1)n_2(c - an_1 - bn_2)\big )\\ \frac{dn_2}{dt}&= n_2\big (1 - (n_1 + n_2) + (x_1 - x_2)n_1(c - an_2 - bn_1)\big ), \end{aligned} \end{aligned}$$
(1.1)

where \(n_1\) and \(n_2\) are populations of the groups having trait values \(x_1\) and \(x_2\) respectively. For this model,

  • In case \(a = b = 0\), this model has been extensively treated in the previous studies, for example, Diekmann (2004) and Brännström et al. (2013).

  • In case \(a = b\), then there exists an associated generating function and hence the existing method using invasion fitness can be applied.

  • In case \(a \ne b\), there exists no associated generating function and hence the existing method using invasion fitness can not be applied.

The dichotonomy between the last two cases is due to Theorem 3.9. Since a tiny perturbation to a system can easily destroy the equality \(a = b\), we need a theory beyond the paradigm of invasion fitness in order to study the stability of the global behavior under small perturbations of a system. Indeed, by our results, we do see that the global behavior of (1.1) is stable under small perturbations of the parameters a, b and c as long as \((b - c)(a + b - 2c) \ne 0\). See Sect. 3.3 for details.

2 Frameworks and rough description of results

To illuminate our aims and to fix ideas, let us clarify our terminologies and frameworks. A monomorphic system is the following system (2.1) of ordinary differential equation, ODE for short, which describes the time evolution of a population consisting of individuals with a single trait value x,

$$\begin{aligned} \begin{aligned} \frac{dn}{dt}&= nf_1(n, N, x), \\ \frac{dN}{dt}&= q_1(n, N, x), \end{aligned} \end{aligned}$$
(2.1)

where n is the population, x is the parameter representing trait value and N is the external environmental factor.

A dimorphic system is the system of ODEs describing the time evolution of a population consisting of individuals with two trait values under an external environmental factor N. In this case the population is divided into two groups depending on trait values and those groups compete with each other. Let \((n_1, x_1)\) and \((n_1, x_2)\) be the pairs of the population and the trait value of two competing groups. In this paper we assume that the growth rate of the population of the group having trait value \(x_1\) is given by

$$\begin{aligned} F(n_1, x_1|n_2, x_2, N) \end{aligned}$$

and hence

$$\begin{aligned} \begin{aligned} \frac{dn_1}{dt}&= n_1F(n_1, x_1| n_2, x_2, N)\\ \frac{dn_2}{dt}&= n_2F(n_2, x_2| n_1, x_1, N) \end{aligned} \end{aligned}$$
(2.2)

For simplicity, set

$$\begin{aligned} f_2(n_1, n_2, N, x_1, x_2) = F(n_1, x_1|n_2, x_2, N). \end{aligned}$$

Then the complete expression of a dimorphic system is

$$\begin{aligned} \begin{aligned} \frac{dn_1}{dt}&= n_1f_2(n_1, n_2, N, x_1, x_2)\\ \frac{dn_2}{dt}&= n_2f_2(n_2, n_1, N, x_2, x_1)\\ \frac{dN}{dt}&= q_2(n_1, n_2, N, x_1, x_2), \end{aligned} \end{aligned}$$
(2.3)

where

$$\begin{aligned} q_2(n_1, n_2, N, x_1, x_2) = q_2(n_2, n_1, N, x_2, x_1). \end{aligned}$$
(2.4)

should hold since the effect of \((n_1, x_1)\) and \((n_2, x_2)\) to the growth of N does not depend on their order. We call the system of ODE’s (2.3) satisfying the symmetry (2.4) as a dimorphic system.

As a model of the competition of two groups within a single species, it is natural to impose two relations between a monomorphic system (2.1) and a dimorphic system (2.3) :

First, if \(n_2 = 0\) in (2.3), then no competition is present and hence the system is reduced to a monomorphic system (2.1). Namely it is required that

$$\begin{aligned} \begin{aligned} f_2(n_1, 0, N, x_1, x_2)&= F(n_1, x_1|0, x_2, N) = f_1(n_1, N, x_1)\\ q_2(n_1, 0, N, x_1, x_2)&= q_1(n_1, N, x_1). \end{aligned} \end{aligned}$$
(2.5)

Secondly if the trait values \(x_1\) and \(x_2\) are equal in (2.3), then it should be reduced to the monomorphic system (2.1) with \(n = n_1 + n_2\). Mathematically, it is required that

$$\begin{aligned} \begin{aligned} f_2(n_1, n_2, N, x, x)&= F(n_1, x| n_2, x, N) = f_1(n_1 + n_2, N, x)\\ q_2(n_1, n_2, N, x, x)&= q_1(n_1 + n_2, N, x). \end{aligned} \end{aligned}$$
(2.6)

As a whole, our mathematical framework of this paper is the systems of ODEs, (2.3) and a monomorphic system (2.1) with the properties of (2.5) and (2.6). Such a pair of a monomorphic system and a dimorphic system is called a 2-hierarchical system, whose exact definition is as follows.

Definition 2.1

(2-hierarchical system) A pair \(((f_1, q_1), (f_2, q_2))\) is called a 2-hierarchical system if and only if \((f_1, q_1)\) is a monomorphic system, \((f_2, q_2)\) is a dimorphic system and the consistency conditions (2.5) and (2.6) are satisfied.

For the sake of simplicity, we are going to assume that for all parameter x, a monomorphic system (2.1) has a unique equilibrium point \((\widehat{n}_x, \widehat{N}_x)\) which is a global attractor, i.e. \(\lim _{t \rightarrow \infty } (n(t), N(t)) = (\widehat{n}_x, \widehat{N}_x)\) for every nonnegative solution (n(t), N(t)) of (2.1). (See Assumption 3.1 for the precise statement.)

The course of events in this model is as follows: suppose that the population is dominated by residents with a single trait value \(x_*\), i.e. the monomorphic system (2.1) with the parameter \(x_*\) stays at the stable equilibrium \((\widehat{n}_{x_*}, \widehat{N}_{x_*})\). At a certain point, a mutation occurs and a small group of mutants with a new trait value x is introduced into the system. Accordingly, the system of interest has been changed to the dimorphic system with parameter \(x_*\) and x starting from near the equilibrium \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\), which is not necessarily stable as a dimorphic system. Our main interest is to analyze the global behavior of this dimorphic system (2.3). In particular, plausible outcomes of our concern are the following three (A), (B) and (C):

(A) The equilibrium \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\) is globally stable, i.e. mutants are going to extinct eventually and the system will return to the monomorphic system with the original trait value \(x_*\).

(B) The new trait value x is superior to the original one \(x_*\) and eventually mutants will dominate the population. In our framework, this means that the equilibrium \((0, \widehat{n}_x, \widehat{N}_x)\) is globally stable and every solution of (2.3) starting near the original equilibrium \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\) is going to converge to \((0, \widehat{n}_x, \widehat{N}_x)\).

(C) Two trait values \(x_*\) and \(x_*\) are going to coexist in certain proportion, i.e. there exists a stable equilibrium \((\widetilde{n}_{x_*}, \widetilde{n}_x, \widetilde{N})\) of (2.3) such that \(\widetilde{n}_{x_*}, \widetilde{n}_x > 0\) and every solution starting near the original equilibrium \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\) is going to converge to \((\widetilde{n}_{x_*}, \widetilde{n}_x, \widetilde{N})\).

Our main results are the followings:

(I) First we have established a sufficient condition for the global shift between (A) and (B). To be exact, we introduce the notion of raw invasion fitness \(\Theta (n_1, n_2, N, x_1, x_2)\) as the difference between the fitnesses of mutants and residents. i.e.

$$\begin{aligned} \Theta (n_1, n_2, N, x_1, x_2) = f_2(n_2, n_1, N, x_2, x_1) - f_2(n_1, n_2, N, x_1, x_2) \end{aligned}$$
(2.7)

Note that \(\Theta = 0\) on the line segment \(L(x_*)\) defined by

$$\begin{aligned} L(x_*) = \{(n_1, n_2, \widehat{N}_{x_*}, x_*, x_*)|n_1 + n_2 = \widehat{n}_{x_*}, n_1, n_2 \ge 0\}. \end{aligned}$$
(2.8)

The “classical” invasion fitness \(\theta (\cdot , \cdot )\) turns out to be a special value of our raw invasion fitness as follows:

$$\begin{aligned} \theta (x_1, x_2) = f_2(0, \widehat{n}_{x_*}, \widehat{N}_{x_*}, x_2, x_1) = \Theta (\widehat{n}_{x_*}, 0, \widehat{N}_{x_*}, x_1, x_2). \end{aligned}$$
(2.9)

Our theorem, Theorem 3.2, shows that if

$$\begin{aligned} \frac{\partial \Theta }{\partial {x_2}}\,\,\text {is uniformly positive on}\ L(x_*), \end{aligned}$$
(2.10)

then as x crosses \(x_*\), (B) happens while \(x_* < x\) and (A) happens while \(x < x_*\). Under our condition (2.10), \(\Theta \) is uniformly positive (resp. negative) around \(L(x_*)\) when \(x < x_*\) (resp. \(x_* < x\)). Thus our result matches the intuition that whichever has the higher fitness wins the competition.

(II) Secondly, we are going to show that the invasion implies substitution principle, IIS principle for short, by Dercole and Rinaldi (2008) can be obtained as a corollary of our general result mentioned above. More specifically, we introduce the notion of a trimorphic system, which is a system of ODE’s describing the competition of tree groups having different trait values. As is the case of 2-hierarchical system, we call a consistent triple of a monomorphic system, a dimorphic system and a trimorphic system a 3-hierarchical system. Under these terminologies, a careful examination of the discussions by Dercole and Rinaldi (2008) yields that their result can be divided into the following two steps:

  • If a dimorphic system is a part of 3-hierarchical system, then there exists a generating function associated with the dimorphic system.

  • If there exists a generating function associated with a dimorphic system, then IIS principle holds.

The notion of generating function has been introduced by Brown and Vincent (1987) and Vincent and Brown (2005). In fact, we are going to present a characterization of the existence of generating function in terms of raw invasion fitness \(\Theta \). Namely, in Theorem 3.9, the existence of associated generating function is shown to be equivalent to the condition that \(\frac{\partial \Theta }{\partial {x_2}}(n_1, n_2, N, x_1, x_1)\) only depends on the values of \(n_1 + n_2\), N and \(x_1\). In view of (2.9), this characterization will lead to IIS principle under the existence of generating function. See Sect. 3.2 for details. Furthermore, we are going to present the following relations of classes of dimorphic systems, where we use DMS as an abbreviation of a dimorphic system:

$$\begin{aligned}&\{\text {DMS as a part of}\ 3-\text {hierarchical system}\}\nonumber \\&\underset{(1)}{\subsetneq } \{\text {DMS having associated generating function}\}\\&\underset{(2)}{=} \text {the scope of the method using the invasion fitness}\\&\underset{(3)}{\subsetneq } \{\text {DMS as a part of} \ 2-\text {hierarchical system}\}\\&\underset{(4)}{=} \text {the scope of the method using the raw invasion fitness}. \end{aligned}$$

The proper subset symbol (1) is derived from Theorem 3.7 and Proposition 3.10.

The equality (2) is concluded by Theorems 3.2, 3.8 and 3.9.

The proper subset symbol (3) is due to Propositions 3.6 and 3.12.

The euqality (4) is due to Theorem 3.2.

(III) Thirdly, we have obtained a simple class of examples who have no associated generating functions and where IIS principle may fail. Precisely our example is the following 2-hierarchical system:

$$\begin{aligned} \begin{aligned} \frac{dn_1}{dt}&= n_1\big (1 - (n_1 + n_2) + (x_2 - x_1)n_2(c - an_1 - bn_2)\big )\\ \frac{dn_2}{dt}&= n_2\big (1 - (n_1 + n_2) + (x_1 - x_2)n_1(c - an_2 - bn_1)\big )\\ \frac{dN}{dt}&= N(1 - N). \end{aligned} \end{aligned}$$
(2.11)

Although the third equation is noting to do with the first and second ones, we put it here for the sake of formality to match (2.8) with (2.3). Immediately, one sees \(\widehat{N} = 1\). Furthermore since the associated monomorphic system (2.1) is

$$\begin{aligned} \frac{dn}{dt} = n(1 - n), \end{aligned}$$

it follows that \(\widehat{n}_x = 1\) for any x. In this class, an associated generating function exists if and only if \(a = b\). If

$$\begin{aligned} (b - c)(a + b - 2c) > 0, \end{aligned}$$

then we can apply our result in part (I) and show the shift of global stability between the resident dominant and the mutant dominant equilibriums. On the contrary, if

$$\begin{aligned} (b - c)(a + b - 2c) < 0, \end{aligned}$$

\(x_2 < x_1\) and \(x_2\) is sufficiently close to \(x_1\), then (C) occurs, i.e. there exists a stable equilibrium \((\widetilde{n}_{x_1}, \widetilde{n}_{x_2}, 1)\) such that \(\widetilde{n}_{x_1}, \widetilde{n}_{x_2} > 0\) and any solution starting from near the resident dominant equilibrium (1, 0, 1) converges to \((\widetilde{n}_{x_1}, \widetilde{n}_{x_2}, 1)\). Consequently, IIS principle fails in this example. Note that due to the above result (II), this won’t happen under the existence of a generating function. See Sect. 3.3 for exact statements.

3 Main results

In this section, we are going to give exact statements of our results in three subsections according as the rough description (I), (II) and (III) in the last section. In Sect. 3.1, first we provide the notion of shift of global stability called SU-shift and US-shift, where the symbol “S” and “U” stand for “stable” and “unstable” respectively, and give a sufficient condition for shifts of stability as we outlined in (I). In Sect. 3.2, assuming the existence of generating function, we obtain IIS principle originally proven by Dercole and Rinaldi as a corollary of Theorem 3.2 in Sect. 3.1 by using certain characterization of the existence of generating function obtained in Theorem 3.9. In the last Sect. 3.3, we give a simple class of examples where we observe all the variety of plausible outcomes (A), (B) and (C) in the introduction.

Our domain for a monomorphic system (2.1) is

$$\begin{aligned} \mathcal {U}_1=\{(n, N, x)| n \in \mathbb {R}_+, N \in \mathbb {R}, x \in \mathbb {R}\}, \end{aligned}$$

where the variables n, N, and x represent a population, an external environmental factor and a trait value respectively. The external environmental factor may represent amount of available nutrition, population of a predator species and so on. The functions \(f_1\) and \(q_1\) are assumed to be smooth, to be exact, \(C^{\infty }\) in a neighborhood of \(\mathcal {U}_1\), i.e. they can be extended to open neighborhoods of \(\mathcal {U}_1\) and are \(C^{\infty }\) in their extended domains.

In the similar manner, the domain for a dimorphic system (2.3) is

$$\begin{aligned} \mathcal {U}_2 = \{(n_1, n_2, N, x_1, x_2)| n_1, n_2 \in \mathbb {R}_+, N, x_1, x_2 \in \mathbb {R}\}, \end{aligned}$$

where \(n_1\) (resp. \(n_2\)) represents a population of individuals with a trait value \(x_1\) (resp. \(x_2\)) and N represents an external environmental factor. Note that the first trait value \(x_1\) belongs to residents and the second one belongs to mutants in our model. The functions \(f_2\) and \(q_2\) are assumed to be sufficiently smooth, to be exact, \(C^{\infty }\) in a neighborhood of \(\mathcal {U}_2\), i.e. they can be extended open neighborhoods of \(\mathcal {U}_2\) and are \(C^{\infty }\) on their extended domains.

Furthermore, for the sake of simplicity of statements, we assume the following property.

Assumption 3.1

For any \(x \in \mathbb {R}\), there exists a global attractor \((\widehat{n}_x, \widehat{N}_x)\) such that any solution of a monomorphic system (2.1), (n(t), N(t)) converges to \((\widehat{n}_x, \widehat{N}_x)\) as \(t \rightarrow \infty \). Moreover, \((\widehat{n}_x, \widehat{N}_x)\) is hyperbolic and the real parts of all the eigenvalues of the linearization of (2.1) at \((\widehat{n}_x, \widehat{N}_x)\) ,

$$\begin{aligned} \begin{pmatrix} \displaystyle \widehat{n}_x\frac{\partial {f_1}}{\partial {n}} (\widehat{n}_x, \widehat{N}_x, x) &{} \displaystyle \widehat{n}_x \frac{\partial {f_1}}{\partial {N}}(\widehat{n}_x, \widehat{N}_x, x)\\ \displaystyle \frac{\partial {q_1}}{\partial {n}}(\widehat{n}_x, \widehat{N}_x, x)&{} \displaystyle \frac{\partial {q_1}}{\partial {N}} (\widehat{n}_x, \widehat{N}_x, x) \end{pmatrix} \end{aligned}$$
(3.1)

are negative.

The second assumption about eigenvalues of the linearization ensures the local stability of the equilibrium \((\widehat{n}_x, \widehat{N}_x)\).

Even without the assumption that \((\widehat{n}_{x_*}, \widehat{N}_{x_*})\) is a global attractor, if the eigenvalues of (3.1) has negative real parts, then our theorems in this paper still hold with some (rather complicated but non-essential) modifications in the statements.

3.1 Shifts of stability

The shift of global stability in this paper means the global transition between the resident dominant state and the mutant dominant state as the trait value of mutants varies around the trait value of residents. Throughout this subsection, we consider a 2-hierarchical system \((f_1, q_1), (f_2, q_2)\) satisfying Assumption 3.1. To present an explicit statement, we need the notion of a tubular neighborhood \(S_{\epsilon }(x_*)\) of \(L(x_*)\) defined as

$$\begin{aligned} S_{\epsilon }(x_*) = \bigg (\bigcup _{(n_1, n_2, \widehat{N}_{x_*}, x_*, x_*) \in L(x_*)} B((n_1, n_2, \widehat{N}_{x_*}), \epsilon ) \bigg ) \bigcap \,\, \bigg (0, \infty \bigg ) \times \bigg (0, \infty \bigg ) \times \mathbb {R}, \end{aligned}$$

where \(B(x, \epsilon )\) is a Euclidean ball given by \(\{y : |x - y| < \epsilon \}\).

Definition 3.1

Let \(x_* \in \mathbb {R}\). We say that SU-shift (resp. US-shift) occurs at \(x_*\) if there exist \(\epsilon , \delta > 0\) such that if \(\{(n_1(t), n_2(t), N(t))\}_{t \ge 0}\) is a solution of the dimorphic system (2.3) and \((n_1(0), n_2(0), N(0)) \in S_{\epsilon }(x_*)\), then

$$\begin{aligned} \lim _{t \rightarrow \infty }(n_1(t), n_2(t), N(t)) = (\widehat{n}_{x_*}, 0, \widehat{N}_{x_*}) \end{aligned}$$
(S)

whenever \(x_1 = x_*\) and \(x_2 \in (x_* - \delta , x_*)\) (resp. \(x_2 \in (x_*, x_* + \delta )\)) and

$$\begin{aligned} \lim _{t \rightarrow \infty }(n_1(t), n_2(t), N(t)) = (0, \widehat{n}_{x_2}, \widehat{N}_{x_2}) \end{aligned}$$
(U)

whenever \(x_1 = x_*\) and \(x_2 \in (x_*, x_* + \delta )\) (resp. \(x_2 \in (x_* - \delta , x_*)\)).

Recall that the trait values \(x_*\) and \(x_2\) belong to residents and mutants respectively. The statement (S) (resp. (U)) means that any solution starting from near \(L(x_*)\) converges to the resident (resp. mutant) dominant state \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\) (resp. \((0, \widehat{n}_{x_2}, \widehat{N}_{x_2})\)) as \(t \rightarrow \infty \). Thus SU-shift and US-shift at \(x_*\) are global qualitative transitions between (S) and (U) with the critical value \(x_*\).

The following theorem gives a sufficient condition for shift of global stability.

Theorem 3.2

Let \(x_* \in \mathbb {R}\). SU-shift (resp. US-shift) occurs at \(x_*\) if the following condition (3.2) [resp. (3.3)] holds;

$$\begin{aligned}&\inf _{(n_1, n_2, N, x_1, x_2) \in L(x_*)} \frac{\partial \Theta }{\partial x_2}(n_1,n_2,N,x_1,x_2) > 0, \end{aligned}$$
(3.2)
$$\begin{aligned}&\sup _{(n_1, n_2, N, x_1, x_2) \in L(x_*)}\frac{\partial \Theta }{\partial x_2}(n_1,n_2,N,x_1,x_2) < 0. \end{aligned}$$
(3.3)

We will prove this theorem in “Appendix A”. Here we give a rough idea why it is true. Note that \(\Theta = 0\) if \(x_2 = x_*\). Hence

$$\begin{aligned} \Theta \approx (x_2 - x_*)\frac{\partial \Theta }{\partial {x_2}} \end{aligned}$$
(3.4)

if \(x_2\) is sufficiently close to \(x_*\). Suppose that (3.2) is true. If \(x_2 < x_*\), then \(\Theta < 0\) in a small neighborhood of \(L(x_*)\), i.e. \(S_{\epsilon }(x_*)\). Namely, the fitness of residents is uniformly higher than that of mutants. Consequently, residents will be dominant. If \(x_2 > x_*\), then everything becomes opposite and so we have SU-shift.

3.2 Invasion implies substitution principle

In this subsection, we are going to show that “invasion implies substitution principle”, IIS principle for short, can be shown as a corollary of our Theorem 3.2. As we have mentioned in the introduction, the essential claim of IIS principle is that the local stability of the resident dominant equilibrium determines the global stability of both the resident dominant and the mutant dominant equilibriums. To begin with, let us make an observation on the local stability of the resident dominant equilibrium \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\) of a dimorphic system (2.3) with parameters \((x_*, x_2)\). One can easily see that the eigenvalues of the linearization of (2.3) at \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\) are given by the eigenvalues of (3.1) and the invasion fitness \(\theta (x_*, x_2)\). By Assumption 3.1, the sign of \(\theta (x_*, x_2)\) determines the local stability of \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\), i.e. if \(\theta (x_*, x_2) > 0\) (reps. \(\theta (x_*, x_2) < 0\)), then it is locally unstable (resp. stable).

At this point, we are going to revisit the original proof of IIS principle by Dercole and Rinaldi (2008, “Appendix B”). They started with a 2-hierarchical system and assumed the existence of a trimorphic system behind, which has turned out to be the key to fill the gap between local and global stabilities.

A trimorphic system is a system of ODE’s representing competition of three groups inside a single species having three (different) trait values. As a dimorphic system, let \((n_i, x_i)\) for \(i = 1, 2, 3\) be the pair of the population and the trait value of i-th group and let N be an external environmental factor. Suppose \(\{i, j, k\} = \{1, 2, 3\}\). Then it is natural to assume that the fitness of a group i is effected only by the current state of itself, \((n_i, x_i)\), the current state of the opponent groups, \(\{(n_j, x_j), (n_k, x_k)\}\), and the external environmental factor N including possible effect of another living organism. As a result, the fitness of the group having the trait value \(x_i\) must be written as

$$\begin{aligned} F_*(n_i, x_i|\{(n_j, x_j), (n_k, x_k)\}, N). \end{aligned}$$
(3.5)

Consequently, the time evolution of the group i is governed by

$$\begin{aligned} \frac{dn_i}{dt} = n_iF_*(n_i, x_i|\{(n_j, x_j), (n_k, x_k)\}, N). \end{aligned}$$

By the same line of reasoning, we assume that the growth rate of the external environmental factor N is given by

$$\begin{aligned} H(N|\{(n_i, x_i), (n_j, x_j), (n_k, x_k)\}). \end{aligned}$$
(3.6)

Consequently the time evolution of N is governed by

$$\begin{aligned} \frac{dN}{dt} = H(N|\{(n_i, x_i), (n_j, x_j), (n_k, x_k)\}) \end{aligned}$$

Hence if we introduce functions \(f_3: (\mathbb {R}_+)^3 \times \mathbb {R}\times \mathbb {R}^3 \rightarrow \mathbb {R}\) and \(q_3: (\mathbb {R}_+)^3 \times \mathbb {R}\times \mathbb {R}^3 \rightarrow \mathbb {R}\) as

$$\begin{aligned} f_3(n_1, n_2, n_3, N, x_1, x_2, x_3) = F_*(n_1, x_1|\{(n_2, x_2), (n_3, x_3)\}, N), \end{aligned}$$

and

$$\begin{aligned} q_3(n_1, n_2, n_3, N, x_1, x_2, x_3) = H(N|\{(n_1, x_1), (n_2, x_2), (n_3, x_3)\}), \end{aligned}$$

then the full equation of a trimorphic system is

$$\begin{aligned} \begin{aligned} \frac{dn_1}{dt}&= n_1f_3(n_1,n_2,n_3,N,x_1,x_2,x_3),\\ \frac{dn_2}{dt}&= n_2f_3(n_2,n_3,n_1,N,x_2,x_3,x_1),\\ \frac{dn_3}{dt}&= n_3f_3(n_3,n_1,n_2,N,x_3,x_1,x_2),\\ \frac{dN}{dt}&= q_3(n_1,n_2,n_3,N,x_1,x_2,x_3). \end{aligned} \end{aligned}$$
(3.7)

Additionally, since the values of \(F_*\) given by (3.5) and H given by (3.6) are independent of the order of j and k and the order of i, j and k respectively, it is natural to assume that

$$\begin{aligned} f_3(n_i, n_j, n_k, N, x_i, x_j, x_k) = f_3(n_i, n_k, n_j, N, x_i, x_k, x_j) \end{aligned}$$
(3.8)

and

$$\begin{aligned} q_3(n_1, n_2, n_3, N, x_1, x_2, x_3) = q_3(n_i, n_j, n_k, N, x_i, x_j, x_k), \end{aligned}$$
(3.9)

where (i, j, k) is an arbitrary permutation of (1, 2, 3).

Definition 3.3

(Trimorphic system) Write \(\mathcal {U}_3 = (\mathbb {R}_+)^3 \times \mathbb {R}\times \mathbb {R}^3\). A system of ODE’s (3.7) is called a trimorphic system if and only if \(f_3\) and \(q_3\) are \(C^{\infty }\) function defined on a neighborhood of \(\mathcal {U}_3\) and satisfy (3.8) and (3.9) on \(\mathcal {U}_3\) respectively.

There are natural consistency conditions (ET) and (CT) between a dimorphic system and a trimorphic system as was the case between a monomorphic system and a dimorphic system.

(ET)  Extinction of a trait value: If \(n_3 = 0\), then the third group is no longer existent and the system becomes dimorphic with the groups of trait values \(x_1\) and \(x_2\). Mathematically, this requires

$$\begin{aligned} f_3(n_1, n_2, 0, N, x_1, x_2, x_3) = f_2(n_1, n_2, N, x_1, x_2) \end{aligned}$$
(3.10)

and

$$\begin{aligned} q_3(n_1, n_2, 0, N, x_1, x_2, x_3) = q_2(n_1, n_2, N, x_1, x_2). \end{aligned}$$
(3.11)

(CT) Coincidence of trait values: In case two trait values coincide, then two groups sharing the same trait value behave as one. Hence the system becomes dimorphic. Mathematically this requires

$$\begin{aligned} f_3(n_1, n_2, n_3, N, x_1, x_1, x_3) = f_2(n_1 + n_2, n_3, N, x_1, x_3), \end{aligned}$$
(3.12)
$$\begin{aligned} f_3(n_1, n_2, n_3, N, x_1, x_2, x_2) = f_2(n_1, n_2 + n_3, N, x_1, x_2) \end{aligned}$$
(3.13)

and

$$\begin{aligned} q_3(n_1, n_2, n_3, N, x_1, x_1, x_2) = q_2(n_1 + n_2, n_3, N, x_1, x_3). \end{aligned}$$
(3.14)

There are other variations like the case \(n_1 = 0\) or \(x_3 = x_1\) but the associated mathematical relation are all deduced form the above requirements in (CT) and (ET) due to the symmetries (3.8) and (3.9).

The conditions in (ET) and (CT) ensure the consistency between a dimorphic system and a trimorphic system.

Now, we fix terminologies without ambiguity.

Definition 3.4

  1. (1)

    A triple \(((f_1, q_1), (f_2, q_2), (f_3, q_3))\) is called a 3-hierarchical system if and only if \(((f_1, q_1), (f_2, q_2))\) is a 2-hierarchical system, \((f_3, q_3)\) is a trimorphic system defined in Definition 3.3 and all the consistency conditions (3.10), (3.11), (3.12), (3.13) and (3.14) are satisfied for any \((n_1, n_2, n_3, N, x_1, x_2, x_3) \in \mathcal {U}_3\).

  2. (2)

    \(f \in C^{\infty }(\mathcal {U}_2)\) is said to be a part of a 2-hierarchical system if and only if there exists a 2-hierarchical system, \(((f_1, q_1), (f_2, q_2))\), such that \(f = f_2\).

  3. (3)

    \(f \in C^{\infty }(\mathcal {U}_2)\) is said to be a part of a –hierarchical system if and only if there exists a 3-hierarchical system, \(((f_1, q_1), (f_2, q_2),(f_3, q_3))\), such that \(f = f_2\).

There is one more notion playing a key role, which is the notion of generating function introduced by Brown and Vincent (1987) and Vincent and Brown (2005).

Definition 3.5

(Generating function)

  1. (1)

    A function \(G:\mathcal {U}_2 \times \mathbb {R}\rightarrow \mathbb {R}\) which is \(C^{\infty }\) in a neighborhood of \(\mathcal {U}_2 \times \mathbb {R}\), is called a generating function if and only if it satisfies the following conditions (G1),(G2) and (G3).

    1. (G1)

      For any \(n_1 >0\), \(x_1, x_2 \in \mathbb {R}\) and \(N \in \mathbb {R}\),

      $$\begin{aligned} G(n_1, 0, N, x_1, x_2, x_1) = G(n_1, 0, N, x_1, x_1, x_1) \end{aligned}$$
      (3.15)
    2. (G2)

      For any \(s > 0\), \(r_1, r_2 \in [0, 1]\) and \(N, x, y \in \mathbb {R}\),

      $$\begin{aligned} G((1-r_1)s, r_1s, N, x, x, y) = G((1 - r_2)s, r_2s, N, x, x, y) \end{aligned}$$
      (3.16)
    3. (G3)

      For any \((n_1,n_2,N,x_1,x_2,y)\in \mathcal {U}_2\times \mathbb {R}\),

      $$\begin{aligned} G(n_1,n_2,N,x_1,x_2,y) = G(n_2,n_1,N,x_2,x_1,y). \end{aligned}$$
      (3.17)
  2. (2)

    \(f \in C^{\infty }(\mathcal {U}_2)\) is said to have an associated generating function if and only if there exists a generating function \(G: \mathcal {U}_2 \times \mathbb {R}\rightarrow \mathbb {R}\) such that

    $$\begin{aligned} f(n_1, n_2, N, x_1, x_2) = G(n_1, n_2, N, x_1, x_2, x_1) \end{aligned}$$

    for any \((n_1, n_2, N, x_1, x_2) \in \mathcal {U}_2\). In this situation, G is called a generating function associated with f.

As a model, the variables \(n_1, n_2, N, x_1, x_2\) have the same roles as before. The sixth variable y has been called virtual strategy in Brown and Vincent (1987) and Vincent and Brown (2005).

The conditions (G1), (G2) and (G3) correspond to the conditions (P1), (P2) and (P3) in Dercole and Geritz (2016), where their definition of a generating function contains an additional condition (P4).

Let G be a generating function. If \(f_1\) and \(f_2\) are defined by

$$\begin{aligned} f_2(n_1, n_2, N, x_1, x_2) = G(n_1, n_2, N, x_1, x_2, x_1) \end{aligned}$$
(3.18)

and

$$\begin{aligned} f_1(n_1, x_1) = G(n_1, 0, N, x_1, x_1, x_1), \end{aligned}$$
(3.19)

then, with appropriate choice of \(q_1\) and \(q_2\), \(q_1 \equiv 0\) and \(q_2 \equiv 0\) for example, \(((f_1, q_1), (f_2, q_2))\) is a 2-hierarchical system. Thus we have the following fact.

Proposition 3.6

If \(f \in C^{\infty }(\mathcal {U}_2)\) has an associated generating function, then f is a part of 2-hierarchical system.

In our terminologies, two steps of arguments by Dercole and Rinaldi (2008) mentioned in the introduction can be stated as the following two theorems, Theorems 3.7 and 3.8.

Theorem 3.7

(Dercole and Rinaldi 2008) If \(f \in C^{\infty }(\mathcal {U}_2)\) is a part of a 3-hierarchical system, then f has an associated generating function.

The following proof of the above theorem is based on the idea of Dercole and Rinaldi.

Proof

Let \(((f_1, q_1), (f_2, q_2), (f_3, q_3))\) be a 3-hierarchical system and \(f = f_2\). Set

$$\begin{aligned} G(n_1, n_2, N, x_1, x_2, y) = f_3(0, n_1, n_2, N, y, x_1, x_2). \end{aligned}$$

Then by (3.12),

$$\begin{aligned} G(n_1, n_2, N, x_1, x_2, x_1) = f_3(0, n_1, n_2, N, x_1, x_1, x_2) = f_2(n_1, n_2, N, x_1, x_2). \end{aligned}$$

Therefore, by (2.5)

$$\begin{aligned} G(n_1, 0, N, x_1, x_2, x_1) = f_2(n_1, 0, N, x_1, x_2) = f_1(n_1, x_1) \end{aligned}$$

and hence we have (G1). By (3.13), it follows that

$$\begin{aligned} G(rs, (1 - r)s, N, x_1, x_1, y) = f_3(0, (1 - r)s, rs, N, y, x_1, x_1) \!=\! f_2(0, s, N, y, x_1). \end{aligned}$$

This immediately implies (G2). Moreover, we have (G3) by (3.8). Thus we have shown that G is a generating function associated with f. \(\square \)

Theorem 3.8

(Dercole and Rinaldi’s IIS principle) Let \(((f_1, q_1), (f_2, q_2))\) be a 2-hierarchical system and \(f_2\) have an associated generating function. If

$$\begin{aligned} \frac{\partial \theta }{\partial x_2}(x_*,x_*) \end{aligned}$$
(3.20)

is positive (resp. negative), then SU-shift (resp. US-shift) occurs at \(x_*\).

Let us clarify how this theorem is deduced from our main theorem, Theorem 3.2. By (2.9), it follows that

$$\begin{aligned} \frac{\partial \theta }{\partial x_2}(x_*, x_*) = \frac{\partial \Theta }{\partial x_2}(\widehat{n}_{x_*}, 0, \widehat{N}_{x_*}, x_*, x_*). \end{aligned}$$
(3.21)

Since \(\theta (x_*, x_*) = 0\), we see that

$$\begin{aligned} \theta (x_*, x_2) \approx (x_2 - x_*)\frac{\partial \theta }{\partial x_2}(x_*, x_*) = (x_2 - x_*)\frac{\partial \Theta }{\partial x_2}(\widehat{n}_{x_*}, 0, \widehat{N}_{x_*}, x_*, x_*). \end{aligned}$$
(3.22)

So, in case \(\frac{\partial {\theta }}{\partial {x_2}}(x_*, x_*) > 0\) for example, the locally stability of \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*})\) changes from being stable to being unstable as \(x_2\) crosses \(x_*\) form below. Comparing this with (3.4) and our Theorem 3.2, one can clearly recognize the gap between the local and the global stabilities. Namely, the shift of global stability is determined by the sign of \(\frac{\partial \Theta }{\partial {x_2}}\) on the whole line segment \(L(x_*)\) while the change of local stability is determined by that of the one point \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*}, x_*, x_*)\) in \(L(x_*)\).

So, how is it possible that the sign of a value at one point can determine that of the whole points in \(L(x_*)\)? Our answer is simple: if \(f_2\) has an associated generating function, then the value of \(\frac{\partial {\Theta }}{\partial {x_2}}\) is constant on \(L(x_*)\) so that the value at one point \((\widehat{n}_{x_*}, 0, \widehat{N}_{x_*}, x_*, x_*)\) is the values of the whole points in \(L(x_*)\). Actually such a property is the essence of generating function as the next theorem says.

Theorem 3.9

Let \(((f_1, q_1), (f_2, q_2))\) be a 2-hierarchical system. Then \(f_2\) has an associated generating function if and only if \(\frac{\partial \Theta }{\partial {x_2}}(n_1, n_2, N, x_1, x_1)\) only depends on the values of \(n_1 + n_2\), N and \(x_1\).

This theorem will be proven in “Appendix C”.

Given this theorem, it is now clear that Dercole and Rinaldi’s IIS principle is an immediate corollary of our main theorem, Theorem 3.2 as follows.

Proof of Theorem 3.8

Assume that \(((f_1, q_1), (f_2, q_2))\) is a 2-hierarchical system and \(f_2\) has an associated generating function. Then by Theorem 3.9, it follows that \(\frac{\partial \Theta }{\partial {x_2}}\) is constant on \(L(x_*)\). Hence it coincides with \(\frac{\partial {\theta }}{\partial {x_2}}(x_*, x_*)\). Now Theorem 3.2 immediately yields the desired conclusions. \(\square \)

At this point, we have fulfilled our original aim of this section, which has been to show that the original IIS principle of Dercole and Rinaldi can be obtained as a corollary of our main theorem. There still remain, however, intriguing questions concerning generating functions. One of them is the converse of Theorem 3.7: if f has an associated generating function, then is f a part of a 3-hierarchical system? This turns out to be false since we have the following counterexample.

Proposition 3.10

Define

$$\begin{aligned}&f(n_1, n_2, N, x_1, x_2) \nonumber \\&\quad = 1 - (n_1 + n_2) + (x_2 - x_1)n_2({\alpha }\big (n_1)^2 + {\beta }n_1n_2 + {\gamma }(n_2)^2\big ). \end{aligned}$$
(3.23)

Then f is a part of a 2-hierarchical system for any \(\alpha , \beta \) and \(\gamma \). Furthermore,

  1. (1)

    f has an associated generating function if and only if \(\beta + \gamma = 3\alpha \).

  2. (2)

    f is a part of a 3-hierarchical system if and only if \(\alpha = \gamma \) and \(\beta = 2\alpha \).

So, if \(\alpha = 1, \beta = 0\) and \(\gamma = 3\) for example, then f has an associated generating function but it is not a part of any 3-hierarchical system. The key fact to show Proposition 3.10 is the following proposition.

Theorem 3.11

A smooth function \(f: \mathcal {U}_2 \rightarrow \mathbb {R}\) is a part of a 3-hierarchical system if and only if there exist smooth functions \(\xi , f_*: \mathcal {U}_1 \rightarrow \mathbb {R}\) and \(\rho : \mathcal {U}_2 \rightarrow \mathbb {R}\) satisfying

$$\begin{aligned}&f(n_1, n_2, N, x_1, x_2) = f_*(n_1 + n_2, N, x_1)\nonumber \\&\quad + (x_1 - x_2)n_2\big (\xi (n_1 + n_2, N, x_1) + (x_1 - x_2) \rho (n_1, n_2, N, x_1, x_2)\big )\qquad \end{aligned}$$
(3.24)

for any \((n_1, n_2, N, x_1, x_2) \in \mathcal {U}_2\).

A generalized version of this theorem in the case of \(\mathcal {U}_k\) will be proven in “Appendix B”.

Proof of Proposition 3.10

Set \(f_1(n_1, N, x_1) = 1 - (n_1 + n_2)\), \(q_1(n_1, N, x_1) = N(1 - N)\) and \(q_2(n_1, n_2, N, x_1, x_2) = N(1 - N)\). Then \(((f_1, q_1), (f, q_2))\) is a 2-hierarchical system.

  1. (1)

    Set \(\varphi (n_1, n_2) = \alpha (n_1)^2 + {\beta }n_1n_2 + {\gamma }(n_2)^2\) and define

    $$\begin{aligned} G(n_1, n_2, N, x_1, x_2, y)= & {} 1 - (n_1 + n_2) + (x_2 - y)n_2\varphi (n_1, n_2) \nonumber \\&+ (x_1 - y)n_1\varphi (n_2, n_1). \end{aligned}$$

    Then \(G(n_1, n_2, N, x_1, x_2, x_1) = f(n_1, n_2, N, x_1, x_2)\). Moreover (G1) and (G3) hold. Furthermore, (G2) holds if and only if \(n_2\varphi (n_1, n_2) + n_1\varphi (n_2, n_1)\) only depends on \(n_1 + n_2\). A routine calculation shows that this is equivalent to the condition that \(\beta + \gamma = 3\alpha \).

  2. (2)

    Comparing (3.23) and (3.24), we see that f is a part of a 3-hierarchical system if and only if \(\varphi (n_1, n_2)\) depends only on \(n_1 + n_2\). This turns out to be equivalent to the condition that \(\alpha = \gamma \) and \(\beta = 2\alpha \).\(\square \)

3.3 Example

In this subsection, we give a class of examples which is simple enough as the fitness function \(f_2\) is a polynomial of degree 2 in \(n_1\) and \(n_2\) but is out of the scope of the preceding framework by Dercole and Rinaldi. Indeed, we do show in Proposition 3.12 that no generating function is associated with it except the case where \(a = b\) in the following example. Still we can show the occurrence of SU-shift and US-shift due to Theorem 3.2. As a reminder, our example is (2.11) given by

$$\begin{aligned} \begin{aligned} \frac{dn_1}{dt}&= n_1\big (1 - (n_1 + n_2) + (x_2 - x_1)n_2(c - an_1 - bn_2)\big )\\ \frac{dn_2}{dt}&= n_2\big (1 - (n_1 + n_2) + (x_1 - x_2)n_1(c - an_2 - bn_1)\big )\\ \frac{dN}{dt}&= N(1 - N), \end{aligned} \end{aligned}$$

where a, b and c are real-valued parameters. In this case, if

$$\begin{aligned} \begin{aligned} f_2(n_1,n_2, N, x_1, x_2)&= 1-(n_1+ n_2) + (x_2 - x_1)n_2(c - an_1 - bn_2),\\ q_2(n_1, n_2, N, x_1, x_2)&= N(1 - N),\\ f_1(n_1, N, x_1)&= 1 - n_1\\ q_1(n_1, N, x_1)&= N(1 - N), \end{aligned} \end{aligned}$$

then \((f_1, q_1), (f_2, q_2))\) is a 2-hierarchical system corresponding (2.11).

Proposition 3.12

\(f_2\) has an associated generating function if and only if \(a = b\)

Proof

It follows that

$$\begin{aligned} \frac{\partial {\Theta }}{\partial {x_2}}(n_1, n_2, N, x_1, x_2) = b(n_1)^2 + 2an_1n_2 + b(n_2)^2 - c(n_1 + n_2). \end{aligned}$$
(3.25)

By Theorem 3.9, the desired conclusion is immediate. \(\square \)

The following theorem gives us variety of asymptotic behaviors of solutions of (2.11) according to the values of parameters a, b and c. In particular, it tells us that invasion does not always imply substitution.

Theorem 3.13

Let \(x_* \in \mathbb {R}\). Then

  1. (1)

    If \(b - c > 0\) and \(a + b- 2c > 0\), then SU-shift occurs at \(x_*\).

  2. (2)

    If \(b - c < 0\) and \(a + b - 2c < 0\), then US-shift occurs at \(x_*\).

  3. (3)

    Suppose that \((b - c)(a + b - 2c) < 0\). Then two distinct locally stable equilibrium coexist if \(x_2 \ne x_*\) and \(|x_2 - x_*|\) is sufficiently small. More precisely, assume \(b > c\) (resp. \(b < c\).) Then there exists \(\delta > 0\) and \(\epsilon \) such that the following two cases occur.

    1. (3A)

      \(x_2 \in (x_*, x_* + \delta )\) (resp. \((x_* - \delta , x_*)\)):  There exists a locally stable equilibrium point \((\widetilde{n}_{x_*},\widetilde{n}_{x_2}, 1)\) such that any solution starting from \(B((1,0,1), \epsilon ) \cap (0, \infty )^3\) converges to \((\widetilde{n}_{x_*},\widetilde{n}_{x_2}, 1)\)as \(t\rightarrow \infty \). The mutant dominant equilibrium point (0, 1, 1) is also locally stable.

    2. (3B)

      \(x _2 \in (x_* - \delta , x_*)\) (resp. \((x_*, x_* + \delta )\)):  The resident dominant equilibrium (1, 0, 1) is locally stable. There exists a locally stable equilibrium point \((\overline{n}_{x_*},\overline{n}_{x_2}, 1)\) such that any solution starting from \(B((0,1,1), \epsilon ) \cap (0, \infty )^3\) converges to \((\overline{n}_{x_*},\overline{n}_{x_2}, 1)\)as \(t\rightarrow \infty \).

Proof

For (1) and (2), making use of (3.23), we verify (3.2) and (3.3) in Theorem 3.2 respectively. The proof of (3) is in “Appendix D” \(\square \)

As we have already mentioned in the introduction, the case (3) of the above theorem reveals a phenomenon beyond IIS principle. There exist two locally stable equilibria. In the case of (3A), if the initial population of mutants is relatively small, then residents and mutants will coexist in a certain proportion. If the initial population of mutants is large enough mutants will dominate the entire population eventually, although this may not sound realistic in the real world. In summary, the final outcome of the competition really depends on the initial configuration right after a mutation.

4 Discussions

The shift of global stability between resident dominant state and mutant dominant state has been one of the basic concerns in the theory of adaptive dynamics, where the notion of invasion fitness plays a central role. In fact, Dercole and Rinaldi have shown the “invasion implies substitution” principle, IIS principle for short, in Dercole and Rinaldi (2008). Since the IIS principle means mathematically that the local stability of resident dominant state determines the global behavior of solutions of the focal demographic system, there must be strong constraints in the system of interest such as the existence of an associated generating function. This study answers the natural question: what happens without such a strong constraint?

To fix the framework of our study, we first clarify the terminologies such as monomorphic system (2.1), dimorphic system (2.3) and trimorphic system defined in Definition 3.3 which are systems of differential equations describing the time evolutions of populations with a single trait value, two trait values and three trait values respectively. As a model of the competition of groups having different trait values within a single species, a monomorphic system and a dimorphic system fulfill natural consistency conditions. For example, if one of the competing groups is extinct, then a dimorphic system becomes a monomorphic system and if trait values of the two groups coincide, then the union of two groups behaves as a monomorphic system. A pair of a monomorphic system and a dimorphic system satisfying such requirements is called 2-hierarchical system. Similarly, a triple of a monomorphic system, a dimorphic system and a trimorphic system satisfying natural consistency conditions is called 3-hierarchical system. We think of 2-hierarchical system and 3-hierarchical system as the systems of ODE’s meeting minimal set of requirements as models of competitions within a single species. On the other hand, some authors have studied models based on the notion of generating functions. For example, this was the case in Dercole and Rinaldi’s proof of IIS principle in (2008). There exists an associated generation function for Geritz’s model in (2005) as well. By our results, given a 2-hierarchical system, we have found that the following two conditions are equivalent:

  • there exists an associated generating function.

  • The global stabilities of the resident dominant state and the mutant dominant state can be determined by the local gradient of invasion fitness, i.e. invasion implies substitution principle can be applied.

At the same time, establishing an equivalent condition for the existence of an associated generating function in Theorem 3.9, we have shown that

  • There exists a 2–hierarchical system which does not have any associated generating function.

  • Any 3–hierarchical system has an associated generating function but the converse is not true.

The existence of a 2–hierarchical system which does not have any associated generating function is not just an unrealistic exception. As we have seen in the end of the introduction, such 2-hierarchical systems occupy most of small perturbations of a system having associated generating function. Hence one has to investigate such a 2-hierarchical system which is out of the scope of invasion implies substitution principle/invasion fitness in order to consider the stability of the global behavior of the system under small perturbations.

To study 2-hierarchical systems without an associated generating function, we have introduced the notion of raw invasion fitness as a natural extension of the invasion fitness. In our main result, Theorem 3.2, the general condition for the shift of global stability between resident dominant state and mutant dominant state has given in terms of uniform positiveness/negativeness of the gradient of raw invasion fitness. Note that our general condition can be applied to a dimorphic system having no associated generating function.

As a showcase example, in Sect. 3.3, we have given a class of dimorphic systems where the growth rate has quadratic nature. For this class, we can apply our main result to analyze the global behaviors of their solutions regardless of the presence/absence of generating functions. Moreover, in this class, there exists a dimorphic system that has an attractor at which two different traits can coexist, even if the corresponding resident trait value is not evolutionarily singular in the conventional sense, i.e. the selection gradient at the trait value does not vanish. Such a phenomena can not occur in the presence of a generating function as a small perturbation of resident dominant monomorphic system.