Optimal Trading with a Trailing Stop

Abstract

Trailing stop is a popular stop-loss trading strategy by which the investor will sell the asset once its price experiences a pre-specified percentage drawdown. In this paper, we study the problem of timing to buy and then sell an asset subject to a trailing stop. Under a general linear diffusion framework, we study an optimal double stopping problem with a random path-dependent maturity. Specifically, we first analytically solve the optimal liquidation problem with a trailing stop, and in turn derive the optimal timing to buy the asset. Our method of solution reduces the problem of determining the optimal trading regions to solving the associated differential equations. For illustration, we implement an example and conduct a sensitivity analysis under the exponential Ornstein–Uhlenbeck model.

1 Introduction

Trailing stops are a popular trade order widely used by proprietary traders and retail investors to provide downside protection for an existing position. In contrast to a stop-loss exit that closes a position at a fixed price, a trailing stop is characterized by a stochastic floor that moves based on the running maximum of the asset price. This provides a dynamic downside protection as the stochastic floor is automatically adjusted upward whenever the asset price moves to a new high. A trailing stop is triggered when the prevailing price of an asset falls below the stochastic floor. In essence, it allows an investor to specify a limit on the maximum possible loss while not limiting the maximum possible gain. This is particularly relevant in common trend-following strategies, and trailing stop provides an automatic trigger to exit when prices start to trend downward due to, for example, regime switching [1].

In addition to setting a trailing stop order, the investor can also use a limit order to sell at a certain price target. If the price is sufficiently high, the investor may prefer to take profit immediately, rather than waiting further with the possibility of setting off the trailing stop. The investor’s position will be liquidated by either order, whichever comes first.

In this paper, we investigate the mathematical problem of optimal timing to liquidate a position subject to a trailing stop. Mathematically, we recognize the trailing stop as a stochastic timing constraint in the sense that it installs a path-dependent random maturity into the liquidation problem, rending the problem significantly more difficult to analyze or solve. Furthermore, the investor can decide when to establish the position in the first place. This leads us to also analyze the optimal timing to enter the market. In sum, we study an optimal double stopping problem subject to a trailing stop. Using excursion theory of linear diffusion, we derive the value functions using the smallest concave majorant characterization, and discuss the effect of trailing stopping on the optimal trading strategies analytically and numerically. Among our results, we reduce the problem of finding the optimal timing strategies to solving an ODE problem, which forms the basis of our numerical scheme in determining the optimal asset acquisition and liquidation regions.

In general, a trailing stop can be defined as the first time when the asset price X drops below $f(\overline{X})$, where $\overline{X}$ is the running maximum process of X, and f is an increasing function such that $f(x)<x$ for all x in the support of X. In applied probability literature, such a stopping time is related to the drawdown process and its first passage time. We refer to [2,3,4], for a partial list of studies on drawdowns under linear diffusions. Moreover, the optimality of trailing stops in exercising (generalized) Russian options and detecting abrupt changes can be found in [5,6,7], respectively

Despite being commonly used by practitioners, trailing stops have been scarcely studied in the mathematical finance literature. We trace back to [8], who studied the expected discounted reward at a trailing stop under a discrete-time random walk or a geometric Brownian motion (GBM) model, and found that it would be optimal to never use the trailing stop if the stock followed a GBM with a positive drift. In contrast, our study is conducted in a more general linear diffusion framework, and provides concrete illustrative example on how to the use of a trailing stop will affect the optimal timing to sell an asset under the exponential Ornstein-Uhlenbeck model. In a random walk model, [9] performed a probabilistic analysis of a variant of trailing stop. [10] implemented a stochastic approximation scheme to determine the optimal percentage trailing stop level that maximizes the expected discounted simple return from liquidation. The recent study by [11] compared the performance of a number of trading rules with fixed and trailing stops under an arithmetic Brownian motion model.

Compared to these works, we tackle the trading problem by formulating an optimal double stopping with a stochastic timing constraint induced by the trailing stop, and we rigorously derive the optimal trading strategy. Our method of solution applies to a general linear diffusion framework, and our analytical results facilitate computation of the value function and optimal timing strategies (see Sect. 5). In our optimal liquidation problem subject to the trailing stop, we show that it is optimal to use a limit sell order at a sufficiently high price. In other words, once the investor enters the market, he/she can immediately set the optimal limit sell order together with the trailing stop order, and wait for either order to be executed automatically.

The trailing stop can be viewed as a random maturity or stopping time constraint in the optimal stopping problem, in the sense that any admissible stopping time must come before triggering the trailing stop. Related studies by the authors include optimal stopping problems with maturities determined by an occupation time ([12, 13]) or by a default time ([14]), and optimal mean reversion trading with a fixed stop-loss exit ([15]). In particular, part of our study (Sect. 3) generalizes the analytical framework of [15] to general linear diffusions, and the results from optimal stopping subject to a fixed stop-loss exit will prove to be directly useful for solving the analogous problem with a trailing stop.

The remaining of the paper is structured as follows. Section 2 presents stochastic framework for our trading problem. In Sect. 3, we study an optimal trading problem with a fixed stop-loss. Then, in Sect. 4, we study the optimal stopping problems for trading with a trailing stop. To illustrate our analytical results, we consider trading under the exponential Ornstein-Uhlenbeck model, and numerically compute the optimal acquisition and liquidation regions in Sect. 5. We also provide a sensitivity analysis on the optimal trading strategies with respect to model parameters. Detailed proofs are collected in the Appendix.

2 Model Formulation

Let us consider a risky asset value process $X_\cdot =\{X_t\}_{t\ge 0}$ modeled by a linear diffusion on $I\equiv (l,r)\subset \mathbb {R}$ with the infinitesimal generator:

$$\begin{aligned} \mathcal {L}=\frac{1}{2}\sigma ^2(x)\frac{\partial ^2}{\partial x^2}+\mu (x)\frac{\partial }{\partial x},\quad \forall x\in I, \end{aligned}$$

(1)

where $(\mu (\cdot ),\sigma (\cdot ))$ is a pair of real-valued functions on I such that

$$\begin{aligned} \frac{1+|\mu (\cdot )|}{\sigma ^2(\cdot )}\in {\mathbb {L}}^1_{Loc }(I)\quad \text { and }\quad \sigma (x)>0,\,\quad \forall x\in I. \end{aligned}$$

For any ${\bar{x}}\in I$, the running maximum of X is denoted by

$$\begin{aligned} \overline{X}_t:={\bar{x}}\vee \sup _{s\in [0,t]}X_s,\qquad t\ge 0. \end{aligned}$$

We denote the unique probability law of $X_\cdot$ by $\mathbb {P}_{x,{\bar{x}}}$ given $\{X_0=x,\overline{X}_0={\bar{x}}\}$ for any $x,{\bar{x}}\in I$ with $x\le {\bar{x}}$. The expectation associated with $\mathbb {P}_{x,{\bar{x}}}$ is denoted by $\mathbb {E}_{x,{\bar{x}}}$. In calculations and results where the initial value $\overline{X}_0={\bar{x}}$ is irrelevant, we simply write $\mathbb {P}_{x}$ and $\mathbb {E}_{x}$ to denote the probability law of $X_\cdot$ and the associated expectation given $\{X_0=x\}$. Throughout, we assume that the both boundaries l, r are inaccessible.

We consider an investor who holds long one unit of the risky asset X. Our objective is to investigate the optimal trading strategy with a trailing stop. To this end, we consider the problem of optimal early liquidation of this risky asset, given a pre-specified trailing stop mandatory liquidation order. Specifically, we will model liquidation time by a stopping time $\tau$ of the underlying process $X_\cdot$, and the reward to be realized upon liquidation by $h(X_\tau )$, where $h(\cdot )$ is a real-valued increasing function on I, such that $\{x\in I:h(x)>0\}\ne \emptyset$. Fix a function $f(\cdot )$ on I, such that

$$\begin{aligned} \begin{array}{ll} f(\cdot )\text { is continuous, strictly increasing on }I,\\ \text {for all }x\in I, f(x)\in I, f(x)<x. \end{array} \end{aligned}$$

(2)

Then, we define the stochastic floor by $f(\overline{X})$, where $\overline{X}$ is the running maximum of X. The trailing stop, denoted by $\rho _f$, is defined as the first time the asset value X reaches the stochastic floor $f(\overline{X})$ from above. That is,¹

$$\begin{aligned} \rho _f:=\inf \{t>0: X_t<f(\overline{X}_t)\}. \end{aligned}$$

(3)

Remark 2.1

We give two standard choices of the floor function $f(\cdot )$ here. For example, if $I={\mathbb {R}}$, setting $f(x)=x-a$ for some $a>0$ gives the absolute drawdown floor, and $\rho _f$ is the first time X falls from its maximum $\overline{X}$ by a units. Another specification when $I={\mathbb {R}}_+$, $f(x)=(1-\alpha )x$ for some $\alpha \in (0,1)$, gives the percentage drawdown, and $\rho _f$ is the first time X falls from its maximum $\overline{X}$ by $(100\times \alpha )\%$, as depicted in Fig. 1 with $\alpha =0.3$.

Fig. 1

Sample paths of the asset price (solid black), its running maximum (gray dashed), and the $30\%$-drawdown floor representing the trailing stop (red dashed) (Color figure online)

The investor faces the following optimal stopping problem:

$$\begin{aligned} v_f(x,{\bar{x}}):=\sup _{\tau \in \mathcal {T}_f^\mathsf{T}}\mathbb {E}_{x,{\bar{x}}}(\mathrm {e}^{-q\tau }h(X_\tau ) \mathbf {1}_{\{\tau <\infty \}}). \end{aligned}$$

(4)

where $q>0$ is a subjective discounting rate, and $\mathcal {T}_f^\mathsf{T}$ is the set of all stopping times of X that stop no later than the trailing stop $\rho _f$. Notice that $\rho _f$ puts a mandatory selling order of the risky asset, pre-specified by the investor.

To quantify the gain in terms of expected discounted reward from liquidating earlier than the trailing stop time $\rho _f$, we define the early liquidation premium by the difference

$$\begin{aligned} p_f(x,{\bar{x}}):=&v_f(x,{\bar{x}})-g_f(x,{\bar{x}}), \end{aligned}$$

(5)

where the second term represents the expected discounted reward from waiting to sell at the trailing stop, that is,

$$\begin{aligned} g_f(x,{\bar{x}}):=\mathbb {E}_{x,{\bar{x}}}(\mathrm {e}^{-q\rho _f}h(X_{\rho _f})\mathbf {1}_{\{\rho _f<\infty \}}). \end{aligned}$$

(6)

As a convention, we define $\infty -\infty =\infty$ if both terms on the right-hand side of (5) are infinity. Clearly, we have $p_f(x,{\bar{x}})\ge 0$ for all $x,{\bar{x}}\in I$ with $x\le {\bar{x}}$. For our study, the early liquidation premium turns out to be amenable to analysis and give intuitive interpretations. The related concepts of early/delayed exercise/purchase premium have been analyzed in pricing American options (see [16]) and derivatives trading ([17]), among other applications.

Remark 2.2

If floor functions $f_1(\cdot ), f_2(\cdot )$ both satisfy (2), and $f_1(x)\le f_2(x)$ for all $x\in I$, then for every fixed $x\in I$, we have the inequalities:

$$\begin{aligned} h(x) \le v_{f_2}(x,{\bar{x}})\le v_{f_1}(x,{\bar{x}})\le \sup _{\tau \in \mathcal {T}}\mathbb {E}_{x}(\mathrm {e}^{-q\tau }h(X_\tau )\mathbf {1}_{\{\tau <\infty \}}), \end{aligned}$$

(7)

where $\mathcal {T}$ is the set of all stopping times of X.

Given the optimal value $v_f(x,{\bar{x}})$, another related problem is

$$\begin{aligned} v_f^{(1)}(x)=\sup _{\tau \in \mathcal {T}}\mathbb {E}_{x}(\mathrm {e}^{-q\tau }(v_f(X_\tau ,X_\tau )-h_b(X_\tau ))\mathbf {1}_{\{\tau <\infty \}}), \end{aligned}$$

(8)

where $h_b(\cdot )$ is an increasing function on I such that $h_b(x)\ge h(x)$ for all $x\in I$,² and $\sup _{x\in I}(v_f(x,x)-h_b(x))>0$, $\mathcal {T}$ is the set of all stopping times w.r.t. the filtration generated by X. The problem arises, for example, in optimal acquisition of the asset X when $h_b(x)=x+c_b$, where $c_b\ge 0$ is a transaction fee.³ In general, if we assume that $h_b(X)$ is the price the investor need to pay to acquire one unit of the risky asset, then (8) represents the problem of finding the optimal time to purchase this risk asset. Note that the investor will select the optimal time to sell but subject to a trailing stop exit. For this reason, we will call the problem in (8) the optimal acquisition problem with a trailing stop, even for a general reward $h_b(\cdot )$.

Remark 2.3

Note that in (8), we apply the value function $v_f(x,{\bar{x}})$ only with $x={\bar{x}}$. From a practical point of view, this is the most relevant case since a trailing stop should be placed based on the price at which the asset was purchased, rather than an arbitrary reference price.

In summary, the solutions to (8) and (4) yield the optimal trading strategy that involves buying a risky asset and selling it later while being protected by a trailing stop.

2.1 Preliminaries of Linear Diffusions

It is well known that (see, for example, [18]), for any $q>0$, the Sturm-Liouville equation $({\mathcal {L}}-q)u(x)=0$ has a positive increasing solution $\phi _q^+(\cdot )$ and a positive decreasing solution $\phi _q^-(\cdot )$. In fact, for an arbitrary fixed $\kappa \in I$, the solutions can be expressed as

$$\begin{aligned} {\phi _q^+(x)=} {\left\{ \begin{array}{ll} \mathbb {E}_x(e ^{-q\tau _X^+(\kappa )}), &{}\text {if }x\le \kappa \\ \frac{1}{\mathbb {E}_\kappa (e ^{-q\tau _X^+(x)})}, &{}\text {if }x>\kappa \end{array}\right. },\quad {\phi _q^-(x)=} {\left\{ \begin{array}{ll} \frac{1}{\mathbb {E}_\kappa (e ^{-q\tau _X^-(x)})},&{}\text {if }x\le \kappa \\ {\mathbb {E}_x(e ^{-q\tau _X^-(\kappa )})},&{}\text {if }x>\kappa \end{array}\right. }, \end{aligned}$$

(9)

where $\tau _X^+(y)$ and $\tau _X^-(y)$ are the first passage times of X to level $y\in I$ from below and above, respectively,

$$\begin{aligned} \tau _X^\pm (y):=\inf \{t>0: X_t\gtrless y\},\quad \forall y\in I. \end{aligned}$$

(10)

The functions $\phi _q^\pm (\cdot )$ are also closely related to two-sided exit problems of X. Specifically, we have:

Lemma 2.1

[2] Suppose that $l<y\le x\le z<r$, then for $q>0$, we have

$$\begin{aligned} \mathbb {E}_x(e ^{-q\tau _X^-(y)}\mathbf {1}_{\{\tau _X^-(y)<\tau _X^+(z)\}})&= \frac{\phi _q^-(x)}{\phi _q^-(y)}\frac{\psi _q(z)-\psi _q(x)}{\psi _q(z)-\psi _q(y)},\\ \mathbb {E}_x(e ^{-q\tau _X^+(z)}\mathbf {1}_{\{\tau _X^-(y)>\tau _X^+(z)\}})&=\frac{ \phi _q^-(x)}{\phi _q^-(z)}\frac{\psi _q(x)-\psi _q(y)}{\psi _q(z)-\psi _q(y)}, \end{aligned}$$

where $\psi _q:I\mapsto \mathbb {R}_+$ is a strictly increasing function defined as

$$\begin{aligned} \psi _q(x):=\frac{\phi _q^+(x)}{\phi _q^-(x)},\quad \forall x\in I. \end{aligned}$$

(11)

Remark 2.4

By the boundary behavior of X, we have $\phi _q^-(l+)=\phi _q^+(r-)=\infty$, hence $\psi _q(I)=(0,\infty )$. See [18, pp. 18–19] for more details.

2.2 Standing Assumption and Its Implications

We now discuss the following standing assumption on the reward function $h(\cdot )$.

Assumption 2.1

The reward function $h(\cdot )$ is increasing, twice differentiable on I, and there is an $x_0$ in the interior of I such that

$$\begin{aligned} ({\mathcal {L}}-q)h(x)\ge 0\text { if and only if }x\le x_0. \end{aligned}$$

(12)

Moreover, we have

$$\begin{aligned} \lim _{x\rightarrow r}\frac{h(x)}{\phi _q^+(x)}<\sup _{x>x_0}\frac{h(x)}{\phi _q^+(x)}<\infty , \end{aligned}$$

(13)

Remark 2.5

By [19, Proposition 5.10], it is easily seen that Assumption 2.1 ensures the finiteness of the upper bound in (7) for all $x\in I$. Moreover, the assumption implies that the optimal stopping time for the upper bound is of threshold type, as proved in the following lemma.

Lemma 2.2

Under Assumption 2.1, there is an $x^\star \in [x_0,r)$ such that,

$$\begin{aligned} \sup _{\tau \in \mathcal {T}}\mathbb {E}_x(\mathrm {e}^{-r\tau }h(X_\tau )\mathbf {1}_{\{\tau<\infty \}})=\mathbb {E}_x(\mathrm {e}^{-r\tau _X^+(x^\star )}h(X_{\tau _X^+(x^\star )})\mathbf {1}_{\{\tau _X^+(x^\star )<\infty \}}). \end{aligned}$$

Lemma 2.2 shows that Assumption 2.1 is sufficient for the optimality of upcrossing strategy $T_{x^\star }^+$ in optimal stopping problem $\sup _{\tau \in \mathcal {T}}\mathbb {E}_x(\mathrm {e}^{-r\tau }h(X_\tau )\mathbf {1}_{\{\tau <\infty \}})$, where $x^\star$ is a constant in $(x_0,r)$. Since $h(X_\tau )$ represents the proceeds from selling the risky asset, the economic insight of Lemma 2.2 is that, under no constraint (i.e. no trailing stop), it is optimal to sell the asset when its price is sufficiently high. Thus, apart from analytical tractability considerations, Assumption 2.1 is also economically reasonable for our trading problem.

Remark 2.6

We give a few examples in which Assumption 2.1 holds. First, let $h(x)=x-K$ for some constant $K>0$, and $X_\cdot$ be the Black-Scholes model, i.e. $\mu (x)=\mu x, \sigma (x)=\sigma x$ for all $x\in I={\mathbb {R}}_+$, with constants $\mu <q, \sigma >0$.⁴ Second, we can let $h(x)=x$ and $X_\cdot$ be the Ornstein-Uhlenbeck process, i.e. $\mu (x)=\lambda (\theta -x)$ and $\sigma (x)=\sigma$ for $x\in I=\mathbb {R}$, with constants $\lambda ,\sigma >0$ and $\theta \in \mathbb {R}$.

3 Optimal Trading with a Fixed Stop-Loss

To gain some intuition for our solution method for the problem in (4) with a trailing stop, we first consider the optimal stopping problems when the investor uses a fixed stop-loss exit instead of a trailing stop. Precisely, arbitrarily fix a $y\in I$, we consider the following class of problems indexed by y:

$$\begin{aligned} V_y(x):=&\sup _{\tau \in \mathcal {T}_y^\mathsf{S}}\mathbb {E}_{x}(\mathrm {e}^{-q\tau }h(X_\tau )\mathbf {1}_{\{\tau <\infty \}}), \end{aligned}$$

(14)

where $\mathcal {T}_y^\mathsf{S}$ is the set of all stopping times of X that stops no later than the first passage time to level y, i.e.

$$\begin{aligned} \tau _X^-(y)=\inf \{t>0: X_t<y\}, \end{aligned}$$

(15)

and $c\in [0,\sup _{x\in I}(V_y(x)-h(x)))$ is a transaction fee for asset acquisition. The problem in (14) puts a mandatory liquidation constraint upon hitting the fixed stop-loss level y from above.

The special cases of the problem in (14) with the reward function $h(x)=x-c$ driven by the OU and CIR processes have been studied in [15, 20,21,22]. In this section, we present the analysis of problem (14) driven by a general linear diffusion.

3.1 Optimal Liquidation Subject to a Stop-Loss Exit

We now study the optimal liquidation problem (14) where X follows a general linear diffusion (see (1)). To facilitate our analysis, we also consider the extended case of (14) for $y=l$, in which case we have

$$\begin{aligned} V_l(x)=\sup _{\tau \in \mathcal {T}}\mathbb {E}_x(\mathrm {e}^{-q\tau }h(X_\tau )\mathbf {1}_{\{\tau <\infty \}}). \end{aligned}$$

(16)

Notice that the value function $V_l(\cdot )$ has already been derived in Lemma 2.2.

Remark 3.1

For each fixed $x\in I$, the mapping $y\mapsto V_y(x)$ is obviously non-increasing over [l, r).

Remark 3.2

The connection between (4) and (14) can be seen as follows. For any $x,{\bar{x}}\in I$ such that $x\in (f({\bar{x}}),{\bar{x}}]$, by the $\mathbb {P}_{x,{\bar{x}}}$-a.s. inequality that $\rho _f\le \tau _X^-(f({\bar{x}}))$, we know that $\mathcal {T}_f^\mathsf{T}\subset \mathcal {T}_{f({\bar{x}})}^\mathsf{S}$. Hence, $v_f(x,{\bar{x}})\le V_{f({\bar{x}})}(x)$. As a consequence, if we define the optimal liquidation regions

$$\begin{aligned} \mathcal {S}_f^\mathsf{T, L}({\bar{x}}):= & {} \{x\in (l,{\bar{x}}]: v_f(x,{\bar{x}})=h(x)\},\quad \forall {\bar{x}}\in I, \end{aligned}$$

(17)

$$\begin{aligned} \mathcal {S}_{y}^\mathsf{S, L}:= & {} \{x\in I: V_y(x)=h(x)\},\quad \forall y\in I, \end{aligned}$$

(18)

then we have

$$\begin{aligned} \left( \mathcal {S}_{f({\bar{x}})}^\mathsf{S, L}\cap (l,{\bar{x}}]\right) \subset \mathcal {S}_f^\mathsf{T, L}({\bar{x}}), \qquad \forall {\bar{x}}>0. \end{aligned}$$

Additionally, if ${\bar{x}}\in \mathcal {S}_{f({\bar{x}})}^\mathsf{S, L}$ then we have $\left( \mathcal {S}_{f({\bar{x}})}^\mathsf{S, L}\cap (l,{\bar{x}}]\right) =\mathcal {S}_f^\mathsf{T, L}({\bar{x}})$, since in this case it is optimal to liquidate before X reaching a new maximum.

Proposition 3.1

Under Assumption 2.1, for any fixed $y\in (l,x_0)$, there is a finite threshold $b(y)\in (x_0, r)$ such that⁵

$$\begin{aligned} V_y(x)=\mathbb {E}_x(\mathrm {e}^{-q(\tau _X^+(b(y))\wedge \tau _X^-(y))}h(X_{\tau _X^+(b(y))\wedge \tau _X^-(y)})),\quad \forall x\in I. \end{aligned}$$

(19)

Here b(y) can be identified as the smallest solution over $(x_0,r)$ to

$$\begin{aligned} h'(b)-h(b)\frac{\phi _q^{-,\prime }(b)}{\phi _q^-(b)}=\frac{\phi _q^-(b)\psi _q'(b)}{\psi _q(b)-\psi _q(y)}\left( \frac{h(b)}{\phi _q^-(b)}-\frac{h(y)}{\phi _q^-(y)}\right) . \end{aligned}$$

(20)

Moreover, the mapping $y:\mapsto b(y)$ is strictly decreasing and differentiable over $(l,x_0)$, with limits $b(x_0-)=x_0$, and $b(l+)\le x_*<r$, where $x_*$ is defined in Lemma 2.2.

Corollary 3.1

If $y\in [x_0,r)$, then the stopping region $\mathcal {S}_y^\mathsf{S, L}=I$, i.e. there is no continuation region.

4 Optimal Trading with a Trailing Stop

In this section, we apply the results we obtained to study the optimal liquidation problem (4) and the optimal acquisition problem (8).

4.1 Optimal Liquidation

Returning to the problem in (4), we will first using results in Theorem 3.1 to construct a candidate threshold type strategy for liquidation before the trailing stop $\rho _f$.

Corollary 4.1

There is a unique $b_f^\star \ge x_0$ such that $b(f({\bar{x}}))>{\bar{x}}$ if and only if ${\bar{x}}<b_f^\star$. Moreover, $b_f^\star$ can be identified as the unique solution over $(x_0,f^{-1}(x_0))$ to $\Gamma ({\bar{x}})=0$, where

$$\begin{aligned} \Gamma ({\bar{x}}):= & {} \frac{1}{\psi _q'({\bar{x}})}\bigg (\frac{h'({\bar{x}})}{ \phi _q^-({\bar{x}})}-\frac{h({\bar{x}})\phi _q^{-,\prime }({\bar{x}})}{(\phi _q^-({\bar{x}}))^2}\bigg )\nonumber \\&-\frac{1}{\psi _q({\bar{x}})-\psi _q(f({\bar{x}}))}\left( \frac{h({\bar{x}})}{\phi _q^-({\bar{x}})}-\frac{h(f({\bar{x}}))}{\phi _q^-(f({\bar{x}}))}\right) . \end{aligned}$$

(21)

Moreover, $\Gamma ({\bar{x}})>0$ if $l<{\bar{x}}<b_f^\star$, and $\Gamma ({\bar{x}})<0$ if $f^{-1}(x_0)>{\bar{x}}>b_f^\star$.

Remark 4.1

We briefly explain the rationale behind the characterization of $b_f^\star$ in Corollary 4.1 here. Instead of solving the stopping problem with a trailing stop (4) optimally, let us consider a sub-optimal, myopic strategy. The strategy that will be considered is the optimal strategy given in Theorem 3.1 when $y=f(\overline{x})$, where $\overline{x}$ is the initial level of the running maximum. We call this strategy myopic because the strategy is obtained by fixing a stop-loss level, instead of allowing the stop level moving along with the running maximum. Typically, it is impossible to attain the optimal myopic stopping threshold without establishing a new high for the running maximum, unless the initial maximum level is already sufficiently high. The threshold $b_f^\star$ is the critical level beyond which, the above myopic strategy becomes optimal. In fact, when the initial running maximum $\overline{x}=b_f^\star$, the optimal stopping threshold for the fixed stop-loss level at $y=f(b_f^\star )$ is exactly at $b_f^\star$. Hence, (21) is obtained by imposing (20) to hold when $b=\overline{x}$ and $y=f(\overline{x})$.

Let us suppose for now that ${\bar{x}}\ge b_f^\star$. Then,

• 1. If we still have $f({\bar{x}})<x_0$, then by the definition of $b_f^\star$ given in Corollary 4.1, we have $b(f({\bar{x}}))\le {\bar{x}}$. Thus, by Remark 3.2,

  $$\begin{aligned}&h(x)\le v_f(x,{\bar{x}})\le V_{f({\bar{x}})}(x),\quad \forall x,{ \bar{x}}\in I\text { with }x\le {\bar{x}},\\&\left( (l,f({\bar{x}})]\cap [b(f({\bar{x}})),{\bar{x}}]\right) \equiv \left( \mathcal {S}_{f({\bar{x}})}^\mathsf{S, L}\cup (l,{\bar{x}}] \right) =\mathcal {S}_f^\mathsf{T, L}({\bar{x}}). \end{aligned}$$

• 2. If $f({\bar{x}})\ge x_0$, then by Corollary 3.1, we can use the same argument as above to conclude that $(l,{\bar{x}}]\equiv \left( \mathcal {S}_{f({\bar{x}})}^\mathsf{S, L}\cap (l,{\bar{x}}]\right) =\mathcal {S}_f^\mathsf{T, L}({\bar{x}})$.

As a consequence we obtain the following theorem:

Theorem 4.1

Under Assumption 2.1, for $x,{\bar{x}}\in I$ with $x\le {\bar{x}}$ and ${\bar{x}}\ge b_f^\star$, we have

$$\begin{aligned} v_f(x,{\bar{x}})\equiv V_{f({\bar{x}})}(x). \end{aligned}$$

So the optimal stopping time is $\rho _f\wedge \tau _{X}^+(b(f({\bar{x}})))$.

In what follows we consider the remaining case $l<x\le {\bar{x}}<b_f^\star$ and we shall establish the optimality of the stopping rule $\tau _X^+(b_f^\star )\wedge \rho _f$. To this end, we first calculate the associated value of this strategy, denoted by $u_f(x,{\bar{x}})$. In particular, by the strong Markov property of X, applying Lemma 2.1 we have for any $x\in (f({\bar{x}}), {\bar{x}})$ with ${\bar{x}}<b_f^\star$,

$$\begin{aligned}&u_f(x,{\bar{x}}):=\mathbb {E}_{x,{\bar{x}}}(\mathrm {e}^{-r(\rho _f\wedge \tau _X^+(b_f^\star ))}h(X_{\rho _f\wedge \tau _X^+(b_f^\star ))}))\nonumber \\&\quad = h(f({\bar{x}}))\mathbb {E}_x(\mathrm {e}^{-q\tau _X^-(f({\bar{x}}))}\mathbf {1}_{\{\tau _X^-(f({\bar{x}}))<\tau _X^+({\bar{x}})\}})+u_f({\bar{x}},{\bar{x}})\mathbb {E}_x(\mathrm {e}^{-q\tau _X^+({\bar{x}})}\mathbf {1}_{\{\tau _X^+({\bar{x}})<\tau _X^-(f({\bar{x}}))\}})\nonumber \\&\quad = \phi _q^-(x)\bigg (\frac{h(f({\bar{x}}))}{\phi _q^-(f({\bar{x}}))}\frac{\psi _q({\bar{x}})-\psi _q(x)}{\psi _q({\bar{x}})-\psi _q(f({\bar{x}}))}+\frac{u_f({\bar{x}},{\bar{x}})}{\phi _q^-({\bar{x}})}\frac{\psi _q(x)-\psi _q(f({\bar{x}}))}{\psi _q({\bar{x}})-\psi _q(f({\bar{x}}))}\bigg ), \end{aligned}$$

(22)

where for ${\bar{x}}<b_f^\star$, we have

$$\begin{aligned} \frac{u_f({\bar{x}},{\bar{x}})}{\phi _q^-({\bar{x}})}&=\frac{h(b_f^\star )}{ \phi _q^-({\bar{x}})}\mathbb {E}_{{\bar{x}},{\bar{x}}}(\mathrm {e}^{-q\tau _X^+(b_f^\star )} \mathbf {1}_{\{\tau _X^+(b_f^\star )<\rho _f\}})\nonumber \\&\quad +\frac{1}{\phi _q^-({\bar{x}})} \mathbb {E}_{{\bar{x}},{\bar{x}}}(\mathrm {e}^{-q\rho _f}h(X_{\rho _f})\mathbf {1}_{\{\rho _f< \tau _X^+(b_f^\star )\}}). \end{aligned}$$

(23)

The two expectations in (23) can be computed using standard calculation using excursion theory:

Lemma 4.1

For any $b>{\bar{x}}$, we have

$$\begin{aligned}&\mathbb {E}_{{\bar{x}},{\bar{x}}}(\mathrm {e}^{-q\rho _f}h(X_{\rho _f})\mathbf {1}_{\{\rho _f<\tau _X^+(b)\}})\\&\quad =\phi _q^-({\bar{x}})\int _{{\bar{x}}}^{b}\frac{h(f(v))}{\phi _q^-(f(v))} \frac{\psi _q'(v)}{\psi _q(v)-\psi _q(f(v))}\exp \left( -\int _{{ \bar{x}}}^v\frac{\psi _q'(u)\,d u}{\psi _q(u)-\psi _q(f(u))}\right) d v, \end{aligned}$$

and

$$\begin{aligned} \mathbb {E}_{{\bar{x}},{\bar{x}}}(\mathrm {e}^{-q\tau _X^+(b)}\mathbf {1}_{\{\tau _X^+(b)<\rho _f\}})= \frac{\phi _q^-({\bar{x}})}{\phi _q^-(b)}\exp \left( -\int _{{\bar{x}}}^b\frac{\psi _q'(u)d u}{\psi _q(u)-\psi _q(f(u))}\right) . \end{aligned}$$

In particular, as $b\rightarrow r$ we obtain the value of the plain trailing stop (defined in (6))

$$\begin{aligned} g_f({\bar{x}},{\bar{x}})=\phi _q^-({\bar{x}})\int _{{\bar{x}}}^{r} \frac{h(f(v))}{\phi _q^-(f(v))}\frac{\psi _q'(v)}{\psi _q(v)- \psi _q(f(v))}\exp \left( -\int _{{\bar{x}}}^v\frac{\psi _q'(u)\,d u}{\psi _q(u)-\psi _q(f(u))}\right) d v, \end{aligned}$$

and for $f({\bar{x}})<x\le {\bar{x}}$,

$$\begin{aligned} g_f(x,{\bar{x}})=\phi _q^-(x)\bigg (\frac{(hf({\bar{x}}))}{\phi _q^-(f({ \bar{x}}))}\frac{\psi _q({\bar{x}})-\psi _q(x)}{\psi _q({\bar{x}})-\psi _q(f({ \bar{x}}))}+\frac{g_f({\bar{x}},{\bar{x}})}{\phi _q^-({\bar{x}})} \frac{\psi _q(x)-\psi _q(f({\bar{x}}))}{\psi _q({\bar{x}})- \psi _q(f({\bar{x}}))}\bigg ). \end{aligned}$$

To establish the optimality of $\tau _X^+(b_f^\star )\wedge \rho _f$ when $0<x\le {\bar{x}}<b_f^\star$, we need to show that the value of the rule $u_f(x,{\bar{x}})$ dominates the reward function h(x). This claim can be proved by using (22) and the optimality of $b_f^\star$ (see Corollary 4.1).

Lemma 4.2

For all ${\bar{x}}\in (l,b_f^\star )$ and $x\in (f({\bar{x}}),{\bar{x}}]$, we have $u_f(x,{\bar{x}})>h({\bar{x}})$.

Lemma 4.2 says that waiting until $\tau _X^+(b_f^\star )\wedge \rho _f$ yields positive “time value” $u_f(x,{\bar{x}})-h(x)>0$ for all $f({\bar{x}})<x\le {\bar{x}}<b_f^\star$, so this region should be part of the optimal continuation region. On the one hand, before hitting $b_f^\star$, this region is obviously the maximum possible continuation region. Furthermore, upon hitting $b_f^\star$ we have ${\bar{x}}= b_f^\star$, and the case has already been treated in Theorem 4.1, which suggest immediate stopping at $\tau _X^+(b_f^\star )$. So we know that the stopping time $\tau _X^+(b_f^\star )\wedge \rho _f$ is optimal for problem (4) if ${\bar{x}}<b_f^\star$.

Theorem 4.2

Under Assumption 2.1, we have for all $l<x\le {\bar{x}}<b_f^\star$ that,

$$\begin{aligned} v_f(x,{\bar{x}})\equiv u_f(x,{\bar{x}})=\mathbb {E}_{x,{\bar{x}}}(\mathrm {e}^{-q( \tau _X^+(b_f^\star )\wedge \rho _f)})h(X_{\tau _X^+(b_f^\star )\wedge \rho _f}), \end{aligned}$$

where $b_f^\star$ is defined in Corollary 4.1. Moreover, the mapping $f\mapsto b_f^\star$ is non-increasing over all functions satisfying (2).

Proof

The only claim that needs a proof is the monotonicity of $f\mapsto b_f^\star$. But that is due to Remark 2.2 and the structure of the optimal stopping region. $\square$

Corollary 4.2

The value of the plain trailing stop $g_f(x,{\bar{x}})$ given in Lemma 4.1 is finite. Moreover, for any $f({\bar{x}})<x\le {\bar{x}}<b_f^\star$, the early liquidation premium given the trailing stop $\rho _f$ is given by

$$\begin{aligned} p_f(x,{\bar{x}})&=\frac{\phi _q^-(x)}{\phi _q^-(b_f^\star )}\frac{\psi _q(x)-\psi _q(f({\bar{x}}))}{\psi _q({\bar{x}})-\psi _q(f({\bar{x}}))}\exp \left( \int _{{\bar{x}}}^{b_f^\star }\frac{-\psi _q'(u)d u}{\psi _q(u)-\psi _q(f(u))}\right) \\&\quad \left( h(b_f^\star )-g_f(b_f^\star , b_f^\star )\right) , \end{aligned}$$

where $g_f(b_f^\star , b_f^\star )$ is given in Lemma 4.1. If $f({\bar{x}})<x_0$, ${\bar{x}}\ge b_f^\star$ and $f({\bar{x}})<x<b(f({\bar{x}}))$ (see Proposition 3.1 for the existence of b(y)), then the early liquidation premium given the trailing stop $\rho _f$ is

$$\begin{aligned} p_f(x,{\bar{x}})=&\frac{\phi _q^-(x)}{\phi _q^-(b(f({\bar{x}})))}\frac{\psi _q(x)-\psi _q(f({\bar{x}}))}{\psi (b(f({\bar{x}})))-\psi _q(f({\bar{x}}))}\left( h(b(f({\bar{x}})))-g_f(b(f({\bar{x}})),{\bar{x}})\right) . \end{aligned}$$

Finally, if $f({\bar{x}})<x_0$, ${\bar{x}}\ge b_f^\star$ and $b(f({\bar{x}}))\le x\le {\bar{x}}$, or $f({\bar{x}})\ge x_0$ and $f({\bar{x}})<x\le {\bar{x}}$, then the early liquidation premium given the trailing stop $\rho _f$ is

$$\begin{aligned} p_f(x,{\bar{x}})=&h(x)-g_f(x,{\bar{x}}). \end{aligned}$$

Remark 4.2

If the first inequality in (13) is an equality, then the optimal threshold $b_f^\star$ may be at the boundary r, in which case, it will be optimal not to liquidate before the trailing stop. That is, $p_f(x,{\bar{x}})=0$ for all $x,{\bar{x}}\in I$ such that $x\in (f({\bar{x}}),{\bar{x}}]$.

4.2 Optimal Acquisition with a Trailing Stop

In this section, we solve the optimal stopping problem related to acquisition with a trailing stop, which we recall as follows:

$$\begin{aligned} v_f^{(1)}(x)=\sup _{\tau \in \mathcal {T}}\mathbb {E}_x(\mathrm {e}^{-q\tau }(v_f(X_\tau ,X_\tau )-h_b(X_\tau ))\mathbf {1}_{\{\tau <\infty \}}), \end{aligned}$$

(24)

where $\mathcal {T}$ is the set of all stopping times of X, and $\sup _{x\in I}(v_f(x,x)-h_b(x))>0$.

Let us define the optimal acquisition region with a trailing stop as

$$\begin{aligned} \mathcal {S}_f^\mathsf{T, A}:=\{x\in I: v_f^{(1)}(x)=v_f(x,x)-h_b(x)\}. \end{aligned}$$

Following [19, Proposition 5.10] and (23), to determine $\mathcal {S}_f^\mathsf{T, A}$, it suffices to obtain the smallest concave majorant of

$$\begin{aligned} H^{(1)}(z):=\frac{v_f(x,x)-h_b(x)}{\phi _{q}^-(x)},\quad \text {where }z=\psi _{q}(x)\in \mathbb {R}_+, x\in I. \end{aligned}$$

(25)

In light of Theorem 4.1, we know that for $x\ge b_f^\star$, we have $v_f(x,x)-h_b(x)=h(x)-h_b(x)\le 0$, so we must have $\mathcal {S}_f^\mathsf{T, A}\subset I\backslash [b_f^\star ,r)=(l,b_f^\star )$. Therefore, if we denote by

$$\begin{aligned} \overline{z}_f^\star :=\sup \mathrm {arg}\max _{z\in \mathbb {R}_+} H^{(1)}(z). \end{aligned}$$

(26)

Then we have $H^{(1)}(\overline{z}_f^\star )>0$ (since $\sup _{x>0}(v_f(x,x)-h_b(x))>0$), and $\overline{z}_f^\star \in [0,\psi _{q}(b_f^\star ))$, and the smallest concave majorant of $H^{(1)}(\cdot )$ over $[\overline{z}_f^\star ,\infty )$ must be given by the constant function $H^{(1)}(\overline{z}_f^\star )$, so we can deduce that $\mathcal {S}_f^\mathsf{T,A}\subset (l,\psi _{q}^{-1}(\overline{z}_f^\star )]$. However, no further information about $\mathcal {S}_f^\mathsf{T,A}$ is available under general diffusions, mainly due to lack of information about the concavity of $H^{(1)}(\cdot )$. In fact, as seen in Lemma 4.3 below, even in the special case $h_b(\cdot )\equiv h(\cdot )$, function $H^{(1)}(\cdot )$ over $(0,\psi _q(b_f^\star ))$ is the difference between a convex function $H_f(\cdot )$ over $(0,\psi _q(b_f^\star ))$ and a function $H(\cdot )$ that is convex over $(0,\psi _q(x_0))$ and is strictly concave over $(\psi _q(x_0),\psi _q(b_f^\star ))$, so we only know that $H^{(1)}(\cdot )$ is convex on $(\psi _q(x_0),\psi _q(b_f^\star ))$, but the concavity of this function over $(0,\psi _q(x_0))$ is not available to us.

Lemma 4.3

Consider function

$$\begin{aligned} H_f(z):=\frac{v_f(x,x)}{\phi _q^-(x)}, \quad H(z):=\frac{h(x)}{\phi _q^-(x)},\quad \text {where }z=\psi _q(x)\in {\mathbb {R}}_+. \end{aligned}$$

(27)

Then $H_f(\cdot )$ is convex on $(0,\psi _q(b_f^\star ))$, and $H(\cdot )$ is strictly concave on $(\psi _q(x_0),\infty )$ and is convex on $(0,\psi _q(x_0))$.

Remark 4.3

If X follows the Black-Scholes model with drift $\mu <q$, and volatility $\sigma >0$, then as in [22], it is never optimal to acquire the stock given $h(x)=x-c_s$ and $h_b(x)=x+c_b$, with transaction fees $c_s>0$ and $c_b\ge 0$. To see this, we recall that $v_f(x,x)<V_0(x)=\mathbf {1}_{\{x< b\}}(\frac{x}{b})^{\beta ^+}(b-c_s)+\mathbf {1}_{\{x\ge b\}}(x-c_s)$, where $\beta ^+=\delta +\sqrt{\delta ^2+\frac{2q}{\sigma ^2}}>1$ with $\delta =\frac{\mu }{\sigma ^2}-\frac{1}{2}$, and $b=\frac{\beta c_s}{\beta -1}$. The convexity of $V_0(\cdot )$ implies that $V_0(x)-h(x)<c_s$ for all $x\in \mathbb {R}_+$, so $v_f(x,x)-h(x)<c_s$ for all $x\in \mathbb {R}_+$, for any floor function $f(\cdot )$ that satisfies (2). Thus, we have $v_f(x,x)-h_b(x)=v_f(x,x)-h(x)-(c_b+c_s)<-c_b\le 0$, so the payoff function for problem (24) to be negative throughout $\mathbb {R}_+$, yielding an empty optimal stopping region. For some other forms of $h(\cdot )$, one may obtain a non-empty stopping region for problem (24) (see Example 4.1 below).

Example 4.1

Assuming that $\mu (x)=\mu x, \sigma (x)=\sigma x, h(x)=h_b(x)=x-Kx^{-\epsilon }$ for all $x\in I\equiv {\mathbb {R}}_+$, where $\mu \in \mathbb {R}$ such that $\mu <q$, and $\sigma ,K>0$ and $\epsilon \ge 0$ such that $\frac{1}{2}\sigma ^2\epsilon (\epsilon +1)-\mu \epsilon -q<0$. Let $f(x)=(1-\alpha )x$ for some $\alpha \in (0,1)$. Then we have $\mathcal {S}_f^\mathsf{T,A}=(0,\underline{b}_f^\star ]$, where $\underline{b}_f^\star :=\psi _{q}^{-1}(\overline{z}_f^\star )$ with $\overline{z}_f^\star$ given in (26), or equivalently, with $\overline{z}_f^\star$ as the unique root to (50) in the Appendix. That is, for all $x\in I$

$$\begin{aligned} v_f^{(1)}(x)=\mathbb {E}_x(\mathrm {e}^{-q\tau _X^-(\underline{b}_f^\star )}(v_f(X_{ \tau _X^-(\underline{b}_f^\star )},X_{\tau _X^-(\underline{b}_f^\star )})-h_b(X_{\tau _X^-(\underline{b}_f^\star )}))\mathbf {1}_{\{\tau _X^-(\underline{b}_f^\star )<\infty \}}). \end{aligned}$$

In general, one can analyze the concavity of $H^{(1)}(\cdot )$ (and hence the optimal stopping region) on a case-by-case basis with possibly helps of numerical computation. To demonstrate the idea, let us define

$$\begin{aligned} z_f^\star :=\psi _{q}(b_f^\star ),\quad \varphi (z):=\psi _q(f(\psi _q^{-1}(z))),\quad \forall z\in \mathbb {R}_+. \end{aligned}$$

(28)

It is clear that $\varphi (\cdot )$ is an increasing function such that $0<\varphi (z)<z$. From Lemma 4.1 we have for all $z\in (0,z_f^\star )$

$$\begin{aligned} H_f(z)&= \exp \left( -\int _z^{z_f^\star }\frac{d \nu }{\nu -\varphi (\nu )}\right) H(z_f^\star )+\int _z^{z_f^\star }H(\varphi (\nu ))\nonumber \\&\quad \exp \left( -\int _{z}^{\nu }\frac{d w}{w-\varphi (w)}\right) \frac{d \nu }{\nu -\varphi (\nu )}, \end{aligned}$$

(29)

where $H_f(\cdot )$ is defined in (27). To obtain the smallest concave majorant of $H^{(1)}(z)=H_f(z)-H(z)-c/\phi _q^-(\psi _q^{-1}(z))$, we need to numerically evaluate $H_f(\cdot )$. To that end, it will be more convenient to rewrite (29) into an equivalent first-order linear ODE form:

$$\begin{aligned} {\left\{ \begin{array}{ll} H_f^{\prime }(z)=\frac{H_f(z)-H(\varphi (z))}{z-\varphi (z)},\quad &{} \forall z\in (0,z_f^\star ),\\ \text {subject to }H_f(z_f^\star )=H(z_f^\star ). \end{array}\right. } \end{aligned}$$

(30)

Then we can use Mathematica’s NDSolve command to efficiently compute the values of $H^{(1)}(\cdot )$ and its derivatives.⁶

5 Case Study: Trading with a Trailing Stop Under the Exponential OU Model

In this section, we apply our results in Sect. 4 to an exponential Ornstein-Uhlenbeck (OU) model:

$$\begin{aligned} dX_t=X_t\bigg (\lambda (\theta -\log X_t)+\frac{1}{2}\sigma ^2\bigg )d t+\sigma X_t dW_t,\quad X_0=x\in I\equiv \mathbb {R}_+, \end{aligned}$$

(31)

where W is a standard Brownian motion, $\lambda ,\sigma >0$ are positive constants, and $\theta \in \mathbb {R}$ is the long term average for the log-price $\log X$:

$$\begin{aligned} d (\log X_t)=\lambda (\theta -\log X_t)d t+\sigma d W_t. \end{aligned}$$

With reference to (9), it is well-known (see p. 542 of [18]) that

$$\begin{aligned} \phi _q^+(x)&=\,\mathrm {e}^{\frac{\lambda }{2\sigma ^2}(y-\theta )^2}D_{- \frac{q}{\lambda }}\Big (\frac{\sqrt{2\lambda }}{\sigma }(y-\theta )\Big ),\\ \phi _q^-(x)&=\,\mathrm {e}^{\frac{\lambda }{2\sigma ^2}(y-\theta )^2}D_{- \frac{q}{\lambda }}\Big (\frac{\sqrt{2\lambda }}{\sigma }(\theta -y)\Big ), \end{aligned}$$

where $y=\log x$, and $D_\nu (\cdot )$ is the parabolic cylinder function with parameter $\nu$. We are interested in optimal liquidation and acquisition of one unit of an risky asset whose price is modeled by X. To that end, we let

$$\begin{aligned} h(x)=x-c_0,\quad , h_b(x)=x+c_0,\quad \forall x\in I, \end{aligned}$$

where $c_0\ge 0$ is a transaction cost to buy or sell. Then it follows that, for any $q>0$

$$\begin{aligned} (\mathcal {L}-q)h(x)=\bigg (\lambda (\theta -\log x)+\frac{1}{2}\sigma ^2-q\bigg )x+qc_0,\quad \forall x\in I, \end{aligned}$$

which is a strictly decreasing function with range equal to $\mathbb {R}$. Moreover, by the asymptotic behavior of $D_{\nu }(\cdot )$ (see e.g. equation (1.8) of [23]), we know that the reward function $h(\cdot )$ satisfies Assumption 2.1. A number of related studies, such as [24,25,26], have also analyzed the optimal buy-low-sell-high strategy under the OU or exponential OU model, with or without a fixed stop-loss exit. Compared to them, we study a different optimal stopping problem with a random maturity due to the trailing stop.

Fig. 2

Numerical results under the exponential OU model (31): a Plots of function H(z) (dashed gray) and $H_f(z)$ (solid black). The “pasting point” $\psi _q(b_f^\star )=1.0674$ is indicated by the black dot. b Plots of the reward function h(x) (dashed gray) and the value function $v_f(x,x)$ (solid black). The “pasting point” is $b_f^\star =2.8845$ (black dot). c Plots of the reward function $H^{(1)}(z)$ (dashed gray) and its smallest concave majorant (solid black), along with the “pasting point” ${\bar{z}}_f^\star =0.5441$ (black dot). d Plots of the reward function $v_f(x,x)-h_b(x)$ (dashed gray) and the value function $v_f^{(1)}(x)$ (solid black), and the “pasting point” $\underline{b}_f^\star =1.9488$ (black dot)

5.1 Value Function and Optimal Strategy

Upon purchasing of the asset, we set a percentage drawdown trailing stop, i.e. $f(x)=(1-\alpha )x$, where $\alpha \in (0,1)$ is a constant.

In this study, we select the following parameter values:

$$\begin{aligned} \lambda =0.6, \theta =1, \sigma =0.2, q=0.05, c_0=0.02, \alpha =0.3. \end{aligned}$$

(32)

This means that we will liquidate the asset whenever its price drops from its running maximum since the acquisition by more than $30\%$.

In Fig. 2a, we plot the function $H(\cdot )$ defined as in (27). We also have plotted the function $H_f(\cdot )$ defined as in (23) (see also (29)), which is obtained by first solving equation (21) with $f(x)=(1-\alpha )x$ for $b_f^\star (=2.8845)$, and then using ODE (29) to numerically obtain $H_f(\cdot )$. We notice that, in contrast to the value function for a fixed stop-loss level (Theorem 3.1, see also [15]), the function $H_f(\cdot )$ is not concave over $(0,\psi _q(b_f^\star ))$. This is because, although $\phi _q^-(x)H_f(\psi _q(x))=v_f(x,x)$ is the value function for the optimal stopping problem (4) when $x={\bar{x}}$, it does not yield a martingale of $(X_t,\overline{X}_t)$, which requires using the function $v_f(x,{\bar{x}})$, not $v_f(x,x)$.

In Fig. 2b, we plot the reward function h(x) and the value function $v_f(x,x)$ for the optimal liquidation problem (4) with $x={\bar{x}}$.

In Fig. 2c, we plot the function $H^{(1)}(z)$ defined in (25) under the current exponential OU model. By checking the function’s derivative numerically, we conclude that it is concave to the left of its maximum point. Hence, the smallest concave majorant is given by

$$\begin{aligned} {\hat{H}}_{f,q}^{(1)}(z)=H^{(1)}(z\wedge \overline{z}_f^\star ),\quad \forall z\in \mathbb {R}_+. \end{aligned}$$

Therefore, in this case, the optimal acquisition strategy is to purchase the asset once the price is lower than $\underline{b}_f^\star =1.9488$.

In Fig. 2d, we plot the function $v_f(x,x)-h_b(x)$ and the value function $v_f^{(1)}(x)$ for the optimal acquisition problem (8), and the “pasting point” is at $\psi _q^{-1}({\bar{z}}_f^\star )=1.9488$.

In summary, for the exponential OU model (31) with parameters as given in (32), the optimal trading strategy is to purchase the asset when price is lower than $\psi _q^{-1}({\bar{z}}_f^\star )=1.9488$, and setup the $30\%$ trailing stop order as an exit plan, and then wait until either the trailing stop is being activated or the price reaches target $b_f^\star =2.8845$.

Fig. 3

Earlier liquidation premium (black) $p_f(x,x)$ and function $x-f(x)=\alpha x$ (dashed) under the exponential OU model (31)

Lastly, in Fig. 3 we plot the early liquidation premium of $\rho _f\wedge \tau _X^+(b_f^\star )$ over the plain trailing stop $\rho _f$ when $x={\bar{x}}$. This measure the “value” of our result in problem (4). By Corollary 4.2, we know that, for each $x\in I$,

$$\begin{aligned} p_f(x,x)=\exp \left( \int _{x}^{b_f^\star \vee x}\frac{-\psi _q'(u)d u}{\psi _q(u)-\psi _q(f(u))}\right) \left( h(b_f^\star \vee x){-}g_f(b_f^\star \vee x, b_f^\star \vee x)\right) .\nonumber \\ \end{aligned}$$

(33)

To numerically evaluate (33), we use the fusion of a “limiting order” $\tau _X^+(b)$ and the trailing stop $\rho _f$, with b chosen sufficiently large so that

$$\begin{aligned}&\mathbb {E}_x(\mathrm {e}^{-q(\tau _X^+(b)\wedge \rho _f)}\mathbf {1}_{\{\tau _X^+(b)<\rho _f\}})<0.005, \\&0<h(b)\mathbb {E}_x(\mathrm {e}^{-q(\tau _X^+(b)\wedge \rho _f)}\mathbf {1}_{\{\tau _X^+(b)<\rho _f\}})<0.03, \end{aligned}$$

for all x in the plotting region of Fig. 3. Then $g_f(x,x)$ is approximated by the value of this strategy, which is subsequently solved using an ODE similar as (30).

In Fig. 3, we compare the early liquidation premium $p_f(x,x)$ with the function $x-f(x)=\alpha x$ ($\alpha =0.3$), which is the maximum loss of the trailing stop order if the price X reaches the trailing floor immediately (but without an overshoot). We notice that, for large x, the gain from our strategy over the plain trailing stop approaches 30% of the price level. Take into account of discounting and transaction costs, this example suggests that setting a trailing stop when the asset price is high will almost always incur a 30% loss at exit.

5.2 Sensitivity Analysis and Financial Interpretations

The following illustrative numerical examples will shed light on the sensitivity of the optimal acquisition and liquidation thresholds, $\underline{b}_f^\star$ and $b_f^\star$, with respect to the trailing stop level $\alpha$, and transaction cost $c_0$. This involve numerical computation of the thresholds, as well as the critical level where function $(\mathcal {L}-q)h(x)$ vanishes. In Fig. 4a, we plot $(b_f^\star ,x_0,\underline{b}_f^\star )$ as a function of the trailing stop level $\alpha$, with $x_0$ (the dashed line) defined in Assumption 2.1. The optimal liquidation level $b_f^\star$ is increasing in $\alpha$, confirming our result in Theorem 4.2. Moreover, the optimal acquisition level $\underline{b}_f^\star$ is also increasing in $\alpha$. Recalling that a higher $\alpha$ means a lower trailing stop trigger, this means that a larger downside protection induces the investor to enter the market earlier. As seen in Fig. 4a, the investor with a higher $\alpha$ will acquire the asset at a price level closer to the critical level $x_0$. Our numerical results also suggest that, for small $\alpha$, it may not be optimal to initiate the position at all, because the gain to be realized at the sell order at $b_f^\star$ or at the trailing stop will be too low compared to the transaction cost $c_0$. In such cases, we observe that $\sup _{x\in \mathbb {R}}(v_f(x,x)-h(x))<c_0=0.02$.

Fig. 4

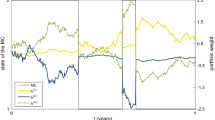
Sensitivity of thresholds $b_f^\star$ (black), $\underline{b}_f^\star$ (gray), and the root $x_0$ (red dashed) of $(\mathcal {L}-q)h(x)=0$, under the exponential OU model (31): a Dependence on $\alpha \in [0.1,0.4]$; b Dependence of on $\sigma \in [0.1,0.4]$; c Dependence of on $\lambda \in [0.2,1.2]$, and d Dependence of on $c_0\in [0, 0.04]$. In all figures, other parameters are set as in (32) (Color figure online)

In Fig. 4b, we plot $(b_f^\star ,x_0,\underline{b}_f^\star )$ as a function of the asset’s volatility parameter $\sigma$. We see that, as $\sigma$ increases, the optimal liquidation level increases, thanks to stronger force from the Brownian motion. However, the acquisition price level is lower for higher $\sigma$, which means that the investor is willing to establish a position at a lower price. However, higher volatility will increase the likelihood for the asset price to reach low levels earlier, so the actual entry time by the investor may be earlier or later. The decreasing pattern of $\underline{b}_f^\star$ with respect to $\sigma$ suggests that the investor voluntarily lowers the take-profit level to mitigate the risk of realizing a reduced profit or a loss at the trailing stop in a more volatile market.

Figure  4c illustrates the effect of the asset’s rate of mean reversion $\lambda$. A higher $\lambda$ means that the log-price will move around its long-term mean $\theta$ faster. As a response, the investor enters the market earlier at a higher entry level and exit at a lower level, resulting in a quick roundtrip, as reflected in the plot by the increasing trends of $b_f^\star$ and $\underline{b}_f^\star$ with respect to $\lambda$. Moreover, their distance is shrinking as $\lambda$ continues to increase. Intuitively, since the asset price tends to rapidly revert to the mean, it does not make sense to select entry and exit price levels that are far apart and away from the mean as the chance of execution is too low.

The effect of transaction cost $c_0$ is shown in Fig. 4d, where we plot $(b_f^\star ,x_0,\underline{b}_f^\star )$ as a function of $c_0$. The optimal liquidation level $b_f^\star$ increases slightly with respect to $c_0$ while the optimal acquisition level $\underline{b}_f^\star$ decreases in $c_0$. To interpret, higher transaction costs discourage both acquisition and liquidation, though the effect is not significant. Nevertheless, as pointed out in our analysis above, while there is always a finite optimal liquidation price $b_f^\star$ given any transaction cost, a high transaction cost may make the trade unprofitable and thus exclude market entry.

A Proofs

Proof of Lemma 2.2

Following [19], let us define For any $b\in I$, let us define

$$\begin{aligned} H(z):=\frac{h(x)}{\phi _q^-(x)},\text { where }z=\psi _q(x)\in {\mathbb {R}}_+. \end{aligned}$$

(34)

By [19, Proposition 5.11], we know that the value function

$$\begin{aligned} V(x):=\sup _{\tau \in \mathcal {T}}\mathbb {E}_x(\mathrm {e}^{-r\tau }h(X_\tau )\mathbf {1}_{\{\tau <\infty \}}), \end{aligned}$$

is given by $\phi _q^-(x){\hat{H}}(\psi _q(x))$, where ${\hat{H}}(\cdot )$ is the smallest nonnegative concave majorant of $H(\cdot )$ on ${\mathbb {R}}_+$. On the other hand, by [19, Section 6], we have

$$\begin{aligned} H''(z)=\frac{2}{\sigma ^2(x)\phi _q^-(x)(\psi _q'(x))^2}\left( (\mathcal {L}-q)h(x)\right) , \quad \text {for }z=\psi _q(x). \end{aligned}$$

So Assumption 2.1 implies that $H(\cdot )$ is convex on $(0,\psi _q(x_0))$, and concave on $(\psi _q(x_0),\infty )$. We now examine the behavior of $H(\cdot )$ near 0 and $\infty$. From (34) we know that,

• 1. if $h(l+)\ge 0$, then $h(l+)$ is finite, and $H(0+)=\lim _{x\downarrow l}\frac{h(x)}{\phi _q^-(x)}=0$;

• 2. if $h(l+)<0$, then $H(z)<0$ for sufficiently small $z>0$.

Moreover, from

$$\begin{aligned} F(z):=\frac{H(z)}{z}=\frac{h(x)}{\phi _q^+(x)},\text { where }z=\psi _q(x) \end{aligned}$$

we know $H(z)>0$ for sufficiently large $z>0$. Here, function $F(\cdot )$ is twice continuously differentiable on $\mathbb {R}_+$, and by Assumption 2.1 we know that $\sup _{z\ge \psi _q(x_0)}F(z)=F(z_*)$ for some $z_*\in [\psi _q(x_0),\infty )$. Obviously $F(z_*)>0$, which implies that $H(z)=\frac{h(x)}{\phi _q^-(x)}>0$ for all $z>z_*$ since $h(\cdot )$ is monotone. Furthermore, $z_*$ must satisfy the first order condition

$$\begin{aligned} \frac{1}{z_*}(H'(z_*)-F(z_*))=0. \end{aligned}$$

(35)

Now define function

$$\begin{aligned} {\tilde{H}}(z)=F(z_*)z\mathbf {1}_{\{z<z_*\}}+H(z)\mathbf {1}_{\{z\ge z_*\}}, \end{aligned}$$

which is clearly continuously differentiable and concave on ${\mathbb {R}}_+$, thanks to (35). Function ${\tilde{H}}(\cdot )$ is also positive on ${\mathbb {R}}_+$, which is evident from the construction. Hence we conclude that ${\tilde{H}}(\cdot )$ is the smallest concave majorant of $H(\cdot )$. So the optimal stopping region is given by

$$\begin{aligned} \psi _q^{-1}(\{z\in \mathbb {R}_+: {\tilde{H}}(z)=H(z)\})=(\psi _q^{-1}(z_*),r). \end{aligned}$$

Therefore, $x^\star =\psi _q^{-1}(z_*)$ is the optimal stopping threshold. $\square$

Proof of Proposition 3.1

The proof is similar as that for Lemma 2.2. In the spirit of [19], we derive the optimal value function and the stopping region by constructing the smallest concave majorant of H(z) on $[\psi _q(y),\infty )$. By the convexity of $H(\cdot )$, we know this concave majorant is given by

$$\begin{aligned} {\hat{H}}_y(z) = {\left\{ \begin{array}{ll} H(\psi _q(y))\frac{z(y)-z}{z(y)-\psi _q(y)}+H(z(y))\frac{z- \psi _q(y)}{z(y)-\psi _q(y)}, &{}\forall z\in (\psi _q(y),z(y)),\\ H(z), &{}\forall z\not \in (\psi _q(y),z(y)), \end{array}\right. }\qquad \end{aligned}$$

(36)

where z(y) is defined as

$$\begin{aligned} z(y):=\inf \mathop {\arg \max }_{z>\psi _q(x_0)}\frac{H(z)-H(\psi _q(y))}{z-\psi _q(y)}. \end{aligned}$$

(37)

Thus, the optimal stopping region is given by

$$\begin{aligned} \mathcal {S}_y^\mathsf{S,L}=\psi _q^{-1}(\mathbb {R}_+\backslash (\psi _q(y),z(y)))=(l,y]\cup [\psi _q^{-1}(z(y)),r). \end{aligned}$$

Therefore, the optimal stopping barrier is given by $b(y):=\psi _q^{-1}(z(y))$.

From Remark 3.1 we know that, for $l\le y_1<y_2<x_0$, the equalities hold:

$$\begin{aligned} \left( (l,y_1]\cup [b(y_1),r)\right) \equiv \mathcal {S}_{y_1}^\mathsf{S, L}\subset \mathcal {S}_{y_2}^\mathsf{S, L}\equiv \left( (l,y_2]\cup [b(y_2),r)\right) . \end{aligned}$$

Thus necessarily, $b(y_2)\le b(y_1)\le b(l)=x_*<r$. Because z(y) is an interior maximizer in the objective function in (37), it must satisfy the first order condition:

$$\begin{aligned} \frac{1}{z(y)-\psi _q(y)}\bigg (H'(z(y))-\frac{H(z(y))-H(\psi _q(y))}{z(y)-\psi _q(y)}\bigg )=0. \end{aligned}$$

(38)

This gives (20).

As $y\uparrow x_0$, b(y) converges to some limit in $[x_0,r)$. Suppose that $b(x_0-)\equiv {\underline{b}}>x_0$, then the concavity of $H(\cdot )$ over $(\psi _q(x_0),\infty )$ implies that

$$\begin{aligned} H'(\psi _q({\underline{b}}))\le \frac{H(\psi _q({\underline{b}}))-H(\psi _q(x_0))}{\psi _q({\underline{b}})-\psi _q(x_0)}. \end{aligned}$$

However, taking limit in (38) as $y\uparrow x_0$, we know that the above inequality is in fact an equality. This, together with the concavity of $H(\cdot )$ implies that $H(\cdot )$ is in fact a straight line over $[\psi _q(x_0), \psi _q({\underline{b}})]$, but then (by the definition of z(y), again) we must have $b(x_0-)=x_0$ instead.

We use implicit differentiation to prove b(y) is strictly decreasing and differentiable on $(l,x_0)$. To that end, we denote $z=z(y)$ and $u=\psi _q(y)$, then the first order equation in (38) reads as

$$\begin{aligned} f(z,u)=0, \text { where }f(z,w)=H'(z)-\frac{H(z)-H(u)}{z-u}. \end{aligned}$$

By the definition of $z\equiv z(y)$ we have

$$\begin{aligned} \frac{\partial f}{\partial u}&=H'(u)-\frac{H(z)-H(u)}{(z-u)}<0,\\ \frac{\partial f}{\partial z}&=H''(z)-\frac{1}{z-u}f(z,u)=H''(z)<0. \end{aligned}$$

Thus, we know that z(y) is strictly decreasing and differentiable in $\psi _q(y)$. In order words, z(y) is differentiable in y and $z'(y)<0$ for any $y\in (l,x_0)$. $\square$

Proof of Corollary 4.1

From Theorem 3.1 we know that ${\bar{x}}\mapsto b(f({\bar{x}}))$ is strictly decreasing and continuous over $(f^{-1}(l),f^{-1}(x_0))$, and the mapping ${\bar{x}}:\mapsto {\bar{x}}$ is strictly increasing over the same domain. Therefore, the difference $D({\bar{x}}):=b(f({\bar{x}}))-{\bar{x}}$ is strictly decreasing, and $D({\bar{x}})\ge D(x_0)> 0$ for all ${\bar{x}}\in (f^{-1}(l),x_0]$, and by Proposition 3.1,

$$\begin{aligned} \lim _{{\bar{x}}\uparrow f^{-1}(x_0)}D({\bar{x}})=x_0-f^{-1}(x_0)<0. \end{aligned}$$

As a consequence, we can define $b_f^\star :=\inf \{{\bar{x}}<f^{-1}(x_0): D({\bar{x}})\le 0\}$, and $b_f^\star \in (x_0,f^{-1}(x_0))$, so $f(b_f^\star )\le x_0$.

Now for all ${\bar{x}}<b_f^\star$, by the construction of $b_f^\star$ we have $b(f({\bar{x}}))>{\bar{x}}$, by definition of $z(f({\bar{x}}))\equiv \psi _q(b(f({\bar{x}})))$ in the proof of Proposition 3.1 we know that $z(f({\bar{x}}))>\psi _q({\bar{x}})$. Because the line segment $l_0$ connecting $(\psi _q(f({\bar{x}})), H(\psi _q(f({\bar{x}}))))$ and $(z(f({\bar{x}})), H(\psi _q(f({\bar{x}}))))$ gives part of the concave majorant of $H(\cdot )$, we know that the line segment $l_1$ connecting $(\psi _q(f({\bar{x}})), H(\psi _q(f({\bar{x}}))))$ and $(\psi _q({\bar{x}}), H(\psi _q({\bar{x}})))$, which is below line segment $l_0$, must go below the graph of $H(\cdot )$ at $\psi _q({\bar{x}})$. This implies that the derivative of $H(\cdot )$ at $\psi _q({\bar{x}})$ must be strictly greater than that of line segment $l_1$. That is,

$$\begin{aligned} H'(\psi _q({\bar{x}}))>\frac{H(\psi _q({\bar{x}}))-H(\psi _q(f({\bar{x}})))}{\psi _q({\bar{x}})-\psi _q(f({\bar{x}}))}\quad \Leftrightarrow \quad \Gamma ({\bar{x}})>0. \end{aligned}$$

On the other hand, for all $f^{-1}(x_0)>{\bar{x}}>b_f^\star$, we have $b(f({\bar{x}}))<{\bar{x}}$. Using similar argument as above, we know that $z(f({\bar{x}}))=\psi _q(b(f({\bar{x}})))<\psi _q({\bar{x}})$. Since the line segment $l_1$ connecting $(\psi _q(f({\bar{x}})), H(\psi _q(f({\bar{x}}))))$ and $(\psi _q({\bar{x}}), H(\psi _q({\bar{x}})))$ is a line segment connecting two points on the graph of a concave function ${\hat{H}}(\cdot )$, which is the smallest concave majorant of $H(\cdot )$ over $[\psi _q(f({\bar{x}})),\infty )$, we know that

$$\begin{aligned} {\hat{H}}'(\psi _q({\bar{x}}))=H'(\psi _q({\bar{x}}))<\frac{H(\psi _q({\bar{x}}))-H(\psi _q(f({\bar{x}})))}{\psi _q({\bar{x}})-\psi _q(f({\bar{x}}))}\quad \Leftrightarrow \quad \Gamma ({\bar{x}})<0. \end{aligned}$$

Expressing $H(\cdot )$ and its derivative with $h(\cdot ), \phi _q^-(\cdot ), \psi _q(\cdot )$ and their derivatives yields (21) and completes the proof. $\square$

Proof of Lemma 4.1

Let us denote by $\mathbf {e}_q$ an exponential random variable with mean 1 / q, which is independent of X. Then we notice that

$$\begin{aligned} \mathbb {E}_{{\bar{x}},{\bar{x}}}(\mathrm {e}^{-q\rho _f}h(X_{\rho _f})\mathbf {1}_{\{\tau _X^+(b)<\rho _f\}})=&\mathbb {E}_{{\bar{x}},{\bar{x}}}(h(X_{\rho _f})\mathbf {1}_{\{\rho _f<\tau _X^+(b)\wedge \mathbf {e}_q\}}),\\ \mathbb {E}_{{\bar{x}},{\bar{x}}}(\mathrm {e}^{-q\tau _X^+(b)}\mathbf {1}_{\{\tau _X^+(b)<\rho _f\}})=&\mathbb {P}_{{\bar{x}},{\bar{x}}}(\tau _X^+(b)<\rho _f\wedge \mathbf {e}_q). \end{aligned}$$

To calculate the right-hand sides of the above, we consider an excursion of X below u (notice that $\tau _X^+(u-)=\inf \{t>0: X_t\ge u\}$ is the first hitting time of X to u):

$$\begin{aligned} \epsilon _u=\{\epsilon _u(s):=X_{\tau _X^+(u-)}-X_{\tau _{X}^+(u-)+s}\}_{0<s\le \tau _X^+(u)-\tau _X^+(u-)}, \end{aligned}$$

which is defined for all $u\ge X_0=\overline{X}_0={\bar{x}}$ such that its lifetime $\zeta (\epsilon _u):=\tau _X^+(u)-\tau _X^+(u-)>0$. When $\zeta (\epsilon _u)=0$ we set $\epsilon _u=\partial$, an isolated point. Then the process $\{(u,\epsilon _u)\}_{u\ge {\bar{x}}}$ is a Poisson point process with jump measure $d u\times d n_u$, where $n_u$ is the excursion measure for $\epsilon _u$. Define $T_f(\epsilon _u):=\inf \{0<s<\zeta (\epsilon _u): \epsilon _{u}(s)>u-f(u)\}$. It is known from [27] and Lemma 2.1 that,

$$\begin{aligned}&n_u(\mathbf {e}_q<\zeta (\epsilon _u)\wedge T_f(\epsilon _u))=\lim _{x\uparrow u}\frac{1}{u-x}\left( 1-\mathbb {E}_{x}(\mathrm {e}^{-q\tau _X^+(u)}\mathbf {1}_{\{ \tau _X^+(u)<\tau _X^-(f(u))\}})\right) \\&-\lim _{x\uparrow u}\frac{\mathbb {E}_{x}(\mathrm {e}^{-q\tau _X^-(f(u))}\mathbf {1}_{\{\tau _X^-(f(u))< \tau _X^+(u)\}})}{u-x}\\&=\frac{\phi _q^{-,\prime }(u)}{\phi _q^-(u)}+\bigg (1-\frac{ \phi _q^-(u)}{\phi _q^-(f(u))}\bigg )\frac{\psi _q'(u)}{\psi _q(u)-\psi _q(f(u))},\\&n_u(T_f(\epsilon _u)<\zeta (\epsilon _u)\wedge \mathbf {e}_q) =\lim _{x\uparrow u}\frac{\mathbb {E}_{x}(\mathrm {e}^{-q\tau _X^-(f(u))}\mathbf {1}_{\{\tau _X^-(f(u))< \tau _X^+(u)\}})}{u-x}\\&=\frac{\phi _q^-(u)}{\phi _q^-(f(u))}\frac{ \psi _q'(u)}{\psi _q(u)-\psi _q(f(u))}. \end{aligned}$$

Hence,

$$\begin{aligned} n_u(\mathbf {e}_q<\zeta (\epsilon _u)\wedge T_f(\epsilon _u)\text { or }T_f(\epsilon _u)<\zeta (\epsilon _u)\wedge \mathbf {e}_q)=\frac{\phi _q^{-,\prime }(u)}{\phi _q^-(u)}-\frac{\psi _q'(u)}{\psi _q(u)-\psi _q(f(u))}. \end{aligned}$$

Let A be the space of all excursions $\epsilon _u$ such that $T_f(\epsilon _u)<\zeta (\epsilon _u)\wedge \mathbf {e}_q$, and B be the space of all excursions $\epsilon _u$ such that $\mathbf {e}_q<\zeta (\epsilon _u)\wedge T_f(\epsilon _u)$. We have that $A\cap B=\emptyset$. Consider a Poisson process (with time indexed by the running maximum $\overline{X}$) that jumps whenever the current excursion $\epsilon _{\overline{X}}\in A\cup B$, then from the above calculation, we know that this Poisson process has jump intensity $n_u(\mathbf {e}_q<\zeta (\epsilon _u)\wedge T_f(\epsilon _u)\text { or }T_f(\epsilon _u)<\zeta (\epsilon _u)\wedge \mathbf {e}_q)$. So $\mathbb {P}_{{\bar{x}},{\bar{x}}}(\tau _X^+(b)<\rho _f\wedge \mathbf {e}_q)$ is the same as the probability that this Poisson process has no jump over $[{\bar{x}},b)$, which is given by

$$\begin{aligned}&\exp \Big (-\int _{{\bar{x}}}^bn_u(\mathbf {e}_q<\zeta (\epsilon _u)\wedge T_f(\epsilon _u)\text { or }T_f(\epsilon _u)<\\&\zeta (\epsilon _u)\wedge \mathbf {e}_q)d u\Big )=\frac{\phi _q^-({\bar{x}})}{\phi _q^-(b)}\exp \left( -\int _{{\bar{x}}}^b \frac{\psi _q'(u)d u}{\psi _q(u)-\psi _q(f(u))}\right) . \end{aligned}$$

Moreover, for any $v\in [{\bar{x}},b)$, the probability that the Poisson process will have the first jump at “time” $d v$ as a result of $\epsilon _v\in A$, is given by

$$\begin{aligned}&\exp \left( -\int _{{\bar{x}}}^vn_u(\mathbf {e}_q<\zeta (\epsilon _u)\wedge T_f(\epsilon _u)\text { or }T_f(\epsilon _u) \right. \\&\qquad \left. \left.<\zeta (\epsilon _u)\wedge \mathbf {e}_q)d u \phantom {-\int _{{\bar{x}}}^vn_u}\right) \cdot n_v(T_f(\epsilon _v)<\zeta (\epsilon _v)\wedge \mathbf {e}_q\right) d v\\ =&\frac{\phi _q^-({\bar{x}})}{\phi _q^-(v)}\exp \left( -\int _{{\bar{x}}}^v\frac{\psi _q'(u)d u}{\psi _q(u)-\psi _q(f(u))}\right) \times \frac{\phi _q^-(v)}{\phi _q^-(f(v))}\frac{\psi _q'(v)}{\psi _q(v)-\psi _q(f(v))}d v\\ =&\frac{\phi _q^-({\bar{x}})}{\phi _q^-(f(v))}\frac{\psi _q'(v)}{\psi _q(v)-\psi _q(f(v))}\exp \left( -\int _{{\bar{x}}}^v\frac{\psi _q'(u)d u}{\psi _q(u)-\psi _q(f(u))}\right) d v, \end{aligned}$$

which is the same as $\mathbb {P}_{{\bar{x}},{\bar{x}}}(\overline{X}_{\rho _f}\in d v, \rho _f<\tau _X^+(b)\wedge \mathbf {e}_q)$. The proof is complete by integrating in v over $[{\bar{x}},b)$. $\square$

Proof of Lemma 4.2

Let us define for any $b\ge {\bar{x}}$

$$\begin{aligned}&{\bar{H}}(\psi _q({\bar{x}}), b):=H(\psi _q(b))\exp \left( -\int _{{\bar{x}}}^{b} \frac{\psi _q'(u)\,d u}{\psi _q(u)-\psi _q(f(u))}\right) \\&\quad +\int _{{\bar{x}}}^{b}\frac{\psi _q'(v)\,H(\psi _q(f(v)))}{w(v)-w(f(v))} \exp \left( -\int _{{\bar{x}}}^{v}\frac{\psi _q'(u)}{\psi _q(u)-\psi _q(f(u))}d u\right) d v. \end{aligned}$$

It is clear that ${\bar{H}}(\psi _q({\bar{x}}),{\bar{x}})=H(\psi _q({\bar{x}}))=\frac{h({\bar{x}})}{\phi _q^-({\bar{x}})}$, and for $b>{\bar{x}}$ we have the right derivative of $H_f(\psi _q({\bar{x}}),b)$ in b:

$$\begin{aligned}&\frac{\partial }{\partial b}{\bar{H}}(\psi _q({\bar{x}}), b)=\psi _q'(b)\exp \left( -\int _{{\bar{x}}}^{b}\frac{\psi _q'(u)d u}{\psi _q(u)-\psi _q(f(u))}\right) \\&\quad \bigg (H_+'(\psi _q(b))-\frac{H(\psi _q(b))-H( \psi _q(f(b)))}{\psi _q(b)-\psi _q(f(b))}\bigg ). \end{aligned}$$

It follows that the sign of $\frac{\partial }{\partial b}{\bar{H}}(\psi _q({\bar{x}}), b)$ depends on that of

$$\begin{aligned} \Gamma (b)=H'(\psi _q(b))-\frac{H(\psi _q(b))-H(\psi _q(f(b)))}{\psi _q(b)-\psi _q(f(b))}. \end{aligned}$$

But the latter is known to be positive for all $b<b_f^\star$, thanks to Corollary 4.1. Because $H'(\psi _q(\cdot ))$ is continuous, so is $\Gamma (\cdot )$. So we know that

$$\begin{aligned}&\frac{u_f(x,{\bar{x}})}{\phi _q^-(x)}={\bar{H}}(\psi _q({\bar{x}}),b_f^ \star )=H(\psi _q({\bar{x}}))+\int _{{\bar{x}}}^{b_f^\star }\frac{\partial }{ \partial u}{\bar{H}}(\psi _q({\bar{x}}), u)d u>H(\psi _q({\bar{x}}))\\&\quad = \frac{h(x)}{\phi _q^-(x)}, \forall {\bar{x}}<b_f^\star . \end{aligned}$$

This completes the proof. $\square$

Proof of Corollary 4.2

If $f({\bar{x}})<x\le {\bar{x}}<b_f^\star$, then by the strong Markov property of X, we have

$$\begin{aligned} p_f(x,{\bar{x}})&=\,\mathbb {E}_{x,{\bar{x}}}([\mathrm {e}^{-q\tau _X^+(b_f^\star )}h(X_{\tau _X^+(b_f^\star )})-\mathrm {e}^{-q\rho _f}h(X_{\rho _f})]\mathbf {1}_{\{\tau _X^+(b_f^\star )<\rho _f<\infty \}}) \\&=\,\mathbb {E}_{x,{\bar{x}}}(\mathrm {e}^{-q\tau _X^+(b_f^\star )}\mathbf {1}_{\{\tau _X^+(b_f^\star )<\rho _f\}})\, \left( h(b_f^\star )-\mathbb {E}_{b_f^\star ,b_f^\star }(\mathrm {e}^{-q\rho _f}h(X_{\rho _f})\mathbf {1}_{\{\rho _f<\infty \}})\right) , \end{aligned}$$

where $\mathbb {E}_{b_f^\star ,b_f^\star }(\mathrm {e}^{-q\rho _f}h(X_{\rho _f})\mathbf {1}_{\{\rho _f<\infty \}})=g_f(b_f^\star ,b_f^\star )$ is given in Lemma 4.1, which is finite since we know that it is dominated from above by $v_f(b_f^\star ,b_f^\star )=h(b_f^\star )$. On the other hand, by the analysis in (22) and the results in Lemma 4.1, we have

$$\begin{aligned} \mathbb {E}_{x,{\bar{x}}}(\mathrm {e}^{-q\tau _X^+(b_f^\star )}\mathbf {1}_{\{\tau _X^+(b_f^\star )<\rho _f\}})&=\frac{\phi _q^-(x)}{\phi _q^-(b_f^\star )}\frac{\psi _q(x)-\psi _q(f({\bar{x}}))}{\psi _q({\bar{x}})-\psi _q(f({\bar{x}}))}\\&\quad \exp \left( -\int _{{\bar{x}}}^{b_f^\star }\frac{\psi _q'(u)d u}{\psi _q(u)-\psi _q(f(u))}\right) . \end{aligned}$$

We obtain the claimed formula by combining the above results.

If $f({\bar{x}})<x_0$ and ${\bar{x}}\ge b_f^\star$, then from Theorem 3.1 and Theorem 4.1 we know that $b(f({\bar{x}}))\le {\bar{x}}$, and for all $f({\bar{x}})<x<b(f({\bar{x}}))$,

$$\begin{aligned} p_f(x,{\bar{x}})&=\mathbb {E}_x(\mathrm {e}^{-q\tau _X^+(b(f({\bar{x}})))}\mathbf {1}_{\{ \tau _X^+(b(f({\bar{x}})))<\tau _X^-(f({\bar{x}}))\}})\left( h(b(f({\bar{x}})))\right. \\&\left. -\,\mathbb {E}_b(f({\bar{x}}),{\bar{x}}(\mathrm {e}^{-q\rho _f}h(X_{\rho _f}) \mathbf {1}_{\{\rho _f<\infty \}})\right) . \end{aligned}$$

By using Lemma 2.1 we obtain that

$$\begin{aligned} \mathbb {E}_x(\mathrm {e}^{-q\tau _X^+(b(f({\bar{x}})))}\mathbf {1}_{\{\tau _X^+(b(f({\bar{x}})))<\tau _X^-(f({\bar{x}}))\}})=&\frac{\phi _q^-(x)}{\phi _q^-(b(f({\bar{x}})))}\frac{\psi _q(x)-\psi _q(f({\bar{x}}))}{\psi (b(f({\bar{x}})))-\psi _q(f({\bar{x}}))}. \end{aligned}$$

The claim in this case follows from Lemma 4.1.

In the last case that $f({\bar{x}})<x_0$, ${\bar{x}}\ge b_f^\star$ and $b(f({\bar{x}}))\le x\le {\bar{x}}$, or $f({\bar{x}})\ge x_0$ and $f({\bar{x}})<x\le {\bar{x}}$, from Theorem 3.1 and Theorem 4.1 we know that the optimal stopping rule for problem (4) is 0, so we have

$$\begin{aligned} p_f(x,{\bar{x}})=h(x)-\mathbb {E}_{x,{\bar{x}}}(\mathrm {e}^{-q\rho _f}h(X_{\rho _f})\mathbf {1}_{\{\rho _f<\infty \}}). \end{aligned}$$

The completes the proof. $\square$

Proof of Lemma 4.3

The convexity of $H(\cdot )$ has already been proved in the proof of Lemma 2.2, so we only need to prove that for $H_f(\cdot )$. To that end, we recall (30) that

$$\begin{aligned} H_f^{\prime }(z)=\frac{H_f(z)-H(\varphi (z))}{z-\varphi (z)},\quad \forall z\in (0,z_f^\star ), \end{aligned}$$

from which we obtain that, for $z\in (0,z_f^\star )$,

$$\begin{aligned} d H_f^{\prime }(z)&=\frac{\frac{H_f(z)-H(\varphi (z))}{z-\varphi (z)}d z-H'(\varphi (z))d \varphi (z)}{z-\varphi (z)}-\frac{H_f(z)-H(\varphi (z))}{(z-\varphi (z))^2}(d z-d \varphi (z))\nonumber \\&=\bigg (\frac{H_f(z)-H(\varphi (z))}{z-\varphi (z)}-H'(\varphi (z))\bigg )\frac{d \varphi (z)}{z-\varphi (z)}\nonumber \\&\ge \bigg (\frac{H(z)-H(\varphi (z))}{z-\varphi (z)}-H'(\varphi (z))\bigg )\frac{d \varphi (z)}{z-\varphi (z)}. \end{aligned}$$

(39)

We prove that the embraced expression in (39) is positive, which implies that $H_f'(\cdot )$ is increasing so $H_f(\cdot )$ is convex.

To prove the claim, we notice that for $z\in (0,z_f^\star )$, we have $\varphi (z)<\varphi (z_f^\star )=\psi _q(f(\psi _q^{-1}(z_f^\star )))=\psi _q(f(b_f^\star ))<\psi _q(x_0)$, thanks to Corollary 4.1. We now prove that the line segment connecting $(\varphi (z),H(\varphi (z)))$ and (z, H(z)) stays above the graph of $H(\cdot )$. Suppose not, then by the convexity of $H(\cdot )$ this can happen only if the line segment crosses the graph of $H(\cdot )$ twice, and $z>\psi _q(b(\psi _q^{-1}(\varphi (z))))$, the latter of which is the point where the tangent line of $H(\cdot )$ that crosses $(\varphi (z),H(\varphi (z)))$ touches the graph of $H(\cdot )$. In other words,

$$\begin{aligned} \psi _q^{-1}(z)>b(\psi _q^{-1}(\varphi (z)). \end{aligned}$$

(40)

On the other hand, by the monotonicity of b(y) (see Proposition 3.1) we know that

$$\begin{aligned} b(\psi _q^{-1}(\varphi (z))>b(\psi _q^{-1}(\varphi (z_f^\star ))=b_f^\star , \end{aligned}$$

(41)

where we used the definition of $b_f^\star$ in Corollary 4.1. However, (40) is contradictory to (41). Thus, the the line segment connecting $(\varphi (z),H(\varphi (z)))$ and (z, H(z)) stays above the graph of $H(\cdot )$. Given that $H(\cdot )$ is convex at $\varphi (z)$, we know that the slope of this line segment, $\frac{H(z)-H(\varphi (z))}{z-\varphi (z)}$, is larger than $H'(\varphi (z))$. $\square$

Lemma A.1

Define the constant $\beta ^\pm := -\delta \pm \gamma ,$ where

$$\begin{aligned} \delta =\frac{\mu }{\sigma ^2}-\frac{1}{2},\quad \gamma =\sqrt{\delta ^2+\frac{2q}{\sigma ^2}}. \end{aligned}$$

Then, we have $\beta ^+>1$ and

$$\begin{aligned} \frac{-\epsilon -\beta ^-}{2\gamma }, \quad \frac{1-\beta ^-}{2\gamma }\in (0,1). \end{aligned}$$

(42)

Proof

First, since $g(1)=\mu -q<g(\beta ^+)=0$ where $g(\beta )=\frac{1}{2}\sigma ^2\beta (\beta -1)+\mu \beta -q$, we conclude that $1<\beta ^+$. It follows from $\delta <\gamma$ that $-\beta ^-=\delta +\gamma <2\gamma$, so $-\frac{\beta ^-}{2\gamma }<1$. From $g(-\epsilon )<g(\beta ^-)=0$ where $g(\beta )=\frac{1}{2}\sigma ^2\beta (\beta -1)+\mu \beta -q$, we know that $-\epsilon >\beta ^-$. Moreover, $1-\beta ^--2\gamma =1+\delta -\gamma =1+\delta -\sqrt{\delta ^2+\frac{2q}{\sigma ^2}}<\delta +1-\sqrt{\delta ^2+\frac{2\mu }{\sigma ^2}}=\delta +1-\sqrt{\delta ^2+2\delta +1}\le 0$, so $\frac{1-\beta ^-}{2\gamma }<1$. $\square$

Proof of Example 4.1

First of all, we verify that $h(\cdot )$ satisfies Assumption 2.1. To that end, we calculate

$$\begin{aligned} (\mathcal {L}-q)h(x)=(\mu -q)x-\left[ \frac{1}{2}\sigma ^2\epsilon (1+\epsilon )-\mu \epsilon -q\right] Kx^{-\epsilon }, \end{aligned}$$

from which we know that (12) holds. From [18] we know that

$$\begin{aligned} \phi _q^\pm (x)=x^{\beta ^\pm }, \psi _q(x)=x^{\beta ^+-\beta ^-}=x^{2\gamma }, \end{aligned}$$

(43)

where $\beta ^\pm$ is defined in Lemma A.1. Condition (13) holds since $\beta ^+>1$, and thus, Assumption 2.1 holds.

Using (43) and $f(x)=(1-\alpha )x$ we obtain that

$$\begin{aligned}&H(z)=z^{\frac{1-\beta ^-}{2\gamma }}-Kz^{\frac{-\epsilon -\beta ^-}{2 \gamma }},\quad \varphi (z)=(z^{\frac{1}{2\gamma }}(1-\alpha ))^{2\gamma }=(1- \alpha )^{2\gamma }z=:{\bar{\alpha }}z. \nonumber \\&H''(z)=n_1(n_1-1)z^{n_1-2}-K n_2(n_2-1)z^{n_2-2}\nonumber \\&\quad =z^{n_2-2}[n_1(n_1-1)z^{n_1-n_2}+K n_2(1-n_2)]\nonumber \\&\frac{1}{2}\sigma ^2(-\epsilon )(-\epsilon -1)-\mu \epsilon -q<0, \frac{1}{2}\sigma ^2\epsilon (\epsilon +1)-\mu \epsilon -q<0. \end{aligned}$$

(44)

It follows that

$$\begin{aligned} H_f(z)&=\exp \left( -\int _z^{z_f^\star }\frac{d \nu }{\nu -\varphi (\nu )}\right) H(z_f^ \star )+\int _z^{z_f^\star }H(\varphi (\nu )) \nonumber \\&\quad \exp \left( -\int _{z}^{\nu }\frac{ d w}{w-\varphi (w)}\right) \frac{d \nu }{\nu -\varphi (\nu )}\nonumber \\ =&\bigg (\frac{z}{z_f^\star }\bigg )^{\frac{1}{1-{\bar{\alpha }}}}\left[ (z_f^ \star )^{\frac{1-\beta ^-}{2\gamma }}-K(z_f^\star )^{\frac{-\epsilon -\beta ^-}{2 \gamma }}\right] \nonumber \\&\quad +\frac{({\bar{\alpha }})^{\frac{1-\beta ^-}{2\gamma }}}{(1-{\bar{\alpha }}) \frac{1-\beta ^-}{2\gamma }-1}\left[ (z_f^\star )^{\frac{1-\beta ^-}{2\gamma }}\bigg (\frac{z}{z_f^\star }\bigg )^{\frac{1}{1-{\bar{\alpha }}}}-z^{\frac{1-\beta ^-}{2\gamma }}\right] \nonumber \\&-K\frac{({\bar{\alpha }})^{\frac{-\epsilon -\beta ^-}{2\gamma }}}{(1-{\bar{\alpha }})\frac{-\epsilon -\beta ^-}{2\gamma }-1}\left[ (z_f^\star )^{\frac{-\epsilon -\beta ^-}{2\gamma }}\bigg (\frac{z}{z_f^\star }\bigg )^{\frac{1}{1-{\bar{\alpha }}}}-z^{\frac{-\epsilon -\beta ^-}{2\gamma }}\right] . \end{aligned}$$

(45)

Notice that (42) ensures that two detonators in the last line of (45) are negative.

Using (43), (44) and (45), we obtain

$$\begin{aligned}&H^{(1)}(z)\nonumber \\&=H_f(z)-H(z)\nonumber \\&=\bigg (\frac{({\bar{\alpha }})^{\frac{1-\beta ^-}{2\gamma }}+(1-{\bar{\alpha }}) \frac{1-\beta ^-}{2\gamma }-1}{(1-{\bar{\alpha }})\frac{1-\beta ^-}{2 \gamma }-1}(z_f^\star )^{\frac{1-\beta ^-}{2\gamma }} \nonumber \\&\quad -K\frac{({\bar{\alpha }})^{ \frac{-\epsilon -\beta ^-}{2\gamma }}+(1-{\bar{\alpha }})\frac{-\epsilon -\beta ^-}{2 \gamma }-1}{(1-{\bar{\alpha }})\frac{-\epsilon -\beta ^-}{2\gamma }-1}(z_f^\star )^{\frac{- \beta ^-}{2\gamma }}\bigg )\bigg (\frac{z}{z_f^\star }\bigg )^{\frac{1}{1-{\bar{\alpha }}}}\nonumber \\&-\frac{({\bar{\alpha }})^{\frac{1-\beta ^-}{2\gamma }}+(1-{\bar{\alpha }}) \frac{1-\beta ^-}{2\gamma }-1}{(1-{\bar{\alpha }})\frac{1-\beta ^-}{2\gamma }-1}(z_f^\star )^{\frac{1-\beta ^-}{2 \gamma }}\bigg (\frac{z}{z_f^\star }\bigg )^{\frac{1-\beta ^-}{2\gamma }}\nonumber \\&\quad +K\frac{({\bar{\alpha }})^{ \frac{-\epsilon -\beta ^-}{2\gamma }}+(1-{\bar{\alpha }})\frac{-\epsilon -\beta ^-}{2 \gamma }-1}{(1-{\bar{\alpha }})\frac{-\epsilon -\beta ^-}{2\gamma }-1}(z_f^\star )^{\frac{- \beta ^-}{2\gamma }}\bigg (\frac{z}{z_f^\star }\bigg )^{\frac{-\epsilon -\beta ^-}{2\gamma }}\nonumber \\&=: k(\frac{z}{z_f^\star }), \end{aligned}$$

(46)

where k(u) is a polynomial in u:

$$\begin{aligned} k(u)=Au^{n_1}+Bu^{n_2}+Cu^{n_3},\quad \forall u\in (0,1] \end{aligned}$$

(47)

with

$$\begin{aligned} \frac{1}{1-{\bar{\alpha }}}\equiv n_1>1>n_2\equiv \frac{1-\beta ^-}{2\gamma }>n_3\equiv \frac{-\epsilon -\beta ^-}{2\gamma }>0, \end{aligned}$$

and unambiguous definitions of the coefficients A, B,  and C. We can show that $C>0$. In view of the fraction inside C, we let $g(x)=x^p+p(1-x)-1$ for $p=\frac{-\epsilon -\beta ^-}{2\gamma }\in (0,1)$. Then $g(1)=0$ and $g'(x)=p(x^{p-1}-1)>0$ for all $x\in (0,1)$ so $g(\cdot )$ is strictly increasing over (0, 1). In particular, $g({\bar{\alpha }})<g(1)=0$. Since the denominator in C is also negative, we conclude that $C>0$.

Also, observe that $k(0+)=0=H^{(1)}(0+)$. Now, taking derivative of k(u) in (47), we get

$$\begin{aligned} u^{1-n_3}k'(u)=An_1u^{n_1-n_3}+Bn_2u^{n_2-n_3}+Cn_3. \end{aligned}$$

(48)

From $\lim _{u\downarrow 0}u^{1-n_3}k'(u)=Cn_3>0$ we know that $H^{(1),\prime }(z)>0$ for sufficiently small $z>0$. Moreover,

$$\begin{aligned} u^{2-n_3}k''(u)=An_1(n_1-1)u^{n_1-n_3}+Bn_2(n_2-1)u^{n_2-n_3}+Cn_3(n_3-1). \end{aligned}$$

(49)

Using standard argument by taking the derivative, it can be shown that functions like the right hand side of (49) can change monotonicity at most once over (0, 1). Clearly, the right hand side of (49) converges to $Cn_3(n_3-1)<0$ as $u\downarrow 0$. On the other hand, because $H_f(z)-H(z)$ is convex over $(\psi _q(x_0), \psi _q(b_f^\star ))$ (see Lemma 4.3), we know that the right hand side of (49) is positive as $u\uparrow 1$. Given that k(u) is maximized at $\frac{\overline{z}_f^\star }{z_f^\star }$, we know that $k''(u)$ changes sign exactly once over (0, 1). More specifically, there are $u_1\in (0,1)$ such that $k''(u)<0$ for all $u\in (0,u_1)$, and $k''(u)>0$ for all $u\in (u_1,1)$. This proves the pattern of convexity change for $H^{(1)}(\cdot )$. It follows that $H^{(1)}(\cdot )$ is strictly increasing from 0 to $\overline{z}_f^\star$, in particular, $H^{(1)}(z)>0$ for all $z\in (0,z_f^\star )$. Thus, the smallest nonnegative concave majorant of $H^{(1)}(\cdot )$ is given by

$$\begin{aligned} H^{(1)}(z\wedge \overline{z}_f^\star ), \end{aligned}$$

and the optimal stopping region for (24) is given by $\psi _q^{-1}((0,\overline{z}_f^\star ])=(0,\underline{b}_f^\star ]$. Finally, the global maximum $\overline{z}_f^\star$ is the unique solution to

$$\begin{aligned} k'(\frac{z}{z_f^\star })=0, \frac{\overline{z}_f^\star }{z_f^\star }\in (0,u_1). \end{aligned}$$

(50)

$\square$