Optimal mean-reverting spread trading: nonlinear integral equation approach

Abstract

We study several optimal stopping problems that arise from trading a mean-reverting price spread over a finite horizon. Modeling the spread by the Ornstein–Uhlenbeck process, we analyze three different trading strategies: (i) the long-short strategy; (ii) the short-long strategy, and (iii) the chooser strategy, i.e. the trader can enter into the spread by taking either long or short position. In each of these cases, we solve an optimal double stopping problem to determine the optimal timing for starting and subsequently closing the position. We utilize the local time-space calculus of Peskir (J Theor Probab 18:499–535, 2005a) and derive the nonlinear integral equations of Volterra-type that uniquely characterize the boundaries associated with the optimal timing decisions in all three problems. These integral equations are used to numerically compute the optimal boundaries.

1 Introduction

Spread trading is a common strategy used by many traders in various markets, including equity, fixed income, currency, and futures markets. In a spread trade, traders construct a mean-reverting spread by simultaneously taking positions in two or more highly correlated or co-moving assets. The proliferation of exchange-traded funds (ETFs) has further popularized spread trading as some ETFs are designed to replicate identical or similar assets. The strategy involves opening and subsequently closing a position based on the sign and magnitude of the spread. Therefore, the risk of trading changes from the directional price movements of each asset to the fluctuation of the spread over time.

The core of the spread trading strategies lies in the timing to enter and exit the market. For example, Gatev et al. (2006) examined the historical returns from the buy-low-sell-high strategy where the entry and exit levels are set as $\pm 1$ standard deviation from the long-run mean. Similarly, Avellaneda and Lee (2010) considered starting and ending a pairs trade based on a fixed distance of the spread from its mean. In Elliott et al. (2005), the market entry timing is modelled by the first passage time of an Ornstein–Uhlenbeck (OU) process, followed by an exit on a fixed future date. In these studies, the trading rules are not derived endogenously based on a given objective but are prescribed in an ad hoc manner. While these naive trading rules have the advantage of being very simple and explicit, their common drawback is the lack of optimality justification.

Alternatively, a host of related studies apply stochastic optimal control and optimal stopping techniques to determine the optimal timing strategies for an OU price spread. Ekström et al. (2010) analyzed a optimal single stopping problem for liquidating a spread position on an infinite horizon under the OU model with no transaction costs. Song and Zhang (2013) considered an optimal switching approach for trading a spread repeated over an infinite horizon with transaction costs, and solved for the optimal entry and exit thresholds. Also over an infinite horizon, Leung and Li (2015), Leung et al. (2015), Leung and Li (2016), solved analytically and numerically a number of optimal double stopping problems to determine the entry and exit levels for trading under the OU and exponential OU models with transaction costs. Also, Song et al. (2009) proposed and implemented a numerical stochastic approximation scheme to solve for the optimal buy-low-sell-high strategies over a finite horizon.

In this paper, we study several optimal stopping problems that arise from trading a mean-reverting price spread over a finite horizon. We model the stochastic spread directly by an OU process, and analyze three different trading strategies. The first one involves starting by going long on the spread and reverse the position to close, and the second represents the opposite sequence of trades—short to open, long to close. Moreover, as the trader ponders when to enter the market, he/she can enter by starting either with a long or short position. This gives the trader a chooser option to be exercised upon market entry. Once the first position is committed, the trader faces an optimal timing problem to exit the market. For each of these strategies, we solve an optimal double stopping problem to determine the optimal timing for starting and subsequently closing the position.

Our method of solution utilizes local time-space calculus of Peskir (2005a) to derive the Volterra-type integral equations that uniquely characterize the boundaries associated with the optimal timing decisions in all three trading problems. The nonlinear equations are useful not only for the analytical representation but also numerical computation of the value functions and optimal boundaries. Unlike its perpetual analogue (see e.g. Cartea et al. (2015), and Leung and Li (2015)), the finite-horizon trading problems studied herein do not admit closed-form expressions for the value functions or optimal boundaries. Nevertheless, our application of local time-space calculus allows us to express the optimal enter and exit boundaries as unique solutions to recursive integral equations. We provide illustrations of the boundaries and discuss their properties and financial implications.

Our paper contributes to the literature of optimal spread trading by providing an optimal double stopping approach together with Volterra-type integral equations for determining and analyzing the optimal boundaries over a finite horizon. It also introduces a number of new Volterra-type integral equations based on an OU underlying process. To the best of our knowledge, the integral equations and analytical results for optimal pair trading herein are new. Our integral equation approach has been recently applied to the valuation of swing options with multiple stopping opportunities, see De Angelis and Kitapbayev (2016). Modeling the spread between the futures and spot by a Brownian bridge, Dai et al. (2011) also consider a chooser option embedded in the trader’s timing to enter the market.

The paper is organized as follows. We formulate the optimal trading problem in Sect. 2. The solutions for the three trading problems and analyses of the optimal timing strategies are presented in Sects. 3, 4, and 5, respectively. Section 6 is included to discuss the incorporation of transaction costs and associated challenges.

2 Problem overview

We fix a finite trading horizon [0, T], and filtered probability space $(\varOmega , \mathcal{F}, (\mathcal{F}_t), \mathsf {P})$, where $\mathsf {P}$ is a subjective probability measure held by the trader, and $(\mathcal{F}_t)_{0\le t\le T}$ is the filtration to which every process defined herein is adapted.

We model the price spread X by the Ornstein–Uhlenbeck (OU) process introduced by Ornstein and Uhlenbeck (1930):

$$\begin{aligned} dX_t=\mu (\theta \! -\! X_t)dt+\sigma dB_t, \quad X_0=x, \end{aligned}$$

(1)

where B is a standard Brownian motion, and the parameters $\mu , \sigma >0$, and $\theta \in \mathbb {R}$, represent the speed of mean reversion, volatility, and long-run mean of the process, respectively. We refer the reader to, e.g., Section 2.1 of Leung and Li (2015), for the detailed maximum likelihood procedure to estimate the parameters for this model with backtested examples of spread trading.

The solution to (1) is well-known as

$$\begin{aligned} X_t=x\text {e}^{-\mu t}+\theta (1\! -\! \text {e}^{-\mu t})+\sigma \int _0^t \text {e}^{-\mu (t-s)}dB_s, \qquad t\ge 0. \end{aligned}$$

(2)

At any fixed time t, the random variable $X_t$ has a normal distribution with the probability density function

$$\begin{aligned} p(\widetilde{x};t,x)=\frac{1}{\sqrt{2 \pi \; var(t,x)}}\,\text {e}^{-\frac{(\widetilde{x}-m(t,x))^2}{2\;var(t,x)}}\,, \end{aligned}$$

(3)

where the mean m(t, x) and variance var(t, x) functions are given by

$$\begin{aligned} m(t,x)&=x\text {e}^{-\mu t}+\theta (1\! -\! \text {e}^{-\mu t}), \end{aligned}$$

(4)

$$\begin{aligned} var(t,x)&=\frac{\sigma ^2}{2\mu }(1-\text {e}^{-2\mu t}), \end{aligned}$$

(5)

for $(t,x) \in \mathbb {R}_+\times \mathbb {R}$. The infinitesimal operator of X is given as

$$\begin{aligned} \mathbb {L}_X F(x)=\mu (\theta \! -\! x)F'(x)+\frac{\sigma ^2}{2} F''(x) \end{aligned}$$

(6)

for $x\in \mathbb {R}$ and $F\in C^2 (\mathbb {R})$.

The trader seeks to establish a position and subsequently closes it by time $T>0$. We analyze three trading strategies: (i) the long-short strategy, whereby the trader longs the spread first and later reverses the position to close (see Sect. 3); (ii) short-long strategy, whereby the trader shorts the spread to start and then close by taking the opposite (long) position (see Sect. 4), and (iii) the chooser strategy, i.e. the trader can take either a long or short position in the spread when entering the market (see Sect. 5), and subsequently liquidates by taking the opposite position. For each trading problem, if it is optimal for the trader not to trade at all, then in the absence of trading fees we represent it as if she/he enters and exits simultaneously at T, giving a zero return. In other words, the trader must enter and exit by time T. In the presence of transaction costs, simultaneous entry and exit will generate a strictly negative return, so the problem is more delicate and difficult (see Sect. 6).

3 Optimal long-short strategy

The trader who enters the market by taking a long position and subsequently closes it before time T faces the following optimal double stopping problem:

$$\begin{aligned} V^1(t,x)=\sup \limits _{0\le \tau \le \zeta \le T-t}\mathsf {E}\left[ \text {e}^{-r\zeta } X^x_\zeta \! -\! \text {e}^{-r\tau } X^x_\tau \right] , \end{aligned}$$

(7)

defined at current time $t\in [0,T)$ and spread value $x\in \mathbb {R}$. Here, $X^x$ represents the process X starting at $X^x_0=x$, $r>0$ is the trader’s discount rate, and the supremum is taken over all pairs of $\mathcal{F}^{X}$- stopping times $(\tau ,\zeta )$ such that $\tau \le \zeta \le T-t$. The time $\tau$ represents the strategy for buying the spread and $\zeta$ is the liquidation time.

Using standard arguments (see e.g. Carmona and Touzi (2008)), the problem (7) can be reduced to a sequence of two optimal single stopping problems. Precisely, the optimal liquidation timing problem is represented by

$$\begin{aligned} V^{1,L}(t,x)=\sup \limits _{0\le \zeta \le T-t}\mathsf {E}\left[ \text {e}^{-r\zeta } X^x_\zeta \right] . \end{aligned}$$

(8)

This value function $V^{1,L}$ represents the maximum expected value of a long position in the spread X, but the trader will need to pay the spread value for this position. Therefore, the difference between this value function and the spread value is viewed as the reward the trader received upon entry. Therefore, the trader’s optimal entry timing problem is given by

$$\begin{aligned} V^{1,E}(t,x)=\sup \limits _{0\le \tau \le T-t}\mathsf {E}\left[ \text {e}^{-r\tau }(V^{1,L}(t\! +\! \tau ,X^x_\tau )\! -\! X^x_\tau )\right] . \end{aligned}$$

(9)

We have the equality: $V^1=V^{1,E}$, and that the optimal stopping times in problems (8)-(9) are optimal for the original problem in (7). We first solve the problem (8) in Sect. 3.1 and then the problem (9) in Sect. 3.2.

3.1 Optimal exit problem

We now discuss how to represent the optimal stopping problem (8) as a free boundary problem, which is then analyzed using the local time-space calculus (see Peskir (2005a)). First, using that the payoff function in (8) is continuous and standard arguments (see e.g. Corollary 2.9 (finite horizon) with Remark 2.10 in Peskir and Shiryaev (2006)), we define the continuation and exit regions:

$$\begin{aligned} \mathcal {C}^{1,L}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:V^{1,L}(t,x)>x\}, \end{aligned}$$

(10)

$$\begin{aligned} \mathcal {D}^{1,L}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:V^{1,L}(t,x)=x\}, \end{aligned}$$

(11)

which are linked to the optimal exit time in (8) given by

$$\begin{aligned} \zeta _*^{1,L}=\inf \ \{0\le s\le T\! -\! t:(t\! +\! s,X^x_{s})\in \mathcal {D}^{1,L}\}. \end{aligned}$$

(12)

Let us define the function

$$\begin{aligned} \mathcal {K}^{1,L}(u,x,z):=&-\text {e}^{-ru}\mathsf {E}\big [H^{1,L}(X^x_u) I(X^x_u \ge z)\big ] \end{aligned}$$

(13)

$$\begin{aligned} =&-\text {e}^{-ru}\int _z^{\infty } H^{1,L}(\widetilde{x})\,p(\widetilde{x};u,x)\,d\widetilde{x} \end{aligned}$$

(14)

for $u\ge 0$ and $x,z\in \mathbb {R}$, where the normal density p is given in (3) and the function $H^{1,L}$ is an affine function in x defined by

$$\begin{aligned} H^{1,L}(x)=-(\mu \! +\! r)x+\mu \theta . \end{aligned}$$

(15)

The main result of this section is the integral equation representation of the free boundary associated with the optimal exit time $\zeta _*^{1,L}$.

Theorem 1

The optimal stopping time for (8) is given by

$$\begin{aligned} \zeta _*^{1,L}=\inf \ \{0\le s\le T\! -\! t:X^x_{s}\ge b^{1,L}(t\! +\! s) \}. \end{aligned}$$

(16)

The function $b^{1,L}(\cdot )$ is the optimal exit boundary corresponding to (8), and it can be characterized as the unique solution to a nonlinear integral equation of Volterra type, that is,

$$\begin{aligned} b^{1,L}(t)=\text {e}^{-r(T-t)}m(T\! -\! t,b^{1,L}(t)) +\int _0^{T-t} \mathcal {K}^{1,L}(u,b^{1,L}(t),b^{1,L}(t\! +\! u))du \end{aligned}$$

(17)

for $t\in [0,T]$ in the class of continuous decreasing functions $t\mapsto b^{1,L}(t)$ with $b^{1,L}(T)=x^*=\mu \theta /(\mu +r)$. The value function $V^{1,L}$ in (8) admits the representation

$$\begin{aligned} V^{1,L}(t,x)=\text {e}^{-r(T-t)}m(T\! -\! t,x) +\int _0^{T-t}\mathcal {K}^{1,L}(u,x,b^{1,L}(t\! +\! u))du \end{aligned}$$

(18)

for $t\in [0,T]$ and $x\in \mathbb {R}$.

Proof

The proof is provided in several steps.

• 1. Continuity of $V^{1,L}$. Here we show that the price function $V^{1,L}$ is continuous on $[0,T)\times \mathbb {R}$. For this, let $t\in [0,T]$ and $x>y\in \mathbb {R}$ be given and fixed. We let $\zeta _x$ denote the optimal stopping time for $V^{1,L}(t,x)$. We then have

  $$\begin{aligned} 0&\le V^{1,L}(t,x)-V^{1,L}(t,y)\le \mathsf {E}\left[ \text {e}^{-r\zeta _x} (X^x_{\zeta _x}- X^y_{\zeta _x})\right] \nonumber \\&= \mathsf {E}\left[ \text {e}^{-(r+\mu )\zeta _x}(x-y) \right] \le x-y \end{aligned}$$

  (19)

  where we used (2). Thus, we see that $x\mapsto V^{1,L} (t, x)$ is continuous on $\mathbb {R}$ uniformly over $t\in [0, T ]$ since the right-hand side of (19) does not depend on t. It is therefore enough to show that $t \mapsto V^{1,L} (t, x)$ is continuous on [0, T] for each $x\in \mathbb {R}$ given and fixed. For this, fix arbitrary $0 \le t_1 < t_2 \le T$ and $x\in \mathbb {R}$, and let $\zeta _1$ denote the optimal stopping time for $V^{1,L}(t_1,x)$. As the payoff function in (8) is time-independent and the process X is time-homogeneous, it follows that the map $t\mapsto V^{1,L}(t,x)$ is decreasing on [0, T] for each $x\in \mathbb {R}$. In turn, setting $\zeta _2 =\zeta _1\wedge (T-t_2)$, we obtain

  $$\begin{aligned} 0&\le V^{1,L}(t_1,x)-V^{1,L}(t_2,x)\le \mathsf {E}\left[ \text {e}^{-r\zeta _1} X^x_{\zeta _1}\right] -\mathsf {E}\left[ \text {e}^{-r\zeta _2} X^x_{\zeta _2}\right] \nonumber \\&\le \mathsf {E}\left[ |X^x_{\zeta _1}\! -\! X^x_{\zeta _2}|\right] . \end{aligned}$$

  (20)

  Letting first $t_2-t_1\rightarrow 0$ and using $\zeta _1-\zeta _2\rightarrow 0$ we see that $V^{1,L}(t_1,x)-V^{1,L}(t_2,x)\rightarrow 0$ by the dominated convergence theorem. This shows that $t\mapsto V^{1,L}(t,x)$ is continuous on [0, T] for each $x\in \mathbb {R}$ fixed, and the proof of the initial claim is complete.

• 2. Now we obtain some initial insights into the structure of the exit region $\mathcal {D}^{1,L}$. For this, we use Ito’s formula and the optional sampling theorem to see that

  $$\begin{aligned} \mathsf {E}\left[ \text {e}^{-r\zeta }X^{x}_\zeta \right] =\;x+\mathsf {E}\left[ \int _0^\zeta \text {e}^{-rs}H^{1,L}(X^{x}_s)ds\right] \end{aligned}$$

  (21)

  for $x\in \mathbb {R}$ and any stopping time $\zeta \in [0,T]$ where the function $H^{1,L}$ was defined in (15).

  The function $H^{1,L}$ is strictly decreasing with single root $x^*=\mu \theta /(\mu + r)$. The Eq. (21) shows that it is not optimal to exit the position when $X_t< x^*$ as $H^{1,L}(X_t)>0$ in this region and thus the integral term on the right-hand side of (21) is positive. For this one can make use of the first exit time from a sufficiently small time-space ball centered at the point where $H^{1,L}>0$. Another implication of (21) is that the exit region is non-empty for all $t\in [0,T)$, as for large $x\uparrow \infty$ the integrand $H^{1,L}$ is very negative and thus due to the lack of time to compensate the negative $H^{1,L}$, it is optimal to exit at once.

• 3. Optimal exit boundary. Next we prove further properties of the exit region $\mathcal {D}^{1,L}$ and define the optimal exit boundary.

  • (i) Recall that the map $t\mapsto V^{1,L}(t,x)$ is decreasing on [0, T] for each $x\in \mathbb {R}$ so that $V^{1,L}(t_1,x)\! -\! x\ge V^{1,L}(t_2,x)\! -\! x\ge 0$ for $0\le t_1<t_2 <T$ and $x\in \mathbb {R}$. Now if we take a point $(t_1,x)\in \mathcal {D}^{1,L}$, i.e. $V^{1,L}(t_1,x)=x$, then $(t_2,x)\in \mathcal {D}^{1,L}$ as well, which shows that the exit region expands when t increases. In other words, $\mathcal {D}^{1,L}$ is right-connected.

  • (ii) Now let us take $t>0$, $x>y$, and we denote by $\zeta =\zeta (t,x)$ the optimal stopping time for $V^{1,L}(t,x)$. Then using (21) we have

    $$\begin{aligned} V^{1,L}(t,x)-V^{1,L}(t,y)&\le \mathsf {E}\left[ \text {e}^{-r\zeta } X^{x}_\zeta \right] - \mathsf {E}\left[ \text {e}^{-r\zeta }X^{y}_\zeta \right] \nonumber \\&=x-y+\mathsf {E}\left[ \int _0^\zeta \text {e}^{-rs}\left( H^{1,L}(X^{x}_s)\! -\! H^{1,L}(X^y_s)\right) ds\right] \nonumber \\&\le x-y \end{aligned}$$

    (22)

    where we used that $H^{1,L}$ is decreasing and $X^x_{\cdot }\ge X^y_{\cdot }$ by (2). Now if we let $(t,y)\in \mathcal {D}^{1,L}$, i.e. $V^{1,L}(t,y)=y$, we have $V^{1,L}(t,x)=x$, i.e. $(t,x)\in \mathcal {D}^{1,L}$. Therefore we obtain an up-connectedness of the exit region $\mathcal {D}^{1,L}$.

  • (iii) From (i)-(ii) and paragraph 2 above we can conclude that there exists an optimal exit boundary $b^{1,L}:[0,T]\rightarrow \mathbb {R}$ such that

  $$\begin{aligned} \zeta _*^{1,L}=\inf \ \{0\le s\le T\! -\! t:X^x_{s}\ge b^{1,L}(t\! +\! s) \} \end{aligned}$$

  (23)

  is optimal in (8) and $x^*<b^{1,L}(t)<\infty$ for $t\in [0,T)$. Moreover, $b^{1,L}$ is decreasing on [0, T).

• 4. Smooth-fit. Now we prove that the smooth-fit condition along the boundary $b^{1,L}$ holds

  $$\begin{aligned} V^{1,L}_x (t, b^{1,L}(t)-)=V^{1,L}_x(t,b^{1,L}(t)+)=1 \end{aligned}$$

  (24)

  for all $t\in [0,T)$.

  • (i) First let us fix a point $(t,x)\in [0,T)\times \mathbb {R}$ lying on the boundary $b^{1,L}$ so that $x=b^{1,L}(t)$. Then we have

    $$\begin{aligned} \frac{V^{1,L}(t,x)-V^{1,L}(t,x\! -\! \varepsilon )}{\varepsilon }&\le \frac{x-(x\! -\! \varepsilon )}{\varepsilon }=1 \end{aligned}$$

    (25)

    and taking the limit as $\varepsilon \downarrow 0$, we get

    $$\begin{aligned} V^{1,L}_x (t,x-)\le 1 \end{aligned}$$

    (26)

    where the left-hand derivative exists by the convexity of $x\mapsto V^{1,L}(t,x)$ on $\mathbb {R}$ for any fixed $t\in [0,T)$.

  • (ii) To prove the reverse inequality, we set $\zeta _\varepsilon =\zeta _\varepsilon (t,x\! -\! \varepsilon )$ as an optimal stopping time for $V^{1,L}(t,x-\varepsilon )$. Using that X is a regular diffusion and $t\mapsto b^{1,L}(t)$ is decreasing, we see that $\zeta _\varepsilon \rightarrow 0$ as $\varepsilon \rightarrow 0$ $\mathsf {P}$-a.s. We get

  $$\begin{aligned} \frac{1}{\varepsilon }\Big (&V^{1,L}(t,x)-V^{1,L}(t,x\! -\! \varepsilon )\Big )\nonumber \\&\ge \frac{1}{\varepsilon }\mathsf {E}\left[ \text {e}^{-r\zeta _{\varepsilon }}\left( X_{\zeta _{\varepsilon }}^{x}\! -\! X_{\zeta _{\varepsilon }}^{x-\varepsilon }\right) \right] =\mathsf {E}\left[ \text {e}^{-(r+\mu )\zeta _{\varepsilon }}\right] \end{aligned}$$

  (27)

  where we used the solution (2) for X. Clearly, the right-hand side of (27) goes to 1 as $\varepsilon \rightarrow 0$. Thus taking the limits as $\varepsilon \rightarrow 0$, we get the inequality

  $$\begin{aligned} V^{1,L}_x (t,x-)\ge 1 \end{aligned}$$

  (28)

  for $t\in [0,T)$. Combining (26) and (28), we obtain (24).

• 5. Continuity of $b^{1,L}$. Here we prove that the boundary $b^{1,L}$ is continuous on [0, T] and that $b^{1,L}(T-)=x^*$. The proof is provided in 3 steps and follows the approach proposed by De Angelis (2014).

  • (i) We first show that $b^{1,L}$ is right-continuous. Let us fix $t\in [0,T)$ and take a sequence $t_n \downarrow t$ as $n\rightarrow \infty$. As $b^{1,L}$ is decreasing, the right-limit $b^{1,L}(t+)$ exists and $(t_n, b^{1,L}(t_n))$ belongs to $\mathcal {D}^{1,L}$ for all $n\ge 1$. Recall that $\mathcal {D}^{1,L}$ is closed so that $(t_n,b^{1,L}(t_n))\rightarrow (t,b^{1,L}(t+))\in \mathcal {D}^{1,L}$ as $n\rightarrow \infty$ and we may conclude that $b^{1,L}(t+)\ge b^{1,L}(t)$. The fact that $b^{1,L}$ is decreasing gives the reverse inequality and thus $b^{1,L}$ is right-continuous as claimed.

  • (ii) Now we prove that $b^{1,L}$ is also left-continuous. Assume that there exists $t_0\in (0,T)$ such that $b^{1,L}(t_0-)>b^{1,L}(t_0)$. Let us set $x_1 = b^{1,L}(t_0)$ and $x_2 = b^{1,L}(t_0-)$ so that $x_1 < x_2$. For $\varepsilon \in (0,(x_2- x_1)/2)$ given and fixed, let $\varphi _\varepsilon : (-\infty ,\infty ) \rightarrow [0,1]$ be a $C^\infty$- function satisfying (i) $\varphi _\varepsilon (x) = 1$ for $x\in [x_1 +\varepsilon , x_2 -\varepsilon ]$ and (ii) $\varphi _\varepsilon (x) = 0$ for $x\in (-\infty ,x_1\! +\! \varepsilon /2]\cup [x_2\! -\! \varepsilon /2,\infty )$. Letting $\mathbb {L}^*_X$ denote the adjoint of $\mathbb {L}_X$, recalling that $t\rightarrow V^{1,L}(t,x)$ is decreasing on [0, T] and that $V^{1,L}_t\! +\! \mathbb {L}_X V^{1,L} \! -\! rV^{1,L}= 0$ on $\mathcal {C}^{1,L}$, we find integrating by parts (twice) that

    $$\begin{aligned} 0&\ge \int ^{x_2}_{x_1}{\varphi (x)V^{1,L}_t(t_0 \! -\! \delta ,x)dx}\nonumber \\&=-\int ^{x_2}_{x_1}{V^{1,L}(t_0 \! -\! \delta ,x)\left( \mathbb {L}_X^*\varphi (x)\! -\! r\varphi (x)\right) dx} \end{aligned}$$

    (29)

    for $\delta \in (0,t_0\wedge (\varepsilon /2))$ so that $\varphi _\varepsilon (x_2\! -\! \delta ) = \varphi '_\varepsilon (x_2\! -\! \delta ) = 0$ as needed. Letting $\delta \downarrow 0$ it follows using the dominated convergence theorem and integrating by parts (twice) that

    $$\begin{aligned} 0&\ge -\int ^{x_2}_{x_1}{V^{1,L}(t_0,x)\left( \mathbb {L}_X^*\varphi (x)\! -\! r\varphi (x)\right) dx}\nonumber \\&=-\int ^{x_2}_{x_1}{x\left( \mathbb {L}_X^*\varphi (x)\! -\! r\varphi (x)\right) dx}\nonumber \\&=-\int ^{x_2}_{x_1}{\left( \mathbb {L}_X x\! -\! rx\right) \varphi (x) dx}=-\int ^{x_2}_{x_1}{H^{1,L}(x)\varphi (x)dx}. \end{aligned}$$

    (30)

    Letting $\varepsilon \downarrow 0$ we obtain

    $$\begin{aligned} 0\ge -\int ^{x_2}_{x_1}{H^{1,L}(x)dx}>0 \end{aligned}$$

    (31)

    as $x\rightarrow H^{1,L}(x)$ is strictly negative on $(x_1,x_2]$. We thus have a contradiction and therefore we may conclude that $b^{1,L}$ is continuous on [0, T) as claimed.

  • (iii) To prove that $b^{1,L}(T-)=x^*$ we can use the same arguments as those in (ii) above with $t_0=T$ and suppose that $b^{1,L}(T-)>x^*$.

• 6. Free-boundary problem. The facts proved in paragraphs 1–5 above and standard arguments based on the strong Markov property (see e.g. Peskir and Shiryaev (2006)) lead to the following free-boundary problem for the value function $V^{1,L}$ and unknown boundary $b^{1,L}$:

  $$\begin{aligned}&V^{1,L}_t \! +\! \mathbb {L}_X V^{1,L} \! -\! rV^{1,L}=0&\quad \text { in }\; \mathcal {C}^{1,L} \end{aligned}$$

  (32)
  $$\begin{aligned}&\quad V^{1,L}(t,b^{1,L}(t))=b^{1,L}(t)&\quad \text { for }\; t\in [0,T) \end{aligned}$$

  (33)
  $$\begin{aligned}&\quad V^{1,L}_x (t,b(t))=1&\quad \text { for }\; t\in [0,T) \end{aligned}$$

  (34)
  $$\begin{aligned}&\quad V^{1,L}(t,x)>x&\quad \text { in }\; \mathcal {C}^{1,L} \end{aligned}$$

  (35)
  $$\begin{aligned}&\quad V^{1,L}(t,x)=x&\quad \text { in }\; \mathcal {D}^{1,L} \end{aligned}$$

  (36)

  where the continuation set $\mathcal {C}^{1,L}$ and the exit region $\mathcal {D}^{1,L}$ are given by

  $$\begin{aligned} \mathcal {C}^{1,L}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:x<b^{1,L}(t)\} \end{aligned}$$

  (37)
  $$\begin{aligned} \mathcal {D}^{1,L}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:x\ge b^{1,L}(t)\}. \end{aligned}$$

  (38)

  The following properties of $V^{1,L}$ and $b^{1,L}$ were also verified above:

  $$\begin{aligned}&V^{1,L}\;\text {is continuous on}\; [0,T]\times \mathbb {R}\end{aligned}$$

  (39)
  $$\begin{aligned}&\quad V^{1,L}\;\text {is }\; C^{1,2}\;\text { on }\; \mathcal {C}^{1,L} \end{aligned}$$

  (40)
  $$\begin{aligned}&\quad x\mapsto V^{1,L}(t,x)\;\text { is increasing and convex on }\mathbb {R}\hbox { for each } t\in [0,T] \end{aligned}$$

  (41)
  $$\begin{aligned}&\quad t\mapsto V^{1,L}(t,x)\;\text { is decreasing on }[0,T] \hbox { for each } x\in \mathbb {R}\end{aligned}$$

  (42)
  $$\begin{aligned}&\quad t\mapsto b^{1,L}(t)\;\text { is decreasing and continuous on }[0,T] \hbox { with }\; b^{1,L}(T-)=x^*. \end{aligned}$$

  (43)

• 7. Integral equation. We clearly have that the following conditions hold: (i) $V^{1,L}$ is $C^{1,2}$ on $\mathcal {C}^{1,L}\cup \mathcal {D}^{1,L}$; (ii) $b^{1,L}$ is of bounded variation (due to monotonicity); (iii) $V^{1,L}_t\! +\! \mathbb {L}_{X}V^{1,L}-rV^{1,L}$ is locally bounded; (iv) $x\mapsto V^{1,L}(t,x)$ is convex; (v) $t\mapsto V^{1,L}_x (t,b^{1,L}(t)\pm )$ is continuous (recall (34)). Hence we can apply the local time-space formula on curves Peskir (2005a)) for $\text {e}^{-rs}V^{1,L}(t+s,X^x_s)$, along with (32), (34), and (36), to get

  $$\begin{aligned}&\text {e}^{-rs}V^{1,L}(t\! +\! s,X^x_s)\nonumber \\&\quad =\;V^{1,L}(t,x)+M_s\nonumber \\&\quad + \int _0^{s} \text {e}^{-ru}\left( V^{1,L}_t \! +\! \mathbb {L}_X V^{1,L} \! -\! rV^{1,L}\right) (t\! +\! u,X^x_u) I(X^x_u \ne b^{1,L}(t\! +\! u))du\nonumber \\&\quad +\frac{1}{2}\int _0^{s} \text {e}^{-ru}\left( V^{1,L}_x (t\! +\! u,X^x_u {+}){-}V^{1,L}_x (t\! +\! u,X^x_u {-})\right) I\big (X^x_u{=}b^{1,L}(t\! +\! u)\big )d\ell ^{b^{1,L}}_u\nonumber \\&\quad =\;V^{1,L}(t,x)+M_s +\int _0^{s} \text {e}^{-ru}H^{1,L}(X^x_u) I(X^x_u \ge b^{1,L}(t\! +\! u))du \end{aligned}$$

  (44)

  where $M=(M_s)_{s\ge 0}$ is the martingale part, and $(\ell ^{b^{1,L}}_t(X^x))_{t\ge 0}$ is the local time process of $X^x$ at the boundary $b^{1,L}$, given by

  $$\begin{aligned} \ell ^{b^{1,L}}_t=\mathsf {P}-\lim _{\varepsilon \downarrow 0}\frac{1}{2\varepsilon }\int _0^{t} I(b^{1,L}(t\! +\! u)\! -\! \varepsilon<X^x_u<b^{1,L}(t\! +\! u)\! +\! \varepsilon )d\left\langle X,X \right\rangle _u. \end{aligned}$$

  (45)

  Now upon letting $s=T\! -\! t$, taking the expectation $\mathsf {E}$, using the optional sampling theorem for M, rearranging terms, noting that $V^{1,L}(T,x)=x$ for all $x\in \mathbb {R}$ and recalling (4), we get (18). The integral equation (17) is obtained by inserting $x=b^{1,L}(t)$ into (18) and using (33).

• 8. Uniqueness of the solution. The proof of that $b^{1,L}$ is the unique solution to the Eq. (17) in the class of continuous decreasing functions $t\mapsto b^{1,L}(t)$ is based on arguments originally employed by Peskir (2005b) and omitted here.

Numerical algorithm for solution to integral equation. We proved above that $b^{1,L}$ is the unique solution to the integral equation (17). Even though this equation cannot be solved analytically, it can be solved numerically in a straightforward and efficient manner, as we illustrate below and refer to Chap. 8 of Detemple (2005) for more details. In order to numerically solve the integral equation, it is crucial to be able to compute $\mathcal {K}^{1,L}$ efficiently. Fortunately, we have the closed-form expression for the function $\mathcal {K}^{1,L}$ since the (marginal) distribution of $X_t$ is Gaussian.

Let N be the number of time discretizations, and set $h=T/N$ and $t_k=kh$ for $k=0,1,...,N$. This leads to the following discrete approximation of the integral equation (17):

$$\begin{aligned} b^{1,L}(t_k)=\;&\text {e}^{-r(T-t)}m(T-t,b^{1,L}(t_k))\nonumber \\&+h\sum _{l=k}^{N-1} \mathcal {K}^{1,L}\left( t_k,t_{l+1}\! -\! t_k,b^{1,L}(t_k),b^{1,L}(t_{l+1})\right) \end{aligned}$$

(46)

for $k= 0,1,...,N\! -\! 1$. Setting $k=N\! -\! 1$ and $b^{1,L}(t_N)=x^*$ we solve the Eq. (46) numerically and obtain the value of $b^{1,L}(t_{N- 1})$. Setting $k=N\! -\! 2$ and using the values $b^{1,L}(t_{N- 1})$ and $b^{1,L}(t_{N})$, we solve (46) numerically for the value $b^{1,L}(t_{N- 2})$. Continuing this recursion we obtain all $b^{1,L}(t_{N})$, $b^{1,L}(t_{N-1})$,...,$b^{1,L}(t_1)$, $b^{1,L}(t_0)$ as approximations to the continuous optimal boundary $b^{1,L}$ at the points $T, T- h,..., h, 0$.

Finally, the value function (18) can be approximated as follows:

$$\begin{aligned} V^{1,L}(t_k,x)=\;&\text {e}^{-r(T-t)}m(T-t,x)\nonumber \\&+h\sum _{l=k}^{N-1} \mathcal {K}^{1,L}\left( t_k,t_{l+1}\! -\! t_k,x,b^{1,L}(t_{l+1})\right) \end{aligned}$$

(47)

for $k= 0,1,...,N\! -\! 1$ and $x\in \mathbb {R}$.

3.2 Optimal entry problem

Having solved for the optimal timing to exit, we now turn to the optimal entry problem

$$\begin{aligned} V^{1,E}(t,x)=\sup \limits _{0\le \tau \le T-t}\mathsf {E}\left[ \text {e}^{-r\tau }\left( V^{1,L}(t\! +\! \tau ,X^x_\tau )-X^x_\tau \right) \right] \end{aligned}$$

(48)

where the supremum is taken over all stopping times $\tau \in [0,T-t]$ of X. We define the payoff function $G^{1,E}(t,x)=V^{1,L}(t,x)-x$ for $(t,x)\in [0,T)\times \mathbb {R}$.

We tackle the problem (48) using similar arguments as for (8). We define the continuation and entry regions

$$\begin{aligned} \mathcal {C}^{1,E}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:V^{1,E}(t,x)>G^{1,E}(t,x)\} \end{aligned}$$

(49)

$$\begin{aligned} \mathcal {D}^{1,E}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:V^{1,E}(t,x)=G^{1,E}(t,x)\}. \end{aligned}$$

(50)

In turn, the optimal exit time in (48) is given by

$$\begin{aligned} \tau ^{1,E}_*=\inf \ \{0\le s\le T\! -\! t:(t\! +\! s,X^x_{s})\in \mathcal {D}^{1,E}\}. \end{aligned}$$

(51)

Let us define the function $\mathcal {K}^{1,E}$ as

$$\begin{aligned} \mathcal {K}^{1,E}(u,x,z)&=-\text {e}^{-ru}\mathsf {E}\big [H^{1,E}(u, X^x_u) I(X^x_u \le z)\big ]\nonumber \\&=-\text {e}^{-ru}\int _{-\infty }^z H^{1,E}(u, \widetilde{x})\,p(\widetilde{x};u,x)\,d\widetilde{x} \end{aligned}$$

(52)

for $u\ge 0$ and $x,z\in \mathbb {R}$, where

$$\begin{aligned} H^{1,E}(t,x)=((\mu + r)x-\mu \theta )I(x <b^{1,L}(t)) \end{aligned}$$

(53)

for $(t,x)\in [0,T)\times \mathbb {R}$.

We now state the main theorem of this section. We do not provide full proof since it is very similar to the one in Theorem 3.1 above and outline only important details.

Theorem 2

The optimal entry boundary $b^{1,E}$ in (48) can be characterized as the unique solution to a nonlinear integral equation

$$\begin{aligned} V^{1,L}(t,b^{1,E}(t))\! -\! b^{1,E}(t)=\int _0^{T-t} \mathcal {K}^{1,E}(u,b^{1,E}(t),b^{1,E}(t\! +\! u))du \end{aligned}$$

(54)

for $t\in [0,T]$ in the class of continuous increasing functions $t\mapsto b^{1,E}(t)$ with $b^{1,E}(T)=x^*$. The value function $V^{1,E}$ in (48) can be represented as

$$\begin{aligned} V^{1,E}(t,x)=\int _0^{T-t}\mathcal {K}^{1,E}(u,x,b^{1,E}(t\! +\! u))du \end{aligned}$$

(55)

for $t\in [0,T]$ and $x\in \mathbb {R}$.

Proof

• 1. We use the local time-space formula on curves (Peskir (2005a)), the smooth-fit property (34) and the option sampling theorem to obtain

  $$\begin{aligned} \mathsf {E}\left[ \text {e}^{-r\tau }G^{1,E}(t\! +\! \tau ,X^{x}_\tau )\right] =\;G^{1,E}(t,x)+\mathsf {E}\left[ \int _0^\tau \text {e}^{-rs}H^{1,E}(t\! +\! s,X^{x}_s)ds\right] \end{aligned}$$

  (56)

  for $t\in [0,T)$, $x\in \mathbb {R}$, any stopping time $\tau \in [0,T-t]$ of process X and where the function $H^{1,E}$ is defined as $H^{1,E}(t,x):=(\mathbb {L}_X G^{1,E} \! -\! rG^{1,E})(t,x)$ for $(t,x)\in [0,T)\times \mathbb {R}$ and equals

  $$\begin{aligned} H^{1,E}(t,x)=((\mu \! +\! r)x-\mu \theta )I(x <b^{1,L}(t)) \end{aligned}$$

  (57)

  for $(t,x)\in [0,T)\times \mathbb {R}$.

  The function $H^{1,E}$ is strictly increasing and linear in x on $(-\infty ,b^{1,L}(t))$ for fixed t and has unique root $x^*=\mu \theta /(\mu \! +\! r)<b^{1,L}(t)$. Hence, it is not optimal to enter into the position when $X_t>x^*$ and as the integral term on the right-hand side of (56) is non-negative. The Eq. (56) also gives that the entry region is non-empty for all $t\in [0,T)$, as for large negative $x\downarrow -\infty$ the integrand $H^{1,E}$ is very negative and thus it is optimal to enter immediately.

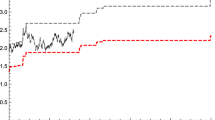
• 2. We can prove similarly as in the previous section that the entry region $\mathcal {D}^{1,E}$ is right-connected and down-connected. Hence there exists an optimal entry boundary $b^{1,E}:[0,T]\rightarrow \mathbb {R}$ (see Fig. 1) such that

  $$\begin{aligned}&\tau ^{1,E}_*=\inf \ \{0\le s\le T\! -\! t:X^x_{s}\le b^{1,E}(t\! +\! s) \} \end{aligned}$$

  (58)

  is optimal in (48) and $-\infty<b^{1,E}(t)<x^*$ for $t\in [0,T)$. Moreover, $b^{1,E}$ is increasing on [0, T) and is bounded from below.

• 3. Standard methods based on the strong Markov property and arguments from the previous section lead to the following free-boundary problem for the value function $V^{1,E}$ and the boundary $b^{1,E}$:

  $$\begin{aligned}&V^{1,E}_t \! +\! \mathbb {L}_X V^{1,E} \! -\! rV^{1,E}=0&\quad \text {in}\; \mathcal {C}^{1,E} \end{aligned}$$

  (59)
  $$\begin{aligned}&\quad V^{1,E}(t,b^{1,E}(t))=V^{1,L}(t,b^{1,E}(t))\! -\! b^{1,E}(t)&\quad \text { for }\; t\in [0,T) \end{aligned}$$

  (60)
  $$\begin{aligned}&\quad V^{1,E}_x(t,b^{1,E}(t))=V^{1,L}_x(t,b^{1,E}(t))\! -\! 1&\quad \text { for }\; t\in [0,T) \end{aligned}$$

  (61)
  $$\begin{aligned}&\quad V^{1,E}(t,x)>G^{1,E}(t,x)&\quad \text {in }\; \mathcal {C}^{1,E} \end{aligned}$$

  (62)
  $$\begin{aligned}&\quad V^{1,E}(t,x)=G^{1,E}(t,x)&\quad \text {in }\; \mathcal {D}^{1,E} \end{aligned}$$

  (63)

  where the continuation set $\mathcal {C}^{1,E}$ and the entry region $\mathcal {D}^{1,E}$ are given by

  $$\begin{aligned} \mathcal {C}^{1,E}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:x>b^{1,E}(t)\} \end{aligned}$$

  (64)
  $$\begin{aligned} \mathcal {D}^{1,E}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:x\le b^{1,E}(t)\}. \end{aligned}$$

  (65)

  The following properties of $V^{1,E}$ and $b^{1,E}$ hold:

  $$\begin{aligned}&V^{1,E}\;\text {is continuous on}\; [0,T]\times \mathbb {R}\end{aligned}$$

  (66)
  $$\begin{aligned}&\quad V^{1,E}\;\text {is}\; C^{1,2}\;\text {on}\; \mathcal {C}^{1,E} \end{aligned}$$

  (67)
  $$\begin{aligned}&\quad x\mapsto V^{1,E}(t,x)\;\text {is convex on }\mathbb {R}\hbox { for each } t\in [0,T] \end{aligned}$$

  (68)
  $$\begin{aligned}&\quad t\mapsto V^{1,E}(t,x)\;\text {is decreasing on }[0,T] \hbox { for each } x\in \mathbb {R}\end{aligned}$$

  (69)
  $$\begin{aligned}&\quad t\mapsto b^{1,E}(t)\;\text {is increasing and continuous on }[0,T] \hbox { with }\; b^{1,E}(T-)=x^*. \end{aligned}$$

  (70)

• 4. We then verify the conditions of local time-space formula and apply it for $\text {e}^{-rs}V^{1,E}(t+s,X^x_s)$ to obtain representation (55). The integral equation (55) is derived by inserting $x=b^{1,E}(t)$ into (55).

Fig. 1

The optimal entry boundary (lower) and the optimal exit boundary (upper) for the long-short strategy problem (7) computed as the solutions to integral equations (54) and (17), respectively. The parameters are: $T=1$ year, $r=0.01$, $\theta =0$, $\mu =16$, $\zeta =0.16.$ A time discretization with 500 steps for the interval [0, T] is used

4 Optimal short-long strategy

In this section, we consider the short-long strategy: short the spread to open, long the spread to close the position. This problem is analogous to the one in Sect. 3, and thus we only state the optimal stopping problems and main results, and omit the proofs.

At time $t\in [0,T)$ with the current spread value $x\in \mathbb {R}$, the trader solves the optimal double stopping problem

$$\begin{aligned} V^2(t,x)=\sup \limits _{0\le \zeta \le \tau \le T-t}\mathsf {E}\left[ \text {e}^{-r\zeta } X^x_\zeta \! -\! \text {e}^{-r\tau } X^x_\tau \right] \end{aligned}$$

(71)

where $X^x$ represents that the process X starts from $X^x_0=x$, $r>0$ is the interest rate, and the supremum is taken over all pairs of $\mathcal{F}^{X}$- stopping times $(\tau ,\zeta )$ such that $\zeta \le \tau \le T-t$. As in the previous section, $\tau$ is time for long position and $\zeta$ is the strategy for short position.

Remark 1

If $\theta =0$, then X and $-X$ have the same law. As such, the problems (7) and (71) are symmetric, i.e., $V^{2}=-V^{1}$.

We reduce (71) into the two single optimal stopping problems:

$$\begin{aligned} V^{2,L}(t,x)=\inf \limits _{0\le \tau \le T-t}\mathsf {E}\left[ \text {e}^{-r\tau } X^x_\tau \right] \end{aligned}$$

(72)

which is the optimal exit problem under this strategy. After solving (72) we will turn to the entry problem, i.e. optimal timing to enter into the long position

$$\begin{aligned} V^{2}(t,x)=V^{2,E}(t,x)=\sup \limits _{0\le \zeta \le T-t}\mathsf {E}\left[ \text {e}^{-r\zeta }(X^x_\zeta \! -\! V^{2,L}(t\! +\! \zeta ,X^x_\zeta ))\right] \end{aligned}$$

(73)

as at time $t\! +\! \zeta$ we receive $X^x_\zeta$ and get the short position with the value $-V^{2,L}(t\! +\! \zeta ,X^x_\zeta )$.

As in the previous section, we reduce (72) to the free-boundary problem for the value function $V^{2,L}$ and optimal exit boundary $b^{2,L}$:

$$\begin{aligned}&V^{2,L}_t \! +\! \mathbb {L}_X V^{2,L} \! -\! rV^{2,L}=0&\quad \text {in }\; \mathcal {C}^{2,L} \end{aligned}$$

(74)

$$\begin{aligned}&\quad V^{2,L}(t,b^{2,L}(t))=b^{2,L}(t)&\quad \text {for }\; t\in [0,T) \end{aligned}$$

(75)

$$\begin{aligned}&\quad V^{2,L}_x (t,b^{2,L}(t))=1&\quad \text {for }\; t\in [0,T) \end{aligned}$$

(76)

$$\begin{aligned}&\quad V^{2,L}(t,x)<x&\quad \text {in }\; \mathcal {C}^{2,L} \end{aligned}$$

(77)

$$\begin{aligned}&\quad V^{2,L}(t,x)=x&\quad \text {in }\; \mathcal {D}^{2,L} \end{aligned}$$

(78)

where the continuation set $\mathcal {C}^{2,L}$ and the exit region $\mathcal {D}^{2,L}$ are given by

$$\begin{aligned} \mathcal {C}^{2,L}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:x>b^{2,L}(t)\} \end{aligned}$$

(79)

$$\begin{aligned} \mathcal {D}^{2,L}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:x\le b^{2,L}(t)\}. \end{aligned}$$

(80)

The value function $V^{2,L}$ and optimal boundary $b^{2,L}$ admit the following properties:

$$\begin{aligned}&V^{2,L}\;\text {is continuous on}\; [0,T]\times \mathbb {R}\end{aligned}$$

(81)

$$\begin{aligned}&\quad V^{2,L}\;\text {is}\; C^{1,2}\;\text {on}\; \mathcal {C}^{2,L} \end{aligned}$$

(82)

$$\begin{aligned}&\quad x\mapsto V^{2,L}(t,x)\;\text {is increasing and concave on }\mathbb {R}\hbox { for each } t\in [0,T] \end{aligned}$$

(83)

$$\begin{aligned}&\quad t\mapsto V^{2,L}(t,x)\;\text {is increasing on }[0,T] \hbox { for each } x\in \mathbb {R}\end{aligned}$$

(84)

$$\begin{aligned}&\quad t\mapsto b^{2,L}(t)\;\text {is increasing and continuous on }[0,T] \hbox { with }\; b^{2,L}(T-)=x^*. \end{aligned}$$

(85)

The main theorem is stated as follows.

Theorem 3

The value function $V^{2,L}$ in (72) has the following representation

$$\begin{aligned} V^{2,L}(t,x)=\text {e}^{-r(T-t)} m(T-t,x) +\int _0^{T-t}\mathcal {K}^{2,L}(u,x,b^{2,L}(t\! +\! u))du \end{aligned}$$

(86)

for $t\in [0,T]$ and $x\in \mathbb {R}$. The optimal exit boundary $b^{2,L}$ in (72) can be characterized as the unique solution to a nonlinear integral equation

$$\begin{aligned} b^{2,L}(t)=\text {e}^{-r(T-t)} m(T-t,b^{2,L}(t)) +\int _0^{T-t} \mathcal {K}^{2,L}(u,b^{2,L}(t),b^{2,L}(t\! +\! u))du \end{aligned}$$

(87)

for $t\in [0,T]$ in the class of continuous increasing functions $t\mapsto b^{2,L}(t)$ with $b^{2,L}(T)=x^*$. and where the function $\mathcal {K}^{2,L}$ is defined as

$$\begin{aligned} \mathcal {K}^{2,L}(u,x,z)=-\text {e}^{-ru}\mathsf {E}\big [H^{1,L}(X^x_u) I(X^x_u \le z)\big ] \end{aligned}$$

(88)

for $u\ge 0$, $x,z\in \mathbb {R}$ and $H^{1,L}$ is given in (15).

Applying the results for exit problem, we now analyze the following free-boundary problem for the optimal entry value function $V^{2,E}$ in (73), and the associated boundary $b^{2,E}$:

$$\begin{aligned}&V^{2,E}_t \! +\! \mathbb {L}_X V^{2,E} \! -\! rV^{2,E}=0&\quad \text {in}\; \mathcal {C}^{2,E} \end{aligned}$$

(89)

$$\begin{aligned}&\quad V^{2,E}(t,b^{2,E}(t))=b^{2,E}(t)\! -\! V^{2,L}(t,b^{2,E}(t))&\quad \text {for}\; t\in [0,T) \end{aligned}$$

(90)

$$\begin{aligned}&\quad V^{2,E}_x (t,b^{2,E}(t))=1\! -\! V^{2,L}_x(t,b^{2,E}(t))&\quad \text {for}\; t\in [0,T) \end{aligned}$$

(91)

$$\begin{aligned}&\quad V^{2,E}(t,x)>x\! -\! V^{2,L}(t,x)&\quad \text {in}\; \mathcal {C}^{2,E} \end{aligned}$$

(92)

$$\begin{aligned}&\quad V^{2,E}(t,x)=x\! -\! V^{2,L}(t,x)&\quad \text {in}\; \mathcal {D}^{2,E} \end{aligned}$$

(93)

where the continuation and entry regions, respectively, are given by

$$\begin{aligned} \mathcal {C}^{2,E}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:x<b^{2,E}(t)\} \end{aligned}$$

(94)

$$\begin{aligned} \mathcal {D}^{2,E}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:x\ge b^{2,E}(t)\}. \end{aligned}$$

(95)

The following properties of $V^{2,E}$ and $b^{2,E}$ hold:

$$\begin{aligned}&V^{2,E}\;\text {is continuous on}\; [0,T]\times \mathbb {R}\end{aligned}$$

(96)

$$\begin{aligned}&\quad V^{2,E}\;\text {is}\; C^{1,2}\;\text {on }\; \mathcal {C}^{2,E} \end{aligned}$$

(97)

$$\begin{aligned}&\quad x\mapsto V^{2,E}(t,x)\;\text {is convex on }\mathbb {R}\hbox { for each } t\in [0,T] \end{aligned}$$

(98)

$$\begin{aligned}&\quad t\mapsto V^{2,E}(t,x)\;\text {is decreasing on }[0,T] \hbox { for each } x\in \mathbb {R}\end{aligned}$$

(99)

$$\begin{aligned}&\quad t\mapsto b^{2,E}(t)\;\text {is decreasing and continuous on }[0,T] \hbox { with }\; b^{2,E}(T-)=x^*. \end{aligned}$$

(100)

To prepare the following result, we define the function

$$\begin{aligned} \mathcal {K}^{2,E}(u,x,z)=-\text {e}^{-ru}\mathsf {E}\big [H^{1,L}(X^x_u) I(X^x_u \ge z)\big ] \end{aligned}$$

(101)

for $t, u\ge 0$, $x,z\in \mathbb {R}$, with $H^{1,L}$ defined in (15).

Theorem 4

The value function $V^{2,L}$ in (73) admits the integral representation:

$$\begin{aligned} V^{2,E}(t,x)=\int _0^{T-t}\mathcal {K}^{2,E}(u,x,b^{2,E}(t\! +\! u))du \end{aligned}$$

(102)

for $t\in [0,T]$ and $x\in \mathbb {R}$. The optimal entry boundary $b^{2,E}$ in (73) can be characterized as the unique solution to a nonlinear integral equation

$$\begin{aligned} b^{2,E}(t)\! -\! V^{2,L}(t,b^{2,E}(t))=\int _0^{T-t} \mathcal {K}^{2,E}(u,b^{2,E}(t),b^{2,E}(t\! +\! u))du \end{aligned}$$

(103)

for $t\in [0,T]$ in the class of continuous decreasing functions $t\mapsto b^{2,E}(t)$ with $b^{2,E}(T)=x^*$.

5 Chooser strategy

In this section, the trader in the spread trading problem can choose whether to long or short his position first. Thus she/he is not pre-committed to the strategies in Sects. 3 and 4, and clearly this flexibility increases his overall expected profit from the trading. The trading problem again can be formulated as the double optimal stopping one

$$\begin{aligned} V^0(t,x)=\sup \limits _{0\le \tau ,\zeta \le T-t}\mathsf {E}\left[ \text {e}^{-r\zeta } X^x_\zeta \! -\! \text {e}^{-r\tau } X^x_\tau \right] \end{aligned}$$

(104)

for $(t,x)\in [0,T)\times \mathbb {R}$ where $X^x$ represents that the process X starts from $X^x_0=x$, $r>0$ is the interest rate, and the supremum is taken over all pairs of $\mathcal{F}^{X}$- stopping times $(\tau ,\zeta )$ such that $\tau ,\zeta \le T-t$. As before, $\tau$ is time for long position and $\zeta$ is time for short position. The main difference of (104) compare to both long-short and short-long strategies is that there is no order and constraint between $\tau$ and $\zeta$. We do not need to consider sequentially exit and entry problems, but just solve optimal problems for both long and short positions independently. Therefore we split the trading problem into the two separate problems

$$\begin{aligned} V^{1,L}(t,x)&=\sup \limits _{0\le \zeta \le T-t}\mathsf {E}\left[ \text {e}^{-r\zeta } X^x_\zeta \right] \end{aligned}$$

(105)

$$\begin{aligned} V^{2,L}(t,x)&=\inf \limits _{0\le \tau \le T-t}\mathsf {E}\left[ \text {e}^{-r\tau } X^x_\tau \right] \end{aligned}$$

(106)

and we have

$$\begin{aligned} V^0(t,x)=V^{1,L}(t,x)-V^{2,L}(t,x) \end{aligned}$$

(107)

for $(t,x)\in [0,T)\times \mathbb {R}$ and where $V^{1,L}$ and $V^{2,L}$ are given in (18)–(86).

Both problems (105)–(106) have been solved already in previous sections. The optimal entry time in (104) is given by $\zeta _*^{1,L}\wedge \tau _*^{2,L}$ and the exit time is $\zeta _*^{1,L}\vee \tau _*^{2,L}$, where $\zeta _*^{1,L}$ and $\tau _*^{2,L}$ have been characterized as well.

In Fig. 2, we illustrate the two optimal boundaries representing the long and short entering positions under the chooser strategy. We compare it to the optimal entering thresholds in the perpetual version of the problem (see Chap. 14 of Cartea et al. (2015)). Intuitively, with an infinite horizon ahead, the trader can afford to wait longer and enter the market when the spread is wider in either direction. This is confirmed in Fig. 2 as the optimal boundary to long (resp. short) is above (resp. below) the optimal thresholds from the perpetual case. In other words, the continuation region, in which the trader waits to enter the market, is larger in the perpetual case than in the current finite-horizon problem.

Fig. 2

The optimal boundaries $(b^{1,L},b^{2,L})$ (solid line) for the chooser strategy problem (104) computed as the solution to integral equations (17) and (87). Dashed lines represent optimal thresholds for the perpetual case. The parameter set is $T=1$ year, $r=0.01$, $\theta =0$, $\mu =16$, $\zeta =0.16$. We used $N=500$ steps for the time discretization of interval [0, T]

Here we reformulate the problem (104) sequentially as for the long-short and short-long strategies. We already know the solution to the problem from previous paragraph, but would like to show that the solution satisfies the free-boundary problem for the entry problem. Once the trader enters into the position, she/he solves one of the optimal liquidation problems and both of them were already solved Sects. 3.1 and 4. Therefore we only need to study the optimal entry problem and this can be formulated as follows

$$\begin{aligned} V^{0,E}(t,x)=\sup \limits _{0\le \tau \le T-t}\mathsf {E}\left[ \text {e}^{-r\tau }G(t\! +\! \tau ,X^x_\tau )\right] \end{aligned}$$

(108)

where the payoff function G reads

$$\begin{aligned} G(t,x)=\max (V^{1,L}(t,x)\! -\! x,x\! -\! V^{2,L}(t,x)) \end{aligned}$$

(109)

for $t\in [0,T)$ and $x\in \mathbb {R}$. The payoff function G shows that at entry time the trader maximizes his value and chooses the best option, i.e. whether to go long or short the spread. Below we show that $V^{0,E}$ is the same as $V^0$ from (107).

It can be seen that $V^{1,L}(t,x)- x=0$ for $x\ge b^{1,L}(t)$ and $x-V^{2,L}(t,x)=0$ for $x\le b^{2,L}(t)$. Also since $V^{1,L}$ and $V^{2,L}$ are convex and concave, respectively, we have $V^{1,L}_x \le 1$ and $V^{2,L}_x \le 1$. Hence the function $V^{1,L}(t,x)\! -\! x$ is decreasing for $x< b^{1,L}(t)$ and $x\! -\! V^{2,L}(t,x)$ is increasing $x> b^{2,L}(t)$, and we can conclude that there exists threshold m(t) for fixed $t\in [0,T)$ such that

$$\begin{aligned} G(t,x)=(V^{1,L}(t,x)\! -\! x) I(x\le m(t)) + (x\! -\! V^{2,L}(t,x))I(x> m(t)) \end{aligned}$$

(110)

for $t\in [0,T)$ and $x\in \mathbb {R}$. Clearly, the function G is convex in x for fixed $t\in [0,T)$.

Given that we already know the solution to the problem (104), we will use “guess-verify” method for the finite horizon optimal entry problem (104) unlike in Sects. 3.1 and 4 where the optimal boundaries were constructed directly (as solutions to the integral equations). Let us take the pair of optimal exit strategies $(b^{1,L},b^{2,L})$ as the candidate for the optimal entry boundaries such that the entry time is given by

$$\begin{aligned} \tau _{0,E}=\inf \ \{0\le s\le T\! -\! t:X^x_{s}\le b^{2,L}(t\! +\! s)\;\text {or}\;X^x_{s}\ge b^{1,L}(t\! +\! s) \} \end{aligned}$$

(111)

and define

$$\begin{aligned} \widehat{V}^{0,E}(t,x)=V^{1,L}(t,x)-V^{2,L}(t,x) \end{aligned}$$

(112)

for $t\in [0,T)$ and $x\in \mathbb {R}$ as the candidate value function for $V^{0,E}$.

Using established properties (32)–(36) and (74)–(78) of the value functions ${V}^{1,L}$ and $V^{2,L}$, and boundaries $b^{1,L}$ and $b^{2,L}$, we can verify that $\widehat{V}^{0,E}$ and $(b^{1,L},b^{2,L})$ solve the following free-boundary problem

$$\begin{aligned}&\widehat{V}^{0,E}_t \! +\! \mathbb {L}_X \widehat{V}^{0,E} \! -\! r\widehat{V}^{0,E} =0&\quad \text {in}\; \mathcal {C}^{0,E} \end{aligned}$$

(113)

$$\begin{aligned}&\quad \widehat{V}^{0,E} (t,b^{1,L}(t))=G(t,b^{1,L}(t))&\quad \text {for}\; t\in [0,T) \end{aligned}$$

(114)

$$\begin{aligned}&\quad \widehat{V}^{0,E} (t,b^{2,L}(t))=G(t,b^{2,L}(t))&\quad \text {for}\; t\in [0,T) \end{aligned}$$

(115)

$$\begin{aligned}&\quad \widehat{V}^{0,E}_x (t,b^{1,L}(t))=G_x(t,b^{1,L}(t))&\quad \text {for}\; t\in [0,T) \end{aligned}$$

(116)

$$\begin{aligned}&\quad \widehat{V}^{0,E}_x (t,b^{2,L}(t))=G_x(t,b^{2,L}(t))&\quad \text {for}\; t\in [0,T) \end{aligned}$$

(117)

$$\begin{aligned}&\quad \widehat{V}^{0,E}(t,x)>G(t,x)&\quad \text {in}\; \mathcal {C}^{0,E} \end{aligned}$$

(118)

$$\begin{aligned}&\quad \widehat{V}^{0,E}(t,x)=G(t,x)&\quad \text {in}\; \mathcal {D}^{0,E} \end{aligned}$$

(119)

where the continuation set $\mathcal {C}^{0,E}$ and the entry set $\mathcal {D}^{0,E}$ are given by

$$\begin{aligned} \mathcal {C}^{0,E}&= \{ (t,x)\in [0,T)\! \times \! \mathbb {R}:b^{2,L}(t)<x<b^{1,L}(t)\} \end{aligned}$$

(120)

$$\begin{aligned} \mathcal {D}^{0,E}&= \{ (t,x)\in [0,T)\! \times \!\mathbb {R}:x\le b^{2,L}(t)\,\text {or}\,x\ge b^{1,L}(t)\}. \end{aligned}$$

(121)

Let us show, for example, that (114) holds indeed. This condition is equivalent to $V^{1,L}(t,b^{1,L}(t))-V^{2,L}(t,b^{1,L}(t))=b^{1,L}(t)- V^{2,L}(t,b^{1,L}(t))$ as $b^{1,L}(t)>m(t)$. The latter is true as $V^{1,L}(t,b^{1,L}(t))=b^{1,L}(t)$ due to (33). The conditions (114)–(117) can be shown in similar way.

Finally, standard verification arguments indicate that $\widehat{V}^{0,E}$ and $(b^{1,L},b^{2,L})$ are indeed the value function and optimal boundaries, respectively. In Fig. 3, we compare the value function of the chooser strategy over a finite horizon ($T=1$ year) to the value of the perpetual counterpart. As we can see, the difference is quite significant as a longer horizon allows the trader to wait longer to capture a wider spread. This also shows the practical importance of studying the optimal spread problem over the finite horizon.

Fig. 3

The value function $V^{0,E}$ (solid line) of the chooser strategy (104) over a finite horizon lies below the value function for the perpetual case (dashed line). The parameters are: $T=1$ year, $r=0.01$, $\theta =0$, $\mu =16$, $\zeta =0.16$

Remark 2

We note that the analytical results above can be extended to other mean-reverting models of the form

$$\begin{aligned} dX_t=\mu (\theta \! -\! X_t)dt+\sigma (X_t) dB_t, \quad X_0=x, \end{aligned}$$

(122)

where $\sigma (x)$ is some smooth function of X, but not necessarily a constant. The corresponding integral equations and value function representations will be of the same form as those under the OU model derived above. Indeed, the linear payoffs considered herein render the diffusion coefficient $\sigma (x)$ irrelevant when we apply Ito’s calculus. However, for numerical analysis and computation, it is crucial to know marginal distributions of X. For example, $X_t$ is Gaussian when $\sigma (x)=\sigma$, and $X_t$ is non-central chi-squared when $\sigma (x)=\sigma \sqrt{x}$ (CIR process). Hence, our results can be extended to models in (122) with a known probability density for $X_t$ that is explicit or can be approximated. We refer to Leung et al. (2014) for optimal double stopping of the CIR process.

6 Incorporating transaction costs

In this section, we incorporate fixed transaction costs when the trader is pre-committed to the long-short strategy. We assume that she/he may not enter into the long position, e.g., if we enter very close to T it is more likely that we end up with the loss since we pay transaction costs twice and gain at most small difference from the spread. Thus it would be optimal not to enter at all and get zero payoff.

We formulate this problem sequentially, first assume that there is open long position in the spread which want to liquidate optimally

$$\begin{aligned} V^{1,L,c}(t,x)=\sup \limits _{0\le \zeta \le T-t}\mathsf {E}\left[ \text {e}^{-r\zeta } (X^x_\zeta -c)\right] \end{aligned}$$

(123)

and the only difference with the problem (8) above is that we add fixed trading fee $c>0$. Then having solved (123) we consider optimal entry problem

$$\begin{aligned} V^{1,E,c}(t,x)=\sup \limits _{0\le \tau \le T-t}\mathsf {E}\left[ \text {e}^{-r\tau }(V^{1,L,c}(t\! +\! \tau ,X^x_\tau )\! -\! X^x_\tau \! -\! c)^+\right] \end{aligned}$$

(124)

as at time $t\! +\! \tau$ we pay $X^x_\tau +c$ and get the long position with the value $V^{1,L,c}(t\! +\! \tau ,X^x_\tau )$ and we will go long only if the payoff of this strategy is positive, otherwise we use our right not to enter into it at this instance.

Observe that the optimal stopping problem in (123) is a slight generalization of that in (8). Therefore, to avoid repetition, we only state the results below.

Theorem 5

The value function $V^{1,L,c}$ has the following representation

$$\begin{aligned} V^{1,L,c}(t,x)=\;&\text {e}^{-r(T-t)}(m(T\! -\! t,x)\! -\! c) \nonumber \\&+\int _0^{T-t}\mathcal {K}^{1,L,c}(u,x,b^{1,L}(t\! +\! u))du \end{aligned}$$

(125)

for $t\in [0,T]$ and $x\in \mathbb {R}$. The optimal exit boundary $b^{1,L,c}$ can be characterized as the unique solution to a nonlinear integral equation

$$\begin{aligned} b^{1,L,c}(t)=\;&\text {e}^{-r(T-t)}(m(T\! -\! t,b^{1,L,c}(t))\! -\! c) \nonumber \\&+\int _0^{T-t} \mathcal {K}^{1,L,c}(u,b^{1,L,c}(t),b^{1,L,c}(t\! +\! u))du \end{aligned}$$

(126)

for $t\in [0,T]$ in the class of continuous decreasing functions $t\mapsto b^{1,L,c}(t)$ with $b^{1,L,c}(T)=(\mu \theta \! +\! rc)/(\mu \! +\! r)$ where

$$\begin{aligned} \mathcal {K}^{1,L,c}(u,x,z)&=-\text {e}^{-ru}\mathsf {E}\big [H^{1,L,c}(X^x_u) I(X^x_u \ge z)\big ]\\ H^{1,L,c}(x)&=-(\mu \! +\! r)x+\mu \theta +rc. \end{aligned}$$

Now we turn to the entry problem (124). It differs from (9) in two ways: there is transaction fee c and, more importantly, the right not to enter into the position. Indeed, when t goes T, the value of long position $V^{1,L,c}(t,x)$ is close to $x-c$ so that the payoff $V^{1,L,c}(t,x)-x-c$ tends to $-2c$ and thus it almost always not rational to go long near T. To formalize this observation, we define the curve $\gamma$ on [0, T) as

$$\begin{aligned} V^{1,L,c}(t,\gamma (t))-\gamma (t)-c=0 \end{aligned}$$

(127)

for $t\in [0,T)$. Hence when $x\ge \gamma (t)$ we should not enter as the value is non-positive. From the properties of $V^{1,L,c}(t,x)$, it can be seen that $\gamma$ is decreasing with $\gamma (T-)=-\infty$ and that $\gamma <b^{1,L,c}$.

The optionality is the key component that precludes us to perform the complete theoretical analysis and prove regularity properties. The problem becomes very challenging and is left for future research. Here, we conclude the paper with a number of open questions with our remarks:

• The existence of the optimal entry boundary $b^{1,E,c}$ that separates the continuation and exercise sets. Intuitively, it is should be true that $\mathcal {D}^{1,E,c}= \{ (t,x)\in [0,T)\! \times \!\mathbb {R}:x\le b^{1,E,c}(t)\}$.

• Monotonicity of the boundary $b^{1,E,c}$. Most likely, it is decreasing and explodes to $-\infty$ at T. For another example of this boundary behavior, we refer to Leung et al. (2016), where the optimal futures trading problem with the transaction costs has been numerically solved using a finite-difference method applied to the associated variational inequality.

• Smooth-fit property at $b^{1,E,c}$. The standard proof uses that the process enters immediately into the exercise region if starts slightly above $b^{1,E,c}$. However, if the boundary is decreasing, it is not clear that this property holds. Thus one has to compare the asymptotic behavior of the process at 0 and the slope of the boundary. The latter is unknown. In particular, the slope is very negative near T and we do not see strong evidence that the smooth fit holds close to T. This open problem is general for optimal stopping problems when the immediate hitting of the boundary is not guaranteed.

• Local time. It is unclear whether the local time term is present in the expression for the value function and/or in the integral equation for the optimal exercise boundary for problem (124). The local time term will add significant challenges to the analysis and numerical implementation of the associated integral equations.