1 Introduction

Flows in nano- and micro-channels have been widely investigated in the past few years, since current nanotechnology methods have enabled fabrication of small-scale systems and devices used in water desalination [1], nanofiltration systems [2], CO2 separation and storage [3] and many more, as reviewed in [4]. When downsizing at the nanoscale, flows are difficult to be implemented due to strong confinement and wall interaction on fluid atoms. Theoretical investigations on gas and liquid flows in micro devices (MEMS/NEMS) have to take into account properties not previously taken into account at the macroscale [5–7]. From a fundamental point of view, relations from classical fluid dynamics, such as the Navier–Stokes (NS) equations, have been incorporated and scaled down to the nanometer range so as to explain fluid behavior. The validity of the macroscopic relations has been tested against results from molecular dynamics (MD) simulations, a method that applies directly at the nanoscale and provides a well-established theory for fluid flow investigation [8, 9]. Multiscale/hybrid system simulations are also being used in order to explain fluid behavior near the solid boundary (with MD) and away from their effect, in the channel interior (with NS) [10–14].

Researchers have incorporated, either in theoretical basis or experimental setups, novel materials and channel architectures that enhance flow [15–17]. One of the reasons that flow enhancement is possible at the nanoscale is the slip length, a quantity that results when the macroscopic hypothesis of no-slip breaks down [18]. Slip existence or not leads to studies on super- (or ultra-) hydrophobic surfaces. Voronov et al. [19] reviewed current simulation and experimental methods aiming to correlate slip length and fluid contact angle in either flat or patterned surfaces.

Most studies on slip involve the incorporation of either rough, patterned surface of channels during flows or a kind of control over the surface wettability degree [20] or, even, the spring force that connects wall atoms [21]. Asproulis and Drikakis [22] suggested that the amount of slip versus wall stiffness can be modeled through a fifth-order polynomial function. Experiments on slip have shown that larger slips lengths occur with smaller surface roughness [23] and hydrophobic walls [24]. Niavarani and Priezjev [25], among others, pointed out that in the presence of periodic surface roughness, the magnitude of the effective slip length is significantly reduced. Cheng et al. [26] calculated slip length for various roughness patterns and found greater slips for longitudinal grooves compared to transverse ones. The same result obtained in Priezjev et al. [27] for flat-wall channels with stripes of different shear behavior, where larger slip calculated in longitudinal configuration than transverse. Moreover, larger slip was also found when wall/fluid interaction decreases. Yen [28] noticed that hydrophobic behavior has more pronounced effect than roughness on slip. More details on boundary slip can be found in the review of Cao et al. [7], where molecular momentum transport is investigated, with emphasis on molecular behaviors near fluid–solid interfaces at the nano/microscale.

Studies in nanoflows have been also directed towards the calculation of transport properties of fluids. Three of the most important transport properties that reveal the mechanisms of mass, momentum and heat transfer, i.e., the diffusion coefficient, shear viscosity and thermal conductivity, have been calculated with equilibrium or non-equilibrium molecular dynamics methods [29–31]. Transport properties are difficult to define experimentally or with relations from classical fluid dynamics, especially when extensive shear stresses or non-linearities are present [32, 33]. Apart from individual calculations for each one of the three transport properties [34–39] diffusion coefficient has been calculated with molecular dynamics simulations and connected with shear viscosity [40], as well as with thermal conductivity [41] through classical algebraic relations.

In this work, we model duct flows in nanochannels with flat, ribbed and grooved walls of various hydrophobicity/hydrophilicity degrees, and argue on each channel effect on flow parameters, such as density profiles, velocity profiles and slip length calculation. Both hydrophobic and hydrophilic channels are incorporated for our wall geometries. Moreover, we present detailed transport properties calculation (diffusion coefficients, shear viscosity and thermal conductivity) along the channel, both in layer and channel average values, by incorporating microscopic relations in conjunction with relations from the continuum theory. We analyze simulation details in Sect. 2, plot and discuss the results in Sect. 3 and conclude in Sect. 4.

2 Simulation methods

2.1 System model

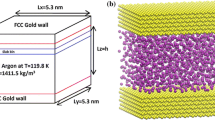
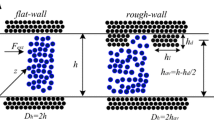
Liquid monoatomic flow is simulated in channels with flat, grooved and ribbed walls (Fig. 1a–c, respectively). Flow is considered equivalent to Poiseuille flow, where liquid argon flows between two parallel plates. The system is periodic along the x-, and y-directions, while, in z-direction, h is the wall separation (channel height). Wall separation for the flat-wall channel is h = 18.58 σ, while groove height and length are g h  = 1.9 σ and g l  = 5.3 σ, respectively. The choice of the specific channel height is based on the fact that, as it has been presented in the literature, simple fluid transport properties (as an average across the channel) tend to obtain their bulk values in channels above 10 σ [31], so h = 18.58 σ lies above this limit. In this way, the calculated results are mainly affected by the wall grooves/ribs. The distinction between a grooved and a ribbed channel is made by the flow direction; when the fluid flows in transverse direction to the protrusions, we have a grooved-wall channel, while, in longitudinal direction, we have a ribbed-wall channel flow.

Fig. 1
figure 1

Channel model showing implementations of a flat-, b grooved-, c ribbed-wall channels and d channel division in 48 × 48 bins and 9 layers for numerical calculations

Full size image

Fluid/fluid, wall/fluid and wall/wall interactions are described by Lennard–Jones (LJ) 12–6 potential \(u^{LJ} (r_{ij} ) = 4\varepsilon ((\sigma /r_{ij} )^{12} - (\sigma /r_{ij} )^{6} )\), with the energy parameter \({\varepsilon \mathord{\left/ {\vphantom {\varepsilon {k_{B} }}} \right. \kern-0pt} {k_{B} }} = 119.8\;{\rm K}\), constant mean fluid density \(\rho_{f} = 0.642\;\sigma^{ - 3}\) (from now on, ρ), wall density \(\rho_{w} = 0.87\;\sigma^{ - 3}\) and cut-off radius, e.g., the distance above which the potential energy between two particles is zero, is r c = 2.5 σ. Flow originates due to the application of an external force \(F_{ext}^{x,y} = 0.01344\;\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon \sigma }} \right. \kern-0pt} \sigma }} \right)\) to all fluid atoms (\(F_{ext}^{y}\) for the ribbed–\(F_{ext}^{x}\) for the grooved), which acts as an analog to the application of pressure difference to induce the flow in macroscopic systems.

Wall atoms are bound on fcc sites and remain approximately at their original positions due to the effect of an elastic spring force \({\mathbf{F}} = - K\left( {{\mathbf{r}}(t) - {\mathbf{r}}_{eq} } \right),\) where \({\mathbf{r}}(t)\) is the vector position of a wall atom at time t, \({\mathbf{r}}_{eq}\) is its initial lattice position vector and \(K = 57.15{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {\sigma^{2} }}} \right. \kern-0pt} {\sigma^{2} }}\) is the wall spring constant which defines the stiffness of the channel wall, i.e., the bonding strength between wall atoms, and large K leads to a stiffer wall. This choice of K was found to satisfy the Lindemann criterion for melting and does not result in oscillating motion of wall particles being outside the regime that can be addressed in the molecular simulation time step.

The system is simulated for two different wall/fluid interaction energy ratios \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 0.5\) and 1.5 (w: wall and f: fluid), which is a means of estimating the slippage of fluid atoms close to the channels walls [42]. This ratio was also found to be analogous to surface wettability (hydrophobic or hydrophilic wall), as potential energy values reveal wall/fluid attraction for values \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 1.5\) (hydrophilic) and fluid atom repel from the wall when \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 0.5\) (hydrophobic) in [43].

Simulations are held under constant temperature Τ = 1 \({\varepsilon \mathord{\left/ {\vphantom {\varepsilon {k_{B} }}} \right. \kern-0pt} {k_{B} }}\), with the application of Nosé-Hoover thermostats. The simulation step for is Δt = 0.005 τ (τ: in units of \(\sqrt {{{m\sigma^{2} } \mathord{\left/ {\vphantom {{m\sigma^{2} } \varepsilon }} \right. \kern-0pt} \varepsilon }}\)). Simulation begins with fluid atoms given appropriate initial velocities in order to reach the desired temperature (T = 1). The system reaches equilibrium after an equilibrium run of 2 × 106 time steps. Then, a number of NEMD simulations for each channel type are performed, each with duration of 5 × 105 time steps.

2.2 Calculations

We calculate number density and velocity values and present the results in profiles across the channel. Number density and fluid velocity values are evaluated locally at various xz-positions of the channels. To achieve this, the channel is divided into a n × n square grid of bins in the xz-plane (Fig. 1d), with each bin of volume \(V_{bin} = \left( {{{L_{x} } \mathord{\left/ {\vphantom {{L_{x} } n}} \right. \kern-0pt} n}} \right) \times L_{y} \times \left( {{h \mathord{\left/ {\vphantom {h n}} \right. \kern-0pt} n}} \right)\), where n = 48. The bin size in the z-direction is <0.5 σ, ensuring adequate accuracy and smoothness of the results.

Number density is calculated by dividing the average number of particles located in the corresponding bin by the volume of the bin. The number of atoms is calculated during the whole simulation time and the average is

$$N(z) = \frac{{\left\langle {N_{bin} (z,z + h_{bin} )} \right\rangle }}{{N_{f} }}$$
(1)

where, N f : number of fluid atoms in the whole channel, N bin : fluid atoms inside the bin under investigation and h bin the bin height in z-direction. Brackets 〈 〉 denote time averaging.

Fluid velocity values (in the x-direction for the flat- and grooved-wall and in the y-direction for the ribbed-wall channel) averaged in time for every bin is given by

$$u(z) = \frac{{\left\langle {u_{x/y} (z,z + h_{bin} )} \right\rangle }}{N(z)}$$
(2)

The slip length at the solid boundary, L s , is generally calculated from the linear Navier boundary condition as \(L_{s} = {{\upsilon_{w} }/{\left.{\frac{d\upsilon }{dz}} \right|}}_{w} ,\) where the subscript w denotes quantities evaluated at the wall. Due to the existence of grooves/ribs on the upper wall, we first extract the mean velocity profile across the channel and calculated the effective slip length as \(L_{s,eff} = {{\langle \upsilon_{w} \rangle }/{\left.{\frac{d\left\langle \upsilon \right\rangle }{dz}}\right|}}_{w}.\)

The channel diffusion coefficient is obtained from the Einstein’s relation [31]

$$D_{ch} = \mathop {\lim }\limits_{t \to \infty } \frac{1}{2dNt}\left\langle {\sum\limits_{j = 1}^{N} {\left[ {{\mathbf{r}}_{j} (t) - {\mathbf{r}}_{j} (0)} \right]}^{2} } \right\rangle$$
(3)

We also consider the diffusion coefficient as parallel D | (x- and y-direction of the position vector r) and transverse D T (z-direction of the position vector r) to the flow as [44]

$$D^{||} = \frac{{D^{x} + D^{y} }}{2} = \frac{1}{2}\mathop {\lim }\limits_{t \to \infty } \frac{1}{2Nt}\left\langle {\sum\limits_{j = 1}^{N} {\left[ {{\mathbf{r}}_{j}^{x} (t) - {\mathbf{r}}_{j}^{x} (0)} \right]}^{2} + \sum\limits_{j = 1}^{N} {\left[ {{\mathbf{r}}_{j}^{y} (t) - {\mathbf{r}}_{j}^{y} (0)} \right]}^{2} } \right\rangle$$
(4)
$$D^{T} = D^{z} = \mathop {\lim }\limits_{t \to \infty } \frac{1}{2Nt}\left\langle {\sum\limits_{j = 1}^{N} {\left[ {{\mathbf{r}}_{j}^{z} (t) - {\mathbf{r}}_{j}^{z} (0)} \right]}^{2} } \right\rangle$$
(5)

From Eqs. (3–5) we derive that \(D_{ch} = \frac{{D^{x} + D^{y} + D^{z} }}{3} = \frac{{2D^{||} + D^{T} }}{3}\).

In order to have a detailed insight of diffusion in fluid layers adjacent to the wall and estimate the range of wall effect, we consider 9 layers (division in the z-direction) as shown in Fig. 1d and calculate the local diffusion coefficients for each layer as

$$D_{lay}^{||} = \frac{1}{2}\mathop {\lim }\limits_{t \to \infty } \frac{1}{{2N_{lay} t}}\left\langle {\sum\limits_{j = 1}^{N} {\left[ {{\mathbf{r}}_{j}^{x} (t) - {\mathbf{r}}_{j}^{x} (0)} \right]}^{2} + \sum\limits_{j = 1}^{N} {\left[ {{\mathbf{r}}_{j}^{y} (t) - {\mathbf{r}}_{j}^{y} (0)} \right]}^{2} } \right\rangle$$
(6)
$$D_{lay}^{T} = \mathop {\lim }\limits_{t \to \infty } \frac{1}{{2N_{lay} t}}\left\langle {\sum\limits_{j = 1}^{N} {\left[ {{\mathbf{r}}_{j}^{z} (t) - {\mathbf{r}}_{j}^{z} (0)} \right]}^{2} } \right\rangle$$
(7)

From Eqs. (6, 7) we derive that \(D_{lay} = \frac{{2D_{lay}^{||} + D_{lay}^{T} }}{3}.\)

Shear viscosity and thermal conductivity are usually calculated using the Green–Kubo formalism, as described in [29], for systems at or close to equilibrium. Apart from GK relations, shear viscosity can be also calculated by NEMD methods, which take into account the induced strain rates in a confined channel [33].

Diffusion coefficient, as long as fluid atom trajectories can be mapped in a simulation system, is computationally expensive to define, but, on the other hand, calculations are straightforward. This is not the case, however, for shear viscosity and thermal conductivity. Both GK and NEMD methods can be difficult to obtain, with increased computational burden, and calculations can be imprecise when high strain rates and complex channel architectures are present [32]. Giannakopoulos et al. [41] proposed a linking scheme that connects transport properties of fluids. For flat-wall channels, if we know the values of the diffusion coefficient, then we can obtain channel shear viscosity η s,ch through the well-known relations

$$D_{ch} = \frac{{k_{\rm B} {\rm T}}}{{6\pi \eta_{s,ch} \sigma }}\,\left( {\text{Stokes}{-}\text{Einstein}} \right)$$
(8)
$$D_{ch} = \frac{{k_{\rm B} {\rm T}}}{{4\pi \eta_{s,ch} \sigma }}\,\left( {\text{Sutherland}} \right)$$
(9)

The Sutherland relation was found as a good estimate for channels of height \(h > 20\;\sigma ,\) while the Stokes–Einstein is a good estimate for \(h < 20\;\sigma ,\) as also seen in [40] where results obtained from this estimate where compare to results obtained from molecular dynamics simulation. Simulations held in this work incorporate channels of h = 18.58 σ, so the Stokes–Einstein relation is used for shear viscosity calculation. In a layer manner, for the same channel division used in layer diffusion coefficient calculations, local shear viscosity is

$$\eta_{s,lay} = \frac{{k_{\rm B} {\rm T}}}{{6\pi \text{D}_{lay} \sigma }}$$
(10)

Based on the GK method, as presented in [29] and applied in flat-wall nanochannels in [31], the channel thermal conductivity λ is calculated by the integration of the time-autocorrelation function of the microscopic heat flow \(J_{q}^{x} ,\) i.e.,

$$\lambda = \frac{1}{{Vk_{B} T^{2} }}\int\limits_{0}^{\infty } {dt\left\langle {J_{q}^{x} (t) \cdot J_{q}^{x} (0)} \right\rangle }$$
(11)

where the microscopic heat flow \(J_{q}^{x}\) is given by

$$J_{q}^{x} = \frac{1}{2}\sum\limits_{i = 1}^{N} {m_{i} } (\upsilon_{i} )^{2} \upsilon_{i}^{x} - \sum\limits_{i = 1}^{N} {\sum\limits_{j > 1}^{N} {\left[ {r_{ij}^{x} :\frac{{\partial u({\mathbf{r}}_{ij} )}}{{\partial r_{ij}^{x} }} - {\mathbf{I}} \cdot u({\mathbf{r}}_{ij} )} \right] \cdot \upsilon_{i}^{x} } }$$
(12)

where \(\upsilon_{i}\) is the speed velocity magnitude of atom i and \({\mathbf{I}}\) is the unitary matrix. For layer calculations,

$$\lambda_{lay} = \frac{1}{{V_{lay} k_{B} T^{2} }}\int\limits_{0}^{\infty } {dt\left\langle {J_{q,lay}^{x} (t) \cdot J_{q,lay}^{x} (0)} \right\rangle }$$
(13)

and

$$J_{q,lay}^{x} = \frac{1}{2}\sum\limits_{i = 1}^{{N_{lay} }} {m_{i} \left( {\upsilon_{i} } \right)^{2} \upsilon_{i}^{x} } - \sum\limits_{i = 1}^{{N_{lay} }} {\sum\limits_{j > 1}^{{N_{lay} }} {\left[ {r_{ij}^{x} :\frac{{\partial u\left( {{\mathbf{r}}_{ij} } \right)}}{{\partial r_{ij}^{x} }} - {\mathbf{I}} \cdot u\left( {{\mathbf{r}}_{ij} } \right)} \right] \cdot \upsilon_{i}^{x} } }$$
(14)

3 Results and discussion

3.1 Number density, velocity and slip length

Number density profiles of liquid argon in various nanochannels are presented in Fig. 2. We consider three channel types; channel with ribbed walls (y- flow direction), channel with grooves (x- flow direction) and flat-wall channel for comparison. For every channel type, we examine two wall/fluid interactions, \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 1.5,\) which is analogous to hydrophilic wall behavior, and \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 0.5,\) which is analogous to hydrophobic wall behavior.

Fig. 2
figure 2

Channel number density profiles. Solid lines are a guide for the eye. Bin number is shown in z-axis, starting from 0 (lower wall)

Full size image

Argon Poiseuille flow in a flat-wall channel presents increased fluid ordering in layers adjacent to the walls, while it is constant in the channel interior, symmetrical with respect to the channel mid-plane. The fluid density peak values decrease as \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }}\) decreases, corresponding to less fluid atom localization past an hydrophobic wall. Similar behavior is observed for ribbed- and grooved-wall channels, with lower ordering peaks near the grooves. We observe, however, that groove orientation does not affect number density. Another point worth mentioning is that the presence of wall grooves, ribs and the effect of either hydrophobic (repelling) or hydrophilic (attractive) wall, seem to affect number density even at the center of the channel. All hydrophobic channels present variation (increase) of number density in the middle, since fluid particles are “pushed” away from the walls. We emphasize that the variation of number density does not mean that we change thermodynamic states between simulations, as fluid density is the same for all cases investigated here \(\left( {\rho = 0.642\,\sigma^{ - 3} } \right).\)

Velocity profiles for all cases investigated are presented in Fig. 3. At first sight, we observe that an effective means of facilitating fluid flow in nanochannels is wall hydrophobicity, as, for a flat-wall channel, we obtain the maximum velocity value when \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 0.5,\) while velocity values are also greater for the grooved- and ribbed-wall channels when \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 0.5\) than they are for \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 1.5.\) However, the presence of grooves on channel walls slows down velocity values, compared to the flat-wall case.

Fig. 3
figure 3

Channel velocity profiles. Solid lines are a guide for the eye. Values shown in reduced LJ units \(\sigma /\tau\)

Full size image

A significant difference between a grooved- and a ribbed-wall channel velocity profile is the existence of asymmetry in a grooved-wall channel; the profile is asymmetric to the channel centerline. This is attributed to the fact that grooves introduce an asymmetry to the flow, which is more pronounced for the hydrophilic cases, as the effect of the walls on fluid atoms extends over a greater range (see potential maps in [43]). Wall ribs do not seem to induce any kind of asymmetry. Moreover, we observe that, for the same \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }}\) value, in the region close to the grooved wall, velocity profile for the ribbed-wall channel approaches closer to the wall and presents greater values compared to the grooved-wall channel. We attribute this behavior to fluid atom trapping inside the grooves when the flow is in transverse direction to the grooves [43], which is not possible when the grooves are in longitudinal direction (ribs).

Fluid atoms are trapped for a significant amount of time inside rough wall grooves as it can be shown from the calculated average time that atoms remain inside cavity regions. In Fig. 4 we present a representative trajectory for two liquid atoms: one trapped in the cavity region and one in the main flow region.

Fig. 4
figure 4

Two characteristic fluid atom trajectories in the xz-plane (x * and z * are in reduced units), where trapping inside the wall grooves is shown

Full size image

The effective slip length calculation is shown in Fig. 5. We point out that L s,eff is about 15 % greater for the ribbed-wall channel compared to grooved- and flat-wall channels. This effect is multiplied when \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 0.5\) (hydrophobic behavior), providing slip increase for the ribbed-wall of about 15 % towards the grooved-wall and about 90 % towards the flat-wall channel. Similar results (theoretical and experimental) have been reported in Cao et al. [45], where a nanostructured surface, when combined with an hydrophobic behavior, gives a super-hydrophobic wall, and Maynes et al. [46], where they correlate slip length behavior near a rough wall to the significant reduction in the surface contact area between the flowing liquid and the solid wall due to the nonpenetration of the liquid meniscus into the cavity regions, and, as a result, a dramatic decrease in the overall flow resistance is possible. On the other hand, a contradicting result has been found in Yang [47], where it is noted that the fluid molecules flowing over a rough surface (both hydrophobic and hydrophilic, for various geometrical characteristics of wall roughness) lose more tangential momentum than the smooth surfaces, resulting in the reduction of slip length, while in [48], the effective slip length decreases when interfacial roughness increases. Both findings do not agree to the work of Ou et al. [49] for drag reduction in ultra hydrophobic surfaces and this is attributed to different pressure conditions.

Fig. 5
figure 5

Effective slip length bar-plot

Full size image

In our study, conclusively, the important finding from slip length calculations is that we can accelerate surface slippage by employing ribs on the channel wall rather than grooves, as was also revealed in Priezjev et al. [27], although for different channel models. Furthermore, wall wettability effect is stronger compared to roughness for the cases shown here, as also pointed out in [28].

3.2 Transport properties

Diffusion coefficient calculations in layers across the channel are shown in Fig. 6a. For the flat- and hydrophobic-wall channel, the diffusion coefficient increases at the two fluid layers near the wall and is constant, about 15 % smaller, in the remaining channel layers. Opposite behavior is observed for the flat-, hydrophilic-wall channel, where the diffusion coefficient at the first fluid layer near the wall has almost half value than it has in the remaining internal channel layers. This behavior is attributed to limited fluid mobility in layers adjacent to an hydrophilic wall (\({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 1.5\)), as was also shown in the flat-wall velocity profiles in Fig. 3.

Fig. 6
figure 6

Diffusion coefficient in a layer average value, b layer, parallel to the flow (xy-direction) and c layer, transverse to the flow (z-direction). Dotted lines are guide to the eye. Values shown in reduced LJ units \(\frac{{\sqrt {{m \mathord{\left/ {\vphantom {m \varepsilon }} \right. \kern-0pt} \varepsilon }} }}{\sigma }\)

Full size image

As for the rough-wall channels, the diffusion coefficients are rather constant and of the same value across the channel (from lower flat wall to channel layers near the grooves/ribs) for \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 0.5.\) However, at the adjacent to the rough wall layer, the ribs have slightly decreasing D lay value compared to the grooves. For \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 1.5,\) the diffusion coefficients behavior are similar to those in a flat-wall channel, with small values at the adjacent to wall layers and bulk values in channel interior. Wall wettability has a prominent effect on diffusion coefficients compared to roughness, while ribs and grooves have almost similar effect on their values. We attribute this behavior to the rather small protrusion height (g h  = 1.9 σ) in our investigations, which is overstepped by the strong wall/fluid interaction.

We have to point out that diffusion coefficient values are different at the channel layer adjacent to the lower flat wall and the lower side (also flat) of the upper grooved/ribbed wall (this is also observed in calculated shear viscosity and thermal conductivity values that follow). We believe that this is a result of the modification of the wall/fluid interactions and fluid atom trapping near the rough wall [43].

The diffusion coefficient variations across the channel can be clearly revealed when we investigate the behavior in parallel and transverse direction to the flow and their participation in the overall diffusion coefficient value. We present parallel diffusion coefficient values \(D_{lay}^{||}\) in Fig. 6b. In a general view, it is shown that \(D_{lay}^{||}\) near the walls are greater than their respective average \(D_{lay}\) values shown in Fig. 6a for hydrophobic channels. Hydrophobicity, as a wall parameter, enhances diffusivity towards the direction of the flow, as fluid atoms are not attracted by wall particles and are “free” to diffuse. In other words, an hydrophobic wall leads in diffusion coefficient anisotropy in fluid layers adjacent to the wall. The hydrophilic wall does not seem to affect \(D_{lay}^{||} .\)

The investigation of diffusion coefficient for all hydrophilic channel cases in the transverse to the flow direction, \(D_{lay}^{T}\) (see Fig. 6c), reveals no anisotropy in channel layers away from the walls and, in general, it does not differ much from the respective \(D_{lay}^{||}\) values. The impact of hydrophobicity, though, is significant in a way that \(D_{lay}^{T}\) is smaller than \(D_{lay}^{||}\) close to the wall, which is expected because of the confinement, as the wall acts as a barrier in z-direction.

In order to have a view of diffusion coefficients as channel properties, we present their calculated values in Table 1. In a previous work [31] we found that strong anisotropy is present in calculated diffusion coefficient values for channels of height less than \(h \approx 10\;\sigma.\) Isotropic diffusion was found at h = 18.58 σ (for \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }} = 1.2,\) slightly hydrophilic). Now, we observe that wall/fluid interaction that resembles a hydrophobic surface, adds anisotropy in channels of height h = 18.58 σ, no matter if the upper wall is flat or rough. This anisotropy is calculated about 7–8 % for hydrophobic walls and 3–4 % for hydrophilic ones. No significant difference is observed in the comparison between a ribbed- and a grooved-wall channel, implying that groove orientation does not have an effect on system dynamics related to mass transfer.

Table 1 Average channel diffusion coefficient, in reduced LJ units \(\frac{{\sqrt {{m \mathord{\left/ {\vphantom {m \varepsilon }} \right. \kern-0pt} \varepsilon }} }}{\sigma }\)
Full size table

Shear viscosity results are summarized in Fig. 7. We stress that, in a qualitative manner, shear viscosity profiles for hydrophobic grooved/ribbed-wall channels are almost constant across the channels we investigated here and slightly increase close to the rough wall. However, in a flat-wall hydrophobic channel, fluid atoms adjacent to the flat wall present smaller shear viscosity values than the channel interior. This is evidence that flat, hydrophobic walls facilitate fluid flow at the boundary, while roughness might lead to stick effects on the walls, as stated in [47]. This is not the case for strong wall/fluid interaction (hydrophilic wall). Shear viscosity increases at the layer adjacent to the lower wall, and does not differ significantly either in flat, ribbed or grooved channels. Maximum shear viscosity values are obtained near the rough wall in all hydrophilic nanochannels, while channel interior values are almost similar for all channel geometries investigated here.

Fig. 7
figure 7

Shear viscosity in layer average value. Dotted lines are guide to the eye. Values shown in reduced LJ units \({{\sigma^{2} } \mathord{\left/ {\vphantom {{\sigma^{2} } {\sqrt {m\varepsilon } }}} \right. \kern-0pt} {\sqrt {m\varepsilon } }}\)

Full size image

Figure 8 present layer values for thermal conductivity calculated from Eq. (13). Thermal conductivity values for all channels investigated vary across the channel, as also shown in [31], where we found that that λ is significantly smaller near the flat channel walls, compared to the channel interior. The effect of wall wettability is pronounced in flat-wall channels, as thermal conductivity values are increasing in a hydrophobic channel compared to a hydrophilic one. This trend also persists in cases of flow in grooved- wall channels, at least in channel region away from the upper rough wall. We observe decreased thermal conductivity values in channel layers adjacent and inside the grooves. This is attributed to fluid atom trapping inside the grooves, as fluid atom velocities slow-down at this region resulting lower heat transfer. A ribbed-wall channel presents asymmetry in thermal conductivity profiles, with hydrophobic values being slightly larger compared to hydrophilic. In this case, it seems that the effect of the ribs is more important than that of wall wettability.

Fig. 8
figure 8

Thermal conductivity in layer average value. Dotted lines are guide to the eye. Values shown in reduced LJ units \({{\sigma^{2} } \mathord{\left/ {\vphantom {{\sigma^{2} } {kB}}} \right. \kern-0pt} {kB}}\sqrt {m/\varepsilon }\)

Full size image

If we consider channel average thermal conductivity values (see Table 2), we conclude that flows over hydrophobic walls (at least in the range examined here) enhance heat transfer compared to flows over hydrophilic walls. Moreover, a ribbed-wall channel presents greater λ ch values compared to flat- and grooved-wall channels.

Table 2 Average channel thermal conductivity, in reduced LJ units \({{\sigma^{2} } \mathord{\left/ {\vphantom {{\sigma^{2} } {kB}}} \right. \kern-0pt} {kB}}\sqrt {m/\varepsilon }\)
Full size table

4 Conclusions

Nanoscale MD simulations were performed for channels with various roughness patterns and wall/fluid interactions in order to extract flow and transport properties of a simple monoatomic liquid. The most important findings are:

  1. 1.

    Fluid number density for ribbed- and grooved-wall channels presents similar ordering, indicating that groove orientation does not affect number density.

  2. 2.

    The presence of grooves on channel walls slows down velocity values, however, flows over a ribbed-wall channel present greater velocity values compared to the grooved-wall channel, which, furthermore, present velocity profile asymmetry.

  3. 3.

    Surface slippage is maximized by fluid flow in longitudinal compared to transverse direction of the grooves and increased wall wettability ratio \({{\varepsilon_{w} } \mathord{\left/ {\vphantom {{\varepsilon_{w} } {\varepsilon_{f} }}} \right. \kern-0pt} {\varepsilon_{f} }}\).

  4. 4.

    A hydrophobic surface adds anisotropy in diffusion coefficient values, no matter if the upper wall is flat or rough. This anisotropy is calculated about 7–8 % for hydrophobic walls and 3–4 % for hydrophilic ones. Diffusion coefficients do not differ significantly either in ribbed- or in grooved-wall channel flows.

  5. 5.

    Due to small values on shear viscosity calculations, we conclude that flat, hydrophobic walls facilitate fluid flow, but, in contradistinction, hydrophobic grooved or ribbed walls present larger shear viscosity values. Maximum shear viscosity values are obtained near the rough wall in grooved, hydrophilic nanochannels.

  6. 6.

    Thermal conductivity calculations reveal small values near the channel walls and wall grooves or ribbs and significantly larger near the channel centerline. Wall ribs also seem to enhance heat transfer, as depicted by the increased λ lay values, while thermal conductivity is decreased in a grooved-wall channel due to fluid atom sticking inside and near the grooves. In bulk channel values, flows over hydrophobic walls present greater λ ch values compared to flows over hydrophilic walls.

All above findings can be encapsulated in fluid dynamics theory, for both fundamental research and technological guidance, in order to be able to describe in detail fluid behavior at the nanoscale.