1 Introduction

Attention has grown in the last decades on the nanoscale regime of fluid mechanics as the scientific community re-investigates the classical theory and tries to bridge models at different scales, in order to understand the complex mechanisms involved in solid/fluid interactions. Theoretical and experimental studies in fields such as carbon dioxide separation, drug delivery, friction and lubrication, membrane science, water desalination and purification, have been embedded in innovative technological applications (Bernardo et al. 2009; Gargiuli et al. 2006; Grannick 1991; Kleinstreuer et al. 2008; Noy et al. 2007; Walther et al. 2013; Asproulis et al. 2012). However, there are still numerous ambiguities to be resolved as far as the limits of applicability of classical theory on micro- and nanoflows are concerned.

For pipe flows, as dimensions decrease dramatically, the impact of surface roughness is significant. Moody’s diagram (Moody 1944) is a point of reference, as a convenient method of determining the pressure drop in macroscopic pipe flows and has been extended to conduits of non-circular cross-section. In the analysis by Kandlikar et al. (2005), suggestions are made to the extension of the Moody diagram by incorporating three additional geometrical parameters of roughness. Herwig et al. (2008) tried to provide a theoretical background to the well-established experimental measurements (Nikuradse 1933) that constitute most of the information incorporated in the diagram. In the work of Valdés et al. (2007, 2008) a numerical model is proposed, where wall roughness is substituted by appropriate factors embedded in a respective smooth (flat-wall) channel.

The effect of surface roughness on micro- and nanoflows has been studied extensively over the last decade, mainly because of the finding, in both theoretical studies and experimental proves, that the classical hypothesis of the no-slip condition breaks down when downsizing to the micro/nanoscale. Davies et al. (2006) showed that, under specific rough-wall characteristics, significant reductions in the frictional pressure drop and greater effective fluid slip at the walls can be achieved relative to the classical smooth channel Stokes flow. Priezjev (2007) noticed that slip length reduces by periodic and random surface roughness, compared to atomically smooth rigid walls, while in Sofos et al. (2012) it is observed that roughness geometrical characteristics could affect slip length values, through fluid atom trapping inside the grooves. Wall roughness is also induced by wall particle oscillating frequencies and, along with wall mass; it is found to connect with slip length (Asproulis and Drikakis 2011). Experimental work reveals how large surface roughness must be to produce the no-slip boundary condition (Zhu and Granick 2002), while in Tretheway and Meinhart (2002) it is noted that fluid slip exists at small scales under the limit of 1 mm.

The effect of surface characteristics on flows is not only limited to roughness. Terms like super- or ultra-hydrophobic surfaces have been incorporated in order to describe hydrophobic surfaces (and rough at the same time) where the contact angle, θ, is greater than 150° (Cao et al. 2011). It is also noted that the slip length can be considered as a quantity used to quantify hydrophobicity at the micro- or nanoscale (Voronov et al. 2006; Koplik and Banavar 2006); however, for super-hydrophobic surfaces, hydrophobicity and roughness have a coupled effect (Sbragaglia et al. 2006). In Maynes et al. (2007), a dramatic decrease in the overall flow resistance is observed due to reduction in the surface contact area between the flowing liquid and the solid (hydrophobic, patterned) wall. Ybert et al. (2007) presented a method of calculating frictional properties of super-hydrophobic surfaces as a function of the generic geometrical parameters of the surface and showed that very large slip lengths can be obtained for an ultra-hydrophobic surface (θ ≈ 180°).

However, the contact angle θ is not sufficient to infer the amount of slip. For example, it was shown that there are cases where strongly super-hydrophobic fractal-patterned surfaces may be not efficient in terms of drag reduction (Cottin-Bizonne et al. 2012). The effect of the size and geometrical characteristics of wall protrusions, wall wettability and wall stiffness on nanochannel flows is intensified by the channel width, h, which is the main parameter that controls how close or far from the continuum regime we are.

In the present work, we calculate the Darcy–Weisbach friction factor, f, based on data compiled from molecular dynamics simulations. We focus mainly: (a) on how wall hydrophobicity/hydrophilicity affects f and (b) on quantifying the effect of wall roughness on f. Dimensional analysis is applied in order to derive correlations for the friction factor. The results show that construction of Moody-like diagrams is possible in the case of nanochannels, provided that some appropriate modifications related to the scale characteristics are taken into account. Furthermore, the clustering of the computed friction factor values allows us to delineate the rough-wall regime from the grooved-wall regime, at least for the particular idealized form of orthogonal wall protrusions studied in the present work. Our investigation could also serve as an intermediate step toward a hybrid (atomistic and continuum) simulation design (Asproulis and Drikakis 2013; Kalweit and Drikakis 2010).

2 Theoretical relations and modeling

2.1 Molecular dynamics simulations

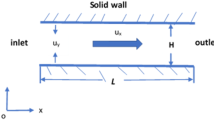
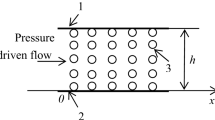
The Lennard-Jones (LJ) 12-6 type potential, \(u^{\text{LJ}} (r_{ij} ) = 4\varepsilon \left[ {(\sigma /r_{ij} )^{12} - (\sigma /r_{ij} )^{6} } \right]\), is widely used to describe interatomic interaction within the non-equilibrium molecular dynamics (NEMD) method. Monoatomic LJ particles (argon) are incorporated for walls and fluid, with \(\sigma_{\text{f}} = \sigma_{\text{w}} = \sigma\) = 0.3405 nm, \(\varepsilon_{\text{f}} /k_{\text{B}} = \varepsilon_{\text{w}} /k_{\text{B}} = \varepsilon /k_{\text{B}}\) = 119.8 Κ, fluid density \(\rho_{\text{f}}\) = 1078 kg/m3 and wall density \(\rho_{\text{w}}\) = 1477 kg/m3. The simulation cell resembles a flat-wall nanochannel (Fig. 1), which is equivalent to macroscopic Poiseuille flow. The system is periodic along the x- and y-directions, while the distance, h, between the two walls is examined for h = 3.15 and 6.3 nm, i.e., 9.3 and 18.6σ, respectively. The respective hydraulic diameter is \(D_{\text{h}} = 2h\).

Fig. 1
figure 1

Model of flat-wall and rough-wall nanochannel

Full size image

We also investigate monoatomic LJ liquid flow in rough-wall simulation cells (Fig. 1), with periodic grooves of various length and height, h l and h d, respectively. The simulation cases studied here involve roughness length \(h_{l} = 1.8\;{\text{nm}}\) and various roughness heights, \(0.6 \le h_{\text{d}} \le 1.96\,{\text{nm}}\), which correspond to \(h_{\text{d}}\) = 5–20 %h. We choose the theoretical channel width as \(h_{\text{av}} = h - h_{\text{d}} /2\), so the hydraulic diameter is \(D_{\text{h}} = 2h_{\text{av}} = 2h - h_{\text{d}}\). A qualitative wall wettability parameter representing hydrophobic or hydrophilic behavior is \({{\varepsilon_{\text{wall}} } / {\varepsilon_{\text{fluid}} }}\) (from now on, \({{\varepsilon_{\text{w}} } /{\varepsilon_{\text{f}} }}\)). We investigate wall wettability effect over the range \({{0.1 < \varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }} < 1.0\).

The wall/fluid interaction is a means of characterizing the degree of wall wettability. In Cao et al. (2009), wettability is characterized by the contact angle θ (taken from Young’s Law, \(\cos \theta = - 1 + 2\frac{{\rho_{\text{S}} c_{\text{LS}} }}{{\rho_{\text{L}} c_{\text{LL}} }}\), where ρ is density and subscripts S and L indicate solid wall and fluid, respectively) which, in turn, depends on a constant c embedded in the original LJ equation, \(u^{\text{LJ}} (r_{ij} ) = 4\varepsilon ((\sigma /r_{ij} )^{12} - c(\sigma /r_{ij} )^{6} )\). In Voronov et al. (2006), by varying the relative energy parameter \(\varepsilon_{\text{r}} = \varepsilon_{\text{wf}} /\varepsilon_{\text{f}}\), the authors change the wall affinity from hydrophilic (large e r) to hydrophobic (small e r), and this is analogous to the contact angle change. Our method is similar to Voronov et al. (2006), where if Lorentz–Berthelot rule applies, then \(\varepsilon_{\text{r}} = \varepsilon_{\text{wf}} /\varepsilon_{\text{f}} = {{\sqrt {\varepsilon_{\text{w}} \cdot \varepsilon_{\text{f}} } } / {\varepsilon_{\text{f}} }} = \sqrt {\frac{{\varepsilon_{\text{w}} }}{{\varepsilon_{\text{f}} }}}\). Furthermore, in Sofos et al. (2012), potential energy contours near the walls show that a large \({{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}\) ratio leads in increased fluid atom presence near the walls (hydrophilic wall), while a small \({{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}\) ratio leads in decreased fluid atom presence near the walls (hydrophobic wall).

Wall atoms are bound on fcc (101) sites and remain fixed to their original positions due to the effect of an elastic spring force \({\mathbf{F}} = - K({\mathbf{r}}(t) - {\mathbf{r}}_{\text{eq}} )\), where r(t) is the vector position of a wall atom at time t, r eq is its initial lattice position vector, and K = 0.816 N/m, the wall spring constant. An external driving force \(f_{\text{ext}}\) is applied along the x-direction to every fluid particle during the simulation, with magnitude ranging from 0.009 to 0.045 pN. A Nosé–Hoover thermostat scheme is applied independently to each thermal wall to keep fluid temperature constant to T = 120 K.

2.2 Theoretical relations

The relation giving the Darcy–Weisbach friction factor is

$$f = \frac{{\left( {\frac{{\Delta p}}{L}} \right)D_{\text{h}} }}{{\frac{1}{2}\rho v^{2} }}$$
(1)

where ρ is the mass density, Δp denotes the pressure drop along a channel segment of length L, v is the average fluid velocity at a channel cross-section and D h the hydraulic diameter. If \(\rlap{--} V\) denotes the volume inside the channel and M the total mass between two successive channel cross-sections, then

$$f = \frac{{\left( {\frac{{{\varDelta }p}}{L}} \right){\rlap{--} V}D_{\text{h}} }}{{\frac{1}{2}Mv^{2} }}$$
(2)

For fluid flows at the nanoscale, it is common to use periodic conditions for the channel in order to simulate the flow. The flow is driven not by a pressure difference Δp, but by an external force f ext applied to each of the N fluid particles in the atomistic model. Consequently, \(Nf_{\text{ext}} \leftrightarrow (\Delta p)A\), where A is the cross-sectional area. Equation (2) now becomes

$$f = \frac{{Nf_{\text{ext}} \left( {\frac{1}{A}\frac{{\rlap{--} V}}{L}} \right)D_{\text{h}} }}{{\frac{1}{2}Mv^{2} }}$$
(3)

We note that \(\frac{{\rlap{--} V}}{AL} \approx 1\), so Eq. (3) becomes

$$f = \frac{{f_{\text{ext}} D_{\text{h}} }}{{\frac{1}{2}\left( {\frac{M}{N}} \right)v^{2} }}$$
(4)

and by substituting the particle mass \(m = {M / N}\) we obtain

$$f = \frac{{f_{\text{ext}} D_{\text{h}} }}{{\frac{1}{2}mv^{2} }}$$
(5)

so that the friction factor can be calculated based on MD simulation parameters

The Reynolds number is defined here as

$$Re = \frac{{vD_{\text{h}} }}{\nu }$$
(6)

or

$$Re = \frac{{vD_{\text{h}} }}{\mu /\rho }$$
(7)

where ν is the coefficient of kinematic viscosity and μ the coefficient of shear viscosity.

Shear viscosity in nanochannels can be calculated by Green–Kubo (Sofos et al. 2009) or NEMD (Delhommelle et al. 2004; Sofos et al. 2010) relations. Green–Kubo methods are mainly used in systems close to or at equilibrium state, and they do not take into account the induced strain rates, while NEMD methods do. The Green–Kubo formula for shear viscosity μ GK is

$$\mu_{\text{GK}} = \frac{1}{{\rlap{--} Vk_{\text{B}} T}}\int\limits_{0}^{\infty } {{\text{d}}t\left\langle {{\mathbf{J}}_{\text{p}}^{xz} (t) \cdot {\mathbf{J}}_{\text{p}}^{xz} (0)} \right\rangle }$$
(8)

where \({\mathbf{J}}_{\text{p}}^{xy}\) is the off-diagonal component of the microscopic stress tensor

$${\mathbf{J}}_{\text{p}}^{xz} = \sum\limits_{i = 1}^{N} {m_{i} v_{i}^{x} v_{i}^{z} } - \sum\limits_{i = 1}^{N} {\sum\limits_{j > 1}^{N} {r_{ij}^{x} \frac{{\partial u(r_{ij} )}}{{\partial r_{ij}^{z} }}} }$$
(9)

Shear viscosity μ NEMD computed by NEMD methods is

$$\mu_{\text{NEMD}} = \mathop {\lim }\limits_{{F_{{{\text{ext}} \to 0}} }} \left[ { - \frac{{\left\langle {J_{xz} } \right\rangle }}{{\dot{\gamma }}}} \right]$$
(10)

where the strain rate \(\dot{\gamma }\) is

$$\dot{\gamma } = \frac{{\partial {\text{v}}_{x} }}{\partial z}$$
(11)

However, there are cases where other methods have been employed. In Markesteijn et al. (2012) and Koplik et al. (1988), a method based on curve fitting that connects the MD with the continuum velocity profile is proposed, while continuum relations have been employed in Giannakopoulos et al. (2012), Ohara and Suzuki (2001), Ritos et al. (2014) and Thomas and McGaughey (2007). If the diffusion coefficient is known, equation

$$D = \frac{{k_{\text{B}} T}}{\alpha \pi \mu \sigma }$$
(12)

relates D, μ and σ. Our results suggest that Eq. (12) can be used with constant α = 6 for channels of width below h = 5 nm (lower bound, known as the Einstein equation), and α = 4 (upper bound, known as the Sutherland equation) for about h > 5 nm. Equation (12) showed excellent agreement to our Green–Kubo calculations on shear viscosity (Giannakopoulos et al. 2012).

In previous works (Sofos et al. 2009, 2010), we employed diffusion coefficient calculations based on Einstein’s relation

$$D_{{}} = \mathop {\lim }\limits_{t \to \infty } \frac{1}{6Nt}\left\langle {\sum\limits_{j = 1}^{N} {\left[ {{\mathbf{r}}_{j} (t) - {\mathbf{r}}_{j} (0)} \right]}^{2} } \right\rangle$$
(13)

The combination of Eqs. (12, 13) is used in this work for shear viscosity calculations in order to avoid complications coming from the induced strain rates due to various rough-wall channel geometries and hydrophobic/hydrophilic wall/fluid interactions.

2.3 Dimensional analysis

The energy loss per unit mass, H loss, depends on the average cross-sectional velocity, v, the channel geometrical characteristics (h and h d, or, equivalently D h), the fluid properties (ρ, μ), as well as the atomistic model parameters (ε w, ε f, σ w, σ f, K*, r c). Simulation evidence supports the assumption that ε w, ε f are the most important atomistic parameters affecting H loss in nanochannels, i.e., our starting point is that there exists a functional relation of the form.

$$H_{\text{loss}} = g(v,D_{\text{h}} ,h_{\text{d}} ,\rho ,\mu ,\varepsilon_{\text{w}} ,\varepsilon_{\text{f}} )$$
(14)

for the flows considered in this work.

A straightforward application of dimensional analysis of Eq. (14) yields five independent dimensionless groups: \(\varPi_{1} = H_{\text{loss}} \frac{{2D_{\text{h}} }}{{Lv^{2} }} = f\), \(\varPi_{2} = \frac{{vD_{\text{h}} }}{v} = \frac{{\rho vD_{\text{h}} }}{\mu } = Re\), \(\varPi_{3} = \frac{{h_{\text{d}} }}{h}\), \(\varPi_{4} = \frac{{\varepsilon_{\text{w}} }}{{v^{2} D_{\text{h}}^{ 3} \rho }}\), \(\varPi_{5} = \frac{{\varepsilon_{\text{f}} }}{{v^{2} D_{\text{h}}^{3} \rho }}\), where f is the Darcy–Weisbach friction factor and Re is the Reynolds number. Consequently,

$$f = \hat{G}\left( {Re,\frac{{h_{d} }}{{D_{h} }},\varPi_{4} ,\varPi_{5} } \right)$$
(15)

or equivalently

$$f = \bar{G}\left( {Re,\frac{{h_{\text{d}} }}{{D_{\text{h}} }},\frac{{\varepsilon_{\text{w}} }}{{\varepsilon_{\text{f}} }},\varPi_{5} } \right)$$
(16)

where \(\frac{{\varepsilon_{\text{w}} }}{{\varepsilon_{\text{f}} }} = \frac{{\varPi_{4} }}{{\varPi_{5} }} = \varPi_{\varepsilon }\).

We drop Π 5 in favor of \(\varPi_{\varepsilon } = \frac{{\varepsilon_{\text{w}} }}{{\varepsilon_{\text{f}} }}\) as being more relevant and important dimensionless parameter in our analysis. Consequently, in the remainder of the paper we work with the non-dimensional functional relation

$$f = G\left( {Re,\frac{{h_{\text{d}} }}{{D_{\text{h}} }},\frac{{\varepsilon_{\text{w}} }}{{\varepsilon_{\text{f}} }}} \right)$$
(17)

3 Calculated results

3.1 Shear viscosity

Figure 2 displays shear viscosity values over each flow parameter investigated. Shear viscosity decreases as the channel width increases and has its bulk value at the h = 6.3 nm channel. Calculated shear viscosity values for argon presented here are in good agreement with values reported in the literature for flat-wall channels (Ashurst and Hoover 1975; Ohara and Suzuki 2001; Pas and Zwolinski 1991).

Fig. 2
figure 2

Shear viscosity values investigated versus the effect of various parameters, such as channel height, wall wettability ratio, and roughness height. Each parameter on the horizontal axis is normalized to its maximum value for presentation reasons

Full size image

The diagram reveals a monotonic increase in shear viscosity past a wall with increased hydrophilicity. On the other hand, hydrophobic walls give rise to lower shear viscosity values, which is in agreement with slip length calculations in the literature, where a viscosity layer adjacent to the wall exists and correlates with slippage over a hydrophobic surface (Vinogradova 1995; Cao et al. 2009; Myers 2011).

We also report increasing shear viscosity values as wall groove height increases from 5 to 20 %h (for the h = 6.3 nm channel) as expected, since, practically, an increase in h d resembles a channel width decrease.

3.2 Friction factor

In Fig. 3a, we present a fully logarithmic plot of f versus Re for two flat-wall channels, of width h = 3.15 nm and h = 6.3 nm. The two channels are investigated for the same values of the dimensionless group Π ε  = \({{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}\). We observe that the data points are well organized in power-law curves for each wettability ratio. No channel size effect is observed, as one would expect based on our dimensional analysis arguments. A power-law least-squares approximation of the form \(f = bRe^{a}\) represents the data very well. The value of parameter a is very close to −1, and consequently, a correlation of the form \(f = \frac{b}{Re}\) approximates data fairly good. Such an approximation would lead to the conclusion that the constancy of Poiseuille number, that holds for laminar flow in macrochannels, is also valid in the case of nanochannel flows, provided that b is now understood as depending on \({{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}\). However, we restrain from adopting this approximation (here and in the remainder of the paper) in order to report only the best approximations (in the least-squares sense) to our computed values of friction factor.

Fig. 3
figure 3

a Friction factor \(f\) for two flat-wall channels of width h = 3.15 and 6.3 nm for various \(\varepsilon_{w} /\varepsilon_{f}\) ratios. Filled symbols represent h = 3.15 nm and empty symbols h = 6.3 nm data points. Lines are power-law least-squares fits, b correlation of parameter b with wettability parameter \(\sqrt {{{\varepsilon_{w} } / {\varepsilon_{f} }}} = {{\varepsilon_{wf} } / {\varepsilon_{f} }}\)

Full size image

Figure 3b presents the dependence of parameter b on \(\sqrt {{{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}}\). A linear fit seems to apply well on the data points (R 2 = 0.987) yielding the relationship \(b = 170.2{{\varepsilon_{\text{wf}} } / {\varepsilon_{\text{f}} }} + 44.8 = 170.2\sqrt {{{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}} + 44.8\), for flat-wall channels.

To elaborate on the different effects of roughness elements and blocking elements, we examine the flow characteristics for various \({{h_{\text{d}} } / h}\), fixed \({{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}\) = 0.1 (hydrophobic channel walls) for h = 3.15 nm and h = 6.3 nm. Figure 4 depicts the calculated f values for protrusion heights \(h_{\text{d}} = 0\,\% h\) (flat-wall), \(h_{\text{d}}\) = 5 and 10 %h as well as \(h_{\text{d}}\) = 15 and 20 %h. Note that no data points for h = 3.15 nm exist for \(h_{\text{d}}\) = 5 and 15 %h as the channel upper wall morphology is impossible for the specific channel-height/groove-height ratio. Evidently, protrusions of height greater than 15 %h generate highly perturbed flow fields which, in turn, lead to values of f that are materially affected by the size (scale) of the channel. Similar diagrams are obtained for other \({{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}\) ratios. To differentiate between the two cases, we use here the term grooved nanochannels (for \(h_{\text{d}} \ge 15\,\% h\)) in contradistinction with the rough-wall nanochannels (for \(h_{\text{d}} \le 10\,\% h\)) considered before.

Fig. 4
figure 4

Friction factor f versus Re for various h d/h ratios and \(\varepsilon_{w} /\varepsilon_{f}\) = 0.1. Filled symbols represent h = 3.15 nm and empty symbols h = 6.3 nm data points. Lines are power-law least-squares fits

Full size image

Moreover, we observed that the power-law coefficient a in \(f = bRe^{a}\) deviates from −1 (\(a = - 1 \pm 0.1\), within statistical error) in hydrophilic channels with \(h_{\text{d}} > 10\,\% h\). This is evidence that a hydrophilic wall in a channel with groove height comparable to channel height can induce irregularities that make the constancy of the Poiseuille number not valid.

The trend that the friction factor decreases as the channel walls become more hydrophobic persists in the case of rough- and grooved-wall nanochannels. However, as shown in Cao et al. (2006) the combined effect of wall roughness and hydrophobicity on friction factor is not a monotonic function.

4 Conclusions

We believe that the fact that the friction factor values (computed based on the output of MD simulations) are organized on well-defined curves lends strong support to the choice of the most relevant dimensional parameters for the family of nanoflows studied. These friction factor curves are approximated very well by power laws of the form \(f = bRe^{a}\) when either \({{h_{\text{d}} } / h}\) or \({{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}\) is kept constant.

Based on the MD simulations, we constructed diagrams and developed correlations that are useful in estimating the friction factor over a range of Reynolds number values relevant to nanoflows. These diagrams allow one to estimate the effect that the wettability ratio (as expressed by the ratio \({{\varepsilon_{\text{w}} }/ {\varepsilon_{\text{f}} }}\)) has on f. As a rule (at least in all cases investigated in this work), the friction factor decreases as the channel walls become more hydrophobic. The influence of the relative protrusion height on the friction factor was also quantified. Nanoconduits with wall protrusions of relative height (\(h_{\text{d}} / h\)) up to 10 % can be classified as rough-wall nanochannels. Above this threshold value, nanoconduits with protrusions of relative height 15, 20 % and higher should be classified as grooved.

Summarizing, the MD results show a dependence of friction factor not only on geometric characteristics, e.g., \(h_{\text{d}} / h\), but also on the nature of interactions between the fluid and the walls (through the \({{\varepsilon_{\text{w}} } / {\varepsilon_{\text{f}} }}\) parameter), and the behavior of friction factor is approximated very well by power law of the form \(f = bRe^{a}\). As a result, one can expect that the knowledge of such relations can lead to tailor-made nanochannels leading to lower power loses, an issue that is important for nanodevices where energy consumption is an important issue. The friction factor predicted by the proposed correlation can be used in conceptual preliminary and even advanced stages of design. The detailed relations that can be extracted from MD simulations could be incorporated in a multiscale design tool for nanodevices incorporating nanochannels, since they would take into account both geometry and surface fluid interactions.