1 Introduction

In 1961, Perelman [1] used for the first time the phrase “conjugate heat transfer” to describe the heat transfer between an internally heated semi-infinite flat plate and a fluid in laminar flow in which the interface temperature is unknown. Variations of the problem originally formulated in Ref. [1] were solved analytically or numerically in Refs. [2–25] (in agreement with the aims of this work, we restricted the citation only to the forced convection analysis). Except for Pozzi and coworkers [16, 23, 24], the analysis of the mathematical models used in Refs. [1–25] reveals the following main characteristics:

  • the flow is steady and laminar;

  • in the fluid phase and inside the plate, a steady temperature profile is considered; in almost all cases, the boundary layer assumptions were used to model the heat transfer in the fluid; the temperature in the plate was calculated by solving the heat conduction equation or considering simplified models (one-dimensional, linear variation in the direction normal to the interface—assumption used for the first time by Luikov [4]).

A steady temperature profile inside the plate and in the fluid phase can be achieved only if a heat/mass source is present in the system. Note that a constant temperature for one of the unwetted sides of the plate indicates the presence of a heat source.

Pozzi and coworkers [16, 23, 24] (and the references cited herein), focussed on the unsteady conjugate heat transfer problem. The plate is considered semi-infinite. At the initial time, a fluid at rest is impulsively accelerated to a constant speed. The initial temperature field is uniform and equal in both the fluid and the solid. The unwetted side of the plate is kept at a constant temperature [16, 23] or it is considered adiabatic [24]. The fluid flow is laminar and compressible. The physico-mathematical model is based on: (a) an integral formulation of the boundary layer equations in the fluid phase; (b) the conduction equation in the solid; the heat transfer in the axial direction is neglected (one dimensional, linear variation in the direction normal to interface). However, we think that Pozzi and co-workers are closer to Refs. [1–25] than to the present work.

When there is no heat/mass source in the system, the conjugate problem must be rewritten and solved as an unsteady one. One of the boundary cases of the conjugate problem is the transfer from a body with uniform properties (temperature/concentration) (the so-called external problem).

The aim of this paper is to analyse the unsteady heat/mass transfer from a flat plate with uniform temperature/concentration. From our knowledge, this problem was not investigated until now. The influence of the product (physical properties ratio) × (aspect ratio) on the heat/mass transfer rate is investigated at Re = 10.0, 40.0, 100.0 and 400.0 (Re is the plate Reynolds number). For each Re number, three values of the fluid phase Prandtl number, Pr = 0.1, 1.0 and 10.0, were considered. The appearance and the development of the thermal/mass wake phenomenon are studied.

2 Model equations

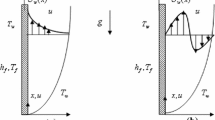
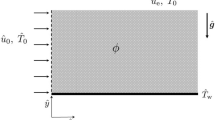
Consider the steady, laminar, two-dimensional motion of Newtonian fluid at zero incidence past a hot or cold flate plate occupying the region—L/2 ≤ x ≤ L/2, −ɛ L ≤ y ≤ 0.0. The plate has finite length L and thickness ɛ L. The free stream velocity and concentration/temperature are denoted by U∞ and C∞/ T∞, respectively. The sides of the plate located at y = −ɛ L and x = ±(L/2) are insulated. Assume that there are no gradients within the plate at each instant of time (the concentration/temperature inside the plate is uniform). Due to the complexities of the problem, we consider also valid the following statements:

  • the effects of buoyancy and viscous dissipation are negligible;

  • the physical properties of the material of the plate and the fluid are considered to be uniform, isotropic and constant;

  • no emission or absorption of radiant energy;

  • no phase change;

  • no chemical reaction inside the plate or in the surrounding fluid;

  • no pressure diffusion or thermal diffusion.

For purposes of obtaining a numerical solution to this problem, it is convenient to use the elliptical cylindrical coordinate system. Denote by X = x/L and Y = y/L the dimensionless cartezian coordinates. The elliptical cylindrical coordinate system (ξ, η) is defined by

$$ X = \frac{1} {2}\cosh \xi \cos \eta ,\quad \quad Y = \frac{1} {2}\sinh \xi \sin \eta $$
(1)

This transformation maps the upper half of the XY—plane (which by symmetry is all that need to be considered) into the semi-infinite strip ξ ≥ 0, 0 ≤ η≤ π. The plate transforms to ξ = 0, with leading edge at η = π and trailing edge at η = 0. In the elliptical cylindrical coordinate system, the nondimensional governing equations are:

  • fluid motion

    $$ \frac{{\partial ^{2} \psi }} {{\partial \xi ^{2} }} + \frac{{\partial ^{2} \psi }} {{\partial \eta ^{2} }} = - J\omega $$
    (2a)
    $$ \operatorname{Re} {\left( {\frac{{\partial \psi }} {{\partial \eta }}\frac{{\partial \omega }} {{\partial \xi }} - \frac{{\partial \psi }} {{\partial \xi }}\frac{{\partial \omega }} {{\partial \eta }}} \right)} = \frac{{\partial ^{2} \omega }} {{\partial \xi ^{2} }} + \frac{{\partial ^{2} \omega }} {{\partial \eta ^{2} }} $$
    (2b)

  • energy

    $$ \frac{{\partial Z}} {{\partial \tau }} + \frac{{Re\,Pr}} {J}{\left( {\frac{{\partial \psi }} {{\partial \eta }}\frac{{\partial Z}} {{\partial \xi }} - \frac{{\partial \psi }} {{\partial \xi }}\frac{{\partial Z}} {{\partial \eta }}} \right)} = \frac{1} {J}{\left( {\frac{{\partial ^{2} Z}} {{\partial \xi ^{2} }} + \frac{{\partial ^{2} Z}} {{\partial \eta ^{2} }}} \right)} $$
    (3a)
    $$ \frac{{\partial Z_{{\text{p}}} }} {{\partial \tau }} = \frac{1} {{\varepsilon \Xi }}{\int\limits_0^\pi {\left. {\frac{{\partial Z}} {{\partial \xi }}} \right|_{{\xi = 0}} {\text{d}}} }\eta $$
    (3b)

    where J = (1/8)(cosh 2ξ − cos 2η).

The boundary conditions to be satisfied are:

  • interface (ξ = 0)

    $$ \psi = 0,\quad \quad Z_{{\text{p}}} = Z $$
    (4a)

  • free stream (ξ = ∞)

    $$ \psi \to \frac{1} {2}{\text{sinh}}\,\xi \,{\text{cos}}\eta {\text{,}}\quad \quad \omega \to {\text{0,}}\quad \quad {\text{Z}} \to {\text{0}}{\text{.0}} $$
    (4b)

  • symmetry axis (η = 0, π)

    $$ \psi = \omega = 0,\quad \quad \frac{{\partial Z}} {{\partial \eta }} = 0.0 $$
    (4c)

The dimensionless initial conditions are:

$$ \tau = 0.0,\quad \quad Z_{{\text{p}}} = 1.0,\quad \quad Z(\xi > 0) = 0.0 $$
(5)

The dimensionless variables Zp and Z have a double signification, dimensionless concentration–dimensionless temperature (the assumptions practiced in this work are those usually employed in the analysis of the analogy between heat and mass transfer). For the simplicity and clarity of the presentation, in the remainder of this work, we will use only the terminology specific to heat transfer. This does not mean that the implication of the present results in mass transfer should be ignored.

The physical quantities of interest are the plate temperature Zp, the local Nusselt number, Nuη, and the average Nusselt number, Nu. Considering as driving force the difference between the plate temperature and the free stream temperature, the local and average Nu numbers are given by

$$ Nu_{\eta } = - \frac{1} {{Z_{{\text{p}}} }}\frac{1} {{1/2\sin \eta }}\left. {\frac{{\partial Z}} {{\partial \xi }}} \right|_{{\xi = 0}} $$
(6a)
$$ Nu = - \frac{1} {{Z_{{\text{p}}} }}{\int\limits_0^\pi {\left. {\frac{{\partial Z}} {{\partial \xi }}} \right|_{{\xi = 0}} {\text{d}}} }\eta $$
(6b)

3 Method of solution

The energy balance equations and the Navier–Stokes equations were solved numerically. The finite difference method was used for discretization.

The Navier–Stokes equations being uncoupled from the energy balance equations can be solved independently of them. Equation 2a was discretized with the central second order accurate finite difference scheme. A double discretization (upwind and central finite difference schemes), necessary for the defect correction iteration, was used for Eq. 2b. Numerical experiments were made with the discretization steps Δ ξ = Δ η = π/64, π/128 and π/256. The algorithm employed is the nested defect-correction iteration [26, 27].

The main problem in solving numerically the present Navier–Stokes equations is the boundary conditions at infinity. Dennis and Dunwoody [28] and Robertson et al. [29] analysed in detail this problem. Useful discussions about this aspect can be viewed in Ref. [30] for a similar flow problem.

Some ideas in solving the steady, laminar flow past a finite flat plate were lent from the steady, laminar flow past a circular cylinder. A reference study in this field may be considered [31]. According to Ref. [31], at ξ∞, the boundary conditions

$$ \frac{{\partial \ifmmode\expandafter\hat\else\expandafter\^\fi{\psi }}} {{\partial \xi }} = \frac{{\partial \omega }} {{\partial \xi }} = 0.0 $$
(7)

provide accurate results at moderate Re values. In (7), \( \ifmmode\expandafter\hat\else\expandafter\^\fi{\psi } = \psi - 1/2\sinh \xi \sin \eta \) is the deviation from the uniform flow.

In this work, both relations (4b) and (7) were used as boundary conditions at infinity. In each case, a carefully investigation of the influence of these boundary conditions on the solutions was made. The comparison between the solutions calculated with boundary conditions (4b) and (7) had shown that the only practical result of using (7) is to decrease the values of ξ∞ necessary to provide an accurate solution in the region near to the body.

The mathematical model Eqs. 3a and b is a system formed by a 2D parabolic partial differential equation (PDE) that describes the heat transfer in the fluid phase and an ordinary differential equation (ODE) that describes the energy balance of the plate. Equation 3a was discretized with the exponentially fitted scheme [32]. The discretization steps in both spatial directions are equal and took the values π/64, π/129 and π/256. The discrete parabolic equation was solved by the implicit ADI method. The ODE was integrated by an explicit modified Euler algorithm. The integral from relation (3b) was calculated by the Newton 3/8 rule using the values of ∂Z/∂ξ |ξ=0 available at time τ. The time step was variable and changed from the start of the computation to the final stage. The initial and final values of the time step depend on the parameter values.

4 Results

The dimensionless Eqs. 2 and 3 and the boundary and initial conditions (4) and (5) depend on four dimensionless parameters: Re,Pr, ɛ and Ξ . The first question discussed in this section is the selection of the numerical values of these parameters.

Four values of the Re number were used: Re = 10.0, 40.0, 100.0 and 400.0. We considered Re = 400.0 as superior boundary in order to avoid a disturbing increase in the numerical errors. At very small values of the product Re Pr, the system has a distinct behaviour and deserves a distinct analysis. For this reason, values of the Re number smaller than 10.0 were not used in this work.

The forced convection heat transfer from a flat plate is usually studied for three distinct sets of Pr values, e.g. Pr → 0.0, Pr ≈ 1.0 and Pr ≫ 1.0. In this work, for each Re value, Pr takes the values, Pr = 0.1, 1.0 and 10.0.

For a heat transfer process, the dimensionless parameter Ξ is the ratio (plate/surrounding medium) of the thermodynamic quantity volume heat capacity (for a mass transfer process this parameter is the Henry number, also called distribution coefficient). For brevity, Ξ will be referred as the thermodynamic ratio. In the mathematical model Eqs. 2–5, the thermodynamic ratio and the aspect ratio ɛ appear only as the product ɛ Ξ in relation (3b). Thus, we may consider the product ɛ Ξ as a single parameter. Values of ɛ Ξ in the range 10−2 –102 cover the situations of practical interest and allow the study of asymptotic behaviour.

The first task in any numerical work is to validate the code’s ability to reproduce published results accurately. A comparison of the present results for the drag coefficient, CD, with published solutions, over the entire range of Reynolds numbers considered, is shown in Table 1. Unfortunately, there are no data in literature to verify the accuracy of the present heat transfer computations. One of the tests that can be made consists of the numerical solving of the forced convection heat transfer from a plate with constant temperature. For this problem, a comparison of the present average Nu values with published solutions is also shown in Table 1. For both CD and Nu, Table 1 shows that the present numerical results are in good agreement to the published results.

Table 1 Comparison of CD and average Nu with previous studies
Full size table

The main problem of this work is the influence of ɛ Ξ on heat transfer. We will try to hit two targets: (1) first, to extend the results obtained at cylinder [35] (i.e. the heat/mass transfer from a cylinder with uniform temperature/concentration) and sphere [36–38] to a new geometry; secondly, to provide new results of interest for the flat plate. At this point, we think that the following aspect should be emphasized. For the sphere and cylinder, the geometry of the body influences the transfer only by means of the dimensionless groups Reynolds, Peclet, and so on. For the flat plate, a geometric parameter, the aspect ratio ɛ, appears explicitly in the mathematical model and influences directly the transfer. As example: for a metallic sphere/cylinder in a fluid environment, Ξ takes values greater or considerably greater than one; for a metallic flat plate, ɛ Ξ can take, theoretically at least, any value.

The time variation of plate temperature at Re = 40.0 and Pr = 1.0 is plotted in Fig. 1. The curves obtained for the other Re and Pr numbers have the same shape and for this reason were not presented. The asymptotic (i.e. the values corresponding to τ → ∞) values of the average Nu numbers are presented in Table 2 and plotted in Fig. 2. The presence of the superscript * in a cell indicates that the time variation of Nu does not reach a frozen value (in the other cases, the time variation of average Nu stabilizes to a constant, frozen value). The values depicted in this case correspond to the integration final, when the time variation of Nu becomes small. The last column of Table 2 shows the values provided by the plate with constant temperature.

Fig. 1
figure 1

Variation of the plate dimensionless temperature with dimensionless time at Re = 40.0 and Pr = 1.0

Full size image
Table 2 Asymptotic (τ → ∞) average Nu values
Full size table
Fig. 2
figure 2

Asymptotic values of the average Nu numbers function of ɛ Ξ ; a Re = 10.0; b Re = 40.0; c Re = 100.0; d Re = 400.0

Full size image

Thermal wake phenomenon is described by the transfer inversion point, TrIP [35, 37]. The TrIP steady values, measured from the trailing edge, are plotted in Fig. 3, only for Re = 10.0 and 100.0. At Re = 40.0 and 400.0, the wake phenomenon is similar to that presented at Re = 100.0. We must mention that the wake phenomenon for flat plate was also reported in Ref. [39].

Fig. 3
figure 3

Steady state position of TrIP on the plate surface, measured with respect to the trailing edge: a Re = 10.0; b Re = 100.0

Full size image

The present results and the sphere’s/cylinder’s results have some common and some distinct features. The common features, that express the general characteristics of the influence of the thermodynamic ratio (for the present case, ɛ Ξ rather than Ξ) on the time variation of plate temperature and asymptotic values of the average Nu numbers, are:

  • the heat transfer rate is strongly influenced by ɛ Ξ ; the increase in ɛ Ξ increases the average Nu number;

  • independently of the ɛ Ξ value, for a given Re number, the increase in Pr increases Nu; also, at a given Pr number, the increase in Re increases Nu; the increase in Re by a given number with the simultaneously decrease in Pr by the same number (i.e. the product Re Pr remains constant) leads to the increase in Nu (the aspect observed only at cylinder is not present here).

The distinct features refer especially to the local effects of ɛ Ξ variation on average Nu number and to the wake phenomenon. Table 2 and Fig. 2 show that, except for the case Re = 10.0 and Pr = 0.1, the influence of ɛ Ξ on average Nu becomes significant when ɛ Ξ < 0.5 (the influence is less significant in comparison with the sphere and cylinder). The wake phenomenon has smaller dimensions in comparison with the sphere and the cylinder. The behaviour of the system at Re = 10.0 and Pr = 0.1 is similar to that described in Ref. [40] for a sphere in creeping flow and small Peclet numbers.

Concerning the wake phenomenon, there is an interesting aspect that deserves to be presented. At sphere and cylinder the thermal wake occurs and develops from the stagnation points. At the plate, the thermal wake occurs in a region delimited by the middle of the plate and the trailing edge (see Fig. 4). In these moments, there are two TrIPs. With the increase in time, the wake evolves toward the trailing edge and finally occupies a region between the trailing edge and a single TrIP.

Fig. 4
figure 4

Local Nu numbers at different times for Re = 40.0, Pr = 1.0 and ɛ Ξ = 0.1

Full size image

The heat transfer from a plate with constant temperature was intensively analysed using boundary layer theory (BLA). In the context of the present work (i.e. the same assumptions are valid), when Re → ∞, the fundamental results provided by BLA are [41]:

$$ {\mathbf{Nu}} = 1.128{\sqrt {{\mathbf{Pr}}} }{\sqrt {{\mathbf{Re}}} }\quad {\text{if}}\;Pr \to {\text{0}}{\text{.0}} $$
(8a)
$$ {\mathbf{Nu}} = 0.664\sqrt[3]{{{\mathbf{Pr}}}}{\sqrt {{\mathbf{Re}}} }\quad {\text{if}}\;0.6 < \Pr < 10.0 $$
(8b)
$$ {\mathbf{Nu}} = 0.678\sqrt[3]{{{\mathbf{Pr}}}}{\sqrt {{\mathbf{Re}}} }\quad {\text{if}}\;Pr \to \infty {\text{.}} $$
(8c)

The Reynolds analogy between the fluid flow and the heat transfer for the flat plate at Pr = 1.0 is expressed by the relation [41]

$ $$ \frac{{{\mathbf{Re}}\,C_{{\text{D}}} }} {{2.0{\mathbf{Nu}}}} \to 1.0\quad {\text{when}}\;Re \to \infty {\text{.}} $$

Fig. 5 shows that for ɛ Ξ > 0.10, the groups Nu/f (Re,Pr) tend to an asymptotic value when Re tends to infinite. At Pr = 0.1, the asymptotic value differs from that predicted by BLA. However, we think that this result cannot be considered an invalidation of BLA. We think that Pr = 0.1 is too higher a value for the limit Pr → 0.0. For Pr = 1.0 and 10.0, the asymptotic values agree well with the BLA values. For ɛ Ξ = 0.1, 0.01 it is difficult to state that the present numerical results tend to the BLA asymptotic value.

Fig. 5
figure 5

Values of the group Nu/(Re1/2 Pry) function of plate Re number; symbol * refer to the asymptotic value provided by boundary layer theory; a Pr = 0.1, y = 1/2, * = 1.128; b Pr = 1.0, * = 0.664; c Pr = 10.0, y = 1/3, * = 0.678

Full size image

For the Reynolds analogy, Fig. 6 shows a similar situation with that described previously. For ɛ Ξ > 0.10 it is obviously that the ratio Re CD/2 Nu tends to unity. At ɛ Ξ = 0.1, 0.01 (especially for ɛ Ξ = 0.01) the asymptotic behaviour is difficult to foresee.

Fig. 6
figure 6

Values of the group Re CD/2 Nu function of plate Re number

Full size image

5 Conclusions

The physical heat transfer from a flat plate with uniform temperature was investigated. The flow past the flat plate was considered steady, laminar at zero incidence. The plate Re number takes the values 10.0, 40.0, 100.0 and 400.0. For each Re value, the fluid phase Pr number was considered equal to 0.1, 1.0 and 10.0. The main aspect analysed was the influence of the product (aspect ratio) × (thermodynamic ratio) on the transfer rate.

The numerical results presented in the previous section show that the heat/mass transfer from a flat plate with uniform temperature exhibits the same main characteristics as the transfer from a sphere or cylinder with uniform properties. The influence on the transfer rate of the thermodynamic ratio, plate Re number and fluid Pr number follows the same rules. Only the wake phenomenon shows a distinct behaviour.