Boundary Layer Flow Over a Moving Vertical Flat Plate with Convective Thermal Boundary Condition

Abstract

This paper studies the steady boundary layer flow over an impermeable moving vertical flat plate with convective boundary condition at the left side of the flat plate. The governing partial differential equations are transformed into a system of ordinary (similarity) differential equations by using corresponding similarity variables. These equations were then solved numerically using the function bvp4c from Matlab for different values of the Rayleigh number Ra, the convective heat transfer parameter $\gamma$, and the Prandtl number Pr. This paper demonstrates that a similarity solution is possible if the convective boundary condition heat transfer is associated with the hot or cooled fluid on the left side of the flat plate proportional to $x^{-1/4}$. For the sake of comparison of the numerical results, the case of the static flat plate $(\sigma =0)$ has been also studied. For the case of a moving flat plate $(\sigma =1)$, it is shown that the solutions have two branches in a certain range of the positive (assisting flow) and negative (opposing flow) values of the Rayleigh number Ra. In order to test the physically available solutions, a stability analysis has been also performed. The effects of the governing parameters on the skin friction, heat transfer, wall temperature, velocity and temperature profiles, as well as on the streamlines and isotherms are investigated. Comparison with results from the open literature shows a very good agreement.

1 Introduction

The boundary layer flow due to a moving flat plate is a relevant type of flow appearing in many industrial processes, such as manufacture and extraction of polymer and rubber sheets, paper production, wire drawing and glass-fiber production, melt spinning, continuous casting, etc. (Tadmor and Klein [39]). It seems that Sakiadis [37] initiated the problem of boundary layer flow and heat transfer past a moving surface, which is different by the boundary layer flow past a stationary surface or the famous Blasius [10] problem due to the entering of the boundary layer. This problem has also many industrial applications such as heat treatment of material traveling between a feed roll and wind-up roll or conveyer belts, extrusion of steel, cooling of a large metallic plate in a bath, liquid films in condensation process and in aerodynamics, etc. A considerable amount of research has been reported on this topic (Jaluria [23], Karve and Jaluria [24], Hayat et al. [15], etc.). Similarity solutions for moving plates were investigated also by many authors. Among them, Afzal et al. [3], Afzal [1, 2], Fang [12], Fang and Lee [13], Weidman et al. [40], Ishak et al. [22] studied the boundary layer flow on a moving permeable plate parallel to a moving stream and concluded that dual solution exists if the plate and the free stream move in the opposite directions. Further, we mention that Hayat et al. [15–20], Nawaz et al. [33], Aman et al. [5], and Mansur and Ishak [32] have studied different problems on convective boundary layers flows.

As per standard text books by Bejan [8], Kays and Crawford [26], Bergman et al. [9] and other literature, the convective flow occurs in atmospheric and oceanic circulation, electronic machinery, heated or cooled enclosures, electronic power supplies, etc. This topic has many applications such as its influence on operating temperatures of power generating and electronic devices. It also plays a great role in thermal manufacturing applications and is important in establishing the temperature distribution within buildings as well as heat losses or heat loads for heating, ventilating, and air conditioning systems. As it is well known, the difference between convective heat transfer and forced convection problems is thermodynamic and mathematical, as well, the convective flows being driven by buoyancy effect due to the presence of gravitational acceleration and density variations from one fluid layer to another (Bejan [8]). It seems that Karwe and Jaluria [24, 25] are the first who have studied the fluid flow and mixed convection transport from a moving plate in rolling and extrusion processes. Ali [4] investigated the effect of temperature-dependent viscosity on laminar mixed convection boundary layer flow and heat transfer on a continuously moving vertical isothermal surface and obtained the local similarity solutions. Further, Aziz [6] has studied the classical problem of hydrodynamic and thermal boundary layers over an impermeable flat plate in a uniform stream of fluid with convective boundary condition. Magyari [27] presented an exact solution of the problem considered by Aziz [6] for the thermal boundary layer in a compact integral form, while Ishak [21] extended Aziz’s [6] problem for a permeable flat plate. Yao et al. [42] obtained exact analytical solutions of the momentum and the energy equations of a viscous fluid flow over a stretching/shrinking sheet with a convective boundary condition. Makinde and Olanrewaju [28] considered the buoyancy effects on the thermal boundary layer over a vertical flat plate with a convective surface boundary condition, while Makinde [29] investigated MHD heat and mass transfer over a moving vertical plate with a convective surface boundary condition. In another paper, Makinde [30] presented similarity solution for natural convection from a moving vertical plate with internal heat generation and a convective boundary condition. Makinde and Aziz [31] analyzed the boundary layer flow of a nanofluid past a stretching sheet with convective boundary condition. Finally, we mention that Aziz and Khan [7] have very recently studied the natural convective boundary layer flow of a nanofluid past a convectively heated vertical plate.

The objectives of the present study are to find new similarity transformations and the corresponding similarity solutions for the problem of steady viscous incompressible fluid past a moving vertical flat plate with thermal convective boundary condition and to solve the transformed coupled ordinary differential equations numerically. The effects of the convective heat transfer parameter $\gamma$, the Prandtl number Pr, and the Rayleigh number Ra on the flow and heat transfer characteristics are investigated numerically. To our best of knowledge, this is a novel problem with new and original results. On the other hand, it should be mentioned that, this is a complete paper with a mathematical stability analysis of the nature of the dual (first and second order or upper branch and lower branch) solutions.

Fig. 1

Flow configuration and coordinate system. a Assisting flow. b Opposing flow

2 Basic Equations

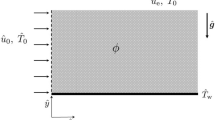
Consider a vertical flat plate moving with the velocity $U_\mathrm{w}(x)$ in an unsteady laminar viscous and incompressible fluid as shown in Fig. 1. It is assumed that the temperature of the ambient fluid is $T_\infty$, the unknown temperature of the plate is $T_\mathrm{w}$, and the left surface of the plate is heated from a hot fluid of temperature $T_\mathrm{f}$ $(>T_\infty )$ or is cooled from a cooled fluid $(T_\mathrm{f}<T_\infty )$ by the process of convection (see Aziz [6] and Ishak [21]). This then yields a heat transfer variable coefficient $h_\mathrm{f}(x)$. It is also assumed that the thermophysical properties of the fluid are constant except the density in the buoyancy force term. Under the assumption of Boussinesq and boundary layer approximations, the governing boundary layer equations relevant to our problem are (Bejan [8], Bergman et al. [9])

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial v}{\partial y}=0 \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial t}+u\displaystyle \frac{\partial u}{\partial x}+v\displaystyle \frac{\partial u}{\partial y} =\nu \displaystyle \frac{\partial ^2 u}{\partial y^2}+g\beta (T-T_\infty ) \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial t}+u\displaystyle \frac{\partial T}{\partial x}+v\displaystyle \frac{\partial T}{\partial y} =\alpha \displaystyle \frac{\partial ^2 T}{\partial y^2}. \end{aligned}$$

(3)

We assume that the initial and boundary conditions of these equations are (Aziz [6], Ishak [21])

$$\begin{aligned} t<0:&\,u=v=0,\ T=T_\infty \quad \text{ for } \text{ any } x,y\nonumber \\ t\ge 0:&\,v=0,\ u=\sigma U_\mathrm{w}(x),\ -k\displaystyle \frac{\partial T}{\partial y}=h_\mathrm{f}(T_\mathrm{f}-T_\mathrm{w})\quad \text{ at } y=0 \\&u\rightarrow 0,\ T\rightarrow T_\infty \quad \text{ as } y\rightarrow \infty \nonumber , \end{aligned}$$

(4)

where t is the time, u and v are the velocity components along the x- and y- axes, T is the temperature, $\nu$ is the kinematic viscosity, k is the thermal conductivity, $\alpha$ is the thermal diffusivity, $\beta$ is the volumetric thermal coefficient, g is the acceleration due to gravity, and $\sigma$ is a constant with $\sigma =0$ for a fixed (static) plate and $\sigma =1$ for a moving plate, respectively. The convective boundary condition is based on the surface energy balance expressed as follows: heat conduction at the surface = heat convection at the surface. This boundary condition encountered in practice as most of the process involving heat transfer are exposed to environment at a specified temperature (see Cengel [11]).

3 Steady-State Flow Analysis

In order to deal with our problem, we introduce the stream function $\psi$ defined in the classical form as $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x$. Thus, Eqs. (2) and (3) can be written as

$$\begin{aligned}&\displaystyle \frac{\partial \psi }{\partial y} \displaystyle \frac{\partial ^2 \psi }{\partial x \partial y} -\displaystyle \frac{\partial \psi }{\partial x} \displaystyle \frac{\partial ^2 \psi }{\partial y^2} =\nu \displaystyle \frac{\partial ^3\psi }{\partial y^3}+g\beta (T-T_\infty ) \end{aligned}$$

(5)

$$\begin{aligned}&\displaystyle \frac{\partial \psi }{\partial y} \displaystyle \frac{\partial T}{\partial x}-\displaystyle \frac{\partial \psi }{\partial x} \displaystyle \frac{\partial T}{\partial y} =\alpha \displaystyle \frac{\partial ^2 T}{\partial y^2} \end{aligned}$$

(6)

and the boundary condition (4) becomes

$$\begin{aligned}&\displaystyle \frac{\partial \psi }{\partial x}=0,\ \displaystyle \frac{\partial \psi }{\partial y}=\sigma U_\mathrm{w}(x),\ -k\displaystyle \frac{\partial T}{\partial y}=h_\mathrm{f}(T_\mathrm{f}-T_\mathrm{w})\quad \text{ at } y=0 \nonumber \\&\displaystyle \frac{\partial \psi }{\partial y}\rightarrow 0,\ T\rightarrow T_\infty \quad \text{ as } y\rightarrow \infty . \end{aligned}$$

(7)

Further, we define the independent and dependent similarity variables in the usual form as (White [41])

$$\begin{aligned} \eta =c_1\displaystyle \frac{y}{x^{1/4}},\quad \psi =c_2x^{3/4}f(\eta ),\quad \theta (\eta )=(T-T_\infty )/\Delta T, \end{aligned}$$

(8)

where $\Delta T=T_\mathrm{f}-T_\infty$ and $c_1$ and $c_2$ are positive constants and will be determined later by using the condition that Eqs. (5) and (6) subject to the boundary condition (7) become similarity equations or ordinary differential equations. Thus, substituting (8) into Eqs. (5) and (6), we get

$$\begin{aligned}&f'''+\displaystyle \frac{c_2}{\nu c_1}\left( \displaystyle \frac{3}{4}ff''-\displaystyle \frac{1}{2}f'^2\right) +\displaystyle \frac{g\beta \Delta T}{\nu c_2c_1^3}=0 \end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle \frac{1}{Pr}\theta ''+\displaystyle \frac{3}{4}\displaystyle \frac{c_2}{\nu c_1}f\theta '=0 \end{aligned}$$

(10)

along with

$$\begin{aligned} c_1c_2x^{1/2}f'(0)=U_\mathrm{w}(x), \end{aligned}$$

(11)

where primes denote differentiation with respect to the similarity independent variable $\eta$. To get the dimensionless form of $\eta$, $f(\eta )$, and $\theta (\eta )$ and to get rid of the fluid properties appearing in the coefficients of the Eqs. (9) and (10),

$$\begin{aligned} \displaystyle \frac{c_2}{\nu c_1}=1,\quad c_1c_2\equiv A \end{aligned}$$

(12)

so that in the wall condition $U_\mathrm{w}(x)=Ax^{1/2}$, where the constant $A(m^{1/2}/s)$ corresponds to the prescribed plate velocity at the distance $x=1m$ from the origin, namely $A=U_\mathrm{w}(1)$. Accordingly, the first Eq. (12), $c_2\equiv \nu c_1$ along with the prescribed equation $c_1c_2=A$, determines the constants $c_1$ and $c_2$ in terms of A uniquely, yielding

$$\begin{aligned} c_1=\sqrt{\displaystyle \frac{A}{\nu }},\quad c_2=\sqrt{A\nu }. \end{aligned}$$

(13)

In this way, the coefficient $g\beta \Delta T/(\nu c_2c_1^3)$ in Eq. (9) leads to an essential parameter of the problem, namely to the mixed convection parameter

$$\begin{aligned} \displaystyle \frac{g\beta \Delta T}{\nu c_2c_1^3}=\displaystyle \frac{g\beta \Delta T}{A^2}. \end{aligned}$$

(14)

Bearing in mind that the present problem does not possess a natural length scale, the length unit L is to our disposal. Thus, choosing L as

$$\begin{aligned} L=\left( \displaystyle \frac{\nu \alpha }{A^2}\right) ^{1/3}, \end{aligned}$$

(15)

one obtains from Eq. (14) the Rayleigh number Ra defined as

$$\begin{aligned} \displaystyle \frac{g\beta \Delta T}{\nu c_2c_1^3}=\displaystyle \frac{g\beta \Delta T}{A^2} =\displaystyle \frac{g\beta \Delta TL^3}{\nu \alpha }\equiv Ra. \end{aligned}$$

(16)

Thus, Eqs. (9) and (10) become

$$\begin{aligned}&f'''+\displaystyle \frac{3}{4}ff''-\displaystyle \frac{1}{2} f'^2+Ra\theta =0 \end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle \frac{1}{Pr}\theta ''+\displaystyle \frac{3}{4}f\theta '=0 \end{aligned}$$

(18)

and the boundary condition (7) can be written as

$$\begin{aligned} \begin{aligned}&f(0)=0,\ f'(0)=\sigma ,\ \theta '(0)=-\gamma [1-\theta (0)]\\&f'(\eta )\rightarrow 0,\ \theta (\eta )=0 \text{ as } \eta \rightarrow \infty , \end{aligned} \end{aligned}$$

(19)

where $Pr=\nu /\alpha$ is the Prandtl number and $\gamma$ is the convective heat transfer parameter, which is given by

$$\begin{aligned} \gamma =\displaystyle \frac{h_\mathrm{f}}{c_1k}x^{1/4}. \end{aligned}$$

(20)

In order that Eqs. (17) and (18) have similarity solutions, the quantity $\gamma$ must be a constant and not a function of x as in Eq. (20) (see Aziz [6] and Ishak et al. [22]). This condition can happen if the heat transfer coefficient $h_\mathrm{f}(x)$ is proportional to $x^{-1/4}$. We therefore assume

$$\begin{aligned} h_\mathrm{f}=ax^{-1/4}, \end{aligned}$$

(21)

where a is a constant. With the introduction of Eq. (21) into Eq. (20), we have $\gamma =a/(c_1k)$. Thus, the solutions of Eqs. (17) and (18) with the boundary condition (19) yield the similarity solutions. Therefore, the investigation of this problem has to be conducted with respect to three characteristic parameters of the model, namely $\gamma$, Pr, and Ra. It is worth emphasizing that Ra is a proper physical characteristic of the problem, depending on the temperature prescription $\Delta T$ for the fluid, as well as on the velocity prescription A for the moving plate. Obviously, $\Delta T$ and A are two physically independent input data. Moreover, Ra can be positive ($\Delta T$, aiding flow) or negative ($\Delta T<0$ opposing flow), respectively.

The physical parameters of interest in the present problem are the skin friction factor $C_\mathrm{f}$ and the local Nusselt number $Nu_x$, which are given by

$$\begin{aligned} C_\mathrm{f}=\displaystyle \frac{\mu }{\rho U_\mathrm{w}^2(x)}\left( \displaystyle \frac{\partial u}{\partial y}\right) _{y=0},\quad Nu_x=\displaystyle \frac{x}{\Delta T}\left( -\displaystyle \frac{\partial T}{\partial y}\right) _{y=0}. \end{aligned}$$

(22)

Substituting (8) into (22), we get

$$\begin{aligned} Re_x^{1/2}C_\mathrm{f}=f''(0),\quad Re_x^{-1/2}Nu_x=-\theta '(0), \end{aligned}$$

(23)

where $Re_x=U_\mathrm{w}(x)x/\nu$ is the local Reynolds number.

4 Flow Stability

Weidman et al. [40], Postelnicu and Pop [35], and Roşca and Pop [36] have shown for the forced convection boundary layer flow past a permeable flat plate and, respectively, for the forced convection flow of a non-Newtonian fluid past a wedge, that the lower branch solutions are unstable (not realizable physically), while the upper branch solutions are stable (physically realizable). We test these features by considering the unsteady equations (2) and (3). Following Weidman et al. [40], we introduce the new dimensionless time variable $\tau =ct$. The use of $\tau$ is associated with an initial value problem and is consistent with the question of which solution will be obtained in practice (physically realizable). Using the variables $\tau$ and (8), we have

$$\begin{aligned} \begin{aligned}&u=Ax^{1/2}\displaystyle \frac{\partial f}{\partial \eta },\ v =-\displaystyle \frac{c_2}{4}x^{-1/4}\left( 3f-\eta \displaystyle \frac{\partial f}{\partial \eta }\right) \\&\theta (\eta ,\tau )=(T-T_\infty )/\Delta T,\ \tau =c_1^2 x^{-1/2}t,\ \eta =c_1\displaystyle \frac{y}{x^{1/4}} \end{aligned} \end{aligned}$$

(24)

so that Eqs. (3) and (5) can be written as

$$\begin{aligned}&\displaystyle \frac{\partial ^3 f}{\partial \eta ^3}+\displaystyle \frac{3}{4}f\displaystyle \frac{\partial ^2 f}{\partial \eta ^2} -\displaystyle \frac{1}{2}\left( \displaystyle \frac{\partial f}{\partial \eta }\right) ^2 -\displaystyle \frac{\partial ^2 f}{\partial \eta \partial \tau }+Ra\theta =0 \end{aligned}$$

(25)

$$\begin{aligned}&\displaystyle \frac{1}{Pr}\displaystyle \frac{\partial ^2 \theta }{\partial \eta ^2}+\displaystyle \frac{3}{4}f\displaystyle \frac{\partial \theta }{\partial \eta } -\displaystyle \frac{\partial \theta }{\partial \tau }=0 \end{aligned}$$

(26)

subject to the boundary conditions

$$\begin{aligned} \begin{aligned}&f(0,\tau )=0,\ \displaystyle \frac{\partial f}{\partial \eta }(0,\tau )=\sigma ,\ \displaystyle \frac{\partial \theta }{\partial \eta }(0,\tau )=-\gamma [1-\theta (0,\tau )] \\&\displaystyle \frac{\partial f}{\partial \eta }(n,\tau )\rightarrow 0,\ \theta (\eta ,\tau )\rightarrow 0\quad \text{ as } \eta \rightarrow \infty . \end{aligned} \end{aligned}$$

(27)

To test stability of the steady flow solution $f(\eta )=f_0(\eta )$ and $\theta (\eta )=\theta _0(\eta )$ satisfying the boundary-value problem (17)–(19), we write (see Weidman et al. [40] or Roşca and Pop [36]),

$$\begin{aligned} f(\eta ,\tau )=f_0(\eta )+e^{-\varepsilon \tau }F(\eta ,\tau ),\quad \theta (\eta ,\tau )=\theta _0(\eta )+e^{-\varepsilon \tau }G(\eta ,\tau ), \end{aligned}$$

(28)

where $\varepsilon$ is an unknown eigenvalue parameter, and $F(\eta ,\tau )$ and $G(\eta ,\tau )$ are small relative to $f_0(\eta )$ and $\theta _0(\eta )$. Substituting (28) into Eqs. (25) and (26), we obtain the following linearized problem

$$\begin{aligned}&\displaystyle \frac{\partial ^3 F}{\partial \eta ^3}+\displaystyle \frac{3}{4}\left( f_0 \displaystyle \frac{\partial ^2 F}{\partial \eta ^2}+f''_0F\right) -(f'_0-\varepsilon )\displaystyle \frac{\partial F}{\partial \eta }-\displaystyle \frac{\partial ^2 F}{\partial \eta \partial \tau }+Ra\, G=0 \end{aligned}$$

(29)

$$\begin{aligned}&\displaystyle \frac{1}{Pr}\displaystyle \frac{\partial ^2 G}{\partial \eta ^2}+\displaystyle \frac{3}{4}\left( f_0\displaystyle \frac{\partial G}{\partial \eta }+F\theta '_0\right) +\varepsilon G-\displaystyle \frac{\partial G}{\partial \tau }=0 \end{aligned}$$

(30)

along with the boundary conditions

$$\begin{aligned} \begin{aligned}&F(0,\tau )=0,\ \displaystyle \frac{\partial F}{\partial \eta }(0,\tau )=0,\ \displaystyle \frac{\partial G}{\partial \eta }(0,\tau )=\gamma G(0,\tau )\\&\displaystyle \frac{\partial F}{\partial \eta }(\eta ,\tau )\rightarrow 0,\ G(\eta ,\tau )\rightarrow 0\quad \text{ as } \eta \rightarrow \infty . \end{aligned} \end{aligned}$$

(31)

As suggested by Weidman et al. [40], we investigate the stability of the steady flow and heat transfer solution $f_0(\eta )$ and $\theta _0(\eta )$ by setting $\tau =0$, and hence $F=F_0(\eta )$ and $G=G_0(\eta )$ in (29) and (30) to identify initial growth or decay of the solution (26). To test our numerical procedure, we have to solve the linear eigenvalue problem

$$\begin{aligned}&F'''_0+\displaystyle \frac{3}{4}(f_0 F''_0+f''_0F_0)-(f'_0-\varepsilon )F'_0+Ra\, G_0=0 \end{aligned}$$

(32)

$$\begin{aligned}&\displaystyle \frac{1}{Pr}G''_0+\displaystyle \frac{3}{4}(f_0 G'_0+F_0 \theta '_0)+\varepsilon G_0=0 \end{aligned}$$

(33)

along with the boundary conditions

$$\begin{aligned} \begin{aligned}&F_0(0)=0,\ F'_0(0)=0,\ G'_0(0)=\gamma G_0(0)\\&F'_0(\eta )\rightarrow 0,\ G_0(\eta )\rightarrow 0\quad \text{ as } \eta \rightarrow \infty . \end{aligned} \end{aligned}$$

(34)

It should be mentioned that for particular values of $\varepsilon$, Pr, and Ra the corresponding steady flow solution $f_0(\eta )$ and $\theta _0(\eta )$, the stability of the steady flow solution is determined by the smallest eigenvalue $\varepsilon$. According to Harris et al. [14], the range of possible eigenvalues can be determined by relaxing a boundary condition on $F_0(\eta )$ or $G_0(\eta )$. For the present problem, we relax the condition that $G_0(\eta )\rightarrow 0$ as $\eta \rightarrow \infty$ and for a fixed value of $\gamma$, we solve the system (32,33) along with the new boundary condition $G_0(0)=1$.

5 Results and Discussion

The set of coupled non-linear ordinary differential Eqs. (17) and (18) with boundary conditions in Eq. (16) forms a two-point boundary-value problem and has been solved numerically using the function bvp4c from Matlab for different values of the Rayleigh number Ra, the convective heat transfer parameter $\gamma$, and the Prandtl number Pr. Both the cases of assisting flow $(Ra>0)$ and opposing flow $(Ra<0)$ and also both cases of static $(\sigma =0)$ and moving $(\sigma =1)$ flat plate have been considered. The relative tolerance was set to $10^{-10}$. In this method, we have chosen a suitable finite value of $\eta \rightarrow \infty$, namely $\eta =\eta _\infty =12$. It was noticed by Pantokratotars [34] that some results are erroneous as the graphs for velocity and temperature distributions in the boundary layers do not approach the correct values in a asymptotic manner due to a small value of $\eta _{\max }$. Since the present problem may have more than one (dual) solution, the bvp4c function requires an initial guess of the desired solution for the ordinary differential equations (17) and (18) with the boundary condition (19). The guess should satisfy the boundary conditions and reveal the behavior of the solution. Determining an initial guess for the first (upper branch) solution is not difficult because the bvp4c method will converge to the first solution even for poor guesses. However, it is difficult to come up with a sufficiently good guess for the solution of the system of the ordinary differential equations (17) and (18) in the case of opposing flow. To overcome this difficulty, we start with a set of parameter values for which the problem is easy to be solved. Then, we use the obtained result as initial guess for the solution of the problem with small variation of the parameters. This is repeated until the right values of the parameters are reached. This technique is called continuation (Shampine et al. [38]). Table 1 shows the comparison of heat transfer for several values of Pr when $\sigma =0$ (fixed plate), $\gamma \rightarrow \infty$ (isothermal plate), and $Ra=1$ (assisting flow) with those reported by Bejan [7]. It is seen that the results are in very good agreement. Further, Eqs. (17) and (18) have been also numerically solved using the Runge–Kutta–Fehlberg fourth–fifth order numerical method proposed by Aziz [6]. The values of $-f''(0)$ and $\theta (0)$ for different values of the Prandtl number Pr and the convective heat transfer parameter $\gamma$ are given in Table 2 for $Ra=1$ (assisting flow) and a moving plate $(\sigma =1)$. The results are shown in Table 2. Also, this table shows a very agreement. Therefore, the results presented in the both Tables 1 and 2 support the validity of the present numerical results. We are, therefore, confident that these results are accurate and correct.

Table 1 Comparison of heat transfer for several values of Pr when $\sigma =0$ (fixed plate), $\gamma \rightarrow \infty$ (isothermal plate), and $Ra=1$ (assisting flow)

Table 2 Values of $-f''(0)$ and $\theta (0)$ for various of Pr and $\gamma$ when $\sigma =1$ (moving plate) and $Ra=1$ (assists flow)

Fig. 2

Variation of $f''(0)$ with Ra for several values of $\gamma$ when $Pr=1$ and a moving plate $(\sigma =1)$

Fig. 3

Variation of $-\theta (0)$ with Ra for several values of $\gamma$ when $Pr=1$ and a moving plate $(\sigma =1)$

In Figs. 2 and 3, we plot the reduced skin friction $f''(0)$ and the reduced heat transfer from the plate $-\theta '(0)$ against the Rayleigh number Ra for different values of the convective heat transfer parameter $\gamma$ when the Prandtl number $Pr=1$ and the plate is moving $(\sigma =1)$. In this case, we find the existence of dual solutions, an upper brunch (or first) solution (shown by full lines), and lower brunch (or second) solution (shown by dot lines) for $f''(0)$ and $-\theta '(0)$ for both the cases of assisting $(Ra>0)$ and opposing $(Ra<0)$ flows. It is seen that there are critical values $Ra_\mathrm{c}<0$ of $Ra<0$, with the values of $|Ra_\mathrm{c}|$ decreasing with increasing $\gamma$ for $f''(0)$ and increasing with $\gamma$ for $-\theta '(0)$, respectively. Further, it is seen that there is a saddle-node bifurcation at $Ra=Ra_\mathrm{c}$ giving rise to the two solution branches for $Ra_\mathrm{c}<Ra<0$. Both solution branches continue into the aiding flow region $(Ra>0)$ with the upper solution branch passing through the forced convection solution at $Ra=0$ for $f''(0)$. On this upper solution branch, $f''(0)$ increases with $\gamma$. The numerical solutions for the both upper and lower brunch solutions pass smoothly through $Ra=0$ without a singularity appearing, as seen for example in Weidman et al. [40]. Further, it has been shown from the stability analysis that the upper branch solutions are stable and physically realizable, while the lower branch solutions are unstable and, therefore, not physically realizable. The smallest eigenvalues $\varepsilon$ for $Ra=-0.5$ and $-1$ (opposing flow), $\gamma =0.05$ and 0.1, and $Pr=1$ are given in Table 3.

Table 3 Smallest eigenvalues of $\varepsilon$ for several values of $\gamma$ when $Ra=-0.5$ and $-1$ (opposing flow) with $Pr=1$

Fig. 4

Velocity profiles $f'(\eta )$ for several values of $Ra<0$ (opposing flow) when $\gamma =0.01$, $Pr=1$, and $\sigma =1$

Fig. 5

Temperature profiles $\theta (\eta )$ for several values of $Ra<0$ (opposing flow) when $\gamma =0.01$, $Pr=1$, and $\sigma =1$

Fig. 6

Velocity profiles $f'(\eta )$ for several values of $\gamma$ when $Ra=-1$ (opposing flow), $Pr=1$, and $\sigma =1$

Fig. 7

Temperature profiles $\theta (\eta )$ for several values of $\gamma$ when $Ra=-1$ (opposing flow), $Pr=1$, and $\sigma =1$

Fig. 8

Velocity profiles $f'(\eta )$ for several values of $Ra>0$ (assisting flow) when $\gamma =0.01$, $Pr=1$, and $\sigma =1$

Fig. 9

Temperature profiles $\theta (\eta )$ for several values of $Ra>0$ (assisting flow) when $\gamma =0.01$, $Pr=1$, and $\sigma =1$

Fig. 10

Velocity profiles $f'(\eta )$ for several values of $\gamma$ when $Ra=1$ (assisting flow), $Pr=1$, and $\sigma =1$

Fig. 11

Temperature profiles $\theta (\eta )$ for several values of $\gamma$ when $Ra=1$ (assisting flow), $Pr=1$, and $\sigma =1$

Fig. 12

Streamlines for the first solution branch (a) and second solution branch (b) when $\gamma =0.05$ (solid line) and $\gamma =0.06$ (dotted line), $Ra=-1$, and $Pr=1$

Fig. 13

Isotherm lines for the first solution branch (a) and second solution branch (b) when $\gamma =0.05$ (solid line) and $\gamma =0.06$ (dotted line), $Ra=-1$, and $Pr=1$

We next illustrate in Figs. 4, 5, 6, 7, 8, 9, 10, and 11, the velocity $f'(\eta )$ and temperature $\theta (\eta )$ profiles for several values of Ra both positive (assisting flow, $Ra>0$) and negative (opposing flow, $Ra<0$) and for several values of $\gamma$, $Pr=1$ when the flat plate is moving $(\sigma =1)$. These figures show that there are also dual (upper and lower brunch) solutions for the velocity and temperature profiles. Figures 4 and 5 display the velocity $f'(\eta )$ and temperature $\theta (\eta )$ profiles for several values of $Ra<0$ (opposing flow) and $\gamma =0.01$. We notice that the velocity profiles decrease, while the temperature profiles increase as |Ra| increases for the both branch solutions. For the velocity field, the boundary layer thickness is higher for the upper branch than the lower branch solutions. However, reverse happens for the temperature profiles. Further, the velocity $f'(\eta )$ and the temperature $\theta (\eta )$ profiles for several values of $\gamma$ when $Ra=-1$ (opposing flow), $Pr=1$, and $\sigma =1$ are illustrated in Figs. 6 and 7. It is seen that $f'(\eta )$ decreases, while $\theta (\eta )$ increases with $\gamma$ for the both branch solutions. Physically, this is because fluids on the right side of the flat plate are cooled, so that higher values of $\gamma$ increase the temperature. Further, Figs. 8 and 9 show the velocity $f'(\eta )$ and temperature $\theta (\eta )$ profiles for several values of $Ra>0$ (assisting flow) when $\gamma =0.01$, $Pr=1$, and $\sigma =1$. It can be seen that $f'(\eta )$ increases, while $\theta (\eta )$ decreases with Ra for the both branch solutions. Fluids on the right side surface of the plate are heated up making it to become lighter and flow faster. Also, the velocity $f'(\eta )$ and temperature $\theta (\eta )$ profiles are given in Figs. 10 and 11 for several values of $\gamma$ when $Ra=1$ (assisting flow), $Pr=1$, and $\sigma =1$. It is found that for the velocity profiles, the upper branch solutions increase, while the lower branch solutions decrease with $\gamma$. However, both the upper and lower branch solutions continuously increase with $\gamma$. For an opposing flow, effects of these parameters are reverse to that of the effect for the assisting case. It is worth mentioning to this end that for both dual solutions, the velocity $f'(\eta )$ and temperature $\theta (\eta )$ profiles attain smoothly the boundary condition (19) as $\eta \rightarrow \infty$ and it shows again that the present results are accurate. Finally, the streamlines and isotherms for the first (upper branch) and the second (lower branch) solutions are illustrated in Figs. 12 and 13 when $\gamma =0.05$ and 0.06, $Ra=-1$, and $Pr=1$.

6 Conclusions

The steady two-dimensional boundary layer flow of a viscous and incompressible fluid over a moving vertical flat plate subject to the thermal convective boundary condition has been examined in this paper. The analysis revealed that similarity solutions exist if the convective heat transfer coefficient $\gamma$ is inversely proportional to $x^{-1/4}$. The numerical solutions have been reported for various governing parameters. The following conclusions can be made:

• Multiple (dual) solutions exist for both the cases of assisting $(Ra>0)$ and opposing $(Ra<0)$.

• The stability analysis has revealed that the upper branch solutions are stable and physically realizable, while the lower branch solutions are unstable and, therefore, not physically realizable.

• It is found that there are critical values $Ra_\mathrm{c}<0$ of $Ra<0$, with the values of $|Ra_\mathrm{c}|$ decreasing with increasing $\gamma$ for $f''(0)$ and increasing with $\gamma$ for $-\theta '(0)$, respectively.

• The reduced skin friction $f''(0)$ decreases, while the rate of heat transfer increases with the increase of $\gamma$ when the flow is opposing $(Ra<0)$.

• The velocity and temperature profiles are also affected by the governing parameters Ra and $\gamma$.