Global solvability of real analytic involutive systems on compact manifolds

Abstract

The focus of this work is the smooth global solvability of a linear partial differential operator ${\mathbb {L}}$ associated to a real analytic closed non-exact 1-form b—defined on a real analytic closed n-manifold—that may be naturally regarded as the first operator of the complex induced by a locally integrable structure of tube type and co-rank one. We define an appropriate covering projection $\widetilde{M}\rightarrow M$ such that the pullback of b has a primitive $\widetilde{B}$ and prove that the operator is globally solvable if and only if the superlevel and sublevel sets of $\widetilde{B}$ are connected. As a byproduct we obtain a new geometric characterization for the global hypoellipticity of the operator. When M is orientable we prove a connection between the global solvability of ${\mathbb {L}}$ and that of ${\mathbb {L}}^{n-1}$ which is the last non-trivial operator of the complex, in particular, we prove that ${\mathbb {L}}$ is globally solvable if and only if ${\mathbb {L}}^{n-1}$ is globally solvable. In the smooth category, we are able to provide analogous geometric characterizations of the global solvability and the global hypoellipticity when b is a Morse 1-form, i.e., when the structure is of Mizohata type.

1 Introduction

Let b be a real analytic closed non-exact 1-form defined on a real analytic closed (i.e., compact and without boundary) connected n-dimensional manifold M $(n>1)$. The focus of this work is the differential operator $\mathbb {L}: C^\infty (M\times \mathbb S^1) \rightarrow \bigwedge ^1 C^\infty (M\times \mathbb S^1)$ defined by

$$\begin{aligned} \mathbb {L}u=d_tu+ib(t)\wedge \partial _x u, \end{aligned}$$

(1)

where x belongs to the unit circle $\mathbb S^1$ and $d_t:C^\infty (M)\rightarrow \bigwedge ^{1}C^\infty (M)$ is the exterior derivative on M. Consider the vector fields

$$\begin{aligned} L_j=\frac{\partial }{\partial t_j}+i\frac{\partial B}{\partial t_j}(t)\frac{\partial }{\partial x},\quad j=1,\ldots ,n, \end{aligned}$$

where $(t_1,\ldots ,t_n)$ are local coordinates on M and B is a local primitive of b. They are local generators of the bundle $\mathscr {V}\doteq (T')^{\perp }\subset \mathbb {C}\otimes T(M\times \mathbb S^1)$ where $T'$ is the line sub-bundle of $\mathbb {C}\otimes T^*(M\times \mathbb S^1)$ generated by the 1-form $dx-ib$. Any involutive structure defines in a natural way a complex of differential operators (see [10, Ch.VII], [36]) which in the case of $\mathscr {V}$ is given by (1) when acting on functions. Thus, we have a complex of differential operators

$$\begin{aligned} C^\infty (M\times \mathbb S^1)&\mathop {\longrightarrow }\limits ^{\mathbb {L}}&\mathfrak {U}^1(M\times \mathbb S^1)\mathop {\longrightarrow }\limits ^{\mathbb {L}^1}\nonumber \\ \mathop {\longrightarrow }\limits ^{\mathbb {L}^1}\mathfrak {U}^2(M\times \mathbb S^1) \mathop {\longrightarrow }\limits ^{\mathbb {L}^2}&\cdots&\mathop {\longrightarrow }\limits ^{\mathbb {L}^{n-1}}\mathfrak {U}^{n}(M\times \mathbb S^1) \mathop {\longrightarrow }\limits ^{\mathbb {L}^{n}}0 \end{aligned}$$

(2)

analogous to the de Rham complex where the space $\mathfrak {U}^j(M\times \mathbb S^1)$, $j=1,\ldots ,n-1$, is obtained by taking an appropriate quotient on the space of j-forms on $M\times {\mathbb {S}}^1$ (we refer to [10, p.311] for details).

The global hypoellipticity of (1) was studied and completely characterized by Bergamasco, Cordaro and Malagutti [3].

Here, we will study the smooth global solvability of the equation $\mathbb {L}u=f$, i.e., the possibility of finding a globally defined solution $u\in C^\infty (M\times \mathbb S^1)$ when f is smooth. Of course, if f is in the range of $\mathbb {L}$ it must satisfy two obvious conditions analogous to the fact that an exact form is both closed and orthogonal to the closed cocyles: (i) $\mathbb {L}^1f=0$ (a consequence of the complex property $\mathbb {L}^1\mathbb {L}=0$), and (ii) f must be orthogonal to the kernel of the dual operator $\mathbb {L}^*$. They are usually referred to as the compatibility conditions for f and they may be formulated in equivalent different ways that turn out to be best suited for the operator under study.

Note that (i) is of local nature while the homology of M plays a role in (ii). In general, given f satisfying the compatibility conditions, the equation $\mathbb {L}u=f$ might or might not have a solution. We say that $\mathbb {L}$ is globally solvable if the equation $\mathbb {L}u=f$ has a globally defined smooth solution whenever the right-hand side satisfies the compatibility conditions.

We now recall some previous work. In his seminal paper [34], Treves studied and characterized the semi-global solvability of a similar complex (defined in the context of pseudo-differential operators) in terms of the homological properties of the semilevel sets (sublevel sets and superlevel sets) of an appropriate locally defined function associated to the complex (for the first operator of the complex this amounts to the connectedness of the semilevel sets). This link between homological properties of semilevel sets of an appropriate function and solvability led to several papers on the local solvability of structures of co-rank 1, e.g., [13, 15–20, 28, 35].

While the local solvability of structures of co-rank 1 has been extensively studied and is well understood at all levels, much less is known about the global solvability of the complex (2) except at the top level, a case that was extensively studied in [4]. Hence, we focus on the first level and start by mentioning some previous results. If $g(x)\in C^\infty (\mathbb S^1),$ denote the Fourier coefficients of g(x) by $\hat{g}(\xi )\doteq (2\pi )^{-1}\int _0^{2\pi }e^{-i\xi x} g(x)\,dx$, $\xi \in \mathbb Z$. Suppose that M is a closed orientable manifold M and b is smooth and exact, then define a primitive on M by $B(t)=\int _{t_0}^tb$. The global solvability of the equation ${\mathbb {L}}u=f$ when b is exact was characterized in [12] as follows.

Theorem

[12] If b is exact the following statements are equivalent:

• (I) For every $f\in \bigwedge ^1 C^{\infty }(M\times \mathbb S^1)$ such that $e^{-\xi B(t)}\hat{f}(t,\xi )$ is exact for all $\xi \in \mathbb Z,$ there exists $u\in C^{\infty }(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}u=f$.

• (II) The semilevel sets $\{t\in M: B(t)<r\}$ and $\{t\in M: B(t)>r\}$ are connected for every $r\in \mathbb {R}$.

When b is smooth and closed but not exact we may pull back b to the universal covering of M and consider the semilevel sets of a primitive B of the pullback of b. In [6, 7], the authors studied the case of a torus $M=\mathbb {T}^2$ and proved

Theorem

[6, 7] The following statements are equivalent:

• (I) For every $f=f_1(t,x)dt_1+f_2(t,x)dt_2\in \bigwedge ^1 C^{\infty }(\mathbb T^3)$ such that

  $$\begin{aligned} \mathbb {L}^1f=0 \quad \text { and }\quad \int \limits _0^{2\pi }\int \limits _0^{2\pi }f_1(t_1,0,x)dt_1dx=\int \limits _0^{2\pi }\int \limits _0^{2\pi }f_2(0,t_2,x)dt_2dx=0, \end{aligned}$$

  there exists $u\in C^\infty (\mathbb T^3)$ satisfying ${\mathbb {L}}u=f$, where $(t,x)=(t_1,t_2,x)$ are global coordinates in $\mathbb T^3.$

• (II) The semilevel sets $\{t\in \mathbb {R}^2: B(t)<r\}$ and $\{t\in \mathbb {R}^2: B(t)>r\}$ are connected for every $r\in \mathbb {R}$.

We now state our main result and describe the organization of the paper. It involves a covering space $\widetilde{M}$ such that the pullback of b to $\widetilde{M}$ has a primitive $\widetilde{B}$ and is minimal in the sense that any other covering with this property is above $\widetilde{M}$ in the usual partial order of covering projections (see Sect. 2 for details). The natural compatibility conditions for the right-hand side of the equation are described in detail in Sect. 3.

Theorem 1

Assume that b is real analytic, closed and not exact. The following statements are equivalent:

• (I) For every $f\in \bigwedge ^1 C^{\infty }(M\times \mathbb S^1)$ that satisfies the compatibility conditions, there exists $u\in C^{\infty }(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}u=f$.

• (II) For every $r\in \mathbb {R}$, the semilevel sets $\{t\in \widetilde{M}: \widetilde{B}(t)<r\}$ and $\{t\in \widetilde{M}: \widetilde{B}(t)>r\}$ are connected.

The proof of (I) $\implies$ (II) involves a refinement of the ideas in [37] and a related submitted work by Bergamasco, Parmeggiani, Zani and the second author, where necessary conditions for global solvability are considered for closed orientable surfaces M although some of the arguments are strictly two dimensional. We emphasize that this implication remains valid when b is a smooth—not necessarily real analytic—closed non-exact 1-form defined on a smooth closed connected n-dimensional manifold M. The reverse implication is discussed in Sect. 6 where we take advantage of some special properties of real analytic functions proved in [24, 27, 33] and also make decisive use of Lojasiewicz’s inequality (see, e.g., [11]) which states that if $\Phi$ is a real analytic function on a neighborhood of the origin and $\Phi (0)=0,$ then there exist $C_0>0$ and $\theta \in (0,1)$ such that

$$\begin{aligned} \Vert \nabla \Phi (s)\Vert \geqslant C_0|\Phi (s)|^{\theta } \end{aligned}$$

for every s sufficiently close to 0. Let us denote by $\Sigma$ the set of the critical points of b, that is,

$$\begin{aligned} \Sigma \doteq \{t\in M: b(t)=0\}. \end{aligned}$$

In Sect. 6.1, we recall the existence shown in [3] of a primitive $B^{\dag }$ of b defined on a neighborhood of $\Sigma$ and prove what is a crucial ingredient in the proof of (II)$\implies$(I) in Theorem 1, namely the fact that the connectedness of the semilevel sets of $\widetilde{B}$ in $\widetilde{M}$ is equivalent to the following property:

$$\begin{aligned}&{} Every\, connected\, component \Sigma _0 \, { of} \, \Sigma \text { contains\, a \,point\,} p^* { \,such \,that\, a \,local\, primitive\, of\,} \\&b ~{ is\, open\, at\,} p^*. \quad \quad (\star ) \end{aligned}$$

This geometric property was known [8] to provide a necessary condition for the global solvability of (1) in the special case $M=\mathbb T^2$ when b is real analytic. Furthermore, it is a theorem of Bergamasco, Cordaro and Malagutti [3] that holds in the real analytic setup that, for general M, property ($\star$) is equivalent to the global hypoellipticity of (1). Hence we get

Corollary 2

Assume that b is real analytic, closed and not exact. The following statements are equivalent:

• (I) For every $f\in \bigwedge ^1 C^{\infty }(M\times \mathbb S^1)$ that satisfies the compatibility conditions, there exists $u\in C^{\infty }(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}u=f$.

• (II) For every $r\in \mathbb {R}$, the semilevel sets $\{t\in \widetilde{M}: \widetilde{B}(t)<r\}$ and $\{t\in \widetilde{M}: \widetilde{B}(t)>r\}$ are connected.

• (III) Property ($\star$) holds.

• (IV) ${\mathbb {L}}$ is globally hypoelliptic.

In particular, (II) furnishes a new geometric condition that may be used to characterize the global hypoellipticity of ${\mathbb {L}}$ and it turns out that ${\mathbb {L}}$ is globally solvable if and only if it is globally hypoelliptic. On the other hand, property $(\star )$ characterizes global solvability in geometric terms that are formulated without recurring to any covering of M. Note that the assumption that b is not exact is essential since when $b\equiv 0$ the operator ${\mathbb {L}}$ is globally solvable but not globally hypoelliptic. We recall that (1) is defined by a real form b,  and we observe that when dealing with general complex forms the global solvability and the global hypoellipticity are also related to some Diophantine conditions, as in [3, 5, 9], or in [14, 21, 25] for single vector fields.

When M is orientable, there is a natural pairing on $\mathfrak {U}^k(M\times \mathbb S^1)\times \mathfrak {U}^{n-k}(M\times \mathbb S^1)$, $0\leqslant k\leqslant n$, which may be used to interpret the operators ${\mathbb {L}}^k$ and $\mathbb L^{k-1}$, $0\leqslant k\leqslant n$, as dual of each other (here $\mathfrak {U}^0(M\times \mathbb S^1)$ means $C^\infty (M\times \mathbb S^1)$). This duality is exploited in [4] to show that ${\mathbb {L}}^{n-1}$ is globally solvable if and only if ${\mathbb {L}}$ is globally hypoelliptic. Since (I) and (IV) of Corollary 2 are equivalent properties we get

Corollary 3

Assume that M is orientable and b is real analytic, closed and not exact. The following statements are equivalent:

• (I) For every $f\in \bigwedge ^1 C^{\infty }(M\times \mathbb S^1)$ that satisfies the compatibility conditions, there exists $u\in C^{\infty }(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}u=f$.

• (II) For every $f\in \mathfrak {U}^n(M\times \mathbb S^1)$ orthogonal to $\mathrm{Ker}{\mathbb {L}}$, there exists $u\in \bigwedge ^{n-1}\mathscr {D}'(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}^{n-1}u=f$.

While (I) $\implies$ (II) in Corollary 2 holds when b is just smooth, it is not clear that the reverse implication remains true in general. In the smooth category, we prove in Sect. 7 the equivalence of (I), (II), (III) and (IV) under the assumption that b is a non-exact Morse form, which is equivalent to requiring that the structure $\mathcal V$ is a Mizohata structure. Mizohata structures have deserved considerable attention. The local integrability question for Mizohata structures was studied in [26, 29] and completely solved in [30]. Concerning global aspects of such structures, we mention [22, 31]. For further information and details we refer the reader to [10, 36]. In Sect. 7.1 we compare briefly the local solvability of our system with its global solvability when b is Morse. Finally, in Sect. 8, we discuss examples of globally solvable systems and mention some open questions.

We are thankful to the anonymous referee whose thorough review and comments helped us improve the presentation of the paper.

2 Preliminaries

Suppose we are given a closed manifold M where a real smooth closed and non-exact 1-form b is defined.

Recall that the group of deck transformations of the universal covering space of M is isomorphic to the first homotopy group $\pi _1(M,p_0)$ ([23, Prop. 1.39]). We will construct a covering space $\widetilde{M}$ of M with special properties, one of them being that the pullback of b to $\widetilde{M}$ is exact. More precisely, take the subgroup G of $\pi _1(M,p_0)$ equal to the kernel of the homomorphism $T: \pi _1(M,p_0) \rightarrow \mathbb {R}$ given by

$$\begin{aligned} \gamma \mapsto \int _{\gamma } b. \end{aligned}$$

By of [23, Theorem 1.38] there exists a covering space $(\widetilde{M},\widetilde{p_0})\rightarrow (M,p_0)$ such that $\pi _1(\widetilde{M},\widetilde{p_0})$ is isomorphic to G and for each pair of liftings of $p_0$ in $(\widetilde{M},\widetilde{p_0})$ there is a deck transformation mapping one to the other ([23, Prop. 1.39]). Because of this, $(\widetilde{M},\widetilde{p_0})$ is called a normal covering space. Moreover, the group $\mathsf {D}$ of deck transformations of $(\widetilde{M},\widetilde{p_0})$ is $\pi _1(M,p_0)/G$ which is finitely generated. We will denote a minimal set of generators of $\mathsf {D}$ by $\{\sigma _k\},$ $k=1,\ldots ,\ell .$

Definition 4

We call $(\widetilde{M},\widetilde{p_0})$ the minimal covering of M (with respect to b).

It is minimal in the sense that G must contain a copy of the fundamental group of any covering space on which a primitive of b is defined. The definition above is a natural generalization of the concept of minimal covering considered in [5, 7].

This covering space is unique up to homeomorphisms and the basepoints can be omitted since G is normal.

Let us fix the projection $\Pi :\widetilde{M}\rightarrow M$ and define a primitive $\widetilde{B}$ of the pullback $\Pi ^*(b)$ in $\widetilde{M}$ by integration from $t_0\in \widetilde{M}$. Note that, for each $\sigma \in \mathsf D$, we have

$$\begin{aligned} \widetilde{B}(\sigma (t))=\int \limits _{t_0}^{\sigma (t)}\Pi ^*(b)=\int \limits _{t_0}^{\sigma (t_0)}\Pi ^*(b) +\int \limits _{\sigma (t_0)}^{\sigma (t)}\Pi ^*(b)=\int \limits _{t_0}^{\sigma (t_0)}\Pi ^*(b)+B(t), \end{aligned}$$

since $\Pi =\Pi \circ \sigma$ and, thus, $\Pi ^*(b)=(\Pi \circ \sigma )^*(b)=\sigma ^*(\Pi ^*(b))$.

The numbers $\int _{t_0}^{\sigma (t_0)}\Pi ^*(b)$ do not depend on $t_0$. Indeed, if $t'_0\in \widetilde{M},$

$$\begin{aligned} \int \limits _{t'_0}^{\sigma (t'_0)}\Pi ^*(b)&=\int \limits _{t'_0}^{t_0}\Pi ^*(b) +\int \limits _{t_0}^{\sigma (t_0)}\Pi ^*(b)+\int \limits _{\sigma (t_0)}^{\sigma (t'_0)}\Pi ^*(b)\\&=-\int \limits _{t_0}^{t'_0}\Pi ^*(b)+\int \limits _{t_0}^{\sigma (t_0)}\Pi ^*(b) +\int \limits _{t_0}^{t'_0}\sigma ^*(\Pi ^*(b))=\int \limits _{t_0}^{\sigma (t_0)}\Pi ^*(b). \end{aligned}$$

Thus, we may write

$$\begin{aligned} \widetilde{B}(\sigma (t))=\widetilde{B}(t)+b_{\sigma },\quad t\in \widetilde{M}, \end{aligned}$$

(3)

where the constant $b_{\sigma }$ is not 0 unless $\sigma$ is the identity transformation.

Example 5

In Fig. 1 (page 12) we illustrate a case when M is an orientable surface of genus 2. Assume that $\{c_i,d_i\}$, $i=1,2$, are the canonical generators of the homology of the tori whose connected sum is M. The 1-form b will be such that $\displaystyle {\int _{c_2}b=\int _{d_1}b=0},$ and $\displaystyle {\int _{c_1}b}$ and $\displaystyle {\int _{d_2}b}$ are linearly independent over $\mathbb Z.$ We cut along $c_1$ and $d_2$ and we glue infinitely many copies of this surface with boundary by identifying them properly, in the sense that a primitive of b satisfying (3) is defined on the covering space.

We pick a complete Riemannian metric m on M and consider the induced Riemannian metric $m^*$ on $\widetilde{M}$ given by

$$\begin{aligned} m^*(X_{\tilde{p}}, Y_{\tilde{p}})\doteq m(D_{\tilde{p}}\Pi (X_{\tilde{p}}),D_{\tilde{p}}\Pi (Y_{\tilde{p}})). \end{aligned}$$

Recall that if $\sigma (\tilde{p})=\tilde{q}$ then

$$\begin{aligned} m^*(D_{\tilde{p}}\sigma (X_{\tilde{p}}), D_{\tilde{p}}\sigma (Y_{\tilde{p}}))= & {} m(D_{\tilde{q}}\Pi (D_{\tilde{p}}\sigma (X_{\tilde{p}})),D_{\tilde{q}}\Pi (D_{\tilde{p}}\sigma (Y_{\tilde{p}})))\nonumber \\= & {} m(D_{\tilde{p}}(\Pi \circ \sigma )(X_{\tilde{p}}), D_{\tilde{p}}(\Pi \circ \sigma )(Y_{\tilde{p}}))=m^*(X_{\tilde{p}}, Y_{\tilde{p}}) \end{aligned}$$

so we get the well known

Fact 1

For every $\sigma \in \mathsf D,$ $D_{\tilde{p}}\sigma$ is an isometry.

3 Compatibility conditions and global solvability

Now we are ready to define the compatibility conditions for our system. The space of plausible right-hand sides for the equation ${\mathbb {L}}u=f$ will be denoted by $\mathbb E$.

Definition 6

(Compatibility conditions) We say that a 1-form $f\in \bigwedge ^1 C^{\infty }(M\times \mathbb S^1)$ belongs to $\mathbb {E}$ if

• (i) for each $\xi \in \mathbb {Z}{\setminus } \{0\}$ and each smooth closed curve $\gamma$ in $\widetilde{M},$

  $$\begin{aligned} \int _{\gamma }e^{-\xi \widetilde{B}(s)}\hat{f}(s,\xi )=0, \end{aligned}$$

• (ii) and for each smooth closed curve $\gamma$ in M, 

  $$\begin{aligned} \int _{\gamma }\hat{f}(s,0)=0. \end{aligned}$$

A few words about this definition. In (i), $\hat{f}(s,\xi )$ denotes (with a slight abuse of notation) the pullback to $\widetilde{M}$ of the non-zero Fourier coefficients of f. For the sake of simplicity, we will use the same notation for a form in M and its pullback to $\widetilde{M}$ except when doing so might lead to confusion. Also, note that this definition is independent of the choice of a primitive $\widetilde{B}$. If we suppose that $\mathscr {M}$ is a covering space where a primitive $B'$ of b is defined and $\gamma \in \pi _1(\mathscr {M}),$ then $\gamma \in G=\pi _1(\widetilde{M}),$ and

$$\begin{aligned} \int _{\gamma }e^{-\xi \widetilde{B}(s)}\hat{f}(s,\xi )=0\implies \int _{\gamma }e^{-\xi B'(s)}\hat{f}(s,\xi )=0 \end{aligned}$$

for $\xi \in \mathbb {Z}{\setminus } \{0\}.$

The conditions then say that

$$\begin{aligned} e^{-\xi B'(t)}\hat{f}(t,\xi ) \text { is an exact } 1\text {-form on }\mathscr {M}\text { for every }\xi \in \mathbb Z{\setminus }\{0\}. \end{aligned}$$

By taking Fourier coefficients, a candidate to a solution of ${\mathbb {L}}u=f$ should satisfy, for every $\xi \in \mathbb {Z}$, the differential equation

$$\begin{aligned} d_t\hat{u}(t,\xi )-\xi b(t)\hat{u}(t,\xi )=\hat{f}(t,\xi ) \end{aligned}$$

(4)

which can be rewritten as

$$\begin{aligned} d_t(e^{-\xi B'(t)}\hat{u}(t,\xi ))=e^{-\xi B'(t)}\hat{f}(t,\xi ). \end{aligned}$$

(5)

Definition 7

We say that the operator (1) is globally solvable if given any 1-form $f\in \mathbb {E}$ there exists $u\in \mathscr {D}'(M\times \mathbb S^1)$ such that $\mathbb {L}u=f$.

We say that the operator (1) is globally hypoelliptic if $u\in C^\infty (M\times \mathbb S^1)$ whenever $\mathbb {L}u\in \bigwedge ^1C^\infty (M\times \mathbb S^1)$.

Recall that if f is in the range of $\mathbb {L}$ we must have $\mathbb {L}^1f=0$ by involutivity, a property that holds for any $f\in \mathbb {E}$.

4 A necessary condition and auxiliary lemmas

In the proof of the part “(I) implies (II)” in Theorem 1 we will only need to assume that M is a smooth closed manifold equipped with a Riemannian metric rather than a real analytic one. Hence, in Sects. 4 and 5 no analyticity assumptions will be made and b will be a smooth closed non-exact 1-form.

When b is exact, the connectedness of the semilevel sets of a primitive defined on the manifold is a necessary and a sufficient condition for the global solvability in [12] (in this case, the minimal covering is M itself). In [6, 7], when M is the torus and b is closed but not exact, the connectedness of the semilevel sets in the universal covering space is a necessary and a sufficient condition for the global solvability. There, the non-connectedness of a semilevel set in the universal covering space is equivalent to the non-connectedness of a semilevel set in the minimal covering space which might be the plane or the cylinder. Nevertheless, due to [37] one can construct examples of globally solvable systems when b is non-exact and defined on a surface of genus $g>1,$ where a primitive of the pullback of b to the universal covering possesses a disconnected semilevel set. This shows the relevance of considering all coverings for which the pullback of b has a primitive rather than focusing on the universal covering alone.

Consider the minimal covering $\Pi :\widetilde{M}\rightarrow M$ of M and for any $r\in \mathbb R$ denote by $\Omega ^r$ the superlevel set $\{t\in \widetilde{M}: \widetilde{B}(t)>r\}$ and by $\Omega _r$ the sublevel set $\{t\in \widetilde{M}: \widetilde{B}(t)<r\}$. One of the essential observations in the proof of Theorem 1 is the fact that for any $r\in \mathbb R$ each of the sets $\Omega ^r$ and $\Omega _r$ have exactly one component as stated in the proposition below. We will need a couple of lemmas in its proof. In the remainder of this section we will focus on superlevel sets for the sake of simplicity but the corresponding claims for sublevel sets are true as well. We now start preparing for the proposition below.

Fix a base point $p_0\in M$ and a base point $\widetilde{p_0}\in \widetilde{M}$ such that $\Pi (\widetilde{p_0})=p_0$. Consider loops $\gamma _j\in \pi _1(M,p_0)$, $j=1,\ldots ,\ell$ at $p_0$ such that their equivalence classes $[\gamma _j] \in \pi _1(M,p_0)/G$ make up a minimal set of generators of $\pi _1(M,p_0)/G\simeq \mathsf D$ . Let $\widetilde{\gamma }_j$, $j=1,\ldots ,\ell$ be the lifting of $\gamma _j$ stemming from $\widetilde{p_0}$. Then $\widetilde{\gamma }_j$ connects $\widetilde{p_0}$ to $t_j=\sigma _j(\widetilde{p_0})$ where $\sigma _j\in D$ is the deck transformation corresponding to $[\gamma _j]$. We will assume without loss of generality that $\beta _j\doteq \int _{t_0}^{t_j}\Pi ^*(b)>0$, $j=1,\ldots ,\ell$. Define the set $\mathscr {K}\doteq \cup _{j=1}^{\ell }\widetilde{\gamma }_j\subset \widetilde{M}$. Note that $\mathscr {K}$ is connected and $t_j \in \widetilde{\gamma }_j\cap \sigma _j(\widetilde{\gamma }_j)\subset \mathscr {K} \cap \,\sigma _j(\mathscr {K})$ so $\mathcal K \cap \sigma _j(\mathscr {K})$ is connected for any $j=1,\ldots ,\ell$ and, more generally, $\bigcup _{k=0}^{k_0}\sigma _j^k(\mathscr {K})$ is connected as well.

Lemma 8

Let $r\in \mathbb R$, let $\mathscr {O}\subset \Omega ^r$ be a connected component of $\Omega ^r$ and set

$$\begin{aligned} \mu =\Vert b\Vert _{L^\infty }\mathrm{diam}\,(M)=\Vert b\Vert _{L^\infty } \sup _{t\in M} \mathrm{dist}\,(t,p_0). \end{aligned}$$

Assume that there is a point $\widetilde{y}_0\in \mathscr {O}$ such that $\widetilde{B}(\widetilde{y}_0)>r+\mu$. Then we can find a deck transformation $\tau \in \mathsf D$ such that $\tau (\widetilde{p_0})\in \mathscr {O}$.

Proof

Set $y_0=\Pi (\widetilde{y}_0)$, let $\gamma$ be the minimal geodesic from $y_0$ to $p_0$ and consider the lifting $\widetilde{\gamma }$ that starts at $\widetilde{y}_0$ and reaches a point $\tau (\widetilde{p}_0)\in \Pi ^{-1}(\{p_0\})$ for some $\tau \in \mathsf D$. Thus

$$\begin{aligned} |\widetilde{B}(\tau (\widetilde{p_0}))-\widetilde{B}(\widetilde{y}_0)|=\left| \int _{y_0}^{\tau (\widetilde{p_0})}\Pi ^*(b)\right| =\left| \int _{\gamma }b\right| \leqslant \mu \end{aligned}$$

and similarly $|\widetilde{B}(\widetilde{\gamma }(s))-\widetilde{B}(\widetilde{y}_0)|\leqslant \mu$ for any intermediate point $\widetilde{\gamma }(s)$ in the lifting of $\gamma$. It follows that $\widetilde{B}>r$ on $\widetilde{\gamma }$ so $\widetilde{\gamma }\subset \mathscr {O}$ and $\tau (\widetilde{p_0})\in \mathscr {O}$. $\square$

Lemma 9

Set

$$\begin{aligned} \nu =\mathrm{osc}\,_{\mathscr {K}}\doteq \sup _{t,t'\in \mathscr {K}}|\widetilde{B}(t)-\widetilde{B}(t')|. \end{aligned}$$

Assume that there is a point $\widetilde{y}_0\in \mathscr {O}$ such that $\widetilde{B}(\widetilde{y}_0)>r+\mu +\nu$. Then we can find a deck transformation $\tau \in \mathsf D$ such that $\tau (\mathscr {K})\subset \mathscr {O}$.

Proof

The proof of the previous lemma shows that we may find $\tau \in \mathsf D$ such that $\tau (\widetilde{p}_0)\in \mathscr {O}$ and $\widetilde{B}(\tau (\widetilde{p}_0))>r+\nu$. Since the oscillation of $\widetilde{B}$ is the same on $\mathscr {K}$ and on $\tau (\mathscr {K})$ and $\tau (\mathscr {K})$ is connected, we conclude that $\widetilde{B}>r$ on $\tau (\mathscr {K})$ and $\tau (\mathscr {K})\subset \mathscr {O}$.   $\square$

The following proposition is crucial.

Proposition 10

For every $r\in \mathbb R,$ there is exactly one component of $\Omega ^r$ on which $\widetilde{B}$ is unbounded.

Proof

First we prove the existence of a component of $\Omega ^r$ on which $\widetilde{B}$ is unbounded. As $\beta _1>0,$ $\widetilde{B}(\sigma _1^n(t))=\widetilde{B}(t)+n\beta _1>r$ for $t\in \mathscr {K}$ and any integer $n>n_0$ if $n_0$ is chosen sufficiently large. Hence, $K\doteq \cup _{n>n_0}\sigma _1^n(\mathscr {K})$ is a connected subset of $\Omega ^r.$ Since $\widetilde{B}$ is unbounded on K,  $\widetilde{B}$ is unbounded a component $\mathscr {O}$ of $\Omega ^r$.

Now suppose that $\mathscr {O}$ and $\mathscr {O}'$ are components of $\Omega ^r$ and $\widetilde{B}$ is unbounded on both of them. We must prove that $\mathscr {O}$ and $\mathscr {O}'$ coincide. Since $\widetilde{B}$ assumes arbitrary large values on $\mathscr {O}$ and $\mathscr {O}'$ we may apply Lemma 9 to find deck transformations $\tau ,\tau '\in \mathsf D$ such that $\tau (\mathscr {K})\subset \mathscr {O}$ and $\tau '(\mathscr {K})\subset \mathscr {O}'$. We now write

$$\begin{aligned} \tau '(\mathscr {K})=\sigma _1^{n_1}\cdots \sigma _{\ell }^{n_{\ell }}(\tau (\mathscr {K})) \end{aligned}$$

for some $n_1,\ldots ,n_{\ell }\in \mathbb Z{\setminus }\{0\},$ where, recall, $\sigma _1=[\gamma _1],\ldots ,\sigma _{\ell }=[\gamma _{\ell }]$ are the generators of $\mathsf D$ and we assume $\beta _{1},\ldots ,\beta _{\ell }>0$. Moreover, we may assume that $\{n_1,\ldots ,n_{\ell }\}\cap \mathbb Z^{+}=\{n_1,\ldots ,n_{k-1}\}$ since $\mathsf D$ is abelian. Thus, we have

$$\begin{aligned} \sigma _1^{n_1}\cdots \sigma _{k-1}^{n_{k-1}}(\tau (\mathscr {K}))=\sigma _k^{-n_k}\cdots \sigma _{\ell }^{-n_{\ell }}(\tau '(\mathscr {K})). \end{aligned}$$

(6)

The sets

$$\begin{aligned} A=\bigcup _{\begin{array}{c} 0\leqslant m_j\leqslant n_j\\ j=1,\ldots ,k-1 \end{array}}\sigma _1^{m_1}\cdots \sigma _{j}^{m_{j}}\cdots \sigma _{k-1}^{m_{k-1}}(\tau (\mathscr {K})) \end{aligned}$$

and

$$\begin{aligned} A'=\bigcup _{\begin{array}{c} 0\leqslant m_j\leqslant -n_j\\ j=k,\ldots ,\ell \end{array}} \sigma _k^{m_k}\cdots \sigma _{j}^{m_{j}}\cdots \sigma _{\ell }^{m_{\ell }}(\tau '(\mathscr {K})) \end{aligned}$$

are connected. Since $\tau (\mathscr {K})\subset A$ and $\tau '(\mathscr {K})\subset A',$ $\widetilde{B}$ is greater than r on $A\cup A'$. The identity (6) shows that $A\cap A'\ne \emptyset$. Therefore, $\mathscr {O}$ and $O'$ are the same component of $\Omega ^r.$ $\square$

Remark 11

Let $\mathscr {M}$ be a covering space of M where a primitive $B'$ of b is defined. Notice that there exists $r\in \mathbb R$ and a component $\mathscr {O}$ of $\Omega ^r=\{t\in \mathscr {M}: \widetilde{B}(t)>r\}$ such that $\widetilde{B}$ is bounded $\mathscr {O}$ if and only if $B'$ is bounded on a component $\mathscr {O}'$ of $\{t\in \widetilde{M}: B'(t)>r'\}$ for some $r'\in \mathbb R.$ Therefore, the previous proposition shows that, when b is non-exact, the non-connectedness of a semilevel set in the minimal covering space is equivalent to the existence of a component $\mathscr {O}'$ of a semilevel set such that $B'$ is bounded on $\mathscr {O}'.$

We now state two additional key lemmas. The first one is proved in [1] although we include the proof, which is quite short. The second one is a standard variation of a celebrated lemma of Hörmander’s. The version presented here is quite similar to the one in [34] and need not be proved.

If $X\subset \widetilde{M}$ and $\sigma \in \mathsf D,$ the set $\sigma (X)$ is referred to as a translate of X.

Lemma 12

If $\widetilde{B}$ is bounded on a component $\mathscr {O}$ of $\Omega ^r,$ a translate $\sigma (\mathscr {O})$, with $\sigma \ne 1$, is disjoint from $\mathscr {O}.$

Proof

Suppose that $\sigma \in \mathsf D$ is not the identity and let us show that $\mathscr {O}\cap \sigma (\mathscr {O})=\emptyset$. Note that $\sigma (\mathscr {O})$ is connected and contained in the $(r+\beta )$-superlevel set with $\beta =\int _t^{\sigma (t)}\Pi ^*(b)$ for any $t\in \widetilde{M}$. Recall that $\beta \ne 0$ and assume first that $\beta >0$. If $\sigma (\mathscr {O})\cap \mathscr {O}\ne \emptyset$ then $\sigma (\mathscr {O})\subset \mathscr {O}$ and therefore $\sigma ^k(\mathscr {O})\subset \mathscr {O}$ for $k\in \mathbb N$ contradicting the boundedness of $\widetilde{B}$ on $\mathscr {O}$. The case $\beta <0$ is analogous. $\square$

Lemma 13

If $\mathbb {L}$ is globally solvable, there exist constants $C>0$ and $m\in \mathbb {N}$ such that, for all $f\in \mathbb E$ (see Definition 6) and $g\in \bigwedge ^{1}C^{\infty }_c(\widetilde{M}\times \mathbb S^1),$

$$\begin{aligned} \left| \int _{\widetilde{M}\times \mathbb S^1}\langle \tilde{f}, g\rangle \right| \leqslant C \Vert \tilde{f}\Vert _{m}\Vert \mathbb {L}^*g\Vert _{m}, \end{aligned}$$

where $\tilde{f}=\Pi ^*(f)$ and ${\mathbb {L}}^*$ is the adjoint operator of ${\mathbb {L}}$.

Here $\Vert v\Vert _m=\mathrm{sup}_{\widetilde{M}\times \mathbb S^1}\sum _{|\beta |\leqslant m}|\partial ^{\beta }v(t,x)|,$ where $|\beta |$ denotes the order of a multi-index $\beta$.

In the proof of “(I) implies (II)” of Theorem 1 we will construct sequences of 1-forms $f_k\in \mathbb {E}$ and $g_k \in \bigwedge ^1C^{\infty }_c(\widetilde{M}\times \mathbb S^1)$ that violate the inequality above when k goes to infinity under the assumption that a semilevel set is disconnected.

5 Proof of Theorem 1: (I) implies (II)

Assume the presence of a disconnected superlevel set of $\widetilde{B}$ (the proof for a disconnected sublevel set is similar). Due to Proposition 10, in $\widetilde{M}$ there exists a component $\mathscr {O}$ of a superlevel set, say $\Omega ^{r}$, such that $\widetilde{B}$ is bounded on $\mathscr {O}.$ Consider levels $r_1$ and $r_2$ both smaller than the supremum K of $\widetilde{B}$ on $\mathscr {O},$ with $r<r_1<r_2.$

Set $\Gamma ^{s}\doteq \{t\in \mathscr {O}: \widetilde{B}(t)>s\}.$ We have $\Gamma ^{r_2}\subset \Gamma ^{r_1}\subset \mathscr {O},$ and all of these sets are disjoint from their non-trivial translates by Lemma 12.

Let $\chi :\widetilde{M}\rightarrow \{0,1\}$ be the characteristic function of $\mathscr {O}$:

$$\begin{aligned}\chi (t) = \left\{ \begin{array}{lll} 1, &{}\quad t\in \mathscr {O}\\ 0, &{}\quad t\notin \mathscr {O}. \end{array} \right. \end{aligned}$$

Next let $\psi :\mathbb R\rightarrow [0,1]$ be a smooth non-negative function on $\mathbb R$ satisfying

• $\psi ^{-1}(\{1\})=[r_2,\infty );$

• $\psi ^{-1}(\{0\})=(-\infty ,r_1].$

We then define a smooth function $F:\widetilde{M}\rightarrow [0,1]$ by

$$\begin{aligned} F(t)=\chi (t)\psi (\widetilde{B}(t)). \end{aligned}$$

Notice that F has support contained in $\overline{\Gamma ^{r_1}}.$ We deduce that

$$\begin{aligned} \widetilde{B}(t)\leqslant r_2, \quad \forall t\in \mathrm{supp}(d_tF). \end{aligned}$$

(7)

Let $P_1$ be a point in $\in \Gamma ^{r_2}.$ Call $P_2$ a translate $\sigma ^{-1}(P_1)$ of $P_1$, with $b_{\sigma }<0.$ Consider small balls $\mathscr {B}_1$ and $\mathscr {B}_2$ respectively centered at $P_1$ and $P_2,$ such that $\widetilde{B}(t)>r_2+\varepsilon$ on them, for some $\varepsilon >0.$ The covering space $\widetilde{M}$ is path-connected, hence there exists a simple smooth path $\alpha$ such that

• $\alpha ([0,\varepsilon '])\subset \mathscr {B}_1;$

• $\alpha ([1-\varepsilon ',1])\subset \mathscr {B}_2;$

• $\alpha (\varepsilon ')=P_1$ and $\alpha (1-\varepsilon ')=P_2.$

Let $\mathscr {U}$ be a tubular neighborhood of $\alpha ,$ with coordinates $t_1,\ldots ,t_n$ ($t_1$ being tangent to $\alpha$). Let $\theta$ be a function defined on $\mathscr {U}$ such that $\partial _1\theta =1$ and $\partial _j\theta =0,$ $j=2,\ldots ,n.$ Take now $g\in C^{\infty }_c(\mathbb R)$ with $g(s)=1$ if $\theta (P_1)<s<\theta (P_2)$ and with support lying inside $[\theta (\alpha (0)),\theta (\alpha (1))].$

We construct the 1-form $v_0$ by

$$\begin{aligned} v_0(t)=h(t)g(\theta (t))dt_1, \end{aligned}$$

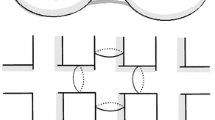
where h is a function defined on $\mathscr {U},$ which is strictly positive on a tubular neighborhood $\mathscr {U}'\subset \mathscr {U}$ of $\alpha ,$ vanishes on $\mathscr {U}{\setminus } \mathscr {U}',$ and satisfies $\partial _1h=0.$ Moreover, assume that $\mathscr {U}$ is chosen so as to make the support of $t\mapsto h(t)g'(\theta (t))$ lie inside $\mathscr {B}_1\cup \mathscr {B}_2.$ Furthermore, since $\mathscr {U}$ is a tubular neighborhood of a simple arc with different endpoints, we may assume that $\mathscr {U}$ is orientable even if M is not. We will take advantage of these observations later. We illustrate the construction in Fig. 1.

Fig. 1

Construction of $v_0$

We define, for $t\in \widetilde{M}$ and $k\in \mathbb N,$

$$\begin{aligned} \widetilde{F_k}(t)=\sum _{\sigma \in \mathsf D}e^{k(\widetilde{B}(\sigma (t))-\widetilde{B}(t))}F(\sigma (t)). \end{aligned}$$

(8)

Finally, define

$$\begin{aligned} f_k(t,x)=e^{ikx+k\widetilde{B}(t)}d_t\widetilde{F_k}(t) \end{aligned}$$

and

$$\begin{aligned} g_k(t,x)=e^{-ikx-k\widetilde{B}(t)}v_0(t). \end{aligned}$$

Claim $\widetilde{F_k}\in C^{\infty }(\widetilde{M})$ and $f_k\in \mathbb E.$

Proof

Notice that, if $t_0\in \widetilde{M}$ is such that $\widetilde{F_k}(t_0)\ne 0,$ then there is only one $\sigma \in \mathsf D$ such that $t\in \mathrm{supp}(F\circ \sigma )$ for t close to $t_0.$ Hence, $\widetilde{F_k}$ is indeed well-defined and smooth on $\bigcup _{\sigma \in \mathsf D}\sigma (\mathscr {O}).$

Now suppose that $t_0$ is in $\overline{\bigcup _{\sigma \in \mathsf D}\sigma (\Gamma _{r_1})}{\setminus } \bigcup _{\sigma \in \mathsf D}\sigma (\Gamma _{r_1})$ (in particular, $\widetilde{F_k}(t_0)=0$). Let us show that

$$\begin{aligned} |e^{k(\widetilde{B}(\sigma (t))-\widetilde{B}(t))}F(\sigma (t))|\rightarrow 0 \end{aligned}$$

(9)

when $t\rightarrow t_0,$ uniformly with respect to $\sigma \in \mathsf D.$ Indeed, if $t\in \widetilde{M}$ and $\sigma \in \mathsf D$ are such that $F(\sigma (t))\ne 0,$ then $\widetilde{B}(\sigma (t))<K.$ Hence, $e^{k(\widetilde{B}(\sigma (t))-\widetilde{B}(t))}\leqslant K_1$ for t close to $t_0.$

Moreover, if $\varphi$ is a local chart defined on a neighborhood W of $t_0,$ and $\varphi (W)$ is a ball centered at $\varphi (t_0)=0,$

$$\begin{aligned}|F(\sigma (\varphi ^{-1}(s)))|\leqslant \Vert s\Vert \mathrm{sup}_{\lambda \in [0,1]}\Vert D_{\lambda s}F\circ \sigma \circ \varphi ^{-1}\Vert . \end{aligned}$$

Now, using that b is defined on M and Fact 1, we finish the proof of (9).

Therefore, the convergence in (8) is uniform on W and we conclude that $\widetilde{F_k}$ is continuous everywhere. Applying the same procedure to the derivatives of the terms in (8) we obtain the smoothness of $\widetilde{F_k}.$

We have defined $f_k$ on $\widetilde{M}\times \mathbb S^1$ and in order to prove that $f_k$ defines a function on $M\times \mathbb S^1$ (that we will denote again by $f_k$) it suffices to notice that it is invariant in the t variable under any deck transformations $\sigma \in \mathsf D$, which follows from the expression

$$\begin{aligned} \widehat{f_k}(t,k)= & {} e^{k\widetilde{B}(t)}\sum _{\sigma \in \mathsf D}e^{k(\widetilde{B}(\sigma (t))-\widetilde{B}(t))}d_tF(\sigma (t))\nonumber \\= & {} \sum _{\sigma \in \mathsf D}e^{k\widetilde{B}(\sigma (t))}d_tF(\sigma (t)). \end{aligned}$$

(10)

$\square$

We are in a position to apply the inequalities of Lemma 13. Since $\mathscr {U}$ is orientable there is no loss of generality in assuming that the restriction to $\mathscr {U}$ of the Riemannian metric given on $\widetilde{M}$ is the Hodge metric, i.e.,

$$\begin{aligned} (\rho ,\phi )=\int _{\mathscr {U}}\rho \wedge *\phi ,\quad \rho ,\phi \in \bigwedge \nolimits ^1C^{\infty }_c(\mathscr {U}), \end{aligned}$$

where $*$ denotes the Hodge star operator on $\mathscr {U}.$ On $\mathscr {U}\times S^1$ the integral in Lemma 13 becomes $\int f_k\wedge *g_k \wedge dx$ and the adjoint ${\mathbb {L}}^*$ may be expressed as ${\mathbb {L}}^*g_k=*\mathbb L^{n-1}*g_k$ [recall that ${\mathbb {L}}^{n-1}$ is the previous to last operator in the complex (2)]. We have

$$\begin{aligned} \mathbb {L}^{n-1}(*g_k)(t,x)=e^{-ikx-k\widetilde{B}(t)}d_t(*v_0)(t), \end{aligned}$$

and a computation gives

$$\begin{aligned} d_t(*v_0)(t)=h(t)g'(\theta (t))dt_1\wedge \cdots \wedge dt_n. \end{aligned}$$

By (7) and (10),

$$\begin{aligned} \Vert f_k\Vert _m\leqslant C_mk^me^{kr_2}. \end{aligned}$$

(11)

Hence, in view of the construction of $v_0$, we have $\Vert f_k\Vert _m\Vert {\mathbb {L}}^{*}g_k\Vert _m\leqslant C'_mk^{2m}e^{-k\varepsilon },$ which goes to 0 when k goes to infinity. However, by Stokes’ Theorem,

$$\begin{aligned} \left| \int f_k\wedge *g_k \wedge dx\right|&=2\pi \left| \int d_t\widetilde{F_k}\wedge *v_0\right| \\&=2\pi \left| \int \widetilde{F_k}(t)h(t)g'(\theta (t))dt_1\wedge \cdots \wedge dt_n\right| . \end{aligned}$$

By choosing conveniently the functions h and g,  one obtains the latter value arbitrarily close to $2\pi |\widetilde{F_k}(P_1)-\widetilde{F_k}(P_2)|.$

Recall that we have taken $P_1$ and $P_2$ satisfying $F(P_1)=1$ and $\widetilde{F_k}(P_2)=e^{kb_{\sigma }},$ with $b_{\sigma }<0.$ Therefore, $2\pi |\widetilde{F_k}(P_1)-\widetilde{F_k}(P_2)|$ can be made strictly positive.

This contradiction leads us to conclude that there is $f\in \mathbb {E}$ so that the equation $\mathbb {L}u=f$ does not have solution on $M\times \mathbb S^1.$ $\square$

6 Proof of Theorem 1: (II) implies (I)

The proof of the remaining implication is constructive and it will involve several steps. In this part the analyticity assumptions will be essential in the arguments and we will work in the analytic category.

First notice that, given f belonging to the space $\mathbb E$ of compatible right-hand sides, we can compute the Fourier coefficients of a candidate to a solution of (1) on $\widetilde{M}$ by solving a differential equation as in (5) for each $\xi \in \mathbb {Z},$ which yields

$$\begin{aligned} \widehat{u}(t,\xi )=\int \limits _{t_0}^{t}\upsilon +K_{\xi }e^{\xi \widetilde{B}(t)}, \end{aligned}$$

where $\displaystyle {\upsilon (s,\xi )=e^{-\xi [\widetilde{B}(s)-\widetilde{B}(t)]}\hat{f}(s,\xi )}.$

In order to have a solution on M we need that $\widehat{u}(\sigma (t),\xi )=\widehat{u}(t,\xi )$, $\sigma \in \mathsf D$, which uniquely determines $K_{\xi }$ and the coefficients of the sought-after solution for $\xi \ne 0$, namely

$$\begin{aligned} \widehat{u}(t,\xi )=\rho (\xi )\int \limits _{t}^{\sigma (t)}\upsilon ,\quad \upsilon (s,\xi )=e^{-\xi [\widetilde{B}(s)-\widetilde{B}(t)]}\hat{f}(s,\xi ), \end{aligned}$$

(12)

where $\rho (\xi )=(e^{-\xi b_{\sigma }}-1)^{-1},$ and $\sigma \in \mathsf {D}$ is such that $b_{\sigma }\ne 0.$

On the other hand, we also obtain

$$\begin{aligned} \widehat{u}(t,\xi )=\rho (-\xi )\int \limits _{t}^{\sigma ^{-1}(t)}\upsilon , \quad \upsilon (s,\xi )=e^{-\xi [\widetilde{B}(s)-\widetilde{B}(t)]}\hat{f}(s,\xi ). \end{aligned}$$

(13)

For $\xi =0,$ we have

$$\begin{aligned} \widehat{u}(t,0)=\int \limits _{t_0}^{t}\hat{f}(s,0), \end{aligned}$$

(14)

which is well-defined on M due to Definition 6.

We know that $\widehat{f}(t,\xi )$ is rapidly decreasing in $\xi \in \mathbb Z$, i.e., for every $N\in \mathbb Z^+,$ there is a constant $C_N>0$ such that

$$\begin{aligned} |\widehat{f}(t,\xi )|\leqslant \frac{C_N}{(1+|\xi |)^N} \end{aligned}$$

and we wish to prove that $\{\widehat{u}(t,\xi )\}_{\xi \in \mathbb Z}$ defined by (12) when $\xi >0,$ and by (13) when $\xi <0,$ decays rapidly as well. Since we are free to choose the path joining t to $\sigma (t)$ (or to $\sigma ^{-1}(t)$), the idea is to select a convenient path, which becomes possible provided that $\Omega _r$ and in $\Omega ^r$ are connected in $\widetilde{M}$. The path will depend on t and the sign of $\xi \in \mathbb Z$, in particular, for each fixed t there will be two paths, one for $\xi >0$ and another one for $\xi <0$. The choice will further obey the following rules: (i) the exponential term $e^{-\xi [\widetilde{B}(s)-\widetilde{B}(t)]}$ will remain bounded on each path with a bound independent of $|\xi |$; (ii) the path will be of finite length; (iii) the previous bounds will be locally constant with respect to t. The detailed construction will be carried out in Sect. 6.3 and, as a preparation, the next two subsections will be dedicated to some useful technical results. The real analyticity of b allows us to prove a key ingredient in Sect. 6.1—which is the equivalence between the connectedness of the semilevel sets of $\widetilde{B}$ and property ($\star$)—and Sect. 6.2 deals with special paths.

6.1 A semi-global primitive and property ($\star$)

We consider here the following property:

$$\begin{aligned}&Every\, connected \,component ~\Sigma _0 ~ { of\,} ~\Sigma ~{ contains\, a\, point\,} p^* { \,such \,that\, a\, local}\\&\quad { \,primitive\, of\,} b { is\, open \,at\,} p^*. \quad \quad (\star ) \end{aligned}$$

Note that since b is closed it has a local primitive around a small neighborhood of any given point but since it is not exact it does not have a primitive defined throughout M. Yet it may have primitives defined on large proper open subsets of M. We will make use of a primitive of b defined on a neighborhood of the singular set of b whose existence was originally proved in [3]. We recall that we denote by $\Sigma \subset M$ the set of the critical points of b,  that is,

$$\begin{aligned} \Sigma \doteq \{t\in M: b(t)=0\}. \end{aligned}$$

Proposition 14

[3, Proposition 3.1] There exist an open set U such that $\Sigma \subset U\subset M$ and a real analytic function $B^{\dag }$ on U satisfying

$$\begin{aligned} d_tB^{\dag }=b\quad \text {on}\quad U\quad \text {and}\quad B^{\dag }\equiv 0\quad \text {on}\quad \Sigma . \end{aligned}$$

We will need also a strengthened version of Proposition 10 that holds in the real-analytic setup and is due to Arnol’d.

Proposition 15

[1, Theorem 1$'$, p. 4] Every semilevel set has exactly one non relatively compact component.

We may now prove

Proposition 16

The sets $\Omega _r$ and $\Omega ^r$ are connected for every $r\in \mathbb R$ if and only if property ($\star$) holds.

Proof

First we suppose that property ($\star$) fails, which means that there is a component $\Sigma _0$ of $\Sigma$ such that $B^{\dag }$ is not an open map at any of its points. Thus, for every $x\in \Sigma _0,$ there exists a ball $\mathscr {B}(x)\subset U,$ with U as in Proposition 14, such that $B^\dag \geqslant 0$ on $\mathscr {B}(x)$ or $B^\dag \leqslant 0$ on $\mathscr {B}(x).$ By the compactness of $\Sigma _0,$ the radius of such balls can be assumed equal. Set $U_1\doteq \bigcup _{x\in \Sigma _0}\mathscr {B}(x).$ Define the function

$$\begin{aligned} f(x)=\mathrm{inf}_{\mathscr {B}(x)} B^\dag ,\quad x\in \Sigma _0. \end{aligned}$$

Now f is continuous on $\Sigma _0,$ and the set $S\doteq \{x\in \Sigma _0: f(x)=0\}$ is both closed and open on $\Sigma _0.$ Indeed, if $x_0\in S$ and $x\in \Sigma _0\cap \mathscr {B}(x_0),$ then $B^{\dag }\geqslant 0$ on $\mathscr {B}(x)\cap \mathscr {B}(x_0).$ If $B^\dag \leqslant 0$ on $\mathscr {B}(x),$ then we would have $B^{\dag }\equiv 0$ on $\mathscr {B}(x)\cap \mathscr {B}(x_0),$ which is a contradiction. Therefore, $x\in S.$ As $\Sigma _0$ is connected, we have that $B^{\dag }\geqslant 0$ or $B^{\dag }\leqslant 0$ on $U_1.$

We will assume first that $B^{\dag }\geqslant 0$ on $U_1.$ Due to the compactness of $\Sigma$ we may assume that

$$\begin{aligned} \Sigma \cap U_1=\Sigma _0. \end{aligned}$$

By taking balls $\mathscr {B}'(x)$, with $\overline{\mathscr {B}'(x)}\subset U_1,$ we also define the set $U_2\doteq \bigcup _{x\in \Sigma _0}\mathscr {B}'(x).$ Thus, $\Sigma _0\subset U_2,$ and $\overline{U}_2\subset U_1 \subset U.$ Notice that, if $s\in \partial U_2,$ then $B^{\dag }(s)>0.$ Indeed, s would be a regular point and then, if $B^{\dag }(s)=0,$ there would be arbitrary close points to s where $B^{\dag }$ is negative.

Set $m\doteq \mathrm{min}B^{\dag }|_{\partial U_2},$ and consider $r\in (0,m).$ Then $\{s\in U_1: B^{\dag }(s)<r\}$ has a non-empty component $\mathscr {O}^{\dag }\subset U_2.$ Take a component W of $\Pi ^{-1}(U_1)$ containing a component $\mathscr {O}$ of $\Pi ^{-1}(\mathscr {O}^{\dag }).$ For the sake of simplicity, assume that $\widetilde{B}(s_0)=0$ with $s_0\in W$ and $\Pi (s_0)\in \Sigma _0.$ We then have

$$\begin{aligned} B^{\dag }\circ \Pi \equiv \widetilde{B}\text { on }W. \end{aligned}$$

Claim

The component $\mathscr {O}$ is a component of $\Omega _{r}$ on which $\widetilde{B}$ is bounded.

We postpone the proof of the claim and take it for granted. Now we may invoke Proposition 10 to assert that $\Omega _r$ is not connected.

Similarly, if $B^{\dag }\leqslant 0$ on $U_1,$ we may find that some $\Omega ^r$ that is not connected. This ends the first half of the proof.

Suppose now that $\Omega _r$ is not connected for some $r\in \mathbb R.$ By Proposition 15, there exists a relatively compact component $\mathscr {O}$ of $\Omega _r$ and $\widetilde{B}(t)$ assumes a minimum value on $\overline{\mathscr {O}}$. This minimum cannot be attained on $\partial \mathscr {O}$ where $\widetilde{B}\equiv r$, so there exists $t_0\in \mathscr {O}$ such that $\widetilde{B}(t_0)\leqslant \widetilde{B}(t)$ for every $t\in \mathscr {O}.$ Thus, $p\doteq \Pi (t_0)\in \Sigma ,$ and we denote by $\Sigma _0$ the component of $\Sigma$ containing p. We may assume that $\widetilde{B}(t_0)=0.$ If there were some $p^*\in \Sigma _0$ such that $B^{\dag }$ is open at $p^*,$ then there would exist $p'$ sufficiently close to $p^*$ with $B^{\dag }(p')<B^{\dag }(p^*).$ Since $\Sigma _0$ is path-connected (see, e.g., Proposition 20 below), we would have $t'\in \Pi ^{-1}(\{p'\})\cap \mathscr {O}$ such that $\widetilde{B}(t')=B^{\dag }(p')<B^{\dag }(p^*)=B^{\dag }(p)=\widetilde{B}(t_0),$ which is a contradiction. We proceed similarly if $\Omega ^r$ is not connected. This shows that property ($\star$) does not hold and finishes the proof. $\square$

Next, to complete the proof of the proposition, we prove the claim.

Proof

(of the Claim) It is clear that $0\leqslant \widetilde{B}|_{\mathscr {O}}<r.$ Let $\mathscr {O}'$ be the component of $\Omega _r$ containing $\mathscr {O}.$ Take $t\in \mathscr {O}$ and $t'\in \mathscr {O}',$ and $\beta$ a path in $\mathscr {O}'$ connecting t to $t'.$ It suffices to show that $\Pi (\beta )\subset \mathscr {O}^{\dag }.$ Indeed, if not, as $\Pi (t)\in \mathscr {O}^{\dag },$ there would exist a first $s\in \Pi (\beta )$ with $s\in \partial \mathscr {O}^{\dag }.$ Hence, $s=\Pi (\bar{t})$ with $\bar{t}$ in W,  and then $\widetilde{B} (\bar{t})=B^{\dag }(s)=r,$ which contradicts the fact that $\bar{t}\in \Omega _r.$ $\square$

6.2 Paths and estimates

In this subsection we state three key results from the literature that we will be crucial in Sect. 6.3. The first one is a result by Teissier that we will need it in the following form.

Proposition 17

[33, Proposition 3] Let U and $B^{\dag }$ be as in Proposition 14. Given a compact set $\mathscr {K}\subset U,$ there exists $C_1\doteq C_1(\mathscr {K})>0$ such that, for every $r\in B^{\dag }(\mathscr {K}),$ any two points in a component of $(B^{\dag })^{-1}(r)\cap \mathscr {K}$ can be joined by a piecewise real analytic path $\varsigma$ in $(B^{\dag })^{-1}(r)\cap \mathscr {K}$ whose length is less than $C_1.$

The second one is due to Maire.

Lemma 18

[27, Lemma 25] Let O be an open set in $\mathbb R^m$ and $\Phi \in C^{\infty }(O)$ satisfying

$$\begin{aligned} \Vert \nabla \Phi (s)\Vert \geqslant C_0|\Phi (s)|^{\theta } \end{aligned}$$

for constants $C>0$ and $\theta \in [0,1),$ and every $s\in O.$ For $s\in O$ with $\nabla \Phi (s)\ne 0,$ the maximal solution $\gamma _s:[0,\delta (s))\rightarrow O$ of

$$\begin{aligned} \left\{ \begin{array}{lll} y'&{}=\displaystyle {\frac{\nabla \Phi (y)}{\Vert \nabla \Phi (y)\Vert }}\\ y(0)&{}=s. \end{array} \right. \end{aligned}$$

satisfies

$$\begin{aligned}\Phi (\gamma _s(\tau ))\geqslant \Phi (s)+C_0\tau ^{\frac{1}{1-\theta }},\end{aligned}$$

for $\tau \in [0,\delta (s)).$

The last one follows from the work of Hironaka [24]. We denote by $\mathscr {B}_r$ the ball of radius r and centered at $0\in \mathbb R^n.$

Definition 19

A set $E\subset \mathscr {B}_{r_0}$ is said to be semi-analytic at $s\in E$ if there exist an open neighborhood O of s and a finite number of real analytic functions $\{g_{ij},f_{ij}\}$ on O such that

$$\begin{aligned} E\cap O=\cup _{i}\{s'\in O: g_{ij}(s')=0, f_{ij}(s')>0, \forall j\}. \end{aligned}$$

Proposition 20

[24, p. 462] Let $a^*$ be a non-isolated point belonging to the closure of a semi-analytic set $E\subset \mathscr {B}_{r_0}.$ Then, for every $a\in E{\setminus } \{a^*\}$ sufficiently close to $a^*,$ there exists a real analytic map $\gamma ^*:(-1,1)\rightarrow \mathscr {B}_{r_0}$ such that $\gamma ^*(0)=a^*$ and $a\in \gamma ^*(0,1)\subset E.$

6.3 Construction of the global solution

Here we obtain the needed decay of the Fourier coefficients (12) when $\xi >0$ and (13) when $\xi <0.$ Given $t_0\in \widetilde{M},$ set $p\doteq \Pi (t_0),$ and let $\varphi :V\rightarrow \mathscr {B}_{r_0}$ be a local chart of M,  with $p\in V$ and $\varphi (p)=0.$ Assume that $\Pi ^{-1}(V)$ consists of sets diffeomorphic to V by $\Pi .$ Take a component $\mathscr {U}'$ containing $t_0.$ Our goal is to select a path $\gamma ^t$ that connects t in a neighborhood $\mathscr {U} \subset \mathscr {U}'$ of $t_0$ to $\sigma (t)$ or $\sigma ^{-1}(t)$ in a convenient way.

Consider $\sigma \in \mathsf D$ with $b_{\sigma }>0.$ First let us state an auxiliary lemma. We can assume that

$$\begin{aligned} \mathrm{sup}_{\mathscr {U}'}\widetilde{B}(t)<\mathrm{inf}_{\mathscr {U}'}\widetilde{B}(\sigma (t)). \end{aligned}$$

Lemma 21

If t and $\widetilde{m_j}$ are in $\mathscr {U}'$ and $\widetilde{B}(\widetilde{m}_j)>\widetilde{B}(t),$ $j=0,\ldots ,N,$ we can select paths $\gamma _j$ connecting $\widetilde{m}_j$ to $\sigma (t),$ with $\widetilde{B} (t')>\widetilde{B}(t)$ for $t'\in \gamma _j.$ If $|\gamma _j|$ stands for the length of $\gamma _j,$ then

$$\begin{aligned} |\gamma _j|\leqslant C' \doteq C'(m_0,\ldots ,m_N). \end{aligned}$$

Indeed, in this case, as $\widetilde{B}(\sigma (\widetilde{m}_j))>\widetilde{B}(\widetilde{m}_j),$ both $\widetilde{m}_j$ and $\sigma (\widetilde{m}_j)$ belong to $\Omega ^{\widetilde{B}(t)},$ which is connected by hypothesis. Now it only remains to connect $\sigma (\widetilde{m}_j)$ to $\sigma (t).$ This can be achieved by the lifting starting at $\sigma (\widetilde{m}_j)$ of the path $\varphi ^{-1}(\ell ),$ where $\ell$ is the segment connecting $\varphi (m_j)$ to $\varphi (\Pi (t)).$ If necessary, we can modify the obtained path in order to have a smooth path $\gamma _j$ such that $\widetilde{B} (t')>\widetilde{B}(t)$ for $t'\in \gamma _j.$

We will now construct $\gamma ^t$ by composing paths, some of which are local. Let then $B:V\rightarrow \mathbb R$ be a local primitive of b,  with $B(p)=0.$ We have the following

Proposition 22

Consider $\sigma \in \mathsf D$ with $b_{\sigma }>0.$ Then, for every t in a certain neighborhood of $t_0\in \widetilde{M},$ there exists a piecewise smooth path $\gamma ^t$ connecting t to $\sigma (t)$ satisfying:

• (i) $\displaystyle {\widetilde{B}(t)\leqslant \widetilde{B}(t'),\quad t'\in \gamma ^t;}$

• (ii) $\displaystyle {|\gamma ^t|\leqslant C=C(t_0).}$

Proof

Case I First we suppose that p is a regular point of b. Take a local chart $\varphi : V\rightarrow \mathscr {B}_{r_0}$ such that $B\circ \varphi ^{-1}(t_1,\ldots ,t_n)=t_1.$

Let $\mathcal Q',\mathcal Q$ be open squares inside $\mathscr {B}_{r_0}$, both centered at 0,  with $\overline{\mathcal Q'}\subset \mathcal Q$ and $\mathcal Q'$ having side-length equal to 2A.

Let $\ell :[0,1]\rightarrow \mathcal Q'$ be the segment joining $\varphi (\Pi (t))=(t_1,\ldots ,t_n)\in \mathcal Q'$ to $m\doteq (A,0,\ldots ,0).$ We have, for $\lambda \in [0,1],$

$$\begin{aligned} \ell (\lambda )=(1-\lambda )\varphi (\Pi (t))+\lambda m=((1-\lambda )t_1+\lambda A,(1-\lambda )t_2,\ldots ,(1-\lambda )t_n), \end{aligned}$$

and

$$\begin{aligned} B\circ \varphi ^{-1}(\ell (\lambda ))=(1-\lambda )t_1+\lambda A. \end{aligned}$$

Since $A\geqslant t_1,$ we have $B\circ \varphi ^{-1}(\ell (\lambda ))\geqslant t_1= B\circ \Pi (t).$ Now join $t\in \mathcal Q$ to $\sigma (t)$ by the path following the lifting of $\varphi ^{-1}(\ell ),$ and $\gamma _0$ given by Lemma 21. We then obtain the estimate (i).

As for the estimate (ii), set

$$\begin{aligned} 2A\sqrt{2}\mathrm{sup}_{\overline{\mathcal Q'}}\Vert D\varphi ^{-1}\Vert +C\doteq C(t_0). \end{aligned}$$

Case II Suppose p is a critical point of b. Take a local chart $\varphi : V\rightarrow \mathscr {B}_{r_0}.$ Call $\mathscr {U}$ a component of $(\varphi \circ \Pi )^{-1}(\mathscr {B}_{r}),$ with $r<r_0,$ containing $t_0.$

Step 1 We suppose that $t\in \mathscr {U}$ is such that $\Pi (t)=q$ and $B(q)>0.$ We apply Lojasiewicz’s inequality to $B\circ \varphi ^{-1}.$ Hence, Lemma 18 says that the solution $\gamma _{\varphi (q)}$ necessarily encounters $\partial \mathscr {B}_{r}.$ Consider then $s \in \partial \mathscr {B}_{r}$ with $s =\gamma _{\varphi (q)}(\tau ).$ Notice that

$$\begin{aligned} \tau \leqslant \left( \frac{2}{C_0}\mathrm{sup}_{\overline{\mathscr {B}_r}}|B\circ \varphi ^{-1}|\right) ^{1-\theta }. \end{aligned}$$

Denote by $\Sigma '$ the critical points of $\varphi _*b|_{\partial \mathscr {B}_{r}}.$ We write $\Sigma '_j$ for the components of $\Sigma ',$ j in a finite set J. Fix a regular point $\varphi (m_j)\in \Sigma '_j$ if $\varphi ^{-1}(\Sigma '_j)$ is not contained in $\Sigma .$

If s is not in $\Sigma ',$ we apply now Lemma 18 for $\partial \mathscr {B}_{r}$ (with constant $C^{\natural }_0$) to obtain $\gamma ^{\natural }_{s}:[0,\delta (s)]\rightarrow \partial \mathscr {B}_r$ such that

$$\begin{aligned} \mathrm{lim}_{\tau \rightarrow \delta (s)}\gamma ^{\natural }_{s}(\tau )=s' \in \Sigma '. \end{aligned}$$

If $s\in \Sigma _j$ for some $j\in J,$ we put $s'\doteq s.$

We connect $\varphi (q)$ to s and s to $s'$ respectively by using $\gamma _{\varphi (q)}$ and $\gamma ^{\natural }_{s}.$ Notice that, since $B\circ \varphi ^{-1}(s')>0,$ Proposition 20 implies that $\varphi ^{-1}(s')\notin \Sigma ,$ hence we can connect $\varphi ^{-1}(s')$ to $m_j$ by a path $\varsigma$ in $\varphi ^{-1}(\Sigma '_j),$ with $|\varsigma |\leqslant C^{\natural }_1$ thanks to Proposition 17.

Therefore, we have a path $\gamma ^+,$ connecting q to $m_j,$ with $B\circ \gamma ^+$ greater than B(q). If $\tilde{C}_0\doteq \mathrm{min}\{C_0,C^{\natural }_0\},$ put

$$\begin{aligned} \tilde{C}\doteq \left( \frac{2}{\tilde{C}_0}\mathrm{sup}_{\overline{\mathscr {B}_r}}|B\circ \varphi ^{-1}|\right) ^{1-\theta }, \end{aligned}$$

and then the lifting of $\gamma ^+$ to $\widetilde{M},$ starting at t,  has length less than or equal to

$$\begin{aligned} 2\tilde{C} \mathrm{sup}_{\overline{\mathscr {B}_r}}\Vert D\varphi ^{-1}\Vert + C^{\natural }_1. \end{aligned}$$

Now join $t\in \mathscr {U}$ to $\sigma (t)$ by the path $\gamma ^t$ following the lifting of $\gamma ^+$ (starting at t) and $\gamma _j$ is given by Lemma 21. It is clear that we have constructed $\gamma ^t$ satisfying (i) and

$$\begin{aligned} |\gamma ^t|\leqslant 2\tilde{C} \mathrm{sup}_{\overline{\mathscr {B}_r}}\Vert D\varphi ^{-1}\Vert + C^{\natural }_1+C'. \end{aligned}$$

(15)

Step 2 Now we will deal with those points $t\in \mathscr {U}$ such that $\Pi (t)=q$ and $B(q)\leqslant 0.$ According to Lemma 18, a possibility for the solution $\gamma _{\varphi (q)}$ is that there is $\tau$ satisfying $\gamma _{\varphi (q)}(\tau )=s\in \partial \mathscr {B}_r.$ Keeping the notation as in Step 1, if $\varphi ^{-1}(s')\notin \Sigma ,$ we follow exactly the same proof there.

The second possibility is that

$$\begin{aligned} \mathrm{lim}_{\tau \rightarrow \delta (\varphi (q))}\gamma _{\varphi (q)}(\tau )\text { is a critical point of }B\circ \varphi ^{-1}. \end{aligned}$$

Therefore, it suffices to assume that we have a path $\gamma ^-$ (consisting of orbits in $\overline{\mathscr {B}_r}$) connecting q to a critical point $q^*$ of B,  with $B\circ \gamma ^-$ greater than or equal to B(q) and

$$\begin{aligned} |\gamma ^-|\leqslant 2\tilde{C} \mathrm{sup}_{\overline{\mathscr {B}_r}}\Vert D\varphi ^{-1}\Vert . \end{aligned}$$

Since property ($\star$) holds, we can connect $q^*$ to $p^*$ by a path $\varsigma$ in a component $\Sigma _0$ of $\Sigma$ such that the semi-global primitive $B^{\dag }$ is open at $p^*.$ Moreover, due to Proposition 17, we can require that $|\varsigma |\leqslant C_1.$

As $B^{\dag }$ is open at $p^*,$ Proposition 20 allow us to connect $p^*$ to a sufficiently close point $p^+$ by a path $\gamma ^*$ on which $B^{\dag }$ is greater than or equal to 0 and $B^{\dag }(p^+)>0.$

Hence, we have a path $\eta ^*$ in U connecting $q^*$ to $p^+$ such that $B^{\dag }\circ \eta ^*$ is greater than or equal to 0 and

$$\begin{aligned} |\eta ^*|\leqslant C_1+|\gamma ^*|. \end{aligned}$$

Consider a path $\eta$ by following the lifting of $\gamma ^-$ to $\widetilde{M},$ starting at t,  and then a lifting of $\eta ^*.$ For the final point $t^+$ of $\eta$ ($\Pi (t^+)=p^+$), we can apply Step 1 and obtain path $\gamma ^{t^+}$.

Then we will join $t\in \mathscr {U}$ to $\sigma (t)$ by a path $\gamma ^t$ following $\eta ,$ $\gamma ^{t^+},$ and $\sigma (\eta ^{-1}).$ We have that $\gamma ^t$ satisfies (i). Since

$$\begin{aligned} |\eta |\leqslant 2\tilde{C} \mathrm{sup}_{\overline{\mathscr {B}_r}}\Vert D\varphi ^{-1}\Vert +C_1+|\gamma ^*|, \end{aligned}$$

and $|\gamma ^{t^+}|$ is estimated in (15), we put $\tilde{C}_1\doteq \mathrm{max}\{C_1,C^{\natural }_1\}$ and

$$\begin{aligned} C(t_0)\doteq 6\tilde{C}\mathrm{sup}_{\overline{\mathscr {B}_r}}\Vert D\varphi ^{-1}\Vert +3\tilde{C}_1+2|\gamma ^*|+C'. \end{aligned}$$

Then, after Step 1 and Step 2, the estimate (ii) holds and the proof is complete. $\square$

Similarly, we have

Proposition 23

Consider $\sigma \in \mathsf D$ with $b_{\sigma }<0.$ Then, for every t in a certain neighborhood of $t_0\in \widetilde{M},$ there exists a piecewise smooth path $\gamma ^t$ connecting t to $\sigma (t)$ satisfying:

• (i) $\displaystyle {\widetilde{B}(t')\leqslant \widetilde{B}(t),\quad t'\in \gamma ^t;}$

• (ii) $\displaystyle {|\gamma ^t|\leqslant C=C(t_0).}$

Recall that, as $f\in \mathbb E,$ each integral that defines the Fourier coefficients does not depend on the path. Take $\sigma \in \mathsf D$ with $b_{\sigma }>0$. By using the path of Proposition 22 in (12), we conclude for $\xi >0$ and $t\in \mathscr {U}$ that

$$\begin{aligned} \displaystyle {|\widehat{u}(t,\xi )|\leqslant (1-e^{-b_{\sigma }})^{-1}C\mathrm{sup}_{\gamma ^t}|\widehat{f}(s,\xi )|.} \end{aligned}$$

Therefore, for every $N\in \mathbb {Z}^+$ and $t\in \mathscr {U},$ there exists $C'_N>0$ such that

$$\begin{aligned} \displaystyle {|\widehat{u}(t,\xi )|\leqslant \frac{C'_N}{(1+|\xi |)^{N}}.} \end{aligned}$$

For $\xi <0,$ we use $\sigma ^{-1}$ and the path of Proposition 23 in (13), which means that we have the uniform decay of the Fourier coefficients on a neighborhood of $t_0\in \widetilde{M}.$ Set now

$$\begin{aligned} u(t,x)\doteq \sum _{\xi \in \mathbb {Z}}\widehat{u}(t,\xi )e^{ix\xi } \end{aligned}$$

and note that u(t, x) is continuous since the series is absolutely and uniformly convergent. Since the coefficients satisfy

$$\begin{aligned} d_t(\hat{u}(t,\xi ))-\xi b(t)\widehat{u}(t,\xi )=\widehat{f}(t,\xi ), \end{aligned}$$

in any local charts of M we have

$$\begin{aligned} \partial _j\widehat{u}(t,\xi )=\xi \partial _jB(t)\widehat{u}(t,\xi )+\widehat{f}(t,\xi ) \end{aligned}$$

(16)

for $j=1,\ldots ,n$ showing that we have found a continuous function that satisfies the equation ${\mathbb {L}}u=f$ in the weak sense and it remains to be shown that u(t, x) is smooth. This will follow by proving the appropriate decay for the derivatives of the coefficients, which will involve and induction argument on the differentiation order. We recall that we denote the order of a multi-index $\alpha$ by $|\alpha |$ and suppose that we have $|\alpha |\geqslant 0$ such that, for every $N\in \mathbb Z^+,$ there is $C_{|\alpha |,N}>0$ with

$$\begin{aligned} \displaystyle {\max \{|\partial ^{\alpha '}\widehat{f}(t,\xi )|,|\partial ^{\alpha '}\widehat{u}(t,\xi )|\}\leqslant \frac{C_{|\alpha |,N}}{(1+|\xi |)^{N}}} \end{aligned}$$

for $|\alpha '|\leqslant |\alpha |$ and every $\xi \in \mathbb Z.$ If we consider a derivative of order $|\beta |=|\alpha |+1,$ then, by (16), we have, for some $j=1,\ldots ,n,$ that

$$\begin{aligned} \partial ^{\alpha }\partial _j\widehat{u}(t,\xi )=\xi \partial ^{\alpha }[\partial _jB(t)\widehat{u}(t,\xi )]+\partial ^{\alpha }\widehat{f}(t,\xi ). \end{aligned}$$

Each term in $\partial ^{\alpha }[\partial _iB(t)\widehat{u}(t,\xi )]$ is $\partial ^{\alpha '}\partial _iB(t)\partial ^{\alpha ''}\widehat{u}(t,\xi )$ for some $\alpha ',\alpha ''$ with $|\alpha '|+|\alpha ''|=|\alpha |,$ and since M is compact there is a constant $C_{|\beta |}\geqslant 0$ such that $|\partial ^{\beta '}B_k(t)|\leqslant \tilde{C}_{|\beta |}$ for every $t\in M$ and $0<|\beta '|\leqslant |\beta |.$ Hence, for every $N\in \mathbb Z^+,$ $\xi \in \mathbb Z,$ and $t\in V,$

$$\begin{aligned} \displaystyle {|\partial ^{\beta }\widehat{u}(t,\xi )|\leqslant |\xi |\tilde{C}_{|\beta |}\frac{C'_{|\alpha |,N+1}}{(1+|\xi |)^{N+1}}+\frac{C_{|\alpha |,N+1}}{(1+|\xi |)^{N+1}}.} \end{aligned}$$

This allows us to conclude the infinite differentiability of u on $M\times \mathbb S^1.$ $\square$

Remark 24

An alternative way to prove that the continuous solution u(t, x) is actually smooth is to invoke the global hypoellipticity of (1) given by Corollary 4.8 in [3].

7 Global solvability for Mizohata structures

In this section we abandon the analyticity assumptions, assume that b is a smooth closed non-exact 1-form defined on a smooth closed connected manifold M of dimension $n>1$ and discuss the global solvability of the differential operator $\mathbb {L}: C^\infty (M\times \mathbb S^1) \rightarrow \bigwedge ^1 C^\infty (M\times \mathbb S^1)$ defined by

$$\begin{aligned} \mathbb {L}u=d_tu+ib(t)\wedge \partial _x u, \end{aligned}$$

where x belongs to the unit circle $\mathbb S^1$ and $d_t:C^\infty (M)\rightarrow \bigwedge ^{1}C^\infty (M)$ is the exterior derivative on M. We will impose additional restrictions on b that we describe now. Recall that the vector fields

$$\begin{aligned} L_j=\frac{\partial }{\partial t_j}+i\frac{\partial B}{\partial t_j}(t)\frac{\partial }{\partial x},\quad j=1,\ldots ,n, \end{aligned}$$

where $(t_1,\ldots ,t_n)$ are local coordinates on M and B is a local primitive of b,  are local generators of the bundle $\mathscr {V}\subset \mathbb {C}\otimes T(M\times \mathbb {S}^1)$ orthogonal to the line sub-bundle $T'\subset \mathbb {C}\otimes T^*(M\times \mathbb {S}^1)$ generated by the 1-form $dx-ib$. Denote by $T^0=T'\cap T^*(M\times \mathbb {S}^1)$ the characteristic set of $\mathscr {V}$. A point $\eta =\sum _{j=1}^n\eta _j dt_j+\eta _0\,dx\in T^*_{(t,x)}(M\times \mathbb {S}^1){\setminus }\{0\}$ belongs to $T^0_{(t,x)}$ if and only if $\displaystyle {\frac{\partial B}{\partial t_1}(t)}=\cdots =\displaystyle {\frac{\partial B}{\partial t_n}(t)}=0$ and $\eta =\eta _0\,dx,$ with $\eta _0\in \mathbb R{\setminus }\{0\}.$ Hence the set of critical points of b,  $\Sigma ,$ is the image of the characteristic set under the canonical projection $T^*(M\times \mathbb S^1)\rightarrow M.$ Recall that

Definition 25

The Levi form of an involutive (or formally integrable) structure $\mathscr {V}$ at the characteristic point $\eta \in T^0_{(t,x)}$, $\eta \ne 0$, is the hermitian form on $\mathscr {V}_{p}$, $p=(t,x)$, defined by

$$\begin{aligned} \mathscr {L}_{(p,\eta )}(\mathsf v,\mathsf w) = \frac{1}{2i} \eta \left( [X,\overline{Y}]_{p}\right) , \end{aligned}$$

where X and Y are smooth sections of $\mathscr {V}$ defined in a neighborhood of $p=(t,x)$ and satisfying $X_{p}=\mathsf v$, $Y_{p}=\mathsf w$. A non-elliptic formally integrable structure of codimension 1 with non-degenerate Levi form is called a Mizohata structure.

From now on we will assume that our structure $\mathscr {V}$ is a Mizohata structure. Thus, if $X=v_1L_1+\cdots +v_nL_n$ and $Y=w_1L_1+\cdots +w_nL_n,$ with $v_j,w_j\in \mathbb C$, $j=1,\ldots n,$ we have

$$\begin{aligned} \mathscr {L} _{(p,\eta )}(X,Y)&=\frac{1}{2i}\eta \left( \sum ^n_{j,k=1}v_j\overline{w_k}[L_j,\overline{L_k}]\right) \\&=\frac{1}{2i}\eta \left( \sum ^n_{j,k=1}v_j\overline{w_k}(-2i)\frac{\partial ^2B}{\partial t_j\partial t_k}(t)\partial _x\right) \\&=-\eta _0\,(v_1,\ldots ,v_n)\mathrm{Hess}_t B (\overline{w_1},\ldots ,\overline{w_n})^t. \end{aligned}$$

Hence, requiring that the Levi form is non-degenerate at any $\eta \in T^0_{(t,x)},$ $\eta \ne 0$, is equivalent to considering a system defined by a Morse 1-form b, i.e., a smooth closed 1-form whose local primitives have only non-degenerate critical points (the primitives defined on a covering space have the same property). The set $\Sigma$ is finite since there is a local chart in a neighborhood of $p\in \Sigma$ such that $B\circ \varphi ^{-1}(t_1,\ldots ,t_n)=\pm t_1^2\pm \cdots \pm t_n^2.$

Our goal is to prove the following theorem, where $\widetilde{M}$ is the minimal covering of M, $\widetilde{B}$ a primitive of the pullback of b to $\widetilde{M}$ and property $(\star )$ was defined at the beginning of Sect. 6.1:

Theorem 26

Assume that b is a non-exact Morse 1-form. The following statements are equivalent:

• (I) For every $f\in \bigwedge ^1 C^{\infty }(M\times \mathbb S^1)$ that satisfies the compatibility conditions, there exists $u\in C^{\infty }(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}u=f$.

• (II) For every $r\in \mathbb {R}$, the semilevel sets $\{t\in \widetilde{M}: \widetilde{B}(t)<r\}$ and $\{t\in \widetilde{M}: \widetilde{B}(t)>r\}$ are connected.

• (III) Property ($\star$) holds.

• (IV) The Levy form of $\mathcal V$ is neither positive definite nor negative definite at any critical point.

• (V) ${\mathbb {L}}$ is globally hypoelliptic.

The index of $p\in \Sigma$ will be the number of negative eigenvalues of $\mathrm{Hess}_{p}B.$ Note that (IV), i.e., the non-existence of critical points of index 0 or n—which are points of a local maximum or a local minimum of a local primitive—is clearly equivalent to (III).

Proof

(of (I) $\iff$ (II)) The implication (I) $\implies$ (II) was proved in Theorem 1. To prove the converse we will exploit the connectedness of the semilevel sets to we construct some paths that allow us estimate the decay of the Fourier coefficients as in Sect. 6.3. We maintain the notation used there.

Proposition 27

Fix $\sigma \in \mathsf D$ with $b_{\sigma }<0$ and $t_0\in \widetilde{M}$. There exists a neighborhood V of $t_0$ such that for every $t\in V$ there exists a piecewise smooth path $\gamma ^t$ connecting t to $\sigma (t)$ satisfying:

• (i) $\displaystyle {\widetilde{B}(t')\leqslant \widetilde{B}(t),\quad t'\in \gamma ^t;}$

• (ii) $\displaystyle {|\gamma ^t|\leqslant C=C(t_0).}$

Proof (of Proposition 27)

Case I If $p=\Pi (t_0)$ is a regular point we may argue as in Case I of Proposition 22.

Case II Suppose $p\in \Sigma$ (with index $s\in \{1,\ldots ,n-1\}$). Take a local chart $\varphi : V\rightarrow \mathscr {B}_{r_0}$ such that $B\circ \varphi ^{-1}(t_1,\ldots ,t_n)=-t_1^2-\cdots -t_s^2+\cdots +t_n^2.$ We introduce $A<r_0,$ $\varphi (m_1)\doteq (A,0,\ldots ,0),$ and $\varphi (m_2)\doteq (-A,0,\ldots ,0).$

Step 1 ($s=1$) Let $\ell _1:[0,1]\rightarrow \mathscr {B}_A$ be the segment joining $\varphi (\Pi (t))=(t_1,\ldots ,t_n)\in \mathscr {B}_A$ to $\varphi (m_1)$ and $\ell _2:[0,1]\rightarrow \mathscr {B}_A$ be the segment joining $\varphi (\Pi (t))$ to $\varphi (m_2).$ We have, for $\lambda \in [0,1],$

$$\begin{aligned} \ell _1(\lambda )=\lambda m_1+(1-\lambda )\varphi (\Pi (t)) \end{aligned}$$

and

$$\begin{aligned}&\nabla (B\circ \varphi ^{-1})(\ell _1(\lambda ))\cdot \ell _1'(\lambda )=\nabla (B\circ \varphi ^{-1})(\ell _1(\lambda ))\cdot (m_1-\varphi (\Pi (t)))\nonumber \\&\quad =(-2[(\lambda A+(1-\lambda )t_1)],2(1-\lambda )t_2,\ldots ,2(1-\lambda )t_n)\cdot (A-t_1,-t_2\ldots ,-t_n)\nonumber \\&\quad =2(-\lambda A (A-t_1)+(\lambda -1)t_1(A-t_1)-(1-\lambda )t^2_2-\cdots -(1-\lambda )t^2_n). \end{aligned}$$

If $t_1\geqslant 0$, then $B\circ \varphi ^{-1}(\ell _1(\lambda ))\leqslant B\circ \Pi (t)$ for $\lambda \in [0,1].$ Otherwise, we conclude that $B\circ \varphi ^{-1}(\ell _2(\lambda ))\leqslant B\circ \Pi (t)$ for $\lambda \in [0,1].$

Step 2 ($s>1$) Here we write $-t_1^2-\cdots -t_s^2=N.$

We connect $\varphi (\Pi (t))=(t_1,\ldots ,t_s,t_{s+1},\ldots , t_n)$ to $(\sqrt{-N},0,\ldots ,0, t_{s+1},\ldots , t_n)$ by the path

$$\begin{aligned} \zeta (\lambda )=(\mathscr {C}(\lambda ),t_{s+1},\ldots , t_n), \end{aligned}$$

where $\mathscr {C}(\lambda )$ is in an arc of a circle of radius $\sqrt{-N}$ (and length at most $\pi \sqrt{-N}).$

Clearly $B\circ \varphi ^{-1}(\zeta (\lambda ))=\widetilde{B}(t)$ for $\lambda \in [0,1].$

Now we apply Step 1 in order to connect $(\sqrt{-N},0,\ldots ,0, t_{s+1},\ldots , t_n)$ to $m_j$ (where $j=1,2$) by a segment $\ell _j$ such that $B\circ \varphi ^{-1}(\ell _j(\lambda ))\leqslant \widetilde{B}(t).$

Finally, join t to $\sigma (t)$ by the path following liftings of $\varphi ^{-1}(\zeta )$ and $\varphi ^{-1}(\ell _j),$ and $\gamma _j$ (given by Lemma 21). We then obtain the estimate (i).

As for estimate (ii), since $\sqrt{-N}\leqslant A,$ put

$$\begin{aligned} (\pi +2)A\mathrm{sup}_{\overline{\mathscr {B}_A}}\Vert D\varphi ^{-1}\Vert +C\doteq C(t_0). \end{aligned}$$

$\square$

Similarly, we have

Proposition 28

Consider $\sigma \in \mathsf D$ with $b_{\sigma }>0.$ Then, for every t in a certain neighborhood of $t_0\in \widetilde{M},$ there exists a piecewise smooth path $\gamma ^t$ connecting t to $\sigma (t)$ satisfying:

• (i) $\displaystyle {\widetilde{B}(t')\geqslant \widetilde{B}(t),\quad t'\in \gamma ^t;}$

• (ii) $\displaystyle {|\gamma ^t|\leqslant C=C(t_0).}$

In view of Propositions 27 and 28 we may reason as we did in Sect. 6.3 to one obtain a smooth solution on $M\times \mathbb S^1$, showing that (II) implies (I). $\square$

Proof

(of (II) $\iff$ (III)) If (III) fails, (IV) also fails and then it is plain by Proposition 10 that $\Omega _r$ or $\Omega ^r$ is not connected for some $r\in \mathbb R.$ Hence (II) $\implies$ (III).

Assume now that $\Omega ^{r}$ is disconnected (the proof is analogue if $\Omega _r$ is disconnected). By Proposition 10, there would exist a component $\mathscr {O}$ of $\Omega ^{r}$ on which $\widetilde{B}$ is bounded (and also disjoint from its non-trivial translates by Lemma 12).

Take a sequence $\{\widetilde{p_n}\}_{n\in \mathbb N}$ of points in $\mathscr {O}$ such that $\widetilde{B}(p_1)=r+\varepsilon _0,$ $\varepsilon _0>0,$ and $\widetilde{B}(p_n)\nearrow K\doteq \mathrm{sup}_{\mathscr {O}}\widetilde{B}(t).$ Set $p_n\doteq \Pi (\widetilde{p_n});$ we may suppose that $p_n\rightarrow q\in M.$ Choose a sufficiently small connected neighborhood N of q evenly covered by $\Pi$ such that, if $\widetilde{x}$ and $\widetilde{y}$ belong to a component of $\Pi ^{-1}(N)$ (thus isometric to N), then $|\widetilde{B}(\widetilde{x})-\widetilde{B}(\widetilde{y})|<\varepsilon _0.$ This shows that the components of $\Pi ^{-1}(N)$ which intercept $\{\widetilde{p_n}\}_{n\in \mathbb N}$ are in $\mathscr {O}.$

Note that for any $\widetilde{q}_1, \widetilde{q}_2\in \Pi ^{-1}(\{q\})$ there is some $\sigma \in \mathsf D$ such that $\sigma (\widetilde{q}_1)=\widetilde{q}_2$. Hence, only one component of $\Pi ^{-1}(N)$ intercepts $\{\widetilde{p_n}\}_{n\in \mathbb N}.$ Denote by $q^*$ the point in this component such that $\Pi (q^*)=q.$ Therefore, $\widetilde{B}(q^*)=K,$ which implies that (III) fails. $\square$

Proof

(of (I) $\implies$ (V)) Suppose that there exists $v\in \mathscr {D}'(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}v=f\in \bigwedge ^1 C^{\infty }(M\times \mathbb S^1).$ Then $f\in \mathbb E$ and by (I) there exists $u\in C^\infty (M\times \mathbb S^1)$ such that ${\mathbb {L}}(u-v)=0.$ From the computation at the beginning of Sect. 6, we conclude that the Fourier coefficients of $u-v$ are 0 if $\xi \ne 0,$ and then $u-v$ is constant. Hence $v\in C^\infty (M\times \mathbb S^1)$ and (V) holds. $\square$

Proof

(of (V) $\implies$ (III)) If (III) fails, there exists $t_0\in M$ and a neighborhood $U_0$ of $t_0$ such that a local primitive B of b is defined on $U_0$ and $B(t_0)<B(t)$ or $B(t_0)>B(t)$ for $t\in U_0{\setminus } \{t_0\}.$ Assume that $B(t_0)<B(t).$ We can define the function $(t,x)\mapsto (1-e^{B(t_0)-B(t)-ix})^{1/2}$ on $U_0,$ denoted by u,  which satisfies ${\mathbb {L}}u=0$ on $U_0$ in the weak sense. By using a smooth function $\chi \in C^\infty _c(U_0)$ equals 1 on a neighborhood $V_0\subset U_0$ containing $t_0,$ we have that $\chi u$ is singular at $(t_0,(1,0))$ and ${\mathbb {L}}(\chi u)\in \bigwedge ^1 C^\infty (M\times \mathbb S^1).$ If we assume $B(t_0)>B(t)$ on $U_0,$ the proof is similar. Therefore, (V) does not hold. $\square$

The proof of Theorem 26 is now complete.

7.1 Local solvability versus global solvability

We now compare the properties of local and global solvability for $\mathbb {L}=d_t+ib(t)\wedge \partial _x$ when the closed non-exact form b has only non-degenerate critical points $\{t_j\}$. Recall that $\mathbb {L}$ is (smoothly) locally solvable at $p=(t,x)\in M\times \mathbb S^1$ if every neighborhood U of p contains a neighborhood V of p such that for every $f\in \mathfrak {U}^1(U)$ satisfying $\mathbb {L}^1f=0$ there exists $u\in C^\infty (V)$ satisfying ${\mathbb {L}}u=f$ in V. If $\mathbb {L}$ is elliptic at p it is fairly easy to prove that it is locally solvable at p. Furthermore, the local solvability at each non elliptic point $(t_j,x)$ is characterized by the results of Treves [34]:

Theorem

[34] The operator ${\mathbb {L}}$ is locally solvable at $(t_j,x)$ if and only if the index of the critical point $t_j$ is neither 1 nor $n-1.$

We see from Example B below that the system can be both globally solvable and not locally solvable at $(t_j,x),$ for every j. Example C below, in turn, shows that the system can be globally solvable but locally solvable at $(t_j,x),$ for some j,  and not locally solvable at $(t_k,x),$ for some k. Other combinations are possible by examples similar to this.

In fact, the case $n=2$ is a special case since when M has dimension 2 the system is globally solvable if and only if it is not locally solvable at $(t_j,x),$ for every j. In particular, if $M=\mathbb T^2,$ the Euler characteristic $\chi (M)$ is 0,  and if there are critical points, there are always critical points of index 0 (or n) and index 1,  hence there exists a point $(t_j,x)$ such that ${\mathbb {L}}$ is not locally solvable at $(t_j,x)$ and the system is not globally solvable. Now if M is an orientable surface of genus $g>1,$ $\chi (M)<0$, and there always exists a point $(t_j,x)$ such that ${\mathbb {L}}$ is not locally solvable at $(t_j,x)$.

7.2 Global solvability of ${\mathbb {L}}^{n-1}$

Here we want to prove the version of Corollary 3 for a Morse 1-form b,  that is,

Corollary 29

Assume that M is orientable and b is Morse and not exact. The following statements are equivalent:

• (I) For every $f\in \bigwedge ^1 C^{\infty }(M\times \mathbb S^1)$ that satisfies the compatibility conditions, there exists $u\in C^{\infty }(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}u=f$.

• (II) For every $f\in \mathfrak {U}^n(M\times \mathbb S^1)$ orthogonal to $\mathrm{Ker}{\mathbb {L}}$ there exists $u\in \bigwedge ^{n-1}\mathscr {D}'(M\times \mathbb S^1)$ satisfying ${\mathbb {L}}^{n-1}u=f$.

Proof

(of (I) $\implies$ (II)) We know that (I) implies the global hypoellipticity of ${\mathbb {L}}$ by Theorem 26. That the global hypoellipticity of ${\mathbb {L}}$ implies (II) is a general result of functional analysis and details can be found in [4]. $\square$

Proof

(of (II) $\implies$ (I)) If (I) does not hold, there exists a disconnected semilevel set by Theorem 26. The proof is then complete after the following proposition. $\square$

Proposition 30

If $\Omega ^r$ or $\Omega _r$ is not connected, then (II) does not hold.

We point out that the proof of Proposition 30 holds for a smooth closed non-exact 1-form b.

Proof (of Proposition 30)

The proof follows the ideas in [4]. As in Lemma 13, we have the following a priori estimates:

Lemma 31

If (II) holds, there exist constants $C>0$ and $m\in \mathbb {N}$ such that, for all $f\in \mathfrak {U}^n(M\times \mathbb S^1)$ orthogonal to $\mathrm{Ker}{\mathbb {L}}$ and $g\in C^{\infty }(M\times \mathbb S^1),$

$$\begin{aligned} \left| \int _{M\times \mathbb S^1}f\wedge g \wedge dx\right| \leqslant C \Vert f\Vert _{m}\Vert \mathbb {L}g\Vert _{m}. \end{aligned}$$

(17)

Here $\Vert v\Vert _m=\mathrm{sup}_{M\times \mathbb S^1}\sum _{|\beta |\leqslant m}|\partial ^{\beta }v(t,x)|.$ We will violate this a priori estimate by defining sequences $f_k$, $g_k$, plugging them in (17) and checking that, as in Sect. 5, the left hand side is bounded below by a positive constant while the right hand side tends to zero as $k\rightarrow \infty$.

Assume the presence of a disconnected superlevel set of $\widetilde{B}$ (the proof for a disconnected sublevel set is similar). Due to Proposition 10, in $\widetilde{M}$ there exists a component $\mathscr {O}$ of a superlevel set, say $\Omega ^{r}$, such that $\widetilde{B}$ is bounded on $\mathscr {O}.$ By Lemma 12, $\mathscr {O}$ is disjoint from their non-trivial translates and then a primitive B of b is defined on $\Pi (\mathscr {O}).$ We assume that $\widetilde{B}\equiv B\circ \Pi$ on $\mathscr {O}.$

Let $\chi :M\rightarrow \{0,1\}$ be the characteristic function of $\Pi (\mathscr {O})$. Consider $\varepsilon >0$ such that $r+3\varepsilon <K,$ where K is the supremum of $\widetilde{B}$ on $\mathscr {O}.$ Define smooth non-negative functions $\psi _1,\psi _2:\mathbb R\rightarrow [0,1]$ satisfying

• $\psi _1^{-1}(\{1\})=[r+2\varepsilon ,\infty );$

• $\psi _1^{-1}(\{0\})=(-\infty , r+\varepsilon ];$

• $\mathrm{supp}(\psi _2)\subset (r+3\varepsilon , \infty ).$

We then define smooth functions $\varphi ,\theta : M\rightarrow [0,1]$ by

$$\begin{aligned}&\varphi (t)=\chi (t)(\psi _1\circ B)(t),\\&\theta (t)=\chi (t)(\psi _2\circ B)(t).\end{aligned}$$

Notice that

$$\begin{aligned} B(t)\leqslant r+2\varepsilon , \quad \forall t\in \mathrm{supp}(d_t\varphi ). \end{aligned}$$

As M is orientable, take $\Omega \in \bigwedge ^nC^\infty (M)$ nowhere vanishing. Finally, set for $k\in \mathbb N$

$$\begin{aligned} f_k(t,x)=e^{-ikx-kB(t)}\theta (t)\Omega (t) \end{aligned}$$

and

$$\begin{aligned} g_k(t,x)=e^{ikx+kB(t)}\varphi (t). \end{aligned}$$

Each $f_k$ is orthogonal to $\mathrm{Ker}{\mathbb {L}}\cong \mathbb C.$ Since

$$\begin{aligned} \mathbb {L}g_k(t,x)=e^{ikx+kB(t)}d_t\varphi (t) \end{aligned}$$

and

$$\begin{aligned} \int f_k\wedge g_k \wedge dx=I_0\ne 0, \end{aligned}$$

we may conclude the proof by reasoning as in Sect. 5. $\square$

8 Examples, comments and open problems

Example A Consider the torus $\mathbb T^n$ and identify $\mathbb S^1$ with $\mathbb R/(2\pi \mathbb Z).$ The functions defined on $\mathbb T^n$ are identified with the functions in $\mathbb R^n$ $2\pi$-periodic on each variable.

Now consider the real analytic function $B^{\natural }:\mathbb R^n\rightarrow \mathbb R$ given by

$$\begin{aligned} B^{\natural }(t_1,\ldots , t_n)=\alpha _1\int _0^{t_1}\sin ^2\theta d\theta +\cdots +\alpha _n\int _0^{t_n}\sin ^2\theta d\theta , \end{aligned}$$

where $\alpha _1,\ldots ,\alpha _n$ are linearly independent over $\mathbb Z.$ Therefore, $b\doteq d_t B^{\natural }$ is a closed non-exact 1-form defined on $\mathbb T^n$ and $\widetilde{M}=\mathbb R^n.$

In this case $\Sigma =(\pi \mathbb Z)^n,$ and we have only degenerate critical points. Nevertheless, $B^{\natural }$ is open at every point of $\Sigma .$ Then property ($\star$) holds, and the system defined by b is globally solvable.

Example B We will construct a smooth Morse 1-form b without critical points of index 0 or n on the connected sum of closed n-manifolds $M_1$ and $M_2.$ In particular, the corresponding operator ${\mathbb {L}}$ will be globally solvable. This example is inspired by [2] and a similar one, as well as more examples of Morse forms, can be found in [37].

Start by taking two Morse 1-forms $\omega _1$ and $\omega _2$ respectively defined on $M_1$ and $M_2.$ Assume that $\omega _1$ and $\omega _2$ do not have critical points of index 0 or n,  and consider sufficiently small open sets $N_1\ni p_1$ and $N_2\ni p_2$, which are neighborhoods of regular points $p_k\in M_k$ for $k=1,2.$

In $\mathbb R^{N}$ (with $(t_1,\ldots ,t_N)$ as the canonical global coordinates, $N>n$), set $Q\doteq [-2,2]^N,$ and let $\varphi _k$ be a diffeomorphism between $N^{\natural }_k$ and $N_k$, where

• $N^{\natural }_1$ is the intersection of Q with $\{(t_1,\ldots ,t_n,-1,0,\ldots ,0)\},$

• and $N^{\natural }_2$ is the intersection of Q with $\{(t_1,\ldots ,t_n,1,0,\ldots ,0)\}$.

We apply the Local Submersion Theorem to choose diffeomorphisms $\varphi _k$ between $N^{\natural }_k$ and $N_k$ satisfying

$$\begin{aligned} \varphi _k^*(\omega _k)=dt_1\quad \text { for }k=1,2. \end{aligned}$$

Consider now disjoint n-manifolds $M^{\natural }_1$ and $M^{\natural }_2$, both embedded on $\mathbb R^N,$ respectively diffeomorphic to $M_1$ and $M_2,$ such that $M^{\natural }_k\cap Q=N^{\natural }_k$. We will obtain a connected sum of $M^{\natural }_1$ and $M^{\natural }_2$ and define a closed 1-form b on it.

In order to do this, take a smooth concave function $h:[1,1+\varepsilon ]\rightarrow [0,\varepsilon ]$ satisfying:

• $h(r)=2(r-1)$ for r close to 1; 

• $h(r)=\varepsilon$ for r close to $1+\varepsilon .$

Now let $T\subset Q$ be the set consisting of the points $(t_1,\ldots ,t_{n+1},0,\ldots ,0)$ such that

$$\begin{aligned} 1\leqslant \Vert (t_1,\ldots ,t_{n},0,\ldots ,0)\Vert \leqslant 1+\varepsilon \quad \text { and }\quad \varepsilon t^2_{n+1}=h(\Vert (t_1,\ldots ,t_n,0,\ldots ,0)\Vert ). \end{aligned}$$

Then T is diffeomorphic to $S^{n-1}\times [-1,1].$ Take open disks $D'_k\subset D_k\subset N^{\natural }_k,$ such that $T\cap M^{\natural }_k=\overline{D_k}{\setminus } D'_k,$ and remove $D'_k$ ($k=1,2$).

By choosing orientation preserving diffeomorphisms $\varphi _k,$ Theorem 5.5 of [32] allows us extended them to diffeomorphisms $\varphi _k:M^{\natural }_k\rightarrow M_k.$ We put

$$\begin{aligned} b|_T=dt_1, \quad b|_{M^{\natural }_k{\setminus } D'_k}=\varphi ^*_k(\omega _k), \quad \mathrm{for}\quad k=1,2. \end{aligned}$$

Notice that b has only two critical points on T,  namely $(1,0,\ldots ,0),$ of index $n-1$ and $(-1,0,\ldots ,0),$ of index 1. In particular, b is non-exact.

Example C In this example, we will construct a Morse 1-form b on $\mathbb T^4\simeq \mathbb {R}^4/(2\pi \mathbb {Z})^4$ without critical points of index 0 or 4. Define

$$\begin{aligned} f(x,y)=(\sin x)(2-\cos y),\quad x,y\in \mathbb R. \end{aligned}$$

The critical points of f in $\mathbb T^2\simeq \mathbb {R}^2/(2\pi \mathbb {Z})^2$ are:

• $P_1=(3\pi /2,\pi ),$ $f(P_1)=-3$ (minimum);

• $P_2=(3\pi /2,0),$ $f(P_2)=-1$ (saddle);

• $P_3=(\pi /2,0),$ $f(P_3)=1$ (saddle);

• $P_4=(\pi /2,\pi ),$ $f(P_4)=3$ (maximum).

Define now a function $B^{\natural }:\mathbb R^4\rightarrow \mathbb R$ by

$$\begin{aligned} B^{\natural }(u,v,x,y)= b_1u+b_2v+f(x,y)-\psi (f(x,y))(\sin u+\sin v)/2, \end{aligned}$$

where the numbers $0<b_1,b_2<1/2$ are linearly independent over $\mathbb Z,$ and $\psi \in C^{\infty }(\mathbb R)$ satisfies:

• $\psi (1)=1;$

• $\psi (s)=0$ for $s=-3,-1,3;$

• $|\psi '(s)|<1$ for $s\in \mathbb R.$

Note that $b\doteq d_t B^{\natural }$ defines a closed non-exact 1-form on $\mathbb T^4.$ It is easily seen that $\widetilde{M}=\mathbb R^2\times \mathbb T^2$ and $\mathsf D$ is generated by two deck transformations.

Let $\varepsilon _j\in (0,\pi /2)$ be the two roots of the equation $2b_j =\cos t,$ $0<t<\pi /2,$ $j=1,2,$ and $\lambda _j\in (3\pi /2,2\pi )$ the roots of the equation $2b_j =\cos t,$ $3\pi /2<t<2\pi ,$ $j=1,2.$

Claim

If $P=(u,v,x,y)\in \mathbb R^2\times [-\pi ,\pi ]\times [-\pi ,\pi ]$ is a critical point of $B^{\natural },$ then $(x,y)=P_3$ and, for some $k\in \mathbb Z,$ $u=\varepsilon _1+2k\pi$ or $u=\lambda _1+2k\pi ,$ and $v=\varepsilon _2+2k\pi$ or $v=\lambda _2+2k\pi$. In all these cases the index is neither 0 nor 4.

Indeed, we have

$$\begin{aligned} \partial _u B^{\natural }(P)= & {} b_1-\psi \circ f(x,y)(\cos u)/2;\nonumber \\ \partial _v B^{\natural }(P)= & {} b_2-\psi \circ f(x,y)(\cos v)/2;\nonumber \\ \partial _x B^{\natural }(P)= & {} (1-\psi '\circ f(x,y)(\sin u+\sin v)/2)\partial _xf(x,y);\nonumber \\ \partial _y B^{\natural }(P)= & {} (1-\psi '\circ f(x,y)(\sin u+\sin v)/2)\partial _yf(x,y).\nonumber \end{aligned}$$

Suppose that $b(P)=0.$ Since $1-\psi '\circ f(x,y)(\sin u+\sin v)/2\ne 0,$ we conclude that $(x_0,y_0)$ is a critical point of f, hence $(x_0,y_0)=P_j$ for some $1\leqslant j\leqslant 4.$ However, if $j\ne 3,$ then $\partial _uB^{\natural }(P)=b_1\ne 0$. Therefore, $(x_0,y_0)=P_3,$ and we have

$$\begin{aligned} \partial _uB^{\natural }(P)=b_1-(\cos u)/2=0\quad \text { and }\quad \partial _vB^{\natural }(P)=b_2-(\cos v)/2=0. \end{aligned}$$

Finally, we have

$$\begin{aligned} \mathrm{Hess}_P B^{\natural }&= \left( \begin{array}{llll} (\sin u)/2 &{} 0 &{} 0 &{} 0\\ 0 &{} (\sin v)/2 &{} 0 &{} 0\\ 0 &{} 0 &{} \partial ^{ 2}_{ {xx}}f(P_3) &{} \partial ^{ 2}_{ {xy}}f(P_3)\\ 0 &{} 0 &{} \partial ^{ 2}_{ {xy}}f(P_3) &{} \partial ^{ 2}_{ {yy}}f(P_3). \end{array} \right) \\ \\&= \left( \begin{array}{llll} (\sin u)/2 &{} 0 &{} 0 &{} 0\\ 0 &{} (\sin v)/2 &{} 0 &{} 0\\ 0 &{} 0 &{} -1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1. \end{array} \right) . \end{aligned}$$

This proves the claim.

The four possibilities of critical points yield four determinants of $\mathrm{Hess}_P B^{\natural }$, two positives and two negatives (recall that the Euler characteristic $\chi (\mathbb T^4)$ is 0).

A similar example can be constructed by taking f defined on $\mathbb T^4$ and having a critical point of index 2 in order to have a globally solvable system (in $\widetilde{M}=\mathbb R^2\times \mathbb T^4$) which is locally solvable at $(t_j,x),$ for every j.

8.1 Open problems

While Theorem 1 and Corollary 2 give satisfactory characterizations of the global solvability of $\mathbb L=d_t+ib(t)\wedge \partial _x$ on $M\times \mathbb S^1$ when the coefficients of the closed and non-exact 1-form b are real analytic, our knowledge is not as complete in the general smooth case. Historically, several results concerning the link between geometric properties of the operator symbol and solvability (or hypoellipticity) properties of the operator itself where proved first in the real analytic case and later extended to the technically harder smooth setup. It is in this spirit that we state below some open problems that aim at the solution of this question. In the sequel b will always be a smooth, closed, non-exact 1-form on a compact, connected, n-dimensional smooth manifold M of dimension $n>1$.

Open Problem 1 Assume that the primitive of b defined on the minimal covering of $M\times \mathbb S^1$ has connected semilevel sets (i.e., property (II) of Theorem 1 holds). Is it true that $\mathbb {L}=d_t+ib(t)\wedge \partial _x$ is globally solvable?

This is known to be true when $M=\mathbb T^2$ [6, 7] and there are additional partial results for $M=\mathbb T^n$ in [5].

Open Problem 2 If ${\mathbb {L}}=d_t+ib(t)\wedge \partial _x$ is (smoothly) globally solvable then ${\mathbb {L}}$ is globally hypoelliptic because we can find a particular smooth solution for any smooth form in the range of ${\mathbb {L}}$ and any two solution differ by a constant. We have seen that the converse is also true in the real analytic case and when b is a smooth Morse form (Theorems 1 and 26). Is the converse true in the general case?

Note that the converse holds when $M=\mathbb T^2$ because the proofs of (V) $\implies$ (III) and (III) $\implies$ (II) in Theorem 26 hold when b is a smooth closed non-exact form on a smooth closed connected manifold and Problem 1 has a positive answer when $M=\mathbb T^2$.

Open Problem 3 Let $\mathscr {O}\subset \widetilde{M}$ be a component of a semilevel set and suppose that $\widetilde{B}$ is bounded on $\mathscr {O}$. Is then $\mathscr {O}$ relatively compact?

It was conjectured by Arnol’d [1] that this is true and he proved it in the real analytic setup and in the case $M=\mathbb T^2.$ A weaker version of the conjecture goes as follows. Let $\mathscr {O}\subset \widetilde{M}$ be a component of the superlevel set $\Omega ^r$ and suppose that $\widetilde{B}$ is bounded on $\mathscr {O}$. Does there exist $s>r$ such that $\Omega ^s$ possesses a relatively compact component contained in $\mathscr {O}$? (Similar question for sublevel sets.)

It is not difficult to answer this version once it is proved for Morse forms. Since when M is n-dimensional and b is a Morse form it follows from the proof of (III) $\implies$ (II) in Theorem 26, the weaker version has a positive answer.

Open Problem 4 While property ($\star$)—originally proposed in [3] to deal with global hypoellipticity in the real analytic case—is relevant and quite useful when the form b is either Morse or real analytic, its present form does not seem adequate for the general smooth case. How should property ($\star$) be formulated in the general case?