1 Introduction

The electricity to consumption centers is fundamental to society and required the creation of requirements for studies of the operation of power systems to achieve this objective. One of these studies is the Small-Signal Stability which seeks to evaluate the dynamics of power systems to small disturbances [44]. The focus of analysis is the identification and mitigation of low-frequency oscillation modes in the linearized models. If these low-frequency oscillation modes are not properly damped, they can damage the adequate supply of electrical energy, damage the system’s equipment and even cause a blackout [44].

In the last decades, the Power System Stabilizers (PSSs) coupled in close proximity to the excitation systems of synchronous machines has been traditional and relatively effective in increasing the damping of local oscillation modes of the system in the frequency from 0.8 to 2.0 Hz [44]. Over the years, different models of power systems such as Heffron and Phillips Linear Model, Power Sensitivity Model and Current Sensitivity Model were developed for the coordinated design of PSSs and later these same models were applied to the design of other damping controllers [45, 50]. Nevertheless, due to the expansion and interconnection of power systems and the increase in electricity consumption, PSSs have a reduced effect in mitigating inter-area oscillation modes in the frequency range of 0.1–0.8 Hz which can also damage the power system stability if not properly mitigated [44].

The development of communication technologies allowed the creation of Wide-Area Measurement Systems (WAMSs) that have Phasor Measurement Units (PMUs) installed in certain buses of the grid and are capable of measuring electrical quantities in these buses with high sampling rates and time synchronization due to the use of Global Positioning System (GPS) [32]. The WAMSs have opened different research fronts for improving the power system operation [1, 8, 9, 11, 14, 15, 19, 34, 41, 42].

PMU data from different locations of the grid for a central damping controller or Wide-Area Damping Controller (WADC) proved to be effective in mitigating inter-area oscillation modes. Different design methods have been proposed and shown to be effective in improving the dynamic performance of power systems [6, 10, 17, 54]. Unlike the PSS-type controller designs, the WADC-type controller design presents additional challenges that still persist as a field of research such as: (i) the presence of variable delays for data transmission from PMUs and (ii) failures in the communication channels or data packets caused by cyber-attacks as Denial-of-Service attacks. Solution proposals were made to solve this problem and ensure the power systems stability with good performance requirements. The field of cybersecurity research is recent and has aroused interest in the scientific community as cyberattacks can affect all proposed applications that rely on data from PMUs.

Time delays in communication channels have been studied in different ways by the scientific community. Some authors initially considered fixed models of time delays given by an approximation of Padé [4, 5, 12, 18, 26]. In this case, the data packets would be retained by a buffer until this stipulated time delay. So, it is possible to define a minimum and maximum time that the buffer can hold PMU data to be effectively used by the controller. In [25], the authors consider time delays as system uncertainties and apply deep neural network techniques to deal with these uncertainties. Other methods propose to use adaptive delay compensator [2, 38, 40], database-based time-delay compensator [35], machine learning technique [43], delay scheduling [22], sliding mode control [33] and predictive control [52] to deal directly with variable delays. Although variable time delays are considered, the controller is able to identify the current scenario and improve performance according to its optimization functions. The majority of research presented by the scientific community considers time delays as a detrimental effect on the design and functioning of the WADC. There is consensus that the presence of time delays affects the closed-loop control system and so far it has been considered the detrimental effect of time delays on the performance of control systems dependent on PMU data. Recent research such as that carried out in [48] indicates that the appropriate use of the time delay model can bring benefits to the design and functioning of the central controller.

The presence of communication technologies in all the infrastructure of power systems caused the vulnerability to cyber-attacks [47]. In 2015, a false data injection attack on the Ukrainian power system triggered control actions that caused a blackout in the system [30]. Different cyber-attacks can also hinder the proper functioning of central controllers in different ways. As the WADC relies on data from PMUs that are transmitted over certain well-defined protocols, cyber-attacks can damage the transmitted data and compromise the central controller operation. False Data Injection Attacks and Denial-of-Service Attacks have already been pointed out in the literature as types of harmful attacks on smart grids.

Recent research has proposed WADC designs considering temporary or permanent data loss. The authors in [5, 7, 13] considered possible losses of a WADC channel at the design stage. The authors in [53] propose to use redundant signals to deal with intermittent data losses from PMUs. In [36], the authors propose to employ the Gilbert model to design a WADC with a robustness step in the PMU data dropout. In [29], the authors proposed a control design strategy to deal with communication failures due to False Data Injection attacks. In [37], the authors proposed to use Linear Matrix Inequalities to handle a packet dropout limit. In [55], the authors proposed an index is to quantify the strongest attack that the power system with a given WADC can tolerate. In [3], the authors propose a simple strategy to deal with communication failures by replacing the lost signal with a healthy signal. In [23], the authors proposed a method for detecting and correcting data from PMUs subject to attacks before being effectively applied to the WADC. In [31], the authors proposed an event-triggered mechanism to deal with denial of service (DoS) attacks and deception attacks. The works are promising but challenges still persist, such as: (i) designing a WADC that provides high damping rates even if a channel is lost, (ii) robustness to system operating uncertainties and (iii) robustness to variations in time delays.

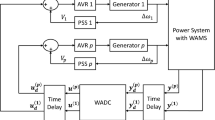
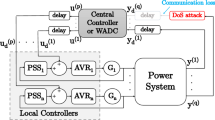
This paper proposes a procedure based on optimization model for the WADC design to improve the damping ratio of the power system modes and that is robust to power system operating conditions. The optimization model can be solved by any metaheuristic. Marine Predators Algorithm (MPA) [24] was chosen for the proposed method due to the good results found by the scientific community in engineering problems [21, 28, 39, 49]. Furthermore, Genetic Algorithms (GA) [46] and Particle Swarm Optimization (PSO) [27], traditional metaheuristics, were applied and evaluated in the proposed optimization model. The value of the time delay will be a variable of the WADC design with the purpose of assisting in the control problem. Figure 1 describes the control structure (PSSs more WADC) used in this work. In this Fig. 1, the possible locations of communication channel losses are also highlighted in dashed lines. The PSSs will be fixed and the control design is reduced to tuning the WADC according to the proposed optimization procedure. The WADC can contain multiple input and output signals with different time delays. However, if we consider the existence of a buffer that holds the signals up to a maximum time limit for the signals to be effectively used, the control project can also look for this maximum time limit that benefits the control objectives. Case studies are showed and analyzed using IEEE 68-bus test system. The proposed method was evaluated by other design method for WADC damping controllers: the method based on Linear Matrix Inequalities (LMIs) [16].

This paper follows this organization: Sect. 2 introduces the power system modeling, Sect. 3 presents the method based on Marine Predators Algorithm for the WADC design, Sect. 4 presents cases studies, and Sect. 5 concludes the article.

Fig. 1
figure 1

Power system with two-level control structure

Full size image

2 Problem formulation

2.1 Power system model

A power system is composed of synchronous and asynchronous generators, transmission lines, Automatic Voltage Regulators, Power System Stabilizers, loads, transformers, capacitor banks, reactor banks, among other devices that present a nonlinear dynamic operation and that may be subject to disturbances. A power system can have its operating dynamics described by the following set of nonlinear differential-algebraic equations [44]

$$\begin{aligned} \dot{\textbf{x}}_k= & {} f(\textbf{x}_k,\textbf{y}_k) \end{aligned}$$
(1)
$$\begin{aligned} \textbf{0}= & {} g(\textbf{x}_k,\textbf{y}_k) \end{aligned}$$
(2)

where \(\textbf{x}_k\) and \(\textbf{y}_k\) describe the vectors of state and algebraic variables, respectively, and \(f(\cdot )\) and \(g(\cdot )\) are functions that describe the differential and static behavior of the power system, respectively.

We are interested in evaluating the system subject to small disturbances, and in this branch of study, we can use a linearized model of the system described by (1)–(2) for each point of operation given by the [44]

$$\begin{aligned} \dot{\textbf{x}}_k= & {} \textbf{A}_k\textbf{x}_k + \textbf{B}_k\textbf{u}_k \end{aligned}$$
(3)
$$\begin{aligned} \textbf{y}_k= & {} \textbf{C}_k\textbf{x}_k \end{aligned}$$
(4)

where \(\textbf{x}_k\in \mathbb {R}^n\) is the vector of power system variables such as angular velocity, \(\textbf{y}_k\in \mathbb {R}^p\) is the vector of system outputs and the outputs will be the speed signals of selected generators \((\varDelta \omega _p\), \(\textbf{u}_k\in \mathbb {R}^p\) is the vector of input variables and the inputs will be the control signals provided by the WADC, \(k=1,...,N_\textrm{op}\) corresponds to each of the \(N_\textrm{op}\) operating conditions of the system considered in the WADC design.

As presented in the introduction of this article, there are different models that can be used to represent power systems. In this research, the authors used the model available in [20] that describes the dynamics of the IEEE 68-bus test system used in this research for case studies. All nonlinear differential-algebraic equations and linearized models of the test system are described in [20].

2.2 Time delay model

Different models and strategies have been proposed in the scientific community to consider time delays (T). This research will consider the model given by the second-order Padé approximation [5]

$$\begin{aligned} \textbf{G}_{\textbf{T}}(s) = \frac{-2Ts+6}{s^2T^2+4Ts+6} \end{aligned}$$
(5)

The WADC can have multiple inputs and outputs with different time delays, but if we consider a buffer that holds the data synchronized for T until the arrival of all data, the WADC can operate normally. Thus, defining this time delay that the buffer holds the PMU data is a project variable in this work. This time delay will have a minimum value \((T_0)\) inherent to the characteristics of data transmission.

From (5), it is possible to obtain the state space model given by

$$\begin{aligned} \dot{\textbf{x}}_{\textbf{d}}= & {} \textbf{A}_{\textbf{d}}\textbf{x}_{\textbf{d}}+\textbf{B}_{\textbf{d}}\textbf{u}_{\textbf{d}} \end{aligned}$$
(6)
$$\begin{aligned} \textbf{y}_{\textbf{d}}= & {} \textbf{C}_{\textbf{d}}\textbf{x}_{\textbf{d}} \end{aligned}$$
(7)

using the observable canonical representation [44] and so each \(\textbf{G}_{\textbf{T}}(s)\) can be represented by the following matrices

$$\begin{aligned} \textbf{A}_{\textbf{d}}= & {} \left[ \begin{array}{cc} 0 &{} -\frac{6}{T}\\ 1 &{} -\frac{4}{T} \end{array}\right] \end{aligned}$$
(8)
$$\begin{aligned} \textbf{B}_{\textbf{d}}= & {} \left[ \begin{array}{cc} \frac{6}{T^2}\\ -\frac{2}{T} \end{array}\right] \end{aligned}$$
(9)
$$\begin{aligned} \textbf{C}_{\textbf{d}}= & {} \left[ \begin{array}{cc} 0&1 \end{array}\right] \end{aligned}$$
(10)

and so \(\textbf{G}_{\textbf{T}}(s)=\textbf{C}_{\textbf{d}}\left( s\textbf{I}-\textbf{A}_{\textbf{d}}\right) ^{-1}\textbf{B}_{\textbf{d}}\).

2.3 Central controller or WADC model

The objective of the WADC of this research is the improvement of the inter-area oscillation modes, and to achieve this objective, the WADC will present multiple input and output signals to guarantee a greater observability of the system. Thus, the WADC to be designed can be modeled by a matrix of transfer functions as

$$\begin{aligned} \textbf{W}(s) = \left[ \begin{array}{cccc} w_{1,1}(s) &{} \cdots &{} w_{1,p}(s) \\ \vdots &{} \ddots &{} \vdots \\ w_{p,1}(s) &{} \cdots &{} w_{p,p}(s) \\ \end{array}\right] \end{aligned}$$
(11)

and the component \(w_{a,b}(s)\), \(a=1,...,p\) and \(b=1,...,p\) is formulated as

$$\begin{aligned} w_{a,b}(s) = K_{a,b}\cdot \frac{T1_{a,b}s+1}{T2_{a,b}s+1}\cdot \frac{T3_{a,b}s+1}{T4_{a,b}s+1} \end{aligned}$$
(12)

From (11), the state-space equations that define the WADC are

$$\begin{aligned} \dot{\textbf{x}}_{\textbf{c}}= & {} \textbf{A}_{\textbf{c}}\textbf{x}_{\textbf{c}}+\textbf{B}_{\textbf{c}}\textbf{u}_{\textbf{c}} \end{aligned}$$
(13)
$$\begin{aligned} \textbf{y}_{\textbf{c}}= & {} \textbf{C}_{\textbf{c}}\textbf{x}_{\textbf{c}}+\textbf{D}_{\textbf{c}}\textbf{u}_{\textbf{c}} \end{aligned}$$
(14)

The WADC parameters \(K_{a,b}\), \(T1_{a,b}\), \(T2_{a,b}\), \(T3_{a,b}\) and \(T4_{a,b}\) defined by (12) are also considered variables in the optimization problem.

2.4 Closed-loop model

The closed-loop system model includes the power system models (3)–(4), the time delay model (6)–(7) and the central controller model (13)–(14). Thus, by defining the state vector \(\bar{\textbf{x}} = \left[ \begin{array}{ccc}\textbf{x}_k^T&\textbf{x}_{\textbf{di}}^T&\textbf{x}_{\textbf{do}}^T\end{array}\right] ^T\), the state-space model is

$$\begin{aligned} \dot{\bar{\textbf{x}}}_{\textbf{k}}= & {} \bar{\textbf{A}}_{\textbf{k}}\bar{\textbf{x}}_{\textbf{k}}+\bar{\textbf{B}}_{\textbf{k}}\bar{\textbf{u}}_{\textbf{k}} \end{aligned}$$
(15)
$$\begin{aligned} \bar{\textbf{y}}_{\textbf{k}}= & {} \bar{\textbf{C}}_{\textbf{k}}\bar{\textbf{x}}_{\textbf{k}} \end{aligned}$$
(16)

From (15) to (16), the closed-loop model including the central controller is given by

$$\begin{aligned} \dot{\widehat{\textbf{x}}}_k = \widehat{\textbf{A}}_k\widehat{\textbf{x}}_k \end{aligned}$$
(17)

where \(\widehat{\textbf{x}}_k = \left[ \begin{array}{cc}\bar{\textbf{x}}_k^T&\textbf{x}_{\textbf{c}}^T\end{array}\right] ^T\) and

$$\begin{aligned} \widehat{\textbf{A}}_k = \left[ \begin{array}{cc} \bar{\textbf{A}}_k + \bar{\textbf{B}}_k\textbf{D}_{\textbf{c}}\bar{\textbf{C}}_k &{} \bar{\textbf{B}}_k\textbf{C}_{\textbf{c}} \\ \textbf{B}_{\textbf{c}}\bar{\textbf{C}}_k &{} \textbf{A}_{\textbf{c}} \end{array}\right] \end{aligned}$$
(18)

In control projects, it is recommended a minimum damping of 5% for all eigenvalues of the system [44]. The parameters of the WADC and the time delay will be variables of the optimization problem in this work. The goal will be to achieve high damping ratios with adequate tuning of controller parameters and buffer actuation time.

2.5 Resiliency to communication loss

In addition to providing an adequate damping rate for all eigenvalues of the closed-loop system for a set of operating points, the central controller will be robust to the permanent loss of one communication channel due to a physical failure or cyber-attack [5].

The controller will present p inputs and p outputs. If the t-th WADC output is lost \((t\in \mathbb {N}, t = 1,..., p)\), then this contingency is equivalent to zeroing the t-th column of \(\textbf{B}_k\) for \(N_\textrm{op}\) operating points. If the s-th WADC input is lost \((s\in \mathbb {N}, s = 1,..., p)\), then this contingency is equivalent to zeroing the s-th row of \(\textbf{C}_k\) for \(N_\textrm{op}\) operating points. Thus, this simple procedure of zeroing columns or rows relates to the loss of the controller communication channels based on PMU data.

Thus, three sets of matrices can be considered: (i) all WADC channels operating properly (18), (ii) loss of one WADC output channel (19) and (iii) loss of one WADC input channel (20).

$$\begin{aligned} \breve{\textbf{A}}_k^t= & {} \left[ \begin{array}{cc} \bar{\textbf{A}}_k + \bar{\textbf{B}}_k^t\textbf{D}_{\textbf{c}}\bar{\textbf{C}}_k &{} \bar{\textbf{B}}_k^t\textbf{C}_{\textbf{c}} \\ \mathbf {B_c}\bar{\textbf{C}}_k &{} \mathbf {A_c} \end{array}\right] \end{aligned}$$
(19)
$$\begin{aligned} \widetilde{\textbf{A}}_k^s= & {} \left[ \begin{array}{cc} \bar{\textbf{A}}_k + \bar{\textbf{B}}_k\mathbf {D_c}\bar{\textbf{C}}_k^s &{} \bar{\textbf{B}}_k^t\mathbf {C_c} \\ \mathbf {B_c}\bar{\textbf{C}}_k^s &{} \mathbf {A_c} \end{array}\right] \end{aligned}$$
(20)

Thus, when evaluating the eigenvalues of these three matrices, the system with possible permanent losses of WADC channels is being evaluated.

3 Proposed control design method

In this research, the control objective is the design of a damping controller of the WADC type. If the system has PSSs, these PSS-type damping controllers will be kept fixed in the analyses and the benefits of a WADC for the dynamics of the test system will be evaluated. As already mentioned, the WADC must guarantee high damping rates \((\zeta > 0.05)\) for all eigenvalues of the system for a set of operation conditions and also be robust to losses of one central controller channel. This control problem was formulated as an optimization problem and the details are presented in Sect. 3.1 and search for parameters was done using the Marine Predators Algorithm, a recent metaheuristic, that is described in Sect. 3.2. Furthermore, Genetic Algorithms and Particle Swarm Optimization, two traditional metaheuristics, were applied to the proposed optimization model in order to compare with the performance of the MPA. Section 3.4 describes Genetic Algorithms, and Sect. 3.3 describes Particle Swarm Optimization. The method was implemented in the MATLAB software, version 2018, on a computer with Intel Core 2.56 GHz and 16GB of RAM.

The WADC can present many communication channels, and each channel is subject to different time delays. However, it was assumed that at the output and input of the WADC there are buffers capable of waiting all the data for a stipulated time and then using the data in the control objective. This research consists of adjusting this time of the buffers that meet control objectives.

3.1 Proposed optimization problem

The variables of the optimization problem are the time delay associated with the transmission of PMU data packets (T) and the parameters of the central controller: \(K_{a,b}\), \(T1_{a,b}\) and \(T3_{a,b}\), for \(a = 1,..., p\) and \(b = 1,..., p\). These variables will present minimum and maximum values in the search space because this controller will be subject to an output limiter with minimum and maximum values of \(-\)0.2 p.u. and 0.2 p.u. so as not to compromise the operation of the closed-loop system. Thus, the vector of variables can be defined as

$$\begin{aligned} \textbf{Z} =\left[ \begin{array}{cccccccccccc} T &{} K_{1,1} &{} T1_{1,1} &{} T3_{1,1} &{} K_{1,2} &{} \cdots &{} K_{p,p} &{} T1_{p,p} &{} T3_{p,p} \\ \end{array}\right] \end{aligned}$$
(21)

The optimization problem used in this work can be described as

$$\begin{aligned} \begin{array}{ll} \text {Find} &{} \textbf{Z} \\ \text {Maximize} &{} \mathcal {F}(\textbf{Z})\\ \text {Subject to} &{} T > T_0 \\ &{} K_{\min }< K_{a,b}< K_{\max } \\ &{} 0< T1_{a,b}< 1 \\ &{} 0< T3_{a,b} < 1 \\ \end{array} \end{aligned}$$
(22)

where \(T_0\) is the minimum time delay associated with the transmission of PMUs data on the communication channels and \(\mathcal {F}(\textbf{Z})\) is the function that returns the minimum damping rate among all \(N_\textrm{op}\) operating points and the three types of matrices of the closed-loop system (Equations (18), (19) and (20)) with the candidate \(\textbf{Z}\) for central controller. This is a nonlinear search problem and this optimization problem can be easily solved with any metaheuristic developed by researchers to date. The authors decided to use the Marine Predators Algorithm because of its easy implementation and recent good results in optimization problems. The next section details this recent metaheuristic.

3.2 Marine predators algorithm

In recent years, a set of metaheuristics has been developed and proved to be effective in solving different optimization problems in engineering. It was decided to use the Marine Predators Algorithm (MPA) to solve the optimization problem described in (22). This choice was based on the fact that this bio-inspired algorithm presents good recent results in engineering optimization problems. Classical metaheuristics such as Genetic Algorithms and Particle Swarm Optimization will also be applied to the proposed optimization model and will be evaluated in terms of the results achieved.

The metaheuristic approach called Marine Predators Algorithm (MPA) recently proposed by the authors at [24] and which is seen as promising in optimization problems [51] is a population-based algorithm inspirited by the actions of predator and prey in nature. In MPA, the prey and predator are viewed as search representatives, since the predator searching for the prey, meanwhile the prey itself looking for its food in nature. The variables of the optimization problem are started randomly and respecting the limits imposed as

$$\begin{aligned} X_0 = X_{\min } + \textrm{rand}\left( X_{\max }-X_{\min }\right) \end{aligned}$$
(23)

where \(X_{\min }\) and \(X_{\max }\) are the lower and upper limits, respectively, and rand() is a function that provides values between 0 and 1 for a uniform distribution.

The best predators in the wild are more talented at foraging in nature. From the best objective function results of the optimization problem, the best predators are chosen to build a matrix called Elite described as

$$\begin{aligned} Elite =\left[ \begin{array}{cccc} X_{1,1}^l &{} X_{1,2}^l &{} \cdots &{} X_{1,d}^l \\ X_{2,1}^l &{} X_{2,2}^l &{} \cdots &{} X_{2,d}^l \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ X_{n,1}^l &{} X_{n,2}^l &{} \cdots &{} X_{n,d}^l \\ \end{array}\right] \end{aligned}$$
(24)

where \(\vec {X}^l\) is the best predator vector, which is replicated n times to construct the Elite matrix, n is the number of search agents, while d is the number of dimensions. The behavior of the predator and the prey in nature describes an iterative process where they are constantly changing their position until they reach their optimum in the optimization problem. Prey also presents its own matrix described by

$$\begin{aligned} Prey =\left[ \begin{array}{cccc} X_{1,1} &{} X_{1,2} &{} \cdots &{} X_{1,d} \\ X_{2,1} &{} X_{2,2} &{} \cdots &{} X_{2,d} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ X_{n,1} &{} X_{n,2} &{} \cdots &{} X_{n,d} \\ \end{array}\right] \end{aligned}$$
(25)

where the \(X_{i,j}\) represents the j-th dimension of the i-th prey. The optimization process is based on the evaluation of these two matrices: Elite and Prey.

As described in the reference [24], MPA is composed of three phases of the optimization process and depends on the speed rates and the behavior of the predator and prey in nature: (i) in high velocity ratio or when prey is moving faster than predator, (ii) in unit velocity ratio or when both predator and prey are moving at almost same pace and (iii) in low velocity ratio when predator is moving faster than prey.

  • Phase 1: high velocity ratio or when prey is moving faster than predator. This phase has the objective of evaluating the search space and is performed in one-third of the first interactions \((N_I/3)\) of the defined \(N_I\) iterations. The prey update process follows the mathematical formulation

    $$\begin{aligned} \vec {stepsize}_i= & {} \vec {R}_B \otimes \left( \vec {Elite}_i-\vec {R}_B\otimes \vec {Prey}_i\right) \end{aligned}$$
    (26)
    $$\begin{aligned} i= & {} 1,...,n \end{aligned}$$
    (27)
    $$\begin{aligned} \vec {Prey}_i= & {} \vec {Prey}_i + P\cdot \vec {R} \otimes \vec {stepsize}_i \end{aligned}$$
    (28)

    where \(R_B\) is a vector containing random numbers based on normal distribution representing the Brownian motion. The notation \(\otimes \) shows entry-wise multiplications. The multiplication of \(R_B\) by prey simulates the movement of prey. \(P = 0.5\) is a constant number, and R is a vector of uniform random numbers in [0, 1].

  • Phase 2: In unit velocity ratio or when both predator and prey are moving at the same pace. This phase occurs between one-third and two-thirds of the number of iterations \((N_I/3<Iter<2\cdot N_I/3)\). In this phase, both exploration and exploitation matter. Consequently, half of the population is designated for exploration and the other half for exploitations. For the first half of the population

    $$\begin{aligned} \vec {stepsize}_i= & {} \vec {R}_L \otimes \left( \vec {Elite}_i-\vec {R}_L\otimes \vec {Prey}_i\right) \end{aligned}$$
    (29)
    $$\begin{aligned} i= & {} 1,...,n/2 \end{aligned}$$
    (30)
    $$\begin{aligned} \vec {Prey}_i= & {} \vec {Prey}_i + P\cdot \vec {R}\otimes \vec {stepsize}_i \end{aligned}$$
    (31)

    where \(\vec {R}_L\) is a vector of random numbers based on Lévy distribution representing Lévy movement. The multiplication of \(\vec {R}_L\) and Prey simulates the movement of prey in Lévy manner, while adding the step size to prey position simulates the movement of prey. For the second half of the populations

    $$\begin{aligned} \vec {stepsize}_i= & {} \vec {R}_B \otimes \left( \vec {R}_B\otimes \vec {Elite}_i-\vec {Prey}_i\right) \end{aligned}$$
    (32)
    $$\begin{aligned} i= & {} n/2,...,n \end{aligned}$$
    (33)
    $$\begin{aligned} \vec {Prey}_i= & {} \vec {Elite}_i + P\cdot CF\otimes \vec {stepsize}_i \end{aligned}$$
    (34)
    $$\begin{aligned} CF= & {} \left( 1 - \frac{Iter}{N_I}\right) ^{\left( \frac{2\cdot Iter}{N_I}\right) } \end{aligned}$$
    (35)

    where CF is an adaptive parameter to control the step size for predator movement. Multiplication of \(\vec {R}_B\) and Elite simulates the movement of predator in Brownian manner, while prey updates its position based on the movement of predators in Brownian motion.

  • Phase 3: In low-velocity ratio or when predator is moving faster than prey. This phase occurs between two-third and the total of iterations \((2\cdot N_I/3<Iter< N_I)\) and presents the following mathematical formulation

    $$\begin{aligned} \vec {stepsize}_i= & {} \vec {R}_L \otimes \left( \vec {R}_L\otimes \vec {Elite}_i-\vec {Prey}_i\right) \end{aligned}$$
    (36)
    $$\begin{aligned} i= & {} 1,...,n \end{aligned}$$
    (37)
    $$\begin{aligned} \vec {Prey}_i= & {} \vec {Elite}_i + P\cdot CF\otimes \vec {stepsize}_i \end{aligned}$$
    (38)

    where the multiplication of \(\vec {R}_L\) and Elite simulates the movement of predator in Lévy strategy while adding the step size to Elite position simulates the movement of predator to help the update of prey position.

  • Eddy formation and Fish Aggregating Devices (FADs) effect. The eddy formation or Fish Aggregating Devices (FADs) effects is a type of environmental issues that can change the behavior of marine predators. The mathematical formula for this stage can be modeled as below:

    • if \(r\le FADs\)

      $$\begin{aligned} \vec {Prey}_i = \vec {Prey}_i+CF\cdot \left[ \vec {X}_{\min }+\vec {R}\otimes \left( \vec {X}_{\max }-\vec {X}_{\min }\right) \right] \otimes \vec {U} \end{aligned}$$
      (39)

    • if \(r > FADs\)

      $$\begin{aligned} \vec {Prey}_i = \vec {Prey}_i+\left[ FADs\cdot (1-r)+r\right] \cdot \left( \vec {Prey}_{r1}-\vec {Prey}_{r2}\right) \end{aligned}$$
      (40)

    where \(FADs = 0.2\) is the probability of FADs effect on the optimization process. \(\vec {U}\) is the binary vector with arrays including zero and one, r is the uniform random number in [0, 1], \(X_{\min }\) and \(X_{\max }\) are the vectors containing the lower and upper bounds of the dimensions, r1 and r2 subscripts denote random indexes of Prey matrix.

  • Marine Memory. Marine predators have a powerful memory of the place in which they have been effective in foraging. This particular function is applied by saving the optimal solutions in each iteration. The saved solutions are updated upon better solutions identified.

3.3 Particle swarm optimization

Particle Swarm Optimization (PSO) is a metaheuristic or swarm intelligence technique proposed by the authors [27]. Such a method seeks to imitate the behavior of swarms through their positions and speeds in the search for an optimal objective. Initially, the vector of positions \((\textbf{x}_i^k)\) and velocities of the particles \((\textbf{v}_i^k)\) are randomly generated respecting the minimum and maximum limits. This vector of positions corresponds to the vector of variables of the optimization problem. As we are dealing with a swarm of particles, there is a vector of particles \((\textbf{X}^k=\left[ \begin{array}{ccc} \textbf{x}_1^k&\cdots&\textbf{x}_{N_p}^k \end{array}\right] )\) of the problem. At each k epoch \((k=1,...,N_e)\) the velocity \((\textbf{v}_i^k)\) and position \((\textbf{x}_i^k)\) of each particle \((n_p=1,...,N_p)\) are updated according to (41) and (42).

$$\begin{aligned} \textbf{v}_i^{k+1}= & {} w\textbf{v}_i^k+c_1r_1(\textbf{x}_i^l-\textbf{x}_i^k)+c_2r_2(\textbf{x}^g-\textbf{x}_i^k) \end{aligned}$$
(41)
$$\begin{aligned} \textbf{x}_i^{k+1}= & {} \textbf{x}_i^{k} + \textbf{v}_i^{k+1} \end{aligned}$$
(42)

where w is a parameter that evaluates how much the speed of the current iteration considers the speed of the previous iteration, \(c_1\) and \(c_2\) are parameters with fixed values, \(r_1\) and \(r_2\) are parameters that vary at each epoch and assume values of a uniform distribution between 0 and 1, \(\textbf{x}^g\) is the position vector that provided the best objective function among all swarm particles in all iterations so far, and \(\textbf{x}_i^l\) is the best position vector for each particle up to the current iteration.

3.4 Genetic Algorithms

Genetic Algorithms (GA) are a special type of evolutionary algorithms that apply operators inspired by evolutionary biology such as mutation, recombination, crossover and natural selection to find optimal solutions to an optimization problem [46].

The algorithm works with a population of individuals \(\textbf{X}=\left[ \begin{array}{ccc}\textbf{x}_1&\cdots&\textbf{x}_{N_I}\end{array}\right] \), where each individual corresponds to a vector of optimization problem variables \(\textbf{x}_i=\left[ \begin{array}{ccc}x_1&\cdots&x_{N_A}\end{array}\right] \). At each generation the crossover and mutation operators will be applied to the individuals and only the individuals that provided the best objective functions will go to the next generation.

The crossover operator consists of exchanging two elements of two individuals of the population (\(\textbf{x}_i\) and \(\textbf{x}_{i+1}\)), thus generating two new individuals (\(\textbf{x}_{N_I+i}\) and \(\textbf{x}_{N_I+i+1}\)). This crossover operator is applied to all \(N_I\) individuals in the population. After this step, the mutation operator will be applied to MR (Mutation Rate) of all individuals and consists of randomly generating a new element \((x_j)\) from the individual. At the end of these two steps, there are \(2\cdot N_I\) individuals in the population and only the \(N_I\) that presented the best objective functions go to the next generation. This process ends when reaching the epoch limit \((N_E)\).

4 Case studies

The test system used in this work was the IEEE 68-bus power system model composed of 16 synchronous generators, and the complete details are in [20]. The single-line diagram of this test system is available in [20]. This test system contains an AVR on 12 synchronous generators and 12 PSSs already tuned. In this research, the PSSs will have their parameters fixed and the benefits of a WADC for the dynamics of the test system will be evaluated. In this research, the authors used the model available in [20] that describes the dynamics of the IEEE 68-bus test system used in this research for case studies. All nonlinear differential-algebraic equations and linearized models of the test system are described in [20]. In [20], only one operation condition is available (Base Case (BC)) and their dominant eigenvalues are described in Table 1. If we consider a second operation condition, C1, given by the increase in load of areas 1 and 2 by 3% and areas 3, 4 and 5 by 6%, Table 1 presents the dominant eigenvalues of low damping rates. There are operating conditions with damping rates below 5% and motivate the design of a central damping controller with the purpose of improving the damping rates of these eigenvalues and ensure good dynamic performance for the system.

Table 1 Dominant oscillation modes
Full size table
Table 2 Results of one hundred simulations of the proposed method using MPA, PSO and GA
Full size table

4.1 Control design stage

Using the geometric measures for the inter-area modes E1 to E5 [44], the signals from the five synchronous generators 5, 9, 10, 11 and 12 were chosen to receive WADC output signals (control signals) and the speed signals from the five synchronous generators 12, 13, 14, 15 and 16 were chosen as inputs of the WADC to be designed. It was stipulated that the minimum time delay is 100 ms for this test system, that is, \( T_0 = 0.100\) s, but the optimization problem can find desired values of time delays greater than this value.

The method was implemented in the MATLAB software, version 2018, on a computer with Intel Core 2.56 GHz and 16GB of RAM. The limits of the WADC design variables were: \(K_{\min }=-30\) and \(K_{\max }=30\). The WADC poles were set to the same poles as the PSSs already installed in the test system: \(T2_{a,b}=0.04\) and \(T4_{a,b}=0.04\). A population composed of 20 individuals \((N_I=20)\) was defined for the three GA, PSO and MPA metaheuristics. The stopping criterion of the optimization model is the number of epochs which was set to 1000 \((N_E=1000)\). The Marine Predators Algorithm presented the following simulation parameters: \(P = 0.5\) and \(FADs = 0.2\). The Particle Swarm Optimization presented the following simulation parameters: \(w=0.7\), \(c_1=1\) and \(c_2=1.5\). The Genetic Algorithms presented the following simulation parameter: \(MR=50\%\). The three metaheuristics had few parameters to be adjusted.

To evaluate the performance of the proposed method, one hundred simulations were performed for the proposed method using MPA, PSO and GA considering the time delay as a variable and considering the time delay fixed at 100 ms and 200 ms. Table 2 provides the results of minimum, maximum, average and standard deviation values of the damping rates of these simulations for these three scenarios. Based on the results, the following evaluations are possible.

  • The proposed method achieved controllers with higher damping rates than the method considering a fixed time delay of 100 ms or 200 ms in all cases. Thus, considering time delays as a design variable can be beneficial in the optimization problem to achieve higher objective function values.

  • In all cases, the damping rates of the proposed method using MPA were above 5%, a margin considered desirable for power system operation. However, the method that considers fixed time delays provided controllers with rates well below 5% in many cases showing that fixed values can define regions where the objective function has difficulty finding optimal values. Furthermore, the application of PSO and GA in the proposed method provided damping rates of the closed-loop system with values below 5% for the three analysis scenarios.

  • The standard deviation of the proposed method is smaller than the method that considers fixed time delays. This shows a lower dependence of the proposed method on initial conditions and how this can affect the outcome of the optimization problem.

The next step in this control design analysis is to evaluate the projected WADC in the time domain using nonlinear simulations and contingencies applied to the system. The WADCs designed by the MPA, PSO and GA metaheuristics that provided the highest damping rate values were chosen to be evaluated, and their parameters are described in Tables 3, 4 and 5, respectively. For these designed controllers, the MPA, PSO and GA WADCs buffers converged with time delays of 108 ms, 143 ms and 191 ms, respectively.

The proposed method based on Linear Matrix Inequalities (LMIs) proposed in [16] for the design of robust WADC was applied to the test system of this research for the same operating scenarios. As method [16] considers fixed time delays, a fixed time delay of 100 ms was chosen for the simulations. The method [16] was implemented in the same software using the same parameters as the authors. The parameters of this WADC after its convergence are described in detail in Table 6.

Table 3 WADC parameters from MPA
Full size table
Table 4 WADC parameters from PSO
Full size table
Table 5 WADC parameters from GA
Full size table
Table 6 WADC parameters from LMI
Full size table

4.2 Time-domain simulations

The designed controllers will be evaluated through dynamic simulations. Two operating conditions were evaluated: condition C1 described in Table 1 and condition C2 which presents the same load level as condition C1 and the disconnection of the line 31–53 of the grid. Three operating scenarios of the designed controller were evaluated: (i) operating with all channels (Y1), (ii) operating with the permanent loss of the channel that would provide the control signal for the synchronous generator 12 and (iii) operating with the permanent loss of the channel that would supply the signal from the synchronous generator 13 to the central controller (Y3). A three-phase fault of 100 ms was applied to bus 40. Figures 2, 3 and 4 show the angle of the synchronous generator 14 for C1 and the three scenarios of the WADC operation. Figures 5, 6 and 7 show the angle of the synchronous generator 14 for C2 and the three scenarios of the WADC operation considered in this control research.

Fig. 2
figure 2

Angle of the generator 14 for C1 case considering all WADC channels operating

Full size image
Fig. 3
figure 3

Angle of the generator 14 for C1 case considering the loss of the \(\varDelta \omega _{13}\) signal

Full size image
Fig. 4
figure 4

Angle of the generator 14 for C1 case considering the loss of the \(VCC_{12}\) signal

Full size image
Fig. 5
figure 5

Angle of the generator 14 for C1 case with transmission line disconnection 31–53 considering all WADC channels operating

Full size image
Fig. 6
figure 6

Angle of the generator 14 for C1 case with transmission line disconnection 31–53 considering the loss of the \(\varDelta \omega _{13}\) signal

Full size image
Fig. 7
figure 7

Angle of the generator 14 for C1 case with transmission line disconnection 31–53 considering the loss of the \(VCC_{12}\) signal

Full size image

From the results of the control design stage and the nonlinear dynamic simulations, the following assessments can be made:

  • The proposed algorithm based on Marine Predators Algorithm, Particle Swarm Optimization and Genetic Algorithms were promising in finding the parameters of the central controller and the time delay to use in the buffer, respecting the imposed restrictions and maximizing the minimum damping rate of the closed-loop system.

  • The proposed design algorithm found a time delay greater than the minimum desired, which provided a damping rate higher than the value of 5% considered satisfactory in control designs. Thus, the system operator can adjust the buffer to receive and send signals from the central controller for a time delay of 0.108 s.

  • The application of MPA in the proposed optimization model provided better results for the damping rate of the closed-loop control system than the application of PSO and GA. Furthermore, angular responses from dynamic simulations were much more damped for the system with the WADC designed by the MPA.

  • The design based on linear models was able to provide a controller with good performance in nonlinear operations of the system subject to small perturbations as can be analyzed in Figs. 2, 3, 4, 5, 6 and 7.

  • The application of the method proposed in [16] and based on LMIs provided a WADC-type controller with fixed time delay that was not able to provide well-damped angular responses. This method then requires an appropriate choice of fixed time delay for good damping ratio performances of the closed-loop control system.

  • According to the results presented, different bio-inspired algorithms can present different performances in the control design. Therefore, appropriate choice of the bio-inspired algorithm is critical to the successful development of the damping controller.

  • There are guarantees of good performance of the controllers designed for the set of operating points considered in the design stage. Different operating conditions of the database may present unsatisfactory performance and require a new control and validation project.

  • Bio-inspired algorithms need few parameters to be defined, and the parameters defined by the author allowed us to achieve the results presented. Better performance can be achieved in the future through a sensitivity analysis of the parameter values of each algorithm.

The vulnerability of communication channels to failures or cyber-attacks is currently the main obstacle to the practical implementation of this type of damping controller. This is the main motivation for growing research into the development of damping controllers resilient to communication failures or cyber-attacks.

5 Conclusions

This article proposes an optimization model for tuning the parameters of the WADC damping controller and the buffer parameter associated with the time delay in the communication channels. The MPA, PSO and GA metaheuristics were applied and evaluated in the proposed optimization model. In addition, the LMI-based method for designing a WADC was also applied and evaluated. Time delays associated with WADC channels can be beneficial in improving the damping rate of power systems when properly tuned. Thus, it is desirable to consider time delays as a design variable for the operation of a WADC whether it can be tuned into a receive and transmit data buffer. The robustness of the WADC at the loss of a channel ensures stability of power systems and cybersecurity requirements. The loss of the communication channel can occur due to cyber-attacks such as Denial-of-Service attack or data packets with a longer than expected time delay. The metaheuristics MPA, PSO and GA used were effective in solving the optimization problem. However, MPA was the only one capable of providing the desired performance requirements in all simulations and was able to provide high damping ratio values and well-damped angular responses.

Future work includes developing probabilistic methods to evaluate different combinations of communication channel losses without unduly affecting the control design. Full WADC shutdown conditions subject to multiple attacks will also be evaluated. Different time delay models will be evaluated in future research and how different strategies can be developed to improve the dynamic performance of the system. In addition, the method will be evaluated in systems with direct current electrical energy transmission.