1 Introduction

1.1 Motivation

In recent years, the development of the Wide-Area Measurement Systems (WAMS) capable to acquired synchronized electrical quantities in different locations of the power system through the installation of Phasor Measurement Units (PMUs) and the use of the Global Positioning System (GPS) has aroused the attention in potential solutions, strategies and improvements in the operation of power systems [44]. Remarkable work has been done over the years in proposing tools based on PMUs’ measures like power system protection [52, 83], monitoring [8, 9, 26, 77], control [1, 14, 32, 33, 79], electromechanical oscillation mode estimation [38], detection and classification of disturbances [75], fault location [19], among others.

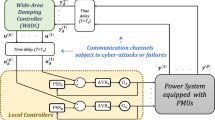
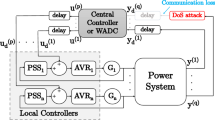
In small-signal stability, the use of the synchronized data for the improvement of the low-frequency oscillation modes has been done by the appropriate tune of the parameters of a central controller or Wide-Area Damping Controller (WADC). Traditionally, the low-frequency oscillation modes of the power system are enhanced by the use of Power System Stabilizer (PSS), properly tuned, providing a control signal for the Automatic Voltage Regulator (AVR) [7, 11, 15, 61, 62]. The PSSs showed to be effective to improve local modes in the range frequency 0.8–2.0 Hz, but they have limited effect in the inter-area mode in the range frequency 0.2–0.8 Hz. The central controller can be a multi-variable controller and, then, it can use different combinations of remote signal to improve the inter-area modes. Because of this, the two-level control structure, PSSs more the WADC, are often proposed for the small-signal stability enhancement [5, 12, 41, 58, 69, 72]. Unlike the design of PSS-type controllers, the central controller design has additional features. In addition to being a multivariate controller, time delays inherent in transmitting PMU data to the control center should be considered since it has already been proven that its disregard affects the performance of the controller. By making use of communication channels that can assume high distances, the controller is subject to loss of information packets due to equipment failure or cyber-attacks. Over the last few years, research has been done on central controller design. However, due to the constant challenges, the WADC design continues an open field of research and improvements are still needed.

1.2 Literature review

Many techniques have been presented in the last years to design a central controller and the research is still ongoing. Firstly, the time delays inherent in transmitting PMU data to the central controller operation were the first problem in the control design stage. A solution proposed by the researches was to consider a fixed time delay represented by the Padé approximation considering different transfer function orders. In [30], the authors present an algorithm based on the Linear Quadratic Regulator theory to design a central controller to improve the low-frequency oscillations using the second-order Padé approximation. The authors in [20] proposed a procedure based on Linear Matrix Inequalities (LMIs) to design a WADC considering multiple load conditions using the first- and second-order Padé approximation. A different LMI-based method was proposed by the authors in [16] and the authors in [60] using the second-order Padé approximation. The authors in [17] present a non-convex optimization algorithm using the second-order Padé approximation to design a WADC. Procedures based on Genetic Algorithms (GAs) were proposed by the authors in [6, 14] using also the second-order Padé approximation. The authors in [72] considered also the second-order Padé approximation to design a central controller using design functions such as \(H_{\infty }\) norm, spectral abscissa and complex stability radius. These methods using the Padé approximation proved the efficacy to improve the low-frequency oscillations of the power system, specially the inter-area oscillations.

However, the PMU data for the central controller operation come from different locations and, then, the next step of the researches was to consider time-variant delays in the control designs. If the communication channels of the central controller are optical fiber cables, the authors mentioned in [57] that the delay could be of the order 100–150 ms. In [80] and [71], the authors proposed to calculate the time delay margin by incorporating a time delay model in the control design stage. The authors in [73] proposed an adaptive delay compensation with penetration of photovoltaic power plants. The authors in [34] used four swarm intelligence-based optimization algorithms to design power oscillation damping controllers under stochastic time delay. In [88], the authors used a theorem based on \(H_{\infty }\) norm to guarantee the asymptotic stability of the power system with a WADC in an interval-time delay. In [65], the authors used a toolbox called Simevents available in the MatLab software to consider the time delay variability. In [45], the authors propose a method based on LMIs and they consider the varying-delay of the wide-area signal during the controller design. The authors in [81], the authors proposed a networked predictive control approach to compensate the constant and the random time delays. In [46], the authors presented a hardware and software design procedure for the Wide-Area Damping control considering different algorithms and the variability of the delay in the wide-area signal.

Due to the need of communication channels to transmit the PMU data to the control center for the proper operation of the WADC, another concern was to evaluate the susceptibility of the channels to failures and cyber-attacks and to propose solutions for these problems. The IEEE C37.118 standards present the most common communication protocol employed nowadays by PMUs to transmit their data. However, this communication protocol is susceptible to cyber attacks such as false data injection attacks, denial-of-service (DoS) attacks and cyber-physical switching attacks and these attacks can damage the dynamic performance of the power system [78]. The authors [47] demonstrated that a properly designed DoS attack sequence on the communication channels of the PMUs can make the power system unstable. Besides, if a communication channel is compromised, then the data signals sent from sensors through this channel will be lost. The authors in [23] investigated the impacts of cyber contingencies such as disordered, delayed, distorted and dropped data in the Wide-Area Damping Control center through an information flow based co-simulation model. The set of results presented allowed the authors to conclude that these contingencies may damage the dynamic performance of the cyber-physical power system. This research proposes a procedure to enhance the resilience of the power system subject to cyber attacks that permanently disrupt a communication channel of a WADC. As per author’s knowledge few works are available in the literature considering this issue. The authors in [84] proposed a control structure that employs both a local signal and a wide-area signal and when a communication failure is detected the operation center employs only the local signals. The authors in [40] proposed a central controller reconfiguration to deal with the communication channel failure, but this failure must be temporary. The authors in [59] and [82] also considered a temporary failures during the WADC operation. The authors in [70, 74, 85] proposed to use redundant communication signals when a channel fails, but there are some limitation in this strategy. The authors in [5, 10, 16] proposed approaches to the design of central controllers considering only a loss of communication channel but considered only fixed time delays in the project, which does not match reality and therefore if there is any a temporary variation of the time delay the communication channel will be considered completely lost. As can be seen, there are few studies dealing with loss of communication channels due to failures and these are considered temporary and not permanent. So the research that will be presented in this article aims to contribute in this area in addition to dealing with time delay uncertainties within a range and uncertainties in the power system operation conditions using a polytopic model.

1.3 Contributions

This paper presents a procedure based on Particle Swarm Optimization (PSO) to design a WADC robust to multiple operating conditions, to time delay variation in a specific range and to permanent failure of one communication channel. An Initialization Process will be presented and it provided satisfactory initial conditions for the Search Process of the procedure. The particle swarm optimization was chosen because of its easy implementation and because it is frequently used in the literature in optimization problems [2, 27, 28, 35, 36, 39, 43, 48, 49, 56, 64, 66,67,68]. However, to evaluate the proposed method, three other meta-heuristics were used to determine the parameters of the central controller: Genetic Algorithms (GA) [3, 4, 50, 53, 55], Grey Wolf Optimizer (GWO) [54] and Ant Colony Optimization (ACO) [29]. The procedure will use linear models, so a set of operating conditions of the power system is linearized around the equilibrium conditions and the purpose will be to improve the damping ratio of these operating conditions. The Padé approximation will be used to build the time delay model considering an upper and lower limit. If the packed data is not in the time delay interval, it will be considered lost and then a permanent failure occurred in this channel. The resulting central controller will also present quadratic stability given by a polytopic model. This work will use a two-level control structure, local controllers (PSSs) more the central controller (WADC) to be designed, described in Fig. 1 where the parameters of the PSSs will be fixed. The Phasor Measurement Units connected to certain buses of the power system allow the measurement of magnitudes and angles of voltage and current [51] and through these data it is possible to estimate the speed signals [37]. In this research, it was considered that the system has a sufficient number of PMUs to estimate the speed signals of the generators whose information will be used by the central controller to be designed. Modal analysis and time-domain nonlinear simulations were conducted in the IEEE 68-bus system, the largest benchmark model present in [22] for small-signal stability studies.

Fig. 1
figure 1

Two-level control structure

Full size image

1.4 Paper organization

The paper is organized as follows: Sect. 2 presents the power system modeling, the time delay model and the structure of the central controller to be determined; Sect. 3 provides the proposed procedure based on PSO; Sect. 4 evaluates the performance of the proposed procedure by its application in the IEEE 68 bus system; Sect. 5 presents the conclusions of the paper.

2 Modeling

2.1 Power system model

The electric power system is a typical example of a differential-algebraic nonlinear system with high dimension. The components that make up the power system at the levels of generation, transmission and distribution such as synchronous generators, automatic voltage regulators, power system stabilizers, transmission lines, loads, transformers, among others can be represented by state space equations. In small-signal stability studies, it is a common process to linearize the complete nonlinear equations for some purpose [42]. In this paper, the main goal is to design a central controller to improve the dyamic performance of the power system and, then, the original state-space nonlinear power system model including the PSSs and AVRs was linearized around a nominal operating condition. The resulting linear model can be described as

$$\begin{aligned} \dot{\mathbf{x}}_n&= {} \mathbf {A}_n\mathbf {x}_n + \mathbf {B}_n\mathbf {u}_{\mathbf {d}n} \end{aligned}$$
(1)
$$\begin{aligned} \mathbf {y}_n&= {} \mathbf {C}_n\mathbf {x}_n \end{aligned}$$
(2)

where \(\mathbf {x}\in \mathbb {R}^m\) is the state vector, \(\mathbf {u}\in \mathbb {R}^p\) is input vector (control signals provided by the WADC), \(y\in \mathbb {R}^p\) is the output vector (speed signals deviation), \(n=1, \ldots ,N\) is an index representing N operation conditions, \(\mathbf {A}_n\in \mathbb {R}^{m \times m}\), \(\mathbf {B}_n\in \mathbb {R}^{m \times p}\) and \(\mathbf {C}_n\in \mathbb {R}^{p \times m}\) are the matrices of the linear model for each operating condition. Each of these sets of matrices \((\mathbf {A}_n,\mathbf {B}_n,\mathbf {C}_n)\) represents an uncertainty of the power system operating condition and the objective is to improve the damping ratio of all eigenvalues in this predefined set.

2.2 Time delay model

As described in Fig. 1, time delays must be considered in the input and output of the central controller to be designed. It was decided to use in this work the second-order Padé approximation given by [13, 30, 72]

$$\begin{aligned} G_d(s) = \frac{6-2Ts}{6+4Ts+T^2s^2} = \frac{- \frac{2}{T}s + \frac{6}{T^2}}{s^2 + \frac{4}{T}s + \frac{6}{T^2}} \end{aligned}$$
(3)

and T represents the time delay to transmit the data. This transfer function can also be represented in state-space equations as

$$\begin{aligned} \dot{\mathbf{x}_d} &= {} \mathbf {A_d}\mathbf {x_d} + \mathbf {B_d}\mathbf {u_d} \end{aligned}$$
(4)
$$\begin{aligned} \mathbf {y_d} &= {} \mathbf {C_d}\mathbf {x_d} \end{aligned}$$
(5)

where the matrices \(\mathbf {A_d}\), \(\mathbf {B_d}\) and \(\mathbf {C_d}\) can be built as

$$\begin{aligned} \mathbf {A_d} = \left[ \begin{array}{cc} 0 &{} -\frac{6}{T^2} \\ 1 &{} -\frac{4}{T} \end{array}\right] \quad \mathbf {B_d} = \left[ \begin{array}{c} \frac{6}{T^2} \\ -\frac{2}{T} \end{array}\right] \quad \mathbf {C_d} = \left[ \begin{array}{cc} 0&1 \end{array}\right] \end{aligned}$$
(6)

in order to fulfill the relation \(\mathbf {G_d}(s)=\mathbf {C_d}\left( s\mathbf {I}-\mathbf {A_d}\right) ^{-1}\mathbf {B_d}\)

To represent the time delay model in the input and output of the central controller, we must use two state-space equations. The first one related to the output of the controller is given as

$$\begin{aligned} \dot{\mathbf{x}_{di}} &= {} \mathbf {A_{di}}\mathbf {x_{di}} + \mathbf {B_{di}}\mathbf {u} \end{aligned}$$
(7)
$$\begin{aligned} \mathbf {u_{d}} &= {} \mathbf {C_{di}}\mathbf {x_{di}} \end{aligned}$$
(8)

where \(\mathbf {x_{di}}\) is state vector related to the input time delay model and \(\mathbf {u} = \left[ \begin{array}{cccc}u^{(1)}&u^{(2)}&\cdots&u^{(p)}\end{array}\right] ^T \in \mathbb {R}^p\) in the vector with the control signal provided by the WADC (output signals). The state-space equations related to the input of the central controller is given as

$$\begin{aligned} \dot{\mathbf{x}_{do}}& = {} \mathbf {A_{do}}\mathbf {x_{do}} + \mathbf {B_{do}}\mathbf {u_{do}} \end{aligned}$$
(9)
$$\begin{aligned} \mathbf {y_{do}}& = {} \mathbf {C_{do}}\mathbf {x_{do}} \end{aligned}$$
(10)

where \(\mathbf {x_{do}}\) is state vector related to the output time delay model and \(\mathbf {y_d} = \left[ \begin{array}{cccc}y_d^{(1)}&y_d^{(2)}&\cdots&y_d^{(p)}\end{array}\right] ^T \in \mathbb {R}^p\) in the vector with the speed deviation signal for the WADC (input signals).

The time delay, as well as, the power system model will consider fixed and, then, we can join their state-space equations to form just one, described as

$$\begin{aligned} \dot{\bar{\mathbf{x}}}_n& = {} \bar{\mathbf{A}}_n\bar{\mathbf{x}}_n + \bar{\mathbf{B}}_n\mathbf {u}_n \end{aligned}$$
(11)
$$\begin{aligned} \mathbf {y}_{\mathbf {d}n}& = {} \bar{\mathbf{C}}_n\bar{\mathbf{x}}_n \end{aligned}$$
(12)

where \(\bar{\mathbf{x}}_n = \left[ \begin{array}{ccc}\mathbf {x}_n^T&\mathbf {x_{di}}^T&\mathbf {x_{do}}^T \end{array}\right] ^T\), \(n=1, \ldots ,N\) and

$$\begin{aligned} \bar{\mathbf{A}}_n = \left[ \begin{array}{ccc} \mathbf {A}_n &{} \mathbf {B}_n\mathbf {C_{di}} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {A_{di}} &{} \mathbf {0} \\ \mathbf {B_{do}}\mathbf {C}_n &{} \mathbf {0} &{} \mathbf {A_{do}} \end{array}\right] \qquad \bar{\mathbf{B}}_n = \left[ \begin{array}{c} \mathbf {0} \\ \mathbf {B_{di}} \\ \mathbf {0} \end{array}\right] \qquad \bar{\mathbf{C}}_n = \left[ \begin{array}{ccc} \mathbf {0}&\mathbf {0}&\mathbf {C_{do}} \end{array}\right] \end{aligned}$$
(13)

and \(\bar{\mathbf{A}}_n \in \mathbb {R}^{r \times r}\), \(\bar{\mathbf{B}}_n \in \mathbb {R}^{r \times p}\) and \(\bar{\mathbf{C}}_n \in \mathbb {R}^{p \times r}\).

2.3 Central controller or WADC

As already mentioned, the central controller will be a multivariable controller with multiple inputs (speed signal deviation) and multiple outputs (control signals for the AVR) to effectively mitigate inter-area oscillation modes. So, the central controller will be a transfer function matrix described as

$$\begin{aligned} \mathbf {CC}(s) = \left[ \begin{array}{cccc} cc_{11}(s) &{} cc_{12}(s) &{} \cdots &{} cc_{1p}(s) \\ cc_{21}(s) &{} cc_{22}(s) &{} \cdots &{} cc_{2p}(s) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ cc_{p1}(s) &{} cc_{p2}(s) &{} \cdots &{} cc_{pp}(s) \\ \end{array}\right] \end{aligned}$$
(14)

where each transfer function \(cc_{kl}\) will present the same configuration of a typical PSS:

$$\begin{aligned} cc_{kl}(s) = K_{kl}\frac{\left( T1_{kl}s+1\right) }{\left( T3_{kl}s+1\right) }\frac{\left( T2_{kl}s+1\right) }{\left( T4_{kl}s+1\right) } \end{aligned}$$
(15)

where \(K_{kl} \subset [K_{min},K_{max}], K_{min},K_{max}\in \mathbb {R}\) is the gain of a typical PSS and \(T1_{kl}, T2_{kl}, T3_{kl}, T4_{kl} \subset [0,0.1]\) are related to the phase lead-lag blocks.

From the transfer function matrix (14) is possible to construct the state-space equations

$$\begin{aligned} \dot{\mathbf{x}_c}& = {} \mathbf {A_c}\mathbf {x_c} + \mathbf {B_c}\mathbf {u_c} \end{aligned}$$
(16)
$$\begin{aligned} \mathbf {y_c}& = {} \mathbf {C_c}\mathbf {x_c} + \mathbf {D_c}\mathbf {u_c} \end{aligned}$$
(17)

and then \(\mathbf {CC}(s) = \mathbf {C_c}\left( s\mathbf {I}-\mathbf {A_c}\right) ^{-1}\mathbf {B_c}+\mathbf {D_c}\).

2.4 Closed loop power system

From the state-space equations described in the last sections, the closed loop system, power system model with time delay model more the designed central controller, is given by

$$\begin{aligned} \dot{\widehat{\mathbf{x}}}_n = \widehat{\mathbf{A}}_n\widehat{\mathbf{x}}_n \end{aligned}$$
(18)

where \(\widehat{\mathbf{x}}_n = \left[ \begin{array}{cc}\bar{\mathbf{x}}_n^T&\mathbf {x_c}^T\end{array}\right] ^T\), \(n=1, \ldots ,N\) and

$$\begin{aligned} \widehat{\mathbf{A}}_n = \left[ \begin{array}{cc} \bar{\mathbf{A}}_n + \bar{\mathbf{B}}_n\mathbf {D_c}\bar{\mathbf{C}}_n &{} \bar{\mathbf{B}}_n\mathbf {C_c} \\ \mathbf {B_c}\bar{\mathbf{C}}_n &{} \mathbf {A_c} \end{array}\right] \end{aligned}$$
(19)

It is common in small-signal stability studies to design controllers that guarantee a minimum damping ratio for all eigenvalues of the closed loop system. This paper adopts the minimum damping ratio of 5% considered satisfactory for the authors in [31] for the power system dynamic performance.

2.5 Robustness analysis to time delay variation

As already mentioned, the time delay model is given by a second-order transfer function (3), where a fixed value T must be provided. However, it is well known that time delays can have different values and, then, it is necessary to consider this in the central control design stage. In this work, is was decided to use a lower and upper limit for the time delay \((T_{min},T_{max})\) and two sets of the models described in (13) were used in the control design stage. After the convergence of the proposed procedure, an analysis will be done in order to evaluate if any time delay in the range \((T_{min},T_{max})\) guarantee appropriate damping ratio for the power system.

2.6 Robustness to permanent communication failure

A permanent communication failure of the channels of the central controller will cause the complete loss of information of the data related to this channel. This problem can be interpreted in another way. The loss of certain channel is the same of zeroing the gains of the central controller related to this specific channel. Considering a central controller of the structure defined in (15) with p inputs and p outputs, so \(k=1,\ldots ,p\) and \(l=1,\ldots ,p\). If the speed deviation signal of the second input \((l=2)\) is permanent lost, so the gains of the second column of the central controller must be zeroed: \(K_{k,2} = 0\) for \(k=1,\ldots ,p\).

Based on the idea of zeroing the gains of the central controller, each candidate of the search process of the controller parameters can have its performance evaluated to permanent communication failure of the channels by zeroing the gains. In this work, it was considered only one permanent communication failure at a time: in the input or in the output of the central controller.

As already mentioned in the last section, it is desirable to guarantee at least 5% of minimum damping ratio for all eigenvalues of the closed loop system for each operating condition. Considering the function \(f_{\zeta }(\cdot )\)

$$\begin{aligned} F_{\zeta }(s_q) = \zeta _{min} \left( \left[ \begin{array}{cc} \bar{\mathbf{A}}_n + \bar{\mathbf{B}}_n\mathbf {D}_{\mathbf {c}_q}\bar{\mathbf{C}}_n &{} \bar{\mathbf{B}}_n\mathbf {C}_{\mathbf {c}_q} \\ \mathbf {B}_{\mathbf {c}_q}\bar{\mathbf{C}}_j &{} \mathbf {A}_{\mathbf {c}_q} \end{array}\right] \right) \end{aligned}$$
(20)

that provides the lowest damping ratio \((\zeta _{min})\) of whole set of operation conditions of the power system \((n=1,\ldots ,N)\) for each central controller candidate \((s_q = \{K_{kl}, T1_{kl}, T2_{kl}, T3_{kl}, T4_{kl}\}, q = 1,\ldots ,NP)\), there are three scenarios of the central controller operation that must be evaluated

  • All central controller channels are working: in this scenario, the lowest damping ratio \((\zeta _1)\) for a set of operating conditions will be compute without modifying the parameters of the central controller candidate (\(K_{kl}\), \(T1_{kl}\), \(T2_{kl}\), \(T3_{kl}\), \(T4_{kl}\)).

  • One permanent loss of the WADC input channel \((l=1,\ldots ,p)\): in this scenario, the matrix gains \(K_{k,l}\) will have one column zeroed lp times \((lp=1,\ldots ,p)\) and for each lp process the lowest damping ratio will be calculated. The final result is the lowest damping ratio \((\zeta _2)\) for these p processes.

  • One permanent loss of the WADC output channel \((k=1,\ldots ,p)\): in this scenario, the matrix gains \(K_{k,l}\) will have one row zeroed kp times \((kp=1,\ldots ,p)\) and for each kp process the lowest damping ratio will be calculated. The final result is the lowest damping ratio \((\zeta _3)\) for these p processes.

After calculating \(\zeta _1\), \(\zeta _2\) and \(\zeta _3\), the lowest value \((\zeta _{min})\) of them must be calculated. The main goal is to improve \(\zeta _{min}\) in such way that \(\zeta _{min} \ge 0.05\).

Then, we can formulate the objective function of the optimization problem as

$$\begin{aligned} F_{\zeta }(s_q) = \zeta _{min} \left\{ \begin{array}{l} \zeta _1\left( \left[ \begin{array}{cc} \bar{\mathbf{A}}_n + \bar{\mathbf{B}}_n\mathbf {D}_{\mathbf {c}_q}\bar{\mathbf{C}}_n &{} \bar{\mathbf{B}}_n\mathbf {C}_{\mathbf {c}_q} \\ \mathbf {B}_{\mathbf {c}_q}\bar{\mathbf{C}}_n &{} \mathbf {A}_{\mathbf {c}_q} \end{array}\right] \right) \\ \\ \zeta _2\left( \left[ \begin{array}{cc} \bar{\mathbf{A}}_n + \bar{\mathbf{B}}_n\mathbf {D}_{\mathbf {c}_q}^{lp}\bar{\mathbf{C}}_n &{} \bar{\mathbf{B}}_n\mathbf {C}_{\mathbf {c}_q}^{lp} \\ \mathbf {B}_{\mathbf {c}_q}^{lp}\bar{\mathbf{C}}_n &{} \mathbf {A}_{\mathbf {c}_q}^{lp} \end{array}\right] \right) \\ \\ \zeta _3\left( \left[ \begin{array}{cc} \bar{\mathbf{A}}_n + \bar{\mathbf{B}}_n\mathbf {D}_{\mathbf {c}_q}^{kp}\bar{\mathbf{C}}_n &{} \bar{\mathbf{B}}_n\mathbf {C}_{\mathbf {c}_q}^{kp} \\ \mathbf {B}_{\mathbf {c}_q}^{kp}\bar{\mathbf{C}}_n &{} \mathbf {A}_{\mathbf {c}_q}^{kp} \end{array}\right] \right) \end{array}\right. \end{aligned}$$
(21)

where \(n=1,\ldots ,N\), \(q=1,\ldots ,NP\), \(lp=1,\ldots ,p\), \(kp=1,\ldots ,p\) and \(s_q\) is a candidate as central controller.

2.7 Quadratic stability

The central controller resulting from the PSO-based procedure provides a desired damping rate for the set of operating points considered in the design stage, but it would be interesting to guarantee a robustness for the closed loop system for any variation within this set of operating points. The robustness of the closed loop system for one central controller was evaluated by the polytopic modeling. The polytopic model comprehends the set of N operating conditions in the form of \(\widehat{\mathbf{A}}_n\), \(n=1,\ldots ,N\), considering the lower and upper limit of the time delay. These models are the vertices of the polytopic set and the closed loop system will present quadratic stability if we find a unique matrix \(\mathbf {P}\) that satisfies [42]

$$\begin{aligned}&\mathbf {P} = \mathbf {P}^T \succ \mathbf {0} \end{aligned}$$
(22)
$$\begin{aligned}&\widehat{\mathbf{A}}_n^T\mathbf {P} + \mathbf {P}\widehat{\mathbf{A}}_n \prec \mathbf {0} \end{aligned}$$
(23)

for \(n=1,\ldots ,N\). If this matrix is found, there is a guarantee of stability in the Lyapunov sense for this set of operation points [1]. If this matrix is not found, new controller parameters must be obtained [18]. It is important to mention that in this set of closed-loop systems, the minimum and maximum limits of time delays were considered in order to also guarantee the quadratic stability for this time delay interval and not only to variations in the load level of the power system.

The SeDuMi solver [76] was used to find the matrix \(\mathbf {P}\) satisfying the inequalities above for a central controller candidate.

3 Proposed procedure

The proposed procedure to design the robust WADC is based on particle swarm optimization with some incremental stages to guarantee the desirable central controller. A flowchart of the general procedure is presented in Fig. 2 and the detailed information are presented below.

Fig. 2
figure 2

Flowchart of the proposed procedure

Full size image

3.1 Problem formulation

The vector of variables (s) of the search process will be the parameters of the central controller to be determined

$$\begin{aligned} s = \left[ \begin{array}{cccccccccccc} K_{1,1}&K_{1,2}&\cdots&K_{m,m}&T1_{1,1}&T1_{1,2}&\cdots&T1_{m,m}&T2_{1,1}&T2_{1,2}&\cdots&T2_{m,m} \end{array}\right] \end{aligned}$$
(24)

where \(K_{kl} \in [K_{min},K_{max}], K_{min},K_{max}\in \mathbb {R}\) for \(k,l=1,\ldots ,p\) and \(T1_{kl}, T2_{kl} \in [0,1]\) for \(k,l=1,\ldots ,p\). It was decided to fix the values of for \(T3_{kl}\) and \(T4_{kl}\) as the same of the PSSs.

The objective function (21) will be to maximize the minimum damping ratio \((\zeta _{min})\) considering the three scenarios presented in Sect. 2.6.

Then, we can define the optimization problem as

$$\begin{aligned} \begin{array}{ll} \text {find} &{} s \\ \text {max} &{} F_{\zeta }(s) \\ \text {s. t.} &{} K_{min} \le K_{kl} \le K_{max} \\ &{} 0 \le T1_{kl} \le 1 \\ &{} 0 \le T2_{kl} \le 1 \\ \end{array} \end{aligned}$$
(25)

for \(k,l=1,\ldots ,p\), s described in (24) and \(F_{\zeta }(s)\) described in (21). This optimization problem can solved by a meta-heuristic and it was chosen the Partcile Swarm Optimization. The termination condition of this optimization problem will be number of epochs (NE). However, it is desirable that the objective function provides at least 0.05 (5% of damping ration of all eigenvalues of the set of operating conditions) for the next steps.

3.2 Initialization process

It is well known from the literature that the initial values of an algorithm based on metaheuristics can affect its convergence. The objective is to improve the damping ratio of the closed loop system and, then, it is recommendable to avoid particles that provides damping ratio of \(-1 (-100\%)\). To avoid this, a set of initial particles \((s_{q},q=1,\ldots ,NP)\) for the search process was built as follows. The \(T3_{kl}\) and \(T4_{kl}\) will be fixed as already mentioned and \(T1_{kl}\) and \(T2_{kl}\) will be calculated in the range [0.01, 0.50]. The gains \(K_{k,l}\) will be generated randomly in the interval \([K_{min}^0,K_{max}^0]\) where \(K_{min}< K_{min}^0< 0< K_{max}^0 < K_{max}\). Thus, the initial particles of the algorithm will be generated for smaller gain values. The main goal is to generate particles with \(\zeta _{min} \ne -1\).

3.3 Search process

After initializing the NP particles \((s_{q,0},q=1,\ldots ,NP)\), we must calculate the objective function for each particle as \(f_{q,0} = F_{\zeta }(s_{q,0})\), define the number of epochs as NE \((e=1,\ldots ,NE)\), calculate the velocity \(v_{q,0}\) of each q particle in the range [0, 1], define the parameter \(\omega \) that defines how much will be retained from the previous velocity, define the parameters \(\phi ^l\) and \(\phi ^g\) in the range [0, 1] that are step size related to the best local particle (\(s^l_q\), the best q particle (the best objective function) until the e epoch), and the best global particle (\(s^g\) the particle of best objective function until the e epoch) respectively, calculate the terms \(rp_q\) and \(rg_q\) in the range [0, 1] for each epoch.

At each epoch, the velocities \((v_{q,e+1})\) of each particle are calculated as follows

$$\begin{aligned} v_{q,e+1} = \omega \cdot v_{q,e} + \phi ^l\cdot rp_q\cdot \left( s^l_q - s_{q,e}\right) + \phi ^g\cdot rg_q\cdot \left( s^g - s_{q,e}\right) \end{aligned}$$
(26)

and each particle will be updated as follows

$$\begin{aligned} s_{q,e+1} = s_{q,e} + v_{q,e+1} \end{aligned}$$
(27)

if the values of the particle \((s_{q,e+1})\) do not respect the limits imposed, this particle remains with the same value of the previous time \((s_{q,e+1} = s_{q,e})\).

This new particle \((s_{q,e+1})\) should also have its objective function value \((f_{q,e+1})\) also updated

$$\begin{aligned} f_{q,e+1} = F_{\zeta }(s_{q,e+1}) \end{aligned}$$
(28)

For each particle is evaluated if the objective function has been improved. If there is improvement, the variable \(s^l_q\) is updated. The particle with the best objective function value \((s^g)\) must also be updated.

This iterative process continues until the number of epochs is reached \((e=NE)\) or the particle with the best objective function value \((s^g)\) already fulfills a certain value considered satisfying to the programmer.

3.4 Quadratic stability evaluation process

This process will be carried out according to the theory presented in Sect. 2.7 only when the search process is finished. If no matrix \(\mathbf {P}\) is found, the initialization and the search processes will be carried out again. Otherwise, the next step will be the time delay variation evaluation process.

3.5 Time delay variation evaluation process

As already mentioned in Sect. 2.5, this work uses two sets of the models described in (13) representing the lower and upper limit for the time delay \((T_{min},T_{max})\). The central controller will have p inputs and p outputs, so \(2\times p\) signals can have different time delays in the range \((T_{min},T_{max})\) to transmit the data.

After finding the unique matrix \(\mathbf {P}\) of the Quadratic Stability Evaluation Process for the closed-loop systems, the objective function \((F_{\zeta }(\cdot ))\) for the candidate as central controller \((s^g)\) will be evaluated considering values of time delays in the interval \((T_{min},T_{max})\) for each one of the \(2\times p\) communication channels. The process will be simple, the eigenvalues of the closed-loop system including the designed controller will be calculated for each increment in fixed steps of the time delay starting from the minimum limit \((T_{min})\) until reaching the maximum limit \((T_{max})\). If, for all evaluations, the minimum damping rate is greater than 5%, the designed central controller has been found and the proposed procedure is completed. Otherwise, the proposed procedure must be restarted from the initialization process.

3.6 Proposed algorithm

The step-by-step algorithm to design the WADC is given as follows

Inputs: \(\mathbf {A}_n\), \(\mathbf {B}_n\), \(\mathbf {C}_n\), \(T_{min}\), \(T_{max}\), \(K_{min}\), \(K_{max}\), \(K_{min}^0\), \(K_{max}^0\), \(T3_{k,l}\), \(T4_{k,l}\), NE, NP, \(\omega \), \(\phi ^l\), \(\phi ^g\) and NR.

Outputs: \(s^g\), \(F_{\zeta }(s^g)\), \(\mathbf {CC}(s)\),

Step 01: Initialization Process as described in Sect. 3.2

Step 02: Search process as described in Sect. 3.3 until the number of epoch be reached \((e=NE)\)

Step 02.01: For each e epoch, update the velocities

$$\begin{aligned} v_{q,e+1} = \omega \cdot v_{q,e} + \phi ^l\cdot rp_q\cdot \left( s^l_q - s_{q,e}\right) + \phi ^g\cdot rg_q\cdot \left( s^g - s_{q,e}\right) \end{aligned}$$
(29)

Step 02.02: Update the particles and their objective function values if the restrictions are respected

$$\begin{aligned} s_{q,e+1}& = {} s_{q,e} + v_{q,e+1} \end{aligned}$$
(30)
$$\begin{aligned} f_{q,e+1}& = {} F_{\zeta }(s_{q,e+1}) \end{aligned}$$
(31)

Step 02.03: Update \(s^l_q\) and \(s^g\), randomly generate \(rp_q\) and \(rq_q\) in the range [0, 1], increment in one unit e and go to Step 02.01.

Step 03: Quadratic Stability Evaluation Process as described in Sect. 3.4. Find a unique matrix \(\mathbf {P}\) that satisfies

$$\begin{aligned}&\mathbf {P} = \mathbf {P}^T \succ \mathbf {0} \end{aligned}$$
(32)
$$\begin{aligned}&\widehat{\mathbf{A}}_n^T\mathbf {P} + \mathbf {P}\widehat{\mathbf{A}}_n \prec \mathbf {0} \end{aligned}$$
(33)

considering all operating conditions, \(n = 1,\ldots ,N\), and the upper and lower time delay, \(T_{min}\) and \(T_{max}\).

If there is an matrix \(\mathbf {P}\), go to Step 04, otherwise go to Step 01.

Step 04: Time Delay Variation Evaluation Process as described in Sect. 3.5.

Step 04.01: For each t evaluation, randomly generate the \(2\times p\) time delays in the interval \([T_{min},T_{max}]\), update all system matrices with the time delay model \((\bar{\mathbf{A}}_{n,t}, \bar{\mathbf{B}}_{n,t}, \bar{\mathbf{C}}_{n,t}, n=1,\ldots ,N)\) and the compute the objective function for the fixed candidate as central controller \((s^g)\)

$$\begin{aligned} F_{\zeta }(s^g) = \zeta _{min} \left\{ \begin{array}{l} \zeta _1\left( \left[ \begin{array}{cc} \bar{\mathbf{A}}_{n,t} + \bar{\mathbf{B}}_{n,t}\mathbf {D}_{\mathbf {c}_q}\bar{\mathbf{C}}_{n,t} &{} \bar{\mathbf{B}}_{n,t}\mathbf {C}_{\mathbf {c}_q} \\ \mathbf {B}_{\mathbf {c}_q}\bar{\mathbf{C}}_{n,t} &{} \mathbf {A}_{\mathbf {c}_q} \end{array}\right] \right) \\ \\ \zeta _2\left( \left[ \begin{array}{cc} \bar{\mathbf{A}}_{n,t} + \bar{\mathbf{B}}_{n,t}\mathbf {D}_{\mathbf {c}_q}^{lp}\bar{\mathbf{C}}_{n,t} &{} \bar{\mathbf{B}}_{n,t}\mathbf {C}_{\mathbf {c}_q}^{lp} \\ \mathbf {B}_{\mathbf {c}_q}^{lp}\bar{\mathbf{C}}_{n,t} &{} \mathbf {A}_{\mathbf {c}_q}^{lp} \end{array}\right] \right) \\ \\ \zeta _3\left( \left[ \begin{array}{cc} \bar{\mathbf{A}}_{n,t} + \bar{\mathbf{B}}_{n,t}\mathbf {D}_{\mathbf {c}_q}^{kp}\bar{\mathbf{C}}_{n,t} &{} \bar{\mathbf{B}}_{n,t}\mathbf {C}_{\mathbf {c}_q}^{kp} \\ \mathbf {B}_{\mathbf {c}_q}^{kp}\bar{\mathbf{C}}_{n,t} &{} \mathbf {A}_{\mathbf {c}_q}^{kp} \end{array}\right] \right) \end{array}\right. \end{aligned}$$
(34)

where \(n=1,\ldots ,N\), \(q=1,\ldots ,NP\), \(lp=1,\ldots ,p\) and \(kp=1,\ldots ,p\)

If \(F_{\zeta }(s^g) > 0.05\) and \(t < NR\), increment in one unit t and go to Step 04.01. If \(F_{\zeta }(s^g) \le 0.05\), go to Step 01 (a new central controller must be found). If \(t = NR\) and in all NR evaluations \(F_{\zeta }(s^g) > 0.05\), so the algorithm ends and the parameters of the central controller are in the vector \(s^g\).

After the convergence of the proposed algorithm, the resulting controller is evaluated in a software called ANATEM [24] for time-domain nonlinear simulations and it was not implemented in a real power system because there is a set of norms for that. Usually, wide-area damping controllers are evaluated through simulation [25, 86, 87]. However, some preliminary results in wide-area damping controller implementation are presents by the authors [63].

4 Test results and discussion

The proposed procedure presented in Sect. 3 was evaluated though its application in the IEEE 68 bus system showed in Fig. 3, the highest benchmark model for small-signal stability studies available in [22]. This power system model presents only one operation condition in [22] and it will be called BL (Base Load) where only the generators 1–12 present an Automatic Voltage Regulator and a Power System Stabilizer. The set of algebraic-differential equations that describes this power system diagram can be found in [21]. Due to space limitations it will not be described here.

Fig. 3
figure 3

Diagram of the IEEE 68-bus power system model [22]

Full size image

A set of operating conditions was built increasing the load levels of all buses of each one of the five areas in different rates. Areas 1 and 2 will present a load maximum increase of 3% and areas 3, 4 and 5, a maximum increase of 6%. The C1 case is the base case BL with these load limits. Table 1 presents the dominant oscillation modes for these two load levels: BL and C1 operation conditions. Using the mode shape analysis, modes M1 and M4 of Table 1 are related to generator 14 against generators 15 and 16. The modes M2 and M5 are related to generator 15 against generators 10–13. The mode 13 is related to generator 16 against generators 14 and 15. Based on this mode shape analysis, it is possible to conclude that the modes with low-damping are related to generators not equipped with AVR and PSS. However, it is possible to estimate the speed signal of each one of the generators 13–16 and these signals can be used for a central controller operation.

Table 1 Dominant oscillation modes of the IEEE 68 bus with all 12 PSSs
Full size table

4.1 Control design stage

The fist step to design the robust WADC is to select the appropriate signals for the input and output of the controller. Another concern is to decide the number of inputs and outputs of the controller to guarantee a satisfactory damping ratio even when one permanent communication failure occurs. It was decided to use five signals \((p=5)\) for the inputs and outputs of the central controller. Using controllability factors [42], the generators 5, 9, 10, 11 and 12 that are equipped with a AVR were selected for the outputs of the WADC and, then \(k=5,9,10,11,12\). The results of observability factors showed that the speed signals of the generators 12, 13, 14, 15 and 16 are appropriated to be the five inputs of the WADC and, then, \(l=12,13,14,15,16\). Figure 4 describes the central controller to be designed illustrating the input and output signals.

Fig. 4
figure 4

Diagram of the IEEE 68-bus power system model with the WADC

Full size image

The parameters of the procedure for search process was defined as \(K_{min}=-30\), \(K_{min}=+30\), \(T1_{k,l} \in [0,1]\), \(T2_{k,l} \in [0,1]\). In this work was decided to use the same time constants of the PSSs related to the poles and, then, \(T3_{k,l} = 0.04\) and \(T4_{k,l} = 0.04\) \((k,l=1,\ldots ,p)\). The number of epochs was 100 \((NE=100)\), the number of particles was 20 \((NP=20)\) and \(\omega = 0.70\), \(\phi ^l = 0.01\), \(\phi ^g = 0.02\).

As already mentioned in Sect. 3.2, the initialization process of the variables is fundamental for better results in shorter simulation time. This case study will have 75 variables to be determined: 25 \(K_{k,l}\), 25 \(T1_{k,l}\) and 25 \(T2_{k,l}\). In the initialization process, the lower and upper limit of the time constants are maintained in [0.01, 0.5] but the lower and upper limit of \(K_{k,l}\) was reduced to \([-10,+10]\) only in this process. The primary purpose in the initialization process is to provide variables such that the objective function is different from \(-1.\)

It was used the SeDuMi solver [76] to find the matrix \(\mathbf {P}\) in the Quadratic Stability Evaluation Process and the number of executions of the Time Delay Variation Evaluation Process was 100 \((NR=10{,}000)\). Figure 5 presents the minimum damping ratio of all operating conditions considering time delay variations in the range 100–150 ms in the input and output of the central controller. It is possible to observe that in this interval, the minimum damping rates were higher than 5%, a value considered satisfactory for stability at small signals [31].

Fig. 5
figure 5

Minimum damping ratio of all operating conditions considering time delay variations in the range 100–150 ms in 0.5 ms step

Full size image

In order to evaluate how the gain limits affect the objective function in the Initialization Process, an analysis was made with the following two limits for the gain: \(L_1=[-10,+10]\) and \(L_2=[-30,+30]\). The lower and upper limit of the time constants are maintained in [0.01, 0.5]. Hundred executions of the Initialization Process for 20 particles \((NP=20)\) were randomly generated for each of these limits and Fig. 6 presented the results: histograms of the particles that provide the highest minimum damping ratio for each one of 100 executions of the Initialization Process. When the limits of the gain were in the range \(L_1\), Fig. 6a, the minimum damping ratio values were in the range [0.1, 1.6] (%), considered satisfactory because the objective was to generate particles whose minimum damping was different from \(-1 (-100\%)\). Figure 6b shows the results when the limits of the gain were in the range \(L_2\): 83 executions provide particles with minimum damping ratio of \(-1 (-100\%),\) undesirable, and 17 executions provide particles with minimum damping ratio in the range \([-9,-3]\) (%). The results demonstrate the importance of properly defining gain limits and time constants in order to provide initial conditions with satisfying values of objective functions for the search process.

Fig. 6
figure 6

Histograms of the particles that provide the highest minimum damping ratio for the 100 executions of the Initialization Process for (a) \(K_{k,l} \in [-10,+10]\) and (b) \(K_{k,l} \in [-30,+30]\)

Full size image

Applying the proposed procedure on a machine with Intel(R) Xeon (R) CPU 2.40 GHz, 64 GB RAM running on a Microsoft 10 Home 64-bit, the procedure took almost 19 min to converge: 8 min in the Step 02 (Search Process), 7 min in the Step 03 (Quadratic Stability Evaluation Process) and 4 min in Step 04 (Time Delay Variation Evaluation Process). The parameters of the robust WADC designed by the proposed procedure are presented in the Table 2. The proposed procedure successfully found the matrix \(\mathbf {P}\) guaranteeing quadratic stability of the power system for all operating points considered and the minimum damping ratio found for the 1000 executions of the Time Delay Variation Evaluation Process was the 5.61%.

Table 2 Parameters of the designed central controller—PSO-WADC(s)
Full size table

4.2 Time-domain nonlinear simulations

The resulting robust central controller, PSO-WADC(s), obtained by linear models was evaluated by time-domain nonlinear simulations using the ANATEM software [24]. The lower and upper limit of the central controller is the same of the PSSs available in the IEEE 69-bus system. Besides, the ideal time delay was used, not a second-order approximation of the function \(\epsilon ^{-sT}\). This controller were also evaluated by other central controllers designed by the meta-heuristics: Genetic Algorithms, GA-WADC, [50], Grey Wolf Optimizer, GWO-WADC, [54] and Ant Colony Optimization, ACO-WADC [29].

Different operating conditions (C) of the power system and different scenarios (S) of the central controller were consider to evaluate the performance of the controller:

  • C1: load condition described in the second paragraph of Sect. 4;

  • C2: the same load level of C1 case and the permanently disconnection of the transmission line 31–53;

  • C3: the following load levels: increase of 3% in area 1, increase of 2% in area 2, increase 4% in area 3, increase of 5% in area 4 and increase of 6% in area 5.

  • C4: the same load level of C1 case and the permanently disconnection of the transmission line 31–53;

  • S1: time delay of 100 ms in all communication channels;

  • S2: different time delays in the communication channels;

  • S3: time delay of 100 ms in all communication channels and permanent loss of the speed signal of generator 13, the second input signal of the central controller;

  • S4: different time delays in the communication channels and permanent loss of the speed signal of generator 13, the second input signal of the central controller;

The output limits of the designed central controller are the same of the PSSs present in [22]. Figure 7a–d present, for the C1 case, the angular response of generator 15 in relation to generator 16 when a temporary three-phase fault-circuit of 50 ms is applied in the bus 40 considering the different fou scenarios: S1, S2, S3 and S4 without and with the designed central controllers: ACO-WADC, GA-WADC, GWO-WADC and PSO-WADC. Figure 8a–d present, for the C2 case, the angular response of generator 14 in relation to generator 16 considering the same temporary three-phase fault-circuit of 50 ms and the four scenarios. Figures 9a–d and 10a–d present, for the C3 and C4 cases respectively, the angular responses of generators 8 and 14 in relation to generator 16 respectively considering the same temporary three-phase fault-circuit of 50 ms. It is interesting to mention that the choice of these generators to present the angular responses was based on the fact that these same generators present their electromechanical state variables with a greater participation factor in the oscillation modes of lower damping rates.

Considering the results of the Figs. 7a–10d, is possible to conclude that the power system with the designed central controller (two-level control structure) present a better damping performance than without the central controller (only the local controllers, PSSs, are working) even when variations occur in the nominal operating condition or in the time delay of the communication channel. Besides, the angular responses of the power system are also stable even when one communication channel loss occurs. The angular responses of the PSO-WADC designed by the proposed procedure in this paper presented a better performance than the other central controllers: ACO-WADC, GA-WADC and GWO-WADC.

Fig. 7
figure 7

Angular deviation responses of generators 15 and 16

Full size image
Fig. 8
figure 8

Angular deviation responses of generators 14 and 16

Full size image
Fig. 9
figure 9

Angular deviation responses of generators 8 and 16

Full size image
Fig. 10
figure 10

Angular deviation responses of generators 14 and 16

Full size image

5 Conclusions

This paper presents a procedure based on Particle Swarm Optimization to design a robust wide-area damping controller considering different operating conditions, a range for the time delay and the permanent loss of signal from a communication channel, unlike the approaches found in the literature that deal only with temporary losses. An Initialization Process was presented and it provided satisfactory initial conditions for the Search Process of the procedure. Besides, the power system with the resulting controller presents quadratic stability using the polytopic model. Based on the time-domain nonlinear simulations for the IEEE 68-bus system for a set of operating conditions and scenarios, the two-level control structure provided good damping performance in the angular responses even when one communication channel loss occurs.

The main disadvantages of the proposed method that will be the subject of future research are: (i) the controller is designed for a set of operating points, if the system presents operating scenarios that were not considered in the design, the performance of the system with the controller may be unsatisfactory, (ii) the controller design is based on linear models of a non-linear system, so depending on the system and approximations, the result can be compromised, (iii) the order of the system may require that the controller has many inputs and outputs and thus many parameters for the control design. Optimization problems with many variables can present convergence problems and, therefore, improvement of meta-heuristics may be necessary.