1 Introduction

In industrial activities, local and instantaneous high pressures are utilized for applications such as mining and blast excavation. To obtain the high pressures, high energy density materials are often used because they release large amounts of energy rapidly and generate local high pressures on the order of gigapascals that fracture hard materials such as rock. However, accidental initiation results in a blast wave that poses a physical hazard whose severity is determined by blast parameters such as the peak overpressure and positive impulse. Here, the positive impulse is calculated as the time integral of the positive overpressure from the time at which the first incident blast wave is recorded to the time at which the overpressure first returns to zero. Therefore, some way of attenuating explosions is required for safer commercial applications and storage of high energy density materials.

Ways to minimize the effects of an explosion have been investigated for many years. Encircling an explosive with water sprays and a layer of particles such as sand is effective for attenuating the blast wave. These methods disturb the propagation of the blast wave, thereby attenuating it directly. Blast-wave mitigation is induced by transferring some of the internal and kinetic energy of the blast wave and the flow induced by it to the particle layer. When the blast wave collides with water sprays, large droplets extract energy from the blast wave, break up into finer mist, and evaporate. To understand quantitatively how the blast wave is mitigated, we must address the associated complex physics, including the interactions among the drag, the heat transfer between the fluid and the particles, and evaporation (if the cloud contains liquid).

Homae et al. [1] conducted experiments in which 100 g of pentolite (50 mm in diameter) was encircled by sand. The peak overpressure and positive impulse were measured to understand how the sand mitigated the blast wave. The sand was contained in acrylic containers of 100 mm and 200 mm in diameter. Homae et al. discussed the effect of the sand mass (67 g for the 100-mm container and 403 g for the 200-mm container). A larger sand barrier achieved greater attenuation of the peak overpressure and positive impulse. Rigby et al. [2] conducted experiments on the detonation of an explosive buried in dry sand and found that the blast parameters were much lower in magnitude for a greater standoff distance between the explosive and the air/sand surface. Sugiyama et al. [3] conducted two-dimensional experimental explosions to understand how a blast wave interacts with a sand hill. The explosive used was a 1-m-long detonating cord initiated in a sand hill shaped like a triangular prism whose cross section was an isosceles triangle with base angles of 30\(^\circ \). The sand-hill height was a parameter used to discuss how the sand mass affected the blast-wave strength. Interaction with the sand/air interface induced multiple peaks in the blast wave, which were generated by successive transmissions at this interface, and an increased mass of sand offered further mitigation.

Pontalier et al. studied blast mitigation by particle–blast interaction during the explosive dispersal of particles and liquids [4]. The dependence of the particle–blast interaction and the blast mitigation effectiveness were investigated. The reduction in peak overpressure depended primarily on the mass ratio between the explosive and the barrier material. The aforementioned studies show that the length of the particle layer through which the blast wave propagates is important for understanding how the blast wave is mitigated. Annamalai et al. [5] conducted numerical simulations in which a dense layer of solid particles surrounding a high-energy reactive material is dispersed, and the interaction between a dense layer and the blast wave was discussed. When the effects of drag force and heat transfer are separately estimated, the blast-wave mitigation mechanism could be quantitatively understood.

However, the attenuation mechanism is yet to be elucidated quantitatively because factors such as (i) the physical properties of the particle layer and (ii) the energy transferred between materials are difficult to assess by experiments alone. If water sprays are utilized for the barrier materials, evaporation and breakup will need to be included in the numerical method to discuss the blast-wave mitigation mechanism [6, 7]. Because numerical simulations can be used to explore quantitatively the mechanisms for transferring energy from the blast wave to the materials, a reliable numerical method is very important for (i) understanding how the blast wave is mitigated and (ii) developing a new way to reduce physical hazards. Recently, Sugiyama et al. [8] and Pontalier et al. [9] used numerical simulations to calculate the energy transferred from the explosive to the barrier materials [mixtures of water and foamed polystyrene (Sugiyama et al.) and glass, steel, and water (Pontalier et al.)] to understand how the blast wave is mitigated.

To understand quantitatively the complex flow behavior associated with the interaction of a blast wave and a particle layer, we must formulate a model that includes their physics. Some methods treat phenomena including the continuum fluid and the particle layer using Eulerian–Eulerian approaches [10], Lagrangian–Lagrangian approaches such as smoothed particle hydrodynamics [11], or Eulerian–Lagrangian approaches such as computational fluid dynamics coupled with the discrete element method [12] (CFD–DEM), the particle-in-cell (PIC) technique [13], and pairwise interaction extended point-particle model  [14]. The Eulerian view of the particle layer is as a continuous material, whereas the Lagrangian view of it is as a collection of discrete, solid, and macroscopic particles with collision and friction interactions. The Lagrangian approach has the advantage that the particle–particle interactions are easy to calculate directly, but it is usually very computationally expensive. Two strategies can be used to calculate the gas–particle interactions: the resolved discrete particle model (RDPM) and the unresolved discrete particle model (UDPM)  [15]. In the RDPM, the computational cells used for the gas phase are smaller than the particle diameter, and the gas–particle interactions are calculated using the boundary conditions at the particle surfaces. This is the most accurate method for studying gas–particle flows, but also the most computationally expensive, due to the fine grid required. In contrast, the UDPM uses computational cells that are larger than the particle diameter and uses a drag force model to calculate the gas–particle interactions.

To validate these methods, some simple experiments can be conducted. Some researchers have used a shock tube in which a generated shock wave collides with a particle layer [16,17,18,19,20,21,22]. They reported on the one-dimensional reflection and transmission of the shock wave at the air/particle interface and the movement of the particle layer induced by the gas flow. Theofanous et al. [19] studied experimentally the interaction between a planar shock wave and a curtain of falling particles that occupied fully the cross section inside a shock tube. Because gravity generated the curtain similar to a waterfall, there was a gradient in gas volume fraction between the top and bottom of the shock tube. This gradient generated a curved transmitted wave and the complex two-dimensional behavior of the dense particle curtain.

Some studies focused on the propagation of the planar shock wave along the particle layer [10, 23, 24], showing uplift of the particle layer by (i) propagation of the shock wave along it or (ii) partial collision of the shock wave with the layer. The Magnus force induced by the relative rotation between the shocked flow and the particles is an important mechanism for lifting the particles behind the shock wave [24]. Other studies [25, 26] focused on shock-driven multiphase instabilities (SDMI), which are unique physical phenomenon induced by gradients in particle–gas momentum transfer.

As the Lagrangian approach directly estimates the contact force, the Eulerian–Lagrangian approach could be utilized to understand the physics of the interaction between the shock-induced flow and particles described above. This paper presents a validation study of the two-dimensional CFD–DEM with UDPM. We modeled a previous experimental study [19] that we consider as a two-dimensional manifestation of the interaction between a shock wave and a particle layer with an initial gradient of its volume fraction in height. We discuss the interaction between the shock wave and the particle cloud curtain (PCC), and we calculate (i) the drag force and convective heat transfer between the air and PCC and (ii) the contact force between two particles. This numerical method can be used to elucidate how the particle layer mitigates the blast wave, providing information for future studies.

2 Investigation details

2.1 Numerical method

The governing equation for the gas phase is the same as in the well-known two-fluid models [24, 27], with the volume fraction, denoted \({\alpha }\). Herein, the subscripts \(\mathrm {g}\) and \(\mathrm {p}\) denote the gas phase and the particle phase, respectively. Then, \({\alpha }_{\mathrm {g}} + {\alpha }_{\mathrm {p}} = 1\) is satisfied in the present study. The gas phase is assumed to be air composed of \(\hbox {O}_{{2}}\) and \(\hbox {N}_{{2}}\) in the molar ratio 1:3.76 and treated as a single fluid. Thus, the conservation laws for mass, momentum, and total energy are expressed as

$$\begin{aligned}&\frac{\partial {\alpha _{\mathrm {g}}}{\rho _{\mathrm {g}}}}{\partial {t}}+\nabla \cdot ({\alpha _{\mathrm {g}}}{\rho _{\mathrm {g}}}{} \mathbf{u}{_{\mathrm {g}}})=0, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial {\alpha _{\mathrm {g}}}{\rho _{\mathrm {g}}}{} \mathbf{u}{_{\mathrm {g}}}}{\partial {t}}+\nabla \cdot ({\alpha _{\mathrm {g}}}{\rho _{\mathrm {g}}}{} \mathbf{u}{_{\mathrm {g}}}{} \mathbf{u}{_{\mathrm {g}}})+{\alpha _{\mathrm {g}}}\nabla p_{\mathrm {g}}=\mathbf{f}_{\mathrm {gp}},\end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial {\alpha _{\mathrm {g}}}{\rho _{\mathrm {g}}}{E_{\mathrm {g}}}}{\partial {t}}+\nabla \cdot [{\alpha _{\mathrm {g}}}({\rho _{\mathrm {g}}}E_{\mathrm {g}}+p_{\mathrm {g}})\mathbf{u}{_{\mathrm {g}}}]\nonumber \\&\quad =-{p_{\mathrm {g}}}\frac{\partial {\alpha _{\mathrm {g}}}}{\partial {t}}+s_{\mathrm {gp}}+q_{\mathrm {gp}}. \end{aligned}$$
(3)

Here, \({\rho _{\mathrm {g}}}\), \(\mathbf{u}{_{\mathrm {g}}}\), \({p_{\mathrm {g}}}\), and \({E_{\mathrm {g}}}\) are the density, velocity vector in Cartesian coordinates, pressure, and total energy per unit mass, respectively. The source terms \(\mathbf{f_{\mathrm {gp}}}\) and \({s_{\mathrm {gp}}}\) are the momentum and energy, respectively, exchanged by aerodynamic forces between the air and the particles, and \({q_{\mathrm {gp}}}\) denotes the energy transferred by the temperature difference between the air and the particles. The equation of state for the air is assumed to be that of a thermally perfect gas, and the heat capacity and enthalpy are estimated using the NASA polynomials with coefficients taken from the CETPC table [28].

The particles are treated as being discrete and are described by the DEM of the soft-sphere model. The individual particles are governed by the equations of motion for translation and by conservation of energy, with their heat capacity assumed to be constant. Thus, the governing equations for particle i are described as

$$\begin{aligned} \frac{ \mathrm {d} {\mathbf{x}_{\mathrm {p},i}}}{ \mathrm {d} {t}}= & {} \mathbf{u}_{\mathrm {p},i},\end{aligned}$$
(4)
$$\begin{aligned} m_{\mathrm {p}}\frac{ \mathrm {d} \mathbf{u}_{\mathrm {p},i}}{ \mathrm {d} t}= & {} \mathbf{F}_{\mathrm {quasi},i}+\mathbf{F}_{\mathrm {pres},i}+\sum _{\forall _j \in \mathrm collision} \mathbf{F}_{\mathrm {pp},ij},\end{aligned}$$
(5)
$$\begin{aligned} I_{\mathrm {p},i}\frac{ \mathrm {d} {\varvec{\omega }}_{\mathrm {p},i}}{ \mathrm {d} t}= & {} \sum _{\forall _j \in \mathrm collision} \mathbf{M}_{\mathrm {pp},ij},\end{aligned}$$
(6)
$$\begin{aligned} m_{\mathrm {p}} c_{p\mathrm {p}}\frac{ \mathrm {d} {T_{\mathrm {p},i}}}{{\mathrm {d} t}}= & {} Q_{\mathrm {heat},i}. \end{aligned}$$
(7)

Here, \(\rho _{\mathrm {p}}\), \(m_{\mathrm {p}}\), \(\mathbf{x}_{\mathrm {p},i}\), \(\mathbf{u}_{\mathrm {p},i}\), \(I_{\mathrm {p},i}\), \({{\varvec{\omega }}_{\mathrm {p},i}}\), \(V_{\mathrm {p}}\), \(c_{p\mathrm {p}}\), and \(T_{\mathrm {p},i}\) are the density, mass, position vector of the center of gravity, velocity vector, moment, rotational velocity vector, volume, specific heat capacity, and surface temperature of particle i, respectively. All particles have the same radius \(r_{\mathrm {p}}\) and density \(\rho _{\mathrm {p}}\) and are assumed to be an incompressible [29] sphere, whereupon \(V_{\mathrm {p}}\) and \(m_{\mathrm {p}}\) are taken as \(4\pi r_{\mathrm {p}}^3/3\) and \(\rho _{\mathrm {p}}V_{\mathrm {p}}\), respectively. In the two-dimensional simulation, \(I_{\mathrm {p},i}\) has a component in the z-direction only. Because of its low Biot number, we neglect the internal temperature gradient of the particle, whereupon the internal energy is dictated by the surface temperature. \(Q_{\mathrm {heat},i}\) is the amount of heat transferred convectively between the air and particle i.

In the present study, the forces acting on a particle are the particle–particle contact force \(\mathbf{F}_{\mathrm {pp},ij}\), the quasi-steady drag force \(\mathbf{F}_{\mathrm {quasi},i}\), and the pressure gradient force \(\mathbf{F}_{\mathrm {pres},i}\). The contact torque \(\mathbf{M}_{\mathrm {pp},ij}\) is generated by the tangential contact force. The contact force and contact torque between two particles i and j are determined as follows:

$$\begin{aligned}&\mathbf{F}_{\mathrm {pp},ij}=\mathbf{F}_{\mathrm {pp},ij}^{n}+\mathbf{F}_{\mathrm {pp},ij}^{t},\end{aligned}$$
(8)
$$\begin{aligned}&\mathbf{F}_{\mathrm {pp},ij}^{n}=-k_{n}{\varvec{\delta }}_{ij}^{n}+\eta _{n}{} \mathbf{u}_{ij}^{n},\end{aligned}$$
(9)
$$\begin{aligned}&\mathbf{F}_{\mathrm {pp},ij}^{t} \nonumber \\&\quad = \left\{ \begin{array}{ll} -k_{t}{\varvec{\delta }}_{ij}^{t}+\eta _{t}{} \mathbf{u}_{ij}^{t} &{} |\mathbf{F}_{\mathrm {pp},i,j}^{t}|< \nu _{t} |\mathbf{F}_{\mathrm {pp},i,j}^{n}| \\ -\nu _{t}{} \mathbf{F}_{\mathrm {pp},i,j}^{n}({\varvec{\delta }}_{ij}^{t})/|{\varvec{\delta }}_{ij}^{t}| &{} |\mathbf{F}_{\mathrm {pp},i,j}^{t}|> \nu _{t} |\mathbf{F}_{\mathrm {pp},i,j}^{n}|\\ \end{array} \right. \end{aligned}$$
(10)
$$\begin{aligned}&\mathbf{M}_{\mathrm {pp},ij}=r_{\mathrm {p}}{} \mathbf{n}_{ij} \times \mathbf{F}_{\mathrm {pp},i,j}^{t},\end{aligned}$$
(11)
$$\begin{aligned}&\mathbf{u}_{ij}=\mathbf{u}_{j}-\mathbf{u}_{i}-(r_{\mathrm {p}} {\varvec{\omega }}_{i}+r_{\mathrm {p}}{\varvec{\omega }}_{j}) \times \mathbf{n}_{ij},\end{aligned}$$
(12)
$$\begin{aligned}&{\varvec{\delta }}_{ij}^{n}=[2r_{\mathrm {p}}-\mathbf{R}_{ij}\cdot \mathbf{n}_{ij}]\mathbf{R}_{ij},\end{aligned}$$
(13)
$$\begin{aligned}&{\varvec{\delta }}_{ij}^{t}= \left\{ \begin{array}{ll} {\varvec{\delta }}_{ij, 0}^{t}+\int _{T_{0}}^{T}{} \mathbf{u}_{ij}^{t} \mathrm {d} t\ &{} |\mathbf{F}_{\mathrm {pp},i,j}^{t}|< \eta _{t} |\mathbf{F}_{\mathrm {pp},i,j}^{n}| \\ \frac{\eta _{t}}{k_{t}}|\mathbf{F}_{\mathrm {pp},i,j}^{n}|\mathbf{n}_{ij}^{t} &{} |\mathbf{F}_{\mathrm {pp},i,j}^{t}|> \eta _{t} |\mathbf{F}_{\mathrm {pp},i,j}^{n}|\\ \end{array} \right. \end{aligned}$$
(14)
$$\begin{aligned}&\mathbf{R}_{ij}=\mathbf{x}_{i}-\mathbf{x}_{j},\end{aligned}$$
(15)
$$\begin{aligned}&\mathbf{n}_{ij}=\mathbf{R}_{ij}/|\mathbf{R}_{ij}|. \end{aligned}$$
(16)

The superscripts n and t denote the normal and tangential directions, respectively. \(\mathbf{u}_{ij}\), \(\mathbf{R}_{ij}\), and \(\mathbf{n}_{ij}\) describe the interparticle relative velocity, the relative position vector from the center of particle i to that of particle j, and its unit vector, respectively. \({\varvec{\delta }}_{ij}^{t}\) and \({\varvec{\delta }}_{ij}^{n}\) denote the tangential and normal displacements, respectively. \(k_{t}\) and \(k_{n}\) are the spring constants, \(\eta _{t}\) and \(\eta _{n}\) are the damping constants, and \(\nu _{t}\) is the kinematic viscosity. When \(|\mathbf{R}_{ij}| < 2r_{\mathrm {p}}\), the contact force and contact torque are activated in the simulation.

The pressure gradient force is given by

$$\begin{aligned}&\mathbf{F}_{\mathrm {pres},i}=-{ V}_{\mathrm {p}}\nabla {p}_{\mathrm {g}}. \end{aligned}$$
(17)

The energy transferred between particle i and the gas is considered to be only the heat transferred by the temperature difference between the two, namely

$$\begin{aligned} Q_{\mathrm {heat},i}= & {} S_{\mathrm {p}}h_{\mathrm {p},i}(T_{\mathrm {g}}-T_{\mathrm {p},i}),\end{aligned}$$
(18)
$$\begin{aligned} h_{\mathrm {p},i}= & {} \frac{\mathrm{Nu}_{\mathrm {p},i}{\kappa }_{\mathrm {g}}}{d_{\mathrm {p}}},\end{aligned}$$
(19)
$$\begin{aligned} \mathrm{Re}_{\mathrm {p},i}= & {} \frac{\rho _{\mathrm {g}}{|\mathbf{u}_{\mathrm {g}}-\mathbf{u}_{\mathrm {p},i}|}d_{\mathrm {p}}}{\mu _{\mathrm {g}}},\end{aligned}$$
(20)
$$\begin{aligned} \mathrm{Nu}_{\mathrm {p},i}= & {} \left( 7-10\alpha _{\mathrm {g}}+5\alpha _{\mathrm {g}}^{2}\right) \left( 1+\mathrm{Re}_{\mathrm {p},i}^{1/5}0.7\mathrm{Pr}_{\mathrm {p}}^{1/3}\right) \nonumber \\&+\left( 1.33-2.4\alpha _{\mathrm {g}}+1.2\alpha _{\mathrm {g}}^{2}\right) \mathrm{Re}_{\mathrm {p},i}^{7/10}\mathrm{Pr}_{\mathrm {p}}^{1/3},\end{aligned}$$
(21)
$$\begin{aligned} \mathrm{M}_{\mathrm {p},i}= & {} \frac{|\mathbf{u}_{\mathrm {g}}-\mathbf{u}_{\mathrm {p},i}|}{a_{\mathrm {g}}},\end{aligned}$$
(22)
$$\begin{aligned} \mathbf{F}_{\mathrm {quasi},i}= & {} 3\pi \mu _{\mathrm {g}}d_{\mathrm {p}}(\mathbf{u}_{\mathrm {g}}-\mathbf{u}_{\mathrm {p},i})\times {\hat{F}}(\mathrm{Re}_{\mathrm {p},i}, \mathrm{M}_{\mathrm {p},i}, \alpha _{\mathrm {g}}). \end{aligned}$$
(23)

Here, \(\mathrm{M}_{\mathrm {p},i}\), \(S_{\mathrm {p}}\), \(d_{\mathrm {p}}(=2r_{\mathrm {p}}\)), and \(h_{\mathrm {p},i}\) are the relative Mach number, the surface area, the diameter, and the coefficient of local heat transfer for particle i, respectively. The viscosity \(\mu _\mathrm{g}\) and thermal conductivity \(\kappa _{\mathrm {g}}\) are calculated using the Gordon equation [30] with the Wilke combination rule to account for the temperature dependency. \(a_{\mathrm {g}}\) is the speed of sound. \(\mathrm{Re}_{\mathrm {p},i}\) and \(\mathrm{Nu}_{\mathrm {p},i}\) are the particle Reynolds number and Nusselt number, respectively. We use the Gunn model [31] to estimate \(\mathrm{Nu}_{\mathrm {p},i}\) as shown in (21). To estimate \({\hat{F}}(\mathrm{Re}_{\mathrm {p},i}, \mathrm{M}_{\mathrm {p},i}, \alpha _{\mathrm {g}})\), we used the Ling model [17]. Black et al. [32] discussed the particle force model effects of pressure gradient, added-mass, and interparticle forces and showed that a SDMI is dependent on the models utilized in the numerical simulation. We activated the added-mass force for the preliminary calculation, but its value was much smaller than those of the pressure gradient force and the quasi-steady drag force. Theofanous et al.  [33] also claimed that the importance of added-mass and history forces was negligible in the present numerical problem. Thus, we neglected them in the present paper.

The governing equations for the gas phase and the equations for the individual particles are coupled by the volume fraction of air \(\alpha _{\mathrm {g}}\) and the interphase exchanges \(\mathbf{f}_{\mathrm {gp}}\), \(s_{\mathrm {gp}}\), and \(q_{\mathrm {gp}}\) as given by  (24)–(27):

$$\begin{aligned}&{\alpha }_{\mathrm {g}}=1-\frac{1}{V_{\mathrm {CFD,cell}}}\sum _{\forall _i \in \mathrm {cell}}n_i^{z}V_{\mathrm {p}},\end{aligned}$$
(24)
$$\begin{aligned}&\mathbf{f}_{\mathrm {gp}}=-\frac{1}{V_{\mathrm {CFD,cell}}}\sum _{\forall _i \in \mathrm {cell}}n_i^{z}\mathbf{F}_{\mathrm {quasi},i},\end{aligned}$$
(25)
$$\begin{aligned}&{s}_{\mathrm {gp}}=-\frac{1}{V_{\mathrm {CFD,cell}}}\sum _{\forall _i \in \mathrm {cell}}n_i^{z}{} \mathbf{F}_{\mathrm {quasi},i} \cdot \mathbf{u}_{\mathrm {p},i},\end{aligned}$$
(26)
$$\begin{aligned}&{q}_{\mathrm {gp}}=-\frac{1}{V_{\mathrm {CFD,cell}}}\sum _{\forall _i \in \mathrm {cell}}n_i^{z}{Q}_{\mathrm {heat},i}. \end{aligned}$$
(27)

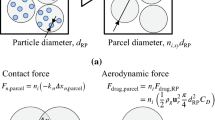
We used the coarse-grained model whose details are described in Refs. [24, 34] and simulated a representative particle known as a parcel to reduce the computational cost. Sakai’s method [34] was used to connect the DEM equations for the parcels with those for the real particles. The particles’ translational motion is assumed to be the same as that of each parcel. From the assumption relating the translational motions of parcels and real particles, the displacements between parcels are the same as those between particles, and the aerodynamic forces are n times greater than those acting on particles. Here, n denotes the number of particles in one parcel. This allows the contact forces and torques acting on individual particles to be calculated using the displacements between parcels, and the aerodynamic forces to be calculated using the real particles’ physical properties.

To solve for spherical (i.e., three-dimensional) particles that are uniformly distributed in the z-direction with two-dimensional CFD, the parcel is modeled as a cylinder extending in the z-direction. The number of particles in one parcel per unit length in the z-direction is \(n_{i}^{z} = 1447\) to match the number of particles estimated from the experimental conditions, and we assume that these 1447 actual particles in one parcel have the same physical properties and move in the same way. Herein, the parcel radius is the same as that of the particle, namely \(r_{\mathrm {p}}\). In the two-dimensional simulation, \({V_{\mathrm {CFD,cell}}}\) is the volume per unit length in the z-direction; therefore, the surface area of each cell of the structured mesh is used in the CFD. This facilitates the coupling of the two-dimensional CFD and the spherical particles put along the z-direction. We used triangle-based barycentric interpolation as the CFD–DEM coupling method [24].

The fluid calculations were discretized spatially using the third-order simple low-dissipation AUSM 2 (SLAU2) [35] scheme with monotone upstream-centered schemes for conservation laws (MUSCL) interpolation and a minmod limiter for the convective term. The time-integration methods for the gas and particle phases are the third-order total-variation-diminishing (TVD) Runge–Kutta method [36] and the first-order symplectic Euler method, respectively. The time steps for the gas phase (\(\varDelta t_{\mathrm {CFD}}\)) and particle phase (\(\varDelta t_{\mathrm {DEM}}\)) are estimated separately using the Courant–Friedrichs–Lewy (CFL) condition. In general, \(\varDelta t_{\mathrm {DEM}}\) was smaller than \(\varDelta t_{\mathrm {CFD}}\), so the time integral for the particle phase was iterated several times to reach \(\varDelta t_{\mathrm {CFD}}\) [24].

2.2 Numerical target

Figure 1 shows the numerical objective of the present study, which models one of the experiments by Theofanous et al. [19]. The calculation domain in x- and y-directions for CFD is as follows: \(-1~\mathrm {m} \le x \le 1~\mathrm {m}\) and \(0~\mathrm {m} \le y \le 0.2~\mathrm {m}\), respectively. The z-direction is defined as the normal direction of the xy plane. It quantified experimentally the two-dimensional dispersal characteristics of the interaction between the air and a dense particle cloud in a shock tube with square cross-sectional dimensions of 200 mm \(\times \) 200 mm. A shock wave originates from the \(-x\)-direction and interacts at the left-hand side of the particle curtain. For that reason, the origin of the coordinate system is the left-hand side of the particle curtain at the bottom of the shock tube. The Mach number of the shock wave and the width of the particle curtain are 1.66 and 24 mm, respectively. The labels P1 at \(x = -0.732\) m and P2 at \(x = 0.608\) m at the top wall denote the positions at which we measure the pressure time histories of the reflected and transmitted parts of the shock wave to compare the numerical results with the experimental data.

Fig. 1
figure 1

Numerical objective of the present study and modeled experiments [19]

Full size image

For the boundary conditions, we used adiabatic slip walls for the top and bottom of the shock tube and the outflow condition at the right-hand boundary. Gas properties behind a shock wave with Mach number of 1.66 flow were introduced into the computational domain from the left boundary (at \(-1\) m). In the experiments, the shock tube generates the shock wave propagating into the low-pressure region and the expansion wave propagating into the high-pressure region. After the expansion wave reflects off the end wall of the shock tube, it follows the shock wave, resulting in a complex pressure distribution behind the shock wave. However, in the present study, we neglect the expansion wave.

Figure 2 shows the initial properties of the PCC in the y-direction. In the experiments, because the PCC forms under gravity, the particles have negative velocity and the gradient of the volume fraction of the air in the y-direction, which are height dependent [19]. We describe fitting curves, indicated by red in Fig. 2, and model them in the calculation. The grid spacing (\(\varDelta x\) and \(\varDelta y\)) and the number of parcels per unit length in the z-direction for the PCC were constant at 2 mm and 3093 or 4 mm and 3045, respectively, and we will examine the influence of grid resolution in this study. The initial pressure and temperature of the air before the incident shock wave are 101,325 Pa and 293 K, respectively.

Table 1 lists the values of the constants in  (1)–(27) used in the present numerical calculations. We conducted the study of the effect of the spring constants as Shimura et al. [24] did. We confirmed that the spring constants in the present paper could properly simulate the behavior of PCC.

Fig. 2
figure 2

Relationships between height from tube bottom and a initial volume fraction of air and b initial particle velocity

Full size image

3 Results and discussion

When the shock wave interacts with the PCC, the reflected and the transmitted shock waves are generated. The gas flow causes the PCC to move in the \(+x\)-direction. To understand the interaction and the PCC movement, Fig. 3 shows a pressure–time diagram for the gas phase at the top of the shock tube (\(y = 0.2\) m) in the case of the grid spacing of 2 mm. Here, time \(t = 0\) ms is defined as when the incident shock wave collides with the left-hand side of the PCC. The reflected shock wave begins to propagate back through the air also at \(t = 0\). At \(t = 0.05\) ms, when the wave propagating through the PCC reaches its right-hand side, the transmitted shock wave begins to propagate through the air. When the PCC interacts with the compressed air, the quasi-steady drag force, pressure gradient force, and convective heat transfer cause the compressed air to lose momentum and total energy, thereby mitigating the transmitted shock wave.

Table 1 Parameter values used in the present study
Full size table

The PCC clearly divides the high-pressure region originating from the reflected shock wave and the low-pressure region originating from the transmitted shock wave. The pressures behind the incident and transmitted parts of the shock wave at 2 ms are 310 kPa and 200 kPa, respectively. The transmitted-to-incident pressure ratio is roughly 0.65, showing that the PCC mitigates the shock wave. This indicates that encircling an explosive with a particle layer is an effective way to mitigate the blast wave because some of the total released energy enters the particle layer, thereby generating a weaker blast wave into the air.

The two white dashed lines in Fig. 3 denote the upstream and downstream particle fronts (UPF and DPF). They are based on the positions of the particles farthest to the left and right in the present simulation. When the shock wave interacts with the PCC, the reflected and the transmitted shock waves are generated. The gas flow causes the PCC to move in the \(+x\)-direction. As Boiko et al. [37] mentioned, the movement of the PCC generates the compression wave and expansion wave. The expansion wave propagating in the \(-x\)-direction reduces the pressure near the UPF, whereas the compression wave propagating in the \(+x\)-direction increases the pressure near the DPF after 3 ms, as shown in Fig. 3. The UPF-to-DPF width of the PCC increases with time. At the UPF, the contact force in the \(-x\)-direction from a particle near the farthest left particle decelerates the particle in the \(+x\)-direction. At the DPF, the contact force in the \(+x\)-direction from a particle near the farthest right particle accelerates it. The air flow induced by the transmitted wave also accelerates the right-side particles, thereby continuing to widen the PCC.

Fig. 3
figure 3

Pressure–time diagram for gas phase at the top wall of shock tube in the case of the grid spacing of 2 mm

Full size image

Now, we compare quantitatively the CFD–DEM data with the experimental results regarding the movement of the PCC. Figure 4 shows the pressure–time histories at (a) P1 (\(x = -0.732\) m) and (b) P2 (\(x = 0.608\) m). Figure 5 shows the time histories of the UPF and DPF. The black and colored data denote the results of the previous experiments [19] and the present CFD–DEM, respectively. Here, we show the results of the grid resolution study in which grid spacings were 2 mm and 4 mm, respectively, which denotes 12 and 6 points in the initial length of the PCC. In the present study, the numerical results for the arrival times of the reflected and transmitted parts of the shock wave and the time changes in pressure thereafter agree well with the experimental ones, and it is sufficient to solve them with a grid spacing of 4 mm. The green arrow in Fig. 4b denotes the CFD–DEM start time of the pressure oscillation and the arrival of the particles at P2 at 8.5 ms, which also agrees with that determined experimentally. On the other hand, the time histories of UPF and DPF are different between the two grid resolutions, and both the UPF and DPF according to the CFD–DEM data agree with those determined experimentally in the case of 2 mm.

In this study, we utilized the UDPM to reduce the computational cost, and the UDPM uses computational cells that are larger than the particle diameter to calculate the gas–particle interactions. In the orthogonal mesh, the cell’s diagonal length of \(l~(=\sqrt{(\varDelta x)^2+(\varDelta y)^2 }~=\sqrt{2}\varDelta x)\) calculated from the grid spacing should be larger than 1.27 mm because the particle diameter is 0.9 mm. Then in the present study, we used 2 mm to discuss the interaction problem of the shock wave and the PCC, and it is the limitation of UDPM in the present study.

Fig. 4
figure 4

Pressure–time histories at a P1 (\(x = -\,0.732\) m) and b P2 (\(x = 0.608\) m) at the top wall of shock tube. Black and colored lines denote the results of the previous experiments and the present CFD–DEM, respectively

Full size image
Fig. 5
figure 5

Time histories of upstream and downstream particle fronts (UPF and DPF)

Full size image

At P1 in Fig. 4a, the incident shock wave increases the pressure to 310 kPa and the reflected shock wave increases it further to 650 kPa. In the case of the shock-tube problem, when the shock wave reflects off the end wall, the reflected pressure is maintained before the expansion wave reaches the end wall. In the present study, the PCC movement generates the expansion wave in \(-x\)-direction and the compression wave in the \(+x\)-direction, which affects the pressure–time history. As shown in Fig. 4a, after the reflected pressure of 650 kPa, the expansion wave generated by the particle movement in the \(+x\)-direction as shown in Fig. 3 reduces the pressure. In Fig. 4b by contrast, the pressure due to the transmitted shock wave reaches 200 kPa, and the compression wave due to the particle movement increases it gradually. These time gradients agree with those in the experiments.

Because the PCC has a gradient in the y-direction, transmission and reflection of the shock wave are not one-dimensional phenomena. To discuss the movement of the PCC and transmitted shock wave, Fig. 6 shows instantaneous pressure distributions near the PCC, where each black dot denotes a particle. The vertical extent of the images in Fig. 6 corresponds to that between the top and bottom of the shock tube. Our numerical results in time histories of UPF, DPF, and pressures at P1 and P2 agree with the experimental data. Then, Fig. 6 qualitatively represents the flow features of the movement of the PCC. The reflection occurs at \(t = 0.01\) ms (Fig. 6a), and a higher-pressure zone appears nearer the top of the tube. In the present study, the initial values of \(\alpha _{\mathrm {p}}\) are least (0.24) at the bottom of the shock tube and greatest (0.58) at the top. Because the shock wave reflects from the PCC more strongly with higher \(\alpha _{\mathrm {p}}\), higher pressure appears nearer the top of the tube. By contrast, as shown in Fig. 6b, the drag force and heat transfer weaken the transmission of the shock wave through the PCC more with higher \(\alpha _{\mathrm {p}}\). This makes the transmitted part of the shock wave strongest at the bottom of the shock tube and weakest at the top. Because of this locally differing shock-wave strength, the transmitted part of the shock wave is curved at 0.45 ms.

Fig. 6
figure 6

Instantaneous distributions of pressure near the particle cloud curtain (PCC). Black dots denote particles

Full size image

After that, the gas flow pushes the particles. There are fewer particle–particle contacts for smaller \(\alpha _{\mathrm {p}}\) for transmitting the contact force from the farther left to the farther right particles. The particles near the bottom of the tube have the smallest \(\alpha _{\mathrm {p}}\), and it is relatively easy to accelerate and move particles in the \(+x\)-direction. Furthermore, air pockets are generated at the points indicated by arrows in Fig. 6d. This is caused by the initial and local positions of the particles in the x-direction and contact forces between two particles. The air pockets become local stagnation points with higher pressure, thereby accelerating particle dispersion from the center of the air pockets. Because the dispersion widens the PCC, the pressure gradient between the UPF and DPF decreases as shown in Fig. 6e. Figure 6 shows that the CFD–DEM properly resolves (i) the interaction phenomena associated with the reflection and transmission of the shock wave and (ii) the particle motions induced by the drag force, contact force, and convective heat transfer.

To understand the interaction between the particles and the shock wave, we calculate the drag force, pressure gradient force, and contact force. Figure 7 shows time histories of (a) the drag force, (b) the pressure gradient force, and (c) the contact force in the \(+x\)-direction. Each dot denotes a value for one particle, and the lines denote the averaged data of all particles. To show the time evolution of the contact force, we treat it specially: the contact forces shown are averaged over 0.01 ms because they act instantaneously between two particles. Here, we present them by the averaged value of all particles. In the calculation, the incoming flow increases the energy and momentum of the gas phase, and they linearly increase with time. To understand momentum and energy transfer between the gas and particles, the sum or the average of all particles could be representative values which are directly compared to the increase in the energy and momentum by incoming flow.

The drag force is around 0.01 N and decreasing slightly because the dispersion increases the volume fraction of gas, and the Ling model used herein reduces the drag force at larger volume fractions of gas.

DeMauro et al. [38] showed that pressure difference established by the reflected or transmitted shock waves determined drag term. In the present study, the pressure gradient force continues to decrease because the dispersion reduces the reflected pressure, increases the transmitted pressure, and widens the PCC, thereby decreasing the pressure gradient between the UPF and DPF. From comparing the drag and pressure gradient forces, the drag force acting between the flow and the PCC relatively affects the transmitted part of the shock wave through the PCC for long duration in the present study.

The contact force between two particles appears to be 100 times greater than either the drag force or the pressure gradient force. However, when two particles collide with each other, the contact forces of the opposite direction and the same size are acted for the two based on Newton’s third law. Then, the distributions of dots are symmetric about 0 N and the averaged contact force becomes zero. The contact force did not affect the global behavior of the PCC. The quasi-steady drag force and the pressure gradient force are always acted when the flow interacts with the PCC. When two particles collide, the contact force, which is much greater than the two forces, is locally acted as shown in Fig. 7. The contact force is an important factor to resolve the interparticle phenomena such as acceleration and deceleration of particles near UPF and DPF, and generation of air pockets as shown in Fig. 6. To understand the local behaviors of the particles, the contact force needs to be directly modeled by the Lagrangian approach.

Fig. 7
figure 7

Time histories of a drag force, b pressure gradient force, and c contact force in the \(+x\)-direction. Dots denote the values for individual particles, and lines denote the averaged data of all particles

Full size image
Fig. 8
figure 8

Time histories of a particle Reynolds number, b surface temperature, and c energy flux by heat transfer

Full size image
Fig. 9
figure 9

Relationship between the initial height of particles in y-direction [m] and a quasi-steady drag force, b pressure gradient force, and c energy flux by heat transfer, respectively, at 1 ms. Each dot denotes a value for one particle

Full size image

Next, we calculate the convective heat transfer between the air and the PCC. Figure 8 shows time histories of (a) particle Reynolds number, (b) surface temperature, and (c) energy flux due to heat transfer. The particle Reynolds number is almost constant at 50,000 because (i) the particle velocity is much less than the fluid velocity induced by the shock wave in this period and (ii) the relative velocity \(|\mathbf{u}_{\mathrm {g}}-\mathbf{u}_{\mathrm {p}}|\) is almost the same as the flow velocity. The average Nusselt number estimated from the particle Reynolds number is also constant, resulting in the constant gradients of the average surface temperature and the energy flux estimated from \(Q_{\mathrm {heat}}\) in  (18). The difference between the maximum and minimum energy flux is about 6 W, resulting in the wide range of the surface temperature as shown in Fig. 8b.

The average energy flux due to heat transfer is roughly 2 W, and then, its sum of heat transfer (2 W \(\times \) 1447 particles \(\div \) one parcel \(\times \) 3093 parcels/m) is 895 kW/m, whereas that from the left boundary is 7238 kW/m. Twelve percent of the incoming energy flux from the left boundary is transferred from the air to the PCC, and the convective heat transfer may contribute to mitigating the shock wave as it passes through the PCC in addition to the quasi-steady drag force and pressure gradient force. Because the heat transfer is determined by the temperature difference between the air and the particle, it is strongly affected by (i) the high-temperature gas behind the shock wave and (ii) the ambient-temperature particles. This effect increases when the particles are placed nearer to the high explosive or the Mach number of the shock wave increases; this will be investigated in future work.

Since the PCC initially had a gradient of its volume fraction in height, the reflection and transmission locally changed with the height as shown in Fig. 6. To understand the gas–particle interaction in detail, Fig. 9 shows the relationship between the initial height of particles in the y-direction and (a) quasi-steady drag force, (b) pressure gradient force, and (c) energy flux by heat transfer, respectively, at 1 ms. Each dot denotes a value for one particle. Horizontal axis denotes the initial height of particles, and a smaller height corresponds to the region of less \({\alpha }_{\mathrm {p}}\) or greater \({\alpha }_{\mathrm {g}}\). The overviews in Fig. 9a, c show that the quasi-steady drag force and energy flux are a function of the initial height and increase as the initial height and \({\alpha }_{\mathrm {p}}\) decrease. This tendency at 1 ms continued between 0 ms and 2.5 ms in the present study. In the Ling model  [17] and the Gunn model  [31], \({\alpha }_{\mathrm {p}}\) is one of the parameters that determines the quasi-steady drag force and energy flux. For constant values of other parameters, the quasi-steady drag force and energy flux become smaller when \({\alpha }_{\mathrm {p}}\) increases. Then, they became smaller at larger initial height.

Figure 9b shows the pressure gradient force, and it is independent of the initial height. As DeMauro et al. [38] stated, the pressure difference established by the reflected and transmitted shock waves determined the pressure gradient force. Since the pressure difference of the gas phase in the height direction is negligible, the pressure gradient force seems to be independent of the initial height. As time passes, the dispersion of the PCC reduces the pressure difference between UPF and PDF, and the pressure gradient force continues to decrease.

We can thoroughly search each gas–particle interaction behavior by DEM, as shown in Figs. 7, 8, and 9, and the physics of the gas–particle interactions such as SMDI and blast-wave mitigation mechanism would be elucidated quantitatively.

4 Conclusions

In the present study, CFD–DEM was used to investigate the interaction between a shock wave and a PCC, and its applicability was validated by comparing with previous experiments. When the incident shock wave interacted with the PCC, the former was reflected from and transmitted through the PCC. The propagation of the transmitted and reflected parts of the shock wave and the motion of the PCC induced by the shock wave agreed well with the previous experimental data. We calculated the effects of the forces and heat transfer. The quasi-steady drag force, pressure gradient force, and heat transfer were strongly related to the differences of velocity, pressure, and temperature between the gas flow and particles, respectively. When the gas flow interacted with the PCC, they were activated, and the gas flow lost momentum and energy, which weakened the transmitted shock wave. In the present study, the quasi-steady drag force remained almost constant. Because of particle dispersion, the pressure gradient force became small as time increased. The convective heat transfer absorbed 12% of the total energy of the incoming flow, which may have some effect in mitigating the shock wave passing through the PCC. By using and improving the present CFD–DEM, the physics of the gas–particle interactions would be elucidated quantitatively.