1 Introduction

Compressible multiphase systems are involved in a wide range of applications yet involve a multitude of complex physics that challenge our computational and experimental capabilities [1]. The physics involved in these systems are based on relatively well-understood phenomena such as drag, heat transfer from a sphere, and simple compressible flow but quickly develop more complex large-scale phenomena like hydrodynamic instabilities and turbulence. Under rapid accelerations, these flows require a re-evaluation of our simple particle models and the development of unsteady particle models. These systems can appear in terrestrial settings such as volcanic ash production [2], industrial refrigeration and energy production [3, 4], and high-speed combustion systems in scramjets and pulse detonation engines [5, 6]. These systems also have applications in astrophysics, where the inclusion of multiphase components is important in capturing the behavior of supernovae (SNe) dust processing. These SNe create shock waves which drive material out from the core into the interstellar medium and act to process the surrounding stellar dust produced by the star [7]. Like SNe events, inertial confinement fusion (ICF) is another area which can benefit from multiphase research. ICF involves a shock wave penetrating several layers of different densities with perturbations in each layer, and these layers can change phase creating a complex hydrodynamic multiphase system. In many of these applications, not only are hydrodynamics of substantial interest, but including the physics associated with the various phases can improve the accuracy when considering the evolutions of shock-driven multiphase instabilities (SDMIs).

In the case of fast-reacting small-sized particles, the SDMI closely resembles the Richtmyer–Meshkov instability (RMI) [8, 9]. The RMI is a hydrodynamic instability resulting from the interaction of a misaligned impulsive acceleration and a density gradient. It has been studied extensively in experiments and simulations due to its appearance in high-energy-density applications such as ICF and SNe. In fact, some common approximations of the multiphase components reduce this SDMI to a RMI. Once such approximation is the dusty gas approximation presented by Marble [10]. This method reduces the multiphase components by mass averaging their properties with their carrier phase. This creates a new gas species with properties which try to capture some of the effects of the particles in the carrier phase. However, this approximation neglects important physics such as particle lag effects and energy coupling [8]. This simplification also ignores any potential effects which may be important in a dense flow, such as interparticle effects or acoustic wave effects from neighboring particles [11, 12].

While the SDMI is commonly compared to the RMI, as the particle relaxation times are increased, it differentiates itself from the RMI due to particle lag effects. This is because the mechanism for vorticity is fundamentally different from the RMI [13]. The RMI may be explained by the deposition of baroclinic vorticity, while the SDMI results from vorticity produced by a gradient in multiphase momentum transfer. These effects can be seen in terms of the enstrophy equation (1) where \(\overrightarrow{\omega }\) is the vorticity, \(\rho _\mathrm{g}\) is the gas density, P is the pressure, \(u_\mathrm{g}\) is the gas velocity, \(\nu \) is the dynamic viscosity, \(\theta _\mathrm{g}\) is the ratio of volume occupied by the gas to the volume occupied by the multiphase system, and \(\overrightarrow{f}\) is the multiphase momentum source term. The strength of the multiphase enstrophy source term is dependent on the alignment of the previously deposited vorticity and the vorticity deposition from the multiphase momentum transfer. The alignment of the terms is dependent on the momentum relaxation time of the particles. Slow particles will lag behind the previously deposited vorticity and result in competition between new and old vorticity. These source terms for the RMI and SDMI are not mutually exclusive, and both can exist simultaneously. In this case, the presence of particles can suppress or support the development of the RMI [8, 14].

$$\begin{aligned} \mathrm{d}_t \frac{\omega _i \omega _i}{2} + u_{\mathrm {g},j}\partial _j \frac{\omega _i \omega _i}{2}= & {} \omega _i \frac{1}{\rho _\mathrm{g}^2}\varepsilon _{ijk} \partial _j \rho _\mathrm{g} \partial _k P \nonumber \\&+\, \omega _i\omega _j\partial _ju_{\mathrm {g},i} -\omega _i \omega _i \partial _j u_{\mathrm {g},j} \nonumber \\&+\, \nu \partial _j \partial _j \frac{\omega _i \omega _i}{2} - \nu {\partial _j \omega _i \partial _j \omega _i} \nonumber \\&+\, \frac{1}{\rho _\mathrm{g} \theta _\mathrm{g}}\omega _i \varepsilon _{ijk} \partial _{j} F_{k}. \end{aligned}$$
(1)

For the RMI, the strength of the pressure-gradient is represented by the Mach number, M, while the density gradient is quantified by the Atwood number for an interface between two fluids. For a SDMI, we can borrow this terminology to define an effective Atwood number, \(A_\mathrm{e}\), for a multiphase system interface as shown in (2), where \(\rho _\mathrm{e}\) is the effective density of the multiphase system, as shown in (3), and where the additional subscripts 1 and 2 denote the upstream and downstream system, respectively. In (3), the effective density is a function of the carrier phase density, the density of the particles, and the volume fraction of the particles, which is the ratio of the volume occupied by the particles to the available volume, given as (4). In the case of fast-reacting particles, \(A_\mathrm{e}\) would be used to predict the RMI-like growth of an interface. In the case of particles with large relaxation times, the effect of \(A_\mathrm{e}\) becomes less clear as the density gradient is applied slowly over the particle–gas equilibration time.

$$\begin{aligned} A_\mathrm{e}= & {} \frac{\rho _{\mathrm {e},2}-\rho _{\mathrm {e},1}}{\rho _{\mathrm {e},2}+\rho _{\mathrm {e},1}} \end{aligned}$$
(2)
$$\begin{aligned} \rho _\mathrm{e}= & {} \rho _\mathrm{g}(1-\theta _\mathrm{v})+\rho _\mathrm{p}\theta _\mathrm{v} \end{aligned}$$
(3)
$$\begin{aligned} \theta _\mathrm{v}= & {} \frac{V_\mathrm{p}}{V_\mathrm{c}}=1-\theta _\mathrm{g} \end{aligned}$$
(4)

For a simple multiphase system where particle–gas coupling is limited to momentum and energy, the equilibration times can be estimated by the velocity and thermal relaxation times, \(t_\mathrm{V}\) and \(t_\mathrm{T}\), respectively [10] (5, 6). As these times become large compared to the characteristic time of the hydrodynamic instability, particle lag effects become important and the parameter space for the SDMI increases to include the time-varying effects of the particles.

$$\begin{aligned} t_\mathrm{V}= & {} \frac{m_\mathrm{p}}{6 \pi r \nu } \end{aligned}$$
(5)
$$\begin{aligned} t_\mathrm{T}= & {} \frac{m C_\mathrm{p}}{4 \pi r \kappa _\mathrm{g}} \end{aligned}$$
(6)

The SDMI has been explored for fast-reacting [9, 13, 14] and slow-reacting [8] particles in past works; however, these consider only low volume fraction, dilute flows. When in the dilute regime, the effects of particle–particle interactions can be neglected due to the low likelihood of interactions. As the volume the particles occupy increases, however, the flow transitions from dilute flow to dense flow and additional particle–particle effects must be considered. This regime has been explored in simple 1D-like shock tube experiments to explore the interaction of a shock wave with a dense particle curtain [15]. This work found that traditional drag models could not predict the spreading rate of the particle curtain. Explosive-driven particle dispersal was studied in a spherical geometry [16] which showed the organization of 3D hydrodynamic features in the particle field that could not be accounted for by drag forces alone. These experimental works led to the development of additional force models which were implemented in simulations to replicate the results of the particle curtain experiments [17]. These models were developed further in simulations of explosive particle distribution [18].

In this paper, we employ these previous works, using the particle force models presented by Ling et al. [17], to explore the role of particle–particle interactions on the particle and gas fields in a SDMI. We use a simple geometry consisting of a particle-laden cylinder interacting with a planar shock wave (a geometry common in previous RMI works) to replicate conditions which could be explored in a shock tube experiment. Using this setup, this paper explores the effect of particle force models and particle relaxation times on the development of a SDMI.

2 Computational environment

2.1 FLAG code description

The simulations presented in this work were performed using the hydrocode FLAG [19, 20]. FLAG is a multi-material multi-physics hydrodynamics code developed at Los Alamos National Laboratory (LANL). FLAG includes a fully unstructured grid mesh, allowing an arbitrary polyhedral mesh, and can function as an arbitrary Lagrangian–Eulerian (ALE) code utilizing a Lagrangian hydrodynamics step followed by an optional relaxation and remapping step [21, 22]. The relaxation algorithm in the current work is a Laplacian-type smoothing and is performed every cycle. The FLAG remapping step uses the flux-corrected transport (FCT) algorithm of Boris and Book [21, 23] to achieve second-order accuracy for smooth solutions, while preserving monotonicity at discontinuities and ensuring conservation. The implementation is directionally unsplit in 2D/3D, based on Zalesak [24], and limited gradients are computed with the unstructured Barth–Jespersen limiter [25]. Experience suggests both FCT and gradient limiting are necessary for high-strain-rate flows on highly deformed meshes. Multi-material interfaces are reconstructed using Youngs’ volume of fluid method (VOF) [26], but this is not necessary in the current work as the carrier phase is treated as a single material for the purposes of advection. To handle the particles, the multiphase particle-in-cell (MP-PIC) method [27] is employed, which assigns the particles their own discrete points and couples the particle effects to the gas mesh via energy and momentum terms. The particles in FLAG are also known as parcels, representing large numbers of physical particles. These parcels are considered to save computational time and resources by significantly reducing the number of calculations necessary to capture the hydrodynamics. During the particle transport, continuum properties are interpolated to the particle locations to allow effects such as drag, whereas the particle properties including mass, momentum, and energy are accumulated over the gas mesh to act as feedback, allowing for calculations such as drag heating [22].

Equations (7)–(11) present the continuum equations of motion for mass, momentum, and energy as they are given in FLAG, which solves for the density, \(\rho \), pressure, P, and specific internal energy, \(\epsilon \), respectively, and include the continuum velocity, \(u_j\). Equations (8) and (9) also include the two-way momentum and energy coupling source terms represented by \(F_\mathrm{D}\) and \(Q_\mathrm{s}\), respectively. Equations (10) and (11) outline the particle transport equations of particle momentum and energy, where \(m_\mathrm{p}, v_j, \rho _\mathrm{p}, F_\mathrm{D}\), and \(Q_\mathrm{s}\) are the particle mass, particle velocity, particle density, momentum source term, and energy source term, respectively. The gas phases use the ideal gas equations of state, (12) and (13), where \(R, U_\mathrm{g}\), and \(c_{v}\) are the specific gas constant, the integral energy, and the specific heat at constant volume of the gas, respectively. Equations (10) and (11) update the parcels state.

$$\begin{aligned}&\partial _t\rho - \partial _i\rho u_i=0 \end{aligned}$$
(7)
$$\begin{aligned}&\rho \partial _t u_i - \partial _iP + F_\mathrm{D}=0 \end{aligned}$$
(8)
$$\begin{aligned}&\rho \partial _t\epsilon +P\partial _{i}u_{i} +Q_\mathrm{s}=0 \end{aligned}$$
(9)
$$\begin{aligned}&m_\mathrm{p}\partial _tv_j+\frac{m_\mathrm{p}}{\rho _\mathrm{p}}\partial _iP-F_\mathrm{D}=0 \end{aligned}$$
(10)
$$\begin{aligned}&m_\mathrm{p}\partial _t\epsilon -Q_\mathrm{s}=0 \end{aligned}$$
(11)
$$\begin{aligned}&PV=RT \end{aligned}$$
(12)
$$\begin{aligned}&U = c_{v}RT \end{aligned}$$
(13)

The momentum source term, given in (10), relies on the Kliatchko drag model [28] shown below (14, 15) and is a function of the particle Reynolds number. It should be noted that while there exist models which expand upon the Kliatchko drag model to include a relative particle–gas Mach number, this modification to the drag coefficient is slight at the relatively low Mach numbers within these simulations. As such, the standard model was deemed appropriate for this study. The particle Reynolds number is given in (16) where \(d_\mathrm{p}\) and \(\rho _\mathrm{g}\) are the particle diameter and the density of the carrier gas. The particle source term for the energy equation is found using the Ranz–Marshall correlation, (17) [29], where \(r_\mathrm{p}, k, C_\mathrm{p}, \mathrm {Pr}, T_\mathrm{g}\), and \(T_\mathrm{p}\) are the radius of the particle, the thermal conductivity of the fluid, the specific heat of the particle, the Prandtl number of the fluid, and the temperatures of the carrier gas and particle, respectively. Since the particles in this work are considered as solid soda-lime glass particles, the reader should note that the internal specific energy is approximated as \(\mathrm {d}\epsilon =C\mathrm {d}T\), with \(C =840~{\mathrm{J}}/{\mathrm{kg}\,\mathrm{K}}\), and the density is taken as a constant, \(\rho _\mathrm{p}=2252~{\mathrm{kg}}/{\mathrm{m}^{3}}\).

$$\begin{aligned} F_\mathrm{D}= & {} \frac{C_\mathrm{d}A_\mathrm{p} \rho _\mathrm{g}}{2}\left( |u_j-v_j|\right) \left( u_j-v_j\right) \end{aligned}$$
(14)
$$\begin{aligned} C_\mathrm{d}= & {} 0.424, \quad \text { if }\quad \mathrm {Re} < 1000,\nonumber \\= & {} \frac{24}{\mathrm {Re}}+\frac{4}{\mathrm {Re}^{1/3}},\quad \text { if }\quad \mathrm {Re} \ge 1000 \end{aligned}$$
(15)
$$\begin{aligned} \mathrm {Re}= & {} \frac{d_\mathrm{p}\rho _\mathrm{g}|u_j-v_j|}{\mu } \end{aligned}$$
(16)
$$\begin{aligned} \partial _{t}T_\mathrm{p}= & {} \frac{4\pi r_\mathrm{p} k}{C_\mathrm{p}m_\mathrm{p}} \left( 1+0.3\mathrm{Re}^{1/2}\mathrm{Pr}^{1/3}\right) \left( T_\mathrm{g}-T_\mathrm{p}\right) \end{aligned}$$
(17)

2.2 Additional force implementation

To explore the physics involved in more dense flows, the capabilities of FLAG were expanded to include additional particle force models. A literature review for hydrodynamic dense flows finds that there are several important forces which must be modeled. Many of these forces were already included in the FLAG code, but several more were added during this work. Ling et al. [17] suggest the inclusion of several forces, considering an effective-mass, a pressure-gradient, and an interparticle force in addition to the quasi-steady (drag) and unsteady viscous forces. Andrews and O’Rourke [27] also discuss the implementation of the added-mass and interparticle terms in the MP-PIC methodology.

This work will consider the total force on a parcel to be the sum of drag, pressure-gradient, added-mass, and interparticle forces, as shown in (18). Although it is discussed in the literature, this work does not consider the viscous unsteady force. Equations (19)–(21) express the new force terms, while (14) above is used to calculate the drag on a particle. The added-mass force, (20), is a function of the particle volume, a constant, pressure, the particle acceleration, and the density of the carrier phase, or \(V_\mathrm{p}, C_\mathrm{M}, P, \mathrm{d}_{t}v_{i}\), and \(\rho _\mathrm{g}\). The constant \(C_\mathrm{M}\) is set to 0.5, to be consistent with the literature. Similarly, the pressure-gradient force (19) is dependent upon the gradient of pressure and the volume of the particle. While these terms are also included in the added-mass equation, the pressure-gradient force has been shown to be necessary and important during the passage of the shock wave through the particle field [17]. When modeling the interparticle force, (21), it is common to utilize the formulation presented by Harris and Crighton [30]. This formulation neglects individual interparticle events, or collisions, and instead models the force as a kind of diffusion term using the local volume loading as the driving variable behind the force. In this way, (21) is a function of the particle volume, the local particle volume fraction and the gradient of a pressure term, the local volume loading raised to some power, \(\beta \), all over the difference of the close-packed limit and the local volume loading, or \(V_\mathrm{p}, \theta _\mathrm{v}, P_\mathrm{s}, \beta \), and \(\theta _\mathrm{c}\). Ling et al. [17] have done a comprehensive study of \(P_\mathrm{s}\) and \(\beta \) and found that they are best represented as constants. As such, the values used in this work are 1 atm and 3, respectively, as found in this previous work. The close-packed limit represents the fraction of volume mono-sized spheres may occupy in a cube and is taken to be 0.6 here.

$$\begin{aligned}&F_\mathrm{i} = F_\mathrm{D}+F_\mathrm{am}+F_\mathrm{pg}+F_\mathrm{pp} \end{aligned}$$
(18)
$$\begin{aligned}&F_\mathrm{pg}=-V_\mathrm{p}(\partial _{i}P) \end{aligned}$$
(19)
$$\begin{aligned}&F_\mathrm{am}=-V_\mathrm{p}C_\mathrm{M}\left( \partial _iP+\partial _{t}(\rho _\mathrm{g}v_{i})\right) \end{aligned}$$
(20)
$$\begin{aligned}&F_\mathrm{pp} = -\frac{V_\mathrm{p}}{\theta _\mathrm{v}}\partial _i\frac{P_\mathrm{s}\theta _\mathrm{v}^{\beta }}{\theta _{\mathrm {c}}-\theta _{\mathrm {v}}} \end{aligned}$$
(21)
Fig. 1
figure 1

1D Sandia particle curtain validation simulation, where USE and DSE represent the upstream and downstream edges of the particle curtain. This figure shows good agreement with the Sandia particle curtain growth shown in Wagner et al. and Ling et al. For example, the authors consider a comparison with Fig. 4 of Ling et al. In this figure, it can be estimated that at \(t/(L/u_\mathrm{s})=200\) the upstream and downstream edges of the particle curtain reach a non-dimensional distance (x / L) of 11 and 30, respectively, which are close to the values presented in here

Full size image

A validation case was performed in the FLAG code against the simulation results of Ling et al. [17] which included some experimental results from Wagner et al. [15]; this was reproduced and is presented below. The validation case considered a simple pseudo-1D simulation of the Sandia particle curtain experiment and showed good qualitative agreement when considering the spread rate. This simulation considered a particle curtain with a particle volume fraction of 0.21, an initial curtain length of \(2~\mathrm {mm}\), and a shock wave Mach number of 1.66 in air. The resulting particle spread is shown in Fig. 1. This figure uses the same non-dimensional length and time for the x- and y-axes as is presented in Ling et al., which are given as the position of the particles over the length of the particle curtain, x / L, and time over the ratio of length of the curtain to the velocity of the shock wave, \(t/(L/u_\mathrm{s})\). This figure shows great agreement with the particle curtain spread presented in Ling et al. by showing the same growth in the particle curtain upstream and downstream edges. While the flag simulation was able to capture the general trend, it did not necessarily show the exact same behavior—even in this 1D simulation. In part, this is due to the exclusion of the viscous unsteady forces; however, it was found that good agreement could be achieved by refining the mesh and including a higher number of particles. This will be the premise for future work, but is not investigated here. While the above force models have been implemented in other codes and used to simulate particle-spread experiments, our literature review revealed no predictive hydrodynamic simulations. As such, this work was performed to guide potential future dense particle flow hydrodynamic experiments and to explore any potential contributions these models may make in the SDMI.

2.3 Simulation parameters and initial conditions

To investigate the effects of the force models on the SDMI, two 2D studies were performed. The first study presented uses 2-\(\upmu \hbox {m}\) particles and toggles the forces being considered. This leads to five cases: D, DP, DM, DI, and A, or drag-only, drag and pressure-gradient, drag and added-mass, drag and interparticle, and all forces, which denote the force models active. In all simulations, the parcels are given a random uniform distribution. To prevent any variation from small-scale perturbations due to the random parcel locations, the parcel positions were generated in a cylindrical interface once and then used for all simulations presented in this work. Therefore, any difference in morphology or behavior is strictly due to the variation in the force models included. This study is presented as the force study in the Results section.

The second study, termed the relaxation-time study, compares particles of various relaxation times (diameters) and includes both drag-only and all-forces simulations. Careful consideration on how to initialize the parcels had to be included in this study as changing the parcel size changes the particle volume, and therefore the overall parcel volume. As such, the same random distribution from the previous study was used, leaving the total number of parcels in the simulations the same. Thus, the number of particles per parcel varies between the different-sized-particle cases while at the same time keeping the initial interface volume loading the same throughout. The particle sizes investigated include diameters of 2, 25, 50, and 100 \(\upmu \mathrm {m}\). This case also considers both simulations with drag only and all forces for each particle size. The cases in this section will be identified by their diameter followed by D or A to denote drag only or all forces.

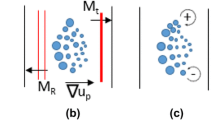
All simulations were performed in a 2D shock tube environment with a cylindrical interface of diameter \(2~\mathrm {cm}\), that is \(d_\mathrm{i}=2\). The computational domain is \(150~\mathrm {cm} \times 12~\mathrm {cm}\), with all boundaries being shock reflecting. The y-dimension was chosen as it was shown to be large enough to prevent boundary effects from interfering with the interface growth. A shock wave is initialized at \(x_0 = -\,10~\mathrm {cm}\) with the interface centered on \({x} = 0~\mathrm {cm}\). Figure 2 shows an enlarged interface, with the left half of the image showing the carrier phase species fraction with point parcels and the right-hand side showing enlarged parcels forming the cylinder interface. These parcels have been enlarged by four times to make qualitative analysis easier at later times; this enlargement will be used throughout the rest of the images. The purpose of the right- and left-side interface visualization is to show that the particle field has been enlarged throughout the rest of the figures and to give the reader a sense of the true computational particle field. The presentation of Fig. 2 is to give the reader an example of the domain and a reference scale for the simulation domain. The following figures will show a limited area, kept to 10 cm in x and 3 cm in y in an effort to fully visualize the interface. The reader should note that the non-carrier and carrier phases were initialized separately despite containing the same species so that they could be easily tracked and interface information could be readily calculated.

Fig. 2
figure 2

Schematic of the simulation initial conditions. Note: the figure is not drawn to scale. The location of the shock wave, \(x_0\), and the position of the interface are pictured. The particles are visualized here as black spheres. The interface is broken into two representations. The left-hand side shows the particle field (black circles) over the carrier species contour, while the right-hand side shows an enlarged particle field. The computational particles here are still represented by black spheres—however, they are now enlarged, and as such, the entirety of interface appears as black. This is meant to show that the carrier phase is entirely seeded and that the particle field is indeed circular

Full size image
Table 1 Initial conditions
Full size table
Fig. 3
figure 3

Evolution over time of the SDMI with 2-\(\upmu \mathrm {m}\) particles. Top row: all-forces case; bottom row: drag-only case

Full size image

The simulations were initialized at atmospheric conditions, with the pressure and temperature at \(101.3~\mathrm {kPa}\) and \(300~\mathrm {K}\), respectively. It was previously mentioned that the effective Atwood number can be used to determine the strength of the instability and can be considered a function of the particle volume fraction for uniform particle material and gas density. As such, the initial effective Atwood number was held to a constant 0.905 for all cases. This was achieved by holding the initial interface volume fraction to 0.01 across all cases. This means that since all simulations use the same initial particle field, which is only populated within the circular interface, for the average USE and DSE representing the upstream and downstream edges of the particle curtain, the particle volume fraction within the interface is set to 0.01, while outside the interface it is set to zero. To compare the different cases together, a post-shock time will be used. This time, \(t^*\), is the time after the shock wave has crossed half of the cylindrical interface and is a function of \(x_\mathrm{{0}}\) and \(w_\mathrm{I}\), or the initial distance from the shock front to the center of the cylindrical interface and incident wave speed, respectively.

$$\begin{aligned} t^* = t- \frac{x_\mathrm{{0}}}{w_\mathrm{I}}. \end{aligned}$$
(22)

For all the simulations, the particles are considered as solid soda-lime glass with a carrier phase of air. Table 1 shows the basic initial conditions which are for the simulations presented in the diameter study; the force study uses the same initial conditions as the 2-\(\upmu \mathrm { m}\) column but toggles the active forces. All data shown in this work were visualized using the CFD visualization program EnSight, a post-processing program made by Computational Engineering International, Inc.

3 Results

Figure 3 shows the evolution of the instability with respect to time. The figure is separated into two rows with three columns. The top row shows the all-forces case, while the bottom shows the drag-only case, both cases having particles of 2-\(\upmu \mathrm {m}\) diameter, with the columns showing the evolution at times \(t^* = 0.1, 0.25\), and \(0.5~\mathrm {ms}\). At early times, the morphology of both the carrier species and the particle fields is very similar between both cases. At \(t^* = 0.25~\mathrm {ms}\), the all-forces case shows a difference in the development of a center spike, as well as more asymmetry developing in the outer particle field. Here the drag-only case shows tighter roll-ups in the carrier phase and more organization in the particle field. By \(t^* = 0.5~\mathrm {ms}\), both cases have broken symmetry due to the random initial particle locations. The all-forces case shows a more concentrated stream of particles located in the downstream reverse spike structure and a greater concentration of carrier mass residing in clumpy vortical features. The drag only case shows a more dispersed carrier gas and particle mass. For both particle and carrier gas mass, the inclusion of the additional force terms seems to result in greater entrainment of concentrated gas and particle clumps but less mixing (diffusion) of gas. Later (Sect. 3.2) it will be seen that for larger particles, the all-forces case results in less hydrodynamic growth, though it is difficult to see this result in the 2-\(\upmu \mathrm {m}\)-particle cases. For brevity, all further discussion on flow field conditions will consider \(t^* = 0.5~\mathrm {ms}\) to observe the most differences between the cases.

3.1 Force study

This section explores the contribution of the various force models to the hydrodynamic evolution of the 2-\(\upmu \mathrm {m}\)-particle field and includes results from the drag-only D, drag and pressure DP, drag and added-mass DM, drag and interparticle DI, and all-force A cases. Figure 4 shows \(\omega \), or the vorticity, at \(t^* = 0.5~\hbox {ms}\), for all-force cases. The vorticity is calculated as shown in (23). As can be expected from the previous figure, all cases have broken symmetry at this late time. However, the inclusion of the additional force models has changed the morphology of each case. The D case, which is the most standard methodology used when considering the SDMI, shows a thin spike and several structures growing out of the vortical roll-ups, including ones off the top right, bottom right, and a few small structures forming upstream of the interface. The particle field of the D case also suggests the particles may collect more at the upstream edge.

$$\begin{aligned} \omega _i = \epsilon _{ijk}\partial _j u_k. \end{aligned}$$
(23)
Fig. 4
figure 4

Vorticity for the force study cases at \(t^* = 0.5~\mathrm {ms}\)

Full size image

The DP case has very similar morphology though with a thinner structure forming in the top downstream area and a slightly thicker structure in the bottom downstream area. However, the upstream particle field is just as thick and has small structures. The DM case has a much larger downstream reverse spike and a thinner, albeit still present upstream particle field. The DI case seems to recover similarities to the D case, with thinner central and downstream spikes. However, the vorticity field here suggests some qualitative departure from the D case. The A case has a more organized vorticity field with less compressed vorticity cores. The particle field also shows a thick downstream spike, and the upstream particle field also shows more structure, spreading out and showing less clumping. Of these cases, the DM case recovers most of the qualitative features of the A case.

Figure 5 presents the enstrophy for the force study. The enstrophy is calculated as shown in (24), where the area considered is limited to the area near the interface over which vorticity acts. Looking at the enstrophy over time, an interesting connection can be seen. The three most similar cases, the D, DP, and DI cases, all have very similar enstrophy throughout and even end at approximately the same value of \(\approx 6.8\times 10^{10}~\mathrm{s}^{-2}\). The A and DM cases are also similar through time, diverging slightly at \(t^* \approx 0.42~\mathrm {ms}\). The enstrophy, which is indicative of the energy contained within the vortices, suggests that the primary modifying force in the A case is the \(F_\mathrm{am}\) term and that the \(F_\mathrm{pg}\) and \(F_\mathrm{pp}\) forces have little effect compared to \(F_\mathrm{am}\). Indeed, it seems all terms but the added-mass term can be neglected when the hydrodynamic evolution and vorticity deposition are considered under these conditions.

$$\begin{aligned} \epsilon = \int _{A}\omega _i\omega _i \mathrm {d}A. \end{aligned}$$
(24)
Fig. 5
figure 5

Enstrophy for the force study cases with respect to \(t^*\)

Full size image
Fig. 6
figure 6

Average particle acceleration for the force study cases with respect to \(t^*\)

Full size image

To observe the effects the force models have on the particles, Fig. 6 shows the average acceleration on the particles. This was found by taking the x- and y-components of velocity for each particle at each time step, using a simple first-order differencing method to approximate the derivative, and then averaging the resulting accelerations across each particle at every time step, as shown in (25). Like the previous figure, the D, DI, and DP cases all have very similar behavior, with the DP case showing a slight increase over the D and DI cases throughout the simulation. The DM and A cases also act similarly, as can be expected from the previous discussion. However, these two cases have less acceleration than the others. This, considered with the lesser enstrophy, or kinetic energy in the vortex cores, supports the suggestion that the added-mass force has the strongest effect on the hydrodynamics when considering the additional force models. The added-mass term acts to decrease the acceleration of the particles from the shock wave. This allows for the particles to lag further behind the carrier gas resulting in a greater misalignment of the deposited vorticity and the multiphase source term (1).

$$\begin{aligned} \frac{\sum _{i=1}^{N}a_\mathrm{p}}{N}=\sum _{i=1}^{N}\frac{v_\mathrm{p}(t)-v_\mathrm{p}\left( t-\delta t\right) }{\delta (t)}. \end{aligned}$$
(25)
Fig. 7
figure 7

Species and particle fields for the diameter-study cases at \(t^* = 0.5~\mathrm {ms}\)

Full size image

3.2 Relaxation-time study

The second study presented in this work explores the role of particle relaxation time and considers simulations which use drag-only and all-force models for four different particle diameters. As seen in (5), the particle velocity relaxation time varying as m/r, which reduces to \(\rho /r^2\). Therefore, increasing the particle size results in particles which are slow to respond to the impulsive acceleration and which damp the hydrodynamics of the interface [8]. Particle velocity relaxation-time estimates are given in Table 1. The larger particle sizes have relaxation times which are much greater than the hydrodynamic timescales considered here and have likely not reached equilibrium with the gas flow by \(t^*=0.5~\mathrm {ms}\).

Figure 7 shows the carrier species contour with the particle field at time \(t^* = 0.5~\mathrm {ms}\). The figure is arranged in two columns and four rows, the columns representing the all-force and the drag-only simulations and each row representing increasing particle diameter from top to bottom. The first row shows the A and D cases from the previous study. Here the particle fields have negligible lag. As the particle size increases, the lag between the particle fields and their carrier phase increases. Aside from the lag, the organization of both the carrier species and the particle field increases with particle size; these simulations do not break symmetry by \(t^* = 0.5~\mathrm {ms}\). When comparing the two columns to each other, the additional force models increase the lag distance between the two interfaces. The D cases for all particle sizes also show more evolution than their counterparts, both in the carrier species and in the particles. For all particle sizes, the D cases show vortical roll-ups in the carrier phase and some evolution in the particle fields. However, the 50-\(\upmu \mathrm {m}\) and 100-\(\upmu \mathrm {m}\,\mathrm{A}\) cases show only compression of the particle field, and the 100-\(\upmu \mathrm {m}\) case shows some stretching in the carrier phase as opposed to only vortical structures.

Figure 8 shows the vorticity for the relaxation-time study and is organized similarly to Fig. 7. This figure shows some of the same behavior as Fig. 7; however, the relative strengths of the vortex cores can now be seen. As can be expected from the morphology of the previous figure, the 25-\(\upmu \mathrm {m}\) cases still have strong vorticity cores but remain more organized than the 2-\(\upmu \mathrm {m}\) cases due to their diminished vorticity deposition. Here, due to the organization of the 25-\(\upmu \mathrm {m}\) cases, we can see that the drag-only case has a single layer of alternating vorticity around its cores and stronger vorticity in its cores. These alternating vortex layers were seen in previous work as well [8]. For all larger particle sizes, the D case has stronger vortex cores as well. The A cases have a tighter, less developed particle field; they also have weaker vortex cores. It appears that the additional forces are dampening the instability as a whole, which is most apparent at larger particle sizes.

Fig. 8
figure 8

Vorticity and particle fields for the diameter-study cases. All rows use their own unique color bars and all images are at \(t^* = 0.5~\mathrm {ms}\)

Full size image

Figure 9 shows the enstrophy over time for the relaxation-time study. The right-hand axis shows the enstrophy for all cases with diameters greater than 2 \(\upmu \mathrm {m}\). The left-hand axis shows the enstrophy for the 2-\(\upmu \mathrm {m}\) A and D cases. This was done because the 2-\(\upmu \mathrm {m}\) cases have enstrophy approximately five times greater than the other cases. As per the previous discussion, when comparing the D and A cases for a single diameter size, the more evolved D cases also show higher enstrophy. The difference in enstrophy deposition is relatively constant for each particle size which results in a greater effect on the large-diameter cases which have a lower initial deposition. This again supports the suggestion that the D cases exhibit more evolution in their instabilities than the A cases of the same diameter and that this effect increases with particle size.

Fig. 9
figure 9

Enstrophy over time for the diameter-study cases with respect to \(t^*\); note the 2-\(\upmu \mathrm {m}\) D and A cases are on the left axis due to the difference in magnitudes

Full size image
Fig. 10
figure 10

Max local particle volume fraction for the A cases highlighting when interparticle effects may be active

Full size image

While the pressure-gradient force has been identified in the literature to work primarily as the shock wave passes through the particle field, and the added-mass force has been shown in this work to dominate the additional force models, it is still of interest to examine regions where the interparticle effects may be important. From (21), it can be seen that the interparticle force is directly related to the local volume fraction, as such this force will have greater effects on the particle field as it transitions from the dilute flow to the dense flow regime. Typically, the flow regime for a multiphase flow can be considered dense with as low a volume fraction as 5%. Though these simulations all consider an initial volume fraction of \(1\%\), as the shock wave penetrates the interface, it compresses the particle field potentially driving the local volume fraction up. Figure 10 shows the max local volume loading with respect to time. The 2-\(\upmu \mathrm {m}\) A case shows an immediate increase in max local volume fraction, due mostly to its ability to closely follow the flow [8]. The 25-\(\upmu \mathrm {m}\) A case also shows an increase, crossing from initially dilute to dense flow and increasing its maximum local volume loading to 10%. The two larger-diameter cases, the 50-\(\upmu \mathrm {m}\) and 100-\(\upmu \mathrm {m}\) A cases, however, do not evolve enough within the simulation time to see an increase in local volume fraction. This perhaps explains why the evolution of the 2-\(\upmu \mathrm {m}\) cases is more complex in morphology and why the 2-\(\upmu \mathrm {m}\) A case shows greater entrainment of particles and carrier gas mass but less mixing by species diffusion. For the 2-\(\upmu \mathrm {m}\) case, the additional forces, other than the added-mass term, may play a role in the distribution of particles at early time due to the higher volume fraction.

4 Conclusions and future work

The additional particle force models increase the particle lag effects and reduce metrics associated with evolution of the SDMI—both qualitatively, in the form of increased particle clumping and decreased carrier phase mixing, and quantitatively in vorticity deposition and particle acceleration. However, not all the models act on the same scales. For instance, the force study showed that the addition of the pressure-gradient term showed a slight increase in acceleration at early times and a slight increase in enstrophy at late times but the added-mass term when included dominates the simulation by significantly decreasing both. In fact, the enstrophy and average particle acceleration through time are very similar between the simulations with drag and added-mass forces and simulations with all forces considered. This suggests that under these conditions the interparticle force models may be neglected but that the added-mass term needs to be used.

Considering the effects of the additional force models, particle relaxation times were then also investigated by changing the particle diameters. As can be expected, the simulations with the additional force models showed an increase in particle lag and a qualitative and quantitative decrease in the evolution of the SDMI, shown as an increase in organization in both the particle and gas fields and a decrease in enstrophy, respectively. The larger size particles, the 50-\(\upmu \mathrm {m}\) and 100-\(\upmu \mathrm {m}\) cases, did not reach momentum equilibrium in the time explored but still show a significant difference due to the additional force models.

The effects of the pressure-gradient force and added-mass forces were both discussed for the force study; however, the interparticle effects are harder to isolate. As such, the maximum local volume fraction, which is the driving variable for the interparticle force, was investigated for the diameter-study A cases. Here it was shown that the interparticle force is mostly inactive for the larger-particle cases due to their large momentum lag time, and that only the 25-\(\upmu \mathrm {m}\) and 2-\(\upmu \mathrm {m}\) cases show a significant increase in the volume fraction, and therefore experience an increase in the interparticle force term.

However, a conclusive answer has yet to be reached as to when high particle volume fraction effects should be considered. As such, future work will be performed on the initial volume fraction as well as the post-shock volume fraction to observe any regions where the flow may transition to dilute, or marginally dense into the dense regime with the goal to approach the closed packing limit. This may help illuminate questions on blast wave-driven or shock-processed ejecta. Future work will also try to observe parcel to particle resolution effects, holding the initial volume fraction constant and varying the number of parcels to see how this effects both the particle forces and the evolution of the SDMI. The authors would like to invite experimentalists with access to multiphase experiments to also consider these regimes in which the various forces might dominate the flow, as currently the experimental literature is lacking but will be necessary to fully discover the physics.