1 Introduction

Nowadays, there is an increasing demand for high-accuracy and reliable positioning in support of some emerging applications such as self-driving cars, unmanned aerial vehicles and mobile robots. To acquire accurate position information, two classical techniques including network-based real-time kinematic (NRTK, Rizos 2002; Landau et al. 2003; Wielgosz et al. 2005) and precise point positioning (PPP, Zumberge et al.1997; Kouba and Heroux 2001) are usually implemented. The NRTK technique can achieve centimeter-level positioning accuracy with the supplement of regional corrections, but it is restricted in service coverage. The PPP technique is able to provide high-precision positions at the global scale, but a comparatively long initialization time of about 30 min is required (Ge et al. 2008). In order to not only make full use of the advantages but also alleviate the limitations of the two techniques, the PPP–RTK method was proposed and has been widely applied in recent years (Wubbena et al. 2005; Teunissen et al. 2010; Li et al. 2011). PPP–RTK shows the similar flexibility with the PPP, which allows users to perform absolute positioning using a stand-alone receiver at the global scale, and even provides more accurate positions with ambiguity resolution (AR) (Zhang et al. 2019). Different from NRTK, the PPP–RTK technique uses the state-space representation (SSR) to provide users with the individual GNSS-related errors instead of the raw or corrected observations (Wang et al. 2017). With the SSR mode, GNSS-related errors of different physical characteristics such as the tropospheric and the ionospheric delays can be represented separately at the server side, leading to potential improvement based on their own properties. Moreover, the undifferenced atmospheric corrections can be broadcasted on reference stations to release the real-time communication burden (Li et al. 2013). In this sense, PPP–RTK, which combines the advantages of both PPP and NRTK, brings innovative opportunities for the emerging mass market and automotive applications.

Generally, the realization of PPP–RTK needs to accomplish two sequential tasks. The first task is to obtain the precise orbits and clocks, the phase and code biases, as well as the atmospheric corrections from data of reference network at the server side (Li et al. 2014; Khodabandeh and Teunissen 2014; Wang et al. 2017). Then, at the user side, PPP rapid ambiguity resolution is implemented with the augmentation of precise corrections. Several studies were conducted to implement PPP–RTK and evaluate its performance (Zhang et al. 2011; Nadarajah et al. 2018; Teunissen and Khodabandeh 2015). Li et al. (2011) developed a PPP–RTK system to integrate PPP and NRTK into a seamless positioning service, which can provide an overall accuracy of about 10 cm, and a positioning accuracy of 3–5 cm can also be obtained with the atmospheric corrections augmentation. Psychas and Verhagen (2020) further investigated the performance of PPP–RTK by applying the ionospheric corrections from a multi-scale network. They demonstrated that the convergence time bears a linear relationship with the network density and a sub-10-cm accuracy can be achieved almost instantaneously for a network with 68-km spacing. In addition, with the rapid development of GNSS, joint corporation of multi-GNSS constellations also brings new opportunities to improve the performance of PPP–RTK (Li et al. 2021).

However, the performance of PPP–RTK is to a large extent constrained by the external environment and the signal availability, which degrades rapidly when the signal blockage occurs in a harsh-signal environment (Zhang and Li 2012). The inertial navigation system (INS) is an autonomous and spontaneous positioning system capable of providing continuous and superior positioning in a short timescale, which has potential to enhance the positioning performance and the ambiguity resolution when the tight integration of INS and GNSS is applied (Zhang and Gao 2008; Roesler and Martell 2009; Gao et al. 2017; Shin and Scherzinger 2009). The INS-augmented method was commonly introduced in RTK processing, and its performance has been widely investigated. Scherzinger (2000) indicated that the ambiguity-fixing time was 1–4 s for the INS-augmented RTK and 10–15 s for the standard RTK after an outage 60 s. Li et al. (2017) proposed an INS aiding multi-GNSS single-frequency ambiguity-fixing method, and their results showed that the fixing rate of 82.2% could be obtained when the cut-off elevation was set 35°. Han et al. (2017) proposed an INS-augmented partial ambiguity resolution method with GPS and BDS observations, where a success fixing percentage over 90% and a fixing time less than 5 s were achieved.

In recent years, more attentions have been paid to PPP/INS tight integration attributing to the superiorities of PPP. Rabbou and El-Rabbany (2014, 2015) developed an integrated navigation system by integrating the between-satellite single-differenced PPP with INS observations, and the system is able to achieve decimeter-level accuracy. Gao et al. (2016) tightly integrated the multi-GNSS ionospheric-constrained PPP with INS to make full use of the current multi-GNSS and INS observations. The results indicated that tight integration of multi-GNSS and INS observations helped improve the positioning performance in terms of accuracy, availability and convergence. Moreover, the introduction of INS also brings benefits to the performance of PPP AR (Liu et al. 2016; Zhang et al. 2018; Du et al. 2020). The high-accuracy information provided by INS will contribute to improve the accuracy of float ambiguities, which will naturally facilitate the rapid identification of correct ambiguity candidates. The ambiguity-fixed PPP/INS is able to achieve centimeter-level positioning, and re-fixing time after a short outage can be confined to few seconds in an open environment (Zhang et al. 2018). However, several minutes are still in need to achieve the first fixing of the ambiguities. In addition, the ambiguity re-fixing for PPP always fails in urban environments resulted from the intermittent signal interruptions.

In this contribution, we proposed a tightly coupled PPP–RTK/INS method aiming to achieve continuous and robust positioning with centimeter-level accuracy under the harsh environments. The atmospheric corrections, derived from the multi-GNSS PPP fixed solutions by using the raw observations of the reference network, are generated to enable the rapid ambiguity resolution in the PPP–RTK/INS integration. To evaluate the performance of the proposed the PPP–RTK/INS method, several experiments are conducted in different scenarios, such as urban roads, urban canyon and overpasses. This study is organized as follows: Sect. 2 describes the method of tightly coupled integration of PPP–RTK and INS. Section 3 details the experimental situation and the processing strategies in the vehicle-bone experiments. Section 4 evaluates the performance of PPP–RTK/INS and presents the experimental results in different scenarios. The conclusions and perspectives are illustrated in Sect. 5.

2 Methods

2.1 PPP–RTK with rapid ambiguity resolution

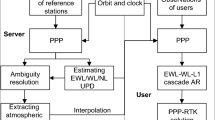
In this section, the multi-GNSS PPP–RTK system developed to achieve rapid ambiguity resolution is described. The flow chart of PPP–RTK processing at both the server and the user modules is illustrated in Fig. 1. It can be seen that the precise atmospheric corrections such as the ionospheric and the tropospheric delays are derived from the multi-GNSS PPP fixed solutions at the server side, which are disseminated to and interpolated at the user stations to enable the PPP rapid ambiguity resolution. To introduce the multi-GNSS PPP–RTK system in detail, the uncombined multi-GNSS ambiguity resolution model, the atmospheric corrections retrieval and the interpolation methods, as well as the PPP rapid ambiguity resolution with atmospheric augmentation, will be introduced afterward.

Fig. 1
figure 1

Flow chart of the PPP–RTK system

Full size image

2.1.1 Uncombined multi-GNSS PPP ambiguity resolution

The GNSS pseudorange (\(P_{r,n}^{s}\)) and phase (\(L_{r,n}^{s}\)) observation equations between station \(r\) and satellite \(s\) at frequency \(n\) can be written as:

$$ P_{r,n}^{s} = \rho_{r}^{s} + c(t_{r} - t^{s} ) + \gamma_{n} \cdot I_{r,1}^{s} { + }T_{r,n}^{s} + b_{r,n} - b_{n}^{s} + e_{r,n}^{s} $$
(1)
$$ L_{r,n}^{s} = \rho_{r}^{s} + c(t_{r} - t^{s} ) - \gamma_{n} \cdot I_{r,1}^{s} { + }T_{r,n}^{s} { + }\lambda_{n}^{{}} \cdot (B_{r,n} - B_{n}^{s} ) + \lambda_{n}^{{}} \cdot N_{r,n}^{s} + \varepsilon_{r,n}^{s} $$
(2)

where

\(\rho_{r}^{s}\) is the geometry distance between the satellite and receiver (m);

\(t_{r}\) and \(t^{s}\) are the receiver and satellite clock offsets, respectively (s);

\(c\) denotes the speed of the light in vacuum (m/s);

\(T_{r,n}^{s}\) represents the slant tropospheric delay (m);

\(I_{r,1}^{s}\) symbolizes the ionospheric propagation delay at the first frequency (m);

\(\lambda_{n}^{{}}\) is the carrier wavelength at frequency \(n\) (m);

\(\gamma_{n}\) denotes the frequency-dependent multiplier factor, which can be expressed as \(\gamma_{n} = {{\lambda_{n}^{2} } \mathord{\left/ {\vphantom {{\lambda_{n}^{2} } {\lambda_{1}^{2} }}} \right. \kern-\nulldelimiterspace} {\lambda_{1}^{2} }}\); \(b_{r,n}^{{}}\) and \(b_{n}^{s}\) denote the code-specific hardware delays at receivers and satellites, respectively (m), while \(B_{r,n}\) and \(B_{n}^{s}\) are the receiver and satellite phase delays, respectively (in cycles);

\(N_{r,n}^{s}\) is the integer carrier-phase ambiguity (in cycles);

\(e_{r,n}^{s}\) and \(\varepsilon_{r,n}^{s}\) denote the sum of measurement noise and multipath error for the code and carrier-phase observations, respectively (m).

It is worthy of noting that while other errors such as the satellite and receiver antenna phase center offsets (PCOs) and variations (PCVs), the relativistic effects, the Sagnac effect, the tidal loadings and the phase wind-up have been omitted from Eqs. (1) and (2) for simplicity, they have been corrected during implementation of the approach according to the existing models (Kouba 2015).

To eliminate the first-order effects of the ionospheric delays, the ionosphere-free (IF) combination is commonly used in the PPP model. Another popular PPP model, called uncombined model, is to process raw observations and the slant ionospheric delays are estimated as unknown parameters. Compared to the IF model, the uncombined PPP model displays several significant advantages. For example, it can directly provide the precise ionospheric information, and the a priori knowledge of ionospheric delays such as temporal correlation, spatial characteristics and the external ionospheric corrections can be utilized to constrain the estimated ionospheric parameters to augment the positioning performance (Li et al. 2013). Here, the uncombined PPP model is selected to retrieve the atmospheric corrections and conduct PPP AR. The general equations of the multi-GNSS PPP uncombined model are written as:

$$ \left\{ \begin{gathered} p_{r,n}^{s,G} = {\mathbf{g}}_{r}^{s,G} \cdot {\mathbf{x}} + c \cdot \overline{t}_{{_{r} }}^{G} + m_{r,w}^{s,G} \cdot Z_{r,w} + \gamma_{n} \cdot \overline{I}_{r,n}^{s,G} + e_{r,n}^{s,G} \hfill \\ p_{r,n}^{s,R} = {\mathbf{g}}_{r}^{s,R} \cdot {\mathbf{x}} + c \cdot \overline{t}_{{_{r} }}^{G} + {\text{ISB}}_{r}^{R} + m_{r,w}^{s,R} \cdot Z_{r,w} + \gamma_{n} \cdot \overline{I}_{r,n}^{s,R} + e_{r,n}^{s,R} \hfill \\ p_{r,n}^{s,E} = {\mathbf{g}}_{r}^{s,E} \cdot {\mathbf{x}} + c \cdot \overline{t}_{{_{r} }}^{G} + {\text{ISB}}_{r}^{E} + m_{r,w}^{s,E} \cdot Z_{r,w} + \gamma_{n} \cdot \overline{I}_{r,n}^{s,E} + e_{r,n}^{s,E} \hfill \\ p_{r,n}^{s,C} = {\mathbf{g}}_{r}^{s,C} \cdot {\mathbf{x}} + c \cdot \overline{t}_{{_{r} }}^{G} + {\text{ISB}}_{r}^{C} + m_{r,w}^{s,C} \cdot Z_{r,w} + \gamma_{n} \cdot \overline{I}_{r,n}^{s,C} + e_{r,n}^{s,C} \hfill \\ \end{gathered} \right. $$
(3)
$$ \left\{ \begin{gathered} l_{r,n}^{s,G} = {\mathbf{g}}_{r}^{s,G} \cdot {\mathbf{x}} + c \cdot \overline{t}_{{_{r} }}^{G} + m_{r,w}^{s,G} \cdot Z_{r,w} - \gamma_{n} \cdot \overline{I}_{r,n}^{s,G} + \lambda_{n} \cdot \overline{N}_{r,n}^{s,G} + \varepsilon_{r,n}^{s,G} \hfill \\ l_{r,n}^{s,R} = {\mathbf{g}}_{r}^{s,R} \cdot {\mathbf{x}} + c \cdot \overline{t}_{{_{r} }}^{G} + m_{r,w}^{s,R} \cdot Z_{r,w} - \gamma_{n} \cdot \overline{I}_{r,n}^{s,R} + \lambda_{n} \cdot \overline{N}_{r,n}^{s,R} + \varepsilon_{r,n}^{s,R} \hfill \\ l_{r,n}^{s,E} = {\mathbf{g}}_{r}^{s,E} \cdot {\mathbf{x}} + c \cdot \overline{t}_{{_{r} }}^{G} + m_{r,w}^{s,E} \cdot Z_{r,w} - \gamma_{n} \cdot \overline{I}_{r,n}^{s,E} + \lambda_{n} \cdot \overline{N}_{r,n}^{s,E} + \varepsilon_{r,n}^{s,E} \hfill \\ l_{r,n}^{s,C} = {\mathbf{g}}_{r}^{s,C} \cdot {\mathbf{x}} + c \cdot \overline{t}_{{_{r} }}^{G} + m_{r,w}^{s,C} \cdot Z_{r,w} - \gamma_{n} \cdot \overline{I}_{r,n}^{s,C} + \lambda_{n} \cdot \overline{N}_{r,n}^{s,C} + \varepsilon_{r,n}^{s,C} \hfill \\ \end{gathered} \right. $$
(4)
$$ with\;\left\{ \begin{gathered} \overline{t}_{{_{r} }}^{G} = t_{r}^{G} + b_{r,IF12}^{G} \hfill \\ \overline{I}_{r}^{s,sys} = I_{r,1}^{s,sys} + \beta_{12}^{sys} \left( {DCB_{r,12}^{sys} - DCB_{12}^{s,sys} } \right) \hfill \\ \overline{N}_{r,n}^{s,sys} = N_{r,n}^{s,sys} + d_{r,n}^{sys} - d_{n}^{s,sys} \hfill \\ \end{gathered} \right. $$
(5)
$$ \left\{ \begin{gathered} DCB_{r,12}^{sys} = b_{r,1}^{sys} - b_{r,2}^{sys} ;DCB_{12}^{s,sys} = b_{1}^{s,sys} - b_{2}^{s,sys} \hfill \\ \alpha_{12}^{sys} = {{\left( {f_{1}^{sys} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {f_{1}^{sys} } \right)^{2} } {\left[ {\left( {f_{1}^{sys} } \right)^{2} - \left( {f_{2}^{sys} } \right)^{2} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\left( {f_{1}^{sys} } \right)^{2} - \left( {f_{2}^{sys} } \right)^{2} } \right]}} \hfill \\ \beta_{12}^{sys} = - {{\left( {f_{{2}}^{sys} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {f_{{2}}^{sys} } \right)^{2} } {\left[ {\left( {f_{1}^{sys} } \right)^{2} - \left( {f_{2}^{sys} } \right)^{2} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\left( {f_{1}^{sys} } \right)^{2} - \left( {f_{2}^{sys} } \right)^{2} } \right]}} \hfill \\ b_{{{\text{IF}}12}}^{s,sys} = \alpha_{12}^{sys} \cdot b_{1}^{s,sys} + \beta_{12}^{sys} \cdot b_{{2}}^{s,sys} ;b_{{{\text{r,IF}}12}}^{s,sys} = \alpha_{12}^{sys} \cdot b_{r,1}^{sys} + \beta_{12}^{sys} \cdot b_{{r,{2}}}^{sys} \hfill \\ d_{r,n}^{sys} = B_{r,n}^{sys} - {{\left( {b_{{{\text{r,IF}}12}}^{G} - \gamma_{n}^{sys} \beta_{12}^{sys} DCB_{r,12}^{sys} } \right)} \mathord{\left/ {\vphantom {{\left( {b_{{{\text{r,IF}}12}}^{G} - \gamma_{n}^{sys} \beta_{12}^{sys} DCB_{r,12}^{sys} } \right)} {\lambda_{n}^{sys} }}} \right. \kern-\nulldelimiterspace} {\lambda_{n}^{sys} }} \hfill \\ d_{n}^{s,sys} = B_{n}^{s,sys} + {{\left( {b_{{{\text{IF}}12}}^{G} + \gamma_{n}^{sys} \beta_{12}^{sys} DCB_{12}^{s,sys} } \right)} \mathord{\left/ {\vphantom {{\left( {b_{{{\text{IF}}12}}^{G} + \gamma_{n}^{sys} \beta_{12}^{sys} DCB_{12}^{s,sys} } \right)} {\lambda_{n}^{sys} }}} \right. \kern-\nulldelimiterspace} {\lambda_{n}^{sys} }} \hfill \\ \end{gathered} \right. $$
(6)

where the superscript \(sys\) indicates the GNSS system and superscripts G, R, E and C refer to GPS, GLONASS, Galileo and BDS systems, respectively; \(p_{r,j}^{s}\) and \(l_{r,j}^{s}\) denote the observed minus computed values of the pseudorange and carrier-phase observations, respectively; \({\mathbf{g}}_{r}^{s}\) is the unit vector of the component from the receiver to the satellite;\({\mathbf{x}}\) (\({\mathbf{x}} = [dx,dy,dz]\)) is the vector of the receiver position increments relative to the a priori position;\(Z_{r,w}\) represents the tropospheric zenith wet delay; and \(m_{r,w}^{s}\) is the corresponding mapping function. It should be noted that the slant tropospheric delay is composed of dry and wet components, where the dry component of tropospheric delays can be corrected with empirical models with sufficient accuracy, such as the Saastamoinen model (Saastamoinen 1972), while the wet component is estimated in the processing procedure. \({\text{ISB}}_{r}\) denotes the receiver code-specific inter-system bias, which is introduced for each system except for GPS under the assumption that the multi-GNSS code observations share the same receiver clock. It is noteworthy that the ISB parameters will be introduced for each frequency for the GLONASS satellites because of the frequency-division multiple-access (FDMA) strategy. \({\overline{\mathbf{N}}}_{r,n}^{s}\) indicates the float ambiguity at frequency \(n\), which is biased by receiver- and satellite-specific hardware delays (\(d_{r,n}^{sys}\) and \(d_{n}^{s,sys}\)). For recovering the integer nature of the ambiguities, the phase biases of the wide-lane (WL) and narrow-lane (NL) combinations are estimated (Li et al. 2018). With the precise satellite orbit, clock and phase bias corrections, PPP AR can be implemented at the reference stations and the parameters \({\mathbf{X}}_{server}\) to be estimated at the server side of the PPP–RTK system will be:

$$ {\mathbf{X}}_{server} = [{\mathbf{x}},\overline{t}_{r}^{G} ,{\text{ISB}}_{{_{r} }}^{sys} ,Z_{r,w} ,{\overline{\mathbf{I}}}_{{_{r} }}^{s} ,{\mathbf{N}}_{{_{r,1} }}^{s} ,{\mathbf{N}}_{{_{r,2} }}^{s} ] $$
(7)

2.1.2 Atmospheric correction retrieval and interpolation

After the ambiguity resolution, the receiver clock (\(\overline{t}_{r}\)), the zenith tropospheric delays (\(Z_{r,w}\)) and the slant ionospheric delays (\(\overline{I}_{r}^{s}\)) can be accurately estimated. In this study, the tropospheric wet delays and the slant ionospheric delays will be utilized directly as the tropospheric and ionospheric corrections (\(\tilde{Z}_{r,w}^{s}\) and \(\tilde{I}_{r,1}^{s}\)), respectively, which can be expressed as:

$$ \left\{ \begin{gathered} \tilde{Z}_{r,w} { = }Z_{r,w} \hfill \\ \tilde{I}_{r,1}^{s} { = }I_{r,1}^{s} \hfill \\ \end{gathered} \right. $$
(8)

Once the precise atmospheric corrections are generated epoch-wisely from a set of reference stations, the interpolation method called modified linear combination method (MLCM) is employed to obtain the precise atmospheric information at the user station (Li et al. 2011), which can be expressed as:

$$ \left( {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & \cdots \hfill & 1 \hfill \\ {X_{1} - X_{u} } \hfill & {X_{2} - X_{u} } \hfill & \cdots \hfill & {X_{n} - X_{u} } \hfill \\ {Y_{1} - Y_{u} } \hfill & {Y_{2} - Y_{u} } \hfill & \cdots \hfill & {Y_{n} - Y_{u} } \hfill \\ \end{array} } \right) \cdot \left (\begin{array}{*{20}c} {\alpha_{1} } \\ {\alpha_{2} } \\ \vdots \\ {\alpha_{m} } \\ \end{array}\right) = \left( {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ \end{array} } \right) $$
(9)
$$ \sum\limits_{i = 1}^{n} {\alpha_{i} } = 1;\;\sum\limits_{i = 1}^{n} {\alpha_{i}^{2} } = Min;\;\tilde{v}_{u} = \sum\limits_{i = 1}^{m} {\alpha_{i} \tilde{v}_{i} } $$
(10)

where subscript \(u\) indicates the user station and \(m\) denotes the number of reference stations; \(X\) and \(Y\) are the station coordinates in the WGS-84 earth-centered earth-fixed (ECEF) frame; \(\alpha_{i}\) is the interpolation coefficient; and \(\tilde{v}_{i}\) and \(\tilde{v}_{u}\) refer to the atmospheric corrections at the reference stations and the user station, respectively. It should be noted that the ionospheric corrections will absorb the receiver- and satellite-specific code biases. The satellite-specific biases in the interpolated corrections share the same values with the user station as the sum of the interpolation coefficients equals one. Thus, the satellite-specific biases absorbed in the atmospheric corrections will compensate the corresponding errors at the user side. However, the receiver-specific code bias absorbed in the ionospheric correction is different from that of the estimated ionospheric parameter at the user side, which will introduce an additional frequency-dependent code bias for PPP–RTK users. Assuming that stations \(r_{1}\) to \(r_{n}\) are selected as reference stations for interpolating atmospheric corrections to user station \(r_{u}\), the frequency-dependent receiver code bias (\(\tilde{b}_{r,u}\)) can be expressed as Eq. (11), which needs to be estimated in the PPP–RTK user model (Psychas and Verhagen 2020).

$$ \tilde{b}_{r,u} = \beta_{12}^{sys} DCB_{{r_{u} ,12}}^{sys} - \beta_{12}^{sys} DCB_{{r_{1} ,r_{2} \cdots r_{n} ,12}}^{sys} $$
(11)

2.1.3 PPP rapid ambiguity resolution with atmospheric corrections augmentation

At the user side, if the precise atmospheric corrections from the reference stations are obtained, the atmospheric constraints will be taken as the virtual observations to realize PPP rapid ambiguity resolution. The constraints for the tropospheric wet delays and ionospheric slant delays are expressed as:

$$ \left\{ \begin{gathered} Z_{{r_{u} ,w}} - \tilde{Z}_{{r_{1} ,r_{2} \cdots r_{n} }} = 0,\quad \sigma_{{Z_{r,w} }}^{2} \hfill \\ \overline{I}_{{r_{u} }}^{s} - \tilde{I}_{{r_{1} ,r_{2} \cdots r_{n} }}^{{s_{i} }} = 0,\quad \sigma_{{I_{r}^{s} }}^{2} \hfill \\ \end{gathered} \right. $$
(12)

where \(\tilde{I}_{{r_{1} ,r_{2} \cdots r_{n} }}^{{s_{i} }}\) and \(\tilde{Z}_{{r_{1} ,r_{2} \cdots r_{n} }}\) are the interpolated tropospheric and ionospheric corrections, respectively. The biases between the estimated atmospheric delay and interpolated corrections are zero mean white process with the variance of \(\sigma_{{I_{r}^{s} }}^{2}\) and \(\sigma_{{Z_{r,w} }}^{2}\) for the ionospheric and tropospheric wet delay, respectively.

With the precise atmospheric corrections, the PPP rapid AR can be achieved. A cascade ambiguity-fixing strategy using WL and L1 ambiguities is employed. The WL ambiguities are derived from the differenced values between the L1 and L2 ambiguities and are fixed according to the round strategy proposed by Dong and Bock (1989). Subsequently, the integer WL ambiguities are used as strong constraints to the norm matrix, and the L1 ambiguities as well as their variance–covariance matrix will be updated. The updated L1 ambiguities present higher precision, which can be fixed easily based on the LAMBDA method (Teunissen 1995). The ratio test will be used to validate the ambiguity validation with a threshold of 2 (Han 1997). Moreover, the partial ambiguity resolution strategy is employed in the multi-GNSS PPP AR processing. The elevation of the satellite less than 10° and the fractional part of the ambiguities larger than 0.25 cycle for WL and 0.15 cycle for L1 will be rejected to ambiguity resolved in advance. Then, the valid ambiguities are removed one by one in the descending order according to their decorrelated variance until the requirement of the ratio test and the success rate has been satisfied (Teunissen et al.1999; Li and Zhang 2015).

2.2 Tightly coupled integration of PPP–RTK and INS

The INS error equations expressed in WGS-84 ECEF frame are given by:

$$ \left[ \begin{gathered} {\dot{\user2{\phi }}} \hfill \\ {\updelta }{\dot{\mathbf{v}}}^{e} \hfill \\ {\updelta }{\dot{\mathbf{r}}}^{e} \hfill \\ \end{gathered} \right]{ = }\left[ \begin{gathered} - {{\varvec{\upomega}}}_{ie}^{e} \times {\varvec{\phi}} - {\mathbf{C}}_{b}^{e} \delta {{\varvec{\upomega}}}_{ib}^{b} \hfill \\ {\mathbf{C}}_{b}^{e} {\mathbf{f}}_{ib}^{b} \times {\varvec{\phi}}{ + }{\mathbf{C}}_{b}^{e} (\delta {\mathbf{f}}_{ib}^{b} ) - (2{{\varvec{\upomega}}}_{ie}^{e} ) \times \delta {{\varvec{\upnu}}}^{e} \hfill \\ \delta {\mathbf{v}} \hfill \\ \end{gathered} \right] $$
(13)

where the dot denotes the difference operator; the cross-product operator means the skew-symmetric form of a vector; superscripts and subscripts \(e\), \(i\) and \(b\) stand for ECEF, earth-centered inertial (ECI) and inertial sensor body frames, respectively; the b-frame is defined as right–front–up axis set which is aligned with the pitch, roll and yaw; \({\varvec{\phi}}\), \(\delta {\mathbf{v}}\) and \(\delta {\mathbf{r}}\) are the misalignment, velocity and position error vectors expressed in the e-frame, respectively; the rotation rate of frame-a relative to frame-b expressed in frame-c is denoted as \({{\varvec{\upomega}}}_{ab}^{c}\); \({\mathbf{C}}_{b}^{e}\) represents the rotation matrix to rotate a vector from frame-b to frame-e; \({\mathbf{f}}_{ib}^{e}\) is the specific force vector obtained from the accelerometers expressed in frame-b; \(\delta\) denotes an error quantity; and \(\delta {{\varvec{\upomega}}}_{ib}^{b}\) and \(\delta {\mathbf{f}}_{ib}^{b}\) are synthetic systematic errors of the gyroscope and accelerometer, respectively. Here, only biases are considered and other inertial sensor errors like the scale factor and the non-orthogonality errors are neglected for a tactical IMU, whose scale factor and non-orthogonality errors range from 10−4 to 10−3 and have the minimal effects on INS. However, for some micro-electro-mechanical system (MEMS) IMUs, the scale factor and non-orthogonality errors can be as large as 10−2, which should be carefully considered (Gao et al. 2017).

The loosely coupled integration and the tightly coupled integration are two common methods for integrating GNSS and INS (Du and Gao 2010). The tight integration architecture is used here as it shows dominate advantages in three aspects: Firstly, it uses raw observations which show less temporal correlation than navigation solutions; then, the tight integration of GNSS and INS is capable of providing continuous solutions when the available satellites are less than four; and finally, it improves the performances of INS augmentation in the cycle slip and fault detection as well as the ambiguity resolution (Kim et al. 1998). For tight integration of PPP and INS, the Kalman filter estimator is used (Brown et al. 1992). Two important parts including the system model and the measurement model need to be developed. Based on the INS error equation shown in the Eq. (13), the system model of tightly coupled PPP/INS is shown as follows:

$$ \left[ \begin{gathered} {\dot{\user2{\phi }}} \hfill \\ \delta {\dot{\textbf{v}}} \hfill \\ \delta {\dot{\textbf{r}}} \hfill \\ \delta {\dot{\textbf{f}}}_{ib}^{b} \hfill \\ \delta {\dot{\varvec{\upomega }}}_{ib}^{b} \hfill \\ \delta \dot{\overline{t}}_{{{r} }}^{G} \hfill \\ \delta {\dot{\textbf{ISB}}} \hfill \\ \delta {\dot{\overline{\textbf{I}}}}_{r}^{s} \hfill \\ \delta {\dot{Z}}_{r,w} \hfill \\ \delta {\dot{\textbf{N}}}_{n}^{s} \hfill \\ \end{gathered} \right]{ = }\left[ {\begin{array}{*{20}c} { - {{\varvec{\upomega}}}_{ie}^{e} \times } & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & { - {\textbf{C}}_{b}^{e} } & 0 & {{{\textbf{0}}} \, {{\textbf{0}}}} & 0 & {{\textbf{0}}} \\ {{\textbf{C}}_{b}^{e} {\textbf{f}}_{ib}^{b} \times } & { - (2{{\varvec{\upomega}}}_{ie}^{e} ) \times } & {{\textbf{0}}} & {{\textbf{C}}_{b}^{e} } & {{\textbf{0}}} & 0 & {{{\textbf{0}}} \, {{\textbf{0}}}} & 0 & {{\textbf{0}}} \\ {{\textbf{0}}} & {\textbf{I}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 & {{{\textbf{0}}} \, {{\textbf{0}}}} & 0 & {{\textbf{0}}} \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 & {{{\textbf{0}}} \, {{\textbf{0}}}} & 0 & {{\textbf{0}}} \\ \begin{gathered} {{\textbf{0}}} \hfill \\ {{\textbf{0}}} \hfill \\ \end{gathered} & \begin{gathered} {{\textbf{0}}} \hfill \\ {{\textbf{0}}} \hfill \\ \end{gathered} & \begin{gathered} {{\textbf{0}}} \hfill \\ {{\textbf{0}}} \hfill \\ \end{gathered} & \begin{gathered} {{\textbf{0}}} \hfill \\ {{\textbf{0}}} \hfill \\ \end{gathered} & \begin{gathered} {{\textbf{0}}} \hfill \\ {{\textbf{0}}} \hfill \\ \end{gathered} & \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} {{\textbf{0}}} \, {{\textbf{0}}} \hfill \\ {{\textbf{0}}} \, {{\textbf{0}}} \hfill \\ \end{gathered} & \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} {{\textbf{0}}} \hfill \\ {{\textbf{0}}} \hfill \\ \end{gathered} \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 & {{{\textbf{0}}} \, {{\textbf{0}}}} & 0 & {{\textbf{0}}} \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 & {{{\textbf{0}}} \, {{\textbf{0}}}} & 0 & {{\textbf{0}}} \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 & {{{\textbf{0}}} \, {{\textbf{0}}}} & 0 & {{\textbf{0}}} \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 & {{{\textbf{0}}} \, {{\textbf{0}}}} & 0 & {{\textbf{0}}} \\ \end{array} \, } \right] \left[ \begin{gathered} {\varvec{\phi}} \hfill \\ \delta {\textbf{v}} \hfill \\ \delta {\textbf{r}} \hfill \\ \delta {\textbf{f}}_{ib}^{b} \hfill \\ \delta {{\varvec{\upomega}}}_{ib}^{b} \hfill \\ \delta \overline{t}_{{{r} }}^{G} \hfill \\ \delta {\textbf{ISB}} \hfill \\ \delta \overline{{\textbf{I}}}_{{{r} }}^{s} \hfill \\ \delta {Z}_{r,w} \hfill \\ \delta {\textbf{N}}_{n}^{s} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}c} { {\textbf{0}}} & {\textbf{C}_{b}^{e}} & {{\textbf{0}}} & 0 & \\ -{{\textbf{C}}_{b}^{e} } & {{\textbf{0}}} & {{\textbf{0}}} & 0 \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 \\{{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 \\{{\textbf{0}}} & {{\textbf{0}}} & {\textbf{I}} & 0 \\ {{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 1 \\{{\textbf{0}}} & {{\textbf{0}}} & {{\textbf{0}}} & 0 \\\\ \end{array} \, } \right] \left[ \begin{gathered} {{\varvec{\upvarepsilon}}}_{{\delta {\textbf{f}}_{ib}^{b} }} \hfill \\ {{\varvec{\upvarepsilon}}}_{{\delta {{\varvec{\upomega}}}_{ib}^{b} }} \hfill \\ {{\varvec{\upvarepsilon}}}_{{\delta {\textbf{ISB}}}} \hfill \\ \varepsilon_{{Z_{r,w} }} \hfill \\ \end{gathered} \right] $$
(14)

where \({\mathbf{I}}\) denotes the identity matrix. It should be noted that the accelerometer biases (\(\delta {{\varvec{\upomega}}}_{ib}^{b}\)), gyro biases (\(\delta {\mathbf{f}}_{ib}^{b}\)), tropospheric zenith wet delay (\(\delta Z_{r,w}\)) and inter-system biases (\(\delta {\mathbf{ISB}}\)) are modeled as random walk process with driving noises denoted by \({{\varvec{\upvarepsilon}}}_{{\delta {\mathbf{f}}_{ib}^{b} }}\), \({{\varvec{\upvarepsilon}}}_{{\delta {{\varvec{\upomega}}}_{ib}^{b} }}\), \({{\varvec{\upvarepsilon}}}_{{\delta {\mathbf{ISB}}}}\) and \(\varepsilon_{{Z_{r,w} }}\), respectively. In addition, the ionospheric error (\(\delta \overline{{\mathbf{I}}}_{{_{r} }}^{s}\)) and receiver clock offset (\(\delta \overline{t}_{{_{r} }}^{G}\)) are estimated as white noise, while the ambiguities (\({\mathbf{N}}_{n}^{s}\)) are estimated as constants in the tightly coupled PPP/INS model.

The measurement model can be written as follows:

$$ \left[ \begin{gathered} \delta {\textbf{P}}^{s} \hfill \\ \delta {\textbf{L}}^{s} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {{\textbf{0}}}\,\,{{\textbf{0}}}\,\, {\textbf {g}}_{r}^{s}\,\, {{\textbf{0}}}\,\,{{\textbf{0}}}\,\,{\textbf {I}}\,\,{\textbf {I}}\,\, {\varvec {\upgamma}}_{n} \,\,{\textbf {m}}_{r,w}^{s}\,\, {{\textbf{0}}} \hfill \\ {{\textbf{0}}}\,\,{{\textbf{0}}}\,\,{\textbf {g}}_{r}^{s}\,\, {{\textbf{0}}}\,\,{{\textbf{0}}}\,\,{\textbf {I}}\,\,{{\textbf{0}}} \,\, {\varvec {\gamma}}_{n} \,\,{\textbf {m}}_{r,w}^{s}\,\,{\textbf {I}} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {\varvec {\upphi}} \hfill \\ \delta {\textbf {v}} \hfill \\ \delta {\textbf{r}} \hfill \\ \delta {\textbf {f}}_{ib}^{b} \hfill \\ \delta {\varvec {\upomega}}_{ib}^{b} \hfill \\ \delta \overline{t}_{{{r} }}^{G} \hfill \\ \delta {\textbf{ISB}} \hfill \\ \delta {\overline {\textbf{I}}}_{{{r} }}^{s} \hfill \\ \delta {{Z}}_{r,w} \hfill \\ \delta {\textbf {N}}_{n}^{s} \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} {\varvec {\upvarepsilon}}_{{P^{s} }} \hfill \\ {\varvec {\upvarepsilon}}_{{L^{s} }} \hfill \\ \end{gathered} \right] $$
(15)

where \(\delta {\mathbf{P}}^{s}\) and \(\delta {\mathbf{L}}^{s}\) denote the observed minus computed values of the undifferenced pseudorange and phase observations, where the compute values are derived from the INS-mechanized position. Since the GNSS antenna and IMU cannot be installed at the same place, the spatial difference between them, which is known as the lever-arm error, must be taken into account in the parameter estimation. Based on Eqs. (14) and (15), the PPP/INS integration model was developed.

To achieve rapid ambiguity resolution, the precise atmospheric corrections are necessary. The generation of the atmospheric corrections and the interpolation method at the user station are illustrated detailedly in Sect. 2.1. Thanks to the precise atmospheric corrections, the related tropospheric and ionospheric errors can be removed from observations. Then, the initial values of \(\delta {\mathbf{I}}_{{{r} }}^{s}\) and \(\delta Z_{r,w}\) are set to zero with a prior variance of \(\sigma_{{I_{r}^{s} }}^{2}\) and \(\sigma_{{Z_{r,w} }}^{2}\) in the filter as Eq. (16):

$$ \left\{ \begin{gathered} \delta {\mathbf{I}}_{{{r} }}^{s} = 0, \, \sigma_{{I_{r}^{s} }}^{2} \hfill \\ \delta Z_{r,w} = 0, \, \sigma_{{Z_{r,w} }}^{2} \hfill \\ \end{gathered} \right. $$
(16)

Meanwhile, the integer feature of ambiguities will be recovered and PPP with rapid ambiguity resolution can be achieved. The algorithm and strategy for ambiguity resolution are described in Sect. 2.1.

The flow chart of the PPP–RTK/INS processing is shown in Fig. 2. When the initial conditions of the system are known, the state (position, velocity and attitude) propagation is performed by the INS mechanization. The high-precision INS-predicted positions will assist in the cycle slip detection in the GNSS processing. When a cycle slip occurs, there will be a significant difference between the current INS-predicted phase observations and the original phase observations. In this study, if the normalized posteriori residual is larger than 3, the current phase observation is considered to have a cycle slip and its ambiguity will be reset. If there are GNSS observations available, the Kalman filter measurement update is conducted to calculate the corrections of state parameters (Brown and Hwang 1992). Finally, the estimated IMU-related parameters will be fed back to the next IMU raw data to restrain the INS divergence.

Fig. 2
figure 2

Flow chart of the PPP–RTK/INS processing

Full size image

3 Experimental validations

To validate the performance of the proposed INS-augmented PPP–RTK method, a series of road vehicular tests were conducted in Wuhan, China. Two experiments consisting of several typical urban sceneries were presented in this paper for detailed analysis. Experiment A was conducted from 5:56:00 to 6:56:00 on October 29, 2020, and the trajectory of the vehicle is shown in the left panel of Fig. 3. The length of the route is about 20.6 km. The experimental vehicle was driven in open-sky environment at the beginning 30 min and then entered into the urban area with several trees, tall buildings and overpasses. Experiment B was conducted in a more complex urban environment with dense high-rise buildings from 8:50:00 to 9:12:00 on December 16, 2020. The trajectory of the vehicle is shown in the right panel of Fig. 3. Six reference stations around Wuhan are selected as the augmentation stations to generate the atmospheric corrections for users. The deployment of the network stations is shown in Fig. 4, where the red pushpins represent augmentation stations. The averaged inter-station distance is about 50 km.

Fig. 3
figure 3

Trajectories of two vehicle experiments (left panel: experiment A conducted from 5:56:00 to 6:56:00 on October 29, 2020; right panel: experiment B conducted from 8:50:00 to 9:12:00 on December 16, 2020)

Full size image
Fig. 4
figure 4

Distribution of regional augmentation stations around Wuhan

Full size image

As shown in Fig. 5, the road vehicle is equipped with a Septentrio PolaRx5 GNSS receiver together with a GNSS antenna (NovAtel GPS-702-GG), a tactical IMU (StarNeto XW-GI7660) and a MEMS IMU (ADIS-16470). The specific information of IMU sensors is provided in Table 1. Time synchronization at hardware level is adopted to unify the timestamps from different sensors to GPS time. As for the spatial synchronization, the shift between the IMU center and the GNSS antenna is measured precisely to calibrate the lever-arm offset. The raw GNSS observations are collected at 1 Hz, while the raw data of the tactical and MEMS IMUs are logged at rates of 200 Hz and 100 Hz, respectively. A reference station equipped with Septentrio PolaRx5 GNSS receiver is set at a location quite close to the route with an open-sky view. With the raw observations of the tactical IMU and two GNSS receivers, the smoothed solutions calculated by tightly coupled multi-GNSS RTK/INS based on commercial Inertial Explorer (IE) 8.9 software are taken as the reference coordinates (NovAtel Corporation 2018).

Fig. 5
figure 5

Illustration of the experimental equipment

Full size image
Table 1 Technical specifications of the IMU sensors used in the experiment
Full size table

The specific strategies for PPP–RTK processing are shown in Table 2. Multi-GNSS observations (GPS, Galileo and BDS) with 1-s interval are used. The orbit and clock errors are corrected by Centre for Orbit Determination in Europe (CODE) products. The satellite phase biases are computed from a set of globally distributed stations using open-source software called GREAT-UPD (https://geodesy.noaa.gov/gps-toolbox/).

Table 2 Processing strategies for PPP–RTK
Full size table

4 Results

In this section, the performance of INS-augmented PPP–RTK was investigated in both open-sky and urban canyon environments. Observations were processed in four modes including float PPP, PPP–RTK, loosely coupled (LC) and tightly coupled (TC) PPP–RTK/INS. The performance of four solutions was carefully analyzed and compared in terms of availability, accuracy and fixing percentage. Here, the availability is defined as the percentage of time that the availability criteria (such as positioning errors below a certain threshold) are met. To evaluate the positioning accuracy, the root mean square (RMS) values of positioning differences with respect to the reference benchmarks were calculated. The fixing percentage here is defined as the percentage of the correctly fixed epochs over the total epochs. A correctly fixed solution is identified when: (1) the requirement of ratio test and success rate has been satisfied; (2) the ambiguity-fixed position agrees well with the reference coordinate (positioning error below 0.1 m), and its accuracy is better than that of the ambiguity-float solutions (Zhang et al.2018).

4.1 Performance of INS-augmented PPP–RTK

Figure 6 shows the positioning series of float PPP, PPP–RTK, LC and TC PPP–RTK/INS, respectively, for experiment A. The number of available satellites (NSAT), position dilution of precision (PDOP), multipath and noise errors are also presented in the figure. Here, the sum of multipath and noise is calculated by the multipath combination (Estey and Meertens 1999) to evaluate the measurement quality of GNSS satellites. During the first 30 min, the number of available GNSS satellites varies between 13 and 22 and PDOP values are mostly less than 2, which ensures a continuous and reliable positioning of PPP. Then, the vehicle runs into a semi-urban operational environment with several trees, tall buildings and overpasses where the signal tracking becomes discontinuous and the NSAT drops frequently. Because of the frequent signal interruptions, the PPP series reconverges several times, and it usually takes about ten minutes for PPP to converge to the centimeter-level accuracy. With the augmentation of precise atmospheric corrections, a rapid ambiguity resolution can be achieved and a centimeter-level accuracy can be obtained within few seconds for PPP–RTK. However, some outliers appear in the positioning series of PPP–RTK, which are attributed to the failure of ambiguity resolution. From Fig. 6, we can see that the appearance of outliers is accompanied by the decrease of NSAT and the increase of PDOP or severe multipath errors. All these factors will degrade the precision of the float ambiguities and lead to the failure of ambiguity resolution (Zhang and Li 2013). It is inevitable in a real kinematic environment where some obstructions such as billboard, trees and buildings will cause the degradation of NSAT and GNSS measurement quality and affect ambiguity resolution. In the loosely coupled PPP–RTK/INS integration, with high-frequency IMU data used for state transfer, the continuity and smoothness of low-frequency GNSS measurement results can be improved. As shown in the shaded area of Fig. 6, PPP and PPP–RTK solutions are almost unavailable during this period because of the frequent signal interruptions lasting for about 3 min. The LC PPP–RTK/INS provides continuous position estimates even when the data gap of GNSS appears. However, it diverges rapidly due to time-increasing INS errors during lengthy GNSS outages. Compared to the loosely coupled solutions, the tightly coupled PPP–RTK/INS provides more accurate position estimates, especially for the situation where available GNSS satellites are less than four. In fact, when the number of the available satellites drops to four or less, the accuracy of LC PPP–RTK/INS mainly depends on the performance of the inertial sensors, while the tightly coupled approach can still make use of available GNSS observations. Moreover, several outliers, appearing in PPP–RTK solutions, can be removed when the INS is used to aid PPP AR. Since INS is free from the external abrupt changes, its superior and stable positioning accuracy in a short timescale will enhance the position and float ambiguity estimation when tight integration is applied. Based on the good quality of float ambiguities, the ambiguity dilution precision (ADOP) and the size of integer ambiguity search space are reduced, and then, the ambiguity resolution of PPP–RTK can be improved (Zhang et al. 2018).

Fig. 6
figure 6

Positioning series of float PPP, PPP–RTK, LC and TC PPP–RTK/INS, respectively (experiment A). The NSAT and PDOP series as well as the multipath series are also presented in this figure

Full size image

The positioning availability for PPP–RTK and PPP–RTK/INS is shown in Table 3 with the availability criteria of 10 cm and 20 cm for the horizontal component, respectively. As shown in Table 3, the PPP–RTK/INS integration exhibits better performance in availability than the PPP–RTK solutions. The percentage of solutions with horizontal accuracy better than 20 cm is 89.25% for PPP–RTK, which is improved to 91.39% and 96.06% for the LC PPP–RTK/INS and TC PPP–RTK/INS solutions, respectively. Compared to the loose integration, the improvement is more significant by the tight integration of PPP–RTK and INS, which is reasonable once we acknowledge that the tightly coupled mode makes full use of GNSS information even in the environment with visible satellites less than four. The fixing percentages of PPP–RTK and PPP–RTK/INS solutions are also presented in Table 3. It can be seen that the fixing percentage also improves from 88.41 to 90.78% by the tightly coupled integration of PPP–RTK and INS. The loosely coupled method brings no improvement for the ambiguity resolution since the GNSS processing is independent of the INS processing in the loose integration.

Table 3 Positioning availability and fixing percentage of PPP–RTK and PPP–RTK/INS
Full size table

Experiment B is conducted in a more complex environment to further investigate the performance of INS-augmented PPP–RTK. The positioning series of PPP–RTK, LC and TC PPP–RTK/INS as well as the multipath/NSAT/PDOP series are presented in Fig. 7. Noted that the NSAT here indicates the number of available satellites with precise atmospheric corrections. There are three shaded areas in this figure, indicating three special situations. The first two shaded areas refer to two reconvergence processes due to the signal interruptions. The first interruption occurs at 8:54:16 lasting only two seconds, and the ambiguity re-fixing is achievable within five seconds for PPP–RTK. The second interruption occurs at 8:57:37 lasting 10 s, and it takes 33 s for PPP–RTK to achieve ambiguity re-fixing. When tight integration of PPP–RTK and INS is applied, the previously accumulated high-precision position information transmitted by the INS can be used as a constraint to obtain more accurate initial float ambiguities when GNSS signals are available, which enables ambiguity re-fixing achieved within 1–2 s in this experiment. The third shadow area is from 9:02:00 to 9:10:00. In this case, GNSS signals are deteriorated and blocked due to several high-rise buildings, and the PPP–RTK solutions diverged to a few decimeters or even a few meters at some epochs. The loose integration of PPP–RTK and INS can improve the smoothness of PPP–RTK solutions; however, it still cannot obtain accurate positions for a long time in a GNSS-degraded environment. The loosely coupled PPP–RTK/INS integration is susceptible to the GNSS degradation since it requires GNSS to compute a position and covariance metrics in the combined solution. By contrast, the PPP–RTK/INS tight integration presents the most stable and accurate positioning series during the whole experimental period, even in an urban canyon environment.

Fig. 7
figure 7

Positioning series of PPP–RTK, LC and TC PPP–RTK/INS, respectively (experiment B). The NSAT and PDOP series as well as the multipath series are also presented in the figure

Full size image

The positioning accuracy of TC PPP–RTK/INS is 0.066, 0.044 and 0.053 m in the east, north and up components, respectively, while that of PPP–RTK and LC PPP–RTK/INS is decimeter level under the GNSS partly blocked environment, and degrades to meter-level under more complex environments. Moreover, the fixing percentage of PPP–RTK and TC PPP–RTK/INS is 48.86% and 81.21%, respectively, which further indicates that the tight integration of PPP–RTK and INS can significantly improve the performance of ambiguity resolution.

4.2 Results analysis in different situations

To investigate the INS aiding effects in precise positioning and ambiguity resolution in different environments, four typical situations are selected for detailed analysis. Figure 8 presents the specific observation environment of four scenarios, which are marked by I, II, III and IV. The red arrows denote the direction of vehicle motion. The first scenario is a road in an open-sky environment, which corresponds to experiment A from 5:57:00 to 6:12:00. The second scenario (6:47:52–6:48:52 of experiment A) presents a GNSS partly blocked environment, where the experiment is influenced by tall buildings and trees along the road. The third scenario (9:01:00–9:03:00 of experiment B) is a typical urban canyon environment with high-rise buildings along the road. The fourth scenario includes several overpasses (6:32:27–6:34:37 of experiment A). The vehicle crosses three overpasses consecutively and then runs under another overpass for few seconds.

Fig. 8
figure 8

Observation environment of four typical situations

Full size image

The positioning series of float PPP, PPP–RTK and TC PPP–RTK/INS in scenario I are plotted in Fig. 9 by blue, green and red lines, respectively. We can find that the performance float PPP is improved dramatically with the atmospheric corrections augmentation. Among all solutions, PPP–RTK/INS shows the fastest convergence, the most stable position series and the highest accuracy for all three components. The statistical results of the positioning accuracy in three processing modes are given in Table 4. The accuracy of the float PPP solutions is 0.385, 0.123 and 0.213 m in the east, north and vertical components, respectively, which is improved remarkably to the centimeter level with PPP–RTK and PPP–RTK/INS. Moreover, the PPP–RTK/INS solution shows the highest accuracy of 0.011, 0.029 and 0.064 m in the east, north and vertical components, respectively, revealing an improvement of 26.6%, 17.1% and 28.0% compared to the PPP–RTK solutions. The results indicate that, under an open-sky environment such as scenario I, both PPP–RTK and PPP–RTK/INS exhibit excellent performance with the positioning accuracy of centimeter level, and INS augmentation can further improve the positioning accuracy of PPP–RTK.

Fig. 9
figure 9

Positioning errors of PPP, PPP–RTK and TC PPP–RTK/INS in scenario I

Full size image
Table 4 Positioning accuracy of PPP, PPP–RTK and TC PPP–RTK/INS in scenario I (unit: m)
Full size table

The positioning series of PPP, PPP–RTK and PPP–RTK/INS solutions in scenario II are plotted in Fig. 10. It can be seen that the positioning performance of PPP degrades suddenly due to the environmental obstructions, which also brings negative effects to ambiguity resolution. Fortunately, the position series of PPP–RTK/INS keep stable during this period. The positioning accuracy is computed and given in Table 5. The positioning accuracy is 0.010, 0.021 and 0.010 m in the east, north and vertical directions for the PPP–RTK/INS solutions, respectively, exhibiting improvements of 93.05%, 92.25% and 98.48% and 85.91%, 89.95% and 94.79% compared to PPP and PPP–RTK solutions, respectively. It is clearly indicated that the augmentation of INS is able to significantly improve the performance of PPP–RTK in a GNSS partly blocked environment.

Fig. 10
figure 10

Positioning errors of PPP, PPP–RTK and TC PPP–RTK/INS in scenario II

Full size image
Table 5 Positioning accuracy of PPP, PPP–RTK and PPP–RTK/INS in scenario II
Full size table

Figure 11 presents the vehicle trajectory overlaid on Google Map for scenario III, which is a typical urban canyon scenario with high-rise buildings along the roads. The red, blue and yellow points indicate the PPP–RTK, the TC PPP–RTK/INS and the reference benchmark solutions, respectively. Results in the box of the left panel of Fig. 11 are zoomed in and shown in the right panel of this figure. It can be seen that few solutions of PPP–RTK are missing due to lack of sufficient visible satellites, while the TC PPP–RTK/INS shows good continuity. In addition, we find that the PPP–RTK solution deviates from the vehicle trajectory, while the TC PPP–RTK/INS solution coincides well with the benchmark solution. The positioning series as well as the multipath, signal–noise-ratio (SNR), NSAT and PDOP series in scenario III are presented in Figs. 12 and 13. The code multipath series behave as random noises basically showing a RMS of 0.282 m. In addition, an obvious deviation during 9:01:00–9:02:00 and a few outliers afterward can be found for the multipath series. The SNR series range between 20 and 50 dB-Hz, and the SNR values after 9:02:00 are obviously lower than former one (usually less than 30). The available GNSS satellites with precise atmospheric corrections vary between 5 and 10, and the PDOP values are mostly larger than two. Also, we find that after 9:02, the NSAT decreases obviously and frequently, and only four satellites are available at some epochs. Meanwhile, the positioning results of PPP–RTK present remarkable deviations. In fact, the lack of satellites, unfavorable tracking geometry and severe multipath may lead to the failure of ambiguity fixing (Zhang and Li 2013). In this scenario, the worse results may mainly be attributed to the limited number of satellites and the poor signal quality, which degrades the accuracy of float ambiguities and hence causes the failure of AR. In contrast, with the accurate positioning information provided by INS, the accuracy of float ambiguities can be improved. Such float ambiguities with enhanced observability will further facilitate the rapid identification of the correct integer candidates. The positioning accuracy is provided in Table 7. Limited by its poor ambiguity-fixing performance, PPP–RTK can only achieve decimeter-level accuracy, while the TC PPP–RTK/INS presents continuous and reliable positioning solutions in the urban canyon environment with an accuracy of 0.055, 0.048 and 0.037 m in the east, north and vertical directions, respectively.

Fig. 11
figure 11

Vehicle trajectory overlaid on Google Map in scenario III. The red, blue and yellow dots refer to the PPP–RTK, the TC PPP–RTK/INS and the reference benchmark solutions, respectively. Results in the box of the left panel are zoomed in and shown in the right panel

Full size image
Fig. 12
figure 12

Positioning series of PPP–RTK (left panel) and TC PPP–RTK/INS (right panel) in scenario III

Full size image
Fig. 13
figure 13

Multipath, SNR, NSAT and PDOP series in scenario III

Full size image

Figure 14 presents the vehicle trajectory overlaid on Google Map in scenario IV (when crossing overpasses). Three overpasses are marked by , and , and the red arrow denotes the direction of vehicle motion. As shown in the figure, PPP–RTK solutions are interrupted when crossing the overpasses, while PPP–RTK/INS can provide continuous positions during the whole period. The positioning availability during the period from 6:32:27 to 6:33:27 with availability criteria of 0.5 m is summarized in Table 7. The availability of positioning solutions is 54.6% when using PPP–RTK method, and it improves to 100% with INS augmentation. The NSAT series during the 1-min period is potted in Fig. 15. The range of two green lines indicates a 33s outage when crossing the overpasses. During this period, signals are interrupted intermittently and the NSAT varies from zero to four. After crossing the overpasses, the number of visible satellites increases gradually. It takes 18 s for PPP–RTK to achieve ambiguity re-fixing. With INS augmentation, a faster ambiguity recovery can be achieved within 5 s. The performance of re-fixing process in scenario IV is also summarized in Table 6.

Fig. 14
figure 14

Vehicle trajectory overlaid on Google Map (when crossing overpasses) in scenario IV. The top and bottom panels denote the results of PPP–RTK and PPP–RTK/INS integration, respectively. The blue and red dots refer to the float and fixed solutions, respectively. Three overpasses are marked by , and , and the red arrow denotes the direction of vehicle motion

Full size image
Fig. 15
figure 15

Satellite availability during the period from 6:32:27 to 6:33:27 in scenario IV. The range of two green lines indicates a 33-s outage when crossing the overpasses

Full size image
Table 6 Availability of positioning solutions and re-fixing performance of PPP–RTK and PPP–RTK/INS in scenario IV
Full size table

Figure 16 presents the vehicle trajectory overlaid on Google Map in scenario IV (when running under an overpass). The NSAT values during the 70-s period are presented in Fig. 17. As can be noticed, the vehicle runs under an overpass for a relatively long period and then enters into a road with tall buildings on both sides. The GNSS signals are blocked by the overpass and tall buildings along the road, and the NSAT decreases to less than four for most of the time. The PPP–RTK solutions are interrupted three times due to the intermittent signal interruptions, while the PPP–RTK/INS integration is capable of continuous operation even when there are less than four satellites available. The positioning availability during the period from 6:33:27 to 6:34:37 is 45.7% and 100% for PPP–RTK and PPP–RTK/INS solutions, respectively. Once GNSS signals can be tracked continuously, instantaneous ambiguity recovery could be obtained by tightly coupled integration of PPP–RTK/INS, while it requires 8 s for PPP–RTK to get converged. The instant accuracy at the fixed epoch is 0.082, 0.036 and 0.055 m and 0.031, 0.020 and 0.054 m in the east, north and vertical components for PPP–RTK and PPP–RTK/INS, respectively. The re-fixing performance of PPP–RTK and PPP–RTK/INS in scenario IV is also summarized in Table 7.

Fig. 16
figure 16

Vehicle trajectory overlaid on Google Map (running under an overpass) in scenario IV. The top and bottom panels denote the results of PPP–RTK and PPP–RTK/INS integration, respectively. The blue and red dots refer to the float and fixed solutions, respectively. The red arrow denotes the direction of vehicle motion

Full size image
Fig. 17
figure 17

Satellite availability during the period from 6:33:27 to 6:34:37. The range of two green lines indicates 27-s outage when running under an overpass

Full size image
Table 7 Availability of positioning solutions and re-fixing performance of PPP–RTK and PPP–RTK/INS in scenario IV
Full size table

Scenario IV represents typical situations in the urban environment where signals are interrupted frequently by the obstructions. Benefiting from the high short-term accuracy and stability of INS, a centimeter to decimeter positioning accuracy over a short period of GNSS outage can be achieved. As a result, the INS information could bridge the gaps in GNSS data and enable continuous positioning in GNSS-challenged environments. The frequent interruptions also lead to ambiguities re-initialized. To obtain reliable positioning information, it is necessary to re-fix ambiguities successfully and fast. Experience in the previous studies indicates that a long period of 30 min or even more is usually required to achieve ambiguity fixing for PPP users (Ge et al. 2008; Li et al. 2018). With the augmentation of precise atmospheric corrections, ambiguities can be fixed quickly in an open-sky environment (Li et al. 2011). Nevertheless, under a GNSS-challenged environment where signals are blocked frequently, the limited number of visible satellites, the poor satellite geometry and the severe multipath errors will degrade the accuracy of float ambiguities. Such float ambiguities with poor accuracy further affect the performance of ambiguity re-fixing. Fortunately, the INS solutions are immune from such re-initialization and could provide continuous and high-accuracy positioning information over a short period. The high-accuracy information will contribute to the decorrelation between positions and ambiguities, which will provide more precise ambiguities for ambiguity re-fixing (Geng and Shi 2017). In fact, the ambiguity re-fixing performance of PPP–RTK/INS integration relies on the positioning accuracy predicted by the INS and the capability of GNSS positioning. Since the accuracy of INS information will decrease with increasing time, the shorter the outages, the shorter time required for ambiguity re-fixing. In addition, more visible satellites and improved observation geometry will undoubtedly contribute to an enhanced performance of the ambiguity re-fixing.

4.3 MEMS-based PPP–RTK/INS integration

The above result analysis for PPP–RTK/INS integration in Sects. 4.1 and 4.2 is based on a tactical-grade IMU. Compared to high-end inertial sensors, MEMS sensors are characterized by lightweight, small size and low cost, which are more suitable for navigation applications such as self-driving cars, unmanned aerial vehicles and mobile robots. In this section, the performance of PPP–RTK integrated with low-cost MEMS inertial sensors is also investigated in experiment A, which was conducted from 5:56:00 to 6:56:00 on October 29, 2020, and the trajectory of vehicle is shown in the left panel of Fig. 3.

The positioning errors of PPP–RTK, tactical-based PPP–RTK/INS (PPP–RTK/T-INS) and MEMS-based PPP–RTK/INS (PPP–RTK/M-INS) are presented in Fig. 18. It can be seen that PPP–RTK/M-INS achieves a comparable performance with PPP–RTK/T-INS under an open-sky environment. Both the PPP–RTK/M-INS and PPP–RTK/M-INS solutions present more stable series with less outliers compared to the PPP–RTK solutions. The shaded area indicates a GNSS-challenging condition where frequent signal interruptions occur and last for about 3 min. During this period, one can see that the position error of PPP–RTK/M-INS drifts more rapidly than those of PPP–RTK/T-INS, and the accuracy decreases to decimeter level or even worse. It can be easily understood by the fact that MEMS sensors generally present relatively poorer performance and stability compared to high-end inertial sensors as the high noise level and the significant bias instability affect the MEMS-based inertial sensors.

Fig. 18
figure 18

Positioning series of PPP–RTK, tactical-based PPP–RTK/INS (PPP–RTK/T-INS) and MEMS-based PPP–RTK/INS (PPP–RTK/M-INS)

Full size image

The positioning availability and fixing percentage are also computed for the MEMS-based PPP–RTK/INS and shown in Table 8. For comparison, the corresponding results of PPP–RTK and PPP–RTK/T-INS are also given in Table 8. It can be seen that the percentage of solutions with horizontal accuracy better than 20 cm is 89.25% for PPP–RTK, which is improved to 93.03% and 96.06% for the MEMS-based and tactical-based PPP–RTK/INS solutions, respectively. The fixing percentage of PPP–RTK is also improved from 88.41 to 90.75% when MEMS IMU is tightly integrated with GNSS. It indicates that the MEMS-based PPP–RTK/INS integration exhibits obviously better performance than the PPP–RTK solution, while it has slightly worse performance with respect to the tactical-based PPP–RTK/INS integration.

Table 8 Positioning availability and fixing percentage of PPP–RTK, PPP–RTK/T-INS and PPP–RTK/M-INS
Full size table

The positioning accuracy in good GNSS observation conditions (5:56:00–6:32:27) and GNSS challenging conditions (6:32:27–6:41:00) is calculated for PPP–RTK, PPP–RTK/T-INS and PPP–RTK/M-INS solutions, respectively. The statistical results are shown in Table 9. When the GNSS availability is good, centimeter-level accuracy is achievable for three processing modes with ambiguity fixed correctly. But under GNSS partly blocked environments, the positioning accuracy of PPP–RTK decreases to meter level. With the aid of MEMS sensors, the positioning accuracy of PPP–RTK is improved to 0.401, 0.398 and 0.509 m in the east, north and vertical components, respectively. It is demonstrated that using MEMS-grade INS to aid PPP–RTK can achieve the positioning accuracy of centimeter level in good GNSS observation conditions and decimeter level in GNSS challenging conditions.

Table 9 Positioning accuracy in good GNSS observation conditions (5:56:00 ~ 6:32:27) and GNSS challenging conditions (6:32:27 ~ 6:41:00)
Full size table

5 Conclusions

In this study, we developed a tightly coupled PPP–RTK/INS integration model aiming to achieve continuous and robust positioning with centimeter-level accuracy in a harsh-signal environment. The performance of INS-augmented PPP–RTK is evaluated in terms of availability, accuracy and fixing percentage. In addition, the INS aiding effects on precise positioning and ambiguity resolution are investigated and discussed in different scenarios.

Several road vehicular tests equipped with the tactical-grade and MEMS-grade IMUs were conducted to verify the effectiveness of the proposed INS-augmented PPP–RTK method. Augmented by the precise atmospheric information, PPP–RTK with rapid ambiguity resolution is achievable, which provides centimeter-level accuracy positioning in an open-sky environment. However, the positioning performance degrades rapidly for PPP–RTK when the vehicle runs into a GNSS-blocked environment. The loose integration of PPP–RTK and INS can improve the smoothness of the PPP–RTK solutions. However, it still cannot obtain accurate positions for a long time in a GNSS-degraded environment. The PPP–RTK/INS tight integration presents the most stable and accurate positioning series during the whole experimental period, even in an urban canyon environment. For a tactical IMU, the horizontal positioning accuracy of tightly coupled PPP–RTK/INS is 1–2 cm in a semi-urban environment and 5–6 cm in a real urban environment with fixing percentages of 90.7% and 81.2%, respectively. Likewise, using MEMS-grade IMU to aid PPP–RTK can also achieve the positioning accuracy of centimeter level in good GNSS observation conditions. However, the accuracy decreases to decimeter-level in GNSS challenging conditions because of the high noise level and significant bias instability of MEMS IMU.

Meanwhile, the INS aiding effects in the different scenarios were carefully investigated. Under an open-sky view environment, both PPP–RTK and PPP–RTK/INS exhibit excellent performance with the positioning accuracy of centimeter level, and INS augmentation can further improve the positioning accuracy of PPP–RTK. In an urban canyon scenario, several factors such as the lack of satellites, the unfavorable tracking geometry and the severe multipath will lead to the failure of ambiguity fixing. But with the accurate positioning information provided by INS, the accuracy of float ambiguities can be improved, and the fixing performance of PPP–RTK is enhanced. Under a GNSS-blocked environment where signals are interrupted frequently by the obstructions such as overpasses, the INS augmentation presents remarkable advantages in terms of continuity and accuracy of positioning. Benefiting from the tightly coupled integration of INS and PPP–RTK, the gaps caused by intermittent signal interruptions can be bridged. Moreover, it takes 1–5 s for PPP–RTK/INS to achieve ambiguity re-fixing after an outage duration lasting up to 30 s, while 8–18 s is required for PPP–RTK.

The results clearly indicate that the augmentation of INS is able to significantly improve the performance of PPP–RTK in real urban environments. However, with increasing GNSS outage time, INS suffers from accumulative position errors which would lead to adverse impacts on ambiguity resolution. Visual–inertial odometry (VIO) can significantly reduce the drift of INS and has been widely applied in the local pose estimation. Therefore, the integration of GNSS, inertial sensors and stereo camera will be investigated in future, which has the potential to further improve the position performance in GNSS-degraded and denied environments.