Robust M–M unscented Kalman filtering for GPS/IMU navigation

Abstract

In this paper, a robust unscented Kalman filter (UKF) based on the generalized maximum likelihood estimation (M-estimation) is proposed to improve the robustness of the integrated navigation system of Global Navigation Satellite System and Inertial Measurement Unit. The UKF is a variation of Kalman filter by which the Jacobian matrix calculation in a nonlinear system state model is not necessary. The proposed robust M–M unscented Kalman filter (RMUKF) applies the M-estimation principle to both functional model errors and measurement errors. Hence, this robust filter attenuates the influences of disturbances in the dynamic model and of measurement outliers without linearizing the nonlinear state space model. In addition, an equivalent weight matrix, composed of the bi-factor shrink elements, is proposed in order to keep the original correlation coefficients of the predicted state unchanged. Furthermore, a nonlinear error model is used as the dynamic equation to verify the performance of the proposed RMUKF with a simulation and field test. Compared with the conventional UKF, the impacts of measurement outliers and system disturbances on the state estimation are both controlled by RMUKF.

1 Introduction

The Kalman filter has been widely applied in real-time navigation using integrated Global Navigation Satellite System (GNSS) and Inertial Measurement Unit (IMU), since it is optimal in linear systems. The filter reduces the effects of errors on the state estimates in a least squares sense, by using weighting information from various sources. In this sense, the state and its covariance matrix are obtained by solving the linear parameter estimation problem. It is well documented, however, that outliers (i.e., data that are inconsistent with the overall pattern of distribution) degrade the estimation quality and render the estimate unreliable (Fitzgerald 1971; Durgaprasad and Thakur 1998).

In static geodetic measurement adjustment, different methods have been applied in an effort to reduce the influence of outliers in observations on the estimated state parameters. These include conventional test procedures (Baarda 1968; Pope 1976) and robust estimation techniques (Huber 1981; Hampel et al. 1986; Rousseeuw and Leroy 1987; Koch 1999; Yang 1999; Xu 2005). The former methods detect, identify and remove the outliers based on statistical hypothesis testing; the latter methods design robust estimation criteria to reduce the influence of outliers on the parameter estimates. Different robust estimators have been proposed, including the so-called L-estimator, L1-norm estimator, M-estimator and M split-estimator (Bickel 1973; Bloomfield and Steiger 1983; Huber 1964, 1981; Andrews 1974; Wiśniewski 2009, 2010), and some of these have been successfully applied in GNSS/INS navigations. Among these robust estimators, the robust M-estimator has received widespread attention due to its high efficiency and high accuracy (Hampel et al. 1986; Wiśniewski 1999, 2009; Yu et al. 2017). The M-estimator has also been extended to deal with correlated observations (Koch 1988; Xu 1989; Yang et al. 2002). Specifically, Koch (1988) uses the Cholesky decomposition to de-correlate the correlated observations; Xu (1989) extends the robust estimator by a bivariate robust function which addresses the correlations between the observations, while Yang et al. (2002) keep the correlations among the observations unchanged using a bi-factor robust equivalent matrix. Nevertheless, the M-estimates may not be robust in some circumstances, if the weights of outlying observations satisfy a certain condition (Xu 2005).

In Kalman filtering, different robust estimators have been studied, such as the Gaussian sum approach, H_∞ filter and robust M-estimation-based Kalman filter (Alspach and Sorenson 1972; Caputi and Moose 1993; Koch and Yang 1998; Yang et al. 2001; He and Han 2010). In addition, Wang et al. (2008) proposed a robust extended Kalman filter (EKF) using W-test statistics based on filtering residuals in order to eliminate the effect of outliers on GNSS navigation solutions. The Gaussian sum approach approximates the non-Gaussian distribution analytically by a finite sum of Gaussian density functions (Alspach and Sorenson 1972; Caputi and Moose 1993; Nikusokhan and Nobahari 2017). The approximation accuracy of the Gaussian sum approach, however, relies on the number of Gaussian terms. If only few Gaussian terms are employed, the poor approximation of true densities could be provided (Stano et al. 2013). The H_∞-based Kalman filter minimizes the worst-case estimate error averaged over all samples by treating process noises, measurement noises and model uncertainties as unknown-but-bounded noise (He and Han 2010). The filter breaks down, however, in the presence of randomly occurring outliers (Gandhi and Mili 2010). The M-estimation technique improves the robustness of the Kalman filter by assuming that the observation errors follow Huber’s distribution (Durgaprasad and Thakur 1998), and then uses the M-estimation approach (Kovacevic et al. 1992; Durovic and Kovacevic 1999). The approaches down weight the contaminated measurements and conduct like least square filters on the other measurements with the assumption that the predicted state is accurate and any of the outliers are uncorrelated. If a correlation exists between the measurements, the Cholesky decomposition can be used to de-correlate the dependent measurements into independent ones, but the outlying errors are also transformed, meaning that the error detection may fail (Xu 1989; Yang 1994).

In general, two types of outliers are assumed: the dynamic model disturbances and the measurement outliers. These two types of outliers arise naturally in many areas of engineering, such as disturbances in the dynamic environment, imprecise knowledge of prior information and faults in hardware, etc. In the literature, adaptive filters and robust filters have been proposed to overcome these two types of outliers. In respect of disturbances in the dynamic environment, adaptive Kalman filter (AKF) is applied. A conventional adaptive method uses a re-weighting technique to re-evaluate the covariance matrices of the predicted state and the measurements with a moving window (Sage and Husa 1969). A more flexible adaptive Kalman filter (AKF) has also been proposed in which an adaptive factor is introduced based on the discrepancy between the estimated and predicted states or based on the predicted residuals (Yang et al. 2001; Yang and Gao 2005). Furthermore, an optimal AKF has been derived based on both the predicted state errors and the predicted residuals (Yang and Gao 2006), while Yang and Xu (2003) proposed a combined AKF based on the moving window variance estimate. By applying the adaptive variance estimation or adaptive factors, the performance of Kalman filter is improved. Furthermore, the robust adaptive estimation techniques have also been applied to control the effects of both the measurement outliers and dynamic model disturbances. Despite the care taken during individual observation solutions, a new robust adaptive Kalman filter with adaptive factors for different state components has been proposed (Yang and Cui 2008). These adaptive factors, however, are constructed under the individual robust solution based on recent measurement information, which is often unavailable. In addition, different robust filters, namely the robust M–LS, LS–M and M–M filters, have been developed to accommodate effects of the outliers or outlying disturbances by using equivalent weights (Yang 1991).

The above approaches are derived based on the Kalman filter or extended Kalman filter (EKF). The latter uses the first-order Taylor expansion, i.e., it calculates the Jacobian matrix in order to analytically linearize the nonlinear model. The cumbersome derivation and determination of the Jacobian matrix not only increases the complexity of the mathematical computation, but also introduces linearization errors. The unscented Kalman filter (UKF), which was introduced by Julier and Uhlman (1997), is another probabilistic approach to approximate the state distribution by Gaussian random variables. The filter utilizes the unscented transform (UT) to estimate the system state vector and its covariance matrix, which undergoes a nonlinear transformation (Wan and van der Merwe 2000; Julier and Uhlmann 2004). An adaptive UKF with a covariance matching technique and a nonlinear strapdown inertial navigation system (SINS) error model with large misalignment angle are used for Doppler Velocity Log (DVL)-aided SINS alignment (Li et al. 2013). A robust adaptive UKF has been proposed to deal simultaneously with dynamic model errors and measurement outliers (Wang et al. 2014). The algorithm uses Huber’s robust function to adjust the measurement weight based on the innovation vector, while the process noise matrix is adjusted by a fading factor, based on the discrepancy between the predicted state and the robust estimated state at the present epoch. A fault-tolerant estimation algorithm based on the UKF, which adaptively estimates the process noise covariance or measurement noise covariance, depending on the type of fault, has also been studied (Hajiyev and Soken 2014). Li et al. (2016) proposed a robust adaptive UKF to handle the uncertainties of process noise and measurement noise. This algorithm uses the moving window and matrix matching technology to estimate the measurement noise and process noise adaptively. It is difficult to determine the length of the moving window, however.

In this paper, we focus on the robust M–M UKF (RMUKF), based on the M–M estimation proposed by Yang (1991), by extending the equivalent weight matrices to bi-factor weight matrices and extending this approach from linear models to the nonlinear models. More precisely, this study extends the robust M–M estimation to a nonlinear state space model, in which the influences of the dynamic model disturbances and measurement outliers are controlled simultaneously by inflating the variances of the outliers. The correlations among the state vector elements are solved by introducing the bi-factor equivalent variance elements, which preserve the original correlation between the states. The rest of the paper is organized as follows. We first review the M–M estimator. The new robust M–M UKF (RMUKF) based on the bi-factor covariance matrix is presented. A simulation and field test are carried out with a loosely coupled integrated Global Positioning System (GPS) and Inertial Measurement Unit (IMU) to verify the performance of the proposed filter. Finally, conclusions are drawn.

2 Mathematical model and M–M robust Kalman filtering

2.1 Dynamic model and measurement model

The classical linear error model for an IMU usually ignores the second-order terms and assumes that the angle error is small. Environmental disturbances and sensor errors, however, may break the small error assumption. Thus, IMU error models for large misalignment angles have been reported in the literature (Yan et al. 2008), in which the nonlinear error model is derived based on the Euler angle errors. The Jacobian matrix of this nonlinear error model is complicated; hence, the UKF is reasonably applied to complete the state estimation. This nonlinear error model states:

$$ \begin{aligned} & \dot{\varphi } = C_{\omega }^{ - 1} \left[ {\left( {I - C_{l}^{p} } \right)\delta \omega_{il}^{l} } \right] \\ & \delta \dot{v}^{l} = \left[ {I - \left( {C_{l}^{p} } \right)^{T} } \right]C_{b}^{p} f^{b} - \left( {2\delta \omega_{ie}^{l} + \delta \omega_{el}^{l} } \right) \\&\qquad\quad\times \tilde{v}^{l} - \left( {2\tilde{\omega }_{ie}^{l} + \tilde{\omega }_{el}^{l} } \right) \times \delta v^{l} + \left( {2\delta \omega_{ie}^{l} + \delta \omega_{el}^{l} } \right) \times \delta v^{l} + \delta g^{l} \\ & \delta \dot{p}^{l} = \left[ {\begin{array}{*{20}c} 0 &\quad {\frac{1}{M + h}} &\quad 0 \\ {\frac{1}{N + h}\cos \phi } &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 \\ \end{array} } \right]\delta v^{l} \\ \end{aligned} $$

(1)

where

$$ C_{\omega }^{ - 1} = \frac{1}{{\cos \varphi_{x} }}\left[ {\begin{array}{*{20}c} {\cos \varphi_{y} \cos \varphi_{x} } &\quad 0 &\quad {\sin \varphi_{y} \cos \varphi_{x} } \\ {\sin \varphi_{y} \sin \varphi_{x} } &\quad {\cos \varphi_{x} } &\quad { - \cos \varphi_{y} \sin \varphi_{x} } \\ { - \sin \varphi_{x} } &\quad 0 &\quad {\cos \varphi_{y} } \\ \end{array} } \right] $$

(2)

$C_{l}^{p}$ is the rotation matrix from the local-level frame $\left( l \right)$ to the platform frame $\left( p \right)$; $\delta \omega_{il}^{l}$ is the angular velocity error of the $l$ frame with respect to the inertial frame $\left( i \right)$. $\tilde{\omega }_{ie}^{l}$ is the earth rotation velocity at the $l$ frame, and $\tilde{\omega }_{el}^{l}$ is the rotation velocity of the $l$ frame with respect to the earth-centered, earth-fixed frame $\left( e \right)$ at the $l$ frame. $f^{b}$ is the measurement of the accelerometer at the body frame $\left( b \right)$. $\tilde{v}^{l} = \left[ {\begin{array}{*{20}c} {V_{\text{E}} } & {V_{\text{N}} } & {V_{\text{U}} } \\ \end{array} } \right]^{\text{T}}$ are the velocity components of the east, north and up directions, and $\delta p^{l} = \left[ {\delta \begin{array}{*{20}c} {\text{L}} & {\delta\uplambda} & {\delta {\text{h}}} \\ \end{array} } \right]^{\text{T}}$ are the position error components of the latitude, longitude and altitude. Thus, the state vector can be expressed as $X = \left[ {\varphi_{1 \times 3} \delta v_{1 \times 3} \delta p_{1 \times 3} } \right]^{\text{T}}$. The dynamic model can be rewritten more economically as:

$$ x_{k} = f_{k,k - 1} \left( {x_{k - 1} } \right) + \omega_{k - 1} $$

(3)

where $x_{k}$ and $x_{k - 1}$ are the state vectors at epoch k and k − 1, respectively, including the position vector and velocity vector; $f_{k,k - 1} \left( {x_{k - 1} } \right)$ is the state transition function; and $\omega_{k - 1}$ is the model error vector.

The measurement equation is written as:

$$ L_{k} = h_{k} \left( {x_{k} } \right) + e_{k} $$

(4)

where $L_{k}$ is an $m \times 1$ measurement vector; $h_{k} \left( {x_{k} } \right)$ is the transformation function that maps the state vector parameters into the measurement domain; and $e_{k}$ is the measurement error vector. In case the velocity and positioning outputs from GPS receivers are taken as measurements, the measurement equation is:

$$ L_{k} = A_{k} x_{k} + e_{k} $$

(5)

where $x_{k}$ is the $n \times 1$ state vector with prior estimated $\bar{x}_{k}$ and covariance matrix $\Sigma _{{\bar{X}}}$; $e_{k}$ is the $6 \times 1$ error vector; and $A_{k}$ is the $6 \times n$ linear map function between the state vector parameters and measurements and is expressed as:

$$ A = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0_{3 \times 3} } &\quad {I_{3 \times 3} } \\ \end{array} } & {\begin{array}{*{20}c} {0_{3 \times 3} } &\quad \ldots &\quad {0_{3 \times n} } \\ \end{array} } \\ {\begin{array}{*{20}c} {0_{3 \times 3} } &\quad {0_{3 \times 3} } \\ \end{array} } & {\begin{array}{*{20}c} {I_{3 \times 3} } &\quad \ldots &\quad {0_{3 \times n} } \\ \end{array} } \\ \end{array} } \right] $$

(6)

where $I_{3 \times 3}$ is an identity matrix.

2.2 M–M robust estimation

Yang (1991) introduced three robust estimators, based on the M-estimation technique, for three corresponding error models, in which the measurements follow a contaminated normal distribution (M–LS), or in which the prior estimate contains outliers (LS–M), or both measurements and prior estimates follow contaminated normal distributions (M–M). This section reviews the methodology of the three estimators. The error equation of the measurement is:

$$ v_{k} = A_{k} \hat{x}_{k} - L_{k} $$

(7)

where $v_{k}$ is the $n \times 1$ correction vector of measurements and $\hat{x}_{k}$ is the estimated state vector of $x$. If the predicted correction vector, $\Delta \bar{x}_{k} = \bar{x}_{k} - x_{k}$, and the measurements are independently and identically distributed with a Gaussian distribution, the risk function, based on the least squares (LS) Bayesian estimation, is:

$$ \varOmega_{k} = v_{k}^{\text{T}}\Sigma _{k}^{ - 1} v_{k} + \left( {\bar{x}_{k} - \hat{x}_{k} } \right)^{\text{T}}\Sigma _{{\bar{x}_{k} }}^{ - 1} \left( {\bar{x}_{k} - \hat{x}_{k} } \right) $$

(8)

where $\Sigma _{k}$ is the covariance matrix of the measurements.

Assuming that the measurements, $L_{k} ,$ and the predicted state vector, $\bar{x}_{k}$, are contaminated by outliers and the corresponding contaminated distributions for both measurement errors and predicted state elements are, respectively,

$$ F_{\Delta } \left( \varepsilon \right) = \left( {1 - \varepsilon } \right)\phi_{\Delta } + \varepsilon H $$

(9)

and

$$ F_{{\Delta \bar{x}}} \left( {\varepsilon_{x} } \right) = \left( {1 - \varepsilon_{x} } \right)\phi_{x} + \varepsilon_{x} H $$

(10)

where $0 < \varepsilon < 1$, $H$ is any symmetric distribution, and $\phi_{\Delta }$ and $\phi_{x}$ are the normal distributions. The risk function based on the robust M-estimation is as follows:

$$ \Omega = \mathop \sum \limits_{i = 1}^{n} \rho \left( {v_{i} } \right) + \mathop \sum \limits_{j = 1}^{m} \beta \left( {\delta \tilde{x}_{j} } \right) $$

(11)

with

$$ \rho \left( {v_{i} } \right) = \left\{ {\begin{array}{*{20}l} {\frac{{v_{i}^{2} }}{2}} \hfill &\quad {\left| {v_{i} } \right| < \tau } \hfill \\ {\tau \left| {v_{i} } \right| - \frac{{\tau^{2} }}{2}} \hfill &\quad {\left| {v_{i} } \right| \ge \tau } \hfill \\ \end{array} } \right. $$

(12)

where $v_{i}$ denotes the $i{\text{th}}$ element of the vector $v_{k}$; $\tau$ is chosen to give the desired efficiency at the Gaussian model (Kovacevic et al. 1992); and the $\beta \left( \cdot \right)$ function is similar to $\rho \left( \cdot \right)$.

The estimator determined by condition function (11) is known as the M–M estimator, since the M-estimation principle is applied for both the measurement and the predicted state vectors. The robust estimator is expressed as:

$$ \hat{x}_{k} = \left( {A_{k}^{\text{T}} \bar{P}_{k} A_{k} + \bar{P}_{{\bar{x}_{k} }} } \right)^{ - 1} \left( {A_{k}^{\text{T}} \bar{P}_{k} L_{k} + \bar{P}_{{\bar{x}_{k} }} \bar{x}_{k} } \right) $$

(13)

where $\bar{P}_{k}$ and $\bar{P}_{{\bar{x}_{k} }}$ are equivalent weight matrices of the measurements and predicted state vector, respectively. The M–M Kalman filter is the combination of LS–M and M–LS estimator. It can also be written as follows (Koch and Yang 1998; Yang et al. 2001):

$$ \hat{x}_{k} = \bar{x}_{k} + {\bar{\varSigma }}_{{\bar{x}}} A_{k}^{\text{T}} \left( {A_{k} {\bar{\varSigma }}_{{\bar{x}}} A_{k}^{\text{T}} + {\bar{\varSigma }}_{k} } \right)^{ - 1} \left( {L_{k} - \bar{L}_{k} } \right) $$

(14)

where ${\bar{\varSigma }}_{k} = \bar{P}_{k}^{ - 1}$ and ${\bar{\varSigma }}_{{\bar{x}}} = \bar{P}_{{\bar{x}_{k} }}^{ - 1}$ are called equivalent covariance matrices of the measurements and predicted state vector, respectively (for the detailed component calculation, please refer to Koch and Yang 1998).

If the dynamic model and measurement equations are linear, the M–M Kalman filter can provide robust estimates of the state vector. In practice, however, the dynamic model and measurement equations may be nonlinear, and the linearization process introduces not only a heavy computational burden but also additional uncertainty in respect of model errors.

3 Robust M–M unscented Kalman filter

The M–M estimator mentioned above reweights the measurements and predicted state elements by using iterated residuals of the measurements and corrections of predicted state elements based on the linear or linearized models. The RMUKF, however, starts from general nonlinear models, Eqs. (3) and (4).

The predicted state vector and its covariance matrix are:

$$ \left( {\tilde{x}_{k} } \right)_{i} = f_{k} \left[ {\left( {\tilde{x}_{k} } \right)_{i} } \right] $$

(15)

$$ \bar{x}_{k} = \mathop \sum \limits_{i = 0}^{2n} w_{i} \left( {\tilde{x}_{k} } \right)_{i} $$

(16)

with the covariance matrix:

$$ \Sigma _{{\bar{x}_{k} }} =\Sigma _{{\omega_{k - 1} }} + \mathop \sum \limits_{i = 0}^{2n} w_{i} \left[ {\left( {\tilde{x}_{k} } \right)_{i} - \bar{x}_{k} } \right]\left[ {\left( {\tilde{x}_{k} } \right)_{i} - \bar{x}_{k} } \right]^{\text{T}} $$

(17)

where $\left( {\tilde{x}_{k} } \right)_{i}$ is the $i{\text{th }}$ sigma point, which is chosen based on the current Gaussian distribution; $w_{i}$ is the weight of the sigma point. The details of the UKF can be found in Yang et al. (2016, 2018). The predicted measurement vector and innovation vector are:

$$ \left( {\tilde{L}_{k} } \right)_{i} = h_{k} \left[ {\left( {\tilde{x}_{k} } \right)_{i} } \right] $$

(18)

$$ \bar{L}_{k} = \mathop \sum \limits_{i = 0}^{2n} w_{i} \left( {\tilde{L}_{k} } \right)_{i} $$

(19)

$$ \bar{V}_{k} = L_{k} - \bar{L}_{k} $$

(20)

with the covariance matrix:

$$ \Sigma _{{\bar{V}_{k} }} =\Sigma _{k} + \mathop \sum \limits_{i = 0}^{2m} w_{i} \left[ {\left( {\tilde{L}_{k} } \right)_{i} - \bar{L}_{k} } \right]\left[ {\left( {\tilde{L}_{k} } \right)_{i} - \bar{L}_{k} } \right]^{\text{T}} =\Sigma _{k} +\Sigma _{{\bar{L}_{k} }} $$

(21)

The cross-covariance matrix is:

$$ \Sigma _{{\bar{x}_{k} \bar{L}_{k} }} = \mathop \sum \limits_{i = 0}^{2m} w_{i} \left[ {\left( {\tilde{x}_{k} } \right)_{i} - \bar{x}_{k} } \right]\left[ {\left( {\tilde{L}_{k} } \right)_{i} - \bar{L}_{k} } \right]^{\text{T}} $$

(22)

where $\left( {\tilde{L}_{k} } \right)_{i}$ is the sigma point of the predicted measurements; $\bar{L}_{k}$ is the weighted mean of the sigma points. If a linear equation is used to describe the measurement model, the linear propagation of the state vector and its covariance matrix have equivalent accuracy as those from the unscented transform, but there is less computational consumption (Yang et al. 2016).

The estimated state vector and its covariance matrix can be obtained as:

$$ \hat{x}_{k} = \bar{x}_{k} + K_{k} \left( {L_{k} - \bar{L}_{k} } \right) $$

(23)

$$ \Sigma _{{\hat{x}_{k} }} =\Sigma _{{\bar{x}_{k} }} - K_{k}\Sigma _{{\bar{y}_{k} }} K_{k}^{\text{T}} $$

(24)

where $K_{k}$ is the Kalman gain matrix (Yang et al. 2018):

$$ K_{k} =\Sigma _{{\bar{x}_{k} \bar{y}_{k} }}\Sigma _{{\bar{y}_{k} }}^{ - 1} $$

(25)

The correction vector of the measurements and the correction vector of the predicted state can be obtained using the estimated state vector. They are:

$$ \hat{L}_{k} = h\left( {\hat{x}_{k} } \right) $$

(26)

$$ V_{k} = \hat{L}_{k} - L_{k} $$

(27)

$$ V_{{\bar{x}_{k} }} = \hat{x}_{k} - \bar{x}_{k} $$

(28)

where $\hat{L}_{k}$ is the estimated measurement vector. Based on the M-estimation principle, the cost function is:

$$ V_{{\bar{x}_{k} }}^{\text{T}} \bar{P}_{{\bar{x}_{k} }} V_{{\bar{x}_{k} }} + V_{k}^{\text{T}} \bar{P}_{k} V_{k} = \hbox{min} $$

(29)

where $\bar{P}_{{\bar{x}_{k} }}$ and $\bar{P}_{k}$ are equivalent weight matrices of the respective predicted state and measurement vectors. An equivalent expression may be written as:

$$ V_{{\bar{x}_{k} }}^{\text{T}} {\bar{\varSigma }}_{{\bar{x}_{k} }}^{ - 1} V_{{\bar{x}_{k} }} + V_{k}^{\text{T}} {\bar{\varSigma }}_{k}^{ - 1} V_{k} = \hbox{min} $$

(30)

where ${\bar{\varSigma }}_{{\bar{x}_{k} }}$ and ${\bar{\varSigma }}_{k}$ are the equivalent covariance matrices of the respective $\bar{x}_{k}$ and $L_{k}$, and

$$ {\bar{\varSigma }}_{{\bar{x}_{k} }} = P_{{\bar{x}_{k} }}^{ - 1} $$

(31)

$$ {\bar{\varSigma }}_{k} = \bar{P}_{k}^{ - 1} $$

(32)

It should be noted that although the observations are independent within a loosely coupled integration, the predicted state elements are correlated. Thus, if both the predicted state and measurement vectors are contaminated by outliers, a bi-factor inflation covariance model is introduced to suppress the impact on the estimated state vector (Yang et al. 2002). The equivalent covariance matrices of the predicted state vector, $\bar{x}_{k}$, and the measurement vector, $L_{k}$, are then:

$$ \begin{aligned} \bar{\sigma }_{i}^{2} & = \lambda_{ii} \sigma_{i}^{2} \quad \lambda_{ii} \ge 1 \\ \bar{\sigma }_{j}^{2} & = \lambda_{jj} \sigma_{j}^{2} \quad \lambda_{jj} \ge 1 \\ \bar{\sigma }_{ij} & = \lambda_{ij} \sigma_{ij} \\ \end{aligned} $$

(33a)

where $\lambda_{ii}$ and $\lambda_{jj}$ are two inflation factors of the covariance elements, and $\lambda_{ij} = \sqrt {\lambda_{ii} \lambda_{jj} }$ is the bi-factor; $\bar{\sigma }_{i}^{2}$, $\bar{\sigma }_{j}^{2}$ and $\bar{\sigma }_{ij}$ are equivalent variances and covariance elements, respectively. The newly generated covariance matrix has thus kept the original correlations unchanged.

$$ {\bar{\varSigma }} = \left[ {\begin{array}{*{20}c} {\bar{\sigma }_{11}^{2} } &\quad \cdots &\quad {\bar{\sigma }_{1n}^{2} } \\ \vdots &\quad \ddots &\quad \vdots \\ {\bar{\sigma }_{n1}^{2} } &\quad \cdots &\quad {\bar{\sigma }_{nn}^{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\lambda_{11} \sigma_{11}^{2} } &\quad \cdots &\quad {\lambda_{1n} \sigma_{1n}^{2} } \\ \vdots &\quad \ddots &\quad \vdots \\ {\lambda_{n1} \sigma_{n1}^{2} } &\quad \cdots &\quad {\lambda_{nn} \sigma_{nn}^{2} } \\ \end{array} } \right] $$

(33b)

The bi-factor can be chosen as follows:

$$ \lambda_{ii} = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {\left| {\tilde{v}_{i} } \right| \le c} \hfill \\ {\frac{{\left| {\tilde{v}_{i} } \right|}}{c}} \hfill &\quad {\left| {\tilde{v}_{i} } \right| > c} \hfill \\ \end{array} } \right. $$

(34)

where $c$ is a constant, usually chosen as 1.0–2.0; $\tilde{v}_{i} = v_{i} /\sigma_{0}$ is the standardized correction corresponding to the $i{\text{th}}$ measurement or standardized correction for the $i{\text{th}}$ predicted state element. The variance scale factor is

$$ \sigma_{0} = {\text{median }}\left\{ {\left| {\tilde{v}_{i} } \right|} \right\}/0.6745 $$

(35)

The constant 1/0.6745 is a correction factor for Fisher consistency at the Gaussian distribution (Fakharian et al. 2011). The robust estimated state vector and its covariance matrix then can be derived via Eqs. (23) and (24), while the iterations can effectively suppress the influences of the outliers.

It can be found from the above derivation that the robust estimation process requires iteration at the present epoch. The estimated state vector at the first iteration acts as the reference state and completes the robust M–M estimation. The RMUKF calculation flow is presented in Fig. 1.

Fig. 1

Flowchart of RMUKF

The following characteristics can be obtained from the above derivation.

• 1. The M–M estimation is limited not only to linear models, but also to nonlinear models if unscented Kalman filter is applied.

• 2. The RMUKF can effectively attenuate the effects of the dynamic disturbances and measurement outliers on the estimated state vector by iteration procedures.

• 3. The algorithm can be modified into an adaptive algorithm by adding an adaptive factor to the innovation vector and its covariance matrix. If the measurement errors were not contaminated by the outliers, the innovation vector could indicate the system discrepancy. The weight function decreases the contribution of the dynamic model to the estimated state vector based on the extent of the discrepancy.

• 4. The equivalent covariance matrices determined by Eqs. (33a) and (33b) are symmetric and keep the original predicted state correlation coefficients unchanged.

• 5. The derivation is carried out with nonlinear state space models. It should be noted that the derivation is also valid for a linear model.

4 Computation and analysis

To verify the proposed RMUKF, both a simulation test and a field test were carried out. A loosely coupled integration strategy was used to fuse the output data from a GPS receiver and IMU. A nine-state nonlinear error model was used as the dynamic equation. The tests were processed in the MATLAB R2010a 64-bit program on a PC with Intel Core i7-3770 CPU at 3.40 GHz, 16-GB RAM equipped with Win10.

4.1 Simulation tests

The simulation tests were based on a moving vehicle with different moving behaviors. The simulation duration was 549 s with a 100-Hz sampling frequency, and the simulation initial conditions are listed in Table 1. In Table 1, the initial state variance elements approximately correspond to the initial state errors. The simulation was processed without initial alignment, and the misalignment angle was randomly set to a considerable number. The simulated trajectory and velocity are presented in Figs. 2 and 3. The measurement outliers at four different epochs are arbitrarily given as presented in Table 2. The differences between the observations with outliers and the simulated true observations, positioning and velocity components are plotted in Figs. 4 and 5. The estimation results were also compared with the simulated true values. A complementary simulation was also carried out with different initial conditions, in which the initial position errors were enlarged to [20 m, 20 m, 30 m], and the velocity errors were enlarged to 2 m/s.

Table 1 Simulation initial conditions

Fig. 2

The simulated trajectory. The red dot is the initial position of the trajectory

Fig. 3

The simulated velocity at east, north and up components

Table 2 Magnitude of input outliers

Fig. 4

The difference between the outlying position components and the simulated true observations in latitude (a), longitude (b) and altitude (c)

Fig. 5

The difference between the outlying velocity components and the simulated true observations in respect of east (a), north (b) and up (c)

The positioning errors of simulation results are illustrated in Fig. 6, in which (a) presents the error of the latitude component, (b) the error in the longitude component and (c) the error in the altitude component. Figure 7 presents the velocity error, in which (a) gives the error of the east component, (b) gives the error of the north component, and (c) gives the error of up component. The absolute maximum error of UKF and RMUKF is given in Fig. 8. The root-mean-square error (RMSE) is given in Table 3.

Fig. 6

Position error in latitude (a), longitude (b) and altitude (c)

Fig. 7

Velocity error in east (a), north (b) and up (c)

Fig. 8

Absolute maximum error of position (a) and velocity (b)

Table 3 RMSE of UKF and RMUKF in simulation

The two cases of the simulation calculation results are labeled as RMUKF1 (with original small initial errors) and RMUKF2 (with enlarged initial errors).

From the calculation results, we observe that:

• 1. The UKF failed to constrain the position error influence between epoch 300 s and 386 s due to the outlying observations, see Fig. 6.

• 2. The maximum positioning error of RMUKF is smaller than that of UKF. It is noted that the error magnitude of UKF is more than 12 m in the longitude component, while that of RMUKF is less than 5 m. This means that the RMUKF proposed in this paper has the ability to reduce the outlying measurement effects to the state parameter estimates. In particular, the peak value is confined.

• 3. The velocity component errors reveal a similar phenomenon as the positioning component errors; that is, the velocity estimated from RMUKF is superior to that of UKF, as shown in Fig. 7.

• 4. It is noted that a large fluctuation occurred after epoch 300 s due to the outlying observation elements, while the fluctuation in RMUKF is smaller and RMUKF converges faster than that of UKF.

• 5. The RMSE presented in Table 3 also proved that RMUKF was better able to minimize the influences of outliers on positioning and velocity results.

• 6. From Table 4 it can be seen that the RMSE of RMUKF with a large initial error is greatly increased. Thus, the proposed RMUKF requires a relatively accurate initial state.

  Table 4 RMSE of RMUKF1 and RMUKF2

4.2 Field test

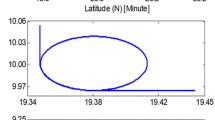
This subsection presents experimental results to demonstrate the performance of the proposed RMUKF when applied to GPS/IMU integrated vehicle navigation. The experiment was conducted next to a lake in Wuhan, China. The vehicle trajectory is shown in Fig. 9a; the three positioning components, which are solved by single-point positioning technique, are presented in Fig. 9b–d. In Fig. 9d, it is noted that the altitude component fluctuated between 6.6 and 49.22 m during the epochs 283310–284248 s. The sampling frequencies of the IMU and GPS were 100 Hz and 10 Hz, respectively. The bias variances of the gyro and accelerometer were 1 °/h and 500 μg, respectively. The initial position errors were set to [7 m, 7 m, 7 m], initial velocity errors to [0.1 m/s, 0.1 m/s, 0.1 m/s] and initial attitude errors to [16, 16, 83].

Fig. 9

The vehicle trajectory (a) and position components in longitude (b), latitude (c) and altitude (d)

The estimated results were compared with double-differenced GPS positioning and velocity. The UKF and RMUKF positioning errors are presented in Fig. 10. The velocity errors are presented in Fig. 11. The RMSE are shown in Fig. 12 and Table 5. The running time for both UKF and RMUKF is presented in Table 6.

Fig. 10

Position error of UKF (a) and RMUKF in latitude (a), longitude (b) and altitude (c)

Fig. 11

Velocity error of UKF versus RMUKF in east (a), north (b) and up (c)

Fig. 12

RMSE of position (a) and velocity (b)

Table 5 RMSE of UKF and RMUKF in field test

Table 6 Running time of UKF and RMUKF

By analyzing from the actual field test, we observe:

• (1) The peak positioning error values provided by RMUKF are smaller than those of UKF. In particular, the outlying effects in the longitude component around epoch 2.84 disappear, see Fig. 10b. The RMUKF controls the outlying measurement effects.

• (2) It is also noted that there are considerable fluctuations in the UKF positioning errors, especially in longitude and altitude components, shown in Fig. 10b, c. The RMUKF not only has fewer peak values in positioning errors than those of UKF, but also converges faster than UKF after the error peaks have occurred.

• (3) The RMUKF velocity error in the east and north components during the initial period is bounded, while the UKF velocity error tends to diverge.

• (4) The RMSE presented in Fig. 12 and Table 5 also demonstrates the superior performance of the RMUKF.

• (5) The proposed RMUKF took 414.19 s to run in the field test, compared to 400.42 s for UKF.

5 Conclusions

This study presents a robust M-unscented Kalman filter, based on an M–M estimation principle. The filter has the ability to suppress the effects of outliers from both the dynamic model and measurements on dynamic state estimates and hence provides a robust solution in an iterative manner, without requiring the linearization of nonlinear models. Furthermore, the correlations of the predicted state parameters are rigorously taken into account by the correlated bi-factor equivalent covariance matrix, in which the original correlations of the predicted parameters are kept unchanged. The performance of RMUKF is verified by simulation and field tests. The influences of measurement outliers and dynamic model disturbances, as well as the stochastic model uncertainties, are controlled well by RMUKF. In addition, RMUKF makes the filter converge quickly. The proposed method, however, requires a relative accurate initial state vector.