Introduction

In kinematic geodetic positioning and navigation, Kalman filtering has been widely applied because of its optimality in linear systems and simplicity in the recursive calculation process. For nonlinear systems, however, the standard Kalman filter may provide biased state estimates due to the nonlinear model approximation (Yang et al. 2016). In addition, the standard Kalman filter may lead to failure if inaccurate prior state estimates or unreasonable statistical information is used.

For the inaccurate prior state estimate and their covariance matrices, the adaptive Kalman filters (AKFs) are applied, two of which are the innovation-based adaptive estimation (IAE) and residual-based adaptive estimation (RAE) (Sage and Husa 1969). These two algorithms use a re-evaluation technique, called Sage window method, to estimate the covariance matrices of the predicted state and measurement vectors by a moving window. The Sage window method is also applied to integrate Global Positioning System (GPS) and an inertial measurement unit (IMU) (Mohamed and Schwarz 1999). A more flexible AKF was proposed by introducing an adaptive factor based on the discrepancy between the estimated and predicted states or based on the innovation vectors (Yang et al. 2001; Yang and Gao 2006). In addition, a combined AKF was constructed by integrating the moving window method with an adaptive factor (Yang and Xu 2003). Furthermore, an optimal AKF was derived based on both the predicted state errors and the innovation vectors (Yang and Gao 2006). Geng and Wang (2008) reported an alternative adaptive Kalman filter with multiple adaptive factors. Chang and Liu (2015) proposed an adaptive filter using Mahalanobis distance to detect the model errors, in which the covariance matrix of the related covariance matrix is inflated by a fading factor. In addition, an adaptive federated Kalman filter was also proposed for the PPP/INS integrated system (Li et al. 2017). By applying the adaptive estimation method, the performance of Kalman filtering is improved. It should be mentioned that all the variations on adaptive Kalman filtering are based on the linear state-space model.

For dealing with nonlinearity of the state-space model, many approximation methods have been developed. A widely accepted method is the extended Kalman filter (EKF), which approximates the nonlinear model by linearization (Sorenson 1985). The EKF uses the first-order Taylor series expansion to linearize the nonlinear model. Thus, the Jacobian matrices of the nonlinear models have to be obtained, and the higher order terms of the derivatives are truncated. Unscented Kalman filter (UKF), proposed by Julier et al. (1995), is another method to deal with the nonlinear state-space model. Julier and Ulhmann (1997) demonstrated that the performance of the UKF was comparable to that of the second-order Gauss filter. Wan and van der Merwe (2000) pointed out that the unscented transform (UT) could capture the state posterior mean and covariance accurately to the third order of Taylor expansion using a sigma point approach. They found that the UKF has better performance than EKF in a number of application domains, including state estimation, dual estimation, and parameter estimation. The performance of the UKF and EKF on solving the problem of optimal estimation of noise-corrupt input and output sequences has also been studied (Zhou et al. 2009). Gustafsson and Hendeby (2012) found that the EKF based on the second-order Taylor expansion was closely related to UKF. Yang et al. (2016) carried out a comparative study of UKF and EKF on integrated vehicle navigation with different integration strategies. The results also indicated that UKF outperforms the EKF in terms of estimation accuracy.

To improve the UKF efficiency, a deterministic sampling approach to capture the state parameters and their covariance matrices with a minimal set of sample points was proposed (Wan and van der Merwe 2000). In addition, Liu et al. (2014) studied high order moment matching filter, like a quadrature rule-based filter and cubature rule-based filter, to improve the UKF efficiency in dealing with the nonlinear state-space model. The UKF and its alternatives, however, do not have adaptation ability between the measurement and kinematic models.

Many researchers have discussed the adaptation methods for UKF. Han et al. (2009) described two distinctive adaptive methods. In the first method, a cost function is constructed to minimize the difference between theoretical covariance and actual covariance matrices of the innovation vector; the adaptive process noise covariance matrix is then estimated by the adaptive law, which is derived by the Massachusetts Institute of Technology (MIT) rule. The presented algorithm, however, requires calculation of partial derivatives. In the second method, two parallel UKFs run in master and slave manners, in which the master UKF estimates system states and the slave UKF estimates the noise covariance matrix for the master UKF in parallel. The computational demand of the algorithm increases obviously due to parallel computations. Hajiyev and Soken (2014) presented a window-based robust adaptive unscented Kalman filter (AUKF). The filter uses the innovation and residual sequences to construct an adaptive matrix and an adaptive factor to adjust the covariance matrices of measurement and process noise, respectively. Gao et al. (2015) also developed an AUKF with the weighted moving window approach using the historical innovation sequences and residual sequences. Li et al. (2016) proposed a robust adaptive UKF with the ability to tune both process and measurement noise covariance matrices. An adaptive algorithm that combines the maximum likelihood principle and moving horizon estimation to improve the performance of UKF regarding inaccurate system noise has been studied (Gao et al. 2018). The moving horizon estimation uses a fixed number of historical measurements to produce estimates of state parameters and smooth the previous estimates by iteration (Robertson et al. 1996). The adaptive estimation methods mentioned above improved the filter performance, because the measurements and the process noise covariance matrices are adjusted according to the real data. However, the heavy burden of theoretical covariance matrix calculation is still a problem and contaminated predicted information, which is caused by disturbances of dynamic model and uncertainties of noise information, has not been well considered.

We first present an alternative derivation and expression of UKF, by which any adjustment for the measurement and process noise covariance matrices is easy to be expressed and explained. The derivation is based on the correlational inference, which uses the predicted state covariance matrix, predicted measurement covariance matrix, and measurement noise covariance matrix to construct a constrained target function. By minimizing this target function, then UKF is derived. Furthermore, the robust and adaptive factors can be embedded in this derived UKF estimator directly and easily. Considering that the disturbances of the dynamic model could contaminate the predicted mean and predicted covariance matrices, the contribution of the predicted state information from UT thus should be controlled. In this case, the adaptive methodology proposed by Yang et al. (2001) can be integrated with derived UKF estimator to reduce the influences of dynamic model errors and to handle the nonlinear state-space model on the state estimation. The corresponding adaptive UKF estimator is deduced, and the adaptive factor is presented in a simple expression and an easy form for calculation.

In the following section, correlational inference and analysis are presented first. An adaptive algorithm based on correlational inference is introduced then. The numerical experiments are analyzed afterward. The last part concludes the findings of the study.

New expression of Unscented Kalman filter

A new derivation and expression of the UKF is presented in this section; the theoretical analysis of the derivation is performed. The derivation focuses on the general state-space model and aims to reveal the relationships among the measurements, predicted states, and predicted measurements, as well as their cross-covariance matrices.

Correlational inference

To derive the UKF without loss of generality, we start with nonlinear equation and estimate the state vector with Kalman filter. Considering the following discrete nonlinear system:

$${L_k}={h_k}\left( {{X_k}} \right)+{e_k}$$
(1)
$${X_k}={f_k}\left( {{X_{k - 1}}} \right)+{w_k},$$
(2)

where \({L_k}\) is the \(m \times 1\) measurement vector; \({e_k}\) is the corresponding error vector; \({X_k}\) and \({X_{k - 1}}\) are \(n \times 1\) state vector at epoch \({t_{k - 1}}\) and \({t_k}\), respectively; \({w_k}\) is the \(n \times 1\) noise vector of dynamic model; and \({h_k}\left( \cdot \right)\) and \({f_k}\left( \cdot \right)\) denote the nonlinear function of measurements and dynamic state. The error equation of measurement is

$${V_k}={h_k}\left( {{{\hat {X}}_k}} \right) - {L_k}={\hat {L}_k} - {L_k},$$
(3)

where \({\hat {L}_k}={h_k}\left( {{{\hat {X}}_k}} \right);\) \({\hat {X}_k}\) is the estimated state vector; and \({V_k}\) is the residual vector of \({L_k}\). The predicted state vector \({\bar {X}_k}\) can be obtained by (2):

$${\bar {X}_k}={f_k}\left( {{{\hat {X}}_{k - 1}}} \right).$$
(4)

The residual vector of \({\bar {X}_k}\) is denoted by \(~{V_{{{\bar {X}}_k}}}\):

$$~{V_{{{\bar {X}}_k}}}={\hat {X}_k} - {\bar {X}_k}.$$
(5)

The predicted measurement vector \({\bar {L}_k}\) is then given by

$${\bar {L}_k}={h_k}\left( {{{\bar {X}}_k}} \right),$$
(6)

with the corresponding covariance matrix \(\Sigma _{{{{\bar {L}}_k}}}^{{\text{*}}}\) at epoch \({t_k}\). If the measurement vector \({L_k}\) at epoch \({t_k}\) is available, the innovation vector \({\bar {V}_k}\) can be obtained at epoch \({t_k}~\):

$${\bar {V}_k}={L_k} - {h_k}\left( {{{\bar {X}}_k}} \right)={L_k} - {\bar {L}_k}.$$
(7)

Given that the two vectors \({L_k}\) and \({\bar {L}_k}\) are independent, the covariance matrix \({\Sigma _{{{\bar {V}}_k}}}\) can be calculated by

$${\Sigma _{{{\bar {V}}_k}}}={\Sigma _k}+\Sigma _{{{{\bar {L}}_k}}}^{{\text{*}}},$$
(8)

where \(\Sigma _{{{{\bar {L}}_k}}}^{{\text{*}}}\) is the covariance matrix of the predicted measurement vector. If the measurement model is nonlinear, the UT can be applied to acquire the covariance matrix \(\Sigma _{{{{\bar {L}}_k}}}^{{\text{*}}}\). If the measurement model is linear or linearized, then the covariance matrix of innovation vector can be obtained by variance–covariance propagation law, which is

$${\Sigma _{{{\bar {V}}_k}}}={\Sigma _k}+{A_k}{\Sigma _{{{\bar {X}}_k}}}A_{k}^{T},$$
(9)

where \({A_k}\) is the linearized form of the measurement function \({h_k}\left( \cdot \right)\), and \({\Sigma _{{{\bar {X}}_k}}}\) is the covariance matrix of the predicted state vector \({\bar {X}_k}\).

In theory, the following equation is valid:

$$E\left( {{{\hat {L}}_k} - {{\hat {\bar {L}}}_k}} \right)=0,$$
(10)

where \({\hat {L}_k}\) is the estimated measurement vector; \({\hat {\bar {L}}_k}\) denotes the estimated vector of the predicted measurement vector \({\bar {L}_k}\). The error equation of \({\hat {\bar {L}}_k}\) is

$${\hat {\bar {L}}_k}={\bar {L}_k}+{V_{{{\bar {L}}_k}}},$$
(11)

where \({V_{{{\bar {L}}_k}}}\) is the residual vector of \({\bar {L}_k}\). Substituting (3) and (11) into (10), we have

$${\hat {\bar {L}}_k}={\hat {L}_k}={h_k}\left( {{{\hat {X}}_k}} \right)={\bar {L}_k}+{V_{{{\bar {L}}_k}}}={L_k}+{V_k}.$$
(12)

Thus

$${V_k} - {V_{{{\bar {L}}_k}}}+\left( {{L_k} - {{\bar {L}}_k}} \right)=0.$$
(13)

Considering (7), Eq. (13) can be written as

$${V_{{{\bar {L}}_k}}} - {\bar {V}_k} - {V_k}=0.$$
(14)

Equations (10) or (14) can be regarded as constraint equations.

Considering that \({\bar {L}_k}\) contains the predicted state vector \({\bar {X}_k}\) from a nonlinear function as shown in (6), the vectors \({\bar {L}_k}\) and \({\bar {X}_k}\) are thus correlated with the cross-covariance matrix \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\). To estimate the state vector \({\hat {X}_k}\) from the measurement vector \({L_k}\), predicted state vector \({\bar {X}_k}\) and predicted measurement vector \({\bar {L}_k}\) with their covariance and cross-covariance matrices \({\Sigma _k}\), \({\Sigma _{{{\bar {X}}_k}}}\) and \(\Sigma _{{{{\bar {L}}_k}}}^{*}\), as well as \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\), the Lagrange objective function can be constructed, considering the constraints (10) and (14):

$$V_{k}^{T}\Sigma _{k}^{{ - 1}}{V_k}+\left[ {\begin{array}{*{20}{c}} {V_{{{{\bar {L}}_k}}}^{T}}&{V_{{{{\bar {X}}_k}}}^{T}} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} {\Sigma _{{{{\bar {L}}_k}}}^{*}}&{{\Sigma _{{{\bar {L}}_k}{{\bar {X}}_k}}}} \\ {{\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}}&{{\Sigma _{{{\bar {X}}_k}}}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{V_{{{\bar {L}}_k}}}} \\ {{V_{{{\bar {X}}_k}}}} \end{array}} \right] - 2{\lambda ^T}\left( {{V_{{{\bar {L}}_k}}} - {{\bar {V}}_k} - {V_k}} \right)={\text{min,}}$$
(15)

where \(\lambda\) is Lagrange multiplier vector. Taking the partial derivatives of (15) with respect to \({V_k}\), \({V_{{{\bar {L}}_k}}}\), \({V_{{{\bar {X}}_k}}}\), \(\lambda\), and setting them to 0, we can obtain

$${V_k}= - {\Sigma _k}\lambda ,$$
(16)
$$\left[ {\begin{array}{*{20}{c}} {{V_{{{\bar {L}}_k}}}} \\ {{V_{{{\bar {X}}_k}}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\Sigma _{{{{\bar {L}}_k}}}^{*}}&{{\Sigma _{{{\bar {L}}_k}{{\bar {X}}_k}}}} \\ {{\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}}&{{\Sigma _{{{\bar {X}}_k}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \lambda \\ 0 \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\Sigma _{{{{\bar {L}}_k}}}^{*}\lambda } \\ {{\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\lambda } \end{array}} \right].$$
(17)

From (17), we obtain the solution

$$\begin{gathered} {V_{{{\bar {L}}_k}}}=\Sigma _{{{{\bar {L}}_k}}}^{*}\lambda \hfill \\ {V_{{{\bar {X}}_k}}}={\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\lambda . \hfill \\ \end{gathered}$$
(18)

Based on (16) and (18), and considering (14), we can obtain

$${\Sigma _k}\lambda +\Sigma _{{{{\bar {L}}_k}}}^{*}\lambda - {\bar {V}_k}=0,$$
(19)
$$\lambda ={\left( {\Sigma _{{{{\bar {L}}_k}}}^{*}+{\Sigma _k}} \right)^{ - 1}}{\bar {V}_k}.$$
(20)

Substituting (20) into (18), the residual vectors of the predicted measurements and predicted state vector are obtained, respectively, as follows:

$${V_{{{\bar {L}}_k}}}=\Sigma _{{{{\bar {L}}_k}}}^{*}{\left( {\Sigma _{{{{\bar {L}}_k}}}^{*}+{\Sigma _k}} \right)^{ - 1}}{\bar {V}_k},$$
(21)
$${V_{{{\bar {X}}_k}}}={\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}{\left( {\Sigma _{{{{\bar {L}}_k}}}^{*}+{\Sigma _k}} \right)^{ - 1}}{\bar {V}_k}.$$
(22)

Because of (8)

$${V_{{{\bar {X}}_k}}}={\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\Sigma _{{{{\bar {V}}_k}}}^{{ - 1}}{\bar {V}_k},$$
(23)

and

$$\begin{aligned} {{\hat {X}}_k}= \,& {{\bar {X}}_k}+{V_{{{\bar {X}}_k}}} \\ = \,& {{\bar {X}}_k}+{\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}{\left( {\sum\nolimits_{{{L_k}}}^{*} + {\Sigma _k}} \right)^{ - 1}}\left( {{L_k} - {{\bar {L}}_k}} \right) \\ =\, & {{\bar {X}}_k}+{K_k}{{\bar {V}}_k}, \\ \end{aligned}$$
(24)

where \({K_k}\) is the Kalman gain matrix

$${K_k}={\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}{\left( {\Sigma _{{{{\bar {L}}_k}}}^{*}+{\Sigma _k}} \right)^{ - 1}}={\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\Sigma _{{{{\bar {K}}_k}}}^{{ - 1}}.$$
(25)

It should be stressed that in the above equations, the estimated state vector \({\hat {X}_k}\) and its Kalman gain matrix \({K_k}\) contain neither Jacobian matrices of the nonlinear measurement model nor dynamic model. Furthermore, since \({\bar {L}_k}\) and \({L_k}\) are stochastically independent, then

$${\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}={\Sigma _{{{\bar {X}}_k}{{\bar {V}}_k}}}.$$
(26)

Thus, from (23)

$${V_{{{\bar {X}}_k}}}={\Sigma _{{{\bar {X}}_k}{{\bar {V}}_k}}}\sum\nolimits_{{{{\bar {V}}_k}}}^{{ - 1}} {{{\bar {V}}_k},}$$
(27)
$${\hat {X}_k}={\bar {X}_k}+{\Sigma _{{{\bar {X}}_k}{{\bar {V}}_k}}}\sum\nolimits_{{{{\bar {V}}_k}}}^{{ - 1}} {{{\bar {V}}_k}} ={\bar {X}_k}+{K_k}{\bar {V}_k}.$$
(28)

The posterior covariance matrix of the estimated state vector reads

$${\Sigma _{{{\hat {X}}_k}}}={\Sigma _{{{\bar {X}}_k}}} - {K_k}{\Sigma _{{{\bar {V}}_k}}}K_{{k.}}^{T}$$
(29)

The above expression shows that the covariance matrix of the estimated state vector is smaller than that of the predicted state vector because of the second term of (29); the matrix product \({K_k}{\Sigma _{{{\bar {V}}_k}}}K_{k}^{T}\) is positive definite. In addition, the posterior covariance matrix of the state vector is not related to any linearization process, since \({K_k}\) is obtained from (25) which is not related to linearization.

Theoretical analysis

From the above derivations, the following interesting facts are obtained:

  1. (i)

    The derivation presented above illustrates a more generalized theoretical framework of Kalman filtering. In this framework, the estimated state vector relates to the innovation vector, predicted state vector and their covariance matrices as well as their cross-covariance matrix. Thus, the estimator expressed by the prior covariance and cross-covariance matrices makes the Kalman filtering more generalized and more flexible.

  2. (ii)

    In the new expression (28), the predicted state vector \({\bar {X}_k}\) with \({\Sigma _{{{\bar {X}}_k}}}\) can be obtained by approximation method, such as UT (Julier and Uhlmann 1997). Then, UKF can be easily expressed. In addition, the correlational inference has proven that the state estimate is not difficult to obtain by the approximation method, and furthermore, the estimate does not need any computation of Jacobian matrix for measurement equation or dynamic equation.

  3. (iii)

    The innovation vector \({\bar {V}_k}\) reflects the consistency between the predicted state and the measurement. The Kalman gain matrix \({K_k}\) is determined by \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\) and \(\Sigma _{{{{\bar {V}}_k}}}^{{ - 1}}\). Hence, the cross-covariance matrix between \({\bar {X}_k}\) and \({\bar {V}_k}\) as well as the weight matrix \(\Sigma _{{{{\bar {V}}_k}}}^{{ - 1}}\) of \({\bar {V}_k}\) are crucial in determining the gain matrix \({\text{~}}{K_k}\). The estimated state vector \({\hat {X}_k}\) can also be easily obtained when the cross-covariance matrices \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\) or \({\Sigma _{{{\bar {X}}_k}{{\bar {V}}_k}}}\) are determined. In UKF, the matrix \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\) is generated according to the sample dispersion of \({\bar {X}_k}\) and \({\bar {L}_k}\), with the predicted state vectors not related to the actual linearized models, and \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\) being usually much more accurate than that propagated from the linearized equations (Yang et al. 2016).

  4. (iv)

    Equation (27) expresses the relationship between the two correlated stochastic vectors \({V_{{{\bar {X}}_k}}}\) and \({\bar {V}_k}\). This relationship illustrates that the stochastic unknown vector \({V_{{{\bar {X}}_k}}}\), which does not appear in the system model, can be derived from the related estimated vector \({\bar {V}_k}\), using the cross-covariance matrix \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\). This relationship has also appeared in collocation (Moritz 1980; Koch 1977; Yang et al. 2009). If two correlated stochastic vectors \(s\) and \({s_1}\) with expectations \(E\left( s \right)=0\) and \(E\left( {{s_1}} \right)=0\) and with the covariance matrices \({\Sigma _s}\) and \({\Sigma _{{s_1}}}\) as well as cross-covariance matrix \({\Sigma _{s{s_1}}}=\Sigma _{{{s_1}s}}^{T}\) exist, the relationship between the two estimated vectors \(\hat {s}\) and \({\hat {s}_1}\) is

$$\hat {s}={\Sigma _{s{s_1}}}\Sigma _{{{s_1}}}^{{ - 1}}{\hat {s}_1}\quad {\text{or}}\quad \hat {s}={\Sigma _{{s_1}s}}\Sigma _{{{s_1}}}^{{ - 1}}\hat {s}.$$
(30)
  1. (v)

    If the state-space model is linear, the basic expression of the newly derived estimator from the correlational inference is equivalent to Kalman filter. Both the linear form of error Eq. (3) and the form of predicted state Eq. (4) are as follows:

$${V_k}={A_k}{\hat {X}_k} - {L_k},$$
(31)
$${\bar {X}_k}={\Phi _{k,k - 1}}{\hat {X}_{k - 1}},$$
(32)

with the covariance matrix \({\Sigma _{{{\bar {X}}_k}}}\)

$${\Sigma _{{{\bar {X}}_k}}}={\Phi _{k,k - 1}}{\Sigma _{{{\hat {X}}_{k - 1}}}}\Phi _{{k,k - 1}}^{T}+{\Sigma _{{W_k}}},$$
(33)

where \({\Phi _{k,k - 1}}\) is the transition matrix, \({\Sigma _{{{\hat {X}}_{k - 1}}}}\) is the estimated state covariance matrix, and \({\Sigma _{{W_k}}}\) is the process noise covariance matrix. Thus, the Kalman filter is obtained (Koch and Yang 1998):

$${\hat {X}_k}={\bar {X}_k}+{\Sigma _{{{\bar {X}}_k}}}A_{k}^{T}{\left( {{A_k}{\Sigma _{{{\bar {X}}_k}}}A_{k}^{T}+{\Sigma _k}} \right)^{ - 1}}\left( {{A_k}{{\bar {X}}_k} - {L_k}} \right).$$
(34)

The innovation vector, or the predicted residual vector, in the above linear form is expressed as

$${\bar {V}_k}={A_k}{\bar {X}_k} - {L_k},$$
(35)

and the corresponding predicted measurement vector is

$${\bar {L}_k}={A_k}{\bar {X}_k}.$$
(36)

The following equations can be easily obtained from (33) and (36):

$${\Sigma _{{{\bar {X}}_k}{{\bar {V}}_k}}}={\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}={\Sigma _{{{\bar {X}}_k}}}A_{k}^{T},$$
(37)
$${\Sigma _{{{\bar {V}}_k}}}=\sum\nolimits_{{{{\bar {L}}_k}}}^{*} +{{\Sigma _k}={A_k}{\Sigma _{{{\bar {X}}_k}}}A_{k}^{T}+{\Sigma _k}.}$$
(38)

The conventional Kalman gain matrix then reads

$${K_k}={\Sigma _{{{\bar {X}}_k}}}A_{k}^{T}{\left( {{A_k}{\Sigma _{{{\bar {X}}_k}}}A_{k}^{T}+{\Sigma _k}} \right)^{ - 1}}={\Sigma _{{{\bar {X}}_k}{{\bar {V}}_k}}}\Sigma _{{{{\bar {V}}_k}}}^{{ - 1}}.$$
(39)

The derivation suggests that the state estimator (24) derived by the correlational inference is equivalent to the standard Kalman filter estimator (34) in the case of the linear system model.

This correlational inference deduces the generalized expression of Kalman filtering by the relationship among the predicted measurement vector \({L_k}\) and the predicted state vector \({\bar {X}_k}\), as well as the cross-covariance matrix \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\). The deduction avoids the linear model requirement of Kalman filter. With the use of the new expression of Kalman filtering, different methods can be deduced in the same framework based on the revealed relationships between the measurement and the state vectors. If the state-space model is linear, the relationship of the measurement vector \(L\) and the state vector \(X\) can be easily obtained with variance propagation law; the Kalman filter estimator is then obtained. If the state-space model is nonlinear and the first-order Taylor expansion is used to approximate the nonlinear equation, the covariance matrix can also be obtained by variance–covariance propagation, we obtain the EKF estimator; if UT is employed to approximate the covariance matrix, we arrive at UKF. The Cubature Kalman filter (CKF) can also be established by generating the sigma points based on the spherical–radial cubature rule (Arasaratnam and Haykin 2009).

Adaptively unscented Kalman filtering based on correlational inference

After new expression of UKF is presented, we then develop an AUKF based on the correlational inference to reduce the influences of the dynamic model disturbances. An adaptive factor is introduced for AUKF to adjust the contribution of the dynamic model and the measurement model.

Unscented Kalman filter

UKF samples a set of sigma points to match the current statistics properties and then propagates the points through the nonlinear function. The predicted mean and covariance matrices of the state parameters and measurements are then estimated by the weighted transformed sigma points (Julier and Uhlmann 1997; Cui et al. 2005). The sigma points are chosen based on the estimated state covariance matrix with a deterministic method (LaViola 2003; Kandepu et al. 2008):

$${\left( {{{\tilde {X}}_{k - 1}}} \right)_0}={\hat {X}_{k - 1}}$$
(40a)
$${\left( {{{\tilde {X}}_{k - 1}}} \right)_{i+n}}={\hat {X}_{k - 1}}+\gamma \left( {{\Sigma _{{{\hat {X}}_{k - 1}}}}} \right)_{i}^{{\frac{1}{2}~}}\quad i=1,~2,~ \cdots ,~n$$
(40b)
$${\left( {{{\tilde {X}}_{k - 1}}} \right)_{i - {\text{n}}}}={\hat {X}_{k - 1}} - \gamma \left( {{\Sigma _{{{\hat {X}}_{k - 1}}}}} \right)_{i}^{{\frac{1}{2}~}},$$
(40c)

where \({\text{n}}\) is the dimension of the state vector, \(i\) denotes the \(i\)th column of covariance matrix, the square root of covariance matrix is normally obtained by Cholesky decomposition, and \(\gamma\) is a scale factor:

$$\gamma =\sqrt {n+\kappa } ,$$
(41)

where parameter \(\kappa\) is a secondary scale parameter which is usually greater than or equal to 0 (Kandepu et al. 2008). A good choice of this scale factor is \(\kappa =0\). The predicted state vector can be derived by the weighted transformed sigma points:

$${\left( {{{\tilde {X}}_k}} \right)_i}={f_k}\left[ {{{\left( {{{\tilde {X}}_k}} \right)}_i}} \right]$$
(42)
$${\bar {X}_k}=\mathop \sum \limits_{{i=0}}^{{2n}} {w_i}{\left( {{{\tilde {X}}_k}} \right)_i},$$
(43)

where \({w_i}\) is the weight of the sigma points (Liu et al. 2014; LaViola 2003):

$${w_0}=\frac{\kappa }{{N+\kappa }},$$
(44a)
$${w_i}=\frac{\kappa }{{2(N+\kappa )}}\quad i \ne 0,$$
(44b)

where \(N\) is the number of the sigma points, \(N=2n+1\).

The corresponding covariance matrix of the predicted state vector is followed by

$${\Sigma _{{{\bar {X}}_k}}}={\Sigma _{{w_k}}}+\mathop \sum \limits_{{i=0}}^{{2n}} {w_i}\left[ {{{\left( {{{\tilde {X}}_k}} \right)}_i} - {{\bar {X}}_k}} \right]{\left[ {{{\left( {{{\tilde {X}}_k}} \right)}_i} - {{\bar {X}}_k}} \right]^T}.$$
(45)

The predicted measurement vectors corresponding to the predicted state vector \({\bar {X}_k}\) are

$${\left( {{{\tilde {L}}_k}} \right)_i}={h_k}\left[ {{{\left( {{{\tilde {X}}_k}} \right)}_i}} \right], \quad i =1,2,\ldots, 2n+1.$$
(46)

The weighted averaged predicted measurement vector is

$${\bar {L}_k}=\mathop \sum \limits_{{i=0}}^{{2n}} {w_i}{\left( {{{\tilde {L}}_k}} \right)_i},$$
(47)

with the corresponding covariance matrix:

$${\Sigma _{{{\bar {V}}_k}}}={\Sigma _k}+\mathop \sum \limits_{{i=0}}^{{2m}} {w_i}\left[ {{{\left( {{{\tilde {L}}_k}} \right)}_i} - {{\bar {L}}_k}} \right]{\left[ {{{\left( {{{\tilde {L}}_k}} \right)}_i} - {{\bar {L}}_k}} \right]^T}.$$
(48)

The cross-covariance matrix \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\) between the predicted state vector \({\bar {X}_k}\) and predicted measurement vector \({\bar {L}_k}\), which is expressed in (26), is required. The approximation equation is similar to formulae (45) and (48):

$${\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}=\mathop \sum \limits_{{i=0}}^{{2m}} {w_i}\left[ {{{\left( {{{\tilde {X}}_k}} \right)}_i} - {{\bar {X}}_k}} \right]{\left[ {{{\left( {{{\tilde {L}}_k}} \right)}_i} - {{\bar {L}}_k}} \right]^T}.$$
(49)

Substituting the predicted state vector \({\bar {X}_k}\) and the predicted measurement vector \({\bar {L}_k}\) with their covariance matrices \({\Sigma _{{{\bar {X}}_k}}}\) and \({\Sigma _{{{\bar {L}}_k}}}\) as well as their cross-covariance matrix \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\) into the estimator, Eq. (24), we obtain the UKF estimated state vector \({\hat {X}_k}\). The estimated covariance matrix can be obtained by (29).

Adaptive unscented Kalman filter

The UKF described above depends on the approximation method for the nonlinear system model. The method, however, is very difficult to accurately predict the distribution or the dynamic errors. In addition, the inaccurate estimation of the last epoch will affect the selection of sigma points at the present epoch. Thus, the state prediction \({\bar {X}_k}\) is influenced, in the same way as the predicted measurement vector \({\bar {L}_k}\) from (5). To control the influences of the dynamic model disturbances, an adaptive factor \({\alpha _k}\) \(\left( {0<{\alpha _k}<1} \right)\) is introduced. The AUKF estimator can be constructed based on the correlational inference. The predicted state vector is assumed to be contaminated by some kinematic disturbing phenomenon; the contribution of \({\bar {X}_k}\), therefore, should be weakened. Thus, Eq. (15) can be rewritten with an adaptive factor \({\alpha _k}\):

$$V_{k}^{T}\Sigma _{k}^{{ - 1}}{V_k}+\left[ {\begin{array}{*{20}{c}} {V_{{{{\bar {L}}_k}}}^{T}}&{V_{{{{\bar {X}}_k}}}^{T}} \end{array}} \right] \cdot {\alpha _k} \cdot {\left[ {\begin{array}{*{20}{c}} {{\Sigma _{{{\bar {L}}_k}}}}&{{\Sigma _{{{\bar {L}}_k}{{\bar {X}}_k}}}} \\ {{\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}}&{{\Sigma _{{{\bar {X}}_k}}}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{V_{{{\bar {L}}_k}}}} \\ {{V_{{{\bar {X}}_k}}}} \end{array}} \right] - 2{\lambda ^T}\left( {{V_{{{\bar {L}}_k}}} - {{\bar {V}}_k} - {V_k}} \right)=\hbox{min} ,$$
(50)

and (18) is updated as

$$\begin{gathered} {V_{{{\bar {L}}_k}}}=\frac{1}{{{\alpha _k}}}{\Sigma _{{{\bar {L}}_k}}}\lambda \hfill \\ {V_{{{\bar {X}}_k}}}=\frac{1}{{{\alpha _k}}}{\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\lambda . \hfill \\ \end{gathered}$$
(51)

The AUKF estimator is

$$\begin{aligned} {{\hat {X}}_{AK}}=\, & {{\bar {X}}_k}+\frac{1}{{{\alpha _k}}}{\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}{\left( {\frac{1}{{{\alpha _k}}}\Sigma _{{{{\bar {L}}_k}}}^{*}+{\Sigma _k}} \right)^{ - 1}}\left( {{L_k} - {{\bar {L}}_k}} \right) \\ =\, & {{\bar {X}}_k}{\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}{\left( {\Sigma _{{{{\bar {L}}_k}}}^{*}+{\alpha _k}{\Sigma _k}} \right)^{ - 1}}\left( {{L_k} - {{\bar {L}}_k}} \right). \\ \end{aligned}$$
(52)

This equation can also be expressed as

$${\hat {X}_k}={\bar {X}_k}+{\tilde {K}_k}\left( {{L_k} - {{\bar {L}}_k}} \right),$$
(53)

where \({\tilde {K}_k}\) is the adaptive Kalman gain matrix, which is expressed as

$${\tilde {K}_k}={\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\tilde {\Sigma }_{{{{\bar {V}}_k}}}^{{ - 1}},$$
(54)

and

$${\tilde {\Sigma }_{{{\bar {V}}_k}}}=\mathop \sum \limits_{{i=0}}^{{2n}} {w_i}\left[ {{{\left( {{{\tilde {L}}_k}} \right)}_i} - {{\bar {L}}_k}} \right]{\left[ {{{\left( {{{\tilde {L}}_k}} \right)}_i} - {{\bar {L}}_k}} \right]^T}+{\alpha _k}{\Sigma _k},$$
(55)

where \({\tilde {\Sigma }_{{{\bar {V}}_k}}}\) is the covariance matrix of innovation vector based on the adaptive estimation.

The larger the errors of \({\bar {X}_k}\) generated from the sigma points, the larger the covariance matrices, \({\Sigma _{{{\bar {X}}_k}{{\bar {L}}_k}}}\) and \({\Sigma _{{{\bar {V}}_k}}}\). Thus, the adaptive factor \({\alpha _k}\) plays a role in weakening the contribution of disturbed or contaminated predicted state vector \({\bar {X}_k}\), or strengthen the contribution of the measurement vector \({L_k}\).

The adaptive factor can be constructed as (Yang and Gao 2006)

$${\alpha _k}=\left\{ {\begin{array}{*{20}{l}} 1&{tr\left( {{{\hat {\Sigma }}_{{{\bar {X}}_k}}}} \right)<tr\left( {{\Sigma _{{{\bar {X}}_k}}}} \right)} \\ {\frac{{\mathop \sum \nolimits_{{i=1}}^{n} \sigma _{{{{\bar {X}}_{{k_i}}}}}^{2}}}{{\mathop \sum \nolimits_{{i=1}}^{n} \Delta \bar {X}_{{{k_i}}}^{2}}}}&{{\text{otherwise}}} \end{array},} \right.$$
(56)

where \(\Delta {\bar {X}_k}\) is the discrepancy between the predicted state and the robust estimated state, and

$$\Delta {\bar {X}_k}={\tilde {X}_k} - {\bar {X}_k},$$
(57)
$$tr\left( {{{\hat {\Sigma }}_{{{\bar {X}}_k}}}} \right) \approx tr\left( {\Delta {{\bar {X}}_k}\Delta \bar {X}_{k}^{T}} \right)=\Delta \bar {X}_{k}^{T}\Delta {\bar {X}_k}=\mathop \sum \limits_{{i=1}}^{n} \Delta \bar {X}_{{{k_i}}}^{2},$$
(58)

where \({\tilde {X}_k}\) is the robust estimate from the measurement information at the present epoch. The robust estimate can be derived with the linearized measurement model by robust least squares method (Yang et al. 2002):

$${V_k}={A_k}{\hat {X}_k} - {L_k},$$
(59)

The robust estimated state from the measurements is then

$${\tilde {X}_k}={\left( {A_{k}^{T}{{\bar {P}}_k}{A_k}} \right)^{ - 1}}A_{k}^{T}{\bar {P}_k}{L_k},$$
(60)

where \({\bar {P}_k}\) denotes the measurement equivalent weight matrix, which is determined by the robust estimation principle.

The robust state is estimated by the linearized measurement model, and the linearization process increases the calculation burden. Thus, another adaptive factor is given by Yang and Gao (2006):

$${\alpha _k}=\left\{ {\begin{array}{*{20}{l}} 1&{tr\left( {{{\hat {\Sigma }}_{{{\bar {V}}_k}}}} \right)<tr\left( {{\Sigma _{{{\bar {V}}_k}}}} \right)} \\ {\frac{{\mathop \sum \nolimits_{{i=1}}^{{{n_k}}} \sigma _{{{{\bar {V}}_{{k_i}}}}}^{2}}}{{\mathop \sum \nolimits_{{i=1}}^{{{n_k}}} \bar {V}_{{{k_i}}}^{2}}}}&{{\text{otherwise}}} \end{array}} \right.,$$
(61)

where \({n_k}\) represents the number of the measurements and \(\sigma _{{{{\bar {V}}_{{k_i}}}}}^{2}\) can be calculated as

$$\sigma _{{{{\bar {V}}_{{k_i}}}}}^{2}=\sigma _{{\bar {L}_{{{k_i}}}^{*}}}^{2}+\sigma _{{{k_i}}}^{2},$$
(62)

where \(\sigma _{{{{\bar {V}}_{{k_i}}}}}^{2}\), \(\sigma _{{\bar {L}_{{{k_i}}}^{*}}}^{2}\), and \(\sigma _{{{k_i}}}^{2}\) are the \(i\)th diagonal element of \({\Sigma _{{{\bar {V}}_k}}},\) \({\Sigma _{{{\bar {L}}_k}}}\), and \({\Sigma _k}\), respectively. \({\Sigma _{{{\bar {V}}_k}}}\) is the covariance matrix of the innovation vector. This covariance matrix can be obtained based on (38) by means of the linearized measurement model or by UT for nonlinear equations. The above two approaches to calculate the adaptive factor, Eqs. (56) and (61), lead to the same result, since the vector solution is a linear equation. The matrix \({\hat {\Sigma }_{{{\bar {V}}_k}}}\) is the estimated covariance matrix of the innovation vector \({\bar {V}_k}\), which can be obtained using Sage window method:

$${\hat {\Sigma }_{{{\bar {V}}_k}}}=\frac{1}{{m - 1}}\mathop \sum \limits_{{i=1}}^{m} {\bar {V}_{k - i}}\bar {V}_{{k - i}}^{T},$$
(63)

where m is the length of the window. Then, the IAE-based AUKF has been established. The Sage window method, however, evaluates the current system noise characteristic within a time window. Thus, the adaptive mechanism response is delayed. In addition, the historical information is equally contributed by the window method to evaluate the current noise characteristic. The outliers in the historical information are thus averaged over all the epochs within the window. Therefore, in this manuscript, the adaptive factor is constructed based on the predicted residuals at the present epoch:

$${\hat {\Sigma }_{{{\bar {V}}_k}}}={\bar {V}_k}\bar {V}_{k}^{T}.$$
(64)

Thus, the historical data storage and the influences of the historical outliers are avoided.

When the discrepancy between the predicted measurement vector and the measurement vector is large, the value of the adaptive factor \({\alpha _k}\) is less than 1. Therefore, the contribution of the predicted information to the estimation results from the UT is weakened.

Discussion

The very core of the window-based adaptive estimation is the matching of the estimated covariance matrices with the theoretical covariance matrix, which is derived by windowing approximation. The two popular windowing approximation methods for adaptive estimation are IAE and RAE. The former uses the innovation vector sequences to approximate the theoretical covariance matrix \({\hat {\Sigma }_{{{\bar {V}}_k}}}\), while the latter approximates the theoretical covariance matrix of measurement by residual vector sequences \({V_k}\). In these two methods, i.e., IAE and RAE, the innovation or residual vectors must be known for several epochs, the storage burden has thus been increased. Furthermore, the windowing method requires that number of measurements at each epoch must be identical and be of the same distribution, which is difficult to achieve in a highly dynamic environment. In contrast, the theoretical covariance matrix, approximated by the innovation vector at the present epoch, can be obtained directly. We derived the adaptive estimator analytically based on the new proposed target function, which is constructed based on the relationships among the covariance matrices of the innovation vector and predicted state vector. Hence, the proposed adaptive estimator does not need any functional model linearization. Compared to the window-based adaptive method, the proposed method is designed to weaken the prior information based on the system discrepancy, while the window-based adaptive schemes balance the noise information of dynamic or measurement models. The proposed method avoids the need to store the historical information and is more sensitive to the discrepancy of the filter at the present epoch.

Mathematical models of the integrated system

The classical linear Strapdown Inertial Navigation System (SINS) error propagation model is derived with the assumption of small misalignment angles, i.e., less than 5° (Kong et al. 1999). However, the environmental disturbances and sensor errors may break this assumption and degrade the filter estimation accuracy (Cao and Guo 2012). Therefore, a nonlinear error model is employed to perform the analysis and thus avoids the small angle assumption and improves the filter stability (Kong et al. 1999; Sun et al. 2015). The model derivation can be found in Yan et al. (2008). The nonlinear IMU dynamic model is

$$\begin{array}{*{20}{c}} {\dot {\varphi }}&=&{C_{\omega }^{{ - 1}}\left[ {\left( {I - C_{l}^{p}} \right)\delta \omega _{{il}}^{l} - C_{b}^{p}\delta \omega _{{ib}}^{b}} \right]} \end{array},$$
(65a)
$$\begin{aligned} \delta {{\dot {v}}^l}= & \left[ {I - {{\left( {C_{l}^{p}} \right)}^T}} \right]C_{b}^{p}{f^b}+{\left( {C_{l}^{p}} \right)^T}C_{b}^{p}\delta {f^b} - \left( {2\delta \omega _{{ie}}^{l}+\delta \omega _{{el}}^{l}} \right) \times {{\tilde {v}}^l} \\ & - \left( {2\tilde {\omega }_{{ie}}^{l}+\tilde {\omega }_{{el}}^{l}} \right) \times \delta {v^l}+\left( {2\delta \omega _{{ie}}^{l}+\delta \omega _{{el}}^{l}} \right) \times \delta {v^l}+\delta {g^l}, \\ \end{aligned}$$
(65b)
$$\delta {\dot {p}^l}=\left[ {\begin{array}{*{20}{c}} 0&{\frac{1}{{M+h}}}&0 \\ {\frac{{\cos \phi }}{{N+h}}}&0&0 \\ 0&0&1 \end{array}} \right]\delta {v^l},$$
(65c)
$${\dot {d}_i}=0,$$
(65d)
$${\dot {b}_i}=0,$$
(65e)

where \(C_{\omega }^{{ - 1}}\) in (65a) is

$$C_{\omega }^{{ - 1}}=\frac{1}{{\cos {\varphi _x}}}\left[ {\begin{array}{*{20}{l}} {\cos {\varphi _y}\cos {\varphi _x}}&0&{\sin {\varphi _y}\cos {\varphi _x}} \\ {\sin {\varphi _y}\sin {\varphi _x}}&{\cos {\varphi _x}}&{ - \cos {\varphi _y}\sin {\varphi _x}} \\ { - \sin {\varphi _x}}&0&{\cos {\varphi _y}} \end{array}} \right].$$
(66)

The rotation matrix \(C_{l}^{p}\) relates the local level frame \(l\) and the platform frame \(p\), \(\delta \omega _{{il}}^{l}\) is the angular velocity error of local level frame with respect to the inertial frame, and \(\delta \omega _{{ib}}^{b}\) is the bias of the gyroscope. \(\tilde {\omega }_{{ie}}^{l}\) is the earth rotation velocity at local level frame, and \(\tilde {\omega }_{{ie}}^{l}\) is the rotation velocity of local level frame with respect to the earth fixed frame at local level frame. \({f^b}\) is the measurement of the accelerometer, and \(\delta {f^b}\) is the bias of the accelerometer. \({\tilde {v}^l}={\left[ {\begin{array}{*{20}{c}} {{V_E}}&{{V_N}}&{{V_U}} \end{array}} \right]^T}\) are the velocity components in east, north and up directions, and \(\delta {p^l}={\left[ {\delta \begin{array}{*{20}{c}} L&{\delta \lambda }&{\delta h} \end{array}} \right]^T}\) are the position error components in latitude, longitude, and height. Thus, the state vector can be expressed as \(X={\left[ {{\varphi _{1 \times 3}}~\delta {v_{1 \times 3}}~\delta {p_{1 \times 3}}~{d_{1 \times 3}}~{b_{1 \times 3}}~} \right]^T}\). The Jacobian matrix of this model has seldom been derived or accurately calculated, and by contrast, the UKF has advantages in estimating the state with this nonlinear model (Yan et al. 2008).

The velocity and position output from GPS receivers are taken as measurements. Therefore, the design matrix for the measurement equation is

$$A=\left[ {\begin{array}{*{20}{c}} {{0_{3 \times 3}}}&{{I_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}} \\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{I_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}} \end{array}} \right],$$
(67)

where \({0_{3 \times 3}}\) denotes the 3 by 3 null matrix; and \({I_{3 \times 3}}\) is the 3 by 3 identity matrix. Thus, the design matrix \(A\) is of size \(15 \times 6\) matrix. The IMU error model expressed by (65) is derived from the time derivative of the rotation matrix \(C_{b}^{l}\), which relates to the rotation from body frame \(\left( b \right)\) to local level frame \(\left( l \right)\). From the attitude error Eq. (65a), the small angle assumption does not exist. The simulation and field test are presented in the next section.

Numerical experiment and analysis

In this section, a simulation and a field test of integrated navigation are discussed to evaluate the performance of AUKF in comparison with that of UKF. In addition, the IAE-based AUKF is also used in the field test and compared with the proposed AUKF in terms of computation time, positioning and velocity estimation accuracy. The loosely coupled configuration is employed to integrate the IMU and GPS. Both the simulation and field test are carried out without initial alignment. The tests are processed in the Matlab R2010a 64-bit program on a PC with Intel Core i7-4600U CPU at 2.10-GHz, 8-GB RAM equipped with Windows 10.

Simulation and analysis

The simulation was based on the moving vehicle with different driving behaviors. The constant gyro drift was set to 100°/h; the angular random walk was 5°/√h; the accelerometer bias was 2000 mg; the velocity random walk was 1000 mg/√Hz. The initial local geographic latitude was 22.31°, longitude was 114.18°, and height was 41 m. The measurement accuracy was 1 m for horizontal positioning and 3 m for the height; the velocity accuracy was 0.2 m/s. Thus, the noise of measurement was \(e={[1\;1\;3\;0.2\;0.2\;0.2]^T}.\) The simulation was processed without initial alignment. The initial misalignment angle was randomly set as \({[ - 20^\circ 37^\circ 80^\circ ]^T}\). Simulation duration was 3000 s.

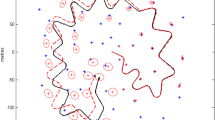
To compare the performance of the AUKF and UKF, the estimated results are compared with the simulated real value. The simulated trajectory is presented in Fig. 1 (blue line), including two circular curves to simulate the traffic circle in real situation, which are marked in red circles in area 1 and area 2. The simulation results of the positioning error are illustrated in Fig. 2. The red dotted line indicates AUKF estimation error, and the blue line represents UKF estimation error. From this figure, it can be observed that the AUKF estimated results have fewer peak values than those estimated by UKF. By comparing the epochs of the error spikes with the simulated trajectory, these epochs coincide with the positions exactly in the marked areas in Fig. 1. From Fig. 2, it also found that the UKF height estimate has a bias, caused by both measurement noise and disturbed predicted information; while AUKF reduces the weight of the predicted information by an adaptive factor, driving the estimate to rely on the measurements. The Root Mean Squares Error (RMSE) of the state estimate by UKF in latitude, longitude, and height components are 1.94, 2.45, and 26.14 m, while the RMSE of those of AUKF are 1.04, 0.98, and 1.61 m. In addition, the maximum state error estimated by UKF in the east, north, and height components are 12.87, 19.12, and 75.94 m, respectively, while those estimated by AUKF are 3.70, 5.01, and 7.93 m.

Fig. 1
figure 1

Simulated trajectory (top), area 1 (middle), and area 2 (bottom). The longitude and latitude values of the plotted trajectory are relative to 114° and 22°, respectively

Full size image
Fig. 2
figure 2

Position error in latitude (top), longitude (middle), and height (bottom)

Full size image

The velocity errors from the two filters are illustrated in Fig. 3. The errors reveal a similar phenomenon to that of the positioning errors. The oscillations of state estimates by AUKF are fewer than those by UKF, and the velocity estimates by UKF in the height direction are divergent. The reason is that the predicted information obtained by the dynamic model is disturbed by IMU error; the inaccurate predicted information creates biased UKF estimates. The AUKF, however, uses an adaptive factor to weaken the contribution of inaccurate predicted information and in turn reduce the bias.

Fig. 3
figure 3

Velocity error in east (top), north (middle), and up (bottom)

Full size image

The RMSE of the state estimates from UKF and AUKF are illustrated in Table 1, which also prove that the performance of AUKF is superior to UKF in terms of positioning and velocity estimate.

Table 1 RMSE of filter solutions
Full size table

Experiments and analysis

This subsection presents experimental results to demonstrate the performance of the proposed AUKF applied to IMU/GPS integrated vehicle navigation. In addition, the IAE-based AUKF and conventional UKF are also presented to compare the performance with the proposed AUKF. The window length of the IAE method was set to 10 epochs. The experiment lasted approximately one and a half hours. The IMU and GPS sampling frequencies were 100 and 10 Hz, respectively. The bias variances of gyro and accelerometer were 1°/h and 500 µg, respectively. The initial position error was set to [7 m, 7 m, 7 m], initial velocity error [0.1 m/s, 0.1 m/s, 0.1 m/s] and initial attitude error was [16ʹ, 16ʹ, 83ʹ]. The estimated results are compared with GPS measured position and velocity, which are solved by IGGIII robust estimation (Yang 1994).

The vehicle trajectory acquired by GPS positioning is presented in Fig. 4. The number of satellites used for positioning and the corresponding Geometric Dilution of Precision (GDOP) values are presented in Figs. 5 and 6. The position errors are shown in Fig. 7, in which the estimated positions of the AUKFs are much closer to GPS measured position than those estimated by UKF. The IAE-based AUKF has similar performance with that of the proposed AUKF. Compared with those of UKF results, the AUKFs constrained the errors at the east component during the process period. The peak value of UKF estimate error at the east component is 2.66 m during the time period (283980s, 284070s), and the peak value of those estimated by the proposed AUKF at the same period is 1.53 and 2.05 m for the IAE-based AUKF estimate. In the north component, the largest spikes of the three estimators occur during the same time period (283980s, 284080s) as the east component, at which the visible satellite number is 5 and the GDOP value is larger than 4, and even up to 17. In such a situation, the GPS-positioning results are not accurate. Thus, the three estimated results are fluctuating in this period. The UKF height error fluctuates between − 40 and 58 m during the process time, while the AUKFs error moves between − 15 and 25 m. The estimation error at the height component is significantly improved by AUKFs. The remaining oscillations around epoch 283300s to 283600s and 283900s to 284200s are caused by GPS measured fluctuations. According to the RMSE of the positioning results presented in Table 2, it can be proven that the overall performance of the proposed AUKF and IAE-based AUKF have similar superior performance than UKF.

Fig. 4
figure 4

Vehicle trajectory. The longitude and latitude values of the plotted trajectory are relative to 114° and 22°, respectively

Full size image
Fig. 5
figure 5

Visible satellites number, the second of week (SOW) is used to represent the GPS time epoch on X axis

Full size image
Fig. 6
figure 6

GDOP Values

Full size image
Fig. 7
figure 7

Positioning error in latitude (top), longitude (middle), and height (bottom)

Full size image
Table 2 RMSE of two filter solutions
Full size table

The velocity errors are shown in Fig. 8. It is seen that the state estimate by UKF is influenced by the disturbances of dynamic model and the AUKFs confine the error effects to the velocity. It is also noticed that the proposed AUKF converges much faster compared with that of UKF or the IAE-based AUKF. Since UKF operates under the Kalman framework and employs the UT to deal with the nonlinear equation, the disturbances of the dynamic model have not been restricted by any strategies. In contrast, the IAE-based AUKF uses the windowing method to estimate the noise stochastic characteristic, which adjusts the contribution of the state parameters produced from the UT. Thus, the performance of IAE-based AUKF is nearly the same as that of UKF at the beginning epochs. The proposed AUKF dynamically adjusts the measurement statistic during the filtering process; thus, the contribution of inaccurate prior information has been reduced at each epoch and the effects of disturbances of the dynamic model are also controlled, which results in much higher accurate state estimates than the standard UKF and shorter converge time than the IAE-based AUKF. The RMSE of velocity estimates are also presented in Table 2, which also proves that the overall performance of AUKFs is superior to that of UKF.

Fig. 8
figure 8

Velocity error in east (top), north (middle), and up (bottom)

Full size image

The run times of three filters, standard UKF, the proposed AUKF, and IAE-based AUKF, are listed in Table 3. The IAE-based AUKF obtains the theoretical covariance matrix using window method to average the storage innovation sequences. Thus, the data process requires the longest process time. The proposed AUKF, which uses the innovation vector at the present epoch to approximate the theoretical covariance matrix, needs slightly longer process time than the standard UKF.

Table 3 Running time of filters in seconds
Full size table

Conclusions

We presented the new derivation and expression of the Unscented Kalman filter (UKF) based on correlational inference, which has been further used to construct an adaptive Unscented Kalman filter (AUKF). The simulation and field test with a loosely coupled configuration and nonlinear dynamic model have been used to validate the proposed AUKF. Therefore, from our theoretical derivation, analysis and numerical tests, the following conclusions can be drawn:

  1. 1.

    The new Kalman filtering estimator reveals the fundamental relationship among the estimated state vector, the innovation vector, and the predicted state vector, as well as their covariance and cross-covariance matrices. Therefore, this new expression is a generalized estimator which can be easily simplified to the standard Kalman filter, EKF, and UKF.

  2. 2.

    The new generalized Kalman filtering expression is based on the constrained target function. This target function is not related to any approximation methods of the linear or nonlinear models by which the UKF estimator can be rigorously derived.

  3. 3.

    The adaptive UKF estimator is directly deduced from the constrained target function by introducing an adaptive factor for balancing the contribution between the predicted information and the measurements. This kind of estimator not only approximates the state parameters and their covariance matrices by UT, but also controls the influences of the contaminated predicted information on the estimated state.

  4. 4.

    The simulation and field test have proven that AUKF outperformed the UKF in terms of positioning and velocity accuracy. In the simulation, the UKF RMSE in latitude, longitude and height components estimate are 1.94, 2.45, and 26.14 m, respectively, while the RMSE of those of AUKF are 1.04, 0.98 and 1.61 m. In the field test, the RMSE of UKF in positioning estimation are 0.55, 1.30 and 13.73 m, while the RMSE of those of AUKF are 0.24, 0.69 and 3.23 m.

  5. 5.

    The field test has also revealed that the two kinds of AUKF have similar performance in terms of RMSE of positioning and velocity components. However, the adaptive factor-based AUKF has less converge time than the IAE-based AUKF, especially in velocity estimate. In addition, the process time of the three filters, UKF, adaptive factor-based AUKF, and IAE-based AUKF, are, respectively, 652.08, 654.53, and 660.78 s. Thus, the IAE-based AUKF requires the longest process time among the three filters.