Abstract
New spherical integral formulas between components of the second- and third-order gravitational tensors are formulated in this article. First, we review the nomenclature and basic properties of the second- and third-order gravitational tensors. Initial points of mathematical derivations, i.e., the second- and third-order differential operators defined in the spherical local North-oriented reference frame and the analytical solutions of the gradiometric boundary-value problem, are also summarized. Secondly, we apply the third-order differential operators to the analytical solutions of the gradiometric boundary-value problem which gives 30 new integral formulas transforming (1) vertical-vertical, (2) vertical-horizontal and (3) horizontal-horizontal second-order gravitational tensor components onto their third-order counterparts. Using spherical polar coordinates related sub-integral kernels can efficiently be decomposed into azimuthal and isotropic parts. Both spectral and closed forms of the isotropic kernels are provided and their limits are investigated. Thirdly, numerical experiments are performed to test the consistency of the new integral transforms and to investigate properties of the sub-integral kernels. The new mathematical apparatus is valid for any harmonic potential field and may be exploited, e.g., when gravitational/magnetic second- and third-order tensor components become available in the future. The new integral formulas also extend the well-known Meissl diagram and enrich the theoretical apparatus of geodesy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Integral transforms represent a fundamental mathematical apparatus which is important in many branches of science. In geodesy, many integral transforms have been formulated to relate scalar-, vector- and tensor-valued gravitational measurements available from sensors on ground (including sea), and at aerial and satellite altitudes. This mathematical tool provides a basis for modelling the gravitational field which in turn is indispensable for understanding the complex Earth’s system.
Surface integral solutions to boundary value-problems of the potential theory form a fundamental class of integral transforms. These allow for determination of the (disturbing) gravitational potential from known boundary values such as the (disturbing) gravitational potential itself (Kellogg 1929), gravity anomalies (e.g., Stokes 1849; Pizzetti 1911; Molodensky et al. 1962; Moritz 1989), gravity disturbances (e.g., Hotine 1969; Koch 1971; Grafarend et al. 1985), deflections of the vertical (e.g., Grafarend 2001; van Gelderen and Rummel 2001; Jekeli 2007) and gravitational tensor components of the second- (e.g., van Gelderen and Rummel 2001; Martinec 2003; Tóth 2003; Bölling and Grafarend 2005; Li 2005; Eshagh 2011a) and third-order (Šprlák and Novák 2016).
An additional class of integral transforms can be obtained by applying respective differential operators to analytical solutions of the boundary-value problems. This effort has led to integrals mapping either the (disturbing) gravitational potential, gravity anomalies or gravity disturbances onto deflections of the vertical (e.g., Vening-Meinesz 1928; Luying and Houze 2006; Jekeli 2007), gravity anomalies (e.g., Lelgemann 1976; Rummel et al. 1978), gravity disturbances (e.g., Zhang 1993), gravity disturbance vector (e.g., Heiskanen and Moritz 1967; Sünkel 1981), line-of-sight gravity disturbances, i.e., generalized gravitational gradients (Garcia 2002; Ardalan and Grafarend 2004; Novák et al. 2006; Novák 2007), gravitational second-order (e.g., Reed 1973; Heck 1979; Thalhammer 1995; Petrovskaya and Zielinski 1997; van Gelderen and Rummel 2001; Denker 2003; Tóth 2003; Kern and Haagmans 2005; Wolf and Denker 2005; Wolf 2007; Šprlák et al. 2015) and third-order (Šprlák and Novák 2015) tensor components.
More complex transforms of the deflections of the vertical onto the line-of-sight gravity disturbances and second-order gravitational tensor components were derived by Šprlák and Novák (2014b). Second-order tensor components were also transformed to gravity anomalies (e.g., Li 2005), gravity disturbances (e.g., Li 2002), deflections of the vertical (e.g., Li 2005), line-of-sight gravity disturbances (Šprlák and Novák 2014a) and second-order components themselves (e.g., Bölling and Grafarend 2005; Tóth 2005; Tóth et al. 2006; Šprlák et al. 2014). Gravity anomalies can also be extracted from satellite orbital elements (Eshagh and Ghorbannia 2013). Satellite-to-satellite velocity differences can be transformed to the disturbing gravitational potential, gravity anomalies and gravity disturbances (Eshagh and Šprlák 2016).
In this study, we establish relations between the gravitational tensors of the second- and third-orders. The second-order gravitational tensor components are observed by gradiometry which is now a well-established technique covering various spatial scales and stimulating new applications in geosciences. The technique was founded by Baron Roland von Eötvös (1896) whose exceptional theoretical and practical efforts provided many terrestrial measurements using torsion balance. Recent technological progress has led to development of more sophisticated terrestrial gradiometers based on atom interferometry, see McGuirk et al. (2002), Fixler (2003) and Sorrentino et al. (2014). Prospects of gradiometry in regional studies have also been tested and analysed on moving platforms, such as airplanes (Jekeli 1988, 1993; Dransfield 2007; Douch et al. 2015) and submarines (Bell et al. 1997). The static part of the global gravitational field was significantly improved with gradiometric observations provided by the GOCE (Gravity field and steady-state Ocean Circulation Explorer, ESA 1999; Rummel 2010) mission.
Also development of sensors for observing the third-order gravitational tensor components have recently been reported. In fact, the first terrestrial measurement of the vertical third-order tensor component have already been performed by Rosi et al. (2015). Other terrestrial sensors for observing the third-order derivatives of the gravitational potential were proposed by Balakin et al. (1997) and patented by, e.g., Meyer (2013), Rothleitner (2013), Klopping et al. (2014). Rothleitner and Francis (2014) proposed observing the vertical third-order tensor component for determination of the Newtonian gravitational constant. DiFrancesco et al. (2009) discussed possible benefits of an airborne sensor for observing the third-order gravitational tensor components. Brieden et al. (2010) introduced the satellite mission called OPTIMA (OPTical Interferometry for global MAss change detection from space) for measuring these parameters in space. Šprlák et al. (2016) studied properties of the third-order gravitational tensor and analysed requirements for an instrument that would eventually observe its components by differential accelerometry at satellite altitudes. Ghobadi-Far et al. (2016) performed a contribution analysis of the third-order gravitational tensor components.
Below, we provide a rigorous mathematical model for transforming six unique second-order gravitational components onto ten unique third-order gravitational tensor components in the form of spherical integral formulas. In this way, we extend the existing theoretical apparatus of geodesy and complete the Meissl diagram (Meissl 1971; Rummel and van Gelderen 1995). The presented mathematical formulations can be applied in any harmonic potential field; thus, they enhance a more general framework of the potential theory. We also expect that the new integral formulas will be exploited, e.g., for gravitational/magnetic field modelling or calibration/validation studies, with more observations of the second- and third-order tensor components available in the future.
The article is organized as follows: preliminaries, i.e., the nomenclature and initial points necessary for the mathematical derivations, are defined in Sect. 2; the new integral transforms among components of the second- and third-order gravitational tensors are derived in Sect. 3; numerical experiments focus on testing the consistency of the new theoretical apparatus with its spectral representation and investigating the sub-integral kernels, see Sect. 4; finally, conclusions summarizing main contributions and findings of the article can be found in Sect. 5.
2 Preliminaries
2.1 Nomenclature
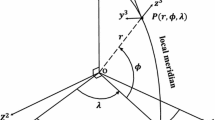
To understand the topic properly, we start with defining the notation used throughout the article. The mathematical apparatus derived below assumes spherical approximation of the Earth. Therefore, it is natural to define spherical geocentric coordinates in terms of the geocentric radius r and two angular coordinates—spherical latitude \(\varphi \) and longitude \(\lambda \). Moreover, a short-hand notation \(\Omega = (\varphi , \lambda )\) representing a geocentric direction is used. The symbol R designates the radius of the mean sphere which approximates the Earth and encloses its solid masses.
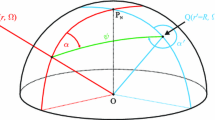
Because the mathematical apparatus presented below is in the form of integral formulas, we distinguish between an evaluation point \((r,\Omega )\), in which a numerical value of a gravitational field parameter is computed, and an integration (running) point \((R, \Omega ')\), where \(\Omega ' = (\varphi ',\lambda ')\), representing an infinitesimal spherical element as the surface integration over the mean sphere will be considered in our derivations, see Fig. 1.
The spherical polar angular coordinates are also exploited, see Fig. 1. The symbol \(\psi \) stands for the spherical distance between the evaluation and integration points. The direct azimuth \(\alpha \) is an azimuth between the evaluation and integration points measured clock-wise from the North at the position of the evaluation point. The backward azimuth \(\alpha '\) is then measured clock-wise from the North at the position of the integration point. Mathematical formulas transforming the spherical geocentric angular coordinates of the evaluation and integration points onto the spherical polar angular coordinates are summarized in “Appendix A”.
Spherical geocentric and polar coordinates. The point P represents an evaluation point with spherical geocentric coordinates \(r,\Omega = (\varphi ,\lambda )\). The point Q is an integration point defined by spherical coordinates \(R,\Omega ' = (\varphi ',\lambda ')\). The spherical polar angular coordinates are the spherical distance \(\psi \), direct azimuth \(\alpha \) and backward azimuth \(\alpha '\). O is the centre of the mean sphere of radius R and \(P_N\) is the North pole. The spherical local North-oriented reference frame with the origin at the evaluation and integration points is also depicted. This reference frame is defined by the right-handed orthonormal basis vectors \(\mathbf{{e}}_x\) (pointing to the North), \(\mathbf{{e}}_y\) (pointing to the West) and \(\mathbf{{e}}_z\) (pointing in the radial direction)
a The second-order disturbing gravitational tensor and b the third-order disturbing gravitational tensor. The second-order tensor illustrated in the form of a 2-D square is defined by nine components \(T_{op}\), \(o, p \in \{x, y, z\}\). If the gravitational field is continuous, the second-order tensor is determined by six components (depicted in blue). The third-order tensor is formed by 27 components \(T_{opq}\), \(o, p, q \in \{x, y, z\}\), and may be depicted as a 3-D cube. In the continuous gravitational field, ten components (depicted in blue) determine the third-order tensor completely
Throughout the article we assume that all parameters of the actual gravitational field are reduced by their normal gravity field counterparts. The normal gravity field is generated by the international reference ellipsoid. The reduced parameters belong to the disturbing gravitational field and are called correspondingly, e.g., disturbing gravitational potential or disturbing gravitational tensor components. We prefer to use the adjective gravitational to gravity as the disturbing field is free of the centrifugal part.
2.2 Disturbing gravitational tensors of the second- and third-orders
Mathematical relations between components of the second- and third-order disturbing gravitational tensors are derived below. We also briefly summarize basic properties of these parameters. We assume that the second- and third-order disturbing gravitational tensor components refer to the spherical local North-oriented reference frame. Such a frame has its origin at the point of interest, e.g., the evaluation or integration points. Its right-handed orthonormal basis is defined by the unit vector \(\mathbf{{e}}_x\) pointing to the North, \(\mathbf{{e}}_y\) pointing to the West and \(\mathbf{{e}}_z\) pointing in the radial direction, see Fig. 1.
The second-order disturbing gravitational tensor is defined by nine components \(T_{op}\), \(o, p \in \{x, y, z\}\), and can be represented by a 2-D square, see Fig. 2a. For the continuous potential field, the tensor is symmetric, i.e., it holds \(T_{op} = T_{po}\), and can completely be described only by six components. Moreover, the Laplace equation \(T_{xx} + T_{yy} + T_{zz} = 0\) holds in the mass free-space for the harmonic potential T. Then the tensor is given only by the five independent components. Throughout the article, we explicitly work with the six second-order tensor components which can systematically be divided into three groups:
-
vertical–vertical (VV) if \(o, p = z\) with one \(T_{zz}\) component,
-
vertical–horizontal (VH) if \(o \in \{x, y\}\) and \(p = z\) with two components \(T_{xz}\) and \(T_{yz}\),
-
horizontal–horizontal (HH) if \(o, p \in \{x, y\}\) with three components \(T_{xx}\), \(T_{xy}\) and \(T_{yy}\).
Mathematically, the second-order disturbing gravitational tensor can be obtained by applying the gradient operator twice onto the disturbing gravitational potential T. We can write the tensor for the continuous disturbing gravitational field as follows:
The symbols \(\mathbf{{e}}_{op} = \mathbf{{e}}_{o} \otimes \mathbf{{e}}_{p}\), \(o, p \in \{x, y, z\}\), represent spherical dyadics which form the basis for unique representation of the second-order disturbing gravitational tensor, see, e.g., Simmonds (1994). The six tensor components \(T_{xx}\), \(T_{xy}\), \(T_{xz}\), \(T_{yy}\), \(T_{yz}\) and \(T_{zz}\) are explicitly defined by the differential operators of Eqs. (6a)–(6f) applied to the disturbing gravitational potential.
The third-order disturbing gravitational tensor is defined by 27 components \(T_{opq}\), \(o, p, q \in \{x, y, z\}\). Such a mathematical object may be illustrated as a 3-D cube, see Fig. 2b. If the disturbing gravitational field is continuous, the tensor is completely represented by ten components only as the order of indices does not matter, i.e., it holds \(T_{opq} = T_{poq} = T_{oqp} = T_{qop}\). The ten third-order tensor components, with which we work below, may be organized into the following four groups:
-
vertical–vertical–vertical (VVV) if \(o, p, q = z\) with one component \(T_{zzz}\),
-
vertical–vertical–horizontal (VVH) if \(o \in \{x, y\}\) and \(p, q = z\) with two components \(T_{xzz}\) and \(T_{yzz}\),
-
vertical–horizontal–horizontal (VHH) if \(o, p \in \{x, y\}\) and \(q = z\) with three components \(T_{xxz}\), \(T_{xyz}\) and \(T_{yyz}\),
-
horizontal–horizontal–horizontal (HHH) if \(o, p, q \in \{x, y\}\) with four components \(T_{xxx}\), \(T_{xxy}\), \(T_{xyy}\) and \(T_{yyy}\).
Three Laplace equations, i.e., \(T_{xxq} + T_{yyq} + T_{zzq} = 0\), \(q \in \{x, y, z\}\), hold in the mass-free space. Then the third-order disturbing gravitational tensor is defined by seven independent components only. In the mathematical sense, the third-order disturbing gravitational tensor may be defined as the triple gradient of the disturbing gravitational potential:
The symbols \(\mathbf{{e}}_{opq} = \mathbf{{e}}_{o} \otimes \mathbf{{e}}_{p} \otimes \mathbf{{e}}_{q}\), \(o, p, q \in \{x, y, z\}\), represent the spherical triads which define the basis for unique representation of the third-order disturbing gravitational tensor. The ten tensor components, which determine the third-order tensor on the right-hand side of Eq. (2), are given by the differential operators of Eqs. (8a)–(8j) acting on the disturbing gravitational potential.
2.3 Spherical gradiometric boundary-value problem
The spherical gradiometric boundary-value problem (GBVP) aims at determining the harmonic disturbing gravitational potential T from the second-order disturbing gravitational tensor components. The disturbing gravitational potential is sought on and outside of the mean sphere. The second-order tensor components are continuously given at the mean sphere, while the regularity condition holds at infinity. Solutions of the spherical GBVP have been provided by, e.g., Rummel et al. (1993), van Gelderen and Rummel (2001), Martinec (2003), Tóth (2003) and Bölling and Grafarend (2005).
In this subsection, we briefly summarize selected integrals of the spherical GBVP as they represent the basis of our derivations. We consider the solutions derived by Martinec (2003) which relate the disturbing gravitational potential and the second-order tensor components by three integral formulas:
Equations (3a)–(3c) show that the disturbing gravitational potential can be computed independently from the three groups, i.e., VV, VH and HH, of the second-order gravitational tensor. The isotropic kernels \({\mathcal {K}}_\mathrm{VV}\), \({\mathcal {K}}_\mathrm{VH}\) and \({\mathcal {K}}_\mathrm{HH}\) are given by the following spectral and closed expressions (Martinec 2003, Eqs. 30–32):
The new parameters t, u and g in Eqs. (3a)–(4c) are defined as follows:
They stand for the attenuation factor, cosine of the spherical distance and the normalized Euclidean distance. The symbol \(P_{n,m}\) designates the non-normalized associated Legendre function of the first kind of degree n and order m. For more details on the solution of the spherical GBVP, such as its existence and uniqueness, and analytical properties of the isotropic kernels, see Martinec (2003).
2.4 Differential operators for the second- and third-order tensor components
Differential operators define relationships between various gravitational field parameters. In this subsection, we summarize differential operators which are necessary for our derivations. We begin with differential operators that relate the disturbing gravitational potential to the six second-order tensor components, see, e.g., Reed (1973), Wolf (2007) and Šprlák et al. (2014):
The superscripts on the left-hand sides of Eqs. (6a)–(6f) specify resulting components. The first equalities in these equations define the operators in terms of the spherical geocentric triad \((r,\Omega )\). Such a representation is of interest when parameters of the disturbing gravitational field are expanded into a series of spherical harmonics. The second equalities then define the same operators in terms of the triad \((t,u,\alpha )\) that allows decomposing into the azimuthal and isotropic parts. This fact can efficiently be exploited in relating various disturbing gravitational field parameters, e.g., through integral transforms. The isotropic part is defined by the four isotropic differential operators \(\mathcal{{D}}^{1}_{2}\), \(\mathcal{{D}}^{2}_{2}\), \(\mathcal{{D}}^{3}_{2}\) and \(\mathcal{{D}}^{4}_{2}\) which read:
The subscript on the left-hand sides of Eq. (7) explicitly indicates the order of the tensor components, while the superscript value distinguishes between the individual isotropic differential operators.
The corresponding differential operators for the ten components of the third-order disturbing gravitational tensor are more complex. They are defined in terms of the triads \((r,\Omega )\) and \((t,u,\alpha )\) as follows, see, e.g., Tóth (2005), Šprlák and Novák (2015):
The six isotropic differential operators \(\mathcal{{D}}^{1}_{3}, \mathcal{{D}}^{2}_{3}, \mathcal{{D}}^{3}_{3}, \mathcal{{D}}^{4}_{3}, \mathcal{{D}}^{5}_{3}\) and \(\mathcal{{D}}^{6}_{3}\) in Eqs. (8a)–(8j) are defined as follows:
Expressions for the third-order differential operators in terms of the triad \((t,u,\alpha )\) can significantly be simplified if applied to the isotropic kernels of the form \(\mathcal{{K}}(t,u) = \sum _{n=0}^{\infty }\ t^{n+1}\ h_n\ P_{n,0}(u)\) with \(h_n\) being eigenvalues of the isotropic kernel. In this case, the third-order differential operators read (Šprlák and Novák 2015):
where
Note that the asterisk is used in the superscripts of Eqs. (10) and (11) to avoid any confusion with the operators of Eqs. (8a)–(9).
We will also apply recursive relationships between the differential operators for the second- and third-order tensor components defined as follows (Šprlák and Novák 2015):
It can be seen from Eq. (12) that the third-order differential operators are either linear combinations of their second-order counterparts and/or their first-order derivatives with respect to the spherical geocentric coordinates. The recursions are more efficient in some mathematical derivations as compared to the original differential operators of Eqs. (8a)–(8j) which are composed of the derivatives with respect to the spherical geocentric coordinates up to the third-order.
3 Integral transforms between the second- and third-order disturbing gravitational tensor components
In the following subsections, we provide 30 new integral formulas that transform the VV, VH and HH second-order tensor components onto the ten third-order tensor components, see Fig. 3. With more measurements of the second- and third-order gravitational tensor components available in the future, such mathematical connections can be exploited for validation purposes or gravitational field modelling. Besides, the development of the mathematical apparatus is challenging theoretically and reveals interesting properties of the new integral transforms.
Schematic relations between the vertical–vertical (black lines), vertical–horizontal (blue lines) and horizontal–horizontal (red lines) second-order disturbing gravitational components and their third-order counterparts. The second-order components are depicted at the lower level as functions of the position of the integration point \((R,\Omega ')\). The corresponding isotropic kernels are located in the middle level along the connecting lines. The third-order components are functions of the position of the evaluation point \((r,\Omega )\) and are placed at the upper level
3.1 Transformation of the VV disturbing gravitational component onto the third-order disturbing gravitational components
We begin with the mathematical derivation of the integral transforms which map the VV disturbing gravitational component onto the third-order disturbing gravitational components. Such transforms may be obtained in a relatively simple way that originates from the isotropic property of the kernel \(\mathcal{{K}}_\mathrm{VV}\) in Eq. (3a). In other words, the kernel in Eq. (3a) is of the form \(\mathcal{{K}}_\mathrm{VV} (t, u) = \sum \nolimits _{n=0}^{\infty } t^{n+1}\ h_n\ P_{n,0} (u)\), where \(h_n = \frac{2n + 1}{(n + 1) (n + 2)}\). Therefore, the differential operators of Eqs. (10) and (11) can directly be applied to Eq. (3a) to get the required transforms. After performing this mathematical operation, we obtain ten integral transforms of the form:
The sub-integral kernels \(\mathcal{{D}}^{opq}\ \mathcal{{K}}_\mathrm{VV}\) are:
Obviously, they reflect the structure of the differential operators of Eq. (10), such as the decomposition into the azimuthal and isotropic parts. The azimuthal part is represented by cosines and sines of the multiples of the direct azimuth \(\alpha \). The isotropic part is defined by the isotropic kernels \(\mathcal{{K}}_\mathrm{VV}^{k}\), \(k = 0, 1, 2, 3\).
Equations (14a)–(14j) reveal symmetries of the sub-integral kernels. One can see that every group of the third-order disturbing gravitational components, i.e., VVV, VVH, VHH and HHH, is defined by the same isotropic kernels, see also Fig. 3. For example, the evaluation of the purely horizontal third-order disturbing gravitational components \(T_{xxx}\), \(T_{xxy}\), \(T_{xyy}\) and \(T_{yyy}\) requires only the isotropic kernels \(K_\mathrm{VV}^{1}\) and \(K_\mathrm{VV}^{3}\). Moreover, the numbers in the superscripts of the isotropic kernels and the corresponding multiples of the direct azimuth are the same. By inspecting the isotropic differential operators of Eq. (11) we can observe that the number in the superscript of the isotropic kernels agrees with the order of differentiation with respect to the parameter u.
The spectral forms of the isotropic kernels \(\mathcal{{K}}_\mathrm{VV}^{k}\), \(k = 0, 1, 2, 3\), can concisely be written as follows:
where \(a_0 = 1/2\), \(a_1 = -3/4\), \(a_2 = -1/2\) and \(a_3 = 1/4\). We can arrive at Eq. (15) by applying the operators of Eq. (11) to the spectral form of the isotropic kernel \({\mathcal {K}}_\mathrm{VV}\) of Eq. (4a) and by exploiting the definition of the non-normalized Legendre functions of the first kind (Heiskanen and Moritz 1967, Eq. 1–60):
The spectral forms of the isotropic kernels are of importance when the second- or third-order disturbing gravitational components are band-limited. However, when the disturbing gravitational components contain all frequencies, the closed forms of the isotropic kernels are necessary. They can be obtained by summing up the corresponding infinite series of Eq. (15). For this purpose, we apply the summation rules provided by, e.g., Pick et al. (1973, Appendix 18) and get:
Alternatively, the differential operators of Eq. (11) can directly be applied to the closed form of the isotropic kernel \({\mathcal {K}}_\mathrm{VV}\) of Eq. (4a).
Equations (17a)–(17d) may become singular for some limiting values of the parameters t and u. Therefore, we also provide explicit expressions for their limiting values which follow from the L’Hospital rule:
It can be seen that each of the four isotropic kernels is singular for \(t = u = 1\). On the other hand, they are bounded for the other limiting values, while only the kernel \(\mathcal{{K}}_\mathrm{VV}^{0}\) is non-zero.
3.2 Transformation of the VH disturbing gravitational components onto the third-order disturbing gravitational components
We now proceed with the transformation between the VH disturbing gravitational components and their third-order counterparts. The starting point for such relationships is given by Eq. (3b). However, by inspecting this formula, we can observe that its sub-integral kernels are no longer isotropic as they depend also on the backward azimuth \(\alpha '\). Therefore, to derive the desired integral transforms, we must apply the more general differential operators of Eqs. (8a)–(9). By employing these operators to Eq. (3b), we derive ten integral transforms:
The sub-integral kernels of Eq. (19) represent the action of the differential operators \(\mathcal{{D}}^{opq}\) to the multiplications of \(\cos \alpha '\) and \(\sin \alpha '\) by \(\mathcal{{K}}_\mathrm{VH}\). Such a mathematical operation is investigated in “Appendix B” for two general functions \(f = f(\Omega ,\Omega ')\) and \(h = h(r,R,\Omega ,\Omega ')\). Equations (36a)–(36j) reveal that the action is composed of three parts (1) the application of the third-order differential operators to the functions f and h, (2) the action of the second-order differential operators to the functions f and h, and (3) the auxiliary terms, i.e., the derivatives of the functions f and h with respect to the spherical geocentric coordinates.
We can arrive at the resulting formulas for the sub-integral kernels of Eq. (19) in terms of the parameters \((t,u,\alpha ,\alpha ')\) by considering \(f = \cos \alpha '\), or \(f = \sin \alpha '\), and \(h = \mathcal{{K}}_\mathrm{VH}\) in Eqs. (36a)–(36j). Explicit expressions for the individual terms are obtained as follows:
-
the terms of the type \(f\ \mathcal{{D}}^{opq}\ h\) are defined by the action of the third-order differential operators in terms of the parameters \((t,u,\alpha )\), see Eqs. (8a)–(9), to the isotropic kernel \(\mathcal{{K}}_\mathrm{VH}\),
-
the terms of the type \(h\ \mathcal{{D}}^{opq}\ f\) originate from Eqs. (39a)–(39i), see also the paragraph below these equations, which are defined in “Appendix C”,
-
the terms of the type \(\frac{\partial f}{\partial \varphi }\ \mathcal{{D}}^{op}\ h\) and \(\frac{\partial f}{\partial \lambda }\ \mathcal{{D}}^{op}\ h\) are given by Eqs. (37a) and (37b), see also the paragraph below these equations, together with the action of the second-order differential operators in terms of the parameters \((t,u,\alpha )\), see Eqs. (6a), (7), to the isotropic kernel \(\mathcal{{K}}_\mathrm{VH}\),
-
the terms of the type \(\frac{\partial h}{\partial r}\ \mathcal{{D}}^{op}\ f\), \(\frac{1}{r} \frac{\partial h}{\partial \varphi }\ \mathcal{{D}}^{op}\ f\) and \(\frac{1}{r \cos \varphi } \frac{\partial h}{\partial \lambda }\ \mathcal{{D}}^{op}\ f\) make use of the expressions:
$$\begin{aligned}&\frac{\partial }{\partial r} = - \frac{t^2}{R}\ \frac{\partial }{\partial t}, \quad \frac{1}{r}\ \frac{\partial }{\partial \varphi } = \frac{t \cos \alpha \sqrt{1-u^2}}{R}\ \frac{\partial }{\partial u},\nonumber \\&\frac{1}{r \cos \varphi } \frac{\partial }{\partial \lambda } = \frac{t \sin \alpha \sqrt{1-u^2}}{R}\ \frac{\partial }{\partial u}, \end{aligned}$$(20)when differentiating the isotropic kernel \(\mathcal{{K}}_\mathrm{VH}\). Equations (38a)–(38e), see also the paragraph below these equations, define the action of the second-order operators to \(\cos \alpha '\) or \(\sin \alpha '\),
-
formulas for the auxiliary terms are summarized in “Appendix D”.
By combining the individual terms, we obtain the resulting formulas for the sub-integral kernels of Eq. (19):
By changing \(\cos \alpha ' \rightarrow \sin \alpha '\) and \(\sin \alpha ' \rightarrow - \cos \alpha '\) in these equations, we get the sub-integral kernels \(\mathcal{{D}}^{opq}\ (\sin \alpha '\ \mathcal{{K}}_\mathrm{VH})\), \(o, p, q \in \{x, y, z\}\).
The sub-integral kernels of Eqs. (21a)–(21j) posses analogous properties as those of Eqs. (14a)–(14j) in the previous subsection. Namely, we can clearly resolve the decomposition into their azimuthal and isotropic parts. Similarly, every group of the third-order disturbing gravitational components can be evaluated from the same isotropic kernels, see Fig. 3. On the other hand, the azimuthal part is now more complex as it is composed of multiplications of the trigonometric functions of both the direct and backward azimuth. Moreover, seven isotropic kernels are introduced in Eqs. (21a)–(21j) as compared to only four in Eqs. (14a)–(14j), i.e.:
The numbers in the superscripts on the left-hand sides indicate the highest order of differentiation with respect to the parameter u. Such a notation is in correspondence to the isotropic kernels in the previous subsection, see Eq. (15) or Eqs. (17a)–(17d). However, we append the asterisk to distinguish between different kernels with the same numerical value in the superscripts.
The seven isotropic kernels in the spectral form read:
We arrive at these equations by substituting the spectral form of the kernel \(\mathcal{{K}}_\mathrm{VH}\), see Eq. (4b), into Eqs. (22a)–(22g). Moreover, the following identities for the Legendre functions of the first kind are exploited, see, e.g., Arfken and Weber (2005, Sect. 12.5), Eshagh (2008):
We can see in Eqs. (23a)–(23g) that the kernel \(\mathcal{{K}}_\mathrm{VH}^{0}\) needs only the Legendre function of the first order. The other isotropic kernels are defined by two distinct Legendre functions with the orders which differ by two. Moreover, the pairs of the isotropic kernels (\(\mathcal{{K}}_\mathrm{VH}^{0*}\), \(\mathcal{{K}}_\mathrm{VH}^{1}\)), (\(\mathcal{{K}}_\mathrm{VH}^{1*}\), \(\mathcal{{K}}_\mathrm{VH}^{2}\)) and (\(\mathcal{{K}}_\mathrm{VH}^{2*}\), \(\mathcal{{K}}_\mathrm{VH}^{3}\)) are defined by the Legendre functions of the same orders.
The spatial forms of the isotropic kernels can be derived by summing up the infinite series of Eqs. (23a)–(23g). Such a mathematical operation gives:
By exploiting the L’Hospital rule, we obtain the corresponding limits:
Equations (27a)–(27d) show that the seven isotropic kernels are singular for \(t = u = 1\). For the other limiting values of the parameters t and u, only the kernels \(\mathcal{{K}}_\mathrm{VH}^{0*}\) and \(\mathcal{{K}}_\mathrm{VH}^{1}\) have non-zero values.
3.3 Transformation of the HH disturbing gravitational components onto the third-order disturbing gravitational components
We complete our mathematical derivations with the integral formulas transforming the HH disturbing gravitational components onto the third-order components. For this purpose, we exploit Eq. (3c) as our initial point. Obviously, the sub-integral kernels of Eq. (3c) are again non-isotropic as they are functions of the backward azimuth \(\alpha '\). Therefore, the differential operators of Eqs. (8a)–(9) are applied to Eq. (3c) that yields ten integral transforms:
Taking \(f = \cos 2 \alpha '\) or \(f = \sin 2 \alpha '\), \(h = \mathcal{{K}}_\mathrm{HH}\), and following the steps described in the paragraphs below Eq. (19), the sub-integral kernels of Eq. (28) read:
It is not necessary to provide explicit expressions for the sub-integral kernels \(\mathcal{{D}}^{opq}\ (\sin 2\alpha '\ \mathcal{{K}}_\mathrm{HH})\), \(o, p, q \in \{x, y, z\},\) as they come directly from Eqs. (29a)–(29j) by changing \(\cos 2\alpha ' \rightarrow \sin 2\alpha '\) and \(\sin 2\alpha ' \rightarrow - \cos 2\alpha '\). In fact, Eqs. (29a)–(29j) do not have to be presented either as they can be obtained by changing \(\cos \alpha ' \rightarrow \cos 2 \alpha '\), \(\sin \alpha ' \rightarrow \sin 2 \alpha '\) and \(\mathcal{{K}}_\mathrm{VH} \rightarrow \mathcal{{K}}_\mathrm{HH}\) in Eqs. (21a)–(21j). Such a transition implies that properties of sub-integral kernels for the integral formulas of Eqs. (19) and (28), e.g., decomposition into the azimuthal and isotropic parts or definition of the third-order components by the same set of isotropic kernels, are equivalent; they are discussed in detail in the paragraphs below Eq. (21j).
The isotropic parts of the sub-integral kernels of Eqs. (29a)–(29j) are represented by the seven isotropic kernels. These are defined as follows:
The notation used for the isotropic kernels is in correspondence with that of Eqs. (22a)–(22g). Namely, the numbers in the superscripts on the left-hand sides are the same as the highest order of differentiation with respect to the parameter u. The asterisk is added to distinguish between various kernels with the same superscript value.
Note that some similarities between the defining isotropic differential operators may be observed by comparing Eqs. (30a)–(30g) with those of Eqs. (22a)–(22g). The corresponding differential operators for the isotropic kernels \(\mathcal{{K}}_\mathrm{HH}^{0}\) and \(\mathcal{{K}}_\mathrm{HH}^{1}\) are identical to those of \(\mathcal{{K}}_\mathrm{VH}^{0}\) and \(\mathcal{{K}}_\mathrm{VH}^{1}\). The differential operators for the kernels \(\mathcal{{K}}_\mathrm{HH}^{0*}\) and \(\mathcal{{K}}_\mathrm{HH}^{1*}\) differ only by the factor of two from those of the kernels \(\mathcal{{K}}_\mathrm{VH}^{0*}\) and \(\mathcal{{K}}_\mathrm{VH}^{1*}\). The differential operators for the kernels \(\mathcal{{K}}_\mathrm{HH}^{2}\) and \(\mathcal{{K}}_\mathrm{VH}^{2}\) differ by the factor of four in the first term inside the curly brackets. On the other hand, the defining operators for \(\mathcal{{K}}_\mathrm{HH}^{2*}\) and \(\mathcal{{K}}_\mathrm{HH}^{3}\) are significantly different from those of the kernels \(\mathcal{{K}}_\mathrm{VH}^{2*}\) and \(\mathcal{{K}}_\mathrm{VH}^{3}\).
The spectral forms of the isotropic kernels can be derived by substituting the series representation of the kernel \(\mathcal{{K}}_\mathrm{HH}\) of Eq. (4c) into Eqs. (30a)–(30g). After applying the identities of Eqs. (24) and (25), we get:
Clearly, the kernel \(\mathcal{{K}}_\mathrm{HH}^{0}\) requires only the Legendre function of the second order, while the kernels \(\mathcal{{K}}_\mathrm{HH}^{0*}\) and \(\mathcal{{K}}_\mathrm{HH}^{1}\) are defined by two different Legendre functions of the orders one and three. On the other hand, three distinct Legendre functions are necessary to compute the isotropic kernels \(\mathcal{{K}}_\mathrm{HH}^{1*}\), \(\mathcal{{K}}_\mathrm{HH}^{2}\), \(\mathcal{{K}}_\mathrm{HH}^{2*}\) and \(\mathcal{{K}}_\mathrm{HH}^{3}\).
By exploiting the summation rules for the infinite series of Legendre polynomials and their derivatives, we get the closed forms of the isotropic kernels:
It can be observed that the closed forms of the isotropic kernels are more complex as those of Eqs. (26a)–(26g). The complexity originates mainly from the spectral forms which are composed of more terms and contain the Legendre functions of higher orders.
We conclude our mathematical derivations with the limiting values of the isotropic kernels of Eqs. (32a)–(32g). By employing the L’Hospital rule, they read as follows:
In correspondence to Eqs. (27a)–(27d), each of the seven isotropic kernels is singular for \(t = u = 1\). For the other limiting values, these are bounded and only two kernels, i.e., \(\mathcal{{K}}_\mathrm{HH}^{1*}\) and \(\mathcal{{K}}_\mathrm{HH}^{2}\), are non-zero.
Generally, the isotropic kernels of the integral transforms of Eqs. (13), (19) and (28) are bounded for \(t < 1\) and \(-1 \le u \le 1\). In other words, the upward continuation of the second-order disturbing gravitational tensor components onto the third-order disturbing gravitational tensor components is not problematic. However, all isotropic kernels are singular for \(t = u = 1\), see Eqs. (18c), (27c), (33c). The singularities indicate that the transformation of the second-order disturbing gravitational tensor components onto their third-order counterparts is inherently unstable when both tensor quantities are given at the same sphere. This is very similar to the much simpler and more frequent transformation of the disturbing gravitational potential (or geoid undulation) onto gravity anomalies, see, e.g., Vaníček and Krakiwsky (1986, p. 562).
4 Numerical experiments
4.1 Closed-loop test of the new integral transforms
The complex mathematical derivations performed in the previous section may be prone to potential errors. Therefore, the resulting integral transforms of Eqs. (13), (19) and (28) are implemented in the form of computer programs written in the programming language C. The accuracy of the computer programs, thus also the internal consistency of the new mathematical apparatus with respect to its spectral representation, is subsequently verified in a closed-loop test.
We opt for testing the integral transforms of Eqs. (13), (19) and (28) by solving the direct problem. Namely, the second-order disturbing gravitational components are assumed to be known at the mean sphere of radius R, while their third-order counterparts are evaluated at the sphere of radius \(r = R + 250\) km. In this way, both transformation and upward continuation of the input data are validated.
Such a geometric configuration may also be exploited in the future for calibration/validation of satellite third-order gravitational components (potentially observed by the mission OPTIMA) through ground gradiometric measurements. However, terrestrial data does not cover the entire Earth and is usually available only in limited geographic areas. Therefore, the ground gradiometric measurements would have to be combined with a global gravitational model in realistic calibration/validation experiments.
We firstly synthesize the six second-order disturbing gravitational components from the global gravitational model EGM2008 (Pavlis et al. 2012) in the form of global equiangular grids with the steps \(\Delta \varphi = \Delta \lambda = 0.5^{\circ }\). Correspondingly, the synthesis is performed between the degrees 2-360 on the mean sphere of radius \(R = 6378.1363\) km. The normal gravity field generated by the international equipotential ellipsoid GRS80 (Moritz 2000) is adopted throughout all numerical simulations.
Secondly, the true values of the ten third-order disturbing gravitational components are synthesized from EGM2008 at the sphere of radius \(r = R + 250\) km. We calculate the true values with the steps \(\Delta \varphi = \Delta \lambda = 0.5^{\circ }\) in the test area bounded by the spherical geocentric angular coordinates \(\varphi \in [-50^{\circ }, 0^{\circ }]\) and \(\lambda \in [-85^{\circ }, -60^{\circ }]\). For the reasons explained below, the true third-order disturbing gravitational components are synthesized in the two different bandwidths (1) between the degrees 2–360 and (2) between the degrees 100–200.
The test area covers the majority of the Andes. Variations of the third-order disturbing gravitational components in this region are twice as high as their corresponding global averages. Thus, the closed-loop test is performed for the case of a complex gravitational field. The statistics of the true values for both spectral bandwidths are summarized in Table 1 reaching magnitudes of the order of \(10^{-15}\) m\(^{-1}\) s\(^{-2}\). We can also see that the variations of the third-order gravitational components between the degrees 100–200 are approximately four times lower as compared to those between the degrees 2–360. For both bandwidths, the largest signal is observed for the vertical component \(T_{zzz}\). Also, we can clearly identify larger signals for \(T_{yyy}\), \(T_{yyz}\) and \(T_{yzz}\) as compared to \(T_{xxx}\), \(T_{xxz}\) and \(T_{xzz}\). This is in correspondence with larger variations of the gravitational field in the East-West direction, i.e., in the direction of the y axis, over the Andes.
Thirdly, the numerical integration over the global grids of the second-order disturbing gravitational components is performed according to the integral transforms of Eqs. (13), (19) and (28). The evaluation points are identical to those for the true values of the third-order disturbing gravitational components. Both the spectral and isotropic kernels are validated by the numerical integration. When the closed isotropic kernels are employed, the expected spectral content must be consistent with the input data, i.e., between the degrees 2–360 as for the second-order disturbing gravitational components. On the other hand, the spectral isotropic kernels are limited to the degrees 100–200 corresponding to the limited bandwidth of the true values.
Finally, the third-order disturbing gravitational components calculated by the numerical integration and their true values are compared. The corresponding statistics for the integral transform of Eq. (13) is provided in Table 2. It can be seen that the magnitudes of the differences between the third-order disturbing gravitational components computed by the numerical integration and their true values are of the order of \(10^{-18}\) m\(^{-1}\) s\(^{-2}\). Compared to the signals in Table 1, the differences are three orders of magnitude smaller. Almost identical statistics, differing by several hundredths of \(10^{-18}\) m\(^{-1}\) s\(^{-2}\) for the minima and maxima, are obtained for the integrals of Eqs. (19) and (28). Thus, we show the consistency of the new integral transforms of Eqs. (13), (19) and (28) derived in Sect. 3 with their corresponding spectral representations.
4.2 Properties of the sub-integral kernels in the spatial domain
We now examine the spatial behaviour of the new sub-integral kernels. The investigation is performed to better understand properties of the corresponding integral transforms, e.g., symmetries of the sub-integral kernels, or position and occurrence of their extreme values. These properties are closely related to practical aspects of the integral transforms, such as exploitation of fast numerical algorithms for their numerical evaluation, significance of the distant zones or suitability of the integral transforms for solving inverse problems.
Šprlák and Novák (2015) studied the performance of the sub-integral kernels for the integral formulas transforming the mass density, disturbing gravitational potential, gravity anomaly and gravity disturbance onto the third-order disturbing gravitational components. Similar findings may also be extended for the kernel functions of the integral transform of Eq. (13). Examination of these properties is not duplicated in this article. Therefore, we restrict to the sub-integral kernels for the integral formulas of Eqs. (19) and (28), which are investigated for the first time. However, some properties of the sub-integral kernels are commented for all three integral transforms to illustrate possible similarities and contrasts between them.
The investigation is performed for the same geometric configuration as already discussed above, i.e., the second-order components are prescribed at the mean sphere of radius \(R = 6378.1363\) km and the third-order components at the sphere of radius \(r = R + 250\) km. The geometric formation may be of practical importance for solving both the direct and inverse problems when the third-order components become observable in space in the future.
The first idea on the general behaviour of the sub-integral kernels can be obtained by inspecting the corresponding mathematical formulas derived in Sect. 3. The kernel function of Eq. (14j) for the integral formula of Eq. (13) is isotropic as it depends only on the spherical distance \(\psi \). The other sub-integral kernels for the same integral transform are functions of the direct azimuth \(\alpha \), thus they are anisotropic, see also Šprlák and Novák (2015). On the other hand, the kernel functions for the integrals of Eqs. (19) and (28) are anisotropic and also non-homogeneous with the spherical latitude of the evaluation point. The non-homogeneity originates from the backward azimuth \(\alpha '\), see Eqs. (21a)–(21j) and (29a)–(29j).
The behaviour of the sub-integral kernels: a) \(\mathcal{{D}}^{xxx} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), b) \(\mathcal{{D}}^{xxy} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), c) \(\mathcal{{D}}^{xxz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), d) \(\mathcal{{D}}^{xyy} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), e) \(\mathcal{{D}}^{xyz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), f) \(\mathcal{{D}}^{xzz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), g) \(\mathcal{{D}}^{yyy} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), h) \(\mathcal{{D}}^{yyz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), i) \(\mathcal{{D}}^{yzz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and j) \(\mathcal{{D}}^{zzz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), see Eqs. (21a)–(21j). The kernels are calculated for \(R = 6378.1363\) km and \(r = R + 250\) km with the closed isotropic kernels of Eqs. (26a)–(26g) as functions of the spherical distance \(\psi \in [0^{\circ }, 30^{\circ }]\) and direct azimuth \(\alpha \in [0^{\circ }, 360^{\circ })\). The spherical distance \(\psi \) is measured from the centres of the polar plots and indicated by the dashed concentric circles. The direct azimuth \(\alpha \) is measured clock-wise from the North and marked along the circumference of each of the polar plots. The evaluation point with the spherical coordinates \(\varphi = 60^{\circ }\) and \(\lambda = 0^{\circ }\) is located at the centres of the polar plots. The kernel values are unitless as they are multiplied by the factor \(R^3\) for numerical reasons. Black lines inside the plots indicate zero crossings of the sub-integral kernels.
The ten kernel functions \(\mathcal{{D}}^{opq} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big ), o, p, q \in \{x, y, z\}\), defined by Eqs. (21a)–(21j) are illustrated in Fig. 4. For numerical reasons, they are multiplied by the factor of \(R^3\). The computation is performed at the evaluation point with the spherical coordinates \(\varphi = 60^{\circ }\) and \(\lambda = 0^{\circ }\) that is located in the centres of the polar plots. The kernels are depicted as functions of the spherical polar coordinates, i.e., the spherical distance \(\psi \in [0^{\circ }, 30^{\circ }]\) and the direct azimuth \(\alpha \in [0^{\circ }, 360^{\circ })\). The spherical distance is measured from the centres of the polar plots and indicated by the concentric dashed circles. Values of the direct azimuth are measured clock-wise from the North and are marked along the circumference of each polar plot.
Figure 4 reveals that there are no mutual symmetries between the ten kernel functions as their behaviours are different. In other words, the kernels are not interrelated by any azimuthal rotation. This is in contrast to the sub-integral kernels of Eqs. (14a)–(14j). Among them the pairs (\(\mathcal{{D}}^{xxx}\ \mathcal{{K}}_\mathrm{VV}\), \(\mathcal{{D}}^{yyy}\ \mathcal{{K}}_\mathrm{VV}\)), (\(\mathcal{{D}}^{xyy}\ \mathcal{{K}}_\mathrm{VV}\), \(\mathcal{{D}}^{xxy}\ \mathcal{{K}}_\mathrm{VV}\)) and (\(\mathcal{{D}}^{xzz}\ \mathcal{{K}}_\mathrm{VV}\), \(\mathcal{{D}}^{yzz}\ \mathcal{{K}}_\mathrm{VV}\)) are related by the azimuthal rotation of \(\pi /2\). In addition, the pair (\(\mathcal{{D}}^{xxz}\ \mathcal{{K}}_\mathrm{VV}\), \(\mathcal{{D}}^{yyz}\ \mathcal{{K}}_\mathrm{VV}\)) is symmetric by rotating the direct azimuth \(\alpha \) by \(\pm \pi /2\), see Šprlák and Novák (2015).
By inspecting the individual sub-integral kernels in Fig. 4, we can clearly identify their symmetry or anti-symmetry with respect to the meridional plane passing through the computational point. Specifically, the sub-integral kernels with the y coordinate either missing or occurring twice in the superscript, i.e., \(\mathcal{{D}}^{xxx} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{xxz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{xzz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{zzz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{xyy} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and \(\mathcal{{D}}^{yyz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), are symmetric with respect to the meridional plane. On the other hand, the kernels with the y coordinate occurring an odd number of times in the superscript, i.e., \(\mathcal{{D}}^{xxy} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{xyz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{yzz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and \(\mathcal{{D}}^{yyy} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), are anti-symmetric with respect to the meridional plane. Both the symmetry and anti-symmetry require only half of the kernel values to be computed. Moreover, values of the sub-integral kernels do not change with the spherical longitude of the evaluation point. Thus, assuming a regular equiangular grid of evaluation points, the sub-integral kernels need to be calculated only once for all evaluation points with the same spherical latitude. These properties allow for exploiting fast and rigorous numerical algorithms, e.g., the 1-D fast Fourier transform (Haagmans et al. 1993) or the fast numerical integration (Huang et al. 2000), in practical computations of the corresponding integral transforms.
Looking at the position and occurrence of the extremes, we can distinguish between two types of kernel functions. Obviously, the kernels \(\mathcal{{D}}^{xxx} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{xyy} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and \(\mathcal{{D}}^{xzz} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) reach their extreme magnitudes at the evaluation point. However, the other kernels are exactly zero at the evaluation point, while their extremes can be seen for the spherical distances of several degrees of arc. The magnitudes of all kernels are significantly reduced by at least two orders beyond \(\psi = 8^{\circ }\).
The behaviour of the sub-integral kernels: a \(\mathcal{{D}}^{xxx} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), b \(\mathcal{{D}}^{xxy} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), c \(\mathcal{{D}}^{xxz} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), d \(\mathcal{{D}}^{xyy} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), e \(\mathcal{{D}}^{xyz} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), f \(\mathcal{{D}}^{xzz} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), g \(\mathcal{{D}}^{yyy} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), h \(\mathcal{{D}}^{yyz} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), i \(\mathcal{{D}}^{yzz} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\) and j \(\mathcal{{D}}^{zzz} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), see Eqs. (29a)–(29j). The kernels are calculated for \(R = 6378.1363\) km and \(r = R + 250\) km with the closed isotropic kernels of Eqs. (32a)–(32g) as functions of the spherical distance \(\psi \in [0^{\circ }, 30^{\circ }]\) and direct azimuth \(\alpha \in [0^{\circ }, 360^{\circ })\). The spherical distance \(\psi \) is measured from the centres of the polar plots and indicated by the dashed concentric circles. The direct azimuth \(\alpha \) is measured clock-wise from the North and marked along the circumference of each of the polar plots. The evaluation point with the spherical coordinates \(\varphi = 60^{\circ }\) and \(\lambda = 0^{\circ }\) is located at the centres of the polar plots. The kernel values are unitless as they are multiplied by the factor \(R^3\) for numerical reasons. Black lines inside the plots indicate zero crossings of the sub-integral kernels
The two types of kernel functions can determine suitability of the integral transforms for solving inverse problems. Eshagh (2011b) showed that the first type of the sub-integral kernels is superior for integral inversions. However, he considered different gravitational field parameters, i.e., integral inversion of the second-order disturbing gravitational components onto the gravity anomaly and only small integration radii. Therefore, we do not definitely conclude on this issue as the suitability of the integral transforms of Eq. (19) for inverse problems should be shown by an independent numerical experiment. This task is left for our future research.
The spatial behaviour of the sub-integral kernels \(\mathcal{{D}}^{opq} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), \(o, p, q \in \{ x, y, z \}\), see Eqs. (29a)–(29j), is depicted in Fig. 5. They are again multiplied by the factor of \(R^3\). Clearly, we do not observe any mutual symmetries between the kernels. The symmetry or anti-symmetry with respect to the meridional plane according to the occurrence of the y coordinate in the superscripts can also be seen. Also, the two types of kernel functions may be identified based on the position and occurrence of the extremes. These properties are in correspondence to those for the kernel functions illustrated in Fig. 4.
However, the spatial behaviour for the kernels in Fig. 5 is different as compared to their counterparts in Fig. 4. Different kernel functions, i.e., \(\mathcal{{D}}^{xxz} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\) and \(\mathcal{{D}}^{yyz} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), reach their extreme values at the computational point. In addition, the magnitudes of the sub-integral kernels are still significant even at \(\psi = 10^{\circ }\). Therefore, we suppose that the effect of the truncation error could be more crucial for the integral transforms of Eq. (28) as compared to those of Eq. (19) when assuming a truncated integration of input data.
The sub-integral kernels \(\mathcal{{D}}^{opq} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and \(\mathcal{{D}}^{opq} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), \(o, p, q \in \{x, y, z \}\), are illustrated in two animations which are included in the electronic supplementary material. The animations are created for the same parameters as already discussed above for Figs. 4 and 5, i.e., \(R = 6378.1363\) km, \(r = R + 250\) km, \(\psi \in [0^{\circ }, 30^{\circ }], \alpha \in [0^{\circ }, 360^{\circ })\) and \(\lambda = 0^{\circ }\). However, each animation sequence differs by the spherical latitude of the evaluation point \(\varphi \in [-80^{\circ }, 80^{\circ }]\) with the changes of \(20^{\circ }\).
The animations show the non-homogeneity of the sub-integral kernels. Obviously, the non-homogeneity still possesses a symmetric feature for the evaluation points which are symmetric with respect to the equatorial plane. For example, the sub-integral kernels at \(\varphi = -60^{\circ }\) can be retrieved from those at \(\varphi = 60^{\circ }\) by the azimuthal rotation of \(\pm \pi \) and vice versa. However, the spatial behaviour of the kernels changes as a function of the spherical latitude of the evaluation point. This is clearly indicated by the zero crossing lines which form different shapes for different values of the spherical latitude of the evaluation point \(\varphi \) and originate from the trigonometric functions of the backward azimuth \(\alpha '\).
So far, the functions \(\mathcal{{D}}^{opq} \big (\cos \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and \(\mathcal{{D}}^{opq} \big (\cos 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big ), o, p, q \in \{x, y, z \}\), were investigated. They represent only half of the sub-integral kernels of the integral transforms of Eqs. (19) and (28). The other half of the kernel functions is completed by 20 functions, i.e., \(\mathcal{{D}}^{opq} \big (\sin \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and \(\mathcal{{D}}^{opq} \big (\sin 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big ), o, p, q \in \{x, y, z \}\). For the sake of brevity, the properties of these functions are only briefly summarized and contrasted to their formerly investigated counterparts.
The spatial behaviour of \(\mathcal{{D}}^{opq} \big (\sin \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and \(\mathcal{{D}}^{opq} \big (\sin 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big ), o, p, q \in \{x, y, z \}\), differs from the kernels discussed above. This originates from the fact that there is no mutual azimuthal symmetry between the pairs \((\cos \alpha ', \sin \alpha ')\) and \((\cos 2\alpha ', \sin 2\alpha ')\), i.e., the trigonometric functions of the backward azimuth \(\alpha '\). Another distinct point is that these kernel functions are anti-symmetric with respect to the meridional plane for the y coordinate either missing or occurring twice in the superscript. The symmetry with respect to the meridional plane holds for the kernel functions with the y coordinate occurring an odd number of times. Also, there is a difference when looking at the position and occurrence of the extreme values. In particular, the extreme values at the evaluation point can be found for the functions \(\mathcal{{D}}^{xxy} \big (\sin \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{yyy} \big (\sin \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), \(\mathcal{{D}}^{yzz} \big (\sin \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\), and \(\mathcal{{D}}^{xyz} \big (\sin 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\). Note that the other properties observed in Figs. 4 and 5 may also be extended to the sub-integrals kernels \(\mathcal{{D}}^{opq} \big (\sin \alpha '\ \mathcal{{K}}_\mathrm{VH} \big )\) and \(\mathcal{{D}}^{opq} \big (\sin 2\alpha '\ \mathcal{{K}}_\mathrm{HH} \big )\), \(o, p, q \in \{ x, y, z \}\).
5 Conclusions
New spherical integral formulas transforming the second-order gravitational components onto their third-order counterparts were presented in this article. For this purpose, we firstly defined the preliminaries necessary for the mathematical derivations, see Sect. 2. Namely, we reviewed the nomenclature exploited throughout the article, basic properties of the second- and third-order gravitational tensors and of the related differential operators, and summarized the analytical solutions of the gradiometric boundary-value problem. Secondly, the third-order differential operators were applied to the three analytical solutions of the gradiometric boundary-value problem, see Sect. 3. In this way, we obtained 30 new integral formulas transforming (1) vertical–vertical, (2) vertical–horizontal and (3) horizontal–horizontal second-order gravitational tensor components onto their third-order counterparts, see Eqs. (13), (19) and (28). The corresponding sub-integral kernels were concisely expressed in terms of the spherical polar coordinates, see Eqs. (14a)–(14j), (21a)–(21j) and (29a)–(29j) which allow for decomposing the kernel functions into their azimuthal and isotropic parts. The isotropic kernels were provided both in the spectral and closed forms; their limits were also estimated. Thirdly, the consistency of the new integral transforms with corresponding spectral representations was successfully verified by a closed loop test over the test area of the Andes, see Sect. 4.1. Moreover, the properties of the sub-integral kernels were investigated in detail in Sect. 4.2.
The new mathematical formulas enrich the theoretical apparatus of physical geodesy by extending the Meissl diagram, see Fig. 3, which concisely connects various parameters of the gravitational field. The new integral transforms can be applied, e.g., for calibration/validation studies or gravitational field modelling, when observations of the second and third-order gravitational components become available in the future. The new mathematical apparatus formulated in this article can also be exploited for other potential fields, such as the geomagnetic field; moreover, it also enhances the general framework of the potential theory.
References
Abramowitz M, Stegun IA (1972) Handbook of mathematical functions with formulas, graphs, and mathematical tables. Tenth Printing, National Bureau of Standards, Department of Commerce, Washington DC, USA, p 1046
Ardalan AA, Grafarend EW (2004) High-resolution regional geoid computation without applying Stokes’s formula: a case study of the Iranian geoid. J Geodesy 78:138–156
Arfken GB, Weber HJ (2005) Mathematical methods for physicists, 6th edn. Elsevier Academic Press, New York, p 1182
Balakin AB, Daishev RA, Murzakhanov ZG, Skochilov AF (1997) Laser-interferometric detector of the first, second and third derivatives of the potential of the Earth gravitational field. Izvestiya vysshikh uchebnykh zavedenii, seriya Geologiya i Razvedka 1:101–107
Bell RE, Anderson RN, Pratson LF (1997) Gravity gradiometry resurfaces. Lead Edge 16:55–60
Bölling C, Grafarend EW (2005) Ellipsoidal spectral properties of the Earth’s gravitational potential and its first and second derivatives. J Geodesy 79:300–330
Brieden P, Müller J, Flury J, Heinzel G (2010) The mission OPTIMA -novelties and benefit. Geotechnologien, Science Report no. 17, Potsdam, Germany, pp. 134–139
Chauvenet W (1875) A treatise on plane and spherical trigonometry, 9th edn. JB Lippincott & Co., Philadelphia, p 270
DiFrancesco D, Meyer TJ, Christensen A, FitzGerald D (2009) Gravity gradiometry—today and tomorrow. In: 11th SAGA Biennial Technical Meeting and Exhibition, September 13–18, 2009. Swaziland, South Africa, pp 80–83
Denker H (2003) Computation of gravity gradients for Europe for calibration/validation of GOCE data. In: Tziavos IN (ed) Gravity and Geoid 2002, 3rd Meeting of the International Gravity and Geoid Commission, August 26–30 2002. Thessaloniki, Greece, Ziti Publishing, Thessaloniki, Greece, pp 287–292
Douch K, Panet I, Pajot-Métivier G, Christophe B, Foulon B, Lequentrec-Lalancette M-F, Diament M (2015) Error analysis of a new planar electrostatic gravity gradiometer for airborne surveys. J Geodesy 89:1217–1231
Dransfield M (2007) Airborne gravity gradiometry in the search for mineral deposits. In: Milkereit B (ed) Proceedings of Exploration 07: Fifth Decennial International Conference on Mineral Exploration, September 9–12, 2007. Canada, Toronto, pp 341–354
Eötvös L (1896) Untersuchungen über gravitation und erdmagnetismus. Annalen der Physik und Chemie, Neue Folge 59:354–400
ESA (1999) Gravity field and steady-state ocean circulation mission. In: Reports for mission selection, ESA SP-1233(1)—the four candidate earth explorer core missions, ESA Publication Division, ESTEC, Noordwijk, The Netherlands, p 217
Eshagh M (2008) Non-singular expressions for the vector and the gradient tensor of gravitation in a geocentric spherical frame. Comput Geosci 34:1762–1768
Eshagh M (2011a) On integral approach to regional gravity field modelling from satellite gradiometric data. Acta Geophys 59:29–54
Eshagh M (2011b) The effect of spatial truncation error on the integral inversion of satellite gravity gradiometry data. Adv Space Res 45:1238–1247
Eshagh M, Ghorbannia M (2013) The use of Gaussian equations of motions of a satellite for local gravity anomaly recovery. Adv Space Res 52:30–38
Eshagh M, Šprlák M (2016) On the integral inversion of satellite-to-satellite velocity differences for local gravity field recovery: a theoretical study. Celest Mech Dyn Astron 124:127–144
Fixler JB (2003) Atom interferometer-based gravity gradiometer measurements. Doctoral Thesis, Faculty of Graduate School, Yale University, New Haven, Connecticut, USA, p 138
Garcia RV (2002) Local geoid determination from GRACE mission. Report No. 460, Department of Civil and Environmental Engineering and Geodetic Science, The Ohio State University, Columbus, Ohio, USA, p 106
Ghobadi-Far K, Sharifi MA, Sneeuw N (2016) 2D Fourier series representation of gravitational functionals in spherical coordinates. J Geodesy 90:871–881
Grafarend EW (2001) The spherical horizontal and spherical vertical boundary value problem—vertical deflections and geoid undulations - the completed Meissl diagram. J Geodesy 75:363–390
Grafarend EW, Heck B, Knickmeyer EH (1985) The free versus fixed geodetic boundary value problem for different combinations of geodetic observables. Bull Géodésique 59:11–32
Haagmans R, de Min E, van Gelderen M (1993) Fast evaluation of convolution integral on the sphere using 1D-FFT and a comparison with existing methods for Stokes integral. Manuscr Geod 18:227–241
Heck B (1979) Zur lokalen Geoidbestimmung aus terrestrischen Messungen vertikaler Schweregradienten. Deutsche Geodätische Kommission, Reihe C, Nr. 259, München, Germany
Heiskanen WA, Moritz H (1967) Physical geodesy. Freeman and Co., San Francisco, USA, p 364
Hotine M (1969) Mathematical geodesy. Environmental science services administration, monograph no. 2, US Department of Commerce, Washington DC, USA, p 416
Huang J, Vaníček P, Novák P (2000) An alternative algorithm to FFT for the numerical evaluation of Stokes’s integral. Stud Geophys Geod 44:374–380
Jekeli C (1988) The gravity gradiometer survey system (GGSS). Eos Trans Am Geophys Union 69:105–117
Jekeli C (1993) A review of gravity gradiometer survey system data analyses. Geophysics 58:508–514
Jekeli C (2007) Potential theory and static gravity field of the Earth. In: Schubert G (ed) Treatise on geophysics, vol 3. Elsevier, Oxford, pp 11–42
Kellogg OD (1929) Foundations of potential theory. Verlag von Julius Springer, Berlin 384 p
Kern M, Haagmans R (2005) Determination of gravity gradients from terrestrial gravity data for calibration and validation of gradiometric data. In: Jekeli C, Bastos L, Fernandes L (eds) Gravity, geoid and space missions, IAG symposia series, vol 129. Springer-Verlag, Berlin, pp 95–100
Klopping FJ, Billson RM, Niebauer TM (2014) Interferometric differential gradiometer apparatus and method. United States Patent, Patent no. US 20140026654 A1, Washington DC, USA
Koch KR (1971) Die geodätische Randwertaufgabe bei bekannter Erdoberfläche. Zeitschrift für Vermessungswesen 96:218–224
Lelgemann D (1976) On the recovery of gravity anomalies from high precision altimeter data. Report No. 239, Department of Geodetic Science and Surveying, The Ohio State University, Columbus, Ohio, USA, p 52
Li J (2002) A formula for computing the gravity disturbance from the second radial derivative of the disturbing potential. J Geodesy 76:226–231
Li J (2005) Integral formulas for computing the disturbing potential, gravity anomaly and the deflection of the vertical from the second-order radial gradient of the disturbing potential. J Geodesy 79:64–70
Luying C, Houze X (2006) General inverse of Stokes, Vening-Meinesz and Molodensky formulae. Sci China Ser D Earth Sci 49:499–504
Martinec Z (2003) Green’s function solution to spherical gradiometric boundary-value problems. J Geodesy 77:41–49
McGuirk JM, Foster GT, Fixler JB, Snadden MJ, Kasevich MA (2002) Sensitive absolute-gravity gradiometry using atom interferometry. Phys Rev A 65:033608, p 13
Meissl P (1971) A study of covariance functions related to the Earth’s disturbing potential. Report No. 151, Department of Geodetic Science, The Ohio State University, Columbus, Ohio, USA, p 86
Meyer TJ (2013) Gravity sensing instrument. United States Patent, Patent no. US 8359920 B2, Washington DC, USA
Molodensky MS, Eremeev VF, Yurkina MI (1962) Methods for study of the external gravitational field and figure of the Earth. The Israel Program for Scientific Translations, Department of Commerce, Washington DC, USA, p 248
Moritz H (1967) Kinematical geodesy. Report no. 92, Department of Geodetic Science, Ohio State University, Columbus, Ohio, USA, p 65
Moritz H (1989) Advanced physical geodesy, 2nd edn. Herbert Wichmann Verlag, Karlsruhe 500 p
Moritz H (2000) Geodetic reference system 1980. J Geodesy 74:128–133
Novák P (2007) Integral inversion of SST data of type GRACE. Stud Geophys Geod 51:351–367
Novák P, Austen G, Sharifi MA, Grafarend EW (2006) Mapping Earth’s gravitation using GRACE data. In: Flury J, Rummel R, Reigber C, Rothacher M, Boedecker G, Schreiber U (eds) Observation of the earth system from space. Springer-Verlag, Berlin Heidelberg, pp 149–164
Pavlis NK, Holmes SA, Kenyon SC, Factor JK (2012) The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J Geophys Res (Solid Earth) 117:B04406, p 38
Petrovskaya MS, Zielinski JB (1997) Determination of the global and regional gravitational fields from satellite and balloon gradiometry missions. Adv Space Res 19:1723–1728
Pick M, Pícha J, Vyskočil V (1973) Theory of the Earth’s gravity field. Elsevier, Amsterdam 538 p
Pizzetti P (1911) Sopra il calcolo teorico delle deviazioni del geoide dall’ ellissoide. Atti della Reale Accademia della Scienze di Torino 46:331–350
Reed GB (1973) Application of kinematical geodesy for determining the short wavelength components of the gravity field by satellite gradiometry. Report No. 201, Ohio State University, Department of Geodetic Sciences, Columbus, USA, p 164
Rothleitner C (2013) Interferometric differential free-fall gradiometer. United States Patent, Patent no. US 20130205894 A1, Washington DC, USA
Rothleitner C, Francis O (2014) Measuring the Newtonian constant of gravitation with a differential free-fall gradiometer: a feasibility study. Rev Sci Instrum 85: 044501, p 14
Rosi G, Cacciapuoti L, Sorrentino F, Menchetti M, Prevedelli M, Tino GM (2015) Measurements of the gravity-field curvature by atom interferometry. Phys Rev Lett 114:013001, p 5
Rummel R (2010) GOCE: gravitational gradiometry in a satellite. In: Freeden W, Nashed ZM, Sonar T (eds) Handbook of geomathematics. Springer-Verlag, Berlin, pp 93–103
Rummel R, van Gelderen M (1995) Meissl scheme—spectral characteristics of physical geodesy. Manuscr Geod 20:379–385
Rummel R, Sjöberg LE, Rapp R (1978) The determination of gravity anomalies from geoid heights using the inverse Stokes’ formula, Fourier transforms, and least squares collocation. NASA Contract Report 141442, Department of Geodetic Science, The Ohio State University, Columbus, Ohio, USA, p 65
Rummel R, van Gelderen M, Koop R, Schrama E, Sansó F, Brovelli M, Miggliaccio F, Sacerdote F (1993) Spherical harmonic analysis of satellite gradiometry. Report no. 39, Publications on Geodesy, New Series, Netherlands Geodetic Commission, Delft, The Netherlands, p 124
Simmonds JG (1994) A brief on tensor analysis. Undergraduate texts in mathematics, 2nd edn. Springer-Verlag, New York, p 112
Sorrentino F, Bodart Q, Cacciapuoti L, Lien Y-H, Prevedelli M, Rosi G, Salvi L, Tino GM (2014) Sensitivity limits of a Raman atom interferometer as a gravity gradiometer. Phys Rev 89:023607, p 14
Stokes GG (1849) On the variation of gravity on the surface of the Earth. Trans Camb Philos Soc 8:672–695
Sünkel H (1981) Feasibility studies for the prediction of the gravity disturbance vector in high altitudes. Report No. 311, Department of Geodetic Science, The Ohio State University, Columbus, Ohio, USA, p 53
Šprlák M, Novák P (2014a) Integral transformations of deflections of the vertical onto satellite-to-satellite tracking and gradiometric data. J Geodesy 88:643–657
Šprlák M, Novák P (2014b) Integral transformations of gradiometric data onto GRACE type of observable. J Geodesy 88:377–390
Šprlák M, Novák P (2015) Integral formulas for computing a third-order gravitational tensor from volumetric mass density, disturbing gravitational potential, gravity anomaly and gravity disturbance. J Geodesy 89:141–157
Šprlák M, Novák P (2016) Spherical gravitational curvature boundary-value problem. J Geodesy 90:727–739
Šprlák M, Hamáčková E, Novák P (2015) Alternative validation method of satellite gradiometric data by integral transform of satellite altimetry data. J Geodesy 89:757–773
Šprlák M, Novák P, Pitoňák M (2016) Spherical harmonic analysis of gravitational curvatures and its implications for future satellite missions. Surveys Geophy 37:681–700
Šprlák M, Sebera J, Vaľko M, Novák P (2014) Spherical integral formulas for upward/downward continuation of gravitational gradients onto gravitational gradients. J Geodesy 88:179–197
Thalhammer M (1995) Regionale Gravitationsfeldbestimmung mit zukünftigen Satellitenmissionen (SST und Gradiometrie). Deutsche Geodätische Kommission, Reihe C, Nr. 437, München, Germany
Tóth G (2003) The Eötvös spherical horizontal gradiometric boundary value problem—gravity anomalies from gravity gradients of the torsion balance. In: Tziavos IN (ed) Gravity and Geoid 2002, 3rd Meeting of the International Gravity and Geoid Commission, August 26–30 2002. Thessaloniki, Greece, Ziti Publishing, Thessaloniki, Greece, pp 102–107
Tóth G (2005) The gradiometric-geodynamic boundary value problem. In: Jekeli C, Bastos L, Fernandes L (eds) Gravity, geoid and space missions, IAG Symposia, vol 129. Springer-Verlag Berlin, Germany, pp 352–357
Tóth G, Földváry L, Tziavos IN, Ádám J (2006) Upward/downward continuation of gravity gradients for precise geoid determination. Acta Geod Geophys Hung 41:21–30
Tóth G, Ádám J, Földváry L, Tziavos IN, Denker H (2005) Calibration/validation of GOCE data by terrestrial torsion balance observations. In: Sansó F (ed) A window on the future geodesy, IAG Symposia Series, vol 128. Springer-Verlag Berlin, Germany, pp 214–219
van Gelderen M, Rummel R (2001) The solution of the general geodetic boundary value problem by least squares. J Geodesy 75:1–11
Vaníček P, Krakiwsky EJ (1986) Geodesy: the concepts, 2nd edn. Elsevier Science Publishers B.V., Amsterdam, p 697
Vening-Meinesz FA (1928) A formula expressing the deflection of the plumb-lines in the gravity anomalies and some formulae for the gravity field and the gravity potential outside the geoid. Koninklijke Nederlandsche Akademie van Wetenschappen 31:315–331
Winch DE, Roberts PH (1995) Derivatives of addition theorem for Legendre functions. J Aust Math Soc Ser B Appl Math 37:212–234
Wolf KI (2007) Kombination globaler Potentialmodelle mit terrestrische Schweredaten für die Berechnung der zweiten Ableitungen des Gravitationspotentials in Satelitenbahnhöhe. Deutsche Geodätische Kommission, Reihe C, Nr. 603, München, Germany
Wolf KI, Denker H (2005) Upward continuation of ground data for GOCE calibration. In: Jekeli C, Bastos L, Fernandes L (eds) Gravity, geoid and space missions, IAG symposia series, vol 129. Springer-Verlag, Berlin, pp 60–65
Zhang C (1993) Recovery of gravity information from satellite altimetry data and associated forward geopotential models. UCGE Report No. 20058, University of Calgary, Calgary, Canada, p 160
Acknowledgments
The authors were supported by the project No. GA15-08045S of the Czech Science Foundation. Thoughtful and constructive comments of the three anonymous reviewers are gratefully acknowledged. Thanks are also extended to the editor-in-chief Prof. Jürgen Kusche and the responsible editor Prof. Wolfgang Keller for handling our manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 2 (mpeg 7694 KB)
Supplementary material 3 (mpeg 8000 KB)
Appendices
Appendix A: Formulas for \(u = \cos \psi \), direct azimuth \(\alpha \) and backward azimuth \(\alpha '\)
In this appendix, we provide equations for numerical calculation of the parameter \(u = \cos \psi \), direct azimuth \(\alpha \) and backward azimuth \(\alpha '\). Given the spherical coordinates of the evaluation and integration points, these parameters are defined as follows:
Equations (34a)–(34e) can be derived by using cosine, sine and sine-cosine rules of spherical trigonometry, see, e.g., Chauvenet (1875, pp. 151–154).
Cosines and sines of multiples of \(\alpha \) and \(\alpha '\) also appear in Sect. 3. They read
Equations (35a)–(35f) can be obtained from the multiple-angle formulas for trigonometric functions, see, e.g., Abramowitz and Stegun (1972), p. 72.
Appendix B: Action of the third-order differential operators on multiplication of two functions
In this appendix, the general form resulting from the application of the third-order differential operators on multiplication of two functions is provided. This is exploited in Sects. 3.2 and 3.3 to derive integral transforms of the VH and HH gravitational tensor components onto the third-order gravitational tensor components.
We suppose two functions, i.e., \(f = f(\Omega ,\Omega ')\) and \(h = h (r,R,\Omega ,\Omega ')\). The function f depends only on the geocentric angular coordinates, while h also depends on the geocentric radii of the evaluation and integration points. We now apply the recursive formulas between the second- and third-order differential operators of Eq. (12) to the multiplication of f and h that gives:
Appendix C: Derivatives of the backward azimuth \(\alpha '\)
In Eqs. (36a)–(36i), the first-order derivatives with respect to the spherical geocentric angular coordinates \(\varphi \) and \(\lambda \) as well as the second- and third-order differential operators are applied to the function f. In this appendix, we provide formulas for the action of such differential operators assuming \(f = \cos \alpha '\), \(\sin \alpha '\), \(\cos 2 \alpha '\) and \(\sin 2\alpha '\). These are expressed in terms of the parameters \(t, u, \alpha \) and \(\alpha '\), and exploited for the mathematical derivations in Sect. 3.
The first-order derivatives of \(\cos \alpha '\) read as follows, see, e.g., Winch and Roberts (1995):
We can easily obtain:
-
derivatives of \(\sin \alpha '\) by changing \(\sin \alpha ' \rightarrow - \cos \alpha '\),
-
derivatives of \(\cos 2\alpha '\) by changing \(\sin \alpha ' \rightarrow 2\sin 2\alpha '\),
-
derivatives of \(\sin 2\alpha '\) by changing \(\sin \alpha ' \rightarrow - 2\cos 2\alpha '\),
Formulas for the action of the second-order operators \(\mathcal{{D}}^{xx}\), \(\mathcal{{D}}^{xy}\), \(\mathcal{{D}}^{xz}\), \(\mathcal{{D}}^{yy}\) and \(\mathcal{{D}}^{yz}\) to \(\cos \alpha '\) are of the form (Šprlák et al. 2014):
One can also obtain the action of the second-order differential operators to:
-
\(\sin \alpha '\) by changing \(\sin \alpha ' \rightarrow - \cos \alpha '\) and \(\cos \alpha ' \rightarrow \sin \alpha '\),
-
\(\cos 2\alpha '\) by changing \(\sin \alpha ' \rightarrow 2\sin 2\alpha '\) and \(\cos \alpha ' \rightarrow 4 \cos 2\alpha '\),
-
\(\sin 2\alpha '\) by changing \(\sin \alpha ' \rightarrow - 2\cos 2\alpha '\) and \(\cos \alpha ' \rightarrow 4 \sin 2\alpha '\),
By applying the third-order differential operators \(\mathcal{{D}}^{xxx}\), \(\mathcal{{D}}^{xxy}\), \(\mathcal{{D}}^{xxz}\), \(\mathcal{{D}}^{xyy}\), \(\mathcal{{D}}^{xyz}\), \(\mathcal{{D}}^{xzz}\), \(\mathcal{{D}}^{yyy}\), \(\mathcal{{D}}^{yyz}\) and \(\mathcal{{D}}^{yzz}\) to \(\cos \alpha '\) we get:
We arrive at the formulas for the application of the third-order differential operators for:
-
\(\sin \alpha '\) by changing \(\sin \alpha ' \rightarrow - \cos \alpha '\) and \(\cos \alpha ' \rightarrow \sin \alpha '\).
-
\(\cos 2\alpha '\) by changing \(\cos \alpha ' \rightarrow 4 \cos 2\alpha '\); in addition, we change \(\sin \alpha ' \rightarrow 2\sin 2\alpha '\) for the operators \(\mathcal{{D}}^{xxz}\), \(\mathcal{{D}}^{xyz}\), \(\mathcal{{D}}^{xzz}\), \(\mathcal{{D}}^{yyz}\) and also when \(\sin \alpha '\) is multiplied by \(u^2\), i.e., in the third terms inside the square brackets for the operators \(\mathcal{{D}}^{xxx}\), \(\mathcal{{D}}^{xxy}\), \(\mathcal{{D}}^{xyy}\) and \(\mathcal{{D}}^{yyy}\); for the purely horizontal operators, another change \(\sin \alpha ' \rightarrow 4\sin 2\alpha '\) is applied in the first terms inside the square brackets,
-
\(\sin 2\alpha '\) by changing \(\cos \alpha ' \rightarrow 4 \sin 2\alpha '\); moreover, the substitution \(\sin \alpha ' \rightarrow - 2\cos 2\alpha '\) is applied for the operators \(\mathcal{{D}}^{xxz}\), \(\mathcal{{D}}^{xyz}\), \(\mathcal{{D}}^{xzz}\), \(\mathcal{{D}}^{yyz}\) and also when \(\sin \alpha '\) is multiplied by \(u^2\) in the third terms inside the square brackets for the operators \(\mathcal{{D}}^{xxx}\), \(\mathcal{{D}}^{xxy}\), \(\mathcal{{D}}^{xyy}\) and \(\mathcal{{D}}^{yyy}\); for the purely horizontal differential operators, we also change \(\sin \alpha ' \rightarrow -4\cos 2\alpha '\) in the first terms inside the square brackets,
Appendix D: Auxiliary terms from the action of the third-order differential operators on multiplication of two functions
In this appendix, formulas for the auxiliary terms in Eqs. (36a)–(36i), i.e., all terms except for the action of the second and third-order differential operators, are provided. Similar to “Appendix C”, the auxiliary terms are given for \(f = \cos \alpha '\), \(\sin \alpha '\), \(\cos 2 \alpha '\) and \(\sin 2\alpha '\) in terms of the parameters t, u, \(\alpha \) and \(\alpha '\). However, we still assume the general function \(h = h (r,R,\Omega ,\Omega ')\) specified in Sect. 3.
The auxiliary terms of Eqs. (36a)–(36i) for \(f = \cos \alpha '\) read:
We can also obtain the auxiliary terms for:
-
\(f = \sin \alpha '\) by changing \(\sin \alpha ' \rightarrow - \cos \alpha '\) and \(\cos \alpha ' \rightarrow \sin \alpha '\),
-
\(f = \cos 2\alpha '\) by changing \(\sin \alpha ' \rightarrow 2\sin 2\alpha '\) and \(\cos \alpha ' \rightarrow 4 \cos 2\alpha '\),
-
\(f = \sin 2\alpha '\) by changing \(\sin \alpha ' \rightarrow - 2\cos 2\alpha '\) and \(\cos \alpha ' \rightarrow 4 \sin 2\alpha '\),
Rights and permissions
About this article
Cite this article
Šprlák, M., Novák, P. Spherical integral transforms of second-order gravitational tensor components onto third-order gravitational tensor components. J Geod 91, 167–194 (2017). https://doi.org/10.1007/s00190-016-0951-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00190-016-0951-4