1 Introduction

Currently available sensors in geodesy and geophysics allow for measuring scalar, vectorial and second-order tensorial quantities of the Earth’s gravitational potential field, see, e.g. (Torge 1989; Schwarz and Li 1997; Chelton et al. 2001; Seeber 2003; Forsberg and Olesen 2010; Rummel 2010; Timmen 2010; Torge and Müller 2012). Such observables have widely been exploited by geodesists in various parametrization methods, such as harmonic analysis, integral formulas or radial basis function approach, for the purpose of the Earth’s gravitational field modelling. Theoretical aspects of these quantities have also been extensively studied and well understood (Meissl 1971; Rummel and van Gelderen 1995; Rummel 1997; Grafarend 2001; Bölling and Grafarend 2005; Freeden and Schreiner 2009).

On the other hand, new sensors proposed for observing a third-order gravitational tensor are currently under development. This fact may be illustrated by the project Dulkyn (http://www.dulkyn.ru/) which aims at developing a system that would eventually observe directional derivatives of the gravitational potential up to the third order together with their temporal variations on the Earth surface (Balakin et al. 1997). In addition, the gravity-dedicated satellite mission called OPTIMA (OPTical Interferometry for global MAss change detection from space), which should measure third-order derivatives of the Earth’s gravitational potential, was proposed (Brieden et al. 2010).

Although not currently observable, third-order potential derivatives have already been discussed in various contexts in geodesy. Moritz (1967) investigated parameters of the disturbing gravitational field up to the third-order disturbing gravitational tensor. He showed that gravitational tensors of order three and higher were independent of orientation on platforms without inertial stabilization. Thus, any instrument capable of observing such quantities would provide a purely gravitational signal. Cunningham (1970) derived spherical harmonic series for gravitational tensors of an arbitrary order in a geocentric reference frame. This study, which is of particular interest to satellite geodesy and celestial mechanics, was further extended by Metris et al. (1999) and Petrovskaya and Vershkov (2010). Higher-order vertical derivatives of a harmonic function for its analytical continuation in space were also considered by Velkoborský (1982). Rummel (1986), Koop (1993) and Albertella et al. (2000) used a third-order gravitational tensor for error analysis of gradiometric observations. Wang (1989) provided expressions for the third-order derivatives of the normal gravitational potential generated by an equipotential ellipsoid for analysing sensitivity of second-order gradients measured by an airborne gradiometer. Similarly, Ardalan and Grafarend (2001) expanded the normal gravitational potential in the Taylor series up to the third-order potential derivatives in analysing Bruns’s formula. Grafarend (1997) derived a functional relationship between curvature and torsion of a plumb-line to the second- and third-order derivatives of the gravitational potential.

Nagy et al. (2000) provided directional derivatives of the gravitational potential up to third-order for the mass prism. Keller and Sharifi (2005) analysed satellite gradiometry using a pair of satellites and investigated the influence of higher-order gravitational tensors. Tóth (2005) investigated the gradiometric-geodynamic boundary value problem and its linearisation, and provided expressions of the third-order gravitational tensor in a spherical local reference frame. Making use of the same expressions, Tóth and Földváry (2005) studied projection of the second-order gravitational tensor observed by the gradiometric mission GOCE (Gravity field and steady-state Ocean Circulation Explorer, ESA 1999) onto a geocentric sphere approximating its orbit. Casotto and Fantino (2009) provided general equations for gravitational tensors up to the fourth order by tensor analysis. They also derived explicit expressions for gravitational tensors in the local and global reference frames up to the third order. Csapó et al. (2009) exploited third-order derivatives of the gravitational potential for evaluation of the second-order vertical gradient which is not directly observable by a torsion balance apparatus. Sali (2009) modelled the third-order vertical derivative of the gravitational potential to reduce observation noise in aerial gradiometry data caused by aircraft motion.

Computational aspects of harmonic synthesis up to third-order derivatives of Legendre functions were also discussed (Fantino and Casotto 2009; Fukushima 2012, 2013). Motivated by higher sensitivity of the third-order derivatives to short-wavelength structures of potential fields (Jacoby and Smilde 2009), their exploitation has also been suggested for geophysical exploration purposes, see, e.g. (Troshkov and Shalaev 1968; Smith et al. 1998; Fedi and Florio 2001; Thurston et al. 2002; Abdelrahman et al. 2003; Hafez et al. 2006; Pajot et al. 2008; Veryaskin and McRae 2008; Beiki 2010; Klokočník et al. 2010; Eppelbaum 2011).

Higher-order potential tensors have been applied also in other sciences. Jordan et al. (1995) constructed potential energy surfaces from third-order potential derivatives for studies in molecular chemistry. Sun et al. (2011) provided a mathematical formulation, which splits Hamiltonian into both kinetic and potential energy. Such formulation may be defined by an operator containing third-order potential derivatives and allows for solving related problems of astronomy and celestial mechanics.

In this article, we provide a rigorous mathematical model for transformation of the third-order gravitational tensor to other parameters of the Earth’s gravitational field. Namely, we derive differential operators for the components of the third-order (disturbing) gravitational tensor in the spherical local north-oriented frame (LNOF). We also provide integral formulas that relate the volumetric mass density distribution, disturbing gravitational potential, gravity anomaly and gravity disturbance to the components of the third-order (disturbing) gravitational tensor.

The presented study reveals important properties of the third-order gravitational tensor and further extends the Meissl scheme of physical geodesy, i.e. the well-known theoretical paradigm interrelating various parameters of the Earth’s gravitational field. The new formulas may be exploited in geophysical studies, continuation of gravitational field quantities in space, e.g. by Taylor expansions or gravity transport (Marussi 1985), and in analysing the gradiometric-geodynamic boundary value problem (Tóth 2005). Further applications of the new formulas may emerge in the future after successful development of instruments sensing directly the third-order gravitational gradients.

The article is organised as follows: the nomenclature is defined in Sect. 2; in Sect. 3, we define differential operators for the components of the third-order (disturbing) gravitational tensor in LNOF; in Sect. 4, we apply the differential operators to the integrals of Newton, Abel-Poisson, Pizzetti and Hotine and in Sect. 5, we investigate properties of corresponding integral kernels. Finally, main contributions of the article are summarized in the conclusions.

2 Nomenclature

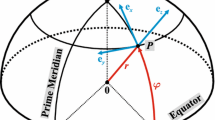
Before we start mathematical derivations, we define the nomenclature used throughout the article. Generally, a gravitational tensor and a gravitational gradient are synonyms, both composed of components. Components of the gravitational tensor will be referred to as gravitational gradients since this terminology has widely been used in geodesy. Whenever important, an order of gravitational gradients will also be specified to indicate the order (or rank) of the respective gravitational tensor. We consider only gravitational gradients referred to the spherical LNOF. Such a reference frame has a moving origin and it is defined by a right-handed orthogonal basis with the following orientation of axes: the \(x\)-axis points to the north, the \(y\)-axis points to the west and the \(z\)-axis is directed radially outward.

In the article, we will use angular geocentric spherical coordinates with the triad \((r, \Omega )\), where \(r\) is the geocentric radius and \(\Omega = (\varphi , \lambda )\) represents a pair of angular spherical geocentric coordinates, i.e. spherical latitude \(\varphi \) and longitude \(\lambda \), to designate the position of an evaluation point. The evaluation point stands for a point in which an integral formula is evaluated. The primed spherical triad \((r', \Omega ')\) stands for the position of an integration volume element, i.e. an infinitesimal tesseroidal volume \({r'}^2\,{{\mathrm {d}} r'}\, {{\mathrm {d}} \Omega '}\). For a constant value of \(r' = R\), where \(R\) represents the radius of a mean geocentric sphere approximating the geoid, the spherical triad \((R, \Omega ')\) designates the position of an integration surface element, i.e. an infinitesimal spherical surface \(R^2\,{{\mathrm {d}} \Omega '}\).

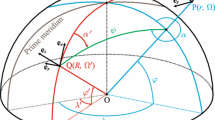
Except for the angular geocentric spherical coordinates, we define the angular spherical polar coordinates \(\alpha = \alpha (\Omega , \Omega ')\), \(\alpha ' = \alpha '(\Omega , \Omega ')\) and \(\psi = \psi (\Omega , \Omega ')\), see Fig. 1. The symbol \(\alpha \) abbreviates the direct azimuth, i.e. the azimuth between an evaluation point and an integration element. It is measured at the evaluation point clockwise from the north. The symbol \(\alpha '\) stands for the backward azimuth, i.e. the azimuth between an integration element and an evaluation point as measured at the integration element clockwise from the north. The symbol \(\psi \) abbreviates the spherical distance between an evaluation point and an integration element.

Fig. 1
figure 1

Graphical illustration of the angular spherical polar coordinates, i.e. the direct azimuth \(\alpha \), the backward azimuth \(\alpha '\) and the spherical distance \(\psi \), between the points \(P\) and \(Q\). \(P\) designates an evaluation point and \(Q\) is the centre of an integration surface element. \(P_\mathrm{N}\) is the North pole and \(O\) is the centre of the mean geocentric sphere with radius \(R\)

Full size image

We also introduce the following substitutions—unitless variables:

$$\begin{aligned} t&= t(r, r') = \frac{r'}{r},\quad r' \le r,\end{aligned}$$
(1)
$$\begin{aligned} u&= u(\Omega , \Omega ') = \cos \psi ,\end{aligned}$$
(2)
$$\begin{aligned} g&= g(t, u) = \sqrt{1 - 2tu + t^2}, \end{aligned}$$
(3)

where \(t\) is the attenuation factor, \(u\) is a cosine of the spherical distance and \(g\) represents the normalised Euclidean distance. These substitutions allow for simpler representations of mathematical formulas.

3 Differential operators for third-order gravitational gradients

A third-order gravitational tensor is generally represented by 27 gravitational gradients \(V_{\mu \nu \tau }\); \(\mu , \nu , \tau \in \{x, y, z\}\). Due to continuity of the gravitational field, the third-order gravitational tensor is symmetric with respect to the pairs of indices \((\mu , \nu )\), \((\nu , \tau )\) and \((\mu , \tau )\), i.e. it holds \(V_{\mu \nu \tau } = V_{\nu \mu \tau }\), \(V_{\mu \nu \tau } = V_{\mu \tau \nu }\) and \(V_{\mu \nu \tau } = V_{\tau \nu \mu }\). By such a symmetry, the third-order gravitational tensor can be defined only by ten gravitational gradients, see, e.g. (Tóth 2005). Another simplification comes from the Laplace differential equation that holds for the gravitational potential in mass-free space and by which \(V_{xx \nu } + V_{yy \nu } + V_{zz \nu } = 0\), \(\nu \in \{x, y, z\}\), see (Casotto and Fantino 2009). In such a case, the third-order gravitational tensor is composed of seven independent components.

Throughout the article, we will provide explicit expressions for ten gravitational gradients of the third order. These may further be divided into the four groups, i.e.

  • horizontal–horizontal–horizontal (HHH) if \(\mu , \nu , \tau \in \{x, y\}\),

  • horizontal–horizontal–vertical (HHV) if \(\mu , \nu \in \{x, y\}\) and \(\tau = z\),

  • horizontal–vertical–vertical (HVV) if \(\mu \in \{x, y\}\) and \(\nu , \tau = z\),

  • and vertical–vertical–vertical (VVV) if \(\mu , \nu , \tau = z\).

Obviously, the third-order gravitational tensor is composed of four HHH, three HHV, two HVV and one VVV gravitational gradients.

The gravitational tensor of the third order is obtained by the successive application of the gradient operator to the gravitational potential. Therefore, the ten gravitational gradients are defined by differential operators. Such differential operators in terms of the spherical geocentric coordinates \((r, \Omega )\) read as follows (Tóth 2005; Casotto and Fantino 2009):

$$\begin{aligned} {\mathcal {D}}^{xxx}&= - \frac{1}{r^2} \left( \frac{2}{r} \frac{\partial }{\partial \varphi } - 3 \frac{\partial ^2}{\partial r \partial \varphi } - \frac{1}{r} \frac{\partial ^3}{\partial \varphi ^3}\right) ,\end{aligned}$$
(4)
$$\begin{aligned} {\mathcal {D}}^{xxy}&= - \frac{1}{r^2 \cos \varphi } \left( \frac{2 \tan ^2 \varphi }{r} \frac{\partial }{\partial \lambda } + \frac{\partial ^2}{\partial r \partial \lambda } \right. \nonumber \\&\left. +\, \frac{2 \tan \varphi }{r} \frac{\partial ^2}{\partial \varphi \partial \lambda } + \frac{1}{r} \frac{\partial ^3}{\partial \varphi ^2 \partial \lambda }\right) ,\end{aligned}$$
(5)
$$\begin{aligned} {\mathcal {D}}^{xxz}&= - \frac{1}{r} \left( \frac{1}{r} \frac{\partial }{\partial r} - \frac{\partial ^2}{\partial r^2} + \frac{2}{r^2} \frac{\partial ^2}{\partial \varphi ^2} - \frac{1}{r} \frac{\partial ^3}{\partial r \partial \varphi ^2}\right) ,\end{aligned}$$
(6)
$$\begin{aligned} {\mathcal {D}}^{xyy}&= - \frac{1}{r^2} \left( \frac{1}{r \cos ^2 \varphi } \frac{\partial }{\partial \varphi } - \frac{\partial ^2}{\partial r \partial \varphi } + \frac{\tan \varphi }{r} \frac{\partial ^2}{\partial \varphi ^2} \right. \nonumber \\&\left. - \frac{2 \tan \varphi }{r \cos ^2 \varphi } \frac{\partial ^2}{\partial \lambda ^2} - \frac{1}{r \cos ^2 \varphi } \frac{\partial ^3}{\partial \varphi \partial \lambda ^2}\right) ,\end{aligned}$$
(7)
$$\begin{aligned} {\mathcal {D}}^{xyz}&= \frac{1}{r^2 \cos \varphi } \left( \frac{2 \tan \varphi }{r} \frac{\partial }{\partial \lambda } - \tan \varphi \frac{\partial ^2}{\partial r \partial \lambda } \right. \nonumber \\&\left. +\,\, \frac{2}{r} \frac{\partial ^2}{\partial \varphi \partial \lambda } - \frac{\partial ^3}{\partial r \partial \varphi \partial \lambda } \right) ,\end{aligned}$$
(8)
$$\begin{aligned} {\mathcal {D}}^{xzz}&= \frac{1}{r} \left( \frac{2}{r^2} \frac{\partial }{\partial \varphi } - \frac{2}{r} \frac{\partial ^2}{\partial r \partial \varphi } + \frac{\partial ^3}{\partial r^2 \partial \varphi } \right) ,\end{aligned}$$
(9)
$$\begin{aligned} {\mathcal {D}}^{yyy}&= \frac{1}{r^2 \cos \varphi } \left( \frac{2}{r \cos ^2 \varphi } \frac{\partial }{\partial \lambda } - 3 \frac{\partial ^2}{\partial r \partial \lambda } + \frac{3 \tan \varphi }{r} \frac{\partial ^2}{\partial \varphi \partial \lambda } \right. \nonumber \\&\left. -\frac{1}{r \cos ^2 \varphi } \frac{\partial ^3}{\partial \lambda ^3}\right) ,\end{aligned}$$
(10)
$$\begin{aligned} {\mathcal {D}}^{yyz}&= - \frac{1}{r} \left( \frac{1}{r} \frac{\partial }{\partial r} - \frac{2 \tan \varphi }{r^2} \frac{\partial }{\partial \varphi } - \frac{\partial ^2}{\partial r^2} + \frac{\tan \varphi }{r} \frac{\partial ^2}{\partial r \partial \varphi } \right. \nonumber \\&\left. +\, \frac{2}{r^2 \cos ^2 \varphi } \frac{\partial ^2}{\partial \lambda ^2} - \frac{1}{r \cos ^2 \varphi } \frac{\partial ^3}{\partial r \partial \lambda ^2} \right) ,\end{aligned}$$
(11)
$$\begin{aligned} {\mathcal {D}}^{yzz}&= - \frac{1}{r \cos \varphi } \left( \frac{2}{r^2} \frac{\partial }{\partial \lambda } - \frac{2}{r} \frac{\partial ^2}{\partial r \partial \lambda } + \frac{\partial ^3}{\partial r^2 \partial \lambda } \right) ,\end{aligned}$$
(12)
$$\begin{aligned} {\mathcal {D}}^{zzz}&= \frac{\partial ^3}{\partial r^3}. \end{aligned}$$
(13)

The superscripts on the left-hand sides of Eqs. (4)–(13) indicate gravitational gradients that are obtained by applying the differential operators. Note that these differential operators were originally derived in a right-handed spherical LNOF with the \(x\)-axis pointing eastwards and the \(y\)-axis pointing north.

The differential operators of Eqs. (4)–(13) are composed of derivatives with respect to the spherical coordinates \(r\), \(\varphi \) and \(\lambda \) up to the third order. These are of a particular interest when the gravitational potential is expanded in a spherical harmonic series. For parametrization of the Earth’s gravitational field, e.g. by integral transformations, least-squares collocation or radial basis function approach, other representations, such as those in the spherical polar coordinates \((r, \psi , \alpha )\) or in terms of \((t, u, \alpha )\), are more appropriate. These lead to decomposition of the differential operators in Eqs. (4)–(13) into an azimuthal and an isotropic part and significantly simplify subsequent mathematical derivations and numerical evaluation.

At least two different ways may be followed to get the differential operators for the third-order gravitational gradients in terms of \((r, \psi , \alpha )\) or \((t, u, \alpha )\). In the first approach, one starts with Eqs. (4)–(13) and applies the chain rule up to the third-order derivatives with respect to \(r\), \(\varphi \) and \(\lambda \). In the second approach, recursive relations between the differential operators for the second-order gravitational gradients, which are summarized in Appendix , and their third-order counterparts are sought. Such a transition involves only first-order differentiation with respect to \(r\), \(\varphi \) and \(\lambda \) which may be handled more easily by the chain rule again.

Our experience has shown that the second approach was less laborious; therefore, it will be followed in this article below. To start with the second approach, we need the recursive relation between the differential operators for the second- and third-order gravitational gradients. This relation is defined by the following proposition:

Proposition 1

The recursive relationships between the differential operators for the second- and third-order gravitational gradients are:

$$\begin{aligned} {\mathcal {D}}^{xxx}&= \frac{1}{r} \left( 2 {\mathcal {D}}^{xz} \!+\! \frac{\partial }{\partial \varphi } {\mathcal {D}}^{xx}\right) , \,\,\, \!\!\!{\mathcal {D}}^{xxy} \!=\! \frac{1}{r} \!\left( {\mathcal {D}}^{yz} \!+\! \frac{\partial }{\partial \varphi } {\mathcal {D}}^{xy} \!\right) \!, \nonumber \\ \quad {\mathcal {D}}^{xxz}&= \frac{\partial }{\partial r} {\mathcal {D}}^{xx}, \quad {\mathcal {D}}^{xyy} = \frac{1}{r} \frac{\partial }{\partial \varphi } {\mathcal {D}}^{yy},\nonumber \\ {\mathcal {D}}^{xyz}&= \frac{\partial }{\partial r} {\mathcal {D}}^{xy}, \quad {\mathcal {D}}^{xzz} = \frac{\partial }{\partial r} {\mathcal {D}}^{xz},\nonumber \\ \quad {\mathcal {D}}^{yyy}&= \frac{1}{r} \left[ 2 \left( {\mathcal {D}}^{yz} - \tan \varphi {\mathcal {D}}^{xy}\right) - \frac{1}{\cos \varphi } \frac{\partial }{\partial \lambda } {\mathcal {D}}^{yy} \right] ,\nonumber \\ {\mathcal {D}}^{yyz}&= \frac{\partial }{\partial r} {\mathcal {D}}^{yy}, \quad {\mathcal {D}}^{yzz} = \frac{\partial }{\partial r} {\mathcal {D}}^{yz} , \quad {\mathcal {D}}^{zzz} = \frac{\partial }{\partial r} {\mathcal {D}}^{zz}. \end{aligned}$$
(14)

One may prove Proposition 1 by applying Eq. (14) to those of Eqs. (71)–(76). After performing differentiations and algebraic manipulations, we get expressions for the differential operators of the third-order gravitational gradients defined by Eqs. (4)–(13). Alternatively, Proposition 1 may be proven by the recursive formula of Casotto and Fantino (2009, Eq. 24) requiring the Christoffel symbols of the second kind.

It can be seen from Eq. (14) that the differential operators for the HHV, HVV and VVV gravitational gradients are obtained by the first-order radial derivative of the corresponding second-order differential operators. Generally, the differential operators for the HHH gravitational gradients are linear combinations of two terms: the first term may be either zero, another second-order differential operator or a combination of second-order differential operators; the second term is a first-order derivative either with respect to \(\varphi \) or \(\lambda \) of a second-order differential operator.

We can now formulate representation of the differential operators for the third-order gravitational gradients in terms of the spherical polar triad \((r, \psi , \alpha )\) and in terms of \((t, u, \alpha )\):

Proposition 2

The differential operators for the third-order gravitational gradients in terms of the spherical polar triad \((r, \psi , \alpha )\) and in terms of \((t, u, \alpha )\) are:

$$\begin{aligned} {\mathcal {D}}^{xxx}&= \frac{1}{r'^3} \left( \cos \alpha {\mathcal {D}}_{3}^{1} + \cos 3 \alpha {\mathcal {D}}_{3}^{2}\right) ,\nonumber \\ {\mathcal {D}}^{xxy}&= - \frac{1}{r'^3} \left( \frac{1}{3} \sin \alpha {\mathcal {D}}_{3}^{1} + \sin 3 \alpha {\mathcal {D}}_{3}^{2}\right) ,\nonumber \\ {\mathcal {D}}^{xxz}&= \frac{1}{r'^3} \left( {\mathcal {D}}_{3}^{3} + \cos 2 \alpha {\mathcal {D}}_{3}^{4}\right) ,\nonumber \\ {\mathcal {D}}^{xyy}&= \frac{1}{r'^3} \left( \frac{1}{3} \cos \alpha {\mathcal {D}}_{3}^{1} - \cos 3 \alpha {\mathcal {D}}_{3}^{2}\right) ,\nonumber \\ {\mathcal {D}}^{xyz}&= - \frac{1}{r'^3} \sin 2 \alpha {\mathcal {D}}_{3}^{4},\nonumber \\ {\mathcal {D}}^{xzz}\!&= \!\frac{1}{r'^3} \cos \alpha {\mathcal {D}}_{3}^{5}, \quad {\mathcal {D}}^{yyy} \!=\! - \frac{1}{r'^3} \left( \sin \alpha {\mathcal {D}}_{3}^{1} \!-\! \sin 3 \alpha {\mathcal {D}}_{3}^{2}\right) ,\nonumber \\ {\mathcal {D}}^{yyz}&= \frac{1}{r'^3} \left( {\mathcal {D}}_{3}^{3} - \cos 2 \alpha {\mathcal {D}}_{3}^{4}\right) ,\nonumber \\ {\mathcal {D}}^{yzz}&= - \frac{1}{r'^3} \sin \alpha {\mathcal {D}}_{3}^{5}, \quad {\mathcal {D}}^{zzz} = \frac{1}{r'^3} {\mathcal {D}}_{3}^{6}, \end{aligned}$$
(15)

where

$$\begin{aligned} {\mathcal {D}}_{3}^{1}&= \frac{3 r'^3}{r^2} \left[ \frac{1}{4 r} \left( 2 + \frac{1}{\sin ^2 \psi }\right) \frac{\partial }{\partial \psi } - \frac{\partial ^2}{\partial r \partial \psi } \right. \nonumber \\&\left. -\frac{1}{4 r} \left( \cot \psi \frac{\partial ^2}{\partial \psi ^2} +\frac{\partial ^3}{\partial \psi ^3}\right) \right] \nonumber \\ \!&= \! - 3 t^3 \sqrt{1 - u^2} \left( \frac{\partial }{\partial u} \!+\! t \frac{\partial ^2}{\partial t \partial u} \!+\! u \frac{\partial ^2}{\partial u^2} \!-\! \frac{1 - u^2}{4} \frac{\partial ^3}{\partial u^3}\right) ,\end{aligned}$$
(16)
$$\begin{aligned} {\mathcal {D}}_{3}^{2}&= - \frac{r'^3}{4 r^3} \Bigg [\left( \frac{1}{\sin ^2 \psi } + 2 \cot ^2 \psi \right) \frac{\partial }{\partial \psi } \nonumber \\&- 3 \cot \psi \frac{\partial ^2}{\partial \psi ^2} + \frac{\partial ^3}{\partial \psi ^3}\Bigg ] = \frac{t^3 \sqrt{(1-u^2)^{3}}}{4} \frac{\partial ^3}{\partial u^3},\end{aligned}$$
(17)
$$\begin{aligned} {\mathcal {D}}_{3}^{3}&= - \frac{r'^3}{r} \Bigg (\frac{1}{r} \frac{\partial }{\partial r} + \frac{\cot \psi }{r^2} \frac{\partial }{\partial \psi } - \frac{\partial ^2}{\partial r^2} - \frac{\cot \psi }{2 r} \frac{\partial ^2}{\partial r \partial \psi } \nonumber \\&+ \frac{1}{r^2} \frac{\partial ^2}{\partial \psi ^2} - \frac{1}{2 r}\frac{\partial ^3}{\partial r \partial \psi ^2}\Bigg )\nonumber \\&= t^3 \left[ 3 t \frac{\partial }{\partial t} + 2 u \frac{\partial }{\partial u} + t u \frac{\partial ^2}{\partial t \partial u} + t^2 \frac{\partial ^2}{\partial t^2} \right. \nonumber \\&\left. - (1 - u^2) \left( \frac{\partial ^2}{\partial u^2} + \frac{t}{2} \frac{\partial ^3}{\partial t \partial u^2}\right) \right] , \end{aligned}$$
(18)
$$\begin{aligned} {\mathcal {D}}_{3}^{4}&= \frac{r'^3}{r^2} \Bigg (\frac{\cot \psi }{r} \frac{\partial }{\partial \psi } - \frac{\cot \psi }{2} \frac{\partial ^2}{\partial r \partial \psi } - \frac{1}{r} \frac{\partial ^2}{\partial \psi ^2} + \frac{1}{2} \frac{\partial ^3}{\partial r \partial \psi ^2}\Bigg ) \nonumber \\&= - t^3 (1 - u^2) \left( \frac{\partial ^2}{\partial u^2} + \frac{t}{2} \frac{\partial ^3}{\partial t \partial u^2}\right) ,\end{aligned}$$
(19)
$$\begin{aligned} {\mathcal {D}}_{3}^{5}&= - \frac{r'^3}{r} \Bigg (\frac{2}{r^2} \frac{\partial }{\partial \psi } - \frac{2}{r} \frac{\partial ^2}{\partial r \partial \psi } + \frac{\partial ^3}{\partial r^2 \partial \psi }\Bigg ) \nonumber \\&= t^3 \sqrt{1 - u^2} \left( 2 \frac{\partial }{\partial u} + 4 t \frac{\partial ^2}{\partial t \partial u} + t^2 \frac{\partial ^3}{\partial t^2 \partial u}\right) ,\end{aligned}$$
(20)
$$\begin{aligned} {\mathcal {D}}_{3}^{6}&= r'^3 \frac{\partial ^3}{\partial r^3} = - t^4 \left( 6 \frac{\partial }{\partial t} + 6 t \frac{\partial ^2}{\partial t^2} + t^2 \frac{\partial ^3}{\partial t^3}\right) . \end{aligned}$$
(21)

The proof of Proposition 2 may be performed in several steps. Firstly, the differential operators of Eq. (77) are substituted into those of Eq. (14). Secondly, we make use of the following expressions, see, e.g. (Heiskanen and Moritz 1967, p. 113):

$$\begin{aligned} \frac{\partial }{\partial \varphi } = - \cos \alpha \frac{\partial }{\partial \psi }, \quad \frac{1}{\cos \varphi } \frac{\partial }{\partial \lambda } = - \sin \alpha \frac{\partial }{\partial \psi }, \end{aligned}$$
(22)

and, e.g. (Winch and Roberts 1995):

$$\begin{aligned}&\frac{\partial \sin 2 \alpha }{\partial \varphi }=2 \cot \psi \cos 2 \alpha \sin \alpha , \nonumber \\&\quad \frac{\partial \cos 2 \alpha }{\partial \varphi }=- 2 \cot \psi \sin 2 \alpha \sin \alpha ,\nonumber \\&\frac{\partial \cos 2 \alpha }{\partial \lambda }=\frac{2 \cos \varphi ' \sin 2 \alpha \cos \alpha '}{\sin \psi }. \end{aligned}$$
(23)

After performing some algebraic operations, we get the expressions for the differential operators of the third-order gravitational gradients in terms of the triad \((r, \psi , \alpha )\). Such a representation is defined by Eq. (15) and the first equalities of \({\mathcal {D}}_{3}^{i}\); \(i = 1, \ldots , 6\) of Eqs. (16)–(21). Thirdly, Eqs. (16)–(21) are expressed in terms of the substitutions \(t\) and \(u\), see Eqs. (1) and (2), applying again the chain rule relations:

$$\begin{aligned}&\frac{\partial }{\partial r} = - \frac{t^2}{r'} \frac{\partial }{\partial t}, \quad \frac{\partial }{\partial \psi } = - \sqrt{1 - u^2}\ \frac{\partial }{\partial u},\nonumber \\&\frac{\partial ^2}{\partial r^2} = \frac{t^3}{r'^2} \left( 2 \frac{\partial }{\partial t} + t \frac{\partial ^2}{\partial t^2}\right) , \quad \!\!\! \frac{\partial ^2}{\partial r \partial \psi }\! =\! \frac{t^2 \sqrt{1 - u^2}}{r'} \frac{\partial ^2}{\partial t \, \partial u}, \nonumber \\&\frac{\partial ^2}{\partial \psi ^2} = - u \frac{\partial }{\partial u} + \left( 1 - u^2\right) \frac{\partial ^2}{\partial u^2},\nonumber \\&\frac{\partial ^3}{\partial r^3} = - \frac{t^4}{r'^3} \left( 6 \frac{\partial }{\partial t} + 6 t \frac{\partial ^2}{\partial t^2} + t^2 \frac{\partial ^3}{\partial t^3}\right) ,\nonumber \\&\frac{\partial ^3}{\partial r^2 \partial \psi } = - \frac{t^3 \sqrt{1 - u^2}}{r'^2} \left( 2 \frac{\partial ^2}{\partial t \partial u} + t \frac{\partial ^3}{\partial t^2 \partial u}\right) ,\nonumber \\&\frac{\partial ^3}{\partial r \partial \psi ^2} = \frac{t^2}{r'} \Bigg [u \frac{\partial ^2}{\partial t \partial u} - (1 - u^2) \frac{\partial ^3}{\partial t \partial u^2}\Bigg ], \nonumber \\&\frac{\partial ^3}{\partial \psi ^3} = \sqrt{1 - u^2} \Bigg [\frac{\partial }{\partial u} + 3 u \frac{\partial ^2}{\partial u^2} - (1 - u^2) \frac{\partial ^3}{\partial u^3}\Bigg ]. \end{aligned}$$
(24)

Note that the subscript on the left-hand sides of Eqs. (16)–(21) represents the respective order of the gravitational tensor which distinguishes the operators of Eqs. (16)–(21) from those of Eqs. (78)–(81).

Proposition 2 demonstrates that the differential operators for the third-order gravitational gradients may efficiently be decomposed into the azimuthal and isotropic parts. The azimuthal part is represented by trigonometric functions of multiples of the direct azimuth \(\alpha \). The maximum multiple of the direct azimuth \(\alpha \) corresponds to the order of the gravitational tensor. The isotropic part is defined by the six differential operators \({\mathcal {D}}_{3}^{i}\); \(i = 1, \ldots , 6\) that are rotationally symmetric about the radial direction, i.e. azimuthally isotropic. We will refer to such differential operators as isotropic.

Moreover, the inspection of Eq. (15) reveals that for one group of the gravitational gradients (either HHH, HHV, HVV or VVV), isotropic differential operators occur repeatedly. For example, the four HHH gravitational gradients are expressed by the isotropic differential operators \({\mathcal {D}}_{3}^{1}\) and \({\mathcal {D}}_{3}^{2}\). It may also be seen that some pairs of the differential operators, i.e. \(({\mathcal {D}}^{xxx}, {\mathcal {D}}^{yyy})\), \(({\mathcal {D}}^{xyy}, {\mathcal {D}}^{xxy})\), \(({\mathcal {D}}^{xzz}, {\mathcal {D}}^{yzz})\) and \(({\mathcal {D}}^{xxz}, {\mathcal {D}}^{yyz})\), are symmetric with respect to the rotation of the direct azimuth \(\alpha \). The first three pairs are interrelated by the rotation of \(\pi /2\), e.g. we get \({\mathcal {D}}^{yyy}\) by considering \(\alpha + \pi /2\) for the differential operator \({\mathcal {D}}^{xxx}\). The last pair of the differential operators is rotationally symmetric by rotating \(\alpha \) by angle \(\pm \pi /2\).

The differential operators of Proposition 2 may be simplified for a certain class of isotropic kernels to which they are applied. The more concise definition is defined by the following proposition:

Proposition 3

For the isotropic kernels of the series form:

$$\begin{aligned} {\mathcal {K}} (t, u) = \sum \limits _{n=0}^{\infty } t^{n+1}h_n P_{n,0} (u), \end{aligned}$$
(25)

with \(h_n\) being eigenvalues of the isotropic kernels, the differential operators for the third-order gravitational gradients may be expressed as:

$$\begin{aligned} {\mathcal {D}}^{xxx}&= \frac{1}{r'^3} \left( \cos \alpha {\mathcal {D}}_{3}^{1*} + \cos 3 \alpha {\mathcal {D}}_{3}^{3*}\right) ,\nonumber \\ {\mathcal {D}}^{xxy}&= - \frac{1}{r'^3} \left( \frac{1}{3} \sin \alpha \ {\mathcal {D}}_{3}^{1*} + \sin 3 \alpha {\mathcal {D}}_{3}^{3*}\right) ,\nonumber \\ {\mathcal {D}}^{xxz}&= \frac{1}{r'^3} \left( {\mathcal {D}}_{3}^{0*} + \cos 2 \alpha {\mathcal {D}}_{3}^{2*}\right) ,\nonumber \\ {\mathcal {D}}^{xyy}&= \frac{1}{r'^3} \left( \frac{1}{3} \cos \alpha {\mathcal {D}}_{3}^{1*} - \cos 3 \alpha {\mathcal {D}}_{3}^{3*}\right) ,\nonumber \\ {\mathcal {D}}^{xyz}&= - \frac{1}{r'^3} \sin 2 \alpha {\mathcal {D}}_{3}^{2*}, \quad {\mathcal {D}}^{xzz} = - \frac{4}{3 r'^3} \cos \alpha {\mathcal {D}}_{3}^{1*},\nonumber \\ {\mathcal {D}}_{3}^{yyy}&= - \frac{1}{r'^3} \left( \sin \alpha {\mathcal {D}}_{3}^{1*} - \sin 3 \alpha {\mathcal {D}}_{3}^{3*}\right) ,\nonumber \\ {\mathcal {D}}^{yyz}&= \frac{1}{r'^3} \left( {\mathcal {D}}_{3}^{0*} \!-\! \cos 2 \alpha {\mathcal {D}}_{3}^{2*}\right) , \quad {\mathcal {D}}^{yzz} \!=\! \frac{4}{3 r'^3} \sin \alpha {\mathcal {D}}_{3}^{1*},\nonumber \\ {\mathcal {D}}^{zzz}&= -\frac{2}{r'^3} {\mathcal {D}}_{3}^{0*}, \end{aligned}$$
(26)

where

$$\begin{aligned} {\mathcal {D}}_{3}^{0*}&= {\mathcal {D}}_{3}^{3} = - \frac{1}{2} {\mathcal {D}}_{3}^{6} = \frac{t^4}{2} \frac{\partial ^3}{\partial t^3} \left( t^2 . \right) ,\end{aligned}$$
(27)
$$\begin{aligned} {\mathcal {D}}_{3}^{1*}&= {\mathcal {D}}_{3}^{1} = - \frac{3}{4} {\mathcal {D}}_{3}^{5} = - \frac{3 t^3 \sqrt{1 - u^2}}{4} \frac{\partial ^3}{\partial t^2 \partial u} \left( t^2 . \right) ,\end{aligned}$$
(28)
$$\begin{aligned} {\mathcal {D}}_{3}^{2*}&= {\mathcal {D}}_{3}^{4} = - \frac{t^2 (1 - u^2)}{2} \frac{\partial ^3}{\partial t \partial u^2} \left( t^2 . \right) ,\end{aligned}$$
(29)
$$\begin{aligned} {\mathcal {D}}_{3}^{3*}&= {\mathcal {D}}_{3}^{2} = \frac{t^3 \sqrt{(1 - u^2)^{3}}}{4} \frac{\partial ^3}{\partial u^3}. \end{aligned}$$
(30)

To prove Proposition 3, the isotropic differential operators \({\mathcal {D}}_{3}^{2}\), \({\mathcal {D}}_{3}^{4}\), \({\mathcal {D}}_{3}^{5}\) and \({\mathcal {D}}_{3}^{6}\) of Eqs. (16)–(21) are rewritten in the form of Eqs. (27)–(30) that follows from the rules of differentiation. It can be seen that the isotropic differential operators of Eqs. (27)–(30) have been renamed as indicated by different numbers in the superscript followed by an asterisk. The number in the superscript corresponds to the order of differentiation with respect to \(u\). Note that the symbol \((t^2 . )\) under differentiation in Eqs. (27)–(29) stands for multiplication of \(t^2\) and the isotropic kernel of Eq. (25). To complete the proof of the proposition, we have to show that \({\mathcal {D}}_{3}^{3} = - \frac{1}{2} {\mathcal {D}}_{3}^{6}\) and \({\mathcal {D}}_{3}^{1} = - \frac{3}{4} {\mathcal {D}}_{3}^{5}\). These equalities follow by applying the isotropic differential operators \({\mathcal {D}}_{3}^{1}\), \({\mathcal {D}}_{3}^{3}\), \({\mathcal {D}}_{3}^{5}\) and \({\mathcal {D}}_{3}^{6}\) of Eqs. (16), (18), (20) and (21) to the kernel of Eq. (25). Note that singular terms of the type \(\frac{u}{\sqrt{1 - u^2}} P_{n,m} (u)\) for \(m = 1, 2\) occur after the application of \({\mathcal {D}}_{3}^{1}\) and \({\mathcal {D}}_{3}^{3}\). These can be removed by the following identity (Arfken 1968, p. 456):

$$\begin{aligned} \frac{u}{\sqrt{1 - u^2}} P_{n,m} (u)&= \frac{1}{2m} \left[ (n + m) (n - m + 1) P_{n,m-1} (u) \right. \nonumber \\&\left. +\, P_{n,m+1} (u)\right] . \end{aligned}$$
(31)

Proposition 3 illustrates another symmetry of the differential operators for the third-order gravitational gradients. It can be seen from Eq. (26) that multiples of the direct azimuth \(\alpha \) and the numbers in the superscripts of the corresponding isotropic differential operators agree. The simplification of Proposition 3 is based on the fact that only four isotropic differential operators are required compared to the six isotropic differential operators of Proposition 2. One has to keep in mind that this holds only if the differential operators act on the isotropic kernels of the form defined by Eq. (25).

4 Application to the integrals of Newton, Abel-Poisson, Pizzetti and Hotine

Having the differential operators in hand, we may relate the third-order gravitational gradients to various parameters of the Earth’s gravitational field. We now focus on the application of the differential operators to the integrals of Newton, Abel-Poisson, Pizzetti (also known as extended Stokes’s integral) and Hotine. The first of these transformations relates the volumetric mass density distribution \(\rho \) to the gravitational potential \(V\) by the volume integral, see, e.g. (Kellogg 1929; Martinec 1998):

$$\begin{aligned} V \left( r, \Omega \right) = G \int \limits _{\Omega '} \int \limits _{r'} \rho \left( r', \Omega '\right) \, {\mathcal {K}}^{N} (t, u) \, r'~{{\mathrm {d}}}r' {{\mathrm {d}}}\Omega ', \end{aligned}$$
(32)

where \(G\) stands for the Newtonian gravitational constant. Note that the first power of \(r'\) in Eq. (32), as opposed to the second power usually presented in geodetic literature, appears due to definition of the Newtonian kernel \({\mathcal {K}}^{N}\), see below. The other three surface integral transformations, i.e. Abel-Poisson (Heiskanen and Moritz 1967), Pizzetti (1911) and Hotine (1969), indicated by the respective superscripts \({\mathcal {P}}\), \({\mathcal {S}}\) and \({\mathcal {H}}\), may concisely be written as:

$$\begin{aligned}&T \left( r, \Omega \right) \nonumber \\&\quad = \frac{1}{4 \pi } \int \limits _{\Omega '} T^{j} \left( R, \Omega '\right) \, {\mathcal {K}}^{j}(t, u) \, {{\mathrm {d}}}\Omega ', j \in \{{\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}, \end{aligned}$$
(33)

where \(T^{{\mathcal {P}}} = T\) is the disturbing gravitational potential, \(T^{{\mathcal {S}}} = R\Delta g\), with \(\Delta g\) being the gravity anomaly and \(T^{{\mathcal {H}}}=R\delta g\) with \(\delta g\) standing for the gravity disturbance.

The integral kernels for the four integral formulas of Eqs. (32) and (33) in the closed form read as follows:

$$\begin{aligned} {\mathcal {K}}^{\mathcal {N}} (t, u)&= \frac{t}{g},\end{aligned}$$
(34)
$$\begin{aligned} {\mathcal {K}}^{\mathcal {P}} (t, u)&= \frac{t (1 - t^2)}{g^3},\end{aligned}$$
(35)
$$\begin{aligned} {\mathcal {K}}^{\mathcal {S}} (t, u)&= t + \frac{2 t}{g} - 3 t g - t^2 u \left[ 5 + 3 \ln \left( \frac{1 - t u + g}{2}\right) \right] ,\nonumber \\ \end{aligned}$$
(36)
$$\begin{aligned} {\mathcal {K}}^{\mathcal {H}} (t, u)&= \frac{2 t}{g} - \ln \left( \frac{t - u + g}{1 - u}\right) . \end{aligned}$$
(37)

These correspond to the infinite series, i.e. the spectral forms:

$$\begin{aligned} {\mathcal {K}}^{j} (t, u) = \sum \limits _{n=0}^{\infty } t^{n+1}h_n^{j} P_{n,0}(u),\quad j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}, \end{aligned}$$
(38)

where the corresponding eigenvalues \(h_n^{j}\) are:

$$\begin{aligned} h_n^{\mathcal {N}}&= 1,&\forall \ n \ge 0,\end{aligned}$$
(39)
$$\begin{aligned} h_n^{\mathcal {P}}&= 2 n + 1,&\forall \ n \ge 0,\end{aligned}$$
(40)
$$\begin{aligned} h_0^{\mathcal {S}}&= h_1^{\mathcal {S}} = 0, h_n^{\mathcal {S}} = \frac{2 n + 1}{n - 1},&\forall \ n \ge 2,\end{aligned}$$
(41)
$$\begin{aligned} h_n^{\mathcal {H}}&= \frac{2 n + 1}{n + 1},&\forall \ n \ge 0. \end{aligned}$$
(42)

The symbol \(P_{n,m}(u)\) stands for the non-normalised Legendre function of the first kind of degree \(n\) and order \(m\).

Mathematical relation between the third-order (disturbing) gravitational gradients and the mass density distribution, disturbing gravitational potential, gravity anomaly and gravity disturbance is formulated in the following proposition:

Proposition 4

Integral formulas\(,\) that relate mass density distribution to the third-order gravitational gradients\(,\) are:

$$\begin{aligned}&V_{\mu \nu \tau } \left( r, \Omega \right) =\, G \int \limits _{\Omega '} \int \limits _{r'} \rho \left( r', \Omega '\right) \, {\mathcal {K}^{\mu \nu \tau , N}} (t, u) \, r'^{-2}\ {{\mathrm {d}}}r' {{\mathrm {d}}}\Omega ',\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \mu , \nu , \tau \in \{x, y, z\}. \end{aligned}$$
(43)

Integral formulas transforming the disturbing gravitational potential\(,\) gravity anomaly and gravity disturbance to the third-order disturbing gravitational gradients are of the form:

$$\begin{aligned}&T_{\mu \nu \tau } \left( r, \Omega \right) =\,\! \frac{1}{4 \pi R^3} \!\!\int \limits _{\Omega '}\! T^{j} \left( R, \Omega '\right) \,\! {\mathcal {K}}^{\mu \nu \tau , j}(t, \!u) \, {{\mathrm {d}}}\Omega ',\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \mu , \nu , \tau \!\in \! \{x, y, z\}, \,\, j \in \{{\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}.\nonumber \\ \end{aligned}$$
(44)

The sub-integral kernels \({\mathcal {K}}^{\mu \nu \tau , j} = {\mathcal {D}}^{\mu \nu \tau }\ {\mathcal {K}}^{j}\); \(\mu , \nu , \tau \in \{x, y, z\}\); \(j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}\) of Eqs. (43) and (44) are defined as follows:

$$\begin{aligned}&{\mathcal {K}}^{xxx, j}=\cos \alpha \ {\mathcal {K}}^{1*, j} + \cos 3 \alpha {\mathcal {K}}^{3*, j},\nonumber \\&{\mathcal {K}}^{xxy, j}=- \frac{1}{3} \sin \alpha {\mathcal {K}}^{1*, j} - \sin 3 \alpha {\mathcal {K}}^{3*, j},\nonumber \\&{\mathcal {K}}^{xxz, j}={\mathcal {K}}^{0*, j} + \cos 2 \alpha {\mathcal {K}}^{2*, j},\nonumber \\&{\mathcal {K}}^{xyy, j}=\frac{1}{3} \cos \alpha {\mathcal {K}}^{1*, j} - \cos 3 \alpha {\mathcal {K}}^{3*, j},\nonumber \\&{\mathcal {K}}^{xyz, j}=- \sin 2 \alpha {\mathcal {K}}^{2*, j}, \quad {\mathcal {K}}^{xzz, j} = - \frac{4}{3} \cos \alpha {\mathcal {K}}^{1*, j}\nonumber \\&{\mathcal {K}}^{yyy, j}=- \sin \alpha {\mathcal {K}}^{1*, j} + \sin 3 \alpha {\mathcal {K}}^{3*, j},\nonumber \\&{\mathcal {K}}^{yyz, j}={\mathcal {K}}^{0*, j} - \cos 2 \alpha {\mathcal {K}}^{2*, j}, \quad {\mathcal {K}}^{yzz, j} = \frac{4}{3} \sin \alpha {\mathcal {K}}^{1*, j},\nonumber \\&{\mathcal {K}}^{zzz, j}=- 2{\mathcal {K}}^{0*, j}, \end{aligned}$$
(45)

where the isotropic kernels read:

$$\begin{aligned} {\mathcal {K}}^{i*, j} (t, u) = {\mathcal {D}}_{3}^{i*} {\mathcal {K}}^{j} (t, u);\quad i \in \{0, 1, 2, 3\}. \end{aligned}$$
(46)

Proposition 4 may be proven by the action of the differential operators of Eq. (26) to Newton’s, Abel-Poisson’s, Pizzetti’s and Hotine’s integrals, see Eqs. (32) and (33). Application of the more concise differential operators of Proposition 3 is permitted because the kernels for these integrals, see Eq. (38), are of the form of Eq. (25). Note that \(r' = R\) in Eq. (26) when these are applied to the integrals of Abel-Poisson, Pizzetti and Hotine. In total, 40 new integral formulas, of which 28 are independent due to the Laplace differential equation, are embedded in Eqs. (43) and (44). Obviously, the sub-integral kernels of Eqs. (45) possess the same properties as we have already discussed for the third-order differential operators, see the paragraphs below Propositions 2 and 3.

Connection between the gravitational field quantities of Eqs. (44)–(46) is depicted in Fig. 2 in terms of a Meissl-type scheme in the spatial domain. The scheme summarizes possible applications of Eqs. (44)–(46). The direct problem (upward continuation) allows for computing disturbing gravitational gradients from the disturbing gravitational potential, gravity anomaly or gravity disturbance. On the other hand, the disturbing gravitational potential, gravity anomaly or gravity disturbance are estimated from the disturbing gravitational gradients by solving the inverse problem (downward continuation). Similar scheme may be depicted also for the volumetric mass density and the gravitational gradients, i.e. Eqs. (43), (45) and (46), and would provide another extension of the Meissl scheme in the spatial domain.

Fig. 2
figure 2

Relation between the disturbing gravitational gradients and the disturbing gravitational potential, gravity anomaly and gravity disturbance. The disturbing gravitational gradients at the evaluation point with spherical coordinates \((r, \Omega )\) are located at the upper level. The symbol \(T^j(R, \Omega ')\), \(j \in \{{\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}\), at the lower level substitutes the disturbing gravitational potential, gravity anomaly and gravity disturbance on the surface of the mean geocentric sphere of radius \(R\). The corresponding isotropic kernels are located at the middle level

Full size image

Explicit expressions for the isotropic kernels of Eq. (46) are required for numerical evaluation of the integral formulas of Eq. (43) and (44). Their spectral forms are defined in the next proposition:

Proposition 5

Spectral forms of the isotropic kernels are:

$$\begin{aligned} {\mathcal {K}}^{0*, j} (t, u) \!&= \! \frac{1}{2} \sum \limits _{n=0}^{\infty } t^{n\!+\!4} h_n^{j} (n \!+\! 1) (n \!+\! 2) (n \!+\! 3) P_{n,0} (u),\end{aligned}$$
(47)
$$\begin{aligned} {\mathcal {K}}^{1*, j} (t, u)&= - \frac{3}{4} \sum \limits _{n=0}^{\infty } t^{n+4} h_n^{j} (n + 2) (n + 3) P_{n,1} (u),\end{aligned}$$
(48)
$$\begin{aligned} {\mathcal {K}}^{2*, j} (t, u)&= - \frac{1}{2} \sum \limits _{n=0}^{\infty } t^{n+4}h_n^{j} (n + 3) P_{n,2} (u),\end{aligned}$$
(49)
$$\begin{aligned} {\mathcal {K}}^{3*, j} (t, u)&= \frac{1}{4} \sum \limits _{n=0}^{\infty } t^{n+4}h_n^{j}P_{n,3} (u). \end{aligned}$$
(50)

Looking at the general definition of the isotropic kernels in Eq. (46), we may prove Proposition 5 by applying the isotropic differential operators of Eqs. (27)–(30) to Eq. (38). Proposition 5 demonstrates a very general definition of the isotropic kernels in the spectral form. Corresponding expressions for \(j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}\) may easily be obtained by inserting the eigenvalues of Eqs. (39)–(42) into Eqs. (47)–(50).

The closed (spatial) forms of the isotropic kernels must be given separately for each of the superscripts \(i\) and \(j\). These are summarized in the next proposition:

Proposition 6

The closed \((\)spatial\()\) forms of the isotropic kernels are:

\(\underline{(\mathbf{a}) \text { for }j = {\mathcal {N}}:}\)

$$\begin{aligned}&{\mathcal {K}}^{0*, {\mathcal {N}}} (t, u)=\frac{3 t^4}{2 g} \Bigg \{2 + \frac{t}{g^2} \left[ 3 (2 u - 3 t) \right. \nonumber \\&\quad \left. + \frac{3 t (t - u) (4 t - 3 u)}{g^2} - \frac{5 t^2 (t - u)^3}{g^4} \right] \Bigg \},\end{aligned}$$
(51)
$$\begin{aligned}&{\mathcal {K}}^{1*, {\mathcal {N}}} (t, u)\nonumber \\&=- \frac{9 t^5 \sqrt{1 - u^2}}{4 g^3} \Bigg \{4 + \frac{t}{g^2} \left[ 8 u - 9 t + \frac{5 t (t - u)^2}{g^2}\right] \Bigg \},\end{aligned}$$
(52)
$$\begin{aligned}&{\mathcal {K}}^{2*, {\mathcal {N}}} (t, u)=- \frac{15 t^6 (1 - u^2)}{2 g^5} \left[ 1 + \frac{t (u - t)}{g^2}\right] ,\end{aligned}$$
(53)
$$\begin{aligned}&{\mathcal {K}}^{3*, {\mathcal {N}}} (t, u) =\frac{15 t^7 \sqrt{(1 - u^2)^{3}}}{4 g^7}, \end{aligned}$$
(54)

\(\underline{(\mathbf{b})\text { for } j = {\mathcal {P}}:}\)

$$\begin{aligned} {\mathcal {K}}^{0*, {\mathcal {P}}} (t, u)&= \frac{3 t^4}{2 g} \Bigg \{2 + \frac{t}{g^2} \bigg [22 u - 49 t \nonumber \\&+ \frac{3 t [(t - u) (54 t - 25 u) + 2 u^2]}{g^2} \nonumber \\&- \frac{5 t^2 (t - u)^2 (37 t - 25 u)}{g^4}\nonumber \\&+ \frac{70 t^3 (t - u)^4}{g^6}\bigg ]\Bigg \},\end{aligned}$$
(55)
$$\begin{aligned} {\mathcal {K}}^{1*, {\mathcal {P}}} (t, u) \!&= \! - \frac{9 t^5 \sqrt{1 \!-\! u^2}}{4 g^3} \Bigg \{12 \!+\! \frac{t}{g^2} \left[ 64 u \!-\! 87 t \right. \nonumber \\&\left. + \frac{5 t (t \!-\! u)(29 t\! -\! 23 u)}{g^2} \!-\! \frac{70 t^2 (t - u)^3}{g^4}\right] \Bigg \},\nonumber \\\end{aligned}$$
(56)
$$\begin{aligned} {\mathcal {K}}^{2*, {\mathcal {P}}} (t, u)&= - \frac{15 t^6 (1 - u^2)}{2 g^5} \Bigg \{5 + \frac{t}{g^2} \left[ 17 u - 19 t \right. \nonumber \\&\left. + \frac{14 t (t - u)^2}{g^2}\right] \Bigg \},\end{aligned}$$
(57)
$$\begin{aligned} {\mathcal {K}}^{3*, {\mathcal {P}}} (t, u)&= \frac{105 t^7 (1 - t^2) \sqrt{(1 - u^2)^{3}}}{4 g^9}, \end{aligned}$$
(58)

\(\underline{(\mathbf{c})\text { for }j = {\mathcal {S}}:}\)

$$\begin{aligned} {\mathcal {K}}^{0*, {\mathcal {S}}} (t, u)&= 3 t^4 \Bigg \{\frac{11}{g} - g (12 - g) - t^2 \nonumber \\&-t u \left[ 31 + 12 \ln \left( \frac{1 + g - t u}{2}\right) \right] \nonumber \\&+\, \frac{t}{2 g^3} \left[ 20 u - 27 t + \frac{3 t (t - u) (9 t - 7 u)}{g^2} \right. \nonumber \\&\left. - \frac{10 t^2 (t - u)^3}{g^4}\right] \Bigg \},\end{aligned}$$
(59)
$$\begin{aligned} {\mathcal {K}}^{1*, {\mathcal {S}}} (t, u)&= \frac{9 t^5 \sqrt{1 - u^2}}{4} \Bigg \{3 \left[ 13 + 4 \ln \left( \frac{1 + g - t u}{2}\right) \right. \nonumber \\&\left. -\frac{4 (g + 1)^2}{g (1 + g - t u)}\right] \nonumber \\&-\frac{1}{g^3} \left[ 15 + \frac{t (19 u - 21 t)}{g^2} + \frac{10 t^2 (t - u)^2}{g^4}\right] \Bigg \},\end{aligned}$$
(60)
$$\begin{aligned} {\mathcal {K}}^{2*, {\mathcal {S}}} (t, u) \!&= \! - \frac{3 t^5 (1 \!-\! u^2)}{2} \Bigg \{\frac{4 t}{1 \!+\! g \!-\! t u} \left[ 1 \!+\! \frac{1}{g^3} \right. \nonumber \\&\left. \!+\, \frac{(g \!+\! 1)^3}{g^2 (1 \!+\! g \!-\! t u)}\right] \!+\! \frac{1}{g^5} \left[ 13 t \!+\! \frac{10 t^2 (u \!-\! t)}{g^2}\right] \Bigg \},\end{aligned}$$
(61)
$$\begin{aligned} {\mathcal {K}}^{3*, {\mathcal {S}}} (t, u) \!&= \! \frac{3 t^7 \sqrt{(1 \!-\! u^2)^{3}}}{4} \Bigg \{\frac{10}{g^7} \!+\! \frac{1}{1 \!+\! g \!-\! t u} \left( \frac{3}{g^5} \!+\! \frac{1}{1 \!+\! g \!-\! t u}\right) \nonumber \\&\!+\, \frac{1}{g^3 (1 \!+\! g \!-\! t u)^2} \left[ \frac{4 g \!+\! 3}{g} \!+\! \frac{2 (g \!+\! 1)^4}{1 \!+\! g \!-\! t u}\right] \Bigg \}, \end{aligned}$$
(62)

\(\underline{(\mathbf{d})\text { for }j = {\mathcal {H}}:}\)

$$\begin{aligned}&{\mathcal {K}}^{0*, {\mathcal {H}}} (t, u) = \frac{t^4}{2 g} \Bigg \{6 + \frac{t}{g^2} \Bigg [30 u - 47 t \nonumber \\&\quad + \frac{3 t (t - u) (23 t - 17 u)}{g^2} - \frac{30 t^2 (t - u)^3}{g^4} \Bigg ]\Bigg \}\end{aligned}$$
(63)
$$\begin{aligned}&{\mathcal {K}}^{1*, {\mathcal {H}}} (t, u) = \frac{3 t^3 \sqrt{1 - u^2}}{2} \Bigg \{\frac{1}{1 - u} - \frac{g + t}{g (g + t - u)} \nonumber \\&\quad - \frac{t^2}{2 g^3} \left[ 19 + \frac{3 t (15 u - 17 t)}{g^2} + \frac{30 t^2 (t - u)^2}{g^4}\right] \Bigg \},\end{aligned}$$
(64)
$$\begin{aligned}&{\mathcal {K}}^{2*, {\mathcal {H}}} (t, u) = t^3 (1 - u^2) \Bigg \{\frac{1}{(1 - u)^2} - \frac{1}{g^2 (g + t - u)} \nonumber \\&\quad \times \left[ \frac{t^2}{g}\,+ \frac{(g + t)^2}{g + t - u}\right] - \frac{3 t^3}{2 g^5} \left[ 9 + \frac{10 t (u - t)}{g^2}\right] \Bigg \},\end{aligned}$$
(65)
$$\begin{aligned}&{\mathcal {K}}^{3*, {\mathcal {H}}} (t, u) \!=\! \frac{t^3 \sqrt{(1 \!-\! u^2)^{3}}}{4} \left\{ \frac{30 t^4}{g^7} \!-\! \frac{2}{(1 - u)^3} \!+\! \frac{1}{g^3 (g \!+\! t \!-\! u)}\right. \nonumber \\&\left. \quad \times \left[ \frac{3 t^3}{g^2} + \frac{3 t^2 (g + t)}{g (g + t - u)} + \frac{2 (g + t)^3}{(g + t - u)^2}\right] \right\} . \end{aligned}$$
(66)

Each of Eqs. (51)–(66) may be proven by summing up the corresponding infinite series representation defined in Proposition 5. We describe details of such a derivation for one of the isotropic kernels, e.g. \({\mathcal {K}}^{2*, {\mathcal {S}}}\). First, the corresponding eigenvalue of Eq. (41) is inserted into Eq. (49) and the degree-dependent term, i.e. the term \(h_n^{{\mathcal {S}}} (n + 3)\), is decomposed into partial fractions. Second, based on the partial fraction decomposition in Eq. (92), the original infinite summation is divided into three separate series. Each of the three series is defined by closed expressions defined by Eqs. (110), (111) and (125). Thirdly, making use of the closed expressions and performing some algebraic operations, we get the isotropic kernel \({\mathcal {K}}^{2*, {\mathcal {S}}}\) in closed form, see Eq. (61). Closed forms of the other isotropic kernels may be obtained by repeating the same steps. Due to brevity, we left this task for an interested reader who may find all necessary formulas in Appendices  and .

Proposition 6 may be complemented by inspecting limits of the isotropic kernels for some special values of \(u\) and \(t\). We have inspected four special cases that are concisely summarized in the next proposition:

Proposition 7

Limits of the isotropic kernels \({\mathcal {K}}^{i*, j};\) \(i \in \{0, 1, 2, 3\};\) \(j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}\) are:

\(\underline{(\mathbf{a})\text { for }u = 1\text { and }t < 1:}\)

$$\begin{aligned} {\mathcal {K}}^{0*, {\mathcal {N}}} (t, 1)&= \frac{3 t^4}{(1 - t)^4}, \quad {\mathcal {K}}^{0*, {\mathcal {P}}} (t, 1) = \frac{3 t^4 (1 + 7 t)}{(1 - t)^5},\nonumber \\ {\mathcal {K}}^{0*, {\mathcal {S}}} (t, 1)&= 3 t^5 \left[ \frac{t (38 - 88 t + 73 t^2 - 21 t^3)}{(1 - t)^4} \!-\! 12 \ln (1 \!-\! t)\right] ,\nonumber \\ {\mathcal {K}}^{0*, {\mathcal {H}}} (t, 1)&= \frac{t^4 (3 + 6 t - 4 t^2 + t^3)}{(1 \!-\! t)^4},\nonumber \\ {\mathcal {K}}^{1*, j} (t, 1)&= {\mathcal {K}}^{2*, j} (t, 1) \!=\! {\mathcal {K}}^{3*, j} (t, 1) \!=\! 0, j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\},\nonumber \\ \end{aligned}$$
(67)

\(\underline{(\mathbf{b})\text { for }u = -1\text { and }t<1:}\)

$$\begin{aligned}&{\mathcal {K}}^{0*, {\mathcal {N}}} (t, -1) = \frac{3 t^4}{(1 + t)^4}, \quad {\mathcal {K}}^{0*, {\mathcal {P}}} (t, -1) = \frac{3 t^4 (1 - 7 t)}{(1 + t)^5},\nonumber \\&{\mathcal {K}}^{0*, {\mathcal {S}}} (t, \!-\!1) \!=\! 3 t^5 \left[ \frac{t (38 \!+\! 88 t + 73 t^2 + 21 t^3)}{(1 \!+\! t)^4} \!+\! 12 \ln (1 + t)\right] ,\nonumber \\&\quad {\mathcal {K}}^{0*, {\mathcal {H}}} (t, -1) = \frac{t^4 (3 - 6 t - 4 t^2 - t^3)}{(1 + t)^4},\nonumber \\&{\mathcal {K}}^{1*, j} (t, -1) = {\mathcal {K}}^{2*, j} (t, -1) = {\mathcal {K}}^{3*, j} (t, -1) = 0,\nonumber \\&\quad j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}, \end{aligned}$$
(68)

\(\underline{(\mathbf{c})\text { for }u = 1\text { and }t = 1:}\)

$$\begin{aligned}&{\mathcal {K}}^{1*, {\mathcal {N}}} (1, 1) = {\mathcal {K}}^{3*, {\mathcal {N}}} (1, 1) = {\mathcal {K}}^{0*, {\mathcal {P}}} (1, 1) = {\mathcal {K}}^{1*, {\mathcal {P}}} (1, 1) \nonumber \\&\quad = {\mathcal {K}}^{2*, {\mathcal {P}}} (1, 1) = {\mathcal {K}}^{1*, {\mathcal {S}}} (1, 1) = {\mathcal {K}}^{3*, {\mathcal {S}}} (1, 1)\nonumber \\&\quad = {\mathcal {K}}^{1*, {\mathcal {H}}} (1, 1) = {\mathcal {K}}^{3*, {\mathcal {H}}} (1, 1) = \infty ,\nonumber \\&{\mathcal {K}}^{0*, {\mathcal {N}}} (1, 1) = {\mathcal {K}}^{2*, {\mathcal {N}}} (1, 1) = {\mathcal {K}}^{0*, {\mathcal {S}}} (1, 1) \nonumber \\&\quad = {\mathcal {K}}^{2*, {\mathcal {S}}} (1, 1) = {\mathcal {K}}^{0*, {\mathcal {H}}} (1, 1) = {\mathcal {K}}^{2*, {\mathcal {H}}} (1, 1) = - \infty ,\nonumber \\&{\mathcal {K}}^{3*, {\mathcal {P}}} (1, 1) = 0, \end{aligned}$$
(69)

\(\underline{(\mathbf{d})\text { for }u = -1\text { and }t = 1:}\)

$$\begin{aligned}&{\mathcal {K}}^{0*, {\mathcal {N}}} (1, -1) = \frac{3}{16}, \quad {\mathcal {K}}^{0*, {\mathcal {P}}} (1, -1) = -\frac{9}{16},\nonumber \\&{\mathcal {K}}^{0*, {\mathcal {S}}} (1, -1) = \frac{165}{4} + 36 \ln 2, \quad {\mathcal {K}}^{0*, {\mathcal {H}}} (1, -1) = - \frac{1}{2},\nonumber \\&{\mathcal {K}}^{1*, j} (1, -1) = {\mathcal {K}}^{2*, j} (1, -1) = {\mathcal {K}}^{3*, j} (1, -1) = 0,\nonumber \\&\qquad j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}. \end{aligned}$$
(70)

Proposition 7 may be proven by finding the limits directly or by making use of the L’Hospital rule. Equations (67)–(70)  reveal that the isotropic kernels are bounded for \(t < 1\). On the other hand, the isotropic kernels are unbounded for \(t = 1\) except for \({\mathcal {K}}^{3*, {\mathcal {P}}}\).

5 Investigation of the sub-integral kernels

To get an insight into the integral transformations of Proposition 4, we have further investigated properties of the sub-integral kernels \({\mathcal {K}}^{\mu \nu \tau , j}\); \(\mu , \nu , \tau \in \{x, y, z\}\); \(j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}\). The sub-integral kernels have been evaluated for two different scenarios: (1) assuming \(R=6{,}371\) km and \(r=6{,}621\) km, and (2) \(R = r = 6{,}371\) km. In the first case, the constant height of 250 km above the mean geocentric sphere approximating the geoid is considered. Thus, it may correspond to altitude of an Earth-orbiting satellite that would eventually observe the third-order gravitational gradients, e.g. such as the proposed mission OPTIMA (Brieden et al. 2010). The second case corresponds to a terrestrial system for observing the third-order gravitational gradients, e.g. as proposed by the Dulkyn project (http://www.dulkyn.ru/, Balakin et al. 1997).

Figure 3 illustrates the sub-integral kernels \({\mathcal {K}}^{xxx, {\mathcal {S}}}\), \({\mathcal {K}}^{xxz, {\mathcal {S}}}\), \({\mathcal {K}}^{xyy, {\mathcal {S}}}\), \({\mathcal {K}}^{xyz, {\mathcal {S}}}\), \({\mathcal {K}}^{xzz, {\mathcal {S}}}\) and \({\mathcal {K}}^{zzz, {\mathcal {S}}}\) for the first scenario. The kernels are depicted as functions of the direct azimuth \(\alpha \) (indicated by the values along the circumference of each plot) and spherical distance \(\psi \) (indicated by the dashed concentric circles). Figures are restricted to the limited spherical domain bounded by \(\alpha \in [0^{\circ }, 360^{\circ }]\) and \(\psi \in [0^{\circ }, 7^{\circ }]\).

Fig. 3
figure 3

Behaviour of the sub-integral kernels: a \({\mathcal {K}}^{xxx, {\mathcal {S}}}\), b \({\mathcal {K}}^{xxz, {\mathcal {S}}}\), c \({\mathcal {K}}^{xyy, {\mathcal {S}}}\), d \({\mathcal {K}}^{xyz, {\mathcal {S}}}\), e \({\mathcal {K}}^{xzz, {\mathcal {S}}}\), f \({\mathcal {K}}^{zzz, {\mathcal {S}}}\) in the spatial domain \(\alpha \in [0^{\circ }, 360^{\circ }]\), \(\psi \in [0^{\circ }, 7^{\circ }]\). The kernels were evaluated for \(R = 6{,}371\) km and \(r = 6{,}621\) km. Values of the direct azimuth \(\alpha \) are indicated along the circumference of each of the polar plots. The spherical distance \(\psi \) is measured from the centre of the polar plots (indicated by the dashed concentric circles). Black lines inside the plots indicate zero crossings of the sub-integral kernels

Full size image

Among all 40 sub-integral kernels, only six of them are sufficient to demonstrate their spatial properties due to two reasons: First, the sub-integral kernels \({\mathcal {K}}^{\mu \nu \tau , j}\); \(\mu , \nu , \tau \in \{x, y, z\}\) behave similarly when mutually comparing between each \(j \in \{{\mathcal {N}}, {\mathcal {P}}, {\mathcal {S}}, {\mathcal {H}}\}\). One could also observe that magnitudes of the sub-integral kernels for \(j \in \{{\mathcal {N}}, {\mathcal {S}}, {\mathcal {H}}\}\) are of the same order. On the other hand, these are two orders lower as compared to the sub-integral kernels for \(j = {\mathcal {P}}\). Among the four values of \(j\), we have opted to further investigate those for \(j = {\mathcal {S}}\). Second, for a particular value of \(j\), the sub-integral kernels posses azimuthal symmetries as mentioned in Sect. 3 below Proposition 2. It holds that the pairs of sub-integral kernels \(({\mathcal {K}}^{xxx, j}, {\mathcal {K}}^{yyy, j})\), \(({\mathcal {K}}^{xyy, j}, {\mathcal {K}}^{xxy, j})\) and \(({\mathcal {K}}^{xzz, j}, {\mathcal {K}}^{yzz, j})\) are interrelated by the azimuthal rotation of \(\pi /2\). For example, one has to rotate the polar plot of the sub-integral kernel \({\mathcal {K}}^{xxx, j}\) by \(\pi /2\) counterclockwise to obtain \({\mathcal {K}}^{yyy, j}\). Moreover, the pair of sub-integral kernels \(({\mathcal {K}}^{xxz, j}, {\mathcal {K}}^{yyz, j})\) is azimuthally symmetric by rotating \(\alpha \) by \(\pm \pi /2\).

Figure 3 reveals several interesting properties of the sub-integral kernels. It can be seen that the kernel \({\mathcal {K}}^{zzz, {\mathcal {S}}}\) is isotropic, while the others posses corresponding azimuthal dependencies. Obviously, the kernels reach maxima or minima in a close neighbourhood of the evaluation point (located in the centre of the polar plots) and decay with the increasing spherical distance. One may also observe that the magnitude of the sub-integral kernels \({\mathcal {K}}^{xxx, {\mathcal {S}}}\), \({\mathcal {K}}^{xyy, {\mathcal {S}}}\), \({\mathcal {K}}^{xyz, {\mathcal {S}}}\) and \({\mathcal {K}}^{xzz, {\mathcal {S}}}\) equals zero at the evaluation point. On the other hand, the sub-integral kernels \({\mathcal {K}}^{xxz, {\mathcal {S}}}\) and \({\mathcal {K}}^{zzz, {\mathcal {S}}}\) reach their extreme values at the evaluation point.

On the surface of the mean geocentric sphere, i.e. for the second scenario with \(R = r = 6{,}371\) km, we have to distinguish between two different cases of the sub-integral kernels. The kernels for \(j\in \{{\mathcal {N}}, {\mathcal {S}}, {\mathcal {H}}\}\) degenerate into those illustrated by Fig. 4. Note that only the sub-integral kernels for \(j = {\mathcal {S}}\) are depicted. Moreover, we restrict to the spatial domain bounded by \(\alpha \in [0^{\circ }, 360^{\circ }]\) and \(\psi \in [0.3^{\circ }, 7^{\circ }]\) due to the singularity at the evaluation point. For handling the singular behaviour in practical calculations see, e.g. (Klees 1996; Klees and Lehmann 1998). The omitted domain, for which it holds \(\alpha \in [0^{\circ }, 360^{\circ }]\) and \(\psi \in [0^{\circ }, 0.3^{\circ })\), is indicated by the grey dots located in the centre of each polar plot. We also note that the magnitude of the sub-integral kernels exceeds the maximum and minimum values of the colour bar scale. Therefore, one may see white and black colours in the polar plots revealing strong increase and decrease of the sub-integral kernels. Similar to the first scenario depicted in Fig. 3, it is obvious from Fig. 4 that only the kernel \({\mathcal {K}}^{zzz, {\mathcal {S}}}\) is isotropic, while the other kernels have also azimuthal dependencies. The kernels \({\mathcal {K}}^{xxx, {\mathcal {S}}}\), \({\mathcal {K}}^{xyy, {\mathcal {S}}}\) and \({\mathcal {K}}^{xzz, {\mathcal {S}}}\) reach higher magnitudes for larger values of the spherical distance as compared to \({\mathcal {K}}^{xxz, {\mathcal {S}}}\), \({\mathcal {K}}^{xyz, {\mathcal {S}}}\) and \({\mathcal {K}}^{zzz, {\mathcal {S}}}\). In particular, this is seen for \(\psi \in [1^{\circ }, 3^{\circ }]\).

Fig. 4
figure 4

Behaviour of the sub-integral kernels: a \({\mathcal {K}}^{xxx, {\mathcal {S}}}\), b \({\mathcal {K}}^{xxz, {\mathcal {S}}}\), c \({\mathcal {K}}^{xyy, {\mathcal {S}}}\), d \({\mathcal {K}}^{xyz, {\mathcal {S}}}\), e \({\mathcal {K}}^{xzz, {\mathcal {S}}}\), f \({\mathcal {K}}^{zzz, {\mathcal {S}}}\) in the spatial domain \(\alpha \in [0^{\circ }, 360^{\circ }]\), \(\psi \in [0.3^{\circ }, 7^{\circ }]\). The kernels were evaluated for \(R = r = 6{,}371\) km. Values of the direct azimuth \(\alpha \) are indicated along the circumference of each of the polar plots. The spherical distance \(\psi \) is measured from the centre of the polar plots (indicated by the dashed concentric circles). Black lines inside the plots indicate zero crossings of the sub-integral kernels

Full size image

The second case of the sub-integral kernels is represented for \(j = {\mathcal {P}}\). On the mean geocentric sphere, the isotropic kernel \({\mathcal {K}}^{3*, {\mathcal {P}}} = 0\) for \(-1 \le u \le 1\) that may be proven by inserting \(t = 1\) into Eq. (58). Considering this in Eq. (45) of Proposition 4, we get \({\mathcal {K}}^{xxx, {\mathcal {P}}} = 3\ {\mathcal {K}}^{xyy, {\mathcal {P}}} = - 3/4\ {\mathcal {K}}^{xzz, {\mathcal {P}}}\) revealing another symmetry of the sub-integral kernels. Consequently, only four sub-integral kernels, which are depicted in Fig. 5, are sufficient to illustrate their complete spatial behaviour for \(j = {\mathcal {P}}\). In correspondence with Figs. 3 and 4, we observe in Fig. 5 the isotropic behaviour of the kernel \({\mathcal {K}}^{zzz, {\mathcal {P}}}\) and the azimuthal dependence for \({\mathcal {K}}^{xxx, {\mathcal {P}}}\), \({\mathcal {K}}^{xxz, {\mathcal {P}}}\) and \({\mathcal {K}}^{xyz, {\mathcal {P}}}\). The kernels \({\mathcal {K}}^{xxz, {\mathcal {P}}}\), \({\mathcal {K}}^{xyz, {\mathcal {P}}}\) and \({\mathcal {K}}^{zzz, {\mathcal {P}}}\) are more significant compared to \({\mathcal {K}}^{xxx, {\mathcal {S}}}\), especially for \(\psi \in [1^{\circ }, 2^{\circ }]\).

Fig. 5
figure 5

Behaviour of the sub-integral kernels: a \({\mathcal {K}}^{xxx, {\mathcal {P}}}\), b \({\mathcal {K}}^{xxz, {\mathcal {P}}}\), c \({\mathcal {K}}^{xyz, {\mathcal {P}}}\), d \({\mathcal {K}}^{zzz, {\mathcal {P}}}\) in the spatial domain \(\alpha \in [0^{\circ }, 360^{\circ }]\), \(\psi \in [0.3^{\circ }, 7^{\circ }]\). The kernels were evaluated for \(R = r=6,371\) km. Values of the direct azimuth \(\alpha \) are indicated along the circumference of each of the polar plots. The spherical distance \(\psi \) is measured from the centre of the polar plots (indicated by the dashed concentric circles). Black lines inside the plots indicate zero crossings of the sub-integral kernels

Full size image

6 Conclusions

A new mathematical model for evaluation of the third-order (disturbing) gravitational gradients is formulated in this article. Required differential operators in the spherical local north-oriented frame were derived first, see Sect. 3. The operators were subsequently applied to integral equations of Newton, Abel-Poisson, Pizzetti and Hotine that link the volumetric mass density, disturbing gravitational potential, gravity anomaly and gravity disturbance with the (disturbing) gravitational potential. The new integral equations can then be used for transformations between third-order (disturbing) gravitational gradients and the volumetric mass density, disturbing gravitational potential, gravity anomaly and gravity disturbance, respectively; see Proposition 4. Spatial properties of the new integral kernels were then studied in Sect. 5, where several plots illustrating their characteristic features and properties are shown.

The new mathematical formulas extend the theoretical apparatus of geodesy, i.e. the well-known Meissl scheme of physical geodesy, and reveal important properties of the third-order gravitational tensor. They may be exploited in future geophysical studies, continuation of gravitational field quantities and analysing the gradiometric-geodynamic boundary value problem.