Inventory control and pricing for perishable products under age and price dependent stochastic demand

Abstract

Perishable products have a short lifetime and cause a high amount of wastage when managed ineffectively, due to their deterioration over time. We consider coordinated inventory and pricing decisions for perishable products in a periodically-reviewed inventory system with an age and price dependent random demand. We consider the products with a fixed shelf lifetime and use dynamic programming to model this system. We prove certain structural characteristics of the optimal solution and also analyze the effect of different parameters on the optimal solution through numerical experiments. In addition, we analyze simple-to-implement inventory control policies, namely quantity-based and age-based policies, and investigate their effectiveness.

1 Introduction

Global grocery and supermarket sales are among the largest markets in the world and perishable products such as fresh produce, dairy and meat constitute the biggest section of these markets. Due to their deterioration over time, the demand for these products depends highly on their freshness. They become totally obsolete after a certain amount of time causing a high amount of wastage and decreases in grocery profits. In addition, customers are asking for higher product variety in perishable product categories, leading to less predictable demand per product and higher losses. Effective management of these perishable products is an important issue since it is observed that billions of dollars’ worth of food is expired and wasted every month (Minner and Transchel 2010). Donselaar and Broekmeulen (2012) state that the average annual food losses in supermarkets were 11.4% for fresh fruit, 9.7% for fresh vegetables and 4.5% for fresh meat, poultry and seafood in 2005 and 2006, according to the United States Department of Agriculture (USDA). Different from non-perishable products, the freshness or age of these products is also a major concern for the managers in addition to the amount of these products on hand. The demand rate for these products will decrease as the products on hand start to age, and the managers need to decide when to order a new batch and what price to charge for the products on hand in order to control the demand and increase the profits. As a result, the time dependency of demand and the perishability of these products make the management of inventory and pricing much harder.

Fresh foods, groceries, pharmaceuticals, composite materials, packaged chemical products, blood and its derivatives are a few examples of perishable goods found in a wide variety of industries. Due to their common occurrence and importance, a broad literature has developed over the years on management of perishable inventories. We analyze the coordinated inventory control and dynamic pricing decisions for perishable products with a fixed lifetime, such as dairy products. These products generally have a short shelf-life and have a certain expiration date. The managers need to decide when to get rid of the old products and order a new batch in order to increase the demand and improve the revenues. If they order the new batch too soon, then there will be a big loss due to the wastage of the current products that could be sold. Alternatively, if the managers wait too long to order the new batch, then the demand will decrease too much and the company loses sales during that period leading to decreased profits. Thus, it is important to determine the optimal time to order the new batch for perishable products in order to maximize the profits. We consider a time and price dependent random demand function in a periodically-reviewed inventory system and use dynamic programming in order to determine the best times for replenishment, optimal replenishment quantities and the optimal prices to charge depending on the state of the system. We also develop easy-to-use heuristics for these decisions and analyze the effectiveness of these heuristics under different conditions.

There is a stream of research that considers the pricing and inventory control decisions under deterministic demand. Benkherouf (1995) and Mishra and Singh (2010) analyze the inventory control decisions for perishable products with time-dependent demand but they do not consider pricing. Transchel and Minner (2009) consider coordinated pricing and inventory control for non-perishable products under a deterministic demand. Rajan and Steinberg (1992), Abad (1996, 1997, 2001, 2003), Burwell et al. (1991), Wee (1999), Mukhopadhyay et al. (2004), Sana (2010), You (2005), Avinadav et al. (2013) and Kaya and Polat (2017) are the studies that consider coordinated pricing and inventory control for perishable products but they all assume a deterministic demand function.

Inventory and pricing decisions for perishable products under stochastic demand are generally studied separately in the literature. Most of the inventory models assume that inventories can be held in stock indefinitely to satisfy future demands and the demand is independent of the age of the products on hand. Nahmias (1975), Fries (1975) and Weiss (1980) consider the age information in inventory control. Haijema et al. (2007) take the age information into account by differentiating the products into two categories: young and old items, and they develop two different replenishment strategies. Broekmeulen and van Donselaar (2009) also focus on a perishable product system considering the age of products and they propose a heuristic policy for the replenishment of perishable inventories without the consideration of pricing. They use simulation to compare their heuristic results with the optimal policy that does not take into account the age of inventories. Minner and Transchel (2010) consider the ordering policies for perishable products in the food retail industry under service-level constraints and present a method to determine the order quantities. However, none of the studies above consider pricing. Nahmias (1982) reviews related literature about determining the ordering policies for perishable inventory systems for products having exponential decay over time as well as the products with fixed lifetime. Rafaat (1991), Goyal and Giri (2001) and Bakker et al. (2012) also present surveys about the inventory management of deteriorating items.

In the dynamic pricing literature, there are many models for which a fixed amount of inventory needs to be sold until a certain time, without any replenishment opportunities, as in the airline or hotel management industries. Gallego and van Ryzin (1994), Zhao and Zheng (2000), Monahan et al. (2004), Gayon et al. (2009) are a few examples of these studies. Bitran and Caldentey (2003) present an extensive review of dynamic pricing policies in the literature. However, in most of these models, the demand is assumed to be independent of time and there is no inventory replenishment decisions.

There are also several studies considering the inventory and pricing problems for perishable products with time dependent demand. Chen et al. (2014) focus on the joint pricing and inventory control problem for perishable inventory systems with stochastic demand and lead times and focus on the structural properties of the optimal solution. Chen and Sapra (2013) consider the joint inventory and pricing decisions for perishable products in a periodic review model with a fixed lifetime of two periods. Chew Peng et al. (2009) develop a discrete time dynamic programming model to determine the optimal inventory allocations and the optimal prices for a perishable product with a two-period lifetime and they obtain several optimality properties. They also propose three heuristics to obtain the inventory allocations and the prices when the lifetime of the product is longer than two periods, since the optimality properties for two period lifetime in their model do not hold for longer lifetimes.

We consider the coordinated inventory control and pricing decisions for perishable products with fixed shelf lifetimes under an age and price dependent random demand function. We consider a periodically-reviewed inventory system with fixed ordering costs and use dynamic programming in order to determine the optimal times to order a new batch, optimal quantity to order and the optimal prices to set depending on the state of the inventory at hand. Most of the studies in the literature regarding inventory control for perishable products assume a First-In-First-Out (FIFO) policy and either consider simple replenishment policies or assume that the perishable products have a two-period lifetime in order to obtain a tractable model. In this study, we don’t restrict ourselves for products with only two-period lifetimes and propose a new model as explained in the following section. Development of this model for the coordination of inventory control with pricing and the analysis of the optimal solution of this model bring significant novelties to the literature. We prove certain structural results about the optimal policy in our model and develop easy-to-use heuristics for the managers of perishable products. We also analyze the effects of the system parameters on the optimal solution and investigate the effectiveness of the heuristics under different conditions. We also present managerial insights about the management of perishable products. These insights will improve the sustainability of this system as well as increase the system wide profits.

2 Model

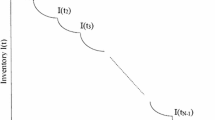
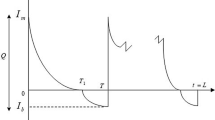
We consider a perishable product with a fixed shelf lifetime of m periods in a periodically-reviewed inventory system. At the beginning of every period we need to decide whether to order a new batch of products or to continue one more period with the current products. In our model, q denotes the number of units of product on hand, t denotes the remaining shelf lifetime of these products and at every period the remaining shelf lifetime of the unsold products decreases by 1. However, if we decide to order a new batch at state (q, t), we assume that there is no replenishment lead time and Q(q, t) units of new products with a shelf lifetime of m periods will arrive in the same period, which is a common assumption used in the inventory control literature. Whenever a new batch is ordered, there is a fixed cost of ordering, denoted as K, and we let c denote the unit cost of products.

When the same type of products with different ages co-exist on the shelves and sold at the same price, we assume that the customers prefer fresher ones and thus a Last-In-First-Out policy is used in the sale of inventories. This policy will lead to the older products to be remained as unsold items on the shelves unless all the fresher ones are sold out. As an approximation to this system, we assume that when a new batch is ordered, the older products are sold in a secondary market with ample demand or salvaged. It is also possible to sell the older products at a cheaper price than the fresh ones leading to a customer segmentation. Since they target different customer segments, we assume that the demand for these products are independent from each other and the sale of older products do not affect the demand for the fresh ones. Thus, we consider the new batch of products independently from the older ones. We let s denote the salvage value of the unsold products from the previous batch. Even though this assumption might seem restrictive at first, we believe that it is consistent with many practices in reality. For example, Intermarch, a French supermarket chain, takes the older fruits and vegetables from the shelves when fresh products arrive and they make soup and juices from these spoiled-looking products and sell them at a certain price in their market. In real life, customers generally prefer fresher products and when they go to the store, if there are two types of the same product, only differing in their freshness, they will prefer the fresh ones, leading the older ones to be unsold. The older products can only be sold during a small time interval in which the fresh products are depleted and the new batch has not arrived yet. However, it rarely happens that the new products are sold out, the older ones have still some remaining shelf lifetime and there is a demand for them in that period. Even if this happens the demand for them will be generally low and a new batch will be ordered in the next period. For example, if we consider a product with a 7-day shelf life and after 4 days let us assume that we decide to order a new batch. If the older products are not salvaged, then they need to wait until the new batch is sold out which might take more than 3 days and the older products will already be expired. However, if they are sold out in 2 days, then at that day, some of the older products with a remaining shelf life of 1 day can be sold but the demand for those products will be very low and a new batch will be ordered in the next day. Thus, we assume that the sales of the older products will not be significant for our model and salvaging the older products at a certain price when a new batch is ordered seems logical and consistent with real life practices. In Sect. 4, we analyze this assumption and compare the systems, for products with 2 and 3 period lifetimes, when older products are salvaged and when they are kept in store after a new replenishment is made. We show the validity of this assumption with our numerical experiments in Sect. 7.2 using different parameter settings.

The assumption stated above is analytically critical for us in order to develop a tractable dynamic programming model and leads to a different model than the ones in the literature. We note that, one needs to keep track of the quantities at all possible ages of the product and because of this reason it is widely assumed that the perishable products have a two-period lifetime in the inventory control literature [e.g. Chen and Sapra (2013), Chew Peng et al. (2009), etc.]. For example, if a product has an m-period lifetime, then we need an m-dimensional state space, each dimension showing the amount of products at that age. Using a dynamic programming formulation with an m-dimensional state space becomes very difficult to solve as m gets larger than 2. However, we do not restrict ourselves to two-period lifetimes and instead we assume that the older products are salvaged when a new batch arrives. With this assumption, all the products on hand will have the same age and at any time, the system can be modeled using two state variables, the number of products on hand, and their remaining lifetime.

In addition to the inventory ordering decisions, at the beginning of every period, we also decide on the price in that period, denoted as p(q, t), depending on the state of the system at that period, (q, t). The demand at every period, denoted as D(p(q, t), t), is then a random function of the price and the remaining shelf lifetime of the products. Below, we present the notations used throughout the paper. We start our analysis by considering the static pricing model in the next section, such that the price is fixed for all (q, t). In the next section, we assume that $p(q,t)=p$ for all (q, t). Then, we analyse the dynamic pricing model, such that different prices can be charged at different states, in Sect. 6.

Parameters

m :

Maximum shelf lifetime

c :

Cost per product

K :

Fixed ordering cost

s :

Salvage value of older products when a new batch is ordered

System states

q :

Inventory amount at hand

t :

Remaining shelf lifetime of the products in inventory

Decisions variables

Q(q, t):

Order size at state (q,t)

p(q, t):

Price at state (q,t)

System disturbance

D(p, t):

Random demand that depends on price and remaining shelf lifetime of the products in inventory

3 Coordinated inventory control and static pricing

We aim to maximize the average system profit per unit time by deciding on when to order a new batch and how much to order depending on the system state, (q, t), in addition to the optimal static price p, to set. In this section, we assume that a single price p is used at all possible states (q, t). We consider an infinite planning horizon and use an average cost dynamic programming (DP) formulation [see Bertsekas (2005) for detailed information on average cost DP formulations]. For a given p, the Bellman’s equation for our model is as follows:

$$\begin{aligned} \Pi ^*+ h(q,t)= & {} \max \Big \{f_c(q,t), f_o(q,t)\Big \}\nonumber \\ f_c(q,t)= & {} p\,E\Big [\min \big \{q,D(p,t)\big \}\Big ] +E\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ]\nonumber \\ f_o(q,t)= & {} \max _{Q(q,t)}\Big \{-K-cQ(q,t)+sq+f_c(Q(q,t),m)\Big \} \end{aligned}$$

(3.1)

with the boundary conditions $\Pi ^*+h(q,0)=\max _Q(q,0)\{-K-cQ(q,0)+sq+f_c(Q(q,0),m)\}$.

In order to obtain the optimal static price p, we also need to solve the following problem, where $\Pi ^*$ is the optimal average profit value in the solution of the above problem. We do a one-dimensional search over p and solve the above problem and determine the value of p that provides the maximum $\Pi ^*$ value.

$$\begin{aligned} \max _p\Big \{\Pi ^*\Big \} \end{aligned}$$

In the above formulation 3.1, $\Pi ^*$ denotes the optimal average profit value per unit time, h(q, t) denotes the relative (differential) profit values, $f_c(q,t)$ denotes the profit value if we decide to continue with the current products on hand and $f_o(q,t)$ denotes the profit value if we decide to order a new batch at state (q, t). Note that if we decide to continue, then the profit function includes an immediate expected profit from selling the products in this period, denoted as $p\,E[\min \{q,D(p,t)\}]$ and a future expected profit of the system, denoted as $E[h([q-D(p,t)]^+,t-1)]$. In this case, the next state will be $([q-D(p,t)]^+,t-1)$, in which the products have one less remaining shelf lifetime. If we decide to have a new order, we need to choose the best Q(q, t) to maximize the expected profit. In this case, first we have an ordering cost, K, and the cost of the purchased products cQ(q, t). Then, we have salvage revenue sq and we come to the state (Q(q, t), m) with the new batch whose profit value will be equal to $f_c(Q(q,t),m)$.

Since we aim to focus on the perishability of the products and time-dependency of demand, we do not include any inventory holding cost explicitly in our model. The perishability of the products and the time dependency of demand have a similar effect in our decisions as the inventory holding costs. The expiration risk of the products and the decrease of demand rate by time prevents us from ordering too much as the inventory holding cost does in the classical inventory control literature. Thus, inventory holding costs are implicitly embedded in the expiration process of the perishable products. In addition, since we consider short time periods, the inventory holding costs per period will be very small compared to the revenues and the costs per period. Thus, we choose not to include the inventory holding cost explicitly in our formulation for the sake of simplicity.

3.1 Structural results

In this section, we focus on the problem 3.1 to analyze the optimal inventory control policy for fixed p. We prove some structural properties about the optimal policy by analyzing the DP formulation 3.1.

Proposition 1

Optimal order size, $Q^*$ is independent of q and t.

Due to Proposition 1, for the sake of simplicity, from this point onwards, we use Q instead of Q(q, t) in our formulations. In that case, we can rewrite our DP formulation as below

$$\begin{aligned} \Pi ^*+ h(q,t)= & {} \max \Big \{f_c(q,t), f_o(q)\Big \}\nonumber \\ f_c(q,t)= & {} p\,E\Big [\min \big \{q,D(p,t)\big \}\Big ] +E\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ]\nonumber \\ f_o(q)= & {} \max _Q\{-K-cQ+sq+f_c(Q,m)\} \end{aligned}$$

(3.2)

with the boundary conditions $\Pi ^*+h(q,0)=\max _Q\{-K-cQ+sq+f_c(Q,m)\}$.

However, we observe in our numerical studies that the optimal average profit value is not a concave function of Q. Thus, in order to determine the value of $Q^*$ we need to do a line search between the lower bound L and the upper bound U stated in Proposition 2 in which $F_{m}$ denotes the cumulative distribution function of total demand for m periods and $F_{1}$ denotes the cumulative distribution function of the demand in the first period.

Proposition 2

For a given p, the optimal order size $Q^*$ is between the lower bound L and the upper bound U, where L and U are denoted as below

$$\begin{aligned} U= & {} min \Big \{ Q | F^{-1}_{m}(Q) \ge \frac{p-c}{p-s}\Big \}\\ L= & {} min \Big \{Q | F^{-1}_{1}(Q) \ge \frac{p-c}{p-s}\Big \} \end{aligned}$$

In order to define the structure for the optimal ordering states, we present the following lemmas and propositions.

Lemma 1

h(q, t) is non-decreasing in q for any given t. In addition, $h(q+1,t)-h(q,t)\ge s$ for any given t.

Lemma 2

h(q, t) is non-decreasing in t for any given q.

Using Lemmas 1 and 2, we now prove the structure about the optimal ordering policy in Propositions 3 and 4.

Proposition 3

There is a critical value q(t) for any t such that a new batch should be ordered if $q<q(t)$ and we should continue with the current products if $q\ge q(t)$. In addition, q(t) is non-increasing in t.

Proposition 4

There is a critical value t(q) for any q such that a new batch should be ordered if $t<t(q)$ and we should continue with the current products if $t\ge t(q)$. In addition, t(q) is non-increasing in q.

We essentially show with Propositions 3 and 4 that there is a monotonic structure in the optimal ordering decision policy. In Fig. 1 is a typical structure of the optimal ordering policy with respect to inventory size and remaining shelf lifetime. As seen in Fig. 1, there is a monotone curve that separates the ordering and non-ordering states.

Fig. 1

Optimal ordering decision policy—typical monotone structure

We present numerical experiments and the solutions for the optimal static pricing and inventory decisions in the numerical results section.

4 A comparison of the models with and without the salvaging assumption for perishable products with two and three period lifetimes

Recall that in our model, it is assumed that when a new batch is ordered the older products are salvaged or sold in a secondary market. Hence, products with different ages do not co-exist. This assumption enables us to have a state definition with two states; on-hand inventory and remaining shelf life. However, if products with different ages are allowed to co-exist, i.e. if the older products are kept in store instead of being salvaged when a new batch is ordered, it might be possible to obtain higher profits in the system. However, in order to model such a system, we need to keep track of the amount of products at each age, and thus the state space of the system grows exponentially. The state space of such a model can be denoted as $(q_1, q_2, ..., q_{m-1})$ where $q_i$ denotes the products with age i. The solution of such a model in a reasonable time limit becomes impossible, especially when the maximum lifetime of the product, m, gets larger, mainly due to the size of the state space. In addition, when products with different ages co-exist in the system, there is a need for a proper allocation of demand among these products. Consumer choice models or demand spillovers need to be incorporated into the model, which makes the solution even more difficult.

Besides the difficulties explained above, for $m=2$ and $m=3$, we model the system without the assumption that the older products are salvaged when a new batch is ordered. We compare the results of our proposed model in Sect. 2 with the results of the model without this assumption. We present these models for $m=2$ and $m=3$ in the following sections.

4.1 Coordinated pricing and inventory control for products with two-period lifetimes

In this section, we consider a product with two-period lifetime, $m=2$, and allow products with different ages co-exist. We let q denote the number of products that are left over from the previous period and Q denote the number of products that are ordered at the beginning of that period. If we do not salvage the older products when this new batch is ordered, both Q new products and q old products will be available on the shelf. In this model, consistent with our initial model, we assume that the customers prefer fresher products if both products are sold at the same price, and thus the products are sold on a Last-In-First-Out (LIFO) basis. An arriving customer is assumed to buy the new product, if available. However, if all the new products are depleted, then the later arriving customers might also buy the old product. Similar to our initial model, for products with different ages, we use an age and price dependent random demand function D(p, t) where p denotes the price of the product and t denotes the age of the product. We let $D(p)=D(p,m)$ denote the demand for the most fresh products (i.e. new batch) with m periods of lifetime remaining at the price p. However, if the demand is more than Q, then the new batch will be depleted and the later arriving customers need to decide whether to buy the old product or not. Consistent with the age-dependency of demand, we assume that an $\alpha$ portion of these customers will buy the old products. Thus the sales amount from the new and old products will be min(Q, D(p)) and $min(q, \left\lfloor \alpha [D(p)-Q]^+ \right\rfloor )$, respectively. Note that, we take the floor of the value $\alpha [D(p)-Q]^+$, since this value needs to be an integer value denoting the demand. Also note that when $\alpha =1$, the demand will be independent of age and the customers will be indifferent between old and new products. Observe that, since the maximum lifetime of the product is 2, the unsold portion of the old q products will not be carried over to the next period and will be salvaged at the price s. Since Q is a variable that will be decided at the beginning of each period based on the state of the system, we only need to keep track of the number of products that are leftover from the previous period. Thus, q denotes the state variable in our model. Then, we can write the infinite-horizon average cost dynamic programming formulation for this model as below.

$$\begin{aligned} \Pi ^*+ h(q)= & {} \max _Q\Bigg \{\,-K1_{Q>0}-cQ+pE\Big [\min \big \{Q, D(p)\big \}\nonumber \\&+\,\min \Big \{q, \left\lfloor \alpha [D(p)-Q]^+ \right\rfloor \Big \}\Big ]\nonumber \\&+\,sE\big [q-\left\lfloor \alpha (D(p)-Q)^+ \right\rfloor \big ]^+ +\,E\bigg [h\Big (\big [Q-D(p)\big ]^+\Big )\bigg ]\Bigg \}\qquad \end{aligned}$$

(4.1)

In the above formulation, $\Pi ^*$ denotes the optimal average profit value per unit time and h(q) denotes the relative (differential) profit value when q units are left over from the previous period. In order to accommodate the fixed order cost in our model, we use the function $1_{Q\,>\,0}$, which takes the value 1 if a batch with $Q>0$ is ordered in that period and takes the value 0 if a batch order is not made in that period. Observe that the unsold portion of the new batch of Q units are carried over to the next period and the unsold portion of the old q products are salvaged. Thus the state variable for the next state is written as $E[h([Q-D(p)]^+)]$.

In order for them to be comparable with each other, below we also present the dynamic programming formulation for the original model given in Sect. 3 for $m=2$ with the assumption that the older products are salvaged when a new batch is ordered. Since $m=2$, the products at hand can only have 1 period lifetime remaining and thus the time index t in our original model can only take the value 1. Because of this reason, we can drop the index t from the state space representation of the original model and write the model as below. Consistent with the above model, we use a demand function $D(p,t)=\alpha ^{m-t}D(p)$ where $m=2$, and $t=1$ for the old products and $t=2$ for the new batch. Observe that if a new batch is ordered, the demand for that batch will be D(p) and if a new batch is not ordered, the demand will be $\left\lfloor \alpha D(p) \right\rfloor$ since $\alpha$ portion of these customers will buy the old products at the price p. The unsold portion of these products will be salvaged and the next state will be 0 if a batch is not ordered in this period. However, when a batch of Q units are ordered, all the old products of q units are salvaged at that time and only the new batch is sold at the price p with demand equal to D(p).

$$\begin{aligned} \Pi ^*+ h(q)= & {} \max \Bigg \{pE\Big [\min \big \{q, \left\lfloor \alpha D(p) \right\rfloor \big \}\Big ]+sE\big [q-\left\lfloor \alpha D(p) \right\rfloor \big ]^{+}\nonumber \\&+\,h(0),\max _Q\Bigg \{\,-K-cQ+sq\nonumber \\&+\,pE\Big [\min \big \{Q, D(p)\big \}\Big ]+E\bigg [h\Big (\big [Q-D(p)\big ]^+\Big )\bigg ]\Bigg \}\Bigg \} \end{aligned}$$

(4.2)

We compare the results of these two models in order to analyze the effect of our assumption that the older products are salvaged when a new batch is ordered. In the numerical results section, we analyze the results with and without this assumption by comparing the results of the above models under different parameter settings.

4.2 Coordinated pricing and inventory control for products with three-period lifetimes

In this section, we consider a product with three-period lifetime, $m=3$, and allow products with different ages co-exist. Similar to the previous section, we present the infinite-horizon average cost dynamic programming formulation for this model as below.

$$\begin{aligned} \Pi ^*+ h(q_1,q_2)= & {} \max _Q\Bigg \{\,-K1_{Q>0}-cQ + pE\Big [\min \big \{Q,D(p)\big \}+\min \Big \{q_1, \left\lfloor \alpha [D(p)-Q]^+ \right\rfloor \nonumber \\&+\,\min \Big \{q_2,\left\lfloor \alpha [\alpha [D(p)-Q]^+-q_1]^+ \right\rfloor \Big \}\Big \}\Big ]\nonumber \\&+\,sE\big [q_2-\left\lfloor [\alpha [\alpha [D(p)-Q]^+-q_1]^+]^+ \right\rfloor \big ]^+\nonumber \\&+\,E\bigg [h\Big (\big [Q-D(p)\big ]^+, (q_1-\left\lfloor \alpha [D(p)-Q]^+ \right\rfloor )^+\Big )\bigg ]\Bigg \}\qquad \end{aligned}$$

(4.3)

In the above model, we denote the state space as $(q_1, q_2)$ denoting the number of products at age 1 and 2, respectively. The products are again assumed to be sold on a LIFO basis and $\alpha$ portion of the leftover demand from the fresher products is attributed to the older products. Any unsold portion of $q_2$ units will be salvaged and the next state will be $([Q-D(p)]^+, (q_1-\left\lfloor \alpha [D(p)-Q]^+ \right\rfloor )^+)$.

Then, we consider our original model given in Sect. 3 for $m=3$, which can be written as below, where (q, t) denotes the state space with q units of product with $t\in \{1,2\}$ time periods remaining lifetime. We use the demand function $D(p,t)=\left\lfloor \alpha ^{m-t}D(p) \right\rfloor$, where $m=3$ and $t=3$ for the new batch and $t=2$ or 1 for the older products.

$$\begin{aligned} \Pi ^*+ h(q,t)= & {} \max \Bigg \{pE\Big [\min \big \{q, D(p,t)\big \}\Big ]+E\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ],\nonumber \\&\max _Q\Bigg \{\,-K-cQ+sq+pE\Big [\min \big \{Q, D(p)\big \}\Big ]\nonumber \\&+\,E\bigg [h\Big (\big [Q-D(p,3)\big ]^+, 2\Big )\bigg ]\Bigg \}\Bigg \} \end{aligned}$$

(4.4)

We again compare the results of these two models in our numerical results section and analyze the effect of the assumption that the older products are salvaged when a new batch is ordered.

Observe that as m gets larger, the state space of our original model is not affected much. However, the state space of the model without the critical assumption, increases exponentially and the model easily becomes unsolvable in a reasonable time limit, as m gets larger. Even for $m=3$, in our numerical experiments, it took over half an hour to solve some of the instances of the above model without the critical assumption, while it took only a few minutes at most, to solve the same instance with our original model.

We also note that, in our models we assume that a single price is used for all products even if products with different ages co-exist in the system. This is a general practice in many retail stores. We can observe that even though the products on the shelves have different ages, they are generally sold at the same price in real life. It is clear that higher profits can be obtained if products with different ages have different prices, however, modeling such a system needs a very different approach. A consumer choice model might be needed in that system since the customers need to choose between the fresh but more expensive products and the old but cheaper products. LIFO assumption on the order of sales can not be applied anymore in that situation. Because of the complexity and the differences in the allocation of demand among products with different ages, it will not be fair to compare the results of our initial model with a model that allows different prices for products with different ages at the same time. Thus, the analysis of such a system is out of the scope of this paper and is thought to be a future area of study.

5 Heuristics for inventory control under static pricing

In Sect. 3, through DP for a given p, we prove that there exists a critical value of q(t) that determines the ordering time decision. Even though the optimal decision depends both on the age of products and the amount at hand, following this strategy can be difficult to implement and use for the managers. In reality, similar to the inventory control of durable products, it is observed that a policy that only considers the amount of products on hand and does not take the age of products into account is commonly employed. Alternatively, a policy that only considers the age of products and ignores the amount at hand is also seen to be implemented. In this section, we model these two heuristics in order to compare their performances with the optimal solution.

5.1 Single quantity threshold (r) heuristic

In this heuristic, we consider a single threshold level r for the amount at hand, instead of different q(t) values for different t as stated in the previous section. This heuristic is like a modified (s, S) policy in the classical inventory literature such that if the inventory at hand at the beginning of any period is less than r, we order a new batch of Q units and since we discard the old ones, our inventory level goes up to Q. If the inventory never goes below r in m periods, then we order a new batch after m periods since all the products on hand will be expired at that time. This heuristic can be considered as a quantity-based replenishment policy. Also note that the demand is age dependent and we also need to decide on the optimal price, p, to set in this system.

In this heuristic, since it is a simplified version of the model in the previous section, we use the same equations as above but use the single unknown r, and the optimal value of it will be determined through a one-dimensional line search using the equations below:

• If $q > r$: $\Pi ^*+h(q,t)=f_c(q,t)=p\,E\Big [\min \big \{q,D(p,t)\big \}\Big ]+E\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ]$

• If $q \le r$: $\Pi ^*+h(q,t)=f_o(q)=\max _Q\{-K-cQ+sq+f_c(Q,m)\}$

We determine the optimal p, Q and r values that maximize $\Pi ^*$ value in the above equations. We present and compare the results of this heuristic with the optimal DP solution in the Table 2 in the numerical results section.

5.2 Single lifetime threshold (l) heuristic

In this heuristic, similar to the previous one, we again consider a single threshold level but this threshold level is based on the remaining shelf lifetime of the products, instead of the remaining quantity of the products. As stated in Proposition 4, the optimal policy requires us to find the critical time threshold levels, denoted as t(q) for all possible q. However, in this heuristic, we consider a single time threshold level l such that we give a new order when the remaining lifetime of the products becomes less than l, independent of the quantity at hand. We also note that if all the products are sold before l periods, we also give a new order at that time even though l periods have not passed yet. This heuristic can be considered as a time-based replenishment policy.

Since this heuristic is also a simplified version of the model in the previous sections, we use similar equations as stated below and in order to determine the optimal value of l, we employ a one-dimensional line search.

• If $t > l$: $\Pi ^*+h(q,t)=f_c(q,t)=p\,E\Big [\min \big \{q,D(p,t)\big \}\Big ]+E\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ]$

• If $t \le l$: $\Pi ^*+h(q,t)=f_o(q)=\max _Q\{-K-cQ+sq+f_c(Q,m)\}$

We determine the optimal p, Q and l values that maximize $\Pi ^*$ value in the above equations. We present and compare the results of this heuristic with the optimal DP solution in Table 2 in the numerical results section.

6 Coordinated inventory control and dynamic pricing model

In this section, we consider dynamic pricing such that instead of using a single price value p for all states (q, t), we allow different prices, p(q, t), to be used at different states (q, t). In this case, the DP equation to be solved will be as follows:

$$\begin{aligned} \Pi ^*+ h(q,t)= & {} \max \Big \{f_c(q,t), f_o(q,t)\Big \}\nonumber \\ f_c(q,t)= & {} \max _{p(q,t)} \Bigg \{p(q,t)\,E\Big [\min \big \{q,D(p(q,t),t)\big \}\Big ]\nonumber \\&+\,E\bigg [h\Big (\big [q-D(p(q,t),t)\big ]^+,t-1\Big )\bigg ]\Bigg \}\nonumber \\ f_o(q,t)= & {} \max _{Q(q,t)}\{-K-cQ(q,t)+sq+f_c(Q(q,t),m)\} \end{aligned}$$

(6.1)

with the boundary conditions $\Pi ^*+h(q,0)=\max _{Q(q,0)}\{-K-cQ(q,0)+sq+f_c(Q(q,0),m)\}$.

In this formulation, different from the static pricing model, for all states (q, t), we also need to pick the best p(q, t) to maximize the expected profit. We note that all the propositions stated for the static pricing model related to the inventory policy are also valid under the dynamic pricing strategy as stated below.

Proposition 5

Under the dynamic pricing model, optimal order size, $Q^*$ is independent of q and t.

Due to Proposition 5, from this point onwards, we again use Q instead of Q(q, t) in our formulations and the function $f_o(q,t)$ can bedenoted as $f_o(q)$ since it no longer depends on t. We also note that the optimal order size $Q^*$ is searched between the lower and upper bounds obtained in a similar manner as explained in Proposition 6. In the dynamic pricing case, since the price, p, is not fixed, we can not directly use the lower and upper bounds as given in Proposition 2. Instead, we use $p_{min}$ and $p_{max}$, which denote the minimum and maximum possible prices that can be set for p(q, t), i.e. $p(q, t)\in \{p_{min}, p_{max}\}$. In addition, we let $F_{m, p_{min}}$ denote the cumulative distribution function of total demand for m periods under fixed price $p_{min}$ and $F_{1, p_{max}}$ denote the cumulative distribution function of the demand in the first period when the price is $p_{max}$. Then, the lower and upper bounds under the dynamic pricing model can be stated as below.

Proposition 6

Under the dynamic pricing model, the optimal order size $Q^*$ is between the lower bound L and the upper bound U, where L and U are denoted as below

$$\begin{aligned} U= & {} min \Big \{ Q | F^{-1}_{m, p_{min}}(Q) \ge \frac{p_{min}-c}{p_{min}-s}\Big \}\\ L= & {} min \Big \{Q | F^{-1}_{1, p_{max}}(Q) \ge \frac{p_{max}-c}{p_{max}-s}\Big \} \end{aligned}$$

In order to define the structure for the optimal ordering states under the dynamic pricing model, we present the following lemmas and propositions that are similar to the ones stated for the static pricing model.

Lemma 3

Under the dynamic pricing model, h(q, t) is non-decreasing in q for any given t. In addition, $h(q+1,t)-h(q,t)\ge s$ for any given t.

Lemma 4

Under the dynamic pricing model, h(q, t) is non-decreasing in t for any given q.

Proposition 7

Under the dynamic pricing model, there is a critical value q(t) for any t such that a new batch should be ordered if $q<q(t)$ and we should continue with the current products if $q\ge q(t)$. In addition, q(t) is non-increasing in t.

Proposition 8

Under the dynamic pricing model, there is a critical value t(q) for any q such that a new batch should be ordered if $t<t(q)$ and we should continue with the current products if $t\ge t(q)$. In addition, t(q) is non-increasing in q.

For the sake of space, we don’t repeat the proofs for Propositions 5 and 6 since they are almost the same as the proofs given for the static pricing model. However, we present outlines for the proofs of Lemmas 3 and 4, and Propositions 7 and 8 in the “Appendix”.

When we look at the optimal pricing decisions, first we can say that if the optimal policy is to order a new batch at any two states $(q_1,t_1)$ and $(q_2,t_2)$, then the optimal prices for these states are the same, i.e. $p(q_1,t_1)=p(q_2,t_2)$. For the non-ordering states, we observe numerically that these prices are non-decreasing in the remaining shelf lifetime, meaning that higher prices should be charged for fresher products. However, when we look at the relationship between the prices and the inventory size, we observe that they do not have such a monotonic structure in the inventory size as seen in the numerical results section. We present detailed numerical experiments and analyze the optimal pricing decisions in the numerical results section.

7 Numerical results

In this section, we present our numerical results for both static and dynamic pricing models. We analyze the effects of different parameters on the system and investigate the benefit of dynamic pricing. We also analyze the effect of the assumption that the older products are salvaged when a new batch is ordered by comparing the results of our proposed model with the model without that assumption. The efficiencies of the heuristics presented above are also presented.

7.1 Numerical results for inventory control under static pricing

First, we analyze the static pricing model. In our experiments, similar to the demand functions used in Banerjee and Agrawal (2017) and Avinadav et al. (2013, 2014), we assume a demand function that has a Poisson distribution with rate $\lambda (p,t)=a (\frac{t}{m})^n e^{\beta (1-\frac{p}{c})}$ where t is the remaining lifetime of the product, $\frac{p}{c}$ is the profit margin (p is the price and c is the unit cost of the product), a is the demand coefficient constant, $\beta$ denotes the price sensitivity of demand and n represents the time sensitivity of demand. As a base case for our numerical experiments, we use the parameters $c= 1000$, $K= 20000$, $a = 60$, $m = 7$, $s= 400$, $\beta = 2$ and $n = 1$. For these parameters, using the DP equation 3.2, we find out that the optimal static price is 1497 and the optimal order quantity is 78. We note that the couple (Q, p) = (78, 1497) is the optimal value that maximizes the profit in our system, however, in some cases, one of these decisions might be fixed and the optimal value of the other variable can be searched. Figure 2 shows the optimal values of these variables as the other one is fixed, presenting the effect of price on optimal order quantity and the effect of order quantity on optimal price value. In this chart we see a monotone structure in these relations, and the optimal couple (Q,p) is the intersection point of these two lines in Fig. 2.

Fig. 2

Optimal ordering size and optimal price behaviour with respect to each other

In Fig. 3, we illustrate the structure of the function h(q, t), that is also stated in Propositions 1 and 2. You can see in part (a) of Fig. 3 that for any remaining shelf lifetime value, relative profit function h(q, t) is increasing in inventory size. Similarly, in part (b) of Fig. 3, for any inventory size value, h(q, t) in non-decreasing in remaining shelf lifetime. In Fig. 4, we present the optimal inventory replenishment strategy denoting at which states, we should order a new batch and at which states we should continue with the current inventory at hand. Observe that Fig. 4 is consistent with the structure stated in Propositions 3 and 4.

Fig. 3

Relative profit function versus a inventory size for different remaining shelf lifetime values, b remaining shelf lifetime for different inventory size values

Fig. 4

Optimal decision policy structure for any inventory size and remaining shelf lifetime

Fig. 5

The effect of the product’s shelf lifetime on a optimal ordering size, b optimal average profit, c optimal price

In the following charts we consider the effect of different parameters on optimal average profit, optimal price and optimal order size. Part (a) of Fig. 5 shows that as the shelf lifetime of the product increases, the optimal order size also increases. It means that when products have more time before expiration, we can order more. But we also observe that this increase is in a concave manner and after a while, even though the product’s shelf lifetime increases, the order quantity stays constant. A similar structure is also seen in part (b) of Fig. 5 in which we present the average profit value as opposed to the shelf lifetime of the products denoting that products with a short lifetime are more riskier and bring less profit. In part (c) of Fig. 5 we see how optimal price value changes with respect to the shelf lifetime of the products. We observe that the optimal price value has a non-monotonic structure with respect to the shelf lifetime of the product, especially when the shelf lifetime is small. The reason for this is that when the shelf lifetime increases, the order size also increases and increased shelf lifetime and increased order size work in opposite directions for the price. For example, in part (c) of Fig. 5, when the shelf lifetime increases from 5 to 6, the order size also increases and the optimal price decreases because of the higher order size overcoming the effect of longer shelf lifetime. However, as the shelf lifetime is above a certain value, the optimal price seems to increase monotonically with the shelf lifetime. For example, when the shelf lifetime goes from 15 to 16, the increase in order size is smaller and the effect of longer lifetime overcomes the effect of higher order size and the optimal price increases. When we fix the value of the order size Q and analyze the optimal price under fixed Q, we observe that the optimal price is monotonically increasing with the shelf lifetime. When Q is fixed, if a product has a longer shelf lifetime, it has higher demand at the same price p, and there is a longer time to sell these products. As a result higher prices are set as the shelf lifetime increases. Figure 6 shows the effect of the fixed ordering cost and we observe that the order size increases with the fixed cost in order to decrease the order frequencies to avoid high fixed costs. But, the order size converges concavely to a certain value as the fixed cost goes beyond a certain level because ordering more than a certain amount will not be profitable since they can not be sold before their expiration dates and even though the fixed cost is too high, the order size will never be more than a certain amount. We note that the value that the order size eventually converges to is equal to the upper bound that we introduced in Proposition 2. When we consider the average profit value, we observe that it decreases as the fixed cost increases, as expected, and the optimal price again does not have a monotonic structure with respect to the fixed ordering cost. Figure 7 shows the effect of the salvage value on the system. When we can salvage the products with higher prices, there is less risk to order more. So, it is reasonable that by increasing the salvage value, the optimal ordering size increases. Furthermore, we can simply conclude that, if salvage value gets close enough to the unit cost value, the optimal ordering size goes to infinity, since there is no risk in ordering more when we can salvage the product with same value that we paid for them. This behavior is also true for the optimal average profit. When salvage value increases and the difference between product cost and salvage value decreases, it is obvious that we can make more profit in the system. We observe that the optimal price again does not have a monotonic structure with respect to the salvage value. Figure 8 shows the effect of the price sensitivity of demand, $\beta$, on the order size, the average profit values and the optimal price. Note that for a given price, when $\beta$ increases, demand decreases. Thus, when $\beta$ increases, having less demand for products, it is reasonable to order less number of products and it obviously decreases the optimal average profit in the system. In part (c) of Fig. 8, we observe that the optimal price monotonically decreases as $\beta$ increases. When the demand becomes more sensitive to price, we should charge lower prices in order not to lose the demand.

Fig. 6

The effect of the fixed order cost on a optimal ordering size, b optimal average profit, c optimal price

Fig. 7

The effect of the salvage value on a optimal ordering size, b optimal average profit, c optimal price

Fig. 8

The effect of the price sensitivity of demand on a optimal ordering size, b optimal average profit, c optimal price

We assume that the salvage value of the products are not affected by their remaining shelf lifetimes when they are salvaged. However, here we also analyze the system behavior numerically when the salvage value depends on the freshness of the product. In the example below, we observe that when the salvage value is different for products with different ages, the system shows a different behavior regarding the optimal ordering decision policy and the monotonic structure no longer holds. In this example, we assume that the salvage value increases linearly with the remaining shelf lifetime instead of being a constant value, such that $s=\frac{800t}{m}$. In Fig. 9, you can see that the optimal ordering decision policy has a different structure than the figure given in Fig. 4 and the structural results given in Propositions 3 and 4 do not hold under this condition. The main reason for this structure is that when the inventory size is high considering the remaining shelf time, such that most of them are less likely to be sold during the remaining shelf lifetime, it is better to salvage all of them at the current value instead of keeping them. Since the salvage value decreases over time, the value obtained through salvaging these products become higher than the value obtained by selling some of them and salvaging the rest later at the decreased value.

Fig. 9

Optimal ordering decision Policy for an example with salvage value linearly increasing in remaining shelf lifetime

7.2 Numerical results for the comparison of the proposed model with the optimal solution for products with m = 2 and m = 3

In this section, in order to analyze the effect of the assumption that the older products are salvaged when a new batch is ordered, we compare the results of the models with and without this assumption for products with two and three period lifetimes. In this section, we use a random demand function of the form $D(p,t)=\left\lfloor \alpha ^{m-t}D(p) \right\rfloor$ where D(p) is Poisson distributed with rate $\delta -\gamma p$. We use different parameter values as stated in Table 1 and present a comparison of the profits and the static prices set in each case.

Table 1 Comparison of the proposed model with the optimal solution for products with m = 2 and m = 3

Table 2 Solutions obtained with the heuristics and the DP model

We observe that both models provide very similar results and our assumption, that the unsold products are salvaged when a new replenishment is made, does not significantly change the results compared to the optimal solutions. The percentage difference between the profits of the models with and without the assumption is about $0.5\%$ on average and $2.492\%$ in the worst case based on the results in Table 1. We can state that our model with this assumption can be used as a close approximation to the optimal solution without the assumption. Our model provides especially better approximations as K, s, $\alpha$ or $\gamma$ gets larger or c or $\delta$ gets smaller. We observe that as the shelf life of the product, m, gets larger, the percentage differences between the profits slightly increase. When shelf life is significantly larger than 3, the differences might increase even further and the performance of the approximation might decrease. However, note that the approximation provides the optimal result when $m=1$ and the differences between profits for $m=2$ and $m=3$ are 0.397 and $0.557\%$ on average, and 1.994 and $2.492\%$ in the worst cases, respectively. The value of m affects the performance of the approximation the most between $m=1$ and $m=2$. It has a smaller effect between $m=2$ and $m=3$, and it is expected to have decreasing effects between m and $m+1$ for larger m. The differences between profits are expected to increase in a concave manner, with even further decreasing rates as m gets significantly larger. Thus, even though the performance of the approximation worsens for larger m, we expect that it will still provide close enough results to the optimal solution, even when shelf lifetimes are significantly longer. The analysis about the performance of this approximation for larger m values can be analyzed in more detail in future studies. In addition, more research might need to be done in the future when multiple aged products with long shelf lives co-exist in the system.

7.3 Analysis of heuristics for inventory control under static pricing

In this section, we compare the solutions obtained by the heuristics described above with the optimal DP model solutions through numerical examples. In Table 2, we present the optimal order size ($Q^*$) for the DP model and the heuristics, for different sets of parameters as given in the table. In addition, in the last columns of Table 2, we also present the percentage differences of the average profit values ($\frac{\Pi _{DP}-\Pi _H}{\Pi _{DP}}*100$) obtained by the DP model and the heuristics.

We observe that the Single Quantity Threshold heuristic gives us better solutions than Single Lifetime Threshold heuristic in these experiments and they both seem to be efficient and easy to use in real life. The performances of both heuristics increase as s, m or $\beta$ decrease; or K or a increase.

7.4 Numerical results for the coordinated inventory control and dynamic pricing

In this section, we present the numerical results for the same parameters that we use in static pricing section but now we use dynamic pricing and the price is not fixed for all states. For any inventory size and remaining shelf lifetime, the optimal price is chosen to maximize the system profit.

We observe in Fig. 10 that the relative value function h(q, t) is non-decreasing in inventory size and in remaining shelf lifetime, as expected.

Fig. 10

The behaviour of the relative value function h(q, t) versus a inventory size for different remaining shelf lifetimes, b remaining shelf lifetime for different inventory sizes

In Fig. 11, we present the optimal solution of the dynamic pricing DP model and how the optimal price value changes with respect to inventory size and remaining shelf lifetime. The yellow region denotes the states at which a replenishment is made and when a replenishment is made, the optimal price to use is found to be 1504. We note that the optimal static pricing for this example is 1497, which is close to the price at the replenishment time. However, as time passes, depending on the demand, very different prices between 900 and 2500 are seen to be charged at different states of the system. For the sake of illustration, in Fig. 11, different colours are used for different ranges of prices and a monotone behavior of optimal price values in inventory size and remaining shelf lifetime is observed. However, when we look at the behaviour of the optimal price with respect to inventory size and remaining shelf lifetime, we observe in Fig. 12 that even though the optimal price value increases in remaining shelf lifetime, it does not have a monotonic structure with respect to the inventory size. In general, we observe that the price decreases when there are more inventory in the system, however at certain states this structure does not hold and the reason for this might be the fact that at those states when the inventory decreases, the system might choose to decrease the price, too, in order to make more sales and quickly reach to a state at which a replenishment is made instead of waiting for one more period in order to make more profit. So, at those critical states, a non-monotonic structure happens.

Fig. 11

Optimal replenishment decisions and the optimal prices at different states

Fig. 12

Optimal Price value versus a remaining shelf lifetime for different inventory size values, b inventory size for different remaining shelf lifetime values

7.5 Comparison of static pricing and dynamic pricing

In this section we analyze the effect of the dynamic pricing policy and compare the results of the static pricing model with the dynamic pricing model. Using the parameters stated above, part (a) of Fig. 13 shows the states at which a replenishment is made for both the static pricing and dynamic pricing models. We also consider another example in which all the parameters are the same as above except that the fixed order cost $K=0$ now and part (b) of Fig. 13 shows the optimal solutions for the replenishment decisions for the static and dynamic pricing models. We observe in both examples that higher quantities are ordered under dynamic pricing, i.e. $Q_D\ge Q_S$, and considering only the states with quantities less than $Q_S$, we observe that the set of ordering states under the dynamic pricing model is a subset of the set of ordering states under the static pricing model. This means that if a replenishment is made at a state, with quantity less than $Q_S$, under the dynamic pricing model, a replenishment is also made at that state under the static pricing model. But there also exists some states at which a replenishment is made under the static pricing model but not under the dynamic pricing case. In such states, the old products are salvaged under the static pricing model since the demand becomes too low at those states with the static price, but we continue to try to sell the older products under the dynamic pricing model by decreasing the price and increasing the demand since we have that option under dynamic pricing. Thus, dynamic pricing allows the managers to salvage less products by changing the price and the demand structure. As a result, we can say that less products are wasted with dynamic pricing. However, since higher quantities are ordered under the dynamic pricing model, we also note that there also exists some ordering states of the dynamic pricing model with quantities more than $Q_S$ but less than $Q_D$, that are not included in the set of ordering states of the static pricing model.

Fig. 13

Optimal replenishment decisions at different states when a K = 20,000, b K = 0

In Table 3, we compare the optimal order sizes under the static and dynamic pricing models, $Q_S$ and $Q_D$ respectively, and the improvement in average profit values with dynamic pricing as opposed to static pricing. We observe that significant improvements can be made via dynamic pricing compared to static pricing but the amount of improvement depends highly on the system parameters. Dynamic pricing seems especially beneficial when fixed order cost is high (since orders need to be made less frequently and more price changes need to be done in a cycle), market size is small (since a small change in price makes a big effect on revenue percentages), or price sensitivity of demand is high (since price changes have more significant effects on demand). In addition, we note that higher quantities are ordered in most of the examples under dynamic pricing. The reason for this is that by changing the price through the period, we are able to control the demand better and manage to have higher sales amount.

Table 3 Comparison of static and dynamic pricing models

8 Conclusion

We model a coordinated inventory control and pricing problem for perishable products with fixed shelf lifetime by considering a general stochastic demand function that is dependent on both price and remaining shelf lifetime of the products. We design a dynamic programming model for this system that gives us the optimal ordering decision policy, optimal quantity to order and price that should be charged to the products. Under the given assumptions, we prove that the optimal ordering decision scenario has a monotone structure in both static and dynamic pricing models. In the dynamic pricing model, we observe that the optimal price value decreases as time passes in a period. However, the optimal price changes in a non-monotonic structure with respect to inventory size. The proven properties of monotone structure of optimal ordering decision policy and ordering quantity and also the behavior of the optimal dynamic price versus inventory size and remaining shelf lifetime facilitate the use of the model outputs in perishable inventory systems and gives valuable insights to the managers of these systems. We perform numerical experiments for static and dynamic pricing cases and analyze the effects of the parameters on the results. We also analyze two heuristics that give us near optimal solutions with considerably less computational effort and easier-to-use for the managers. We check their performances for different sets of parameters to see which one is more reliable and efficient to use in each case, and compare their results with the optimal solution.

As possible future studies for this research, we may generalize some of the assumptions that we use in our model. Firstly, explicit inventory holding costs and lead times can be incorporated into the model, which will make the model a little bit more complicated. In addition, we assume that all the older products are salvaged when a new batch is ordered, however, as an extension, one may assume that the older products are kept at store and sold at a different price than the fresh products. This new assumption can be applicable for systems in which there is discount for old products as an attraction for different demand market sections. For this new model, we will also need to decide for how many periods we should keep old products in the inventory to sell. We also note that in this study a periodically-reviewed inventory system is analyzed and in the future we plan to analyze the pricing and replenishment decisions for a continuously-reviewed inventory system for perishable products.

Appendix

1.1 Proof of Proposition 1

In any state (q, t), we should choose an ordering size, Q(q, t), that maximizes $-K-cQ(q,t)+sq+f_c(Q(q,t),m)$ and the maximizer value will be independent of q and t. So, we can simply say that the optimal order size is same for all q and t values.

1.2 Proof of Proposition 2

Note that the maximum time before ordering a new batch is m periods since it is the maximum life of the product. In our model, we may not wait until the end of m periods and we can make a replenishment before that time. If we neglect the replenishment opportunities before m periods and assume that we make replenishments in every m periods, then the problem turns into a newsvendor problem in which the demand is the total demand of m periods. Hence, it is obvious that the optimal ordering size for our model is always less than the optimal ordering quantity of this newsvendor problem. If we assume that we have a standard newsvendor problem where the demand is equal to the total demand of m periods in our model, we know that the optimal ordering quantity for the newsvendor problem is equal to

$$\begin{aligned} min \Big \{ Q | F^{-1}_{m}(Q) \ge \frac{p-c}{p-s}\Big \} \end{aligned}$$

Thus, the optimal ordering size of the newsvendor problem stated above is an upper-bound for $Q^*$ in our problem.

Similarly, if we assume that we have another newsvendor problem in which the demand is equal to the demand of the first period in our model (where the remaining shelf lifetime is equal to m), the optimal ordering size for this newsvendor problem stated as below, will be a lower bound for $Q^*$ in our problem.

$$\begin{aligned} min \Big \{ Q | F^{-1}_{1}(Q) \ge \frac{p-c}{p-s}\Big \} \end{aligned}$$

1.3 Proof of Lemma 1

We can write the Bellman’s equation in 3.1 as $h=T(h)$ where T is an appropriate transformation function for the vector h. We prove that $h(q+1,t)\ge h(q,t)$ by showing that the transformation function used in the DP equation 3.1 preserves the monotonicity of the function h as stated in the equation below.

$$\begin{aligned} \Pi ^*+h(q,t)= & {} \max \Bigg \{\max _Q\big \{-K-cQ+sq+f_c(Q,m)\big \}, p\,E_D\nonumber \\&\Big [\min \big \{q,D(p,t)\big \}\Big ]+\,E_D\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ]\Bigg \}\nonumber \\\le & {} \max \Bigg \{\max _Q\{-K-cQ+s(q+1)+f_c(Q,m)\},\nonumber \\&p\,E_D \Big [\min \big \{q+1,D(p,t)\big \}\Big ]\nonumber \\&+\,E_D\bigg [h\Big (\big [q+1-D(p,t)\big ]^+,t-1\Big )\bigg ]\Bigg \} = \Pi ^*+h(q+1,t)\nonumber \\ \end{aligned}$$

(9.1)

In the above inequality, it can be easily seen that the second line is greater than the first line due to the assumption that $h(q+1,t)\ge h(q,t)$. As a result, we can say that the transformation function T given in the DP equation 3.1 preserves the monotonicity assumption that $h(q+1,t)\ge h(q,t)$ and thus it is proved that h(q, t) is non-decreasing in q for any given t.

For the second part of the Lemma, observe that each product at hand will either be sold at price $p>s$ or salvaged at price s at the end of the period, if not sold until that time. Thus, the value of having 1 more product on hand now is at least s and at most p.

$$\begin{aligned} s \le h(q+1,t)-h(q,t) \le p \end{aligned}$$

(9.2)

1.4 Proof of Lemma 2

We need to show that $h(q,t+1) \ge h(q,t)$ for any q and t. First, note that $\Pi ^*+ h(q,t)=\max \Big \{f_c(q,t), f_o(q)\Big \}$ and $f_o(q)$ is independent of t. Thus it is enough just to show that $f_c(q,t+1) \ge f_c(q,t)$. To prove this statement, we use a sample path argument. Using the sample path argument, we assume that we have two sets of products:

• Set 1: q products in inventory with $t+1$ remaining shelf lifetime

• Set 2: q products in inventory with t remaining shelf lifetime

Now, consider the case when the same customer arrives to these two sets and decides to buy or not a product. Three cases can happen in this system:

• Case I: Customer decides not to buy from both sets

• Case II: Customer decides to buy in both sets

• Case III: Customer decides to buy from set 1 and not to buy from set 2

Note that, it is not possible for the customer to buy from set 2 but not from set 1 because we assume that the customers always prefer fresher products and set 1 has fresher products than set 2 and they both have the same price. So, at a certain day after all customers visit the market, three cases can happen:

• Case 1: All products in both sets are sold out (the number of customers that decide to buy are more than q for both sets)

• Case 2: k number of products are sold in both conditions ($k \le q$)

• Case 3: k number of products are sold from set 1 and m number of products are sold from set 2, ($m \le k \le q$)

Now, using induction we will show that in all these three cases $h(q,t+1) \ge h(q,t)$ for any q and t values.

First for the boundary condition, for $t=0$,

• $h(q,1)=\max \Big \{f_c(q,1), f_o(q)\Big \}-\Pi ^*$

• $h(q,0)=f_o(q)-\Pi ^*$

So, it is obvious that $h(q,1) \ge h(q,0)$ (in all cases)

For $t \ge 1$, using the induction assumption that $h(q,t) \ge h(q,t-1)$

Case 1:

• $f_c(q,t+1) = pq+h(0,t)$ where $h(0,t)=f_o(0)-\Pi ^*$

• $f_c(q,t) = pq+h(0,t-1)$ where $h(0,t-1)=f_o(0)-\Pi ^*$

• So, $h(q,t+1) \ge h(q,t)$

Case 2:

• $f_c(q,t+1) = pk+h(q-k,t)$

• $f_c(q,t) = pk+h(q-k,t-1)$

Due to the induction assumption that $h(q-k,t)\ge h(q-k,t-1)$, we can state that $f_c(q,t+1) \ge f_c(q,t)$ for any q and t.

Case 3:

• $f_c(q,t+1) = pk+h(q-k,t)$

• $f_c(q,t)= pm+h(q-m,t-1)$

$f_c(q,t+1)-f_c(q,t)=p(k-m)+h(q-k,t)-h(q-m,t-1)\ge p(k-m)+h(q-k,t)-h(q-m,t)$ due to the induction assumption that $h(q-m,t)\ge h(q-m,t-1)$.

Now, we note the following inequality, since each product at hand will be sold or salvaged until the end of the period and thus the value of having k more products on hand now is at least sk and at most pk.

$$\begin{aligned} sk \le h(q+k,t)-h(q,t) \le pk \end{aligned}$$

(9.3)

Then, due to the above inequality, we have $s(k-m) \le h(q-m,t)-h(q-k,t) \le p(k-m)$. Thus, $p(k-m)+h(q-k,t)-h(q-m,t) \ge 0$ and we have $f_c(q,t+1)-f_c(q,t)\ge 0$.

As a result, we can say that in all three cases $h(q,t+1) \ge h(q,t)$ for any q and t and we can conclude that h(q, t) is non-decreasing in t for any q value.

1.5 Proof of Proposition 3

If we decide to order, the profit will be $f_o(q)$ that is an increasing function of q with the slope of s. On the other hand, if we decide to continue, the profit will be $f_c(q,t)$ that is again an increasing function of q. Since, a product in inventory will be sold or salvaged at the end, each product will have either a value of p or s for the system. So, it means that $s<f_c(q+1,t)-f_c(q,t)<p$. Hence, $f_c(q,t)$ is increasing with respect to q with a slope higher than s for all q and t. Since, $f_c(0,t)<f_o(0)$ and $f_c(q,t)$ is increasing with a faster rate than $f_o(q)$ for all q and t, $f_c(q,t)$ and $f_o(q)$ will intersect at a single point q for any t and we label it as q(t).

$f_o(q)$ function is independent of t and $f_c(q,t)$ is non-decreasing in remaining shelf lifetime value, t. So, by increasing t, the intersection point will happen at a lower q value meaning that q(t) is non-increasing in t.

1.6 Proof of Proposition 4

We know that $f_o(q)$ is independent of t and $f_c(q,t)$ is non-decreasing in t due to Lemma 2. So for a given q value, $f_o$ and $f_c(t)$ will have exactly one intersection point, denoted as t(q). Hence, t(q) is the critical value for any q such that we should give an order if $t<t(q)$ and do not order if $t\ge t(q)$.

It is obvious that q(t) and t(q) show the same curve for ordering states. In other words $t(q(t))=t$.

We proved in Proposition 3 that q(t) is non-increasing in t. So, for any $t_1\ge t_2$, $q(t_1)\le q(t_2)$. Let $q_1=q(t_1)$ and $q_2=q(t_2)$. Then, since $t_1=t(q(t_1))$ and $t_2=t(q(t_2))$, we can equivalently write that $t_1=t(q_1)$ and $t_2=t(q_2)$. Since $t_1\ge t_2$, $t(q_1)\ge t(q_2)$ for $q_1\le q_2$, which means that t(q) is non-increasing in q.

1.7 Proof of Lemma 3

Let’s assume that a given price p is applied at state (q, t) and define $f_c(q,t,p)=p\,E\Big [\min \big \{q,D(p,t)\big \}\Big ]+E\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ]$. Also, let $\Pi ^*+ h(q,t,p)=\max \Big \{f_c(q,t,p), f_o(q)\Big \}$. Then, observe that $f_c(q,t)=\max _{p}\{f_c(q,t,p)\}$ and $h(q,t)=\max _{p}\{h(q,t,p)\}$.

Let $p_1$ denote the optimal price at state (q, t) and $p_2$ denote the optimal price at state $(q+1,t)$, such that $h(q,t)=h(q,t,p_1)$ and $h(q+1,t)=h(q+1,t,p_2)$. Now, assume that, the same price $p_1$ is applied at both states (q, t) and $(q+1,t)$, even though it is not the optimal price for state (q+1,t). Note that $h(q+1,t,p_2)\ge h(q+1,t,p_1)$ since $p_2$ is the optimal price at state $(q+1,t)$. Observe that, under the same price $p_1$, due to Lemma 1, $h(q+1,t,p_1)\ge h(q,t,p_1)$. Then $h(q+1,t)=h(q+1,t,p_2)\ge h(q+1,t,p_1)\ge h(q,t,p1)=h(q,t)$. As a result, h(q, t) is non-decreasing in q for any given t, even though the prices are different at different states.

1.8 Proof of Lemma 4

Similar to the previous case, let $p_1$ denote the optimal price at state (q, t) and $p_2$ denote the optimal price at state $(q,t+1)$, such that $h(q,t)=h(q,t,p_1)$ and $h(q,t+1)=h(q,t+1,p_2)$. Now, assume that, the same price $p_1$ is applied at both states (q, t) and $(q,t+1)$, even though it is not the optimal price for state (q, t + 1). Note that $h(q,t+1,p_2)\ge h(q,t+1,p_1)$ since $p_2$ is the optimal price at state $(q,t+1)$. Observe that, under the same price $p_1$, due to Lemma 2, $h(q,t+1,p_1)\ge h(q,t,p_1)$. Then $h(q,t+1)=h(q,t+1,p_2)\ge h(q,t+1,p_1)\ge h(q,t,p1)=h(q,t)$. As a result, h(q, t) is non-decreasing in t for any given q, even though the prices are different at different states.

1.9 Proof of Proposition 7

If we decide to order, the profit will be $f_o(q)$ that is an increasing function of q with the slope of s. On the other hand, if we decide to continue, even though the prices at different states are different, the minimum price still needs to be more than the salvage value s. Since Lemma 1 also applies under dynamic pricing, the profit $f_c(q,t)$ is again an increasing function of q with a slope that is at least equal to s, i.e. $s \le f_c(q+1,t)-f_c(q,t)$. Hence, $f_c(q,t)$ is increasing with respect to q with a slope higher than s for all q and t. Since, $f_c(0,t)<f_o(0)$ and $f_c(q,t)$ is increasing with a faster rate than $f_o(q)$ for all q and t, $f_c(q,t)$ and $f_o(q)$ will again intersect at a single point q for any t and we label it as q(t).

Again, observe that the function $f_o(q)$ is independent of t and $f_c(q,t)$ is non-decreasing in remaining shelf lifetime value, t due to Lemma 2. So, by increasing t, the intersection point will happen at a lower q value meaning that q(t) is non-increasing in t.

1.10 Proof of Proposition 8

We know that $f_o(q)$ is independent of t and $f_c(q,t)$ is non-decreasing in t due to Lemma 2, even though different prices are applied at different states. So for a given q value, $f_o$ and $f_c(t)$ will have exactly one intersection point, denoted as t(q). Hence, t(q) is the critical value for any q such that we should give an order if $t<t(q)$ and do not order if $t\ge t(q)$.

It is obvious that q(t) and t(q) show the same curve for ordering states. In other words: $t(q(t))=t$.

We proved in Proposition 7 that q(t) is non-increasing in t. So, for any $t_1\ge t_2$, $q(t_1)\le q(t_2)$. Let $q_1=q(t_1)$ and $q_2=q(t_2)$. Then, since $t_1=t(q(t_1))$ and $t_2=t(q(t_2))$, we can equivalently write that $t_1=t(q_1)$ and $t_2=t(q_2)$. Since $t_1\ge t_2$, $t(q_1)\ge t(q_2)$ for $q_1\le q_2$, which means that t(q) is non-increasing in q.