1 Introduction

We consider inventory management and pricing of perishable products such as fresh fruits, vegetables, milk, yogurt, eggs, and bread, considering a price and time-dependent demand function. Effective management of these perishable products is an important issue since it is observed that billions of dollars’ worth of food is expired and wasted every month (Minner and Transchel 2010). Different than durable products, as the perishable products age, the demand for these products starts to decline and in a short time these products can become completely obsolete making the management of these products especially difficult. Thus, not only the amount of these products on shelf but also their status or age is also a major concern for the managers in their decisions. As the products on shelf start to deteriorate, the managers need to decide whether to continue with the products on hand which might cause a decrease in sales and loss in revenues or order a new batch which will lead to the wastage of the products on hand, since they will no longer be sold when the new batch arrives. In addition, the managers also have the option to change the prices of the products as they age in order to control the demand and to increase the revenues. As a result, the perishability and the time dependency of demand make the management of inventory and pricing for these products much harder.

In the literature, most of the inventory models assume that inventories can be held in stock indefinitely to satisfy future demands and the demand is independent of the age of the products on hand. However, in reality, there exists many perishable products that either deteriorate or become outdated by time. Thus, the inventory on hand not only decreases by demand, but it also decreases due to the expiration of products. In addition, because of the change in demand over time, it might also be better to charge different prices at different times and employing a dynamic pricing strategy might improve the profits substantially. Therefore, if the rate of deterioration is not sufficiently low, its impact on modeling of the inventory becomes a major concern.

The stream of literature considering dynamic pricing under stochastic demand includes a wide range of applications from airline companies to hotel reservation systems. There are many models, in which a fixed amount of inventory needs to be sold until a certain time, without any replenishment opportunities (e.g., Gallego and van Ryzin 1994; Zhao and Zheng 2000; Monahan et al. 2004; Gayon et al. 2009, etc.). In these studies, demand is mostly assumed to be independent of time and they mainly focus on the structural characteristics of the optimal solution. Bitran and Caldentey (2003) present an extensive review of dynamic pricing policies in the literature. Minner and Transchel (2010) consider the ordering policies for perishable products in the food retail industry under service level constraints and present a method to determine the order quantities, but they do not consider pricing in their study. Nahmias (1982) reviews related literature about determining the ordering policies for perishable inventory systems for products with both fixed life and having exponential decay over time. Interested readers can also refer to the surveys done by Rafaat (1991), Goyal and Giri (2001) and Bakker et al. (2012) about the inventory management of deteriorating items. There are also several studies in the literature considering the inventory and pricing problems for perishable products with time-dependent demand. Chen et al. (2014) focus on the joint pricing and inventory control problem for perishable inventory systems with stochastic demand and lead times and also focus on the structural properties of the optimal solution. Chen and Sapra (2013) consider the joint inventory and pricing decisions for perishable products in a periodic review model with a fixed lifetime of two periods. Chew Peng and Chulung (2009) develop a discrete time dynamic programming model to determine the optimal inventory allocations and the optimal prices for a perishable product with a two period lifetime and they obtain several optimality properties.

Benkherouf (1995) and Mishra and Singh (2010) consider deterministic demand in their inventory models for deteriorating items with a time-dependent demand function, but they only focus on the replenishment schedule and do not consider pricing. Broekmeulen and van Donselaar (2009) also focus on a perishable product system considering the age of products and they propose a heuristic policy for the replenishment of perishable inventories without the consideration of pricing. They compare their heuristic results with the optimal policy that does not take into account the age of inventories using simulation. Transchel and Minner (2009) consider discrete pricing of non-perishable products with deterministic demand, assuming a fixed cost for changing prices. Abad (1996) and Rajan and Steinberg (1992) consider the relationship between pricing and ordering decisions for perishable products by allowing a continuous price function p(t) over the cycle. Abad (1997, 2001, 2003) works on optimal pricing and lot sizing problem for perishable products with deterministic demand allowing a single price in the system. Burwell et al. (1991) extend the results of Abad (1997) by offering shortages in addition to all unit quantity discounts. Wee (1999) has developed a joint pricing and replenishment policy for deteriorating items, with a lifetime that has a Weibull distribution, with partial backordering and quantity discounts, but he only considers a single price and does not allow price changes. Similarly, Mukhopadhyay et al. (2004) and Sana (2010) also consider perishable products assuming a single price to be charged over the whole cycle without allowing price changes in a cycle. In addition, they assume that the demand function is independent of time. You (2005) deals with perishable inventory models with price and time-dependent demand and aims to determine the optimal number of prices, price values and order quantities in her proposed model assuming fixed time intervals between price changes.

In Table 1, we present the comparison of our study with the most related papers with deterministic models in the literature. As seen in Table 1, none of the studies in the literature, except Transchel and Minner (2009), considers discrete pricing over time allowing the times of price changes to be decision variables. For example, Rajan and Steinberg (1992) and Abad (1996) consider continuous pricing and do not analyze discrete prices. You (2005) considers discrete prices, but she assumes fixed time intervals and does not consider different timings of price changes. She also does not consider any deterioration process for the products. Transchel and Minner (2009) do not consider perishable products and, thus, they do not consider deteriorating inventory over time. In addition, the demand function used in their model only depends on the price and the age or freshness of the products does not affect the demand function. Our study combines all the different elements in these studies and is the only study in the literature that considers discrete pricing for perishable products that decides on the optimal times to change the prices in addition to the optimal price values.

Table 1 Comparison of this study with the most related deterministic models in the literature
Full size table

As stated above, most of the researchers in the literature consider the pricing and inventory decisions for perishable products separate from each other or allow a single price over the planning horizon. Only a few studies consider multiple pricing, but they either allow a continuous price function without considering price changing costs or price changes are made at predefined times. However, in reality, it is not possible to continuously change prices at no cost and timing of price changes is an important factor that can significantly affect the revenues. In this study, we construct a model by giving the seller the ability to change the prices multiple times at any time he wants at a certain cost over the planning horizon so as to maximize the total profit. We aim to find the best times to change the prices as well as the optimal values of these prices. We investigate the effects of dynamic pricing on ordering decisions with an optimized number of price changes and timings in every cycle. We also compare the multi-pricing case with the constant pricing strategy. In addition, most of the studies in the literature related to coordinated pricing and inventory decisions assume that demand is independent of time. However, we consider perishable products with time- and price-dependent demand that decay at a certain rate, and we provide explicit analytical and numerical results for this system. In addition to modeling and analyzing the optimal solution of this system, different from the literature, we also propose solution algorithms and present their performances compared to the optimal solution.

2 Model

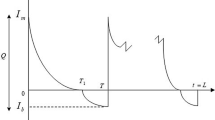
We use an economic order quantity (EOQ)-based approach without allowing backorders, since the customers for perishable products will not be willing to wait to get these products. We denote the time between two successive orders for new products to replenish inventory as an inventory cycle. During an inventory cycle, the price of the product is changed several times to obtain the maximum possible profit. We let h denote the inventory cost per unit per unit time, N denote the number of different prices used in an inventory cycle and C(N) denote the cost of changing prices when N different prices are used in an inventory cycle. In our model, \(t_i\), \(i=1,2\ldots N-1\), denotes the time of the ith price change with \(t_0=0\) and \(t_N\) denotes the end of an inventory cycle at which time new and fresh products are ordered. We let \(p_i\), for \(i=1,2 \ldots N\), denote the price during the time interval \([t_{i-1}, t_i)\). Figure 1 presents an illustration of an inventory cycle.

Fig. 1
figure 1

Illustration of inventory process

Full size image

Due to perishability of the product, the inventory is depleted partly to meet the demand and partly for deterioration. We assume that each product on hand decays at a constant rate \(\theta \) independent of the other products since it is a common assumption in literature (e.g., Abad 1996, 2001, 2003; Mukhopadhyay et al. 2004 etc.). In this case, the decay rate of all inventory at any time t is given by \(w(t)=\theta I(t)\) as a function of the instantaneous inventory level at that time, denoted as I(t). Note that \(Q = I(0)\) denotes the maximum inventory level, i.e., batch size ordered at the beginning of each cycle. Every time an inventory replenishment order is given, a fixed order cost A and per unit cost c are incurred such that the total cost at the time of order will be \(A+cQ\). In Fig. 1, x axis is the time line and y axis is the inventory level at each time. In this figure, \(t_1,t_2 \ldots ,t_N\) are the times where we apply price adjustments and \(I(t_1),I(t_2) \ldots ,I(t_N) \) are the corresponding inventory levels at those times. We describe the inventory function I(t) by the differential equation (1) which consists of the decay rate and the price- and time-dependent demand rate, D(p, t), such that

$$\begin{aligned} \frac{\partial {I(t)}}{\partial t}= -D(p(t),t)-\theta I(t) \end{aligned}$$
(2.1)

Since the inventory function changes every time the price is changed, we let \(I_i(t)\) denote the inventory function for any time \(t \in [t_{i-1}, t_i)\). We also let \(I(t_i)\) denote the inventory level at the end of the time period \([t_{i-1}, t_i)\). Note that the inventory level \(I_i(t)\) will be equal to the inventory consumed from time t to \(t_i\) due to sales and decay plus \(I(t_i)\) as stated below.

$$\begin{aligned} I_i(t) = \int _{t}^{t_i} (D(p,s) +I(s)\theta )\mathrm{d}s+I(t_i) \end{aligned}$$

Equation 2.1 is a first-order differential equation with variable coefficients. This equation can be solved using an integrating factor \(e^{\theta t}\). Multiplying Eq. 2.1 by \(e^{\theta t} \), we obtain

$$\begin{aligned} e^{\theta t}\frac{\partial {I_i(t)}}{\partial t}+\theta e^{\theta t} I_i(t)= -e^{\theta t}D(p_i,t)\nonumber \\ \frac{\mathrm{d} (e^{\theta t}I_i(t))}{\mathrm{d} t}=-e^{\theta t} D(p_i,t) \end{aligned}$$
(2.2)

By integrating both sides of Eq. 2.2, we find that

$$\begin{aligned} e^{\theta t}I_i(t)=\int _{t}^{t_i} e^{\theta s} D(p_i,s) ds + c \end{aligned}$$
(2.3)

where c is an arbitrary constant. By solving Eq. 2.3 for \( I_i(t) \), we obtain the general solution

$$\begin{aligned} I_i(t)=e^{-\theta t}\int _{t}^{t_i} e^{\theta s}D(p_i,s) \mathrm{d}s + c e^{-\theta t} \end{aligned}$$
(2.4)

Then, for any time \(t \in [t_{i-1}, t_i)\), using the differential Eq. 2.4 with the boundary condition \(I_i(t_i)=I(t_i)\), we get the following instantaneous inventory equation for \(I_i(t)\).

$$\begin{aligned} I_i(t)=\int _{t}^{t_i} D(p,s)e^{\theta (s-t)}\mathrm{d}s +I(t_{i})e^{\theta (t_i-t)} \end{aligned}$$

From now on, in order to obtain explicit analytical results, we use a linear demand function, that is commonly used in literature (e.g., Rajan and Steinberg 1992; Transchel and Minner 2009, etc.), which depends on both price and time as \(D(p_i,t)=a-\beta p_{i}-kt \) where \(p_{i}\) denotes the price at ith time interval, \(\beta \) is the price sensitivity of demand and k is the time sensitivity of demand. Using the linear demand function, the inventory equation can be written as:

$$\begin{aligned} I_i(t)= & {} \int _{t}^{t_i} (a-\beta p_{i}-ks)e^{\theta (s-t)} \mathrm{d}s +I(t_{i}) e^{\theta (t_{i}-t)}\nonumber \\ I_i(t)= & {} \frac{a-\beta p_{i}-kt_i}{\theta } e^{\theta (t_{i}-t)}+\frac{k}{\theta ^2}e^{\theta (t_{i}-t)}-\frac{a-\beta p_{i}-kt}{\theta }-\frac{k}{\theta ^2}+I(t_{i})e^{\theta (t_{i}-t)}\nonumber \\ \end{aligned}$$
(2.5)

We note that since at the end of the cycle all the inventory will be consumed (otherwise, it will not be an optimal solution and ordering one less at time zero will yield a better result), i.e., \(I(t_N)=0\), using the above equation and going backwards, one can find all \(I(t_i)\) values and \(I_i(t)\) equations explicitly. Similarly, we can find the order level \(Q=I(t_0)\) where \(t_0=0\) from the above equation. Explicitly, we can write Q and \(I(t_i)\) as below:

$$\begin{aligned} I(0)= & {} Q=\frac{a-\beta p_{1}-kt_1}{\theta } e^{\theta t_{1}}+\frac{k}{\theta ^2}e^{\theta t_{1}}-\frac{a-\beta p_{1}}{\theta }-\frac{k}{\theta ^2}+I(t_{1})e^{\theta t_{1}}\\ Q= & {} \sum _{i=1}^{N}\left( \frac{a-\beta p_i-kt_i}{\theta }e^{\theta t_i}+\frac{k}{\theta ^2}e^{\theta t_i}-\frac{a-\beta p_i-kt_{i-1}}{\theta }e^{\theta t_{i-1}}-\frac{k}{\theta ^2}e^{\theta t_{i-1}}\right) \\ I(t_i)= & {} \sum _{j=i+1}^{N}\left( \frac{a-\beta p_j-kt_j}{\theta }e^{\theta (t_j-t_i)}+\frac{k}{\theta ^2}e^{\theta (t_j-t_i)}-\frac{a-\beta p_j-kt_{j-1}}{\theta }e^{\theta (t_{j-1}-t_i)}\right. \nonumber \\&\times \left. -\frac{k}{\theta ^2}e^{\theta (t_{j-1}-t_i)}\right) \end{aligned}$$

We let \(S_i\) denote the sales amount of the product at ith interval:

$$\begin{aligned} S_i= & {} \int _{t_{i-1}}^{t_i} (a-\beta p_i -kt) \mathrm{d}t\\= & {} (a-\beta p_i)(t_{i}-t_{i-1})-\frac{k}{2}\left( t_{i}^2-t_{i-1}^2\right) \end{aligned}$$

Then, we find the revenue in an interval by multiplying the demand with the price in that cycle and total revenue in an inventory cycle will be the sum of all the revenues earned at each interval. The total revenue, \(\Pi _R\), is found as follows:

$$\begin{aligned} \Pi _R=\sum _{i=1}^{n} p_i(a-\beta p_i)(t_{i}-t_{i-1})-\frac{kp_i}{2}\left( t_{i}^2-t_{i-1}^2\right) \end{aligned}$$

We also calculate the inventory cost, \(\Pi _H\), in the system by taking the area under the inventory curve in Fig. 1 and then multiply with the unit holding cost to find the total inventory cost. Using Eq. (2.5),

$$\begin{aligned} \Pi _H= & {} h\sum _{i=1}^n \int _{t_i-1}^{t_i} I_i(t) \mathrm{d}t\\= & {} h \left( \sum _{i=1}^{n} \int _{t_{i-1}}^{t_i} \big ( \frac{a-\beta p_i-kt_{i}}{\theta }e^{\theta (t_{i}-t)}\right. \\&\left. +\frac{k}{\theta ^2}e^{\theta (t_{i}-t)}-\frac{a-\beta p_i-kt}{\theta }-\frac{k}{\theta ^2}+I(t_i)e^{\theta (t_{i}-t)} \big ) dt \right) \\= & {} h\sum _{i=1}^{n} \left( -\frac{a-\beta p_i-kt_i}{\theta ^2}(1-e^{\theta (t_{i}-t_{i-1})})\right. \\&\left. -\frac{k}{\theta ^3}(1-e^{\theta (t_{i}-t_{i-1})})-\frac{a-\beta p_i}{\theta }(t_{i}-t_{i-1})\right. \\&\left. +\frac{k}{2\theta }\left( t_{i}^2-t_{i-1}^2\right) -\frac{k}{\theta ^2}(t_{i}-t_{i-1})-\frac{I(t_i)}{\theta }(1-e^{\theta (t_i-t_{i-1})}) \right) \end{aligned}$$

Finally, the profit per unit time function is obtained by taking the difference between total revenue and total cost during an inventory cycle and dividing that value by the length of an inventory cycle. As a result, we can write our problem as below:

$$\begin{aligned} \max _{N,p_i,t_i} \pi ^{(N)}= & {} \bigg \{\frac{1}{t_N}\bigg [\sum _{i=1}^{N}\bigg \{ p_i(a-\beta p_i)(t_i-t_{i-1})-\frac{kp_i}{2}(t_i^2-t_{i-1}^2)\nonumber \\&-h\left[ -\frac{a-\beta p_i-kt_i}{\theta ^2}(1-e^{\theta (t_i-t_{i-1})})-\frac{k}{\theta ^3}(1-e^{\theta (t_i-t_{i-1})})\right. \nonumber \\&-\frac{a-\beta p_i}{\theta }(t_i-t_{i-1})+\frac{k}{2\theta }(t_i^2-t_{i-1}^2)\nonumber \\&\left. -\frac{k}{\theta ^2}(t_{i}-t_{i-1}) -\frac{I(t_i)}{\theta }(1-e^{\theta (t_i-t_{i-1})})\right] \bigg \}-(A+cQ+C(N))\bigg ]\bigg \}\nonumber \\&s.t \nonumber \\&a-\beta p_i-kt_i\ge 0 \qquad \forall i \in \{1,\ldots ,N\} \nonumber \\&t_{i}-t_{i-1}\ge 0 \qquad \forall i \in \{1,\ldots ,N\} \nonumber \\&p_{i}\ge 0 \qquad \forall i \in \{1,\ldots ,N\} \nonumber \\&\qquad t_0 = 0 \nonumber \\&\qquad N \in \{1,2,\ldots \} \end{aligned}$$
(2.6)

For given N and \(t_i\) values for all \(i=1,2,\ldots ,N\), we can find the optimal prices \(p_i\) using the first-order derivatives of the above equation as stated in the following Theorem.

Theorem 1

For a given set of N and \(t_i\) values, let \(p_i^1\) and \(p_i^2\) be defined as below.

$$\begin{aligned} p_i^1= & {} \frac{a}{2\beta }-\frac{k}{4\beta }(t_i+t_{i-1})+\frac{c(e^{\theta t_i}-e^{\theta t_{i-1}})}{2\theta (t_i-t_{i-1})}\\&+\frac{h}{2\theta }\bigg (\frac{e^{\theta (t_i-t_{i-1})}-1-\sum _{j=1}^{i-1}((e^{\theta (t_i-t_j)}-e^{\theta (t_{i-1}-t_j)})(1-e^{\theta (t_j-t_{j-1})}))}{\theta (t_i-t_{i-1})}-1\bigg )\\ p_i^2= & {} \frac{a-kt_i}{\beta } \end{aligned}$$

Then, the optimal prices \(p_i^*\) are as given by the following equation:

$$\begin{aligned} p_i^*=\left\{ \begin{array}{ll} p_i^1, &{} \mathrm{if} a-\beta p_i^1-kt_i\ge 0; \\ p_i^2, &{} \mathrm{otherwise.} \end{array} \right. \end{aligned}$$

Proof

We find the optimal prices using the result of first- and second-order derivatives of the profit function given in Eq. (2.6). \(\pi ^N\) is a function which is twice differentiable at each \(p_i\) and satisfies \( \frac{\partial ^2 \pi ^N}{\partial p_i^2}=\frac{-2\beta (t_i-t_{i-1})}{t_N} < 0\) for all \(i=1,\ldots ,N\) and \(\frac{\partial ^2 \pi ^N}{\partial p_i\partial p_j} = 0\) for all \(i=1,\ldots ,N\) and \(j\ne i\). Hence, \(\pi ^N\) is jointly concave in \(p_i\) for \(\forall i\) and the optimal prices \(p_i\) are the values which make the first-order derivatives, which are stated as below, equal to 0.

$$\begin{aligned} \frac{\partial \pi }{\partial p_i}= & {} \frac{1}{t_N}\left[ a(t_i-t_{i-1})-2\beta p_i (t_i-t_{i-1})-\frac{k}{2}(t_i^2-t_{i-1}^2)+\frac{c \beta (e^{\theta t_i}-e^{\theta t_{i-1}})}{\theta }\right. \\&-h \left[ \frac{\beta }{\theta ^2}(1-e^{\theta (t_i - t_{i-1})})+\frac{\beta }{\theta }(t_i -t_{i-1})\right. \\&\left. \left. +\frac{\beta }{\theta ^2}\sum _{j=1}^{i-1}((e^{\theta (t_i-t_j)}-e^{\theta (t_{i-1}-t_j)})(1-e^{\theta (t_j-t_{j-1})}))\right] \right] \\ p_i^1= & {} \frac{a}{2\beta }-\frac{k}{4\beta }(t_i+t_{i-1})+\frac{c(e^{\theta t_i}-e^{\theta t_{i-1}})}{2\theta (t_i-t_{i-1})}\\&+\frac{h}{2\theta }\bigg (\frac{e^{\theta (t_i-t_{i-1})}-1-\sum _{j=1}^{i-1}((e^{\theta (t_i-t_j)}-e^{\theta (t_{i-1}-t_j)})(1-e^{\theta (t_j-t_{j-1})}))}{\theta (t_i-t_{i-1})}-1\bigg ) \end{aligned}$$

However, for \(p_i^1\) to be optimal, it should also satisfy the constraints in the problem. Since \(a>kt_i\) should hold for all i (otherwise, the demand function \(a-\beta p_i-kt_i\) will be non-positive even for \(p_i=0\) and such \(t_i\) can never be optimal), \(p_i^1 \ge 0\) will always hold. However, \(p_i^1\) might not satisfy the constraint \(a-\beta p_i^1-kt_i \ge 0\) for all i. In those cases, since the objective function is jointly concave w.r.t. \(p_i\), the optimal price will be \(p_i^2=\frac{a-kt_i}{\beta }\). \(\square \)

Even though we can find analytical results for the optimal prices for given \(t_i\) and N values, due to the constraints in the problem and N being an integer variable, we could not determine the optimal values of N and \(t_i\) explicitly, for all \(i=1,2,\ldots ,N\). Thus, we try to solve the above problem with the commercial nonlinear programming solver BARON with GAMS. We use \(p_i\) values from Theorem 1 to decrease the number of variables in the model and aim to solve for the unknowns N and \(t_i\) only. We do a one-dimensional search over N and run the solver for our problem for varying N values given as input and try to find the optimal \(t_i\) values for all \(i=1,2,\ldots ,N\). As a result, even though we could obtain the optimal solution when N is small (e.g., less than 10), the commercial solver failed to give any results as N increases under a time limit of 4 hours. In addition, the commercial solver is seen to fail to guarantee the global optimality in many cases. We note that running the model with \(p_i\) values also as decision variables results in worse solutions. Hence, we develop heuristic algorithms to determine the optimal values of N and \(t_i\) as presented in the next section.

2.1 Special case: single price model \((N=1)\)

In this section, we analyze the static pricing model in which a single price is used over the inventory cycle with no price changes (\(N=1\) case). In this case, the profit function and the problem can be written as below:

$$\begin{aligned} \max _{p_1,t_1}&\pi ^{1}=\bigg [p_1(a-\beta p_1)-\frac{kp_1}{2}t_1-h\left[ -\frac{a-\beta p_1-kt_1}{\theta ^2 t_1}(1-e^{\theta t_1})-\frac{k}{\theta ^3 t_1}(1-e^{\theta t_1})\right. \nonumber \\&\left. -\frac{a-\beta p_1}{\theta }+\frac{k}{2\theta }t_1-\frac{k}{\theta ^2}\right] -c\frac{(a-\beta p_{1}-kt_1)\theta e^{\theta t_{1}}+k e^{\theta t_{1}}-(a-\beta p_{1})\theta -k}{\theta ^2 t_1}\nonumber \\&-\frac{A}{t_1}\bigg ]\nonumber \\&s.t \nonumber \\&a-\beta p_1-kt_1\ge 0 \nonumber \\&t_1\ge 0 \nonumber \\&p_1\ge 0 \end{aligned}$$
(2.7)

For this case, the first-order derivatives of the objective function will be as below:

$$\begin{aligned} \frac{\partial \pi ^1 }{\partial p_1}=a-2\beta p_1-\frac{k t_1}{2}+\frac{c \beta (e^{\theta t_1}-1)}{\theta t_1}-h \left[ \frac{\beta }{\theta ^2 t_1}(1-e^{\theta t_1})+\frac{\beta }{\theta }\right] \end{aligned}$$
(2.8)
$$\begin{aligned} \frac{\partial \pi ^1 }{\partial t_1}= & {} -\frac{kp_1}{2}-h\nonumber \\&\times \left[ \frac{[k(1-e^{\theta t_1})+(a-\beta p_1-kt_1)(\theta e^{\theta t_1})]t_1+(a-\beta p_1-kt_1)(1-e^{\theta t_1})}{\theta ^2 t_1^2}\right. \nonumber \\&\quad \left. +\,\frac{k\theta e^{\theta t_1}t_1+k (1-e^{\theta t_1})}{\theta ^3 t_1^2}+\frac{k}{2\theta }\right] +\frac{A}{t_1^2}\nonumber \\&\quad -\,c\frac{(-ke^{\theta t_1}+(a-\beta p_1-kt_1)\theta e^{\theta t_1})\theta t_1-\theta (a-\beta p_1-kt_1)e^{\theta t_1}}{\theta ^2 t_1^2}\nonumber \\&\quad +\,\frac{k e^{\theta t_1}\theta t_1- ke^{\theta t_1}}{\theta ^2 t_1^2} \end{aligned}$$
(2.9)

Even though the optimal price can be obtained from Eq. 2.8 as a function of \(t_1\) as stated in Theorem 1 for \(i=1\), due to the complexity of Eq. 2.9, it is not possible to obtain a closed form solution for \(t_1\) even when \(N=1\). However, since the objective function is jointly concave w.r.t. \(p_1\) and \(t_1\), the optimal price and cycle length can be obtained from the above equations numerically, if they satisfy the constraints. Otherwise, one of the constraints will be binding and in the optimal solution, either \(t_1=0\) or \(p_1=\frac{a-kt_1}{\beta }\) should be satisfied. If \(t_1=0\), it means that the business should be closed and zero profit will be made. On the other hand, if \(p_1=\frac{a-kt_1}{\beta }\), then the optimal \(t_1\) can be found from the solution of the first-order derivative of the objective function, as stated below:

$$\begin{aligned} \frac{A}{t_1^2}-\frac{k^2 t_1}{\theta }+\frac{hk(e^{\theta t_1}-1)}{t_1^2\theta ^3}+\frac{ck(e^{\theta t_1}-1)}{t_1^2\theta ^2}+\frac{ak}{2\beta }+\frac{hk}{2\theta }-\frac{hke^{\theta t_1}}{\theta ^2 t_1}-\frac{cke^{\theta t_1}}{\theta t_1}=0\nonumber \\ \end{aligned}$$
(2.10)

3 Approximate solutions

3.1 Price changes at equal intervals

In this approximation algorithm, we assume that the times between any two price changes are equal to each other, such that \(t_i-t_{i-1}=t\) for all \(i=1,2\ldots N\) for some t. Under this assumption, in addition to the variables N and \(p_i\), instead of the variables \(t_i\) for all \(i=1,2 \ldots N\), we only have a single variable t that determines the time length between any two price changes. For a given t, time of the ith price change, \(t_i\), will be \(i*t\). Since we can determine the optimal \(p_i\) values as a function of \(t_i\) as given in Theorem 1, the only problem remains to determine the optimal N and t, which can easily be determined through a two-dimensional search in a reasonable time. We present the efficiency of this approximation algorithm in our computational studies.

3.2 Genetic algorithm

Genetic algorithm is an optimization method based on naturally inspired genetic operations. It uses selection, mutation and crossover operations to achieve its optimization goal. A chromosome in our model is an array with N values, where the element at the ihposition denotes the value of \(t_i\). We note that, since N is a decision variable, the algorithm is run for different N values and optimal N is obtained through enumeration. Figure 2 shows an illustration of such chromosomes.

Fig. 2
figure 2

Illustration of chromosomes

Full size image

As a result of our initial experiments, where we tried different initial population sizes of 20, 30, 50 and 100, we choose to start with 30 different chromosomes, each with a different random value of \(t_N\). For the initial solution, we generate all other \(t_i\) values in a chromosome by equally spacing them up to \(t_N\). Then, for a given array of \(t_i\) values, we calculate the optimal prices and the profit function for each chromosome using the equations in the previous section, and determine the fitness value of each chromosome as the value of the profit function for that time array.

After evaluating the profit values for each chromosome, we allocate reproductive opportunities in such a way that the chromosomes which represent a better solution for the problem are given higher chances to reproduce than other chromosomes with lower objective function value. We apply roulette wheel selection as the reproduction mechanism. In the roulette wheel selection method, the first step is to calculate the cumulative fitness of the whole population through the sum of the fitness of all individuals. After that, the probability of selection is calculated for each individual as being wheel \(=\) fitness/total fitness. Then, an array is built containing cumulative probabilities of the individuals and individuals are selected according to their probabilities.

We apply crossover operations to generate new populations using one point variable length crossover. We form a mating pool with the offspring and the original population, then by generating random numbers, chromosomes with higher fitness values are selected into the next generation. We take two parents and cut them at a random position and swap them. For each chromosome pair, probability of crossover is randomly generated at each time. The pairs are selected randomly from a 30-member population. Therefore, at each iteration, fifteen pairs are created and crossover is applied if default crossover probability is less than the random number generated by code as crossover probability.

In order to have diversification, we also apply mutation to the chromosomes. After crossover is performed, we apply the mutation operator to change only one point of the genome to diversify the solution. Every genome is mutated by a predefined probability of 0.07, which is found to be the best value according to our initial experiments.

Until a termination criterion is met, this procedure is repeated and the best time array is selected. The pseudo-code for our algorithm is as follows:

Pseudo-Code for Genetic Algorithm

  • Step 1. Generate an initial population of chromosomes which are constructed from feasible solutions of time arrays

  • Step 2. Evaluate objective function values of chromosomes using profit functions with the corresponding price functions.

  • Step 3. Select two chromosomes from the population according to their objective values (higher probability of selection for higher objective values)

  • Step 4. According to crossover probabilities, by crossover operator, form new offspring from parents.

  • Step 5. According to the mutation probabilities, mutate new offspring at each randomly selected locus

  • Step 6. Place new offspring in the population

  • Step 7. Select the next population according to their objective function values.

  • Step 8. Use new generated population for the further run of the algorithm

  • Step 9. If end condition is satisfied, stop and return the best solution in the population.

Table 2 Comparison of multi-pricing strategy with single pricing
Full size table

4 Computational studies

In this section, we present our numerical results to analyze the multi-pricing strategy for the management of perishable inventories. As a base case for our numerical examples, we use the parameters a (market size)\(=100\), \(\beta \)(price sensitivity of demand)\(=1\), k(age sensitivity of demand)\(=5\), c(unit cost of products)\(=5\), h(holding cost per product per unit time)\(=0.1\), \(\theta \)(decay rate of products)\(=0.05\), A(fixed order cost)\(=5000\). In addition, when N prices are used in an inventory cycle, it means that \(N-1\) price changes are made and we use a linear cost function \(C(N)=(N-1)f\) for changing prices where \(f=10\). In Table 2, we present the results for the dynamic pricing model as well as the results for the static pricing case, as a benchmark, in which the price is not allowed to change during a cycle. In the first row of Table 2, we present the results for this base case and in the following rows of this table, we do a sensitivity analysis by changing one of these parameters as stated in the first column of Table 2. In Table 2, we compare the multi-pricing strategy with the static pricing strategy, in which only one price is allowed to be used. We obtain the optimal results for the static pricing case by fixing \(N=1\) and doing a one-dimensional search for the optimal length of the cycle \(t_N\) to maximize the total profit function 2.6 with the help of Theorem 1. For the multi-pricing case, we use the commercial solver BARON with GAMS since the number of price changes in the optimal solution is small in these examples. Experiments are done on a workstation with an Intel(R) Core(TM)2 Duo processor, 2.53 GHz speed, and 2GB of RAM.

In Table 2, we observe that dynamic pricing might result in significant gains in profits as opposed to single pricing. In our base case, the difference of the profits between multiple pricing and single pricing is about 2.5%, but this difference changes depending on the system parameters. For example, when a decreases to 80 or k increases to 10, the gain in profits with multiple pricing increases up to 30%. On the other hand, when a is high or k is small, the percentage difference of profits between multi-pricing and single pricing becomes less than 1%. We observe that multiple pricing becomes more beneficial as a, f, h or \(\theta \) decreases; or A, \(\beta \), c or k increases. When we look at the other values, we observe that multiple pricing leads to longer cycle lengths and higher order quantities in all cases; however, this also leads to higher decay ratios of products which seem counterintuitive at first, since we expect that multiple pricing might decrease the wastage amounts. However, due to longer cycles and higher order sizes, even though higher profits are obtained, multiple pricing also leads to higher decay amounts. When we look at the prices, we observe that the average price values with multiple pricing are lower than the static price value. It is seen that, when multiple prices are used, at first a high price is charged at the beginning (which is generally larger than the single price value), and then the prices are decreased over time. For example, in our base case the single price value is 44.4, but in the multiple pricing model, the price 49.7 is charged at the beginning and then it is decreased to 44.11 at time 2.42 and then to 38.56 at time 4.85 and this price is charged until the end of the cycle.

When we look at the effects of the parameters on the system, we observe that as a increases, the order size increases, the cycle length decreases and the profits increase substantially. In addition, the benefit of dynamic pricing decreases with a. As \(\beta \) increases, less profit is obtained since lower prices need to be charged but the order size and the cycle length increase. In addition, as \(\beta \) increases, since the system will be more sensitive to pricing, the benefit of dynamic pricing compared to the static pricing model increases. When k increases, multiple pricing becomes more beneficial while the order size and the cycle length decrease. Next, we observe that as c increases, order size, cycle length and profits decrease. In addition, the benefit of dynamic pricing also increases with c. We observe that as the inventory holding cost increases, profits decrease and less units are ordered in each cycle leading to shorter cycle lengths. When the wastage rate increases, we see that the cycle length decreases but the order size increases. The reason for this is that since more products will be wasted, the company needs to order more products to satisfy the demand during a cycle. As f decreases, dynamic pricing will be more useful and the prices are changed more often, leading to increased profits. Lastly, we observe that as A increases, more units are ordered and the cycle length increases. In addition, multiple pricing becomes more beneficial as A increases.

Number of price changes, N, is one of the main parameters in order to see the effects of multi-pricing on the system. Hence, we try different numbers of price changes by letting \(f=0\) and we observe in Table 3 that the profit is concavely increasing with the number of price changes. That is, the effect of increasing the number of price changes on profit is high at first but the increase in profit converges to 0 as N gets larger. For example, the profits increase by \(2.25\%\) when a single price change is made (\(N=2\)), instead of using a constant price over the cycle (\(N=1\)). However, when N is increased from 2 to 3, the profits increase by \(0.42\%\) and when N is increased from 3 to 4, the profits only increase by \(0.15\%\). In addition, when N is changed from 2 to 10, the increase in profits is only \(0.73\%\). Thus, it is observed that most of the benefits are obtainable through a single price change, and it enables the retailer to be close enough to the optimal solution.

Table 3 Effect of the number of price changes on profit
Full size table

In general, since the price changes are costly, we can conclude that it will be optimal to use just a few price changes in a cycle rather than making too many changes in price. However, the cost of changing prices might vary a lot in different industries. When C(N) is small, as in sales made online, more frequent price changes can be done since changing the prices online is much less costly, but, as C(N) gets higher, less number of price changes need to be done. Thus, depending on the cost of price changes, a manager can decide on the optimal number of price changes N in his business by considering the effect of C(N) in his profits.

Table 4 Efficiency of heuristics
Full size table

We analyze the efficiency of the proposed heuristics in Table 4. Heuristic methods are coded in C programming language and the run times are seen to be less than a few seconds in all cases. We observe that both heuristics perform very well and the differences between the profits obtained by the heuristics and the optimal value of profits are less than \(0.5\%\) in all cases. For the base case, when equal time intervals are used, it is observed that the prices are changed at times 2.43 and 4.86 where the cycle length is 7.3 and the prices at these intervals are 49.68, 44.08 and 38.54, which are very close to the optimal solution stated above for this case, even though not optimal. The results suggest that employing a simple strategy with equal time intervals to change the prices is very efficient. It is stated by Transchel and Minner (2009) that changing the prices at equal time intervals is essentially optimal for non-perishable products and we observe that this strategy gives very good results for the perishable products, too. Such a strategy is also easy to use for the managers; thus instead of trying to determine the optimal times to change the prices, using equal time intervals seems to be an effective strategy to follow. When we look at the genetic algorithm, we observe that it gives even better results than the equal time interval approximation. We note that the genetic algorithm gives different results at each run due to the stochastic nature of the algorithm and the results given in Table 4 are the best results obtained in 10 runs of the algorithm.

5 Conclusions

We analyze the coordinated pricing and inventory decisions for perishable products in a deterministic setting in which the demand not only depends on the price but also on the freshness of the products. In addition, the products in inventory are assumed to decay at a certain rate which adds another dimension to the problem. We derive explicit analytical results for the optimal prices, given the times to change the prices. We can determine the optimal times to change the prices by solving a nonlinear program using a commercial solver and we propose two heuristic algorithms to approximate the optimal solution. Through numerical experiments, we compare the multi-pricing strategy with single pricing case in which the price is not allowed to change throughout the selling period. We observe that multiple pricing can lead to significant savings depending on the system parameters. When we look at the efficiencies of the heuristics, we observe that changing the prices at equal time intervals is very efficient and gives very close results to the optimal solution. Since it is also much easier to use for the managers, it might be logical to use equal time intervals to change the prices.

We plan to extend our model in the future in several ways. Firstly, different types of demand functions or decay processes can be analyzed in detail. For example, instead of using a constant decay rate, time-dependent decay functions can be used in the future. Also, exponential or nonlinear demand functions can be employed. Even though different types of demand functions will generate different analytical results for the optimal solutions, the analysis of the problem will be the same. We expect that similar results and managerial implications will be obtained for different types of demand functions as seen in the literature for similar problems (e.g., Transchel and Minner 2009; Rajan and Steinberg 1992; Benkherouf 1995, etc.) even though the sensitivity of the optimal solution will be different depending on the demand parameters. In addition, this problem can be analyzed in a stochastic setting in which the demand and also the decaying process are random. Even though our results can form a basis for developing coordinated pricing and inventory policies that can be also applied in stochastic environments, the performances of such policies need to be investigated and effective policies need to be developed for stochastic systems.