On the invertibility of seasonally adjusted series

Abstract

This paper examines the implications of the seasonal adjustment by an ARIMA model based (AMB) approach in the context of seasonal fractional integration. According to the AMB approach, if the model identified from the data contains seasonal unit roots, the adjusted series will not be invertible that has serious implications for the posterior analysis. We show that even if the ARIMA model identified from the data contains seasonal unit roots, if the true data generating process is stationary seasonally fractionally integrated (as it is often found in economic data), the AMB seasonal adjustment produces dips in the periodogram at seasonal frequencies, but the adjusted series still can be approximated by an invertible process. We also perform a small Monte Carlo study of the log-periodogram regression with tapered data for negative seasonal fractional integration. An empirical application for the Spanish economy that illustrates our results is also carried out at the end of the article.

1 Introduction

Given the seasonal nature of many macroeconomic time series, seasonal adjustment is a widespread practice and millions of series are routinely adjusted, some of them are not even publicly available in the nonadjusted version. Seasonal adjustment is believed to remove undesirable fluctuations at seasonal frequencies without producing significant changes at other frequencies (especially at the low part of the spectrum) making the data easily tractable, thereby simplifying posterior modeling and analysis. However, the properties of the adjusted series crucially depend on the method used for the adjustment and the initial properties of the series, and they may result just as unattractive for analysts as seasonality itself.

In this paper, we examine one of the important features of the adjusted data: dips in the periodogram at seasonal frequencies and the resulting noninvertibility of the adjusted series. The spectral dips (or zeros) are produced by all seasonal adjustment methods used in practice, regardless of whether it is a naive adjustment by seasonal dummies or a sophisticated ARIMA-model-based (AMB) signal extraction produced by specialized programs. Ooms and Hassler (1997) point out that the regression on seasonal dummies generates zeros in the periodogram at seasonal frequencies that can lead to the singularities in the log-periodogram regression. Nerlove (1965) applies Census X-11 and the modified ‘Hannan’ method and concludes that both methods remove more than just the seasonal component. Grether and Nerlove (1970) show that the phenomenon observed in Nerlove (1965), namely dips created near the seasonal frequencies after adjustment, is obtained as a result of ‘optimal’ adjustment procedure as well. The consequent seasonal adjustment routines of Census, X-11-ARIMA, and X-12 produce the same result by construction. Gomez and Maravall (2001) call attention to the fact that TRAMO-Seats generates dips at seasonal frequencies whenever the model identified for the data contains seasonal unit roots. According to Gomez and Maravall (2001), the spectral zeros are the frequency counterpart of the unit MA roots and therefore the adjusted series is not invertible and does not accept autoregressive AR (or VAR) approximations to its Wold representation. Although often ignored, this is, perhaps, the most important practical implication of AMB adjustment, since AR (and VAR) approximations to seasonally adjusted data are typically carried out in the applied econometric work.

In this work we analyze in detail the dips at the seasonal frequencies and the apparent noninvertibility produced by the AMB approach, within the fractional integration (FI) framework, which admits a wider definition of the invertibility condition than the one applied by Gomez and Maravall (2001). In particular, a fractionally integrated (FI) process is (seasonally) invertible whenever the FI coefficients at seasonal frequencies are higher than −0.5. In addition, notice that the negative seasonal FI parameters correspond to the spectral zeros at seasonal frequencies. Thus, the process can have spectral zeros at seasonal frequencies but still remain invertible.

We choose TRAMO-Seats for Windows (TSW) as the representative AMB seasonal adjustment program. TSW is a pair of the data adjustment programs developed by the Bank of Spain that have been intensively employed by Eurostat since 1994, and nowadays their use has been extended to various European countries (Gomez and Maravall 2001; Eurostat 2009).¹

To check for the invertibility of the series adjusted by TSW, we produce simulations for a set of processes. We do not restrict the analysis to processes with integer orders of integration at zero and the seasonal frequencies since it has been shown by many authors that FI at seasonal frequencies is a widespread phenomenon in economics (Porter-Hudak 1990; Gil-Alana and Robinson 2001; etc.). However, we also make simulations for a set of Airline models, which are the default models in TSW. For each model, we simulated 500 series, we adjust them by TSW and then, we estimate the fractional differencing parameters at the seasonal frequencies in the adjusted series with the log-periodogram regression with tapered data.

We find that if the data generating process (DGP) follows the default Airline model, TSW always identifies seasonally nonstationary ARIMA models for the data, and the adjusted series produced by TSW are indeed noninvertible, which is in line with the results of Gomez and Maravall (2001). However, if the original series is FI at the seasonal frequencies, which is less restrictive and very plausible in many cases according to the empirical evidence, the adjusted series may be approximated by an invertible process depending on the stationarity of the original series. If the DGP is a seasonally stationary FI model, TSW is less prone to identifying a seasonally nonstationary model. Moreover, even if the model chosen by the program is a seasonally nonstationary, the adjusted series does contain dips at the seasonal frequencies but these dips correspond to negative seasonal FI with coefficients greater than −0.5. Hence the adjusted series still can be approximated by an invertible process. On the contrary, the adjustment of a series generated from a model with nonstationary FI seasonality results in noninvertible negative FI coefficients. Note that this last result is not straightforward since overdifferencing is expected to be larger for data generated from seasonal stationary models when a nonstationary model is employed for adjustment.

The paper is organized as follows. Section 2 describes the problem. Section 3 briefly introduces the ideas behind the concept of seasonal FI. The simulation set-up and the results are presented in Sect. 4. Section 5 contains a small empirical application illustrating the results reported in Sect. 4. Section 6 concludes the paper.

2 The problem

SEATS is an “ARIMA-model-based” (AMB) seasonal adjustment routine. Within the AMB approach, the program TSW starts by identifying an ARIMA model to the observed data

$$\begin{aligned} \Phi (B) x_t = \Theta (B) a_t , \end{aligned}$$

(1)

where B is backward shift operator, $B^{i}x_t =x_{t-i}$, $a_t$ is an iid $N\left( {0,\sigma ^{2}} \right)$ innovation, the polynomial $\Phi \left( B \right) =F\left( B \right) \left( {1-B} \right) ^{D}\left( {1-B^{\tau }} \right) ^{D_\tau }$ contains nonseasonal and seasonal roots respectively, ${\uptau }$ is the number of observations per year, D is the (integer) order of integration at frequency zero, while $D_\tau$ is the (integer) seasonal order of differentiation. The polynomials $F\left( B \right)$ and $\Theta \left( B \right)$ are finite in B, the first one includes stationary seasonal and nonseasonal AR roots and the second is an invertible MA polynomial.

If the aim of the application of the TSW is the seasonal adjustment, the observed series $x_t$ is decomposed into the mutually orthogonal seasonally adjusted (SA) component $n_t$ and seasonal component $s_t$:

$$\begin{aligned} x_t =n_t +s_t \end{aligned}$$

The processes for the SA (or signal) and the seasonal components follow ARIMA processes:

$$\begin{aligned} \Phi _n (B) n_t= & {} \Theta _n (B) a_{nt} ,\quad {a_{nt} \sim niid (0, \sigma _n^2 )} \end{aligned}$$

(2)

$$\begin{aligned} \Phi _s (B) s_t= & {} \Theta _s (B) a_{st} ,\quad {a_{st} \sim niid (0, \sigma _s^2 )} \end{aligned}$$

(3)

such that $\Phi (B) = \Phi _n \left( B \right) \Phi _s \left( B \right)$ and $\Theta (B) a_t = \Phi _n \left( B \right) \Theta _s \left( B \right) a_{st} +\Phi _s \left( B \right) \Theta _n \left( B \right) a_{nt}$.

Thus, the seasonal component captures the peaks around the seasonal frequencies, which may be subtracted by the filter.

For the seasonal adjustment, the purpose is, given $x_t$, to obtain the estimator of $\hat{{n}}_t$ such that $E\left[ {\left( {n_t -\hat{{n}}_t } \right) ^{2}|x_t } \right]$ is minimized, i.e. the MMSE estimator of $n_t$.

Denote $n_t =\Psi _n \left( B \right) a_{nt}$, with $\Psi _n \left( B \right) ={\Theta _n \left( B \right) }/{\Phi _n \left( B \right) }$; $x_t$ and $s_t$ are defined in the same way. As it is shown in Whittle (1963), $\hat{{n}}_t$ is obtained by means of the Wiener-Kolmogorov (WK) filter as the MMSE estimator of the signal given the observed series:

$$\begin{aligned} \hat{{n}}_t = \left[ {\frac{\sigma _n^2 \Psi _n (B) \Psi _n (F) }{\sigma ^{2}\Psi (B) \Psi (F)}} \right] x_t = \nu (B, F)x_t \end{aligned}$$

(4)

where F is a forward-shift operator (i.e. $F^{i}x_t =x_{t+i}$). The estimator given by (4) is called historical estimator. The WK filter can be expressed after simplification as

$$\begin{aligned} \nu (B, F) = \frac{\sigma _n^2 }{\sigma ^{2}}\frac{\Theta _n (B)\;\Phi _s (B)\Theta _n (F)\;\Phi _s (F)}{\Theta (B)\;\Theta (F)} \end{aligned}$$

(5)

From (1), (4) and (5) it can be obtained

$$\begin{aligned} \Phi _n (B) \hat{{n}}_t = \Theta _n (B) \frac{\Theta _n (F) \Phi _s (F) \sigma _n^2 }{\Theta (F) \sigma ^{2}} a_t . \end{aligned}$$

(6)

It is clear that the process for the SA component (2) is different from the process for its historical estimator (6). If the process (1) is seasonally stationary, the seasonal component (3) will not contain the seasonal unit roots and, as a result, the polynomial $\Phi _s \left( F \right)$ will be stationary. In this case $\hat{{n}}_t$ given by (6) is going to be invertible. If the seasonal component is a nonstationary I(1) process (i.e. it contains unit roots at seasonal frequencies) $\Phi _s \left( F \right) =1+F+F^{2}+\cdots +F^{r-1}=S\left( F \right)$, these unit roots will show up as MA in the model generating $\hat{{n}}_t$ and will produce spectral zeros for the associated seasonal frequencies.

Thus, if the seasonal component identified within AMB approach is nonstationary, the historical estimator of the series will not be invertible. An important implication of this result according to Gomez and Maravall (2001) is that the estimator of the SA series“...will not accept, in general, an AR (or VAR) approximation to its Wold representation”.²

3 Seasonal fractional integration

The AMB approach assumes that the data follows an ARIMA-type process. This assumption restricts the DGP to be either stationary I(0) or, alternatively integrated of order one, I(1), at zero and/or the seasonal frequencies. In this article, we extend the seasonal I(1)/I(0) approach to the fractional case and examine cases where the original series have noninteger orders of integration at seasonal frequencies. In such a case, the process is said to be seasonally fractionally integrated or seasonal I(d).

For the purpose of the present work, we first define an I(0) process as a covariance stationary process with a positive and bounded spectral density at all frequencies in the spectrum. Then, we say that a process $x_{t}$ is seasonal I(d) if it can be represented as:

$$\begin{aligned} (1 - B^{\tau })^{d}x_t = a_t , \end{aligned}$$

(7)

where $B^{\tau }$ is the seasonal lag operator (i.e., $B^{\tau }x_{t}=x_{t-\tau }$) and $\tau$ represents the number of periods per year (e.g., $\tau = 4$ with quarterly data, $\tau = 12$ in case of monthly data, etc.), d is a real value and $a_{t}$ is an I(0) process that may include seasonal and nonseasonal weakly autocorrelated (e.g., ARMA) terms. If $d>0$ in (7), $x_{t}$ is said to be a seasonal long memory process, so-named because of the strong degree of association between observations widely (seasonally) separated in time. However, the specification in (7) is rather restrictive in the sense that it imposes the same degree of integration at all frequencies, noting that ($1 - B^{\tau }$) can be decomposed into $(1- B)S(B)$ where $S(B) = 1 + B + B^{2} + {\cdots } + B^{\tau -1}$ refers exclusively to the seasonal frequencies. Thus, for example, in the case of the polynomial $\left( {1-B^{4}} \right) ^{d}$, it can be expressed as $\left( {1-B} \right) ^{d}\left( {1+B+B^{2}+B^{3}} \right) ^{d}=\left( {1-B} \right) ^{d}\left( {1+B} \right) ^{d}\left( {1+B^{2}} \right) ^{d}$, implying the same degree of integration, d, at zero and the seasonal frequencies $\pi ,\pi /2$ ($3\pi /2$) (of a $2\pi$ cycle). Extending this model, we may consider a more general specification that permits different degrees of integration at each of the frequencies. In particular, for the case of quarterly data, in the paper we will examine models of the form:

$$\begin{aligned} (1 - B)^{d_0 }(1 + B)^{d_2 }(1 + B^{2})^{d_1 }x_t = a_t , \end{aligned}$$

(8)

where $d_{0}$ refers to the order of integration at the long run or zero frequency; $d_{2}$ is the order of integration at the semiannual frequency $\pi$, and $d_{1}$ corresponds to the annual frequencies $\pi /2$ and $3\pi /2$. Applications using the flexible model (8) can be found in Arteche and Robinson (2000), Gil-Alana and Robinson (2001), Arteche (2003) and Hassler et al. (2009).

If the true process for (quarterly) data is fractionally integrated and it is given by (8), then TSW will find the best possible integer framework approximation to model seasonality, which can be stationary or not.

Theoretically, the process for the historical estimator of the SA series has the following form:

$$\begin{aligned} \nabla ^{d_0 }\hat{{N}}_t = \frac{\sigma _n^2 }{\sigma ^{2}}\;\frac{\Theta _n (B)\Phi _s (B)\;}{\Theta (B)\;}\frac{\Theta _n (F)\Phi _s (F)}{\Theta (F)}\left( {1+B} \right) ^{-d_2 }\left( {1+B^{2}} \right) ^{-d_1 }a_t \end{aligned}$$

(9)

where $\nabla =1-B$. If we separate seasonal and non-seasonal MA roots in the process, TSW chooses for the data, $\Theta \left( k \right) =\Theta _{SS} \left( k \right) \Theta _{NN} \left( k \right) ,k=B,F$, then the terms $\frac{\Phi _s (B)\;}{\Theta _{SS} (B)\;}$ and $\frac{\Phi _s (F)}{\Theta _{SS} (F)}$ are parts of the two-sided WK filter (with backward and forward operators correspondingly) aimed to subtract the seasonal component given by $\left( {1+B} \right) ^{d_2 }\left( {1+B^{2}} \right) ^{d_1 }$. In other words, $\frac{\Phi _s (B)\;}{\Theta _{SS} (B)\;}$is the TSW integer framework approximation to the fractionally ingenerated seasonal component.

Note that the (pseudo) spectrum of the process in (9) is the same as that of

$$\begin{aligned} \nabla ^{d_0}{\mathop {N}\limits ^{\smile }}_t = \frac{\sigma _n^2 }{\sigma ^{2}}\frac{\Theta _n^2 (B)}{\Theta _{NN}^2 (B)}\;\left[ {\frac{\Phi _s (B)\;}{\Theta _{SS} (B)\;}} \right] ^{2}\left( {1+B} \right) ^{-d_2 }\left( {1+B^{2}} \right) ^{-d_1 }\alpha _t \end{aligned}$$

with $\hbox {var}\left( {a_t } \right) =\hbox {var}\left( {\alpha _t } \right)$.³

If TSW chooses a nonstationary SARIMA to fit the data, then $\Phi _s (B)=\left( {1+B} \right) \left( {1+B^{2}} \right)$ and therefore:

$$\begin{aligned} \nabla ^{d_0} {\mathop {N}\limits ^{\smile }}_t = \frac{\sigma _n^2 }{\sigma ^{2}}\frac{\Theta _n^2 (B)}{\Theta _{NN}^2 (B)}\;\frac{\left( {1+B} \right) ^{2-d_2 }\left( {1+B^{2}} \right) ^{2-d_1 }}{\Theta _{SS}^2 (B)}\alpha _t \end{aligned}$$

(10)

If $d_1 ,d_2 <1$, the adjusted series should have a seasonal fractionally integrated MA polynomial with coefficients larger than 1, thus being, hypothetically, not invertible. In the following section, we investigate this issue in practice by means of simulations.

4 Simulation study

4.1 Simulation set-up

To study invertibility of the time series adjusted by TSW, we generate quarterly data from different specifications of seasonal fractionally integrated ARIMA (SARFIMA) models. The parameters for the simulated SARFIMA processes of the form as in (8) are $d_{0} = \{0.3, 0.7, 1, 1.5\}, d_{i} = \{0.1, 0.3, 0.5, 0.7\}, i = \{1, 2\}$, and ${\upsigma }^{2} = 1$. For $d_{0} = 1$ we simulate additionally $d_{i} = 1$. The choice of the values is justified by the empirical evidence. The number of observations for each series is set T $=$ 500.

To generate the data, the long memory polynomials in (8) have to be expanded. We choose the lag truncation 1000 for each of the three polynomials $\left( {1-B} \right) ^{d_0 }$, $\left( {1+B^{2}} \right) ^{d_1 }$, and $\left( {1+B} \right) ^{d_2 }$. Thereafter, we multiply the expanded long memory polynomials and, following Bhardwaj and Swanson (2006), we truncate the resulting polynomial when the coefficients become smaller than 1.0e−004 (the truncation lag is always smaller than 1000). All observations are generated using standard normal errors. For each process and each replication, we generate 3000 observations and we use just the last T observations to avoid the initial values problem, which is especially important when taking into account the long-memory properties of the DGP.

To each simulated series, we apply TSW. If TSW chooses a seasonally nonstationary ARIMA model for this series, we collect it for the future analysis. If the model chosen by TSW contains stationary seasonality we discard the simulated series. We proceed until we have I $=$ 500 simulated series for each specification identified by TSW as seasonally nonstationary.

In addition to SARFIMA, we produce simulations for a set of quarterly Airline models of Box and Jenkins (1970) which are believed to approximate reasonably well the stochastic properties of many series

$$\begin{aligned} (1 - B) (1 - B^{\tau })x_t = (1 + Q_1 B) (1 + Q_\tau B^{\tau }) a_t \end{aligned}$$

(11)

with $\tau =4$ and negative values for $Q_{1}$ and $Q_{4}$: $Q_i =\left\{ {-0.8,-0.6,-0.3} \right\}$, $i=1,4$ and $\left[ {Q_1 ,Q_4 } \right] =\left\{ {\left[ {-1,-0.8} \right] ,\left[ {-1,-0.6} \right] ,\left[ {-1,-0.3} \right] } \right\}$. In the same way as for SARFIMA, we collect I $=$ 500 series for each specification identified by TSW as seasonally nonstationary.

Thereafter, each selected series for each specification is adjusted by TSW and coefficients of FI at seasonal frequencies are estimated.⁴ It is important to remark that, even if several series are simulated from the same SARFIMA specification, the TSW may choose distinct SARIMA models for each of the simulated series. Moreover, even if the model chosen is the same, the estimated SARIMA parameters may be very different. Since the seasonal filters applied to the data are based on the identified SARIMA model, different filters may be applied to each of the series simulated from the same SARFIMA specification. In this way, the mean of the estimated parameters of FI at seasonal frequencies of the adjusted series does not have statistical meaning. Therefore, to build conclusions on the invertibility of the adjusted series we propose the following testing procedure. After estimating the FI parameters at seasonal frequencies, we test if we can reject the null hypothesis $d_i \ge -0.5$ in favor of the alternative $d_i <-0.5$ at least for one of the two parameters of seasonal FI. If this is the case, we say that the adjusted series is statistically noninvertible. Also, we test if the series is statistically invertible, i.e., if we can reject the null hypothesis $d_i \le -0.5$ in favor of the alternative $d_i >-0.5$ for both estimated parameters of seasonal FI. As a result, for each Airline and SARFIMA specification, we can compute both the percentage of statistically noninvertible and the percentage of statistically invertible series (in the adjusted I = 500 series chosen by TSW to be seasonally nonstationary before adjustment).

To estimate the coefficients of FI at the seasonal frequencies, we use the log-periodogram regression with a complex-valued taper proposed by Hurvich and Chen (2000):

$$\begin{aligned} h_t =0.5\left[ {1-\exp \left\{ {\frac{i2\pi \left( {t-0.5} \right) }{T}} \right\} } \right] ,\quad t=1,\ldots ,T. \end{aligned}$$

The choice of the log-periodogram regression is justified by several reasons. Since we do not know what the correct specification after adjustment is, we avoid the parameterization of the whole spectrum by choosing a local estimation method. Tapering is particularly suitable when the estimated coefficients of FI are expected to be negative, possibly smaller than −0.5. In these circumstances, the estimation results based on the nontapered data will have a strong positive bias, making the method not appropriate for the purposes of this work. As Hurvich and Ray (1995) and Velasco (1999) point out, the use of a taper can alleviate the negative effects of overdifferencing, reducing the bias in FI estimates. Finally, tapering also reduces the bias that appears due to contamination of the periodogram from the short memory component of the spectral density and allows for a less restrictive trimming of frequencies in presence of asymmetries, as it happens at the frequency $\pi /2$. A comprehensive discussion of the performance of the method for seasonal and cyclical time series with asymmetric long memory properties is presented in Arteche and Velasco (2005). Nevertheless, we also perform a small Monte Carlo study to check the performance of the estimation method in the presence of negative seasonal fractional integration at seasonal frequencies in the following way. For each specification, after simulating the data and before applying the TSW (i.e. when we still know the true DGP), we take yearly differences, making sure that the resulting series are over-differenced at seasonal frequencies having negative FI coefficients. We estimate these coefficients computing the mean for each specification to assess the estimation bias.

Also, note that the classification of an adjusted series as statistically noninvertible or statistically invertible requires the one-tailed testing of two different seasonal FI parameters (one for each seasonal frequency), and thus is subject to a multiple-testing problem. Given that independence of the estimates at different frequencies is satisfied asymptotically, we can control for the experiment-wide type-I error.⁵ Statistical noninvertibility requires the rejection of at least one of the two nulls, so it faces the increase in type I error that occurs when statistical tests are used repeatedly. If two independent tests are performed, the experiment-wide significance level is given by $\bar{{\alpha }}=1-\left( {1-\alpha } \right) ^{2}$, being $\alpha$ the significance level employed testing at each frequency (Sidak 1967). Thus, an $\bar{{\alpha }}=10\%$ implies the use of the significance level $\alpha =5.01\% \approx 5\%$ at individual tests. As for statistical invertibility, it requires the rejection of exactly the two one-tailed nulls. Although the experiment-wide significance level cannot be computed exactly, it can be bounded by $\alpha$ under independence. Note that the process would be incorrectly classified as statistically invertible if the two nulls are rejected when in fact, either both hypotheses are true or only one is true. In the former case, the experiment-wide significance level under independence is $\bar{{\alpha }}=\alpha ^{2}$. In the latter case, the experiment-wide significance level can be bounded as $\alpha ^{2}\le \bar{{\alpha }}=\alpha (1-\beta )\le \alpha$, where $\beta$ is the probability of type II error. Therefore, we remain conservative by testing each frequency at significance level $\alpha =10\%$, ensuring that the experiment-wide significance level $\bar{{\alpha }}$ does not exceed 10%.

All the simulations and estimations were produced in Matlab. The programs are available from the authors upon request. For seasonal adjustment, we use the last release of the TSW for Matlab developed by the Bank of Spain.

4.2 Simulation results

The results of the simulation study for the different Airline and SARFIMA specifications are presented in Tables 1 and 2 respectively. In both tables, the particular specification, chosen as DGP, appears in the first column (i.e., the values for the MA parameters $Q_{1}$ and $Q_{4}$ for the Airline model and the parameters of FI at seasonal frequencies $d_{1}$ and $d_{2}$ for SARFIMA).

Table 1 Simulation results, airline model

Table 2 Simulation results, SARFIMA model

4.2.1 Monte Carlo results for the tapered log-periodogram regression for seasonal frequencies with negative FI

The Monte Carlo study is presented in the columns 2 and 3 of Tables 1 and 2. The coefficients in the table are $\hat{{d}}_i =1+\hat{{d}}_i^*$, where $\hat{{d}}_i^*$ denotes the mean of the estimates obtained with yearly differenced data.⁶

The estimated parameters are slightly positively biased. The bias is higher when the negative FI is greater in absolute value. Thus, the highest bias is observed for the process $\{d_0 =0.3, d_1 =0.1, d_2 =0.1\}$. Recall that after taking yearly difference it becomes $\{d_0^*=-0.7, d_1^*=-0.9, d_2^*=-0.9\}$.

The simulation results for the Airline specifications are useful to study the performance of the method in the presence of short memory components. Results are presented in Table 1. The estimation method always detects seasonal unit roots. The precision of the estimates depends on the value of the seasonal MA parameter $Q_4$: the larger this value in absolute terms, the larger is the bias.

Finally, note that no matter the specification, the coefficient $d_1$ tends to be estimated less precisely than the coefficient $d_2$ due to the asymmetries presented in the periodogram around frequency $\pi /2$.

Overall, the performance of the method at seasonal frequencies is similar to its performance at frequency zero, documented in previous studies. The log-periodogram regression with tapered data performs well for negative seasonal FI even for coefficients from the noninvertible region and also for the estimation of the parameter at frequency $\pi /2$, where the spectrum is not symmetric. The method works also well in the presence of short memory components, as shown in Table 1. Thus, the results from the Monte Carlo study confirm that the log-periodogram regression with tapered data is appropriate for the purposes of the present work.

4.2.2 Results on the invertibility of the adjusted series

The column four of Tables 1 and 2 presents the percentage of cases for which TSW chooses a seasonally nonstationary model to fit the data for each of the simulated processes (NS). As can be seen in Table 1, TSW always chooses a nonstationary model when the true DGP follows the Airline model. As expected for the SARFIMA specifications (Table 2) this percentage increases together with the magnitude of both $d_{1}$ and $d_{2}$.

Next three columns of Tables 1 and 2 contain results of the statistical testing described in the simulation set-up. Column five presents the percentage of cases in which the seasonally adjusted processes are estimated invertible (I), i.e., with the two estimated coefficients of FI at seasonal frequencies greater than −0.5. Thereafter we compute the percentage of replications in which the SA series have at least one estimated coefficient of seasonal FI statistically smaller than −0.5—that is to say, the series is statistically noninvertible (SNI). Thereafter, we test statistical invertibility: both estimated coefficients are statistically greater than −0.5. The percentage of statistically invertible results is given in column seven (SI). When the data are simulated from the Airline model (Table 1), the estimated coefficients of FI at frequencies $\pi /2$ ($3\pi /2$) and $\pi$ are almost always smaller than −0.5, which indicates the (possible) noninvertibility of the corresponding SA series. Moreover, in a high percentage of cases, this noninvertibility is statistically significant. This result is not surprising and it is completely in line with the implications of the TSW for this class of models (Gomez and Maravall 2001). For the SARFIMA specifications (Table 2), the result of the application of TSW depends on the initial properties of the simulated data. Thus, if the two coefficients of the seasonal FI are within the stationary region ($d_{i}<0.5, i = \{1, 2\}$), even if the TSW identifies a nonstationary seasonal model (this occurs in a relatively small percentage of cases), the estimated coefficients of seasonal FI of the SA series are greater than −0.5 in most of the cases. Only a very small percentage of series are (possibly) statistically noninvertible. The percentage of statistically invertible results decreases as the seasonal FI coefficients of the original series approach the nonstationary region. For example, for $d_{0} = 0.3$, if the original series have both coefficients of seasonal FI $d_{i} = 0.1$, TSW only selects a seasonal nonstationary representation in 32% of the cases. In addition, even if this is the case and a nonstationary SARIMA is chosen, the estimated coefficients of the SA series almost always lie (99%) in the invertible region. Moreover, in 91% of the cases both parameters are statistically greater than −0.5 and the series are statistically invertible. The percentage of statistically invertible results decreases to 45% if $d_{1}$ and $d_{2}$ are equal to 0.3. Still, the estimated parameters are greater than −0.5 in 92 % of the cases and the percentage of statistically invertible results is 56%.

On the contrary, if one of the coefficients of seasonal FI in the DGP is greater than 0.5, TSW fits a seasonally nonstationary model a higher percentage of times, and for these cases, the SA series are often estimated to be noninvertible. Once more, the percentage of statistically noninvertible results increases with the parameters of seasonal FI of the original series. Thus, (again for $d_{0} = 0.3$) if $d_{i} = 0.7$ for the two coefficients, TSW selects a nonstationary representation in almost 100% of the cases. Only in 13.2% of the cases, the SA series are invertible (and only in 7.6% the invertibility is statistically significant) whereas in 42% of the replicas the SA series were found to be statistically noninvertible. It is also interesting to note that, although the parameter of fractional integration at zero is not neutral, the same conclusions are obtained for all simulated $d_{0.}$

If $d_1$ and $d_2$ in the DGP are very different in magnitude, the TSW chooses the model with nonstationary seasonality for the process with higher $d_1$ more often. After the adjustment, these processes present lower percentage of invertible and statistically invertible cases. For example, if parameters in the DGP are $d_0 =0.3$, $d_1 =0.1$ and $d_2 =0.5$, the TSW chooses models with non-stationary seasonality 58.1% of times, while this percentage reaches 96% when $d_1 =0.5$ and $d_2 =0.1$. The SA data is invertible in 85% of the cases (and statistically invertible in 46%) for the initial process with $d_1 =0.1$ and $d_2 =0.5$, and in 67% (26%) of the cases for data generated with $d_1 =0.5$ and $d_2 =0.1$. Thus, we find that the TSW seems to react strongly to long memory at the yearly frequency.

The previous results indicate that invertibility may not be a severe issue in many circumstances. However, they contradict the theoretical findings derived in Sect. 3. Recall that the simulations are based on data identified by TSW as seasonally nonstationary and, according to the Eq. (10), the adjusted series should contain seasonal unit MA roots. To aid in the explanation of this apparent puzzle, the columns eight and nine in Tables 1 and 2 report the median with the 16th and 84th percentiles (68% band) of the estimated seasonal FI parameters after adjustment. Several results emerge from these columns:

• 1. If the DGP contains stationary seasonality with relatively low parameters of FI, the adjusted series is not only usually estimated (statistically) invertible, but also the estimated parameters of FI are indeed very small in magnitude, with no sign of unit MA roots. For example, if the data is generated from an SARFIMA with $d_0 =0.3, d_1 =0.1$ and $d_2 =0.1$, the median of the estimated values after adjustment is ${\tilde{d}}_1 =-0.116$ and ${\tilde{d}}_2=-0.096$.

• 2. If the DGP contains seasonal FI with equal parameters ($d_1 =d_2$), the medians of parameter estimates after adjustment are also close to each other and very similar to the values employed to generate the data but with opposite sign.

• 3. If $d_1$ and $d_2$ in the DGP are very different in magnitude, the median values after adjustment are negative but smaller in magnitude than the larger parameter in the DGP. For example, if parameters in the DGP are $d_0 =0.3$, $d_1 =0.7$ and $d_2 =0.1$, the median estimated values after adjustment are ${\tilde{d}}_1 =-0.476$ and ${\tilde{d}}_2 =-0.465$.

The most likely explanation for these results is that for a given data length, frequency and bandwidth employed in the simulations, the integer framework process resulting from TSW seasonal adjustment is difficult to distinguish from FI integration at seasonal frequencies, i.e., $\left[ {\frac{\Phi _s (B)\;}{\Theta _{SS} (B)\;}} \right] ^{2}\left( {1+B} \right) ^{-d_2 }\left( {1+B^{2}} \right) ^{-d_1 }\approx \left( {1+B} \right) ^{\delta _2 }\left( {1+B^{2}} \right) ^{\delta _1 }$.⁷ Therefore (10) can be approximated by:

$$\begin{aligned} \nabla ^{d_0 } {\mathop {N}\limits ^{\smile }}_t^{*} = \frac{\sigma _n^2 }{\sigma ^{2}}\;\frac{\Theta _n^2 (B)}{\Theta _{NN}^2 \left( B \right) }\left( {1+B} \right) ^{\delta _2 }\left( {1+B^{2}} \right) ^{\delta _1 }\alpha _t \end{aligned}$$

(12)

To illustrate the approximation of (10) by (12), we provide a numerical example in Table 3.

Table 3 Model for the signal and its approximation

Consider that the true DGP is an SARFIMA model with stationary FI at seasonal frequencies and that TSW identifies an Airline model to fit the data. The respective parameterizations appear in the first part of Table 3.⁸ The table also shows the models for the separate components and the model for the SA data derived by TSW if the program uses the Airline specifications in the table for the seasonal adjustment. Finally, the last row of the table presents the approximation ${\mathop {N}\limits ^{\smile }}_t^*$ to the historical estimator of the SA series ${\mathop {N}\limits ^{\smile }}_t$.

Fig. 1

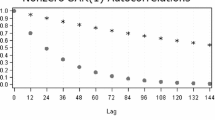
(pseudo) Spectrums of the signal $S\left( N \right)$ and its approximation $S\left( {N^{*}} \right)$ of the process of the illustrative example of Table 3

Figure 1 plots the (pseudo) spectrums of both, ${\mathop {N}\limits ^{\smile }}_t$ and ${\mathop {N}\limits ^{\smile }}_t^{{*}}$. Note that the (pseudo) spectrum of ${\mathop {N}\limits ^{\smile }}_t$ presents strong dips at the two seasonal frequencies which correspond to the MA roots of a noninvertible process. These dips are also present in the spectrum of the approximation ${\mathop {N}\limits ^{\smile }}_t^{{*}}$. However, in this last case the dips correspond to invertible negative seasonal fractional integration. To assess the quality of the approximation of ${\mathop {N}\limits ^{\smile }}_t$ by ${\mathop {N}\limits ^{\smile }}_t^{{*}}$, we perform the following exercise. From the spectrum of the historical estimator of the SA series, $S\left( {\mathop {N}\limits ^{\smile }}_t,\omega \right)$, we draw $k=1,\ldots ,1000$ periodograms $I^{\left( k \right) }\left( {{\mathop {N}\limits ^{\smile }} ,\omega _j } \right) =\frac{1}{2}S\left( {{\mathop {N}\limits ^{\smile }} ,\omega _j } \right) {^{*}} \upsilon _j^k$, where $\upsilon _j^{\left( k \right) }$ are independently and identically distributed $\chi _2^2$ errors, $j=1,\ldots ,T/2-1$.⁹ If we fit ${\mathop {N}\limits ^{\smile }}_t^{{*}}$ instead of ${\mathop {N}\limits ^{\smile }}_t$ to the simulated periodograms, we can test the null hypothesis that ${2I^{\left( k \right) }\left( {{\mathop {N}\limits ^{\smile }} ,\omega _j } \right) }/{S\left( {{\mathop {N}\limits ^{\smile }}^{*},\omega _j } \right) }= \upsilon _j^{\left( k \right) *}$ in the neighborhood of the two seasonal frequencies is distributed as $\chi _2^2$. If for a given sample size, frequency and bandwidth ($T=500$, quarterly data, the same bandwidth as we use in simulations), we cannot reject this null, the processes ${\mathop {N}\limits ^{\smile }}_t$ and ${\mathop {N}\limits ^{\smile }}_t^{{*}}$ are statistically not distinguishable around the seasonal frequencies, that is to say that the approximation of (10) by (12) is good. In this example, the null is rejected only a 13% and a 6% of times for the frequencies $\pi /2$ and $\pi$ respectively.¹⁰ This empirical example suggests that in many cases the noninvertible process resulting from the seasonal adjustment by TSW may not be distinguished in practice from an invertible process with seasonal fractional integration.

This explanation can also accommodate the second and third findings. Our results show that the integer SARIMA framework where TSW operates is quite successful approximating processes with equal orders of FI at seasonal frequencies. However, the integer framework is not flexible enough to correctly approximate SARFIMA processes with different (and not related) orders of FI at seasonal frequencies. In these cases, TSW reacts more to the FI coefficient at a frequency $\pi /2$ and selects an SARIMA model with stronger seasonality for data simulated with $d_1>>d_2$ than for data simulated with $d_1<<d_2$. However, the main result still holds: if the true DGP is stationary FI at seasonal frequencies, then the TSW adjusted data usually is virtually not distinguishable from a process with invertible seasonal FI MA roots.

Overall, simulation results are in line with Gomez and Maravall (2001), but using a more flexible definition of invertibility: if the process contains strong nonstationary seasonality (including FI) then the SA series estimated by TSW will be in general noninvertible. However, if the original series were stationary fractionally integrated at seasonal frequencies, TSW will choose a nonstationary representation in a smaller percentage of cases and, even if a nonstationary seasonal model is chosen, the resulting SA series is likely to be not distinguishable from an invertible process.This result is important because an econometrician never knows what the DGP for the real data is, and always works with approximations which fit the data reasonably well according to the results of statistical testing.We illustrate our results with real data in the following section.

5 Empirical examples

To illustrate the simulation results, we consider several quarterly series of the Spanish economy: Industrial Production Index (IPI), airline passengers (AIR), employment (EMP) and three quarterly cyclical economic indicators, namely: cement consumption (CC), car registrations (CR) and housing starts (HS). The IPI and these three indicators are considered to be the cycle drivers for an economy in Leamer (2009) and have been recently used by Bujosa et al. (2013) to construct a composite leading indicator for the Spanish economy. All the series start in the late 60s or early 70s and they are non-stationary in the mean and strongly seasonal. Monthly data for IPI, CC, CR, HS and AIR are obtained from the Bank of Spain. To convert the IPI to quarterly, we use the simple average of the monthly observations inside each quarter. The other series are converted to quarterly by adding the observations inside the quarter. Employment has been obtained from the OECD stats database. We apply a logarithmic transformation to IPI, CR, and AIR to stabilize volatility.

Fig. 2

Nonadjusted and adjusted data (left panel) and their respective periodogram (right panel) from the empirical application

Figure 2 (left panels) plots the original series and the series after adjustment by TSW. A strong seasonal pattern is observed in all the original series. We exclude the last years of data from the analysis to circumvent the strong nonlinearities consequence of the late 2000s recession.¹¹ This nonlinear pattern is clearly visible in Fig. 2 and may disturb the interpretation of the results.

The right panel in Fig. 2 depicts the periodogram of both differenced series: original and adjusted by TSW. As expected, the periodograms of the differenced original series have strong peaks at the two seasonal frequencies, while those of the differenced adjusted series present dips at the same frequencies. The models identified by TSW for the original series are provided in Table 4.

Table 4 Empirical example: models identified by TSW

As can be seen in the table, all the series except ln(IPI), HS and EMP follow a standard Airline model. For CC and ln(CR) the trend is very strong and $Q_{1 }$ is equal to zero. The model identified for ln(IPI) does not accept the admissible decomposition and is modified by SEATS. Given that AR(1) polynomials with $\Phi _{1 }$ in the interval (−0.2, −0.4) are practically indistinguishable from the MA(1) with $\hbox {Q}_{1} = - \Phi _{1,}$ SEATS replaces the original model with the Airline model (Maravall 2009). TSW chooses a stationary seasonal model for HS and SARIMA for EMP.

We estimate the coefficients of FI at seasonal frequencies before and after the adjustment by TSW. These results are presented in Table 5.

Table 5 Empirical example: estimation results after adjustment

It is interesting to note that the examined series seem to follow the SARIMA model. Note that the estimated seasonal FI coefficients before the adjustment (columns four and five) are both statistically different from one in all the cases. In particular, CC, ln(CR) and EMP seem to be seasonally stationary before adjustment. Overall, in line with the simulation results, even though TSW has selected seasonally nonstationary models for the three series, the estimated coefficients after the adjustment are substantially higher than −0.5, suggesting that the adjusted series can be approximated by an invertible process. That also seems to be the case of HS, for which TSW has selected a stationary representation before adjustment. For the ln(IPI) and ln(AIR) series, the estimated coefficients of FI at frequency $\pi /2$ are larger than 0.5, albeit we cannot reject the null of $d_1 =0.5$ at any significance level. After adjustment, the estimated coefficient of FI at the frequency $\pi$ is smaller than −0.5 and the adjusted series may then be noninvertible, although we cannot reject the null of $d_2 \ge -0.5$ in favor of the alternative $d_2 <-0.5$. Overall, the empirical results are in line with the results of the simulation study.

6 Conclusions

In this paper, we have examined the invertibility property of seasonal series adjusted by TSW. According to Gomez and Maravall (2001) whenever the process chosen by TSW to fit the data contains seasonal unit roots, the adjusted series estimated by the program has MA unit roots and, as a result, it is not invertible and cannot be approximated by an AR (VAR) process as it is ordinarily done in practice.

In the simulation study carried out in this work, we found that the invertibility issue may not be in many circumstances a strong concern. In particular, we found that if the true DGP follows the Airline model, the adjusted series produced by TSW are indeed noninvertible. However, if the series is fractionally integrated at the seasonal frequencies, which is less restrictive and very plausible in some cases according to the empirical evidence, the adjusted series still can be approximated by an invertible process, depending on the stationarity of the original series. Thus, if the original series is seasonally stationary with coefficients of FI at seasonal frequencies smaller than 0.5, the SA series adjusted by TSW is likely to be statistically invertible or indistinguishable from an invertible process even if the program chose a nonstationary model for the data, therefore still admitting AR (or VAR) approximation. This approximation is more plausible the further the seasonal FI parameters of the original series are from the nonstationary region. On the contrary, if the original series is seasonally nonstationary, the resulting adjusted series are expected to be noninvertible. As shown in the empirical examples, these results are interesting since stationary FI seasonality is not a rare event in economic data.