A Comparison Between Direct and Indirect Seasonal Adjustment of the Chilean GDP 1986–2009 with X-12-ARIMA

Abstract

It is well known among practitioners that the seasonal adjustment applied to economic time series involves several decisions to be made by the econometrician. As such, it would always be desirable to have an informed opinion on the risks taken by each of those decisions. In this paper, I assess which disaggregation strategy delivers the best results for the case of the Chilean 1986–2009 GDP quarterly dataset (base year: 2003). This is done by performing an aggregate-by-disaggregate analysis under different schemes, as the fixed base year dataset allows this fair comparison. The analysis is based on seasonal adjustment diagnostics contained in the X-12-ARIMA program plus some statistical tests for robustness. This exercise is relevant for conjunctural economic assessment, as it concerns signal extraction from seasonal, noisy series, direction of change detection, and econometric applications based on reliable and accurate unobserved variables. The results show that it is preferable, in terms of stability, to use the first block of supply-side disaggregation, while demand-side disaggregation tends to be less reliable. This result carries important implications for policymakers aiming to evaluate its short-term effectiveness in both households and firms.

1 Introduction

It is well known among practitioners that seasonal adjustment applied to economic time series involves several decisions to be made by the econometrician. Many of these decisions concern parameters to be fixed prior to the adjustment process and are included in traditional programs such as X-12-ARIMA or TRAMO-SEATS.¹ Despite these advances, there is no consensus on a particular method to obtain reliable and accurate results. Specifically, the econometrician’s decisions seem to be case dependent and based merely on empirics.² In the case of an aggregate series—already a weighted sum of disaggregates—there are several strategies to perform a seasonal adjustment; for instance, by: (1) adjusting an aggregate series by itself, (2) adjusting components of the aggregate with the same methodology and then aggregate to the original, and (3) adjusting components with a different methodology and adding up to the original. These strategies could deliver results that strongly differ from each other; while partial aggregations may be useful for many econometric purposes. Some reasons for this difference are nonlinearities in the components, different seasonal patterns through themselves, outliers, and difficulties in identifying the trading day effect.

In this paper, I assess the question of which of these strategies yields the most robust (stable, reliable, and accurate) results for the case of the Chilean Gross Domestic Product (GDP) 1986–2009 quarterly dataset (base year: 2003). I perform an aggregate-by-disaggregate analysis under different schemes, based on the diagnostics for seasonal adjustment contained in the X-12-ARIMA program plus some statistical tests for robustness. These capabilities include spectral plots, sliding-spans-based diagnostics, and revision history diagnostics; all of them simple checks that cast for both quality and stability of results.³ By performing this exercise, I will be able to provide an informed opinion about which scheme provides the most stable seasonal adjustment for the mentioned Chilean GDP vintage.

The exercise performed in this article is relevant for several reasons. First, since 2009 the GDP dataset is released under the linked-chain methodology, losing its additive property. Therefore, this exercise should be read as a benchmark for further extensions using the datasets released with the new methodology (base years 2009 and 2013).⁴ Second, to have an informed opinion on the reliability of seasonally adjusted disaggregations that compound total GDP. This is relevant for conjunctural economic assessment, as it concerns signal extraction from seasonal, noisy series; direction of change detection; and econometric applications (i.e. modelling) using seasonal variables. Finally, policymakers whose effectiveness is strongly attached to the current business cycle outlook, should be aware of the sources of instability and the difficulties for obtaining reliable information from both the demand- and supply-side.

Note that as seasonal adjustment lacks an objective definition, the term “accurate” does not operate as in other traditional circumstances. Instead, I considered the more stable as the best result (Di Fonzo 2005). The exercise is carried out on the automatic X-12-ARIMA program default mode, according to the suggestions presented in Maravall (2002). Then, if a component does not fulfill the statistical criteria of an acceptable result, minimal interventions are made one-by-one until all tests are fulfilled, as probably made by most of the users.

The question about how we know if it is better to use direct or indirect adjustment is similar to that treated in Astolfi et al. (2001), Hood and Findley (2001), Otranto and Triacca (2002), among other papers. Nevertheless, to the author’s knowledge, no similar study has been carried out with Chilean GDP data. It is worth mentioning that despite several testing procedures contained in X-12-ARIMA, choosing between direct and indirect adjustment constitutes a different, separate question. This is so because the challenge consists of choosing appropriate diagnostics to compare among several adjustments applied to the same variable. Some diagnostics would be replicated while others, as those of stability and quality, need more attention and careful treatment.

This would lead to proceed without, for instance, the M1-M11 and Q statistics (Lothian and Morry 1978)—placed at the core of X-12-ARIMA. Furthermore, as Hood and Findley (2001) suggest, the ratio of one adjustment to another is also not valid, because spurious seasonality emerges. Many other examples remark the importance of a tailored quality assessment: different users would weigh different diagnostic outputs pursuing their own objectives. Take the case, for instance, of an adjuster making use of seasonally adjusted series in a turning point detection analysis. The smoothness in the resulting series will likely be a desirable outcome.

For these and other reasons to be discussed later, I make use of diagnostics that allow a quality and stability assessment for indirect adjustment, namely, spectral analysis in the frequency domain, sliding spans⁵, and revision history; all of them built-in X-12-ARIMA. I also use bias significance to statistically assess the distance to the direct method. The key is to have always in mind the goal of absence of residual seasonality; that is, absence of seasonality in series that theoretically should not have it. This is also analyzed through a rolling regression exercise. Finally, the exercise is re-done using the linked-chain dataset using a 1996–2017 sample (base year: 2013)—with evident aggregation bias in the aggregation schemes.

The results show that, in terms of stability, it is advisable to use the first stage of disaggregation by supply-side. Moreover, the results for the second and third stage of disaggregation by demand-side are very poor, according to the standard automatic setup described below. A deeper supply-side disaggregation results in a noisy estimation with many outliers in the adjusted series, but provides useful information regarding the sources of instability. Particularly powerful tools to discriminate are spectral plots and sliding spans, both estimated to the final seasonally adjusted series. Some economic intuition behind the statistical results is also provided. When using a linked-chain dataset, the first stage of disaggregation by supply-side is less biased in both actual and adjusted series, showing even more stability than the GDP itself.

The paper proceeds as follows. In Sect. 2, I provide some reasons about why the two kinds of adjustments (direct and indirect) may differ, along with some elements to consider reverting poor results. In Sect. 3, I apply these procedures to the Chilean GDP obtained by five different aggregation schemes—by supply- and demand-side—plus the GDP itself. I conclude in Sect. 4.

2 The Statistics of the Indirect Adjustment

As mentioned above, indirect seasonal adjustment is useful for benchmarking. I also addressed the reliability of subsets of seasonally adjusted series to be used with econometric purposes. One of these applications is to identify sources of methodological uncertainty which could redound in a poor adjustment of the aggregate. This section deals with the reasons behind the discrepancy between the indirect and direct methods. This is relevant as it stresses the difference between methodological versus purely empirical drivers behind mentioned discrepancy.

As expected, it is possible to obtain more than one indirectly adjusted series using the same dataset. This result is certainly due to different manipulation of the program. Consequently, this section also explores some possibilities to revert poor adjustment results, also aiming to stress the instability emerged exclusively from the method.

2.1 Why May Direct and Indirect Adjustment Results Differ?

There are several reasons why both kinds of adjustments may differ. I discuss some of these reasons next, supposing that the same methodology and sample span are applied for both adjustments.⁶ I follow closely the discussion provided in Ladiray and Mazzi (2003), and also, but to a lesser extent, in Peronacci (2003). Firstly, note that several unrealistic conditions should fulfill the adjustments in order to deliver the same results. These include: when the combination and adjustment are linear, the series does not exhibit outliers, the same filter is applied to all series, and, if with multiplicative adjustment there is no irregular component; then it is more likely that both adjustments will coincide. In the same way, similar results between both adjustments can be obtained if the statistical characteristics of the series are similar. This is a very uncommon fact with GDP datasets, but more likely with interest rates.

The adjustment made directly or by means of its disaggregation may differ because of:

• The use of a multiplicative adjustment in disaggregates This is especially the case with an aggregate compound by an algebraic sum of components, such as GDP. Note that when components are adjusted in a multiplicative way, the original series are divided by a specified seasonal factor. Since the seasonal factors are not common across sectors, or even more, imperfectly correlated, the sum of those components should exhibit a different behavior to that of by, say, an additive adjustment of the aggregate.

• Presence of outliers and differences in the trading day effect of the disaggregation As in the previous case, idiosyncratic effects of components could cast for different parameters in the adjustment. A rough example consists of an aggregate of two equally weighted components. Suppose that both components exhibit the typical behavior of an economic series, and also related between them, except for its outliers. Also, the first series experience several outliers across sample span, followed by outliers in the second component in the same direction. Obviously, they will be corrected separately implying that they can still share the same filter characteristics. But the aggregate will exhibit a very noisy behavior as it adds up both kinds of outliers or shocks. Thus, it will be hard to find a stable filter for adjusting the aggregate, implying that different estimates could emerge.

• Use of different filters Even in a series without outliers and with the same kind of adjustment, the results may diverge. This could be the case when different filters are used. Note that sensitivity of moving averages (MA) to its order leads to dramatically different results in cases with volatile series. Recall that the order of an MA is closely related to the independence—lower correlation—of the series observations. So, the more independent the observations are, the more sensitive to its order the MA is. In the case of seasonal adjustment, it could occur that when only one component has a different filter than the rest, the indirect adjustment result moves away from that of the direct one. This point is amplified when the observations of the aggregate are less independent of those of its disaggregation.⁷

• Different forecasting models If disaggregation is forecast with different autoregressive integrated moving average (ARIMA) models, and consequently different from that of the aggregate, it is more likely that both adjustments will not coincide. This is so because different forecasting models could induce major revisions due to forecasting accuracy. Furthermore, the forecasting model can account for different MA filters between disaggregations. Hence, they redound into differences between direct and indirect adjustment.

• Harshness of aggregation Obviously, as the number of series included in the aggregation increases, their weight in the aggregate decreases. This happens in any context such as, for instance, original and seasonally adjusted series. Thus, a series composed of $n_{1}$ subseries, is more likely to deliver more unstable results than the one built with $n_{2}\gg n_{1}$ subseries. This is not necessarily always true as it still depends on how the aggregation is made. If the aggregation of components with erratic seasonality converges to a series with stable seasonality, it is desirable to aggregate just a little number of series in terms of stability. But, if the assumption $n_{2}\gg n_{1}$ is computed with a large enough $n_{2}$ relative to $n_{1}$, the marginal contribution of a series with erratic seasonality will not affect the result of the aggregate.

• Fading out of judgment As will be discussed later, a way to improve poor adjustment results consists in fixing some diagnostics by means of user’s judgment. This is common with series that exhibit erratic seasonal components, requiring fine expertise rather than those with stable seasonality. It could be the case that the choice based on user judgment of a specific filter, forecasting model, specific fixed effect, or any other user intervention may help to correct some diagnostics. Nevertheless, as a result of this intervention, the disaggregation becomes adjusted under a different setup from that of the aggregate. This leads to almost surely divergent results between the direct and indirect adjustments.

2.2 How to Revert Poor Results?

There are several strategies to evaluate when some diagnostics fail in order to extract seasonality. These corrections arise supposing that a more stable adjustment is preferable with most recent data. All these corrections require user intervention. Expert judgment is always desirable. Manipulations can be made at any stage of the process or even prior to the analysis without affecting the results’ validation. Some recommendations found in the literature include the following:

• Regarding seasonality detection, spectrum diagnostics tend to fail when changing seasonality is present. Spectra work well with medium-sized series. With a long series, spectral plots show little change when more observations are added. This could hide most recent data seasonality (Hood and McDonald-Johnson 2009). Hence, analysis of more recent data (latest 60 observations) leads directly to the detection of seasonality with the spectrum of the original series.

• For the same abovementioned problem, a reduction of spectrum bandwidth increases the probability of detection of seasonality. As Hood (2007) finds, the use of an AR(10) model instead of an AR(30) casts for less smoother spectral plots. This change brings attached the risk of finding more false negative cases. Nevertheless, this represents a minor shortcoming when seasonality is hard to detect. This is especially the case when the AR(30) model cannot discriminate because of short peaks at seasonal or trading day frequencies.

• Another way to find seasonality relies on the suggestion proposed by Maravall (2005). This consists of a joint test of seasonal dummies contained in a regression of original series. The theoretical distribution is based on the nonparametric Kendall-Ord test (Kendall and Ord 1990). As it constitutes a nonparametric test, its use with a short sample span, however, is not entirely recommended.

• The goal of seasonal adjustment is to achieve absence of residual seasonality. This task could be eased with a series that has already been controlled for effects that facilitate residual seasonality—by removing outliers, for instance. With this purpose in mind, Soukup and Findley (1999) suggest testing residual RegARIMA (Findley et al. 1998) series for seasonality through spectral plots. This check, as the authors suggest, improves the capacity of remaining diagnostics contained in the program to dissipate residual seasonality.

• Several rough interventions also facilitate both detection and quality improvement. This category includes fix data transformation—such as a logarithm—, change filters’ lengths, avoid sample span flagged as unstable—according to sliding span and revision history—, RegARIMA fixed effects manipulation and/or fix RegARIMA model, among others. Note that X-12-ARIMA has the option of deactivating specific stability diagnostics, such as sliding spans or RegARIMA residual outliers’ detection. An iterative process fixing one control at a time is recommended, basically to ensure consistency as new information arrives.

• A typical undesirable effect are outliers. RegARIMA specifically controls for additive outliers. Nevertheless, a second check is recommended specifically when it appears in recent observations. Take the case of, for instance, an outlier at the last observation available. For sure, RegARIMA will replace this observation with one affine to the series prior to outlier arrival, and no further intervention will be required. But, if it is expected that few of the next observations will exhibit the same value, then it is recommended to include the observation in the adjustment process. Keeping the outlier observation for processing can be managed in several ways inside the RegARIMA module. For instance, by using the span or types=(ls tc) options within outlier command when manipulating the software. Of course, a different situation arises when the outlier is located near the half of the series length. Obviously, the most ideal case with outliers is when they are at the beginning of the sample, and the sample is long enough.

• For stability purposes, Bobbit and Otto (1990) suggest using long-horizon backcasts and forecasts. The authors conclude that revisions are smaller when a series is extended with enough long-horizon forecasts. This finding is achieved by comparing the stability of adjusted series with extended original series—using a symmetric filter—versus not extended or extended by just one year. It is also interesting, especially from a practitioners’ point of view, that a simple automatic procedure is equally accurate as modeling individual ARIMA processes.

3 Empirical Application: The Case of Chile’s 1986–2009 GDP

In this section, I focus on applying the three abovementioned X-12-ARIMA diagnostics to determine which indirect seasonal adjustment for the Chilean GDP 1986-2009 (base year: 2003) is preferable. The diagnostics considered are all those that are robust to direct and indirect adjustment, namely spectral plots, sliding spans, and revision history. The analysis is complemented with several statistics that resume part of the adjustment quality assessment as, for instance, bias in seasonally adjusted series and residual seasonality checking. Finally, the same exercise is re-done using the most up-to-date dataset 1996–2017 (base year: 2013) which is released under the linked-chain methodology (losing the additivity property across aggregations).

Notice that the particular vintage used has several desirable characteristics for an economic-statistical analysis, such as: (1) it does not have induced breaks or level shifts due to methodological changes, (2) it is prepared and released on a quarterly basis, (3) it is compounded by a number of sectors with different seasonal patterns, and (4) it does not have any missing values, mismatches, or any other shortcoming to deal with prior to the adjustment.

3.1 Data: Descriptive Statistics and Aggregations

I use the first 96 observations of the Central Bank of Chile’s Quarterly National Accounts (QNA), from 1986.I to 2009.IV, starting with GDP as the most aggregated, and with three levels of disaggregation on the demand side and two on the supply side. The construction of the dataset is as follows. First, I use the dataset detailed in the official volume “National Accounts of Chile 2003–2009” (Banco Central de Chile 2010). The original series are in levels, denominated in millions of 2003 Chilean pesos. Hence, the additivity (or subtraction) is ensured as the components are denominated in the same units and constructed with the same base year. This also implies a weight equal to 1 (or − 1) for an added (or subtracted) component (Ladiray and Mazzi 2003). Second, I calculate the quarterly variation of the dataset provided in Stanger (2007). This dataset contains quarterly data from the period 1986–2002 denominated also in millions of 2003 Chilean pesos. Finally, the quarterly overlapping method is used backwards by fixing the base year 2003 and building the series back to 1986 with the quarterly rates calculated previously. Nevertheless, I use only the first 96 observations, counting from 1986.I onwards, as they constitute the minimum length suggested by X-12-ARIMA developers to stress its capabilities, even though the minimum length of a series to perform a routine is 60 observations.

The original series comprise the Chilean GDP by demand side and supply side. A scheme of demand-side aggregations of all series with acronyms used in this paper is shown in “Appendix A”, and those of supply-side in “Appendix B”. There are a total of five different aggregations, labelled as “Aggregation i”, $i =$ {1-5}, plus the GDP by itself (“Aggregation 6”). All five aggregation blocks as well as aggregation 6 deliver the GDP, calculated as a sum of every corresponding component.⁸

Since 2008 the Central Bank of Chile has adopted the linked-chain methodology to produce the GDP dataset. This methodology, used to improve representativeness, implies that the dataset loses its additive property. Under this scheme, the disaggregation added to an aggregate does not necessarily coincide with the direct aggregate. The indirect seasonal adjustment quality and its stability depends in this context, among other factors, on the so-called non-additive term that emerges from the difference between both aggregates. A method to adjust indirectly a linked-chain variable is presented in Scheiblecker (2014), but it has not been widely accepted yet. A deeper analysis of the indirect adjustment made with linked-chain data is left to further research. However, in this article it is explored preliminary results using a 1996–2017 dataset (base year: 2013) released under linked-chain methodology. The statistical properties of the non-additive term play a crucial role to understand why different indirect adjustments differ diametrically. The same exercises are performed with this dataset in order to produce comparable results.

The analysis provided in this article makes use of the information already contained in the dataset when additivity was ensured. This result acts as a natural benchmark when the dataset may be updated with subsequent 2009 and 2013 available vintages; these two built under the linked-chain methodology. Again, the relevance of the exercise lies in the awareness of the user on the accuracy exhibited by certain disaggregates.

3.2 Setting Up the Exercise

The exercise consists of adjusting all the components by demand side and supply side to then add up according to the aggregation schemes (“Appendix E”). Note that some parameters governing the adjustment of each component may differ between them. The exercise is carried on the automatic program default mode, according to the suggestions presented in Maravall (2002). Then, if a component does not fulfill the statistical criteria of an acceptable result, minimal interventions are made one-by-one until all tests are fulfilled. These interventions are chosen considering stability as a criterion. That is, trying to keep the adjustment parameters fixed along the evaluation sample span; from the 60th to the 96th observation (2000.IV–2009.IV). Note that this dynamic scheme is made to compute the sliding span, revision history, and residual seasonality checking. On the opposite side, spectral plots are computed with the whole sample, same as bias significance.

The adjustment is made through Eviews 7.2 interface for X-12-ARIMA version 0.2.10. Notice that Eviews makes use of its own notation for X-12-ARIMA options. These options used by Eviews are the following (while the script used for the adjustment is presented in Medel 2014):

• Mode: For setting up the seasonal adjustment method: “m” for multiplicative, “a” for additive, “p” for pseudo-additive, and “l” for log-additive seasonal adjustment.

• Filter: For setting up the seasonal filter: “msr” for automatic, moving seasonality ratio, “x11” for X11 default, “stable” for stable, and “s3xj” for $3\times j$ MA, $j\in \{1,5,9,15\}$.

• Trans.: For setting up a transformation for RegARIMA: “logit” for logit, “auto” for automatically choose between no transformation and log transformation, number for Box-Cox power transformation using a specified parameter, where “0” is for log transformation.

• SSpan: For analyzing the stability with sliding spans: “sspan”.

• Check: For checking the residuals of RegARIMA: “check”.

• ARIMA: For setting up the ARIMA specification of RegARIMA: “f” for using forecasts from the chosen model, “b” for using forecasts and backcasts from the chosen model, “(p,d,q)” for manually entering specification. When this option is used, it could also be accompanied by “oos” for using out-of-sample forecasts for automatic model selection.

• Model: For knowing the RegARIMA model estimated to each of the series previous to apply the adjustment. Parsimonious models are chosen to more stylized series, while models imposing numerous coefficients are used for volatile, unstable series. The basic RegARIMA specification is written as:

  $$\begin{aligned} \phi (L)\Phi (L^{s})(1-L)^{d}(1-L^{s})^{D}(y_{t}-\underset{i}{\sum }\beta _{i}x_{it})=\theta (L)\Theta (L^{s})z_{t}, \end{aligned}$$

  (1)

  where L is the backshift operator ($L^{p}y_{t}=y_{t-p}$), s is the seasonal period, $\phi (L)$ is the nonseasonal AR operator (of order p), $\Phi (L^{s})$ is the seasonal AR operator (of order P), $\theta (L)$ is the nonseasonal MA operator (of order q), $\Theta (L^{s})$ is the seasonal MA operator (of order Q), and $z_{t}$ is iid with zero mean and variance equal to $\sigma _{z}^{2}$ (white noise). Note that $z_{t}$ is modeled with an ARIMA process as the series $y_{t}$ after these controls commonly exhibits autocorrelation. Some controls ($\mathbf {x}_{t}$) already incorporated in the program are: trend constant, fixed seasonal effect, trading day effect, length-of-month (or quarter), leap year, Labor Day effect, additive outliers, level shift, temporary change, and ramp, among others. Under this multiplicative presentation, the model is represented as (p,d,q)(P,D,Q), where d and D are the differencing order of $y_{t}$ and $z_{t}$ to achieve stationarity.

• Outlier: For analyzing the presence of outliers of RegARIMA: “outlier”. However, for the purposes of this article, the most relevant result relates to the number of observations $\Delta y_{t}^{sa}=y_{t}^{sa}-y_{t-1}^{sa}$ lying outside the range $\Delta \overline{y}_{t-1}\pm Z_{\alpha }\widehat{\sigma }_{t-1}$, where $Z_{\alpha }$ is the inverse normal distribution evaluated at probability $\alpha$. In other words, it refers to the quarterly rate of the period t which lies outside the $\alpha = 5$% (and symmetrically at 95%) and $\alpha = 1$% (99%) confidence interval calculated with the sample until $t-1$.

The adjustment options of each component are presented schematically in Table 1. Note that a logarithmic multiplicative adjustment with automatic filter selection is the preferred specification. The sliding span for trend-cycle and seasonally adjusted, along with the diagnostics used for resultant RegARIMA residual series, are also selected. The trading day effect cannot be identified in these series because of sample length. All remaining parameters are left in Eviews’ default mode. The chosen RegARIMA model is presented under the “Model” heading. “Outliers” stands for the number of observations lying outside the confidence ranges.

Table 1 Seasonal adjustment options of each sector.

Several adjustments deserve mentioning. The Change in inventories (ci) series does not show seasonality according to X-12-ARIMA diagnostics. When series containing this component are added up to its aggregation, ci is included in its original version. The External demand (ed) series corresponds to a series in levels that allows for negative and zero values. Therefore, an additive adjustment was tried but with negative outcome. As a result, I used an indirect adjustment corresponding to its definition but with seasonally adjusted series: $x_{t}^{sa}-m_{t}^{sa}$. The seasonality of the Exports of services (xs) series is found with two RegARIMA specifications at two different sample spans. The first, with a (0, 0, 1)(0, 0, 0) specification is obtained in 1986.I through 2003.I, while the second, for 2003.II–2009.IV is found using a RegARIMA specification supported by an out-of-sample criterion. In general, all those series in which the RegARIMA specification is fixed (to the (0, 0, 1)(0, 0, 0) model) or sliding span option deactivated, correspond to cases with an erratic behavior across time, with a relatively high variance (see “Appendix E”), specially at the first stages of the sample.

3.3 Results

In this subsection, I analyze the estimates of diagnostics checks for all six aggregations. In some cases (bias), aggregation 6 acts as a benchmark; hence, deviations from seasonally adjusted series of that aggregation are considered a low-quality adjustment. However, this result must be considered just as a benchmark given the discussion of previous sections about the possibilities among which the different schemes may differ. Specifically, disaggregates can handle RegARIMA outliers and nonlinearities better, and when adding up to the original, different seasonal patterns do not cancel noisy effects at all. A corollary of this discussion is that an “actual seasonally adjusted” series does not exist, while many minor changes in some parameters for the aggregate and all its diagnostics fall on the acceptance region. This implies that expert judgment plays a key role in determining which strategy is the best.

To have a general overview of the adjusted series, in Fig. 1, panel A, I plot the seasonally adjusted series in logarithmic levels (whole sample), while in panel B, its quarterly variation (quarter-on-quarter changes). The latter panel is useful since it exhibits the observations exceeding the confidence interval (5, 95%) in a schematic way. Quick comparisons regarding these observations are conducted with ease, particularly with respect to aggregation 6 (see Sect. 3.3.5 for an economic interpretation of these results).

The first result concerns bias. As X-12-ARIMA adjusts the series within a year across all years of available sample, the mean of seasonally adjusted series should coincide with that of the original series. Table 2 displays this result, showing a downward bias for the demand side aggregations (− 1.0% on average) and an upward bias for those of supply side (1.2% on average). As displayed in the table, aggregations 4 and 6 are the least biased adjusted series.

Fig. 1

Source: Author’s elaboration based on Central Bank of Chile’s database

Chilean GDP—Seasonally adjusted and log-differenced series. a Seasonally adjusted series. b Log-differenced series. Shaded areas indicate an observation lying outside the confidence interval (5, 95%) of any of depicted series.

Table 2 Bias and covariance analysis.

Regarding second moments, panel B shows the covariance of the first to fifth aggregations with respect to adjusted GDP. Panel B also shows statistical inference on the significance of estimated bias, in the spirit of the exercise presented in Di Fonzo (2005). The inference is applied to the coefficient c (null hypothesis: $c=0$) in the regression $y_{t}^{Agg(i)}-y_{t}^{Agg(6)}=c+\varepsilon _{t}$, $\varepsilon _{t}\sim iid \mathcal {N}(0,\widehat{\sigma }^{2})$, where $i =$ {1-5}, and the standard deviation of $\widehat{c}$ is corrected with the Newey-West heteroskedasticity and autocorrelation method. As with the mean, aggregation 4 is the closest to the benchmark, along with aggregation 3. Moreover, aggregation 4 exhibits a different dynamic than the aggregation 6 at the 12.3% level of confidence, quite far from those obtained with demand-side disaggregations.

The original dataset described in Stanger (2007) and Banco Central de Chile (2010) recognizes that the data construction method comprises bias, but with values surrounding 0.2–0.0% of total GDP. Thus, the results presented in Table 2 are possibly due to the nonparametric characteristic of the program, being unable to detect special data effects without user intervention, namely outliers, at the sectoral level.

3.3.1 Spectra-Based Diagnostics

Spectral graphics are computed with gretl 1.9.12cvs software.⁹ As mentioned, they are computed with the whole sample for the final seasonally adjusted and the irregular component. The quality assessment should be easy considering pairwise comparisons of one aggregation to another. Anchoring to aggregation 6—whose adjustment fulfill all statistical tests—is recommended.

The results are presented in “Appendix F”. From the first panel of figures, concerned with seasonally adjusted series, it is easy to be aware of the inefficiencies of aggregations 1 and 2: they exhibit clearly a peak at $\pi /2$ frequency—thereof seasonality—but also in the irregular component (second panel). Regarding the four remaining cases, the three first are all visually congruent with aggregation 6. However, considering the irregular component, note that the spectrum of aggregation 4 is most alike to the benchmark. It is worth to mention that aggregation 6 positively overpass all X-12-ARIMA diagnostics, despite of a peak between frequencies ($\pi /2,3\pi /4$)—associated with trading day effect; but no robust identification was possible due to sample size. As a result, aggregations 4 and 6 remain with promissory results.

3.3.2 Sliding-Span-Based Diagnostics

The sliding spans (Findley et al. 1990) are estimated with the minimum length of observations required by X-12-ARIMA: 60 observations. As I dispose of the shortest length, the estimation of sliding spans is made in recursive scheme rather than a rolling-window alike, adding one year at a time. This treatment starts from a “lower bound quality” to then becoming more demanding for the sliding spans, given two forces behind the dynamics that emerge while the span is increased.

On the one hand, if more observations are available, they will be added while the initials will be dropped. The new data, similar to most recent dynamic, will redound in a better-quality adjustment. Furthermore, with long enough series, it is possible to exclude observations that show different behavior from that of the more recent data. On the other hand, as Otto (1985) suggests, adding more observations to series—being actual as well as (back)forecasted—result in smaller revisions. To the matter of this empirical application, however, these both excluded possible improvements seem to have a minor impact. This is so because the first years of data seem well behaved in most sectors.

The sliding spans are computed for final seasonally adjusted and trend-cycle series with two transformations: logarithmic and log-differenced levels. These four sets of variables are analyzed because those are the series that attract the attention of the users. The log-differentiation stands for quarter-on-quarter change approximation. The results are provided in terms of descriptive statistics of the span $S_{t}(k)$ (see Medel 2014, for more details). Recall that for the series in logarithmic units, the sliding span measure $S_{t}(k)=\left[ \max _{k}y_{t}^{sa}(k)-\min _{k}y_{t}^{sa}(k)\right] /\min _{k}y_{t}^{sa}(k)$ is computed for the seasonally adjusted series $y_{t}^{sa}$ using the span k, so the mean of $S_{t}(k)$ until K available spans corresponds to (s is the sample size of the span):

$$\begin{aligned} \overline{S}=\overset{T}{\underset{t=1}{\sum }}\frac{\max _{k}y_{t}^{sa}(k)- \min _{k}y_{t}^{sa}(k)}{\min _{k}y_{t}^{sa}(k)},\text { }\quad \forall k\in K|K=\left\{ 1,\ldots ,\frac{T}{s}\right\} , \end{aligned}$$

(2)

quantifying the average deviation from the minimum to maximum estimates of each observation. For log-differenced series, the analyzed statistic corresponds also to the mean of $S_{t}(k)$, but defined as:

$$\begin{aligned} \overline{S}=\overset{T}{\underset{t=1}{\sum }}\left[ \max _{k}QQ_{t}(k)- \min _{k}QQ_{t}(k)\right] ,\text { }\quad \forall k\in K|K=\left\{ 1,...,\frac{T}{s}\right\} , \end{aligned}$$

(3)

where $QQ_{t}(k)=[y_{t}^{sa}(k)-y_{t-1}^{sa}(k)]/y_{t-1}^{sa}(k)$. Note that if $S_{t}(k)>\alpha \%$, then observation t is flagged as unstable. The value of $\alpha$ used as a threshold is 3% for seasonally adjusted series and 33.3% for trend-cycle series. This latter value is considered as an approximation to the 3% threshold applied to seasonal factors. Thus, it supposes a null expectation on irregular component movements. The adjustment is considered of inferior quality if the number of observations flagged as unstable exceeds 25% with logarithmic and 40% with log-differenced series.

To make a more demanding comparison, I find the maximum and minimum values of $y_{t}^{sa}(k)$ through 3–10 spans, recalling that X-12-ARIMA finds from 2 to 4 spans (Findley et al. 1998). Thus, including a higher number of spans gives more chances to consider more distant estimates. Given the recursive scheme, available data allows to estimate 10 sliding spans. The first is estimated up until 2000.IV (1st–60th observation) while the last, until 2009.IV (1st–96th observation). Note that the last span that allows for a joint triple comparison includes observations until 2007.IV—that is, the last span where $\#k^{min}=3$.

The results are calculated for trend-cycle and seasonally adjusted series, for two transformations (log and log-differenced). The detailed extensive results of each span for each series can be found in Medel (2014). Table 3 summarizes reports some descriptive statistics of $\overline{S}$ series. As can be seen in Table 3, most of the divergence between aggregations occurs with the log-differenced series. In the case of seasonally adjusted series, note that the benchmark achieves a 34% of unstable cases (threshold: 40%). Recall that the adjustment made to aggregation 6 overpasses all the diagnostics in the default mode. This 34% of unstable cases are achieved with the modifications made to the sliding-span basic scheme and threshold impositions. These modifications are made basically to stress the differences between aggregations. The results with this kind of data show that two aggregations exhibit better results than the benchmark, both belong to the supply side: aggregations 4 and 5, for median, mean and times flagged as unstable. A similar result is replicated qualitatively with trend-cycle series, but excluding aggregation 5. In this case, aggregation 4 also seems an alternative, especially given the stability of its point estimates. So, overall, aggregation 4 remains as the most stable (along with aggregation 6) with both log and log-differenced data.

In the case of logarithmic series, just minor differences can be adverted. However, aggregation 4 for seasonally adjusted data and aggregation 6 for trend-cycle, provide the most stable estimates, with aggregation 4 for trend-cycle being also strongly suggested to use. Among all possibilities, undoubtedly aggregation 3 has the worst performance, representing the case where adding up components with different seasonality results in the worst aggregate performance.

Table 3 Summary of sliding-span-based diagnostics.

3.3.3 Revision History Diagnostics

The basic revision calculated by the program is the difference between the earliest adjustment of a quarter’s datum obtained when that quarter is the final quarter in the series (concurrent) and a later adjustment based on all future data available at the time of the diagnostic analysis (most recent) (see Findley et al. 1998, pp. 137). Often, the informational content of last observations is more important for users, especially for those involved with conjunctural assessment.

The revision is calculated as follows. Suppose that the series to be seasonally adjusted is $\{y_{t}\}_{t=t_{0}}^{t=T}$, and $t_{0}\le t\le T$. Hence, if $y^{sa}$ is the seasonally adjusted series, then $y_{t|t}^{sa}$ is the concurrent seasonal adjustment of observation t, and $y_{t|T}^{sa}$ is the final adjustment of observation t, made with the full sample, T. The revision is:

$$\begin{aligned} R_{t}=\frac{y_{t|T}^{sa}-y_{t|t}^{sa}}{y_{t|t}^{sa}}. \end{aligned}$$

(4)

As concerns the stability of the overall process, this measure has the advantage of quantifying, and making comparable through different methods, the dynamic effect of adding new data. Hence, it clearly exposes the methodological instability of the X-12-ARIMA program. Notice that this instability arises mainly from the sensitivity of moving average estimates to change in the dynamics of the series. Furthermore, the instability has to be observed through a set of observations and not by one observation alone. In that case, RegARIMA will treat it as an outlier and drop it from the adjustment.

The results are presented graphically in “Appendix G”. The figures show, plotted for log-differenced trend-cycle (panel A) and seasonally adjusted series (panel B), the concurrent and the most recent (marked with ${\blacktriangledown }$) estimates of each observation across time. Hence, two statistics are reported: (1) the absolute average change, and (2) the number of times that the movement from concurrent to most recent (or vice versa) includes the zero. The absolute average change is the average of the distance between concurrent and most recent, across time. So, a shorter average result in better stability. The second statistic accounts for the undesirable case that is reporting firstly a decrease in the series to, quarters later, notice that the series actually increases, or vice versa.

Table 4 reports a summary of both statistics analyzed. As shown, aggregation 4 exhibits better statistics than aggregation 6 for both trend-cycle and seasonally adjusted series jointly. In particular, the absolute change for trend-cycle reaches 0.255 with aggregation 6, while just 0.135 with aggregation 4. Notice that the best case of demand-side—aggregation 2—is not fully disposable. With seasonally adjusted series, the benchmark achieves an average of 0.269 and 0.279, in a virtual tie between aggregations 4 and 5. With these series, however, demand-side aggregations exhibit a worse performance than in the previous case. Regarding the “Times equal to zero” measure, notice that the results are not generally scattered, except with aggregation 3. Undoubtedly, aggregation 4 represents the best case where never the estimates change their direction as new data are incorporated into the adjustment. Hence, aggregation 4 comes out as the most stable aggregation.

Table 4 Revision history results summary.

3.3.4 Residual Seasonality Check

Recall that the purpose of the program is to decompose a time series ($y_{t}$) into a trend-cycle component ($y_{t}^{\tau }$) plus (or times, depending on the kind of seasonality) a seasonally adjusted component ($y_{t}^{sa}$), plus (or times) a residual irregular component ($y_{t}^{ir}$; then $y_{t}=y_{t}^{\tau }+y_{t}^{sa}+y_{t}^{ir}$, or $y_{t}=y_{t}^{\tau }\times y_{t}^{sa}\times y_{t}^{ir}$). Hence, the two latter components, $y_{t}^{sa}$ and $y_{t}^{ir}$, should not exhibit a cyclical behavior. Furthermore, trends and seasonally adjusted series (the log-difference) tend to attract a lot of attention, which redounds on the importance of stability as a measure of economic diagnostic reliability. As Granger (1979) pointed out, this decomposition is relevant because seasonality explains most of the variance of a series being economically insignificant.

Accordingly, this subsection focuses on the systematic component that could be present in the resulting irregular component ($y_{t}^{ir}$). In particular, the attention is posed on the to-be-estimated autocorrelation of both the nonseasonal and seasonal parts of $y_{t}^{ir}$. Note that this component should be stationary by construction, as any unit-root-alike component should be contained in the trend-cycle component ($y_{t}^{\tau }$ ). To have a fairer comparison between the different aggregations, the t-statistic of the $\phi _{i}$ coefficients of the following two regressions in a rolling-window scheme for each aggregation are reported:

$$\begin{aligned} {\mathsf {AR(1)}} :y_{t}^{ir}= {} \mu _{1}+\phi _{1}y_{t-1}^{ir}+\varepsilon _{t},\nonumber \\ {\mathsf {AR(4)}} :y_{t}^{ir}= {} \mu _{4}+\phi _{4}y_{t-4}^{ir}+\nu _{t}, \end{aligned}$$

(5)

where {$\mu _{i},\phi _{i}$} are parameters to be estimated, and {$\varepsilon _{t},\nu _{t}$} are white noises. Note that X-12-ARIMA does not distinguish between trend and cycle, basically because the series traditionally analyzed does not provide enough sample span to determine whether it is trend or cycle.¹⁰ Hence, if one of the $\phi _{i}$ parameters is significant, the identified residual seasonality could belong to the seasonally adjusted ($y_{t}^{sa}$) and/or the trend-cycle series ($y_{t}^{\tau }$). Whatever the case, statistical significance of the $\phi _{i}$ parameters indicate the presence of residual seasonality, particularly $\phi _{4}$. A significant $\phi _{1}$ parameter, in turn, goes beyond residual seasonality, as it indicates the presence of a systematic component in a series that supposedly must be “irregular”.

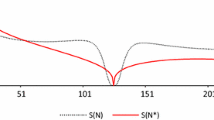
The results are presented in Fig. 2. Notice that aggregation 6 turns out to be an appropriate benchmark since, despite the significant first-order autocorrelation, it does not contain a seasonal component in the irregular series, and fulfil all statistical X-12-ARIMA requirements. Aggregations 1 and 2 exhibit both kinds of autocorrelation, despite some observations free of residual seasonality during the 2006–2008 for aggregation 2. Aggregation 3 exhibits stronger autocorrelation during the evaluation sample while being of short-memory, making the AR(4) coefficient non-significant. Aggregations 4 and 5 exhibit a closer pattern to that of aggregation 6, in the sense that the first-order autocorrelation is the only significant one, implying the absence of residual seasonality in a stricter sense. Aggregation 4, in particular, is closer to having the required characteristics being easier to handle for those purposes (following the directions of Sect. 2).

3.3.5 Economics-Based Results

Aggregation 4 stands out as the most reliable indirectly adjusted GDP series, while demand-side aggregations 1–3 are characterized by the presence of residual seasonality, and an overall inferior adjustment. This subsection analyses to what extent these results have a relation with the economic developments of involved sectors, and the Chilean economy in general.

Fig. 2

Source: Author’s elaboration

Irregular components’ residual seasonality: rolling estimate of the AR(1) and AR(4) coefficients’ t-statistic. Shaded area  =  0  ${\pm }$ 1.644 (null hypothesis rejection region)

First of all, that demand-side aggregations are more difficult to adjust rather than supply-side schemes, suggests that shocks may persist for a longer time in the former than in the latter group of series. Consequently, the identification of seasonality given a fixed time span will be spoiled out due to shocks, either more persistent or more in number. An outliers account describes well the difficulty found by X-12-ARIMA to deal with supply-side series at the most disaggregated level. Notice that when widening the confidence interval to find outliers in the log-differences series (see Table 1), they move in tandem with the most volatile series. Most disaggregated data from the supply side (aggregation 5) exhibit a disproportionate number of outliers, which are cancelled out when aggregated to the next level (aggregation 4).

For users concerned with signal extraction at the aggregate level, these results suggest that a way to proceed would be to consider series conforming aggregation 4. Moreover, this result is also likely to be present even in further vintages of the dataset, as it represents consumer habits and government consumption behavior with infrequent changes versus activity disruptions in a diversified small open economy.

Note also that most disaggregate supply-side adjusted series are also noisy, with some tests not completely fulfilled. This result suggests that, despite a number of shocks present at the sectoral level, the net effect is offset resulting in an appealing set of series when they are aggregated accordingly. This is the case when moving from aggregation 5–4, becoming the seasonally adjusted GDP Non-natural resources a convenient representation for the overall state of the economy.

The different results arising from this aggregation problem, strictly relates to Sect. 2 contents, i.e. the aggregation of noisy, volatile series may result in a smooth, appealing aggregate. In line with the outlier figures shown in Table 1, the way how aggregation 4 is built results in a better indirect adjustment. Nevertheless, the results are not necessarily within the boundaries of the best adjustment. Hence, a suggestion for further analysis goes in the direction of depurate or re-grouping of GDP Non-natural resources aggregate.

When seasonally adjusted levels of GDP are needed (e.g. measuring economic slack through the output gap), an immediate recommendation for modelling purposes is the use of the GDP Non-natural resources series. In the same line, base conjunctural economic assessment at the most disaggregate supply-side level should be avoided. From the demand side, in turn, external demand adjustment could be greatly improved by analyzing it at the most disaggregated level in order to identify and isolate inner sources of instability.

3.3.6 What Happens when Linked-Chain Data are Used?

From a practitioner’s point of view, it is impractical to conduct an up-to-date analysis using the 1986–2009 sample. However, as above mentioned, since 2009 the Central Bank of Chile releases the QNA using the linked-chain methodology. This means that each series is augmented with a surveyed rate of growth, and hence, when adding up the corresponding series to have an aggregate, it does not necessarily match the surveyed rate of growth of the aggregate, generating a difference or a “non-additive term” in actual series. As in this article five aggregations target the same aggregate, it is likely that they may differ between them.

Despite this latent discrepancy at the aggregate level, in this subsection the same previous diagnostics are applied to an official Central Bank of Chile dataset released with linked-chain methodology for the available sample 1996.I–2017.II (base year: 2013). Some minor differences are noticed in the sub-aggregates by the demand side, such as, Changes in inventories are already included in the Investment series, and Households’ consumption expenditures differentiates Nondurable consumption from Services.

Overall, these robustness results are plainly supporting aggregation 4 as the most reliable seasonally adjusted series, and even more suitable than the direct method according to some specific diagnostics.

Same as above, first result concerns bias. In this case, bias is present at the first level of aggregation, which is depicted in Table 5 mimicking, to some extent, the results of Table 2 (in this case, figures are denominated in millions of pesos of 2013).

Table 5 reveals that aggregation 3 originally exhibits the greatest downward bias with respect to aggregation 6 (acting as a pivot), showing a mean 13.7605% lower. Remaining aggregations show smaller bias surrounding 1 and 0.3%. Remarkably, aggregations 4 and 5 show equal estimates, as will happen with some other diagnostics.

When comparing bias in seasonally adjusted series, similar results to actual series are obtained. A clearly biased result is observed for aggregation 3, which is also statistically significant unlike the remaining results. Aggregations 4 and 5 are positively biased by 0.2784% whereas aggregation 1 by (virtually) the same amount but positively. Bias estimates are quite reduced with respect to previous figures despite disruptions in all the series, particularly due to the Global Financial Crisis impact perceived in 2009–2010. Marginally, aggregation 4 shows the preferred results in terms of bias in both actual and seasonally adjusted series.

Table 5 Bias analysis with linked-chain data.

Regarding spectral plots, estimates are depicted in “Appendix F”, in an analogous manner of “Appendix H” for the logarithmic-difference and the irregular components. Generally speaking, all the results are much better-behaved than the previous case. Demand-side aggregations exhibit a notorious peak at 2.25/4 frequency (Fig. 9) which is present in all other aggregations, to a lesser extent, except in aggregation 6. Aggregations 4 and 5 show very similar spectral shape, accruing mass at higher frequencies, as is expected for this kind of series.

Regarding the spectral shape of the irregular component, results for aggregation 6 are in line with those of Fig. 3: at higher frequencies there is still some evidence of systematicity in its dynamics. On the other hand, aggregations 3 and 5 accumulate mass at smaller frequencies, which could be considered as a benign outcome; however, differing dramatically from the aggregation 6 used for benchmarking. The results for aggregation 3 are basically explained by the influence of the External demand series, whereas for aggregation 5 the results are presumably due to a too rugged aggregation, as explained in Sect. 2. In general, aggregations 1, 2, and 4 are very similar to aggregation 6 and, therefore, the regression analysis of the irregular components through AR models becomes more worthwhile.

Summary results of sliding span estimates are presented in Table 6, similar to that of Table 3. Among trend-cycle series, log-series are easier to interpret because all of them are well-behaved. Aggregation 3 shows the poorest result whereas aggregations 4 and 6 do a fairly good job in terms of stability. More diverse results are obtained with log-differenced series. An interesting result is obtained for aggregation 4, which may be more stable than aggregation 6 (median of − 4.86 vs. 7.00) but with a greater dispersion ([42.56; − 444.86] vs. [87.77; − 36.55]).

Table 6 Summary of sliding-span-based diagnostics using linked-chain dataset.

Regarding the sliding spans of seasonally adjusted series, logarithmic series are all well-behaved and the results for aggregation 3 are by far much more stable than the 1986–2009 case. Same as above, log-differenced series are more scattered, and the best result is obtained with aggregation 6, followed by both supply-side aggregations. In this case, statistics goes in the opposite direction for aggregation 4, that is, it exhibits a lesser min-max range but with a mean 4.5 times higher than aggregation 6. This fact could be understood merely as volatility and greater uncertainty in the point estimate of the most recent observation of the seasonally adjusted series. Still, aggregation 4 stands out as the best alternative to the direct approach (Table 7).

Table 7 Revision history results summary using linked-chain dataset.

In terms of revision history, aggregate 4 stands as more stable than aggregation 6 for a very small difference in both trend-cycle and seasonally adjusted series, compared to the performance exhibited by the remaining aggregations. All aggregations have a smaller absolute average change compared to the 1986–2009 case, except for aggregation 3 which increases about seven times the average of trend-cycle series.¹¹

Fig. 3

Source: Author’s elaboration

Irregular component’s residual seasonality: rolling estimate of the AR(1) and AR(4) coefficients’ t-statistic. Shaded area  =  0  ${\pm }$  1.644 (null hypothesis rejection region).

Finally, the regression analysis of the residual seasonality check is presented in Fig. 3. All these figures describe an analogous situation to the 1986–2009 case. However, some minor details are noticed producing significant differences. For instance, demand-side aggregations 1 and 2 exhibit a better-behaved irregular component with linked-chain data, where both AR(1) and AR(4) are statistically non significant most of the time—a fact not observed with the 1986–2009 dataset. Aggregations 3 and 5 remain equal, describing a deficient performance where both parameters are statistically significant and, therefore, a systematic dynamic is still present. Aggregations 4 and 6 show a similar pattern to the previous case, whereas aggregation 4 marginally improves delivering a non-significant AR(4) coefficient since 2006 onwards.

In sum, aggregation 4 stands out as the best alternative to the direct method using both kinds of datasets. When using the 1996–2017 dataset, aggregation 4 becomes even more stable according to some diagnostics to aggregation 6; therefore, recommending its use for econometric applications and conjunctural assessment.

4 Concluding Remarks

This paper addresses the question of which aggregation scheme provides the best results for an overall seasonal adjusting process for the Chilean GDP 1986–2009 (base year: 2003) using the X-12-ARIMA program version 0.2.10. These are understood as the best results that achieve the most stability in the resulting series. This stability is tested with specific tools contained in the X-12-ARIMA program; specifically, spectral plots, sliding spans, and revision history. I also make use of bias significance to statistically assess the distance to the direct method. The key is to always bear in mind the goal of the absence of residual seasonality; that is, absence of seasonality in series that theoretically should not have it, which is analyzed through a rolling regression exercise. Finally, the exercise is re-done using the linked-chain dataset using a 1996–2017 sample (base year: 2013)—with evident aggregation bias in the aggregation schemes.

Spectral plots are used commonly to analyze a series through its frequency domain. It is used in this context as a model-free diagnostic to associate the cycles of series with their strengths. Therefore, spectral plots for final seasonally adjusted series as well as for irregular components are especially useful to detect residual seasonality. Hence, it evaluates the quality of the overall process. Sliding-span diagnostics and revision history can be seen as pure stability measures. Sliding spans allow the user to detect unstable passages of the sample, indicating also if a user’s intervention is required. Revision history quantifies how reliable the adjustment applied to certain series is as the sample is increasing in length. Regression-based results are useful for both instability and the detection of residual seasonality, which in this case, is tested on the irregular component.

The results show that, in terms of stability, the use of the first stage of disaggregation by supply-side is recommended. Moreover, the results for the second and third stages of disaggregation by demand-side are very poor, according to the standard setup used for the adjustment. These results are not surprising at all, given that the aggregation made by supply side already groups components with more affine dynamics, with a small number of atypical values and virtually without residual seasonality. Regarding methodological issues, particularly powerful tools to discriminate between stable aggregations are spectral plots and sliding spans, both estimated to the final seasonally adjusted series. When using the linked-chain dataset the results are plainly supporting of those previously obtained.

This exercise is relevant for several reasons. First, since 2009 the GDP dataset is released under the linked-chain methodology, losing its additive property. Therefore, this exercise should be read as a benchmark for further extensions beyond that offered in this article. Second, to have an informed opinion on the reliability of seasonally adjusted disaggregations that compound total GDP. This is relevant for conjunctural economic assessment, as it concerns signal extraction from seasonal, noisy series; direction of change detection; and econometric applications using seasonal variables. Third, policymakers whose effectiveness is strongly attached to the current business cycle outlook, should be aware of the sources of instability and the difficulties in obtaining reliable information from both demand and supply side.

Finally, several topics emerge for future investigation. Especially relevant are the calibration of some thresholds used by diagnostics to certain, and relevant, cases as Chilean GDP, or if there are cross-sector differences in the thresholds used.

Appendices

Chilean GDP by Demand Side

See Table 8.

Table 8 Chilean GDP in levels by demand side.

Chilean GDP by Supply Side

See Table 9.

Table 9 Chilean GDP in levels by supply side.

Shares of Sectorial Components on Real GDP

See Table 10.

Table 10 Shares of sectorial components on real GDP of 2003 (average of the base year).

Typical Statistics of Time Series

See Tables 11 and 12.

Table 11 Typical statistics of demand side series, full sample.

Table 12 Typical statistics of supply side series, full sample.

GDP Components: Original Series in Levels

See Fig. 4.

Fig. 4

Source: Author’s elaboration based on Central Bank of Chile’s database

Chilean GDP—Original series in logarithmic levels.

Diagnostic Result 1

1.1 Spectral Plots of Final Seasonally Adjusted and Irregular Series

See Figs. 5 and 6.

Fig. 5

Source: Author’s elaboration

Spectral plots of final seasonally adjusted series. 10 ${\times }$ (log-diff.). Bartlett window length = 30.

Fig. 6

Source: Author’s elaboration

Spectral plots of irregular series. Bartlett window length = 30.

Diagnostic Result 3

1.1 Revision History of Trend-Cycle and Final Seasonally Adjusted Series

See Figs. 7 and 8.

Fig. 7

Source: Author’s elaboration

Revision history of trend-cycle series (log-differenced). ${\blacktriangledown }$ = Most recent.

Fig. 8

Source: Author’s elaboration

Revision history of seasonally adjusted series (log-differenced). Aggregation 3 contains an outlier at 2008.III: from − 106.9 (concurrent) to − 0.4 (most recent) ${\blacktriangledown }$ = Most recent.

Diagnostic Result 1: Linked-Chain Dataset

1.1 Spectral Plots of Final Seasonally Adjusted and Irregular Series

See Fig. 9 and 10.

Fig. 9

Source: Author’s elaboration

Spectral plots of final seasonally adjusted series. 10 ${\times }$ (log-diff.). Bartlett window length = 30.

Fig. 10

Source: Author’s elaboration

Spectral plots of irregular series. Bartlett window length = 30.