On estimation of measurement error models with replication under heavy-tailed distributions

Abstract

Measurement error (errors-in-variables) models are frequently used in various scientific fields, such as engineering, medicine, chemistry, etc. In this work, we consider a new replicated structural measurement error model in which the replicated observations jointly follow scale mixtures of normal (SMN) distributions. Maximum likelihood estimates are computed via an EM type algorithm method. A closed expression is presented for the asymptotic covariance matrix of those estimators. The SMN measurement error model provides an appealing robust alternative to the usual model based on normal distributions. The results of simulation studies and a real data set analysis confirm the robustness of SMN measurement error model.

1 Introduction

It is often assumed in classical statistical regression models that the covariates or explanatory variables are observed exactly. However, this assumption can be challenged since observed values of variables can often be considered error-prone measurements of the true covariates. Dramatically, ignoring such errors in covariates usually results in biased estimates of the regression coefficients. As a more realistic representation of classical regression models, measurement error (errors-in-variables) models assume that the independent variables are subject to error. A comprehensive study in measurement error models (MEM) can be found in Fuller (1987), Cheng and Van Ness (1999) and Carroll et al. (2006).

The linear MEM can be described as follows,

$$\begin{aligned} x_t=\xi _t+\delta _t, y_t=\eta _t+\varepsilon _t, \eta _t=\alpha +\beta \xi _t, \quad t=1,\ldots ,n, \end{aligned}$$

(1)

where $(x_t, y_t)$ are observed values, which are equal to true (latent) unobserved variables $(\xi _t,\eta _t)$ plus the additive measurement errors $(\delta _t,\varepsilon _t)$. The latent variables $\xi _t$ can be regarded as fixed unknown parameters (a functional model), or as independent, identically distributed random variables (a structural model). In this work, we only focus on the structural type model. As Reiersol (1950) showed, when normality is assumed, this model is not identifiable unless further information about the parameters can be found. This occurs because one can not establish a single relationship between the parameters of the distribution for $(x_t,y_t)$ and the parameters of the model. A common solution of this problem is to assume some prior knowledge about the error variance (Cheng and Van Ness 1999). However, the non-identifiability issue will not appear in the replicated measurement error model (RMEM), in which the error variances can be estimated through the replicated data. Maximum likelihood (ML) estimation of the replicated structural model under normal distributions was solved by Chan and Mak (1979) and Isogawa (1985). Recently, Lin et al. (2004) derived an iterative EM algorithm to compute the ML estimators of the replicated model also under the normal distribution. However, the normality assumption is doubtful and suffers from a lack of robustness against outlying observations on the parameter estimates. Hence, it is very important to develop more robust model to fit the replicated measurement error data.

In this paper, we will assume scale mixtures of normal (SMN) distributions (Andrews and Mallows 1974) for the accommodation of extreme and outlying observations in RMEM. As the most important subclass of the elliptical symmetric distributions (Fang et al. 1990), the class of SMN distributions is a very flexible extension of normal distribution. Models based on SMN distributions will present more appealing robustness compared to the normal ones. Details about SMN distributions can be found in Andrews and Mallows (1974), Fang et al. (1990) and Lange and Sinsheimer (1993). Recently, SMN distributions have been applied to some special MEM. For example, Osorio et al. (2009) studied estimation and influence diagnostics for the Grubbs’ model under SMN distributions; same issues on non-replicated MEM model based on SMN distributions are investigated by Lachos et al. (2011). Furthermore, scale mixtures of the skew-normal distributions have also been applied to MEM by Lachos et al. (2010). In this work, we discuss the ML estimation of RMEM, where the replicated observed values jointly follow SMN distributions. The hierarchical representation proposed by Pinheiro et al. (2001) is considered, which make it convenient to apply the EM algorithm for parameter estimation.

The rest of this paper is organized as follows. A brief sketch of SMN distributions is presented in Sect. 2. In Sect. 3, the replicated structural measurement error model with scale mixtures of normal distributions (SMN-RMEM) is defined, and an EM-type algorithm is applied to obtain the maximum likelihood estimates. A closed form expression is also obtained for the asymptotic covariance matrix of the ML estimators. Results of simulation studies are reported in Sect. 4. In Sect. 5, the CSFII (Continuing Survey of Food Intakes by Individuals) data (Thompson et al. 1992) is analyzed under the proposed SMN-RMEM. Some concluding remarks are given in the last section.

2 SMN distributions

SMN distributions, which play very important roles in statistical modeling, can be defined as the following $m$-dimensional random vector

$$\begin{aligned} Y=\varvec{\mu }+\kappa ^{1/2}(V)W, \end{aligned}$$

(2)

where $\varvec{\mu }$ is an $m$-dimensional location vector, $W$ is an $m$-dimensional normal random vector with mean vector $\mathbf 0$, and covariance matrix $\Sigma$, and $\kappa (\cdot )$ is a strictly positive weight function which is associated to the independent mixture variable $V$, a positive random variable with cumulative distribution function $H(v;\nu )$. It is easy to see from (2) that, the conditional distribution of $Y$ given $V$ is a multi-normal distribution, i.e., $Y|V=v\sim \text{ N}_m(\varvec{\mu },\kappa (v)\Sigma )$. Therefore, the marginal density function of $Y$ takes the form as

$$\begin{aligned} f(\varvec{y})=|2\pi \Sigma |^{-1/2} \int \limits _{0}^{\infty }{\{\kappa (v)\}^{-m/2}\exp \{-\kappa ^{-1}(v)u/2\}}dH(v), \end{aligned}$$

(3)

where $u=(\varvec{y}-\varvec{\mu })^{\top }\Sigma ^{-1}(\varvec{y}-\varvec{\mu })$ is the Mahalanobis distance. If $Y$ has the form as (2) or has the density as (3), we will denote $Y\sim \text{ SMN}_m(\varvec{\mu },\Sigma ;H)$. Owing to its special structure, the class of SMN distributions has similar properties to the normal distribution. With a suitable choice of $\kappa (\cdot )$ and the distribution function $H(\cdot ;\nu )$, many heavy-tailed distributions can be generated, which are very useful for robust inference. Note that when $\kappa (\cdot )=1$, the distribution of $Y$ is just the normal one (N-SMN). Members of SMN distributions may be found, for instance, in Andrews and Mallows (1974). Here, three important examples are listed and will be applied in our study. We also compute the conditional expectation $\text{ E}[\kappa ^{-1}(V)|Y]$ under the following distributions, which is helpful to carry out the EM algorithm.

(i) Multivariate Student-$t$ distribution (T-SMN)

The multivariate Student-$t$ distribution (Cornish 1954, Dunnett and Sobel 1954) with $\nu$ degrees of freedom, $t_m(\varvec{\mu },\Sigma ;\nu )$, can be derived from the mixture structure (2), by taking $\kappa (v)=1/v$ and $V\sim Gamma(\nu /2,\nu /2)$. The Cauchy distribution is obtained when $\nu =1$, and one also gets the normal distribution when $\nu \rightarrow \infty$. In this case, the conditional expectation is

$$\begin{aligned} \text{ E}[\kappa ^{-1}(V)|Y]=\frac{\nu +m}{\nu +u}, \end{aligned}$$

where $u$ is the Mahalanobis distance we mentioned above.

(ii) Slash distribution (S-SMN)

To get the multivariate slash distribution (Rogers and Tukey 1972), denoted by $\text{ SL}_m(\varvec{\mu },\Sigma ;\nu )$, one needs to take $\kappa (v)=1/v$ and $V\sim Beta(\nu ,1)$, which has the density function as

$$\begin{aligned} h(v;\nu )=\nu v^{\nu -1},\quad 0<v\le 1, \nu >0. \end{aligned}$$

It follows that

$$\begin{aligned} \text{ E}[\kappa ^{-1}(V)|Y]=\left(\frac{2\nu +m}{u}\right) \frac{P_1(m/2+\nu +1,u/2)}{P_1(m/2+\nu ,u/2)}, \end{aligned}$$

where $P_x(a,b)$ denotes the cumulative distribution function of the $Gamma(a,b)$ distribution, i.e.,

$$\begin{aligned} P_x(a,b)=\frac{b^a}{\Gamma (a)}\int \limits _{0}^{x} t^{a-1}e^{-bt}dt. \end{aligned}$$

(iii) Contaminated normal distribution (C-SMN)

The multivariate contaminated normal distribution (Tukey 1960), $\text{ CN}_m(\varvec{\mu },\Sigma ;\nu ,\gamma )$, can be obtained from (2) by taking $\kappa (v)=1/v$, and supposing $V$ follows a discrete random probability function

$$\begin{aligned} h(v;\nu ,\gamma )=\nu \text{ I}(v=\gamma )+(1-\nu )\text{ I}(v=1),\quad 0\le \nu \le 1, 0<\gamma \le 1. \end{aligned}$$

The density of $Y$ has a mixture form as

$$\begin{aligned} f(\varvec{y})=|2\pi \Sigma |^{-1/2}[\nu \gamma ^{m/2}e^{-\gamma u/2} +(1-\nu )e^{-u/2}], \end{aligned}$$

and the conditional expectation is

$$\begin{aligned} \text{ E}[\kappa ^{-1}(V)|Y]=\frac{1-\nu +\nu \gamma ^{m/2+1}e^{(1-\gamma )u/2}}{1-\nu +\nu \gamma ^{m/2}e^{(1-\gamma )u/2}}. \end{aligned}$$

3 Estimation of SMN-RMEM model

In this section, we will describe the SMN-RMEM model and investigate the EM algorithm and asymptotic covariance for the parameter estimators.

3.1 The SMN-RMEM model

Consider a bivariate random variable $(\xi ,\eta )$ satisfying a linear relationship $\eta =\alpha +\beta \xi$, in which $\xi$ and $\eta$ cannot be observed directly and we observe the values of $x=\xi +\delta$ and $y=\eta +\varepsilon$ with measurement errors $\delta$ and $\varepsilon$. For each $\xi$ and $\eta$, $p$ and $q$ repeated observations $x_t^{(i)}, i=1,\ldots ,p$, $y_t^{(j)},j=1,\ldots ,q$ are obtained, respectively. Then the SMN-RMEM model is given by

$$\begin{aligned} x_t^{(i)}&= \xi _t+\delta _t^{(i)},\quad i=1,\ldots ,p,\nonumber \\ y_t^{(j)}&= \eta _t+\varepsilon _t^{(j)},\quad j=1,\ldots ,q,\\ \eta _t&= \alpha +\beta \xi _t, \quad t=1,\ldots ,n,\nonumber \end{aligned}$$

(4)

where $Z_t=(x_t^{(1)},\ldots ,x_t^{(p)},y_t^{(1)},\ldots ,y_t^{(q)})^{\top }$ follows a SMN distribution, with the hierarchical structure form, which based on the suggestion of Pinheiro et al. (2001), as

$$\begin{aligned} Z_t|\xi _t,v_t&\stackrel{ind}{\sim }&\text{ N}_{m}(\varvec{a}+\varvec{b}\xi _t,\kappa (v_t)\varvec{D}(\varvec{\phi })),\nonumber \\ \xi _t|v_t&\stackrel{ind}{\sim }&\text{ N}(\lambda ,\kappa (v_t)\phi _{\xi }),\ v_t\stackrel{iid}{\sim } H(v;\nu ),\ t=1,\ldots ,n, \end{aligned}$$

(5)

where $m=p+q$, $\varvec{a}=(\stackrel{p}{\overbrace{0,\ldots ,0}},\alpha \varvec{1}_q^{\top })^{\top }$, $\varvec{b}=(\varvec{1}_p^{\top },\beta \varvec{1}_q^{\top })^{\top }$, in which $\varvec{1}_p$ and $\varvec{1}_q$ are, respectively, $p$- and $q$-dimensional vector with all elements are equal to 1, $\varvec{\phi }=(\phi _{\delta }\varvec{1}_p^{\top }, \phi _{\varepsilon }\varvec{1}_q^{\top })^{\top }$, and $\varvec{D}(\cdot )$ denotes the diagonal transformation which transforms a vector to a diagonal matrix. In fact, it can be inferred from above that $Z_t\stackrel{iid}{\sim } \text{ SMN}_{m}(\varvec{\mu },\Sigma ;H)$, where the location and scale parameter can be expressed as $\varvec{\mu }=(\lambda \varvec{1}_p^{\top },(\alpha +\beta \lambda )\varvec{1}_q^{\top })^{\top }$, $\Sigma =\phi _{\xi }\varvec{b}\varvec{b}^{\top }+\varvec{D}(\varvec{\phi })$. Note that, model (4) is the same as model (1) when $p=q=1$.

3.2 EM algorithm

As a special case, Lin et al. (2004) obtained ML estimators through an EM iteration for model (4) under normal distributions. Due to the hierarchical structure of (5), it is natural to also use the EM algorithm (Dempster et al. 1977, McLachlan and Krishnan 1997) to calculate the ML estimates of the parameters.

Let $\varvec{\theta }=(\lambda ,\alpha ,\beta ,\phi _\delta ,\phi _{\varepsilon }, \phi _{\xi })^{\top }$ be the parameter vector of model (4), and $\varvec{\theta }^{(k)}$ denotes the estimates of $\varvec{\theta }$ at the $k$-th iteration. Let $Z_c=(Z,\varvec{\xi },\varvec{v})$ be the complete data set of model (4), where $Z=(Z_1^{\top },\ldots ,Z_n^{\top })^{\top }$, $\varvec{\xi }=(\xi _1,\ldots ,\xi _n)^{\top }$ and $\varvec{v}=(v_1,\ldots ,v_n)^{\top }$. It follows from (5) that the complete log-likelihood function associated with $Z_c$ has the form as

$$\begin{aligned} l_c(\varvec{\theta }|Z_c)&=-\frac{n}{2}\log \big (|\varvec{D}(\varvec{\phi })|\big ) \!-\!\frac{1}{2}\sum _{t=1}^{n}\kappa ^{-1}(v_t)(Z_t-\varvec{a} \!-\!\varvec{b}\xi _t)^{\top }\varvec{D}^{-1}(\varvec{\phi })(Z_t-\varvec{a} \!-\!\varvec{b}\xi _t)\\&\quad -\frac{n}{2}\log (\phi _{\xi })-\frac{1}{2\phi _{\xi }}\sum _{t=1}^{n} \kappa ^{-1}(v_t)(\xi _t-\lambda )^2+C, \end{aligned}$$

where $\log (|\varvec{D}(\varvec{\phi })|)=p\log (\phi _{\delta }) +q\log (\phi _{\varepsilon })$, and $C$ is a constant that is independent of $\varvec{\theta }$. The EM algorithm is listed as follows.

E-step: Given the current estimate $\varvec{\theta }^{(k)}$, the expected complete data log-likelihood function $\text{ E}[l_c(\varvec{\theta }|Z_c)|\varvec{\theta }^{(k)},Z]$, also called the $Q$-function in Dempster et al. (1977), may be expressed as

$$\begin{aligned} Q(\varvec{\theta }|\varvec{\theta }^{(k)})&= \!-\!\frac{n}{2}\log \big (|\varvec{D}(\varvec{\phi })|\big )\!-\!\frac{1}{2}\sum _{t=1}^{n} \kappa _t^{(k)}(Z_t-\varvec{a}-\varvec{b}\xi _t^{(k)})^{\top }\varvec{D}^{-1}(\varvec{\phi }) (Z_t\!-\!\varvec{a}\!-\!\varvec{b}\xi _t^{(k)})\\&-\frac{1}{2}\sum _{t=1}^{n} \tau ^{(k)}\varvec{b}^{\top }\varvec{D}^{-1}(\varvec{\phi })\varvec{b} \!-\!\frac{n}{2}\log (\phi _{\xi })\!-\!\frac{1}{2\phi _{\xi }}\sum _{t=1}^{n} \Big [\kappa _t^{(k)}(\xi _t^{(k)}\!-\!\lambda )^2+\tau ^{(k)}\!\Big ]. \end{aligned}$$

where $\kappa _t^{(k)}=\text{ E}[\kappa ^{-1}(v_t)|\varvec{\theta }^{(k)},Z_t]$, $\tau ^{(k)}=\phi _{\xi }^{(k)}/S^{(k)}$ with $S^{(k)}=1+\phi _{\xi }^{(k)}\varvec{b}^{(k)\top } \varvec{D}^{-1}(\varvec{\phi }^{(k)})\varvec{b}^{(k)}$, and $\xi _t^{(k)}=\lambda ^{(k)}+\tau ^{(k)}\varvec{b}^{(k)\top } \varvec{D}^{-1}(\varvec{\phi }^{(k)})(Z_t-\varvec{a}^{(k)}-\varvec{b}^{(k)}\lambda ^{(k)})$.

M-step: Based on the $Q$-function, a new parameter estimate $\varvec{\theta }^{(k+1)}$ can be obtained by maximize $Q(\varvec{\theta }|\varvec{\theta }^{(k)})$ with respect to $\varvec{\theta }$. The details of these steps are described as follows.

Firstly, the regression coefficients are updated by

$$\begin{aligned} \alpha ^{(k+1)}&= {(b_1^{(k)}a_{22}^{(k)}-b_2^{(k)}a_{12}^{(k)})}\big / (a_{11}^{(k)}a_{22}^{(k)}-a_{12}^{2(k)}),\\ \beta ^{(k+1)}&= (b_2^{(k)}a_{11}^{(k)}-b_1^{(k)}a_{12}^{(k)})\big / (a_{11}^{(k)}a_{22}^{(k)}-a_{12}^{2(k)}), \end{aligned}$$

where $a_{11}^{(k)}=\sum _{t=1}^{n}\kappa _t^{(k)}$, $a_{22}^{(k)}=n\tau ^{(k)}+\sum _{t=1}^{n}\kappa _t^{(k)}\xi _t^{2(k)}$, $a_{12}^{(k)}=\sum _{t=1}^{n}\kappa _t^{(k)}\xi _t^{(k)}$, $b_1^{(k)}=\sum _{t=1}^{n}\kappa _t^{(k)}\overline{y}_t$, $b_2^{(k)}=\sum _{t=1}^{n}\kappa _t^{(k)}\xi _t^{(k)}\overline{y}_t$, and $\overline{y}_t=\sum _{j=1}^{q} y_t^{(j)}/q$.

Then, other parameters can be updated by the following equations:

$$\begin{aligned} \lambda ^{(k+1)}&= a_{12}^{(k)}/a_{11}^{(k)},\ \phi _{\xi }^{(k+1)}=\tau ^{(k)}+\frac{1}{n} \sum _{t=1}^{n}\kappa _t^{(k)}(\xi _t^{(k)}-\lambda ^{(k+1)})^2,\\ \phi _{\varepsilon }^{(k+1)}&= \tau ^{(k)}(\beta ^{(k+1)})^2 +\sum _{t=1}^{n}\kappa _t^{(k)}\left[\sum _{j=1}^{q}(y_t^{(j)} -\alpha ^{(k+1)}-\beta ^{(k+1)}\xi _t^{(k)})^2\right],\\ \phi _{\delta }^{(k+1)}&= \tau ^{(k)}+\frac{1}{np}\sum _{t=1}^{n} \kappa _t^{(k)}\left[\sum _{i=1}^{p}(x_t^{(i)}-\xi _t^{(k)})^2\right]. \end{aligned}$$

Starting with a suitable initial vector value $\varvec{\theta }^{(0)}$, the algorithm iterates between the E- and M-steps until it reaches convergence. To ensure it is positive, the inverse of matrix $\Sigma$ used in each E-step is computed by a closed form (Harville 1997) as

$$\begin{aligned} \Sigma ^{-1}=\varvec{D}^{-1}(\varvec{\phi })-\varvec{D}^{-1}(\varvec{\phi })\varvec{b} \varvec{b}^{\top }\varvec{D}^{-1}(\varvec{\phi }) /(\phi _{\xi }^{-1}+\varvec{b}^{\top }\varvec{D}^{-1}(\varvec{\phi })\varvec{b}). \end{aligned}$$

3.3 The expected information matrix

Since the SMN distributions belong to the elliptical distribution class (Fang et al. 1990), the replicated observations $Z_t$ of model (4) can also be regarded as following an elliptical distribution $\text{ EL}_m(\varvec{\mu },\Sigma ,g)$, where $\varvec{\mu }$ and $\Sigma$ are the same as those in Sect. 3.1, and $g(\cdot ): \mathbb R \rightarrow [0,\infty )$ is called the density generator such that $\int _0^{\infty }{g(u)du}<\infty$. Hence, the density function of $Z_t$ takes the form

$$\begin{aligned} f(Z_t)=|\Sigma |^{-1/2}g(u_t),\ t=1,\ldots ,n, \end{aligned}$$

where $u_t=(Z_t-\varvec{\mu })^{\top }\Sigma ^{-1}(Z_t-\varvec{\mu })$, and $g(u_t)$ can be expressed as

$$\begin{aligned} g(u_t)=(2\pi )^{-m/2}\int \limits _0^{\infty } {\kappa (v)}^{-m/2}\exp \{-\kappa ^{-1}(v)u_t/2\}dH(v). \end{aligned}$$

The log-likelihood function for model (4) is given by

$$\begin{aligned} l(\varvec{\theta })=-\frac{n}{2} \log (|\Sigma |)+ \sum _{t=1}^n \log \{g(u_t)\}, \end{aligned}$$

(6)

By calculating the expectations of the second-order derivatives of (6), we obtain the Fisher information matrix of $\varvec{\theta }$ as $\mathbf I (\varvec{\theta })=(\text{ I}_{ij})_{6\times 6}$, with

$$\begin{aligned} \text{ I}_{ij}&= \frac{4n}{m}d_g\dot{\varvec{\mu }}_i^{\top }\Sigma ^{-1} \dot{\varvec{\mu }}_j, \ i\le 3,\ j\le 3,\quad \text{ and}\quad (i,j)\ne (3,3);\\ \text{ I}_{ij}&= na\text{ tr}(\Sigma ^{-1}\dot{\Sigma }_i\Sigma ^{-1}\dot{\Sigma }_j) +nb\text{ tr}(\Sigma ^{-1}\dot{\Sigma }_i)\text{ tr}(\Sigma ^{-1}\dot{\Sigma }_j),\\&\ i\ge 3,\ j\ge 3,\quad \text{ and}\quad (i,j)\ne (3,3);\\ \text{ I}_{33}&= \frac{4n}{m}d_g\dot{\varvec{\mu }}_3^{\top }\Sigma ^{-1} \dot{\varvec{\mu }}_3 +na\text{ tr}(\Sigma ^{-1}\dot{\Sigma }_3\Sigma ^{-1}\dot{\Sigma }_3) +nb\text{ tr}^2(\Sigma ^{-1}\dot{\Sigma }_3);\\ \text{ I}_{ij}&= 0, \ \text{ for}\ i\le 2,\ j\ge 4 \ \text{ or}\ i\ge 4,\ j\le 2, \end{aligned}$$

where $a=\frac{2f_g}{m(m+2)}$, $b=\frac{f_g}{m(m+2)}-\frac{1}{4}$, $f_g=\text{ E}\{W_g^2(u)u^2\}$, $d_g=\text{ E}\{W_g^2(u)u\}$, in which $W_g(u)=\frac{\dot{g}(u)}{g(u)}$ with $u=\varvec{e}^{\top }\varvec{e}$ and $\varvec{e}\sim \text{ EL}_m(\varvec{0},I_m)$, $\dot{\varvec{\mu }}_i=\partial \varvec{\mu }/ \partial \theta _i$ and $\dot{\Sigma }_i=\partial \Sigma /\partial \theta _i$.

Due to the similarity between the inference for elliptical models and normal models, it is reasonable to expect that under suitable regularity conditions, the approximate distribution of the ML estimator $\widehat{\varvec{\theta }}$ in large samples is $\text{ N}_6(\varvec{\theta }, \mathbf I ^{-1}(\varvec{\theta }))$. Hence, the variance-covariance matrix of $\widehat{\varvec{\theta }}$ can be estimated by $\mathbf I ^{-1}(\widehat{\varvec{\theta }})$.

4 Simulation study

In this section, we perform Monte-Carlo simulations to compare the performance of the ML estimators of RMEM under four different type SMN distributions: N-SMN, T-SMN, S-SMN and C-SMN. Note that all of the other three distributions have heavier tails than the normal one, which indicates that statistical models based on those distributions are more robust to outliers. The degrees of freedom are set as follows: $\nu =4$ (for T-SMN), $\nu =3$ (for S-SMN) and $\nu =0.1$, $\gamma =0.2$ (for C-SMN). Other parameters in model (4) are set as: $\lambda =3$, $\alpha =2$, $\beta =1$, $\phi _{\delta }=1$ and $\phi _{\xi }=1$. The values of $\phi _{\varepsilon }$ has two values for comparison: 1 and 0.2, corresponding to the ratio of the error variances $\phi _{\varepsilon }/\phi _{\delta }$ of 1 and 0.2, respectively. The replicated numbers of the observations are chosen as $p=3$ and $q=2$.

In order to maintain the general and consistent form of the estimators among different SMN distributions, the degrees of freedom for the SMN model will not be estimated together with the interested parameters. In the simulation study, the main motivation is to confirm the heavy-tailed model’s robustness and accuracy. Hence, we selected some heavy-tailed distributions with fixed degrees of freedom. While in the application, to find the best distribution for the data, we will choose the degrees of freedom by some usual criterions.

4.1 The first simulation

It is well known that misspecification of model’s distribution will lead to the biases of parameter estimates. In the first simulation, we want to show that the ML estimates based on the heavy-tailed RMEMs will be more accurate than normal ones, when the true distribution of the data is heavy-tailed. In this simulation, we independently generate 2000 random samples with sample sizes $n=20$, 50, and 100 from model (4) under one of the four SMN distributions. Then, we compute the ML estimators of $\varvec{\theta }$ through the EM algorithm under all the four SMN distributions, respectively. Tables 1, 2, 3 and 4 display both the simulated sample means and standard deviations (SD) of interesting parameters $\lambda$, $\alpha$ and $\beta$, under simulated datasets generated by four different SMN distributions, respectively.

Some valuable conclusions can be drawn from the simulation study. For each case, the bias and the SD values are almost smallest when the true distribution is used. As expected, the SD of all estimates become smaller as $n$ increases and as the variance radio $\phi _{\varepsilon }/\phi _{\delta }$ decreases. The most important information of Tables 2, 3 and 4 is that, when one of the three heavy-tailed distributions is assumed, the estimators under the normal distribution are worst at all times, since their SD values are largest among all estimators based on the four distributions. It is confirmed that RMEM under heavy-tailed distributions are more effective than the normal one, even if the distribution we used is not the true distribution.

Table 1 Performance of estimators under N-SMN-RMEM datasets

Table 2 Performance of estimators under T-SMN-RMEM datasets

Table 3 Performance of estimators under S-SMN-RMEM datasets

Table 4 Performance of estimators under C-SMN-RMEM datasets

4.2 The second simulation

In the second simulation, we will compare the performance of the estimators based on different methods in the presence of outliers. Regression calibration (RC) is also considered in the simulation. RC is an important estimation method for the MEM which can correct biases of the naive estimators. Details of this method may be found, for instance, in Carroll et al. (2006). Note that, we use analysis of variance formulae to get the consistent estimates of $\lambda$ and variance components $\phi _{\delta }$ and $\phi _{\xi }$. Then, the RC estimator is obtained based on the adjustment of regression on averages of the observed variables, which is the same as the adjusting ordinary least squares mentioned in Lin et al. (2004).

We first generate 1,000 datasets with sample sizes $n=50$ and $100$ from model (4) under normal distribution. Similar to Vanegas and Cysneiros (2010), we shift the observed value $x_t^{(i)}$ to $x_t^{(i)}+\lambda d$, where $t=n/2$ and $d=0,0.5,1,\ldots ,5$ to guarantee the presence of one outlier in the individuals. For each data set, we calculate all the five estimators (ML estimators based on four type SMN-RMEMs, and the RC estimators) of $\alpha$, $\beta$ and $\lambda$ under the shifted and non-shifted data, respectively. Then, we compute the relative changes of the estimates (i.e., $|(Est_{(s)}-Est)/Est|$, where $Est$ is the estimate under non-shifted data, $Est_{(s)}$ is the estimate under shifted data).

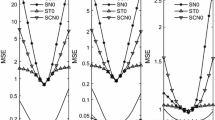
Figures 1, 2 and 3, respectively display the average relative changes on the estimates $\widehat{\alpha }$, $\widehat{\beta }$ and $\widehat{\lambda }$ at different values of $d$ under all the five estimation methods. In all situations, the change ratios of RC and N-SMN estimates increase with $d$, which indicates that the influence of the outlier become serious when $d$ increases for the RC and N-SMN estimates. On the contrary, the relative changes on the estimates based on T-SMN and S-SMN models are almost not increasing with $d$. Though the change ratios on the estimates based on C-SMN model show a slightly increasing trend with $d$, they are still much smaller than those on the RC and N-SMN estimates. As the sample size $n$ increases, we find that the influences of the outlier on the estimates become smaller for all the five estimates. However, the advantage of the robustness based on heavy-tailed models is still obvious. Thus, we draw a conclusion from the simulations that ML estimation method based on heavy-tailed SMSN-RMEM is more appealing since it can present more robustness compared to the traditional normal ones and the RC method.

Fig. 1

Average relative changes of $\widehat{\alpha }$ under five estimation methods

Fig. 2

Average relative changes of $\widehat{\beta }$ under five estimation methods

Fig. 3

Average relative changes of $\widehat{\lambda }$ under five estimation methods

5 Application

In this section, we consider the CSFII data (Thompson et al. 1992) as a numerical example. This dataset has also been used by Carroll et al. (2006) as an additional information to analyze the NHANES data (Jones et al. 1987). The CSFII data contains the 24-h recall measures, as well as three additional 24-h recall phone interviews of 1,722 women who were recorded about their diet habits. We consider the calorie intake/5,000 as $\xi$, and the saturated fat intake/100 as $\eta$. Instead of $\xi$ and $\eta$, the nutrition variables $x$ and $y$ are computed by four 24-h recalls, which are supposed to follow model (4) with $p=q=4$.

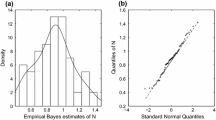
Figure 4 displays the linear tendency between the average calories ($\bar{x}$) and the average saturated fat ($\bar{y}$). The QQ plot of the differences between replicates $x_t$ and between replicates $y_t$ are given in Fig. 5a, b, respectively, which show that non-normality is evident in the presence of heavier-than-normal tails. If the CSFII data we used follows a normal RMEM, then it is true that $\{u_t=(Z_t-\varvec{\mu })^{\top }\Sigma ^{-1}(Z_t-\varvec{\mu }),\ t=1,\ldots ,1{,}722\}$ are mutually independent and follow a chi-square distribution with 8 degrees of freedom. By applying the Wilson-Hilferty transformation (Johnson et al. 1994), we obtain a set of $iid$ variables $\{r_t=3u_t^{1/3}-35/6,\ t=1,\ldots ,1{,}722\}$ which approximately follows the standard normal distribution. The QQ plot of $\{r_t,\ t=1,\ldots ,1{,}722\}$ is shown in Fig. 5c, which gives obvious evidence against the normal assumption.

Fig. 4

The linear tendency and four fitted lines between the average calories and the average saturated fat

Fig. 5

QQ plots for the CSFII data: a differences between replicates of calorie intakes, b differences between replicates of saturated fat intakes, and c transformation of the Mahalanobis distances

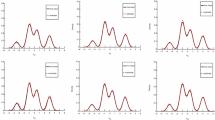
Now we consider the ML estimates for the CSFII data based on RMEM under four proposed SMN distributions. The degrees of freedom for T-SMN, S-SMN, and C-SMN distributions are selected by the Schwarz information criterion (Schwarz 1978). We plot the profile log-likelihood functions for the three models in Fig. 6. By getting the largest values of the profile log-likelihood, the degrees of freedom are found as $\nu \!=\!4.3$ for T-SMN, $\nu \!=\!1.3$ for S-SMN, and $\nu \!=\!0.29$, $\gamma \!=\!0.22$ for C-SMN.

Fig. 6

Degrees of freedom versus the profile log-likelihood under three heavy-tailed RMEMs, a T-SMN, b S-SMN, c, d C-SMN

Table 5 gives the ML estimates of parameter $\varvec{\theta }$ with standard errors in parenthesis, and also the AIC (Akaike 1974) and BIC (Schwarz 1978) values of the four SMN-RMEMs. The estimates of the scale parameters are not comparable among different distributions due to the different scales. Note that, the original AIC is used for model selection since the four type distributions we discussed are all members of the SMN distribution class. Compared with the conditional AIC (Vaida and Blanchard 2005), we prefer original AIC in this situation. First, in the RMEM, the most interest is in the population parameters $\alpha$ and $\beta$, and not in the individual clusters. Second, as we mentioned, the SMN distributions belong to the elliptical distribution family. The reason we use the SMN form to represent Student-$t$, slash and contaminated normal distribution is its hierarchical structure makes the EM algorithm become feasible. However, instead of the hierarchical form, the elliptical structure is still the major form of the RMEM model when we do other statistical inference.

From Table 5, we find that the standard errors of $\lambda$, $\alpha$ and $\beta$, and the values of AIC and BIC under the three heavy-tailed distributions are always smaller than those under the normal one, which indicates that the heavy-than-normal RMEMs fit the data better than N-SMN-RMEM. Moreover, it is suggested that T-SMN-RMEM is the best one among the four models, since it has the smallest values of BIC and standard errors of location parameters. It should be noted that the estimates of $\beta$ under three heavy-tailed models are all smaller than that under the normal one. This attenuation phenomenon is displayed in Fig.4, in which four regression lines between the average calories and the average saturated fat are plotted, based on the four models, respectively.

Table 5 Parameter estimators of the CSFII data under SMN-RMEM

6 Conclusions

In this work, we have discussed the ML estimations of the proposed SMN-RMEM. A major advantage of SMN model is its flexibility, due to it contains different types of distributions, which offers us the opportunity to compare with each other. Iterative equations are obtained to estimate the parameters of the model by the EM algorithm method. It is important to emphasize the capacity of this model to attenuate outlying observations by using heavy-tailed SMN distributions. Monte Carlo simulations displayed the robustness of heavy-tailed SMN-RMEM. A real data analysis also confirms some robustness aspects of our SMN-RMEM.