1 Introduction

With the development of social economy and the improvement of living standard, people’s dietary patterns have been greatly changed. Chronic diseases, such as hypertension, dyslipidemia, cardiovascular disease, diabetes mellitus, dietary obesity, have often appeared among different ages in the past decades. The food-consumption behavior and the nutrition arrangement have become hot issues in economical or medical researches (Gori and Sodini 2011; le Coutre et al. 2013, among others). Continuing Survey of Food Intakes by Individuals (CSFII), conducted annually by the US Department of Agriculture (USDA), gathers regular food-consumption information through 24-h individual recalls in 48 conterminous United States. These survey data primarily aim at assessing food consumption behavior and nutritional content of diets for policy implications with respect to food production and marketing, food safety, food assistance and nutrition education (Jacobs et al. 1998). For each CSFII survey, data collection starts in April of the given year and is finished in March of the following year. Harnack et al. (1999) analyzed CSFII data using a logistic regression model, while Carroll et al. (2006) used a similar data set, the National Health and Nutrition Examination Survey data (NHANES) (Jones et al. 1987), to model measurement error directly. In addition, Sun and Empie (2007) carried out a primary statistical analysis using population dietary survey databases of USDA CSFII combined with NHANES 1999–2002.

It is noted that during the process of data collection, measurement error (ME) would inevitably occur in observations of covariates as well as response variables. It may be caused by using different measurement methods and instruments or by human or other external factors. Just like the CSFII data, the ME appears in 24-h individual recalls due to randomness and unidentifiable systematic bias. Ignoring such errors would bring a certain degree of deviations to statistical inferences. As a special tool for handling ME, measurement error models (MEMs) have been comprehensively studied and discussed in literature, see for example, Fuller (1987), Cheng and Ness (1999) and Carroll et al. (2006). According to Reiersol (1950), there exists a non-identifiability problem in normal MEMs, and we have to make some assumptions on error variances in advance, while such assumptions are usually not easy to justify. Fortunately, this problem can be solved if we have replicated data, since the error variance can be estimated either separately or together with other parameters. In CSFII data, the long-term daily intake is measured by daily diets, which is collected repeatedly for several days. An abundant literature discussed the maximum likelihood estimation (MLE) for structural replicated measurement error model (RMEM) (Chan and Mak 1979; Isogawa 1985; Lin et al. 2004; Giménez and Patat 2005; Wimmer and Witkovský 2007; Bartlett et al. 2009, among others). But these studies were all under the normal distribution assumption. However, the normality assumption can be doubtful and the related model lacks robustness against departure from the normal distribution or outlying observations, which may result in misleading conclusions in practice. Recently, Lin and Cao (2013) took advantage of scale mixtures of normal (SMN) distributions for the accommodation of extreme and outlying observations in RMEM (SMN-RMEM) and derived an iterative formulas of MLE through expectation-maximization (EM) algorithm (Dempster et al. 1977; McLachlan and Krishnan 1997). SMN distributions, as a very flexible extension of normal distribution, was developed by Andrews and Mallows (1974), and contains Student t, slash, contaminated normal and other symmetric distributions (Fang et al. 1990; Lange and Sinsheimer 1993). A comprehensive list of applications on SMN distributions in MEMs can be found, for instance, in Osorio et al. (2009), Lachos et al. (2011) and Zeller et al. (2012). Cao et al. (2015) showed appealing robustness compared to normal ones for the multivariate RMEM. However, the SMN distributions may be violated when a data set contains asymmetric outcomes. Currently, a new class of robust distributions, called scale mixtures of skew-normal (SMSN) distributions, has been developed by Branco and Dey (2001) and becomes very attractive since it can model skewness and heavy tails simultaneously. It includes the whole symmetric family of SMN distributions and its skew version. More details about SMSN distributions can be found in Genton (2004). SMSN distributions have been applied into many models in recent years, for example, linear mixed models (Arellano-Valle et al. 2005; Jara et al. 2008; Lachos et al. 2010a), nonlinear regression models (Xie et al. 2008; Cancho et al. 2008; Cao et al. 2014), MEMs (Lachos et al. 2010b; Montenegro et al. 2010; Zeller et al. 2014).

In this paper, we will develop the RMEM under SMSN distributions (SMSN-RMEM). In particularly, the equation error is considered to cope with the random relationship between true covariates and response. In practice, the non-equation error model is often used in natural science, for instance, physics and chemistry, while the equation error model is frequently used in econometrics and the medical sciences (Cheng and Riu 2006). The presence of equation error could significantly affect the estimation results, as what we will discuss later in this paper. Using EM algorithm, we will calculate MLEs of SMSN-RMEMs with or without equation error. The proposed model shows its effectiveness and robustness of MLEs, which is confirmed by simulation studies and the application.

The rest of this paper is organized as follows. Section 2 gives a brief description of the SMSN distributions. Section 3 proposes the SMSN-RMEM and presents iterative formulas using EM algorithm. The observed information matrix as well as empirical Bayes estimations and predictions are also reported. In Sect. 4, the performance of the model and the importance of equation error are examined via simulation studies. Section 5 applies the model to analyze the inner relationship between saturated fat and caloric intake in CSFII data. Some conclusions are given in Sect. 6.

2 The Scale Mixtures of Skew-Normal Distributions

In this section, we give a brief description of the definition and properties of SMSN distributions. The details can been found in Branco and Dey (2001), Genton (2004) and Basso et al. (2010). An m-dimensional random vector \(\varvec{Y}\) has a skew-normal (SN) distribution, denoted by \(\varvec{Y}\sim SN _m(\varvec{\mu }, {\varvec{\Sigma }}, \varvec{\lambda })\), if its probability density function (pdf) is given by

$$\begin{aligned} f(\varvec{y})=2\phi _m(\varvec{y}|\varvec{\mu }, {\varvec{\Sigma }})\Phi (A), \end{aligned}$$
(1)

where \(\varvec{\mu }\) is an m-dimensional location vector, \({\varvec{\Sigma }}\) is a covariance matrix, \(\varvec{\lambda }\) is a skewness parameter vector and \(A=\varvec{\lambda }^{\top }{\varvec{\Sigma }}^{-1/2}(\varvec{y}-\varvec{\mu })\); \(\phi _m\) is the probability density function (pdf) of m-dimensional normal distribution while \(\Phi \) is the cumulative distribution function (cdf) of the standard normal distribution. The SMSN random vector \(\varvec{Y}\) can be expressed as

$$\begin{aligned} \varvec{Y}=\varvec{\mu }+\kappa ^{1/2}(U)\varvec{Z}, \end{aligned}$$

where \(\varvec{Z}\sim SN _m(\varvec{0},{\varvec{\Sigma }},\varvec{\lambda })\), \(\kappa (\cdot )\) is a strictly positive weight function, and U is a positive random variable with cdf \(H (\cdot ;\varvec{\nu })\) and pdf \(h(\cdot ;\varvec{\nu })\), independent of \(\varvec{Z}\). Here \(\varvec{\nu }\) is a scalar or vector indexing the distribution of U.

We now use the notation \(\varvec{Y}\sim SMSN _m(\varvec{\mu }, {\varvec{\Sigma }}, \varvec{\lambda }; H )\) to stand for scale mixtures of skew-normal distributions. Given \(U=u\), the conditional distribution of \(\varvec{Y}\) is a multi-SN distribution, i.e.,\(\varvec{Y}|U=u \sim SN _m(\varvec{\mu }, \kappa (u){\varvec{\Sigma }}, \varvec{\lambda })\). When \(\varvec{\lambda }=\varvec{0}\), SMSN distributions are deteriorated to SMN distributions \(SMN _m(\varvec{\mu }, {\varvec{\Sigma }};H )\).

Note that when \(\kappa (u)\equiv 1\), SMSN is a SN distribution. Another special case is the one with \(\kappa (u)=1/u\), i.e., the skew-normal/independent distribution (Lachos et al. 2010a). We define the conditional moments by

$$\begin{aligned} u_r=E \left[ \kappa ^{-r}(U)|\varvec{y}\right] ,\quad \eta _r=E \left[ \kappa ^{-r/2}(U)W_{\Phi }\left( \kappa ^{-1/2}(U)A\right) |\varvec{y}\right] , \end{aligned}$$

where \(W_\Phi (x)=\phi (x)/\Phi (x)\), \(x\in \mathbb {R}\). The pdf of \(\varvec{Y}\) and the conditional moments under some heavy-tailed SMSN distributions, such as the multivariate skew-Student t (ST), skew-slash (SS), skew-contaminated normal (SCN) distributions, are given in “Appendix A”.

3 Model Description and Parameter Estimation

Let x, y be the unobserved (true) covariate and response, respectively. They satisfy an incomplete linear relationship \(y=\alpha +\beta x+e\), in which the equation error e means that the true variables x and y are not perfectly related if other factors besides x are also accountable for the variation in y. We usually observe \(X=x+\delta \) and \(Y=y+\varepsilon \) with measurement errors \(\delta \) and \(\varepsilon \), as the surrogates of x and y. Suppose x and y are respectively observed p and q times to bring out replicated observations \(X_t^{(i)}, i=1,\ldots ,p\) and \(Y_t^{(j)}, j=1,\ldots ,q\). Then the SMSN-RMEM with equation error is given by

$$\begin{aligned} \begin{aligned} X_t^{(i)}=&\,x_t+\delta _t^{(i)},\ i=1,\ldots ,p,\\ Y_t^{(j)}=&\,y_t+\varepsilon _t^{(j)},\ j=1,\ldots ,q,\\ y_t=&\,\alpha +\beta x_t+e_t,\ t=1,\ldots ,n,\\ \end{aligned} \end{aligned}$$
(2)

where, \(\delta _t^{(i)}\), \(\varepsilon _t^{(j)}\) and \(e_t\) are uncorrelated each other, and

$$\begin{aligned}&\displaystyle U_t\mathop {\sim }\limits ^{iid}H \left( u;\varvec{\nu }\right) , \ t=1,\ldots ,n,\nonumber \\&\displaystyle x_t|U_t=u_t\mathop {\sim }\limits ^{ind}SN \left( \mu _x,\kappa (u_t)\phi _x,\lambda _x\right) , \ \text {i.e.}, x_t\mathop {\sim }\limits ^{iid}SMSN (\mu _x, \phi _x, \lambda _x; H ),\nonumber \\&\displaystyle \delta _t^{(i)}|U_t=u_t\mathop {\sim }\limits ^{ind}N (0,\kappa (u_t)\phi _{\delta }), \ \text {i.e.}, \delta _t^{(i)}\mathop {\sim }\limits ^{iid}SMN (0,\phi _{\delta };H ),\nonumber \\&\displaystyle \varepsilon _t^{(j)}|U_t=u_t\mathop {\sim }\limits ^{ind}N (0,\kappa (u_t)\phi _{\varepsilon }), \ \text {i.e.}, \varepsilon _t^{(j)}\mathop {\sim }\limits ^{iid}SMN (0,\phi _{\varepsilon };H ),\nonumber \\&\displaystyle e_t|U_t=u_t\mathop {\sim }\limits ^{ind}N (0,\kappa (u_t)\phi _e), \ \text {i.e.}, e_t\mathop {\sim }\limits ^{iid}SMN (0,\phi _e;H ). \end{aligned}$$

Note that the observation vector is \(\varvec{Z}_t={(\varvec{X}_t^{\top },\varvec{Y}_t^{\top })}^{\top }\), where \(\varvec{X}_t={(X_t^{(1)},\ldots ,X_t^{(p)})}^{\top }\) and \(\varvec{Y}_t={(Y_t^{(1)},\ldots ,Y_t^{(q)})}^{\top }\). Motivated by Montenegro et al. (2010) and Zeller et al. (2011), we express model (2) by the following hierarchical representation

$$\begin{aligned} \begin{aligned} \varvec{Z}_t|x_t,U_t=&\,u_t\mathop {\sim }\limits ^{ind}N _m(\varvec{a}+\varvec{b}x_t, \kappa (u_t){\varvec{\Sigma }}_1),\\ x_t|U_t=&\,u_t,V_t=v_t\mathop {\sim }\limits ^{ind}N (\mu _x+\tau _x v_t,\kappa (u_t)\gamma _x),\\ V_t|U_t=&\,u_t\mathop {\sim }\limits ^{ind}HN (0,\kappa (u_t)),\\ U_t\mathop {\sim }\limits ^{iid}&H (u; \varvec{\nu }), \end{aligned} \end{aligned}$$
(3)

where \(m=p+q\), \(\varvec{a}={(\varvec{0}_p^{\top },\alpha \varvec{1}_q^{\top })}^{\top }\), \(\varvec{b}={(\varvec{1}_p^{\top },\beta \varvec{1}_q^{\top })}^{\top }\), \(\varvec{c}={(\varvec{0}_p^{\top },\varvec{1}_q^{\top })}^{\top }\), \({\varvec{\Sigma }}_1=\varvec{D}({\varvec{\phi }})+\phi _e\varvec{c}\varvec{c}^{\top }\) with \(\varvec{\phi }={(\phi _{\delta }\varvec{1}_p^{\top }, \phi _{\varepsilon }\varvec{1}_q^{\top })}^{\top }\), \(\tau _x=\phi _x^{1/2}\delta _x\) with \(\delta _x=\lambda _x(1+\lambda _x^2)^{-1/2}, \gamma _x=(1-\delta _x^2)\phi _x=\phi _x/(1+\lambda _x^2)\), and \(\varvec{D}(\cdot )\) denotes a diagonal matrix whose diagonal elements are formed by a vector.

It is straightforward to know that \(\varvec{Z}_t{\sim }SMSN _m(\varvec{\mu },{\varvec{\Sigma }},\varvec{\lambda };H )\), and its conditional distribution \(\varvec{Z}_t|u_t{\sim }SN _m(\varvec{\mu },\kappa (u_t){\varvec{\Sigma }},\varvec{\lambda })\), where the location, scale and skewness parameters can be expressed as \(\varvec{\mu }=\varvec{a}+\mu _x\varvec{b}\), \({\varvec{\Sigma }}=\varvec{\Sigma }_1+\phi _x\varvec{b}\varvec{b}^{\top }\) and \(\varvec{\lambda }=\frac{\lambda _x\phi _x{\varvec{\Sigma }}^{-1/2}\varvec{b}}{\sqrt{\phi _x+\lambda _x^2\Lambda _x}}\) respectively, with \(\Lambda _x=\phi _x/c\) and \(c=1+\phi _x\varvec{b}^{\top }{\varvec{\Sigma }}_1^{-1}\varvec{b}\).

3.1 EM Algorithm

It is intractable to calculate MLEs effectively through common likelihood method. In the assumption of SMN distributions, Lin and Cao (2013) proposed an iterative approach using EM algorithm in RMEM without assuming equation errors. Here we devote to get the MLEs of model (2) by EM algorithm.

Denoting the parameter vector of model (2) by \(\varvec{\theta }={(\mu _x,\alpha ,\beta ,\lambda _x,\phi _x,\phi _{\delta },\phi _{\varepsilon },\phi _e)}^{\top }\), the estimates of \(\varvec{\theta }\) at the k-th iteration by \({\widehat{\varvec{\theta }}}^{(k)}\) and the complete data set of model (2) by \(\varvec{Z}_c=\{\varvec{Z},\varvec{x},\varvec{v},\varvec{u}\}\), where \(\varvec{Z}=\{\varvec{Z}_1,\ldots ,\varvec{Z}_n\},\varvec{x}=(x_1,\ldots ,x_n)^{\top },\varvec{v}=(v_1,\ldots ,v_n)^{\top },\varvec{u}=(u_1,\ldots ,u_n)^{\top }\), then the complete log-likelihood function based on \(\varvec{Z}_c\) is given by

$$\begin{aligned} l(\varvec{\theta }\big |\varvec{Z}_c)=\sum _{t=1}^n {\left( l_{x_t|v_t,u_t}+l_{\varvec{Z}_t|x_t,u_t}\right) }, \end{aligned}$$

where,

$$\begin{aligned}&l_{x_t|v_t,u_t}=-\frac{1}{2}\log (\gamma _x)-\frac{1}{2}\gamma _x^{-1}\kappa ^{-1}(u_t)\left( x_t-\mu _x-\tau _x v_t\right) ^2,\\&l_{\varvec{Z}_t|x_t,u_t} =-\frac{1}{2}\log \left( |{\varvec{\Sigma }}_1|\right) -\frac{1}{2}\kappa ^{-1}(u_t) {\left( \varvec{Z}_t-\varvec{a}-\varvec{b}x_t\right) }^{\top }{\varvec{\Sigma }}_1^{-1}{\left( \varvec{Z}_t-\varvec{a}-\varvec{b}x_t\right) }. \end{aligned}$$

with \({\varvec{\Sigma }}_1^{-1}=diag \{\frac{1}{\phi _{\delta }}\mathbf I _p,\frac{1}{\phi _{\varepsilon }}\mathbf I _q-\frac{\phi _e}{\phi _{\varepsilon }(\phi _{\varepsilon }+q\phi _e)}\varvec{1}_q\varvec{1}_q^{\top }\}\) and \(|{\varvec{\Sigma }}_1|=\phi _{\delta }^p\phi _{\varepsilon }^{q-1}(\phi _{\varepsilon }+q\phi _e)\). We ignore the constant which is independent of \(\varvec{\theta }\) in above expressions. The EM algorithm is constructed as follows.

E-step: Given the value of \({\widehat{\varvec{\theta }}}^{(k)}\), we calculate the Q-function by using the property of conditional expectation \(E \big [l(\varvec{\theta }|\varvec{Z}_c)\big |{\widehat{\varvec{\theta }}}^{(k)}, \varvec{Z}\big ]\). The Q-function takes the following form

$$\begin{aligned} Q\left( \varvec{\theta }|{\widehat{\varvec{\theta }}}^{(k)}\right) =\sum _{t=1}^n\left[ Q_{1t}\left( \varvec{\theta }|{\widehat{\varvec{\theta }}}^{(k)}\right) +Q_{2t}\left( \varvec{\theta }|{\widehat{\varvec{\theta }}}^{(k)}\right) \right] , \end{aligned}$$
(4)

where

$$\begin{aligned} Q_{1t}\left( \varvec{\theta }|{\widehat{\varvec{\theta }}}^{(k)}\right) =&-\frac{1}{2}\log (\gamma _x)-\frac{1}{2}\gamma _x^{-1}\left( \widehat{ux^2}_t^{(k)}+\mu _x^2\widehat{u}_t^{(k)}+\tau _x^2\widehat{uv^2}_t^{(k)}\right. \\&\quad \left. -\,2\mu _x\widehat{ux}_t^{(k)}-2\tau _x\widehat{uxv}_t^{(k)}+2\mu _x\tau _x\widehat{uv}_t^{(k)}\right) ,\\ Q_{2t}\left( \varvec{\theta }|{\widehat{\varvec{\theta }}}^{(k)}\right) =&-\frac{1}{2}\log \left( |{\varvec{\Sigma }}_1|\right) -\frac{1}{2}\left[ \widehat{u}_t^{(k)}\left( \varvec{Z}_t-\varvec{a}\right) ^{\top }{\varvec{\Sigma }}_1^{-1}(\varvec{Z}_t-\varvec{a})\right. \\&\quad \left. -\,2\widehat{ux}_t^{(k)}\left( \varvec{Z}_t-\varvec{a}\right) ^{\top }{\varvec{\Sigma }}_1^{-1}\varvec{b} +\widehat{ux^2}_t^{(k)}\varvec{b}^{\top }{\varvec{\Sigma }}_1^{-1}\varvec{b}\right] , \end{aligned}$$

with \(\widehat{u}_t^{(k)}=E [\kappa ^{-1}(U_t)|{\widehat{\varvec{\theta }}}^{(k)},\varvec{Z}_t]\), \(\widehat{uv}_t^{(k)}=E [\kappa ^{-1}(U_t)v_t|{\widehat{\varvec{\theta }}}^{(k)},\varvec{Z}_t]\), \(\widehat{uv^2}_t^{(k)}=E [\kappa ^{-1}(U_t)v_t^2|{\widehat{\varvec{\theta }}}^{(k)},\varvec{Z}_t]\), \(\widehat{ux}_t^{(k)}=E [\kappa ^{-1}(U_t)x_t|{\widehat{\varvec{\theta }}}^{(k)},\varvec{Z}_t]\), \(\widehat{ux^2}_t^{(k)}=E [\kappa ^{-1}(U_t)x_t^2|{\widehat{\varvec{\theta }}}^{(k)},\varvec{Z}_t]\), \(\widehat{uxv}_t^{(k)}=E [\kappa ^{-1}(U_t)x_tv_t|{\widehat{\varvec{\theta }}}^{(k)},\varvec{Z}_t]\), and they can be readily evaluated by

$$\begin{aligned}&\widehat{uv}_t^{(k)}=\widehat{u}_t^{(k)}\widehat{\mu }_{v_t}^{(k)}+\widehat{M}_v^{(k)}\widehat{\eta }_{1,t}^{(k)},\\&\widehat{uv^2}_t^{(k)}=\widehat{u}_t^{(k)}{\widehat{\mu }_{v_t}}^{2(k)} +{\widehat{M}_v}^{2(k)}+\widehat{M}_v^{(k)}\widehat{\mu }_{v_t}^{(k)}\widehat{\eta }_{1,t}^{(k)},\\&\widehat{ux}_t^{(k)}=\widehat{u}_t^{(k)}\widehat{r}_t^{(k)}+\widehat{uv}_t^{(k)}\widehat{s}^{(k)},\\&\widehat{ux^2}_t^{(k)}=\widehat{u}_t^{(k)}{\widehat{r}_t}^{2(k)}+2\widehat{uv}_t^{(k)}\widehat{r}_t^{(k)}\widehat{s}^{(k)} +\widehat{uv^2}_t^{(k)}{\widehat{s}}^{2(k)}+\widehat{\gamma }_x^{(k)}/\widehat{c}_1^{(k)},\\&\widehat{uxv}_t^{(k)}=\widehat{uv}_t^{(k)}\widehat{r}_t^{(k)}+\widehat{uv^2}_t^{(k)}\widehat{s}^{(k)}, \end{aligned}$$

with \(\widehat{\mu }_{v_t}=\widehat{\tau }_x\widehat{a}_t/\widehat{c}\), \(\widehat{M}_v=\sqrt{\widehat{c}_1/\widehat{c}}\), \(\widehat{\eta }_{1,t}^{(k)}=E \big [\kappa ^{-1/2}(U_t)W_\Phi \big (\kappa ^{-1/2}(U_t)\widehat{\mu }_{v_t}/\widehat{M}_v\big ) \big |{\widehat{\varvec{\theta }}}^{(k)},\varvec{Z}_t\big ]\), \(\widehat{r}_t=\widehat{\mu }_x+\widehat{\gamma }_x\widehat{a}_t/\widehat{c}_1\), \(\widehat{s}=\widehat{\tau }_x/\widehat{c}_1\), \(a_t=(\varvec{Z}_t-\varvec{\mu })^{\top }{\varvec{\Sigma }}_1^{-1}\varvec{b}\), \(c_1=1+\gamma _x\varvec{b}^{\top }{\varvec{\Sigma }}_1^{-1}\varvec{b}\).

M-step: Maximizing \(Q(\varvec{\theta }|{\widehat{\varvec{\theta }}}^{(k)})\) with respect to \(\varvec{\theta }\), we achieve the updated estimates \({\widehat{\varvec{\theta }}}^{(k+1)}\) by the following iterative equations:

$$\begin{aligned}&\displaystyle \widehat{\mu }_x^{(k+1)}=\frac{\sum _{t=1}^n \widehat{ux}_t^{(k)}\sum _{t=1}^n \widehat{uv^2}_t^{(k)}-\sum _{t=1}^n \widehat{uv}_t^{(k)}\sum _{t=1}^n \widehat{uxv}_t^{(k)}}{\sum _{t=1}^n \widehat{u}_t^{(k)}\sum _{t=1}^n \widehat{uv^2}_t^{(k)}-\left( \sum _{t=1}^n \widehat{uv}_t^{(k)}\right) ^2},\\&\displaystyle \widehat{\tau }_x^{(k+1)}=\frac{\sum _{t=1}^n \widehat{u}_t^{(k)}\sum _{t=1}^n \widehat{uxv}_t^{(k)}-\sum _{t=1}^n \widehat{uv}_t^{(k)}\sum _{t=1}^n \widehat{ux}_t^{(k)}}{\sum _{t=1}^n \widehat{u}_t^{(k)}\sum _{t=1}^n \widehat{uv^2}_t^{(k)}-\left( \sum _{t=1}^n \widehat{uv}_t^{(k)}\right) ^2},\\&\displaystyle \widehat{\gamma }_x^{(k+1)}=\frac{1}{n}\sum _{t=1}^n \left( \widehat{ux^2}_t^{(k)}+\left( \widehat{\mu }_x^{(k+1)}\right) ^2\widehat{u}_t^{(k)}+\left( \widehat{\tau }_x^{(k+1)}\right) ^2\widehat{uv^2}_t^{(k)}\right. \\&\displaystyle \left. -2\widehat{\mu }_x^{(k+1)}\widehat{ux}_t^{(k)}-2\widehat{\tau }_x^{(k+1)}\widehat{uxv}_t^{(k)} +2\widehat{\mu }_x^{(k+1)}\widehat{\tau }_x^{(k+1)}\widehat{uv}_t^{(k)}\right) ,\\&\displaystyle \widehat{\alpha }^{(k+1)}=\frac{\sum _{t=1}^n \left( \widehat{u}_t^{(k)}\bar{Y}_t\right) \sum _{t=1}^n \widehat{ux^2}_t^{(k)}-\sum _{t=1}^n \widehat{ux}_t^{(k)}\sum _{t=1}^n \left( \widehat{ux}_t^{(k)}\bar{Y}_t\right) }{\sum _{t=1}^n \widehat{u}_t^{(k)}\sum _{t=1}^n \widehat{ux^2}_t^{(k)}-\left( \sum _{t=1}^n \widehat{ux}_t^{(k)}\right) ^2},\\&\displaystyle \widehat{\beta }^{(k+1)}=\frac{\sum _{t=1}^n \widehat{u}_t^{(k)}\sum _{t=1}^n \left( \widehat{ux}_t^{(k)}\bar{Y}_t\right) -\sum _{t=1}^n \widehat{ux}_t^{(k)}\sum _{t=1}^n \left( \widehat{u}_t^{(k)}\bar{Y}_t\right) }{\sum _{t=1}^n \widehat{u}_t^{(k)}\sum _{t=1}^n \widehat{ux^2}_t^{(k)}-\left( \sum _{t=1}^n \widehat{ux}_t^{(k)}\right) ^2},\\&\displaystyle \widehat{\phi }_{\delta }^{(k+1)}=\frac{1}{n}\sum _{t=1}^n \left[ \frac{1}{p}\widehat{u}_t^{(k)}\sum _{i=1}^p {(X_t^{(i)})}^2-2\widehat{ux}_t^{(k)}\bar{X}_t+\widehat{ux^2}_t^{(k)}\right] ,\\&\displaystyle \widehat{\phi }_{\varepsilon }^{(k+1)}=\frac{1}{n(q-1)}\left( \sum _{t=1}^n \widehat{\pi }_{1t}^{(k+1)}-q\sum _{t=1}^n \widehat{\pi }_{2t}^{(k+1)}\right) ,\\&\displaystyle \widehat{\phi }_{e}^{(k+1)}=\frac{1}{n(q-1)}\left( q\sum _{t=1}^n \widehat{\pi }_{2t}^{(k+1)}-\frac{1}{q}\sum _{t=1}^n \widehat{\pi }_{1t}^{(k+1)}\right) , \end{aligned}$$

where,

$$\begin{aligned}&\displaystyle \bar{X}_t=\frac{1}{p}\sum _{i=1}^p X_t^{(i)},\bar{Y}_t=\frac{1}{q}\sum _{j=1}^q Y_t^{(j)},\\&\displaystyle \begin{aligned}\widehat{\pi }_{1t}^{(k+1)}&=\widehat{u}_t^{(k)}\sum _{j=1}^q \left( Y_t^{(j)}-{\widehat{\alpha }}^{(k+1)}\right) ^2-2q\widehat{ux}_t^{(k)}\left( \bar{Y}_t-\widehat{\alpha }^{(k+1)}\right) \widehat{\beta }^{(k+1)}\\&\displaystyle \quad +\,q\widehat{ux^2}_t^{(k)}{\left( \widehat{\beta }^{(k+1)}\right) }^2, \end{aligned}\\&\displaystyle \widehat{\pi }_{2t}^{(k+1)}=\widehat{u}_t^{(k)}{\left( \bar{Y}_t-\widehat{\alpha }^{(k+1)}\right) }^2 -2\widehat{ux}_t^{(k)}\left( \bar{Y}_t-\widehat{\alpha }^{(k+1)}\right) \widehat{\beta }^{(k+1)}+\widehat{ux^2}_t^{(k)}{\left( \widehat{\beta }^{(k+1)}\right) }^2. \end{aligned}$$

Note that the estimators \(\widehat{\lambda }_x\) and \(\widehat{\phi }_x\) can be inferred from the one-to-one transformation \(\lambda _x=\tau _x/\sqrt{\gamma _x}\) and \(\phi _x=\gamma _x+\tau _x^2\). Thus the iterative expressions for these two parameters can be written as

$$\begin{aligned}&\widehat{\lambda }_x^{(k+1)}=\widehat{\tau }_x^{(k+1)}\big /\sqrt{\widehat{\gamma }_x^{(k+1)}},\\&\widehat{\phi }_x^{(k+1)}=\widehat{\gamma }_x^{(k+1)}+{\left( {\widehat{\tau }_x^{(k+1)}}\right) }^2. \end{aligned}$$

Starting from suitable initial values (for example, the MLEs from the SMN-RMEM or the moment estimators), the iterations of the above EM algorithm between E-step and M-step are repeated until a suitable convergence rule is satisfied, e.g., \(\Vert {\widehat{\varvec{\theta }}}^{(k+1)}-\widehat{\varvec{\theta }}^{(k)}\Vert \) is sufficiently small. We will apply a closed form (Harville 1997) to compute the inverse of matrix \({\varvec{\Sigma }}_1\) as

$$\begin{aligned} {\varvec{\Sigma }}_1^{-1}= \varvec{D}^{-1}(\varvec{\phi })-\frac{\phi _e\varvec{D}^{-1}(\varvec{\phi })\varvec{c}\varvec{c}^{\top }\varvec{D}^{-1}(\varvec{\phi })}{1+\phi _e\varvec{c}^{\top }\varvec{D}^{-1}(\varvec{\phi })\varvec{c}}. \end{aligned}$$

This can guarantee a positive covariance matrix.

3.2 The Observed Information Matrix

Asymptotic confidence intervals of the MLEs can be constructed using the observed information matrix. We have inferred \(\varvec{Z}_t{\sim }SMSN _m(\varvec{\mu },{\varvec{\Sigma }},\varvec{\lambda };H )\), so the log-likelihood function of \(\varvec{Z}\) respect to \(\varvec{\theta }\) is given by \(l(\varvec{\theta })=\sum _{t=1}^n l_t(\varvec{\theta })\), where

$$\begin{aligned} l_t(\varvec{\theta })=\log 2-\frac{m}{2}\log (2\pi )-\frac{1}{2}\log |{\varvec{\Sigma }}|+\log (K_t), \end{aligned}$$
(5)

with \(K_t=\int \nolimits _0^{\infty }\kappa ^{-m/2}(u_t)\exp \{-\kappa ^{-1}(u_t)d_t/2\}\Phi \big (\kappa ^{-1/2}(u_t)A_t\big )d H (u_t)\), \(d_t=(\varvec{Z}_t-\varvec{\mu })^\top {\varvec{\Sigma }}^{-1}(\varvec{Z}_t-\varvec{\mu })\), and \(A_t=\varvec{\lambda }^\top {\varvec{\Sigma }}^{-1/2}(\varvec{Z}_t-\varvec{\mu })\).

We use the observed information matrix with the help of score function for \({\varvec{\theta }}\). It is expressed by

$$\begin{aligned} \frac{\partial l_t({\varvec{\theta }})}{\partial {\varvec{\theta }}}=-\frac{1}{2}\frac{\partial \log |{{\varvec{\Sigma }}}|}{\partial {\varvec{\theta }}}+\frac{1}{K_t}\frac{\partial K_t}{\partial {\varvec{\theta }}}, \end{aligned}$$
(6)

where, \(\frac{\partial K_t}{\partial \varvec{\theta }}= I_t^{\phi }\left( \frac{m+1}{2}\right) \frac{\partial A_t}{\partial \varvec{\theta }} -\frac{1}{2}I_t^{\Phi }\left( \frac{m+2}{2}\right) \frac{\partial d_t}{\partial \varvec{\theta }}\), and in which,

$$\begin{aligned} I_t^\Phi (w)&=\int \nolimits _0^{\infty }\kappa ^{-w}(u_t)\exp \left\{ -\kappa ^{-1}(u_t)d_t/2\right\} \Phi \left( \kappa ^{-1/2}(u_t)A_t\right) d H (u_t),\\ I_t^\phi (w)&=\int \nolimits _0^{\infty }\kappa ^{-w}(u_t)\exp \left\{ -\kappa ^{-1}(u_t)d_t/2\right\} \phi \left( \kappa ^{-1/2}(u_t)A_t\right) d H (u_t). \end{aligned}$$

Then the asymptotic covariance of the MLEs can be estimated by the inverse of the observed information matrix \(\varvec{I }\left( {{\widehat{\varvec{\theta }}}}\right) = \sum _{t=1}^n{\left( \frac{\partial l_t({\varvec{\theta }})}{\partial {\varvec{\theta }}}\right) {\left( \frac{\partial l_t({\varvec{\theta }})}{\partial {\varvec{\theta }}}\right) }^{\top }|_{\varvec{\theta }={{\widehat{\varvec{\theta }}}}}}\). Explicit expressions of \(I_t^\Phi (w)\) and \(I_t^\phi (w)\) for some SMSN distributions can be found in Lachos et al. (2010a) and Zeller et al. (2011). The derivatives of the score function are given in “Appendix B”.

3.3 Empirical Bayes Estimation and Prediction

In this section, we consider an empirical Bayes approach to estimate the true variable \(x_t\) and to predict \(\varvec{Y}_t\) given \(\varvec{X}_t\). From the definition of the models, it is not difficult to derive that the conditional distribution of \(x_t\) given \(\varvec{Z}_t\) and \(u_t\) belongs to the extended SN (ESN) distributions (Azzalini and Capitanio 1999), with the conditional pdf as

$$\begin{aligned} f(x_t|\varvec{Z}_t, u_t)=\phi (x_t; \mu _x+\Lambda _x a_t, \kappa (u_t)\Lambda _x)\frac{\Phi \left( \kappa ^{-1/2}(u_t)\lambda _x \phi _x^{-1/2} (x_t-\mu _x)\right) }{\Phi (\kappa ^{-1/2}(u_t)A_t)}. \end{aligned}$$

Thus, we get the conditional expectation of \(x_t\) given \(\varvec{Z}_t\) and \(u_t\) as

$$\begin{aligned} E [x_t|\varvec{Z}_t, u_t]=\mu _x+\Lambda _x a_t+\kappa ^{1/2}(u_t)\frac{\lambda _x\Lambda _x}{\sqrt{1+\lambda _x^2\Lambda _x}}W_{\Phi }\left( \kappa ^{-1/2}(u_t)A_t\right) . \end{aligned}$$

Then

$$\begin{aligned} \widehat{x}_t=&\,E [x_t|\varvec{Z}_t]=E \{E [x_t|\varvec{Z}_t, u_t]|\varvec{Z}_t\}\\ =&\,\mu _x+\Lambda _x a_t+\frac{\lambda _x\Lambda _x}{\sqrt{1+\lambda _x^2\Lambda _x}}\eta _{-1,t}, \end{aligned}$$

where \(\eta _{-1,t}=E [\kappa ^{1/2}(U_t)W_{\Phi }(\kappa ^{-1/2}(U_t)A_t)|\varvec{Z}_t]\).

Next, we will predict \(\varvec{Y}_t\) given \(\varvec{X}_t\). From the previous conclusions, we know that \(\varvec{Z}_t\sim SMSN _m(\varvec{\mu },{\varvec{\Sigma }},\varvec{\lambda };H )\), and \(\varvec{Z}_t|u_t\sim SN _m(\varvec{\mu },\kappa (u_t){\varvec{\Sigma }},\varvec{\lambda })\). Now, partition \({\varvec{\Sigma }}\) as

$$\begin{aligned} {\varvec{\Sigma }}=\left( \begin{array}{cc} {\varvec{\Sigma }}_{11} &{} \varvec{\Sigma }_{12} \\ {\varvec{\Sigma }}_{21} &{} \varvec{\Sigma }_{22} \\ \end{array} \right) , \end{aligned}$$

where \({\varvec{\Sigma }}_{11}=\phi _{\delta }\varvec{I }_p+\phi _x\varvec{1}_p\varvec{1}_p^{\top }\), \({\varvec{\Sigma }}_{12}=\beta \phi _x\varvec{1}_p\varvec{1}_q^{\top }\), \({\varvec{\Sigma }}_{21}=\varvec{\Sigma }_{12}^{\top }\), \({\varvec{\Sigma }}_{22}=\phi _{\varepsilon }\varvec{I }_q+(\phi _e+\beta ^2\phi _x)\varvec{1}_q\varvec{1}_q^{\top }\). Then we have marginal distribution

$$\begin{aligned} \varvec{X}_t\sim SMSN _p\left( \mu _x\varvec{1}_p,{\varvec{\Sigma }}_{11},\varvec{\lambda }_{1t};H \right) , \end{aligned}$$

where \(\varvec{\lambda }_{1t}= \frac{\lambda _x\phi _x}{\sqrt{1+\varvec{\lambda }^{\top }\varvec{\lambda }}}{\varvec{\Sigma }}_{11,t}^{-1/2}\varvec{1}_{p_t}\big / \sqrt{1-\frac{\rho ^2p_t}{\phi _{\delta _t}+p_t\phi _x}}\), i.e., \(\varvec{X}_t|u_t\sim SN _{p_t}(\mu _x\varvec{1}_{p_t},\kappa (u_t){\varvec{\Sigma }}_{11,t},\varvec{\lambda }_{1t})\).

Denote \(A_{1,t}=\varvec{\lambda }_1^{\top }{\varvec{\Sigma }}_{11}^{-1/2}(\varvec{X}_t-\mu _x\varvec{1}_p) =\frac{\rho p}{\phi _{\delta }+p\phi _x}(\bar{X}_t-\mu _x)/\sqrt{1-\frac{\rho ^2 p}{\phi _{\delta }+p\phi _x}}\), with \(\rho =\lambda _x\phi _x/\sqrt{1+\varvec{\lambda }^{\top }\varvec{\lambda }}\), then \(\varvec{Y}_t|\varvec{X}_t, u_t\sim ESN _q(\varvec{\mu }_{2\cdot 1,t},\kappa (u_t){\varvec{\Sigma }}_{22\cdot 1};\lambda _{0,t},\varvec{\lambda }_{1,t})\), where

$$\begin{aligned} \varvec{\mu }_{2\cdot 1,t}=&\,\left[ \alpha +\beta \mu _x+\frac{p\phi _x}{\phi _{\delta }+p\phi _x}\beta (\bar{X}_t-\mu _x)\right] \varvec{1}_q,\\ {\varvec{\Sigma }}_{22\cdot 1}=&\,{\varvec{\Sigma }}_{22}-\varvec{\Sigma }_{21}{\varvec{\Sigma }}_{11}^{-1}\varvec{\Sigma }_{12} =\phi _{\varepsilon }\mathbf I _q+\left( \phi _e+\frac{\phi _{\delta }\phi _x\beta ^2}{\phi _{\delta }+p\phi _x}\right) \varvec{1}_q\varvec{1}_q^{\top },\\ \lambda _{0,t}=&\,\kappa ^{-1/2}(u_t)\frac{\rho p}{\phi _{\delta }+p\phi _x}(\bar{X}_t-\mu _x)/\sqrt{1-\rho ^2\varvec{b}{\varvec{\Sigma }}^{-1}\varvec{b}},\\ \varvec{\lambda }_{1,t}=&\frac{\rho \beta \phi _{\delta }}{\phi _{\delta }+p\phi _x}{\varvec{\Sigma }}_{22\cdot 1}^{-1/2}\varvec{1}_q/\sqrt{1-\rho ^2\varvec{b}{\varvec{\Sigma }}^{-1}\varvec{b}}. \end{aligned}$$

Accordingly, we get the conditional expectation of \(\varvec{Y}_t\) given \(\varvec{X}_t\) and \(u_t\) as

$$\begin{aligned} \begin{aligned} E [\varvec{Y}_t|\varvec{X}_t,u_t]=&\,\varvec{\mu }_{2\cdot 1,t}+\kappa ^{1/2}(u_t){\varvec{\Sigma }}_{22\cdot 1}^{1/2}\frac{\varvec{\lambda }_{1,t}}{1+{\varvec{\lambda }}_{1,t}^{\top }{\varvec{\lambda }}_{1,t}}W_{\Phi }\left( \kappa ^{-1/2}(u_t)A_{1,t}\right) \\ =&\,\varvec{\mu }_{2\cdot 1,t}+\kappa ^{1/2}(u_t)W_{\Phi }\left( \kappa ^{-1/2}(u_t)A_{1,t}\right) \frac{\rho \beta \phi _{\delta }}{\phi _{\delta }+p\phi _x}\varvec{1}_q\big /\sqrt{1-\frac{\rho ^2 p}{\phi _{\delta }+p\phi _x}}, \end{aligned} \end{aligned}$$

Then, the prediction of \(\varvec{Y}_t\) is given by

$$\begin{aligned} \begin{aligned} \widehat{\varvec{Y}}_t=&\,E [\varvec{Y}_t|\varvec{X}_t]=E \{E [\varvec{Y}_t|\varvec{X}_t,u_t]|\varvec{X}_t\}\\ =&\,\varvec{\mu }_{2\cdot 1,t}+\tilde{\eta }_{-1,t}\frac{\rho \beta \phi _{\delta }}{\phi _{\delta }+p\phi _x}\varvec{1}_q\big /\sqrt{1-\frac{\rho ^2 p}{\phi _{\delta }+p\phi _x}}, \end{aligned} \end{aligned}$$
(7)

where \(\tilde{\eta }_{-1,t}=E [\kappa ^{1/2}(U_t)W_{\Phi }(\kappa ^{-1/2}(U_t)A_{1,t})|\varvec{X}_t]\).

4 Simulation Studies

In this section, we will report the results of two simulation studies. The first one is to confirm the effectiveness and accuracy of the MLEs under SMSN distributions. The second one is to investigate the robustness of SMSN-RMEM when there has outliers. In each simulation study, we consider three skew distributions, including SN, ST with \(\nu =4\) and SCN with \(\nu =0.2, \gamma =0.3\), in RMEM with or without equation error, respectively. Under the circumstances of no equation error, we denote the SN, ST and SCN distributions by SN0, ST0 and SCN0 correspondingly. The regression parameters \(\alpha \) and \(\beta \) will be regarded as parameters of interest in both simulation studies.

Table 1 Performances of estimators under ST-RMEM with or without equation error
Full size table

4.1 The First Simulation Study

In this simulation study, the parameters of SMSN-RMEM model are set as \(\mu _x=1.5, \alpha =2, \beta =1, \lambda _x=0.5, \phi _x=1, \phi _{\delta }=1\) and \(\phi _{\varepsilon }=0.5\). For comparison, we set \(\phi _e=0.5\), 1 and 1.5 respectively, which shows that the matching degree between the true covariate and response tends from strong to weak. The replicated numbers of the observations are chosen as \(p=4\) and \(q=3\). We generate data from model (2) with sample size \(n=50\) or 100 under ST distribution (\(\nu =4\)). Based on the sample data, we compute the MLEs of \(\varvec{\theta }\) using EM algorithm under SN, ST and SCN distributions with or without equation error, respectively. After 1000 times repetition, we calculate the sample bias (BIAS) and the standard deviation (SD) as assessments for the estimates.

Table 1 displays the estimations of \(\alpha \) and \(\beta \) based on six type SMSN-RMEMs (SN-RMEM, ST-RMEM, SCN-RMEM, SN0-RMEM, ST0-RMEM, SCN0-RMEM). As we expected, No matter it is \(\alpha \) or \(\beta \), the BIAS and SD of all estimates get smaller as samples size increasing from 50 to 100. The BIAS and SD under ST distribution are almost always the smallest for all cases, which fully reflects the effectiveness and accuracy of the ML estimates. Moreover, the performance under SCN and ST distribution behaves better than SN distribution, which may attribute to their heavy-tailed features.

Obviously, the estimates with equation error consistently perform better than the estimates without equation error. Especially, when \(\phi _e\) increases from 0.5 to 1.5, the ratios of SD without equation error and with equation error become clearly larger. It states that for the data with skewness or heavy-tailed features, ignoring equation error will bring serious deviation for statistical inference. The equation error plays an important role in expressing the uncertain relationship between the true covariates and the response.

4.2 The Second Simulation Study

In this simulation study, we aim at examining the robustness of skew-heavy tailed models by comparing the performance of estimates in the presence of outliers. We first generate a data set with sample size \(n=100\) from model (2) under SN distribution, and take the first half as training data and the rest as testing data. Then we shift the observed value \(X_t^{(i)}\) to \(X_t^{(i)}+w\mu _x\) and \(Y_{t'}^{(j)}\) to \(Y_{t'}^{(j)}+w(\alpha +\beta \mu _x)\) for all i, j, respectively, where the two subject number t and \(t^{\prime }\) are chosen randomly from training data each time. The value of w, from \(-3\) to 3, indicates the degree of contamination. All the true values of parameters are the same as the first simulation study. After that, we calculate the MLEs of \(\alpha \) and \(\beta \) based on six type SMSN-RMEMs (mentioned in the first simulation study) under the shifted data and the non-shifted data, respectively. For the testing data, we use the empirical Bayes method to predict \(\varvec{Y}_t\) according to the observed values of \(\varvec{X}_t\) under the aforementioned six type SMSN-RMEMs. Based on 1000 simulations, the mean squared error (MSE) values of \(\alpha \), \(\beta \) and the predictions at different w are computed and shown in Fig. 1 for the six models. The smaller MSE value is, the better robustness of model will behave.

Whether it is \(\alpha \) or \(\beta \), MSEs of estimates without assuming equation error are always larger than the ones assuming equation error. It indicates the significant importance of equation error for skew or heavy-tailed data. This finding matches the results from the first simulation study. The MSEs of estimates based on SN, SN0, ST0 and SCN0 models increase quickly along with w, which shows that the influence of the outliers become serious when the absolute value of w increases. On the contrary, the MSEs of estimates based on ST and SCN models almost do not change with w, which reveals the robustness of ST and SCN models. As expected, the MSEs are the smallest at the zero point (i.e., no perturbation in the data) for all the cases. The impacts of positive disturbance are almost as much as negative disturbance. Although the true data follow the SN distribution, the superiority of robustness based on heavy-tailed models is obvious. Similar conclusions for predictions can be drawn from Fig. 1c. That is to say, the robustness of skew-heavy tailed distributions are also efficient for Bayes prediction approach.

To sum up, the MLEs based on skew-heavy tailed models are more appealing since they behave better than the traditional SN ones in terms of robustness and accuracy.

Fig. 1
figure 1

Performances of estimates in the presence of outliers: MSE versus w, for a \(\alpha \); b \(\beta \); c predictions

Full size image

5 Application

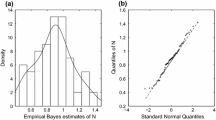
We give an illustrative example using the CSFII dataset. This dataset has conducted the 24-h recall measures, as well as three additional 24-h recall phone interviews of 1827 women who were recorded about their daily diet intake (for example, saturated fat, calories, vitamin, and so on). Carroll et al. (2006) have indicated that saturated fat has great relationship with the risk of breast cancer and other diseases, but the statistical significance for saturated fat disappeared when adding caloric intake into the logistic regression model. Thus it is really necessary to reveal the inner relationship between saturated fat and caloric intake. In this illustrative example, we take the calorie intake/5000 as x and the saturated fat intake/100 as y (Carroll et al. 2006; Lin and Cao 2013). Instead of x and y, the nutrition variables X and Y are calculated by four 24-h recalls, and suppose that they follow model (2) with \(p=q=4\). Acceptable saturated fat daily intake has been considered as an important reference index for health in the survey (le Coutre et al. 2013). There are some differences for daily diet habits for people in different ages, which may be aroused by their different lifestyles or nutrition awareness. In order to compare the difference of adults at different ages, we divide the dataset into two groups. Group 1 is younger than 40 years old, and group 2 is over 40. With the purpose of verifying the existence of skewness and heavy-tails in the latent covariate x, we fit the data using normal RMEM without equation error. Figure 2 presents the corresponding histogram and Q–Q plot of the empirical Bayes estimates of \(x_t\), both showing that the latent covariate is positively skewed and heavy-tailed in each group. This hints that a normal model may not offer a good fit. We now consider SMSN distributions for \(x_t\) and SMN distributions for measurement errors \(\delta _t, \varepsilon _t\) and equation error \(e_t\) in the RMEM, i.e., the SMSN-RMEM proposed in this paper. For the sake of comparison, we also consider the SMN distributions for \(x_t\), i.e. the distributions without assuming skewness.

Fig. 2
figure 2

Histogram and normal Q–Q plot of empirical Bayes estimates of \(x_t\) under N0 model, a, b for group 1, and c, d for group 2

Full size image

We calculate the MLEs of parameter \(\varvec{\theta }\) and their standard errors (SEs) and also Akaike information criterion (AIC) (Akaike 1974) values based on RMEM model under above distributions. This estimates are displayed in Table 2 for group 1 and Table 3 for group 2, where ST, ST0, SS, SS0, SCN, SCN0, T, T0, S, S0 and CN, CN0 denote the skew-t, skew-slash, skew-contaminated normal, Student t, slash and contaminated normal distributions with or without equation error correspondingly. The degrees of freedom for different distributions, chosen by the Schwarz (1978) information criterion, are also reported in the tables.

We draw some conclusions from Tables 2 and 3. The AIC values are used for model selection. The smaller the AIC value is, the better the model is. We find that the AIC value under Student-t distribution is always the smallest for each group, whether there are equation error or skewness or not, and it gets the smallest value under ST0 distribution in all situations. Thus, ST0-RMEM is more suitable for the two group data. Moreover, the heavy-tailed models show smaller SEs than the normal model. Meanwhile, we’d better consider skewness in the models for their smaller AIC values.

Table 2 Parameter estimations of group 1 (age \(\leqslant \) 40) for CSFII data
Full size table
Table 3 Parameter estimations of group 2 (age > 40) for CSFII data
Full size table

We now do a test to compare the robustness among each model. We aim at \(\alpha , \beta \) and \(\lambda _x\) as our test targets. Figure 3 shows the index plots of Mahalanobis distance \(d_t, t=1,\ldots ,n\) (mentioned in Sect. 3.2) under the normal RMEM. In this case, we have \(d_t\sim \chi ^2(8)\). Here, we adopt the cutoff lines correspond to the quantile \(\chi ^2_{0.01}\) for the distribution of \(d_t\). As we can see, there are 69 potential outliers in group 1 and 36 points in group 2. Removing these observations, we calculate the change ratios of \(\alpha \), \(\beta \) and \(\lambda _x\) under above models and display their values in Tables 4 (for group 1) and 5 (for group 2). The estimated values get slightly smaller after deleting the influential observations in all situations. Specially, both the cases with and without equation error, the change ratios of estimators under heavy-tailed distributions are smaller than those under normal distribution, which also implies that heavy-tailed models fit the data better than normal ones.

Fig. 3
figure 3

Performances of the influential points, a for group 1 and b for group 2

Full size image
Table 4 Change ratios of \(\alpha , \beta , \lambda _x\) after deleting outliers in Group 1 (in%)
Full size table
Table 5 Change ratios of \(\alpha , \beta , \lambda _x\) after deleting outliers in Group 2 (in%)
Full size table

Now, we explain the data by parameters of interest \(\beta \), \(\lambda _x\) and \(\phi _e\). From Table 2, The values of \(\phi _e\) seem very small and only slightly changes among different models, indicating that there is inapparent random relationship between calorie and saturated fat intake. The almost same conclusions can be drawn from Table 3 for group 2. The practical significance of parameter \(\beta \) can be described as the positive proportion of saturated fat in calorie. It takes a smaller value in the younger group than the older group. Thus it can be seen that age factor has a certain effect on their diet habits. The younger people may react quickly than the older ones when acquiring new nutrition knowledge. Besides, it should be noted that the estimates of \(\beta \) under heavy-tailed models are smaller than the normal ones. Skew parameter \(\lambda _x\) is positive, suggesting that the two group data skewed to the right. Moreover, the value of \(\mu _x\) in group 1 is consistently larger than group 2, that may due to younger’s demands on more calories.

6 Conclusions

In this paper, we proposed a RMEM under the SMSN distribution class, called SMSN-RMEM, which is suitable for asymmetric and heavy-tailed data. It includes many special cases, such as non-replicated MEM under SMN distributions (Lachos et al. 2011), RMEM under normal distribution (Lin et al. 2004) or SMN distributions (Lin and Cao 2013). Considering the SMSN-RMEM with equation error, we provided the explicit iterative expressions of MLEs via an EM type algorithm. Additionally, empirical Bayes estimations have been conducted for predicting the true covariate and response. Simulation studies and the application on CSFII data demonstrated the effectiveness and robustness of inferences under the SMSN-RMEM model. The proposed model has good features in terms of robustness against outlying observations, adaptation to general data type and convenience for extensive applications. We expect that the model provides satisfactory results for data in presence of measurement error, skewness and outliers, etc., which are often observed in many areas, particularly in economics, medicine and environment.

We assume a SMSN distribution for the true error-prone covariate while the random errors are all assumed following SMN distributions, which is similar as those in Lachos et al. (2010b) and Zeller et al. (2014), etc. Owing to the hierarchical structure of the model, the features of skewness of both covariate and response can be captured under this assumptions. We may also assume that some random errors follow skew distributions, if we have an evidence from the data collection process. However, we need consider carefully the identification of the model. This may be an interest research later. We conducted model selection mainly through AIC criterion. Other criteria, such as BIC and EDC can also be chosen. For the CSFII data, the order of the candidate models does not change and the advantage of heavy-tailed models is always maintained under different criteria. The computing code is available from the authors upon request. In the future work, it is also necessary to perform some statistic diagnostics and hypothesis tests for the significance of parameters or equation error. Furthermore, the model can be extended to multivariate cases for some statistical studies, or analyzed under a Bayesian paradigm.