A flexible method to correct tooth surface deviation for CNC power skiving of face gears

Abstract

In contemporary gear manufacturing, power skiving stands out as an efficient process. Therefore, several investigations have applied the skiving process to face gear. However, obtaining the precision of the skived tooth surface is a challenge. So, this study introduces a groundbreaking approach to enhancing face gear manufacturing productivity by addressing deviations in the spur face gear tooth surface arising from geometric and kinematic constraints in the conventional power skiving method. To overcome the limitations in traditional approaches, the development of a flexible model for calculating coefficients that adjust CNC axes’ motion and modify the rack cutter was established. The modified tooth topology of the face gear can be obtained by adjusting the machine axis of the CNC machine. A sensitivity correction technique is employed to implement this flexible correction method, utilizing the Levenberg–Marquardt (LM) algorithm to determine the coefficients governing machine motion. The primary objective is to achieve the necessary normal deviations on the tooth surface of the spur face gear. The effectiveness of the proposed method is confirmed by using numerical examples featuring various predetermined target surfaces alongside corresponding machining simulations.

1 Introduction

Face-gear drives have been widely used in aerospace drive systems and enable the transmission of drive systems through an angle. Particularly in helicopter transmission boxes [1], such gear drives offer the advantages of splitting torque between two face-gear drives, reducing the load on the bearings, having a high contact ratio, and being lightweight. The common methods to manufacture face gears are shaping and hobbing processes. Litvin and Fuentes [2] presented a basic approach for face-gear geometry generation based on the meshing of the envelope to the family of shaper surfaces. Miller [3] proposed a new efficient method for manufacturing face gears with a hobbing cutter. Litvin et al. [4] presented the generation of the face gear based on a grinding process by the cutting worm, which can improve the profile errors of the spur face gear by correcting the machine-tool settings to avoid misalignment in bearing contact. Zschippang et al. [5] proposed a method to produce crowning for the face gear to prevent edge contact caused by minor alignment errors. They studied the pointing and undercutting conditions in geometry generation. Wang et al. [6] developed a geometric design of a spherical hobbing cutter to improve machining accuracy and shorten the processing cycle time in face-gear hobbing. To enhance the accuracy of the machining process, Wang et al. [7] proposed a milling cutter design and milling principle following face-gear geometry requirements to simulate the cutting process in a five-axis CNC milling machine. Yang and Tang [8] proposed a flexible rough machining method for spur face-gears using a plunge milling method and re-calculated the NC processing code to improve the machine error in the plunge milling process.

Recently, gear power skiving, which is a modern gear machining method, has been introduced that can achieve high productivity and optimization. The skiving process demands high machine structure rigidity and accuracy synchronization between the tool and the skived gear. The first gear skiving model was proposed in 1910 [9] and included a helical shaping cutter conjugate with an internal straight-tooth gear, in which the crossed-axis angle corresponds precisely to the helix angle value of the cutting tool. As technological limitations gradually improved, after over half a century, the power skiving process performed some applications in internal gear manufacturing. In 1974, Kojima and Nishijima [10] presented the conjugating principle between the skiving cutter and the internal gear and then developed a method to determine the exact profile of the cutting edge. Due to the geometric design of the skiving cutter to facilitate machining, the mismatch between the cutting-edge and the theoretical conjugating helical pinion would cause normal deviations on the generated gear surface. Many previous researchers have proposed correction methods to improve the normal deviations by modifying the geometric structure of the skiving cutter. Guo et al. [11] presented a tool modification method to correct the deviation based on the optimization of the cutter profile using B-spline curves. These same authors [12] proposed a novel power skiving method that optimizes machine setting parameters using a common shaper cutter instead of a specialized skiving cutter, making the process more flexible and economical. The method can be applied to involute spur gears, helical gears, and non-involute cylinder gears based on constructing a sensitive coefficient matrix and linear regression. Huang et al. [13] proposed a method to minimize twist errors by optimizing machine motions using machine motions formulated up to six-order polynomials and evaluated at topographical grid points with a dynamic sensitivity matrix, which is more efficient for double flank grinding. Chen et al. [14] developed a conical error-free slice cutter, in which the cutter tooth-flank is formed by several slices of conjugating pinions with corresponding profile-shifting coefficient values. Tsai [15] presented a design method for an interference-free skiving tool based on a barrel shape and adjusting the initial installation of the skiving tool in the skiving process. Luu and Wu [16] proposed a correction method to attain pre-defined grinding stock on the generating gear by defining a polynomial rack cutter profile using linear and quadratic functions, which were used to generate the skiving cutter.

Nomenclature
mi,r	Polynomial coefficient of the modified rack cutter
C	Machine axes
ei	Modified amount of the rack cutter
h	Rack height
$\mathbf{L}$	Upper-left 3 × 3 submatrix of the transformation matrix
${m}_{n}$	Normal module of gear
M	Transformation matrix
n	Normal vector
$N$	Number of teeth
$P$	Gear pitch
r	Position vector
$r$	Pitch radius
$S$	Coordinate system
t	Tangent vector
$u$	Rack cutter profile parameter
$\theta$	Lengthwise parameter of the rack cutter
$\alpha$	Pressure angle
$\beta$	Helix angle
$\tau$	Normal deviation
$\sum$	Crossed-axis angle
$\xi$	Damping parameter
$\varphi$	Rotational angle
$\varsigma$	Side clearance angle of the cutting tool
$\lambda$	Top clearance angle of the cutting tool
$\zeta$	Twist angle of the cutting tool transverse section
Subscripts
A	Installation angle of the work gear axis
B	Installation angle of the cutting tool axis
c	Skiving cutting tool
C1	Rotation of the work gear
C2	Rotation of the skiving cutting tool
f	Theoretical face gear
g	Spur gear
r	Modified rack cutter
$w$	Skived face gear
X	x-axis component
Y	y-axis component
Z	z-axis component

However, with several complex geometric tooth flanks, such as the face-gear tooth, the bevel gear tooth, or the target surface with a particular geometric form similar to a double-crowning surface, it would be difficult to achieve the desired surface with the correction method by modifying the cutter geometry, modification of machining motion is considered. Based on technological developments, especially in the electronic gearbox of the movement axis in the CNC machine, motion modification has been popularly applied due to high efficiency and flexibility to improve the gear tooth accuracy. To obtain the helical gear with an anti-twist tooth flank, Jiang and Fang [17] proposed a correction method in which the motion axis of the CNC hobbing machine is formed as a high-order polynomial function, and the corrective polynomial coefficients are calculated through an optimization algorithm based on the pre-designed target. Tran and Wu [18] presented a modification method to grind the helical gear with a double-crowning tooth flank on the gear honing machine. Using the disc grinding wheel six-axis CNC machine for the face-gear grinding process, Shen et al. [19] developed a universal optimization solution for solving the additional motion to obtain the face-gear crowned tooth surface. To improve the flexibility of the correction method for the desired tooth surfaces, Luu and Wu [20] proposed a numerical approach for correcting the helical tooth flank by combining both modification methods, i.e., the geometric design of the cutting tool and the motion of the CNC machine axis, in the gear power skiving process. Han et al. [21] presented a machining principle for generating the face gear by the power skiving method to increase machining efficiency and presented experiments to validate the proposed method. In addition, Guo et al. [22] proposed a method to improve the normal deviation and contact region on the skived face-gear tooth flank based on evaluating the influences of adjusting the skiving cutter parameters. Mo et al. [23] presented a novel skiving method for face gear using a modified rack cutter to decrease tooth surface error. They used the Newton iterative method to solve the rake and conjugate surface intersection. Nevertheless, it remains difficult to calculate the polynomial coefficients necessary to attain the desired tooth surface, particularly in optimizing the adjustment of the cutter profile along with the correction of the machine axis motion.

Therefore, this paper proposes a flexible modification approach to generate and correct the face-gear tooth surface using the power skiving method in a multi-axis CNC machine. The meshing principle of the spur face-gear and the spur pinion is presented to generate the theoretical face-gear tooth surface. Based on the power skiving process principle, mathematical modeling of the cutting tool geometry is established. The mathematical modeling of power skiving for the face gear on the multi-axis CNC machine is proposed. The normal rack cutter profile and machine-axis motions are modified by adding a high-order form of the polynomial coefficients to correct the error on the gear-tooth surfaces. Finally, an optimization method using the Levenberg–Marquardt (LM) algorithm is proposed, wherein the modified amounts of cutter profile and the polynomial coefficients of the machine-axis motion are obtained by applying closed-loop modification. The efficacy of the proposed methodology is demonstrated through numerical examples featuring various predetermined target surfaces alongside corresponding machining simulations, thereby affirming its validity and applicability.

2 Mathematical model of generating the face gear by power skiving

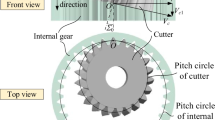
This proposed mathematical model focuses on the meshing conjugation between the spur face gear and the spur pinion in the face-gear drive, wherein a tapered helical gear type cutter is utilized to generate the spur face gear. The relative motion of the skiving tool to the face gear is shown in Fig. 1. The rotating axis of the skiving tool is positioned at a crossed-axis angle, Ʃ, relative to the horizontal axis of the face gear. In this investigation, the crossed-axis angle coincides with the helix angle β_f of the skiving tool for machining the spur face gear. Moreover, precise synchronization of the cutter and face-gear rotational motions ensures accuracy throughout the machining process.

Fig. 1

Machining principle of the power skiving face-gear

2.1 Mathematical model of the power skiving cutter

Many previous researchers have proposed various skiving cutters, such as conical and cylindrical shape cutters. This paper presents the design of a conical skiving cutter for manufacturing face-gears. The tooth flank of the conical skiving tool embodies a helical pinion design featuring geometric modifications aimed at preventing interference and enhancing accuracy during the cutting operation. The geometrical profile of the cutter flank is derived from the enveloping surface of the rack cutter utilizing the generating helical pinion.

Due to the uneven normal deviation on the face-gear tooth topography resulting from the asymmetry on the cutting-edge profile and the differences in profiles along the face-gear tooth length, geometrical modification of the rack profile is considered. As shown in Fig. 2, the rack cutter profile is defined as a quadratic function with ${m}_{r,i}$ and ${n}_{r,i}$ as the parabola coefficients, respectively; ${u}_{r}$ is the curve parameter; ${\alpha }_{r}$ is the pressure angle on the normal section; e_i is the modification amount of the parabolic curve; and parameter $i$ indicates the side of the rack profile, with $i=1$ for the left side and $i=2$ for the right side. When ${m}_{r,i}=0$, ${n}_{r,i}=0$, and ${e}_{i}=0$, the rack profile is a standard straight line. The modified parameter coefficients of the skiving cutter profile will be calculated along with the motion polynomial coefficients, which will be presented in Sect. 3.

Fig. 2

Schematic representation of the rack cutter and the skiving tool generation process: a transverse section of the quadratic rack cutter and b generation of a cutter-flank transverse section

The involute segment e–f of the rack profile, which generates the involute part of the spur gear, is described as the following equation:

$$\left\{\begin{array}{l}{x}_{i}=\pm \left(\frac{P}{4}+{u}_{r}\sin{\alpha }_{rc}+\left({m}_{r,i}{u}_{r}^{2}+{n}_{r,i}{u}_{r}\right)\cos{\alpha }_{r}+{e}_{i}\right)\\ {y}_{i}={u}_{r}\cos{\alpha }_{r}+\left({m}_{r,i}{u}_{r}^{2}+{n}_{r,i}{u}_{r}\right)\sin{\alpha }_{r}\end{array}\right.,\frac{-{h}_{d}}{\cos{\alpha }_{r}}\le {u}_{i}\le \frac{{h}_{a}}{\cos{\alpha }_{r}}$$

(1)

The fillet segment f-g of the rack profile is described as the following equation:

$$\left\{\begin{array}{l}{x}_{f}=\pm \left({\rho }_{f,i}\cos{u}_{f}+\left({m}_{r,i}{u}_{f}^{2}+{n}_{r,i}{u}_{f}\right)\cos{\alpha }_{r}+{e}_{i}\right)\\ {y}_{f}=-\left({h}_{d}-{\rho }_{f,i}\sin{\alpha }_{r}+\left({m}_{r,i}{u}_{f}^{2}+{n}_{r,i}{u}_{f}\right)\sin{\alpha }_{r}\right)+{\rho }_{f,i}\sin{u}_{f}\end{array}\right.,-\frac{\pi }{2}\le {u}_{f}\le -{\alpha }_{r}$$

(2)

Accordingly, the position and normal vectors of the modified rack cutter are briefly presented as follows:

$${\mathbf{r}}_{r,i}\left({u}_{r}\right)={\left[{x}_{r,i},{y}_{r,i},{z}_{r,i},1\right]}^{T}$$

(3)

$${\mathbf{n}}_{r,i}\left({u}_{r}\right)=\frac{\partial \left[{x}_{r,i},{y}_{r,i},{z}_{r,i}\right]}{\partial {u}_{r}}\times \mathbf{k}$$

(4)

where the positive sign in ± is used for the right-side rack profile, the negative sign for the left-side rack profile; and the unit vector $\mathbf{k}=\left[0,0,1\right]$ of the z-axis.

The approach for obtaining the mathematical modeling of the skiving tool flank comprises the following steps:

(i) Rack cutter profiles are applied through a similar transformation matrix, as shown in Fig. 2b, to determine the transverse section of the generating helical pinion.

(ii) The conical skiving cutter design performs a top relief angle to prevent interference with the tooth flank surface by changing the profile shifting amount of the rack cutter transverse profile corresponding to the cutter flank transverse section along the gear face width.

(iii) The entire helical cutter tooth flank is obtained by positioning each transverse generating profile with the corresponding twist angle ${\zeta }_{c}$, as presented in Fig. 3.

Fig. 3

Geometrical generation of cutter tooth flank

As shown in Fig. 3, the coordinate system ${S}_{c}\left({x}_{c},{y}_{c},{z}_{c}\right)$ is connected to the cutter flank; ${S}_{s}\left({x}_{s},{y}_{s},{z}_{s}\right)$ is connected to the transverse section of the cutter flank with the corresponding twist angle ${\zeta }_{c}$; and ${S}_{1}\left({x}_{1},{y}_{1},{z}_{1}\right)$ is the auxiliary coordinate transformation. Derivation of the cutter tooth flank is generated in the coordinate system ${S}_{s}$ through a homogenous coordinate transformation matrix ${\mathbf{M}}_{sr}$ as follows:

$${\mathbf{r}}_{s,i}\left({u}_{r},{\varphi }_{c},{\zeta }_{c},{v}_{c}\right)={\left[{x}_{s,i},{y}_{s,i},{z}_{s,i},1\right]}^{T}={\mathbf{M}}_{sr}\left({\varphi }_{c},{\zeta }_{c},{v}_{c}\right){\mathbf{r}}_{r,i}\left({u}_{r}\right)$$

(5)

$${\mathbf{n}}_{s,i}\left({u}_{r},{\varphi }_{c},{\zeta }_{c},{v}_{c}\right)={\mathbf{L}}_{sr}\left({\varphi }_{c},{\zeta }_{c},{v}_{c}\right){\mathbf{n}}_{r,i}\left({u}_{r}\right)$$

(6)

$${\mathbf{M}}_{sr}\left({\varphi }_{c},{\zeta }_{c},{v}_{c}\right)={\mathbf{M}}_{sc}{\mathbf{M}}_{cr}$$

(7)

$${\mathbf{M}}_{cr}=\left[\begin{array}{cccc}\cos{\varphi }_{c}& -\sin{\varphi }_{c}& 0& {r}_{pc}{\varphi }_{c}\cos{\varphi }_{c}-\left({x}_{ps}+{r}_{pc}\right)\sin{\varphi }_{c}\\ \sin{\varphi }_{c}& \cos{\varphi }_{c}& 0& {r}_{pc}{\varphi }_{c}\sin{\varphi }_{c}+\left({x}_{ps}+{r}_{pc}\right)\cos{\varphi }_{c}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right], {\;\mathbf{M}}_{sc}=\left[\begin{array}{cccc}\cos{\zeta }_{c}& \sin{\zeta }_{c}& 0& 0\\ -\sin{\zeta }_{c}& \cos{\zeta }_{c}& 0& 0\\ 0& 0& 1& {v}_{c}\\ 0& 0& 0& 1\end{array}\right]$$

where ${\mathbf{L}}_{sr}\left({\varphi }_{c},{\delta }_{c},{v}_{c}\right)$ is the upper-left $3\times 3$ of ${\mathbf{M}}_{sr}\left({\varphi }_{c},{\delta }_{c},{v}_{c}\right)$, wherein ${v}_{c}$ is the cutter flank longitudinal parameter, and ${\varphi }_{c}$ is the cutter flank rotational angle, and ${r}_{pc}$ is the pitch radius of the skiving cutter. The profile shifting amount ${x}_{ps}$ and the twist angle ${\zeta }_{c}$ at each transverse section can be defined by

$${x}_{ps}={v}_{c}\tan\lambda$$

(8)

$${\zeta }_{c}=\frac{{v}_{c}\tan{\beta }_{c}}{{r}_{pc}}$$

(9)

where $\lambda$ is the top clearance angle of the cutter; ${\zeta }_{c}$ is the twist angle of the cutter tooth transverse section along the tooth flank width; and ${\beta }_{c}$ is the skiving tool helix angle.

According to the enveloping method [1], the envelope surface of the cutter flank satisfies the meshing equation, which is determined as follows:

$${f}_{c}\left({u}_{r},{\varphi }_{c},{\zeta }_{c},{v}_{c}\right)={\mathbf{n}}_{c,i}\left({u}_{r},{\varphi }_{c},{\zeta }_{c},{v}_{c}\right).\frac{\partial \left[{x}_{s,i},{y}_{s,i},{z}_{s,i}\right]}{\partial {\varphi }_{c}}=0$$

(10)

According to the meshing equation Eq. (10), the unknown ${\varphi }_{c}$ can be solved by substituting specific values of the rack parameter ${u}_{r}$, z-component of transverse section ${v}_{c}$ and corresponding shifting coefficient ${\zeta }_{c}$ into Eq. (10); then, the tooth surfaces of the skiving cutter blanks are completely defined from Eq. (5) based on a set of the above-adopted values $\left({u}_{r},{\varphi }_{c},{\zeta }_{c},{v}_{c}\right)$.

As shown in Fig. 4, the front rake plane with geometric parameter design is presented. The rake plane is firstly rotated about the y-axis with an angle equal to the helix angle to balance the cutting force on both sides of the cutting tool profile. In addition, the rake plane is rotated about the x-axis in the rake angle ${\gamma }_{c}$, allowing the cutting chip to flow easily and reduce cutting force. Reference point P is located on the pitch radius with corresponding profile shifting amounts. The intersecting profile between the tooth flank surface of the skiving tool and the rake plane is used to obtain the cutting-edge profile on the tooth of the cutting tool. An expression for the equation of the rake plane and the plane normal vector passing through a reference point P is given as follows:

Fig. 4

Geometric structure design of skiving cutting tool

$${n}_{xrp}\left(x-{x}_{p}\right)+{n}_{yrp}\left(y-{y}_{p}\right)+{n}_{zrp}\left(z-{z}_{p}\right)=0$$

(11)

$${\mathbf{n}}_{rp}={\left[{n}_{xrp},{n}_{yrp},{n}_{zrp}\right]}^{T}={\left[-\cos\gamma \sin{\beta }_{c},-\sin\gamma ,\cos{\beta }_{c}\cos\gamma \right]}^{T}$$

(12)

The position vector of the reference point P is expressed as follows:

$${\mathbf{r}}_{p}={\left[{x}_{p},{y}_{p},{z}_{p}\right]}^{T}={\left[-{r}_{pc}\sin{\zeta }_{rp},{r}_{pc}\cos{\zeta }_{rp},{v}_{p}\right]}^{T}$$

(13)

$${\zeta }_{rp}=\frac{{v}_{p}\tan{\beta }_{c}}{{r}_{pc}}, {v}_{p}=\frac{{x}_{ps}\cos{\beta }_{c}}{\tan\lambda }$$

(14)

where $\varsigma$ is the side clearance angle; $\gamma$ is the rake angle; and ${\zeta }_{rp}$ and ${v}_{p}$ are the twist angle and the z-axis component of the transverse section passing through the reference point P, respectively.

The cutting tool profile is determined by the equation of meshing Eq. (10) and the equation of rake plane Eq. (11). Additionally, the tangent vector of a point on the cutting-edge profile is obtained as follows:

$${\mathbf{t}}_{c}={\mathbf{n}}_{c}\times {\mathbf{n}}_{rp}=\left({\mathbf{t}}_{\varphi c}\times {\mathbf{t}}_{\theta c}\right)\times {\mathbf{n}}_{rp}=\left(\frac{\partial \left[{x}_{s,i},{y}_{s,i},{z}_{s,i}\right]}{\partial {\varphi }_{c}}\times \frac{\partial \left[{x}_{s,i},{y}_{s,i},{z}_{s,i}\right]}{\partial {v}_{c}}\right)\times {\mathbf{n}}_{rp}$$

(15)

where ${\mathbf{n}}_{c}$ is the normal vector of the cutting tool flank and ${\mathbf{t}}_{\varphi c}$ and ${\mathbf{t}}_{\theta c}$ are the tangent vectors of the profile and the longitudinal direction of the cutter, respectively.

2.2 Mathematical model of the skiving face gear on the CNC gear skiving machine

By the principles of power skiving, the cutting speed is generated by the angular position of the cutting tool with respect to the manufactured gear. Furthermore, due to the face-gear characteristic geometry, the rotational axis of the shaft angle is required. To meet these prerequisites, a conceptual schematic form of a CNC gear skiving machine for manufacturing the face gear is proposed in Fig. 5. The machine structure is based on a conventional CNC gear skiving machine, such as the Gleason PS series or the Liebherr LK series, with an additional shaft angle rotational axis. The machine structure includes X, Y, and Z, which are the translational axes; A and B are installation axes for the shaft angle of the workpiece and the tilted angle of the skiving cutting tool, respectively; and C₁ and C₂ are the rotation spindle of the face-gear workpiece and the skiving tool, respectively.

Fig. 5

Schematic representation of the face-gear skiving machining process: a multi-axis CNC machine for the face-gear skiving process and b relative motion coordinate system in the face-gear power skiving process

The relative motion coordinate system for the face-gear skiving process is presented in Fig. 5b. The coordinate systems ${S}_{w}\left({x}_{w},{y}_{w},{z}_{w}\right)$ and ${S}_{c}\left({x}_{c},{y}_{c},{z}_{c}\right)$ are connected to the workpiece and the cutting tool, respectively, in which the coordinate systems ${S}_{1}\left({x}_{1},{y}_{1},{z}_{1}\right)$, ${S}_{2}\left({x}_{2},{y}_{2},{z}_{2}\right)$, and ${S}_{3}\left({x}_{3},{y}_{3},{z}_{3}\right)$ are auxiliary coordinate systems. The face-gear tooth surface can be derived by transforming the cutting tool profile from the coordinate system ${S}_{c}$ to the coordinate system ${S}_{w}$. The position and tangent vectors of the face-gear tooth flank in the coordinate system ${S}_{w}$ can be expressed as follows:

$${\mathbf{r}}_{w}\left({\varphi }_{c1},{l}_{z}\right)={\left[{x}_{w},{y}_{w},{z}_{w},1\right]}^{T}={\mathbf{M}}_{wc}\left({\varphi }_{c1},{l}_{z}\right){\mathbf{r}}_{c}$$

(16)

$${\mathbf{t}}_{w}\left({\varphi }_{c1},{l}_{z}\right)={\left[{t}_{xw},{t}_{yw},{t}_{zw}\right]}^{T}={\mathbf{L}}_{wc}\left({\varphi }_{c1},{l}_{z}\right){\mathbf{t}}_{c}$$

(17)

$${\mathbf{M}}_{wc}\left({\varphi }_{c1},{l}_{z}\right)={\mathbf{M}}_{w3}{\mathbf{M}}_{32}{\mathbf{M}}_{21}{\mathbf{M}}_{1c}$$

(18)

$${\mathbf{M}}_{w3}=\left[\begin{array}{cccc}\cos{\varphi }_{c1}& -\sin{\varphi }_{c1}& 0& 0\\ \sin{\varphi }_{c1}& \cos{\varphi }_{c1}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right], {\;\mathbf{M}}_{32}=\left[\begin{array}{cccc}1& 0& 0& {l}_{x}\\ 0& \cos\gamma & \sin\gamma & {l}_{z}\\ 0& -\sin\gamma & \cos\gamma & {l}_{y}\\ 0& 0& 0& 1\end{array}\right],{\;\mathbf{M}}_{21}=\left[\begin{array}{cccc}\cos{\psi }_{c}& 0& \sin{\psi }_{c}& 0\\ 0& 1& 0& 0\\ -\sin{\psi }_{c}& 0& \cos{\psi }_{c}& 0\\ 0& 0& 0& 1\end{array}\right], {\;\mathbf{M}}_{1c}=\left[\begin{array}{cccc}\cos{\varphi }_{c2}& \sin{\varphi }_{c2}& 0& 0\\ -\sin{\varphi }_{c2}& \cos{\varphi }_{c2}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

where ${\mathbf{r}}_{c}$ is the position and ${\mathbf{t}}_{c}$ is the tangent vector of the skiving tool profile; the ${\mathbf{M}}_{wc}\left({\varphi }_{c1},{l}_{z}\right)$ matrix describes the transformation from ${S}_{c}$ to ${S}_{w}$; ${\mathbf{L}}_{wc}\left({\varphi }_{c1},{l}_{z}\right)$ is the upper-left $3\times 3$ of ${\mathbf{M}}_{wc}\left({\varphi }_{c1},{l}_{z}\right)$; ${\varphi }_{c1}$ and ${\varphi }_{c2}$ are the workpiece spindle and the cutting tool spindle rotational angles, respectively; $\gamma$ is the shaft angle between the cutting tool and the workpiece rotation axis; $\sum$ is the crossed-axis angle of the skiving tool spindle axis; ${l}_{y}$ is the radial installation value of the skiving cutter; and ${l}_{z}$ is the axial-feed amount of the skiving cutter, which are given as

$$\left\{\begin{array}{l}{l}_{X}=0\\ {l}_{Y}=-{r}_{sc}\\ {l}_{Z}={v}_{f}t\\ {l}_{A}=\gamma \\ {l}_{B}=\sum ={\beta }_{c}\\ {\varphi }_{c1}={\varphi }_{c2}\frac{{N}_{c}}{{N}_{f}}\end{array}\right.$$

(19)

In this case, the shaft angle is installed in a perpendicular direction $\gamma =\pi /2$; ${r}_{sc}$ is the reference radius that corresponds to the cutting-edge geometry design; ${v}_{f}$ is the moving rate of the cutting tool; and ${N}_{c}$ and ${N}_{f}$ are the tooth number of the skiving cutter and the generated face-gear, respectively. The rotational angle of the workpiece and skiving cutter spindles are implemented with a synchronous rotation relationship as follows:

$$\frac{{\varphi }_{c1}}{{\varphi }_{c2}}=\frac{{N}_{c}}{{N}_{f}}$$

(20)

As shown in Fig. 6, the meshing condition for every generated point on the face-gear tooth surface by the skiving cutter can be derived as follows: the normal vector ${\mathbf{n}}_{f}$ of the generated point G on the tooth surface is certainly perpendicular to the tangent vector ${\mathbf{t}}_{w}$ of the corresponding point on the skiving cutting tool profile.

$${f}_{w}={\mathbf{n}}_{f}.{\mathbf{t}}_{w}=\left({\mathbf{t}}_{\varphi c1}\times {\mathbf{t}}_{lz}\right).{\mathbf{t}}_{w}=\left(\frac{\partial \left[{x}_{w},{y}_{w},{z}_{w}\right]}{\partial {\varphi }_{c1}}\times \frac{\partial \left[{x}_{w},{y}_{w},{z}_{w}\right]}{\partial {l}_{z}}\right).{\mathbf{t}}_{w}=0$$

(21)

where ${\mathbf{t}}_{\varphi c1}$ and ${\mathbf{t}}_{lz}$ are the tangent vectors related to the parameters ${\varphi }_{c1}$ and ${l}_{z}$ of the face-gear tooth flank, respectively.

Fig. 6

Illustration of meshing condition

A set of solutions $\left({\varphi }_{c1},{l}_{z}\right)$ can be obtained by simultaneously giving a known z-component value for each transverse section of the skived face-gear tooth flank in Eq. (16) and solving the meshing equation Eq. (21). The tooth surfaces of the skived face gear are attained by substituting the solution sets $\left({\varphi }_{c1},{l}_{z}\right)$ into Eq. (16).

3 Numerical approach for topology modification in face-gear power skiving

In the gear skiving process, the skiving cutter is a helical pinion type with geometry modification for cutting purposes such as the top relief and rake angles to optimize cutting efficacy. Theoretically, an imaginary helical pinion with the same design parameter as the skiving tool conjugates with the generated face gear at a crossed-axis angle. However, achieving the desired accuracy in the face gear tooth surface poses challenges due to the inherent mismatch between the cutting tool profile and the conjugating transverse section of an imaginary helical gear. This mismatch results in errors in tool geometry and subsequent normal deviations on the tooth surface. To address these challenges, previous researchers have proposed two primary correction methods:

• Cutting tool design correction: One approach involves modifying the cutting tool geometry, considering factors such as top relief and rake angles [11, 12, 16]. This correction is efficient in addressing the complex tooth geometry of the face gear, particularly in correcting normal deviations along the tooth flank profile direction. Besides, achieving the designed accuracy solely through this method can be labor-intensive. Because each profile section along the tooth length direction is different, it is difficult to calculate the corrected profile of the cutter.

• Machine-axis motion modification: this method focuses on modifying the motion axis using a high-order form of an independent motion parameter. This adjustment aims to obtain the requisite accuracy, especially in the lengthwise direction. It is less effective to obtain the coefficient value through experiments or to attempt different values to obtain the optimal value because changes in gear geometries affect the value of the polynomial coefficients of machine motions [12, 13, 18, 20].

The idea combines correcting the cutting tool geometry to handle tooth flank profile deviations and simultaneously modifying the machine-axis motion to enhance accuracy. This study proposes a closed-loop optimization to simultaneously calculate the adjusting coefficients of machine-axis motion and the modification amount of the rack cutter profile. Simultaneously, the modified amounts on the normal section of the rack cutter and the motion parameters of the machining axes are corrected using the Levenberg–Marquardt (LM) algorithm [24, 25], combined with the sensitivity matrix [26]. The proposed method is presented in turn in the following sections.

3.1 Mathematical modeling for machine-axis modification of the multi-axis CNC machine in gear skiving process

The skiving process operates in two movements: the synchronizing rotation between the workpiece and the skiving cutter at a constant ratio and the feeding motion of the cutting tool along the z-axis direction of the machine, as shown in Fig. 5. To adjust the movement of the cutting tool and the workpiece, machine-axis motion is modified by adding the high-order forms of additional coefficients. In some previous public articles, axis motion can be formulated up to a six-order polynomial function; however, based on some reference gear skiving machines, the limitation of adding polynomial function order depends on the motion-axis characteristic and the limit of the electronic gearbox. In this study, four machine axes are modified as a polynomial form of independent motion parameter ${C}_{Z}$. As proposed in previous studies [12, 13, 18, 20], machine-axis motions in CNC power skiving could be expressed as a six-order polynomial function to achieve the accuracy of the tooth surface. Therefore, machine axes are modified by adding a sixth-order term of polynomials as follows:

$$\left\{\begin{array}{l}{C}_{Y}=-{r}_{sc}+\Delta {C}_{Y}\\ {C}_{X}=\Delta {C}_{X}\\ {C}_{C1}={C}_{C2}\frac{{N}_{c}}{{N}_{f}}+\Delta {C}_{C1}\\ {C}_{B}={\beta }_{c}+\Delta {C}_{B}\\ {C}_{A}=\gamma \end{array}\right.$$

(22)

wherein.

$\begin{array}{c}\Delta {C}_{y}=\sum \limits_{i=0}^{k}{a}_{i}{{C}_{Z}}^{i}\\ \Delta {C}_{C1}=\sum \limits_{i=0}^{k}{b}_{i}{{C}_{Z}}^{i}\\ \Delta {C}_{X}=\sum \limits_{i=0}^{k}{c}_{i}{{C}_{Z}}^{i}\\ \Delta {C}_{B}=\sum \limits_{i=0}^{k}{d}_{i}{{C}_{Z}}^{i}\end{array}, k=6$  

where ${C}_{Z}$ is the feeding motion of the skiving cutter. The polynomial coefficients a_i, b_i, c_i, and d_i are polynomial parameters that modify the face-gear tooth topology.

The relative motion coordinate system for the face-gear skiving process considering axis-movement modification is presented in Fig. 7. The coordinate systems ${S}_{w}\left({x}_{w},{y}_{w},{z}_{w}\right)$ and ${S}_{c}\left({x}_{c},{y}_{c},{z}_{c}\right)$ are connected to the workpiece and the cutting tool, respectively; ${S}_{1}\left({x}_{1},{y}_{1},{z}_{1}\right)$, ${S}_{2}\left({x}_{2},{y}_{2},{z}_{2}\right)$, ${S}_{3}\left({x}_{3},{y}_{3},{z}_{3}\right)$, and ${S}_{4}\left({x}_{4},{y}_{4},{z}_{4}\right)$ are the auxiliary coordinate system for the coordinate transformation. Coordinate transformation matrixes for axis-movement modification are expressed as follows:

Fig. 7

Relative motion coordinate system in the face-gear skiving process considering additional motion

$${\mathbf{M}}_{wc}\left({C}_{C1},{C}_{Z}\right)={\mathbf{M}}_{w4}{\mathbf{M}}_{43}{\mathbf{M}}_{32}{\mathbf{M}}_{21}{\mathbf{M}}_{1c}$$

(23)

$${\mathbf{M}}_{w4}=\left[\begin{array}{cccc}\cos{C}_{C1}& -\sin{C}_{C1}& 0& 0\\ \sin{C}_{C1}& \cos{C}_{C1}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right], {\;\mathbf{M}}_{43}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos{C}_{A}& \sin{C}_{A}& 0\\ 0& -\sin{C}_{A}& \cos{C}_{A}& 0\\ 0& 0& 0& 1\end{array}\right], {\;\mathbf{M}}_{32}=\left[\begin{array}{cccc}1& 0& 0& -{C}_{X}\\ 0& 1& 0& {C}_{Y}\\ 0& 0& 1& {C}_{Z}\\ 0& 0& 0& 1\end{array}\right], {\;\mathbf{M}}_{21}=\left[\begin{array}{cccc}\cos{C}_{B}& 0& \sin{C}_{B}& 0\\ 0& 1& 0& 0\\ -\sin{C}_{B}& 0& \cos{C}_{B}& 0\\ 0& 0& 0& 1\end{array}\right], {\mathbf{M}}_{1c}=\left[\begin{array}{cccc}\cos{C}_{C2}& \sin{C}_{C2}& 0& 0\\ -\sin{C}_{C2}& \cos{C}_{C2}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

where ${C}_{C1}$ and ${C}_{C2}$ are the rotational angle of the workpiece and the cutting tool, respectively; ${C}_{A}$ is the shaft angle of the cutting tool spindle axis and the workpiece axis; ${C}_{B}$ is the tilted angle of the cutting tool spindle axis; ${C}_{Y}$ is the radial installation value of the skiving tool; and ${C}_{Z}$ is the axial-feed amount of the skiving tool.

3.2 Optimization model for calculating adjusting modified cutter and machine-axis settings

For topology modification purposes, it is necessary to calculate the tooth flank normal deviations between the generated and the theoretical tooth flank. The schematic of measurement points is based on the coordinate measuring machine (CMM) measurement. It is presented in Fig. 8. The measurement region must not be too close to the tip, end face, and fillet region. The measurement grid is defined in which the top and the bottom of the grid are 5% of the working depth from the start of the working depth, and 10% of the face width from the end face. The measurement grid is defined as a set of $5\times 9$ grid points divided into 45 points, i.e., 5 points placed from root to tip and 9 points placed from toe to heel. The normal deviation of each point $\tau$, calculated in a direction normal to the tooth flank surface between the generated and theoretical tooth surface, is given as

$$\tau =\left({\mathbf{r}}_{w}^{\prime}-{\mathbf{r}}_{f}^{\prime}\right)\cdot {\mathbf{n}}_{fg}=\left({x}_{w}-{x}_{f}\right){n}_{fgx}+\left({y}_{w}-{y}_{f}\right){n}_{fgy}+\left({z}_{w}-{z}_{f}\right){n}_{fgz}$$

(24)

where ${\mathbf{r}}_{w}^{\prime}$ and ${\mathbf{r}}_{f}^{\prime}$ are the first three position values of the position vector ${\mathbf{r}}_{w}$ and ${\mathbf{r}}_{f}$, respectively; and ${\mathbf{n}}_{f}$ is the normal vector of the theoretical tooth surface.

Fig. 8

Definition of face-gear tooth measurement: a illustration of the measurement region on the tooth flank and b topography of the face-gear tooth surface

According to the effect of each polynomial coefficient in Eq. (22) and limitations of practical machines, such as motion characteristics and the limit of the electronic gearbox. There are twenty coefficients approaching zero, ${a}_{i}\approx {b}_{i}\approx {c}_{i}\approx {d}_{i}\approx 0$, 2 ≤ i ≤ 6. Therefore, eight polynomial coefficients, a₀, a₁, b₀, b₁, c₀, c₁, d₀, and d₁, are considered in the sensitivity calculation, including the radial feed y-axis, tangential feed x-axis, the installation axes C1 for the shaft angle of the workpiece, and the rotary axis B. By substituting polynomial coefficients into Eq. (22), the motion axes are expressed as follows:

$$\left\{\begin{array}{l}{C}_{Y}=-{r}_{sc}+{a}_{0}+{a}_{1}{C}_{z}\\ {C}_{X}={c}_{0}+{c}_{1}{C}_{z}\\ {C}_{C1}={C}_{C2}\frac{{N}_{c}}{{N}_{f}}+{b}_{0}+{b}_{1}{C}_{z}\\ {C}_{B}={\beta }_{c}+{d}_{0}+{d}_{1}{C}_{z}\\ {C}_{A}=\gamma \end{array}\right.$$

(25)

An optimization model is proposed using the Levenberg–Marquardt (LM) algorithm to simultaneously calculate the adjusting coefficients of machine-axis motion and the modification amount of the rack cutter profile. Fourteen unknown values need to be determined, including eight polynomial coefficients (a₀, a₁, b₀, b₁, c₀, c₁, d₀, and d₁) in Eq. (25) and six coefficients of the modified rack (m_r,1, n_r,1, m_r,2, n_r,2, e₁ and e₂) in Eq. (1). Following the solving algorithm; it is necessary to provide an initial guess for each polynomial coefficient. The sensitivity matrix can be defined through the effect of each polynomial coefficient on the normal deviation ${\mathbf{M}}_{s}$:

$${\mathbf{M}}_{s}=\left[\frac{\partial {\tau }_{i}}{\partial {c}_{j}}\right]=\left[\begin{array}{cccc}\frac{\partial {\tau }_{1}}{\partial {c}_{1}}& \frac{\partial {\tau }_{1}}{\partial {c}_{2}}& \cdots & \frac{\partial {\tau }_{1}}{\partial {c}_{j}}\\ \frac{\partial {\tau }_{2}}{\partial {c}_{1}}& \frac{\partial {\tau }_{2}}{\partial {c}_{2}}& \cdots & \frac{\partial {\tau }_{2}}{\partial {c}_{j}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial {\tau }_{i}}{\partial {c}_{1}}& \frac{\partial {\tau }_{i}}{\partial {c}_{2}}& \cdots & \frac{\partial {\tau }_{i}}{\partial {c}_{j}}\end{array}\right]$$

(26)

where $i=1\sim 90$ indicates the number of measurement points on both sides of the gear tooth flank and $j=1\sim 14$ is the number of additional polynomial coefficients.

Applying the Levenberg–Marquardt (LM) algorithm [23,24,25], with the target normal deviations on the gear tooth flank given, the polynomial coefficients $\delta {c}_{j}$ for the axis-movement modification can be calculated through the following equation:

$$\left\{\delta {c}_{j}\right\}={\left({\mathbf{M}}_{s}^{T}{\mathbf{M}}_{s}+\xi \mathbf{I}\right)}^{-1}{\mathbf{M}}_{s}^{T}\left\{{\delta \tau }_{i}\right\}$$

(27)

where ${\delta \tau }_{i}$ is the normal deviation of all measurement points; $\xi$ is the damping coefficient, defined as max $\left\{{\mathbf{M}}_{s}^{T}{\mathbf{M}}_{s}\right\}$; and I is the identity matrix.

Following the flowchart, as shown in Fig. 9, the iterative procedure for face-gear tooth flank modification is: (a) define the target surface of the desired tooth flanks; (b) input the design parameters of the skiving tool that corresponds to the target surface. The different amounts between the normal deviations on the target surface and normal deviations on skived gear with the non-modified skiving cutter are defined as mismatched amounts; (c) the modification amounts on the rack profiles can be calculated; (d) generate the skiving cutter; (e) define the sensitivity matrix and calculate the polynomial coefficients by the LM algorithm; (f) simulate the skiving process with the additional polynomial coefficients; (g) calculate the normal deviations on both sides of the gear tooth flank; (h) check the required conditions R¹ and R². If the generated surface meets the requirement, the iterative loop will end. If the calculated normal deviation does not meet the requirement, the algorithm will return to step (c) to re-calculate the modification amounts on the rack profiles. For each iteration, the target surface and the polynomial coefficients will be updated by adding the value of the normal deviation and coefficients calculated from the previous iteration.

Fig. 9

Flowchart for tooth flank modification based on the Levenberg–Marquardt (LM) algorithm in the face-gear skiving process

The required condition to terminate the loop is given as

$$\max\left|{\mathbf{M}}_{s}^{T}\left\{{\delta \varepsilon }_{i}\right\}\right|<\varsigma$$

(28)

where $\varsigma ={10}^{-4}$ is the convergence value for the loop.

4 Numerical examples

Based on the proposed topology modification method, three cases of different pre-designed target surfaces, as shown in Fig. 10, are applied to verify the proposed method. Case 1: target surface with accuracy following the standard grade (Sect. 4.1); Case 2: target surface is a pre-defined grinding stock amount surface for the finishing process (Sect. 4.2); and as presented in Sect. 4.3, Case 3: target surface with a pre-defined double-crowning surface for meshing contact purposes. The basic parameters for the face gear and the skiving cutter are listed in Table 1.

Fig. 10

Three pre-designed target surfaces of gear tooth surface modification

Table 1 Design parameters for the face-gear skiving process

As shown in Fig. 11, the topography of the original generated face-gear tooth surface in the skiving process is presented, in which all geometric modifying parameters of the skiving cutter and all additional polynomial coefficients of machine-axis motion are not considered.

Fig. 11

Illustration of face-gear tooth topography

4.1 Non-grinding face-gear tooth surface with pre-defined accuracy grade

The gear power skiving process is efficient for rough machining, particularly for non-grinding gear machining. Therefore, in Case 1, in which the target surface is based on the ANSI/AGMA 2009-B01 [27] gear accuracy standard for the bevel gear, the generated face-gear tooth achieves an accuracy grade of B3. According to the ANSI/AGMA standard accuracy grade B3 with the corresponding normal module, total profile deviation ${F}_{p}=\left({\max\tau }_{i}^{p}-{\min\tau }_{i}^{p}\right)\le 5$ μm Furthermore, all measured normal deviations on the generated surface ${\tau }_{pi}\ge 0$ shall be positive values. Therefore, the target amount for all measured normal deviations ${\tau }_{i}^{t}$ is equal to 1.0 μm, as shown in Fig. 12a.

Fig. 12

Gear tooth topographies in Case 1: a target surface; b generated surface considering modification

As shown in Fig. 12b, the topography of the gear tooth has considered skiving cutter modification; after twenty-five iterations, the required condition R¹ is satisfied. The obtained normal deviations on the gear tooth surface are shown in Table 2. The maximum and minimum normal deviations are 1.44 μm and 0.53 μm, respectively, and the total profile deviation ${F}_{p}$ = 0.91 μm < 5.0 μm. The generated surface satisfies the accuracy grade B3 requirement. Table 3 shows the value of the calculated parameters of the cutting tool and calculated polynomial coefficients of machine-axis motion in Case 1.

Table 2 Obtained normal deviations in Case 1 with consideration of machine-axis modification (unit: μm)

Table 3 Calculated cutter parameters and polynomial coefficients in Case 1

4.2 Face-gear tooth surface with a pre-defined even grinding stock amount

The grinding allowance refers to a predefined quantity of material allocated on the gear tooth surface, primarily intended for the surface finishing process, particularly for the grinding process. The amount of grinding stock is crucial in determining various aspects, such as the gear tooth surface quality, grinding productivity, and manufacturing cost. This study applies the proposed modification method to accurately determine the required grinding stock on the face-gear tooth surface. The objective is to optimize the grinding process and minimize friction to enhance the grinding tool life and improve the quality of the grinding surface. The designated target surface is the tooth surface with an even grinding stock, in which the given amount is 100.0 μm, as shown in Fig. 13a.

Fig. 13

Gear tooth topographies in Case 2: a target surface; b generated surface considering modification

After thirty iterations in the calculation loop for axis-machine motion, the required condition R¹ is satisfied. The topography of the generated gear tooth with calculated parameters is presented in Fig. 13b, and the obtained normal deviations on the gear tooth surface are shown in Table 4. The maximum and minimum normal deviations are 100.49 μm and 99.53 μm, respectively. The proposed method has successfully generated the face-gear tooth surface with an even grinding-stock amount, with the largest normal deviation compared to the target surface ${F}_{t\max}$ = 0.96 μm < 5.0 μm. According to the computed result, the calculated parameters of the cutting tool and the polynomial coefficients of machine-axis motion are presented in Table 5.

Table 4 Obtained normal deviations in Case 2 with consideration of machine-axis modification (unit: μm)

Table 5 Calculated cutter parameters and polynomial coefficients in Case 2

4.3 Double-crowning face-gear tooth surface with a pre-defined crowning amount

The tooth contact pattern for the face gear or bevel gear is a necessary indication for inspecting the mating region and load distribution over the tooth surface. Many previous studies have proven the advantages of double-crown gear tooth surfaces. The double-crowning gear tooth surface, which performs a high-efficiency tooth contact region, optimizes the loaded tooth contact and prevents edge contact in gear mating [16] ,20. In this case, the proposed modification method is applied to obtain the non-grinding face-gear tooth surfaces with a pre-defined crowning amount for a double-crowning surface, considering the crown in both profile and longitudinal directions. The target surface is shown in Fig. 14a, and the pre-defined crowning amount on the gear-tooth surface is presented in Table 6.

Fig. 14

Gear tooth topographies in Case 3: a target surface; b generated surface considering modification

Table 6 Target normal deviations on the face-gear tooth surface with the double-crowning pre-defined amount (unit: μm)

Due to the complex target surface with crowning amounts on both profile and longitudinal directions, the generated tooth surfaces considering cutter modification are required to fit the distribution of the deviations on the desired surface. The modification axis process is applied to achieve the desired tolerance. After thirty iterations in the calculating loop, the required condition R¹ is satisfied. The calculated parameters of the cutting tool and the additional polynomial coefficients are listed in Table 7. With the modified axis-machine motions, the topography of the generated surface is shown in Fig. 14b, and the normal deviation distribution is listed in Table 8. Compared to the pre-defined target amounts, the maximum tolerance of the generated tooth surface is F_tmax = 3.29 μm ≤ 5.0 μm.

Table 7 Calculated cutter parameters and polynomial coefficients in Case 3

Table 8 Obtained normal deviations in Case 3 with consideration of machine-axis modification (unit: μm)

To simulate the changing in the contact status of face gears under load at various rotational angles, a load tooth contact analysis for face gear pairs was conducted using finite element analysis (FEA) in the ANSYS software, incorporating Hertz contact theory. The semi-major and semi-minor axes of the contact ellipse were determined based on the applied load, contact ratio, longitudinal position, and effective Young’s modulus, as presented in the Appendix. The pressure distribution on the tooth flank of the face gear was calculated using Hertzian contact theory [28, 29]. The load application in the FEA model involved setting up a detailed 3D model of the face gear and pinion, applying appropriate boundary conditions, and simulating the gear meshing process under load. The load was positioned on the tooth flank, taking into account the contact ratio and load distribution during operation. The contact analysis was performed using FEA software to determine the pressure distribution and stress on the tooth flank. Specifically, the rotation angles of the face gear were set at 2° and 4°, and the moment applied to the pinion was 800.0 Nm. The face gear sector was constrained by fixing the lateral and bottom surfaces of the rim. Simultaneously, the nodes on the lateral surfaces of the pinion sector were constrained to rotate rigidly around the axis of the pinion. The loading condition involved applying a torque to a node defined on the pinion axis, as shown in Fig. 15. The design parameters of the face-gear drive are shown in Table 1, and Young's modulus E = 2.1 ×10¹¹ Pa.

Fig. 15

FEM constrained and loaded model of Face gear drives using ANSYS software

Initially, the analysis results of tooth contact pressure were obtained for the theoretical face gear without any modifications, designed based on the gear shaping process, as shown on the left side in Figs. 16 and 17. Subsequently, tooth contact pressure analysis was performed for face gears featuring double-crowning modifications, as shown on the right side in Figs. 16 and 17, which show the trend of contact pressure on the tooth surface. The contact pressure on the right-side tooth surface was predominantly distributed near the middle of the tooth surface, with no instances of edge contact. Similarly, contact pressure on the left-side tooth surface exhibited a similar distribution pattern, primarily concentrated around the middle sections, without any edge contact on the tooth surfaces. As shown in Fig. 18, the contact pressure and contact stress of the modified tooth surface are more evenly distributed. This reduces localized high-stress areas on the tooth flank of the face gear. According to the results of the analysis, the proposed modification method can successfully generate a double-crowning surface for both sides of the face-gear tooth based on the desired target surface.

Fig. 16

The contact pressure on the face gear tooth flank at the rotation angle 2°

Fig. 17

The contact pressure on the face gear tooth flank at the rotation angle 4°

Fig. 18

Contact pressure and contact stress of theoretical and modified face gear drives: a contact pressure and b contact stress

4.4 Verification based on VERICUT software

A virtual machining model is established in VERICUT software based on a computer numerical control (CNC) machining machine to validate the methodology proposed in this study. The structure of the machine model follows from the conceptual machine model presented in Sect. 2. The CNC machine comprises six machining axes, including three translation axes and three rotation axes. Three rotation axes include the workpiece rotation axis, the tool rotation axis, and the axis for the cross angle. The NC code file has been created based on the value of calculated coefficients and the principle of generation [30]. Additionally, the following machining simulations utilized the numerical cases in Sect. 4.1.

The generated face-gear tooth surfaces in the VERICUT simulation are shown in Fig. 9. With the cut stock exported from simulation software, normal deviations on the profile of generated tooth surfaces can be calculated. By overlapping two generated surfaces, as shown in Fig. 19, it is observed that the deviations on the generated surface in the VERICUT simulation result very close to the normal deviations in the proposed mathematical method. As shown in Fig. 20, the distribution of deviations obtained by the simulation result follows the distribution trend of normal deviations on the tooth surfaces generated by the skiving process (as shown in Fig. 12b and Table 2), indicating that the proposed computing method is correct even though there is a slight difference between the two curves caused by the grid quality of the CAD workpiece model in VERICUT software.

Fig. 19

Simulation model of machining spur face gear in multi-axis CNC gear skiving machine

Fig. 20

Comparing errors between the mathematical model and the VERICUT simulation model

The errors between the generated tooth surfaces from VERICUT software and the proposed mathematical model are caused by some reasons: generating the skiving cutter from numerical result to CAD model involves a mismatch in the generated cutting edge profile; setting tolerance of virtual machining system, including developed CAD model and virtual simulation software; solving the skived gear profile using the VERICUT with triangle mesh cut stock, the mismatch between the approximation point from a triangle mesh.

The correctness and flexibility of the proposed method are evident based on the findings from three numerical examples and software simulations.

5 Conclusions

This study presented a pioneering approach to obtaining accuracy in the face-gear skiving process through a comprehensive modification method. This method concurrently addresses skiving cutter geometry and machine-axis motion modifications, leveraging advanced mathematical models using the Levenberg–Marquardt algorithm combined with the sensitivity matrix in a closed-loop optimization. Incorporating the target surfaces in the calculation of skiving cutter geometry modifications, coupled with considering high-order function additional coefficients for machine-axis modification, results in successfully realizing the desired face-gear tooth flanks. The generated tooth surface topography has confirmed the effectiveness of the proposed method. The validation through numerical examples and machining simulations underscores the practicability and adaptability of the proposed method for achieving the accuracy of skived tooth surfaces of face gear based on the desired target tooth surfaces.

Appendices

Appendix 1. Contact ratio of face gear pair

The modification for the face gear drive must satisfy several conditions: maintaining a sufficiently large contact ratio, ensuring adequate tooth tip thickness, and preventing interference during engagement. The contact ratio is crucial for distributing the load across the gear teeth during engagement; a higher contact ratio involves more teeth in the meshing process, resulting in smoother gear transmission for continuously profile-shifted modified face gear pairs, variations in the modification coefficient along the tooth’s longitudinal direction cause changes in the tooth addendum and dedendum at different sections. Consequently, the contact ratio for the face gear pair varies along the tooth’s longitudinal direction. However, the modification coefficient for the face gear pair can still be considered constant at any given section. Points D₁ and D₂ represent the start and end points on the meshing line of the face gear drive's tooth surface, with D₁ being the intersection of the meshing line and the pinion addendum circle and D₂ being the intersection of the meshing line and the face gear addendum circle. As shown in Fig. 21, the rotation angle of the pinion during a meshing cycle with face gear is $\widehat{{D}_{1}{O}_{p}{D}_{2}}$. Since the face gear’s tooth profile engaging with the pinion is equivalent to that of a gear rack during the engagement, the working length of the meshing line is the displacement of the contact point along this line during a meshing cycle on the face gear’s tooth surface, which is presented as

Fig. 21

Schematic of contact ratio in face gear drives

$$\overline{{D }_{1}{D}_{2}}={r}_{p}\left(\tan{\alpha }_{c1}-\tan{\alpha }_{c}\right)+\frac{{h}_{af}}{\sin{\alpha }_{c}}$$

(29)

The contact ratio ε can be calculated as follows:

$$\varepsilon =\frac{\overline{{D }_{1}{D}_{2}}}{{p}_{g}}+\frac{v\sin{\beta }_{p}}{\pi m}$$

(30)

wherein ${p}_{g}=\pi m\cos{\alpha }_{c}$ is the base circle tooth pitch of pinion; h_af  is the tooth addendum of face gear; β_p is the helix angle of the pinion; v is the longitudinal position of tooth length; and α_c1 and α_c are addendum pressure angle and pressure angle of pinion, respectively.

Additionally, although the contact ratio values vary, the overall shape of the curve remains consistent when the modification coefficient or longitudinal position v changes. The calculation of the contact ratio for a face gear pair at a single section has already been discussed. Given that the modification coefficient of a continuously profile-shifted face gear pair varies along the tooth's longitudinal direction, the contact ratio will also vary depending on different modification coefficient functions, even at the same longitudinal position. As a result, the distribution of the contact ratio along the tooth's longitudinal direction for the face gear pair changes accordingly.

Appendix 2. Contact pressure distribution

Due to the elastic deformation at the tooth’s contact surface, the instantaneous contact point expands into an elliptical shape, which serves as the center of symmetry. This results in a series of contact ellipses forming the contact trace. These ellipses’ orientation and aspect ratio is determined by the principal curvature and the primary directions of the two contacting tooth surfaces. The elastic deformation at the contact point influences the length of the major axis of these ellipses. This deformation, denoted as δ, is dependent on the applied load, which is generally small when assessing the contact between two tooth surfaces.

As presented in Fig. 22, the two tooth surfaces contact at point P_ct, forming deformation areas A₁P_ctA₂ and B₁P_ctB₂ upon contact, which are originally denoted as A₁P₁A₂ and B₁P₂B₂ before contact. The elastic deformation of the tooth surface at contact point P_ct is represented by the normal offset from the point to the common tangent plane. Assuming the elastic deformations of the two tooth surfaces are ζ₁ and ζ₂, the total elastic deformation ζ at contact point P_ct can be calculated by ζ = ζ₁ + ζ₂. Let points M₁ and M₂ be the next pair of points in continuous tangent contact on the two tooth surfaces. Assuming the elastic deformations at points M₁ and M₂ are equal to zero, which is the case when points M₁ and M₂ are at the edge of the elastic deformation zone on the tooth surface, then the elastic deformation at the edge of the contact ellipse can be calculated $\zeta =\left|\overline{{MM }_{1}}-\overline{{MM }_{2}}\right|$. The vertical offset to the tangent plane l_v of any point on the tooth surface can be determined using the following equation:

$${l}_{v}=\frac{{K}_{n}{\left({\rho }_{e}\right)}^{2}}{2},n=p,f$$

(31)

where K_n is induced normal curvature of tooth surface, ρ_e is tangential offset from point M to point P_ct. Combining with Euler equation, Eq. (32) can be obtained.

$$\overline{{MM }_{1}}-\overline{{MM }_{2}}=\frac{{\left({\rho }_{e}\right)}^{2}}{2}\left[{K}_{f}^{\left(1\right)}{\cos}^{2}{q}_{1}+{K}_{p}^{\left(1\right)}{\sin}^{2}{q}_{1}-\left({K}_{f}^{\left(2\right)}{\cos}^{2}{q}_{2}+{K}_{p}^{\left(2\right)}{\sin}^{2}{q}_{2}\right)\right]=\pm \zeta$$

(32)

where ${K}_{f}^{\left(1\right)}$ and ${K}_{f}^{\left(2\right)}$ are principal curvatures of tooth surface Σ_f; ${K}_{p}^{\left(1\right)}$ and ${K}_{p}^{\left(2\right)}$ are principal curvatures of tooth surface Σ_f; q₁ is directed angle from principal direction d⁽¹⁾ of tooth surface Σ_f to $\stackrel{\rightharpoonup }{{P}_{ct}M}$; and q₂ is directed angle from principal direction d⁽²⁾ of tooth surface Σ_p to $\stackrel{\rightharpoonup }{{P}_{ct}M}$.

Fig. 22

Diagram of contact ellipse for face gear drives

The two coordinate axes (ɳ_a, ɳ_b) on the tangent plane are selected as the two axes of the contact ellipse. Figure 22 presents the relationships between the contact ellipse axes and principal directions angles of the two contact tooth surfaces are. α⁽¹⁾ is principal direction angle of tooth surface Σ_f, and α⁽²⁾ is principal direction angle of tooth surface Σ_p. Substituting ${q}_{1}={\alpha }^{\left(1\right)}+{\mu }_{e} ,{q}_{2}={\alpha }^{\left(2\right)}+{\mu }_{e} ,{\rho }^{e}={\eta }_{a}^{2}+{\eta }_{b}^{2},\sin{\mu }_{e}=\frac{{\eta }_{a}}{{\rho }^{e}}$ and $\cos{\mu }_{e}=\frac{{\eta }_{b}}{{\rho }^{e}}$ into Eq. (32), it becomes:

$$\eta_a^2[K_{f}^{(1)}\cos^2\alpha^{(1)}+K_{p}^{(1)}\sin^2\alpha^{(1)}-(K_{f}^{(2)}\cos^2\alpha^{(2)}+K_{p}^{(2)}\sin^2\alpha^{(2)})]+\eta_b^2[K_{f}^{(1)}\sin^2\alpha^{(1)}+K_{p}^{(1)}\cos^2\alpha^{(1)}-(K_{f}^{(2)}\sin^2\alpha^{(2)}+K_{p}^{(2)}\cos^2\alpha^{(2)})]-\eta_a\eta_b[(K_{f}^{(1)}-K_{p}^{(1)})\sin2\alpha^{(1)}-(K_{f}^{(2)}-K_{p}^{(2)})\sin2\alpha^{(2)}]=\pm2\zeta$$

(33)

There are ${\alpha }^{\left(2\right)}={\alpha }^{\left(1\right)}+{\sigma }_{e}$ and $\left({K}_{f}^{\left(1\right)}-{K}_{p}^{\left(1\right)}\right)\sin2{\alpha }^{\left(1\right)}-\left({K}_{f}^{\left(2\right)}-{K}_{p}^{\left(2\right)}\right)\sin2{\alpha }^{\left(2\right)}=0$. Finally, contact ellipse equation can be presented as follows:

$$\left\{\begin{array}{l}{B}_{el}{\eta }_{a}^{2}+{A}_{el}{\eta }_{b}^{2}=\pm \zeta \\ {B}_{el}=\frac{{K}_{fp}^{\left(1\right)}-{K}_{fp}^{\left(2\right)}-\sqrt{{G}_{1}^{2}-2{G}_{1}{G}_{2}\cos2{\sigma }_{e}+{G}_{2}^{2}}}{4}\\ {A}_{el}=\frac{{K}_{fp}^{\left(1\right)}-{K}_{fp}^{\left(2\right)}+\sqrt{{G}_{1}^{2}-2{G}_{1}{G}_{2}\cos2{\sigma }_{e}+{G}_{2}^{2}}}{4}\end{array}\right.$$

(34)

wherein

$$\left\{\begin{array}{l}{K}_{fp}^{\left(i\right)}={K}_{f}^{\left(i\right)}+{K}_{p}^{\left(i\right)}\\ {G}_{i}={K}_{f}^{\left(i\right)}-{K}_{p}^{\left(i\right)}\end{array}, i=\text{1,2}\right.$$

(35)

The principal curvature of tooth surface ${K}_{fp}^{\left(i\right)}$ can be determined by simultaneously solving the first and second basic quadratic homogeneous polynomials of the tooth surface along with the Rodrigues formula. Consequently, the directions d⁽¹⁾ and d⁽²⁾ and phase difference σ_e in the principal directions of the two tooth surfaces are also determined. Thus, the semi-major axis a_el and semi-minor axis b_el of the contact ellipse can be expressed as follows:

$$\left\{\begin{array}{c}{a}_{el}=\sqrt{\left|\frac{\zeta }{{A}_{el}}\right|}\\ {b}_{el}=\sqrt{\left|\frac{\zeta }{{B}_{el}}\right|}\end{array}\right.$$

(36)

To accurately determine the pressure distribution on the tooth flank of the face gear, we utilized the Hertzian contact theory, which is widely used for gear contact analysis. The contact area between the mating teeth of the face gear and pinion is calculated based on the gear geometry and applied load. The semi-major axis a and semi-minor axis b of the contact ellipse underloaded are determined using the following equations:

$$\begin{array}{c}a=\sqrt{\frac{4F\left(1-{v}^{2}\right)}{\pi Eb}}\\ b=\sqrt{\frac{4F\left(1-{v}^{2}\right)}{\pi Ea}}\end{array}$$

(37)

where F is the applied load; ν is the longitudinal position; and E is the effective Young’s modulus. Start with an initial value of a and b, which are a_el and b_el, respectively. Continue iterating until the changes in a and b between successive iterations are smaller than a predefined tolerance level, indicating convergence.

The contact pressure p(x, y) at any point (x, y) along the contact line is calculated using the Hertzian contact pressure distribution equation:

$$p\left(x,y\right)=\frac{2F}{\pi ab}\sqrt{1-{\left(\frac{x}{a}\right)}^{2}-{\left(\frac{y}{b}\right)}^{2}}$$

(38)