A novel approach to attain tooth flanks with variable pressure and helical angles utilizing the same cutter in the CNC gear skiving process

Abstract

To save manufacturing costs and enhance design flexibility in gear skiving, a dual closed loop, including inner and outer closed loops, is proposed to generate skived gear tooth flanks with different pressure angles and helix angles using the same cutter. The skiving cutter is firstly generated based on the suitable form of the corrected rack, which is defined according to the target tooth surface. The additional motions considering the motion limits of an electronic gearbox for the machining axis are added in the form of polynomials. The inner closed loop based on the Levenberg–Marquardt algorithm is developed to attain the coefficients of polynomials in fitting the skived gear tooth flanks to the target surface. After completing a cycle of the inner closed loop, the skived gear’s pressure/helix angle is changed in the outer closed loop to renew the target surface, and then a new cycle of the inner closed loop is restarted. The suitable range of the skived gear’s pressure/helix angle is satisfied when the dual closed loop is fully ended. The effectiveness and practicality of the proposed method are verified by the presented numerical examples.

1 Introduction

Power skiving has recently received increasing attention in gear production since it constitutes a highly qualitative and productive machining method for external and internal gears [1,2,3,4]. The meshing relationship between a skiving cutter and a work gear is similar to that between a pair of non-intersecting axis gears. Accordingly, one skived gear demands one cutter with pre-defined parameters of pressure angle and helix angle. Therefore, to save manufacturing costs and enhance design flexibility in gear skiving, it is essential to explore a correction tooth flank method that allows using the same cutter for generating skived gears with different pressure angles and helix angles.

According to the theory of gearing [5], the work gear tooth flank can be corrected by cutter modification. Several researchers have found novel methods to improve the skived gear tooth flank more accurately by correcting the skiving cutter. Chen et al. [6, 7] proposed a complete mathematical model to construct and grind the prominent flank face of an error-free spur slice cutter, ensuring non-interference situations. Guo et al. [8] reported a corrected rack method to reduce the normal deviation of the skived gear based on analytical geometrics of the skiving cutter. In another study, the same author [9] developed an optimization method of skiving cutter profile to improve the twist phenomena of the skived gear tooth flank. Guo et al. [10] reported that the tooth profile error of the skived gear is affected by the inherent error of the conventional skiving tools and the longitudinal error of the cutting edge. Moriwaki et al. [11] then generated the cutting edge of a cylindrical skiving cutter from the intersection curve between the rake face and the conjugate barrel-shaped pinion surface to avoid the machining error of the skived gear. Shih and Li [12] presented an error-free flank face constructed by a set of intersection curves between generating gears and rake faces according to re-sharpened lengths. Recently, Tsai [13] established a cylindrical skiving cutter based on a barrel-shaped surface to avoid interference problems and achieve high accuracy of the skived gear surface. Subsequently, Shih et al. [14] proposed a cylindrical skiving cutter for internal circular splines with an error-free tooth flank by generating a cutting edge from the intersection curve of the rake face and barrel generating gear. Luu and Wu [15] developed a conical skiving cutter from a corrected normal rack to obtain even grinding stock on the tooth flank of the skived gear. The abovementioned studies successfully modified the gear surface by correcting the cutter profile with each pressure angle or helix angle of a pre-defined workpiece. However, an investigation into improving the flexibility of the cutter for generating skived gears with different pressure and helix angles has not yet been reported.

Many researchers, however, applied the method of motion modification of the computer numerical control (CNC) machine to modify the work gear tooth flank. For the skiving process, Guo et al. [16] modified the conjugation relationship between the standard shaper cutter and the skived gear by optimizing the setting parameters as a zero-order correction of the center distance, shaft angle, and rotation speed on the CNC machine. Zheng et al. [17] then investigated the effect of adding a coefficient for axis movement on normal deviation, path of contact, and transmission error in the gear skiving process. In addition, the motion modification method was applied in other machining processes. Fong [18] presented the third-order correction for CNC axis movement to improve the error on the universal hypoid generator. Shi and Fong [19] proposed a model to achieve the desired ease-off topographies of spiral bevel and hypoid gears tooth flank by modifying the original motions of the CNC machine up to degree six. Shi and Chen [20] corrected the motions for a CNC grinding machine by adding six-degree polynomials to enhance single-flank and dual-flank grinding accuracy. Tran and Wu [21] developed a closed-loop topology modification to attain double crowning with a minimum amount of twist for the external gear during the gear honing process. Shen et al. [22] used the approximation functions by Taylor expansion for displacement motions to obtain the double-crowned tooth geometry of face gear on a six-axis CNC machine using a disc grinding wheel. Jiang and Fang [23] developed a correction model for each axis motion of a CNC hob machine using the adding function in terms of high-order polynomial function to generate the anti-twist tooth flank of helical gears. The motion modification method, however, can produce a significant error due to the motion modification limit of the machining axis and the pre-defined surface conditions, such as a double-crowning surface or an even grinding stock surface. Furthermore, applying the motion modification method for using the same cutter to generate skived gears with different pressure angles or helix angles has not been considered in previous studies.

Based on the development of CNC machining technologies, many researchers proposed the method of manufacturing gear by combining the adjustments of tool design and tool path. Boa et al. [24, 25], Bizzarri and Barto [26], and Rajain et al. [27] presented the optimization cycle of a custom-shaped tool and its machining motions to attain high manufacturing accuracy and avoid overcutting on screw rotor, gears, or blisks. Accordingly, every tooth groove of the work gear is generated in one machining cycle. In addition, the work gear with a specific pressure angle or helix angle usually requires a customized cutting tool. Therefore, these methods consume manufacturing time and cost. Recently, Sandvik company [28] developed a technique named InvoMilling to productively manufacture gear using the special tool design and cutting path. Accordingly, the gear profile is flexibly changeable and manufactured without re-designing the tool. However, this method is more feasible for external gears, large module parts, and small batch production.

In view of these deficiencies, this paper proposes a novel approach to correct the skived gear tooth flank by combining the geometrical correction of the cutter and motion modification of the CNC machine in one process. Firstly, the segment on the normal rack is identified by a linear function or quadratic function depending on three cases of the target tooth surface: even grinding stock surface; non-grinding stock surface; or double-crowning surface. The cutting edge of the skiving cutter is then achieved by the intersection of the cutter body and the rack plane. The tangential feed, the center distance between the cutter and the skived gear, and the rotation angles of the skived gear on the CNC skiving machine are modified by adding the polynomial functions of the axial feed and rotation angle of the cutter. The motion limit of the electronic gearbox that shows the highest order of additional functions for each axis movement is considered. Finally, after several iterations of the inner closed loop, the skived gear tooth flank will fit the target surface. The coefficients of the machining axes are stored, and the pre-defined conditions of normal deviation on the entire skived gear surface are checked in the outer closed loop. If the conditions are not met, a new cycle of the inner closed loop is activated by a change of the skived gear’s pressure angle or helix angle. If the conditions are met, the changing range of pressure angle or helix angle is completely determined. Numerical examples validate the proposed method for the gear skiving process.

2 Mathematical model for generating a conical power skiving tool

The skiving cutter is divided into two types: conical-shaped and cylindrical-shaped. The clearance angle of the skiving cutter is constructed by either geometric design for the conical type or position correction of the cutter on the CNC machine for the cylindrical type. The conical shape has been shown to be more useful for the skiving cutter in terms of cutting resistance and machine settings than the cylindrical shape [3, 29]. Therefore, this section presents a mathematical model for generating a conical skiving based on the conjugating motion between an inclined rack and the cutter.

Figure 1 presents a helical conical skiving cutter, in which the top relief angle $\lambda$ and side clearance angle $\tau$ are automatically generated due to the continuous changing of shift coefficient between transverse sections. To construct the rake angle $\gamma$, an original plane is firstly located in a perpendicular direction with the lead line of the skiving cutter, and then rotated about the $x$-axis by an angle of $\gamma$ to generate a rake plane ${\uppi }_{{\text{r}}}$. Subsequently, a cutting edge which fully conjugates with the work gear during the skiving process is defined by an intersection curve between ${\uppi }_{{\text{r}}}$ and the cutter tooth flank. After a period of machining time, the skiving cutter will be re-sharpened on the rake plane to construct a new cutting edge for the next time.

Fig. 1

Geometric definitions of the conical skiving cutter

The skiving cutter tooth flank can be generated by the conjugation relationship between an inclined rack and skiving cutter, as shown in Fig. 2a. Accordingly, the inclined rack is constituted by arranging several transverses racks on transverse planes under an incline angle $\lambda$ also called the relief angle of the skiving cutter. Figure 2b illustrates the transformation coordinate system from the inclined rack to the skiving cutter, where the coordinate systems $S_{r} (x_{r} ,y_{r} ,z_{r} )$ and $S_{c} (x_{c} ,y_{c} ,z_{c} )$ are rigidly attached to the inclined rack and the skiving cutter, respectively, and $S_{1} (x_{1} ,y_{1} ,z_{1} )$, $S_{2} (x_{2} ,y_{2} ,z_{2} )$, and $S_{3} (x_{3} ,y_{3} ,z_{3} )$ are auxiliary coordinate systems. The position vector ${\mathbf{r}}_{r}$ and the normal vector ${\mathbf{n}}_{r}$ of the inclined rack in coordinate system $S_{r}$ are presented through the position vector of the corrected normal-rack, ${\mathbf{r}}_{n} \left( u \right) = \left[ {x_{n} \left( u \right),y_{n} \left( u \right),0,1} \right]^{T}$, which was introduced by Luu and Wu [15], as follows:

$$\begin{aligned}{\mathbf{r}}_{r} \left( {u,v} \right)& = \left[ {x_{r} \left( {u,v} \right),y_{r} \left( {u,v} \right),z_{r} \left( {u,v} \right),1} \right]^{T}\\& = \left[ {x_{n} \left( u \right),y_{n} \left( u \right) + v\tan \lambda ,v - x_{n} \left( u \right)\tan \beta_{c} ,1} \right]^{T}\end{aligned}$$

(1)

$${\mathbf{n}}_{r} \left( {u,v} \right) = \frac{{\partial_{u} \left[ {x_{r} ,y_{r} ,z_{r} } \right]^{T} \times \partial_{v} \left[ {x_{r} ,y_{r} ,z_{r} } \right]^{T} }}{{\left| {\partial_{u} \left[ {x_{r} ,y_{r} ,z_{r} } \right]^{T} \times \partial_{v} \left[ {x_{r} ,y_{r} ,z_{r} } \right]^{T} } \right|}}$$

(2)

where $u$ is the curve parameter of the corrected normal-rack; $v$ is the longitudinal parameter of the inclined rack; and $\beta_{c}$ is the helix angle of the skiving cutter. In addition, the explicit equations for each segment of the corrected normal rack are also presented in Table 8 of the Appendix.

Fig. 2

Meshing relationship between a skiving cutter and an inclined rack; a assembly relationship, and b relative coordinate systems

By applying the transformation matrix from coordinate systems $S_{r}$ to $S_{c}$, the position vector ${\mathbf{r}}_{r}$ and normal vector of skiving cutter ${\mathbf{n}}_{r}$ can be derived as:

$${\mathbf{r}}_{c} \left( {u,v,\varphi } \right) = \left[ {x_{c} \left( {u,v,\varphi } \right),y_{c} \left( {u,v,\varphi } \right),z_{c} \left( {u,v,\varphi } \right),1} \right]^{T} = {\mathbf{M}}_{cr} \left( \varphi \right){\mathbf{r}}_{r} \left( {u,v} \right)$$

(3)

$${\mathbf{n}}_{c} \left( {u,v,\varphi } \right) = {\mathbf{L}}_{cr} \left( \varphi \right){\mathbf{n}}_{r} \left( {u,v} \right)$$

(4)

$${\mathbf{M}}_{cr} = {\mathbf{M}}_{c3} {\mathbf{M}}_{32} {\mathbf{M}}_{21} {\mathbf{M}}_{1r}$$

$${\mathbf{M}}_{cr} = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } & {a_{14} } \\ {a_{21} } & {a_{22} } & {a_{23} } & {a_{24} } \\ {a_{31} } & {a_{32} } & {a_{33} } & {a_{34} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],\;{\mathbf{L}}_{cr} = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } \\ {a_{21} } & {a_{22} } & {a_{23} } \\ {a_{31} } & {a_{32} } & {a_{33} } \\ \end{array} } \right]$$

where

$$\begin{aligned}a_{11}& = \cos \beta_{c} \cos \varphi ,\;a_{12} = - \sin \varphi ,\;\\&a_{13} = - \cos \varphi \sin \beta_{c} ,\;a_{14} = \varphi r_{p} \cos \varphi - r_{p} \sin \varphi ,\end{aligned}$$

$$\begin{aligned}a_{21} &= \cos \beta_{c} \sin \varphi ,\;a_{22} = \cos \varphi ,\;\\&a_{23} = - \sin \beta_{c} \sin \varphi ,\;a_{24} = \varphi r_{p} \sin \varphi + r_{p} \cos \varphi ,\end{aligned}$$

$$a_{31} = \sin \beta_{c} ,\;a_{32} = 0,\;a_{33} = \cos \beta_{c} ,\;a_{34} = 0,$$

in which $\varphi$ is the rotational angle of the skiving cutter; and $r_{p}$ is the pitch radius of the skiving cutter.

According to the theory of gearing [5], the meshing relationship between the inclined rack and the skiving cutter in coordinate systems $S_{c}$ could be presented by the meshing equation as follows:

$$f_{0} = {\mathbf{n}}_{c} \cdot \frac{{\partial \left[ {x_{c} ,y_{c} ,z_{c} } \right]}}{\partial \varphi } = 0$$

(5)

The rotational angle $\varphi$ and the longitudinal parameter $v$ for each point on a transverse section of the skiving cutter are acquired by substituting specific values of the rack parameter $u$, and solving a set of Eq. (5) and z-component equation that is in a constant value for each transverse section. Therefore, the position vector and the normal vector of each point on the transverse section of the skiving cutter can be completely defined from Eqs. (3) and (4) based on a set of the above adopted values $\left( {u,v,\varphi } \right)$.

Moreover, the rotational angle $\varphi$ and the longitudinal parameter $v$ for each point on the cutting edge of the skiving cutter can be attained by substituting specific values of the rack parameter $u$ and solving the rake plane equation and Eq. (5) simultaneously. The equation of the rake plane ${\uppi }_{{\text{r}}}$ is given as follows:

$$n_{xf} (x - x_{f} ) + n_{yf} (y - y_{f} ) + n_{zf} (z - z_{f} ) = 0$$

(6)

wherein

$${\mathbf{r}}_{f} = \left[ {x_{f} ,y_{f} ,z_{f} } \right]^{T} = \left[ { - r_{p} \sin \psi ,r_{p} \cos\psi ,l_{f} } \right]^{T} ,\;\psi = \frac{{l_{f} \tan\beta_{c} }}{{r_{p} }},\;l_{f} = \frac{{\xi m_{n} \cos \beta_{c} }}{\tan\lambda }$$

(7)

$${\mathbf{n}}_{f} = \left[ {n_{xf} ,n_{yf} ,n_{zf} } \right]^{T} = \left[ { - \cos \gamma \sin \beta_{c} , - \sin \gamma ,\cos \beta_{c} \cos \gamma } \right]^{T}$$

(8)

where ${\mathbf{r}}_{f}$, ${\mathbf{n}}_{f}$, and $l_{f}$ are the position vector, the normal vector, and the z-component of the reference point on the rake plane in the coordinate system of cutter $S_{c}$, respectively; and $\xi$ and $m_{n}$ are the design shift coefficient and the normal module of the skiving cutter, respectively.

Additionally, the conjugation relationship between the cutting edge and the skived gear dominates the gear skiving process. Therefore, to simulate the cutting process, the tangent vector for each point of cutting edge ${\mathbf{t}}_{c}$ needs to be determined by substituting the value $\left( {u,v,\varphi } \right)$ of each point on the cutting edge into the following equation:

$${\mathbf{t}}_{c} = {\mathbf{n}}_{c} \times {\mathbf{n}}_{rp} = \left( {{\mathbf{t}}_{\varphi } \times {\mathbf{t}}_{v} } \right) \times {\mathbf{n}}_{rp} = \left( {\frac{{\partial \left[ {x_{c} ,y_{c} ,z_{c} } \right]}}{\partial \varphi } \times \frac{{\partial \left[ {x_{c} ,y_{c} ,z_{c} } \right]}}{\partial v}} \right) \times {\mathbf{n}}_{rp}$$

(9)

where ${\mathbf{n}}_{c}$ is the normal vector of the cutter flank face; and ${\mathbf{t}}_{\varphi }$, ${\mathbf{t}}_{v}$ are the tangent vectors corresponding to the variables $\varphi$ and $v$ of the cutter flank face, respectively.

3 Mathematical model for modifying the axis movements on a multi-axis CNC power skiving machine

In manufacturing gear by a CNC skiving machine, modification of each axis movement by adding a polynomial function is used to save manufacturing costs because the same skiving cutter can be used to manufacture the skived gear with different tooth profiles. However, the order of additional functions for each axis movement is limited for different CNC skiving machines. This issue has not yet been considered in extant literature. Therefore, this section presents a motion correction model for a CNC skiving machine considering the motion limit of the electronic gearbox based on an industrial CNC machine named Matrix GBG-3210.

As shown in Fig. 3, a CNC six-axis machine is considered based on the machine structure of GBG-3210 developed by Matrix Co., Ltd., with three linear and three rotational movements: the tangential feed X, radial feed Y, axial feed Z, and the rotation axis C₁ of the skiving cutter, and the tilt axis B and the rotation axis C₂ of the work gear, respectively. The coordinate systems $S_{c} (x_{c} ,y_{c} ,z_{c} )$ and $S_{w} (x_{w} ,y_{w} ,z_{w} )$ are rigidly attached to the cutter and work gear, respectively, while the coordinate systems $S_{1} (x_{1} ,y_{1} ,z_{1} )$, $S_{2} (x_{2} ,y_{2} ,z_{2} )$, and $S_{3} (x_{3} ,y_{3} ,z_{3} )$ are the auxiliary coordinate system for the coordinate transformation between the skiving cutter and the skived gear during the skiving process.

Fig. 3

Coordinate system for multi-axis CNC of the gear skiving machine

Figure 4 presents the motion control diagram for the skiving process. Two tangent circles box icon illustrates the original relative motion between the skiving cutter and the work gear. The curve box icons present the additional motions for the original relative motions. The additional motions for each axis movement are added in the form of polynomials and connected by an electronic gearbox. The maximum degree order of polynomials is based on the control characteristics of the CNC machine for each axis movement. The tangential feed X and radial feed Y axis can be adjusted to second-order; the rotation axis C₂ of the work gear can be adjusted to first-order; and the tilt axis B can be adjusted to zero-order. Therefore, the relative functions between the skiving cutter and the work gear on the CNC machine can be written as:

$$\left\{ \begin{array}{l} C_{y} = a_{w} = r_{oc} + \mu r_{ow} + a_{0} + a_{1} C_{z} + a_{2} C_{z}^{2} \hfill \\ C_{b} = \Sigma = \beta_{ow} + \mu \varepsilon \beta_{oc} + b_{0} \hfill \\ C_{x} = - \mu C_{z} \tan C_{b} + d_{0} + d_{1} C_{z} + d_{2} C_{z}^{2} \hfill \\ C_{c2} = C_{c1} \frac{{Z_{c} }}{{Z_{w} }} - \mu \varepsilon \frac{{C_{z} \tan \beta_{ow} }}{{r_{ow} \cos C_{b} }} + c_{0} + c_{1} C_{c1} + c_{2} C_{z} \hfill \\ \end{array} \right.$$

(10)

where $r_{oc}$, $\beta_{oc}$, and $Z_{c}$ represent the operation pitch, operation helix angle, and tooth number of the skiving cutter, respectively; $r_{ow}$, $\beta_{ow}$, and $Z_{w}$ represent the operation pitch, operation helix angle, and tooth number of the skived gear, respectively; $a_{0} \sim a_{2}$, $b_{0}$, $c_{0} \sim c_{2}$, and $d_{0} \sim d_{2}$ are polynomial coefficients of additional functions.

Fig. 4

Electronic gearbox schematic of the CNC machine for the modified tooth surface

The position vector ${\mathbf{r}}_{w}$ and tangent vector ${\mathbf{t}}_{w}$ of the skived gear can be expressed as follows:

$${\mathbf{r}}_{w} (C_{c1} ,C_{z} ) = \left[ {x_{w} ,y_{w} ,z_{w} ,1} \right]^{T} = {\mathbf{M}}_{wc} (C_{c1} ,C_{z} ){\mathbf{r}}_{c}$$

(11)

$${\mathbf{t}}_{w} (C_{c1} ,C_{z} ) = {\mathbf{L}}_{wc} (C_{c1} ,C_{z} ){\mathbf{t}}_{c}$$

(12)

$${\mathbf{M}}_{wc} = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } & {a_{14} } \\ {a_{21} } & {a_{22} } & {a_{23} } & {a_{24} } \\ {a_{31} } & {a_{32} } & {a_{33} } & {a_{34} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],\;{\mathbf{L}}_{wc} = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } \\ {a_{21} } & {a_{22} } & {a_{23} } \\ {a_{31} } & {a_{32} } & {a_{33} } \\ \end{array} } \right]$$

$$\begin{aligned}a_{11}& = \cos C_{b} \cos C_{c1} \cos C_{c2} - \mu \sin C_{c1} \sin C_{c2} ,\;\\&a_{12} = \cos C_{b} \sin C_{c1} \cos C_{c2} + \mu \cos C_{c1} \sin C_{c2} ,\end{aligned}$$

$$\begin{aligned}a_{13} &= \varepsilon \mu \cos C_{c2} \sin C_{b} ,\;\\&a_{14} = C_{x} \cos C_{c2} \cos C_{b} + \varepsilon \mu C_{z} \cos C_{c2} \sin C_{b} - \mu^{2} C_{y} \sin C_{c2} ,\end{aligned}$$

$$a_{21} = - \sin C_{c1} \cos C_{c2} - \mu \cos C_{b} \cos C_{c1} \sin C_{c2} ,$$

$$a_{22} = \cos C_{c1} \cos C_{c2} - \mu \cos C_{b} \sin C_{c1} \sin C_{c2} ,\;a_{23} = - \varepsilon \mu^{2} \sin C_{c2} \sin C_{b} ,$$

$$a_{24} = - \mu C_{x} \sin C_{c2} \cos C_{cb} - \mu C_{y} \cos C_{c2} - \varepsilon \mu^{2} C_{z} \sin C_{cb} \sin C_{c2} ,$$

$$\begin{aligned}a_{31} &= - \varepsilon \mu \cos C_{c1} \sin C_{b} ,\;\\ &a_{32} = - \varepsilon \mu \sin C_{c1} \sin C_{b} ,\;\\&a_{33} = \cos C_{b} ,\;a_{34} = C_{z} \cos C_{b} - \varepsilon \mu C_{x} \sin C_{b}\end{aligned}$$

where ${\mathbf{r}}_{c}$ and ${\mathbf{t}}_{c}$ are the position vector and the tangent vector of the cutting edge in coordinate system $S_{c}$; $\varepsilon$ indicates the helix direction of the skived gear along the gear-rotating axis, which is equal to 1 or $- 1$ for right-hand or left-hand directions, respectively; $\mu = 1$ denotes the external skived gear; $\mu = - 1$ denotes the internal skived gear; $C_{x}$, $C_{y}$, and $C_{z}$ indicate the three linear feeds of axes x, y, and z, respectively; $C_{c1}$ and $C_{c2}$ are the rotational angle of the skiving cutter and the work gear spindle, respectively; and $C_{b}$ represents the cross-axis angle of the skived-gear rotating axis.

At every instant of time, the position of cutting edge in the coordinate system S_w is determined by specifying $C_{c1}$ and $C_{z}$ in Eq. (11). As shown in Fig. 5a, the cutting edge moves according to the specific path during a period of time (t_in ~ t_out), and contacts with the skived gear flanks along the instant contact curve.

Fig. 5

Gear tooth generation principle; a cutting process, and b skived gear in transverse plane

Based on the theory of gearing, the unknown parameters $C_{c1}$ and $C_{z}$ of the instant contact point can be obtained by solving a set of two equations after substituting each set of the known coefficients, $(a_{0} ,a_{1} ,a_{2} ,b_{0} ,c_{0} ,c_{1} ,c_{2} ,d_{0} ,d_{1} ,d_{2} )$. The first equation is the meshing equation of the skived gear in coordinate system $S_{w}$, and the second is the equation of setting the position for the transverse plane in the z-axis direction. These equations are described as:

$$\left\{ \begin{array}{l} f_{1} = {\mathbf{t}}_{w} \cdot \left( {\frac{{\partial {\mathbf{r}}_{w}^{\prime } }}{{\partial C_{z} }} \times \frac{{\partial {\mathbf{r}}_{w}^{\prime } }}{{\partial C_{c1} }}} \right) = 0 \hfill \\ z_{w} = l_{z} \hfill \\ \end{array} \right.$$

(13)

where $l_{z}$ is the longitudinal length of gear tooth to be defined, and ${\mathbf{r}}_{w}^{\prime }$ is the first three components of ${\mathbf{r}}_{w}$. To solve the instant contact points on a specified transverse tooth section, $l_{z}$ is predefined first, the unknowns $C_{c1}$ and $C_{z}$ are then solved by Eq. (13). By substituting the solved values of $C_{c1}$ and $C_{z}$ into Eq. (11), the position of instant contact points on a transverse section of skived gear is successfully attained, as shown in Fig. 5b.

Furthermore, the trajectory of the skiving tool in the cutting process intersects with the transverse plane by a set of points called the cutting point cloud, where the unknown parameter $C_{c1}$ of these points can be calculated by solving a set of equations:

$$\left\{ \begin{array}{l} z_{w} = l_{z} \hfill \\ C_{z} = C_{z,\min } + j\frac{{C_{z,\max } - C_{z,\min } }}{{N_{z} }}\end{array} \right.,\;j = 0 \sim N_{z}$$

(14)

where $N_{z}$ is the number of cuts when the cutter performs the axial feed motion from $C_{z,\min }$ to $C_{z,\max }$. By substituting the solved values of $C_{c1}$ and $C_{z}$ into Eq. (11), the positions of the cutting point cloud are completely acquired.

To perform the overcutting checking, the point cloud of cutting trajectories and the skived gear tooth profile in one of transverse planes are presented as shown in Fig. 6. Boundary points are first detected among the point cloud. Subsequently, the normal deviation d between the boundary points and the corresponding skived gear profile is calculated by the following equation:

$$d = ({\mathbf{r}}_{w}^{\prime i} - {\mathbf{r}}_{w}^{\prime s} ) \cdot {\mathbf{n}}_{w} = (x_{w}^{i} - x_{w}^{s} )n_{wx} + (y_{w}^{i} - y_{w}^{s} )n_{wy} + (z_{w}^{i} - y_{w}^{s} )n_{wz}$$

(15)

where the superscript i denotes the boundary points of the cutting point cloud; the superscript s denotes the skived gear tooth profile; ${\mathbf{n}}_{w} = \left[ {n_{wx} ,n_{wy} ,n_{wz} } \right]$ is the unit normal vector of the skived gear tooth profile. If the normal deviations at all the boundary points are positive, no overcutting exists during the skiving process.

Fig. 6

Point cloud of cutting trajectories in one of transverse planes

4 A novel approach to correct the tooth flank of the skived gear

In gearing production, to enhance design flexibility and save manufacturing costs in gear skiving on a specific CNC machine, the cutter should be used to generate the topology modification of gear surfaces in complex geometrical forms, and especially reused when changing the geometrical parameters of the skived gear, such as the pressure angle or the helix angle. The topology modification of gear surfaces can be achieved by two methods, i.e., geometrical modification of the cutter or kinematic relationship modification of the cutter and the work gear. For the first method, the geometric structure of the cutter is corrected by modifying the primeval rack on the profile direction or the longitudinal direction, or both. Accordingly, the target surface of the work gear is fully generated by applying the original matching relationship between the cutter and the work gear. However, the cutter needs to be re-designed when the work gear’s pressure angle or helix angle is changed.

For the second method, the topology modification of gear surfaces can be obtained by adding the motions in the form of polynomials for each machining axis of the CNC machine. However, when the target surfaces are in complex geometrical forms, such as double-crowning surfaces or even grinding stock on tooth flanks, the additional motions could be beyond the kinematic control range of a specific CNC machine. Consequently, applying the separate methods is ineffective in completely solving the problem. Therefore, this section presents a novel approach to correct the tooth flank of the skived gear on a specific CNC machine by combining the above methods in dual closed loops, in which the motion limit of the electronic gearbox is also considered. Additionally, this novel method uses the same cutter to generate the skived gears with different pressure and helix angles. After several closed-loop iterations, the skived gear tooth flank can be fitted to the target tooth surface. Furthermore, the changing range of pressure angle or helix angle can also be wholly determined to assure the pre-defined conditions of normal deviation on the skived gear surface.

The algorithm of the proposed method is shown in Fig. 7, and comprises the following steps:

• 1. Input the initial geometric parameters of the skived gear and the cutter.

• 2. The target surface of the skived gear with the initial geometric parameters is firstly determined from one of three cases, as shown in Fig. 8. Case 1 is an even grinding stock surface to which the finishing process will be applied. In contrast, cases 2 and 3 are non-grinding stock surface and double-crowning surface, respectively, and are available for working without applying the finishing process. The grinding stock (s_w) and the double-crowning amounts of work gear for case 1 and case 3, respectively, are pre-defined.

• 3. Define the shape of the normal rack based on three modification cases of the skived gear surface presented in Fig. 8, including the linear correction normal rack for case 1, the standard rack for case 2, and the quadratic correction normal rack for case 3. Accordingly, three skiving cutter modifications are generated, including the linear correction cutter, the standard cutter, and the quadratic correction cutter.

• 4. Define the required condition for the inner closed loop (R₁) and the required condition R₂ for the gear tooth flank.

• 5. Modify the machining axis movements of a specific CNC machine by adding the additional motions in the form of polynomials.

• 6. Calculate the coefficients of polynomials using the Levenberg–Marquardt (LM) algorithm.

• 7. Perform the multi-axis CNC cutting simulation with the axis movements in step 5 to generate the current skived gear surface.

• 8. Calculate the normal deviations on the modification region between the current skived gear surface and the target surface.

• 9. Check the required condition R₁. If the condition is not met, the axis movement of the CNC machine continues to be adjusted, and the algorithm returns to step 6 for the next inner iteration. If the condition is met, the algorithm proceeds to the next step.

• 10. Calculate the normal deviation on the entire skived gear tooth surface.

• 11. Perform overcutting checking for the skived gear profile. If no overcutting is detected, proceed to the next step; otherwise, return to step 5 and restart the inner closed loop.

• 12. Check the required condition R₂. If the condition is not met, the coefficients of polynomials are stored, and the algorithm goes to the next step. If the condition is met, the algorithm goes to the end, and the changing ranges of the geometric parameters of the skived gear, including pressure angle and helix angle, are completely defined.

• 13. Modify either the pressure angle or the helix angle of the skived gear from initial parameters, as shown in Fig. 9. Accordingly, the new datum and target surfaces are defined, in which the target surface corresponds to the given case in step 2. Then, the algorithm returns to step 5 and then restarts the inner closed loop.

Fig. 7

Flowchart for expanding the capability of tooth flank correction on the skived gear

Fig. 8

Three modification cases of the skived gear tooth surface, the normal rack, and the skiving cutter with the initial geometric parameters

Fig. 9

Two modification cases of the skived gear geometric parameters

Among these steps, steps 3 and 6 need to be presented in more detail. Therefore, Sect. 4.1 presents the corrected method for the normal rack mentioned in step 3. Section 4.2 presents the Levenberg Marquardt (LM) method for detecting the coefficients of polynomials mentioned in step 6.

4.1 A correction method for the normal rack of the skiving cutter with the pre-defined topology modification of skived gear surfaces

As shown in Fig. 8, the modification zone on the work gear tooth flank with the initial geometric parameters is divided into five points A, B, …, E and nine points 1, 2, …, 9 according to profile direction and longitudinal direction, respectively. The normal deviations between the target and datum tooth surfaces are either constant, as in case 1 and case 2, or variable, as in case 3, in both profile and longitudinal directions. Therefore, the target tooth surface in case 3 is chosen as the general case. Then, the normal rack can be corrected to generate a skiving cutter that fully conjugates with one section of the target tooth surface in the profile direction.

In a previous study, Luu and Wu [15] developed a conical skiving cutter from a corrected normal rack to obtain an even grinding stock on the tooth flank of the skived gear. This method was based on the relationship between the grinding stock of the skived gear profile and the adjusting amount of the imaginary helical gear profile on the normal plane, in which the grinding stock distribution of the skived gear profile on the normal plane is uniform. Furthermore, the relationship transformations from the rake plane to the normal plane for points on the cutting edge increase the number of equations to solve. Therefore, this section presents a more general approach for a non-linear adjusting amount distribution of skived gear profile and considers the adjusting amount of the imaginary helical gear profile on the rake plane to reduce the number of equations to solve.

As shown in Fig. 10, the fifth section of the target tooth surface in the profile direction is chosen to define the normal profile of imaginary helical gear Σ:

$$s_{ni} = \frac{{s_{ri} \cos \beta_{w} \cos \alpha_{n} }}{\cos \delta },\;\delta = \tan^{ - 1} \left( {\frac{{\tan \alpha_{n} }}{{\cos \beta_{w} }}} \right),\;i = 1\sim 5$$

(16)

where $s_{ri}$ is the normal deviation in the fifth transverse section between the target and datum tooth surfaces from A to E.

Fig. 10

The meshing condition of the work gear and the imaginary helical gear

The normal deviations of imaginary helical gear Σ on the rake plane are calculated as follows:

$$s_{pi} = s_{ni} \cos \alpha_{p} ,\;\alpha_{p} = \tan^{ - 1} (\cos \gamma \tan \alpha_{n} ),\;i = 1\sim 5$$

(17)

As shown in Fig. 11, if the cutting edge of the skiving cutter coincides with intersection curve I₁ between rake plane ${\uppi }_{{\text{r}}}$ and imaginary helical gear $\sum$, the work gear profile will approach the target profile in the smallest error. In practice for manufacturing a conical skiving cutter, however, this condition is impossible to satisfy. To reduce the profile error of the skived gear, (q + 1) points ${\text{T}}_{{\text{j}}}$ in the cutting edge are designed in a coincident position with (q + 1) points ${\text{R}}_{{\text{j}}}$ in I₁, wherein (q + 1) points ${\text{R}}_{{\text{j}}}$ are (q + 1) symmetric points pre-defined by Eq. (17), and q is the degree order of polynomial that is defined in step 2.

Fig. 11

Schematics of designing the skiving cutter for generating the work gear with a pre-defined cross-section profile

According to Sect. 2, the position vector of points ${\text{T}}_{{\text{j}}}$ on the cutting edge ${\mathbf{r}}_{T}^{(j)}$ could be calculated by replacing the position vector of points ${\text{Q}}_{{\text{j}}}$ on corrected rack ${\text{R}}_{{{\text{m1}}}}$ into Eq. (3) as follows:

$${\mathbf{r}}_{T}^{(j)} \left( {u_{j} ,v_{j} ,\varphi_{j} } \right) = \left[ {x_{T}^{(j)} ,y_{T}^{(j)} ,z_{T}^{(j)} ,1} \right]^{T} = {\mathbf{M}}_{cr} \left( {\varphi_{j} } \right)\left[ {x_{Q}^{(j)} (u_{j} ),y_{Q}^{(j)} (u_{j} ) + v_{j} \tan \lambda ,v_{j} - x_{Q}^{(j)} (u_{j} )\tan \beta_{c} ,1} \right]^{T}$$

(18)

in which the position vector of the point ${\text{Q}}_{{\text{j}}}$, ${\mathbf{r}}_{Q}^{(j)}$ is expressed as:

$$\left\{ \begin{array}{l} x_{Q}^{(j)} = ( - 1)^{d} u_{j} \hfill \\ y_{Q}^{(j)} = h_{j} = \sum\limits_{i = 0}^{q} {a_{i} u_{j}^{i} }\end{array} \right.,\;j = 0\sim q$$

(19)

in which $h_{j} = h_{q} + \frac{{(h_{q} - h_{0} )j}}{q + 1}$, $j = 0\sim q$.

In addition, points ${\text{T}}_{{\text{j}}}$ satisfy the meshing condition Eq. (5) and the rake plane equation Eq. (6) as:

$$f_{1}^{(j)} = {\mathbf{n}}_{T}^{(j)} \cdot \frac{{\partial {\mathbf{r}}_{T}^{\prime (j)} \left( {u_{j} ,v_{j} ,\varphi_{j} } \right)}}{\partial \varphi } = 0$$

(20)

$$n_{xf} (x_{T}^{(j)} - x_{f} ) + n_{yf} (y_{T}^{(j)} - y_{f} ) + n_{zf} (z_{T}^{(j)} - z_{f} ) = 0$$

(21)

where ${\mathbf{r}}_{T}^{\prime (j)}$ is a vector of the first three elements of ${\mathbf{r}}_{T}^{(j)}$.

As shown in Fig. 11, the points ${\text{R}}_{{\text{j}}}$ are generated by adjusting points S_j on I₂ along the normal direction with the distances $s_{pj}$, wherein I₂ is the intersection curve between rake plane ${\uppi }_{{\text{r}}}$ and imaginary helical gear $\sum_{s}$. Due to that the points ${\text{S}}_{{\text{j}}}$ are generated by points ${\text{P}}_{{\text{j}}}$ on the standard rack, the position vector ${\mathbf{r}}_{S}^{(j)}$ and unit normal vector ${\mathbf{n}}_{S}^{(j)}$ of points ${\text{S}}_{{\text{j}}}$ can be calculated as follows:

$${\mathbf{r}}_{S}^{(j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} ,\varphi_{j}^{(s)} } \right) = \left[ {x_{S}^{(j)} ,y_{S}^{(j)} ,z_{S}^{(j)} ,1} \right]^{T} = {\mathbf{M}}_{cr}^{(s)} \left( {\varphi_{j}^{(s)} } \right){\mathbf{r}}_{P}^{(j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} } \right)$$

(22)

$${\mathbf{n}}_{S}^{(j)} \left( {u_{j}^{(s)} ,\varphi_{j}^{(s)} ,l_{j}^{(s)} } \right) = {\mathbf{L}}_{cr}^{(s)} \left( {\varphi_{j}^{(s)} } \right){\mathbf{n}}_{P}^{(j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} } \right)$$

(23)

where:

$${\mathbf{r}}_{P}^{(j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} } \right) = \left[ {( - 1)^{d} ({t \mathord{\left/ {\vphantom {t 2}} \right. \kern-\nulldelimiterspace} 2} - u_{j}^{(s)} \sin \alpha_{n} ),u_{j}^{(s)} \cos \alpha_{n} + l_{f} \tan \lambda ,v_{j}^{(s)} ,1} \right]^{T}$$

$${\mathbf{n}}_{P}^{(j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} } \right) = \frac{{\partial_{{u^{(s)} }} {\mathbf{r}}_{P}^{\prime (j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} } \right) \times \partial_{{v^{(s)} }} {\mathbf{r}}_{P}^{\prime (j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} } \right)}}{{\left| {\partial_{{u^{(s)} }} {\mathbf{r}}_{P}^{\prime (j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} } \right) \times \partial_{{v^{(s)} }} {\mathbf{r}}_{P}^{\prime (j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} } \right)} \right|}}$$

wherein the matrixes ${\mathbf{M}}_{cr}^{(s)}$ and ${\mathbf{L}}_{cr}^{(s)}$ are constructed by substituting $\varphi$ and $\lambda$ by $\varphi^{(s)}$ and $0$ into the matrixes ${\mathbf{M}}_{cr}$ and ${\mathbf{L}}_{cr}$, respectively.

The meshing condition $f_{3}^{(j)}$ of points S_j can be attained as:

$$f_{3}^{(j)} = {\mathbf{n}}_{S}^{(j)} \cdot \frac{{\partial {\mathbf{r}}_{S}^{\prime (j)} }}{{\partial \varphi^{(s)} }} = 0$$

(24)

In addition, points ${\text{S}}_{{\text{j}}}$ satisfy the rake plane equation Eq. (6) as follows:

$$n_{xf} (x_{s}^{(j)} - x_{f} ) + n_{yf} (y_{s}^{(j)} - y_{f} ) + n_{zf} (z_{s}^{(j)} - z_{f} ) = 0$$

(25)

Because the points ${\text{T}}_{{\text{j}}}$ coincide with the points ${\text{R}}_{{\text{j}}}$, the distance ${\text{S}}_{{\text{j}}} {\text{T}}_{{\text{j}}}$ matches the distance ${\text{S}}_{{\text{j}}} {\text{R}}_{{\text{j}}}$:

$$\left\{ \begin{array}{l} (x_{R}^{(j)} - x_{S}^{(j)} )^{2} + (y_{R}^{(j)} - y_{S}^{(j)} )^{2} + (z_{R}^{(j)} - z_{S}^{(j)} )^{2} = s_{pj}^{2} \hfill \\ f_{5}^{(j)} = ({\mathbf{r}}_{R}^{\prime (j)} - {\mathbf{r}}_{S}^{\prime (j)} ) \cdot {\mathbf{t}}_{S}^{(j)} = 0 \hfill \\ \end{array} \right.$$

(26)

In which the tangent vector of I₁ at point S_j, ${\mathbf{t}}_{S}^{(j)}$ can be calculated as:

$${\mathbf{t}}_{S}^{(j)} = {\mathbf{n}}_{S}^{(j)} \times {\mathbf{n}}_{f} = \left( {{\mathbf{t}}_{{\varphi_{j} }}^{(s)} \times {\mathbf{t}}_{{l_{j} }}^{(s)} } \right) \times {\mathbf{n}}_{f} = \left( {\frac{{\partial {\mathbf{r}}_{S}^{\prime (j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} ,\varphi_{j}^{(s)} } \right)}}{{\partial \varphi^{(s)} }} \times \frac{{\partial {\mathbf{r}}_{S}^{\prime (j)} \left( {u_{j}^{(s)} ,v_{j}^{(s)} ,\varphi_{j}^{(s)} } \right)}}{{\partial v^{(s)} }}} \right) \times {\mathbf{n}}_{f}$$

Finally, Eqs. (19), (20), (21) and (24)–(26) are available for solving the coefficients, $a_{q}$, $q = 1\sim 2$ of the polynomial function that presents the position vector at segment e–f of the corrected rack, as shown in Fig. 28 in the “Appendix.” Based on this, the whole segments of the corrected rack are defined.

4.2 Solving the machine-axis setting by applying the Levenberg–Marquardt method

According to Sub-sect. 4.1, the skiving cutter is corrected to generate the gear tooth surface, whose cross-sections are the same as one section of the original target tooth surface in step 2. To achieve the entire target tooth surfaces using this corrected skiving cutter, this sub-section presents a method that modifies the axis movement of the CNC machine by adding the motions in the form of polynomials. The polynomial coefficients can be attained after several closed-loop iterations.

The normal deviation at each grid point on the current gear tooth surface in comparison with the new datum surface $\delta \varepsilon$ is given as:

$$\delta \varepsilon = ({\mathbf{r}}_{{\text{w}}}^{\prime } - {\mathbf{r}}_{d}^{\prime } ) \cdot {\mathbf{n}}_{d} = (x_{w} - x_{d} )n_{dx} + (y_{w} - y_{d} )n_{dy} + (z_{w} - z_{d} )n_{dz}$$

(27)

where ${\mathbf{r}}_{d}$ and ${\mathbf{n}}_{d}$ are the position and unit normal vectors of the point on the datum gear tooth surface, respectively; ${\mathbf{r}}_{w}$ is the position vector of the point on the current gear tooth surface; and ${\mathbf{r}}_{w}^{\prime }$ and ${\mathbf{r}}_{d}^{\prime }$ are vectors of the first three elements of ${\mathbf{r}}_{d}$ and ${\mathbf{r}}_{w}$, respectively.

The Levenberg–Marquardt (LM) method [30, 31] is used to determine the polynomial coefficients $a_{0} \sim a_{2}$, $b_{0}$, $c_{0} \sim c_{2}$, and $d_{0} \sim d_{2}$. Based on this method, a sensitivity matrix ${\mathbf{M}}_{s}$ is first identified from the influence of a small change in terms of each polynomial coefficient on the normal deviation of work gear profile ${{\partial \varepsilon_{i} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{i} } {\partial v_{j} }}} \right. \kern-\nulldelimiterspace} {\partial v_{j} }}$. Accordingly, the relationship between the variations of normal deviation and polynomial coefficients can be presented in matrix form as:

$$\left\{ {\delta \varepsilon_{i} } \right\} = \left[ {\frac{{\partial \varepsilon_{i} }}{{\partial v_{j} }}} \right]\left\{ {\delta v_{j} } \right\} = {\mathbf{M}}_{s} \left\{ {\delta v_{j} } \right\}$$

(28)

in which $\left\{ {\delta v_{j} } \right\}$ represents the modifications to the polynomial coefficients, and $\left\{ {v_{j} } \right\}$ indicates the polynomial coefficients in the jth iteration.

Based on the given normal deviation between the target surface and the current surface, the modifications to the polynomial coefficients can be determined as:

$$\left\{ {\delta v_{j} } \right\} = ({\mathbf{M}}_{s}^{T} {\mathbf{M}}_{s} + \eta {\mathbf{I}})^{ - 1} {\mathbf{M}}_{s}^{T} \left\{ {\delta \varepsilon_{i} } \right\}$$

(29)

in which $\eta$ is the damping parameter; and ${\mathbf{I}}$ is the identity matrix.

To proceed the next iteration of the inner closed loop, the updated polynomial coefficients $\left\{ {\delta v_{j} } \right\}$ are obtained by adding the values calculated from Eq. (29) to the values in the previous loop. After several iterations, the final polynomial coefficients are determined when the following required condition (R₁ in Fig. 7) [31] is satisfied:

$$R_{1} {: }\max \left| {{\mathbf{M}}_{s}^{T} \left\{ {\delta \varepsilon_{i} } \right\}} \right| < \varsigma_{1}$$

(30)

or:

$$R_{1} {: }\max \left| {\frac{{\delta v_{j} }}{{v_{j} }}} \right| < \varsigma_{2}$$

(31)

where $\varsigma_{1}$ and $\varsigma_{2}$ are threshold values of convergence (10⁻⁴ is given in this study).

5 Numerical example

5.1 Generation of even grinding stock on skived gears with different pressure and helix angles by the same linear correction skiving cutter

In practical applications, a skived gear with precision grinding stock enhances tool life, work gear profile accuracy, and reduces finishing cost. The linear corrected cutter has been verified by Luu and Wu [15] to generate an even grinding stock on the skived gear. However, this method is only used for generating a skived gear with a specific value of pressure angle and helix angle. Therefore, this section presents an application of the novel approach to expand the machining range of the linear correction skiving cutter for gear tooth flank modification, as in case 1 described in Sect. 4.

The geometric parameters of the cutter and the skived gear used for this instance are shown in Table 1. The initial values of pressure angle $\alpha$ and helix angle $\beta$ of the skived gear are set by 20°. Based on these parameters, a linear correction cutter is firstly generated by applying the methodology presented in Sect. 4.1 with the grinding stock $s_{r}$ of the skived gear of 100 µm. The segments on both sides of the normal rack generated involute parts of the skived gear are presented in the form of linear functions, as illustrated in Table 2. In addition, Fig. 12 presents the complete form of the correction rack and linear correction skiving cutter along with its cutting edge.

Table 1 Parameters of gear skiving and skiving tool

Table 2 Equations of segment e–f on the corrected rack (unit: mm)

Fig. 12

Linear corrected rack and linear corrected skiving cutter

The datum surface of the skived gear is reconstructed by adjusting the pressure or helix angles from the initial values for both internal and external skived gears. The target surface is then obtained by adding more material for the datum surface in the normal direction, equalling the grinding stock $s_{r}$. The meshing relationships between the cutter and the skived gear are set as in Sect. 3 on the multi-axis CNC machine to simulate the cutting process. The coefficients of the adding functions are updated in each inner closed-loop iteration (as presented in Sect. 4.2) until the required condition R₁ is met. Moreover, the required conditions R₂ for the outer closed loop in this instance are set by $\pm 5$ µm for normal deviation of grinding stock on the left and the right involute region, respectively, and $\pm 50$ µm for normal deviation of grinding stock on the addendum diameter. The step size of pressure/helix angle on the outer closed loop is set as 0.1°.

In the first outer closed loop, an external gear with a pressure angle of 20.1° is manufactured by modifying the axis movements of the CNC machine with a linear-corrected skiving cutter. The additional motion functions of machining axes in Eq. (10) are chosen. After 384 iterations of the inner closed loop, the required condition R₁ is met, and then the polynomial coefficients $(a_{0} ,a_{1} ,a_{2} ,b_{0} ,c_{0} ,c_{1} ,c_{2} ,d_{0} ,d_{1} ,d_{2} )$ are obtained, as shown in Table 3. In addition, the point cloud of cutting trajectory on the transverse section $z_{{\text{w}}} = 0$, the boundary points (blue curve), and the skived gear profile (red curve) are generated and presented in Fig. 13. The normal deviations of the boundary points for the left and right tooth flanks are also analyzed. Overcutting (negative normal deviation) is detected on both tooth flanks. It is caused due to the additional motion term with the coefficient c₁. Therefore, as mentioned in Sect. 4, step 5 in the algorithm is considered, the machining axis movements shall be modified by setting the coefficient c₁ as zero.

Table 3 Polynomial coefficients of additional motions for manufacturing external gear with pressure angle 20.1°

Fig. 13

Skived gear profile with overcutting

As shown in Figs. 14a and 15a, the required condition R₁ is satisfied after 416 iterations for the external gear with a 22° pressure angle (case 1), and after 31 iterations for the internal gear with a 21.1° helix angle (case 2). The skived tooth topology for case 1 is presented in Fig. 14b, the normal deviation is evenly distributed on both tooth flanks and approaches to the desired grinding stock (100 µm). A similar result for case 2 can be seen in Fig. 15b. To ensure no overcutting in the skiving process, normal deviation between the boundary points (P_b) and the skived gear profile is also analyzed to assure positive values over the full tooth profile, including the left flank, root, and right flank (Figs. 14c and 15c). The cutting trajectory of the cutter rake profile at every instant of time is fully wrapped within the skived gear profile for both case 1 and case 2. In addition, the virtual cutting simulations using VERICUT software are performed as shown in Figs. 16 and 17 to mutually verify the established machining model and the numerical results.

Fig. 14

Skived external gear with a pressure angle of 22° (case 1); a R₁ with respect to the number of iterations, b tooth topology after inner closed-loop calculation, and c overcutting evaluation

Fig. 15

Skived internal-gear with a helix angle of 21.1° (case 2); a R₁ with respect to the number of iterations, b tooth topology after the inner closed-loop calculation, and c overcutting evaluation

Fig. 16

Virtual cutting experiment in VERICUT software for the case of external gear with pressure angle of 22°

Fig. 17

Virtual cutting experiment in VERICUT software for the case of internal gear with a helix angle of 21.1°

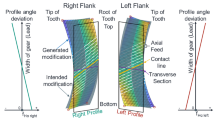
The variations of external and internal skived gear tooth surface with changing pressure angles are shown in Figs. 18 and 19, respectively. The polynomial coefficients of additional motions for machining-axis movements are indicated in the upper half of Table 4. The left side of Figs. 18 and 19 illustrate the tooth surface topography of the external and the internal skived gear, respectively, in nine sections by calculating the normal deviation in comparison between the actual surface (A) and the datum surface (D). The tooth gear profile in Sect. 1 is then demonstrated on the right side of Figs. 18 and 19 for the external and the internal skived gear, respectively, to show the variation of normal deviation in the profile direction. In these figures, the notation Max (Min). D indicates the maximum (minimum) normal deviation of addendum diameter, the notation Max (Min). L(R) presents the maximum (minimum) normal deviation on the left involute region (L_i) or right involute region (R_i), and the notation T_r indicates the top region.

Fig. 18

External gears with different pressure angles skived using the same linear-corrected cutter

Fig. 19

Internal gears with different pressure angles skived using the same linear-corrected cutter

Table 4 Polynomial coefficients of additional motions for machining axes

In the case of external gear skiving, the iteration number in the inner close-loop is 32 for the pressure angle of 18.5° and 416 for the pressure angle of 22°. The involute regions satisfy the required conditions R₂ and no overcutting is found, as shown in Fig. 18. For the internal gear skiving, the iteration number in the inner close-loop is 83 for the pressure angle of 19.0° and 368 for the pressure angle of 20.9°. Also, the required condition R₂ for the involute regions is satisfied without overcutting, as shown in Fig. 19. As a result, the same linear-corrected cutter is practicable for manufacturing external or internal gears with a range of varied pressure angles with satisfying the required conditions.

Figures 20 and 21 show the variation of external and internal skived gear tooth surface when changing helix angle, respectively. The polynomial coefficients of additional motions for machining-axis movements are indicated in the lower half of Table 4. The tooth surface topography is presented on the left side of Figs. 20 and 21 for the external and the internal skived gear, respectively. In the case of external gear skiving, the iteration number in the inner close-loop is 12 and 16 for the helix angle of 18.8° and 22.6°, respectively. The involute regions satisfy the required conditions R₂ and no overcutting is found, as shown in Fig. 20. For the internal gear skiving, the iteration number in the inner close-loop is 33 and 31 for the helix angle of 19.0° and 21.1°, respectively. Also, the required condition R₂ for the involute regions is satisfied without overcutting, as shown in Fig. 21. As a result, the same linear-corrected cutter is practicable for manufacturing external or internal gears with a range of varied helix angles with satisfying the required conditions.

Fig. 20

External gears with different helix angles skived using the same linear-corrected cutter

Fig. 21

Internal gears with different helix angles skived using the same linear-corrected cutter

This example verified that the linear correction skiving cutter could be used for generating precision grinding stock on tooth flanks of the skived gear, and reused when changing the normal pressure angle or helix angle of the skived gear. Therefore, the economic efficiency and flexibility of the gear skiving process could be significantly improved by applying the proposed method.

5.2 Generation of tooth flanks of skived gears archived accuracy grade DIN6 with different pressure angles and helix angles by the same standard skiving cutter

In some cases of gear production, the work gear surface does not require a finishing process if the gear quality can achieve an accuracy grade of five or six. Additionally, the manufacturer wishes to manufacture the gear tooth profile with different helix and pressure angles by one cutter. This skiving cutter is also generated from the standard rack in order to save manufacturing costs. However, the solution to this issue is absent in previous literature. Therefore, this section presents an application of the novel approach to expand the machining range of the standard skiving cutter for gear tooth flank modification, as in case 2 presented in Sect. 4.

The essential geometric parameters of the cutter and the skived gear are similar to those in Sect. 5.1. A standard skiving cutter and its cutting edge are firstly generated by the standard normal rack, in which it is easier to manufacture the cutter. Then, changing the pressure angle or helix angle from the initial value generates a new datum surface of the skived gear, and the new target surface is set coincidentally with the new datum surface. The machining process on the multi-axis CNC machine presented in Sect. 3 for both internal and external skived gears is applied to obtain the actual surface after each inner closed-loop iteration. The required conditions R₁ for the inner closed loop are the same as those in the case presented in Sect. 5.1. The profile of the skived gear at each section will be inspected on profile evaluation range $L_{\alpha }$, which is set from profile control diameter $d_{cf}$ to tip form diameter $d_{fa}$. The normal deviation between the actual profile and the datum profile needs to be smaller than the total profile deviation $F_{f}$, taken from the standard table according to accuracy grade and essential geometric parameter of gear [32]. For this example, based on the gear module of 3 mm, and the chosen gear accuracy grade of six, the total profile deviation $F_{f}$ is 10 µm according to the DIN standard. In addition, the normal deviation of the skived gear profile will be set by a positive value on the profile evaluation range $L_{\alpha }$. Therefore, one of the required conditions R₂ for normal deviation on the profile evaluation range is in the range from 0 to 10 µm. Furthermore, another of the required conditions R₂ for normal deviation of addendum diameter is set in the range from − 50 to 100 µm. After several iterations of the outer closed loop, the required conditions R₂ are met, a set of coefficients for the adding functions are stored, and a changing limit range of pressure or helix angle is obtained.

Figures 22 and 23 show the variation of the external and internal skived gear tooth surface when changing pressure angle, respectively. The polynomial coefficients of additional motions for machining-axis movements are indicated in the upper half of Table 5. For the external skived gear, the required condition R₁ is satisfied after 11 and 12 iterations of the inner closed loop with pressure angles of 18.9° and 22.2°, respectively. In addition, the required conditions R₂ for the involute regions are met, as shown in Fig. 22, and overcutting is not found. For the internal skived gear, the inner closed loop reaches the convergence criteria R₁ after 22 and 408 iterations for pressure angles of 19.4° and 21.2°, respectively. The required condition R₂ on the involute regions is satisfied without overcutting, as shown in Fig. 23. As a result, the gear accuracy of DIN6 is achievable in manufacturing external or internal gears with a range of varied pressure angles using the same standard cutter.

Fig. 22

External gears with different pressure angles skived using the same standard cutter

Fig. 23

Internal gears with different pressure angles skived using the same standard cutter

Table 5 Polynomial coefficients of additional motions for machining axes

Figures 24 and 25 show the external and the internal skived gear tooth surface variation when changing helix angle, respectively. The polynomial coefficients of additional motions for machining-axis movements are indicated in the lower half of Table 5. For the external gear skiving, the iteration number in the inner close-loop is 11 for both the helix angle of 18.8° and 21.8°. The involute regions satisfy the required conditions R₂, as shown in Fig. 24, and no overcutting is found. For the internal gear skiving, the iteration number in the inner close-loop is 24 for the helix angle of 19.4° and 361 for the pressure angle of 21.5°. Also, the required condition R₂ for the involute regions is satisfied without overcutting, as shown in Fig. 25. As a result, the gear accuracy of DIN6 is achievable in manufacturing external or internal gears with a range of varied helix angles using the same standard cutter.

Fig. 24

External gears with different helix angles skived using the same standard cutter

Fig. 25

Internal gears with different helix angles skived using the same standard cutter

This example verified that the proposed method is suitable for generating non-finishing tooth flanks of the skived gear in grade DIN6 with different normal pressure or helix angles by the same standard cutter.

5.3 Generation of double-crowning surface on skived gears with different pressure and helix angles by the same quadratic correction skiving cutter

Double-crowning surfaces can be produced to improve tooth contact efficiency for non-applied finishing cases of the skived gear. However, no previous literature presented double-crowning gear surfaces produced by the skiving cutter, especially using the same cutter for different pressure and helix angles of the skived gear. Therefore, the proposed method is used to design the skiving cutter and modify the motion of the CNC machine axis in order to solve this issue.

In this instance, the target surface of the skived gear is set by the pre-defined double-crowning surface, as shown in Fig. 26, with the essential geometric parameters of the cutter and the skived gear the same as those presented in Sect. 5.1. The initial values of pressure angle $\alpha$ and helix angle $\beta$ of the skived gear are set by 20°, respectively. The target profile shown on the right side of Fig. 26 is chosen to generate the quadratic correction skiving cutter. According to Sect. 4.1, the equation of segment e–f is successfully defined, as shown in Table 6. Consequently, the quadratic correction skiving cutter is completely generated. By changing the pressure angle or helix angle from the initial value, the new datum and target surfaces of the skived gear are identified. The skiving process is performed on the multi-axis CNC machine shown in Sect. 3 for both the internal and the external skived gear to attain the actual surface after each closed-loop iteration. The required condition (R₁) for normal deviation on the modification region is similar to that in Sect. 5.1. In addition, the required conditions (R₂) for normal deviation on the entire tooth surface are from 0 to 2 µm for double-crowning regions, from 0 to 10 µm for involute regions, and from − 50 to 100 µm for addendum diameter, respectively.

Fig. 26

Pre-defined double-crowning target surface

Table 6 Equations of segment e–f on the corrected rack (unit: mm)

Figures 27 and 28 show the variation of the external skived gear tooth surface when changing pressure angle and helix angle, respectively. In these figures, the notation D_c indicates the double-crowning region, and the remaining notations have the same meaning as in the figures in Sect. 5.1. The polynomial coefficients of additional motions for machining-axis movements are indicated in Table 7. For the case of changing pressure angles, the inner closed loop reaches the convergence criteria R₁ after 17 and 15 iterations for pressure angles of 19.7° and 20.4°, respectively; and no overcutting is found. As the topography of tooth flanks in Fig. 27, the required condition R₂ of the double-crowning regions is satisfied. For the case of changing helix angles, the iteration number in the inner close-loop is 17 and 16 for the helix angle of 19.5° and 20.4°, respectively. The required condition R₂ of the double-crowning regions is met as the topography of tooth flanks in Fig. 28. In addition, no overcutting is found. This example verified that the proposed method is suitable for generating double-crowning surfaces of skived gear with different normal pressure or helix angles by the same quadratic correction cutter.

Fig. 27

External gears with different pressure angles skived using the same quadratic-corrected cutter

Fig. 28

External gears with different helix angles skived using the same quadratic-corrected cutter

Table 7 Polynomial coefficients of additional motions for machining axes

6 Conclusion

This study proposes a novel approach with a dual closed loop for correcting skived gears with different normal pressure angles and helix angles based on cutter modification and motion modification of the CNC machine. The corrected rack is firstly defined from the target tooth surface, including the even grinding stock surface, non-grinding stock surface, and double-crowning surface. The additional motions considering the motion limits of an electronic gearbox for the machining axis are added in the form of polynomials. The inner closed loop based on the Levenberg–Marquardt (LM) algorithm is developed to attain the coefficients of polynomials for additional motions in fitting the skived gear tooth flanks to the target tooth surface. After completing a cycle of the inner closed loop, the skived gear’s pressure angle or helix angle is changed in the outer closed loop to renew the target tooth surface, and then a new cycle of the inner closed loop is restarted. The suitable range of the skived gear’s pressure or helix angles is satisfied when the dual closed loops are fully ended.

Appendix

In this paper, the corrected normal rack consists of seven segments, as shown in Fig. 29, proposed by Luu and Wu [15]. Each segment is presented in explicit equations in Table 8.

Fig. 29

Definition of corrected rack (R_m1) [15]

Table 8 Explicit equations of segments of the corrected normal rack [15]