Stability analyses of compressible flat plate boundary layer flow over a mechanically compliant wall

Abstract

Sustained flight at hypersonic speeds is characterized by high pressure and aerothermal loads imposed on the structure of the aerodynamic vehicle. A consequence of lightening the structural design permits fluid–structure interaction phenomena that can significantly alter the flow and initiate unsteady structural responses. We investigate the coupling between high-speed laminar boundary layer flows over a mechanically compliant panel and analyze the dynamic system response of the coupled system to boundary layer instabilities by means of local convective linear stability analysis. The resulting non-dimensional interaction parameters describing the compliant system are shown to affect the boundary layer instabilities in the infinitely thin panel limit, and the transition from the rigid limit is described by two distinctly different responses: (a) a piston-like, one-dimensional panel deflection, or (b) a synchronization with flexural waves. Compliance is shown to non-monotonically change convective wave growth rates and induce uncertainty in the integrated N-factors.

1 Introduction

Wall-bounded flows with mechanically compliant walls have been of interest for incompressible flows for a long time. Gray’s paradox [1] and his observation of the high swimming speeds of dolphins led to a series of experiments of laminar and turbulent boundary layers over a layered compliant surface [2]. The introduction of a rubber coating applied to a rigid surface mimicked the dolphins’ skin and reduced the drag by up to 60% by delaying transition. Benjamin [3] and Landahl [4] tried to understand the transition delay mechanism by applying linear stability analysis to the boundary layer flow over a spring-backed panel with damping and categorized the resulting modes based on their energy transfer mechanism. Benjamin [3] also found that, due to the existence of a compliant coating, flexural waves coalesced with the Tollmien–Schlichting instability to stabilize the boundary layer via an irreversible energy transfer from the flow to the compliant coating [5]. A wider parametric study of this problem was later investigated by [6, 7] by introducing a spring-backed elastic plate submerged in a fluid substrate to include damping effects. They found viscous and viscoelastic damping to be destabilizing, whereas the reduction in flexural rigidity and spring stiffness, as well as an increase in plate mass and the introduction of an inviscid fluid substrate, was stabilizing. The instability behavior for the compliant system was found to be the coalescence of Tollmien–Schlichting waves and traveling wave flutter. Further, they termed turbulent wave flutter to be a “flow-induced surface instability” (FISI) to distinguish it from fluid instabilities present in the rigid limit. The coalescence of fluid and flexural instabilities with similar wave lengths was also found to be relevant by [8] in the coupled system, who found the compliant wall’s response to be a superposition of four waves: fluid, flow-induced upstream-propagating flexural, flow-induced downstream-propagating flexural, and local in-vacuo waves. Most recently, the linear stability analysis for the incompressible flat plate flow was extended to include transient growth, which was found to have a significant impact on the importance of viscous effects in the instability mechanism [9].

In the compressible flow regime, the design of super- and hypersonic aircraft in the mid-twentieth century pushed the development of appropriate tools to focus on aeroelastic flutter and panel divergence, both instability phenomena associated with finite-sized structural panels. The most widely used model has been a linear thin panel description for the solid and inviscid first-order piston theory for the fluid domain [10], later extended to capture nonlinearities in the solid and to higher-order piston theories [11]. These models were able to provide flutter boundaries and are still powerful tools to roughly estimate panel scale instability behavior. The description of the panel used has varied ranging from a simple Kirchhoff–Love plate to a nonlinear van Kàrmàn plate for large deflections. Different problem formulations, such a assumed-mode Euler–Lagrange or direct discretization of the linearized dynamics, have been employed and a temporal response, either in the limit cycle oscillation or including transient behavior [10] have demonstrated the complex behavior of the system. Early investigations showed that, for instance, the damping capabilities of the plate determine whether the experienced instability is of the standing or traveling wave kind and found a close resemblance between finite and infinite panels in that regard. [12] review modern approaches to panel flutter including higher-order fluid and panel models.

However, the piston theory-based fluid model does not capture all instabilities within the fluid, specifically within boundary layers, and thus omits possible mechanisms. These instabilities, specifically in the presence of boundary layers, are relevant features that may influence the design of airframe structures and are not captured in the fluid–structure coupled system analyses to date. In order to overcome the resulting uncertainty, design engineers assume a worst-case scenario which leads to conservative, less performant designs and thus room for optimization [13]. Empirical and linear stability methods have been used and properly calibrated to test flight data in order to gain better insight into the system, but the substantial pressure and temperature loads, especially in the highly compressible flow regime, result in an overly conservative prediction of boundary layer state and airframe structure response [14].

Bondarev and Vedeneev [15] analyzed inviscid instabilities in supersonic boundary layer flow over a nominally flat panel and formulated criteria for stabilized and destabilized systems depending on the boundary layer profile. Sucheendran [16] formulated a reduced order model to predict the panel response under a grazing flow due to acoustic loading and found a critical relation between the system damping and the Mach number of the flow. Acoustic instabilities in super- and hypersonic flow, specifically a second-mode instability in a $M=6$ boundary layer grazing a wavy wall, are highly susceptible to local wall perturbation as was shown by [17]. A hypersonic ramp configuration involving a boundary layer and structural model that are interconnected with a linear stability tool for transition prediction has been developed [18] and has shown a significant impact on the transition onset location. A fully nonlinear, coupled fluid–structure interaction of a $M=2.25$ turbulent flat plate boundary flow with a clamped panel by means of direct numerical simulation by [19] has shown a rich coupling between the fluid and structural domain leading to the alteration of turbulent statistical properties of the fluid domain under a flutter-like response of the panel. More recently, in the hypersonic regime, coupled analyses have been extended to analyze application-specific flow scenarios, such as composite panels coupled to fluid models of varying fidelity [20]. Additionally, the occurrence of strong shock systems in hypersonic flows has led to the analyses of panel response in the presence of impinging shocks [21] and compression ramps [22].

While incompressible boundary layers have been extensively analyzed and fairly well understood, a broader understanding of compressible boundary layers has yet to be established. A systematic, parametric investigation of a flat plate boundary flow grazing a nominally flat panel presented here serves to establish the fundamental mechanics of convective boundary layer instabilities and flexible panels.

Fig. 1

Schematic of a two-dimensional boundary layer grazing a nominally flat panel

2 Theory

2.1 Fluid-side linear stability theory

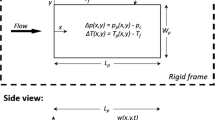
We consider the linear stability analysis of a zero pressure gradient laminar boundary layer (ZPGLBL) flowing over a nominally flat plate and follow the local ansatz described in [23]. (See Fig. 1 for a schematic of the configuration.) We non-dimensionalize using freestream conditions

$$\begin{aligned} \begin{array}{rl@{\qquad }rl@{\qquad }rl@{\qquad }rl@{\quad }rl} \displaystyle U_i &{}= \displaystyle \frac{{\tilde{U}}_i}{{\tilde{U}}_{\infty }}, &{}\rho &{}= \displaystyle \frac{{\tilde{\rho }}}{{\tilde{\rho }}_{\infty }}, &{}T &{}= \displaystyle \frac{{\tilde{T}}}{{\tilde{T}}_{\infty }}, &{} \mu ^F = \displaystyle \frac{{\tilde{\mu }}^F}{{\tilde{\mu }}^F_{\infty }}\\ \displaystyle {\tilde{p}} &{}= \displaystyle \frac{{\tilde{p}}}{{\tilde{\rho }}_{\infty } {\tilde{U}}_{\infty }^2}, &{}{\tilde{L}}_{\text {ref}} &{}= \displaystyle \frac{{\tilde{x}}}{\sqrt{{{Re}}_x}}, &{}{\tilde{t}}_{\text {ref}} &{}= \displaystyle \frac{{\tilde{L}}_{\text {ref}} }{{\tilde{U}}_{\infty }} \end{array} \end{aligned}$$

where $\tilde{(.)}$ denotes a dimensional quantity, subscript ‘$\infty$’ denotes freestream and ‘$\text {ref}$’ a reference quantity. This leads to the non-dimensional equations

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \frac{\partial \left( \rho U_i \right) }{\partial x_i}&= 0 \end{aligned}$$

(1)

$$\begin{aligned} \rho \left[ \frac{\partial U_i}{\partial t} + U_j \frac{\partial U_i}{\partial x_j} \right]&= - \frac{\partial p}{\partial x_j} \delta _{ij} + \frac{1}{{{Re}}} \frac{\partial }{\partial x_j} \left[ \uplambda \frac{\partial U_k}{\partial x_k} \delta _{ij} \right] \nonumber \\&\quad \ \ + \frac{1}{{{Re}}} \frac{\partial }{\partial x_j} \left[ \mu ^F \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \right) \right] \end{aligned}$$

(2)

$$\begin{aligned} \rho \left[ \frac{\partial T}{\partial t} + U_j \frac{\partial T}{\partial x_j} \right] =&\left( \gamma -1 \right) M_{\infty }^2 \left[ \frac{\partial p}{\partial t} + U_j \frac{\partial p}{\partial x_j} \right] + \frac{1}{{{Re}}{{Pr}}} \frac{\partial }{\partial x_j} \left[ \kappa \frac{\partial T}{\partial x_j} \right] \nonumber \\&+ \left( \gamma -1 \right) \frac{M_{\infty }^2}{{{Re}}} \left[ \frac{\partial U_j}{x_j} \right] ^2 + \left( \gamma -1 \right) \frac{M_{\infty }^2}{{{Re}}} \frac{\mu ^F}{2} \left[ \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \right] \end{aligned}$$

(3)

where Stokes’ law is used to describe the second coefficient of viscosity $\uplambda$ and $M_{\infty }={\tilde{U}}_{\infty }/{\tilde{c}}_{\infty }$ is the free stream Mach number with ${\tilde{c}}_{\infty }=\sqrt{\gamma R {\tilde{T}}_{\infty }}$ being the freestream speed of sound. In order to compute the dynamic viscosity ${\tilde{\mu }}^F={\tilde{\mu }}^F({\tilde{T}})$, we make use of the two-part Sutherland’s law following [24].

We invoke the constant Prandtl number assumption and with the appropriate non-dimensionalization for the thermal conductivity ${\tilde{\kappa }}={\tilde{\kappa }}({\tilde{T}})$, we get $\kappa (T) = \mu ^F(T)$. For the flow variables $q=[U,V,W,p,T]^\mathrm{T}$, we assume the decomposition

$$\begin{aligned} q = {\overline{Q}} + q' \quad \text {with} \quad q'(x,y,z,t) = {\hat{q}}(y) \cdot \mathrm{e}^{i \left( \alpha x + \beta z - \omega t \right) }. \end{aligned}$$

(4)

Due to the convective nature of instabilities known to be present in laminar boundary layers, we employ a spatial framework where the instabilities grow in space with the wave numbers $\alpha \!\in \!{\mathbb {C}}$ and real-valued temporal frequency $\omega \!\in \!{\mathbb {R}}$. Using these definitions in combination with subsequent linearization of Eq. (1)–(3), we can write the coupled system of equations as an eigenvalue problem following [23] of the form

$$\begin{aligned} \left[ L_0 + \alpha L_1 + \alpha ^2 L_2 \right] {\hat{q}} = 0. \end{aligned}$$

(5)

The components of the matrices $\left[ L_0, L_1, L_2 \right]$ can be found in “Appendix A”.

We make use of a self-similar solution of the Navier–Stokes equations for a ZPGLBL to serve as a meanflow. We use the Mangler–Levy–Lees self-similarity transformation [25] which leads to the two coupled ordinary differential equations

$$\begin{aligned}&\displaystyle \left( C f'' \right) ' + f f'' = 0 \end{aligned}$$

(6)

$$\begin{aligned}&\displaystyle f g' + \left( \frac{C}{\mathrm{Pr}} g' + \frac{\left( \gamma -1 \right) M^2}{1 + \frac{\gamma -1}{\gamma }M^2} \left( 1 - \frac{1}{\mathrm{Pr}} \right) C f' f'' \right) ' = 0 \end{aligned}$$

(7)

where $\left( ... \right) ' = \frac{\partial }{\partial \zeta }$, $\zeta$ is the scaled wall-normal coordinate, $C=\frac{{\tilde{\mu }}{\tilde{\rho }}}{{\tilde{\mu }}_{\infty } {\tilde{\rho }}_{\infty }}$ is the Chapman parameter, and the aforementioned two-part Sutherland’s law is used for the dynamic viscosity. The validity of the baseflow tool was verified based on boundary layer and displacement thicknesses for both the incompressible and compressible flow regime with [24].

2.2 Boundary conditions

For the baseline system with a rigid, isothermal wall, we set both wall and freestream values for $[{\hat{u}},{\hat{v}},{\hat{T}},{\hat{w}}]$ to zero. It can be shown that thermal compliance, because of its long timescales relative to bending waves, is dynamically unimportant but is critical in determining the effective material properties. For the mechanically compliant, isothermal wall, we allow for a nonzero fluid velocity at the wall coupled to the motion of the plate. For this we use the Kirchhoff–Love plate equation which in dimensional form reads

$$\begin{aligned} {\tilde{\rho }}_s {\tilde{h}} \frac{\partial ^2 {\tilde{\eta }}}{\partial {\tilde{t}}^2} + {\tilde{B}} \left[ \frac{\partial ^4 {\tilde{\eta }}}{\partial {\tilde{x}}^4} + 2 \frac{\partial ^4 {\tilde{\eta }}}{\partial {\tilde{x}}^2 \partial {\tilde{z}}^2} + \frac{\partial ^4 {\tilde{\eta }}}{\partial {\tilde{z}}^4} \right] + {\tilde{p}} ' = 0 \end{aligned}$$

(8)

with the bending stiffness ${\tilde{B}}={\tilde{E}}{\tilde{h}}^3/ \left[ 12 ( 1 - \nu ^2 )\right]$ the same wave-like perturbation ansatz for the plate deflection $\eta$ as for the fluid perturbations, $\eta (x,z,t) = {\hat{\eta }} \mathrm{e}^{i \left( \alpha x + \beta z - \omega t \right) }$, where ${\tilde{L}}_{\text {ref}}$ is used for non-dimensionalization. For the interface treatment, we match both the fluid velocity perturbation with the plate deflection velocity on the undeformed plate location following

$$\begin{aligned} \frac{\partial \eta }{\partial t} = v'_\mathrm{wall},\qquad u'_\mathrm{wall} + \eta \frac{\partial {\overline{U}}}{\partial y}\Big \vert _\mathrm{wall} = 0, \end{aligned}$$

(9)

which leads to the impedance boundary condition

$$\begin{aligned} {\hat{v}} i \omega \mu \left[ \phi \frac{\left( \alpha ^2 + \beta ^2 \right) ^2}{\omega ^2} -1 \right] = - {\hat{p}} \end{aligned}$$

(10)

with

$$\begin{aligned} \phi = \frac{1}{12 \left( 1-\nu ^2 \right) } \left[ \frac{{\tilde{h}}}{{\tilde{L}}_{\text {ref}}} \right] ^2 \left[ \frac{{\tilde{\rho }}_s}{{\tilde{\rho }}_{\infty }} \right] \left[ \frac{{\tilde{E}}}{{\tilde{\rho }}_s {\tilde{U}}^2_{\infty }} \right] \quad \text {and} \quad \mu = \left[ \frac{{\tilde{\rho }}_s}{{\tilde{\rho }}_{\infty }} \right] \left[ \frac{{\tilde{h}}}{{\tilde{L}}_{\text {ref}}} \right] , \end{aligned}$$

(11)

the two resulting additional non-dimensional parameters that uniquely describe the coupled system. $\mu$ is known as the weight ratio between fluid and solid domain, whereas the parameter $\phi$ describes the flexural behavior of the panel. As this boundary condition involves quartic terms in $\alpha$, the originally second-order becomes a fourth-order eigenvalue problem that can be rewritten as a first-order linear system according to

$$\begin{aligned} \begin{bmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad I \\ L^1 &{}\quad L^0 &{}\quad L^2 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad I &{}\quad 0\\ I &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} \begin{bmatrix} {\hat{q}} \\ \alpha {\hat{q}}\\ \alpha ^2 {\hat{q}} \\ \alpha ^3 {\hat{q}} \end{bmatrix} = \alpha \begin{bmatrix} 0 &{}\quad 0 &{}\quad I &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -L^4 &{} \\ I &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad I &{}\quad 0 &{}\quad 0 \end{bmatrix} \begin{bmatrix} {\hat{q}} \\ \alpha {\hat{q}}\\ \alpha ^2 {\hat{q}} \\ \alpha ^3 {\hat{q}} \end{bmatrix}, \end{aligned}$$

(12)

where I denotes the identity matrix and $L^4$ is a matrix containing only zeros except for the interface points where Eq. 10 is enforced. The components of the matrices $\left[ L^0, L^1, L^2, L^4 \right]$ can be found in “Appendix A”.

2.3 Verification of rigid LST solver

The rigid LST solver has been verified in both the subsonic and super-/hypersonic flow regimes. For the incompressible limit, growth rates for three perturbation frequencies that correspond to stable, neutrally stable, and unstable boundary layer instabilities for $M=10^{-6}$ have been compared to [26] DNS results as well as results employing the LST solver NOLOT by [27] and found to be within reasonable accuracy. For the compressible limit, the solver has been verified with Marxen’s DNS and LST results [28] for an unstable second-mode boundary layer instability with non-dimensional temporal wave number $F= 2 \pi {\tilde{f}} {\tilde{\mu }}_{\infty }/( {\tilde{\rho }}_{\infty } {\tilde{U}}^2_{\infty } ) = 1.5 \cdot 10^{-4}$ and $M=4.8$ (see Fig. 2). The minor discrepancy for Marxen’s temperature perturbation distribution is expected due to a discrepancy in baseflow, as his baseflow was not a self-similar but rather a Direct Numerical Simulation solution. Small difference in boundary layer thickness between the full Navier–Stokes equations and self-similar solutions in the highly compressible flow regime shifts perturbation maxima but has only minor effect on the growth rates themselves. While there has been work done in the incompressible, compliant regime [9], the lower-speed structural physical models are different and limit meaningful verification for the present case.

Fig. 2

Comparison of growth rate in the incompressible limit with NOLOT [27] and Fasel and Konzelmann [26] (left) as well as velocity and temperature perturbations in the compressible regime with Marxen et al. [28] (right)

Fig. 3

Stability diagram (rigid) for the three baseflow considerations with the red dot indicating the frequency and Reynolds number for the compliant investigations

3 Results

We investigate the stability characteristics of three baseflows with fixed Reynolds number ${{Re}}=1000$ and frequency $F = {\tilde{\omega }} {\tilde{\nu }}_{\infty }/{\tilde{u}}_{\infty }^2=8 \cdot 10^{-5}$ and $M=[3, 5.8, 10]$ for two-dimensional perturbations ($\beta =0$). These parameters are chosen such that the boundary layer of a rigid system is convectively unstable for all Mach numbers considered (see Fig. 3). A sweep across a wide range for $\phi$ and $\mu$ gives insight into different regions of interest that correspond to the coupled system’s response.

3.1 Non-dimensional parameter space analysis

The fluid instability’s growth rate is shown for all cases investigated in Fig. 4. We can identify three features that are valid for all Mach numbers: (1) There exists a converging rigid limit; (2) there exists a converging free limit; (3) there exist two distinct regions transitioning from rigid to free limit behavior. For the free limit, it can be observed that the fluid instability is damped as the growth rate $-\alpha _i$ converges to a negative value. The fact that the boundary layer instability converges to a finite value in the free limit is a consequence of the impedance boundary condition in Eq. 10. For the limit of $\left( \mu , \phi \right) \rightarrow 0$, ${\hat{p}} \rightarrow 0$ in order for the wall-normal velocity perturbation to be bounded. It can be shown that the compliant eigenvalue problem then reduces—in the free limit—to the rigid eigenvalue problem where we impose ${\hat{p}}_w=0$ instead of ${\hat{v}}_w=0$ for the boundary condition.

Fig. 4

Growth rate $-\alpha _i$ of a $M=3$ (top left), $M=5.8$ (top right), and $M=10$ (bottom middle) compliant system

For the horizontal transition region (see Fig. 4), which we label correlation I, the system behavior transitions monotonically, whereas the other transition region, which we label correlation II, exhibits a non-monotonic behavior. To quantitatively describe these transition regions of compliance based on the impedance boundary condition (Eq. (10)), we define the approximations

$$\begin{aligned} \text {correlation I:} \quad&1 \gg \phi \frac{\left( \alpha ^2 + \beta ^2 \right) ^2}{\omega ^2}\quad \rightarrow \quad {\hat{p}} = i \omega \mu {\hat{v}} \\ \text {correlation II:} \quad&1 \ll \phi \frac{\left( \alpha ^2 + \beta ^2 \right) ^2}{\omega ^2}\quad \rightarrow \quad {\hat{p}} = - i \mu \phi \frac{\left( \alpha ^2 + \beta ^2 \right) ^2}{\omega } {\hat{v}}. \end{aligned}$$

With a given relative deviation from the rigid system following

$$\begin{aligned} \epsilon _{\alpha _i} = \Big \vert \frac{(\alpha _i - \alpha _i^{\mathrm{rigid}})}{\alpha _i^{\mathrm{rigid}}} \Big \vert , \end{aligned}$$

(13)

these relations can be quantitatively specified and used as boundaries for the rigid-compliant system behavior (see Fig. 5). For the intersection of the two correlations, we can see that it occurs for $\log _{10}(\phi ) \approx 3$ for all Mach numbers considered. This independence of $M_{\infty }$ and $\mu$ is supported by considering the flexural phase and group wave speeds, namely

$$\begin{aligned} c_{\mathrm{ph}} = \frac{\omega }{\alpha } = \root 4 \of {\frac{{\tilde{E}} \tilde{h^2}}{12 {\tilde{\rho }}_s \left( 1- \nu ^2 \right) }} \sqrt{\omega } = \root 4 \of {\phi \omega ^2} \quad \text {and} \quad c_{\mathrm{gr}} = \frac{\partial \omega }{\partial \alpha } = 2 \root 4 \of {\phi \omega ^2}. \end{aligned}$$

(14)

Fig. 5

Approximation of rigid-compliant boundaries for $M=5.8$ in non-dimensional parameter space (left) and phase relation between ${\hat{p}}_w$ and ${\hat{v}}_w$ with both phase (dashed) and group (dotted) speed of flexural wave (right)

It can be seen in Eq. (14) that both the phase and group speeds are independent of $\mu$ and there seems to exist a constant value $\phi$ for the intersection of correlation I and II across all Mach numbers considered. Boundary layer instabilities are known to have wave speeds of the same order as the non-dimensional freestream velocity, namely $\approx \!\textit{O}(1)$, and we can compute a corresponding $\phi$ assuming matching wave speeds of fluid instability and flexural wave to find $\phi = 1/\omega ^2$ for $c_{\mathrm{ph}} \approx 1$ and $\phi = 1/(4\omega )^2$ for $c_\mathrm{gr} \approx 1$. For the given parameter analysis with $\omega ={{Re}}\cdot F$, we see that the resulting values $\log _{10}(\phi _{(c_{\mathrm{gr}=1})})=3.05$ and $\log _{10}(\phi _{(c_{\mathrm{ph}=1})})=1.84$ correspond to the intersection of correlations I and II (see Fig. 5). This intersection stems from a flexural wave that synchronizes its phase with the fluid instability’s pressure perturbation and results in a $90^{o}$ phase shift between wall-normal velocity and pressure (see Fig. 5), $\theta ({\hat{p}}_\mathrm{wall})-\theta ({\hat{v}}_\mathrm{wall})$, where $\theta ({\hat{q}})=\arg ({\hat{q}})$ is the argument of the complex amplitude distribution ${\hat{q}}$, which is associated with a nonzero power flux at the interface. Additionally, we can observe a shift in spatial wave structure of the fluid instability (see Fig. 6). Across the correlation I region, we see a smooth decrease in spatial wave length, while there is a more pronounced undershoot across the correlation II region, which is consistent with the observations for the growth rate. This supports the notion of the synchronization of a flexural wave with the imposed pressure perturbation of the fluid instability at the interface for a given critical value $\log (\phi _\mathrm{crit})$. For values above, fluid–structural interaction follows correlation II, whereas for values below, it follows the piston-like behavior described by correlation I.

It is worth mentioning that for the tracking along constant values of $\phi$ and varying $\mu$, we experience a general movement of the boundary layer mode towards the continuous spectrum (see Fig. 6). This phenomenon is more pronounced for lower values of $\mu$ and the transitioning behavior is confined to the correlation II region. While the modes do not intersect in the complex plane, the modal shapes have found to be comparable suggesting a potential synchronization with acoustic modes.

Fig. 6

Eigenspectrum for the rigid case and tracked eigenvalue of boundary layer mode holding $\log _{10}(\mu )=-1.5$ constant and varying $\log _{10}(\phi )=[-4 \ldots 6]$ (left); spatial wave number $\alpha _r$ of second-mode instability for $M=5.8$ (right)

We next conduct an analysis of a $M=5.8$ boundary layer flow with a convecting second-mode instability with $F=2 \cdot 10^{-4}$ for systems corresponding to correlation I/II and the free limit. We compute the resulting N-factor

$$\begin{aligned} N(x) = - \int _{x_0}^{x} \alpha _i(x) \mathrm{d}x \end{aligned}$$

(15)

and visualize its deviation $\epsilon _N=\frac{N-N_{\mathrm{rigid}}}{N_{\mathrm{rigid}}}$ from the rigid system. In Fig. 7, we can see that all three cases converge to a constant value as ${{Re}}\rightarrow \infty$, where the free limit with a value of $\epsilon _N \approx 1$ has the most pronounced effect. Nevertheless, both correlation regions show a drastic deviation for lower Reynolds numbers which suggests a shift of the neutral stability curve in the R-F-plane and that $\epsilon _N \approx 0.1 -0.2$ for larger values of ${{Re}}$.

Fig. 7

Varying relative growth rates for a $M=5.8$ second-mode instability for correlation I/II and free limit cases

It needs to be mentioned that the ansatz for the perturbations (given in Eq. 4) breaks down for the converging free limit region as the physical response of the panel in that domain would represent panel flutter. For this aeroelastic instability, the streamwise domain length is critical as the instability coalesces into up- and downstream propagating flexural waves that reflect off the finite panel’s boundaries. Hence, in this limit, the proposed model of linearized Navier–Stokes and Kirchhoff–Love equation cannot fully capture the physical response of the dynamical system. For a deeper discussion of flutter, please refer to the works of Benjamin [5], Landahl [4], and Dowell [29].

3.2 Comparison to Piston theory

Tools used to investigate dynamic behavior in the presence of inviscid, compressible freestream flow grazing over a compliant panel have primarily focused on employing reduced order models for the fluid domain. Most commonly, this includes a thin plate model such as the Kirchhoff-Love plate equation coupled with Piston Theory representing the grazing, inviscid, compressible flow. The latter is an approximation of the perturbed pressure due to a local deflection velocity and angle which, with Eq. 9 and the perturbation ansatz for the deflection $\eta$, can be written as the impedance condition

$$\begin{aligned} {\hat{p}}^\mathrm{PT}_w = -\frac{1}{\sqrt{M^2 -1}} \left[ \frac{M^2-2}{M^2-1} - \frac{\alpha }{\omega } \right] {\hat{v}}_w. \end{aligned}$$

(16)

As the inverse of phase speed $\alpha /\omega$ only varies insignificantly for varying compliance parameters, the phase angle between pressure and wall-normal velocity perturbation is constant and the magnitude difference is predominantly a parameter of Mach number. With the use of Eqs. 10 and 16, we can compute the pressure ratio for both piston theory and linear stability theory as

$$\begin{aligned} \chi = \frac{{\hat{p}}^\mathrm{LST}_w}{{\hat{p}}^\mathrm{PT}_w} = i \omega \mu \sqrt{M^2-1} \frac{\frac{ \left( \alpha ^2 + \beta ^2 \right) ^2}{\omega ^2} \phi -1}{\frac{M^2-2}{M^2-1}-\frac{\alpha }{\omega }}. \end{aligned}$$

(17)

$\vert \chi \vert$ denotes the magnitude of the pressure ratio and $\text {arg}(\chi )$ the difference in pressure phase, which can be seen Fig. 8.

Fig. 8

Pressure ratio magnitude $\vert \chi \vert$ (left) and pressure phase difference (right) between linear stability and piston theory for a compliant system with a $M=5.8$ grazing flow

Clearly, neither the phase nor the magnitude difference between pressure and wall-normal velocity perturbation is constant in the $\phi$-$\mu$-plane. The magnitude follows a similar pattern to the growth rates where both correlations I/II are visible and the magnitude varies gradually between a converging value in the rigid and free limit. More notably, the pressure phase difference experiences a jump from $-\pi /2$ to $~ \pi /2$ across a constant value of $\log _{10}(\phi )$, which correlates to the intersection between correlation I/II. This is caused by a shift between the dominant terms for the numerator $(\alpha ^2+\beta ^2)^2/\omega ^2-1$, which essentially causes a change in sign and hence a phase shift of $+\pi$. Contrary to the piston theory, we can see that the compliant system captured by the conjunction of linear stability theory and a mechanically compliant panel shows more complex dynamics and allows for a nonzero phase relation between panel deflection and the pressure perturbation at the wall.

4 Conclusion

For this work, the canonical flow problem of a compressible, laminar boundary layer over a flat plate has been extended to account for mechanical compliance of the plate. We study the linear response of the system due to boundary layer instabilities for super- and hypersonic Mach numbers that are known to be convectively unstable. For this, we employ a locally parallel ansatz for the flow assuming spatially growing, two-dimensional modes and couple the fluidal perturbation with the linear response of a Kirchhoff–Love plate. Two additional non-dimensional parameters, $\mu$ and $\phi$, allow for a unique description of the coupled, dynamical system.

To gain insight into the alteration of preexisting boundary layer instabilities, we consider an exemplary set of flow parameters $(F,{{Re}})$ that corresponds to unstable boundary layer modes in the rigid limit for all Mach numbers $M=[3,5.8,10]$ considered. The resulting modal growth rates in the non-dimensional $\mu$-$\phi$-plane show a converging rigid and free limit and two distinct correlation regions. The first corresponds to a piston-like movement of the panel where all streamwise variations of the panel response is negligibly small. The transition onset from a rigid to compliant only depends on the weight ratio $\mu$ only, and its associated value is dependent on the Mach number. The second correlation region corresponds to a flexural plate movement which is not Mach number dependent. The intersection of these regions coincides with the flexural wave speeds of the plate being of the order of the boundary layer instability’s wave speeds. This results in a phase change between pressure and wall-normal velocity perturbations leading to a nonzero power input into the panel which destabilizes the boundary layer mode. Comparison to a $1{\text {st}}$-order piston theory model shows significant differences with respect to pressure magnitude for a given plate deflection as well as a nonzero phase relation that experiences a Mach-independent phase jump of $\pi$ at a constant value $\phi$.

Eigenvalue problem

The quadratic eigenvalue problem described in Eq. 5 can be rewritten as a first-order system following

$$\begin{aligned} \begin{bmatrix} L^1 &{}\quad L^0 \\ I &{}\quad 0 \end{bmatrix} {\hat{z}}= \alpha \begin{bmatrix} -L^2 &{}\quad 0\\ 0 &{}\quad I \end{bmatrix} {\hat{z}} \quad \text {with} \quad {\hat{z}} = \begin{bmatrix} \alpha {\hat{q}}\\ {\hat{q}} \end{bmatrix}, \end{aligned}$$

(18)

where I denotes the identity matrix and 0 is a zero matrix. Similarly, the quartic eigenvalue problem for the compliant system can be rewritten as a first-order system following

$$\begin{aligned} \begin{bmatrix} L^1 &{}\quad L^0 &{}\quad L_2 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad I\\ 0 &{}\quad 0 &{}\quad I &{}\quad 0 \\ I &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} {\hat{z}} = \alpha \begin{bmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad -L_4\\ 0 &{}\quad 0 &{}\quad I &{}\quad 0 \\ I &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad I &{}\quad 0 &{}\quad 0\\ \end{bmatrix} {\hat{z}} \quad \text {with} \quad {\hat{z}}=\begin{bmatrix} \alpha {\hat{q}}\\ {\hat{q}} \\ \alpha ^2 {\hat{q}} \\ \alpha ^3 {\hat{q}} \end{bmatrix}. \end{aligned}$$

(19)

The components to the submatrices $[L^0,L^1,L^2,L^4]$ follow the pattern

$$\begin{aligned} L^i = \begin{bmatrix} L^i_{11} &{}\quad L^i_{12} &{}\quad L^i_{13} &{}\quad L^i_{14} &{}\quad L^i_{15}\\ L^i_{21} &{}\quad L^i_{22} &{}\quad L^i_{23} &{}\quad L^i_{24} &{}\quad L^i_{25}\\ L^i_{31} &{}\quad L^i_{32} &{}\quad L^i_{33} &{}\quad L^i_{34} &{}\quad L^i_{35}\\ L^i_{41} &{}\quad L^i_{42} &{}\quad L^i_{43} &{}\quad L^i_{44} &{}\quad L^i_{45}\\ L^i_{51} &{}\quad L^i_{52} &{}\quad L^i_{53} &{}\quad L^i_{54} &{} \quad L^i_{55}\\ \end{bmatrix} \end{aligned}$$

(20)

with the following nonzero components:

$$\begin{aligned} L^0_{11}&= D_2 + \frac{1}{\mu } \frac{\partial \mu }{\partial T} \frac{\partial T}{\partial T} D_1 - i \left( \beta W - \omega \right) \frac{{{Re}}}{\mu T} -\beta ^2 \\ L^0_{12}&= -\frac{{{Re}}}{\mu T} \frac{\partial U}{\partial y} \\ L^0_{14}&= \frac{1}{\mu } \frac{\partial \mu }{\partial y} \frac{\partial U}{\partial y} D_1 + \frac{1}{\mu } \frac{\partial \mu }{\partial T} \frac{\partial ^2 U}{\partial y^2} + \frac{1}{\mu } \frac{\partial ^2 \mu }{\partial y^2} \frac{\partial T}{\partial y} \frac{\partial U}{\partial y} \\ L^0_{22}&= D_2 + \frac{1}{\mu }\frac{\partial \mu }{\partial T} \frac{\partial T}{\partial y} D_1-i \left( \beta W -\omega \right) \frac{{{Re}}}{l_2 \mu T} - \frac{\beta }{l_2} \\ L^0_{23}&= \frac{{{Re}}}{l_2 \mu } D_1 \\ L^0_{24}&= \frac{i}{l_2 \mu } \frac{\partial \mu }{\partial T} \frac{\partial U}{\partial y} \\ L^0_{25}&= i \beta \frac{l_1}{l_2} D_1 + i \beta \frac{l_0}{l_2 \mu } \frac{\partial \mu }{\partial T} \frac{\partial T}{\partial y} \\ L^0_{32}&= D_1 - \frac{1}{T} \frac{\partial T}{\partial y} \\ L^0_{33}&= i \gamma M^2 \left( \beta W - \omega \right) \\ L^0_{34}&= -\frac{i}{T} \left( \beta W -\omega \right) \\ L^0_{35}&= i \beta \\ L^0_{41}&= 2 {{Pr}}\gamma M^2 \frac{\partial U}{\partial y} D_1 \\ L^0_{42}&= 2 i \left( \gamma -1\right) M^2 Pr \beta \frac{\partial W}{\partial y} - \frac{{{Pr}}{{Re}}}{\mu T} \frac{\partial T}{\partial y} \\ L^0_{43}&= i \left( \beta W -\omega \right) \left( \gamma -1\right) M^2 \frac{{{Pr}}{{Re}}}{\mu } \\ L^0_{44}&= D_2 + \frac{2}{k} \frac{\partial k}{\partial y} D_1 -i \left( \beta W -\omega \right) \frac{{{Pr}}{{Re}}}{\mu T} + \left( \gamma -1 \right) \frac{{{Pr}}}{\mu } \frac{\partial \mu }{\partial y} \left[ \left( \frac{\partial U}{\partial y} \right) ^2 + \left( \frac{\partial W}{\partial y} \right) ^2 \right] \\&\quad + \frac{1}{k} \frac{\partial ^2 k}{\partial y^2} - \beta ^2 \\ L^0_{45}&= 2 {{Pr}}\left( \gamma -1 \right) M^2 \frac{\partial W}{\partial y} D_1 \\ L^0_{52}&= i \beta l_1 D_1 + i \frac{\beta }{\mu } \frac{\partial \mu }{\partial y} \frac{\partial T}{\partial y} - \frac{{{Re}}}{\mu T} \frac{\partial W}{\partial y} \\ L^0_{53}&= -i \beta \frac{Re}{mu} \\ L^0_{54}&= \frac{1}{\mu } \frac{\partial \mu }{\partial T} \frac{\partial W}{\partial y} D_1 + \frac{1}{\mu } \frac{\partial \mu }{\partial T} \frac{\partial ^2 W}{\partial y^2} + \frac{1}{\mu } \frac{\partial ^2 \mu }{\partial T^2} \frac{\partial T}{\partial y} \frac{\partial W}{\partial y} \\ L^0_{55}&= D_2 + \frac{1}{\mu } \frac{\partial \mu }{\partial T} \frac{\partial T}{\partial y} D_1 -i \left( \beta W -\omega \right) \frac{{{Re}}}{\mu T} - l_2 \beta ^2 \\ L^1_{11}&= -i U \frac{{{Re}}}{\mu T} \\ L^1_{12}&= i l_1 D_1 + \frac{i}{\mu } \frac{\partial \mu }{\partial T} \frac{\partial T}{\partial y} \\ L^1_{13}&= -i \frac{Re}{\mu } \\ L^1_{15}&= -\beta l_1 \\ L^1_{21}&= i \frac{l_1}{l_2} D_1 + \frac{i}{\mu } \frac{\partial \mu }{\partial T} \frac{\partial T}{\partial y} \frac{l_0}{l_2} \\ L^1_{22}&= -i U \frac{{{Re}}}{l_2 \mu T} \\ L^1_{24}&= -i U \frac{{{Re}}}{l_2 \mu T} \\ L^1_{31}&= i \\ L^1_{33}&= i \gamma M^2 U \\ L^1_{34}&= -i \frac{U}{T}\\ L^1_{42}&= 2 i \left( \gamma -1\right) M^2 {{Pr}}\frac{\partial U}{\partial y} \\ L^1_{43}&= i \left( \gamma -1\right) M^2 \frac{{{Pr}}{{Re}}}{\mu } \\ L^1_{44}&= -i U \frac{{{Pr}}{{Re}}}{\mu T} \\ L^1_{51}&= -\beta l_1 \\ L^1_{55}&= -i U \frac{{{Re}}}{\mu T} \\ L^2_{11}&= \frac{i}{\mu } \frac{\partial \mu }{\partial T} \frac{\partial T}{\partial y} \frac{l_0}{l_2} \\ L^2_{22}&= - \frac{1}{l_2} \\ L^2_{44}&= -1 \\ L^2_{55}&= -1, \end{aligned}$$

where $D_1$ and $D_2$ denote the discrete first and second derivative operator with respect to wall-normal coordinate y and $l_i = i + k/\mu$. These submatrices arise from sorting the governing perturbation equations (Eqs. 1–3 in conjunction with the perturbation ansatz Eq. 4) in the following order:

$$\begin{aligned} \begin{bmatrix} \text {continuity} \\ \text {x-momentum equation} \\ \text {y-momentum equation} \\ \text {z-momentum equation} \\ \text {energy equation} \\ \end{bmatrix} \end{aligned}$$

(21)

In terms of the boundary conditions of the rigid system, we enforce $[{\hat{u}}_w, {\hat{u}}_{\infty }]=0$ in the x-momentum equation, $[{\hat{v}}_w, {\hat{v}}_{\infty }]=0$ in the y-momentum equation, $[{\hat{w}}_w, {\hat{w}}_{\infty }]=0$ in the z-momentum equation, and $[{\hat{T}}_w, {\hat{T}}_{\infty }]=0$ in the energy equation. For the compliant system, we substitute $[{\hat{v}}_w, {\hat{v}}_{\infty }]=0$ with Eq. 10, which changes the following components of above submatrices $L^i$ at the wall:

$$\begin{aligned} L^0_{22}&= \omega ^2 + i \beta ^4 \mu \phi \\ L^0_{23}&= \omega \\ L^2_{22}&= 2 i \beta ^2 \mu \phi \\ L^4_{22}&= i \mu \phi .\\ \end{aligned}$$