1 Introduction

Topology optimization is a computational method used to automatically generate optimal layouts of material within a design domain (Bendsoe and Sigmund 2013), with common design problems including minimization of compliance for maximally stiff structures (Andreassen et al. 2011) or maximization of an output displacement for compliant mechanism design (Sigmund 1997; Zhu et al. 2020). It is currently standard practice for the boundary conditions in these problems to be predetermined by the user based only on intuition, where the locations of applied loads and rigid supports remain fixed and unchanging during the optimization process. In topology optimization studies such as multiple degree-of-freedom compliant mechanisms (Frecker et al. 1999; Alonso et al. 2014; Zhu and Chen 2018; Sigmund 2001), several input loads are applied which can have complex interactions between each other and desired output displacements. This makes it conceivable that the configuration of the boundary conditions could have a large effect on the final topology and performance of the optimized designs. In another application of topology optimization for the design of a bi-stable airfoil compliant mechanism (Bhattacharyya et al. 2019), the input load and fixed supports were manually placed at particular locations on the domain which the authors noted required specific user inputs to determine. In examples such as these it is unlikely that the loads and supports have been placed in optimal positions and orientations, suggesting that a more systematic way of determining their configuration would be useful. In this paper, we therefore seek to develop an efficient method of including the boundary conditions as automatically optimized parameters in the topology optimization formulation.

Optimizing the locations of mechanical (fixed displacement) supports is not a new idea and has been explored in other studies. An early work by Thomas Buhl (2002) used an additional set of design variables to control the stiffness of support springs connected to each element in the finite element mesh of the structure. With its many design variables representing the supported areas, the method allowed for arbitrary support configurations to appear, but also required a penalization method to avoid supports with intermediate stiffness and extra constraint functions for the total area of the domain being supported. In a similar but more complex method by Zhu and Zhang (2010), supports were modeled using separate movable components subjected to boundary conditions, constraints to prevent component overlap, and a finite element mesh that adapted to the updating component locations. For the design of multi-component systems or assemblies, similar techniques to the mechanical support design methods have been applied. Rakotondrainibe et al. (2020) optimized rigid and bolted connections using a type of Robin boundary condition to model the locations, while using the topological derivative to allow for introduction of new connections during the optimization. Ambrozkiewicz and Kriegesmann (2021) simultaneously optimized the joint locations and topologies of mechanical assemblies using spring connections to transfer the loads between parts. In another study for the design of multi-body mechanisms, Swartz and James (2019) used spring connections between components which were parameterized by a Gaussian function to model the behavior of pin joints and to optimize their locations.

For applied loads that change during the course of the optimization, studies such as those by Lee et al. (2012); Lee and Martins (2012) have implemented design-dependent pressure loads or self-weights, where the nodal forces were computed by using detected solid-void material interfaces for pressure or by using the weights of each element based on their density value. Other problems such as homogenization-based microstructure design and thermal structure design (Alacoque et al. 2021) also feature design-dependent loads, but like with pressure and self-weight, these loads are calculated based on the current design and are not controlled by a design variable to find an optimal way of applying them.

In certain scenarios, such as for distributed loads, we will also need to apply continuously movable non-design regions to ensure that the varying loads are applied to completely solid surfaces, while for supports we may wish to have a predetermined solid shape for manufacturability reasons. In the paper by Ambrozkiewicz and Kriegesmann (2021), they enforced circular and cylindrical non-design regions at the movable connections between components using parametric equations and “mask” vectors, which were combined with the structural topology. With a somewhat similar concept, Pollini and Amir (2020) projected shapes onto the design domain from linear segmented profiles using super-Gaussian functions. They used the projections to control material properties or local constraints in specific parts of the domain that were movable by the optimizer. This method of geometry projection onto a domain discretized by a fixed mesh was first introduced by Norato et al. (2015), who defined the geometry of bars using distance functions and used design variables for the spatial locations of their endpoints. Since then, the geometry projection method has been used for other problems such as multi-material lattice structures (Kazemi et al. 2020) and for problems involving projection of more complex discrete shapes (Zhang et al. 2016, 2018; Jessee et al. 2020).

In this paper, we take inspiration from and combine the concepts of spring connections from Buhl (2002), distance functions from Norato et al. (2015), and projection using Gaussian functions from Swartz and James (2019) and Pollini and Amir (2020) to parameterize and optimize both loads and supports simultaneously with the structural topology. The Gaussian function method we develop using these concepts offers several attractive features: (1) Efficient modeling of variable boundary conditions which adds no additional degrees of freedom and requires no remeshing, (2) geometry projection characteristics that can be easily adjusted by choosing the values of a few scalar parameters in the Gaussian function, (3) projection shapes and topologies that can be changed in a modular way by using different distance functions as the input to the same Gaussian function, (4) overlapping of multiple loads or supports projected by a single Gaussian function which cause no issues because they merge together seamlessly without requiring any additional formulations, and (5) formulations and sensitivities which are simple to derive and to implement in existing topology optimization codes.

We begin the paper with a description of the standard Solid Isotropic Material with Penalization (SIMP) topology optimization method in Sect. 2. In Sect. 3, we extend the finite element model by augmenting it with spring connections and nodal forces to allow for variable load and support boundary conditions. The general higher-order Gaussian function is introduced in Sect. 4, and two different distance functions used for projecting point and line geometries into the domain are given. Sections 5 and 6 describe the specific Gaussian functions and formulations used to model the variable boundary conditions and the movable non-design regions, respectively. The main objective and constraint functions used for the topology optimization example problems are given in Sect. 7 along with their adjoint sensitivity analysis formulations. Numerical examples showing the efficacy of the Gaussian function projection method are shown in Sect. 8, and conclusions and potential for future applications of the method are discussed in Sect. 9.

2 Topology optimization

We base our method on the standard SIMP (Solid Isotropic Material with Penalization) topology optimization formulation. The linear elasticity problem is used, which we discretize into a uniform grid of rectangular 4-node bilinear finite elements. Each finite element e is assigned a design variable \(\rho _e\) which represents the density or volume fraction of material in the element ranging from \(\rho _e=0\) (void) to \(\rho _e=1\) (solid). To avoid checkerboard patterns and enforce a minimum length scale on the optimized designs, we use the density filtering method (Bruns and Tortorelli 2001). The filtered densities, representing the actual physical design to be manufactured, are given by

$$\begin{aligned} {\bar{\rho }}_e&= {} \frac{\sum _{i=1}^{N_e}H_{ei}\rho _i}{\sum _{i=1}^{N_e}H_{ei}}, \end{aligned}$$
(1)
$$\begin{aligned} H_{ei}&= {} \max (0,r_{\text{{min}}}-\Delta (e,i)), \end{aligned}$$
(2)

where \(N_e\) is the number of elements in the mesh, \(r_{\text{{min}}}\) is the filter radius specified by the user, and \(\Delta (e,i)\) is the distance between element e and element i. The physical densities \({\bar{\rho }}_e\) are then used to calculate the Young’s modulus of each element using the SIMP interpolation model:

$$\begin{aligned} E_e = E_{\text{{min}}} + {\bar{\rho }}_e^p(E_0-E_{\text{{min}}}), \end{aligned}$$
(3)

where \(E_{\text{{min}}}\) is a minimum value of Young’s modulus given to void elements to avoid singular stiffness matrices in the finite element analyses, p is the SIMP penalization factor used to avoid intermediate densities by setting it to a value greater than 1, and \(E_0\) is the Young’s modulus of the solid material. The Poisson’s ratio, \(\nu\), is a constant.

3 Finite element formulation

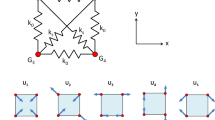
Expanding on the standard SIMP method to allow for simultaneous optimization of the structural topology, mechanical supports, and applied forces, the finite element mesh is connected to a system of spring elements. Like in the method introduced by Buhl (2002), all degrees of freedom in the continuum part of the mesh are connected to rigid fixtures by a spring. In the present paper, we base the stiffness of the support springs on element-centric values \(k^s_e\) assigned to each element. We also apply forces to every node of the continuum mesh at an angle \(\theta\), with a magnitude based on a value \(f_e\) assigned to each of the continuum elements. For the design of compliant mechanisms using the spring model, springs opposing the input forces are also placed at every node at the same angle \(\theta\) and with element-centric stiffness values \(k^{in}_e\). We have used element-centric values rather than nodal values in order to simplify the computations required for creating variable non-design regions of density (which are element-centric values) that follow the boundary condition locations (described in Sect. 6). The general mesh setup is illustrated in Fig. 1. In the following sections of this paper, we explain how to vary the distributions of the spring stiffnesses and force magnitudes in order to control the effective shapes and locations of the boundary conditions.

Fig. 1
figure 1

The general finite element mesh setup with forces, input force springs, and support springs applied to each node

Full size image

The finite element equations for the mesh setup are assembled as follows, where the symbol \({{{\varLambda }\,}}\) is used to denote the finite element assembly operator. The global stiffness matrix \({\varvec{K}}\) of the continuum mesh is assembled in the usual way as

$$\begin{aligned} {\varvec{K}} = {{{\varLambda }\,}}_{e=1}^{N_e} E_e \int _{V_e}^{} {\varvec{B}}_e^\text{{T}}{\varvec{C}}_0{\varvec{B}}_e \text{{d}}V_e = {{{\varLambda }\,}}_{e=1}^{N_e} E_e {\varvec{k}}^0_e, \end{aligned}$$
(4)

where e is the element number, \(V_e\) is the element volume, \({\varvec{B}}_e\) is the element strain–displacement matrix, and \({\varvec{C}}_0\) is the constitutive matrix for a unit Young’s modulus. The integral in Eq. (4) is the element stiffness matrix for a unit Young’s modulus and is written more simply as \({\varvec{k}}^0_e\). The support and input load springs add no additional degrees of freedom to the model, so their contributions to the global stiffness matrix can be simply added to \({\varvec{K}}\). The contribution of the support springs, \({\varvec{K}}^s\), is the assembly of spring element stiffness matrices

$$\begin{aligned} {\varvec{K}}^s = {{{\varLambda }\,}}_{e=1}^{N_e} k^s_e {\varvec{I}}_8, \end{aligned}$$
(5)

where \({\varvec{I}}_8\) is the \(8\times 8\) (8 degrees of freedom per element) identity matrix used to apply \(k^s_e\) to both the x and y degrees of freedom of each node. For the global force vector, the applied forces at each element are assembled as

$$\begin{aligned} {\varvec{F}} = {{{\varLambda }\,}}_{e=1}^{N_e} f_e \varvec{\varTheta }, \end{aligned}$$
(6)

where \(\varvec{\varTheta }\) is an \(8\times 1\) rotation vector that converts the nodal force magnitudes into their corresponding components in the x and y directions based on the global reference frame:

$$\begin{aligned} {\varTheta } = \begin{bmatrix} \cos {\theta }&\quad \sin {\theta }&\quad \cdots \end{bmatrix}^\text{{T}}. \end{aligned}$$
(7)

The contribution of the input springs to the global stiffness matrix is assembled in a similar way to the force vector:

$$\begin{aligned} {\varvec{{K}}}^{\text{{in}}} = {{{\varLambda }\,}}_{e=1}^{N_e} k^{\text{{in}}}_e {\varvec{{I}}}_8\langle \varvec{\varTheta }\rangle . \end{aligned}$$
(8)

Here, the vector \(\langle \varvec{\varTheta }\rangle\) is a smooth approximation of the absolute values of each entry of \(\varvec{\varTheta }\) in order to avoid negative values of spring stiffness while keeping the function differentiable at all values of \(\theta\):

$$\begin{aligned} \langle {\varTheta }\rangle = \begin{bmatrix} \sqrt{\cos ^2{\theta +\epsilon }}&\quad \sqrt{\sin ^2{\theta +\epsilon }}&\quad \cdots \end{bmatrix}^\text{{T}}, \end{aligned}$$
(9)

where a small positive number \(\epsilon\) is added inside the square root of each entry to smooth the sharp corner of the absolute value function. The output spring for compliant mechanism problems is modeled by adding a single spring of stiffness \(k^{\text{{out}}}\) to the output degree of freedom on the main diagonal of the total global stiffness matrix. The global vector of nodal displacements \({\varvec{U}}\) is then found by solving the finite element equilibrium equations, where the spring stiffness matrices are added to the continuum stiffness matrix:

$$\begin{aligned} ({\varvec{{K}}} + {\varvec{{K}}}^s + {\varvec{{K}}}^{\text{{in}}}){\varvec{{U}}} = {\varvec{{F}}}. \end{aligned}$$
(10)

4 Gaussian function parameterization

To control the distributions of force magnitude and support stiffness using only a small number of parameters, we use a super-Gaussian function of the form

$$\begin{aligned} G(x,y) = Ab^{-\left( \frac{d(x,y)^2}{r^2}\right) ^P}. \end{aligned}$$
(11)

The super-Gaussian function has a flat plateau-shaped top with a smooth Gaussian fall-off in the directions of increasing distance represented by the function d(x, y). The parameter P controls the sharpness of the plateau, the coefficient A is the height, and the radius parameter r determines the length from the center of the plateau to a point in the fall-off region with height A divided by the base parameter b:

$$\begin{aligned} G(d=r) = \frac{A}{b}. \end{aligned}$$
(12)

The properties of the super-Gaussian function are illustrated in Fig. 2, where we use a simple one-dimensional distance function describing the distance to the origin point.

Fig. 2
figure 2

Super-Gaussian function with a 1D distance function for several values of the exponent P

Full size image

In two dimensions, we have made use of two different types of distance functions. The first is used to model concentrated loads and small circular supports and is the minimum distance to a number of zero-dimensional points, where the positions of the N points are described by the sets of design variables \({\varvec{{x}}}_D\) and \({\varvec{{y}}}_D\), where \({\varvec{{x}}}_D = \begin{bmatrix} x^{(1)}_D&\quad x^{(2)}_D&\quad \cdots&\quad x^{(N)}_D \end{bmatrix}\) and \({\varvec{{y}}}_D = \begin{bmatrix} y^{(1)}_D&\quad y^{(2)}_D&\quad \cdots&\quad y^{(N)}_D \end{bmatrix}\). The subscript D indicates the coordinate is a design variable and not just a spatial point in the domain. The minimum distance from an element centroid coordinate \({\varvec{{p}}}_e = \begin{bmatrix} x^{(e)}&y^{(e)} \end{bmatrix}\) to the \(N\) points \({\varvec{{c}}}_i = \begin{bmatrix} x^{(i)}&y^{(i)} \end{bmatrix}\) is

$$\begin{aligned} d_e = \min (\Vert {\varvec{{d}}}_1\Vert ,\Vert {\varvec{{d}}}_2\Vert ,\cdots ,\Vert {\varvec{{d}}}_N\Vert ), \end{aligned}$$
(13)

where \({\varvec{{d}}}_i={\varvec{{p}}}_e-{\varvec{{c}}}_i\). An example of the minimum distance function to five different points and the resulting circular shapes with radius r projected into the domain by using the Gaussian function is shown in Fig. 3. Notice that as the circular regions overlap, the value of the Gaussian function is always as if we took the maximum value of separate Gaussian functions applied to each point individually. If multiple points occupy identical coordinates, the Gaussian function produces a distribution exactly as though only a single point were at that position. Although this function is non-smooth, it is continuous and its derivative with respect to all design variables is defined everywhere throughout the domain (see Eq. 52). The discontinuities in the first derivative do not coincide with any local minima within the design space. Therefore, they do not hinder or prevent convergence of the algorithm.

Fig. 3
figure 3

Using the Gaussian function to project circular shapes from zero-dimensional points

Full size image

The second distance function we use is to model distributed loads and supports. This function is the minimum distance to a one-dimensional line, defined by two endpoints \({\varvec{{c}}}_1\) and \({\varvec{{c}}}_2\) as shown in Fig. 4 and described by the piecewise function (Norato et al. 2015)

$$\begin{aligned} d_e = {\left\{ \begin{array}{ll} \Vert {\varvec{{h}}}\Vert &{}\quad \text {if } {\varvec{{a}}} \cdot {\varvec{{h}}} \le 0, \\ \Vert {\varvec{{g}}}\Vert &{}\quad \text {if } 0< {\varvec{{a}}} \cdot {\varvec{{h}}} < {\varvec{{a}}} \cdot {\varvec{{a}}}, \\ \Vert {\varvec{{e}}}\Vert &{}\quad \text {if } {\varvec{{a}}} \cdot {\varvec{{h}}} \ge {\varvec{{a}}} \cdot {\varvec{{a}}}, \end{array}\right. } \end{aligned}$$
(14)

where

$$\begin{aligned} {\varvec{a}}&= {} {\varvec{c}}_2 - {\varvec{c}}_1, \end{aligned}$$
(15)
$$\begin{aligned} {\varvec{h}}&= {} {\varvec{p}}_e - {\varvec{c}}_1, \end{aligned}$$
(16)
$$\begin{aligned} {\varvec{e}}&= {} {\varvec{p}}_e - {\varvec{c}}_2, \end{aligned}$$
(17)
$$\begin{aligned} {\varvec{g}}&= {} \left[ {\varvec{I}}-\frac{1}{\Vert {\varvec{a}}\Vert ^2}{\varvec{a}} \otimes {\varvec{a}} \right] {\varvec{h}}. \end{aligned}$$
(18)

In Eq. (18), \({\varvec{I}}\) is an identity matrix and the symbol \(\otimes\) is the tensor product. This piecewise function and its derivatives are fully smooth and continuous. After passing the line distance function through the Gaussian function, a rounded bar shape of radius r is projected onto the domain.

Fig. 4
figure 4

Using the Gaussian function to project a bar shape from a one-dimensional line

Full size image

5 Variable loads and supports

The locations of the supports are allowed to vary by assigning point coordinates as design variables for the optimizer. We define the vector of all design variables, \({\varvec{z}}\), by concatenating the vector of element densities \(\varvec{\rho }\) with the vectors of support point coordinates \({\varvec{x}}_s\) and \({\varvec{y}}_s\):

$$\begin{aligned} {\varvec{{z}}} = \begin{bmatrix} \varvec{\rho }&{\varvec{x}}_s&{\varvec{y}}_s \end{bmatrix}. \end{aligned}$$
(19)

The support points are then used to define a distance function using either of Eqs. (13) or (14). Using the Gaussian function to define the projection based on the distance function, we obtain the distribution of support spring stiffness throughout the design domain. In the Gaussian function (Eq. 11), the coefficient A is assigned a value of spring stiffness, \(k_0\), chosen by the user which should be large enough to adequately simulate rigid supports but low enough to avoid poor convergence characteristics:

$$\begin{aligned} k^s_e = k_0 b^{-\left( \frac{d_e^2}{r^2}\right) ^P}. \end{aligned}$$
(20)

Through numerical experiments we found that supports of roughly the same stiffness as the solid material gave smoother convergence, where the spring constant corresponding to a certain Young’s modulus can be determined by multiplying it by the element size. The location and orientation of loads are optimized by including the coordinates \({\varvec{x}}_f\) and \({\varvec{y}}_f\) and the orientation of the forces \(\theta\) in the design variable vector. Appending these parameters to the vector of design variables gives

$$\begin{aligned} {\varvec{{z}}} = \begin{bmatrix} \varvec{\rho }&{\varvec{x}}_s&{\varvec{y}}_s&{\varvec{x}}_f&{\varvec{y}}_f&\theta \end{bmatrix}. \end{aligned}$$
(21)

The design variables for the forces are used to define another distance function, which is passed to the Gaussian function to obtain a force value in each element:

$$\begin{aligned} f_e = A_f b^{-\left( \frac{d_e^2}{r^2}\right) ^P}. \end{aligned}$$
(22)

We define the coefficient \(A_f\) such that the user can specify the approximate total load applied in the design domain as a single constant \(f_0\). As the Gaussian function superscript P approaches infinity, the total load in the domain becomes equal to the total load under the projected shape of radius r. For concentrated loads, this is written as

$$\begin{aligned} A_f = \frac{f_0 V_e}{n_n \pi r^2}, \end{aligned}$$
(23)

while for distributed loads it is written as a function of the line length \(\Vert {\varvec{a}}\Vert\), given by

$$\begin{aligned} A_f = \frac{f_0 V_e}{n_n(\pi r^2 + 2r\Vert {\varvec{a}}\Vert )}. \end{aligned}$$
(24)

where \(n_n\) is the number of overlapping nodes between elements (four in the case of 2D rectangular bilinear elements). For the design of compliant mechanisms using the spring model, we scale the stiffness of the input springs proportionally to the force magnitudes using a user-specified constant \(k^{in}_0\):

$$\begin{aligned} k^{\text{{in}}}_e = \frac{k^{\text{{in}}}_0}{A_f} f_e. \end{aligned}$$
(25)

In Eqs. (20) and (22), the radius parameter r can be chosen based on the physical size of the components intended to be providing the load or support. For example, if the structure is held down by a bolted connection, r can be set as the radius of the bolt.

6 Variable non-design regions

To create movable non-design regions that follow the locations of the variable boundary conditions, we use the Gaussian function to project a density distribution onto the domain which is then combined with the filtered densities in a smooth and differentiable way. The filtered element densities are calculated from the density design variables in the same way as before:

$$\begin{aligned} {\tilde{\rho }}_e = \frac{\sum _{i=1}^{N_e}H_{ei}\rho _i}{\sum _{i=1}^{N_e}H_{ei}}. \end{aligned}$$
(26)

The projected density distribution is given by the Gaussian function of unit height (\(A=1\)) with a distance function based on load and support point variables:

$$\begin{aligned} {\hat{\rho }}_e = b^{-\left( \frac{d_e^2}{r^2}\right) ^P}. \end{aligned}$$
(27)

Since the load and supports are based on element-centric values, their distance functions can be directly reused here to define the distribution of element densities. The filtered densities \({\tilde{\rho }}_e\) and the projected densities \({\hat{\rho }}_e\) are then combined into a physical density field using a generalized mean to take the maximum of the two fields:

$$\begin{aligned} {\bar{\rho }}_e = \left( \frac{{\tilde{\rho }}_e^Q + {\hat{\rho }}_e^Q}{2}\right) ^\frac{1}{Q}. \end{aligned}$$
(28)

With \(Q=1\), \({\bar{\rho }}_e\) is the average of \({\tilde{\rho }}_e\) and \({\hat{\rho }}_e\), and as Q approaches infinity, \({\bar{\rho }}_e\) approaches the maximum of the two values from below. Thus, we can set Q to a finite value to approximate the maximum of the filtered and projected density fields in a smooth and differentiable way.

7 Optimization problems and sensitivity analysis

The optimization problem considered in this paper is a minimization of an objective function \(f_{\text{{obj}}}\) subjected to constraints on the design variable upper and lower limits (denoted by the subscripts U and L, respectively, with \(n_s\) representing the number of support design variables and \(n_f\) representing the number of load variables), the amount of material in the domain or overall volume fraction \(V_f\), and any additional number, \(n_c\), of functions \(h_i({\varvec{z}})\) that may be desired in particular problem setups:

$$\begin{array}{lll} \underset{{\varvec{z}}}{\text {min}} &{}\quad f_{obj}({\varvec{z}}) \\ \text {s.t.} &{}\quad 0 \le \rho _e \le 1,&e = 1, \ldots, N_e, \\ &{}\quad x_{sL}^{(i)} \le x_s^{(i)} \le x_{sU}^{(i)},&i = 1, \ldots , n_s, \\ & {}\quad y_{sL}^{(i)} \le y_s^{(i)} \le y_{sU}^{(i)},&i = 1, \ldots , n_s, \\ & {}\quad x_{fL}^{(i)} \le x_f^{(i)} \le x_{fU}^{(i)},&i = 1, \ldots , n_f, \\ & {}\quad y_{fL}^{(i)} \le y_f^{(i)} \le y_{fU}^{(i)},&i = 1, \ldots , n_f, \\ & {}\quad \theta _L \le \theta \le \theta _U, \\ & {}\quad \frac{\sum _{e=1}^{N_e} {\bar{\rho }}_e}{N_e} \le V_f, \\ & {}\quad h_i({\varvec{z}}) \le 0,&i = 1, \ldots , n_c. \end{array} $$
(29)

This problem is solved using the traditional method of moving asymptotes (MMA) (Svanberg 1987), which as a gradient-based numerical optimization method requires the objective and constraint function values along with their first derivatives as inputs. For compliance minimization problems, the objective function \(f_{\text{{obj}}}({\varvec{z}})\) takes the form

$$\begin{aligned} f_{\text{{obj}}}({\varvec{z}}) = C({\varvec{z}}) = {\varvec{F}}({\varvec{z}})^\text{{T}} {\varvec{U}}({\varvec{z}}). \end{aligned}$$
(30)

In the case of compliant mechanism design, the objective is the specified output displacement

$$\begin{aligned} f_{\text{{obj}}}({\varvec{z}}) = U_{\text{{out}}}({\varvec{z}}) = {\varvec{L}}^\text{{T}} {\varvec{U}}({\varvec{z}}), \end{aligned}$$
(31)

where \({\varvec{L}}^\text{{T}}\) is a constant vector of all zeros except at the output degree of freedom, where it has a value of one.

Table 1 Adjoint sensitivity equations for the derivative of the compliance and output displacement functions with respect to each design variable
Full size table

To determine the derivative of the compliance with respect to each of the design variables, we use adjoint sensitivity analysis to find

$$\begin{aligned} \frac{\partial C({\varvec{z}})}{\partial z_i}&= \frac{\partial {\varvec{F}}^\text{{T}}}{\partial z_i} {\varvec{U}} + {\varvec{U}}^\text{{T}} \nonumber \\&\quad \times \left( \frac{\partial {\varvec{F}}}{{\partial z_i}} - \left( \frac{\partial {\varvec{K}}}{\partial z_i} + \frac{\partial {\varvec{K}}^s}{\partial z_i} + \frac{\partial {\varvec{K}}^{\text{{in}}}}{\partial z_i}\right) {\varvec{U}}\right) . \end{aligned}$$
(32)

Similarly for the output displacement objective function, we find the following form:

$$\begin{aligned} \frac{\partial U_{\text{{out}}}({\varvec{z}})}{\partial z_i}&= \varvec{\lambda }^\text{{T}} \nonumber \\&\quad \times \left( \frac{\partial {\varvec{F}}}{{\partial z_i}} - \left( \frac{\partial {\varvec{K}}}{\partial z_i} + \frac{\partial {\varvec{K}}^s}{\partial z_i} + \frac{\partial {\varvec{K}}^{\text{{in}}}}{\partial z_i}\right) {\varvec{U}}\right) . \end{aligned}$$
(33)

where the adjoint vector is first computed as

$$\begin{aligned} \varvec{\lambda } = \left( {\varvec{K}} + {\varvec{K}}^s + {\varvec{K}}^{\text{{in}}}\right) ^{-1}{\varvec{L}}. \end{aligned}$$
(34)

The adjoint sensitivity equations then take on different forms for each design variable type \(\varvec{\rho }\), \({\varvec{x}}_s\) or \({\varvec{y}}_s\), \({\varvec{x}}_f\) or \({\varvec{y}}_f\), and \(\theta\). For the sensitivity with respect to the density variable at each element e (\(z_i= \rho _i\)), the derivative with respect to the physical density \({{\bar{\rho }}_e}\) is taken first and the chain rule is subsequently used to find the sensitivity with respect to the base design variable:

$$\begin{aligned} \frac{\partial f_{\text{{obj}}}({\varvec{z}})}{\partial \rho _i} = \sum _{e=1}^{N_e}\frac{\partial f_{\text{{obj}}}({\varvec{z}})}{\partial {\bar{\rho }}_e} \frac{\partial {\bar{\rho }}_e}{\partial {\tilde{\rho }}_e} \frac{\partial {\tilde{\rho }}_e}{\partial \rho _i}, \end{aligned}$$
(35)

where

$$\begin{aligned} \frac{\partial {\bar{\rho }}_e}{\partial {\tilde{\rho }}_e}&= {} \frac{1}{2} \left( \frac{{\tilde{\rho }}^Q_e + {\hat{\rho }}^Q_e}{2} \right) ^{\frac{1}{Q}-1}{\tilde{\rho }}_e^{Q-1}, \end{aligned}$$
(36)
$$\begin{aligned} \frac{\partial {\tilde{\rho }}_e}{\partial \rho _i}&= {} \frac{H_{ie}}{\sum _{j=1}^{N_e}H_{ij}}. \end{aligned}$$
(37)

The final adjoint sensitivity equations are summarized in Table 1.

We now list the partial derivatives of the stiffness matrices and force vectors. The sensitivity of the global stiffness matrix with respect to the physical densities is given by

$$\begin{aligned} \frac{\partial {\varvec{K}}_e}{{\partial {\bar{\rho }}_e}} = p{\bar{\rho }}_e^{p-1}(E_0-E_{\text{{min}}}) {\varvec{k}}^0_e. \end{aligned}$$
(38)

where the subscript e on the global matrix indicates that we only consider entries within the global stiffness matrix that correspond to degrees of freedom associated with the element e, since the derivatives of all other entries vanish.

For the derivative of the stiffness matrix of the continuum structure with respect to each support variable \(z_i = x^{(i)}_s\) or \(z_i = y^{(i)}_s\) (and similarly with respect to the force location variables), the derivative is

$$\begin{aligned} \frac{\partial {\varvec{K}}}{\partial z^{(i)}_s} = {{{\varLambda }\,}}_{e=1}^{N_e} p{\bar{\rho }}_e^{p-1}\frac{\partial {\bar{\rho }}_e}{\partial z^{(i)}_s} (E_0-E_{\text{{min}}}) {\varvec{k}}^0_e, \end{aligned}$$
(39)

where

$$\begin{aligned} \frac{\partial {\bar{\rho }}_e}{\partial z^{(i)}_s} = \frac{1}{2} \left( \frac{{\tilde{\rho }}^Q_e + {\hat{\rho }}^Q_e}{2} \right) ^{\frac{1}{Q}-1}{\tilde{\rho }}_e^{Q-1} \frac{\partial {\hat{\rho }}_e}{\partial z^{(i)}_s}, \end{aligned}$$
(40)

and

$$\begin{aligned} \frac{\partial {\hat{\rho }}_e}{\partial z^{(i)}_s} = - \frac{2 P}{r^2}b^{-\left( \frac{d^2_e}{r^2}\right) ^P} \ln (b) \left( \frac{d^2_e}{r^2}\right) ^{P-1} d_e \frac{\partial d_e}{\partial z_s^{(i)}}. \end{aligned}$$
(41)

For the support spring component of the global stiffness matrix, it is

$$\begin{aligned} \frac{\partial {\varvec{K}}^s}{\partial z_s^{(i)}} = {{{\varLambda }\,}}_{e=1}^{N_e}\frac{\partial k^s_e}{\partial z_s^{(i)}}{\varvec{{I}}}_8, \end{aligned}$$
(42)

where

$$\begin{aligned} \frac{\partial k^s_e}{\partial z_s^{(i)}} = -\frac{2 k_0 P}{r^2}b^{-\left( \frac{d^2_e}{r^2}\right) ^P} \ln (b) \left( \frac{d^2_e}{r^2}\right) ^{P-1} d_e \frac{\partial d_e}{\partial z_s^{(i)}}. \end{aligned}$$
(43)

For the derivative with respect to each force variable \(z_i = x^{(i)}_f\) or \(z_i = y^{(i)}_f\), The derivative of the input spring stiffness matrix is

$$\begin{aligned} \frac{\partial {\varvec{{K}}}^{\text{{in}}}}{\partial z^{(i)}_f}&= -\frac{k^{\text{{in}}}_0}{A_f^2} \frac{\partial A_f}{\partial z^{(i)}_f} {{{\varLambda }\,}}_{e=1}^{N_e} f_e {\varvec{{I}}}_8\langle {\varTheta }\rangle \nonumber \\&\quad + \frac{k^{\text{{in}}}_0}{A_f} {{{\varLambda }\,}}_{e=1}^{N_e} \frac{\partial f_e}{\partial z^{(i)}_f} {\varvec{{I}}}_8\langle {\varTheta }\rangle . \end{aligned}$$
(44)

The force vector is also a function of the force design variables and its derivative is given by

$$\begin{aligned} \frac{\partial {\varvec{F}}}{{\partial z^{(i)}_f}} = {{{\varLambda }\,}}_{e=1}^{N_e} \frac{\partial f_e}{{\partial z^{(i)}_f}} {\varTheta }, \end{aligned}$$
(45)

where for the case where the coefficient \(A_f\) is a function of the line length

$$\begin{aligned} \frac{\partial f_e}{{\partial z^{(i)}_f}}&= \frac{\partial A_f}{\partial z_f^{(i)}}b^{-\left( \frac{d^2_e}{r^2}\right) ^P} \nonumber \\&\quad - \frac{2 A_f P}{r^2}b^{-\left( \frac{d^2_e}{r^2}\right) ^P} \ln (b) \left( \frac{d^2_e}{r^2}\right) ^{P-1} d_e \frac{\partial d_e}{\partial z_f^{(i)}}. \end{aligned}$$
(46)

The derivative of the coefficient is given by

$$\begin{aligned} \frac{\partial A_f}{\partial z_f^{(i)}} = \frac{2 f_0 V_e r}{n_n (\pi r^2 + 2r\Vert {\varvec{a}}\Vert )^2} \frac{{\varvec{a}}^{(i)}}{\Vert {\varvec{a}}\Vert }, \end{aligned}$$
(47)

for the case of a line load or else is equal to zero for the case of a point load.

For the derivative of the global stiffness matrix with respect to the force angle variable \(\theta\), the input spring stiffness matrix has dependence:

$$\begin{aligned} \frac{\partial {\varvec{{K}}}^{\text{{in}}}}{\partial \theta } = \frac{k^{\text{{in}}}_0}{A_f} {{{\varLambda }\,}}_{e=1}^{N_e} f_e {\varvec{{I}}}_8 \frac{\partial \langle {\varTheta }\rangle }{\partial \theta }, \end{aligned}$$
(48)

where

$$\begin{aligned} \frac{\partial \langle {\varTheta }\rangle }{\partial \theta } = \begin{bmatrix} -\frac{\sin {\theta } \cos {\theta }}{\sqrt{\cos ^2(\theta )+\epsilon }}&\quad \frac{\sin {\theta } \cos {\theta }}{\sqrt{\sin ^2(\theta )+\epsilon }}&\quad \cdots \end{bmatrix}^\text{{T}}. \end{aligned}$$
(49)

Finally, the derivative of the global force vector with respect to the load orientation is given by

$$\begin{aligned} \frac{\partial {\varvec{F}}}{{\partial \theta }} = {{{\varLambda }\,}}_{e=1}^{N_e} f_e \frac{\partial {\varTheta }}{{\partial \theta }}, \end{aligned}$$
(50)

where

$$\begin{aligned} \frac{\partial {\varTheta }}{{\partial \theta }} = \begin{bmatrix} -\sin {\theta }&\quad \cos {\theta }&\quad \cdots \end{bmatrix}^\text{{T}}. \end{aligned}$$
(51)

When zero-dimensional points are being used to construct the minimum distance function, the derivative of the distance function is

$$\begin{aligned}&\frac{\partial d_e}{\partial \begin{bmatrix} x_D^{(i)}&\quad y_D^{(i)} \end{bmatrix}^\text{{T}}} \nonumber \\&\quad = {\left\{ \begin{array}{ll} -\frac{{\varvec{d}}_i}{\Vert {\varvec{d}}_i\Vert } &{}\quad \text {if } \Vert {\varvec{d}}_i\Vert = \min (\Vert {\varvec{{d}}}_1\Vert ,\Vert {\varvec{{d}}}_2\Vert ,\ldots ,\Vert {\varvec{{d}}}_N\Vert ), \\ {\varvec{0}} &{}\quad \text {if } \Vert {\varvec{d}}_i\Vert \ne \min (\Vert {\varvec{{d}}}_1\Vert ,\Vert {\varvec{{d}}}_2\Vert ,\ldots ,\Vert {\varvec{{d}}}_N\Vert ), \end{array}\right. } \end{aligned}$$
(52)

and when one-dimensional lines are being used, it is

$$\begin{aligned}&\frac{\partial d_e}{\partial \begin{bmatrix} x_D^{(1)}&y_D^{(1)} \end{bmatrix}^\text{{T}}} \nonumber \\&\quad ={\left\{ \begin{array}{ll} - \frac{{\varvec{{h}}}}{\Vert {\varvec{{h}}}\Vert } &{} \\ \text {if } {\varvec{{a}}} \cdot {\varvec{{h}}} \le 0, \\ \frac{1}{\Vert {\varvec{{g}}}\Vert } \left[ \frac{1}{\Vert {\varvec{{a}}}\Vert ^2} \left( ({\varvec{{a}}} \otimes {\varvec{{h}}})^\text{{T}}+({\varvec{{a}}} \cdot {\varvec{{h}}}){\varvec{{I}}} \right) -{\varvec{{I}}} \right] {\varvec{{g}}} &{} \\ \text {if } 0< {\varvec{{a}}} \cdot {\varvec{{h}}} < {\varvec{{a}}} \cdot {\varvec{{a}}}, \\ \mathbf{0} &{} \\ \text {if } {\varvec{{a}}} \cdot {\varvec{{h}}} \ge {\varvec{{a}}} \cdot {\varvec{{a}}}. \end{array}\right. } \end{aligned}$$
(53)

for the first point of the line and

$$\begin{aligned}&\frac{\partial d_e}{\partial \begin{bmatrix} x_D^{(2)}&y_D^{(2)} \end{bmatrix}^\text{{T}}} \nonumber \\&\quad = {\left\{ \begin{array}{ll} \mathbf{0} &{} \\ \text {if } {\varvec{{a}}} \cdot {\varvec{{h}}} \le 0, \\ - \frac{1}{\Vert {\varvec{{g}}}\Vert \Vert {\varvec{{a}}}\Vert ^2} \left( ({\varvec{{a}}} \otimes {\varvec{{h}}})^\text{{T}}+({\varvec{{a}}} \cdot {\varvec{{h}}}){\varvec{{I}}} \right) {\varvec{{g}}} &{} \\ \text {if } 0< {\varvec{{a}}} \cdot {\varvec{{h}}} < {\varvec{{a}}} \cdot {\varvec{{a}}}, \\ - \frac{{\varvec{{e}}}}{\Vert {\varvec{{e}}}\Vert } &{} \\ \text {if } {\varvec{{a}}} \cdot {\varvec{{h}}} \ge {\varvec{{a}}} \cdot {\varvec{{a}}}. \end{array}\right. } \end{aligned}$$
(54)

for the second point of the line.

8 Numerical examples

In this section, we demonstrate the performance of the algorithm for several benchmark problems. To avoid letting the designs prematurely converge to local minima, we use a continuation strategy on the SIMP penalty parameter p where the optimization runs with \(p=1\) until the average change in the density design variables from the previous iteration is less than \(10^{-3}\), after which p is increased by 0.5. This process repeats until \(p=3\), and at this point the optimization continues until the average change in density variables is less than \(10^{-4}\), at which point we consider the optimization fully converged and stop the program. We use the average change, rather than the maximum change that is often used in topology optimization (Andreassen et al. 2011), since it is less sensitive to localized changes in the density caused by small oscillations in the load and support design variables (Ferrari and Sigmund 2020).

Table 2 Optimization parameters common to all example problems
Full size table

The common parameters used for all of the following examples are summarized in Table 2. Since we are using linear elasticity, the elastic modulus of the solid material is set to \(E_0=1\) Pa to represent an arbitrary material. The total load is also given a small value by setting \(f_0=1\) N, which prevents extremely large displacements from occurring. To make the supports roughly the same stiffness as the solid material, the values for support spring stiffness are set to \(E_0 \times 10^{-3}\), since all examples have element sizes on the order of \(10^{-3}\) meters. For the smoothing parameter \(\epsilon\), we conservatively chose a relatively large value of 0.1 to ensure differentiability of the input force string stiffness matrix. Smaller values such as \(\epsilon =0.01\) also work acceptably well, although it is not critical that the distribution of input spring stiffness precisely follows the distribution of the input forces. The Gaussian function superscript is set to \(P=4\) to create flat-topped projections which still have smooth fall-off regions. This value can be set to higher values for finer meshes or larger projection radii. The superscript for the generalized mean of the filtered and projected density fields is set to \(Q=10\), which is based on numerical experiments to determine a value that is high enough to approximate a maximum without causing convergence issues due to non-smoothness. The superscript values for similar smooth maximum functions have typically also been set to values of 8 to 10 in the previous studies (Lee et al. 2012; Norato et al. 2015; Alacoque et al. 2021).

For the MMA optimizer, the move limits are set to plus or minus 20% of the current values for the densities, 2r for the load and support locations, and 2 degrees for the load orientation.

In the design plots shown in the following sections, red contour lines represent the support geometry projected by the Gaussian function at a radius r. Loads are similarly shown by blue contour lines, with an arrow pointing in the direction \(\theta\) and originating at the design variable coordinates \((x_f,y_f)\).

8.1 Minimum compliance design

We begin by validating the framework for a simple minimum compliance cantilever beam problem which has a well-known solution with obvious optimal locations for the loads and supports. A rectangular design domain of dimensions \(30\times 7.5\) centimeters and discretized by a grid of \(200\times 50\) elements is initialized with a uniform distribution of 20% density, a distributed line support at the left side with both endpoints at the same position, and a concentrated load at the right side. We note that although the structure is initially supported by only a single point, the Gaussian function projects a circle of finite radius r which provides rotational stiffness. The design variables included are the densities, support line endpoint coordinates, and load point coordinates:

$$\begin{aligned} {\varvec{{z}}} = \begin{bmatrix} \varvec{\rho }&\quad {\varvec{x}}_s&\quad {\varvec{y}}_s&\quad {\varvec{x}}_f&\quad {\varvec{y}}_f\end{bmatrix}. \end{aligned}$$
(55)

The load orientation is set to a constant value of \(\theta =-90^\circ\) (pointing straight downwards). The areas of the design domain where the support and load coordinates are allowed to move in are constrained to one-fourth of the length of domain from the left and right ends, as shown by the red and blue dashed regions in Fig. 5a. Minimum and maximum values of the points are set such that they must remain at least a distance of the Gaussian function radius, r, from the overall domain boundaries.

Fig. 5
figure 5

Results of the cantilever beam problem

Full size image

Running the optimization, we get the design we would expect with fast convergence. The loads and supports move horizontally as close together as possible to minimize the moment arm, and the two endpoints of the distributed support move vertically as far apart as possible to maximize the second moment of area. The density resolves to a cantilever beam design that is typical with the standard SIMP method. The optimized design is shown in Fig. 5b and the convergence history is shown in Fig. 5c. The sharp kinks in the objective function history starting near 25 iterations correspond to the point where the loads and supports reach their vertical and horizontal limits, and the small upward jumps afterwards are caused by the continuation scheme when the SIMP penalty parameter p increases by 0.5.

As a second compliance minimization problem, we optimize a bridge structure. We initialize a \(20\times 20\) centimeter design domain with \(200\times 200\) elements and 15% uniform density as shown in Fig. 6a. One point support is placed in each of the top corners of the domain, and two overlapping supports are placed at each of the two bottom corners for a total of six support points. A distributed line load with a solid non-design region projected underneath is placed across the width of the center of the domain with the orientation initially pointing downwards. These parameters are represented by the following vector of design variables:

$$\begin{aligned} {\varvec{{z}}} = \begin{bmatrix} \varvec{\rho }&\quad {\varvec{x}}_s&\quad {\varvec{y}}_s&\quad {\varvec{x}}_f&\quad {\varvec{y}}_f&\quad \theta \end{bmatrix}. \end{aligned}$$
(56)

The upper bound of the material volume fraction is constrained to 15%, and the supports are allowed to move only along the edges of the domain as shown in Fig. 6a by the red dashed lines. The distributed load is allowed to move in the middle third of the domain as shown in Fig. 6a by the blue dashed region.

Fig. 6
figure 6

Results for the bridge design problem

Full size image

The results of the optimization are shown in Fig. 6b. As would be expected, the distributed load moves as close as possible to the supports along the bottom edge, which distribute themselves underneath it. The load also remains distributed across the entire domain and the orientation does not change from its initial downward direction. The supports allowed to move along the vertical edges place themselves at the ends of the bridge to directly support it.

8.2 Compliant mechanism design

While for the simple compliance minimization problems in the previous section the optimal locations of the loads and supports were somewhat obvious and could be guessed intuitively, typically the same cannot be said for compliant mechanism design problems. The positions and orientations of the boundary conditions have a significant effect on the motion of the output degrees of freedom and initial guesses based on intuition are likely suboptimal.

To demonstrate this, we use the standard benchmark compliant mechanism problem of a displacement inverter. The domain is initialized as a \(20\times 20\) centimeter square with a grid of \(200\times 200\) elements, with a uniform 20% material density. This same 20% value was used for the constraint on the volume fraction upper bound, and the load and support locations are placed in the positions shown in Fig. 7a, which are the typical locations in the inverter mechanism problem. A spring of stiffness \(k^{\text{{out}}}\) is placed on the degree of freedom for the horizontal displacement at the center of the right edge, which is the displacement being minimized as the objective function (to maximize the displacement in the leftward direction). This initial design and volume constraint is the same for each of the following examples. First, we set only the material densities as the design variables:

$$\begin{aligned} {\varvec{{z}}} = \begin{bmatrix} \varvec{\rho } \end{bmatrix}. \end{aligned}$$
(57)

The results of this optimization gives a familiar displacement inverter design, shown in Fig. 7b.

Fig. 7
figure 7

Results for the displacement inverter design problem

Full size image

As a second problem, we add the positions of the load and supports as design variables:

$$\begin{aligned} {\varvec{{z}}} = \begin{bmatrix} \varvec{\rho }&\quad {\varvec{x}}_s&\quad {\varvec{y}}_s&\quad {\varvec{x}}_f&\quad {\varvec{y}}_f \end{bmatrix}. \end{aligned}$$
(58)

These positions are unconstrained and can move anywhere in the design domain, with the exception that they must remain at least a distance of r from the edges of the domain. Since asymmetry in the design was observed, we also include an additional constraint function to prevent the output displacement from deviating significantly in the vertical direction:

$$\begin{aligned} \left( U^y_{\text{{out}}}\right) ^2 \le \left( 0.05U^x_{\text{{out}}}\right) ^2. \end{aligned}$$
(59)

The problem results in a different design, shown in Fig. 7c, where the supports have moved very close to the input load, which shifts to a position further inside the domain. As a result of this change in the boundary condition locations, the output displacement increases by 123% compared to the conventional design that had predetermined boundary conditions.

For a third problem, we include the orientation of the load as a design variable:

$$\begin{aligned} {\varvec{{z}}} = \begin{bmatrix} \varvec{\rho }&\quad {\varvec{x}}_s&\quad {\varvec{y}}_s&\quad {\varvec{x}}_f&\quad {\varvec{y}}_f&\quad \theta \end{bmatrix}. \end{aligned}$$
(60)

Keeping the constraint function for controlling the unwanted vertical output displacement, Eq. (59), this results in an asymmetrical design, shown in Fig. 7d, where the load is applied at an oblique angle relative to the direction of the output displacement. A displacement 151% larger than the conventional fixed boundary condition design is achieved for the same input force magnitude, which shows that the optimizer is able to exploit the additional design freedom to obtain better objective function values. The increase in performance and the counterintuitive, asymmetrical design when the boundary conditions are included as design variables shows the effectiveness of allowing them to be determined automatically by the optimizer.

The asymmetrical design of Fig. 7d performs well based on the finite element analysis, however, the support closest to the applied load is somewhat difficult to interpret as a manufacturable structure. It is surrounded by solid material with a region of soft intermediate density in the middle, making the support rotate and act more like a pin joint than a compliant hinge. To get a fully compliant mechanism design with no need for bearings or significant post-processing, we run the asymmetrical inverter problem once more and include variable non-design solid regions projected on both the load and the supports. We implement this by defining a new distance function of three points, \(d({\varvec{x}}_s,{\varvec{y}}_s,x_f,y_f)\), and using it in the equations of Sect. 6. The initial design and optimized results are shown in Fig. 8, where there are now clearly formed compliant hinges for each boundary condition point. By forcing the material to be solid at the load and support locations, the optimizer was no longer able to take advantage of the soft intermediate density material to make a pin joint. This came at a small cost to the overall performance, with the design achieving 1.7% less displacement at the output point compared to the asymmetrical inverter without the non-design regions. The deformation is visualized in Fig. 9, where the bending of compliant hinges and a substantial geometric advantage can be seen. The locations of the supports translate very little in relation to the input load and the output point, showing that the stiffness of the support springs is adequately high.

Fig. 8
figure 8

Results for the asymmetric displacement inverter problem with variable non-design regions included

Full size image
Fig. 9
figure 9

Deformation of the asymmetrical inverter design superimposed on the undeformed design

Full size image

To validate our methodology, we manufactured a half-scale model of the design of Fig. 8 on an Objet260 Connex3 3D printer using the digital material FLX9885-DM, a blend of VeroWhite and TangoBlack+ polymers. The mechanism’s supports were inserted into a base plate, 3D printed from VeroWhite, with a cutout included to guide the input actuation handle at the correct angle. Figure 10 shows the 3D printed model as it is actuated through a large displacement. While the numerical modeling was only based on linear elasticity, the physical prototype is still able to maintain a small vertical output displacement through the large actuation shown in Fig. 10. In both the partially actuated and fully actuated states shown in Fig. 10, the vertical displacement of the output point is about 8% the magnitude of the horizontal displacement based on measurements of the image. This can be compared to the 5% constraint imposed on the design in the topology optimization by Eq. (59).

Fig. 10
figure 10

3D printed model of the displacement inverter design

Full size image

9 Conclusion

In this paper, we introduced a framework for including variable load and support boundary conditions in topology optimization. Starting with the standard SIMP method with linear elasticity, we extended it to use a system of spring elements to model elastic supports and loads. The stiffness of the springs and the magnitudes of input forces applied to every structural element were parameterized and controlled by a higher-order Gaussian function. By using the distance functions of simple points and lines, the Gaussian function was used to model the effective location and orientation of different boundary conditions in a smooth, differentiable, and optimizable way with minimal numbers of additional design variables.

Two examples of compliance minimization problems were shown, demonstrating the effectiveness and efficiency of the Gaussian function approach in automatically finding optimal placements of the boundary conditions. Several examples of compliant mechanism problems were then presented, resulting in significantly increased performance over designs in which the boundary conditions were defined a priori. Using our method to design displacement inverters, we produced several designs with more than double the performance of the design with conventionally predetermined boundary conditions. The relatively counterintuitive design of these mechanisms shows the usefulness of allowing a numerical optimizer to automatically find the optimal boundary conditions, rather than relying only on experience or trial and error methods.

The super-Gaussian projection method proposed here was applied only to linear elasticity problems with the boundary conditions modeled by simple points and straight lines. However, it should be straightforward to add new features in future applications. Different and more complex boundary condition geometries can be used by defining new distance functions. Movable and rotatable roller supports could be implemented by using a rotation vector in the assembly of the support spring stiffness matrix, like what was done in this paper for the load vector assembly. Extension to three dimensions can be done easily, as long as some attention is paid to maintaining manufacturable supports and load application zones that do not become entirely enclosed in material. The method should also be extendable to more complex problems such as those that include geometric non-linearity or multiple physics disciplines. Future work will utilize the super-Gaussian projection method developed in this paper for problems involving some of these extensions.