Support-free robust topology optimization based on pseudo-inverse stiffness matrix and eigenvalue analysis

Abstract

Current finite element analysis (FEA) and optimizations require boundary conditions, i.e., constrained nodes. These nodes represent structural supports. However, many realistic structures do not have such concrete supports. In a robust optimization, i.e., optimization for uncertain load inputs, it is desirable to involve support uncertainty. However, such a robust optimization has not been available since constrained nodes are required to convert the stiffness matrix to an invertible matrix. This paper demonstrates a quite simple robust optimization based on a pseudo-inverse stiffness matrix and eigenvalue analysis that successfully creates optimal design without constrained nodes. The optimization strategy is to minimize the largest eigenvalue of the pseudo-inverse matrix. It was found that optimization for multiple eigenvalues, i.e., multiple load inputs, is required as the nature of the minimax problem. The created structures are capable of carrying multiple load inputs—bending, torsion, and more complex loads. Configurations created in rectangular design domains exhibited hollow monocoque structures.

1 Introduction

Various realistic structures, such as handheld electronic devices or marine hull structures, are exposed to uncertain load inputs, and these structures do not have concrete supports. Robust structural optimization involves these uncertainties in loading or other conditions. Practically, the concept of ‘uncertain load’ should involve uncertain supports. Therefore, the problem should preferably be “support-free.” However, optimization for such support-free problems have yet to be considered.

There are several approaches to robust optimizations, such as worst-case oriented approaches (Ben-Tal and Nemirovski 2002) and stochastic approaches. Cherkaev and Cherkaev (1999, 2003, 2008) formulated worst loading as a loading that causes maximum strain energy under a certain loading constraint. Takezawa et al. (2011) expanded the formulation to a realistic methodology. Nakazawa et al. (2016) formulated worst loading as an uncertain loading position of a point loading. The concept of “uncertain load” also involves uncertain loading directions (Csébfalvi 2018). Chen et al. (2010) and Zhao and Wang (2014) formulated stochastic approaches as random field loadings.

Other various approaches have also been presented (Leliévre et al. 2016): uncertainty in material property and manufacturing tolerances (Guest and Igusa 2008; Rostami SAL Ghoddosian 2018), uncertain bounded buckling loads (Kaveh et al. 2018), and the game theory approach (Holmberg et al. 2017). Zhang et al. (2016) applied eigenvalue analysis to dynamic compliance problems. An optimization technique to assure robustness against small loading uncertainty has also been described (Liu et al. 2017). Kogiso et al. (2008) considered stability with respect to changes in loading. Beside the density-based approaches of topology optimization, a level-set based structural optimization method (De Gournay et al. 2008), methods for shape optimization (Shimoda et al. 2015; Dambrine and Laurain 2016), and a ground structure approach (Ahmadi et al. 2018) have also been presented.

All of these methods above require a boundary condition, i.e., support consisting of displacement constraints. Basically, static structural analysis cannot determine a solution without a boundary condition. This is the difficulty of support-free problems. Some methods have been developed to deal with such support-free systems. The inertia relief analysis firstly introduced in NASTRAN (Reference Manual 2005) enables analysis of support-free systems by converting the static structural problem into a dynamic problem. A structural optimization method including optimization of supports is also available (Buhl 2002). However, considering simplicity and flexibility, there is a requirement for a straightforward analysis and optimization method for support-free systems.

In finite element analysis, the stiffness matrix is not invertible without boundary conditions (nodal constraints with at least 6 degrees of freedom are required for 3D problems). However, this does not mean that an elastic equation does not have solutions. In principle, an input load set has an elasticity solution without these constrained nodes. If the load input is balanced, the sum of both the loads and moments are zero. For such a non-invertible matrix, eigenvalue analysis is still available. In addition, the pseudo-inverse of a stiffness matrix can substitute for the inverse. This yields an exact solution for balanced load input.

This paper presents a robust structural optimization methodology for support-free systems based on an established topology optimization adopting the density-based approach (Bendsøe 1989; Mlejnek 1992; Bendsøe and Sigmund 2003). This approach to robust optimization is worst-case oriented. The use of a pseudo-inverse matrix and eigenvalues is also widely applicable to other schemes, such as shape optimization, the level set method, and stochastic approaches to robust optimization. The following sections describe the details of this method and the trials that were carried out.

2 Theoretical remarks

2.1 Support-free problems

An elasticity problem with supports is a boundary value problem. The supports provide the essential boundary conditions as displacement constraints. The given loading conditions at the surface of the elastic body also provide the natural boundary conditions as stress constraints. Since the problem is static, the total sum of the loadings must be zero, and the reaction forces on the supports balance the total load.

A support-free problem lacks the essential boundary conditions. The displacement solution is not unique due to uncertainty of the integration constants. If the load input is not balanced, the equation does not have a solution because the problem cannot satisfy the natural boundary conditions.

In realistic physics, the application of an unbalanced load onto an unsupported body results in infinite displacements. However, the load input consists of a balanced component and an unbalanced component. The balanced component may produce internal deformation of the body, and the unbalanced component may produce infinite rigid body motion. It can be expected that the internal deformation produces unique strain and that the rigid body motion does not produce strain. Optimization of the structure is possible using the unique strain. The following subsection proves this suggestion based on finite element systems. A brief explanation for a one-dimensional continuum elasticity problem is shown in Appendix A.

2.2 Eigenvalue analysis and pseudo-inverse matrix for support-free systems

An elasticity problem consisting of finite elements can be described in an elasticity equation as follows:

$$ \textbf{KU} = \textbf{F} $$

(1)

where K is the stiffness matrix, U is the displacement vector, and F is the load input vector. The K matrix is not invertible if the problem is support-free. From basic physical considerations, a balanced load input F_b apparently has a solution U_s. However, the solution is not unique. The sum of a solution of U_s and an arbitrary rigid body motion U_R is also a solution of (1) because KU_R = 0. The non-uniqueness of this solution is attributed to the singularity of the matrix K. To handle the problem, the load input F is separated into the balanced component F_b and the unbalanced component F_R.

$$ \textbf{F} = \textbf{F}_{b} + \textbf{F}_{R}. $$

(2)

The sum of an unbalanced load and an arbitrary balanced load is also an unbalanced load. To determine a unique separation, the unbalanced component is defined as the least norm. It requires that any addition of an arbitrary balanced load F_ba results in increase of the norm of the unbalanced component, namely:

$$ ||\textbf{F}_{R}||^{2} \leq ||\textbf{F}_{R} + \textbf{F}_{ba}||^{2}. $$

(3)

This definition implies that the unbalanced component does not contain any balanced component.

Here, the unbalanced component is assumed to be in the form of a rigid body motion, namely:

$$ \textbf{F}_{R} = \textbf{S}_{R} \textbf{F} $$

(4)

and

$$ \textbf{F}_{ba} = (\textbf{I} - \textbf{S}_{R}) \textbf{F} \equiv \textbf{S}_{d} \textbf{F}_{a} $$

(5)

where, I is an identity matrix, and F_a is an arbitrary load. The matrix S_R is the extraction of the rigid body component from a displacement. S_R can be obtained by applying the least-square method to rigid body motion. Substitution of these equations into inequality (3) gives the following result:

$$ ||\textbf{F}_{R} ||^{2} \leq ||\textbf{F}_{R} ||^{2} + ||\textbf{F}_{ba}||^{2} + \textbf{F}^{T}\textbf{S}_{R}^{T}\textbf{S}_{d}\textbf{F}_{a} + \textbf{F}_{a}^{T}\textbf{S}_{d}^{T}\textbf{S}_{R}\textbf{F}. $$

(6)

S_R and S_d are symmetric, and S_RS_R = S_R. Hence, $\textbf {S}_{R}^{T}\textbf {S}_{d} = \textbf {S}_{R}\textbf {S}_{d}^{T} = 0$. These relationships prove that inequality (3) is always satisfied. Thus, the least-norm unbalanced component is in the form of a rigid body motion.

In general, a support-free problem does not have a solution. Even a balanced load does not provide a unique solution. However, it is possible to find a unique least error solution U_sq that minimizes ||KU_sq −F||² and its norm ||U_sq||². It is known that the pseudo-inverse K⁺ (also referred to as the Moore-Penrose generalized inverse (Moore 1920; Penrose 1955; James 1978)) provides such a solution as U_sq = K⁺F.

The least-squares error is attributed to the least-norm unbalanced component, namely:

$$ ||\textbf{KU}_{sq}-\textbf{F}||^{2} = ||\textbf{F}_{R}||^{2}. $$

(7)

This relationship and (2) suggest the following equation:

$$ \textbf{KU}_{sq}-\textbf{F} = -\textbf{F}_{R}. $$

(8)

The solution U_sq can be regarded as the internal deformation caused by the balanced component of the load.

From the definition of the pseudo-inverse, the following vector is also a least-squares solution (James 1978):

$$ \textbf{U} = \textbf{K}^{+} \textbf{F}_{b} + [\textbf{I} - \textbf{K}^{+}\textbf{K}]\textbf{U}_{w} $$

(9)

where U_w is an arbitrary vector. The second term [I −K⁺K]U_w corresponds to rigid body motion. The absence of a boundary condition results in uncertainty of the solution. However, the uncertain components of the displacements are rigid body motion, and strain energy is not produced. Hence,

the strain energy of the solution is unique, and the pseudo-inverse extracts the component. Thus, the Moore-Penrose generalized inverse consistently solves support-free problems. The simplicity of this approach is a great advantage.

An eigenvalue analysis is also available for the pseudo-inverse K⁺ as follows:

$$ \textbf{K}^{+}\check{\textbf{F}}_{i} = \lambda_{i} \check{\textbf{F}_{i}} = {\check{\textbf{U}}}_{i}. $$

(10)

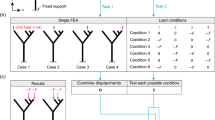
An example of this analysis for a small two-dimensional system is shown in Fig. 1. Although ${\check {\textbf {F}}}_{i}$ may be expected to be balanced, this condition is actually not assured. The considerations above suggest that the eigenvectors also have balanced and unbalanced components as follows:

$$ \check{\textbf{U}}_{i} = \check{\textbf{U}}_{si} + \check{\textbf{U}}_{Ri} = \lambda_{i} (\check{\textbf{F}}_{bi} + \check{\textbf{F}}_{Ri}) . $$

(11)

In the following optimization trials, it was found that the generated eigenvectors contain unbalanced components. However, the compliance (strain energy) in the form $\check {\textbf {U}}_{i}^{T} \textbf {K} \check {\textbf {U}}_{i}$ eliminates the unbalanced components. Optimization based on the strain energy is therefore possible.

Fig. 1

Two-dimensional small elastic system. The displacements for each non-zero eigenvalues κ are shown below. The system has eight degrees of freedom, and three rigid body motions, i.e., parallel displacements in the x and y directions and the rotation, have zero eigenvalues. Hence, the system has five non-zero eigenvalues.

2.3 Robust optimization scheme based on eigenvalue analysis using aggregated system

Takezawa et al. (2011) developed robust optimization based on an aggregated system. The aggregated system provides quite a useful platform. This subsection briefly describes the details of this significant work.

The inverse of (1) is transformed to an aggregated form as follows:

$$ \textbf{U}_{l} = \textbf{CF}_{l} $$

(12)

where C is the aggregated compliance matrix, F_l is the discretized local force vector that consists of only possible load input components, and U_l is the corresponding local displacements.

Eigenvalue analysis is applied to the compliance matrix as follows:

$$ \textbf{C}\check{\textbf{F}}_{li} = \lambda_{i} \check{\textbf{F}}_{li} $$

(13)

where λ_i is the i th largest eigenvalue of C, and $\check {\textbf {F}}_{li}$ is the eigenvector.

The problem formulation is the minimization of the maximum compliance (“robust compliance”) $\textbf {F}_{l}^{T}\textbf {CF}_{l}$ under the constraint ||F_l|| = 1. The corresponding loading distribution F_l is called “worst loading.” According to the Rayleigh-Ritz theorem (a brief introduction is presented in Takezawa et al. (2011)), the worst loading corresponds to the eigenvector belonging to the largest eigenvalue. The robust optimization problem is reduced to a minimax problem of the eigenvalues. Takezawa et al. demonstrated that an optimization for only the largest eigenvalue successfully creates optimum configurations. However, the present work found that optimizations only for the largest eigenvalue are not applicable to support-free problems. The next subsection discusses this issue.

2.4 Physical interpretation of eigenvalues

As mentioned above, optimization only for the largest eigenvalue actually causes unstable premature convergence. To understand this difficulty, physical interpretation of the eigenvalue is crucial.

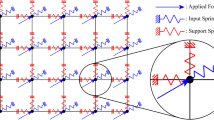
The eigenvector ${\check {\textbf {F}}}_{i}$ denotes the loading distribution, and these distributions exhibit periodic patterns similar to other various eigenvalue analyses like buckling analysis. The present work classifies these periodic patterns as “n th order modes,” where the zeroth order is close to a uniform distribution. A schematic diagram of these periodic patterns is shown in Fig. 2.

Fig. 2

Schematic diagram of loading distributions in each eigenvector of one-dimensional systems: a support-free system and b system with constraints at both ends

As described by Takezawa et al. (2011), for problems with constrained nodes, the worst load patterns involve loading in a certain direction. These modes correspond to the zeroth order. Apparently, such unidirectional loads yield high stress and strain energies around constrained nodes. Thus, the eigenvalue of the zeroth-order mode overwhelms the others. Although the loading distribution changes as the optimization progress, the mode of the largest eigenvalue is unchanged. Hence, the changes in the loading distribution in each iterative calculation are rather small. Consequently, optimization for the worst loading progresses successfully.

In a support-free problem, the zeroth-order mode does not appear because the zeroth-order mode is not balanced. Although lower order modes tend to have larger eigenvalues of the compliance, the first order is not always the worst mode. The worst mode may alternate as the optimization progresses. If the optimization was solely for the worst mode, a discontinuous change in the loading distribution occurs, in which the worst mode alternates. Repeating such alternations of the worst mode, the optimization wanders and does not converge. A robust optimization solely for the worst mode does not progress efficiently in the case of a support-free system. This is an essential difficulty of minimax problems.

3 Method

3.1 Problem formulation

As with a conventional topology optimization, the present scheme requires a volume fraction and design domain. Another design variable that is unique in the present aggregated system approach is the possible load input freedom, i.e., nodes and axes. The system can be described in an aggregated form. Takezawa et al. (2011) showed that the transformations F to F_l, K to C, and U to U_l are given as follows:

$$ \textbf{F}_{l} = \textbf{H}^{T} \textbf{F} $$

(14)

$$ \textbf{U}_{l} = \textbf{H}^{T} \textbf{U} $$

(15)

$$ \textbf{C} = \textbf{H}^{T} \textbf{K}^{-1} \textbf{H} $$

(16)

where H is the conversion matrix connecting the local and global vectors. The non-square conversion matrix H^T can be determined so that it eliminates non-loading components from the force vector F.

An eigenvalue analysis applied to a stiffness matrix may seem to provide an alternative method that does not require an inverse of K. However, the stiffness matrix for the substitute analysis must be in the form of the aggregated system, and the transformation of the stiffness matrix is complex. Eventually, it requires an operation to inverse the global stiffness matrix K. Such an analysis is not practical.

For support-free problems, the aggregated compliance matrix C can be re-defined using the pseudo-inverse of K as follows:

$$ \textbf{C} = \textbf{H}^{T} \textbf{K}^{+} \textbf{H}. $$

(17)

The present work implements an optimization for the worst eigenvalue of the compliance matrix. Hence, the objective function should be the compliance of the largest eigenvalue mode. However, optimization for the worst eigenvalue was found to be unsuccessful due to the alternation of the worst load mode. The present work tried optimizations to minimize the compliance of multiple modes. The compliance of i th eigenmode is as follows:

$$ c_{i}={\check{\textbf{U}}}_{i}^{T} K \check{\textbf{U}}_{i} $$

(18)

and

$$ {\check{\textbf{U}}}_{i}=\textbf{K}^{+} \textbf{H} \check{\textbf{F}}_{li}. $$

(19)

where K⁺ is the pseudo-inverse of K, and ${\check {\textbf {F}}}_{li}$ is the eigenvector of the compliance matrix C.

3.2 Optimization sensitivity for multiple eigenvalues

The present work uses the density-based approach that optimizes the densities of fixed-mesh finite elements ρ_e. As a practical substitute of a minimax problem, the present work uses a weighted sum of optimization sensitivities of N largest eigenvalue modes as the sensitivity, namely:

$$ s_{e} = \sum\limits_{i=1}^{N} w_{i} s_{ei} = -\sum\limits_{i=1}^{N} w_{i} \frac{\partial c_{i}}{\partial \rho_{e}} $$

(20)

where s_ei is the optimization sensitivity of i th mode, and the suffix “_e” denotes the e th element. The weight of the i th worst mode w_i is determined so that a mode with a larger eigenvalue has a larger weight as follows:

$$ w_{i} = \frac{(\lambda_{i} - \lambda_{N+1})^{\mu}}{{\sum}_{i=1}^{N}(\lambda_{i} - \lambda_{N+1})^{\mu}} $$

(21)

where μ is the weighting power factor, and λ_i is the i th largest eigenvalue of C. In the following iterative calculation, previous values of λ_i are used in (21). When the problem has a multiplicity of eigenvalues (Thore 2016), this method is also applicable.

In the present scheme, the structure is optimized mostly for the worst load, and the succeeding modes are also involved. The worst load mode may alternate. However, discontinuous changes in the optimization can be suppressed. An appropriate setting for the factor μ and number of incorporating eigenvalues N may exist. When N is a large number, this may have an adverse effect on convergence and the computation cost. When N is a small number, alternation of the N th and N + 1th mode may make the optimization unstable. When the weighting power factor μ is large, the optimization gives larger weight to the mode with the larger eigenvalue. Although this might mitigate the impact of alternation of the N th and N + 1th mode, it enlarges the impact of the alternation of the worst and the second mode.

The present work adopts the solid isotropic material with penalization (SIMP) method (Bendsøe 1989; Zhou and Rozvany 1991), which penalizes intermediate densities by setting a non-linear relationship between the density and the elastic modulus E as follows:

$$ E = E_{\min} + \tilde{\rho}^{ p}(E_{0} - E_{\min}) $$

(22)

where p > 1 is the penalization factor, and E₀ and E_min are the elastic moduluses of the solid material and the void material, respectively. In the present work, the default setting of the penalization factor was p = 3.

3.3 Iterative calculation

The present work adopts the optimality criteria (OC) method (Bendsøe 1995). In each iterative calculation, the amplification factors B_e for each element are determined based on the sensitivity and the required total volume fraction as follows:

$$ B_{e} = H_{b}(s_{e}) \left( {\Lambda} \frac{\partial v(\rho_{e})}{\partial \rho_{e}}\right)^{-1} $$

(23)

where H_b is a blurring filter that suppresses mesh dependent irregularities such as checkerboards (Bruns and Tortorelli 2001). The Lagrange multiplier Λ is determined so that the total volume v(ρ) (sum of all densities) is kept within the volume fraction limit V_f. The temporal renewed densities ρ_new are calculated from the previous densities ρ_e as follows:

$$ \rho_{new} = \max(\rho_{e} - m, \min(\rho_{e} + m, \rho_{e} B_{e}^{\eta})) $$

(24)

where η is the numerical damping coefficient, and m is the change limit. These convergence control parameters m and η control the speed of the optimization progress. The OC method is historically older than other modern methods, such as sequential quadratic programming (SQP) (Nocedal and Wright 2006) or the method of moving asymptotes (MMA) (Svanberg 1987). However, simple and straightforward speed control plays an important role in this robust optimization. Unlike ordinal structural optimizations, the load input changes as optimization progress, and large changes in each iterative calculation make the optimization unstable. Hence, slower progress—smaller settings of these parameters—is preferable. For ordinal topology optimization, a setting of η = 0.5 and m = 0.2 has been recommended (Bendsøe 1995; Sigmund 2001; Liu and Tovar 2014). In contrast, the present work found that these factors have to be much smaller.

To reduce the computation cost, the present work uses an approximation of $B_{e}^{\eta }$ as follows:

$$ B_{e}^{\eta} \simeq 1 + \eta(B_{e} - 1). $$

(25)

A robust optimization program for a rectangular design domain loaded at the bottom surface was implemented in MATLAB R2018a based on the efficient 3D topology optimization code provided by Liu and Tovar (2014). The MATLAB functions “eigs” and “lsqminnorm” were used for the eigenvalue analysis and the pseudo-inverse computation, respectively. It should be noted that these computations have finite errors. The details of the implementation are described in the latter section.

4 Results and discussion

4.1 Optimization in 3D rectangular design domain

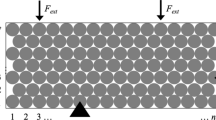
Optimization trials were conducted for several domain sizes and parameter settings. An HP Z420 workstation (Intel Xeon ES-1620, 3.60GHz/16.0GB) was used for the trials. The present methodology can handle arbitrary problems, i.e., any design domains and loading nodes. However, the present program code is specialized for the conditions described in Fig. 3. Table 1 lists the conditions of the trials.

Fig. 3

Design domain and loading inputs. Uncertain loads are applied at the bottom of the domain. The loading vectors are limited to the y-direction. The models consist of unit size elements

Table 1 Trial conditions and results

Figure 4 shows the loading distributions corresponding to each eigenvector for the common initial configuration (rectangular solid) of cases A1 to A4.

Fig. 4

The loading distributions corresponding to each eigenvector for the initial configuration (rectangular solid) of case A1. a The largest eigenvalue: the loading is symmetric torsional input and the first order is in both the x and z directions, i.e., the mode is 1 × 1. b Second largest: loading = bending, mode = 0 × 2. c Third largest: loading = periodic torsion, mode = 1 × 2. d Fourth largest: loading = bending, mode = 2 × 0. e Fifth largest: loading = complex periodic torsion and periodic bending, mode = 2 × 1. f Sixth largest: loading = periodic torsion in both the x and z directions, mode = 1 × 3. The 0 × 0th, 0 × 1th, and 1 × 0th order modes are prohibited because these are not balanced

This sequence of the modes may change as the optimization progresses. The lowest order of torsion and bending in x and z are the most basic load input modes and correspond to the first, second, and fourth largest eigenvalues. These basic input modes should be incorporated in the optimization. This means that the number of incorporated eigenvalues N must be at least four. The present work adopts N = 4. It should be noted that the appropriate setting for N may vary according to the problem. The N th largest eigenvalue must be sufficiently smaller than the largest eigenvalue.

Figure 5 shows the loading distributions of each eigenvalue for the final configuration. The modes are basically maintained, and the sharp peaks at the corners are significantly relaxed. This may be the result of “reinforcements” to high loading areas. The optimization changes the structure to reduce the high strain energies around the corners. Figures 6 and 7 show the convergence history and the final configuration when η = 0.15, m = 0.05, and μ = 1. Although this setting slows down the convergence, it stabilizes the optimization.

Fig. 5

The loading distributions corresponding to each eigenvector for the final configuration of case A1: a the largest eigenvalue, b second largest, c third largest, d fourth largest, e fifth largest, and f sixth largest. Existence of rigid body motion–type components can be seen especially in the fifth and sixth largest modes

Fig. 6

The convergence of the eigenvalues in case A1. The parameters are η = 0.15, m = 0.05, and μ = 1. Smooth convergence was obtained

Fig. 7

The final configuration of case A1. Uncertain loads were applied at the bottom surface of the domain. Voxels are shown when the densities are more than 0.5, and the shades indicate the density. Note that intermediate densities ρ < 0.5 may exist in the hollow spaces

Intermediate densities can be seen in the final configurations. These intermediate densities were not eliminated even if the number of iterations was increased. The SIMP method does not completely remove intermediate densities, which occur around the boundary between black and white regions in ordinal topology optimization. However, in the present work, these intermediate densities occurred in almost the whole structure. An extremely high penalization setting of p = 6 was also tried, but the result was disappointing. Since further processes may solve this problem, these are described in a subsection below.

A more serious problem is the long computation time of the pseudo-inverse matrix and the slow convergence. The present work uses quite a coarse mesh because of the time-consuming pseudo-inverse computation. As listed in Table 1, slightly larger scale problems resulted in unrealistically long computation times or computation interruptions due to memory shortage. The Moore-Penrose pseudo-inverse is notorious for its high computation cost, and new computation methods have been proposed (Courrieu 2005). According to his research, the computation cost is proportional to the third to fourth power of the rank. Although the eigenvalue analysis computation is also a time-consuming process, most of the computation time seems to be taken by the pseudo-inverse computation, especially when the design domain is large.

The slow convergence is the result of securing stability for the worst-mode alternations as well as sensitivity to computation errors. Due to these requirements, the optimization requires a large number of iterations. A long computation time due to this factor above is a major concern related to the industrial application of this method.

Figures 8 and 9 show cases of longer and larger design domains. The larger design domain has an almost similar shape and is 1.4 times larger than the standard condition. The longer design domain is close to the one used by Takezawa et al. (2011). These configurations exhibit hollow “monocoque” structures. Since the present work uses unit size elements, the domain size represents the resolution of the topology. If the optimum “thickness” is smaller than the size of the unit cell, the density stays at an intermediate value. Figure 10 shows the result of the larger volume fraction. The densities of the walls increased, but the “walls” still consist of a single layer. This monocoque structures formation contrasts to two-dimensional problems that exhibit truss structures. As growths of ribbed structures were observed in three-dimensional curved beam optimization (Fukada et al. 2018a, 2018b), three-dimensional problems are crucially important.

Fig. 8

The final configuration of case B. The parameters are standard η = 0.15, m = 0.05, and μ = 1

Fig. 9

The final configuration of case C. The parameters are standard η = 0.15, m = 0.05, and μ = 1

Fig. 10

The final configuration of case A5 with larger volume fraction. The penalization is the same as the standard case (p = 3)

Most structures formed by conventional robust optimization with an uncertain load distribution (Chen et al. 2010; Takezawa et al. 2011) are optimized only for bending. In contrast, the present trials formed monocoque structures for combined torsional and bending loads, and this may be the most prominent difference from these conventional approaches. Monocoque structures are widely used in automobiles, marine vessels, and aircraft fuselages. The present results may demonstrate the excellent characteristics of monocoque structures. Similar results were also found in eigenfrequency optimizations (Ma et al. 1995; Ishii et al. 2001, 2004). Obtained structures optimized for bending and mean eigenfrequencies exhibit hollow thin-walled pipe structures (Ishii and Aomura 2004). When loading direction uncertainty is considered, the formed structures tend to exhibit more complex configurations (Takezawa et al. 2011; Shimoda et al. 2015). If multiple loading points were applied in their trials, monocoques may form to carry torsional loadings.

A monocoque is an excellent structure. However, care may be required when adopting these structures to industrial applications. The present problem formulation adopts the minimum compliance—minimum strain energy. In contrast, industrially realistic requirements often involve minimum displacement. A minimum displacement problem is only equivalent to a minimum strain energy problem when the load inputs areas are small. In the present 3D cases, some elements at the bottom vanished. These parts (actually the elements still maintain finite densities) are apparently structural ‘ weak points.” These weak points are allowed because their contribution to the total strain energy is small. Monocoques are preferred because of their overall structural rigidity and are not designed to support point loadings. If such weak points are not acceptable in the application, the problem formulation should be reconsidered. A scheme involving an uncertain load position (Nakazawa et al. 2016) is also a good means to create structures without weak points.

4.2 Two dimensional cases

Two-dimensional problems enable trials with higher resolution and good validation of the method. Problems with narrow design domains were used to represent quasi-two-dimensional problems. Figure 11 shows the results. Truss bridge–like structures were created in these design domains. The load distributions in conventional robust optimization (Buhl 2002; Zhao and Wang 2014) are basically three-point loading. In contrast, the distributions in the present optimization are combinations of alternative multipoint bending. The difference between the present method and conventional methods is remarkable when the design domain is wide and low.

Fig. 11

The final configuration of two-dimensional condition of case D1 to D3. The parameters are standard η = 0.15, m = 0.05, and μ = 1. a Quasi-two-dimensional cantilever. b Quasi-two-dimensional narrow and tall cantilever. c Quasi-two-dimensional wide and low cantilever

Figure 12 shows the loading distributions for the initial configuration of quasi-two-dimensional case D1. The present MATLAB code is for three-dimensional problems. Although the model consist of a single-element layer in the thickness direction, there are two rows of load input nodes. An asymmetric loading in the front and back is an out-of-plane component. Hence, the trials are not purely two-dimensional. Physically meaningful inputs as a two-dimensional problem are only the modes of the first and the 4th largest eigenvalue, and they correspond to three-point bending and bending with four-point alternative load inputs, respectively. The adequate number of N may be two for this type of pure two-dimensional problem.

Fig. 12

The loading distributions corresponding to each eigenvector for the initial configuration of quasi-two-dimensional case D1. Only the loadings in the front row are indicated. The third largest loading pattern in the back row is the inverse of the largest in the front row. The sixth largest loading pattern in the back row is the inverse of the 4th largest in the front row. The largest and 4th largest are symmetric at the front and back. The others (second, third, 5th, and 6th largest) are asymmetric at the front and back. The symmetry at the front and back is indicated as (sym.) or (asym.). Note that the 5th largest is not balanced

4.3 Low design domain

Figure 13a shows a configuration in the low design domain. A flat hollow monocoque was obtained. This configuration has two “bulkheads,” which may assure torsional rigidity by transferring shear loadings.

Fig. 13

The final configurations of low design domains E1 to E3. a The final configuration of case E1. b The final configuration of case E2 with overhang penalization. c The final configuration of low resolution E3 with overhang penalization

In realistic manufacturing process, hollows or overhangs are troublesome features for casting. To incorporate such manufacturing limitations, an additional overhang penalization, i.e., penalization for negative density gradients in the thickness (y) direction, was introduced. The following penalization factors $p{c_{k}^{u}}$ and $p{c_{k}^{l}}$ are applied to the calculation of B_e.

$$ p{c_{k}^{u}} = \max(1, \min(p_{\text{cmax}}, 1 + g_{c}(r_{cu} - \rho_{k}/\rho_{y-1}))) $$

(26)

and

$$ p{c_{k}^{l}} = \max(p_{\mathrm{\text{cmin}}}, \min(1, 1 + g_{c}(r_{cl} - \rho_{k}/\rho_{y+1}))) $$

(27)

here, ρ_y− 1 and ρ_y+ 1 indicate the densities of the upper and lower adjacent cells, respectively. These factors were applied prior to the smoothing filter. Each parameter was set as follows: p_cmax = 8, p_cmin = 0.125, g_c = 20, r_cu = 1.005, and r_cl = 0.995. Figure 13b shows the obtained configurations. Flanged or cross-ribbed structures were obtained depending on the resolution. These types of configurations are commonly used for reinforcements on flat thin plates. This peculiar mesh dependency requires further investigation.

4.4 Convergence speed and weighting

Figure 14 shows the convergence history when the settings of the convergence control parameters and the weighting power factor are large η = 0.2, m = 0.1, and μ = 2. Singular fluctuations in the largest eigenvalue can be seen, which occur when the mode sequence alternates. Prior to the fluctuations, alternation of the modes at the largest and the second largest eigenvalue occurred. The weighting power factor μ in (21) controls the weight distribution among the worst modes. A higher μ setting provides a heavier weight to the worse mode. Hence, it is likely that mode alternation occurs especially in the worst mode. Figure 15 shows the convergence history when the settings of the convergence control parameters η and m are large, and the weighting power factor μ is unity. Thanks to the lowered weighting power factor, the singularities when mode alternations occur are sufficiently suppressed compared with the case in Fig. 14. The progress of the optimization is rapid due to the higher setting of the convergence control parameters. However, oscillation occurs at a later stage, which was found to be the appearance of asymmetric configurations. These asymmetric configurations appeared periodically in the progress of the optimization. Figure 16 shows the asymmetric configurations. Since the system is completely symmetric, such asymmetric configurations are not supposed to appear. These are probably due to computation errors. The optimization tends to compensate for the asymmetry. However, the optimization likely overcompensates for the asymmetry when the settings of the convergence control parameters are large. As a result, the optimization becomes oscillatory and the oscillation may diverge. Thus, it was found that slow optimization and flat weight distribution are preferable to suppress the effect of computation errors and the impact of eigenvalue alternation.

Fig. 14

The convergence of the eigenvalues of case A2. The parameters are increased parameters η = 0.2, m = 0.1, and μ = 2. Singular fluctuations in the largest eigenvalue can be seen at iteration numbers It = 40, 61, and 71

Fig. 15

The convergence of the eigenvalues of case A3. The parameters are η = 0.2, m = 0.1, and μ = 1. Singular fluctuations in the largest eigenvalue are suppressed. However, oscillation occurred at a later stage

Fig. 16

Asymmetric configurations of case A3. These configurations appeared alternatively and damping of the oscillation did not occur

4.5 Remaining intermediate densities

Intermediate densities still can be seen in the final configurations above. These are created by two factors. One is the variation in the input load distribution. Although a slower optimization speed and a flat weighting scheme significantly improve stability, changes in the input load distribution may retard the convergence. Since the concept of “robust optimization” is actually quite ambiguous, the creation of realistic configurations can be prioritized over mathematical rigorousness. Accordingly, interruption of the loading distribution update, i.e., the fixation of the input load distribution at a later stage of the optimization was tried. An extremely high penalization was also applied with a continuation method involving a gradual increment of the penalty. After the iteration number exceeded 50, the penalty p was increased by factor of 1.015 until it reached p = 6. Figure 17 shows the results. Except for the singular spikes located at the corners, these configuration exhibit more realistic structures, especially in the two-dimensional case. The persistent intermediate densities in the 3D case are results of the thin-walled optimal structure. A limited resolution may result in a space-frame structure.

Fig. 17

The result of high penalization and fixation of input loads. A gradual increment in the penalization p up to p = 6 was applied after iteration number 50. The update of the eigenvectors (input load distributions) was interrupted and the loading distributions were maintained after iteration number 70. a The final configuration of case A4. b The final configuration of the two-dimensional condition of case D4. c The final configuration of the low design domain with overhang penalization E4. It exhibits a double-wall-framed structure. Vertical “spikes” can be seen at the corners in (a) and (b)

As shown by Sigmund (2007), the existence of intermediate densities, i.e., the “measure of discreteness” can be evaluated quantitatively as follows:

$$ M_{nd} \equiv \frac{{\sum}^{N_{e}}_{e=1} \rho_{e}(1-\rho_{e})}{N_{e}} \times 100<percent>, $$

(28)

where N_e is the number of the elements. A low M_nd indicates high discreteness. The values are listed in Table 1. Improvements in high penalization and high resolution (the large design domain) can be seen.

The final eigenvalues are indicated in Table 1 as representative values of the compliance. The values for the high penalization cases are large. This is due to the penalties for intermediate values, and not realistic for actual structures.

Optimizations for multiple load conditions basically yield successful results (Díaz and Bendsøe 1992). However, the loadings (eigenvectors) in the present work are orthogonal. This orthogonality may bring additional difficulty to the removal of intermediate densities. The selection of the optimization algorithm may not be the major factor in the formation of intermediate densities.

Various filtering techniques exist to remove intermediate densities (Sigmund 1997, 2007; Groenwold and Etman 2009; Andreassen et al. 2011; Guest et al. 2004, 2011; Yamasaki et al. 2017; Rong et al. 2017). It will be an interesting future work to observe the responses of these techniques to this support-free robust optimization method. An application of the level set method (Wang et al. 2003; De Gournay et al. 2008; Yamada et al. 2010), which is intermediate-density free, is also an interesting topic for future work.

4.6 Expansion of the method

As mentioned in Section 4.1, the “worst load” does not mean that it produces the “largest displacement.” In the same way, the present approach does not solve stress design problems. An extensive modification may be required to deal with stress design problems. The introduction of a stress constraint instead of a stress minimization seems appropriate. da Silva and Beck (2018) provide an example to approach stress design problems.

An arbitrary load distribution can be expressed as a sum of eigenvectors. Hence, the eigenvalue-based approach can be applied to other problem formulations like stochastic approaches. The problem of this expansion is computation cost since it requires high-order eigenvalue analysis.

The aggregated system approach has great possibilities. The components of the conversion matrices H and H^T take 0 or 1 discrete values and denote “possible load inputs.” It may be possible to give 0–1 continuous values to the components and denote the “load input possibilities.”

5 Conclusion

This paper presented an approach to robust structural topology optimization for support-free problems. The optimization adopts the scheme of minimizing the largest eigenvalue in an aggregated system. A pseudo-inverse matrix was used as a substitution of the inverse stiffness matrix. The characteristics of the eigenvalue and the eigenvector of the pseudo-inverse were also discussed. Optimization solely for the largest eigenvalue does not converge because the mode of the largest eigenvalue alternates as the optimization progress. Accordingly, weighted optimization for multiple largest eigenvalues was proposed. It was found that slow optimization is required to mitigate disturbance from changes in the eigenvectors and computation errors.

Several trials were conducted using rectangular design domains with uncertain vertical loadings at the bottom surface. Under higher resolution conditions, thin-walled monocoque structures were formed. These results show that monocoque structures have superior structural robustness.

There are some remaining issues. The computation time of the optimization trials was long due to the computation of the pseudo-inverse matrix. New efficient algorithms or approximation methods to compute the pseudo-inverse are required for industrial applications.

The created configurations still contain intermediate densities. Extreme penalization was required to remove these intermediates. This may be attributed to the orthogonality of the eigenvectors.

This support-free method is applicable to various problems. However, the concept of “robust” itself is ambiguous and certain variations in requirements and expectations exist. Efforts to find a new problem formulation should be continued.

Although it is difficult to obtain a high-resolution configuration with this method, it may be useful to propose initial designs for support-free structures such as handheld devices or marine hull structures.

6 Replication of results

The present work was performed as a modification to the MATLAB code by Liu and Tovar (2014). Their original code can be downloaded from their web site. This section presents minimum requirements to reproduce the present work. The line numbers presented here are those in their original code. The following lines must be added around the beginning of the code.

eta = 0.15; n = 1;

In the original Liu and Tovar code, the load input nodes are at the edge x = nelx and y = 0. In the present case, the load input nodes are at the y = 0 bottom surface. To change the load input nodes, replace lines 12 to 18 with the following lines:

jl = 0; loadn_index=1; for kl = 0:nelz for il =0:nelx loadnid(loadn_index) = ... kl*(nelx+1)*(nely+1)+il*(nely+1)+ (nely+1-jl); loadn_index=1+loadn_index; end end

To create the H matrix (‘Ht’ in the code) , replace lines 22 to 24 with the following lines:

nload = (nelx+1)*(nelz+1); Hf = zeros(ndof, nload); for nload_i=1:nload Hf(3*loadnid(nload_i)-1, nload_i)=1; end Ht = sparse(Hf); F=zeros(ndof); F1=zeros(ndof); F2=zeros(ndof); F3=zeros(ndof); F4=zeros(ndof); F5=zeros(ndof); F6=zeros(ndof);

In the main part of the optimization, variables Z, C, K⁺ (“Kinv” in the code), F_i, and λ_i (c1, c2... in the code) are obtained. In addition, the sensitivities of each load input (“dc1, dc2...” in the code) are the subject of the weighted sum into “dc.” Replace lines 72 to 76 with the following lines:

Z = lsqminnorm(K,Ht); Kinv = Z*Ht'; C = Ht'*Kinv*Ht; [phi,c_array] = eigs(C); phi1 = phi*([1,0,0,0,0,0])'; phi2 = phi*([0,1,0,0,0,0])'; phi3 = phi*([0,0,1,0,0,0])'; phi4 = phi*([0,0,0,1,0,0])'; phi5 = phi*([0,0,0,0,1,0])'; phi6 = phi*([0,0,0,0,0,1])'; c1 = [1,0,0,0,0,0]*c_array*([1,0,0,0,0,0])'; c2 = [0,1,0,0,0,0]*c_array*([0,1,0,0,0,0])'; c3 = [0,0,1,0,0,0]*c_array*([0,0,1,0,0,0])'; c4 = [0,0,0,1,0,0]*c_array*([0,0,0,1,0,0])'; c5 = [0,0,0,0,1,0]*c_array*([0,0,0,0,1,0])'; c6 = [0,0,0,0,0,1]*c_array*([0,0,0,0,0,1])'; F(:)=0;F1(:)=0;F2(:)=0; F3(:)=0;F4(:)=0;F5(:)=0;F6(:)=0; for nload_i=1:nload F1(3*loadnid(nload_i)-1)=phi1(nload_i); F2(3*loadnid(nload_i)-1)=phi2(nload_i); F3(3*loadnid(nload_i)-1)=phi3(nload_i); F4(3*loadnid(nload_i)-1)=phi4(nload_i); F5(3*loadnid(nload_i)-1)=phi5(nload_i); F6(3*loadnid(nload_i)-1)=phi6(nload_i); end U1 = Kinv*F1; U2 = Kinv*F2; U3 = Kinv*F3; U4 = Kinv*F4; ce1=reshape(sum((U1(edofMat)*KE).*U1 (edofMat),2),... [nely,nelx,nelz]); ce2=reshape(sum((U2(edofMat)*KE).*U2 (edofMat),2),... [nely,nelx,nelz]); ce3=reshape(sum((U3(edofMat)*KE).*U3 (edofMat),2),... [nely,nelx,nelz]); ce4=reshape(sum((U4(edofMat)*KE).*U4 (edofMat),2),... [nely,nelx,nelz]); dc1 = penal*(E0-Emin)*xPhys.^(penal-1).*ce1; dc2 = penal*(E0-Emin)*xPhys.^(penal-1).*ce2; dc3 = penal*(E0-Emin)*xPhys.^(penal-1).*ce3; dc4 = penal*(E0-Emin)*xPhys.^(penal-1).*ce4; wall =(c1-c5)^n +(c2-c5)^n +(c3-c5)^n + ... (c4-c5)^n; w1 = (c1-c5)^n/wall; w2 = (c2-c5)^n/wall; w3 = (c3-c5)^n/wall; w4 = (c4-c5)^n/wall; dc = -(w1*dc1 + w2*dc2 + w3*dc3 + w4*dc4);

The value “move” at the original line 82 corresponds to m in (24). This value should be replaced with a small value around 0.05.

The present work uses the approximation (25), and η is no more than 0.5. Replace line 85 with the following lines:

xnew = max(0.0,max(x-move,min(1,min(x+move, ... x.*(((-dc./dv/lmid)-1)*eta+1) ))));

This code does not calculate the compliance. Hence, the echo back (Line 85) must be modified.

The MATLAB function “lsqminnorm” was introduced since R2017b. For older versions, another function “pinv” is available. Note that this function requires longer computation time. The following line provides a substitute for older versions:

Kinv = pinv(K);

The MATLAB function “eigs” adopts different computation methods for eigenvalue analysis. The ARPACK method was adopted before R2017b and the Krylov-Schur Algorithm method is used in R2017b and later. Significant differences in accuracy exist between these versions.

The penalization for overhang can be activated by adding the following lines after original line 77:

for xc=1:nelx, for zc=1:nelz, for yc=1:nely if yc == 1 pcu = 1; else ru = xPhys(yc,xc,zc)/xPhys(yc-1,xc,zc); pcu = max(1,min(pcmax,1+gc*(rcu-ru))); end if yc == nely pcl = 1; else rl = xPhys(yc,xc,zc)/xPhys(yc+1,xc,zc); pcl = max(pcmin,min(1,1+gc*(rcl-rl))); end dc(yc,xc,zc) = dc(yc,xc,zc)*pcu*pcl; end, end, end

Following lines also must be added around the beginning the code:

pcmax = 40.0; pcmin = 0.025; gc = 20.0; rcu = 1.05; rcl = 0.95;

Appendix A: An example of a continuum elastic body

Consider a one-dimensional elastic body. The equilibrium equation and the formula of strain tensors in the body are as follows:

$$ \frac{d \sigma(x)}{d x} = f(x) $$

(29)

and

$$ \varepsilon = \frac{d u(x)}{d x} $$

(30)

where f(x) is the force per volume.

In the same way as the finite element model, (29) and (30) can be reduced by Hook’s law as follows:

$$ E \frac{d^{2} u(x)}{d x^{2}} = f(x). $$

(31)

The solution of this equation is as follows:

$$ u(x) = \iint \frac{f(x)}{E} dx^{2} + C_{1} x + C_{2} $$

(32)

where C₁ and C₂ are the constants of integration, and C₁ corresponds to an effect of uniform background pressure which should be neglected. The constant C₂ determines the displacement at certain position, and denotes a rigid body motion.

When the problem is support-free and the mean value of the input force is not zero, the natural boundary condition (zero stresses at the free ends of the body) cannot be satisfied.

The force input can be regarded as the sum of the balanced component f_b and the unbalanced component f_R, i.e., the mean value of f(x).

$$ f(x) = f_{b}(x) + f_{R}. $$

(33)

Substituting (33)–(31), the following relationship can be obtained.

$$ E \frac{d^{2} u(x)}{d x^{2}} - f(x) = -f_{R}. $$

(34)

This relationship seems equivalent with (8).

To cope with the difficulty of an unbalanced load, an additional weak constraint k is introduced as follows:

$$ E \frac{d^{2} u(x)}{d x^{2}} - kE\frac{d u(x)}{d x} = f(x). $$

(35)

The exact solution of this equation is as follows:

$$ u(x) = \iint \frac{f_{b}(x)}{E} dx^{2} + C_{3} e^{qx} x + C_{4} e^{-qx}, $$

(36)

and

$$ q = k^{1/2}. $$

(37)

C₃ and C₄ are constants. The natural boundary conditions determine the constants. At the limit of small k, the constants are as follows:

$$ C_{3} = C_{4} = \frac{L f_{R}}{4k} $$

(38)

where L is the length of the body. Thus, the unbalanced component yields infinite rigid-body motion.