1 Introduction

Thin-walled tubal structures, when used as crash energy absorbers in automobiles, improve passenger safety. During a frontal impact, front rails and crash boxes absorb the kinetic energy and dissipate it in the form of plastic deformation. The energy absorption mechanism of these structures makes them interesting to researchers. Several studies have analyzed the effect of the cross-sectional profile on the crashworthiness of thin-walled tubal structures, such as square (Karagiozova et al. 2005; Zhang et al. 2006), circular (Abramowicz and Jones 1986), triangular (Tran and Baroutaji 2018), octagonal (Liu and Day 2007; Zhang et al. 2018a), hexagonal (Hou et al. 2007; Qiu et al. 2018), and hat-shaped (Zhang et al. 2018b). In the automotive industry, the square profile is preferred because of easy coupling with other parts (Chen et al. 2018), and thus the square profile is studied in this paper.

The crashworthiness of single-cell tubes can be enhanced by filling it with foam (foam-filled tubes) and by inserting webs and flanges between the tube walls (multi-cell tubes) (Zhang et al. 2006). When compared together, the multi-cell tubes have 50–100% more energy absorption than the foam-filled tubes (Zhang and Cheng 2007), and thus multi-cell square tubes will be studied in this paper.

A number of researchers have reported that the superior crashworthiness capacity of the multi-cell tubal structure is due to the intersection of its webs and flanges that create joints (corners) (Wierzbicki and Abramowicz 1983; Abramowicz and Jones 1986; Abramowicz and Wierzbicki 1989; Wu et al. 2016). A considerable amount of literature is available about the effect of the number of corners on the crashworthiness performance of multi-cell tubal structures (Zhang et al. 2006; Fang et al. 2015; Wu et al. 2016). Zhang et al. (2006) studied the crashworthiness of single-cell and multi-cell tubes theoretically and numerically. The authors found that if a single-cell is converted to a 3 × 3 multi-cell tube by inserting webs and flanges, the energy absorption increases by 50%. Similar result was reported by Fang et al. (2015), who investigated the effect of the number of corners and proves that energy absorption increase as the number of corners increases. Najafi and Rais-Rohani (2011) studied the effect of the profile geometry on the crashworthiness of multi-cell tubes. The authors concluded that corner angles, number, and size of each web at a corner are the factors responsible for the deformation patterns of multi-cell tubes.

In order to enhance the crashworthiness performance, novel structures with enhanced crashworthiness have also been developed by researchers. In this regard, Chen et al. (2018) developed a five-cell structure with circular corners. The authors achieved a promising results with improved crashworthiness performance. Recently, Duan et al. (2019a) developed a new structure for the front longitudinal beam (FLB) called variable-rolled-blank and variable-cross-sectional-shape (VRB-VCS). The structure has a variable thickness as well as a variable cross-section. The parametric modeling and multi-objective design optimization of the VRB-VCS are covered in Duan et al. (2019b). The numerical results show that the VRB-VCS FLB has significantly higher crashworthiness than the uniform thickness FLB. Pang et al. (2019) proposed a new multi-cell structure with axially varying thickness (AVT). The results show that the thickness gradient significantly reduces the initial peak crushing force. Abdullahi and Gao (2020) developed novel multi-cell tubal structures with varying cell sizes based on Voronoi tessellations. The result indicated that for the same number of cells, the multi-cell Voronoi tubes (MVTs) have more corners than the conventional multi-cell tubes which give the MVTs better crashworthiness.

New methods and modified versions of known methods have been developed by researchers and applied to the crash and topology optimization of structures. Notable methods include hybrid cellular automata (HCA) (Tovar et al. 2004; Penninger et al. 2010; Da et al. 2017; Wang and Xie 2019), level set (Wang et al. 2003; Van Dijk et al. 2013), moving morphable components (MMC) (Zhang et al. 2016; Liu et al. 2018; Zhu et al. 2018), graph-based and heuristic approaches (Patel et al. 2009; Ortmann and Schumacher 2013), and equivalent static loads (ESL) (Cavazzuti et al. 2011; Christensen et al. 2012; Jang et al. 2012; Li et al. 2014). Recently, Duddeck et al. (2016) modified and applied the HCA to automobile thin-walled structures, the improved version of HCA is published in Zeng and Duddeck (2017). Afrousheh et al. (2019) developed yet another modified HCA (MHCA) for enhancing search efficiency in high-impact collisions. Duan et al. (2020) proposed an enhanced version of HCA for the Variable-thickness rolled blanks (VRBs) called eHCA-VRB. The eHCA-VRB algorithm can be used to efficiently solve the optimization problems of VRBs under manufacturing constraints.

The topological configuration in addition to the number of corners is another key parameter that contributes to the crashworthiness. On this note, Fang et al. (2015) investigated the effect of cell number and oblique loadings on the crashworthiness of multi-cell square tubes. The authors’ findings showed that global bending is due to oblique loading which is an inefficient deformation mode. Also, the energy absorption and crushing force increase when the number of cells increases. Wu et al. (2016) studied the effect of topological configurations and the number of cells of the multi-cell square tube. They concluded that the mean crushing force and specific energy absorption increases with an increase in the number of cells. Fang et al. (2017b) performed a topological optimization under different load cases using a modified artificial bee colony (ABC). The optimized structures have more material at the corners and around the outer walls. Qiu et al. (2018) studied multi-cell hexagonal tubes via topology optimization and came up with a range of cross-sections for different loading conditions. Sun et al. (2018a) performed a topological optimization based on integer coded genetic algorithm (ICGA) that results in a series of novel structures with improved crashworthiness. Recently, Bigdeli and Nouri (2019) proposed another five-cell cross-section for circular tubes to enhance the crashworthiness and performed a multi-objective optimization on the geometric parameters. Sun et al. (2018b) studied the effects of cross-sectional configurations and the distribution of foam-filler in the multi-cell tube on the crashworthiness. The optimal foam-filling pattern was found to be a five-cell tube with four cells in the corners filled with foams.

A comprehensive review of design criteria, surrogate modeling, energy absorption, multi-objective optimization, topology optimization, and algorithms related to crashworthiness can be found in Fang et al. (2017a).

The present work seeks to develop a two-staged optimization approach to enhance the crashworthiness of multi-cell square tubal structure. The first stage entails determining the optimal topological configuration, while the second stage entails the parameter optimization to enhance the crashworthiness performance. The paper is structured as follows: the design concept is described in Section 2, the numerical analysis in Section 3. Determination of the optimal topological structure is conducted in Section 4, and the parameter optimization in Section 5. Finally, conclusions are derived in Section 6.

2 Design concept

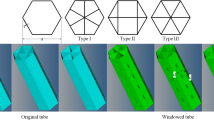
There are different types of corners in a multi-cell tubal structure. The most common being crisscross, T-shaped, and L-shaped (Fig. 1). In the theoretical calculation of the mean crushing force (MCF) of multi-cell tubal structure, the contribution of each type of corner is computed in terms of membrane energy and bending energy using Chen and Wierzbicki’s Simplified Super Folding Element (SSFE) theory (Chen and Wierzbicki 2001).

Fig. 1
figure 1

Corner types in multi-cell tubes. L-shaped (red), crisscross (green), and T-shaped (blue)

Full size image

The membrane energy for each of the corner types is given by:

$$ \begin{aligned} &{{W}_{\text{crisscross}}}&={16{{M}_{o}}{{H}^{2}}}/{t} \\ &{{W}_{\mathrm{T-shaped}}}&={8{{M}_{o}}{{H}^{2}}}/{t} \\ &{{W}_{\mathrm{L-shaped}}}&={4{{M}_{o}}{{H}^{2}}}/{t} \end{aligned} $$
(1)

where M0 is the fully plastic bending moment, t is the thickness of the webs, and H is the half folding wavelength. The total dissipated membrane energy is given by:

$$ \begin{aligned} {{W}_{M}}&={{N}_{L}}{{W}_{\mathrm{L-shaped}}}+{{N}_{C}}{{W}_{\text{crisscross}}}+{{N}_{T}}{{W}_{\mathrm{T-shaped}}} \\ & =(4{{N}_{c}}+16{{N}_{o}}+8{{N}_{T}}){{{M}_{o}}{{H}^{2}}}/{t} \end{aligned} $$
(2)

where NL,NC, and NT indicate the number of L-shaped, crisscross, and T-shaped corners, respectively. The overall mean crushing force is given by:

$$ \begin{aligned} {{P}_{m}}&={\lambda} \frac{{{\sigma }_{0}}t}{2k}\sqrt{2({{N}_{L}}+4{{N}_{C}}+2{{N}_{T}})\pi {{L}_{c}}t} \end{aligned} $$
(3)

where λ is the dynamic loading coefficient, σ0 is the flow stress, k is the effective crushing distance, and Lc is the length of all webs and flanges.

It is now clear that each type of corner affects the overall crashworthiness performance differently. Therefore, a topological and crashworthiness optimization of multi-cell square tubes is proposed such that the different combinations of corners can be achieved. The workflow is as follows: first, a method for representing design configurations is developed, then a binary genetic algorithm (BGA) is implemented to find the optimal topological configuration subject to constraints. The constraints are mass ratio, peak crushing force, functionality, and connectivity. Functionality refers to the functional design of the tube, which in this study is to serve as an energy absorber for an automobile. The cross-section should be square to provide an easy assembly with bumper beams. The connectivity refers to the connection of the webs within the tube cross-section to avoid free or unattached webs that can be difficult to manufacture. Secondly, a parameter optimization is formulated to further optimize the geometric dimensions of the optimal configuration. Figure 2 shows the overall optimization process.

Fig. 2
figure 2

Flowchart of the topological and crashworthiness optimization process

Full size image

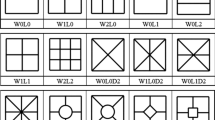
The cross-section of the baseline topological configuration is shown in Fig. 3 along with the design variables shown in red. It can be seen that all the design configurations exhibit symmetry; therefore, only one-eighth of the configuration will be used in defining the topological variables. Note that the symmetry is used only in defining the topological variables and the complete configurations are used in both modeling and finite element simulation. A binary scheme is implemented to represent the presence or not of an edge as x1,x2,...,xn ∈{0,1} where xi (i = 1,2,...,n) are the topological variables. There are twelve binary topological variables as shown in Fig. 3 which results in 212(4096) possible designs. The functionality constraint requires edges 10, 11, and 12 (circled in green) to form the outer wall of the square tube. Therefore, the number of possible designs reduces to (29) 512. For example, the baseline design configuration is represented as X0 = [1,1,1,1,1,1,1,1,1], indicating that all the edges are considered. The connectivity constraint is defined to exclude all topological configurations with unattached edges. Examples of configurations that failed the connectivity test are shown in Fig. 4.

Fig. 3
figure 3

Design variables of multi-cell square tubal structure

Full size image
Fig. 4
figure 4

Different types of unconnected configurations

Full size image

The first stage of the optimization problem is thus formulated as:

$$ \begin{aligned} &\text{Min} ~F(x_{1}, x_{2}, ..., x_{n})\\ &s.t~~ m(x_{1}, x_{2}, ... x_{n})\le m_{0}w\\ &~~~~\text{PCF}(x_{1}, x_{2}, ... x_{9})\le \text{PCF}_{0}\\ &~~~~f_{\text{connectivity}}(x_{1}, x_{2}, ... x_{n}) \ne 0\\ &~~~~f_{\text{functionality}}(x_{1}, x_{2}, ... x_{n}) \ne 0\\ &~~~~ x_{1}, x_{2}, ... ,x_{n} \in \{0,1\} \end{aligned} $$
(4)

where xi, m, m0, PCF0, and w denote the topological variables, the mass of the configuration, the mass of the baseline configuration, peak crushing force of the baseline configuration, and the mass ratio, respectively.

3 Numerical analysis

3.1 Material properties

The tubes’ material is taken to be aluminum alloy. The alloy properties are obtained by performing a tensile test as per Chinese standard GB/T 228.1-2010 on a specimen cut-out from the wall of a single cell tube by Electrical Discharge Machining (EDM). The uniaxial tensile test is performed using SUNS UTM6000 (Shenzhen Suns Technology Co. Ltd, Shenzhen, China) with control and data acquisition via a computer system. The true stress-strain and the test setup curve is shown in Fig. 5. The material properties are as follows: density ρ = 2700 kg/m3, Poisson’s ratio μ = 0.3, and Young’s modulus E = 68.9 GPa.

Fig. 5
figure 5

a, b Result and the setup of the uniaxial tensile test

Full size image

3.2 Finite element model

Tubes with a length of 150 mm and a square cross-section of 60 × 60 mm are created and placed between two rigid plates to simulate axial crushing using LS-DYNA (version R11.0.0), a commercial finite element code. The plates at the top and the bottom are modeled as rigid materials (MAT20). The top plate is 600 kg and moving downwards with a constant velocity of 15 m/s, while the bottom plate is fixed to the ground, the crushing displacement is 100 mm. Shell elements (Belytschko-Lin-Tsay formulation) with five integration points through the thickness are used to model the tube walls. Reduced integration is employed to avoid volumetric locking. The contact option “AUTOMATIC_SINGLE_SURFACE” is used for the tube walls and “AUTOMATIC_SURFACE _TO_SURFACE” option is used for the contact between the rigid plates and the tube. No triggers are used on all the tubes.

To ascertain the quality of the finite element (FE) model and to ensure that the results are not sensitive to mesh element sizes, a mesh sensitivity study is conducted. The baseline topological configuration is meshed with 1.0 × 1.0 mm, 1.5 × 1.5 mm, 2.0 × 2.0 mm, 2.5 × 2.5 mm, and 3.0 × 3.0 mm four-node shell elements. The force-displacement curve is shown in Fig. 6. Based on the results, 2.0 × 2.0 mm is used for the crashworthiness optimization as its sufficient to provide accurate results. The other mesh quality indexes are listed in Table 1.

Fig. 6
figure 6

Force-displacement curve for different element sizes

Full size image
Table 1 Mesh qualities of the FE model
Full size table

3.3 Experimental validation of the FE model

To validate the finite element model, an experiment is conducted. A single-cell specimen (length 150 mm, cross-section 60 × 60 mm, thickness 1 mm ) made from aluminum alloy is subjected to axial loading as depicted in Fig. 7. The speed of the moving plate is 15 m/s.

Fig. 7
figure 7

Loading and boundary condition

Full size image

The experiment is conducted at Zhejiang University Center for Mechanical Experiments. The SUNS UTM6000 (Shenzhen Suns Technology Co. Ltd, Shenzhen, China) is used for the experiment. The equipment uses a computer system for control and data acquisition. The sample and the deformation mode are shown in Fig. 8. Note that there is a slight material failure at the folding areas which is not included in the FE model.

Fig. 8
figure 8

Deformation mode comparison for a single-cell tube

Full size image

Figure 9 shows the force-displacement curve for the experiment and the numerical simulation; the force is recorded from the moving plate. The peak crushing force (PCF) is 24.0 kN and 23.9 kN for the experiment and the numerical simulation, respectively. Therefore, the FE model can adequately estimate the response of the tube and thus can be used for further studies.

Fig. 9
figure 9

Force-displacement curve for a single-cell tube

Full size image

4 Configurational optimization (stage 1)

This section describes the method of determining the optimal topological configuration. First, the criteria used in selecting the optimal topological configuration are described, then a binary topological optimization problem is formulated, and a binary genetic algorithm is introduced to solve the optimization problem.

4.1 Crashworthiness indices

Thin-walled structures like the multi-cell tubes that undergo crushing deformation are investigated based on various indices. Peak crushing force (PCF) is the maximum force that the tubes experienced during the crushing process; in most cases, it coincides with the first fold that leads to the plastic deformation of the tubes. Energy absorption (EA) is the area under the force-displacement curve of the tubes. A key parameter that indicates good crashworthiness is the energy absorbed per unit weight or specific energy absorption (SEA). The mean crushing force (MCF) is the ratio of the EA and the displacement δ. Crushing force efficiency (CFE) is the ratio of MCF and PCF. An ideal thin-walled energy absorber will have a low PCF, a high SEA, and a higher CFE. Table 2 shows the crashworthiness criteria and their respective expressions.

Table 2 Crashworthiness criteria
Full size table

4.2 Problem definition

The first stage of the optimization approach is to find the optimal topological configuration at the selected weight ratios. The optimization problem is thus formulated as:

$$ \begin{aligned} &\text{Min} ~-\text{SEA}(x_{1}, x_{2}, ..., x_{9})\\ &s.t~~ m(x_{1}, x_{2}, ... x_{9})\le m_{0}w\\ &~~~~\text{PCF}(x_{1}, x_{2}, ... x_{9})\le \text{PCF}_{0}\\ &~~~~f_{\text{connectivity}}(x_{1}, x_{2}, ... x_{9}) \ne 0\\ &~~~~ x_{1}, x_{2}, ... ,x_{9} \in \{0,1\} \end{aligned} $$
(5)

where m0 = 0.3402 kg, PCF0 = 185 kN. w is the mass ratio and in this study, it is set as 0.50, 0.75, and 1.0.

4.3 Binary genetic algorithm

BGA is a type of genetic algorithm (GA), a popular evolutionary algorithm among researchers that has been widely studied and applied to optimization problems (Haupt and Haupt 2004). BGA uses the same components of GA, such as initialization, parent selection, cross-over, mutation, sorting, and selection. For configurational optimization, the solutions to the problem are represented by chromosomes. Each chromosome represents a topological configuration. Binary representation is used to represent the topological variables (i.e., the variables can only take a value of 1 or 0) so no decoding is required. A chromosome is denoted as X = [x1,x2,...,x9]. An initial generation of k chromosomes is generated randomly, where k is the population size. The characteristic of the initial generation influences the result and efficiency; therefore, it should be dispersed in the solution space to achieve a global optimum. Each chromosome is evaluated with an objective value. A static objective function with a penalty factor is introduced to penalize chromosomes that violates the constraints (Kuri Morales and Quezada 1998). In this paper, the constraints are the mass ratio, peak crushing force, and connectivity. If the constraints are satisfied, the configuration model is created and finite element analysis is conducted and the objective function (-SEA) is extracted, else a penalty factor is added.

Chromosomes with a smaller value of objective function have a greater fitness value and vice versa. The algorithm sorts the chromosomes based on their respective fitness value. In the current population, the best chromosomes are selected to serve as parents for the next generation. A new population is realized by mating parents through crossover, thereby inheriting many features from the previous generation. High potential parents are expected to produce preferable offspring chromosomes (Marzbanrad and Ebrahimi 2011). Each gene of the chromosome has a chance for mutation controlled by the mutation rate and percentage. Termination criteria are set as one of the following (a) the fitness of the best chromosome and population is not increasing. (b) The maximum number of generations is achieved.

The main steps for the BGA are as follows.

  1. 1.

    Define the optimization problem. This includes the definition of the objective function, design variables, and the design space.

  2. 2.

    Setup the parameters for the BGA and create a random initial population.

  3. 3.

    Convert the generated chromosomes into topological configurations.

  4. 4.

    Perform FE analysis to obtain the objective functions and constraints values.

  5. 5.

    Evaluate the fitness of each configuration and select the best configurations.

  6. 6.

    Check whether the termination criteria are satisfied if yes go to step (9) else continue to step (7).

  7. 7.

    Generate a new population through the following sub-steps.

    1. (a)

      Selection of parents.

    2. (b)

      Cross-over of the parents to generate new children.

    3. (c)

      Mutation of the new children to prevent premature convergence.

  8. 8.

    Return to step (3)

  9. 9.

    End the iteration and output the results.

The BGA parameters are set as follows: population size 15, maximum iteration 100, cross-over percentage 0.8, mutation percentage 0.3, mutation rate 0.02. In this study, random parent selection and the double point cross-over (Neubauer 1997; Sun et al. 2018a) are adopted to produce the next generation of children (configurations).

4.4 Optimization results

The topology evolution for the mass ratios of 0.5 is shown in Fig. 10. The optimization converges after around 20 iterations and the optimal topological configuration is X = [0,0,0,0,1,1,0,0,0] with an SEA of 31.76 kJ/kg, and a PCF of 83.05 kN. Figure 11 shows the topology evolution for the mass ratios of 0.75. The optimization converges after about 35 iterations and the optimal topological configuration is X = [0,0,1,0,1,1,0,1,1] with an SEA of 43.77 kJ/kg, and a PCF of 132.31 kN. The topology evolution for the mass ratios of 1.0 is shown in Fig. 12. The optimization converges after 45 iterations and the optimal topological configuration is X = [0,1,1,1,1,1,1,1,1] with an SEA of 45.28 kJ/kg, and a PCF of 175.97 kN. The summary of results is shown in Table 3. Interestingly, each optimal configuration has a set of different types of corners. For w = 0.5, the optimal configuration has 8 L-shaped, 8 T-shaped, and 0 crisscross corners, and the center of the tube has no webs. Similarly, the optimal configuration for w = 0.75 has only 4 crisscross, 4 L-shaped, and 32 T-shaped corners with no webs in the center. The optimal for w = 1.0 has 4 L-shaped, 22 T-shaped, and 20 crisscross corners without webs in the center.

Fig. 10
figure 10

Topology evolution for w = 0.50

Full size image
Fig. 11
figure 11

Topology evolution for w = 0.75

Full size image
Fig. 12
figure 12

Topology evolution for w = 1.00

Full size image
Table 3 Result of the first stage optimization
Full size table

5 Parameter optimization (stage 2)

5.1 Problem definition

A thin-walled structure like this tube is expected to absorb crash energy per unit weight as much as possible with little crushing force to reduce the degree of injury to the occupants during collisions. Therefore, a multi-objective optimization is proposed to maximize both the CFE and SEA. Due to the symmetric nature of the configuration, three (3) variables (l1,l2,l3) are selected to define the cell sizes, which are then taken as the design variables, as shown in Fig. 13. The minimum value for the design variables is taken as 2 mm due to manufacturing constraints, and the sum of all the variables should be at most 30 mm.

Fig. 13
figure 13

Optimization design variables

Full size image

The optimization problem is formulated as:

$$ \begin{aligned} &\text{Min} ~[-\text{CFE}(l_{1},l_{2},l_{3}),-\text{SEA}(l_{1},l_{2},l_{3} )]\\ &s.t\\ &2\le(l_{1},l_{2},l_{3})\le26\\ &l_{1}+l_{2}+l_{3}\le30 \end{aligned} $$
(6)

To solve the optimization problem, the objective functions, i.e., CFE and SEA have to be defined. In this study, the objective functions are defined by the means of meta-models.

5.2 Meta-models

Due to the non-linearity of the behavior of multi-cell tubes when used as energy absorbers, direct optimization is not efficient. In such cases, the use of surrogate models or meta-models is standard. The meta-model provides an approximate relationship between the objective functions (-CFE, -SEA) and the design variables (l1,l2,l3). The accuracy of the meta-model and computational efficiency are the key factors in selecting the meta-modeling technique. In this paper, the response surface methodology (RSM) is used to establish meta-models for the objective functions; it has been proven to predict the responses with good accuracy especially when the number of variables is less than 10 (Bigdeli and Nouri 2019; Fang et al. 2017a; Abdullahi and Gao 2020).

In RSM, the design variables are expressed as:

$$ \begin{array}{ll} y=&f(x)\approx \eta (x), \\ \eta (x)=&{\sum}_{i=1}^{L}{{{a}_{i}}{{\varphi }_{i}}(x)} \end{array} $$
(7)

the function f(x) is approximated with η(x) which is a set of L primary functions φi(x), and ai are the coefficients to adjust the primary functions. The optimal custom design method with an I-optimal sub-type is used to generate the initial design points in Design-Expert® (Version 11) software. For each of the design points, the model is generated and a finite element analysis is conducted in LS-DYNA (version R11.0.0) and the results are fed into Design-Expert® to get the meta-model. The meta-models are then evaluated for accuracy, if the prediction accuracy is low then additional sampling points are added and the circle is repeated.

The significance of the parameters on the crashworthiness responses is investigated using analysis of variance (ANOVA). Each of the meta-model generated is considered to be significant if the P value of the model and its parameters do not exceed 0.05 (P value < 0.05). Another parameter that indicates the model’s acceptability is the coefficient of determination and its adjusted value (R2 and \(R^{2}_{\text {adj}}\)). Model acceptability increase with the closeness of R2 and \(R_{\text {adj}}^{2}\) values to each other and their closeness to 1. The accuracy of the meta-models is summarized in Table 4

Table 4 Accuracy of the meta-models
Full size table

5.3 Multi-objective particle swarm optimization

Multi-objective particle swarm optimization (MOPSO) with the parameters shown in Table 5 is implemented in MATLAB for Pareto seeking. MOPSO is characterized by good Pareto front distribution and fast convergence as compared with other evolutionary algorithms. It has successfully been used in thin-walled structures optimizations (Qiu et al. 2015; Chen et al. 2018; Bigdeli and Nouri 2019; Fu et al. 2019; Abdullahi and Gao 2020).

Table 5 MOPSO parameters
Full size table

5.4 Optimization results

The Pareto frontier for the multi-objective optimization problem defined in (6) is obtained and shown in Fig. 14 for different mass ratios. It can be seen that the minimization of both the SEA and the CFE strongly conflicts with each other. In order to quantitatively compare the crashworthiness performances for the topological configurations, the “knee point” which is the best compromise solution is selected from the Pareto set using Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) (Chen and Tzeng 2004). For each of the mass ratios, the optimal point selected by TOPSIS is highlighted in Fig. 14 and the result is shown in Table 6.

Fig. 14
figure 14

a–c Pareto frontier for the optimization problem using meta-models

Full size image
Table 6 Crashworthiness performance result for the optimized tube
Full size table

For w = 0.50, the SEA is 34.25 kJ/kg and the CFE is 0.69, and the values of l1, l2, and l3 for the optimal point were 6.82 mm, 10.70 mm, and 12.48 mm. For w = 0.75, the SEA is 42.96 kJ/kg and the CFE is 0.81, and the values of l1, l2, and l3 for the optimal point were 10.68 mm, 7.98 mm, and 11.34 mm. For w = 1.00, the SEA is 46.15 kJ/kg and the CFE is 0.88, and the values of l1, l2, and l3 for the optimal point were 9.97 mm, 9.91 mm, and 10.12 mm. Note that in all the mass ratios considered, the outermost cell size l3 is bigger than the other two. Similar phenomena have been reported in topology optimization where more material is accumulated at the outer boundary (Fang et al. 2017b; Qiu et al. 2018). Although, bigger cell size does not necessarily signify more material, but in this case, the cells at the center of the optimized configurations are empty; therefore, having bigger cells increases the material at the boundary. A finite element model is created for the optimal points and is subjected to the same loading conditions, and the result is shown in Table 6. There is a slight difference (all < 5%) between the meta-model results and the finite element analysis results. This discrepancy is due to the accuracy of the meta-models used. However, the results are still within acceptable limits (Jeyakarthikeyan et al. 2018). The force-displacement curve for the optimized configurations and the baseline configuration is shown in Fig. 15. The baseline configuration has the highest PCF (185 kN). The optimized structures have 89.20 kN, 135.25 kN, and 176.82 kN for w = 0.50, 0.75, and 1.00 respectively. The SEA is shown in Fig. 16. It can be seen that the optimal structure (w = 1.00) has a better SEA (45.63 kJ/kg) than the baseline configuration (44.9 kJ/kg). While the optimal configuration for w = 0.75 has an SEA close to the baseline configuration (44.09 kJ/kg). This clearly shows that optimized structure can perform well as an energy absorber and can be used to replace the baseline configuration for the same loading conditions. For w = 0.5, the optimal structure has an SEA of 32.87 kJ/kg. This is remarkable given that for half the mass, it has an SEA greater than half of the SEA of the baseline configuration.

Fig. 15
figure 15

Force-displacement curve of the optimized structures

Full size image
Fig. 16
figure 16

SEA of the optimized structures

Full size image

5.5 Application

To demonstrate the effectiveness of the two-stage optimization, a simple case of a flat bumper beam and crash box assembly is studied. The assembly consists of two crash boxes welded towards the beam ends as shown in Fig. 17. The bumper and the crash boxes are made of the same material as described in Section 3.1. The contact between the crash boxes and the bumper beam is defined using “TIE_NODES_TO_SURFACE” contact option in LS-DYNA. The other end of the crash boxes is placed against a rigid body that represents the rest of the car body with a mass of 1378 kg. The car is modeled with solid elements and the material is defined as rigid (MAT20) with a velocity of 1.1 m/s. Both the bumper beam and the crash boxes are defined using four-node shell elements having a thickness of 1.5 mm and 1 mm, respectively. The rigid wall is fixed and is defined using “RIGID_WALL_PLANAR” option in LS-DYNA.

Fig. 17
figure 17

Assembly of bumper beam and crash boxes

Full size image

The optimum configuration for w = 0.75 and the baseline study are placed in the bumper beam assembly to replace the crash boxes and a finite element analysis is conducted. The force-displacement curve for the baseline and optimum configuration is shown in Fig. 18. The baseline configuration has a PCF of 122 kN while the optimum has a PCF of 106.5 kN which is 12.7% lower than the baseline configuration. For this type of loading condition (low-speed impact), the force transferred to the rest of the car body should be below 120 kN as per the EURO NCAP standard. Figure 19 shows the SEA of the structures. The baseline configuration has an SEA of 8.84 kJ/kg while the optimum configuration has an SEA of 12.82 kJ/kg which amounts to a 45% increase. Therefore, the two-stage optimization has proven to be applicable in the industrial design of lightweight and crashworthy crash boxes. The configuration profile of the optimized crash box is shown in Fig. 20.

Fig. 18
figure 18

Force-displacement curve of the baseline and optimized structures

Full size image
Fig. 19
figure 19

SEA of the baseline and optimized structures

Full size image
Fig. 20
figure 20

SEA of the baseline and optimized structures

Full size image

6 Conclusion

In the present study, a novel two-stage optimization design of a multi-cell tubal structure is presented. The process addresses an important design problem by combining a discrete and continuous optimization process into a sequential optimization that generates an overall optimum. The first stage entails a configurational optimization which is realized by formulating a discrete topological optimization problem where the webs within the tube configuration are taken as the topological design variables. The constraints in the first stage are connectivity, mass ratio, and PCF. BGA is utilized in searching for the optimal configuration in the first stage. The second stage entails parameter optimization where the cell sizes are the design variables. The objective functions in the second stage are defined using meta-models. MOPSO is employed for Pareto searching and TOPSIS is used to find the optimal point for each of the mass ratios considered. Compared with the baseline configuration, the optimized tubal structures have a significantly improved energy absorption capacity. The two-stage discrete and continuous optimization approach has demonstrated that it not only provides a systematic approach to searching optimal structure but also creates a series of novel multi-cell topological configurations with enhanced crashworthiness. This study has demonstrated that different combination of corners affects the crashworthiness of multi-cell tubal structures and paves the way for the research on the design of multi-cell tubal structures based on corner types to enhance crashworthiness. The direct relation for corner types to crashworthiness criteria should be a focus for future work.