1 Introduction

In order to obtain a design with satisfactory performance, crashworthiness optimization has been widely conducted in automotive industry. Due to the numerical noise and physical bifurcation in crash response, gradient based optimization algorithms cannot be used directly here. On the other hand, because of high computational cost for crash simulation, it is improper to apply evolutionary algorithms directly, such as genetic algorithms (GA), differential evolution (DE), or evolution strategies (ES). To overcome the above problems, surrogate models are generally built to capture the crash response. To improve the accuracy, the optimization is normally done with an adaptive surrogate model. In this concept, a surrogate model is built first and then an optimization is done on this surrogate. When the current best design is obtained, the real response for this point is compared with the predicted one. If the difference is not within the convergence, the surrogate model is improved. For this, there are several approaches like trust region approach (Alexandrov et al. 1998) or kriging with expected improvements (Jones 2001). The optimization is then continued based on the new surrogate model. These steps are repeated until convergence is achieved (Yang et al. 2001; Ryberg et al. 2015). However, the benefit of this concept would be undermined, if the number of design variables is too big. Variable screening techniques might be helpful (Lu and Wang 2011) to reduce the number of relevant parameters. Still, when the importance of the design variables are not so different from each other, it is hard to decide which design variable should be preserved and which can be neglected. Moreover, the computational cost for variable screening is also high when the number of design variables is big.

Based on the above discussion, i.e., taking into account that all of these traditional methods have their drawbacks, HCA exhibits advantages in the following points:

  1. 1.

    It requires no gradient information for updating.

  2. 2.

    It improves the structure fast instead of requiring large number of evaluations.

  3. 3.

    It can handle a large number of design variables without obvious time increase.

Inoue et al. (1994) might have proposed the earliest application of a CA (cellular automata) approach for structural optimization. In this work, they treated the values of Young’s modulus as design variables. The change of the design variable depends on the current stress and the target predefined stress. If the value of Young’s modulus is below a certain value, this cell is deleted; this can hence be regarded as some kind of topology optimization. Later, Tatting and Gürdal (2000) combined simultaneous analysis and design (SAND) and CA for topology optimization of two-dimensional continuum structures. More recently, researchers began to use a hybrid cellular automaton framework for structural optimization. Compared to Tatting and Gürdal (2000), HCA utilizes response information from FEA (finite element analysis). As a result, in each iteration, the residual between external work and internal energy is zero, but in Tatting and Gürdal (2000), this value is iteratively reduced to zero.

For a static loading case, Bochenek and Tajs-Zielińska (2010) applied HCA for the topology optimization of 2D elastic structures. By taking inspiration from PSO (particle swarm optimization), they proposed novel updating rules for design variables. Tovar et al. (2006) discussed different updating rules, namely two-position control, proportional control, derivative control and integral control. They demonstrated the efficiency of HCA by optimizing two-dimensional continuum structures for cantilever problems. Tovar et al. (2004) implemented a HCA in their research where only the surface elements are allowed to change during the structural synthesis process. This concept is inspired by bone remodeling, where only elements on the surface of the mineralized structure can be modified.

With respect to static nonlinear loading cases allowing for large deformations, Patel et al. (2005) illustrated the use of HCA in 2D and 3D compliant mechanism designs. In their approach, they tend to achieve a uniform distribution of the linear combination of mutual potential energy and strain energy for compliant mechanism design.

When it comes to crash optimization, according to the different types of design variables, it can be classified as finite element level optimization and macro level optimization. In the finite element level optimization, the design variables are the relative densities of a material (Bochenek and Tajs-Zielińska 2012). The power-law approach SIMP, i.e., (solid isotropic material with penalization) (Bendsøe 1989; Zhou and Rozvany 1991), is used to eliminate the intermediate elements. Forsberg and Nilsson (2007) have conducted a 2D crash optimization with plane elements. In their research, the design variables are the thicknesses of the elements and a power-law approach is also embedded. Mozumder et al. (2008) have also applied HCA to shell-based structures to obtain the best thickness distribution; but in their optimization, no penalty method is applied. By contrast, for macro level optimization, the design variables are shared not only by one element but by a group of elements. For example, in Patel et al. (2009b), a three dimensional structure is discretized in the plane that is normal to the extrusion axis, and the elements along this axis are grouped together. The responses of the elements are summed in each group and used as input for design variable updating. In Mozumder (2010), an empty crash box beam subjected to axial dynamic load is discretized into non-bulking zone and bulking zone. The thicknesses of each element in these zones are forced to be the same and defined as design variables. More recently, Duddeck et al. (2016) proposed a technique called HCATWS (HCA for Thin-walled Structures). In their work, the thickness of each thin wall is treated as design variable, and it is deleted when it is below a certain value. The effectiveness of HCATWS is demonstrated by comparing to results from commercial software LS-OPT (Stander et al. 2012).

During the last decades, various types of data flow in HCA have been proposed and studied. The simplest form might be the HCA without a predefined mass fraction and extra constraints, such as displacement or force. In this form, the goal is to homogenize a certain kind of response, such as internal energy density or stress, throughout the whole design domain. More specifically, Forsberg and Nilsson (2007) have defined a target value of internal energy density for their crashworthiness optimization. If the shell element’s response is higher than the target value, the thickness is added and vice versa. Without the predefined target value for this specific response, the updating can also be done by comparing the average and its own value. Examples can be found in Khandelwal and Tovar (2010). However, the most popular HCA for topology crash optimization might be the one with a predefined target mass fraction. In this concept, the new set point is calculated according to the previous set point, previous mass fraction and target mass fraction. Then the updating of design variables can be proportional control (Patel et al. 2009a, b; Guo et al. 2012; Aulig et al. 2014; Bandi et al. 2012, 2013), two-position control (Tovar et al. 2004) or even with PID (proportional-integral-derivative) control (Patel et al. 2005, 2006a, b).

A more complex and practical HCA is the one considering some extra displacement or force constraints. In this form, the target mass is not fixed but dynamic. The target mass is usually updated in the outer loop according to the violation of the extra constraints. Mozumder et al. (2008) propose to increase target mass when the displacement constraint is violated and reduce mass when the force constraint is violated for crash optimization. Similar concept of extra constraints handling in HCA can be found in Witowski et al. (2012) and Roux (2011). However, one of the main disadvantages when it applies to crashworthiness optimization is that it tries to homogenize certain field variables but not explicitly minimize mass and the resultant even distribution of energy absorption in the structure cannot ensure the overall maximum of energy absorption (Fang et al. 2016). To improve specific energy absorption, Duddeck et al. (2016) realized an approach by pushing the displacement response to be just within the constraint limit. When the constraint is violated, it increases mass. On the other hand, when there is some gap between the current response and constraint, it reduces mass. Because of the assumed monotonic relationship between the mass and displacement response, this can lead to a design with less mass. However, there might be a design with a high value of mass but its response is just within the boundary. If this situation takes place, the method in Duddeck et al. (2016) improves very slowly because the change of mass is proportional to the gap between the response and constraint.

Hence, in this paper, a new idea called bi-section search with limited length is proposed to define a proper target mass in the outer loop of HCATWS (Duddeck et al. 2016). Further, some new ideas are proposed to assure that the inner loop mass distribution converges exactly to the target mass. The correctness of the optimization results from this improved and more efficient algorithm will be compared with those obtained from the commercial software LS-OPT for the axial crash case. The efficiency of the proposed techniques will be finally demonstrated by more complicated 3 point bending impact cases.

2 Hybrid cellular automaton

The hybrid cellular automaton (HCA) can realize topology optimization for structures consisting of lattices. “Hybrid” means here the combination of cellular automaton (CA) par-adigm and finite element analysis (FEA). The lattice can not only consist of shell, beam or solid elements from the FEA, but also of groups of these elements. During the optimization, after one evaluation of FEA, field variables, such as stress (Gürdal and Tatting 2000), mutual potential energy (MPE) (Patel et al. 2005), strain energy density (SED) (Tovar et al. 2006) and internal energy density (IED) (Forsberg and Nilsson 2007; Guo et al. 2011), can be obtained for each component of the lattice. The information will be utilized by the updating rules to distribute the mass. The goal of the redistribution of mass is to homogenize the field variables.

2.1 Hybrid cellular automaton for thin-walled structures

For automotive, many components are designed as thin-wal-led structures in order to improve crash safety. Therefore, hybrid cellular automaton for thin-walled structures (HCAT-WS) is proposed to deal with crash topology optimization for thin-walled structures. HCATWS can be used for the crash topology optimization problem with one extra displacement constraint.

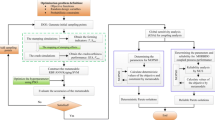
As shown in Fig. 1, HCATWS starts with the initialization of the design, which includes the division of the original structure into lattices. The state of CA is described by its field variable and design variable:

$$ {\beta^{k}_{i}}=\left( \begin{array}{c} {U^{k}_{i}} \\ {x^{k}_{i}} \end{array} \right) $$
(1)

where \({x_{i}^{k}}\) and \({U_{i}^{k}}\) refer to the values of the design variable and field variable of CA in location i and outer loop iteration k.

Fig. 1
figure 1

Flow chart of topology optimization using HCA for thin-walled structures

Full size image

HCATWS has two loops, namely inner loop and outer loop. In the outer loop, as is given in Fig. 1, FEA is conducted to derive the field variables \(({U_{i}^{k}})\) and global output (O k). A new target mass \({m_{t}^{k}}\) will be calculated based on the current structure’s response and the predefined constraint threshold. The goal of the inner loop is to distribute the mass according to the values of the field variable, \({U_{i}^{k}}\), for each cell and its neighborhood, therefore homogenizing the field variable in the design domain. After the completion of the inner loop, mass correction is conducted to assure that the real mass is exactly the same as the target mass. HCATWS will stop when the outer loop convergence is reached.

2.2 Outer loop of HCATWS

HCA tends to make the design more homogeneous and does not explicitly minimize the mass. In HCATWS, the extra constraint considered here is a displacement constraint. There exists a monotonic relationship between the mass and displacement response. HCATWS tries to reduce mass when the design is feasible and increase mass when violated. By this way, it pushes the design’s displacement response to be just within its boundary, therefore minimizing the mass. The main goal of the outer loop is to define a proper target mass for the inner loop. The idea in Duddeck et al. (2016) is that if the design is feasible, it reduces mass while if the design is infeasible it adds mass. The degree of adding or reducing mass is proportional to the gap between the current response and the predefined boundary. It works quite well for comparably small number of design variables. However, the idea of bi-section search with limited length shows its advantage in optimization problems with comparably large number of design variables. The reason is that for designs with different mass, they can have similar responses. Let’s assume the mass of design A is higher than the mass of design B, and their responses of the constraint are just within its boundary. If HCATWS (Duddeck et al. 2016) obtains design A, then the change of target mass is very small. If this happens, for the previous HCATWS method, the mass goes down very slowly to design B or even it converges before it obtains design B. By contrast, bi-section search with limited length keeps pushing the mass to go down every several iterations. At the same time, it searches between the feasible and infeasible points to improve the design because there exists a monotonic relationship between the mass and displacement response. The advantages of this new HCATWS is that it has a higher chance to get design B compared to the previous method proposed in Duddeck et al. (2016).

In order to improve this shortcoming, a new idea based on bi-section search with limited length is proposed for the outer loop to define a proper target mass. Bi-section search is a direct search method where no gradient information is required (Monahan 2011). It abandons half of the feasible region in each step. However, bi-section search cannot be directly used here because the change of mass in two iterations should not be too big. Therefore, a modified approach is proposed here, where the bi-section search is implemented in the outer loop in a sequential way with limited length. More specifically, this idea tends to increase mass if it is feasible and decrease mass if it is infeasible until it encounters a situation where one of the sequential two designs is feasible and the other is infeasible. Because of the monotonic relationship between the mass and displacement response, bi-section search is then conducted within the two designs. The bi-section search within this search step will be stopped by some criterion, which will be discussed later. Compared to the starting point of the bi-section search, the mass of the latest design is more efficiently distributed. The algorithm will try to decrease the target mass to check whether it has more potentiality for a lighter solution. These processes are conducted repeatedly and the detailed steps are shown below:

Step(1): :

FEA is conducted for the initial design. Its mass is depicted as \({m_{t}^{0}}\). The state of the design is described as “feasible” or “violated”, which indicates whether the displacement’s response satisfies the boundary or not.

If the design is feasible, we have

$$ {m_{t}^{1}}={m_{t}^{0}}-\Delta m, $$
(2)

where \({m_{t}^{1}}\) is the new target mass for the inner loop and Δm refers to a predefined search step.

If the design is infeasible, we have

$$ {m_{t}^{1}}={m_{t}^{0}}+\Delta m. $$
(3)

Step (1) is repeated until the situation occurs, where the two states of the sequential designs are different.

Step(2): :

For easy explanation, let’s assume the state of iteration k is “infeasible” and the state of iteration (k − 1) is “feasible”. Then the bi-section search is conducted within the range \([m_{t}^{k-1},{m_{t}^{k}} ]\). The length of the initial section for bi-section search is Δm. The search section is reduced to half of the previous iteration as:

$$ {\Delta m}^{p}={\left( \frac{1}{2}\right)}^{p} \times {\Delta m} $$
(4)

where p indicates the number of bi-section searches having been conducted in this bi-section search step Δm.

Here, we define \(p_{1}^{*}\) and \(p_{2}^{*}\) as two threshold numbers of iterations for bi-section search within this section, and \(p_{2}^{*}>p_{1}^{*}\).

The value of \(p_{1}^{*}\) should satisfy the following requirements:

  1. (1)

    After bi-section search is conducted for several steps within Δm, we expect that the mass distribution is more efficiently distributed than at the starting point for bi-section search. Therefore, we can explore the potentiality for further light weight solutions. Hence, \(p_{1}^{*}\) should be big enough to expect that the mass of design in step \(p_{1}^{*}\) is more efficiently distributed than at the starting point for bi-section search.

  2. (2)

    The nature of bi-section search is that it reduces half of its search length in every step. Then the value of \(p_{1}^{*}\) should not be too big. Otherwise, the change of the target mass will become very small.

The value of \(p_{2}^{*}\) should satisfy the following requirements:

  1. (1)

    \(p_{2}^{*}\) is defined so as to stop the algorithm when the search length becomes extremely small but the design is still infeasible. As a result, the best design is the most previous feasible design. Therefore, the value of \(p_{2}^{*}\) should not be too big.

  2. (2)

    \(p_{2}^{*}\) is defined bigger than \(p_{1}^{*}\) because the algorithm will check whether a feasible design can be obtained after several steps of homogenization of field variables.

To summarize above, the outer loop of this optimization will stop if one of the following criteria is satisfied:

  1. (1)

    The maximum number of evaluations N m a x exceeds a predefined value;

  2. (2)

    During the bi-section search, the situation that \(p>p_{2}^{*}\) and the state is violated takes place;

  3. (3)

    The change of design variables is very small:

    $$ \sum\limits_{i=1}^{N} |x_{i}^{k+1}-{x_{i}^{k}}| < \varepsilon $$
    (5)

    where N indicates the number of cells and ε is a very small predefined value.

As indicated in Fig. 1, for each iteration of the outer loop, it requires only one crash computation. The new approach here doesn’t increase significantly the computational cost compared to the old approach in Duddeck et al. (2016).

2.3 Inner loop of HCATWS

A new target mass is assigned to the inner loop after every iteration of the outer loop. The goal of the inner loop is to distribute the mass according to the field variables of the CA and make the mass converge to the target mass. To distribute the mass, the set point S is introduced. The initial value of this set point S 0 is defined as the average value of the internal energy densities of all cells. The value of the set point is adjusted in the inner loop according to the current mass and the target mass,

$$ S^{j}=S^{j-1} \times \frac{m_{c}^{j-1}}{{m_{t}^{k}}} $$
(6)

where S j indicates the set point in iteration j of the inner loop, \({m_{t}^{k}}\) the target mass in iteration k of the outer loop, \(m_{c}^{j-1}\) the real mass in iteration (j − 1) of the inner loop.

Then the updating of design variables is conducted as,

$$ x_{i}^{k,j}=f_{2} (S^{j-1},\overline{U}_{i}^{k},{x_{i}^{k}}) $$
(7)

where \(x_{i}^{k,j}\) refers to the value of design variable x i in the iteration j of the inner loop and iteration k of the outer loop, f 2 is the updating rule, and \(\overline {U}_{i}^{k}\) represents the weighted field variables in iteration k of the outer loop.

In order to increase the stability for updating, this algorithm uses the weighted sum of field variables in its history instead of the values from only the current iteration (Duddeck et al. 2016).

For iteration k = 0: \(\overline {U}_{i}^{0}={U_{i}^{0}}\)

For iteration k = 1: \(\overline {U}_{i}^{1}=w_{1} {U_{i}^{1}}+w_{2} {U_{i}^{0}} \)

For iteration k>1: \(\overline {U}_{i}^{k}=w_{3} {U_{i}^{k}}+w_{4} U_{i}^{k-1}+w_{5} U_{i}^{k-2} \)

where w 1,w 2,w 3,w 4 and w 5 are weight factors.

The updating of x i is not only decided by the field variable itself but also by its neighborhood. We take the Von Neumann neighborhood (Hunkeler 2013) here. More specifically, for the current thin-walled structure, if extrusion constraints are imposed in longitudinal direction, a cell belongs to the current cell’s neighborhood when they share a common node (Fig. 2a.). If the walls are also discretized in its longitudinal direction, a cell is the current cell’s neighborhood when they share a common line (Fig. 2b.).

Fig. 2
figure 2

Neighborhood for the in-plane (a) and for the out-of-plane case (b)

Full size image

For updating rules, many different ideas have been proposed in the past, such as two-position control (Tovar et al. 2006), proportional control (Patel et al. 2009b; Khandelwal and Tovar 2010; Guo et al. 2012), derivative control (Penninger et al. 2009), integral control (Mozumder et al. 2008) or combination of the mentioned (Patel et al. 2006b; Penninger et al. 2009). For the HCATWS in this paper, we use the hybrid updating rule proposed by Hunkeler and Duddeck (2014), which takes inspiration from Bochenek and Tajs-Zielińska (2010) and Patel (2007). This rule considers separate contributions from each neighbor cell and accounts for the discrepancies between the set point and the IED levels of each neighbor (Duddeck et al. 2016).

The strict convergence of the inner loop is ensured by mass correction as follows,

Step(1): :

The design variables are scaled to make sure the summation of the mass to be the same as the target mass:

$$ x_{i\_new}^{k}={x_{i}^{k}} \times m_{c}/m_{t} $$
(8)

where m c refers to the summation of the current mass.

Step(2): :

Because we have the lower and upper bound for the design variables, this scaling might make the new design variables to exceed these bounds. Then we check the lower bound for deletion: if some of the design variables are deleted, these “deleted masses” are uniformly distributed to the remaining design variables.

Step(3): :

We check the upper bound: if some of the design variables exceed the bound, they are forced to be the upper bound while the “extra mass” is uniformly distributed to the remaining design variables.

Step(4): :

Check whether all design variables have reached their upper bounds. If so, the mass correction is stopped. If not, Step (3) is re-conducted until there is no “extra mass” requiring for a new distribution or all the design variables are at the upper bound.

This new modification, i.e. mass correction, of the original approach in Hunkeler and Duddeck (2014) smoothens the optimization performance.

3 Test cases

3.1 General description

For the chosen test cases, the material of the structure is aluminum. The basic property of this material is given in Table 1 and its hardening is represented by a piecewise linear stress-strain curve as shown in Table 2. Instead of using the real mass directly in the outer loop, we use the average value of design variables (the wall thicknesses x i ), which is proportional to the real mass here. This scaled mass is calculated as,

$$ \overline{m}=\frac{1}{N}\sum\limits_{i=1}^{N}x_{i} $$
(9)
Table 1 Basic properties of aluminum
Full size table
Table 2 Piecewise linear isotropic hardening of the extrusion beam (aluminum) defined by effective plastic strain \(\varepsilon _{eff}^{p}\) and corresponding stress σ [MPa], (Hunkeler 2013)
Full size table

The optimization statement for the testing cases with HCA are,

$$\begin{array}{llllll} & \underset{x_{i}}{\min} & & \sum\limits_{i=1}^{N}|U_{i}-\frac{1}{N}\sum\limits_{i=1}^{N}U_{i}| \quad and \quad \overline{m} \\ & \text{s.t.} & & g \leq g^{*} \\ &&& x_{min} \leq x_{i} \leq x_{max}, \quad \; i = 1, \ldots, N, \end{array} $$

where g refers to the displacement response, g ∗ is the predefined constraint boundary and x m i n and x m a x represent the lower and upper boundary for the design variables.

As shown in the optimization statement, this is a multi-objective optimization problem. One objective is to make the structure more homogenized and the nature of the local rules reflects this feature. The minimization of the mass is achieved by pushing the displacement response to be just within the boundary.

One of most widely used criteria to assess crash performance is specific energy absorption (SEA) (Fang et al. 2016). SEA is defined as energy absorption (EA) per unit mass.

$$ SEA=\frac{EA}{m} $$
(10)

In HCATWS the mass is minimized and the total amount of energy absorption is kept constant, because the rigid pole or wall will bounce back at the end of the simulation. As a result, SEA will be maximized. Nevertheless, it should be noted that topologies having better SEA are possible if the uniformity condition is relaxed. But to the authors’ knowledge there is no method available to identify these geometries with a comparable low computational effort.

In industrial context, displacement constraints are used to protect structures like the radiator in a frontal impact test to assess repair costs as defined by the RCAR organization (www.rcar.org), or battery packs and fuel tanks in case of side or rear crashes. In these cases, impact energy has to be absorbed by cross members allowing only limited intrusions, i.e. relative deformations. Mass-less beams may be used for measurement of these quantities. In additional papers of the authors’ research group, methods have been proposed to enable component-based studies to address full vehicle crashworthiness (Zimmermann and Hössle 2013; Fender et al. 2014). This enables component development by using sub-structures comparable to the studies in this paper. The value of the constraints in industry is normally defined by history data. In other words, the displacement value of the previous component is used for comparison. However, the purpose of this paper is not on the development of a real component but on the assessment of the proposed algorithm. Hence, the value of the constraint is set to be a little smaller than the initial response. We expect that with a more homogenized design, the performance will be improved. Also the value of the constraint is not set to be very small to assure that there exists some possibility to delete some walls during the optimization.

3.2 Axial crash

Axial crash tube box has been widely studied in literature (Liu 2008; Sun et al. 2014; Yin et al. 2014; Tang et al. 2013). Therefore, it is an appropriate choice for comparison. One end of the beam is fixed. Another end of the beam is exposed to a rigid wall impacting with a mass of 500 kg and a velocity of 5 m/s in z direction (Fig. 3a). The outer walls of the tube are not chosen as design variables. They have a constant value of 1.5 mm. There are 31 inner walls, which are modeled as different parts in LS-DYNA. As shown in Fig. 3b, two symmetry planes are used. The number of design variables are hence reduced from 31 to 10. Therefore, the number of design variables is small enough to utilize commercial software, e.g. LS-OPT, for comparison. The initial value of all design variables is 0.50 mm. The range is set from 0.05 to 1.80 mm. If the value of the thickness is less than 0.40 mm, the entire wall is deleted. The constraint in this optimization problem is defined as the maximum displacement of the rigid wall in z-direction. The initial response value of the constraint is 84.24 mm. The constraint is set to be 75.00 mm.

Fig. 3
figure 3

Axial crash test case (a) and symmetry planes to reduce the number of design variables (b)

Full size image

Here, we compare the results from HCATWS in this paper with the results obtained by LS-OPT and HCATWS from Duddeck et al. (2016). In LS-OPT, an iterative response surface method (RSM) using radial basis functions is utilized. In the following, for easy explanation, HCATWS given with the idea in Duddeck et al. (2016) is referred to as HCATWS-1, and HCATWS with the idea of bi-section search with limited length is denoted as HCATWS-2. In Duddeck et al. (2016), LS-OPT required a total number of 255 crash simulations. The best result was found after 187 non-linear simulations. By contrast, HCATWS-1 and HCATWS-2 stopped after 35 and 36 non-linear simulations. The topology of the best design obtained by all three methods is the same and it is shown in Fig. 4a and b. The comparison between LS-OPT, HCATWS-1 and HCATWS-2 is shown in Table 3. For the crushing of the thin-walled tubes, the energy is absorbed through bending deformation along the bending hinge lines and membrane deformation. The severe deformation takes place near the corner. Lee and Wierzbicki (2001) studied this phenomenon for maximum energy absorption. They found that more crash energy will be absorbed when the corner is reinforced with more mass. The results obtained from the LS-OPT (Duddeck et al. 2016), HCATWS-1 and HCATWS-2 have good correspondence with this concept. For this comparably simple optimization problem, HCATWS-1 and HCATWS-2 have similar performance.

Fig. 4
figure 4

Optimized topology for both optimization methods (a) and deformation of crash tube (b) (Duddeck et al. 2016)

Full size image
Table 3 Optimized results comparison between two methods (axial crash case)
Full size table

As discussed in Section 2.2, the value of \(p_{1}^{*}\) should be big enough for homogenization of field variables but not too big to make the search length for bi-section search too small. It is set 5 in this case. For this axial crash case, it is a comparably simple optimization problem with 10 design variables. Based on the complexity of this optimization problem, it is not expected that further improvement can be achieved by setting \(p_{2}^{*}\) with a higher value. Therefore, \(p_{2}^{*}=6\) is used. The performance of the improved HCATWS is depicted in Fig. 5. The initial design is infeasible thus the mass keeps increasing with a scaled change of mass (Δm = 0.1) until iteration 2, where the design is feasible. Due to the monotonic relationship between the mass and displacement response, we assume that between the solution of iteration 1 (\({m_{t}^{1}}\)) and iteration 2 (\({m_{t}^{2}}\)) there exists a design, of which displacement response is just within the boundary. The bi-section search will be used to find this solution. After using 5 (\(p_{1}^{*}\)) times the bi-section search, the search area is already very small and the current design (iteration 7) is feasible. Compared to iteration 2, the mass is more efficiently distributed in iteration 7. Hence, the algorithm tries to push the mass down with Δm = 0.1. This step is repeated until the current design is infeasible (iteration 9). Then the bi-section search is conducted again between the point of iteration 8 (\({m_{t}^{8}}\)) and iteration 9 (\({m_{t}^{9}}\)). This process is repeated until it cannot find a feasible design after 6 searches (\(p_{2}^{*}\)), because the search length is very small \(\left (\Delta m \times \left (\frac {1}{2}\right )^{p_{2}^{*}}\right )\). As a result, the optimization stopped at iteration 35. The best design is the most previous feasible design in iteration 29.

Fig. 5
figure 5

HCA optimization history for axial crash case

Full size image

The topology change history of the improved HCATWS is shown in Fig. 6. As can be seen, most of the inner walls are deleted first. The mass is pushed to the corner where more energy is absorbed. It can be seen that it only requires 17 evaluations to obtain the best topology. As indicated in Fig. 5, the first feasible design obtained by HCATWS-2 is in iteration 2 and its SEA is 5.94 J/g. During the optimization, SEA is increased by minimizing the mass and the optimized structure’s SEA is 7.27 J/g.

Fig. 6
figure 6

Topology evolution for axial crash case

Full size image

3.3 3 Point bending crash case 1

The loading case studied here is a three-point bending crash case (3P Crash 1). As indicated in Fig. 7, the beam is impacted transversely by a pole with an initial velocity of 10 m/s and mass of 85 kg. Two ends of the beam’s outer walls are fixed (all degrees of freedom). The length of the beam is 800 mm and its cross-section is 80×120 mm 2. The thickness of the outer walls is 1.8 mm and they are again not chosen as design variables. The inner walls of this structure are modeled with different parts and they are chosen as design variables. The initial value for all design variables is 0.60 mm. The range of these design variables is set from 0.05 to 3.00 mm. If the thickness is less than 0.50 mm, it is deleted. The total number of inner walls is 446. Two symmetry planes, namely x-y plane and y-z plane as indicated in Fig. 8, are used to reduce the number of design variables from 446 to 123. The constraint of this optimization problem is the maximum displacement of the pole in y-direction. The initial response of the constraint is 99.53 mm. The constraint limitation is chosen to be 80.00 mm.

Fig. 7
figure 7

Three-point bending crash case (1)

Full size image
Fig. 8
figure 8

Symmetry planes to reduce the number of design variables

Full size image

As discussed in Section 2.2, compared to Duddeck et al. (2016), the improved HCATWS proposed here has a higher chance to obtain a better design. To prove this, two crash optimizations are conducted, where all the operators are the same except for the definition of target mass in the outer loop. The values for the stopping index in HCATWS-1 and HCATWS-2 are shown in Table 4. The value of \(p_{1}^{*}\) is defined as 5. For this optimization problem, the number of design variables is comparably higher. Thus we expect that there is a certain probability to obtain a better design by setting \(p_{2}^{*}\) with a comparably higher value. Hence, we set \(p_{2}^{*}=10\).

Table 4 Parameters to define the convergence
Full size table

The performance of HCATWS-1 and HCATWS-2 can be found in Figs. 9 and 10. The optimized results are summarized in Table 5. HCATWS-1 and HCAT-WS-2 stopp-ed because the maximum number of iteration is exceeded. The best design obtained by HCATWS-1 has a scaled mass (\(\overline {m}\)) of 0.601 while in HCATWS-2 it is 0.561. In HCATWS-1, when it obtains a design at iteration 25, its displacement response is 79.85 mm. Thus the gap between the current response and predefined boundary is very small. This results in a very small change of target mass. In Fig. 9, from iteration 25 to iteration 40 the mass goes down very slowly. By contrast, as depicted in Fig. 10, it obtains the first feasible design at iteration 3 with a scaled mass of 0.9. Then bisection search is done between feasible point at iteration 3 and infeasible point at iteration 2. This bisection search is stopped after 5 iterations because here we have set \(p_{1}^{*} = 5\). Then because the current design is feasible, it pushes the target mass to reduce Δm (0.1) to explore more potentiality for a lighter solution. As the design in iteration 9 is infeasible again, bi-section search is conducted between \({m_{t}^{8}}\) and \({m_{t}^{9}}\). This process is repeated until the maximum number of evaluations 60 is achieved.

Fig. 9
figure 9

HCATWS-1 optimization history for 3P crash case 1

Full size image
Fig. 10
figure 10

HCATWS-2 optimization history for 3P crash case 1

Full size image
Table 5 Optimized results comparison between two methods (3P crash case 1)
Full size table

Both responses of the best design obtained by HCATWS-1 and HCATWS-2 are very close to its predefined boundary. The advantage of HCATWS-2 shown in this result is that it can obtain a design with less mass. When it obtains a design whose response is just within its boundary, it will still try to push the mass down. During the optimization process, the structural response becomes more homogeneous and thus the mass is better distributed than in the initial design. Thus there exists some potential to decrease the mass while still satisfying the constraint. By contrast, the idea in Duddeck et al. (2016) might get stuck in a design with more mass when its response is just within its boundary.

The best design’s topology for both methods can be found in Figs. 11 and 12. As depicted in Fig. 12, the mass tends to go to the middle where the beam is impacted by the pole. This helps increasing energy absorption and prevents the pole to move in y direction. At the two ends of the beam mass is also added. This helps preventing local buckling of the structure. The deformation shape for the optimized results from HCATWS-2 is given in Fig. 14. The topology change during the optimization for HCATWS-2 can be found in Fig. 13. As depicted in Fig. 10, HCATWS-2 obtains the first feasible design in iteration 3 with its SEA (1.51 J/g). In the later iterations, SEA is gradually maximized with the minimization of mass and final feasible design’s SEA is 1.96 J/g (Fig. 14).

Fig. 11
figure 11

Optimized result with HCATWS-1 for 3P crash case 1 (outer walls not shown)

Full size image
Fig. 12
figure 12

Optimized result with HCATWS-2 for 3P crash case 1 (outer walls not shown)

Full size image
Fig. 13
figure 13

Topology evolution with HCATWS-2 for 3P crash case 1 (outer walls not shown)

Full size image
Fig. 14
figure 14

Deformation shape of the optimized result with HCATWS-2 for 3P crash case 1

Full size image

3.4 3 Point bending crash case 2

Another advantage of the new method is that it requires no significant increase of the number of finite element analysis when the number of design variables increases. To prove this, the next test example is also a three-point bending crash case (as illustrated in Fig. 15), but it has 1520 inner walls (as indicated in Fig. 16) and they are modeled as different parts in LS-DYNA. As shown in Fig. 17, two planes are used as symmetry planes to reduce the number of design variables from 1520 to 380.

Fig. 15
figure 15

Three-point bending crash case 2

Full size image
Fig. 16
figure 16

Design domain for crash case 2

Full size image
Fig. 17
figure 17

Symmetry planes to reduce the number of design variables

Full size image

As indicated in Fig. 15, the beam is impacted transversely by a pole with an initial velocity of 10 m/s and mass of 85 kg. Two ends of the beam are fully fixed (all degrees of freedom). The length of the beam is 800 mm and its cross-section is 80 × 120 mm 2. The thickness of the outer walls is 1.80 mm, which are not chosen as design variables. For the inner walls, they are regarded as design variables. The initial value for all design variables is 0.60 mm. The range of these design variables is set from 0.05 to 3.00 mm. If the thickness is less than 0.50 mm, it is deleted. The constraint of this optimization problem is the maximum displacement of the pole in y-direction. The initial response of the constraint is 83.28 mm. The structure in the 3 point bending crash case 2 has one more outer wall than the structure of the 3 point bending crash case 1. This extra outer wall will prevent the structure from buckling when it is impacted by the pole. Moreover, the layouts of the inner walls of the two cases are different. In the 3 point bending crash case 1, the thickness is kept to be uniform in y-direction. In 3 point bending crash case 2, the thickness of the walls is the same as in x- direction. The difference in topology results in the different initial values of the displacements. The constraint limitation defined here is 60.00 mm (Table 6).

Table 6 Optimized results comparison between two methods (3P crash case 2)
Full size table

The values for the stopping index in HCATWS-1 and HCATWS-2 are shown in Table 7. The values of \(p_{1}^{*}\) and \(p_{2}^{*}\) are defined as in the 3 point bending crash case 1. The performance of HCATWS-1 and HCATWS-2 can be found in Figs. 18 and 19. HCATWS-1 stopped because the maximum number of evaluations is reached. HCATWS-2 stopped because \(p_{2}^{*}\) is higher than a predefined value 10. As shown in Table 6, the best design obtained by HCATWS-1 obtained at iteration 59 with a scaled mass of 0.611 while the best design obtained by HCATWS-2 has a scaled mass of 0.590 (iteration 34). This shows again that when the number of design variables is quite large, the new idea for the outer loop has a higher potential to lead to a lighter design. The displacement responses of the best designs obtained by both methods are just within the boundary. This reflects the idea that HCATWS tries to minimize the mass by pushing the displacement response to be just within the boundary.

Fig. 18
figure 18

HCATWS-1 optimization history for 3P crash case 2

Full size image
Fig. 19
figure 19

HCATWS-2 optimization history for 3P crash case 2

Full size image
Table 7 Parameters to define the convergence
Full size table

As can be seen in Fig. 18, although the number of design variables has increased a lot compared to the axial crash case, the number of evaluations required by the proposed method (HCATWS-2) is not increased significantly. This advantage is beneficial for automotive crashworthiness design where the simulation cost is high.

The thicknesses distribution for the optimized results obtained from HCATWS-1 and HCATWS-2 can be found in Figs. 20 and 21. The mass tends to be distributed to the part where the pole impacts the beam. It makes sense, because this part contributes strongly to energy absorption and prevents the beam from deforming too much in y direction. The mass also tends to be increased around the corner, while this part prevents local buckling (as indicated in Fig. 22). The topology change history for HCATWS-2 is shown in Fig. 23). In HCATWS-2 (Fig. 19), the first feasible design occurs in iteration 3 with its SEA (1.40 J/g). SEA is then maximized with the minimization of mass and final feasible design’s SEA is 1.68 J/g.

Fig. 20
figure 20

Optimized topology with HCATWS-1 for 3P crash case 2 (outer walls not shown)

Full size image
Fig. 21
figure 21

Optimized topology with HCATWS-2 for 3P crash case 2 (outer walls not shown)

Full size image
Fig. 22
figure 22

Deformation shape of the optimized result with HCATWS-2 for 3P crash case 2 (outer walls not shown)

Full size image
Fig. 23
figure 23

Topology evolution with HCATWS-2 for 3P crash case 2 (outer walls not shown)

Full size image

4 Manufacturing possibility

In the past, the difficulty in interpreting the optimized component obtained by topology optimization prevents its usage in industrial applications. However, the development of Additive Manufacturing (AM) in recent years fills the gap between topology optimization and application (Zegard and Paulino 2016). Additive Manufacturing is defined by a range of technologies that are capable of translating virtual solid model data into physical models in a quick and easy process (Gibson et al. 2014). These virtual solid model data are often generated by 3D computer aided design. AM machines use a layer-based approach to manufacture these 3D models and the various types of AM machines lie in what material they use, how the layers are created and how these layers are bound together (Gibson et al. 2014).

However, the optimized results from traditional element-based topology optimization might still have some difficulties related to manufacturing. For example, in Zegard and Paulino (2016), unnatural thinning at the ends of its optimized structure has to be avoided. They utilized a cubic weighting functions of the filter matrix with weight coefficients to solve this problem and concluded that the resultant structure is more possible for AM. Therefore, some special techniques have to be used to make the optimized design more manufacturable for AM. By contrast, the optimized topology from HCATWS can be more easily manufactured by AM.

5 Conclusion

An improved HCA for thin-walled structure is proposed in this paper. This method tries to homogenize the field variable and minimizes the mass at the same time. The efficiency of the algorithm is compared with a standard approach (LS-OPT) for axial crash case, where similar results are obtained by the new method with a significantly smaller number of FEA evaluations. The bi-section search within limited length outperforms first approach based on HCA for thin-walled structures (Duddeck et al. 2016) such that it has higher possibility to find a lighter design. The 3P bending crash case shows that even with a quite large number of design variables, the number of FEA evaluations for the convergence of the proposed method is not increased significantly. As discussed above, this method requires no gradient information for updating and it improves the structure fast even with large number of design variables. All these advantages are beneficial for automotive crashworthiness design.