1 Introduction

Topology optimization (Bendsøe and Kikuchi 1988) has not been applied only for macroscopic structural design but also for material microstructural design. Sigmund (Sigmund 1994) first employed an inverse homogenization method to tailor materials with prescribed constitutive parameters. Over the past decades, material design using topology optimization has undergone a remarkable development. Homogenization theory (Guedes and Kikuchi 1990) is the most commonly used method to account material heterogeneities and effective properties so as to assess the macroscopic performance. The key hypothesis of this theory is the assumption that the macroscopic characteristic is much larger than that of microscopic structure and the material is composed by the representative unit cell (RUC) periodically. By means of inverse homogenization and density-based topology optimization method, various extreme material properties are obtained by tailoring the architecture of constitution phases in RUC, including the extreme thermal expansion coefficients (Sigmund and Torquato 1997), extreme viscoelastic behavior (Andreassen and Jensen 2014; Huang et al. 2015), combined extreme stiffness and fluid permeability (Guest and Prévost 2006, 2007), and hyperelastic properties (Wang et al. 2014b). Some other typical topology optimization approaches such as ESO-type methods (Huang et al. 2011, 2012; Xia et al. 2016) and level-set methods (Amstutz et al. 2010; Challis et al. 2012; Wang et al. 2014a) also fall into this hot subject, all with the purpose of finding the best material layout within a given design domain which normally is the RUC in material design for specified objectives. A review on design of material microstructures has been recently presented in (Cadman et al. 2013; Xia and Breitkopf 2016).

Note that the topology optimization algorithms formulated in all above-mentioned works are typically gradient-based. Another effective method that requires no gradient information and utilizes cellular automata (CAs) is the hybrid cellular automaton (HCA) method (Tovar et al. 2004a). The CA is a discrete model inspired biologically (Chopard and Droz 1998; Patel 2007). One of the first application of CAs to structural design was presented by Inou et al. (1994, 1998), and the basic idea of this method is that the overall behavior one particular cell is governed by its neighbor neighbors. The HCA method is a CA technique which actually is not explicitly an optimization technique (Tovar et al. 2004b). The physical quantities at all lattices are updated simultaneously based on the local rules such that the material or structural topologies can be tailored to achieve the selected objectives (Kita and Toyoda 2000). During the past decade, structural optimization using the HCA has undergone a remarkable development (Abdalla and Gurdal 2004; Setoodeh et al. 2005, 2006; Tovar et al. 2006; Bochenek and Tajs-Zielinska 2015), and it has been demonstrated that the HCA method is an efficient and robust method in solving topology optimization problems (Tovar et al. 2007; Penninger et al. 2010).

This paper aims to extend the HCA method to the design of periodic microstructures of porous materials with extreme properties. The merits of the HCA method include effectiveness, gradient free and easy implementation with any numerical analysis method (Bochenek and Tajs-Zielinska 2013). In addition, existing works have shown that the used optimization parameters and algorithm could influence final results of material design (Huang et al. 2011; Sigmund 2000; Xia and Breitkopf 2015). With regard to homogenization, this work adopts an energy-based homogenized approach (Xia and Breitkopf 2015) which is based on average stress and strain theorems (Hashin 1983). In the following, the optimization model of material microstructural design using the HCA is described in Section 2. Section 3 gives several numerical examples on the design of periodic porous material with maximum bulk or shear modulus and negative Poisson’s ratio. Finally, conclusion is drawn in Section 4.

2 Material design using the HCA

2.1 Optimization model

The idea of the CA requires decomposition of the considered design domain (RUC) into a set of cells which is also the basic idea of finite element (FE) method. The CA cells and the FE meshes are coincident in this work. The values of elastic modulus of cells or elements are used as the design variables which are updated upon a local rule until convergence is met. Similar to topology optimization of homogeneous structures, the modulus at a cell/element i is defined using the modified solid isotropic material with penalization (SIMP) approach (Sigmund 2007),

$$ {E}_i\left({\rho}_i\right)={E}_{\min }+{\rho}_i^P\left({E}_0-{E}_{\min}\right) $$
(1)

where E 0 is the Young’s modulus of solid cell and E min is the Young’s modulus of void cell, which is a very small value to avoid the singularity of the stiffness matrix. P is the penalization exponent which is artificially introduced to make sure the material distribution converges to a black and white design. ρ i takes values between 0 and 1, and these limits denote the void cells and solid cells, respectively.

The optimization model using the HCA for extreme material properties can be formulated as follows:

$$ \underset{\rho }{ \min }:\kern0.3em c\left({E}_{ijkl}^H\left(\rho \right)\right) $$
(2)
$$ s.t.\kern0.7em :\kern0.3em {S}_i={\overline{C}}_i-{C}_i^{*}=0 $$
(3)
$$ :\kern0.3em \boldsymbol{K}\boldsymbol{U}=\boldsymbol{F} $$
(4)
$$ :0<{\rho}_i\le 1\kern0.4em ,\kern0.3em i=1,\dots, N $$
(5)

The objective c is a function of the homogenized material constitutive components. For example, the maximization of bulk modulus of 2D porous materials can be equivalently formulated into the minimization of

$$ c=-\frac{1}{4}\left({E}_{1111}^H+{E}_{1122}^H+{E}_{2211}^H+{E}_{2222}^H\right) $$
(6)

where E H ijkl is the homogenized stiffness tensor. And the maximization of shear modulus of 2D porous materials can be expressed as the minimization of

$$ c=-{E}_{1212}^H $$
(7)

In Eq. (3), C * i is the local strain energy target and \( {\overline{C}}_i \) is an average element strain energy value. This value is calculated as the average within a fixed proximity of each element in the design domain (Tovar et al. 2006) as

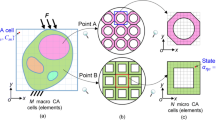
$$ {\overline{C}}_i=\frac{C_i+{\displaystyle \sum_{j=1}^n{C}_j}}{n+1} $$
(8)

where C j corresponds to the strain energy of a neighboring element and n is the number of neighbors defined in the CA neighborhood. Von Neumann neighborhood is employed in this work as illustrated in Fig. 1, and n equals to 4. The C i is defined as the element strain energy and also viewed as the element contribution to the objective function. For instance, when the objective function is chosen as bulk modulus, the C i denotes the element strain energy which corresponds to the bulk modulus. While it comes to maximizing material shear modulus, the C i denotes the element contribution to the shear modulus. Therefore, using the energy-based homogenized approach, the global homogenized material properties formulated in Eq. (2) is governed by discrete elements that interact with their neighbors. The use of average element strain energy instead of an actual value is analogous to the filter technique in classic topology optimization to avoid numerical instabilities such as checkerboard phenomenon and mesh dependency. Equation (3) achieves the zero-error condition between the average value of the strain energies and their optimum value implies that elements which are not void are saturated. When Eq. (3) is not satisfied, a local rule of HCA algorithm formulated in Section 2.2 updates the density design variable ρ i to make this condition hold true.

Fig. 1
figure 1

Two CA neighborhood layouts

Full size image

In Eq. (4), K is the global stiffness matrix, and U and F are the global displacement vector and external force vector, respectively. Under the assumption of periodicity boundary conditions (PBC), the global displacement field of the design domain (RUC) is evaluated by solving the equilibrium problem subjected to the uniform strain fields (three unit test strains for 2D cases, and six unit strains for 3D cases). The PBC in the FE model is directly imposed by constraining the nodal displacements on two opposite faces of the RUC, as also done in (Xia et al. 2003). More details about the numerical implementation of the energy-based homogenization to account for material constituent parameters based on the FEM can refer to (Xia and Breitkopf 2015).

As can be seen, the optimization model using the HCA drives the internal strain energy density of solid cells/elements in design domain to a saturated state. Then, the topology optimization problem considered here can be solved as finding the optimal layout of solid materials so that the extreme effective properties of considered material are satisfied. Note that the volume constraint of solid materials is implicitly presented in optimization model, and a post-processing step given in (Sigmund and Maute 2013) can be employed to minor adjust the final volume fraction.

2.2 Updating rule and convergence criterion

In this work, a local rule in the HCA approach is adopted to update the density design variables ρ i iteratively, and the material which is composed of final relative density distribution processes the extreme material property. The updating rule of the element relatively density is

$$ {\rho}_i\left(t+1\right)=\overline{\rho_i}(t)+\varDelta {\rho}_i(t) $$
(9)
$$ \varDelta {\rho}_i(t)={c}_P\times \kern0.6em {S}_i(t) $$
(10)
$$ \overline{\rho_i}(t)=\frac{\rho_i(t)+{\displaystyle \sum_{j=1}^n{\rho}_j(t)}}{n+1} $$
(11)

where t is the iteration number; \( \overline{\rho_i}(t) \) denotes the effective value of the density design variable which is averaged with neighborhood elements in the same way as it is done for the element strain energy in Eq. (8). Δρ i (t) presents the local control strategy which is the proportion control in the HCA approach. It can be seen that the local rule controls the material distribution in the design domain according the feedback signal S i (t) in Eq. (10). c P is a constant named as the proportional gain. Other updating control rules such as integral and derivative control methods can be find in (Kulakowski et al. 2007).

Typically, the convergence criteria for topology optimization using the HCA algorithm is based on the change in density design variable. Since the structural volume of the current design is determined by density design variable, the iterative optimization process converges when no further change in volume is possible (Tovar et al. 2007). This state can be expressed as

$$ \frac{\left|\varDelta V(t)\left|+\right|\varDelta V\left(t-1\right)\right|}{2\times {V}_0}\le \tau \kern0.9em \mathrm{where}\kern0.3em \varDelta V(t)=V(t)-V\left(t-1\right) $$
(12)

where V(t) and V 0 are the structural volume of t-th iteration step and of initial design, respectively. τ is the convergence tolerance which is set to be 0.01% in this work.

3 Numerical examples

As mentioned in the introduction, there is no unique solution for topological design of materials with extreme properties, and the used algorithm and parameters have influence on the final results. This work considers two initial guesses of the design domain (RUC) as shown in Fig. 2. Following (Huang et al. 2011; Amstutz et al. 2010), four elements and a circular region with void phase at the center of the RUC are named initial design 1 and 2, respectively. The RUC with dimensions 100 × 100 is discretized into 100 × 100 4-node quadrilateral plane stress elements. Young’s modulus and Poisson’s ration of solid phases are set to E = 1 and μ = 0.3, respectively.

Fig. 2
figure 2

Two initial designs

Full size image

3.1 Materials with maximum bulk modulus

Two initial designs of the RUC are employed here, and the penalization exponent P is set to 5. The iterative optimization processes converge with the volume fractions of the solid materials 0.493 and 0.575 starting from initial design 1 and 2, respectively. As for the result starting from initial 1, we used a post-processing step given in (Sigmund and Maute 2013) to satisfy the volume fraction constraint 50%. The final RUCs, corresponding periodic microstructures and their constitutive matrices obtained from two different initial designs are shown in Fig. 3, and the total iteration numbers are 156 and 152, respectively. The bulk moduli from initial designs 1 and 2 are, respectively, 0.180 and 0.224. To verify the developed method, the above problem using the same parameters is solved using the SIMP method (Xia and Breitkopf 2015) with density filtering and filter radius r = 2. When the volume fractions of solid materials are set to 0.5 and 0.575, the resulted bulk moduli are 0.164 and 0.210, respectively, which are lower than that of the proposed method. The corresponding Hashin-Strickman (HS) upper bounds (Hashin and Shtrikman 1963) are 0.185 and 0.229 which shows a good agreement with the present solutions.

Fig. 3
figure 3

Optimized RUC topologies (left), corresponding periodic microstructures (middle), and effective constitutive matrix (right) of materials with maximum bulk modulus starting two initial designs. a Initial design 1. b Initial design 2

Full size image

3.2 Materials with maximum shear modulus

In this section, the objective is to find optimal microstructures with maximum shear modulus and initial design 1 is employed. Two different penalization exponents 5 and 3 are considered. The iterative processes converge with the volume fractions 0.391 and 0.406, respectively. Figure 4 shows the final microstructures and corresponding effective elasticity matrices indicating that both solutions with clearly discernible topology layouts. The total iteration numbers are 37 and 50 and the shear moduli are 0.099 and 0.107, respectively.

Fig. 4
figure 4

Optimized RUC topologies (left), corresponding periodic microstructures (middle), and effective constitutive matrix (right) of materials with maximum shear modulus with two different penalization factors P. a P = 5. b P = 3

Full size image

3.3 Materials with negative Passion’s ratio

Here, we follow the relaxed function of negative Poisson’s ratio (NPR) proposed by Xia and Breitkopf (Xia and Breitkopf 2015) as

$$ c={E}_{1122}^H\mathit{\hbox{-}}{\beta}^t\left({E}_{1111}^H+{E}_{2222}^H\right) $$

where β is a fixed parameter defined as 0.8 and t is the iteration step. Apart from the constant, three remainder items in above c are all homogenized material constitutive. Therefore, the same strategy is employed to design materials with negative Poisson’s ratio as for bulk modulus or shear modulus. The penalization exponent is set to 3 here, and the convergence tolerance changes from 0.01 to 0.1%. The numerical procedure starting from initial design 2 converges to Fig. 5 after 57 iterations, and the final volume fraction and Passion’s ratio are 0.388 and −0.590, respectively. The iteration histories of the objective function and volume fraction for the negative Poisson’s ratio are illustrated in Fig. 6.

Fig. 5
figure 5

Materials with negative Poisson’s ratio starting from initial design 2: final topology (left), corresponding periodic microstructure (middle), and effective constitutive matrix (right)

Full size image
Fig. 6
figure 6

Iteration histories of the objective function, volume fraction, and intermediate microstructural topologies for the negative Poisson’s ratio (NPR)

Full size image

4 Conclusions

This paper has developed a new approach to material design for maximum bulk modulus, maximum shear modulus, and negative Passion’s ratio using the HCA method. Numerical examples have shown the proposed method is effective and robust. Various innovative material microstructural design results have been obtained by the proposed HCA method.