A novel stress influence function (SIF) methodology for stress-constrained continuum topology optimization

Abstract

This study presents a new stress influence function (SIF) methodology for continuum topology optimization under consideration of local strength failure. Firstly, the qp-relaxation criterion is involved to circumvent the stress singularity. To deal with the large-scale stress constraints in topology optimization, the local stress constraint is reflected in the objective along with the material volume by multiplication, and the weight of stress is characterized by stress influence function. Meanwhile, three types of stress influence functions are proposed for comparison. By means of the study on the characteristic of high-stress elements, the rationality of the SIF methodology is illustrated, in which the proposed method may achieve the full-stress state of high-stress element. Numerical examples are given to demonstrate the applicability and validity of the proposed methodology. It is shown that the proposed methodology can obtain reasonable results. Consequently, the proposed SIF methodology provides a novel strategy with high computational efficiency for topology optimization considering local strength failure.

1 Introduction

In the wake of developments in science and technology, topology optimization has become a popular design tool in engineering structures since the pioneering research by Bendsøe and Kikuchi (Bendsøe and Kikuchi 1988). Over the past few decades, a large number of studies on topology optimization have been published (Zhu et al. 2015; Mei and Wang 2004; Xie and Steven 1993; Rozvany et al. 1992; Wang et al. 2019; Xia et al. 2020; Qiu et al. 2019). However, most of the developments have concentrated on minimizing structural compliance with a given amount of material despite the fact that stress constraints are important (Duysinx et al. 2009). Most likely, several challenges arise when including stress constraints in topology optimization.

The first challenge is related to the so-called singular optima. Sved and Ginos (Sved and Ginos 1968) first observed it in truss topology optimization. They demonstrated on a simple three-bar truss problem that the optimum cannot necessarily be reached by gradient-based optimization as the stress constraints prevent reducing the cross-sectional area of the bar to zero. The “singular optima” were further studied in Cheng (Cheng and Jiang 1992) and Kirsch (Kirsch 1989; Kirsch 1990). In density-based topology optimization, the presence of singular optima can lead to large areas of the intermediate densities in the final design (Bendsøe 1989; Duysinx and Bendsøe 1998). To remedy this situation, the stress constraints are relaxed to make singular optima accessible. The commonly used relaxation techniques include smooth envelope functions (SEFs) (Rozvany and Sobieszczanski-Sobieski 1992), ε-relaxation (Cheng and Guo 1997), and the qp-approach (Wang et al. 2019; Bruggi 2008). Le et al. (Le et al. 2009) proposed a solid isotropic material with penalization (SIMP)–motivated stress definition to avoid singular optima.

The second challenge is the local nature of stress, which leads to large-scale constraints. The aggregation is usually applied to reduce the number of constraints by replacing the local stress constraints with a single integrated stress constraint. The common aggregation functions are P-norm (Duysinx and Sigmund 1998) and KS-function (Yang and Chen 1996). However, this global approach does not adequately control the local stress due to the accuracy of aggregation functions. Later, a lot of studies have been aimed at improving accuracy. For example, the block constraints (París et al. 2010) were applied as a compromise between including every local stress constraint and a single aggregation function. Le et al. (Le et al. 2009) and Holmberg et al. (Holmberg et al. 2013) studied the similar approaches in which the regional stress measures are based on the order of the stress values. Luo et al. (Luo et al. 2013) proposed an enhanced aggregation method in which the active set strategy is combined with constraint aggregation. These techniques can improve the accuracy of aggregation functions. Nevertheless, the number of aggregation functions is hard to determine to balance accuracy and computational costs. Zhang et al. (Zhang et al. 2013) studied the stress-constrained topology optimization in a level set framework and presented two novel global form stress constraints. Guo et al. (Guo et al. 2014) used the global measure in (Zhang et al. 2013) to deal with stress-constrained topology optimization involving multiphase materials.

Jeong et al. (Jeong et al. 2012) studied the stress-constrained topology optimization for ductile and brittle materials and considered various static failure criteria. Luo and Kang (Luo and Kang 2012) investigated the stress-based topology optimization of continuum structures exhibiting asymmetrical strength behaviors in compression and tension. Moon and Yoon (Moon and Yoon 2013) studied the stress-constrained topology optimization with geometrical nonlinearity in the framework of the element connectivity parameterization method. Takezawa et al. (Takezawa et al. 2014) investigated the stress-based topology optimization considering thermal stress.

Recently, the damage approaches were proposed for topology optimization with local stress constraints. In these studies, the material with local strength failure is considered damaged, and the stiffness of a damaged material is degraded. The optimization problem formulation using the damage approach does not include any constraints on the stress, and the absence of stress constraints circumvents some of the difficulties associated with stress constraints. James et al. (James and Waisman 2014) presented the strain softening to compute the damage at each material point and imposed a constraint on the approximate maximum damage. Amir (Amir 2016) used elasto-plasticity to describe the damage and imposed a single constraint on the total plastic strains to limit the total damage. These methods replace the local strength failure with damage and set a single constraint on the approximate maximum damage or total damage, which is a simple aggregation of local damage.

Differing from the “hard constraint” damage approach, some researchers proposed the “soft control” damage approach. Verbart et al. (Verbart and Langelaar 2015) used a simplified damage model to penalize the stiffness of elements that suffered local strength failure and imposed a single constraint on the relative compliance to drive the optimization towards a solution with minimal damage. Zelickman (Zelickman and Amir 2018) proposed a novel damage approach, in which the formulation involves minimization of the structure volume and a compliance constraint. As the damaged material is noneconomical, the optimizer will promote a design with a minimal number of damaged materials. The “soft control” damage approach provides an alternative to deal with the large-scale constraints in topology optimization, while the local stress is not well-controlled comparing with the “hard constraint” damage approach.

The damage approaches penalize local strength failure by degrading material, i.e., the stiffness of the material is set lower than its normal value. The nonlinear modeling for the material is required to consider the damage, and it can lead to high finite element computational cost. In this paper, a novel “soft control” method, i.e., the stress influence function (SIF) methodology, is proposed for topology optimization considering local strength failure. To evade the high cost of finite element computation, the local stress constraint is reflected along with the material volume by multiplication based on the idea of specific stiffness, and the weight of stress is characterized by stress influence function. The value of stress influence function increases sharply when the stress exceeds the strength limit to achieve the degradation for the specific stiffness of material with local strength failure. As the goal is to minimize the summation over multiplication of stress influence function and material volume, the material with local strength failure is less likely to appear in the optimal result, and hence, the local stress is implicitly constrained.

In the study, the constraints related to the strength limit is eliminated in the optimization formulation, and thus, the proposed method can achieve high efficiency in dealing with stress-constrained topology optimization. Moreover, the proposed method can achieve less stress variation in the optimal layout than the traditional methods. The remainder of this paper is structured as follows. The construction of element stress criteria is introduced in Section 2. Section 3 discusses the SIF methodology for continuum topology optimization considering local strength failure, in which the optimization formulation is given, and three types of stress influence functions are presented. Furthermore, the characteristic of the high-stress element is discussed, based on which the rationality of the proposed methodology is illustrated in Section 4. The sensitivities with respect to the density design variables are given by the adjoint method in Section 5. The validity and efficiency of the presented methodology are demonstrated in Section 6 through two topology optimization problems. Finally, some conclusions are drawn in Section 7.

2 Construction of element stress criteria

Distinguished from topology optimization with compliance constraint, layout design problems with restricted stress settings need to deal with the singular optima. Under such circumstances, some necessary techniques must be inserted to obtain structural stresses. In this section, the density filtering technique is introduced to get a well-posed topology optimization problem firstly, and then, the solid isotropic material with penalization (SIMP) is reviewed. Finally, the qp-relaxation criterion is applied to avoid singular optima.

2.1 Density filtering

Bruns and Torelli (Bruns and Tortorelli 2001) firstly introduced the density filtering technique to get a well-posed topology optimization problem. With the finite element discretization of density, the design element variables d are filtered to define the element densities ρ as follows:

$$ {\rho}_i=\frac{\sum \limits_{j\in {\Omega}_i}{w}_j{d}_j}{\sum \limits_{j\in {\Omega}_i}{w}_j}\kern0.3em \mathrm{with}\kern0.3em {w}_j=\frac{r_0-{r}_j}{r_0} $$

(1)

where Ω_i of element i stands for a set containing all finite elements j that lie within the filter radius r₀ of the element i as measured from their centroids.

The density filtering technique can avoid designs with narrow members, jagged edges, micro perforations, and sharp interfaces. Moreover, the method allows void elements to become solid elements more easily and vice versa, which enhances its ability to converge to the global optima. For more details, see the study in (Le et al. 2009).

2.2 Solid isotropic material with penalization model

After the density filtering, each element is attached with a density varied between zero and one, representing void and solid material. The governing equations for static equilibrium in terms of the element densities ρ are defined as

$$ \boldsymbol{K}\left(\boldsymbol{\rho} \right)\boldsymbol{u}\left(\boldsymbol{\rho} \right)=\boldsymbol{f} $$

(2)

where ρ = (ρ₁, ρ₂, ⋯, ρ_N)^T represents the vector with N element densities, K denotes the global stiffness matrix, u is the vector with nodal displacements, and f denotes the design-independent load vector.

The global stiffness matrix is composed out of the local element stiffness matrixes, while the elastic modulus of the element i can be obtained by employing the SIMP approach, namely,

$$ {E}_i={\rho}_i^p{E}_0 $$

(3)

where p > 1 is the penalization factor; E₀ is the Young modulus for fully solid material.

2.3 qp-relaxation criterion

As to each intermediate value of ρ_i, an appropriate interpolation scheme should be defined for the stress state to circumvent the singular optima. For this purpose, the “qp-relaxation” is applied to relax the stress involved in the intermediate density materials, namely

$$ {\boldsymbol{\sigma}}_i=\frac{{\boldsymbol{D}}_i{\boldsymbol{\varepsilon}}_i}{{\left({\rho}_i\right)}^q}=\frac{{\boldsymbol{D}}_i{\boldsymbol{Bu}}_i}{{\left({\rho}_i\right)}^q}=\frac{\rho_i^p{\boldsymbol{D}}_0{\boldsymbol{Bu}}_i}{{\left({\rho}_i\right)}^q}={\rho}_i^{p-q}{\boldsymbol{S}}_0{\boldsymbol{u}}_i $$

(4)

where σ_i = [σ_{i, x}, σ_{i, y}, σ_{i, z}, τ_{i, xy}, τ_{i, yz}, τ_{i, zx}]^T is the local stress vector of the element i in the center and ε_i corresponds to the strain vector in the elemental center; D_i is the elastic matrix with intermediate ρ_i and B is the strain matrix; D₀ and S₀ represent the elastic and stress matrixes with full solid; the exponent q < p is a real number.

The equivalent von Mises stress σ_{i, VM} can be solved by the stress vector as follows

$$ {\displaystyle \begin{array}{c}{\sigma}_{i, VM}=\sqrt{{\boldsymbol{\sigma}}_i^T\boldsymbol{\varPi} {\boldsymbol{\sigma}}_i}=\sqrt{{\left({\left({\rho}_i\right)}^{p-q}{\boldsymbol{S}}_0{\boldsymbol{u}}_i\right)}^T\boldsymbol{\varPi} {\left({\rho}_i\right)}^{p-q}{\boldsymbol{S}}_0{\boldsymbol{u}}_i}={\left({\rho}_i\right)}^{p-q}\sqrt{{\left({\boldsymbol{u}}_i\right)}^T{\varXi}_0{\boldsymbol{u}}_i}\\ {}=\sqrt{\frac{1}{2}\left[{\left({\sigma}_{i,x}-{\sigma}_{i,y}\right)}^2+{\left({\sigma}_{i,y}-{\sigma}_{i,z}\right)}^2+{\left({\sigma}_{i,z}-{\sigma}_{i,x}\right)}^2+6\left({\left({\tau}_{i, xy}\right)}^2+{\left({\tau}_{i, yz}\right)}^2+{\left({\tau}_{i, zx}\right)}^2\right)\right]}\\ {}\begin{array}{c}={\left({\rho}_i\right)}^{p-q}\sqrt{\frac{1}{2}\left[{\left({\overset{\sim }{\sigma}}_{i,x}-{\overset{\sim }{\sigma}}_{i,y}\right)}^2+{\left({\overset{\sim }{\sigma}}_{i,y}-{\overset{\sim }{\sigma}}_{i,z}\right)}^2+{\left({\overset{\sim }{\sigma}}_{i,z}-{\overset{\sim }{\sigma}}_{i,x}\right)}^2+6\left({\left({\overset{\sim }{\tau}}_{i, xy}\right)}^2+{\left({\overset{\sim }{\tau}}_{i, yz}\right)}^2+{\left({\overset{\sim }{\tau}}_{i, zx}\right)}^2\right)\right]}\\ {}={\left({\rho}_i\right)}^{p-q}H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)\end{array}\end{array}} $$

(5)

where ${\tilde{\boldsymbol{\sigma}}}_i={\left[{\tilde{\sigma}}_{i,x},{\tilde{\sigma}}_{i,y},{\tilde{\sigma}}_{i,z},{\tilde{\tau}}_{i, xy},{\tilde{\tau}}_{i, yz},{\tilde{\tau}}_{i, zx}\right]}^T$ is the local stress vector of the element i with full solid; Ξ₀ = S₀ΠS₀, and the constant matrix Π is given by

$$ \boldsymbol{\varPi} ={\left[\begin{array}{c}\frac{1}{2}\left(3\boldsymbol{I}-\boldsymbol{\alpha} \right)\kern0.5em {\boldsymbol{O}}_{3\times 3}\\ {}{\boldsymbol{O}}_{3\times 3}\kern0.5em 3\boldsymbol{I}\end{array}\right]}_{6\times 6} $$

(6)

in which I is the 3 × 3 identity matrix and α is the 3 × 3 matrix of ones.

3 Continuum topology optimization considering local strength failure

In most conventional stress-constrained continuum topology optimization, the local strength failure is considered in the constraint, and the aggregation function is always applied to deal with the large-scale stress constraints. However, the optimal settings may be problem-dependent and difficult to determine a priori. In the proposed SIF methodology, the local strength failure is considered in the objective along with the material volume. In this section, the optimization formulation based on the SIF methodology is given, and three types of stress influence functions are further discussed.

3.1 Optimization formulation based on SIF methodology

The common formulation of conventional topology optimization with stress constraints is stated in finite element form as follows:

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\min \\ {}\boldsymbol{\rho} \end{array}V=\sum \limits_{i=1}^N{\rho}_i{V}_i\\ {}\begin{array}{c}s.t.\kern0.5em \boldsymbol{Ku}=\boldsymbol{f}\\ {}{\sigma}_{i, VM}\le {\sigma}_{\mathrm{lim}}\\ {}\begin{array}{c}0<\underset{\_}{\rho}\le {\rho}_i\le 1\\ {}i=1,2,\cdots, N\end{array}\end{array}\end{array}} $$

(7)

where N is the number of elements; V_i denotes the volume of the element i with full solid; σ_lim is the limit stress; $\underset{\_}{\rho }={10}^{-3}$ is set as the lower limit of the design element variables for avoiding singularity of the elemental stiffness matrixes caused by zero density values.

In the study, the SIF methodology is proposed for the topology optimization considering local strength failure, in which the stress constraint is reflected by the stress influence function. The formulation of topology optimization based on the SIF methodology is expressed as follows:

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\min \\ {}\boldsymbol{\rho} \end{array} VS=\sum \limits_{i=1}^N{VS}_i=\sum \limits_{i=1}^N\gamma \left({\sigma}_{i, VM}\right){\rho}_i{V}_i\\ {}\begin{array}{c}s.t.\kern0.5em \boldsymbol{Ku}=\boldsymbol{f}\\ {}\begin{array}{c}0<\underset{\_}{\rho}\le {\rho}_i\le 1\\ {}i=1,2,\cdots, N\end{array}\end{array}\end{array}} $$

(8)

where VS_i = γ(σ_{i, VM})ρ_iV_i denotes the multiplication over material volume and stress influence function γ(σ_{i, VM}) of the element i.

The proposed optimization model in (8) is different from the conventional optimization formulation in (7). In the conventional model, the local strength failure is considered in the constraint, while the proposed model considers the stress constraints in the objective, which is similar to the augmented Lagrangian method (da Silva and Cardoso 2016). Otherwise, the objective is the summation of “material volume items” and “stress constraint items” in the augmented Lagrangian method, while the proposed method takes the summation over the multiplication of “material volume item” and “stress constraint item” as the objective. Therefore, the sensitivity analysis is conducted only for the objective in the SIF methodology, instead of each stress constraint. Consequently, the proposed SIF methodology can achieve higher efficiency in handling large-scale stress-constrained topology optimization.

3.2 Three types of stress influence functions

In the SIF methodology, the weight of stress is characterized by stress influence function in the objective, and thus, a proper stress influence function is significant. On the one hand, the value of γ should be greater than unity to penalize the local strength failure when the stress exceeds the limit. On the other hand, the value is equal to unity when the material is within the strength limit. In summary, the function γ satisfies the condition below:

$$ \left\{\begin{array}{c}\gamma \left({\sigma}_{i, VM}\right)>1,\kern0.5em \mathrm{if}\ {\rho}_i\in \left\{{\rho}_i\left|{\sigma}_{i, VM}\right.>{\sigma}_{\mathrm{lim}}\right\}\ \\ {}\begin{array}{cc}\gamma \left({\sigma}_{i, VM}\right)=1,& \mathrm{if}\ {\rho}_i\in \left\{{\rho}_i\left|{\sigma}_{i, VM}\right.\le {\sigma}_{\mathrm{lim}}\right\}\end{array}\end{array}\right. $$

(9)

To achieve strong penalization on the local strength failure, the value of γ should be large enough when the stress exceeds the strength limit. Moreover, considering the gradient-based optimization is used to solve the problem, the function γ should be at least first-order differentiable, and monotonically increasing once the stress exceeds its allowable value.

The proper function satisfying all the above conditions is hard to search, while many functions partially meet these criteria. In the study, three types of stress influence functions are proposed for comparison, in which the value of γ increases sharply to strongly penalize the local strength failure.

The first function, named as SIF-1, is defined as follows:

$$ \gamma \left({\sigma}_{i, VM}\right)=\left\{\begin{array}{c}1,\kern0.5em \mathrm{if}\ {\sigma}_{i, VM}\le {\sigma}_{\mathrm{lim}}\\ {}{e}^{\alpha \left[{\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^p-1\right]}\begin{array}{cc},& \mathrm{if}\ {\sigma}_{i, VM}>{\sigma}_{\mathrm{lim}}\end{array}\ \end{array}\right. $$

(10)

where α, P > 0 are the parameters which can control the steepness of function γ₁. The SIF-1 is an exponential function, which is similar to one item in the K-S aggregation function. The index is a power function, which is similar to the P-norm aggregation function. The SIF-1 meets all the above criteria except the first-order differentiable condition in σ_{i, VM} = σ_lim.

To satisfy the first-order differentiable condition, the second stress influence function, named as SIF-2, is proposed as:

$$ {\gamma}_2\left({\sigma}_{i, VM}\right)={e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P} $$

(11)

The material within the strength limit is also penalized in (11), and thus, the criterion in (9) is not satisfied in SIF-2.

To reduce the penalization for the material within the strength limit, the third function, named as SIF-3, is proposed as follows:

$$ {\gamma}_3\left({\sigma}_{i, VM}\right)=\left\{\begin{array}{c}{e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^{P^{\hbox{'}}}},\kern0.5em \mathrm{if}\ {\sigma}_{i, VM}\le {\sigma}_{\mathrm{lim}}\\ {}\begin{array}{cc}{e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P},& \mathrm{if}\ {\sigma}_{i, VM}>{\sigma}_{\mathrm{lim}}\end{array}\end{array}\right. $$

(12)

where P^′, P > 0 are the index parameters which can control the steepness of the function. By setting P^′ > P, the penalization for material within the strength limit can be reduced to some degree.

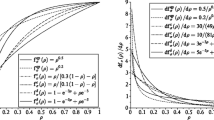
The comparison of SIF-1, SIF-2, and SIF-3 is exhibited in Fig. 1. For the material within the strength limit, i.e., σ_{i, VM}/σ_lim < 1, γ₂(σ_{i, VM}) is greater than γ₃(σ_{i, VM}), and γ₃(σ_{i, VM}) is greater than γ₁(σ_{i, VM}). For the material exceeding the stress limit, i.e., σ_{i, VM}/σ_lim ≥ 1, γ₂(σ_{i, VM}) is equal to γ₃(σ_{i, VM}), which is greater than γ₁(σ_{i, VM}). Remarkably, the SIF-2 is greatly similar to SIF-3 except for the slight difference in value.

Fig. 1

Comparison of SIF-1, SIF-2, and SIF-3

4 Validity interpretation of the proposed SIF methodology

In this section, we give an alternative validity interpretation of the proposed method. Firstly, a small example is given to illustrate the characteristic of high-stress elements in Section 4.1, by means of which the validity of the proposed methodology based on SIF-2 is discussed further in Section 4.2.

4.1 Study on the characteristic of high-stress elements

In this section, we discuss the characteristic of high-stress elements through a small numerical example. It should be noted that the stress-constrained topology optimization is not contained in the example. We only calculate the relaxed elemental stress and compare ∂σ_{i, VM}/∂ρ_i with ∂σ_{i, VM}/∂ρ_j(j ≠ i) in different layouts.

As shown in Fig. 2, a cantilever is fixed on two endpoints of the left side. And a force F is imposed on the lower tip of the right edge, in which F_x = 10N, F_y = 15N. The elastic modulus and Poisson’s ratio are set as E₀ = 70GPa, ν = 0.3 for the fully solid material. The design domain is discretized into 9 elements by using an element size of 1mm. By assigning density value of 0.2, 0.4, 0.6, 0.8, 1 to each element and combining all the 9 elements, one can obtain 5⁹ = 1953125 different layouts.

Fig. 2

Diagram for the small example

The goal is to calculate the sensitivities of each element stress to element densities in different layouts. Considering the few design variables, the finite difference method is applied to solve the sensitivities, in which the step size is set as Δρ_i =  − 0.01. To study the characteristic of element stress, R(σ_{i, VM}) is defined as the ratio of ${\displaystyle \begin{array}{c}\max \\ {}i\ne j\end{array}}\left|\partial {\sigma}_{i, VM}/\partial {\rho}_j\right|$ to |∂σ_{i, VM}/∂ρ_i| , namely,

$$ R\left({\sigma}_{i, VM}\right)=\frac{\begin{array}{c}\max \\ {}j\ne i\end{array}\left|\frac{\partial {\sigma}_{i, VM}}{\partial {\rho}_j}\right|}{\left|\frac{\partial {\sigma}_{i, VM}}{\partial {\rho}_i}\right|} $$

(13)

A total of 5⁹ × 9 = 17578125 ratios are calculated, and the results of R(σ_{i, VM}) on each element in different layouts are exhibited in Fig. 3.

Fig. 3

Results of R(σ_{i, VM}) on each element in different layouts

The horizontal coordinate represents the von Mises stress of element i, while the vertical coordinate represents the natural logarithm of R(σ_{i, VM}). For better exhibition, the horizontal and vertical coordinates are divided into 200 parts and thus make 200 × 200 = 40000 sub-regions. The value of ln(n_ij + 1) is embodied by color, and n_ij represents the number of samples in each sub-region, and the value of each color is shown in the color bar. In the color bar, the color blue represents a low value, while the yellow represents high value.

As shown in Fig. 3, the value of R(σ_{i, VM}) has a wide range for the low-stress element (σ_{i, VM} ≤ 500MPa), while the value is lower than e^−2.16 = 0.115 for the high-stress element (σ_{i, VM} > 500MPa). The results of the small example indicate that the absolute value of ∂σ_{i, VM}/∂ρ_i is 1/0.115 = 8.7 times larger than that of ∂σ_{i, VM}/∂ρ_j(j ≠ i) for high-stress element in all cases.

According to the experimental results, we assume that σ_{i, VM} is only related to its own density ρ_i for high-stress element. In the next section, a special case for the relation is assumed and the validity of the SIF methodology is illustrated based on the assumed relation.

4.2 Discussion about the validity of SIF methodology

As illustrated in Section 4.1, the stress of high-stress element is mostly related to itself. As a special case, the relationship between the stress of high-stress element and its own density is assumed as follows:

$$ {\sigma}_{i, VM}\approx {c}_i{\rho}_i^{t_i} $$

(14)

where c_i > 0 and t_i are the parameters related to the current layout. According to the sign of t_i, two cases are discussed below.

• (1) Case 1: t_i ≥ 0

In this case, the stress and the density are positively correlated, and thus, the stress influence function is also positively correlated with the density. Considering the material volume has a positive correlation with the element density, the density tends to be lower to obtain a better objective and reduce the element stress, and the element stress will be low when the density is close to its lower bound in virtue of the application of the qp-relaxation criterion.

• (2) Case 2: t_i < 0

The stress has a negative correlation with the density, while the material volume is positively correlated with the density. Under such circumstances, the full-stress design of the element can achieve the lightest configuration with stress constraints. To illustrate the relationship between VS_i and the density, the sensitivity of VS_i with respect to the density ρ_i is given as follows:

$$ \frac{\partial V{S}_i}{\partial {\rho}_i}=\gamma \left({\sigma}_{i, VM},{\sigma}_{\mathrm{lim}}\right){V}_1+{\rho}_i\frac{\partial \gamma \left({\sigma}_{i, VM},{\sigma}_{\mathrm{lim}}\right)}{\partial {\rho}_i}{V}_i $$

(15)

Substituting (14) and (11) into (15) yields

$$ \frac{\partial V{S}_i}{\partial {\rho}_i}\approx {e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_1+{\rho}_i{e}^{{\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}\alpha P{\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^{P-1}\frac{1}{\sigma_{\mathrm{lim}}}{c}_i{t}_i{\rho}_i^{t_i}{V}_i $$

(16)

To obtain the minimal value of VS_i, let ∂VS_i/∂ρ_i = 0 yields

$$ \frac{\partial V{S}_i}{\partial {\rho}_i}\approx {e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}\left(1+\alpha P{t}_i{\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P\right){V}_i=0 $$

(17)

The ratio of σ_{i, VM} to σ_lim can be solved from (17) as follows:

$$ \frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}=\sqrt[P]{\frac{1}{-\alpha {Pt}_i}} $$

(18)

By setting a sufficiently large parameter P, one can obtain

$$ \sqrt[P]{\frac{1}{-\alpha {Pt}_i}}\approx 1 $$

(19)

As shown in (19), the proposed method based on SIF-2 can make the high-stress element close to the full-stress state. However, the above discussion is carried out in the absence of lower and upper limits for density values. In practice, the density is located within zero and unity, and the high-stress element may not reach the full-stress state when the density reaches the boundary. Under such circumstances, the stress of high-stress element can be influenced by other elements and thus may achieve the full-stress design of the element.

Considering the property of the high-stress element is mainly affected by itself, the element stress constraint is reflected along with its volume, and the goal is to minimize the summation over multiplication of stress influence function and material volume. As the value of stress influence function increases sharply when the stress exceeds the strength limit, the material with local strength failure is less likely to appear in the final design, and hence, the element stress is implicitly constrained. In summary, the proposed SIF can achieve topology optimization under the consideration of local strength failure.

5 Sensitivity analysis

Generally, if the gradient-based algorithm is employed for solving the topology optimization problem, the sensitivity analysis is necessitated. The adjoint vector principle is applied to obtain the sensitivities of the objective function with respect to the density design variables. The sensitivity analysis for SIF-2 is given in this section, while the sensitivity analysis for SIF-1 and SIF-3 can be obtained in a similar way.

The sensitivity of the objective function in (8), with respect to a density design variable ρ_k, is given by

$$ \frac{\partial VS}{\partial {\rho}_k}=\gamma \left({\sigma}_{k, VM},{\sigma}_{\mathrm{lim}}\right){V}_k+\sum \limits_{i=1}^N{\rho}_i\frac{\partial \gamma \left({\sigma}_{k, VM},{\sigma}_{\mathrm{lim}}\right)}{\partial {\rho}_k}{V}_i $$

(20)

Substituting (11) into (20) yields

$$ \frac{\partial VS}{\partial {\rho}_k}={e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_k+\sum \limits_{i=1}^N{\rho}_i{e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_i\alpha P{\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^{P-1}\frac{1}{\sigma_{\mathrm{lim}}}\frac{{\partial \sigma}_{i, VM}}{\partial {\rho}_k} $$

(21)

Substituting (5) into (21) yields

$$ \frac{\partial VS}{\partial {\rho}_k}={e}^{\alpha {\left(\frac{\sigma_{k, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_k+\sum \limits_{i=1}^N{\rho}_i{e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_i\alpha P{\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^{P-1}\frac{1}{\sigma_{\mathrm{lim}}}\frac{\partial \left[{\left({\rho}_i\right)}^{p-q}H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)\right]}{\partial {\rho}_k} $$

(22)

The partial derivative $\partial \left[{\left({\rho}_i\right)}^{p-q}H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)\right]/\partial {\rho}_k$ can be solved as follows:

$$ \frac{\partial \left[{\left({\rho}_i\right)}^{p-q}H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)\right]}{\partial {\rho}_k}=\left(p-q\right){\left({\rho}_i\right)}^{p-q-1}\frac{\partial {\rho}_i}{\partial {\rho}_k}H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)+{\left({\rho}_i\right)}^{p-q}\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\rho}_k} $$

(23)

where

$$ \frac{\partial {\rho}_i}{\partial {\rho}_k}=\left\{\begin{array}{c}0,\kern0.5em if\ i\ne k\\ {}\begin{array}{cc}1,& if\ i\ne k\end{array}\end{array};\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\rho}_k}\right.=\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_i^T}{\left(\frac{\partial {\overset{\sim }{\sigma}}_i^T}{\partial \boldsymbol{u}}\right)}^T\frac{\partial \boldsymbol{u}}{\partial {\rho}_k} $$

(24)

The partial derivative $\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)/\partial {\overset{\sim }{\sigma}}_i^T$ and $\partial {\tilde{\boldsymbol{\sigma}}}_i^T/\partial \boldsymbol{u}$ can be calculated by

$$ \frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_i^T}=\left[\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_{i,x}},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_{i,y}},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\boldsymbol{\sigma}}}_{\boldsymbol{i},z}},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\tau}}_{i, xy}},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\tau}}_{i, yz}},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\tau}}_{i, zx}}\right] $$

(25)

and

$$ \frac{\partial {\overset{\sim }{\sigma}}_i^T}{\partial \boldsymbol{u}}={\left(\frac{\partial {\overset{\sim }{\sigma}}_i^T}{\partial {\boldsymbol{u}}_{\boldsymbol{i}}}\right)}^T\left(\frac{\partial {\boldsymbol{u}}_i}{\partial \boldsymbol{u}}\right) $$

(26)

where

$$ {\displaystyle \begin{array}{c}\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_{i,x}}=\frac{2{\overset{\sim }{\sigma}}_{i,x}-{\overset{\sim }{\sigma}}_{i,y}-{\overset{\sim }{\sigma}}_{i,y}}{2H},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_{i,y}}=\frac{2{\overset{\sim }{\sigma}}_{i,y}-{\overset{\sim }{\sigma}}_{i,z}-{\overset{\sim }{\sigma}}_{i,x}}{2H},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_{i,z}}=\frac{2{\overset{\sim }{\sigma}}_{i,z}-{\overset{\sim }{\sigma}}_{i,x}-{\overset{\sim }{\sigma}}_{i,y}}{2H}\\ {}\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\tau}}_{i, xy}}=\frac{3{\overset{\sim }{\tau}}_{i, xy}}{H},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\tau}}_{i, yz}},=\frac{3{\overset{\sim }{\tau}}_{i, yz}}{H},\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\tau}}_{i, zx}}=\frac{3{\overset{\sim }{\tau}}_{i, zx}}{H}\end{array}} $$

(27)

To solve the partial derivative ∂u/∂ρ_k, taking the derivative of the equilibrium equation K(ρ)u(ρ) = f with respect to a density design variable ρ_k, it follows

$$ \frac{\partial \boldsymbol{K}\left(\boldsymbol{\rho} \right)}{\partial {\rho}_k}\boldsymbol{u}\left(\boldsymbol{\rho} \right)+\boldsymbol{K}\left(\boldsymbol{\rho} \right)\frac{\partial \boldsymbol{u}\left(\boldsymbol{\rho} \right)}{\partial {\rho}_k}=0 $$

(28)

Solving ∂u(ρ)/∂ρ_k from (28) yields

$$ \frac{\partial \boldsymbol{u}\left(\boldsymbol{\rho} \right)}{\partial {\rho}_k}=-{\boldsymbol{K}}^{-1}\left(\boldsymbol{\rho} \right)\frac{\partial \boldsymbol{K}\left(\boldsymbol{\rho} \right)}{\partial {\rho}_k}\boldsymbol{u}\left(\boldsymbol{\rho} \right) $$

(29)

Substituting (23) and (29) into (22) yields

$$ {\displaystyle \begin{array}{c}\frac{\partial VS}{\partial {\rho}_k}={e}^{\alpha {\left(\frac{\sigma_{k, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_k+{\rho}_k{e}^{\alpha {\left(\frac{\sigma_{k, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_k\alpha P{\left(\frac{\sigma_{k, VM}}{\sigma_{\mathrm{lim}}}\right)}^{P-1}\frac{1}{\sigma_{\mathrm{lim}}}\left(p-q\right){\rho}_k^{p-q-1}H\left({\overset{\sim }{\boldsymbol{\sigma}}}_k\right)-\\ {}\sum \limits_{i=1}^N{e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^{P-1}\frac{V_i\alpha P}{\sigma_{\mathrm{lim}}}{\left({\rho}_i\right)}^{p-q+1}\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_i^T}{\left(\frac{\partial {\overset{\sim }{\sigma}}_i^T}{\partial \boldsymbol{u}}\right)}^T{\boldsymbol{K}}^{-1}\left(\boldsymbol{\rho} \right)\frac{\partial \boldsymbol{K}\left(\boldsymbol{\rho} \right)}{\partial {\rho}_k}\boldsymbol{u}\left(\boldsymbol{\rho} \right)\end{array}} $$

(30)

To solve (30), an adjoint vector λ is introduced, which should be the solution of the equation

$$ \boldsymbol{K}\left(\boldsymbol{\rho} \right)\boldsymbol{\lambda} ={\left(\sum \limits_{i=1}^N{\rho}_i{e}^{\alpha {\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_i\alpha P{\left(\frac{\sigma_{i, VM}}{\sigma_{\mathrm{lim}}}\right)}^{P-1}\frac{1}{\sigma_{\mathrm{lim}}}{\left({\rho}_i\right)}^{p-q}\frac{\partial H\left({\overset{\sim }{\boldsymbol{\sigma}}}_i\right)}{\partial {\overset{\sim }{\sigma}}_i^T}\left(\frac{\partial {\overset{\sim }{\sigma}}_i^T}{\partial \boldsymbol{u}}\right)\right)}^T $$

(31)

Substituting (31) into (30) yields

$$ {\displaystyle \begin{array}{c}\frac{\partial V}{\partial {\rho}_k}={e}^{\alpha {\left(\frac{\sigma_{k, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_k+{\rho}_k{e}^{\alpha {\left(\frac{\sigma_{k, VM}}{\sigma_{\mathrm{lim}}}\right)}^P}{V}_k\alpha P{\left(\frac{\sigma_{k, VM}}{\sigma_{\mathrm{lim}}}\right)}^{P-1}\\ {}-p{\rho}_k^{p-1}{\boldsymbol{\lambda}}_k^T{\overset{\sim }{\boldsymbol{K}}}_k\boldsymbol{u}\end{array}}\frac{1}{\sigma_{\mathrm{lim}}}\left(p-q\right){\rho}_k^{p-q-1}H\left({\overset{\sim }{\boldsymbol{\sigma}}}_k\right) $$

(32)

where λ_k, as the sub-vector of λ, depends on the k − th elemental location. ${\tilde{\boldsymbol{K}}}_k$ is the element stiffness matrix of the element k with full solid material.

6 Numerical examples

In this section, two numerical examples are presented to demonstrate the validity and efficiency of the developed SIF methodology. In these examples, the 4-node plane stress element is used. And the elastic modulus and Poisson’s ratio are set as E₀ = 70GPa, ν = 0.3 for the fully solid material. The FE treatment of the multipoint constraint is adapted to avoid the stress concentration effects.

The method of moving asymptotes (MMA) is used to solve topology optimization problems. The MMA algorithm was first proposed by Svanberg (Svanberg 2010) in 1987. The algorithm takes the first-order inverse Taylor expansion of the structural response at the current design point and establishes the convex linear explicit approximation of the original problem. A series of convex sub-problems are used to approximate the original problem, and the sub-problems are solved by dual method (Fleury and Braibant 2010). Consequently, the solution of the original problem is gradually approached by the solutions of the moving approximation sub-problems. As the stress in statically determinate structural analysis is linear approximation function of inverse design variables (Fleury 1993), the MMA can be used to solve topology optimization under local stress constraints. In the study, the stress influence functions have strong nonlinearity with respect to the elemental stress and an external move limit of 0.05 is set to bound the maximum absolute distance between an asymptote and the design variable. If the move limit is set as 0.1, the results trend to diverge in the examples. Therefore, the proposed method is sensitive to the value of moving limitation in the MMA.

Table 1 lists the characteristic parameters applied to the layout designs. In Table 1, the parameter α is adjusted by the numerical experiments. Firstly, the appropriate value of α is determined to be between 1 and 1.1 by the numerical experiments, in which the value of α is chosen as 1, 1.1, and 1.2. Then, we have chosen a few values 1, 1.02, 1.05, 1.08, and 1.1 for parameter α and conducted the corresponding experiments. The value of α is finally set as 1.08 according to the experimental results.

Table 1 Characteristic parameters applied to the layout designs

For the sake of convenience, the design objective is to minimize the ratio of the current objective to the structure volume with full solid, which it reads

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\min \\ {}\boldsymbol{\rho} \end{array} VSR=\left(\sum \limits_{i=1}^N\gamma \left({\sigma}_{i, VM},{\sigma}_{\mathrm{lim}}\right){\rho}_i{V}_i/\sum \limits_{i=1}^N{V}_i\right)\times 100\%\\ {}\begin{array}{c}s.t\ \boldsymbol{Ku}=\boldsymbol{f}\\ {}0<\underset{\_}{\rho}\le {\rho}_i\le 1\end{array}\end{array}} $$

(33)

6.1 Optimization of L-bracket

As illustrated in Fig. 4, the first example is the topology design for the well-known L-bracket, which is studied by Le in (Le et al. 2009). The design domain is clamped on the top side. An upward force F = 1000N is imposed on the upper tip of the right edge. The strength limit is set as σ_lim = 600MPa. Using an element size of 1mm, the design domain is discretized by 6601 nodes and 6400 elements.

Fig. 4

Schematic diagram for the geometry and FE model of the first example

For comparison’s purpose, the layout design based on Le’s method is also accomplished, in which a large number of P is chosen to achieve good approximation to the maximum stress. The iteration histories of volume ratio from the current layout to the fully solid pattern VR are summarized in Fig. 5, in which the details of the optimal solutions obtained by different methods are also exhibited.

Fig. 5

Iteration procedures of the topology optimization under different methods

As can be seen from Fig. 5, the optimal designs are all featured by a round inner corner, which is significant in eliminating the stress concentration. In Fig. 5a, a few elements of intermediate densities exist at the joints of the optimal design obtained by the Le method. In Fig. 5b–d, the proposed methodology based on different types of stress influence function can achieve quite different optimal results. Among these results, large areas of intermediate densities exist in the final design obtained by the SIF methodology based on SIF-1, while SIF-2 and SIF-3 can achieve final designs with few elements of intermediate densities, which indicates the penalization for material within strength limit is significant to obtain a reasonable design. For further comparison of the Le method and the proposed methodology based on SIF-2 as well as SIF-3, the stress results of the optimal layouts are exhibited in Fig. 6, and the details of optimization results are listed in Table 2. The stress is calculated in the central point of the element and thus the stress calculation is defined on the element level. The stress results shown in Fig. 6 are also plotted on element level.

Fig. 6

Stress results of the optimal layouts obtained by different methods

Table 2 Optimization results obtained by different methods

As shown in Fig. 6 and Table 2, the Le method, as well as the proposed methodology based on SIF-2 and SIF-3, can achieve well control on local stress, in which the maximum stress constraint violation range from 0.000458 to 0.0276. The number of high-stress elements (the red regions in Fig. 6) in the final design obtained by the SIF methodology is fewer than that by the Le method, while the Le method has a better performance than the SIF methodology in controlling the violated stresses (600.275MPa versus 637.833MPa and 616.54MPa). The proposed methodology based on SIF-3 can obtain a bit lighter optimal layout than the Le method (29.73% versus 30.83%), while the final design by SIF-2 is a bit heavier than that by the Le method (30.99% versus 30.83%).

In the conventional stress-constrained topology optimization like the Le method, the aggregation method is applied to deal with the large-scale stress constraints. For the aggregation function like the P-norm, a larger value of P is chosen to achieve good approximation to the maximum stress. The large value of P can lead to a sharp weight drop of other elemental stresses in the aggregation function and thus weaken the control on other elemental stresses. Therefore, many high-stress elements may exist in the optimal layout. In the proposed method, the elemental stress is considered along with the local elemental volume, and thus, the control on all elemental stresses is equally effective. Consequently, the number of high-stress elements obtained by the proposed method is fewer than that by the Le method.

From Figs. 5 and 6, it can be observed that some gray elements still exist along the optimized structure boundary in the results obtained by the SIF methodology. As the proposed method is developed in the SIMP framework, the gray elements may appear in the topology optimization configuration and the stress is calculated based on the elemental density. The existence of gray elements in the structure boundary make the elemental stress smaller than the case for full solid material. As the gray elements do not exist in engineering structure, the value of element stress will increase when the gray elements on structure boundary are changed to solid elements (in the postprocess). Actually, the existence of gray elements in the SIMP framework is inevitable unless some compulsory measures are taken. For stress-based topology optimization, the number of gray elements may be larger than that of stiffness-based topology optimization as the existence of gray elements may decrease the elemental stress. In the experimental tests, we achieved better layout with few gray elements by chosen appropriate values of parameters. Therefore, the optimal selection of the values of the parameters in the proposed method is dependent on the optimization problem in some degree and the selected values of parameters may be more suitable for the second example. The explicit geometry description is an alternative choice to avoid the gray elements. The explicit geometry description uses the position and size of the members to describe the topological configuration, and the gray elements do not exist in the optimization process. For more information about explicit geometry description in topology optimization, see the studies in (Zhang et al. 2018; Zhang et al. 2020).

In summary, the proposed methods based on SIF-2 and SIF-3 are effective ways to deal with the stress-constrained topology optimization problems, and the method based on SIF-3 has a better performance than SIF-2 in controlling the maximum stress and achieving a lighter optimal design (616.54MPa versus 637.833MPa, 29.73% versus 30.99%).

6.2 Optimization of corbel structure

As shown in Fig. 7, the design domain of the topology optimization is a corbel located at the middle height of the column. The domain is clamped on the top and bottom sides. An upward force F = 3000N is imposed on the upper edge of the corbel. Using an element size of 1.25mm, the design domain is discretized by 11,633 nodes and 11,328 elements.

Fig. 7

Schematic diagram for the geometry and FE model of the second example

The proposed methodology based on SIF-3 is applied to obtain the optimal design with three different material strength limits σ_lim = 480,   600,  and  720MPa. More details of optimal solutions are exhibited in Figs. 8 and 9 and Table 3, from which the following conclusions can be summarized:

• (1) As shown in Fig. 8, the proposed method based on SIF-3 can obtain reasonable results in different strength limit, in which the optimal designs have smooth inner corners on the corbel to eliminate the stress concentration. The length of the structure is relatively large for a lower strength limit so that the stress constraint can be satisfied. As listed in Table 3, less material is used for a higher strength limit (σ_lim : 480MPa → 720MPa,VR : 25.50 %  → 18.36%), and all the final designs almost exactly satisfy the stress requirements since the stress constraint violation of maximum stress in the structure are rather small (range from 0.0443 to −0.0134), which indicate the applicability of the proposed method based on SIF-3.

Fig. 8

Iteration procedures of volume ratio VR in different strength limits

Fig. 9

Stress results of the optimal layouts with different strength limits

Table 3 Comparisons of optimal results with different strength limits

• (2) As exhibited in Fig. 9, the maximum structural stress is a bit greater than the strength limit for σ_lim = 480MPa (501.24MPa > 480MPa), while for σ_lim = 600MPa and σ_lim = 720MPa, the maximum structural stress is a bit lower than the strength limit (597.14MPa < 600MPa and 710.33MPa < 720MPa). The ratio of maximum structural stress to strength limit is lower for a higher strength limit under the same stress influence function, which indicates the proposed SIF methodology is slightly problem-dependent.

For generality, the comparison of the proposed method and the Le method is also conducted for σ_lim = 600  MPa in this section. A relatively small value of P in P-norm aggregation function is chosen to guarantee the convergence. The details of the optimal solutions obtained by the two methods are exhibited in Figs. 10 and 11 and Table 4. As shown in Fig. 10, the optimal designs are featured by a round inner corner to eliminate the stress concentration. The topology configurations obtained by the two methods are similar and only some local small differences exist. As shown in Fig. 11, many low-stress elements (the green and blue regions) exist in the configuration based on the Le method, while less low-stress elements exist in the layout by the proposed method. The results indicate that the proposed method can achieve better utilization of materials than the Le method. As listed in Table 4, the maximum stress and the volume ratio of the optimal layout by the proposed method is lower than that by the Le method (597.14MPa versus 600.03MPa, 21.07% versus 25.86%).

Fig. 10

Topology configurations obtained by the proposed method and Le’s method

Fig. 11

Stress results of the optimal layouts obtained by the two methods

Table 4 Comparison of optimal results obtained by the two methods

In the example, a relatively small value of P is chosen in the Le method, and thus, the control on the other elemental stresses is relatively strong. The strong control on the elemental stresses may lead to the reduction of some elemental stresses, and thus, many low-stress elements may exist in the optimal layout. In the proposed method, as the elemental stress is considered in the stress influence function along with the elemental volume and the value of stress influence function changes a little for low-stress element, the density of low-stress element trends to decrease to zero to optimize the objective, and thus, low-stress elements are less likely to appear in the final design.

The proposed method is better than the Le method in weight reduction and maximum stress control in the example. However, it does not mean the proposed method is definitely better than the Le method. Actually, there are many adjustable parameters in the proposed method and the Le method. The results only illustrate that the proposed method is better than the Le method in the current parameters for the current optimization problem.

7 Conclusions

This paper presents the stress influence function (SIF) methodology for continuum stress-constrained topology optimization. To eliminate the large-scale stress constraints in topology optimization, the local stress constraint is reflected in the stress influence function along with the material volume by multiplication. Meanwhile, three types of stress influence functions are proposed for comparison. By means of a small example, the characteristic of high-stress elements is discussed, and the validity of the SIF methodology is illustrated further. It is proved that the proposed methodology may achieve the full-stress design of high-stress elements. Two topology optimization examples are finally presented to illustrating the validity of the proposed methodology. The results show that the present methodology can achieve reasonable designs under stress constraints. The variation of stress in the configuration obtained by the proposed method is less than the conventional stress-constrained topology optimization, i.e., the number of high-stress and low-stress elements in the configuration of the proposed method is lower than that of the conventional method.

In the study, only three possible stress influence functions are provided. Some other functions are urged to achieve better performance in controlling the local stress. In addition, the results of a small example indicate that the stress of high-stress element is mostly related to itself. On this basis, some other new approaches can be developed for stress-constrained topology optimization. Our further work will focus on the two respects.