Non-probabilistic robust continuum topology optimization with stress constraints

Abstract

This paper proposes a non-probabilistic robust design approach, based on optimization with anti-optimization, to handle unknown-but-bounded loading uncertainties in stress-constrained topology optimization. The objective of the proposed topology optimization problem is to find the lightest structure that respects the worst possible scenario of local stress constraints, given predefined bounds on magnitudes and directions of applied loads. A solution procedure based on the augmented Lagrangian method is proposed, where worst-case local stress constraints are handled without employing aggregation techniques. Results are post-processed, demonstrating that maximum stress of robust solutions is almost insensitive with respect to changes in loading scenarios. Numerical examples also demonstrate that obtained robust solutions satisfy the stress failure criterion for any load condition inside the predefined range of unknown-but-bounded uncertainties in applied loads.

1 Introduction

Topology optimization of continuum structures with local stress constraints was introduced in the literature by Duysinx and Bendsøe (1998) considering the density approach. Since then, several papers were developed aiming at overcoming well-known difficulties associated with this formulation: the local nature of stress failure criterion (Pereira et al. 2004), the singularity phenomenon (Cheng and Guo 1997; Duysinx and Bendsøe 1998), and the artificial stress concentration on jagged boundaries (Svärd 2015).

While these difficulties were not completely overcome in the scope of density-based approach, research advanced over parallel topics, such as the consideration of uncertainties in the stress-based formulations. These considerations naturally increase problem nonlinearity and, hence, the difficulty of obtaining topology optimization solutions. In a comprehensive literature review, we identified few papers addressing topology optimization problems of continuum structures with stress constraints under uncertainty (Luo et al. 2014; Holmberg et al. 2017; da Silva and Cardoso 2017; Thore et al. 2017; da Silva et al. 2018; da Silva and Beck 2018). These works can be classified into two categories: probabilistic and non-probabilistic.

In probabilistic approaches, uncertainties are quantified in terms of probabilities, and uncertain variables are represented as random variables. These approaches can be divided in two categories: reliability-based topology optimization (RBTO) and robust topology optimization (RTO). In the RBTO approach, stress constraints are imposed in terms of an allowable probability of failure for each point of stress computation (Luo et al. 2014; da Silva and Beck 2018). In the RTO approach, stress constraints are rewritten as a weighted sum between their expected value and standard deviation (da Silva and Cardoso 2017; da Silva et al. 2018). Both approaches are suitable for handling uncertainties described as random variables. RBTO approaches may be used when marginal probability density functions of random variables are available, whereas RTO approaches require only first- and second-order moments (expected values, standard deviations, and covariances).

Unfortunately, there are situations where there is no sufficient information to evaluate either marginal probability density functions or statistical moments. In some cases, only the bounds of uncertain variables are known. In such situations, one can formulate the problem in terms of these bounds in a non-probabilistic approach. Thus, the development of non-probabilistic approaches is indeed important, also for stress-based problems. Herein, we are not discussing which is the best approach for solving stress-constrained problems under uncertainty. We believe that both probabilistic and non-probabilistic approaches are complementary, and there are situations where one approach may be more suitable than the other. For a deeper discussion on probabilistic and non-probabilistic approaches for optimization under uncertainty, the reader is referred to Elishakoff and Ohsaki (2010).

Non-probabilistic methods for optimization under uncertainty are often formulated as a two-level optimization-anti-optimization problem (Elishakoff and Ohsaki 2010). When the unknown-but-bounded parameters are the only sources of uncertainty in the formulation, and for a deterministic objective function, the optimization problem can be formulated as the minimization (or maximization) of the objective function subjected to the worst-case scenario of constraints. The inner optimization problems solved for achieving the most critical constraints are sometimes called anti-optimization problems in the literature (Elishakoff et al. 1994; Lombardi 1998; Lombardi and Haftka 1998), hence this nomenclature is adopted in this paper.

In recent years, the interest in developing worst-case non-probabilistic approaches for solving continuum topology optimization problems under uncertainty has been growing. Our literature review revealed a variety of formulations developed to solve several kinds of continuum topology optimization problems under the effect of unknown-but-bounded uncertainties. In (Sigmund 2009; Wang et al. 2011b), a formulation is developed to handle uniform boundary variation on optimized topologies, through consideration of eroded and dilated topologies during optimization. This formulation was then extended to solve a variety of problems, like the design of photonic crystal waveguides with tailored dispersion properties (Wang et al. 2011a) and the design of robust electromechanical actuators (Qian and Sigmund 2013). In Guo et al. (2013), a formulation is proposed to solve compliance minimization and fundamental frequency maximization problems under arbitrary boundary variations considered via level set approach. In Guo et al. (2015), concurrent optimization of material and structure under load uncertainties is investigated in a multi-scale framework. In Holmberg et al. (2015), a formulation is proposed to solve the compliance optimization problem, where both load uncertainty due to the worst possible acceleration of applied masses and the weight of the structure itself are addressed. In Holmberg et al. (2017), a game theoretic framework is proposed to solve continuum topology optimization problems (including the stress-constrained problem) under load uncertainty. In Thore et al. (2017), a formulation is developed considering the ellipsoidal uncertainty model for solving continuum problems subjected to Euclidean norm for the stress constraints under load uncertainty. In Liu and Gea (2018), a formulation is developed to solve compliance-based problems under uncertainties in multiple applied loads.

In this work, a novel non-probabilistic RTO approach is proposed for solving stress-constrained topology optimization problems under unknown-but-bounded uncertainty in applied loads.

The main objectives/contributions of this work are:

• 1. Proposing a non-probabilistic robust formulation, based on the two-level optimization with anti-optimization framework, to handle the problem of volume minimization with local stress constraints under unknown-but-bounded uncertainties in magnitude and direction of applied loads;

• 2. Proposing a solution procedure, based on the augmented Lagrangian method (Birgin and Martínez 2014), to handle the worst-case local stress constraints without employing aggregation techniques;

• 3. Showing, through proper post-processing, that optimized structures are truly robust with respect to uncertainties in applied loads, in the sense that local stress constraints are satisfied for any load condition inside given bounds of uncertain variables.

The formulation proposed herein to solve (non-probabilistic robust) stress-constrained topology optimization problems is remarkably similar to the formulation developed in da Silva et al. (2018) for solving the probabilistic version of the robust optimization problem, and in da Silva and Beck (2018), for solving the reliability-based version of the same problem. Although the techniques proposed herein for solving the outer design optimization problem were already explored in da Silva et al. (2018) and da Silva and Beck (2018), it remains fundamental to demonstrate that they are also useful for solving the non-probabilistic robust topology optimization problem.

2 Deterministic topology optimization

In this work, the traditional density approach (Sigmund and Maute 2013) is employed to address the volume minimization problem subjected to local stress constraints.

The deterministic problem, in discrete form, can be written as Le et al. (2010) and Bruggi and Duysinx (2012)

$$\begin{array}{@{}rcl@{}} &&\underset{\boldsymbol{\rho}}{\mathrm{Min.}}V(\overline{\boldsymbol{\rho}}) = {\sum}_{e = 1}^{N_{e}} V_{e} f_{v}\left( \overline{\rho}_{e} \right)\\ &&\begin{array}{cc} \text{s. t.} ~ \frac{\sigma_{eq}^{(k)}(\overline{\boldsymbol{\rho}})}{\sigma_{y}} - 1 \leqslant 0 & \quad k = 1,2,...,N_{k}~, \\ \qquad \mathbf{K}(\overline{\boldsymbol{\rho}})\mathbf{U}(\overline{\boldsymbol{\rho}}) = \mathbf{F} & \\ 0 \leqslant \rho_{e} \leqslant 1 & \quad e = 1,2,...,N_{e} \end{array} \end{array} $$

(1)

where $\boldsymbol {\rho } \in \mathbb {R}^{N_{e}}$ are the design variables of the optimization problem, $V(\overline {\boldsymbol {\rho }})$ is the objective function of the optimization problem, which depends on the physical relative densities $\overline {\boldsymbol {\rho }} \in \mathbb {R}^{N_{e}}$, N_e is the number of elements in the finite element mesh, V_e is the structural volume of finite element e, $\sigma _{eq}^{(k)}(\overline {\boldsymbol {\rho }})$ is the von Mises equivalent stress at point k, σ_y is the yield stress, N_k is the number of points where the von Mises equivalent stress is computed, $\mathbf {K}(\overline {\boldsymbol {\rho }})$ is the global stiffness matrix, $\mathbf {U}(\overline {\boldsymbol {\rho }})$ is the global displacement vector, and F is the global load vector. The local stiffness matrix of element e is computed with the solid isotropic material with penalization (SIMP) approach, as $\mathbf {k}_{e}(\overline {\rho }_{e}) = \left (\overline {\rho }_{e}^{p} + \rho _{min} \right ) \mathbf {k}_{e}^{b}$, following Guest et al. (2011) and Tootkaboni et al. (2012), where ρ_min = 1 × 10^− 9 is adopted to ensure a well-conditioned system of linear equations, p > 1 is a penalization factor, and $\mathbf {k}_{e}^{b}$ is the stiffness matrix considering base material.

The objective function $V(\overline {\boldsymbol {\rho }})$ is chosen equal to $f_{v}\left (\overline {\rho }_{e} \right ) = 1 - \mathrm {e}^{-\delta _{v} \overline {\rho }_{e}} + \overline {\rho }_{e} \mathrm {e}^{-\delta _{v}}$, where $\delta _{v} \geqslant 0$ is the volume penalization parameter (da Silva and Beck 2018).

The von Mises equivalent stress at any point k is computed based on Duysinx and Bendsøe (1998), and can be written as

$$ \sigma_{eq}^{(k)}\left( \overline{\boldsymbol{\rho}}\right) = \sqrt{\boldsymbol{\sigma}_{k}^{T}\left( \overline{\boldsymbol{\rho}}\right) \mathbf{M} \boldsymbol{\sigma}_{k}\left( \overline{\boldsymbol{\rho}}\right) + \sigma_{min}^{2}}, $$

(2)

where the constant σ_min = 1 × 10^− 4σ_y is included in our implementation to ensure a positive von Mises equivalent stress when $\boldsymbol {\sigma }_{k}^{T}\left (\overline {\boldsymbol {\rho }}\right ) \mathbf {M} \boldsymbol {\sigma }_{k}\left (\overline {\boldsymbol {\rho }}\right ) \rightarrow 0$, in order to avoid numerical instabilities during the sensitivity analysis.

$\boldsymbol {\sigma }_{k}\left (\overline {\boldsymbol {\rho }}\right )$ is the stress vector at any point k, computed as

$$ \boldsymbol{\sigma}_{k}\left( \overline{\boldsymbol{\rho}}\right) = \overline{\mathbf{C}}_{k}(\overline{\rho}_{k}) \mathbf{B}_{k} \mathbf{u}_{k}(\overline{\boldsymbol{\rho}}), $$

(3)

and M is a constant matrix, defined as

$$ \mathbf{M} = \left[\begin{array}{ccc} 1 & -\frac{1}{2} & 0 \\ -\frac{1}{2} & 1 & 0 \\ 0 & 0 & 3 \end{array} \right], $$

(4)

for plane stress problems.

In (3), $\overline {\mathbf {C}}_{k}(\overline {\rho }_{k}) = f_{\sigma } \left (\overline {\rho }_{k} \right ) \mathbf {C}_{k}^{b}$ depends on the constitutive matrix of base material of the element which contains point k, $\mathbf {C}_{k}^{b}$; B_k is the strain-displacement transformation matrix evaluated at point k; and $\mathbf {u}_{k}(\overline {\boldsymbol {\rho }})$ is the local displacement vector of the element which contains point k. The local displacement vector can be associated with the global displacement vector through use of a localization operator H_k (Bathe 1996), such that $\mathbf {u}_{k}(\overline {\boldsymbol {\rho }}) = \mathbf {H}_{k} \mathbf {U}(\overline {\boldsymbol {\rho }})$.

In this work, we choose $f_{\sigma }^{\delta } \left (\overline {\rho }_{k} \right ) = 1 - \mathrm {e}^{-\delta _{\sigma } \overline {\rho }_{k}} + \overline {\rho }_{k} \mathrm {e}^{-\delta _{\sigma }}$ for stress constraint relaxation in both deterministic and robust formulations, where δ_σ > 0 is the stress interpolation parameter (da Silva and Beck 2018).

In this work, density filtering with Heaviside step function, originally proposed by Guest et al. (2004), is employed, in order to avoid checkerboard-like areas and to impose a minimum length scale in the solid phase of the optimized solution. Our implementation follows Sigmund (2007). The physical relative density of element e is computed as

$$ \overline{\rho}_{e} = 1 - \mathrm{e}^{-\delta \tilde{\rho}_{e}} + \tilde{\rho}_{e} \mathrm{e}^{-\delta}, $$

(5)

where δ is a penalization parameter which governs nonlinearity of the smoothed Heaviside projection, and $\tilde {\rho }_{e}$ is the filtered relative density of element e, obtained from a linear projection

$$ \tilde{\rho}_{e} = \frac{{\sum}_{n \in \vartheta_{e}} w(\mathbf{x}_{n}) V_{n} \rho_{n}}{{\sum}_{n \in \vartheta_{e}} w(\mathbf{x}_{n}) V_{n}}, $$

(6)

over the design variables ρ, in a circular neighborhood 𝜗_e, centered in element e, which contains all the elements whose center is within a radius R specified by the designer.

A linear weighting function is employed and defined as

$$ w(\mathbf{x}_{n}) = R - \| \mathbf{x}_{n} - \mathbf{x}_{e} \|, $$

(7)

where x_n contains the coordinates of the center of element n and x_e contains the coordinates of the center of the neighborhood 𝜗_e.

For δ = 0, in (5), a linear behavior between physical and filtered relative densities is obtained, $\overline {\rho }_{e} = \tilde {\rho }_{e}$, whereas for δ →∞, the Heaviside step function is approximated (Guest et al. 2004). Large values of δ are usually employed as an attempt to achieve crisp black and white solutions, reducing the blurred boundaries effect related to linear density filtering (Sigmund 2007). In this paper, parameter δ is updated through continuation approach, as described in Section 4.2.

3 Non-probabilistic robust topology optimization

When there is uncertainty in applied loads, optimization problem defined in (1) is no longer appropriate, since von Mises equivalent stresses become uncertain.

Considering a non-probabilistic robust framework, where magnitude and direction of applied loads are unknown-but-bounded, stress constraints should be given for the worst-case scenario, considering any magnitude and direction inside given bounds. In this paper, the non-probabilistic problem is addressed considering the classical nested two-level approach (Elishakoff et al. 1994; Guo et al. 2009), where the outer problem is devoted to finding the optimal topology subjected to worst-case stress constraints and the inner problems are devoted to finding the worst-case von Mises equivalent stresses (due to the worst sets of applied loads).

The outer optimization problem is defined as:

$$ \begin{array}{lll} \begin{array}{cc} \vspace{-12pt} \overset{\displaystyle \mathrm{Min.}}{{~}^{\boldsymbol{\rho}}} \end{array} & V(\overline{\boldsymbol{\rho}}) = {\sum}_{e = 1}^{N_{e}} V_{e} f_{v}\left( \overline{\rho}_{e} \right) & \\ \\ \begin{array}{c} s. t. \end{array} & \frac{\sigma_{eq}^{(k)}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)}\right)^{*},\left( \boldsymbol{\theta}^{(k)}\right)^{*}\right)}{\sigma_{y}} - 1 \leqslant 0 & \quad k = 1,2,...,N_{k} \\ & \mathbf{K}(\overline{\boldsymbol{\rho}})\mathbf{U}(\overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta}) = \mathbf{F}(\mathbf{f},\boldsymbol{\theta}) & \\ & 0 \leqslant \rho_{e} \leqslant 1 & \quad e = 1,2,...,N_{e} \end{array}, $$

(8)

where $\mathbf {f} \in \mathbb {R}^{N}$ and $\boldsymbol {\theta } \in \mathbb {R}^{N}$ are vectors which contain the magnitudes and directions of applied loads, respectively, N is the number of applied loads, and (f^(k))^∗ and (𝜃^(k))^∗ are optimal sets of magnitudes and directions of applied loads, respectively, which leads to the worst possible (maximal) von Mises equivalent stress $\sigma _{eq}^{(k)}\left (\overline {\boldsymbol {\rho }},\left (\mathbf {f}^{(k)}\right )^{*},\left (\boldsymbol {\theta }^{(k)}\right )^{*}\right )$, at point k.

The inner anti-optimization problems are written as maximization problems, defined for each point of stress computation k as

$$ \begin{array}{lll} \begin{array}{cc} \vspace{-12pt} \overset{\displaystyle \mathrm{Max.}}{{~}^{\mathbf{f},\boldsymbol{\theta}}} \end{array} & \sigma_{eq}^{(k)}\left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta}\right) \\ \\ \begin{array}{c} s. t. \end{array} & \mathbf{f}_{inf} \leqslant \mathbf{f} \leqslant \mathbf{f}_{sup} \\ & \boldsymbol{\theta}_{inf} \leqslant \boldsymbol{\theta} \leqslant \boldsymbol{\theta}_{sup} \end{array} $$

(9)

where the uncertain variables of the optimization problem, magnitudes f and directions 𝜃 of applied loads, are the design variables of the anti-optimization problems. In (9), f_inf and f_sup are the bounds for magnitudes, and 𝜃_inf and 𝜃_sup are the bounds for directions of applied loads.

The two-level solution procedure adopted to solve the non-probabilistic problem is very simple: the outer optimization problem (associated with the structural problem), (8), is solved as the deterministic problem, (1), except for the stress constraints, which are evaluated at the worst sets of applied loads, given bounds of uncertain variables. Thus, at each step of outer optimization, (8), one must find the worst possible scenario for the stress constraints by solving N_k anti-optimization problems, (9).

As discussed in Guo et al. (2009), global optimum solutions of anti-optimization problems are essential to guarantee robustness of outer problem solutions. The anti-optimization problems, (9), are in general non-convex; and guaranteeing global optimum for non-convex optimization problems is always a challenging task (Arora 2012). In this paper, each anti-optimization problem is solved with a sequential approach: 1) a simple grid search method (Rao 2009) is first employed; 2) from the best point obtained with the grid search method, a modified steepest descent (here ascent, since maximum stress is desired) method is employed, following implementation proposed in da Silva et al. (2018), until a specified tolerance is attained. In this paper, we use a simple convergence criterion over design variables of anti-optimization problems: maximum change on design variables of anti-optimization problem must be smaller than predefined tolerance specified by the designer, tol_f,𝜃. The outcome of the sequential grid-local search approach is considered as solution of the anti-optimization problem.

Obviously, there is no guarantee that a point obtained from this sequential procedure is a global optimum. However, from our experience with the proposed formulation, good solutions can be achieved. Indeed, numerical results obtained herein confirm that optimized topologies became fully robust with respect to uncertainties in applied loads.

The formulation developed in this paper is quite general, in the sense that solution algorithm employed to solve anti-optimization problems can be replaced, without loss of generality. An alternative, for instance, is employment of algorithms that absolutely guarantee global optimum under a specified tolerance. The authors refer the reader to Thore (2016), where a branch-and-bound algorithm is employed to find the worst possible P-norm von Mises stress value, given bounded uncertainty in applied load.

4 Solution procedure

In this section, details of solution procedure are presented. In Section 4.1, principle of superposition is shown, following da Silva and Beck (2018), but adding uncertainty in direction of applied loads. Principle of superposition is employed herein to speed evaluation of objective functions (von Mises equivalent stresses) and their sensitivities with respect to uncertain parameters (magnitudes and directions of applied loads), during the anti-optimizations. In Section 4.2, the augmented Lagrangian method, employed to solve the outer optimization problem, (8), is briefly explained.

4.1 Principle of superposition

Considering hypothesis of linear elasticity, principle of superposition holds (Bathe 1996; Bucalem and Bathe 2011). Figure 1 shows a solid body (in 2D) where principle of superposition is employed in order to determine global displacements in terms of f and 𝜃. Boundary S of solid body illustrated in Fig. 1 is split in two parts: S_u with prescribed displacements and S_f with prescribed tractions. For simplicity, we assume homogeneous essential boundary conditions on S_u. In this problem, S_f is split in two parts: $S_{f_{0}}$, subjected to surface traction 0; and $S_{f_{i}}$ subjected to concentrated load¹ with magnitude f_i and direction 𝜃_i.

Fig. 1

Illustration of principle of superposition in 2D solid body subjected to null prescribed displacements and concentrated load

Introducing the displacement-based finite element method, with density parameterization, for topology optimization, and generalizing this particular problem for N concentrated loads applied in non-intersecting boundaries $S_{f_{1}}$, $S_{f_{2}}$, ... , $S_{f_{N}}$, one can compute nodal displacements of problem on the left hand side of Fig. 1 as

$$ \mathbf{U}\left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right) = \sum\limits_{i = 1}^{N} f_{i} \left( \overline{\overline{\mathbf{U}}}_{i}^{1}(\overline{\boldsymbol{\rho}}) \cos(\theta_{i}) + \overline{\overline{\mathbf{U}}}_{i}^{2}(\overline{\boldsymbol{\rho}}) \sin(\theta_{i}) \right), $$

(10)

where nodal displacements $\overline {\overline {\mathbf {U}}}_{i}^{1}(\overline {\boldsymbol {\rho }})$ and $\overline {\overline {\mathbf {U}}}_{i}^{2}(\overline {\boldsymbol {\rho }})$ are computed considering unitary magnitude horizontal $\overline {\overline {\mathbf {F}}}_{i}^{1}$ and vertical $\overline {\overline {\mathbf {F}}}_{i}^{2}$ applied loads, respectively, associated with concentrated load i, as

$$ \mathbf{K}(\overline{\boldsymbol{\rho}}) \overline{\overline{\mathbf{U}}}_{i}^{j}(\overline{\boldsymbol{\rho}}) = \overline{\overline{\mathbf{F}}}_{i}^{j}, $$

(11)

for j = 1,2. Equation 11 can be seen as a set of auxiliary equilibrium equations, necessary to obtain the equilibrium configuration of the problem due to horizontal and vertical applied loads with unitary magnitude, $\overline {\overline {\mathbf {F}}}_{i}^{1}$ and $\overline {\overline {\mathbf {F}}}_{i}^{2}$, respectively, for i = 1,2,...,N.

Equation 10 is extremely useful in obtaining solutions of anti-optimization problems, since nodal displacements $\overline {\overline {\mathbf {U}}}_{i}^{1}(\overline {\boldsymbol {\rho }})$ and $\overline {\overline {\mathbf {U}}}_{i}^{2}(\overline {\boldsymbol {\rho }})$ are evaluated only at the beginning of each iteration, for each applied load. The factorization of the global stiffness matrix $\mathbf {K}(\overline {\boldsymbol {\rho }})$ can be performed only once, in the sense that only 2N substitutions are needed to obtain $\overline {\overline {\mathbf {U}}}_{i}^{1}(\overline {\boldsymbol {\rho }})$ and $\overline {\overline {\mathbf {U}}}_{i}^{2}(\overline {\boldsymbol {\rho }})$ for i = 1,2,...,N. Additional calculations are trivial and can be performed explicitly, like the evaluation of $\mathbf {U}\left (\overline {\boldsymbol {\rho }},\mathbf {f},\boldsymbol {\theta } \right )$ at any set of unknown variables f and 𝜃, computation of von Mises equivalent stress, and sensitivity analysis with respect to uncertain variables f and 𝜃.

In the mathematical developments performed in this paper, magnitude and direction of all applied loads are considered uncertain, without loss of generality. If there is a set of deterministic applied loads in the problem being addressed, or applied loads with uncertainty in either magnitude or direction only, one can attribute a deterministic value to f_i and/or 𝜃_i and employ (10) without any difficulty.

Generalization of results presented in (10), in order to explicitly include displacements due to deterministic applied loads, displacements due to applied loads with unknown magnitude only, and displacements due to applied loads with unknown direction only, is straightforward (da Silva and Beck 2018). This generalization is not performed herein, since the expression obtained in (10) is quite general in the sense that attribution of deterministic value to f_i and/or 𝜃_i can be easily performed.

4.2 Augmented Lagrangian method

In this paper, the outer optimization problem, (8), is solved with an augmented Lagrangian method. The augmented Lagrangian method consists in a sequence of optimization subproblems, where the solution of previous subproblem is used as a starting point for solving current subproblem (Birgin and Martínez 2014). Optimization subproblems are derived from original problem, in the sense that desired constraints of original problem are included in the objective function of optimization subproblems, resulting in the augmented Lagrangian function. The included constraints, which are now part of the objective function, are weighted by penalization parameters and are associated with Lagrange multipliers. After solving an optimization subproblem, Lagrange multipliers and penalization parameters are updated, then, another optimization subproblem is solved, and so on, until convergence.

In this work, only stress constraints are included in the augmented Lagrangian function, and only one penalization parameter is considered for the whole set of constraints. The augmented Lagrangian function associated with the outer problem, (8), is defined as

$$\begin{array}{@{}rcl@{}} L\left( \overline{\boldsymbol{\rho}},\underline{\mathbf{f}}^{*},\underline{\boldsymbol{\theta}}^{*},\boldsymbol{\mu},r \right) &=&V(\overline{\boldsymbol{\rho}})+ \frac{r}{2} \sum\limits_{k = 1}^{N_{k}} \left\langle\vphantom{\frac{\sigma_{eq}^{(k)}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)}\right)^{*},\left( \boldsymbol{\theta}^{(k)}\right)^{*}\right)}{\sigma_{y}}} \frac{\mu_{k}}{r}\right.\\ &&\left.+ \frac{\sigma_{eq}^{(k)}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)}\right)^{*},\left( \boldsymbol{\theta}^{(k)}\right)^{*}\right)}{\sigma_{y}} - 1 \right\rangle^{2}, \end{array} $$

(12)

where 〈⋅〉 = max(0,⋅).

Optimization subproblems are subjected to bound constraints, since they are not included in the augmented Lagrangian function. Optimization subproblems are defined as

$$ \begin{array}{lll} \begin{array}{cc} \vspace{-12pt} \overset{\displaystyle \mathrm{Min.}}{{~}^{\boldsymbol{\rho}}} \end{array} & L\left( \overline{\boldsymbol{\rho}},\underline{\mathbf{f}}^{*},\underline{\boldsymbol{\theta}}^{*},\boldsymbol{\mu}^{(c)},r^{(c)} \right) & \\ \\ \begin{array}{c} s. t. \end{array} & \mathbf{K}(\overline{\boldsymbol{\rho}})\mathbf{U}(\overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta}) = \mathbf{F}(\mathbf{f},\boldsymbol{\theta}) & \\ & 0 \leqslant \rho_{e} \leqslant 1 & \quad e = 1,2,...,N_{e} \end{array}, $$

(13)

where $\underline {\mathbf {f}}^{*} \in \mathbb {R}^{N \times N_{k}}$ and $\underline {\boldsymbol {\theta }}^{*} \in \mathbb {R}^{N \times N_{k}}$ are matrices containing all solutions of anti-optimization problems, namely (f^(k))^∗ and (𝜃^(k))^∗, at current step, r is the penalization parameter, $\boldsymbol {\mu } \in \mathbb {R}^{N_{k}}$ is a vector which contains the Lagrange multipliers, and μ_k is the Lagrange multiplier associated with k-th stress constraint. The index c indicates c-th optimization subproblem.

Lagrange multipliers and penalization parameter are updated by:

$$\begin{array}{@{}rcl@{}} &&\mu_{k}^{(c + 1)} \leftarrow \left\langle r^{(c)} \left( \frac{\sigma_{eq}^{(k)}\left( \left( \overline{\boldsymbol{\rho}}^{(c)}\right)^{*},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*}\right)}{\sigma_{y}} - 1\right) + \mu_{k}^{(c)} \right\rangle, \end{array} $$

(14)

and

$$ r^{(c + 1)} \leftarrow \left\lbrace \begin{array}{lll} \min\left( \gamma \ r^{(c)},r_{max}\right) & \quad & if \delta \sigma_{max}^{(c)} > \omega \ \delta \sigma_{max}^{(c-1)} \\ r^{(c)} & \quad & \textit{otherwise} \end{array} \right., $$

(15)

respectively, where $\left (\overline {\boldsymbol {\rho }}^{(c)}\right )^{*}$ is the solution of the c-th subproblem, (13), γ > 1 and ω < 1 are update parameters, r_max is an upper value of penalization parameter and $\delta \sigma _{max} = \left (\frac {\left (\sigma _{eq}^{max}\right )}{\sigma _{y}} - 1\right )$, where $\sigma _{eq}^{max}$ represents the maximum value among all computed von Mises equivalent stresses. In this paper, we choose to increase the value of penalization parameter r by a factor of γ only if maximum value of stress constraints reduces less than a factor of ω, i.e., if there is reasonable progress regarding feasibility of optimized topology, we do not update the penalization parameter, in order to not unnecessarily increase nonlinearity of optimization subproblems.

Convergence is reached when maximum change on design variables max |(ρ^(c))^∗−(ρ^(c− 1))^∗| becomes smaller than tol_ρ and feasibility is guaranteed, such that δσ_max < tol_σ.

After convergence, solution of the optimization problem is obtained for a specific value of δ, which consists in the parameter that controls nonlinearity of Heaviside projection, (5). As an attempt to alleviate blurred boundaries effect and achieve topologies with well-defined interface between solid and void, solution for large values of δ is usually required. In this paper, continuation approach proposed in da Silva et al. (2018) is employed, where the optimization problem is initially solved for δ = 0; then, the obtained topology is used as initial starting point for solving optimization problem with higher value of δ, and so on, until a large value δ_max defined by the designer is reached.

A steepest descent-based method is employed to solve optimization subproblems, as proposed in da Silva et al. (2018); convergence is reached either when maximum change in design variables becomes smaller than tolerance tol_sub imposed by the designer or when maximum number of iterations nit_max is reached.

Figure 2 shows the flowchart of the solution procedure.

Fig. 2

Flowchart of the proposed solution procedure

5 Sensitivity analysis

This section has the purpose of showing analytical first-order derivatives necessary to perform anti-optimization and optimization. In Section 5.1, derivative of von Mises equivalent stress is computed with respect to uncertain parameters f_m and 𝜃_m, that represent the m-th components of the vectors f and 𝜃, which contain the magnitudes and directions of applied loads, respectively, which are design variables of anti-optimization problems. In Section 5.2, derivative of augmented Lagrangian function is computed with respect to ρ_m, that represents the m-th component of the vector ρ, which contains the design variables of the outer optimization problem.

5.1 Anti-optimization problems

The derivatives of von Mises equivalent stress at point k, (2), with respect to uncertain variables f_m and 𝜃_m, are computed as

$$\begin{array}{@{}rcl@{}} &&\frac{\partial \sigma_{eq}^{(k)} \left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)}{\partial f_{m}} = \frac{\mathbf{u}_{k}^{T}\left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)}{\sigma_{eq}^{(k)} \left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)} \mathbf{B}_{k}^{T} \overline{\mathbf{C}}_{k}(\overline{\rho}_{k}) \mathbf{M} \overline{\mathbf{C}}_{k}(\overline{\rho}_{k}) \mathbf{B}_{k} \frac{\partial \mathbf{u}_{k}\left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)}{\partial f_{m}}, \end{array} $$

(16)

and

$$\begin{array}{@{}rcl@{}} &&\frac{\partial \sigma_{eq}^{(k)} \left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)}{\partial \theta_{m}} = \frac{\mathbf{u}_{k}^{T}\left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)}{\sigma_{eq}^{(k)} \left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)} \mathbf{B}_{k}^{T} \overline{\mathbf{C}}_{k}(\overline{\rho}_{k}) \mathbf{M} \overline{\mathbf{C}}_{k}(\overline{\rho}_{k}) \mathbf{B}_{k} \frac{\partial \mathbf{u}_{k}\left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)}{\partial \theta_{m}}, \end{array} $$

(17)

respectively.

Derivatives of local displacements $\mathbf {u}_{k}\left (\overline {\boldsymbol {\rho }},\mathbf {f},\boldsymbol {\theta } \right )$ with respect to f_m and 𝜃_m are directly computed through derivative of (10) and are written as

$$ \frac{\partial \mathbf{u}_{k}\left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)}{\partial f_{m}} = \mathbf{H}_{k}\overline{\overline{\mathbf{U}}}_{m}^{1}(\overline{\boldsymbol{\rho}}) \cos(\theta_{m}) + \mathbf{H}_{k}\overline{\overline{\mathbf{U}}}_{m}^{2}(\overline{\boldsymbol{\rho}}) \sin(\theta_{m}), $$

(18)

and

$$\begin{array}{@{}rcl@{}} &&\frac{\partial \mathbf{u}_{k}\left( \overline{\boldsymbol{\rho}},\mathbf{f},\boldsymbol{\theta} \right)}{\partial \theta_{m}} = f_{m} \left( \mathbf{H}_{k}\overline{\overline{\mathbf{U}}}_{m}^{2}(\overline{\boldsymbol{\rho}}) \cos(\theta_{m}) - \mathbf{H}_{k}\overline{\overline{\mathbf{U}}}_{m}^{1}(\overline{\boldsymbol{\rho}}) \sin(\theta_{m}) \right), \end{array} $$

(19)

respectively, where localization operator H_k is employed.

5.2 Outer optimization problem

Before presenting sensitivity analysis associated with the outer problem, (8), it is important to note that there is an implicit dependence of solutions of anti-optimization problems, namely $\underline {\mathbf {f}}^{*}$ and $\underline {\boldsymbol {\theta }}^{*}$, with respect to physical relative density $\overline {\rho }_{m}$ (Guo et al. 2009). In this paper, this dependence is not taken into consideration. Optimal design variables associated with k-th anti-optimization problem, namely (f^(k))^∗ and (𝜃^(k))^∗, are considered constant during a given iteration in optimization subproblems, (13). This assumption has three implications:

• 1. Derivative of (f^(k))^∗ and (𝜃^(k))^∗ with respect to $\overline {\rho }_{m}$ is assumed equal to 0;

• 2. This simplification saves numerical operations and computational time, since $\underline {\mathbf {f}}^{*}$ and $\underline {\boldsymbol {\theta }}^{*}$ are computed only in the beginning of each iteration, while solving the optimization subproblems;

• 3. With the proposed simplification, there is no guarantee of obtaining even a local minimum point, since $\underline {\mathbf {f}}^{*}$ and $\underline {\boldsymbol {\theta }}^{*}$ may oscillate near optimal solution. However, in the numerical problems addressed herein, no convergence problems were encountered.

This assumption has parallels with the cycle-based method described in Elishakoff and Ohsaki (2010), developed for decoupling the two-level optimization with anti-optimization, in the sense that design variables are kept constant while solving the anti-optimization problems. However, the procedure proposed herein is essentially different than cycle-based method, since anti-optimization problems are solved in each iteration of outer optimization, instead of solving optimization and anti-optimization problems sequentially until convergence, as in the cycle-based method (Elishakoff and Ohsaki 2010).

In the formulation proposed herein, although (f^(k))^∗ and (𝜃^(k))^∗ are kept constant during a given iteration in optimization subproblems, we update these values at every step of outer optimization, hence greatly reducing the gap between two consecutive combinations of worst possible sets of applied loads. This small gap ensures an almost continuum evolution of worst possible sets of applied loads during optimization, eliminating the need of employing additional load conditions to ensure numerical stability of the algorithm, as performed in Holmberg et al. (2017). In this way, we believe our procedure of keeping worst cases unaltered during a given iteration is reasonable.

In order to obtain the derivative of augmented Lagrangian, (12), with respect to design variables, adjoint technique is used. First, derivative of augmented Lagrangian with respect to physical relative density $\overline {\rho }_{m}$ is obtained; then, chain rule is applied to obtain derivative with respect to design variable ρ_m.

In the adjoint technique, auxiliary equilibrium equations, (11), are included in the augmented Lagrangian function, for j = 1,2, to facilitate mathematical manipulations. Hence, the augmented Lagrangian of outer problem, (8), can be written as

$$\begin{array}{@{}rcl@{}} L\left( \overline{\boldsymbol{\rho}},\underline{\mathbf{f}}^{*},\underline{\boldsymbol{\theta}}^{*},\boldsymbol{\mu},r \right) &=& V(\overline{\boldsymbol{\rho}}) \\ && + \frac{r}{2} \sum\limits_{k = 1}^{N_{k}} \left\langle \frac{\mu_{k}}{r} + \frac{\sigma_{eq}^{(k)}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*} \right)}{\sigma_{y}} - 1 \right\rangle^{2} \\ && + \sum\limits_{i = 1}^{N} \left( \boldsymbol{\lambda}_{i}^{1}\right)^{T} \left( \mathbf{K}(\overline{\boldsymbol{\rho}}) \overline{\overline{\mathbf{U}}}_{i}^{1}(\overline{\boldsymbol{\rho}}) - \overline{\overline{\mathbf{F}}}_{i}^{1} \right) \\ && + \sum\limits_{i = 1}^{N} \left( \boldsymbol{\lambda}_{i}^{2}\right)^{T} \left( \mathbf{K}(\overline{\boldsymbol{\rho}}) \overline{\overline{\mathbf{U}}}_{i}^{2}(\overline{\boldsymbol{\rho}}) - \overline{\overline{\mathbf{F}}}_{i}^{2} \right), \end{array} $$

(20)

where $\boldsymbol {\lambda }_{i}^{j}$, for i = 1,2,...,N and j = 1,2, are arbitrary vectors, since $\mathbf {K}(\overline {\boldsymbol {\rho }}) \overline {\overline {\mathbf {U}}}_{i}^{j}(\overline {\boldsymbol {\rho }}) - \overline {\overline {\mathbf {F}}}_{i}^{j} = \mathbf {0}$ for any $\overline {\boldsymbol {\rho }}$. The derivative of the augmented Lagrangian $L\left (\overline {\boldsymbol {\rho }},\underline {\mathbf {f}}^{*},\underline {\boldsymbol {\theta }}^{*},\boldsymbol {\mu },r \right )$ with respect to physical relative density $\overline {\rho }_{m}$ is not straightforward, but it can be easily performed based on detailed sensitivity analysis presented in da Silva and Beck (2018). Thus, in this paper, we do not show the step-by-step development of the sensitivity analysis, only the final derivative. The derivative of the augmented Lagrangian with respect to a physical relative density is written as

$$\begin{array}{@{}rcl@{}} \frac{\partial L}{\partial \overline{\rho}_{m}} &=& \frac{\partial V(\overline{\boldsymbol{\rho}})}{\partial \overline{\rho}_{m}} + \frac{h_{m} \left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(m)} \right)^{*},\left( \boldsymbol{\theta}^{(m)} \right)^{*},\mu_{m},r \right)}{\sigma_{eq}^{(m)}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(m)} \right)^{*},\left( \boldsymbol{\theta}^{(m)} \right)^{*} \right)} \\ &&\times g_{m}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(m)} \right)^{*},\left( \boldsymbol{\theta}^{(m)} \right)^{*} \right) \\ &&+ \sum\limits_{i = 1}^{N} \left[ \left( \boldsymbol{\lambda}_{i}^{1}\right)_{m}^{T} \frac{\partial \mathbf{k}_{m}(\overline{\rho}_{m})}{\partial \overline{\rho}_{m}} \left( \overline{\overline{\mathbf{u}}}_{i}^{1}\right)_{m}(\overline{\boldsymbol{\rho}}) \right. \\ &&+ \left.\left( \boldsymbol{\lambda}_{i}^{2}\right)_{m}^{T} \frac{\partial \mathbf{k}_{m}(\overline{\rho}_{m})}{\partial \overline{\rho}_{m}} \left( \overline{\overline{\mathbf{u}}}_{i}^{2}\right)_{m}(\overline{\boldsymbol{\rho}}) \right], \end{array} $$

(21)

with

$$\begin{array}{@{}rcl@{}} &&h_{m} \left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(m)} \right)^{*},\left( \boldsymbol{\theta}^{(m)} \right)^{*},\mu_{m},r \right)\\ &&\quad=\left\langle \mu_{m}+ r \left( \frac{\sigma_{eq}^{(m)}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(m)} \right)^{*},\left( \boldsymbol{\theta}^{(m)} \right)^{*} \right)}{\sigma_{y}} - 1 \right) \right\rangle \frac{1}{\sigma_{y}}, \end{array} $$

(22)

and

$$\begin{array}{@{}rcl@{}} g_{m} \left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(m)} \right)^{*},\left( \boldsymbol{\theta}^{(m)} \right)^{*} \right)&=& \mathbf{u}_{m}^{T} \left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(m)} \right)^{*},\left( \boldsymbol{\theta}^{(m)} \right)^{*} \right) \mathbf{B}_{m}^{T} \frac{\partial \overline{\mathbf{C}}_{m}(\overline{\rho}_{m})}{\partial \overline{\rho}_{m}} \\ &&\times \mathbf{M} \overline{\mathbf{C}}_{m}(\overline{\rho}_{m}) \mathbf{B}_{m} \mathbf{u}_{m} \left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(m)} \right)^{*},\left( \boldsymbol{\theta}^{(m)} \right)^{*} \right),\\ \end{array} $$

(23)

where $\left (\boldsymbol {\lambda }_{i}^{1}\right )_{m}$, $\left (\boldsymbol {\lambda }_{i}^{2}\right )_{m}$, $\mathbf {k}_{m}(\overline {\rho }_{m})$, $\left (\overline {\overline {\mathbf {u}}}_{i}^{1}\right )_{m}(\overline {\boldsymbol {\rho }})$, and $\left (\overline {\overline {\mathbf {u}}}_{i}^{2}\right )_{m}(\overline {\boldsymbol {\rho }})$ represent local quantities and can be obtained through use of localization operator H_m, as $\left (\overline {\overline {\mathbf {u}}}_{i}^{1}\right )_{m}(\overline {\boldsymbol {\rho }}) = \mathbf {H}_{m} \overline {\overline {\mathbf {U}}}_{i}^{1}(\overline {\boldsymbol {\rho }})$, for instance, allowing fast computation of the derivative of the augmented Lagrangian with respect to physical relative density.

It can be demonstrated that the arbitrary vectors $\boldsymbol {\lambda }_{i}^{1}$ and $\boldsymbol {\lambda }_{i}^{2}$, for i = 1,2,...,N, must be chosen in order to satisfy

$$\begin{array}{@{}rcl@{}} \mathbf{K}(\overline{\boldsymbol{\rho}}) \boldsymbol{\lambda}_{i}^{1} &=& - {\sum}_{k = 1}^{N_{k}} \frac{h_{k} \left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*},\mu_{k},r \right)}{\sigma_{eq}^{(k)}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*} \right)} \\ &&\times \left( f_{i}^{(k)}\right)^{*} \cos{\left( \theta_{i}^{(k)}\right)^{*}} \mathbf{H}_{k}^{T} \mathbf{a}_{k}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*} \right), \end{array} $$

(24)

and

$$\begin{array}{@{}rcl@{}} \mathbf{K}(\overline{\boldsymbol{\rho}}) \boldsymbol{\lambda}_{i}^{2} &=& - {\sum}_{k = 1}^{N_{k}} \frac{h_{k} \left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*},\mu_{k},r \right)}{\sigma_{eq}^{(k)}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*} \right)} \\ &&\times \left( f_{i}^{(k)}\right)^{*} \sin{\left( \theta_{i}^{(k)}\right)^{*}} \mathbf{H}_{k}^{T} \mathbf{a}_{k}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*} \right), \end{array} $$

(25)

respectively, where

$$\begin{array}{@{}rcl@{}} &&\mathbf{a}_{k}^{T} \left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*} \right)\\ &&\quad= \mathbf{u}_{k}^{T}\left( \overline{\boldsymbol{\rho}},\left( \mathbf{f}^{(k)} \right)^{*},\left( \boldsymbol{\theta}^{(k)} \right)^{*} \right) \mathbf{B}_{k}^{T} \overline{\mathbf{C}}_{k}(\overline{\rho}_{k}) \mathbf{M} \overline{\mathbf{C}}_{k}(\overline{\rho}_{k}) \mathbf{B}_{k}. \end{array} $$

(26)

Finally, since density filtering with Heaviside step function is employed, one can compute the derivative of the augmented Lagrangian with respect to design variable ρ_m through a chain rule (Sigmund 2007), such that

$$ \frac{\partial L}{\partial \rho_{m}} = \sum\limits_{n \in \vartheta_{m}} \frac{\partial L}{\partial \overline{\rho}_{n}} \frac{\partial \overline{\rho}_{n}}{\partial \tilde{\rho}_{n}} \frac{\partial \tilde{\rho}_{n}}{\partial \rho_{m}}, $$

(27)

where

$$ \frac{\partial \tilde{\rho}_{n}}{\partial \rho_{m}} = \frac{w(\mathbf{x}_{m})V_{m}}{{\sum}_{j \in \vartheta_{n}} w(\mathbf{x}_{j}) V_{j}}, $$

(28)

is obtained with the derivative of (6) and

$$ \frac{\partial \overline{\rho}_{n}}{\partial \tilde{\rho}_{n}} = \delta \mathrm{e}^{-\delta \tilde{\rho}_{n}} + \mathrm{e}^{-\delta}, $$

(29)

is obtained with the derivative of (5).

6 Numerical results

In this section, three example problems are solved, with several variants. For all problems, hypotheses of plane stress and linear elasticity under static loads are considered. In Section 6.1, two traditional versions of the L-shaped problem are solved, considering one applied load of deterministic magnitude and unknown direction: problem (L1) solved for load at the middle of the rightmost boundary, and problem (L2) solved for load at the top of the same boundary (Fig. 3). In Section 6.2, a variant of the L-shaped problem (L1) is solved (T-shaped problem), considering two applied loads in several loading scenarios, with and without uncertainty in magnitude and direction of applied loads. In Section 6.3, the U-shaped problem is solved, based in Amir (2017), considering two applied loads with uncertain magnitude. Solutions of the robust problem are compared with respective deterministic counterparts.

Fig. 3

L-shaped design domains considered in topology optimization with geometrical dimensions and boundary conditions

Input data associated with optimization solver are as follows: r⁽¹⁾ = 0.01, r_max = 10000, γ = 10, and ω = 0.8, associated with the augmented Lagrangian method, unless specified otherwise; tol_ρ = 0.1 and tol_σ = 0.01 as tolerances of outer problems; tol_f,𝜃 = 1 × 10^− 3 as tolerance of anti-optimization problems; tol_sub = 0.01 or maximum number of iterations of nit_max = 50 as stopping criteria for optimization subproblems. For additional information regarding subproblems solver, as the moving limits updating strategy, the reader may consult (da Silva et al. 2018).

The tolerance tol_ρ may be seem very large at first sight. However, note that this tolerance is applied over maximum change on design variables between solutions of two consecutive optimization subproblems. The authors verified that a smaller tolerance, in this case, would lead to much larger number of iterations, without significantly improving quality of the optimized solutions.

Input data associated with numerical model are as follows: p = 3 for stiffness parameterization (SIMP); δ_σ = 3 for stress interpolation; δ_v = 5 for volume penalization; δ⁽¹⁾ = 0 and δ^(d+ 1) ← min[(δ^(d) + 5),100], associated with continuation approach, related to density filtering with Heaviside step function, where index d indicates d-th iteration that satisfied convergence criteria of outer problems (maximum change on design variables and local feasibility of von Mises equivalent stresses).

Input data associated with material properties and geometrical characteristics are Young’s modulus of 1MPa, thickness of 1 mm, Poisson’s ratio of 0.3, yield stress of 16 kPa, and a filter radius of R = 0.02m, unless specified otherwise.

Additional data: initial value of design variables is ρ⁽¹⁾ = 1 for all problems. In order to properly scale the objective function, the volume is divided by the volume of one finite element V_e in the augmented Lagrangian function. Parameter r_max was reached while δ = 0, in the solution of every problem, such that for δ > 0 only the Lagrangian multipliers were updated at each subproblem iteration. Structural problems are discretized with traditional four-node bilinear isoparametric finite elements and stress is computed at the center of each finite element, since this is the superconvergent point for stress computation (Barlow 1976).

Topologies are illustrated with traditional gray scale: white represents no material ($\overline {\rho } = 0$) and black represents solid material ($\overline {\rho } = 1$). Von Mises stress graphs are illustrated with color images: red represents maximum normalized von Mises equivalent stress (≅ 1) and blue represents minimum stress (≅ 0).

Additional necessary data, as geometrical dimensions, discretization, and boundary conditions, are presented specifically for each problem, in next subsections.

6.1 L-shaped problems with one uncertain variable

As first example, two L-shaped problems are solved. Figure 3 shows design domains with respective dimensions. Structured meshes with 57,600 finite elements are employed to discretize design domains. Note that applied loads are distributed along either 0.06 m, problem (L1), or 0.05 m, problem (L2), in order to avoid stress concentration. Applied loads have deterministic magnitude of 0.3N.

Both L-shaped problems are solved considering four different loading scenarios, as shown in Figs. 4 and 5: (1) only one vertical deterministic load; (2) four deterministic load conditions (not simultaneously applied), with an angle of π/2 rad between them; (3) eight deterministic load conditions (not simultaneously applied), with an angle of π/4 rad between them; (4) direction of applied load is considered unknown, and anti-optimization is employed, considering 𝜃 ∈ [0,2π] rad. Optimized topologies for four and eight loads were obtained under the framework of stress-constrained topology optimization under multiple load conditions (Fancello and Pereira 2003), where stress constraints are satisfied for each load separately. Hence, these problems are solved considering 230,400 and 460,800 stress constraints, respectively (57,600 stress constraints associated with each load condition).

Fig. 4

Optimized topologies obtained as solution of stress-constrained L-shaped problem (L1) considering, from left to right, optimization with: 1 deterministic load; 4 deterministic load conditions; 8 deterministic load conditions; and anti-optimization with 𝜃 ∈ [0,2π] rad

Fig. 5

Optimized topologies obtained as solution of stress-constrained L-shaped problem (L2) considering, from left to right, optimization with: 1 deterministic load; 4 deterministic load conditions; 8 deterministic load conditions; and anti-optimization with 𝜃 ∈ [0,2π] rad

The anti-optimization problems associated with both robust L-shaped problems are initially evaluated for a grid with 10 equally spaced directions for the applied loads: 𝜃_grid = [π/5,2π/5,...,9π/5,2π]^T rad. The direction which gives the largest von Mises stress is then used as initial estimate for the local search method.

Solutions of all problems are post-processed considering 𝜃 ∈ [0,2π] rad, in order to verify maximum von Mises equivalent stress related to each angle 𝜃 of applied load. Post-processed stresses are also shown in Figs. 4 and 5; these are computed considering 1 × 10⁴ equally spaced angles in 0 ≤ 𝜃 ≤ 2π.

Analyzing topologies and post-processed von Mises equivalent stresses in Figs. 4 and 5, one can verify that maximum normalized von Mises equivalent stress, $\max \left (\sigma _{eq}^{max}/\sigma _{y}\right )$, decrease as the number of load conditions increase, up to the limiting case of optimization with anti-optimization. On the other hand, the larger the number of load conditions, up to the limiting case of optimization with anti-optimization, the larger the structural volume of the optimized topology. This is intuitively right, from a structural engineering point of view, since more material is needed in order to guarantee feasibility of optimized topology, considering a larger number of load conditions.

The topologies obtained for only one load condition, considering both problems (L1) and (L2), have no material between the vertical members, unlike the other topologies. Topologies obtained for four and eight load conditions, considering both problems (L1) and (L2), are the same, presenting one member between the vertical ones, differing only in shape. Robust solution for problem (L1) presents two crossed members between the vertical ones, whereas robust solution for problem (L2) presents only one member between the vertical ones, as solutions for four and eight load conditions.

These results demonstrate how deterministic designs are unstable and dependent on the parameters used in optimization, confirming results obtained in Beck and Gomes (2012) and Beck et al. (2015) for simpler design optimization problems. Even when several load conditions are considered (up to eight deterministic load conditions in both of these examples), feasibility of optimized structure can only be guaranteed for the load conditions for which the topology was designed, as clearly seen in Figs. 4 and 5, for four load conditions, where stress constraints are satisfied for 𝜃 = 0.0π,0.5π,1.0π, and 1.5π rad. Any perturbation in the load conditions could cause failure of the structure, as demonstrated by post-processing. The only solutions that resulted truly robust with respect to uncertainty in direction of applied load are the solutions of topology optimization with anti-optimization, for which maximum normalized von Mises equivalent stresses are 1.004 for problem (L1) and 1.009 for problem (L2); hence, maximum von Mises stresses are 0.4% and 0.9% higher than yield stress, respectively, being smaller than specified tolerance tol_σ = 1%.

Moreover, solution of deterministic problems considering several load conditions is rather difficult, due to the necessity of adjusting penalization parameter associated with the augmented Lagrangian method. In this work, penalization parameter r and its maximum value r_max were divided by the number of load conditions, in order to guarantee well-conditioned optimization subproblems.

Figure 6 shows the von Mises equivalent stress graphs for the deterministic (subjected to one load condition) and robust optimized structures. The stress graphs related to the deterministic structure are computed considering the deterministic load condition, whereas the robust stress graphs are computed using the worst possible set of applied loads.

Fig. 6

Deterministic and worst-case von Mises stress distributions for the L-shaped (L1) and (L2) optimized deterministic and robust solutions, respectively

Analyzing the stress graphs, one can verify that both deterministic and robust solutions resulted in stressed structures. Moreover, all solutions successfully avoided the sharp corner on the design domain: the optimized structures show rounded corners in the re-entrant corner region and, more importantly, the stress constraints are satisfied in these regions.

Table 1 shows total number of iterations necessary for convergence, for problems (L1) and (L2). It is verified that total number of iterations for solving robust problems is almost twice the number of iterations for solving traditional deterministic problem, for only one load condition. This additional number of iterations is justified since we are handling with a much more challenging problem, where each local stress constraint must be satisfied for the worst direction, given by a continuum range of load directions.

Table 1 Total number of iterations necessary to reach convergence for problems (L1) and (L2)

Figure 7 shows history of convergence of deterministic (for one load condition) and robust solutions, of the problem (L1). One can verify, at first sight and despite the total number of iterations, that the graphs of the robust solution are similar to the graphs of the deterministic solution, in the sense that both graphs exhibit the same behavior.

Fig. 7

Convergence history of problem (L1): deterministic (left) and robust (right)

Since a small penalization parameter, r⁽¹⁾, is employed to start the optimization process, the stress constraints have a small influence over the augmented Lagrangian function (see (12)), and hence, the optimization is dominated by the volume minimization. This phenomenon is clearly seen in the volume graphs, where the structural volumes reach a very small fraction (≅ 10%, from the graphs) in a few iterations.

Within the first iterations, one can see very large stress values (up to sixteen times the yield stress), as well as some oscillatory behavior in the stresses, which is also explained by the low influence of the stress constraints over the augmented Lagrangian function. In the initial stages of the optimization process, after the Lagrange multipliers and penalization parameter are updated a few times, the weight of the stress constraints over the augmented Lagrangian function is increased, directly affecting behavior of the numerical procedure, which starts becoming stress dominated. The effect caused by increasing the influence of stress constraints over the objective function is verified in both graphs: the maximum von Mises equivalent stress starts decreasing, while the structural volume fraction starts increasing.

From the stress convergence graphs, one can verify that, after the initial stabilization phase, the maximum von Mises stresses decrease in a very stable and smooth manner, without much oscillations. After the maximum normalized stresses get close to 1, one can verify only one stress peak per stress graph: next to 1100 iterations in the deterministic solution, and next to 1500 iterations in the robust solution. These stress peaks indicate the first stage of the optimization process is complete, i.e., the solution of the optimization problems considering the linear density filter (δ = 0) is reached. From this point on, the smoothed Heaviside step is employed to reduce the blurred boundaries effect. Since the employed Heaviside function is a dilation operator (Sigmund 2007), at the first time the Heaviside projection is employed the topology dilates and its boundary hits the re-entrant corner of the design domain, leading to a small stress peak. As one can see in the stress graphs, within a few iterations, the algorithm overcomes this issue, and the maximum normalized stress is reduced again, until reaching a value next to 1. The dilation effect is also observed in volume graphs, where volume increases at the same time that a small stress peak occurs. After occurrence of this small peak of stress, the procedure continues until the maximum value of δ is reached, and the convergence criteria are satisfied.

Regarding computational cost, robust problems are surely more costly than the deterministic ones. In the approach adopted herein for solving the non-probabilistic robust problems, worst-case stress constraints are found at the beginning of each iteration, which can lead to high computational cost if there is no use of parallel computing.

Although not employed in our implementations, the use of parallel computing can greatly improve computational efficiency associated with finding the whole set of worst-case stress constraints, at the beginning of each iteration. Once anti-optimization problems, (9), are independent of each other, and can be solved simultaneously, the use of parallel computing is very effective in reducing total computation cost, as demonstrated in Gurav et al. (2005) for the design of MEMS subjected to unknown-but-bounded uncertainties.

Also, since principle of superposition is employed, computational cost for solving a given anti-optimization problem becomes negligible, since there is no need for solving equilibrium equations in order to evaluate von Mises equivalent stress and their sensitivities with respect to uncertain variables at each iteration of anti-optimization.

6.2 T-shaped problem with up to four uncertain variables

The second problem solved herein is a variant of the L-shaped problem (L1). The design domain consists in a mirrored variant of L-shaped domain, as shown in Fig. 8. A structured mesh with 115,200 finite elements is employed to discretize the design domain.

Fig. 8

Design domain considered in topology optimization with geometrical dimensions and boundary conditions

Three different problems are solved: (1) deterministic problem with two vertical applied loads (simultaneously applied); (2) robust problem with two vertical applied loads of uncertain magnitude; and (3) robust problem with two applied loads of uncertain magnitude and uncertain direction, as shown in Fig. 9. For loads with uncertain magnitude, we have f ∈ [0.0,0.3]N; for loads with uncertain direction we have 𝜃 ∈ [−π/6,π/6]rad. Uncertain variables may assume any value inside prescribed ranges, being independent of each other.

Fig. 9

Optimized topologies (middle) and worst-case von Mises stresses (right) for: (1) two deterministic vertical loads (top); (2) two vertical loads of uncertain magnitude (middle); and (3) two vertical loads of uncertain magnitude and uncertain direction (bottom)

Initial grids for solving the anti-optimization problems are constructed by the combination of the following points: [0.0,0.15,0.3]^T N (magnitudes of applied loads) and [−π/6,0,π/6]^T rad (directions of applied loads); thus, initial grids have 3 × 3 and 3 × 3 × 3 × 3 points, considering the problems subjected to two and four uncertain variables, respectively.

Solutions of both deterministic and robust problems are presented in Fig. 9. The stress graphs demonstrate that the local stress constraints are satisfied in every point the von Mises stress is computed. The obtained structures avoided both re-entrant corners on the design domain, and the stresses in these regions are well distributed on rounded corners.

Analyzing topologies in Fig. 9 and structural volumes in Table 2, one verifies there are differences among topologies and structural volumes of deterministic and robust solutions. Robust solutions have larger number of structural members and larger structural volumes, when compared with the deterministic solution. Interestingly, although the magnitudes f₁ and f₂ and the angles 𝜃₁ and 𝜃₂ can vary independently and asymmetrically, both robust topologies are symmetrical.

Table 2 Total number of iterations necessary to reach convergence and structural volumes for optimized results

Comparison can also be made between both robust solutions. One verifies that solution obtained for applied loads with uncertain magnitude and direction has larger structural volume and larger number of structural members when compared with solution for loads with uncertain magnitude only. This is totally expected from a structural engineering point of view, since in this case, more uncertainty implies in additional sets of load conditions; hence, additional material is needed to satisfy stress feasibility of optimized structure.

As shown in Fig. 9, consideration of uncertainty only in magnitude of applied loads provides a different topology, indicating that we cannot simply substitute the uncertain magnitude by its maximum value, as also observed in Elishakoff et al. (1994) for truss optimization.

Regarding computational cost, although number of iterations necessary for convergence is basically the same, as shown in Table 2, robust solutions are harder to obtain due to the necessity of solving the anti-optimization problems in the beginning of each iteration of the outer problem. However, the possible countermeasure discussed in previous subsection is also valid if more than one unknown variable is considered, i.e., the use of parallel computing is suitable to reduce computational cost associated with solution of whole set of anti-optimization problems, since these problems can be solved simultaneously.

6.3 U-shaped problem with two uncertain variables

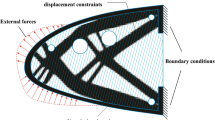
The third problem addressed in this paper is the U-shaped problem (Fig. 10). The U-shaped design domain is non-symmetrical and has two re-entrant corners, being very challenging from a stress-based design point of view. The U-shaped design problems are solved by employing a structured mesh with 70,000 finite elements and a filtering radius of R = 0.03m.

Fig. 10

U-shaped design domain considered in topology optimization with geometrical dimensions and boundary conditions

Two problems are solved: (1) deterministic problem, where the design domain is subjected to two loads of deterministic magnitude; and (2) robust problem, where the magnitude of both applied loads are unknown-but-bounded. Both problems, as well as optimized topologies and worst-case von Mises equivalent stresses, are shown in Fig. 11.

Fig. 11

Optimized topologies (middle) and worst-case von Mises stresses (right) for: (1) two deterministic loads (top); and (2) two loads of uncertain magnitude (bottom)

Initial grids for solving the anti-optimization problems are constructed by the combination of the following points: [0.0,0.2,0.4]^T N (magnitude of horizontal load, f₁) and [0.0,0.1,0.2]^T N (magnitude of vertical load, f₂); thus, initial grid has 3 × 3 points.

Both deterministic and robust topologies avoided the re-entrant corners present on the design domain. The shapes of the optimized topologies at these sharp regions are rounded and, moreover, the von Mises equivalent stresses at these regions satisfy the stress failure criterion, within the tolerance of 1%. The structural volume ratio of robust solution is larger than the deterministic one, indicating that the robust structure requires a larger amount of material to guarantee stress constraints feasibility when applied loads have uncertain magnitude.

Number of iterations to reach convergence is as follows: 1968, for the deterministic problem; and 2180, for the robust problem. However, although number of iterations is almost the same, robust solution becomes more costly than the deterministic one, since the anti-optimization problems are solved to evaluate the worst-case von Mises stresses at each outer iteration, as discussed in previous subsections.

7 Concluding remarks

This work presented a novel formulation for solving continuum stress-constrained topology optimization problems under unknown-but-bounded uncertainty in applied loads. A non-probabilistic robust approach was developed based on the worst-case scenario of stress constraints, resulting in a two-level optimization with anti-optimization. An augmented Lagrangian formulation was employed to solve the problem due to the large number of worst-case stress constraints.

The importance of developing non-probabilistic robust approaches, for solving the stress-constrained problem under uncertainty in applied loads, is demonstrated through numerical examples and post-processing. Deterministic solutions resulted very sensitive to uncertainties in direction of applied loads, in contrast to solutions of the robust problems. Even by increasing the number of load conditions in the deterministic design, robustness with respect to a continuum range of unknown variables could only be ensured through non-probabilistic robust approach.

Although anti-optimization problems are non-convex with respect to unknown variables, post-processing demonstrates that solutions obtained with the proposed approach are indeed robust with respect to uncertainties in applied loads. Maximum von Mises equivalent stresses, among von Mises stresses computed for the whole range of unknown variables, only exceeded yield stress within a predefined convergence tolerance.

Problems with up to four unknown variables were solved to demonstrate the differences between deterministic and robust solutions. It was shown that number of structural members of optimized topology increases as the unknown set of applied loads is increased. It was also shown that we cannot replace uncertainty in magnitude of applied load by its maximum value, since different topology is obtained if the whole range of magnitude uncertainty is considered during optimization.