1 Introduction

Computer-aided engineering (CAE) plays a vital role in designing engineered products. To substitute expensive experiments, in CAE, a computational model that imitates a real engineered product is examined to predict performances of interest. The increased use of CAE requires a more accurate prediction capability in computational models. Because various sources of uncertainties in physical properties, geometric tolerances, and modeling can degrade the accuracy of computational models, scholars have developed statistical approaches to deal with these uncertainties (Oberkampf and Trucano 2002) (Anderson et al. 2007) (Roy and Oberkampf 2010) (Fang et al. 2012) (Mousaviraad et al. 2013) (Park et al. 2016) (Wang et al. 2018) (Lee et al. 2019a). Statistical model improvement, which includes calibration, validation, and refinement, aims to enhance the prediction capability of computational models. Model calibration is used to improve the prediction capability of a computational model by estimating the statistical parameters of unknown input variables; this minimizes the prediction errors of the computational model (Aeschliman et al. 1995) (Kennedy and O'Hagan 2001) (Campbell 2006) (Youn et al. 2011) (Buljak and Pandey 2015). To confirm the validity of a calibrated result, model validation presents a judges of the accuracy of a calibrated computational model (Bayarri et al. 2007) (Ferson et al. 2009) (Wang et al. 2009) (Oberkampf and Roy 2010) (Liu et al. 2011) (Park et al. 2016). If it is possible for a computational model to have model form uncertainties, model refinement is used to reveal the main errors in the modeling and, subsequently, to revise the model accordingly (Xiong et al. 2009) (Youn et al. 2011) (Oh et al. 2016).

Despite the efforts of scholars, engineers in industrial fields still face limitations in their ability to apply statistical model improvement. One issue is that statistical model improvement requires high-quality data for an accurate representation of uncertainties. However, experiments can be expensive. Engineers can spend considerable amounts of time in computational analysis when developing a product. This is a significant issue, especially for products with a limited timeline for development. Even though engineers can simplify computational modeling to reduce the required computational calculation, model simplification can result in invalid modeling information that can degrade the accuracy of the computational model. A computational model that examines the vibrational behaviors of an automobile steering column is an example of the model of a real-world engineered product that suffers from these issues. For statistical model improvement in this case, engineers would require numerous specimens of the steering column of interest, as well as a long period of time for repeated impact testing. The computational model needs expensive calculations for the eigenvalue problem in model analysis. While simplified modeling is an option, it cannot ensure the required level of prediction accuracy. For engineers in industry, time constraints typically do not allow the model form uncertainties to be revealed through trial and error, which could maintain the simplicity of the model.

Some researchers have tried to apply their research ideas to industrial models to address issues related to engineered industrial environments (Youn et al. 2011) (Deng et al. 2013) (Lee et al. 2016). Youn et al. devised a hierarchical model calibration approach to consider different failure mechanisms in an engineered system (Youn et al. 2011). The authors tried to calibrate a cellular phone model; however, the possibility of model form uncertainties in the model was not considered. Deng et al. developed an online Bayesian updating strategy and applied it to soft industrial sensors (Deng et al. 2013). Because five input variables and seven unknown input variables exist in performance responses, the cost for characterization of output uncertainties is lower than that of the automotive steering column examined in the present study. Lee et al. developed a P-box approach and a new area metric to quantify epistemic uncertainties (Lee et al. 2016). The authors used 54 pieces of experimental data for statistical model calibration of a passenger car—this is a large amount of data—which would limit applications of this method in the field. The large amount of experimental data is due to the need to minimize the statistical errors in the experimental data for the demonstration of the proposed idea. Overall, the research has concentrated on demonstrating the suggested ideas through industrial models and has not fully considered the issues that would limit the applicability of approaches in industrial environments.

To address the issues that emerge in real-world engineering settings, it is necessary to identify the reasons for the issues that arise and to suggest appropriate techniques to address these issues. Therefore, this paper discusses the reasons for the principal issues that remain in statistical model improvement that result in its low utility in practice in engineering fields. This paper thus focuses on the practical issues caused by the limited environment of the product development process in industrial fields. This research introduces statistical model improvement techniques that can address current issues in statistical models in real-world industry settings.

The rest of this paper is organized as follows. Section 2 first provides an overview of statistical model improvement. Section 2 continues with a description of the practical issues that arise when examining the statistical model improvement of an automobile steering column model. The automobile steering column model is used as an industrial example to highlight the issues that arise when pursuing statistical model improvement in industrial environments. Section 3 introduces statistical techniques to solve the issues outlined in Section 2. To validate the effectiveness of the suggested solutions, Section 4 outlines a case study of an automobile steering column model. Section 5 summarizes the overall research and outlines the conclusions.

2 Practical issues of a vibration analysis model of an automobile steering column

This section explains three issues that currently limit statistical model improvement, using an automobile steering column as a model for vibration analysis. Section 2.1 provides an overview of the statistical model improvement process. Section 2.2 introduces an automobile steering column model as an industrial example. Section 2.3 provides a detailed explanation of the issues surrounding statistical model improvement in the industry by examining the model of an automobile steering column.

2.1 Overview of statistical model improvement

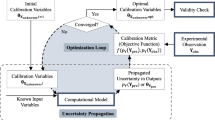
Statistical model improvement is a collective term used to describe technologies related to the enhancement of computational model accuracy. As mentioned in the Introduction, statistical model improvement includes statistical model calibration, validation, and refinement. Figure 1 summarizes the process of statistical model improvement (Youn et al. 2011). The steps in the rectangular boxes present statistical activities used in the model improvement process. The ellipses denote required information and results (e.g., computational model, statistical information of unknown input variables and experimental data) of each activity. Statistical model improvement consists of six steps: (1) uncertainty characterization, (2) uncertainty propagation, (3) calculation of a calibration metric, (4) finding optimal variables, (5) validity check, and (6) model refinement. When computational models include unknown parameters of input variables, the statistical model improvement process starts with the model calibration step. Otherwise, the process skips the model calibration and conducts a validity check first. When the computational model has physically incorrect assumptions, calibrated estimates of the unknown parameters of the input variables are unable to show the validity. In this case, the computational model requires a model refinement. The specific role and purpose of each step are explained as follows:

Fig. 1
figure 1

Framework of statistical model improvement (Youn et al. 2011)

Full size image
  1. 1)

    The first step is uncertainty characterization, which is designed to quantify uncertainties in the experimental data (Trucano et al. 2002). Mean and standard deviation can be descriptors to quantify uncertainties of given data. The probability density function (PDF) is a comprehensive and global method to represent the uncertainty (Mahadevan and Haldar 2000) (Roy and Oberkampf 2010). Generally, statistical model improvement uses the PDF to deal with uncertainties in a global domain.

  2. 2)

    The second step is uncertainty propagation, which is used to quantify uncertainties in the computational responses (Pettit 2004) (Roy and Oberkampf 2010) (Mousaviraad et al. 2013). The uncertainty propagation considers the uncertainties that stem from uncertainties in the input variables, such as material properties and geometric tolerances. Simulation-based methods and numerical integration based methods are representative approaches that can be used for uncertainty propagation (Hurtado and Barbat 1998) (Rahman and Xu 2004) (Youn et al. 2008) (Fang et al. 2012).

  3. 3)

    The third step is the calculation of a calibration metric to evaluate the discrepancy between the experimental and computational responses. Likelihood or probability residual can be used as a calibration metric in a statistical manner (Lee et al. 2018) (Oh et al. 2019). The objective of model calibration is to find the statistical parameters of the input variables that minimize the discrepancy quantified by the calibration metric.

  4. 4)

    The fourth step is model calibration to find optimal values of statistical parameters of unknown input variables in the computational model. Among various deterministic and statistical approaches for model calibration, this paper utilizes optimization-based model calibration (Lee et al. 2018, 2019b). In this approach, an optimization problem is formulated to estimate statistical moments of unknown input variables that minimize the discrepancy of the experimental and computational responses. The value of the calibration metric can be an objective function in the optimization problem. It is worth noting that the optimization-based approach is a deterministic process since the optimal solution derived from the optimization-based approach is a deterministic value. However, the model improvement method in this paper is defined as a statistical approach because the method deals with uncertainties of responses over the whole process. When computational models include model form uncertainties, which arise mainly due to incorrect assumptions or excessive simplification, model calibration fails to find reasonable estimates of the statistical moments of the unknown input variables. The model refinement step can revise the leading cause of the model form uncertainties. To avoid a failure of model calibration, exact computational modeling and simplification of assumptions based on reasonable physics are required.

  5. 5)

    The fifth step is validity check, which is used to verify the validity of computational responses (Oberkampf and Roy 2010). Statistical validation consists of examining the validation metric and decision making. The validation metric quantifies the coincidence or the discrepancy between the experimental and computational responses. The validation metric is technically different from the calibration metric in that it should give information of model validity even in constrained cases, such as where there is a limited number of data or where the experimental data is given in different environments. Validation metrics include the area metric and Bayes factors (Oberkampf and Trucano 2002) (Rebba et al. 2006) (Liu et al. 2011). Using the validation metric value, the statistical validation step is used to determine the validity of the calibrated model. In decision making, hypothesis testing is generally used.

  6. 6)

    The sixth step is model refinement, which explores and revises the root causes of invalid modeling in the computational model (Deng et al. 2013) (Oh et al. 2016). When the model calibration fails, the objective function of the optimization for model calibration does not decrease, regardless of the optimization formulation. The estimates of the statistical moments of the unknown input variables fail to satisfy the desired level of validity in the statistical validation step. In the statistical model improvement process, model refinement is of great importance because model errors interrupt the goal of statistical model improvement to find an exact solution for the statistical parameters of the input variables and decrease the reliability of the improved solution.

2.2 Introduction of the case study: a vibration analysis model of an automobile steering column

An automobile steering column is a device that helps a driver to change the driving direction of an automobile. One issue in the design of an automobile steering column is the desire to reduce the resonated vibration transferred from the engine or the roadway. Transferred vibration may make drivers uncomfortable. The design of an automobile steering column is based on the understanding of vibrational behaviors to avoid resonance. Therefore, the purpose of a computational model for an automobile steering column is to analyze the natural frequency and mode shape of the vibrations. In this paper, we focus on natural frequencies matched to specific mode shapes that arise when a steering wheel vibrates in three axial bending directions. This approach is based on prior knowledge from industrial experts who designed the automobile steering column (offered to us via personal communication). These engineers have found that the vibrating strength of axial bending modes is the most powerful. The target modes of the natural frequency are the 1st, 2nd, and 4th modes. The 3rd mode of the natural frequency is not considered because it has a twisting mode shape.

Figures 2 and 3 show an automobile steering column and the computational model of an automobile steering column, respectively. An automobile steering column consists of two sub-components: a steering wheel and a column assembly. Figures 2a and 3a show a steering wheel and Figs. 2b and 3b show a column assembly. The full steering column and its computational model are shown in Figs. 2c and 3c, respectively. For computational modeling, Hypermesh 13.0 software is used as a preprocessor. Required for exact computation are 298,458 nodes and 214,268 elements. To save computational costs, a computational model simplifies the geometric complexity of a real product. For example, the bolting system is simplified as a rigid body element (RBE2). The airbag in the middle of the steering wheel is simplified as a lumped mass with no geometric inputs. The geometry of the wheel cover uses shell elements, which only considers thicknesses as a geometric input variable.

Fig. 2
figure 2

An automobile steering column: a Steering wheel. b Column assembly. c Entire steering column

Full size image
Fig. 3
figure 3

An automobile steering column model: a Steering wheel. b Column assembly. c Entire computational model of the steering column

Full size image

Using the simplified steering column model, Autodesk Nastran 2018 is employed for a solver and post-processor. The automobile steering column model takes 575.66 s for the calculation of the natural frequencies and mode shapes. The complex design of an automobile steering column requires a significant amount of computational cost for analysis. Despite the calculation cost, however, the computational responses of the model are severely mismatched with experimental data. Therefore, the model requires statistical model improvement. Section 4 explains the process of applying statistical model improvement in detail.

2.3 Issues in statistical model improvement in industrial fields

This section describes three major issues that arise when performing statistical model improvement in industrial engineering models: (1) the issue of a lack of experimental data is discussed in Section 2.3.1, (2) the computational cost for uncertainty propagation of computational responses is outlined in Section 2.3.2, and (3) model form uncertainties are examined in Section 2.3.3.

2.3.1 Issue 1: Lack of experimental data for quantifying the uncertainties of true responses

Variations in true responses are influenced by numerous sorts of uncertainty sources. Uncertainty sources include material properties of specimens, experimental environments, or measurement errors. Random experiments, repeated experiments in the same environment, can consider a variety of uncertainty sources in the experiments. For example, experiments with numerous specimens can give insight into the uncertainties of material properties and geometry. Likewise, a repeated number of experiments can allow consideration of measurement errors. However, in real-world settings, during the product development process, it is difficult to prepare numerous specimens or repeat tests. Overall, the excessive cost of random experiments is a disadvantage in statistical model improvement.

Uncertainty characterization can be performed either in a parametric or nonparametric way. Parametric approaches estimate the best fit of the distribution type and its parameters, usually based on exact information of the distribution type and sufficient data (Mahadevan and Haldar 2000). Kang et al. stated in their paper that the data more than 30 can follow the parametric distribution (Kang et al. 2017). The nonparametric approach overcomes the absence of sufficient number of data set and types of distribution. One commonly used nonparametric approach is kernel density estimation (KDE), which models a distribution directly from data without using a specific type of distribution or parameter. However, the original KDE approach sometimes models a PDF of uneven shape using limited data, due to its high modeling flexibility, even though the true distribution is a smooth distribution. Accordingly, uneven densities of KDE can lead to the identification of incorrect “optimal” solutions from optimization-based model calibration. To overcome this problem, Kang et al. developed a kernel density estimation with estimated bounded data (KDE-ebd) that can use both experimental data and bound information. It thus estimates a more accurate and conservative PDF than the original KDE even using insufficient data (Kang et al. 2018). Further, Moon et al. proposed an input distribution model using a bootstrap method in KDE, which selects an optimal bandwidth of the input variable from the CDF of the bandwidth of the input variables obtained by bootstrap estimation. Since this method can yield a reliable input distribution (Moon et al. 2019a), it can be applied to the statistical model validation (Moon et al. 2019b).

In this study, we prepared three steering wheels and three column assemblies to show the possibility of a successful model improvement process with limited cost. Considering different combinations of the two sub-components, a total of 9 combinations of the automobile steering column were examined in the experiments. With each combination of the automobile steering column, impact tests were performed five times, and the five experimental data were averaged to represent the natural frequency of each combination. Overall, 9 points of experimental data were available for uncertainty characterization. For a successful model improvement process with 9 experimental data, we employed a special technique that has a smooth density shape and simultaneously satisfies the accuracy requirement.

2.3.2 Issue 2: numerous input variables for propagating uncertainties of a computational model

Modeling of an engineered product includes diverse individual design specifications. This is a complex and sophisticated process that requires a combination of numerous components. To complement all specifications, computational models require a large number of input variables. For the uncertainty propagation of the computational model, it is a significant burden to consider all uncertainties of input variables. Meanwhile, uncertainty propagation is the most frequently performed process in statistical model improvement. Uncertainty propagation is necessary for every attempt to quantify the discrepancy between the experimental and computational responses. Therefore, reducing the computation cost for uncertainty propagation is an important issue.

To alleviate the calculation time of the computational model, a surrogate model is generally substituted for the original computational model (Zhao et al. 2011) (Manfren et al. 2013) (Wu et al. 2018). A surrogate model is a numerical model for which calculation time is much shorter than the computational model with CAE. However, when using a surrogate model, minimizing the number of input variables in the model is recommended to ensure accuracy (Schuëller and Jensen 2008). Furthermore, the amount of computational response data for a surrogate model increases with the number of input variables. Overall, reducing the number of input variables is of great importance to reduce the computational cost for uncertainty propagation.

In the case of the automobile steering column model, Table 1 summarizes detailed information for all input variables. The table categorizes input variables into material properties, geometry, and boundary condition. Each variable properties of the materials, such as elastic modulus, density, and Poisson’s ratio, has six input variables because of the six types of materials (e.g., steel, aluminum, polyurethane) used to produce the steering column. Variable properties of geometry include the thicknesses of the six shell elements. In the case of the boundary condition, stiffness of the three main linkage components (e.g., bush, bearing, and spring) is considered. Overall, the automobile steering column model has 46 input variables.

Table 1 Information about the input variables in the steering column model
Full size table

2.3.3 Issue 3: Model form uncertainties in the computational model

Model form uncertainties originate from a misunderstanding of the modeling knowledge required for an exact computational model. The model form uncertainties designate all sources of modeling error, such as wrong assumptions, excessive simplification in the computational model, and inaccurate surrogate modeling. In industrial fields, engineers simplify the computational model as much as possible to improve the computation speed. In this simplification process, excessively simplified modeling can induce model form uncertainties. Given this modeling tendency in real-world industrial settings, this paper only focuses on model form uncertainties that arise from a computational model, such as wrong assumptions and excessive simplification. In a case with surrogate modeling errors, these errors can be managed by the construction of surrogate models with an accurate method.

In computational responses, model form uncertainties generate biased errors. Without revising the sources of model form uncertainties, the calibrated values of statistical parameters of unknown input variables may excessively shift to physically impossible values to complement biased errors. In the optimization of model calibration, the objective function does not decrease, regardless of the optimization formulation. The estimates of the statistical moments of unknown input variables fail to satisfy the desired level of validity in the statistical validation. Thus, model refinement is designed to identify and eliminate the major source of model form uncertainty to prevent the failure of model calibration and to obtain a reasonable estimate of the statistical parameters of the unknown input variables.

In the modeling of the automobile steering column, an airbag located in the steering wheel is simplified as a lumped mass, without detailed geometric modeling. Furthermore, the airbag is modeled with a rigid body element, and the fixed point of the airbag is different from a real specimen. A variety of material properties in the steering column is simplified to representative steel. Even numerous simplified modeling become potential sources of model form uncertainty, it is not advisable to fix all the sources due to calculation costs. Therefore, for engineered product design, an effective way must be found to physically find the most effective source of model form uncertainties.

3 Solutions to the issues of statistical model improvement for an automobile steering column

Section 3 provides suggested solutions to the issues explained in Section 2. Section 3.1 introduces an uncertainty characterization method, kernel density estimation with estimated bounded data (KDE-ebd), for the issue of the lack of experimental data. Section 3.2 describes variable screening and surrogate modeling to address the issue of numerical input variables in uncertainty propagation. Section 3.3 presents a model refinement method for the issue of model form uncertainties.

3.1 Solution 1: Kernel density estimation with estimated bounded data (KDE-ebd)

KDE-ebd was recently developed to improve the original KDE by combining it with interval representation using estimated intervals from given data (Kang et al. 2018). The original KDE method uses given data only to obtain a kernel density function; in contrast, KDE-ebd uses both given and bounded data that are randomly selected within the estimated intervals of the uniform distribution. KDE-ebd can be used whether or not the information about the bounds is given. If there is no bound information, KDE-ebd can estimate the bounds from the given data based on statistical interval estimation theory; otherwise, KDE with bounded data (KDE-bd) can use the known boundary values. The estimated kernel density function using KDE-ebd is expressed as:

$$ \hat{f}(x)=\frac{1}{n_{\mathrm{tot}}\cdotp {h}_{\mathrm{tot}}}\sum \limits_{i=1}^nK\left(\frac{x-{Xebd}_i}{h_{tot}}\right) $$
(1)

where Xebdi is i-th total data, which combines the given and the estimated bounded data for i = 1,…,n, i.e., Xebd = [X, ebd], where X and ebd denote given and bounded data, respectively. ntot is the number of total data samples, htot is the optimal bandwidth for the total data, and K(·) is a kernel function. The estimated bounded data are randomly generated from a uniform distribution with intervals that are estimated by interval representation. The bounded data is added to the given data until the additional bounded data does not affect the shape of the kernel density function. The estimated intervals, l and u, are calculated by:

$$ \left\{l,u\right\}=\left[\hat{b}-\frac{\hat{b}-\hat{a}}{\alpha^{\frac{1}{n}}},\hat{a}+\frac{\hat{b}-\hat{a}}{\alpha^{\frac{1}{n}}}\ \right] $$
(2)

where \( \hat{a} \) and \( \hat{b} \) are point estimators of a uniform distribution for given data, and α is a significance level for the interval estimation of a uniform distribution.

Compared with KDE-ebd, it is possible for KDE to generate a PDF that more accurately represents the given data set. However, KDE may estimate an uneven density shape, such as in the case of a multimodal distribution for an extremely small amount of data. Multimodal PDF is not useful for vibrational analysis of an automobile steering column, because it is impossible to have two different values of the natural frequency in a mode. From the perspective of model calibration, the optimization algorithm has difficulty in finding an optimum to fit a PDF of computational performance with an unevenly shaped PDF that is derived from the experimental data. Since the estimated bounded data supplements the data deficiency, KDE-ebd can model PDF with a smooth density shape, which can yield more easily convergent model calibration. Subsequently, the merits of KDE-ebd in improving statistical models in situations with limited data are as follows: (1) it can increase the modeling accuracy even with limited data, (2) it can improve the efficiency of model calibration by smoothing the PDF of the experimental data, and (3) it can lead to a conservative analysis and design results, regardless of the quality of the data, because the input and output distributions are modeled as heavy-tailed distributions (Kang et al. 2019b).

3.2 Solution 2: variable screening and surrogate model

To address the problem of the computational expense of uncertainty propagation, this research applies two approaches: (1) variance-based variable screening and (2) surrogate modeling with Kriging. Section 3.2.1 explains variance-based variable screening and Section 3.2.2 introduces surrogate modeling with Kriging.

3.2.1 Variance-based variable screening

Variable screening can reduce the dimension of computational responses by considering only effective input variables while maintaining the accuracy of the computational responses (Hamby 1994) (Frey and Patil 2002) (Lee et al. 2019c). Variable screening analysis methods can be categorized into local and global approaches (Campolongo et al. 2007) (Iooss and Lemaître 2015). Local approaches, such as one factor at a time (OAT) or elementary effects (EE), are not suitable for this study. From the perspective of statistical model improvement, statistical model calibration and validation requires the effectiveness of sensitivity analysis in a large boundary of unknown input variables to find an optimal set of unknown input variables. Therefore, global approach is appropriate for the statistical model improvement. Numerous global sensitivity analysis methods, such as the Sobol method or the correlation ratio, only consider the effectiveness of input variables toward the output responses. The statistical model improvement process, however, requires the effectiveness of the uncertainties of input variables toward the uncertainties of output responses. Therefore, this study adopted the efficient variable screening method outlined in the following paper (Cho et al. 2014).

The efficient variable screening is an integration of the absolute discrepancy between a PDF of the computational responses with all input variables and a PDF with all variables except for k-th input variable, expressed as:

$$ {e}_k={\int}_{-\infty}^{\infty}\left|{f}_k(y)-g(y)\right| dy $$
(3)

where ek is an area difference between fk(y) and g(y). fk(y) indicates a PDF of a prediction response y without the effect of the k-th variable, by fixing the value of the input variable to a deterministic value. g(y) denotes a prediction response PDF considering the effects of all variables. When the k-th variable has a large effect on a prediction response, the shape of fk(y) becomes narrow and tall, as compared with g(y). As a result, the change of the PDF shape results in the area difference between fk(y) and g(y).

In addition, the assessment of the effects of input variables can give a guideline for selecting unknown variables. In such a case, the most effective input variables can be unknown variables, with an assumption that more influential input variables can induce more significant errors in computational responses, when the prior information of input variables is incorrect. In the case study of an automobile steering column examined here, the authors selected unknown variables based on variable screening analysis. Section 4.1.2 provides a detailed explanation.

3.2.2 Surrogate modeling with Kriging

Surrogate modeling reduces the computational cost of the response evaluations when expensive CAE analysis is required. Surrogate modeling becomes essential because the statistical model improvement process requires repeated evaluations of the responses. Surrogate modeling includes polynomial chaos expansion (PCE), Kriging, or support vector machine (SVM) groups (Hu and Mahadevan 2016). The PCE group is practical because it is simple to perform; however, it is inaccurate for non-Gaussian cases (Schuëller and Jensen 2008). SVM is mainly used in the field of machine learning as a classification tool. Recently, studies have begun to apply SVM to surrogate modeling (Roy et al. 2019). Kriging is an interpolation-based approach, which is one of the most efficient and accurate surrogate modeling methods for highly nonlinear performance functions (Krige 1951) (Wang 2003) (Clarke et al. 2005) (Marrel et al. 2008) (Lee et al. 2011) (Zhao et al. 2011) (Kang et al. 2019a). The basic idea is to estimate the computational responses using a weighted summation of neighborhood data points, considering spatial relationship. Estimation of a computational response at x0 with Kriging is formulated as:

$$ \hat{\boldsymbol{z}}\left({\boldsymbol{x}}_0\right)=\sum \limits_{i=1}^N{\boldsymbol{\uplambda}}_i\left({\boldsymbol{x}}_0\right)\boldsymbol{z}\left({\boldsymbol{x}}_i\right) $$
(4)

where z(xi) is the i-th computational response data point used for Kriging, and λi is a weight of the i-th computational response data point, indicating spatial correlation. N denotes the number of computational response data points. The objective of Kriging estimation is to calculate the optimal λi, satisfying two conditions:

$$ \mathrm{E}\left(\boldsymbol{\upvarepsilon} \left({\mathbf{x}}_0\right)\right)=\mathrm{E}\left(\hat{\boldsymbol{z}}\left({\boldsymbol{x}}_0\right)-\boldsymbol{z}\left({\boldsymbol{x}}_0\right)\right)=0 $$
(5)
$$ \underset{\boldsymbol{\uplambda}}{\min}\mathrm{Var}\left(\boldsymbol{\upvarepsilon} \left({\mathbf{x}}_0\right)\right)=\mathrm{Var}\left(\hat{\boldsymbol{z}}\left({\boldsymbol{x}}_0\right)-\boldsymbol{z}\left({\boldsymbol{x}}_0\right)\right) $$
(6)

Equation (5) is for unbiased prediction, and Eq. (6) is to minimize the variance of errors. ε(x0) is the discrepancy between the real computational response, and the estimated computational response derived from Kriging. \( \hat{\boldsymbol{z}}\left({\boldsymbol{x}}_0\right) \) denotes the estimation of the computational responses by Kriging; z(x0) signifies the real computational response. Var(·) represents variance. Depending on the stochastic assumption, the type of Kriging method for estimating the optimal λi can be different.

For the case of an automobile steering column model, the natural frequency of the complicated structures is generally highly nonlinear, which is sensitive to the change of input variables (Gholizadeh 2013). Therefore, the Kriging method deals with highly nonlinear response surfaces of the natural frequency for an automobile steering column to reduce the computational cost for uncertainty propagation. This paper uses the universal Kriging method that assumes the computational responses follow a general functional mean with an intrinsic random process, which has zero mean. Detailed description of universal Kriging is referred by the following papers (Armstrong 1984) (Stein and Corsten 1991) (Zimmerman et al. 1999).

3.3 Solution 3: Model refinement

Model refinement is an essential step in that this process directly removes the underlying cause of model form uncertainty. There has been little achievement in academic research towards considering the model form uncertainties in a systematic framework. Xiong et al. stated in their paper that personal experience in modeling gives an intuition for model refinement; however, this is not an applicable process for practical settings. Therefore, model refinement, introduced in this paper, aims to explore the most effective root causes of invalid modeling via a systematic approach (Oh et al. 2016).

The model refinement selects the most invalid sources based on experts’ opinion and numerically quantified criteria. The process involves three steps: (1) model invalidity analysis, (2) an invalidity reasoning tree, and (3) invalidity sensitivity analysis. Model invalidity analysis is a brainstorming step, which gathers all possible invalid sources. This step allows as many invalid sources as possible. The second step is to develop an invalidity reasoning tree that selects only potential invalid sources from among all sources gathered in Step 1. For the selection of invalid sources, related experts should identify the proper reasons for invalidity, from the conceptual, mathematical, and computational perspective. Invalidity sensitivity analysis quantitatively evaluates the importance of invalid sources of computational modeling. A decision matrix is one useful tool for comparing all candidates of the invalid sources of modeling (Dieter 1991). Oh et al. suggested a weighted decision matrix that considers the importance of each criterion by multiplying the weight values (Forman and Gass 2001) (Oh et al. 2016). In this step, engineers in the field can define criteria and weights for quantification appropriate for their situation.

As mentioned in Section 2.3.3, industrial engineers use simplified computational models to increase the speed of calculation or the efficiency of the modeling. The majority of modeling errors arise from the simplification of computational models, rather than a lack of modeling knowledge. Therefore, invalid modeling should be selectively improved by considering the situation and the standards required for each industrial field to ensure that an unconditionally exact and complicated model is not implemented. In addition to the model refinement method, other statistical approaches to deal with the invalidity of a computational model have been developed (Kennedy and O'Hagan 2001) (Xiong et al. 2009) (Qiu et al. 2018). Bias correction with a Bayesian calibration framework can quantify the number of errors that are due to the invalidity of a computational model (Kennedy and O'Hagan 2001) (Arendt et al. 2012) (Xi et al. 2013). To precisely quantify the biased errors, this method requires numerous experimental data samples from a diverse domain of design variables. Because this study deals with the problems that arise from an insufficient amount of data, this approach is not considered here.

4 Industrial demonstration: A case study of an automobile steering column

Section 4 describes the process of statistical model improvement and results for the model case study of an automobile steering column. As mentioned in Section 2.2, the target modes of the natural frequency are the 1st, 2nd, and 4th modes. Among these three modes, the 1st and 4th mode of the natural frequency is used in model calibration; the 2nd-mode natural frequency is used for model validation. Section 4.1 describes the first trial of statistical model improvement. Because of the unrecognized model form uncertainties, the calibration result from the first trial failed to find a valid solution. Therefore, Section 4.2 provides the second trial of statistical model improvement that is implemented after performing model refinement.

4.1 First trial of statistical model improvement

Section 4.1 explains the first trial of the statistical model improvement process. Section 4.1.1 explains the procedure of the random experiment and the results of uncertainty characterization. Because the statistical information of thickness and density of wheel covers are unknown, the process starts with statistical model calibration to estimate the unknown statistical parameters. Section 4.1.2 describes uncertainty propagation results using variable screening and surrogate modeling. Section 4.1.3 introduces the calibration metric used in this study. Section 4.1.4 presents the statistical model calibration result. As the calibrated model shows an invalid result, Section 4.1.5 illustrates the model refinement process.

4.1.1 The first step: uncertainty characterization with a random experiment

The random experiment step can consider a variety of uncertainties in an experiment. Uncertainty sources of the automobile steering column model include material properties, geometric figures, the combination of sub-components (e.g., steering wheel and column), and measurement errors. Three specimens of an automobile steering wheel and column assembly were used to consider the uncertainties of material properties and geometric figures. To consider the uncertainty caused by the assembly of each subcomponent, 9 different combinations of three steering wheels and three steering columns, respectively, are utilized. Measurement errors are reduced by averaging experimental data with repeated experiments five times. For these random experiments, an LMS SCADAS mobile system is used to observe vibrational signals for modal testing. Test Lab software gives the frequency response function and measured natural frequency values using a signal processing tool.

Using this experimental data, the KDE-ebd method characterizes uncertainties. The research outlined in this paper used a critical intersection area of 0.95 and a significance level for an interval estimation of 0.1, as suggested by Kang et al. (Kang et al. 2018). Figure 4 shows a comparison of the uncertainty characterization results from both the KDE and KDE-ebd methods, using 9 experimental data acquired from 9 different steering column combinations. PDFs estimated by KDE for the 1st-mode frequency (Fig. 4b) and the 4th mode frequency (Fig. 4c) show uneven shape. The points of experimental data seem to be separated into two parts due to an insufficient amount of data. The KDE-ebd method smooths the uneven shape of the PDFs caused by the lack of experimental data; KDE does not smooth the shape, as shown in Fig. 4. In the case of the 2nd mode frequency, the estimated PDFs derived from both KDE and KDE-ebd are similar because experimental data for the 2nd-mode frequency are well-distributed and follow a regular-shaped PDF.

Fig. 4
figure 4

Uncertainty characterization of experimental data: (a) 1st-mode natural frequency, (b) 2nd-mode natural frequency, (c) 4th-mode natural frequency

Full size image

4.1.2 The second step: uncertainty propagation with variable screening and surrogate modeling

For variable screening of the input variables, the area differences from Eq. (3) are used to evaluate the effect of each input variable on the 1st, 2nd, and 4th mode of the natural frequencies. To normalize the area metric values with respect to three modes of natural frequencies, each area metric is divided by the sum of the area metrics of all input variables as:

$$ {N}_{e_k}=\frac{e_k}{\sum_{i=1}^n{e}_i} $$
(7)

where \( {N}_{e_k} \) denotes a normalized area metric and n is the number of all input variables in the steering column model. Four input variables with the largest normalized area metric values are summarized in Table 2 which shows that the thickness of the ECU bracket and the elastic modulus of the column frame have dominant effects on the natural frequencies. Therefore, the thickness of the ECU bracket and the elastic modulus of the column frame are considered as unknown input variables.

Table 2 Normalized area metric of each mode frequency
Full size table

A surrogate model is constructed to substitute for the automobile steering column model. The important thing is that the selected unknown input variables should be considered in constructing the surrogate model to find optimal parameters of the unknown input variables using this surrogate model in the model calibration process. Therefore, surrogate models are generated with four input variables: the thickness of the ECU bracket, the elastic modulus of the column frame, thickness, and the density of wheel covers. When generating a Kriging model, this study adopted a Gauss function as a correlation function and the first-order polynomial function. A pattern search algorithm optimized the hyper parameters of the Kriging. Table 3 is the result of a root-mean-square error (RMS) of the Kriging model with 50 test sample points. In this paper, the Kriging modeled the computational responses in a global domain because the DOE points for the Kriging model covered the entire domain of the model calibration. The model calibration domain is defined by the bounds of the input variables. Therefore, once the kriging model is constructed, it can be used in the model calibration.

Table 3 RMS of the Kriging—1st trial
Full size table

4.1.3 The third and fourth step: Calculation of the calibration metric and model calibration

Given the uncertainties of the experimental data and computational responses, this section quantifies the discrepancy between the two responses using a calibration metric. In this paper, model calibration algorithm adopted probability residual as a calibration metric (Lee et al. 2018) (Oh et al. 2019) which is given as:

$$ \mathbf{PR}\left({\boldsymbol{y}}_{\mathrm{exp}}|\boldsymbol{\theta} \right)={\int}_{-\infty}^{\infty }{\boldsymbol{P}}_{{\boldsymbol{y}}_{\mathrm{exp}}}\left(\boldsymbol{y}\right)-{\boldsymbol{P}}_{{\boldsymbol{y}}_{\mathbf{pre}}}\left(\boldsymbol{y}|\boldsymbol{\theta} \right)\ \boldsymbol{dy} $$
(8)

where yexp denotes the PDF of experimental data and \( {\boldsymbol{P}}_{{\boldsymbol{y}}_{\mathbf{pre}}}\left(\boldsymbol{y}|\boldsymbol{\theta} \right) \) denotes the PDF of computational responses. θ represents the statistical parameters of unknown input variables. The probability residual quantifies the difference between experimental and computational PDFs. The advantage of probability residual in the optimization of model calibration is that minimal and maximum values are zero and two, whatever responses we consider. The optimal value of the calibration metric can give intuition about the success or failure of model calibration before the validity check step. To consider the 1st and 4th mode of natural frequencies simultaneously in statistical model calibration, a multi-objective optimization is performed. To formulate a multi-objective optimization, the overall calibration metric for an objective function of optimization is shown as:

$$ \underset{\boldsymbol{\theta}}{\min}\left[\mathbf{PR}\left({\boldsymbol{y}}_{ex{p}_1}|\boldsymbol{\theta} \right)+\mathbf{PR}\left({\boldsymbol{y}}_{ex{p}_4}|\boldsymbol{\theta} \right)\right] $$
(9)

where \( {\boldsymbol{y}}_{ex{p}_1} \) and \( {\boldsymbol{y}}_{ex{p}_4} \) denote experimental data of the 1st and 4th-mode natural frequencies, respectively.

For nonlinear optimization of natural frequency problems, this paper applies a sequential quadratic programming algorithm (SQP). To implement the SQP algorithm, “fmincon” in-build code in MATLAB software is adopted. Table 4 describes the distribution type, bounds of the statistical parameters (e.g., mean and standard deviation), initial values, and optimized values for each input variable Hess’s paper and the ‘Total Materia’ database provide guidance on the distribution types (Hess et al. 2002) (Total Materia 2019). The decision of the bound of statistical parameters requires physical and empirical sense. In-depth physical knowledge and experiences on the computational models and related mechanics help determining the bound.

Table 4 Calibrated statistical parameters of unknown input variables of the 1st trial of statistical model calibration
Full size table

4.1.4 The fifth step: validity check

For a quantitative check of the validity of the calibrated result, an area metric with a u-pooling method is employed. The area metric with a u-pooling method is known as an efficient metric for use when there is an insufficient amount of experimental data (Liu et al. 2011) (Oh et al. 2016). The equation is as follows:

$$ \mathrm{d}\left({P}_{\mathrm{exp}},{P}_{\mathrm{pre}}\right)={\int}_{-\infty}^{\infty}\left|{P}_{\mathrm{exp}}\left(\mathbf{y}\right)-{P}_{\mathrm{pre}}\left(\mathbf{y}\right)\right| dy $$
(10)

where Pexp and Ppre represent the PDF of experimental data and computational responses, respectively. y denotes performances of interest. In this paper, the 2nd mode of the natural frequency is applicable. The u-pooling method deals with the cumulative density function (CDF) of the u-value defined by the probability density of the experimental data and computational responses, as shown in

$$ {u}_i={P}_{\mathrm{pre}}\left({y}_i\right) $$
(11)

where P denotes the CDF of the computational responses and yi presents i-th data. yi can be either experimental or computational data. Using the u-value, the area metric with the u-pooling method is formulated as:

$$ \mathrm{U}={\int}_0^1\left|G\left({u}_{\mathrm{exp}}\right)-G\left({u}_{\mathrm{pre}}\right)\ \right| du $$
(12)

where G(uexp) is an empirical CDF of u-values by experimental data and G(upre) presents the CDF of the u-value by the computational responses.

Figures 5 and 6 show the PDF of the calibrated computational responses and the validity of each mode. In Figs. 5b and 6b), the graph of the black line illustrates the PDF of the area metric values for the 9 data. This graph is obtained from the area metric calculation by 100,000 sets of randomly sampled 9 numbers of data. The u-values of the 9 data are sampled within [0, 1] because the u-value is a cumulative probability density.

Fig. 5
figure 5

Validity of 1st mode frequency: (a) PDF, (b) Validity check with area metric

Full size image

The value of the area metric for the 1st natural frequency is calculated as 0.0890, as shown in Fig. 5b with the star mark (*).The threshold of the area metric at 95% confidence level is 0.1818, which is denoted by the red line. Overall, the calibrated result can guarantee the validity at a 95% confidence level, because the calculated area metric (e.g., 0.0890) is lower than the area metric determined as the criteria (e.g., 0.1818). The value of the area metric for the 4th natural frequency, however, is calculated as 0.4995 as shown in Fig. 6b with the star mark (*). This response is invalid because the value is larger than the threshold (e.g., 0.1818). Therefore, the computational model requires a model refinement.

Fig. 6
figure 6

Validity of 4th mode frequency: (a) PDF, (b) Validity check with area metric

Full size image

4.1.5 The sixth step: Model refinement

Model refinement reveals the invalid modeling sources that cause severe errors of the 4th mode of the natural frequency. The overall step of model refinement came from the following paper (Oh et al. 2016). First, model invalidity analysis gathers candidates of invalid modeling with an affinity diagram, as presented in Table 5. Second, an invalidity reasoning tree, as shown in Fig. 7, reveals the theoretical reasons from the perspective of conceptual, mathematical, and computational modeling. It was determined to ignore the candidate-related geometry of the airbag and steering wheel cover, because the natural frequency is mainly related to mass and stiffness. Therefore, three candidates of invalid modeling sources are considered: (1) simplified material properties in each part in the column assembly, (2) location of the airbag in the steering wheel, and (3) the modeling type of the airbag. The final step is an invalidity sensitivity analysis to evaluate the effects of invalid modeling candidates. To evaluate the effects, the researchers used a weighted decision matrix, shown in Table 6. Table 6 consists of criteria, magnitude (e.g., \( {\mathrm{M}}_j^i \)), standardized magnitude (e.g., \( {S}_j^i \)), and rating.

Table 5 Affinity diagram of an automobile steering column model
Full size table
Fig. 7
figure 7

Invalidity reasoning tree of an automobile steering column model

Full size image
Table 6 Weighted decision matrix for an automobile steering column model
Full size table

The criteria include correctness, robustness, computational cost, and implementation cost with weights allocated according to importance. The weights follow Oh’s paper (Oh et al. 2016). To quantify the magnitude of “correctness” criteria, the authors adopted the following equation:

$$ {\mathrm{M}}_1^i=\frac{\left|\mathrm{E}\left[{\boldsymbol{y}}_{\mathrm{exp}}\right]-\mathrm{E}\left[{\boldsymbol{y}}_{\mathrm{pre}}\left(\boldsymbol{x}\right)\right]\right|}{\mathrm{E}\left[{\boldsymbol{y}}_{\mathrm{exp}}\right]} $$
(13)

where E[·] is an expected value, yexp presents the experimental data, ypre denotes a computational response after revising the invalid modeling source, and x denotes a mean vector of initial unknown input variables. Robustness considers the number of newly added input variables by the refinement of each invalid source. To revise the invalid modeling source of candidate 1, we can specify the material properties of five parts in the column assembly. Therefore, the magnitude of robustness for candidate 1 is five. For candidate 2, there is no need to adopt another input variable. For candidate 3, we can change the modeling type of the airbag from a rigid-body model to a spring-element model. Therefore, the stiffness of the airbag is adopted. The cost of computation and implementation measures the time for computation of the revised model and implementation of modeling revision in minutes. The smaller values of all magnitudes give better impacts on model refinement. This study only quantified the magnitude of four criteria in a deterministic sense, considering the calculation cost in engineering fields. The quantification can be robust and accurate in a statistical manner. Research on fast and accurate approaches in a statistical manner is required in the future.

Standardized magnitude adjusts the magnitude values of all criteria from zero to one. It follows the equation:

$$ {S}_j^i=1-\frac{{\mathrm{M}}_j^i}{\max \left({\mathrm{M}}_1^i,{\mathrm{M}}_2^i,{\mathrm{M}}_3^i\right)} $$
(14)

where \( \max \left({\mathrm{M}}_1^i,{\mathrm{M}}_2^i,{\mathrm{M}}_3^i\right) \) denotes the maximum value of magnitude among the magnitudes of three candidates. \( \max \left({\mathrm{M}}_1^i,{\mathrm{M}}_2^i,{\mathrm{M}}_3^i\right) \)divides \( {\mathrm{M}}_j^i \) for standardization. Furthermore, the standardized term is subtracted from one for the smaller magnitude to give better impacts on model refinement. Rating is a multiplication of weight and \( {S}_j^i \). The summation of all ratings gives the overall sensitivity of each candidate. Based on the summarized results, shown in Table 6, the authors determined to revise candidate 3. The rigid body model of an airbag is modeled as a spring element.

4.2 Second trial of statistical model improvement

Using the revised computational model, this section repeats the statistical model improvement process. Section 4.2.1 describes statistical model calibration. Using the calibrated result, Section 4.2.2 explains the validity check process. Overall, the second trial of the statistical model improvement process succeeded in finding optimal parameters for the unknown input variables.

4.2.1 The second and fourth step: surrogate modeling and statistical model calibration

The second trial model calibration uses the same experimental data, as explained in Section 4.1.1. The characterized uncertainties of the experimental data are the same as those in Fig. 4. In case of uncertainty propagation, however, we should consider another unknown input variable. This is because stiffness of the airbag is newly modeled after the model refinement process, and the parameter information about the stiffness of the airbag was inaccurate. Therefore, the second trial of statistical model calibration estimates statistical parameters of five unknown input variables. Furthermore, the surrogate model is remodeled to consider the newly added unknown input variable in the statistical model calibration. The Kriging model is newly generated with the Gauss correlation function and zeroth order of a polynomial function. The RMS with 50 test sample points are listed in Table 7.

Table 7 RMS of the Kriging—2nd trial
Full size table

Using the same SQP algorithm described in Section 4.1.4, statistical model calibration estimates the statistical parameters of unknown input variables. Table 8 provides calibrated statistical parameters of the unknown input variables.

Table 8 Calibrated statistical parameters of unknown input variables of the 2nd trial of statistical model calibration
Full size table

4.2.2 The fifth step: Validity check

Figures 8 and 9 provides the results of the validity check for the 1st and 4th mode of the natural frequency. The values of the area metrics for the 1st and 4th natural frequencies are calculated as 0.0726 and 0.0824, as shown by star marks in Figs. 8b and 9b. The result shows the validity because area metric values are lower than the threshold (0.1818).

Fig. 8
figure 8

Validity check of the 1st-mode natural frequency: (a) PDF of the calibrated computational responses, (b) Validity check with the area metric

Full size image
Fig. 9
figure 9

Validity check of the 4th-mode natural frequency: (a) PDF of the calibrated computational responses, (b) Validity check with the area metric

Full size image

To show the validity in other modes, 2nd-mode frequency is adopted. The result of the validity check is shown in Fig. 10. Overall, the calibrated result of Table 8 can guarantee the validity at a 95% confidence level, because the calculated area metric (e.g., 0.1557) is lower than the area metric determined as the criteria (e.g., 0.1818).

Fig. 10
figure 10

Validity check of the 2nd-mode natural frequency: (a) PDF of the calibrated computational responses, (b) Validity check with the area metric

Full size image

5 Conclusion

This paper discussed three issues that hinder the widespread use of statistical model improvement in industry and offers solutions to these issues. First, in industrial settings, the number of experimental data may be insufficient for statistical modeling. Lack of experimental data results in erroneous uncertainty characterization. To solve this issue, KDE-ebd was adopted to mitigate an over-fitted PDF for scarcely distributed data, in a manner similar to a regular-shaped PDF. Second, the numerous input variables increase the number of computational analyses required for uncertainty propagation. Therefore, variable screening was used to select effective numbers of input variables for uncertainty propagation. And, the Kriging method was adopted to substitute a sophisticated computational model for reducing the calculation time required for the computational responses. Finally, the model form uncertainties in the computational model seriously reduced the accuracy of the computational responses. To address this issue, model refinement was used to systemically search for the invalid sources of modeling and selectively revise them to improve model prediction.

The statistical model improvement process has a limitation in that a systematic approach for determining the bound of statistical parameters of unknown parameters in model calibration is not provided. This job requires the knowledge and experience of related mechanics. This issue remains a valuable study in the future. Furthermore, the improved computational model enabled by statistical model improvement does not guarantee validity of the global design space. For the use in design activities, additional statistical validation at the new design point is required (Jung et al. 2016) (Jung et al. 2016). To further develop the statistical model improvement process, a validity check in the global design space will be included in the future work.

Statistical model improvement techniques are efficient tools to ensure high fidelity of computational predictions in industrial fields. Therefore, the paper focused on issues related to the significant amount of time needed for statistical model improvement for industrial engineers. By examining the statistical model improvement process of an automobile steering column model case study, this paper demonstrated the effectiveness of the proposed techniques. Once a computational model is evaluated as a valid model, field engineers can expand the use of computational models in other designs to predict performances of interest for various engineered products with high confidence. Eventually, the statistical model improvement process can lead to reliable designs in industrial fields, while offering reduced cost and shortening product development times.