Topology optimization with anisotropic materials, including a filter to smooth fiber pathways

Abstract

In a recent publication, an approach to optimize the orientation of anisotropic materials was presented. This strategy was embedded into the thermodynamic topology optimization based on growth. In this paper, we show that the thermodynamic orientation optimization can also be used in more classical approaches to topology optimization. We furthermore enhance the approach by a novel filtering technique to provide control over the smoothness of the pathway of principal material directions, i.e., the curvature of fibers. The filter is based on a convolution operator and is applied to the material stiffness tensor, so that the filtering technique is not directly bounded to the actual parameterization for the design variables. To this end, the topology is defined by a continuous density approach with penalization of intermediate densities (SIMP) solved via the optimality criteria method (OCM). A set of three continuous Euler angles is used as additional design variables to describe the local material rotation of the anisotropic base material. The thermodynamic optimization of the material orientation is performed by evolution of the Euler angles to minimize the elastic energy. The related evolution equations are derived by means of the Hamilton principle, well-known from material modeling.

1 Introduction

Material laminates or fiber-reinforced materials have a high stiffness-to-weight-ratio and are thus of particular interest in the automotive and aerospace industries to further reduce energy consumption while maintaining structural integrity. These materials possess anisotropic mechanical properties, so that the optimal (local) orientation of the materials must be considered in addition to the topology of the structure. Considerable research effort went into topology optimization over the last decades. Most topology optimization approaches are based on density formulation, i.e., the design variable is a factor to the material stiffness tensor. Usually, the objective is to find a discrete “black-and-white” solution containing either full material or void within a given design space. Different approaches were developed, including “bidirectional evolutionary structural optimization” (BESO), the “level-set” method, “phase-field” methods, and probably the most popular “solid isotropic material with penalization” (SIMP) in conjunction with different mathematical solution algorithms such as the “optimality criteria method” (OCM), “sequential linear/quadratic programming” (SLP/SQP), and “method of moving asymptotes” (MMA). The most popular approaches are reviewed in Sigmund and Maute (2013) and Deaton and Grandhi (2014). Optimization algorithms based on thermodynamic principles were developed and compared with mathematical optimizers to provide a more physical approach to optimization (Junker and Hackl 2015; Jantos et al. 2016). Thermodynamic topology optimization also proved to be suitable for optimization with additional design variables (Jantos et al. 2018; Gaganelis et al. 2019): differential equations, which serve as an update scheme for the design variables, are directly derived from the thermodynamic extremum principle, which are common in material modeling.

Most of these optimization approaches assume isotropic materials. Nevertheless, different approaches were developed to optimize the orientation of anisotropic materials either by solving the topology and material orientation optimization simultaneously or sequentially. Common approaches do not introduce additional design variables for the material orientation. Instead, the principal material direction is assumed to coincide with the principal stress or strain direction which is reasonable for “shear-weak” materials (Hörnlein et al. 2001; Bendsøe and Sigmund 2003; Gea and Luo 2004; Kočvara and Stingl 2007; Klarbring et al. 2017). “Discrete material optimization” (DMO) became quite popular due to its simple formulation based on multi-material topology optimization (Stegmann and Lund 2005; Hvejsel and Lund 2011; Niu et al. 2010): the stiffness tensor of each individual material is defined by an anisotropic base material rotated by a set of fixed angles. Thus, each material phase represents a different material orientation, and implementations for multi-material optimizations are applied for the solution. Thus, density filter techniques can be applied in DMO to control the minimum size of areas containing a single material orientation (Blasques and Stolpe 2012; Sørensen and Lund 2015). For each additional material, an additional design variable must be added, and the calculation effort increases with additional possible material orientations so that the method, especially for three-dimensional problems, becomes less efficient. The restriction to a prescribed set of orientations is resolved in “continuous fiber angle optimization” (CFAO), in which additional (local) design variables are included to parameterize a continuous rotation of an anisotropic base material. For two-dimensional cases, the addition of a single angle is sufficient, whereas for the three-dimensional case at least three or up to six additional design variables can be defined to parameterize the rotation (Stuelpnagel 1964). The rotation of the three-dimensional fourth-order material tensor can be reformulated to a rotation of a six-dimensional second-order material tensor (Mehrabadi and Cowin 1990). Most CFAO approaches consider two-dimensional problems focusing on laminates for shells and plates (Honda et al. 2013; Brampton et al. 2015; Hoglund and Smith 2016). Far less research is dedicated to three-dimensional CFAO (Nomura et al. 2015; Petrovic et al. 2018). The least restricted optimization is the “free material optimization” (FMO) (Zowe et al. 1997; Haslinger et al. 2010; Pedersen and Pedersen 2017), in which the individual entries of the material stiffness tensor are defined as design variables. Although this is the least restricted approach and yields potentially the most optimal design, the results are usually nonmanufacturable, i.e., most approaches do not consider discrete “black-and-white” solutions for the topology and the results are not bounded to a prescribed (set of) base material(s).

To improve the manufacturability of topology optimization results, filtering or projection techniques are often used, although they were intentionally introduced to resolve mesh dependence and checkerboarding due to the non convex minimization problem (Sigmund and Petersson 1998; Sigmund 2007). Checkerboarding or other undesirable numerical effects related to the material orientation are not reported except for mesh dependence when using sensitivity-based optimization (Nomura et al. 2015; Hoglund and Smith 2016). Nevertheless, constraints or filtering techniques to control the smoothness of the material orientation pathways within CFAO approaches are of interest to include manufacturing constraints regarding fiber curvature in conjunction with, e.g., fiber-reinforced composites (Mazumdar 2001), (electro-magnetic) aligned steel fibers in concrete (Mu et al. 2017; Li et al. 2018) or fiber-reinforced-fused deposition modeling (Tekinalp et al. 2014). To this end, a specialized parameterization and projection scheme was developed in Nomura et al. (2015) that is compatible with classical filtering techniques: the orientation is parameterized by the components of an orientation vector defined in a natural coordinate system, including isoparametric shape functions to resolve the quadratic constraint for the unit length of the orientation vector in Cartesian coordinates. No filtering techniques are available for the three-dimensional case based on angles or other intuitive parameterizations.

In this paper, we present a simultaneous topology and continuous fiber angle optimization (CFAO) approach for the three-dimensional case. The design variables are the local density and the rotation of a prescribed anisotropic base material described by a set of Euler angles. We introduce a novel filtering technique to adjust the smoothness of pathways of the material orientation. The filter provides control over the fiber curvature and is based on convolution operators which are well-known in topology optimization. The proposed filter method “filters” the material stiffness tensor. Thus, the filter technique does not depend directly on the actual parameterization for the design variables and is applicable for the filtering of periodic and/or ambivalent design variables, e.g., Euler angles. The approach for the material orientation optimization is adapted from Jantos et al. (2018) in which the material orientation optimization was part of a thermodynamic topology optimization based on the Hamilton principle. However, it is not clear if the mentioned material orientation optimization can be applied to common mathematical optimization, whose numerical behavior differs significantly from the topology optimization approach in Jantos et al. (2018) which is based on structural growth. Thus, we investigate the coupling of the thermodynamic material orientation optimization with classical topology optimization strategies. To this end, the topology is described by a continuous density interpolation with penalization (SIMP). The topology optimization is solved exemplarily via OCM. We show that well-developed classical topology optimizers can be enhanced by the thermodynamic optimization based on the Hamilton principle for additional design variables. The modifications for the inclusion of the material orientation optimization to a given topology optimization are minor, and the optimization algorithms themselves are decoupled from each other. Numerical results are given to show the influence of the filter parameter and convergence behavior compared to isotropic optimization.

This article is structured as follows: model derivations are presented in Section 2, including the material orientation optimization and the material orientation filter. In Section 3, quasi-two-dimensional and three-dimensional numerical results are investigated with respect to their convergence behavior, mesh independence, and properties of the proposed material orientation filter. Finally, we conclude our work in Section 4.

2 Model derivation

2.1 Elastic material

For interpolation between void and solid material, we use a SIMP approach (Bendsøe and Sigmund 2003) and apply it to an anisotropic elasticity tensor; hence,

$$ \mathbb{E}(\chi,\boldsymbol{\alpha}) = \chi^{p} \mathbb{E}^{\mathrm{R}}(\boldsymbol{\alpha}) $$

(1)

where the density variable χ(x) ∈ ]0,1]∀x ∈Ω is used to define the topology. The exponent p = 3 provides a penalization of intermediate densities χ ∈ ]0,1[, which yields distinct “black-and-white” solutions for the topology. The anisotropic elasticity tensor $\mathbb {E}^{\mathrm {0}}$ is rotated by means of rotation matrices Q. Several possibilities for the parameterization of Q are possible, c.f. Stuelpnagel (1964). We chose the most simple one, which is the representation in terms of three Euler angles $\boldsymbol {\alpha }(\boldsymbol {x}) = \left (\varphi (\boldsymbol {x}),\nu (\boldsymbol {x}),\omega (\boldsymbol {x})\right )$ as originally introduced in Junker (2014) and adapted for optimization in Jantos et al. (2018). It turned out that more sophisticated parameterizations, e.g., Rodrigues parameters or quaternions, increase the numerical effort without providing additional benefit. The definition of Q = Q(α) is not unique. However, one possible representation, which describes subsequent rotations firstly around the z-axis by φ followed by a rotation around the rotated x-axis by ν and again around the re-orientated z-axis by ω, is given by the following:

$$ \boldsymbol{Q}(\varphi, \nu, \omega) = \left( \begin{array}{ccc} \cos \varphi \cos \omega - \cos \nu \sin \varphi \sin \omega & -\cos \nu \cos \omega \sin \varphi-\cos \varphi \sin \omega & \sin \nu \sin \varphi \\ \cos \omega \sin \varphi + \cos \nu \cos \varphi \sin \omega & \cos \nu \cos \varphi \cos \omega - \sin \varphi \sin \omega & -\cos \varphi \sin \nu\\ \sin \nu \sin \omega & \cos \omega \sin \nu & \cos \nu \end{array}\right) \ . $$

(2)

To avoid implementations of a fourth-order material tensor, we apply the Mehrabadi–Cowin notation (Mehrabadi and Cowin 1990) to define the rotated six-dimensional second-order material tensor as follows:

$$ \mathbb{E}^{\mathrm{R}}_{6}(\boldsymbol{\alpha}) = {\boldsymbol{Q}_{6}}(\boldsymbol{\alpha})^{\mathrm{T}} \cdot \mathbb{E}^{\mathrm{0}}_{6} \cdot {\boldsymbol{Q}_{6}}(\boldsymbol{\alpha}) $$

(3)

with the orthogonal six-dimensional rotation matrix Q₆, which simply consist of the entries of Q, and the six-dimensional second-order base material tensor $\mathbb {E}^{\mathrm {0}}_{6}$, given in Mehrabadi–Cowin notation. The effective material tensor in Mehrabadi–Cowin notation becomes the following:

$$ \mathbb{E}_{6}(\chi,\boldsymbol{\alpha}) = \chi^{p} {\boldsymbol{Q}_{6}}(\boldsymbol{\alpha})^{\mathrm{T}} \cdot \mathbb{E}^{\mathrm{0}}_{6} \cdot {\boldsymbol{Q}_{6}}(\boldsymbol{\alpha})\ , $$

(4)

which can be easily transformed into the classical Voigt notation (Mehrabadi and Cowin 1990).

2.2 Topology optimization

2.2.1 Optimality criteria method

Although it is possible to derive a thermodynamic topology optimization and the material orientation optimization with the Hamilton principle in a closed form (Jantos et al. 2018), we use a separated topology optimization to show that the proposed material orientation optimization can be combined with other (established) topology optimization algorithms. For instance, we apply the well-known OCM, introduced by Bendsøe in Bendsøe and Sigmund (2003) and Sigmund (2001), due to its rather simple implementation and efficient and fast convergence behavior for the compliance minimization under volume constraint. A comparatively fast convergence is of particular interest to show that the proposed material orientation optimization can “catch-up” (comparable fast convergence) with common topology optimization algorithms to keep the number of required iteration steps at a minimum. Thus, it can be expected that more sophisticated optimization algorithms for the topology optimization could be combined with the proposed material orientation optimization, such as the “method of moving asymptotes” or “sequential linear/quadratic programming.” However, this is beyond the scope of the present work.

A finite element (FE) approach is used to solve the underlying linear elastic mechanical problem. We denote quantities discretized at the integration (Gauß quadrature) points by $(\tilde {\cdot } )$, quantities discretized at the nodes by $(\hat {\cdot } )$, and element-wise–defined quantities by $(\bar {\cdot } )$. The discretized compliance minimization under volume constraints reads as follows:

$$ \begin{array}{@{}rcl@{}} \min_{\bar{\chi},\bar{\alpha}}\text{: } &\quad c = \hat{\boldsymbol{U}}^{\mathrm{T}} \cdot \boldsymbol{K} \cdot \hat{\boldsymbol{U}} = \sum\limits_{e=1}^{N_{e}}{\hat{\boldsymbol{u}}^{\mathrm{T}} \cdot \bar{\boldsymbol{k}} \cdot \hat{\boldsymbol{u}}}\\ \text{subject to: }&\quad \varrho = \displaystyle\frac{1}{\Omega}{\int}_{\Omega}{\chi} \mathrm{d} V = \frac{1}{\Omega}\sum\limits_{e}^{N_{e}}{\bar{\chi}_{e} {\Omega}_{e}} \text{,}\\ &\quad \boldsymbol{K} \cdot \hat{\boldsymbol{U}} = \hat{\boldsymbol{F}} \text{,}\\ &\quad 0 < \chi_{\min} \le \chi \le 1 \end{array} $$

(5)

where c denotes the compliance energy defining the objective of the optimization. The quantities $\hat {\boldsymbol {U}}$ and $\hat {\boldsymbol {F}}$ denote the global nodal displacement and force vector, respectively. The global (assembled) stiffness matrix is represented by K, and the element stiffness matrix is defined by $\bar {\boldsymbol {k}}$. The total number of elements is denoted by N_e and the element’s volumes by Ω_e. The element-wise–discretized design variables are denoted by $\bar {\chi }$ for the density variable and $\bar {\boldsymbol {\alpha }}$ for the material orientation. The prescribed (relative) structure volume is given by ϱ and a minimal density $\chi _{\min \limits } = 0.001$ prevents singular stiffness matrices. The element stiffness matrix is defined as follows:

$$ \bar{\boldsymbol{k}} = \bar{\boldsymbol{k}}(\chi,\boldsymbol{\alpha}) = {\int}_{{\Omega}_{e}}{B^{\mathrm{T}}\cdot\mathbb{E}(\bar{\chi},\bar{\boldsymbol{\alpha}})\cdot\boldsymbol{B}} $$

(6)

with the material tensor $\mathbb {E}(\bar {\chi },\bar {\boldsymbol {\alpha }})$ according to (4) given in its Voigt notation. The operator matrix is denoted by B and yields the strains discretized in the integration points by $\tilde {\boldsymbol {\varepsilon }} = \boldsymbol {B}\cdot \hat {\boldsymbol {u}}$, including linear shape functions for the finite elements.

We apply the OCM algorithm for the update of the density according to Sigmund (2001). The only required modification to the OCM is the application of the rotated anisotropic material tensor given by (4). The element sensitivity for the element density variable $\bar {\chi }$ can be derived with the adjoint method and reads as follows:

$$ \frac{\partial c}{\partial \bar{\chi}} = - \hat{\boldsymbol{u}}^{\mathrm{T}} \cdot \frac{\partial \bar{\boldsymbol{k}}}{\partial \bar{\chi}} \cdot \hat{\boldsymbol{u}} $$

(7)

with

$$ \frac{\partial \bar{\boldsymbol{k}}}{\partial \bar{\chi}} = {\int}_{{\Omega}_{e}}{\boldsymbol{B}^{\mathrm{T}} \cdot \left( p\ {\bar{\chi}}^{p-1} \ \mathbb{E}^{\mathrm{R}}(\bar{\boldsymbol{\alpha}}) \right) \cdot \boldsymbol{B}} \mathrm{d}V $$

(8)

for the proposed anisotropic material with the rotated material stiffness tensor $\mathbb {E}^{\mathrm {R}}(\bar {\boldsymbol {\alpha }})$ according to (3) in its Voigt notation. The Euler angles from the previous iteration step are applied for the calculation of the sensitivities and kept constant within the (explicit) OCM update step. It is well-known that the minimization given in (5) becomes ill-posed for p > 1, resulting in mesh dependence and checkerboarding (Sigmund and Petersson 1998). To regularize the topology optimization problem, we apply the well-known sensitivity filter introduced in Sigmund (2001) with the filter radius denoted by r_χ.

2.3 Material orientation optimization

2.3.1 Evolution equations

A common approach for material orientation optimization is to align the fibers of the materials with principal stress or strain directions. For the proposed method, this is not feasible due to the (later introduced) filtering technique to smooth the fiber path of the material orientation. The filter reduces the admissible set of material orientations which may exclude the principal stress/stain directions. This issue is confirmed by numerical examples (see Section 3.4.1). In addition, the combination of a stress based orientation with the proposed material orientation filter showed poor convergence behavior: the application of the principal stress direction can yield significant changes in the local material orientation which are reversed by the filter-yielding oscillations of the design variables between iterations. Thus, we apply the thermodynamic optimization based on dissipative processes that was introduced in Jantos et al. (2018) to describe a continuous and smooth evolution of the orientation. The approach is based on the Hamilton principle, which has been proven to be beneficial for material modeling based on thermodynamic extremum principles (Junker and Hackl 2014; Junker et al. 2019). More details about the Hamilton principle and related variational techniques may be found, e.g., in Berdichevsky (2009), Pulte (1989), Capecchi and Ruta (2010), Hamilton (1834), Hamilton (1835), and Bedford (1985). The Hamilton principle for dissipative continua reads as follows:

$$ \delta\mathcal{G} + {\int}_{\Omega} \frac{\partial\mathcal{D}}{\partial\dot{\boldsymbol{\alpha}}} \cdot\delta\boldsymbol{\alpha} \ \mathrm{d}V = 0 $$

(9)

with the Gibbs energy

$$ \mathcal{G} = {\int}_{\Omega} \frac{1}{2} \boldsymbol{\sigma} \cdot [\mathbb{E}(\chi,\boldsymbol{\alpha})]^{-1} \cdot \boldsymbol{\sigma} \ \mathrm{d}V - {\int}_{\Omega} \boldsymbol{b}\cdot\boldsymbol{u} \ \mathrm{d}V - {\int}_{\partial{\Omega}} \boldsymbol{t}\cdot\boldsymbol{u} \ \mathrm{d}A \ . $$

(10)

The Gibbs energy with respect to the stresses σ serves as objective function for the optimization and could be replaced by any other appropriate objective functional. Additional constraints could also be added to the variational principle (see, e.g., Jantos et al. (2018, 2019)). However, this is beyond the scope of the present work.

The dissipation function $\mathcal {D}$ defines the form of the later derived evolution equation, which serves as an update scheme. Within the framework of thermodynamic material modeling, the dissipation function $\mathcal {D}$ corresponds to the amount of energy dissipated during microstructural evolution. An experimental evidence has been presented in Junker et al. (2015). Within optimization, the dissipation function is added to include numerical damping and regularize the optimization algorithm. Since we want to decouple the material orientation optimization from the topology optimization, which is solved via OCM, we define a dissipation function that depends only on the material orientation variables α. We define a viscous approach analogous to Jantos et al. (2018) with the following:

$$ \begin{array}{@{}rcl@{}} \mathcal{D} &=& \frac{1}{2} \frac{{\eta_{\boldsymbol{\alpha}}}}{\chi^{p}} \frac{||\boldsymbol{\sigma}||^{2}}{1-\cos^{2} \nu} \left|\left|\dot{\boldsymbol{Q}} \cdot \boldsymbol{Q}^{-1}\right|\right|^{2}\\ &=& \frac{{\eta_{\boldsymbol{\alpha}}}}{\chi^{p}} \frac{||\boldsymbol{\sigma}||^{2}}{1-\cos^{2} \nu} \left( \dot{\varphi}^{2} + \dot{\nu}^{2} + \dot{\omega}^{2} + 2 \ \dot{\varphi} \ \dot{\omega} \ \cos{\nu} \right) \ . \end{array} $$

(11)

where η_α is in terms of physics a viscosity, but serves here as a numerical damping parameter. In contrast to Jantos et al. (2018), we add the penalized density χ^p to yield a higher dissipation for regions with lower density. Thus, the material orientation is not evolving in “void” regions, which improves the numerical stability. For further details on the other terms and a detailed derivation of the following relations, we refer to Jantos et al. (2018).

The variation of (9) must be evaluated with respect to all system variables, which are the displacements u and the material orientation parameters α. The density variable χ is solved via the OCM and is considered as a “known” parameter within the material orientation optimization. The variation with respect to the displacements u results in the balance of linear momentum in its weak form, which yields the same stiffness matrix as given in (6) within the finite element approach. The variation with respect to the orientation parameters α = {φ, ν, ω} yields the evolution equations as follows:

$$ \dot{\bar{\boldsymbol{\alpha}}} = \left( \begin{array}{lll} \dot{\bar{\varphi}} \\ \dot{\bar{\nu}} \\ \dot{\bar{\omega}} \end{array}\right) = \frac{\bar{\chi}^{p}}{\sqrt{2} {\eta_{\boldsymbol{\alpha}}} \bar{\sigma}}\left( \begin{array}{lll} \bar{p}_\varphi - \bar{p}_\omega \cos(\bar{\nu}) \\ \bar{p}_\nu [1-\cos^{2}(\bar{\nu})] \\ \bar{p}_\omega - \bar{p}_\varphi \cos(\bar{\nu}) \end{array}\right) $$

(12)

with

$$ \bar{p}_{k} = \displaystyle{\int}_{{\Omega}_e}{-\frac{1}{2} \boldsymbol{\sigma}_{6} \cdot \frac{\partial \mathbb{E}_{6}^{-1}}{\partial \alpha_{k}} \cdot \boldsymbol{\sigma}_{6}} \mathrm{d} V = \displaystyle{\int}_{{\Omega}_e}{\frac{1}{2} \boldsymbol{\varepsilon}_{6} \cdot \frac{\partial \mathbb{E}_{6}}{\partial \alpha_{k}} \cdot \boldsymbol{\varepsilon}_{6}} \mathrm{d} V $$

(13)

which are called driving forces within the framework of material modeling and fulfill the propose of sensitivities. The derivative of the material stiffness with respect to the material orientation parameters is given by the following expression:

$$ \frac{\partial \mathbb{E}_{6}}{\partial \alpha_{k}} = \chi^{p} \left[ \left( \frac{\partial {\boldsymbol{Q}_{6}}}{\partial \alpha_{k}}\right)^{\mathrm{T}} \cdot \mathbb{E}^{\mathrm{0}}_{6} \cdot {\boldsymbol{Q}_{6}} + {\boldsymbol{Q}_{6}}^{\mathrm{T}} \cdot \mathbb{E}^{\mathrm{0}}_{6} \cdot \frac{\partial {\boldsymbol{Q}_{6}}}{\partial \alpha_{k}} \right] \ . $$

(14)

The evolution (12) can be used as an update scheme by applying the explicit time discretization as follows:

$$ \bar{\boldsymbol{\alpha}}_{i+1} = \bar{\boldsymbol{\alpha}}_{i} + {\Delta} t \left.\dot{\bar{\boldsymbol{\alpha}}}\right|_{i} $$

(15)

where the index i denotes quantities at the previous iteration step and the updated design for the current iteration step is denoted by i + 1. The time increment Δt and the viscosity η_α together account for the numerical damping and are defined as follows:

$$ \frac{\Delta t}{{\eta_{\boldsymbol{\alpha}}}} = m \ \frac{\pi}{4} \ ||\mathbb{E}^{\mathrm{0}}|| $$

(16)

where $||\mathbb {E}^{\mathrm {0}}||$ normalizes the driving forces $\bar {p}_{k}$ in conjunction with $\bar {\sigma }$. The factor $\frac {\pi }{4}$ and the move limit m = 0.2 adjust the maximum angle increment per iteration.

2.3.2 Material orientation filter

The purpose of the material orientation filter is to control the smoothness of the anisotropy, i.e., the curvature of fibers, but also to ensure mesh independence. Euler angles cannot be filtered directly by means of a convolution operator due to their periodicity. For example, the harmonic mean of two angles α_k = {0, π} would yield a “filtered” result of $\alpha _{k}^{*} = \frac {\pi }{2}$, which is obviously wrong because the “filtered” result should be either 0 or π since both describe effectively the same material orientation. We solve this issue by introducing a filtering technique on the effective material tensor instead of the rotation parameters to circumvent the problem of periodicity. The effective material tensor is filtered after each design update by means of a convolution operator. After the filtering step, the orientation parameters must be retrieved from the filtered material tensor. The whole filtering procedure is divided as follows:

$$ \boldsymbol{\alpha} \underbrace{\xrightarrow[\text{definition}]{\text{material}} \mathbb{E}_{6} \xrightarrow[\text{filter}]{\text{convolution}}}_{\text{filtering}} \mathbb{E}_{6}^{*} \underbrace{\xrightarrow[\text{reduction}]{\text{dimension}} \mathbb{E}^{*}_3 \xrightarrow[\text{decomposition}]{\text{spectral}} \boldsymbol{Q}^{*} \xrightarrow[\text{recovery}]{\text{parameter}}}_{\text{extracting variable(s)}} \boldsymbol{\alpha}^{*} $$

(17)

where “filtered” quantities are denoted by (⋅)^∗. In the first step, the effective material tensor must be evaluated as given by (4), which depends on the density χ. Thus, the material orientation is weighted by the actual material density. This is reasonable because the orientation of “void” material has less to no influence on the filtered orientation.¹

The second step is the actual filtering. The filtered material tensor for the element e is via a convolution operator as follows:

$$ \left.{\mathbb{E}_{6}^{*}}\right|_e = \frac{\displaystyle \sum\limits_f^{N_e}{{\Omega}_f \ w_{\alpha}({\Delta} x_{fe}) \ \left.\mathbb{E}_{6}\right|_f}}{\sum\limits_f^{N_e}{{\Omega}_f \ w_{\alpha}({\Delta} x_{fe})}} \ . $$

(18)

For simplicity, we apply a linear convolution operator (weight function) analogously to the sensitivity filter of the density variable as follows:

$$ w_{\alpha}({\Delta} x_{fe}) = \max{\left( 0, 1 - \frac{\Delta x_{fe}}{{r}_{\alpha}}\right)} $$

(19)

where filter radius r_α for the material orientation filter can be chosen independently from the filter radius r_χ for the sensitivity filter of the density variable.

The orientation parameters, which yield the filtered effective material $\mathbb {E}_{6}^{*}$, are required to process further design updates. The third step of (17) is to calculate the associated three-dimensional second-order material tensor $\mathbb {E}^{*}_{3}$, whose eigenvectors coincide with the normals of the material symmetry planes (i.e., principal material directions) and whose eigenvalues coincide with the stiffness in the corresponding direction (i.e., Young’s modulus) (Cowin and Mehrabadi 1987). The associated material tensor is given as follows:

$$ \mathbb{E}^{*}_3 = \left( \begin{array}{lll} (\mathbb{E}_{6}^{*})_{11} + (\mathbb{E}_{6}^{*})_{12} + (\mathbb{E}_{6}^{*})_{13} \ & \ (\mathbb{E}_{6}^{*})_{16} + (\mathbb{E}_{6}^{*})_{26} + (\mathbb{E}_{6}^{*})_{36} \ & \ (\mathbb{E}_{6}^{*})_{15} + (\mathbb{E}_{6}^{*})_{25} + ({\mathbb{E}}_{6}^{*})_{35} \\ (\mathbb{E}_{6}^{*})_{16} + (\mathbb{E}_{6}^{*})_{26} + (\mathbb{E}_{6}^{*})_{36} \ & \ (\mathbb{E}_{6}^{*})_{12} + (\mathbb{E}_{6}^{*})_{22} + (\mathbb{E}_{6}^{*})_{23} \ & \ (\mathbb{E}_{6}^{*})_{14} + (\mathbb{E}_{6}^{*})_{24} + ({\mathbb{E}}_{6}^{*})_{34} \\ (\mathbb{E}_{6}^{*})_{15} + (\mathbb{E}_{6}^{*})_{25} + (\mathbb{E}_{6}^{*})_{35} \ & \ (\mathbb{E}_{6}^{*})_{14} + (\mathbb{E}_{6}^{*})_{24} + (\mathbb{E}_{6}^{*})_{34} \ & \ (\mathbb{E}_{6}^{*})_{13} + (\mathbb{E}_{6}^{*})_{23} + ({\mathbb{E}}_{6}^{*})_{33} \end{array}\right) \ . $$

(20)

The spectral decomposition of $\mathbb {E}^{*}_{3}$ yields an orthogonal basis for orthotropic materials that coincides with a “filtered” rotation matrix Q^∗: the eigenvectors define the three (independent) directions of the rotated basis of the base material. The eigenvalues correspond to the Young’s moduli in each direction and can be used to determine which axis of the base material corresponds to which eigenvector. For example, if the Young’s moduli of the base material are E_z > E_y > E_x, then the first eigenvector (largest eigenvalue) corresponds to the z-axis, the second eigenvector corresponds to the y-axis, and the last eigenvector (smallest eigenvalue) corresponds to the x-axis. Due to the symmetry of the material tensor, the solution for Q^∗ is not unique, especially for transverse isotropic materials that yield two identical eigenvalues. Nevertheless, this is uncritical for practical application as long as any ambivalent solution of Q^∗ yields the correct rotated material tensor for the finite element analysis. The eigenvectors of non-orthotropic material tensors do not form an orthogonal basis and the computation of the rotation matrix Q^∗ is not trivial (Cowin and Mehrabadi 1987). Thus, we apply the material orientation filter only to orthotropic materials (representative for all its subset materials, such as transverse isotropic materials).

The last step of the proposed material orientation filter requires the recovery of the Euler angles from the rotation matrix Q^∗. The Euler angles are calculated with respect to the rotation matrix given in (2) by Slabaugh (1999) as follows:

$$ \begin{array}{@{}rcl@{}} |Q^{*}_{33}| < 1&: \left\{\begin{array}{lllll} \nu = \arccos(Q^{*}_{33})\\ \varphi = \mathrm{atan2}\left( \displaystyle\frac{Q^{*}_{13}}{\sin{\nu}}, -\displaystyle\frac{Q^{*}_{23}}{\sin{\nu}}\right)\\ \omega = \mathrm{atan2}\left( \displaystyle\frac{Q^{*}_{31}}{\sin{\nu}}, \displaystyle\frac{Q^{*}_{32}}{\sin{\nu}}\right) \end{array}\right. \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} Q^{*}_{33} = 1&: \left\{\begin{array}{lllll} \nu = 0\\ \varphi + \omega = \mathrm{atan2}\left( Q^{*}_{21}, Q^{*}_{11}\right) \end{array}\right. \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} Q^{*}_{33} = -1&: \left\{\begin{array}{lllll} \nu = \pi\\ \varphi - \omega = \mathrm{atan2}\left( Q^{*}_{21}, Q^{*}_{11}\right) \end{array}\right. \end{array} $$

(23)

with the inverse tangent function $\mathrm {atan2}\left (\cdot ,\cdot \right )$ defined by the following:

$$ \mathrm{atan2}\left( y,x\right) = \left\{\begin{array}{lllll} \arctan\left( \frac{y}{x}\right) & \text{for } x > 0 \\ \arctan\left( \frac{y}{x}\right) + \pi & \text{for } x < 0 \text{ and } y \ge 0 \\ \arctan\left( \frac{y}{x}\right) - \pi & \text{for } x < 0 \text{ and } y < 0 \\ \frac{\pi}{2} & \text{for } x = 0 \text{ and } y > 0 \\ -\frac{\pi}{2} & \text{for } x = 0 \text{ and } y < 0 \end{array}\right. $$

(24)

which preserves quadrant information of the angles. Either φ or ω can be chosen arbitrarily for cases (22) and (23), resulting in infinite solutions for ν = {0, π}. The non-uniqueness of the solution, as well as the ambiguity of the Euler angles, is uncritical for practical application for the same reason as the non-uniqueness of Q^∗: the Euler angles are used for “internal” calculations (i.e., they do not carry any history information and are also not used for visualization).

The main purpose of the Euler angles is to ensure the definition of feasible orthogonal rotation matrices. The non-uniqueness of the solutions for the Euler angles is resolved for the finite element analysis by the symmetry of the effective material tensor (each ambivalent solution yields the same material tensor). The non-uniqueness is also uncritical for the design update: the driving forces (≈ sensitivities) for the rotation parameters are calculated for each element separately. Thus, the increment for the update fits with the local parameterization and is not influenced by the ambiguity of neighboring elements. The particular choice for the rotation parameterization does not influence the calculation of the sensitivities for the density variable, which depend on the rotation matrix, but not explicitly on the rotation parameters. Nevertheless, it is possible that the numerical values of the Euler angles are sporadically changing by ± π between each optimization step, which reveals to be problematic if the values of the Euler angles are used for visualization of the material orientation. Thus, it is recommended to apply the symmetry axes of the material tensor for visualizations, i.e., the eigenvectors of $\mathbb {E}^{*}_{3}$ or the basis vectors of the rotation matrix Q^∗. The usage of Euler angles is not mandatory for application of the proposed material orientation filter. The filter is applicable for other material orientation parameterizations as long as a mapping $\mathbb {E}^{\mathrm {R}}(\alpha ) \to \alpha$ or Q(α) → α exists.

2.4 Optimization sequence

The results of SIMP are known to the depend on initial conditions for the design variable resulting from the nonconvex minimization problem (Sigmund and Petersson 1998; Rion and Bruyneel 2006). We apply the common initial condition for the density variable χ₀ = ϱ, which is a homogeneous distribution that fulfills the volume constraint. The initial material orientation of anisotropic materials strongly influences the change of the topology in the first iteration steps: the topology optimization tends to “fall” in a local minimum which depends on the (non-optimal) initial material orientation. This can be resolved by continuation methods for the material anisotropy (Nomura et al. 2015). Another possibility is to apply the optimal material orientation for the initial (homogenous) density distribution as initial condition. This could be done by a preceded optimization based on the update scheme in (15) with χ = ϱ. For the applied compliance minimization, the principal stress directions are known to be the optimal orientation at least for “shear-weak” materials.² Thus, we circumvent the additional calculation effort of a preceded material orientation optimization by applying the principal stress directions as initial conditions for the material orientation based on the FE solution with an isotropic material. In the very first FE step, we homogenize the anisotropic elasticity tensor $\mathbb {E}_{6}$ using the Haar measure, c.f. Hackl (1999). This yields the isotropic elasticity tensor as follows:

$$ \begin{array}{@{}rcl@{}} \mathbb{E}_{6}^{\text{iso}}(\chi) &=& \frac{\pi}{(2 \pi)^3} {\int}_{\varphi = 0}^{2\pi} {\int}_{\nu = 0}^{\pi} {\int}_{\omega = 0}^{2\pi}{ \boldsymbol{Q}_{6}}^{\mathrm{T}} \cdot \mathbb{E}_{6}(\chi, \boldsymbol{\alpha})\\ &&\cdot {\boldsymbol{Q}_{6}} \sin \nu \mathrm{d}\omega \mathrm{d}\nu \mathrm{d}\varphi \end{array} $$

(25)

with χ = χ₀ = ϱ to calculate the principal stresses in each element. The implementation to find the local initial material orientation from the principal stresses is based on the material orientation filter: the spectral decomposition of the three-dimensional second-order stress tensor is carried out by replacing the associated three-dimensional second-order material tensor $\mathbb {E}^{*}_{3}$ in (18).

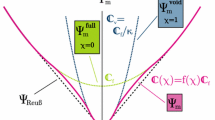
After the initial conditions for the design variables have been defined, the iterative optimization is carried out, which includes alternating single FE solution steps and design updates. This corresponds to the usual operator split applied in structural optimization. The density χ and the material orientation α are updated simultaneously but separately after each FE step: both update algorithms are based on an explicit discretization, i.e., the update depends only on the known design from the current iteration i (given by $\bar {\chi }_{i}$ and $\bar {\boldsymbol {\alpha }}_{i}$) and the resulting element displacements $\hat {\boldsymbol {u}}_{i} = \hat {\boldsymbol {u}}(\bar {\chi }_{i},\bar {\boldsymbol {\alpha }}_{i})$ and strains $\tilde {\boldsymbol {\varepsilon }}_{i} = \tilde {\boldsymbol {\varepsilon }}(\bar {\chi }_{i},\bar {\boldsymbol {\alpha }}_{i})$ calculated via the FEM by solving $\boldsymbol {K}(\bar {\chi }_{i},\bar {\boldsymbol {\alpha }}_{i}) \cdot \hat {\boldsymbol {U}}_{i} = \hat {\boldsymbol {F}}$. Thus, the update for the topology and the update for the material orientation are decoupled and can be implemented separately. The optimization procedure is illustrated in Fig. 1.³

Fig. 1

Flowchart for the proposed method

Fig. 2

Boundary conditions for the Messerschmidt–Bölkow–Blohm (MBB) beam. The initial material orientation is based on the principal stresses for a mesh with 10 × 30 × 1 elements

The $L^{\infty }$ norm of the error of the density variable χ is usually used as a convergence criterion for OCM. This is not reasonable for the presented model because the change in the material orientation is not accounted for. The definition of an appropriate quantity for the change in the material orientation is difficult (or impossible) due to the periodicity of the Euler angles. Thus, we take into account the relative change in the structural compliance (objective function, see (5)) as follows:

$$ c_\text{rel} = \frac{|c_{i} - c_{i-1}|}{c_{i}} < \text{ctol} = 10^{-5} $$

(26)

as a convergence criterion, which automatically includes the influence of all design variables.

3 Numerical results

3.1 Parameters and boundary conditions

For numerical investigations, we apply the orthotropic material tensor (Voigt notation) as follows:

$$ \left( \mathbb{E}^{\mathrm{0}}\right)^{-1} = \left( \begin{array}{llllll} \frac{1}{E_1} & -\frac{\nu_{12}}{E_1} & -\frac{\nu_{13}}{E_1} & 0 & 0 & 0 \\ & \frac{1}{E_2} & -\frac{\nu_{23}}{E_2} & 0 & 0 & 0 \\ & & \frac{1}{E_3} & 0 & 0 & 0 \\ & & & \frac{1}{2 G_{23}} & 0 & 0 \\ & \text{sym} & & & \frac{1}{2 G_{13}} & 0 \\ & & & & & \frac{1}{2 G_{12}} \end{array}\right) $$

(27)

with

$$ \begin{array}{@{}rcl@{}} E_{1} &=& 10 \times 10^{3} \qquad\quad \nu_{12} = 0.4 \qquad\quad G_{12} = 10 \times 10^{3}\\ E_{2} &=& 50 \times 10^{3} \qquad\quad \nu_{13} = 0.3 \qquad\quad G_{13} = 20 \times 10^{3}\\ E_{3} &=& 250 \times 10^{3} \quad\quad ~~ \nu_{23} = 0.2 \qquad\quad G_{23} = 50 \times 10^{3} \end{array} $$

with E₃ > E₂ > E₁. E₃ corresponds to the first principal material direction (highest stiffness), E₂ to the second, and E₁ to the third. The parameters for the OCM are the same as in Sigmund (2001). The viscosity and time increment for the evolution equation of the material orientation optimization are defined in (16). Different filter radii r_α will be applied to investigate the influence of the material orientation filter. The influence of r_χ (sensitivity filter radius for the density variable) is not investigated because there is extensive research in the literature. Figures 2, 3, and 4 show the boundary conditions and the initial material orientation for the quasi-two-dimensional (discretization by a single finite element in the third spatial direction) benchmark problems applied in the following sections. The three-dimensional examples evaluated in Section 3.5 are given in Fig. 5.

Fig. 3

Boundary conditions for the L-shaped cantilever. The initial material orientation is based on the principal stresses for a mesh with 1800 elements

Fig. 4

Boundary conditions for the bending problem. The initial material orientation is based on the principal stresses for L = 2 and a mesh with 30 × 60 × 1 elements

Fig. 5

Boundary conditions for the three-dimensional examples: a cantilever supported on one side subject to a downward pointing load on the lower middle of the opposite free end, b cuboid supported by floating bearings at the lower corners subject to a downward pointing load in the middle of the upper surface, c circular L-shaped cantilever supported by locating bearings at the lower corners subject to a downward pointing load on the lower middle of the opposite free end, and d cube supported by locating bearings at the lower corners subject to a downward pointing load in the middle of the lower surface

The principal material directions are visualized by dashes with the length scaled to the local density χ and are defined by the rotation $\boldsymbol {Q}(\boldsymbol {\alpha }^{*}) \cdot {\boldsymbol {e}}_{k}$, where e_k are the corresponding base unit vectors. Due to the orthotropic material, the three principal directions define an orthogonal base. The first and second principal material directions result to be parallel to the plane of quasi-two-dimensional problems. This is reasonable because the third principal material direction yields the least stiffness and is, therefore, orientated out-of-plane where no loads are applied (Jantos et al. 2018). Thus, only the first principal material direction is displayed for better clearance for quasi-two-dimensional cases. The

structure is validated quantitatively by its stiffness, which is defined as the inverse of the structural compliance c given in (5) normalized to the stiffness of the first FE solution step with ${\mathbb {E}}_{6}^{\text {iso}}(\chi = \varrho )$ given in (25) (Figs. 6 and 7).

3.2 Convergence behavior

We investigate the convergence behavior of the proposed method in comparison with the optimization for an isotropic material with $\mathbb {E}(\chi )_{6} = \mathbb {E}_{6}^{\text {iso}}(\chi )$ given in (25), which yields the Young’s modulus E ≈ 82.4 × 10³ and the Poisson’s ratio ν ≈ 0.153. The final results after convergence according to (26) and after 300 iterations are given in Fig. 6 for the MBB beam and in Fig. 8 for the L-shaped cantilever. The evolution of the normalized stiffness within the iteration process is given in Fig. 7 for the MBB beam and in Fig. 9 for the L-shaped cantilever.

Fig. 6

Topologies obtained for the MBB beam with prescribed structure volume ϱ = 50%. Results after convergence with ctol = 10^− 5 and after 300 iterations

Fig. 7

Change in the normalized stiffness within 100 iteration steps for the for the MBB beam corresponding to Fig. 6

Fig. 8

Topologies obtained for the L-shaped cantilever with 2304 elements for an orthotropic and isotropic material. Filter radii r_α = r_χ = 0.025. Results after convergence with ctol = 10^− 5 and after 300 iterations. Prescribed structure volume ϱ = 50%

Fig. 9

Change in the normalized stiffness within 100 iteration steps for the corresponding results given in Fig. 8 with prescribed structure volume ϱ = 50% and additionally for ϱ = {30,75}%

The stiffness of the anisotropic structure is about three times higher than that of the (orientation-homogenized) isotropic material. The resulting topology for the orthotropic material also differs from the isotropic case. Thus, a (simultaneous) optimization of the material orientation and topology is essential to find an optimal design for structures made of anisotropic materials.

The proposed method yields a smooth convergence of the structural stiffness and does not impair the convergence of the OCM for the topology optimization. For the MBB beam, the anisotropic case is converging even faster than the isotropic case and yields converged results after 63 iterations. The results for the isotropic case still change noticeably after 144 iterations. However, this observation cannot be concluded for the results given in the following section in which the number of required iteration steps for the anisotropic case is similar to the isotropic case. This also applies to the L-shaped cantilever: the number of iteration steps until convergence is higher by 12 steps for the anisotropic case. The proposed convergence criterion given in (26) seems reasonable for the anisotropic case: the relative change in the structural stiffness between the converged and the 300th iteration step is less than 1%. This is also observed for the L-shaped cantilever. Thus, the proposed model seems to converge towards a (local) optimum. The proposed material orientation filter serves as regularization to the material orientation optimization which yields presumably a well-posed problem. The results given in the following section affirm this assumption and show (weak) mesh dependence of the results without the material orientation filter and mesh-independent results by applying the proposed filter.

3.3 Mesh independence

Mesh dependence of results obtained with a sensitivity-based CFAO without regularization of the material orientation are reported in Nomura et al. (2015) and Hoglund and Smith (2016). Thus, we investigate the mesh dependence of the proposed material orientation optimization with and without the proposed material orientation filter. The (mesh-independent) sensitivity filter for the topology optimization is applied so that only the mesh dependence of the material orientation optimization is investigated. The results for the MBB beam, the L-shaped cantilever, and the bending problem with different mesh resolutions are given in Figs. 10, 11, and 12, respectively.

Fig. 10

Topologies and material orientations obtained for the MBB beam with (left column) and without (right column) application of the material orientation filter. The sensitivity filter radius is r_χ = 0.075 for all cases and r_α = 0.075 for the cases with applied material orientation filter. Only the material direction of every forth element is illustrated for the mesh with 240 × 80 × 1 elements (except for the close-up in (a) and (b))

Fig. 11

Topologies and material orientations obtained for the L-shaped cantilever with (left column) and without (right column) application of the material orientation filter. The sensitivity filter radius is r_χ = 0.0375 for all cases and r_α = 0.0375 for the cases with applied material orientation filter. The material direction is illustrated for every element of the mesh with 5184 elements and every fifth element for the mesh with 20,736 elements

Fig. 12

Topologies and material orientations obtained for the bending problem (L = 2) without application of the material orientation filter. The sensitivity filter radius is r_χ = 0.05. The material direction of every element is illustrated for the mesh with 60 × 30 × 1 elements, every second element for the meshes with 100 × 50 × 1 elements, and every twelfth element for the mesh with 200 × 100 × 1 elements

The material orientation optimization without the material orientation filter yields visually mesh-independent results for the bending problem and only slight mesh dependence for the L-shaped cantilever: the unfiltered results of the L-shaped cantilever yield unsteady material pathways near the inner corner of the design space. Those unsteady pathways do not occur if the material orientation filter is applied, resulting in smooth pathways for the material orientation. Two typical effects of the smoothing due to the material orientation filter can be seen in Fig. 10a: within the connection of the lower two trusses, the fiber pathways are shaped in a smooth turn following the structure surface. On the other hand, the two left trusses merge into the third right truss with both fiber pathways converging to the pathway within the third truss. The undesired contrary behavior of non-smooth pathways is observed when our filter has not been applied, cf. Fig. 10b.

Mesh dependence can be observed for the MBB beam, although the results only differ for the coarse mesh with 60 × 20 × 1 elements. This could lead to the assumption that the mesh independence of the material orientation optimization is bounded by mesh convergence, i.e., if the mesh is fine enough, the method becomes mesh-independent. Nevertheless, affirmation of this assumption requires more sophisticated research on different boundary problems, which is beyond the scope of the present work. We conclude that although reasonable results are obtained without the material orientation filter, mesh independence can only be ensured by using the proposed material orientation filter. In addition, the material orientation filter can be used to control the smoothness of the material orientation pathways, i.e., the curvature of fibers. This property is investigated in detail in the following section.

3.4 Material orientation filter properties

3.4.1 Material orientation optimization without topology

In this section, we investigate the influence of the filter radius r_α of the proposed material orientation filter on the smoothness of the material orientation pathways on examples without topology optimization, i.e., we apply full material in the whole design space $\varrho = 1 \leftrightarrow \chi = 1 \forall \boldsymbol {x}\in {\Omega }$ (the influence of r_α in conjunction with the topology optimization is given in the next section). The resulting material orientations for different values of r_α are given in Fig. 13 for the MBB and in Fig. 14 for the L-shaped cantilever. Quarter circles with secant-length of 2 r_α (or its half) are aligned to the fiber path.

Fig. 13

Material orientation obtained for the MBB beam with 30 × 10 × 1 elements having different filter radii r_α = {0.15,0.3,0.45,0.60} for an anisotropic material with a homogeneous density distribution. The quarter circles with secant-length of 2 r_α (or its half) are aligned to the fiber path

Fig. 14

Material orientation obtained for the L-shaped cantilever beam with 2304 elements having different filter radii r_α = {0.03,0.12} for an anisotropic material with a homogeneous density distribution. The quarter circles with secant-length of 2 r_α are aligned to the fiber path

The material orientation filter yields smooth material orientation pathways in all cases. As expected, the pathways become smoother with increasing filter radius r_α. Thus, the resulting material orientations do not coincide with the principal stress direction used as initial condition (see Figs. 2 and 3) and depend on the particular value for the filter radius r_α. The quarter circles with secant-length of 2 r_α coincide with the largest fiber path curvature (smallest arc radius) within the structure. Following simple trigonometric relations, it can be concluded that the maximum fiber curvature is constrained to $\left (\sqrt {2} \ {r}_{\alpha }\right )^{-1}$ by the proposed material orientation filter.

The structural stiffness is decreased with increasing filter radius r_α which results from the reduced set of admissible material orientations: it is not possible for the optimization to develop strong fiber curvatures so that the optimization yields a “worse optimum.” This effect is analogous to the reduced set of possible topologies by applying larger filter radii r_χ which increase the minimum member size. The effect of the filter radius r_α on the resulting topology for a simultaneous optimization of the topology and material orientation is discussed in the next section.

3.4.2 Influence on shape and topology

Figures 15, 16, 17, and 18 show the results of the presented quasi two-dimensional benchmark problems with varying filter radius r_α for the proposed material orientation filter. The sensitivity filter radius r_χ is fixed for each boundary problem. As for the previous results, quarter circles with secant-length of 2 r_α are aligned to the fiber path (except for the results in which the filter radius is to small to be displayed properly).

Fig. 15

Results with ctol = 10^− 5 obtained for the MBB beam with 120 × 40 × 1 elements with r_χ = 0.0375 and different filter radii r_α = {0.0375,0.075,0.1125,0.15}

Fig. 16

Change in the normalized stiffness corresponding to the results given in Fig. 15

Fig. 17

Results with ctol = 10^− 5 obtained for the bending problem with 60 × 30 × 1 elements (L = 2) with r_χ = 0.05 and different filter radii r_α = {0.05,0.1,0.15,0.2}

Fig. 18

Results obtained for the bending problem with 240 × 60 × 1 elements (L = 4) with r_χ = 0.025 for an anisotropic material with different filter radii r_α = {0.025,0.125} and for an isotropic material. The material direction is illustrated for every seventh element

The benchmark problems show the same properties related to the material orientation filter radius r_α: the material orientation pathways are smoothed, i.e., the fiber curvature is reduced, with increasing r_α, especially at corners and truss connection points. As before, the quarter circles with secant-length of 2 r_α coincide with the largest fiber curvature within the structures resulting in a maximum curvature constrained to $\left (\sqrt {2} \ {r}_{\alpha }\right )^{-1}$.

The smoothing effect yields different angles for the trusses to be optimal. These effects are especially remarkable for the bending problem given in Fig. 18 for which the increased filter radius r_α yields a streamlined design. The adopted angles can also yield different topologies to be optimal, for example, two trusses connected by an acute angle are merged, as observed for the MBB beam. The minimum member size is not influenced by r_α. Thus, the filter radius r_α can be used to constrain the fiber curvature independent of the filter radius for the sensitivity filter r_χ which, in turn, can be used to constrain the minimum size of structure members. The structural stiffness decreases with larger filter radii. This is reasonable because larger filter radii restrict the set of possible designs. Thus, the angle optimization seems to work well because less restricted optimizations yield better (quantitative) results which is also reported in Nomura et al. (2015).

3.5 Three-dimensional examples

The examples given in the previous sections are quasi-two-dimensional cases: the mesh is discretized by a single element in the third spatial direction, but a three-dimensional FE solution and optimization are applied. In this section, we present “true” three-dimensional examples. An isosurface representation⁴ is applied for better visualization. For the three-dimensional case, the second principal material direction is also an important information for optimization of the orthotropic material with three distinct material directions used here. Thus, the resulting topologies, including the first and second principal material direction for the boundary problems given in Fig. 5 a and b are presented in Figs. 19 and 20. The results for the boundary problem given in Fig. 5 c and d (including only the first principal material direction) are presented in Fig. 21 and Fig. 22 for varying material orientation filter radii r_α.

Fig. 19

Results for the three-dimensional problem given in Fig. 5a after 142 iterations. First principal material direction in the first line is followed by the second principal material direction in the second line. The results for an isotropic material after 106 iterations is given in the third line. Mesh with 40 × 20 × 20 elements and filter radius r_χ = r_α = 0.075. Relative structure volume ϱ = 15%

Fig. 20

Results for the three-dimensional problem given in Fig. 5b. First and second principal material direction for an anisotropic material after 184 iterations in the first line and results for an isotropic material after 156 iterations in the second line. Mesh with 32 × 32 × 16 elements and filter radius r_χ = r_α = 0.1. Relative structure volume ϱ = 20%

Fig. 21

Results for the three-dimensional problem given in Fig. 5c. First principal material direction for an anisotropic in the first and second line with different filter radii r_α = {0.1,0.5} and for an isotropic material in the third line. Mesh with 41,760 elements, filter radius r_χ = 0.1, and relative structure volume ϱ = 15%

Fig. 22

Results for the three-dimensional problem given in Fig. 5d. Mesh with 26 × 26 × 26 elements and filter radii r_χ = 0.06 and r_α = {0.06,0.12,0.18,0.24}. Relative structure volume ϱ = 10%

Figure 19 shows reasonable results for the first and second principal material direction: the first principal material direction aligns with trusses to reinforce the bending stiffness, whereas the second principal direction aligns with the shear direction within the trusses. The third principal direction (not displayed, but perpendicular to the first and second) aligns with the rotation axis of the bending moment in the trusses. Thus, a weakening of the structure against the bending moment is avoided because the third material direction is the least stiff. In contrast to the two-dimensional benchmark problems, the differences in the resulting topologies are more significant for the three-dimensional examples. The observations regarding the influence of the material orientation filter with increasing filter radius r_α can be reproduced for the three-dimensional case (Fig. 22): larger filter radii smooth the fiber paths which results in different angles of the trusses and some trusses are merged.

4 Conclusions

We presented an approach for simultaneous optimization of the material orientation and topology optimization for anisotropic three-dimensional materials. A continuous density interpolation with penalization of intermediate densities (SIMP) is applied to the topology. The anisotropic base material is subjected to a continuous three-dimensional rotation defined by a set of three Euler angles. Thus, the proposed method can be classified as “continuous fiber angle optimization” (CFAO).

The material orientation optimization is given by a thermodynamic optimization approach that is based on the Hamilton principle which can be enhanced by constraints on the material orientation. For instance, we presented a material orientation filter to control the smoothness of the pathways of the principal material direction, i.e., curvature of fibers. The material orientation filter is based on a convolution operator and “filters” the material stiffness tensor, and is technically independent of the actual parameterization for the material orientation, and is thus applicable for the filtering of periodic and/or ambivalent design variables, e.g., Euler angles. Nevertheless, the filter requires the existence of a mapping from the material stiffness tensor or the rotation matrix to the orientation parameters. A mapping scheme was derived for the applied set of Euler angles for an orthotropic base material. Numerical examples were given that relate to the influence of the material orientation filter on the fiber curvature: the maximum curvature is constrained to $\left (\sqrt {2} \ {r}_{\alpha }\right )^{-1}$ by the proposed filter (with filter radius r_α). Although this relation is not derived mathematically, all numerical (two-dimensional) examples confirm this characteristic.

We combined the material orientation optimization with classical topology optimizers, i.e., the “optimality criteria method” (OCM). The OCM is used as a solution algorithm for the topology optimization, including a sensitivity filter. The modifications required for the topology optimization algorithm are minor: only the base material stiffness matrix must be changed. Due to the explicit update schemes, the optimization procedures for the topology and the material orientation are decoupled. Numerical examples showed that the convergence of the OCM is not impaired by the proposed material orientation optimization, i.e., the number of required iteration steps does not change drastically.

The proposed method for topology and material optimization opens opportunities for future modifications and studies. The rather basic OCM yields promising results. More sophisticated solution algorithms for the topology optimization (e.g., “sequential linear/quadratic programming,” “method of moving asymptotes”), globalization techniques, and filtering techniques (e.g., gradient-based regularization, density filters, and morphological-based filters) could be combined with the proposed material orientation optimization to further improve the convergence and the overall results. The material orientation optimization could be further improved by developing more sophisticated and different types of dissipation functions which determine the update scheme of for the optimization. Furthermore, the proposed material orientation filter is independent of the applied update scheme for the design variables and could be therefore combined with classical (sensitivity based) optimization schemes for the material orientation.