An engineering interpretation of Nesterov’s convex minimization algorithm and time integration: application to optimal fiber orientation

Abstract

Nesterov’s 1983 first-order minimization algorithm is equivalent to the numerical solution of a second-order ODE with non-constant damping. It is known that the algorithm can be obtained by time discretization with asynchronous damping, a long-standing technique in computational explicit dynamics. We extend the solution of the ODE to other time discretization algorithms, analyze their properties and provide an engineering interpretation of the process as well as a prototype implementation, addressing the estimation of the relevant parameters in the computational mechanics context. The main result is that a standard Newmark-type time-integration finite element code can be adopted to perform classical optimization in mechanics. Standard FE analysis, sensitivity analysis and optimization are performed in sequence using a typical FE framework. Geometric nonlinearities in the conservative case are addressed by the adjoint-variable method and examples of optimal fiber orientation are shown, exhibiting remarkable advantages with respect to more traditional optimization algorithms.

1 Introduction

1.1 Context

It is accepted that optimal gradient algorithms for smooth convex minimization were inaugurated by Yurii Nesterov in 1983 [1] as a version of the momentum algorithm by Polyak [2], see also [3]. The word momentum indicates the presence of underlying equations of motion. This is known [4] and has been explored before in applied convex optimization. It is worth mentioning that a unification of the conjugate-gradient method, i.e. Hestenes and Stiefel [5], was proposed by Karimi et al. [6], with a state-of-the-art paper on first-order methods published in 2020, cf. Drori and Taylor [7] pointing out to a unification of the first-order algorithms.

Numerous versions of Nesterov’s algorithm have been successful in the machine-learning community [8] with reported advantages with respect to momentum (or heavy ball) algorithms. In computational mechanics, few applications were published, and none achieved by explicit Newmark time integration. Carlon et al. [9] adopted Donoghue and Candès [10] adaptive restart technique for Nesterov’s algorithm in the context of optimal experimental design, but without the time-integration equivalence shown here. In the context of computational homogenization, Schneider [11] made use of the original asynchronous integrator presented by Su, Boyd and Candès [4]. Convergence of Nesterov’s algorithm in [9, 11] shows the same behavior we observe in this work and the same advantages with respect to the steepest descent method were reported. However, marked differences exist, as no attempt was made toward the use of a damping-insensitive time integrator.

The present work introduces this simple and efficient technique using established time-stepping algorithms to achieve convergence. The fact that a time-stepping algorithm such as Newmark [12] is shown to be equivalent to the application of Nesterov’s algorithm, allows the use of standard dynamic finite element codes to perform the optimization step.

Beyond the original algorithm, we discuss new time integration methods, the line-search scheme and the restarting program. Applications to fiber orientation optimization (DMO), see Stegmann and Lund [13] are performed in both linear and nonlinear regime, with the complete sensitivity analysis being described in detail for the conservative case.

The paper is organized as follows: Sect. 2 presents Nesterov’s algorithm cast as an ordinary differential equation and provides further insights concerning the convergence and solution properties. In Sect. 3 time-integrators are discussed and stability regions are analyzed and the final optimization algorithm is described. In Sect. 4, the adjoint-variable method is described in detail, for both linear and nonlinear cases, with discretization-equivalent formulas and specialization for the strain-energy function. The equations for fiber optimization are introduced in the same section with a particular DMO-like [13,14,15] parametrization. Validation with More’s functions [16] is presented in Sect. 5.2 and Engineering applications of fiber optimization are also presented. The geometrically nonlinear case is also tested, with a simplified hyperelastic constitutive law. Comparisons between the new and existing algorithms are performed. Finally, in Sect. 6 conclusions are drawn concerning this work and its results.

1.2 The original algorithm

We are here concerned with convex unconstrained minimization. We only address functions which are $l-$strongly convex, twice continuously differentiable and with a $L-$Lipschitz-continuous gradient on ${\mathbb {R}}^{n}$ $\phi \left( \mathbf{q }\right) \in {\mathcal {S}}_{L,l}^{2,1}\left( {\mathbb {R}}^{n}\right)$ [3]. Here, $\mathbf{q }\in {\mathbb {R}}^{n}$ are the design-variables and $\phi \left( \mathbf{q }\right)$ is the objective function. The problem consists in

$$\begin{aligned} \underset{\mathbf{q }\in {\mathbb {R}}^{n}}{\min }\phi \left( \mathbf{q }\right) \end{aligned}$$

(1)

using information on value $\phi \left( \mathbf{q }\right)$ and gradient $\nabla _{\mathbf{q }}\phi \left( \mathbf{q }\right)$ for $\mathbf{q }\in {\mathbb {R}}^{n}$. From the aforementioned conditions, the Hessian of $\phi \left( \mathbf{q }\right)$ is eigenvalue-bounded by l and L

$$\begin{aligned} L{{\varvec{I}}}\succeq \nabla _{\mathbf{q }\mathbf{q }}^{2}\phi \left( \mathbf{q }\right) \succeq l{{\varvec{I}}} \end{aligned}$$

(2)

Conditions with the function images are easily interpreted:

$$\begin{aligned} \phi \left( \mathbf{q }'\right)&\le \phi \left( \mathbf{q }\right) +\left[ \nabla _{\mathbf{q }}\phi \left( \mathbf{q }\right) \right] \cdot \left( \mathbf{q }'-\mathbf{q }\right) +\frac{L}{2}\Vert {{\varvec{q}}}-\mathbf{q }'\Vert ^{2} \end{aligned}$$

(3)

$$\begin{aligned} \phi \left( \mathbf{q }'\right)&\ge \phi \left( \mathbf{q }\right) +\left[ \nabla _{\mathbf{q }}\phi \left( \mathbf{q }\right) \right] \cdot \left( \mathbf{q }'-\mathbf{q }\right) +\frac{l}{2}\Vert {{\varvec{q}}}-\mathbf{q }'\Vert ^{2} \end{aligned}$$

(4)

hence, our ${\mathcal {S}}_{L,l}^{2,1}$-function is enveloped by two quadratic models. For first-order methods, the lower complexity bound [3] is given by

(5)

where $\mathbf{q }_{\text {sol}}$ is the minimizer, k is the iteration (or step) number and $\chi$ is the condition number of the Hessian, satisfying the equality .

Nesterov’s algorithm (see [3, 4]) makes use of an auxiliary variable ${{\varvec{p}}}$, see [4, 10], to obtain the required momentum. Starting with the initial condition $\mathbf{q }_{0}$ and ${{\varvec{p}}}_{0}=\mathbf{q }_{0}$, Nesterov’s algorithm with step-size h (see [3, 4]) is based on the following recurrence formula, $k=1,2,\ldots$ is the step number:

$$\begin{aligned} \mathbf{q }_{k}&={{\varvec{p}}}_{k-1}-h\nabla _{\mathbf{q }}\phi \left( {{\varvec{p}}}_{k-1}\right) \end{aligned}$$

(6)

$$\begin{aligned} {{{{\varvec{p}}}_{k}}}&=\mathbf{q }_{k}+\frac{k-1}{k+2}\left( \mathbf{q }_{k}-\mathbf{q }_{k-1}\right) \end{aligned}$$

(7)

It achieves the lower bound (5) for (the corresponding proof is provided on pages 72–77 of [3]). For computational mechanics applications, the difficulty is the estimation of L. Dedicated iterative algorithms [17] exist for estimating L but this is a problem by itself and inconvenient in the computational mechanics context. The rationale for our approach is the following: since an equivalent ODE can be established for (6–7), it can be solved by an alternative form which is compatible with computational mechanics codes, specifically Finite-Element packages, see [18]. We develop a time-stepping algorithm appropriate for optimization and integration in standard Finite-Element packages. Only the unconstrained case is herein treated, but constrained problems can be solved using an extension of this algorithm. For example SUMT [19] can be used for computational mechanics where elements or cliques are used.

2 Equivalent differential equation and insight on Nesterov’s algorithm

Proof of equivalence between Nesterov’s algorithm and the solution of an ODE is provided by Su, Boyd and Candès [4]. For the sake of description, we consider a the scalar case, $n=1$. The final n-dimensional ODE is decoupled and therefore no loss of generality occurs due to this procedure. Let us then consider the following scalar ODE where $t\in {\mathbb {R}}_{+}^{\star }$ and $c\in {\mathbb {N}}$:

$$\begin{aligned} t\ddot{q}\left( t\right) +c{\dot{q}}\left( t\right) +tq\left( t\right) -t&=0 \nonumber \\ \lim _{t\rightarrow 0^{+}}q\left( t\right)&=q_{0^{+}} \end{aligned}$$

(8)

(note that ${\dot{q}}\left( 0\right) =0$). Solution of (8) is written introducing the constant $\alpha$:

(9)

where $J_{\alpha }\left( t\right)$ is the Bessel function of the first kind and . This is an adaptation of a result given by Apostol [20]. To avoid fractional factorials, in (9) we adopt odd values of c so that $\alpha$ is a non-negative integer. Invariance under time-scaling requires a constant c in (8), see [4]. The solution at the limit is one, i.e. $q_{\text {sol}}=\lim _{t\rightarrow +\infty }q(t,c)=1$. Of course, this limit is insufficient to assess convergence to the equilibrium point, we require two additional quantities. By shifting q(t) as ${\overline{q}}(t)=q(t)-1$ (which implies that ${\overline{q}}_{\text {sol}}=q_{\text {sol}}-1=0$), we determine time for the first root and the limit of the product $t^{2}{\overline{q}}^{2}(t)$, $\lim _{t\rightarrow +\infty }t^{2}{\overline{q}}^{2}(t)$. The time for first intersection and the convergence rate are shown in Table 1. The following conclusions are drawn from Table 1:

• Convergence to the exact solution requires that c must be greater or equal than 3.

• The optimal time to obtain the exact solution for the first time is $t_{\text {sol}}=3.8317$ and it is reached for $c=3$.

Arguments of time-scaling invariance and optimality for $c=3$ are key in understanding Nesterov’s idea. We point out that (6–7) is an application of an asynchronous explicit integrator (see, e.g. [21]) to the ODE in (8). The algorithm is not stationary, in the sense that in general ${\dot{q}}(t_{\text {sol}})\ne 0$. A depiction of the solution (9) is presented in Fig. 1 both in the time-domain and in state space.

Table 1 Time for first solution $(q_{\text {sol}}=1)$ and verification of convergence rate

Fig. 1

Behavior of Nesterov ODE for $c=1,3,5$ and 7

We now introduce the following linear variable transformations, where $a>0$ and b are new parameters, to be discussed later:

$$\begin{aligned} t=\sqrt{a}t_{\star } \end{aligned}$$

(10)

and

(11)

With these transformations, the ODE becomes:

$$\begin{aligned} t_{\star }\overset{\star \star }{r}\left( t_{\star }\right) +c\overset{\star }{r}\left( t_{\star }\right) +t_{\star }ar\left( t_{\star }\right) -t_{\star }b&=0 \end{aligned}$$

(12)

where now a can be identified as “stiffness” and b as the constant “force”. Equation (12) has the following solution:

(13)

where the limit of $r(t_{\star },c)$ is now . We note that further time-scaling is possible for the same limit by modifying simultaneously a and b :

(14)

With (14), we can clearly source term $ar\left( t_{\star }\right) -b$ affects the time scale maintaining the solution at the limit. Since damping is inversely proportional to time, scaling of the source term is in fact scaling of damping. Returning to the original notation, the n-degree-of-freedom case is obtained by

$$\begin{aligned} t\ddot{\mathbf{q }}\left( t\right) +c\dot{\mathbf{q }}\left( t\right) +t{{\varvec{A}}}\cdot \mathbf{q }\left( t\right) -t{{\varvec{b}}}&=0 \end{aligned}$$

(15)

with $\mathbf{q }\left( t\right) \in {\mathbb {R}}^{n}$. In (15), ${{\varvec{A}}}$ is a symmetric positive-definite $n\times n$ matrix and ${{\varvec{b}}}$ is a n-dimensional vector. By spectral decomposition of ${{\varvec{A}}}$, we have

$$\begin{aligned} {{\varvec{A}}}=\sum _{i=1}^{n}\lambda _{i}\hat{{\varvec{X}}_{i}} \end{aligned}$$

(16)

where $\lambda _{i}$ are the eigenvalues of ${{\varvec{A}}}$ and $\hat{{\varvec{X}}_{i}}$ are the corresponding normalized eigenvectors, with $\lambda _{i}\le \lambda _{i+1}$.

Modal transformation (see, e.g. [22]) is performed as $\mathbf{q }\left( t\right) ={\hat{{\varvec{X}}}}\cdot {\varvec{\eta }}\left( t\right)$ with ${\hat{{\varvec{X}}}}^{T}\cdot {\hat{{\varvec{X}}}}={{\varvec{I}}}$ with ${{\varvec{I}}}$ being the identity matrix. New unknowns ${\varvec{\eta }}(t)$ are defined from $\mathbf{q }(t)$ by inverting matrix ${\hat{{\varvec{X}}}}$. Matrix ${\hat{{\varvec{X}}}}$ contains the normalized eigenvectors ${\hat{{\varvec{X}}}}_{i}$ disposed by column. This is a standard technique in n-dof vibration [22] and structural dynamics [23]. Classical textbook derivations [22] results in the following modal solution:

(17)

Since the solution converges to ${\varvec{q=}}{{\varvec{A}}}^{-1}\cdot {{\varvec{b}}}$, which is the static limit for a damped system, it is also the solution of the following quadratic minimization problem

$$\begin{aligned}&\min _{\mathbf{q }\in {\mathbb {R}}^{n}}\left[ \phi \left( \mathbf{q }\right) \right] \text {where} \end{aligned}$$

(18a)

$$\begin{aligned}&\phi \left( \mathbf{q }\right) =\frac{1}{2}\mathbf{q }^{T}\cdot {{\varvec{A}}}\cdot \mathbf{q }-\mathbf{q }\cdot {{\varvec{b}}} \end{aligned}$$

(18b)

The relevant contribution of this ODE is that we can obtain the solution of the linear system ${{\varvec{A}}}\cdot \mathbf{q }={{\varvec{b}}}$ by solely using the product ${{\varvec{A}}}\cdot \mathbf{q }$. Generalizing for the condition $\nabla _{\mathbf{q }}\phi (\mathbf{q })={\varvec{0}}$, the ODE for the optimization problem becomes:

$$\begin{aligned} t\ddot{\mathbf{q }}\left( t\right) +c\dot{\mathbf{q }}\left( t\right) +t\nabla _{\mathbf{q }}\phi \left( \mathbf{q }\right)&=0 \end{aligned}$$

(19)

Using principal components and introducing the new unknown $\theta _{i}$, reduction to a first-order system reads:

$$\begin{aligned}&\theta _{i}=\dot{\eta _{i}} \end{aligned}$$

(20)

$$\begin{aligned}&\left\{ \begin{array}{l} {\dot{\theta }}_{i}\\ {\dot{\eta }}_{i} \end{array}\right\} =\left[ \begin{array}{cc} -\frac{c}{t} &{}\quad -\lambda _{i}\\ 1 &{}\quad 0 \end{array}\right] \cdot \left\{ \begin{array}{c} \theta _{i}\\ \eta _{i} \end{array}\right\} +\left\{ \begin{array}{c} \omega _{i}\\ 0 \end{array}\right\} \end{aligned}$$

(21)

Corresponding eigenvalues are given by:

$$\begin{aligned} \chi _{1,2}^{i}=-\sqrt{\lambda _{i}}\left[ \xi _{i}(t)\pm \sqrt{\xi _{i}(t)^{2}-1}\right] \end{aligned}$$

(22)

with $\xi _{i}\left( t\right) =\frac{c}{2t\sqrt{\lambda _{i}}}$ being a time-dependent damping ratio (see, e.g. Meirovitch [22] for this nomenclature). We note that the solution changes from overdamped to underdamped at transition time

$$\begin{aligned} t_{\text {transition}}^{i}=\frac{c}{2\sqrt{\lambda _{i}}} \end{aligned}$$

This actually establishes a one-to-one relation between $\xi _{i}$ and time for each decoupled mode. A global damping scale (replacing the time scale) can also be established, with three regions (all $\xi _{i}<1$, at least one $\xi _{i}<1$ and all $\xi _{i}>1$). This property will be further explored in the following sections.

Fig. 2

Stability region in the ${\widetilde{h}}-\xi \left( t\right)$ domain for various time-step integrators

Fig. 3

Algorithmic flowchart for the time-integration based on Nesterov’s algorithm

3 Algorithm

Concerning the properties of the problem, we ensure that the explicit numerical integrator is stable for all damping ratios, $\xi \in ]0,+\infty [$. Three integrator families are assessed: the Runge–Kutta (RK) of orders 1 up to 4, the central difference explicit integrator, which is a particular case of the Newmark-$\beta$ and the asyncronous explicit integrator. Introducing the scaled step ${\widetilde{h}}_{i}=h\sqrt{\lambda _{i}}$, amplification matrices and stability regions are shown in Table 4 and Fig. 2, respectively. Specializing for the Nesterov algorithm, for the first step we have $\mathbf{q }_{1}=\mathbf{q }_{0}-h^{2}\nabla _{\mathbf{q }}\phi \left( \mathbf{q }_{k}\right)$ and with$k\ge 1$ we have:

• 1. Explicit Newmark: $\mathbf{q }_{k+1}=\mathbf{q }_{k}+\frac{2-hc_{\text {eq}}(k)}{2+hc_{\text {eq}}(k)}\left( \mathbf{q }_{k}-\mathbf{q }_{k-1}\right) -\frac{2h^{2}}{\left[ 2+hc_{\text {eq}}(k)\right] }\nabla _{\mathbf{q }}\phi \left( \mathbf{q }_{k}\right)$

• 2. Explicit Newmark with predictor/corrector: $\widetilde{\mathbf{q }}_{k}=\mathbf{q }_{k}+\frac{2-hc_{\text {eq}}(k)}{2+hc_{\text {eq}}(k)}\left( \mathbf{q }_{k}-\mathbf{q }_{k-1}\right)$

  $\mathbf{q }_{k+1}=\widetilde{\mathbf{q }}_{k}-\frac{2h^{2}}{\left[ 2+hc_{\text {eq}}(k)\right] }\nabla _{\mathbf{q }}\phi \left( \widetilde{\mathbf{q }}_{k}\right)$

• 3. Explicit asyncronous: $\mathbf{q }_{k+1}=\mathbf{q }_{k}+\left[ 1-hc_{\text {eq}}\left( k\right) \right] \left( \mathbf{q }_{k}-\mathbf{q }_{k-1}\right) -h^{2}\nabla _{\mathbf{q }}\phi \left( \mathbf{q }_{k}\right)$

• 4. Explicit asyncronous with predictor/corrector: $\widetilde{\mathbf{q }}_{k}=\mathbf{q }_{k}+\left[ 1-hc_{\text {eq}}\left( k\right) \right] \left( \mathbf{q }_{k}-\mathbf{q }_{k-1}\right)$ $\mathbf{q }_{k+1}=\widetilde{\mathbf{q }}_{k}-h^{2}\nabla _{\mathbf{q }}\phi \left( \widetilde{\mathbf{q }}_{k}\right)$

Figure 2 shows that only the explicit Newmark integrator is immune to the stability region shrinking in overdamped systems. In terms of stability, predictor versions are also not advantageous. Runge–Kutta (RK) integrators are not appropriate for this application, although RK of orders 3 and 4 could be satisfactory in underdamped systems. The corresponding amplification matrices ${{\varvec{C}}}$ (see, Hughes [24] page 492 for the term “amplification matrix” in this context) are shown in Table 4.

A physical interpretation of the previous ODE integrators, which provides a straightforward estimation of h and $c_{\text {eq}}\left( t\right)$ is possible. Given a characteristic number for the elements of the Hessian of $\phi \left( \mathbf{q }_{k}\right)$, a “stiffness” $\chi$, the step size is given by:

(23)

where is a step-scaling, typically a function of the condition number of the Hessian of $\phi \left( \mathbf{q }_{k}\right)$. Of course, “time” t is now the product of time step h by k: $t=hk$. This results in the following recurrence formula for the explicit Newmark algorithm:

(24)

From which a direction ${\varvec{d}}_{k}=\mathbf{q }_{k+1}-\mathbf{q }_{k}$ can be extracted. A few remarks are in order with respect to this direction:

• 1. Nesterov’s choice $c=3$ is clear in (24) as negative momentum would be present otherwise for the first steps.

• 2. Stationarity at the solution is not satisfied, but a more favorable direction is obtained when compared with the original algorithm.

• 3. Not all directions are descent. If $\left( \mathbf{q }_{k}-\mathbf{q }_{k-1}\right) \cdot \nabla _{\mathbf{q }}\phi \left( \mathbf{q }_{k}\right) >0$ the descent condition $\left( \mathbf{q }_{k+1}-\mathbf{q }_{k}\right) \cdot \nabla _{\mathbf{q }}\phi \left( \mathbf{q }_{k}\right) <0$ is only conditionally satisfied for $k\ge 2$ by

  

  (25)

The constant $\chi$ can be replaced by an estimate of the gradient Lipschitz constant L. A value of $\chi$ can be also required in the context of constrained minimization, as part of the penalty term calculations. We now introduce two essential ingredients: conditional restart and line-search procedures. We reset the equivalent damping $c_{\text {eq}}\left( k\right)$ when one of the following descent conditions occurs:

• $k-k_{\star }\ge 2$ and $\left( \mathbf{q }_{k+1}-\mathbf{q }_{k-1}\right) \cdot \nabla _{\mathbf{q }}\phi \left( \mathbf{q }_{k}\right) >0$ or $\left( \mathbf{q }_{k+1}-\mathbf{q }_{k}\right) \cdot \nabla _{\mathbf{q }}\phi \left( \mathbf{q }_{k}\right) >0$

• $c_{\text {eq}}\left( k\right) =\frac{c}{k-k_{\star }}$ where $k_{\star }$ is the last step which failed the aforementioned conditions, which it is initialized as $k_{\star }=1$ .

A version with a two-step descent condition was introduced by Donoghue and Candès [10] who related the interval between restarts with the condition number of a quadratic function as . The ratio is here replaced by 2h,  where h is the step size:

(26)

The value of ${h^{2}}$ is determined by the sufficient decrease rule, see [25, 26]:

$$\begin{aligned} \phi \left( \mathbf{q }_{k}\right) -c_{s}h_{\text {}}^{2}\nabla \phi _{k}^{2}\ge \phi \left( \mathbf{q }_{k}-h^{2}\nabla \phi _{k}\right) \end{aligned}$$

(27)

by the usual backtracking algorithm. A fixed value of $c_{s}=1\times 10^{-4}$ is adopted. In addition, the Dai-Yuan [27] extension of the Barzilai–Borwein method [28] is adopted to calculate $h_{\text {}}$ for steps other than the first:

$$\begin{aligned} h_{\text {}}^{2}=\frac{\Delta \mathbf{q }_{k-1}\cdot \Delta \mathbf{q }_{k-1}}{2\left[ \phi \left( \mathbf{q }_{k-1}\right) -\phi \left( \mathbf{q }_{k}\right) +\nabla _{\mathbf{q }}\phi \left( \mathbf{q }_{k}\right) \cdot \Delta \mathbf{q }_{k-1}\right] } \end{aligned}$$

(28)

where $\Delta \mathbf{q }_{k-1}=\mathbf{q }_{k}-\mathbf{q }_{k-1}$. We therefore employ the minimum step from equations (27–28). The recalculation of h within an explicit integration algorithm such as ours is a delicate operation and cannot be performed too frequently [21] since there is a destabilization effect. As an algorithmic policy, we only update the step at each conditional restart. This ensures that each complete Nesterov iteration is performed with the same . The Algorithm is shown in Fig. 3. The complete code, including all line-search variants and restart policies is public-domain at Github [29].

4 Adjoint variable method and application to fiber-reinforced laminae

When the optimization problem statement contains one function and multiple design variables, the adjoint variable method is the more efficient sensitivity technique to adopt (for the first work in control theory, see [30]). We consider ${{\varvec{x}}}$ to be the state solution, a list of degrees-of-freedom corresponding to displacements. In addition, the design variables are, as previously introduced, arranged in an array $\mathbf{q }$. Let us consider one function $\Psi \left( {{\varvec{x}}},\mathbf{q }\right)$ which is here identified as the objective function. We use a one-to-one mapping between ${{\phi }}\left( \mathbf{q }\right)$ and $\Psi \left( {{\varvec{x}}},\mathbf{q }\right)$ as:

$$\begin{aligned} \phi \left( \mathbf{q }\right) =\Psi \left[ \hat{{{\varvec{x}}}}\left( \mathbf{q }\right) ,\mathbf{q }\right] \end{aligned}$$

(29)

where an implicit relation between ${{\varvec{x}}}$ and $\mathbf{q }$ exists, in this case formalized as $\hat{{{\varvec{x}}}}\left( \mathbf{q }\right)$. To materialize the alternating minimization algorithm, the total derivative with respect to $\mathbf{q }$ follows the analysis stage where ${{\varvec{x}}}$ satisfies equilibrium. Two cases are considered: Case I where state is linear in ${{\varvec{x}}}$ and Case II where state is nonlinear in ${{\varvec{x}}}$.

4.1 Case I: state is linear in ${{\varvec{x}}}$

A linear governing state equation is assumed, ${{\varvec{A}}}(\mathbf{q })\cdot {{\varvec{x}}}={{\varvec{b}}}(\mathbf{q })$ with ${{\varvec{b}}}(\mathbf{q })$ being the load vector and ${{\varvec{A}}}(\mathbf{q })$ the stiffness matrix. Both are for now considered to be functions of $\mathbf{q }$. Sensitivity of $\Psi \left( {{\varvec{x}}},\mathbf{q }\right)$ is defined as:

$$\begin{aligned} \frac{\mathrm {d}\Psi ({{\varvec{x}}},{\mathbf{q }})}{\mathrm {d}q_{j}}=\frac{\partial \Psi ({{\varvec{x}}},\mathbf{q })}{\mathrm {d}q_{j}}+\frac{\partial \Psi \left( {{\varvec{x}}},{\mathbf{q }}\right) }{\partial x_{k}}\frac{\mathrm {d}x_{k}}{\mathrm {d}q_{j}} \end{aligned}$$

(30)

Using the state equation in terms of components, we obtain:

$$\begin{aligned} \frac{\mathrm {d}x_{i}}{\mathrm {d}q_{j}}=\left[ {{\varvec{A}}}^{-1}\left( {\mathbf{q }}\right) \right] _{ik}\left( \frac{\mathrm {d}b_{k}\left( {\mathbf{q }}\right) }{\mathrm {d}q_{j}}-\frac{\partial A_{kl}\left( {\mathbf{q }}\right) }{\partial q_{j}}x_{l}\right) \end{aligned}$$

(31)

By pre-multiplying both sides by $\frac{\partial \Psi \left( {{\varvec{x}}},\mathbf{q }\right) }{\partial x_{i}}$, the following result is achieved:

$$\begin{aligned} \frac{\partial \Psi \left( {{\varvec{x}}},{\mathbf{q }}\right) }{\partial x_{i}}\frac{\mathrm {d}x_{i}}{\mathrm {d}q_{j}}= & {} \frac{\partial \Psi \left( {{\varvec{x}}},{\mathbf{q }}\right) }{\partial x_{i}}\left[ {{\varvec{A}}}^{-1}\left( \mathbf{q }\right) \right] _{ik}\nonumber \\&\times \left( \frac{\mathrm {d}b_{k}\left( {\mathbf{q }}\right) }{\mathrm {d}q_{j}}-\frac{\partial A_{kl}\left( {\mathbf{q }}\right) }{\partial q_{j}}x_{l}\right) \end{aligned}$$

(32)

Therefore, we solve the following adjoint linear system for ${\varvec{\lambda }}$:

(33)

From this solution for ${\varvec{\lambda }}$, the final sensitivity obtained from (32) is given by:

(34)

4.2 Case II: state is nonlinear in ${{\varvec{x}}}$

In this case, the discrete form of equilibrium is written as:

$$\begin{aligned} {\varvec{f}}({{\varvec{x}}},\mathbf{q })={\varvec{0}} \end{aligned}$$

(35)

where ${\varvec{f}}$ is typically identified as the residual. In mechanical engineering circles, it is common to define the residual ${\varvec{f}}({{\varvec{x}}},\mathbf{q })$ as the difference between the internal ${{\varvec{i}}}({{\varvec{x}}},q)$ and external forces ${\varvec{e}}(\mathbf{q })$:

$$\begin{aligned} {\varvec{f}}({{\varvec{x}}},\mathbf{q })={{\varvec{i}}}({{\varvec{x}}},\mathbf{q })-{\varvec{e}}(\mathbf{q }) \end{aligned}$$

(36)

Table 2 Optimization substeps in the nonlinear case

Table 3 Number of function evaluations for the test problems (see [16])

Newton iteration to solve (35) for ${{\varvec{x}}}$ is obtained as:

$$\begin{aligned} {{\varvec{A}}}\left( {{\varvec{x}}}_{(i)},\mathbf{q }\right) \cdot \left( {{\varvec{x}}}_{(i+1)}-{{\varvec{x}}}_{(i)}\right) =-{\varvec{f}}\left( {{\varvec{x}}}_{(i)},\mathbf{q }\right) \end{aligned}$$

(37)

with

$$\begin{aligned} {{\varvec{A}}}({{\varvec{x}}}_{(i)},{\mathbf{q }})=\left. \frac{\partial {\varvec{f}}({{\varvec{x}}},{\mathbf{q }})}{\partial {{\varvec{x}}}}\right| _{{{\varvec{x}}}={{\varvec{x}}}_{(i)}} \end{aligned}$$

(38)

Matrix ${{\varvec{A}}}({{\varvec{x}}},\mathbf{q }),$ which is the Jacobian of ${\varvec{f}}({{\varvec{x}}},\mathbf{q })$ with respect to ${{\varvec{x}}}$ is often called the $\ll \hbox {stiffness}\gg$ matrix. This iteration (37) continues until $\left\| {\varvec{f}}({\varvec{x_{i}}},\mathbf{q })\right\| \cong 0$. After this condition is satisfied, the solution of (35) for ${{\varvec{x}}}$ is typically performed by Newton iteration:

$$\begin{aligned} {{\varvec{A}}}({{\varvec{x}}},\mathbf{q })\cdot \frac{\mathrm {d}{{\varvec{x}}}}{\mathrm {d}\mathbf{q }}=-\frac{\partial {\varvec{f}}({{\varvec{x}}},\mathbf{q })}{\partial \mathbf{q }}\quad \text {if}{\quad {{{\varvec{f}}({{\varvec{x}}},\mathbf{q }})={{\varvec{0}}}}} \end{aligned}$$

Component-wise, the sensitivity of $\Psi ({{\varvec{x}}},{\varvec{q}})$ is written as:

$$\begin{aligned} \frac{\mathrm {d}\Psi ({{\varvec{x}}},{{\mathbf{q }}})}{\mathrm {d}q_{j}}=\frac{\partial \Psi ({{\varvec{x}}},{{\mathbf{q }}})}{\mathrm {d}q_{j}}+\frac{\partial \Psi \left( {{\varvec{x}}},{{\mathbf{q }}}\right) }{\partial x_{k}}\frac{\mathrm {d}x_{k}}{\mathrm {d}q_{j}} \end{aligned}$$

Repeating the process used for the linear case, we obtain

(39)

Therefore, the final formula for the sensitivity is given by:

(40)

4.3 Discretization and specialization to compliance

We now use the FE discretization to calculate the second term. If $\Psi ({{\varvec{x}}},\mathbf{q })$ is defined at the element level as a sum over $n_{e}$ elements, we can write its sensitivity as:

$$\begin{aligned} \frac{\mathrm {d}\Psi ({{\varvec{x}}},{\mathbf{q }})}{\mathrm {d}q_{j}}=\sum _{e=1}^{n_{e}}\frac{\partial \Psi ^{e}({{\varvec{x}}},{{\mathbf{q }}})}{\partial q_{j}^{e}}-\sum _{e=1}^{n_{e}}\frac{\partial f_{k}^{e}({{\varvec{x}}},{\mathbf{q }})}{\partial q_{j}^{e}}\lambda _{k}^{e} \end{aligned}$$

(41)

with

$$\begin{aligned} {{\varvec{A}}}^{T}\cdot \varvec{\lambda }=\frac{\partial \Psi \left( {{\varvec{x}}},\mathbf{q }\right) }{\partial {{\varvec{x}}}} \end{aligned}$$

where element summation applies:

$$\begin{aligned} {{\varvec{A}}}^{T}&=\sum _{e=1}^{n_{e}}{{\varvec{A}}}_{e}^{T} \end{aligned}$$

(42)

$$\begin{aligned} \frac{\partial \Psi \left( {{\varvec{x}}},\mathbf{q }\right) }{\partial {{\varvec{x}}}}&=\sum _{e=1}^{n_{e}}\frac{\partial \Psi ^{e}\left( {{\varvec{x}}},\mathbf{q }\right) }{\partial {{\varvec{x}}}} \end{aligned}$$

(43)

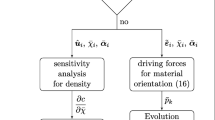
The three steps of our algorithm are summarized in Table 2. A formalization of similar algorithms is presented by Byrne [31] with technical details not explored here.

4.4 Specialization for the strain energy function

We now consider the strain energy to be adopted for $\Psi \left( {{\varvec{x}}},\mathbf{q }\right)$ and assume that the external forces are independent of $\mathbf{q }$, ${\varvec{e}}\left( \mathbf{q }\right) \equiv {\varvec{e}}$. The objective function is written as:

$$\begin{aligned} \Psi ({{\varvec{x}}},\mathbf{q })=\sum _{e=1}^{n_{e}}\Psi ^{e}\left( {{\varvec{x}}},\mathbf{q }\right) =\sum _{e=1}^{n_{e}}\int _{\Omega _{e}}\psi \left[ {{{\varvec{C}}}\left( {{\varvec{x}}}\right) },\mathbf{q }\right] \mathrm {d}V \end{aligned}$$

(44)

where $\Omega _{e}$ is the element integration domain, ${{\varvec{C}}}\left( {{\varvec{x}}}\right)$ is the right Cauchy-Green tensor and $\psi$ is the strain energy density function (see, e.g. Wriggers [32]) for this nomenclature. This results as follows:

$$\begin{aligned} \frac{\partial \Psi \left( {{\varvec{x}}},\mathbf{q }\right) }{\partial {\mathbf{q }}}&=\sum _{e=1}^{n_{e}}\frac{\partial \Psi _{e}\left( {{\varvec{x}}},\mathbf{q }\right) }{\partial \mathbf{q }}=\sum _{e=1}^{n_{e}}\int _{\Omega _{e}}\frac{\partial \psi \left[ {{\varvec{C}}}\left( {{\varvec{x}}}\right) ,\mathbf{q }\right] }{\partial \mathbf{q }}\mathrm {d}V \end{aligned}$$

(45)

$$\begin{aligned} \frac{\partial \Psi \left( {{\varvec{x}}},\mathbf{q }\right) }{\partial {{{\varvec{x}}}}}&={{\varvec{i}}}\left( {{\varvec{x}}},\mathbf{q }\right) =\sum _{e=1}^{n_{e}}\int _{\Omega _{e}}\frac{\partial \psi \left[ {{\varvec{C}}}\left( {{\varvec{x}}}\right) ,\mathbf{q }\right] }{\partial x}\mathrm {d}V \end{aligned}$$

(46)

$$\begin{aligned} \frac{\partial ^{2}\Psi \left( {{\varvec{x}}},\mathbf{q }\right) }{\partial {{{\varvec{x}}}}^{2}}&={{\varvec{A}}}\left( {{\varvec{x}}},\mathbf{q }\right) =\sum _{e=1}^{n_{e}}\int _{\Omega _{e}}\frac{\partial ^{2}\psi \left[ {{\varvec{C}}}\left( {{\varvec{x}}}\right) ,\mathbf{q }\right] }{\partial {{\varvec{x}}}^{2}}\mathrm {d}V \end{aligned}$$

(47)

$$\begin{aligned} \frac{\partial ^{2}\Psi \left( {{\varvec{x}}},\mathbf{q }\right) }{\partial {{{\varvec{x}}}}\partial \mathbf{q }}&=\frac{\partial {{\varvec{i}}}\left( {{\varvec{x}}},\mathbf{q }\right) }{\partial \mathbf{q }}=\sum _{e=1}^{n_{e}}\int _{\Omega _{e}}\frac{\partial ^{2}\psi \left[ {{\varvec{C}}}\left( {{\varvec{x}}}\right) ,\mathbf{q }\right] }{\partial {{{\varvec{x}}}}\partial \mathbf{q }}\mathrm {d}V \end{aligned}$$

(48)

These operations are performed in SimPlas [18] resorting to Wolfram Mathematica [33] and Acegen [34].

Fig. 4

Evolution of $\phi _{k}$ with k for the benchmark functions of Table 3

Fig. 5

Evolution of $\phi _{k}$ and $\left\| \nabla \phi _{k}\right\|$ with k for the benchmark functions of Table 3

Fig. 6

Evolution of $\phi _{k}$ and $\left\| \nabla \phi _{k}\right\|$ with k for the Rosenbrock problem with $c=2,3,5$ and 7.

Fig. 7

Evolution of $\phi _{k}$ and $\left\| \nabla \phi _{k}\right\|$ with k for the Rosenbrock problem with $c=2,3,5$ and 7.

Fig. 8

Cantilever beam from Stegmann and Lund [13]

4.5 Application to fiber-reinforced laminae

Discrete material optimization (DMO) was pioneered by Sigmund and Torquato [35] and further formalized by Stegmann and Lund [13, 36]. We consider a fiber-reinforced material which has a single angle of orientation. For a given finite element e we consider the optimization variables $\mathbf{q }_{e}$ which are here adopted to represent an interpolated quantity $w_{e}\in ]-1,1[$. With that goal, we use the parent-domain coordinates ${{\varvec{\xi }}}$ and obtain $w_{e}$ as:

$$\begin{aligned} w_{e}\left( {{\varvec{\xi }}}\right) =\tanh \left[ {{\varvec{N}}}\left( {{\varvec{\xi }}}\right) \cdot \mathbf{q }_{e}\right] \end{aligned}$$

(49)

where ${{\varvec{N}}}\left( {{\varvec{\xi }}}\right)$ is the traditional shape-function vector and ${{\varvec{\xi }}}$ are the parent-domain coordinates. With this notation, we write the following interpolation:

$$\begin{aligned} {\mathcal {C}}(w_{e})=\sum _{k=1}^{7}L_{k}\left( w_{e}\right) {\mathcal {C}}_{\alpha _{k}} \end{aligned}$$

(50)

with $\alpha _{k}=-\frac{\pi }{2}+\left[ \frac{k-1}{6}\right] \pi$. In (50), $L_{k}\left( w_{e}\right)$ with $k=1,\ldots ,7$ are Lagrange shape function polynomials and ${\mathcal {C}}_{\alpha _{k}}$ is given in plane-stress by:

(51)

with ${{\varvec{T}}}_{\varepsilon }\left( \alpha _{k}\right)$ being the strain transformation matrix in Voigt form:

$$\begin{aligned} {{\varvec{T}}}_{\varepsilon }\left( \alpha _{k}\right)&=\left[ \begin{array}{ccc} \cos ^{2}(\alpha _{k}) &{} \sin ^{2}(\alpha _{k}) &{} \cos (\alpha _{k})\sin (\alpha _{k})\\ \sin ^{2}(\alpha _{k}) &{} \cos ^{2}(\alpha _{k}) &{} -\cos (\alpha _{k})\sin (\alpha _{k})\\ -\sin (2\alpha _{k}) &{} \sin (2\alpha _{k}) &{} \cos (2\alpha _{k}) \end{array}\right] \end{aligned}$$

(52)

Fig. 9

Compliance evolution as a function of the step number

As a side note, ${{\varvec{T}}}_{\sigma }\left( \alpha _{k}\right) =\left[ {{\varvec{T}}}_{\varepsilon }\left( \alpha _{k}\right) \right] ^{-T}=\left[ {{\varvec{T}}}_{\varepsilon }\left( -\alpha _{k}\right) \right] ^{T}$. Lagrange shape functions in (50) correspond to a $6-$th degree polynomial:

$$\begin{aligned} {\varvec{L}}\left( w_{e}\right) =\left( \begin{array}{c} \frac{1}{80}(w_{e}-1)w_{e}(3w_{e}-2)(3w_{e}-1)(3w_{e}+1)(3w_{e}+2)\\ -\frac{9}{40}(w_{e}-1)w_{e}(w_{e}+1)(3w_{e}-2)(3w_{e}-1)(3w_{e}+1)\\ \frac{9}{16}(w_{e}-1)w_{e}(w_{e}+1)(3w_{e}-2)(3w_{e}-1)(3w_{e}+2)\\ \frac{1}{4}\left( 4-w_{e}^{2}\left( 7-9w_{e}^{2}\right) ^{2}\right) \\ \frac{9}{16}(w_{e}-1)w_{e}(w_{e}+1)(3w_{e}-2)(3w_{e}+1)(3w_{e}+2)\\ -\frac{9}{40}(w_{e}-1)w_{e}(w_{e}+1)(3w_{e}-1)(3w_{e}+1)(3w_{e}+2)\\ \frac{1}{80}w_{e}(w_{e}+1)(3w_{e}-2)(3w_{e}-1)(3w_{e}+1)(3w_{e}+2) \end{array}\right) \nonumber \!\!\!\!\!\!\!\!\\ \end{aligned}$$

(53)

Fig. 10

Square plate: relevant data and results from Lund and Stegmann [36]

This is inserted in the framework discussed above into our code [18]. We omit the finite element technology involved, as several papers by our group have been published discussing the details. Note that the derivatives are determined by using Wolfram Mathematica [33] with the Acegen add-on [34].

5 Numerical testing

5.1 Benchmark test functions

For comparison, we use the Polak–Ribière version [37] of the nonlinear conjugate-gradient method [25, 26] with the same line-search algorithm adopted in this work. Tolerance for the gradient norm is here $tol=1\times 10^{-3}$ in both methods. Table 3 shows the number of function evaluations for 8 benchmark problems reported in [16]. In Table 3, the best values are highlighted in bold. We can observe that our algorithm makes use of fewer function and gradient evaluations in all problems except problem #6 where much fewer iterations (and hence gradient evaluations) are performed by the conjugate-gradient method.

Fig. 11

Square plate under uniform pressure: orientation results as a function of mesh density

Fig. 12

Square plate under point load: orientation results as a function of mesh density

Fig. 13

Strain energy evolution as a function of the step number. Plate under point load

Fig. 14

Geometrically nonlinear fiber distribution. Unmagnified configurations

The evolution of $\phi _{k}$ for the 8 problems is shown in Fig. 4 and for $\left\| \nabla \phi _{k}\right\|$ is shown in Fig. 5. We conclude that behavior is clearly excellent for the last part of iteration process, whereas CG tends to perform better in the beginning. An exception is problem 6, where CG outperforms the Nesterov/Newmark algorithm. For the Rosenbrock problem, we inspect the effect of c and the integrator. Figure 6 confirms the advantage of $c=3$ with respect to other choices. In addition, the superiority of the Newmark integrator is confirmed in Fig. 7, even with respect to the asynchronous original proposal by Nesterov. An advantage of the Nesterov/Newmark integration algorithm is that line-search is used infrequently, only at the first iteration and when restarting is flagged. This is particularly useful for Finite Element analysis, since the cost of the objective function evaluation can be nearly as high as the gradient.

5.2 Verification examples: optimization of fiber orientations

We first assess the robustness of the algorithm using solely fiber orientations. The first test is the cantilever beam by Stegmann and Lund [13]. Orthotropic properties and plane-stress conditions are considered, with the relevant properties shown in Fig. 8. In this figure we also show the results from Stegmann and Lund for comparison.

Figure 9 shows the results for the evolution of the strain energy as a function of the step number. Stegmann and Lund mention 100 iterations for convergence, and it can be observed that much fewer steps/iterations are required in our algorithm. We can conclude the following:

• The heavy ball version with $c=0.9$ presents faster convergence than the standard gradient-based optimization.

• Nesterov implementation always outperforms the other two algorithms. We note that with $h^{2}=0.1$ only 20 steps are sufficient for a converged solution, in contrast with the 100 steps reported in [13].

Using a square plate, see Fig. 10, we inspect the effect of the algorithm for the clamped boundary (represented in Fig. 10) and the simply-supported boundary for the two load cases represented in Fig. 10. This example is described in [15, 36]. For simplicity, we here adopt the standard displacement-based H8 hexahedron element, which is known to lock in shear. However, thickness is here 5% of the plate width, which is favorable for our analysis. We test both linear and nonlinear versions of this problem.

One-quarter of the plate is adopted, with up to $80 \times 80 \times 1$ elements, which produces much higher resolution than in Lund and Stegmann [36]. For the two load cases and the two boundary conditions, the fibers are shown in Fig. 11 for the uniform pressure and in Fig. 12 for the point load. Convergence of the strain energy is shown in Fig. 13. The heavy ball algorithm clearly outperforms the standard gradient approach and Nesterov’s algorithm converges much faster, even with small values of ${h^{2}}$. In addition, lower values of the strain energy are reached, with slightly different solutions near the center of the plate.

Fig. 15

Geometrically nonlinear case: Normalized strain energy evolution as a function of the optimization step number and the imposed pressure

For the clamped with uniform pressure, we assess the effect of nonlinearities in the fiber distribution. For that objective we use a Kirchhoff/Saint-Venant (orthotropic) strain energy density function, where ${\varvec{E}}$ is the Green-Lagrange strain. In addition, only one load-step is employed. The configurations of fiber distributions using the deformed mesh are shown in Fig. 14. Upper and lower fiber orientations are distinct since membrane strains are now significant. We normalized the strain energy sensitivity to allow for changes in each state solution stage. This allows for very fast convergence, as depicted in Fig. 15. Higher values of pressure result in higher stiffening effect and stronger decrease in strain energy.

Fig. 16

Cylinder under pressure: geometry, relevant elastic properties and boundary conditions

Fig. 17

Strain energy evolution as a function of the step number for three methods (gradient, heavy ball and Nesterov). Cylinder under pressure

We now present a generalization to shells. With the goal of exhibiting the capability of our time-integration algorithm in this case, a pressure vessel is considered. Dimensions and constitutive properties are presented in Fig. 16. Tensor transformation is adopted to orient the directions to be tangent to the outer surface. Optimized fiber orientation can be observed in the same Figure. A concentric distribution of fibers can be observed in the shell end cap (head) and in the cylindrical surface a crossed pattern is obtained. Near the cap, a transition zone is observed where the fibers become longitudinally aligned. For this problem, two values of ${h^{2}}$ are adopted: ${h^{2}}=0.5,1$. From the observation of Fig. 17a, we can conclude that the Nesterov’s algorithm converges much faster, even with small values of ${h^{2}}$. Attempts to match the performance of Nesterov’s algorithm by the gradient or the heavy ball algorithms with higher values of ${h^{2}}$ result in instability, see Fig. 17b.

6 Conclusions

In this work, we proposed a time-step integration based on an explicit Newmark method for the application of Nesterov’s minimization algorithm in engineering applications. This allows the use of time-integration in a classical FE code to perform optimization. Stability analysis, benchmark test functions and careful assessment of all options were performed. Optimization of fiber orientations was carried out with this alternative method, including the geometrically nonlinear case. For that, a variant of DMO ([13, 36]) design variable definition was used. A complete assessment was presented and the new method consistently outperformed the existing gradient, heavy ball and vanilla conjugate-gradient methods in classical benchmarks and converges faster than gradient and heavy ball methods in the fiber optimization application. Source code for the benchmark tests is available in Github [29].

Appendix

See Table 4.

Table 4 First order amplification matrices (using Hughes terminology [24]) for four ODE explicit integrators