Topology optimization of acoustic mechanical interaction problems: a comparative review

Abstract

The pursuit for design improvements by geometry modifications can easily become prohibitive using a trial and error process. This holds especially when dealing with multi-physics problems—such as acoustic-structure interaction—where it is difficult to realize design improvements intuitively due to the complexity of the coupled physics. Compared to classical shape optimization, where a near optimal shape has to be supplied as an initial guess, topology optimization allows for innovative designs through a completely free material distribution, such that the topology can change during the optimization process. The goal of this article is to provide a comprehensive critical review of the proposed strategies for topology optimization of coupled acoustic-structure interaction problems. The work includes a comparison of topology optimization formulations with density, level set, and evolutionary-based methods and discusses the corresponding strengths and weaknesses through the considered application examples. The review concludes with recommendations for future research directions.

1 Introduction

Since its introduction in the late 1980s, gradient-based topology optimization has diversified significantly both in terms of application areas, but also with emerging variants of the original design parameterization. The initial homogenization approach (Bendsøe and Kikuchi 1988) laid the foundation for the so-called density method, often referred to as the SIMP method (Bendsøe 1989). Here, a pixel (or in 3D: voxel)-based design description is used with continuous element-wise design variables representing a relative “element density” (not to be confused with the mass density of the involved material). Elimination of intermediate-valued (grey) design variables with the penalization approach combined with appropriate regularization of the optimization problem using filtering techniques and length-scale control (Bourdin 2001; Bruns and Tortorelli 2001; Guest et al. 2004; Wang et al. 2011) led to a breakthrough regarding generation of well defined (black-white) pixelized structures. The result is that only limited post-processing (if any, e.g., Christiansen et al. 2015) is needed before fabrication. Combined with efficient adjoint sensitivity analysis and the use of robust and versatile mathematical programming tools, e.g., The Method of Moving Asymptotes (MMA) (Svanberg 1987), this has paved the way for the tremendous popularity of this approach. Recently, a milestone has been reached with the report of giga-scale design of a full aircraft wing with more than one billion 3D elements and corresponding design variables (Aage et al. 2017). Moreover, the method has also proven its worth for a number of other applications, ranging from material design (Larsen et al. 1997), acoustics (Park and Wang 2008), optics (Jensen and Sigmund 2011), and microfluidics (Alexandersen et al. 2016) as well as coupled multi-physics problems such as thermo-electro-mechanical devices (MEMS) (Sigmund 2001), turbulent flow heat transfer systems (Dilgen et al. 2018), and many other application areas.

As an inherent feature of the density-based approach, the structural boundary is constantly evolving during the optimization procedure. That is, boundaries may appear and disappear in a seamless fashion due to the continuous design variables. The corresponding structural appearance with gray scale at intermediate design stages can, however, cause uncertainty and ambiguity in identifying well defined boundaries. This poses a challenge when dealing with structures affected by, e.g., pressure boundary loads and calls for specialized schemes to be developed (Olhoff et al. 1991; Sigmund and Clausen 2007).

The quest for a well-defined boundary has partly motivated the use of level set methods (Osher and Sethian 1988; Sethian and Wiegmann 2000) for structural topology optimization. With the aim of keeping the full design flexibility from the density approach and combining this with the well-defined boundaries known from shape optimization methods, a level set function implicitly defines the structural boundary through its zero level iso-curve. The level set function is evolved via design sensitivities and holes may merge or new holes may appear, partially thanks to the introduction of topological derivatives (Novotny and Sokołowski 2013). Several variants of the method has appeared using the original version based on a boundary-fitted mesh and design updates based on the solution of a Hamilton-Jacobi equation. Since then, many alternative versions have been introduced, of which the one based on fixed meshes, cutfem methods (Hansbo and Hansbo 2004) and the use of mathematical programming tools has been reported well-suited for complex interface problems cf. (Villanueva and Maute 2017). Moreover, variants of the level set methods such as phase field methods and implicit functions have also appeared, which share theoretical and implementation details with the mentioned approaches. It should be mentioned that the numerical implementation of level set methods share many of same issues as the density method, and we refer to the review paper by (Sigmund and Maute 2013) for a thorough review and comparison of the two methods for structural optimization applications.

When considering coupled multi-physics problems like electro-thermo-elastic or elasto-optical, the density and level set methods can be applied with only minor adaptation and usually without altering the basic parametrization scheme. However, a challenge arises when considering coupled problems where different physical fields couple at the structural boundary. Examples include fluid-structure and acoustic-structure interaction. In this paper, we focus exclusively on the acoustic-structure interaction problem, where the fluctuating acoustic pressure field acts as a boundary load on the structure and the structural vibrations act as acoustic sources. In standard solution procedures, it is thus imperative to know the location of this boundary. The level set methods operate with a well-defined boundary and in both Shu et al. (2014) and Desai et al. (2018), the authors adapted the re-meshing-based level set approach to the acoustic-structure interaction problem where the zero level set is now used to separate the structural and the acoustic domains. That is, one solves the standard structural vibration problem where the level set is positive and the acoustic Helmholtz equation is solved in regions where the level set function is negative. Instead of using re-meshing, the level set method has also been used in combination with the density parametrization, i.e., using an erstatz material model and phase field approach to drive the design evolution. In this approach, the level set field is mapped to an indicator function which in turn used to interpolate the material properties of the acoustic and elastic mediums, thus preventing the challenges of tracking the boundary changes throughout the optimization. Using this technique, Noguchi et al. (2015) employed the unified multiphase (UMP) technique based on Biot’s theory for poroelastic waves (Lee et al. 2012). In Noguchi et al. (2016), the authors derived a topological derivative for a vibro-acoustic system modeled by a two-phase material model. Using topological derivatives and the same modeling approach, Noguchi et al. (2017) and Miyata et al. (2018) carried out level set–based topology optimization. The UMP technique has also been used in context of density-based topology optimization of acoustic-mechanical-septa distribution by (Lee et al. 2015). The vibro-acoustic systems have also been studied with a combined Boundary Element (BEM) and FE formulation to take advantage of the BEM’s capabilities of the modeling the unbounded acoustic domains, while relying on FEM for the structural part. Isakari et al. (2017) studied the level set–based topology optimization of an elastic sound scatterer using such a BEM-FEM solver.

As argued, the density method does not naturally provide knowledge of the location of the acoustic-structural interface. However, the mixed FE formulation has been used to circumvent this problem and facilitate a monolithic density-based parametrization approach. This formulation was also used in Sigmund and Clausen (2007) to treat the static pressure-load problem. With this formulation, the pressure is introduced as an auxiliary variable in addition to the displacements which allows one to transfer pressure loads without explicit indication of the boundary location. This formulation was used in the seminal work on acoustic-structure topology optimization presented in Yoon et al. (2007) and has later been applied to design a porous microstructures for increased loss factor (Kook and Jensen 2017).

In addition to these main methods, we will briefly review acoustic-structure interaction problems solved by the bi-directional evolutionary topology optimization (BESO) method as presented in Picelli et al. (2015), Vicente et al. (2015), and Chen et al. (2017). It should be noted also that a number of topology optimization problems have been studied for which the topological changes do not involve a change in the boundary between the structural and acoustic domains. The main part of these involve problems where a plate is coupled to an acoustic domain. For most problems, the in-plane material distribution involving two material constituents is optimized (Yamamoto et al. 2008; 2009; Du and Olhoff 2010; Yang and Du 2013), but also optimal distribution of thin damping layers has been considered (Zhang and Kang 2013) in addition to optimal plate thickness distribution (Akl et al. 2009), laminated composites (Niu et al. 2010), and piezoelectric structures (Yoon et al. 2018). Also, a few studies have appeared where the optimization problem has been defined so as to circumvent the need for modifying the structural boundaries and thus enables the use of standard parameterization schemes (see, e.g., Søndergaard and Pedersen 2014).

In the present paper, we will conduct a review of the methods that have appeared which allows for introducing topological changes in the distribution of acoustic and structural domains, i.e., the level set method, the density-based method using the mixed FE formulation, and the BESO method as a special variant of the density-based method. The computational framework for the density and level set methods will be outlined and results for a series of test problems will be critically examined. All results presented will be based on the authors’ implementation of the optimization algorithm. Based on this comparative review, recommendations for future research will be provided.

2 Topology optimization approaches

The general goal of an acoustic-structure topology optimization problem is to determine the optimal layout of the structural and acoustic domains, such that a given performance measure, that we may denote Φ(u(x,t),p(x,t)), is minimized. This formulation indicates that the performance measure may depend both on both the structural vibration level (the vibration amplitude u) as well as the acoustic pressure amplitude p.

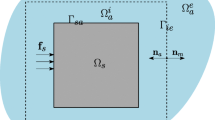
Figure 1a shows an illustration of the initial configuration for a typical acoustic-structure optimization problem. Here, a mechanical structure has two internal acoustic cavities and is surrounded by an external acoustic medium. The structure is excited by a time-harmonic mechanical load f(t) and also a time-harmonic acoustic load q(t). The loads generate vibrations of the structure and also acoustic pressure fluctuation in the acoustic medium. The aim of the optimization problem is now to minimize the prescribed objective function

$$ \min {\Phi}(\mathbf{u}(\mathbf{x},t),p(\mathbf{x},t)) $$

(1)

which in the hypothetical scenario illustrated in Fig. 1 results in the optimized distribution of structural and acoustic domains shown in Fig. 1b. During the optimization process, the structural domain has been reshaped and one of the internal acoustic cavities has been removed. Acoustic-structure optimization problems will most often involve additional constraints on the allowable performance or its configuration. A typical constraint in topology optimization is to enforce a maximum allowable volume of the structure, which we can formulate as

$$ \frac{{\int}_{{\Omega}_{s}}d\Omega}{{\int}_{\Omega}d\Omega}\leq V^{*} $$

(2)

where Ω_s is the domain occupied by the structure, Ω is the total domain under consideration, and V^∗ is the allowable volume fraction.

Fig. 1

Schematic illustration of a typical optimization problem. a Initial configuration. b Optimized configuration

In order to solve this optimization problem, the following key points should be addressed:

• Design parametrization. The methods reviewed apply parametrization based on the density or the level set approach.

• Analysis method. All strategies reviewed rely on finite element analysis of the underlying structural and acoustic problems. The formulations used depend on the choice of parametrization applying either a standard segregated analysis combined with a body-fitted and adaptive FE mesh (level set approach) or a mixed formulation combined with a fixed and regular FE mesh (density approach).

• Sensitivity analysis. The methods reviewed are gradient-based (the BESO method only to a certain extend) and apply sensitivity analysis based on the FE analysis.

• Design updates. The choice of design update method is also linked to the choice of parametrization scheme: The works using the level set approach use an update scheme based on a solution to the Hamilton-Jacobi transport equation. The density approach uses mathematical programming, e.g., MMA, while the BESO uses a heuristic update scheme.

In the following, the strategies outlined in the four key points will be described in details including implementation considerations.

2.1 Design parametrization

Existing approaches for topology optimization of acoustic-structure interaction problems can, as previously stated, be split into two main groups depending on the choice of design parametrization. Note, however, that although the design representations used for the density and level set approaches are conceptually very different, it can be argued that when it comes to a numerical implementation, the similarities actually outweigh the differences as reported for the case of structural optimization in Sigmund and Maute (2013).

2.1.1 The density approach

The basic idea of density-based structural optimization is to describe the topology by a spatially varying design field, here γ(x). In the discretized setting, this is achieved by assigning a design variable to each of the computational domain pixels (2D) or voxels (3D). For the case of acoustic-structure interaction, this means that a pixel with γ = 1 is interpreted as being structure, while γ = 0 corresponds to an acoustic medium. The only difference to classical structural topology optimization is that γ = 0 corresponds to void in that case. Also, it is worth noting that in the density method, the same mesh is often used for both analysis and design and the mesh is usually kept fixed throughout the optimization process. Furthermore, the mesh is often regular which means that elaborate mesh generation or re-meshing is avoided. In order to apply gradient-based optimization methods, the design variable field is represented as continuous, i.e.,

$$ 0\leq \gamma_{i} \leq 1 $$

(3)

where i indicates the pixel (element) number.

A schematic of the entire density-based optimization process is illustrated in Fig. 2. Figure 2a shows a possible initial structure modeled by setting the appropriate design variables to either 1 (black) or 0 (white). However, one of the greatest strengths of the density approach is that initial designs are often not needed. In fact, more often, a uniform distribution of the design variables is applied as illustrated in Fig. 2b. The choice of the initial design distribution is in general arbitrary, but could be chosen to match the volume constraint γ_i = V^∗, if such a constraint is present. Naturally, a random distribution of the densities can be applied as well. As the optimization process progresses, the topology of the design evolves and often grey regions appear as shown in Fig. 2c. Through different filtering and projection methods, the intermediate design variables are slowly suppressed until the design converges to a completely black (1) or white (0) configuration. The optimized design is illustrated in Fig. 2d which also shows how the pixel-based representation leads to the so-called staircasing phenomena. That is, although the design is completely black and white, the interface between solid and acoustic region is jagged. This might pose problems in multiphysics settings, which is why it is sometimes beneficial to allow the interface to be smeared over a couple of pixels.

Fig. 2

Illustration of parametrization using the density approach. a Initial design using a design configuration, b initial design with homogeneous distribution of pixel densities, c intermediate design with grey pixels, and d optimized design

2.1.2 The level set approach

In level set–based topology optimization, the design representation is most often separated from the underlying analysis mesh. This is achieved by representing the topology by a scalar function ϕ, and by defining the different material phases and interface based on the following rule:

$$ \begin{array}{@{}rcl@{}} \phi(x) &>& 0,\qquad x \in {\Omega}_{s} (\text{structural domain}) \\ \phi(x) &=& 0,\qquad x \in \partial {\Omega} (\text{interface})\\ \phi(x) &<& 0,\qquad x \in {\Omega}_{a} (\text{acoustic domain}) \end{array} $$

(4)

Figure 3a illustrates an example of a level set function and how it can be used to define structural and acoustic domains as well as their common interface. This definition is a straightforward extension of the approach usually used for structural topology optimization where ϕ < 0 then corresponds to void.

Fig. 3

Level set model and the design domain: a level set function and its zero level set; bΩ_s and its embedding domain Ω

The level set function is usually discretized on a regular grid, similar to that for the design variables in the density-based method. However, the level set values are most often assigned to nodal points instead of element centers.

Figure 4a shows a representative level set function discretized on a regular grid, whereas Fig. 4b shows the corresponding design configuration described by the the zero-level contour. During the optimization process, the level set function evolves into a new configuration. This is illustrated in Fig. 4c and d which shows the grid-based level set function and its geometric interpretation, respectively.

Fig. 4

Illustration of the discretized level set function. a Grid values of the initial level set function. b Initial design described by the the zero-level iso-curve. c Grid values of the optimized level set function. d Final design described by the zero-level iso-curve

The mapping of the level set function to the mesh used for analysis can be done in several ways. The method most often used in structural optimization is to apply an ersatz material model and in this case the level set method and the density-based method are very similar with only minor differences. To the author’s knowledge, this approach has not yet been applied to acoustic-structure interaction problems. Instead, the approach used in the existing works is to perform a complete remeshing-based on the zero level contour, which ensures a crisp and well-defined interface. However, we should note that recent work on level set–based topology optimization applies novel immersed boundary methods such as cut finite elements or finite cell representations. These methods allow the analysis and level meshes to coincide, while still maintaining the crisp interface by using elaborate integration schemes (see, e.g., Hansbo and Hansbo (2004) and Düster et al. (2008) for more details).

Implicit representation of the interface using the values of the level set function ϕ(x) also allows for easy calculation of the geometric properties such as the unit normal vector and the mean curvature, not only on the design interface ∂Ω, but everywhere in the domain D. The unit normal vector n_a pointing out from the acoustic domain is calculated as

$$ \begin{array}{@{}rcl@{}} \mathbf{n}_{a} = \frac{\nabla \phi}{| \nabla \phi |} \end{array} $$

(5)

Likewise, the calculation of the mean curvature is also tied to the level set function

$$ \begin{array}{@{}rcl@{}} \kappa &=& \nabla \cdot \mathbf{n}_{a} \\ &=& \nabla \cdot \left[ \frac{\nabla \phi}{| \nabla \phi |} \right] \end{array} $$

(6)

2.2 Finite element analysis of acoustic-structural interaction (ASI)

Discretizing and meshing the analysis domain based on the zero-level contour of the scalar level set function makes it possible to employ standard segregated analysis. That is, the structural equation is solved only in the solid region and the acoustic wave equation is solved only in the acoustic region. Thus, this approach is analogous to standard simulation of acoustic-mechanical interaction problems as used in most commercial and open source numerical tool boxes. In the following section, we will describe how to perform the segregated analysis using standard finite elements.

2.2.1 Segregated analysis

The governing equations for the time-harmonic motion of a linear elastic body Ω_s can be written as

$$ \begin{array}{@{}rcl@{}} \nabla^{T}\boldsymbol{\sigma } &+& \omega^{2} \rho_{s} \overline{\mathbf{u}} = 0 \qquad \text{in} \quad {\Omega}_{s} \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\sigma } &=& \boldsymbol{\mathcal{C}} \mathbf{\epsilon } \end{array} $$

(8)

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\epsilon} &=& \{ \epsilon_{11} \epsilon_{22} 2 \epsilon_{12} \}^{T}\qquad \text{(2D)} \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} \epsilon_{11} &=& \frac{\partial \overline{u}_{1}}{\partial x}, \quad \epsilon_{22} = \frac{\partial \overline{u}_{2}}{\partial y}, \quad \epsilon_{12} = \frac{1}{2} \left( \frac{\partial \overline{u}_{1}}{\partial y} + \frac{\partial \overline{u}_{2}}{\partial x} \right) \end{array} $$

(10)

where body forces have been neglected, ρ_s is the density of the solid, and ω is the radial frequency. Moreover, σ is the Cauchy stress vector, $\boldsymbol {\mathcal {C}}$ is the constitutive matrix, and the 𝜖 is the strain vector. We consider the body to be subjected to standard boundary conditions as well as being adjacent to an acoustic medium in a part of the boundary. The boundary conditions read

$$ \begin{array}{@{}rcl@{}} \overline{\mathbf{u}} &=& \mathbf{u}_{0} \qquad \text{in} \quad {\Gamma}_{sd} \end{array} $$

(11)

$$ \begin{array}{@{}rcl@{}} \mathbf{n}_{s}^{T}\boldsymbol{\sigma } &=& \mathbf{f} \qquad \text{in} \quad {\Gamma}_{sn} \end{array} $$

(12)

$$ \begin{array}{@{}rcl@{}} \mathbf{n}_{s}^{T}\boldsymbol{\sigma } &=&p\mathbf{n}_{a} \qquad \text{in} \quad {\Gamma}_{as} \end{array} $$

(13)

where n_a is the normal vector of the acoustic boundary pointing outward from the acoustic domain defined in (5) and n_s is the normal vector of the structural boundary pointing to the acoustic domain. The vector f is the traction force defined on the part of the structural boundary Γ_sn. The definitions for the coupled system is illustrated in Fig. 5 including all boundary conditions used throughout the presented work.

Fig. 5

The coupled acoustic-structure system: the acoustic fluid domain Ω_a and the structural domain Ω_s coupled by integrals over the acoustic-structure interface Γ_as

Similarly, the strong form of the Helmholtz equation describing the pressure fluctuations in the acoustic domain is written as

$$ \nabla^{2} \overline{p} + \left( \frac{\omega}{c_{a}}\right)^{2} \overline{p} = 0 \qquad \text{in} \quad {\Omega}_{a} $$

(14)

along with the following common boundary conditions:

$$ \begin{array}{@{}rcl@{}} \overline{p} &=& p_{0} \qquad \text{in} \quad {\Gamma}_{ad} \end{array} $$

(15)

$$ \begin{array}{@{}rcl@{}} \mathbf{n}_{a}^{T}\nabla \overline{p} &=& a_{n} \qquad \text{in} \quad {\Gamma}_{an} \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} \mathbf{n}_{a}^{T}\nabla \overline{p} &=& - \omega^{2} \rho_{a} \mathbf{n}_{s}^{T} \overline{\mathbf{u}} \qquad \text{in} \quad {\Gamma}_{as} \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} \mathbf{n}_{a}^{T}\nabla \overline{p} &+& \text{i} k \overline{p} = 2 \text{i} k p_{in} \qquad \text{in} \quad {\Gamma}_{ar} \end{array} $$

(18)

where c_a is the speed of sound in the acoustic medium, ρ_a is the density, $k=\frac {\omega }{c_{a}}$ is the wave number, i is the imaginary unit and a_n is the prescribed Neumann boundary condition which is zero for the hard wall boundaries.

Applying the standard Galerkin procedure to carry out the finite element discretization of the governing equations, the following weak form of the elasticity equation is obtained

$$ \begin{array}{ll} &{\int}_{{\Omega}_{s}} \delta \boldsymbol{\epsilon}^{T} \boldsymbol{\mathcal{C}} \boldsymbol{\epsilon} \text{d}{\Omega} - \omega^{2} \rho_{s} {\int}_{{\Omega}_{s}} \delta \overline{\mathbf{u}}^{T} \overline{\mathbf{ u} } \text{d}{\Omega} \\ &- {\int}_{{\Gamma}_{as} } \delta \overline{\mathbf{u}}^{T} \overline{p}\mathbf{n}_{a} \text{d}{\Gamma} = {\int}_{{\Gamma}_{sn} } \delta \overline{\mathbf{u}}^{T} \mathbf{f} \text{d}{\Gamma} \end{array} $$

(19)

Similarly, the weak form of the acoustic domain reads

$$ \begin{array}{ll} &{\int}_{{\Omega}_{a}} (\nabla \delta \overline{p} )^{T} \nabla \overline{p} \text{d}{\Omega} - \frac{\omega^{2}}{ {c_{a}^{2}}} {\int}_{{\Omega}_{a}} \delta \overline{p} \overline{p} \text{d}{\Omega} \\ &- \omega^{2} \rho_{a} {\int}_{{\Gamma}_{as} } \delta \overline{p} \mathbf{n}_{a}^{T} \overline{ \mathbf{u} } \text{d}{\Gamma} = {\int}_{{\Gamma}_{an} } \delta \overline{p} a_{n} \text{d}{\Gamma} \end{array} $$

where the radiation boundary condition in (18) is excluded from the derivation for brevity. Here, δ𝜖 is the virtual strain, $\delta \overline { \mathbf {u}}$ and $\delta \overline {p}$ are the test functions for displacements and the pressure field, respectively. In order to carry out the discretization, the continuous variables $\overline {\mathbf {u}}$ and $\overline {p}$ are approximated using linear iso-parametric shape functions

$$ \begin{array}{@{}rcl@{}} \overline{\mathbf{u}} &=& \mathbf{N}_{u} \mathbf{u}\\ \overline{p} &=& \mathbf{N}_{p} \mathbf{p}\\ \boldsymbol{\epsilon} &=& \boldsymbol{\partial} \mathbf{N}_{u} \mathbf{u} = \mathbf{B}_{u} \mathbf{u} \end{array} $$

(20)

where ∂ is the differential operator and B_u is the linear strain-displacement matrix. The discretized matrix system of the weak form is then

$$ \begin{array}{@{}rcl@{}} \left[\begin{array}{ll} \left( \mathbf{{K}}_{s} - \omega^{2} \mathbf{{M}}_{s} \right) & - \mathbf{{C}} \\ -\rho_{a} \omega^{2} \mathbf{{C}}^{T} & \left( \mathbf{K}_{a} - \omega^{2} \mathbf{M}_{a} \right) \end{array}\right] \left[\begin{array}{l} \mathbf{u} \\ \mathbf{p} \end{array}\right] = \left[\begin{array}{l} \mathbf{f} \\ \mathbf{g} \end{array}\right] \end{array} $$

(21)

with the matrices and vectors being

$$ \begin{array}{@{}rcl@{}} \mathbf{K}_{s} &=& {\int}_{{\Omega}_{s}} \mathbf{B}_{u}^{T} \boldsymbol{\mathcal{C}} \mathbf{B}_{u} \text{d} {\Omega}_{s} \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} \mathbf{M}_{s} &=& {\int}_{{\Omega}_{s}} \rho_{s} \mathbf{N}_{u}^{T} \mathbf{N}_{u} \text{d} {\Omega}_{s} \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} \mathbf{f} &=& {\int}_{{\Gamma}_{sn} } \mathbf{N}_{u}^{T} \mathbf{f} \text{d} {\Gamma}_{sn} \end{array} $$

(24)

for the structural domain and

$$ \begin{array}{@{}rcl@{}} \mathbf{K}_{a} &=& {\int}_{{\Omega}_{a}} \mathbf{B}_{p}^{T} \mathbf{B}_{p} \text{d} {\Omega}_{a} \end{array} $$

(25)

$$ \begin{array}{@{}rcl@{}} \mathbf{M}_{a} &=&{\int}_{{\Omega}_{a}} \frac{1}{{c_{a}^{2}}} \mathbf{N}_{p}^{T} \mathbf{N}_{p} \text{d} {\Omega}_{a} \end{array} $$

(26)

$$ \begin{array}{@{}rcl@{}} \mathbf{g} &=& {\int}_{{\Gamma}_{an}} \mathbf{N}_{p}^{T} a_{n} \text{d} {\Gamma}_{an} \end{array} $$

(27)

for the acoustic domain where the matrix B_p = ∂N_p. The coupling matrix is found as:

$$ \mathbf{C} = {\int}_{{\Gamma}_{as}} \mathbf{N}_{u}^{T} \mathbf{n}_{a} \mathbf{N}_{p} \text{d} {\Gamma}_{as} $$

(28)

As previously mentioned, the mesh is usually adapted to the acoustic-structural boundary in each step of the optimization algorithm. Figure 6 shows an example of a such finite element grid where the the boundary curve is obtained utilizing the marching square algorithm and the curve is fitted to the mesh using simple triangulation.

Fig. 6

Illustration of a fitted finite element mesh to realize the boundary curve. a Whole computation mesh. b Close up view of the mesh showing the triangulation

2.2.2 Mixed formulation

In the case of a density-based parametrization, it is no longer possible to clearly define the acoustic and structural parts of the domain due to the possible appearance of “grey” pixels in the design. Therefore, a single monolithic formulation governing both physics and their coupling is needed. The mixed formulation has been proposed to do exactly this, that is, to model the acoustic-mechanical interaction problems without having an explicit boundary representation. The mixed finite element formulation, also called the u/p (displacement/pressure) formulation, can be found in many references (see, e.g., Zienkiewicz and Taylor (2000)). In Wang and Bathe (1997), the formulation was proposed to model acoustic-mechanical interaction problems. In Sigmund and Clausen (2007), the static mixed FE-formulation was used to solve pressure load problems in density-based topology optimization and in Yoon et al. (2007), the formulation was used for the first time for topology optimization of acoustic-structure interaction problems.

In the following, we present and motivate the use of the mixed formulation for density-based topology optimization. The mixed formulation is derived by first defining a pressure variable using the bulk modulus as follows:

$$ \begin{array}{@{}rcl@{}} \overline{p} = -K \mathbf{m}^{T} \boldsymbol{\epsilon} \end{array} $$

(29)

which is valid for small strains. Here, K is the bulk modulus and m = {1,1,0}^T is the vector formulation for the Kronecker’s delta considering two-dimensional analysis. The stress-strain relationship can then be stated as

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\sigma } = 2 G \mathbf{e} - \mathbf{m} \overline{p} \end{array} $$

(30)

where G is the shear modulus and the deviatoric strain vector e reads

$$ \mathbf{e}= (\mathbf{I}_{0} - \tfrac{1}{2} \mathbf{m} \mathbf{m}^{T} ) \boldsymbol{\epsilon} \qquad \text{(2D)} \\ $$

(31)

with I₀ defined as a diagonal matrix I₀ = diag(1,1,0.5). Moreover, the bulk and shear moduli are defined from the Young’s modulus E and the Poisson’s ratio ν as

$$ K = \frac{E}{2 \left( 1 - \nu \right)},\qquad G=\frac{E}{2\left( 1+\nu\right)} \\ $$

(32)

in the case of 2D plane stress conditions. The coupled equations derived from the mixed formulation can now be written as

$$ \begin{array}{@{}rcl@{}} &&\nabla^{T}\left( 2 G \mathbf{e} - \mathbf{m} \overline{p}\right) + \omega^{2} \rho \overline{\mathbf{u}} = 0 \end{array} $$

(33)

$$ \begin{array}{@{}rcl@{}} &&\frac{\overline{p}}{K} + \mathbf{m}^{T} \boldsymbol{\epsilon} = 0 \end{array} $$

(34)

which can be viewed as an alternative formulation of the original structural equations (with the advantage that it can be applied to perfectly incompressible materials as well).

However, it can also be shown that the Helmholtz equation governing the acoustic pressure can be recovered from this equation by substituting $\overline {\mathbf {u}}$ in (33) into (34) and setting the shear modulus to zero (G = 0). Thus, using the mixed formulation, structural Ω_s and acoustic Ω_a parts of the domain Ω can be realized by defining the bulk modulus K, shear modulus G and density ρ as

$$ \begin{array}{@{}rcl@{}} K &=& K_{s},\qquad G=G_{s},\qquad \rho=\rho_{s}\qquad \text{on } {\Omega}_{s} \\ K &= &K_{a},\qquad G = 0,\qquad \rho=\rho_{a}\qquad \text{on } {\Omega}_{a} \end{array} $$

(35)

In regions with intermediate values of γ, thus not belonging to neither Ω_s nor Ω_a, it is proposed to interpolate the values of K, G, and ρ between the structural and acoustic values in (35). Such an interpolation is found in Yoon et al. (2007):

$$ \begin{array}{@{}rcl@{}} K(\gamma) &=& K_{s} \frac{\gamma}{1 + \left( 1 - \gamma \right) n} + K_{a} \left( 1 - \frac{\gamma}{1 + \left( 1 - \gamma \right)n } \right) \end{array} $$

(36)

$$ \begin{array}{@{}rcl@{}} G(\gamma) &=& G_{s} \frac{\gamma}{1+\left( 1 - \gamma \right) n} \end{array} $$

(37)

$$ \begin{array}{@{}rcl@{}} \rho(\gamma) &=& \rho_{s} \gamma + \rho_{a} \left( 1 - \gamma \right) \end{array} $$

(38)

in which the interpolation of K and G is based on a two material RAMP interpolation scheme (Stolpe and Svanberg 2001) used to avoid the artificial vibration modes in low-density areas reported for the more standard SIMP interpolation function (Pedersen 2000). Here, the parameter n is a positive number that controls the curvature of the interpolation function. As seen from the (38), the mass density ρ is interpolated linearly between the acoustic and the structural domains.

Acoustic boundary conditions for the mixed formulation are derived using that $\nabla \overline {p} = \omega ^{2} \rho _{s} \overline {\mathbf {u}}$. Figure 7 illustrates the most commonly used boundary conditions for the mixed formulation in the acoustic domain. Boundary conditions for the structural domain remain the same and do not require any special attention.

Fig. 7

Boundary conditions for the mixed finite element method in acoustic domain Ω_a. a Radiation, b dirichlet, c hard wall, and d acceleration

The weak form of the mixed formulation given in (33) and (34) are obtained following the standard Galerkin approach

$$ \begin{array}{@{}rcl@{}} &&{\int}_{\Omega} \delta \boldsymbol{\epsilon}^{T} 2 G \mathbf{D} \boldsymbol{\epsilon} \text{d} {\Omega} - {\int}_{\Omega} \delta \boldsymbol{\epsilon}^{T} \mathbf{m} \overline{p} \text{d} {\Omega} - \omega^{2} \rho {\int}_{\Omega} \delta \overline{\mathbf{u}}^{T} \overline{\mathbf{u}} \text{d} {\Omega} = 0 \end{array} $$

(39)

$$ \begin{array}{@{}rcl@{}} &&{\int}_{\Omega} \delta \overline{p} \frac{\overline{p}}{K} \text{d} {\Omega} +{\int}_{\Omega} \delta \overline{p} \mathbf{m}\boldsymbol{\epsilon} \text{d} {\Omega} = 0 \end{array} $$

(40)

where δ𝜖 is the virtual strain, $\delta \overline {\mathbf {u}}$ and $\delta \overline {p}$ are the test functions for the displacement and the pressure field, respectively. Moreover, the matrix D is defined as

$$ \begin{array}{@{}rcl@{}} \mathbf{D} = \mathbf{I}_{0} - \tfrac{1}{2} \mathbf{m}\mathbf{m}^{T} \end{array} $$

(41)

Again the continuous variables $\overline {\mathbf {u}}$ and $\overline {p}$ are approximated by the following shape functions

$$ \begin{array}{@{}rcl@{}} \overline{\mathbf{u}} &=& \mathbf{N}_{u} \mathbf{u}\\ \overline{p} &=& \mathbf{N}_{p} \mathbf{p}\\ \boldsymbol{\epsilon} &=& \boldsymbol{\partial} \mathbf{N}_{u} \mathbf{u} = \mathbf{B}_{u} \mathbf{u} \end{array} $$

(42)

where ∂ is the differential operator and B_u is the linear strain-displacement matrix. Inserting the approximation in (42), into the weak forms in (39) and (40), a matrix formulation of the weak form is obtained as

$$ \begin{array}{@{}rcl@{}} \left[\begin{array}{cc} \left( \mathbf{K} - \omega^{2} \mathbf{M} \right) & - \mathbf{C} \\ - \mathbf{C}^{T} & -\mathbf{A} \end{array}\right] \left[\begin{array}{l} \mathbf{u} \\ \mathbf{p} \end{array}\right] = \left[\begin{array}{l} \mathbf{f} \\ \mathbf{g} \end{array}\right] \end{array} $$

(43)

where

$$ \begin{array}{@{}rcl@{}} \mathbf{K} &=& {\int}_{\Omega} 2 G\mathbf{B}_{u}^{T} \mathbf{D} \mathbf{B}_{u} \text{d} {\Omega} \end{array} $$

(44)

$$ \begin{array}{@{}rcl@{}} \mathbf{M} &=& {\int}_{\Omega} \rho \mathbf{N}_{u}^{T} \mathbf{N}_{u} \text{d} {\Omega} \end{array} $$

(45)

$$ \begin{array}{@{}rcl@{}} \mathbf{C} &=& {\int}_{\Omega} \mathbf{B}_{u}^{T} \mathbf{m} \mathbf{N}_{p} \text{d} {\Omega} \end{array} $$

(46)

$$ \begin{array}{@{}rcl@{}} \mathbf{A} &=& {\int}_{\Omega} \tfrac{1}{K}\mathbf{N}_{p}^{T} \mathbf{N}_{p} \text{d} \Omega \end{array} $$

(47)

In order to realize a stable finite element solution to the mixed u/p formulation, displacement variables should use higher order interpolations than the auxiliary pressure variable (Zienkiewicz and Taylor 2000; Wang and Bathe 1997). To this end, displacement variables are discretized with second order Lagrangian shape functions whereas the pressure field is represented using first order Lagrangian shape function. For triangular and quadrilateral elements, this corresponds to using T6/3 and Q8/4 elements, respectively.

2.3 Sensitivity analysis

A gradient-based optimization approach requires computation of the sensitivities of the objective function and constraints with respect to the design variables. In the following, we will outline the basic procedure followed when using the density and the level set approaches.

2.3.1 Density-based parametrization

In order to carry out the adjoint analysis, firstly the Lagrangian is formed

$$ \begin{array}{@{}rcl@{}} \mathcal{L} = {\Phi}(\boldsymbol{\gamma} , \mathbf{v}(\boldsymbol{\gamma}) ) + \boldsymbol{\lambda}^{T} \mathbf{r}(\boldsymbol{\gamma} , \mathbf{v}(\boldsymbol{\gamma})) \end{array} $$

(48)

where r = Sv −h = 0 defines the residual vector, v = {u,p}^T is the vector of state variables, h = {f,g}^T is the source vector, S is the system matrix found from (43), and λ is a vector of Lagrange multipliers. For zero residual, the Lagrangian coincides with the objective function. The derivative with respect to the design variable can be written following the chain rule as

$$ \begin{array}{@{}rcl@{}} \frac{\text{d} \mathcal{L}}{\text{d} \boldsymbol{\gamma}} &=& \frac{\partial \Phi}{\partial \boldsymbol{\gamma}} + \frac{\partial \Phi}{\partial \mathbf{v}} \frac{\partial \mathbf{v}}{ \partial \boldsymbol{\gamma}} + \boldsymbol{\lambda}^{T} \left( \frac{\partial \mathbf{r}}{\partial \boldsymbol{\gamma}} + \frac{\partial \mathbf{r}}{\partial \mathbf{v}} \frac{\partial \mathbf{v}}{\partial \boldsymbol{\gamma}} \right) \\ &=& \frac{\partial \Phi}{\partial \boldsymbol{\gamma}} + \boldsymbol{\lambda}^{T} \frac{\partial \mathbf{r}}{\partial \boldsymbol{\gamma}} + \underbrace{\left( \frac{\partial \Phi}{\partial \mathbf{v}} + \boldsymbol{\lambda}^{T} \frac{\partial \mathbf{r}}{\partial \mathbf{v}} \right)}_{= 0} \frac{\partial \mathbf{v}}{\partial \boldsymbol{\gamma}} \end{array} $$

(49)

Since the Lagrange multiplier can be freely chosen, it is selected such that the underlined part of the equation becomes zero to avoid the computationally expensive evaluation of the term $\frac {\partial \mathbf {v}}{\partial \boldsymbol {\gamma }}$. The adjoint equation then becomes

$$ \begin{array}{@{}rcl@{}} \mathbf{S}^{T} \boldsymbol{\lambda} = - \left( \frac{ \partial \Phi}{\partial \mathbf{v}}\right)^{T} \end{array} $$

(50)

Here, it is noted that, the state variables can be complex variables if, e.g., the radiation condition given in Fig. 7 is utilized. In this case, the term $\frac {\partial \Phi }{\partial \mathbf {v}}$ on the right hand side of the adjoint equation in (50) is realized as Dühring et al. (2008)

$$ \begin{array}{@{}rcl@{}} \frac{\partial \Phi}{\partial \mathbf{v}} = \frac{\partial \Phi}{\partial \mathbf{v}_{r}} - \text{i} \frac{\partial \Phi}{\partial \mathbf{v}_{i}} \end{array} $$

(51)

where the subscripts r and i denote the real and the imaginary parts of a complex number. Having calculated the Lagrange multipliers that satisfy (50), the sensitivity of the objective function is then calculated as

$$ \begin{array}{@{}rcl@{}} \frac{\text{d} \Phi}{\text{d} \boldsymbol{\gamma}} = \frac{\partial \Phi}{\partial \boldsymbol{\gamma}} + \Re \left( \boldsymbol{\lambda}^{T}\frac{\partial \mathbf{S}}{\partial \boldsymbol{\gamma}}{\mathbf{v}} \right) \end{array} $$

(52)

where R(⋅) denotes the real part of a complex quantity. The R(⋅) operator is used to compress the sensitivity equation into a simplified form and details of this derivation can be extracted from the results in Jensen (2007).

It should be emphasized that the adjoint approach presented here is especially efficient for a very high number of design variables and a low number of constraint functions. The main cost is associated with solving the adjoint equation (50)—a step that is particularly cheap if the original FE equation is solved using a direct solver since the stiffness matrix is then already factorized.

2.3.2 Level set parametrization

Level set sensitivity analysis differs significantly from the density-based analysis presented in Section 2.3.1 where the differentiation was carried out with respect to an element design variable γ. Instead, the derivatives are here handled by treating the domain Ω as a continuous medium and examining what happens when the boundary ∂Ω is perturbed; i.e., the sensitivities take the form of shape derivatives. However, there are also similarities, since the adjoint method is employed for efficient computation. An in depth introduction to shape derivatives can be found in Choi and Kim (2005). Here, it is noted that we have left out the overbar notation for the continuous variables to keep the notation clean for the reminder of this work.

We will assume, without loss of generality, that the objective function to be minimized can be written on the following form:

$$ \begin{array}{@{}rcl@{}} \mathcal{J} = {\int}_{{\Omega}_{obj}} {\Phi}(\mathbf{u},p) \text{d} {\Omega} \end{array} $$

(53)

The shape derivative of the objective function $\mathcal {J}$ is now computed as

$$ \begin{array}{@{}rcl@{}} \dot{\mathcal{J}} = {\int}_{{\Omega}_{obj}} \frac{\partial {\Phi} }{\partial p} p^{\prime} \text{d} {\Omega} &+& {\int}_{{\Omega}_{obj}} \frac{\partial {\Phi} }{\partial \mathbf{u}} \mathbf{u}^{\prime} \text{d} {\Omega}\\ &+& {\int}_{\partial {\Omega}_{obj}} {\Phi} V_{n} \text{d} {\Gamma} \end{array} $$

(54)

where the prime superscript specifies a derivative with respect to a pseudo-time, ∂Ω is the boundary variation and V_n represents a normal (or design) velocity of the boundary. For simplicity, we will assume that Ω_obj is a fixed domain and separate from the design domain. Hence, the third term in (54) vanishes because V_n = 0 for ∂Ω_obj since there is no overlap between the design and objective domains.

In a similar way as for the density-based sensitivity analysis, we will construct an adjoint problem in order to avoid explicit computation of the terms p^′ and u^′. For this purpose, a weak form of the governing equations is constructed, where the test functions are replaced by Lagrange’s multipliers λ_p and λ_u, corresponding to the pressure and displacement fields, respectively. Furthermore, the two weak forms are added into one single equation:

$$ \begin{array}{@{}rcl@{}} &&{\int}_{{\Omega}_{s}} \boldsymbol{\lambda}_{\epsilon}^{T} \mathbf{\mathcal{C} } \boldsymbol{\epsilon} \text{d}{\Omega} - \omega^{2} \rho_{s} {\int}_{{\Omega}_{s}} \boldsymbol{\lambda}_{u}^{T} \mathbf{ u} \text{d}{\Omega}\\ &&+{\int}_{{\Omega}_{a}} (\nabla \lambda_{p} )^{T} \nabla p \text{d}{\Omega} - \frac{\omega^{2}}{ {c_{a}^{2}}} {\int}_{{\Omega}_{a}} \lambda_{p} p \text{d}\Omega\\ &&- {\int}_{{\Gamma}_{as} } \boldsymbol{\lambda}_{u}^{T} \mathbf{n}_{a} p \text{d}{\Gamma} - \omega^{2} \rho_{a} {\int}_{{\Gamma}_{as} } \lambda_{p} \mathbf{n}_{a}^{T} \mathbf{u} \text{d}{\Gamma} = 0 \end{array} $$

(55)

where λ_𝜖 has also been introduced as an adjoint strain field which is calculated as λ_𝜖 = B_uλ_u. In (55), the radiation boundary Γ_ar is not included and the Neumann boundaries for both acoustic and structural domains (Γ_an and Γ_sn) are considered to be zero for clarity.

For use in the subsequent derivation, we now take the shape derivative of (55). Terms containing the pseudo-time derivative of the adjoint fields recover the state equation of the coupled system and sum to zero. This leaves us with the following expression

$$ \begin{array}{@{}rcl@{}} &&{\int}_{{\Omega}_{s}} \boldsymbol{\lambda}_{\epsilon}^{T} \mathbf{\mathcal{C} } \boldsymbol{\epsilon}^{\prime} \text{d}{\Omega} - \omega^{2} \rho_{s} {\int}_{{\Omega}_{s}} \boldsymbol{\lambda}_{u}^{T} \mathbf{ u}^{\prime} \text{d}{\Omega}\\ && + {\int}_{{\Omega}_{a}} (\nabla \lambda_{p} )^{T} \nabla p^{\prime} \text{d}{\Omega} - \frac{\omega^{2}}{ {c_{a}^{2}}} {\int}_{{\Omega}_{a}} \lambda_{p} p^{\prime} \text{d}{\Omega}\\ && - {\int}_{{\Gamma}_{as} } \boldsymbol{\lambda}_{u}^{T} \mathbf{n}_{a} p^{\prime} \text{d}{\Gamma} - \omega^{2} \rho_{a} {\int}_{{\Gamma}_{as} } \lambda_{p} \mathbf{n}_{a}^{T} \mathbf{u}^{\prime} \text{d}{\Gamma} \\ && + {\int}_{\partial {\Omega}_{s}} \mathcal{G}_{s} V_{n} \text{d} {\Gamma} + {\int}_{\partial {\Omega}_{a}} \mathcal{G}_{a} V_{n} \text{d} {\Gamma} + {\int}_{{\Gamma}_{as}} \mathcal{G}_{as} V_{n} \text{d} {\Gamma} \! = 0 \end{array} $$

(56)

where the $\mathcal {G}$ functions collect the boundary terms in (56) that are the coefficients of the normal velocity V_n:

$$ \begin{array}{@{}rcl@{}} \mathcal{G}_{s} &=& \boldsymbol{\lambda}_{\epsilon}^{T} \mathbf{\mathcal{C} } \boldsymbol{\epsilon} - \omega^{2} \rho_{s} \boldsymbol{\lambda}_{u}^{T} \mathbf{ u}\\ \mathcal{G}_{a} &=& (\nabla \lambda_{p} )^{T} \nabla p - \frac{\omega^{2}}{ {c_{a}^{2}}} \lambda_{p} p\\ \mathcal{G}_{as} &=& -\nabla \left( \boldsymbol{\lambda}_{u}^{T} \mathbf{n}_{a} p \right)^{T} \mathbf{n}_{a} - \kappa\left( \boldsymbol{\lambda}_{u}^{T} \mathbf{n}_{a} p \right)\\ &-&\omega^{2}\rho_{a}\left( \nabla \left( \lambda_{p} \mathbf{n}_{a}^{T} \mathbf{u} \right)^{T} \mathbf{n}_{a} - \kappa\left( \lambda_{p} \mathbf{n}_{a}^{T} \mathbf{u} \right)\right) \end{array} $$

(57)

and κ is the mean curvature defined in (6).

In order to construct the adjoint equation, the differentiated weak form in (56) is added to (54) and the terms containing p^′ and u^′ are collected together. The adjoint variables are now chosen so that the following adjoint equation is fulfilled

$$ \begin{array}{@{}rcl@{}} &&{\int}_{{\Omega}_{s}} \boldsymbol{\lambda}_{\epsilon}^{T} \mathbf{\mathcal{C} } \boldsymbol{\epsilon}^{\prime} \text{d}{\Omega} - \omega^{2} \rho_{s} {\int}_{{\Omega}_{s}} \boldsymbol{\lambda}_{u}^{T} \mathbf{ u}^{\prime} \text{d}{\Omega}\\ &&+{\int}_{{\Omega}_{a}} (\nabla \lambda_{p} )^{T} \nabla p^{\prime} \text{d}{\Omega} - \frac{\omega^{2}}{ {c_{a}^{2}}} {\int}_{{\Omega}_{a}} \lambda_{p} p^{\prime} \text{d}{\Omega}\\ &&-{\int}_{{\Gamma}_{as} } \boldsymbol{\lambda}_{u}^{T} \mathbf{n}_{a} p^{\prime} \text{d}{\Gamma} - \omega^{2} \rho_{a} {\int}_{{\Gamma}_{as} } \lambda_{p} \mathbf{n}_{a}^{T} \mathbf{u}^{\prime} \text{d}{\Gamma} =\\ &&-{\int}_{{\Omega}_{obj}} \frac{\partial {\Phi} }{\partial p} p^{\prime} \text{d} {\Omega} - {\int}_{{\Omega}_{obj}} \frac{\partial {\Phi} }{\partial \mathbf{u}} \mathbf{u}^{\prime} \text{d} \Omega \end{array} $$

(58)

Using the discretization approach outlined in (42), the discrete form of the (58) takes the form

$$ \begin{array}{@{}rcl@{}} \left[\begin{array}{cc} \left( \mathbf{K}_{s} - \omega^{2} \mathbf{M}_{s} \right) & - \mathbf{C} \\ -\rho_{a} \omega^{2} \mathbf{C}^{T} & \left( \mathbf{K}_{a} - \omega^{2} \mathbf{M}_{a} \right) \end{array}\right]^{T} \left[\begin{array}{c} \boldsymbol{\lambda}_{u} \\ \mathbf{\lambda_{p}} \end{array}\right] = \left[\begin{array}{c} -\frac{\partial {\Phi} }{\partial \mathbf{u}} \\ -\frac{\partial {\Phi} }{\partial p} \end{array}\right] \end{array} $$

(59)

Considering optimization problems where the parts of the acoustic boundary ∂Ω_a and structural boundary ∂Ω_s subjected to design changes are equal to the boundary of the coupled surface Γ_as and having a set of Lagrange multipliers that satisfies the adjoint equation (58), the expression for the shape derivative of the objective function $\mathcal {J}$ becomes

$$ \dot{\mathcal{J}} = {\int}_{{\Gamma}_{as}} \mathcal{G}_{{\Gamma}_{as}} V_{n} \text{d} {\Gamma} $$

(60)

where

$$ \begin{array}{@{}rcl@{}} &&\mathcal{G}_{{\Gamma}_{as}} = \boldsymbol{\lambda}_{\epsilon}^{T} \mathbf{\mathcal{C} } \boldsymbol{\epsilon} - \omega^{2} \rho_{s} \boldsymbol{\lambda}_{u}^{T} \mathbf{ u} + (\nabla \lambda_{p} )^{T} \nabla p - \frac{\omega^{2}}{ {c_{a}^{2}}} \lambda_{p} p\\ &&- \left[ \nabla \left( \boldsymbol{\lambda}_{u}^{T} \mathbf{n}_{a} p \right)^{T} \mathbf{n}_{a} + \kappa\left( \boldsymbol{\lambda}_{u}^{T} \mathbf{n}_{a} p \right) \right]\\ &&- \omega^{2} \rho_{a} \left[ \nabla \left( \lambda_{p} \mathbf{n}_{a}^{T} \mathbf{u} \right)^{T} \mathbf{n}_{a} + \kappa\left( \lambda_{p} \mathbf{n}_{a}^{T} \mathbf{u} \right) \right] \end{array} $$

(61)

We note that, if the radiation boundary condition is included in the acoustic domain, i.e., (18), the derivation remains the same. However, the state and adjoint variables become complex variables, in which case the shape derivative of the objective function should be replaced by

$$ \begin{array}{@{}rcl@{}} \dot{\mathcal{J}} = {\int}_{{\Gamma}_{as}} \Re \left( \mathcal{G}_{{\Gamma}_{as}} \right) V_{n} \text{d} {\Gamma} \end{array} $$

(62)

In order to convert the optimization problem with an inequality volume constraint to an unconstrained optimization problem (Nocedal and Wright 2006), the following augmented Lagrange function is proposed:

$$ \begin{array}{@{}rcl@{}} \mathcal{L} = \mathcal{J} + \lambda \left[ {\int}_{{\Omega}_{s}} \text{d} {\Omega} - V_{0} \right] + \frac{1}{2{\Lambda} } \left[ {\int}_{{\Omega}_{s}} \text{d} {\Omega} - V_{0} \right]^{2} \end{array} $$

(63)

where λ is the Lagrangian multiplier and Λ is a penalization parameter. The updating scheme is

$$ \begin{array}{@{}rcl@{}} \lambda^{l + 1} = \lambda^{l} + \frac{1}{{\Lambda}^{l}} \left[ {\int}_{{\Omega}_{s}} \text{d} {\Omega} - V_{0} \right], \qquad {\Lambda}^{l + 1} = \eta {\Lambda}^{l} \end{array} $$

(64)

where l is the number of the current iteration of the algorithm and η is a smalll positive number (> 1) which slowly increases the value of the penalization parameter Λ. Thus, the shape derivative of the augmented Lagrange function reads

$$ \begin{array}{@{}rcl@{}} \dot{\mathcal{L}} = {\int}_{{\Gamma}_{as}} \underbrace{\left( \Re\left( \mathcal{G}_{{\Gamma}_{as}} \right) + \lambda^{l} + \frac{1}{{\Lambda}^{l}} \left[ {\int}_{{\Omega}_{s}} \text{d} {\Omega} - V_{0} \right] \right)}_{\mathcal{G}_{tot}} V_{n} \text{d} {\Gamma} \end{array} $$

(65)

Using the steepest decent method in which the decent direction satisfies $\dot {\mathcal {L}} <0$, the design velocity V_n is chosen as

$$ \begin{array}{@{}rcl@{}} V_{n} = - \mathcal{G}_{tot} \end{array} $$

(66)

which will be used in the update scheme presented later.

2.4 Design update methods

Before proceeding, we note that all reviewed methods are based on an optimization cycle that consists of FE analysis, sensitivity analysis, and design updates repeated in an iterative fashion until a convergence criteria is met. The procedures applied for the design updates for the density methods and the level set method will be outlined in the following.

2.4.1 Non-linear mathematical programming

The topology optimization problem can be posed by first defining a real valued cost function Φ. The minimization of this function with respect to the design variables γ is sought while satisfying the given constraints ψ_i. Mathematically, the problem is stated as

$$ \begin{array}{@{}rcl@{}} &&\underset{\boldsymbol{\gamma}}{\min} \quad {\Phi}(\boldsymbol{\gamma} , \mathbf{v}(\boldsymbol{\gamma}) ) \end{array} $$

(67)

$$ \begin{array}{@{}rcl@{}} &&\text{s.t.}\quad \mathbf{r}(\boldsymbol{\gamma} , \mathbf{v}(\boldsymbol{\gamma})) = \mathbf{S} \mathbf{v} - \mathbf{h} = 0 \end{array} $$

(68)

$$ \begin{array}{@{}rcl@{}} &&\qquad \psi_{i} \leq 0 \end{array} $$

(69)

$$ \begin{array}{@{}rcl@{}} &&\qquad 0\leq \boldsymbol{\gamma} \leq 1 \end{array} $$

(70)

The solution to the above stated optimization problem ((67) to (70)) is solved using nonlinear programming tools. A popular choice among the topology optimization community is the method of moving asymptotes (MMA) algorithm (Svanberg 1987, 2001). The algorithm requires the derivatives of both the cost function Φ and the constraints ψ_i with respect to the design variable γ. The problem is solved in a nested manner, such that the state-problem is left out of the optimization problem. It should be noted that topology optimization problems are often characterized by a large number of design variables and few constraints.

To introduce mesh independency and to avoid checkerboard problems, regulation techniques should be applied on the design parametrization. For this purpose, either the convolution type density filtering (Bruns and Tortorelli 2001) or the density filtering based on the solution of a Helmholtz type equation (Lazarov and Sigmund 2011) is applied on the design variable field. Also to achieve crisp designs, projection schemes on the filtered design variable can be applied (Guest et al. 2004; Wang et al. 2011). Additionally, a continuation scheme is applied on the penalization parameter n in the interpolation scheme in (36)–(36) which reduces the risk for the optimization algorithm to get stuck in a local minimum.

The overall algorithm for density-based topology optimization of acoustic-structure interaction problems can be stated as follows

• 1. Initialize the design variable field. This can be either uniform, random or a specified design.

• 2. Apply filtering operation to obtain the physical design.

• 3. Solve the mixed state equation, (43).

• 4. Solve the adjoint equation, (50).

• 5. Calculate the sensitivity, (52), and apply chain rule to take filtering operation into account.

• 6. Update the design using MMA.

• 7. Stop iterations when the change in design variables is below a user defined tolerance or continue from the step 2.

2.4.2 BESO

As an alternative to using mathematical programming for the design updates in density-based topology optimization, the BESO formulation is also included in this work. The overall optimization algorithm is identical to the one presented in the previous section except for step 6 which is replaced by:

• 1. [6.] Heuristic design updates based on the sensitivities evaluated at the discrete design (without any intermediate densities and following a “soft-kill” approach where only structural and acoustic elements are allowed).

This means that at all stages throughout the optimization procedure the design will be fully discrete, meaning that the removed structural elements are replaced with acoustic elements and vice versa. The corresponding material properties of both media are still calculated through the interpolation functions given in the (35) to (38). Various heuristic update schemes have been introduced for the BESO approach (see, e.g., Huang and Xie (2007), (2009), (2010); Huang et al. (2010)). Here, we use the BESO update scheme presented in Huang and Xie (2009) and Huang et al. (2010).

The BESO formulation has previously been presented in Vicente et al. (2015) for acoustic-mechanical interaction problems. However, it should be noted that our BESO implementation is based on the mixed finite element formulation (Section 2.2.2), hence the sensitivities are calculated in the same fashion as presented in Section 2.3.1. This means that our BESO approach differs from the one in Vicente et al. (2015) where a segregated finite element model is used to solve the acoustic-mechanical interaction problem and only the structural part of the domain is included in the sensitivity analysis.

2.4.3 Boundary shape evolution

When using the level set approach, the normal “design” velocity V_n, computed such that $\dot {\mathcal {J}}<0$, is used to update the design. A Hamilton-Jacobi type of equation (Osher and Fedkiw 2003) is obtained by the defining a “time derivative” of the level set function ϕ(x):

$$ \begin{array}{@{}rcl@{}} \frac{\partial \phi }{\partial t} - V_{n} | \nabla \phi | = 0 \text{in} \Omega,\qquad \phi(x,0) = \phi_{0}(x) \end{array} $$

(71)

As seen from the Hamilton-Jacobi equation, the design ∂Ω is updated by moving the zero level set (ϕ = 0) with the normal velocity V_n of the moving boundaries.

Solution of the Hamilton-Jacobi, i.e., (71), is most commonly realized by employing the finite difference method. A number of different explicit upwinded finite difference schemes can be found in the literature (Sethian 1999; Osher and Fedkiw 2003), which provide a robust and stable solution to (71). In a finite element framework, Xing et al. (2010) realized the solution of the Hamilton-Jacobi equation by adding stabilizing diffusion in the streamline direction, whereas (Liu et al. 2005) solved a reaction-diffusion equation obtained by adding an artificial diffusion term.

In our implementation, we make use of the finite volume method and hence solve the following form of the Hamilton-Jacobi equation

$$ \begin{array}{@{}rcl@{}} \frac{\partial \phi }{\partial t} - \mathbf{v}_{n} \cdot \nabla \phi = 0 \end{array} $$

(72)

where $\mathbf {v}_{n} = V_{n} \left (\frac {\nabla \phi }{| \nabla \phi | } \right )$ and the discretization is done on the equivalent divergent form of (72), which reads

$$ \begin{array}{@{}rcl@{}} \frac{\partial \phi }{\partial t} - \left[ \nabla \cdot \left( \mathbf{v}_{n} \phi \right) - \phi \nabla \cdot \mathbf{v}_{n} \right] = 0 \end{array} $$

(73)

First-order upwind scheme is utilized for the discretization of the convective term and the temporal term is discretized by the finite difference method using the first order forward Euler scheme. Stable time evaluation is realized by satisfying the CFL stability condition

$$ \begin{array}{@{}rcl@{}} {\Delta} t \le \frac{h}{\max | V_{n}|} \end{array} $$

(74)

where h is the grid size in the level set mesh.

Furthermore, after a few design iterations, too steep or flat regions can occur in the level set function which can lead to inaccurate representation of the boundaries. In order to regularize the optimization, the level set function is thus periodically re-initialized into a signed distance function by solving the re-initialization equation (Osher and Fedkiw 2003). We remark that many alternative regularization methods exist. For example, Yamada et al. (2010) proposed a level set method from the concept of the phase field model which provides a perimeter constraint method to regularize the optimization problem and does not require solving the reinitialization equation throughout the optimization. The following equation is used for reinitialization of the level set function ϕ

$$ \begin{array}{@{}rcl@{}} \frac{\partial \phi }{\partial t} + \mathbf{s} \cdot \nabla \phi = S(\phi) \end{array} $$

(75)

where $\mathbf {s} = S(\phi ) \left (\frac {\nabla \phi }{| \nabla \phi | } \right )$ and the sign function S(ϕ) is approximated as Peng et al. (1999)

$$ \begin{array}{@{}rcl@{}} S(\phi) = \frac{\phi}{\sqrt{\phi^{2} + | \nabla \phi|^{2} h^{2} }} \end{array} $$

(76)

Here, it is noted that S(ϕ) is updated at every time-step. For the finite volume discretization of the reinitialization equation, the second term on the left hand side of (76) is also written in its equivalent divergent form as

$$ \begin{array}{@{}rcl@{}} \frac{\partial \phi }{\partial t} + \left[ \nabla \cdot \left( \mathbf{s} \phi \right) - \phi \nabla \cdot \mathbf{s} \right] = S(\phi) \end{array} $$

(77)

For the examples considered in this work, the reinitialization equation is discretized with a first-order upwind scheme for the convective term and a first order forward Euler scheme for the temporal term. Selection of the utilized time step Δt is again based on the CFL stability condition given in the (74) where V_n is replaced by |s|.

The overall algorithm for the level set–based topology optimization of acoustic-structure interaction problems is then

• 1. Initialize the level set function to represent the initial design and update the mesh in the structural and acoustic domains either by marching-squares algorithm or by total re-meshing the both domains.

• 2. Solve the state equation (21).

• 3. Solve the adjoint equation (58).

• 4. Update the Lagrange multiplier according to 64.

• 5. Calculate the design velocity V_n (66) and extrapolate it to the level set mesh.

• 6. Solve the Hamilton-Jacobi equation (73) to evolve the shape. (See Section 2.4.3)

• 7. Re-initialize the level set function (77). (See Section 2.4.3)

• 8. Update the mesh from the new level set function.

• 9. Stop iterations when the change in the objective function is below a user defined tolerance or continue from the step 2.

3 Comparison of methods

In the following sections, we use our implementations of the density-based and level set topology optimization methods to solve two representative topology optimization problems in vibro-acoustics. Both problems concern the minimization of the sound pressure in a prescribed objective domain, i.e.,

$$ \begin{array}{@{}rcl@{}} \mathcal{J}(p) = {\int}_{{\Omega}_{obj}} | p | \text{d} \Omega \end{array} $$

(78)

subject to a volume constraint.

3.1 Example 1

The first example is adopted from Yoon et al. (2007) and a schematic illustration of the design problem, including boundary conditions, is given in Fig. 8. The design problem concerns the design of a flexible partition which minimizes the downstream sound pressure in a duct. The model is excited by an incoming plane wave with amplitude p_in = 1kPa to the left and the right most boundary is modelled as open using an absorbing boundary condition. The optimization is carried out for a single frequency of f = 1.0/π Hz. The allowed volume fraction is set to 55% of the design domain. The material properties of the considered structure and the acoustic fields are listed in the Tables 1 and 2. To allow for a fair comparison, the same background mesh is used for both density-based and level set topology optimization methods, i.e., an uniform mesh with an element size of 2 × 10^− 2m.

Fig. 8

Schematic illustration of the example 1 showing the boundary conditions of the optimization problem. Gray color shows the design domain, blue color illustrates the region where the objective function is evaluated

Table 1 Material properties considered for the structure

Table 2 Material properties considered for the acoustic domain

The problem is first solved using the density-based formulation. To regularize the problem, a Helmholtz-type density filtering (Lazarov and Sigmund 2011) with a filtering radius of r = 0.015m is used. Regularized Heaviside projection (Wang et al. 2011) with a threshold η = 0 is employed where the sharpness parameter is taken as β = 3 at the start of the optimization. To avoid getting stuck in a low-quality local minima, we apply a continuation strategy on the convexity parameter n in the RAMP interpolation functions ((36) to (38)) and the sharpness parameter β. The process is started with n = 3 and at every 50th design cycle the value is increased by one until it reaches n = 6. After this β takes the values of 7 and then 14 in the subsequent 50 design iterations. The initial material distribution is a uniform design with γ = 0.5.

The optimized design obtained using the density method with the mixed formulation is shown in Fig. 9. The result is the well-known structure from the literature and it closely resembles the structure reported by Yoon et al. (2007). We note that the problem closely corresponds to the maximization of the clamped beam’s first natural frequency.

Fig. 9

Optimized design with the density-based topology optimization. The objective value of the end design evaluated with mixed formulation, $\mathcal {C} = 48.9 \mathrm {N}$

The example problem is then solved using the level set formulation. In order to avoid too large or too small gradients of the level set function, we re-initialize it as a signed distance function at every 6th iteration. Also, since the level set method is known to be highly dependent on the initial topology (Villanueva and Maute 2014), we use two different initial configurations. First, the design domain is initialized with a straight beam with holes distributed periodically (Fig. 10a). Secondly, the design obtained from the density-based optimization is considered as a “smart” initial guess for the level set optimization. This is included to investigate if the level set optimization keeps and/or improves the structure obtained using the density method.

Fig. 10

Displacement magnitude |u|[m] contours showing a initial structure for the level set method, b optimized design obtained with the level set method, the objective value of the end design $\mathcal {C} = 68.7 \mathrm {N}$, and c optimized design of the level set method where the initial guess is the optimized design from the density-based optimization, objective value of the end design $\mathcal {C} = 34.9 \mathrm {N}$

The optimized designs are given in Fig. 10 where the displacement magnitude of the structures is included for qualitative comparison. The corresponding level set surface for the optimized design in Fig. 10b is shown in Fig. 11. We note that the design obtained using the density-based result as initial guess performs significantly better than the design obtained with an initial configuration based on a beam with holes. Qualitatively, the design obtained using the density-based method is unaltered when used as input for the level set method. However, interestingly, it is found that the objective of the level set design in Fig. 10c constitutes a 28.6% reduction in objective value compared to the density based result evaluated using the mixed formulation, c.f. Fig. 9. To investigate this discrepancy further, we perform a body-fitted mesh analyses of all three designs using the segregated formulation. The density-based design is thresholded at γ = 0.5 using the marching square algorithm and the resulting frequency responses are collected in Fig. 12. From the plot, it is clear that the performance of the density-based design is practically identical to the best result obtained using the level set method. Hence, the discrepancy in objective value is due to the mixed formulation requiring a finer mesh than the segregated analysis (Zienkiewicz and Taylor 2000).

Fig. 11

Level set surface of the optimized design

Fig. 12

Frequency response of the objective function. Black line is the optimized design with the density method (body-fitted mesh), blue line is the optimized design with the level set method, and the red line is the optimized design of the level set method where the initial guess is the optimized design from the density method

Figure 13 shows the sound pressure level (SPL) of the acoustic domain. The plots confirm by visual inspection that the designs obtained by both initial guesses indeed lower the sound pressure level in the objective domain when compared to initial beam structure with holes. It is also clear that the lowest pressure level is obtained for the optimized design using the density-based result as an the initial guess.

Fig. 13

Sound pressure level [dB] contours showing a initial structure for the level set method, b optimized design obtained with the level set method, and c optimized design of the level set method where the initial guess is the optimized design from the density-based optimization

It is important to mention that the objective evolution of any initial guess for the level set method is relatively smooth (c.f. Fig. 14). This means that the design update scheme for the level set function is likely to result in a local mimima, which is similar to solving the density-based problem without a continuation scheme, i.e., using a constant high value for the penalization parameter. However, there is no obvious way to introduce the same convexification in the level set method using the Hamilton-Jacobi equation, and hence, great care must be exerted when designing the initial guess for the level set method.

Fig. 14

The iteration history of the objective function for the level set method

3.2 Example 2

In Example 2, the design of a dome structure is considered. The problem is adopted from Shu et al. (2014) and Vicente et al. (2015) and a schematic illustration of the model problem can be seen in the Fig. 15 along with the dimensions of the computational domain. The boundary condition for the bottom of the computational domain is clamped for the structure and zero Dirichlet for the acoustic domain. All other boundary conditions for the acoustic problem are hard wall conditions. The system is excited with a point pressure load in the acoustic domain inside the dome and the objective is to minimize the absolute pressure over the prescribed objective domain near the top boundary. The design domain is fixed to the dome area shown at the Fig. 15 and 80% of the design domain is allowed to be filled with material. This example is solved for three frequencies, i.e., 4Hz, 5.3Hz, and 6Hz, and the sum of the absolute pressures constitutes the objective function.

Fig. 15

Schematic illustration of example 2 showing the boundary conditions of the optimization problem. Gray color shows the design domain, blue color illustrates the region where the objective function is evaluated. The coordinates of the lower left and upper right corners of the objective domain are (0.06,1.44) and (2.94,1.485), respectively

The material properties of the structure and the acoustic field are listed in the Tables 3 and 4. We construct a uniform mesh with an element size of 1.5 × 10^− 2m for the computational domain and carry out the optimization using the same mesh resolution for both the density-based and the level set–based methods.

Table 3 Material properties considered for the structure

Table 4 Material properties considered for the acoustic domain

The density-based topology optimization approach utilizes a similar continuation strategy for the convexity parameter n and the sharpness parameter β as used in Example 1 (c.f. Section 3.1). In this case, the parameter n is increased at every 100th design cycle and after the final value of n = 6, the parameter β takes the values of 7, 14, and 28 for the subsequent 50 design iterations. The filtering radius and the initial material distribution are taken to be the same as in the previous example.

Figure 16 shows the optimized design obtained using the density-based method. The structure contains one partial hole at the top and the profile of the dome gets thinner towards the sides of the dome. The structure is as thick as the diameter of the prescribed design domain around the top partial hole.

Fig. 16

Optimized design with the density-based topology optimization. The objective value of the end design evaluated with mixed formulation, $\mathcal {C} = 0.0022 \mathrm {N}$

The problem is then solved using the level set formulation. Similar to the first example, the level set function is re-initialized as a signed distance function every 8th iteration. In Fig. 17, the level set surface of the optimized design is shown. The optimized design contains no holes and looks very similar to the structure reported in Shu et al. (2014). Although in Shu et al. (2014), the dome structure is optimized for a distributed load applied at the outer edge of the dome.

Fig. 17

Level set surface of the optimized design

To allow for a fair comparison of the performance of the optimized designs, we once again apply a body-fitted mesh analysis. In Fig. 18, we compare the displacement magnitude of the designs obtained using the density-based and level set–based optimization methods to the initial structure used for the level set optimization. Although the structures obtained with both optimization methods have a similar inner shape, the density-based design in Fig. 18c clearly exhibits smaller displacements at the sides of the dome compared to the level set result in Fig. 18b. Similarly, the sound pressure level contours are shown in Fig. 19 clearly showing that both designs exhibit a significant reduction of the acoustic pressure outside of the dome compared to the initial dome structure with equally spaced holes. Considering the objective values of the end designs listed in Fig. 18, we note that the optimized design using the density method performs approximately 40% percent better than the structure optimized with the level set method.

Fig. 18

Displacement magnitude |u|[m] contours for the frequency f = 6[Hz] showing a initial structure for the level set method, b optimized design obtained with the level set method, the objective value of the end design $\mathcal {C} = 0.0026 \mathrm {N}$, and c body-fitted analysis of optimized design obtained with the density method resulting in an objective value of $\mathcal {C} = 0.0015 \mathrm {N}$. The analysis in c is performed on a thresholded design at γ = 0.5 using the marching squares algorithm

Fig. 19

Sound pressure level [dB] contours for the frequency f = 4[Hz] showing a initial structure for the level set method, b optimized design obtained with the level set method, and c body fitted analysis of the optimized design obtained with the density method, thresholded at γ = 0.5 using the marching squares algorithm

Finally, the frequency responses of the dome structures are shown in Fig. 20. We note that the plot consists of the three designs, i.e., the initial beam with holes and two optimization results as well as an extra design consisting of the design domain fully filled with material. Firstly, it is clear that both optimized designs outperforms the initial design and the fully filled dome. Secondly, it is noted that the optimization results in a minimization of the first resonance frequency and maximization of the second. Third and lastly, it is observed that the density-based method has a better performance for two target frequencies, i.e., f = 4Hz and f = 6Hz. However, from visual inspection of the frequency response, it is clear that the level set method has the lowest response around the target frequency f = 5.3Hz. This advocates the use of a finer frequency range discretization though this is deemed outside the scope of the current review paper.

Fig. 20

Frequency response of the objective function for example 2. The blue line is the optimized design using the level set method, the red line is the initial design with holes, the yellow line is the design domain fully filled with material and the purple line is the optimized design using the density method

3.2.1 BESO

The comparative study is concluded with a single design obtained using the BESO formulation. The optimized design is shown in Fig. 21 along with the sound pressure level contour for a frequency of 4Hz. The resulting topology is found to be in good agreement with the result presented in Vicente et al. (2015).

Fig. 21

Optimized design obtained from the BESO method with mixed FE formulation showing a final optimized design field and b sound pressure level [dB] contour for the frequency f = 4Hz. The objective value of the end design evaluated with mixed formulation, $\mathcal {C} = 0.0029 \mathrm {N}$ and body fitted analysis of optimized design obtained with BESO resulting in an objective value of $\mathcal {C} = 0.0019 \mathrm {N}$

The performance of the BESO design shows a similar reduction of the acoustic pressure outside the optimized dome compared to the level set and density method results given in Fig. 19. The frequency response of the BESO optimized dome is shown in the Fig. 22 which also includes the response for the density-based design, both evaluated using a body fitted mesh and a segregated analysis. The difference in response in the vicinity of the three optimization frequencies are clearly observed, showing that the density-based design has superior performance for the target frequencies of 4Hz and 6Hz, whereas the BESO design exhibits better performance around the second target frequency 5.3Hz similar to the level set design. It is noted that for all methods, the reduction in the sound pressure level in the specified frequency range is obtained by reducing the first resonance frequency and increasing the second resonance frequency of the coupled system. Here, it is noted that, even though the BESO approach provides a crisp design without any gray scale, the calculated objective value of the final design shows a significant discrepancy in the objective value compared to a body fitted analysis of the design, c.f. Fig. 21. This further underlines the previously mentioned inherent limitations of the standard u − p mixed formulation wrt. modelling accuracy.

Fig. 22

Frequency response of the objective function. Black line is the optimized design obtained from BESO approach with mixed formulation, and purple line is the optimized design with the density method

4 Conclusions and recommendations

The aim of this review paper has been to provide an overview and comparison of the different approaches that have currently been applied for solving topology optimization problems in vibro-acoustics. In the following, we summarize the most significant findings, highlight the challenges, and conclude with recommendations for future directions within the field of acoustic-mechanical topology optimization.

For all studied examples, the density-based method was shown to provide the best performing designs from an arbitrary initial guess. We mainly ascribe this to the possibility of designing a continuation scheme on the penalization parameter that effectively and consistently results in better local minima. On the contrary, the level set approach does not facilitate such a continuation scheme making the results more prone to stuck in local minima and highly dependent on the initial design. Also, though not presented here, we emphasize that the use of rigorous mathematics such as non-linear programming methods easily facilitates the inclusion of additional constraints on both physics and geometry (Sigmund and Maute 2013).

However, this should not be interpreted as a rejection of the level set–based methods. On the contrary, problems having a multiphysical nature is often highly dependent on the interface representation, i.e., the coupling conditions. The examples presented here clearly demonstrated the issues arising from intermediate density regions and thus a poor interface representation. That is, poor accuracy in the modeling using mixed formulation makes the density-based optimization approach challenging and problematic for problems which are strongly coupled and sensitive to design changes at the interface. Another significant challenge for the density-based methods is that the optimized designs require a postprocessing step and a subsequent body fitted analysis to verify its performance. This step can be completely avoided when using the level set methods with a crisp interface representation, which together with the possibility to easily enforce complicated coupling conditions advocates the continued use and development of level set methods.

Finally, it was shown that the BESO method provided comparable results in the second example. While the method generally yields very good results for pure static structural optimization where the design sensitivities are of equal sign (more material is always better), its application to more complicated problems involving dynamics and/or multi-physics appears to be more problematic. Throughout the work, the BESO method is found to be the least stable of the considered methods and in some cases it leads to lack of convergence. This we ascribe to the heuristic BESO update algorithm that is not well suited for handling problems with both positive and negative design sensitivities. However, the BESO method also has its justification. That is, the method is very easy to implement in commercial black-box codes without the need to access element integration routines and does not require expensive re-meshing schemes. In fact, for many problems one can use energy expression to get sensitivity information which makes it even simpler to adopt into existing codes.

4.1 Recommendations

Firstly, we recommend that subsequent work on vibro-acoustic optimization always includes a benchmark against previous work as shown in this paper. That is, solving old problems with new methods can only be justified if the new method provides an improvement compared to existing methods. In the following, we provide recommendations for the density and level set method, separately.

For the density-based methods, we have the following recommendations. Firstly, we note that the mixed formulation is an expensive modeling tool since it can lead to poor accuracy on coarse meshes, even with crisp designs, and that the intermediate densities at the interface lack a physical explanation. The mixed formulation is also prone to numerical instabilities arising from the choice of interpolation functions (Wang and Bathe 1997), which means that for a stable solution high order elements must be used which in turn increases the computational complexity even further. Therefore, we suggest that more work should go into new interpolation schemes that, potentially, could alleviate the need for the mixed formulation. On the other hand, a monolithic formulation have many desirable properties and hence another path to follow is to modify, or expand, the standard u − p mixed formulation such that it is better at capturing the sharp jumps in state fields that arise when performing topology optimization.

For the level set–based methods, we have the following recommendations. The main issue with level set methods using the Hamilton-Jacobi update scheme is the problem of adding more constraints. We therefore suggest that focus is put on methods that ensure crisp interfaces, e.g., xFEM (Gerstenberger and Wall 2008) or CutFEM methods (Hansbo and Hansbo 2004; Burman et al. 2014), together with mathematical programming tools. This latter would allow the optimization analyst to include more constraints whereas the first means that tedious post processing can be avoided.

5 Replication of results

All results presented in this work are in fact reproductions of already published and developed methods. For replicating the presented examples, the readers can find the relevant information in the corresponding sections.