1 Introduction

Structural topology optimization problem is concerned with the optimal distribution of material for the load-bearing structures and is applied to a wide range of structural design problems (Bendsøe and Kikuchi 1988). The problem of topology optimization related to dynamic responses is concerned with design of structures subjected to harmonic force excitations. The purpose of the dynamic response topology optimization is to minimize the dynamic compliance of structure at prescribed material volume. In general, it is necessary to incorporate the model reduction methods, such as the mode displacement method (MDM), and mode acceleration method (MAM), into the topology optimization procedure to reduce the computational cost, especially for the large-scale problem (Greene and Haftka 1991). However, due to the changes in the design variables, optimization for the dynamic response requires repetitious solution of generalized eigen-problem, and the process involves repeated and tremendous calculations.

The reanalysis methods are intended to efficiently evaluate the structural responses for various changes in design without solving the full set of modified analysis equations. One of the tools for reanalysis is the Combined Approximations (CA) approach, which attempts to give global qualities local approximations. The CA method uses binomial series terms as basis vectors in reduced basis approximations. Originally, the CA method was proposed for structural static reanalysis (Kirsch and Papalambros 2001). Afterwards, the method had been extended to vibration reanalysis (Kirsch et al. 2007; Kirsch 2010). It has been shown the CA approach can provide accurate results for lower mode shapes (Kirsch and Bogomolni 2004). The CA method, however, calculates a frequency and associated mode shape each time, it is less efficient and accurate, especially for higher order mode shapes. Based on utilizing CA method, some considerable efforts have been made about topology optimization. Leu and Chang (2000) addressed the implementation of structural reanalysis method in both mathematical programming (MP) and optimality criteria (OC) schemes, a reduced basis method extended from Kirsch’s method is employed for the linear reanalysis. Amir et al. (2009) investigated the implementation of CA method in structural topology optimization. It integrated the linear reanalysis into the standard topology optimization for minimum compliance problems. Bogomolny (2010) put forward an extension towards reanalysis-based topology optimization for free vibrations. The CA method involved into the optimization process is utilized for repeated eigenvalue analysis. Xu et al. (2010) applied an adaptive reanalysis method into the optimal design of trusses, where the CA method is adopted for the static analysis. A reanalysis-based genetic algorithm for structural optimization with frequency constrains was presented by Zou et al. (2011). The extended Kirsch CA method is used for the case of repeated eigenvalue problem. The integration of approximate reanalysis procedures in robust topology optimization for a minimum-weight formulation was proposed by Amir et al. (2012). Zuo et al. (2016) presented a new sensitivity reanalysis of static displacement for arbitrary changes of design variables. Taylor series expansion and CA method is utilized to solve the sensitivity equations. Based on CA method, a novel sensitivity reanalysis method of vibration problem (Zou et al. 2017) is proposed to acquire the derivatives of the eigenvalues and eigenvectors.

In this study, the block combined approximation with shifting (BCAS) (Zheng et al. 2015) is implemented in topology optimization related to dynamic responses with multiple frequencies. For the optimization problem, the MAM is adopted because of its compromise between computing accuracy and efficiency (Liu et al. 2015). To implement MAM, however, it generally needs to firstly solve the eigen-problem via subspace iteration or Lanczos algorithms, which is quite time-consuming in optimization process. For improving the efficiency of the topology optimization, the BCAS method is utilized for repetitious solving the eigen-problem invested in MAM. Compared with the CA method, the BCAS method is used to simultaneously compute several frequencies and associated mode shapes of the modified structure at a time. For improving computational efficiency, Basic Linear Algebra Subprograms (BLAS) are adopted. The BLAS are routines that provide standard building blocks for performing basic vector and matrix operations. They were first published as a Fortran library in 1979 (Lawson et al. 1979) and are still used as a building block in higher-level mathematical programming languages and libraries, including LINPACK, LAPACK and so on. The Level-1 BLAS perform scalar, vector and vector-vector operations; the Level-2 BLAS perform matrix-vector operations; the Level-3 BLAS perform matrix-matrix operations and thereby its higher performance is achieved (Goto and Van De Geijn 2008). Because the BLAS are efficient, portable, and widely available, they are commonly used in the development of high quality linear algebra software. For eigenvalue reanalysis, matrix-vector operations in the CA method are based on the Level-2 BLAS; while the matrix-matrix operations in the BCAS method are based on the Level-3 BLAS. The execution efficiency is thus enhanced. When using BCAS for repeated structural analysis, one can substantially reduce the number of required factorized forms of the shifted stiffness matrices, thus removing a significant portion of the computational effort.

The paper is organized as follows. In Section 2, the MAM is firstly introduced for computing the dynamic response of complex structure. The topology optimization problem formulations are reviewed in Section 3, including the polynomial interpolation model, sensitivity analysis and harmonic excitations with multiple frequencies. In section 4, the BCAS method is described generally for completeness. Finally, accuracy and performance comparisons are shown by three numerical examples in section 5 and the conclusions are presented in Section 6.

2 The mode acceleration method

As is known, the governing equation for the structural response of a structure under harmonic external force can be written as

$$ \mathbf{M}\ddot{\mathbf{X}}(t)+\mathbf{C}\dot{\mathbf{X}}(t)+\mathbf{KX}(t)=\mathbf{F}(t) $$
(1)

where X(t) represents the displacement vector, F(t) is the force vector. M, C, K are n × n the mass matrix, damping matrix and stiffness matrix, respectively. F(t) = F 0 e jωt(j 2 =  − 1) is the vector of excitation force with a frequency ω and amplitude F 0.

In this paper, the Rayleigh damping corresponds to

$$ \mathbf{C}=\alpha \mathbf{M}+\beta \mathbf{K} $$
(2)

is considered where α and β are Rayleigh damping coefficients of the structure that may depend on ω.

2.1 Mode acceleration method

To implement MAM (Cornwell et al. 1983), the l lowest eigenpairs need to be computed firstly by solving the following eigen-problem

$$ {\mathbf{K}\boldsymbol{\upvarphi}}_i={\omega}_i^2{\mathbf{M}\boldsymbol{\upvarphi}}_i, i=1,\dots, l $$
(3)

where ω i is the ith circular eigenfrequency and its corresponding eigenvectors is Φ = [φ 1, φ 2,  … , φ l ], both of them satisfy the following orthogonalities

$$ \left\{\begin{array}{l}{\boldsymbol{\upvarphi}}_i^T{\mathbf{K}\boldsymbol{\upvarphi}}_j={\delta}_{i j}{\omega}_i^2\hfill \\ {}\begin{array}{l}{\boldsymbol{\upvarphi}}_i^T{\mathbf{M}\boldsymbol{\upvarphi}}_j={\delta}_{i j}\\ {}{\boldsymbol{\upvarphi}}_i^T{\mathbf{C}\boldsymbol{\upvarphi}}_j=2{\delta}_{i j}{\zeta}_i{\omega}_i\end{array}\hfill \end{array}\right.\kern0.75em i, j=1,2,\dots, l $$
(4)

where δ ij is the Kronecker delta, \( {\zeta}_i=\frac{\alpha +{\beta \omega}_i^2}{2{\omega}_i} \) is damping ratio of the Rayleigh damping.

By using the following transformation

$$ \mathbf{X}(t)=\boldsymbol{\Phi} \mathbf{Y}(t) $$
(5)

where Y(t) = [Y 1(t), Y 2(t),  … , Y n (t)] is the vector of modal coordinate. A set of n uncoupled equations can be obtained by substituting (5) into (1) and by premultiplying Φ T

$$ {\ddot{Y}}_j(t)+2{\zeta}_j{\omega}_j{\dot{Y}}_j(t)+{\omega}_j^2{Y}_j(t)={\boldsymbol{\upvarphi}}_j^T\mathbf{F}(t),\kern0.5em j=1,2,\dots, n $$
(6)

In the MAM, (6) is solved for Y j (t)and gives

$$ {Y}_j(t)=\frac{{\boldsymbol{\upvarphi}}_j^T\mathbf{F}(t)}{\omega_j^2}-\frac{{\ddot{Y}}_j(t)}{\omega_j^2}-\frac{2{\zeta}_j{\dot{Y}}_j(t)}{\omega_j} $$
(7)

The substitution of (7) into (5) yields

$$ \mathbf{X}(t)=\sum_{j=1}^n\left(\frac{{\boldsymbol{\upvarphi}}_j{\boldsymbol{\upvarphi}}_j^T\mathbf{F}(t)}{\omega_j^2}-\frac{{\boldsymbol{\upvarphi}}_j{\ddot{Y}}_j(t)}{\omega_j^2}-\frac{2{\boldsymbol{\upvarphi}}_j{\zeta}_j{\dot{Y}}_j(t)}{\omega_j}\right) $$
(8)

However, the first term in (8) can be represented as (Besselink et al. 2013)

$$ \sum_{j=1}^n\frac{{\boldsymbol{\upvarphi}}_j{\boldsymbol{\upvarphi}}_j^T\mathbf{F}(t)}{\omega_j^2}={\mathbf{K}}^{-1}\mathbf{F}(t) $$
(9)

According to (7), the second and third parts in (8) can be written as

$$ \sum_{j=1}^n\left(\frac{{\boldsymbol{\upvarphi}}_j{\ddot{Y}}_j(t)}{\omega_j^2}+\frac{2{\boldsymbol{\upvarphi}}_j{\zeta}_j{\dot{Y}}_j(t)}{\omega_j}\right)=\sum_{j=1}^n\left(\frac{{\boldsymbol{\upvarphi}}_j{\boldsymbol{\upvarphi}}_j^T\mathbf{F}(t)}{\omega_j^2}-{Y}_j(t)\right) $$
(10)

By inspection of (10), it needs all the n terms for the two parts, which is not practical for the large-scale problem. As a result, only first l(l <  < n) terms are employed in MAM, especially for the large-order problem. Hence, the substitution of first l terms in (10) into (8) and combination with (9) yields

$$ \mathbf{X}(t)={\mathbf{K}}^{-1}\mathbf{F}(t)-\sum_{j=1}^l\left(\frac{{\boldsymbol{\upvarphi}}_j{\boldsymbol{\upvarphi}}_j^T\mathbf{F}(t)}{\omega_j^2}-{\boldsymbol{\upvarphi}}_j{Y}_j(t)\right) $$
(11)

The summation in (11) represents the displacement response approximate result of (1) by MAM.

3 Topology optimization under harmonic force excitation with multiple frequencies

3.1 Statement of topology optimization

Topology optimization of a dynamic problem under harmonic force excitations is formulated as

$$ \begin{array}{l} find\kern0.5em 0<\underset{\bar{\mkern6mu}}{\rho}\le {\rho}_e\le 1\kern0.5em e=1,2,\dots {N}_e\\ {} \min \kern0.5em {f}_s=\left\Vert {X}_s(t)\right\Vert \\ {} s. t.\kern1em \nu \le \overline{\nu}\end{array} $$
(12)

where ρ e (e = 1,  … , N e ) is the pseudo-density of the eth element, \( \underset{\bar{\mkern6mu}}{\rho} \) is a positive lower bound of the set of design variables. Here, \( \underset{\bar{\mkern6mu}}{\rho}=0.001 \) is assigned to ρ e to prevent the mass, stiffness and damping matrices from becoming singular. X s (t) denotes displacement response corresponding the sth DOF. N e and v represent the number of element and material volume, respectively. \( \overline{v} \) is the prescribed volume of available material.

In topology optimization, Solid Isotropic Material with Penalization Model (SIMP) approach would cause localized modes phenomena because of the mismatch between element stiffness and mass (Liu et al. 2015; Zuo and Saitou 2017). In this paper, the Polynomial Interpolation Scheme (PIS) (Zhu et al. 2010) will be used.

$$ \left\{\begin{array}{l}{\mathbf{m}}_e={\rho}_e{\mathbf{m}}_{e0}\hfill \\ {}{\mathbf{k}}_e=\frac{15{\rho}_e^5+{\rho}_e}{16}{\mathbf{k}}_{e0}\hfill \end{array}\right. $$
(13)

where m e and k e are the mass matrix and stiffness matrix of element e. m e0 and k e0 represent the mass matrix and stiffness matrix of solid element e.

3.2 Sensitivity analysis and filtering method

The Globally Convergent Method of Moving Asymptotes (GCMMA) algorithm (Svanberg 1995) is employed as the optimizer. To solve the topological optimization for a harmonic problem, the sensitivity of displacement with respect to design variables ρ e (e = 1,  … , N e ) are firstly required. Suppose X(t) = X 0 e jωt is the solution to (1), its substitution into (1) yields

$$ \left(\mathbf{K}+ j\omega \mathbf{C}-{\omega}^2\mathbf{M}\right){\mathbf{X}}_0={\mathbf{F}}_0 $$
(14)

where X 0 is the complex amplitude vector of displacement response. Take the derivative of (14) with respect to design variable ρ e

$$ \frac{\partial {\overline{\mathbf{K}}}_d}{\partial {\rho}_e}{\mathbf{X}}_0+{\overline{\mathbf{K}}}_d\frac{\partial {\mathbf{X}}_0}{\partial {\rho}_e}=\mathbf{0} $$
(15)

and

$$ {\overline{\mathbf{K}}}_d=\mathbf{K}+ j\omega \mathbf{C}-{\omega}^2\mathbf{M} $$
(16)

Suppose

$$ {\overline{X}}_s={\mathbf{a}}^T{\mathbf{X}}_0 $$
(17)

where a denotes a n × 1 vector with all terms being zero except term s being 1. Based on (15), the sensitivity of the displacement amplitude for the sth DOF is then established

$$ \frac{\partial {\overline{X}}_s}{\partial {\rho}_e}={\mathbf{a}}^T\frac{\partial {\mathbf{X}}_0}{\partial {\rho}_e}=-{\mathbf{a}}^T{\overline{\mathbf{K}}}_d^{-1}\frac{\partial {\overline{\mathbf{K}}}_d}{\partial {\rho}_e}{\mathbf{X}}_0 $$
(18)

So the sensitivity of displacement for the concerned DOF s can be derived through the chain rules as

$$ \frac{\partial {f}_s}{\partial {\rho}_e}=\frac{\partial \left\Vert {X}_s(t)\right\Vert }{\partial {\rho}_e}=\left(\operatorname{Re}\left({\overline{X}}_s\right)\cdot \operatorname{Re}\left(\frac{\partial {\overline{X}}_s}{\partial {\rho}_e}\right)+\operatorname{Im}\left({\overline{X}}_s\right)\cdot \operatorname{Im}\left(\frac{\partial {\overline{X}}_s}{\partial {\rho}_e}\right)\right){\left\Vert {X}_s(t)\right\Vert}^{-1} $$
(19)

To avoid the numerical instabilities (Sigmund and Petersson 1998), such as checkerboards patterns and mesh-dependencies phenomena, some restriction on the design must be imposed. Here a filtering technique (Sigmund 1997) is used to modify the sensitivities \( \frac{\partial {f}_s}{\partial {\rho}_e} \) as follows:

$$ \frac{\overset{\wedge }{\partial {f}_s}}{\partial {\rho}_e}=\frac{1}{\rho_e\sum_{j=1}^{N_j}{H}_j}\sum_{j=1}^{N_j}{H}_j{\rho}_j\frac{\partial {f}_s}{\partial {\rho}_e} $$
(20)

where N j is the set of elements e for which the center-to-center distance dist(e, j) to element e is smaller than the filter radius r min, and the convolution operator (weight factor) H j in (20) is defined as

$$ {H}_j= \max \left(0,{r}_{\min }- dist\left( e, j\right)\right) $$
(21)

3.3 Harmonic excitations with multiple frequencies

In general, frequency response analysis is concerned with dynamic behavior of a structure subjected to harmonic load in a frequency interval, not just at a prescribed frequency value. For the topological optimization under harmonic excitations with multiple frequencies, the object function for minimizing the integral of displacement amplitude in the frequency interval [ω A , ω B ] can be expressed as

$$ \begin{array}{l} find\kern0.5em 0<\underset{\bar{\mkern6mu}}{\rho}\le {\rho}_e\le 1\kern0.5em e=1,2,\dots, {N}_e\\ {} \min \kern0.5em {f}_{\mathrm{si}}={\int}_{\omega_{\mathrm{A}}}^{\omega_{\mathrm{B}}}\left\Vert {X}_s\left(\omega \right)\right\Vert d\omega \\ {} s. t\kern1em \nu \le \overline{\nu}\end{array} $$
(22)

For yielding converged solution (Cheng and Ali 1988; Liu et al. 2015), the Gauss-Legendre integration is utilized to calculate the integral in a frequency interval.

$$ {\int}_{\omega_A}^{\omega_B}\left\Vert {X}_s\left(\omega \right)\right\Vert d\omega \approx \frac{\omega_B-{\omega}_A}{2}\sum_{j=1}^{N_g}{\gamma}_j\left\Vert {X}_s\left(\frac{\omega_B-{\omega}_A}{2}{\mu}_j+\frac{\omega_B+{\omega}_A}{2}\right)\right\Vert $$
(23)

where γ j is the weight factor for the jth Gaussian point, and μ j is the Gaussian point within [−1, 1], N g is the number of Gaussian points.

With the complicated integrand or the large integration interval, it needs to subdivide the integration interval to ensure the computing accuracy. As well-known, the curve of harmonic response has a sharp jump around the resonant eigenfrequency, the large frequency interval can be firstly subdivided by the eigenfrequencies. For each subinterval between the two neighboring eigenfrequencies, it will be further separated by P additional points. The pth point in the subinterval [ω i , ω i + 1] is determined by

$$ {\omega}_{i, p}={\omega}_i+{q}_p\left({\omega}_{i+1}-{\omega}_i\right),\kern0.5em 1\le p\le P,\kern0.5em 0<{q}_p<1 $$
(24)

where q p is the proportional factor of the pth point in the subinterval. For representing the sharp jumps, q p should be chosen properly to form small subintervals near eigenfrequency and large subintervals far from the eigenfrequency. Refer to Liu et al. (2015), theP = 5 addition points are selected between the two neighboring eigenfrequencies as

$$ \begin{array}{l}{\omega}_{i,1}={\omega}_i+0.01\left({\omega}_{i+1}-{\omega}_i\right)\\ {}{\omega}_{i,2}={\omega}_i+0.11\left({\omega}_{i+1}-{\omega}_i\right)\\ {}{\omega}_{i,3}={\omega}_i+0.50\left({\omega}_{i+1}-{\omega}_i\right)\\ {}{\omega}_{i,4}={\omega}_i+0.89\left({\omega}_{i+1}-{\omega}_i\right)\\ {}{\omega}_{i,5}={\omega}_i+0.99\left({\omega}_{i+1}-{\omega}_i\right)\end{array} $$
(25)

4 Block combined approximations method with shifting

In this section, the BCAS method for repeated solution of the generalized eigen-problem is shortly summarized for the sake of completeness. Consider an initial design or a “reference” design with n × n stiffness and mass matrices K 0 and M 0, respectively. The corresponding l lowest eigenpairs can be computed by solving the following eigen-problem via subspace iteration with shifting (Bathe 2013) or shifted Lanczos algorithm (Grimes et al. 1994)

$$ {\mathbf{K}}_0{\boldsymbol{\Phi}}_0={\mathbf{M}}_0{\boldsymbol{\Phi}}_0{\boldsymbol{\Lambda}}_0 $$
(26)

where \( {\boldsymbol{\Lambda}}_0=\mathit{\operatorname{diag}}\left({\omega}_{01}^2,{\omega}_{02}^2,\dots, {\omega}_{0 l}^2\right) \) and Φ0 = [Φ01, Φ02,  … , Φ0l ] represent the matrices of l computed eigenvalues and the corresponding eigenvectors, respectively. Whereas the solution procedure involves a series of LDLT factorized forms of the shifted stiffness matrices K 0 − μ 0j M 0(j = 1, …m, μ 0j  ≥ 0), m is the number of these triangular factorizations. Assume a change in the structure, the corresponding changes in the stiffness and mass matrices are denoted as ΔK and ΔM, respectively, where the modified eigen-problem can be written as

$$ \mathbf{K}\boldsymbol{\Phi } \coloneq \left({\mathbf{K}}_0+\Delta \mathbf{K}\right)\boldsymbol{\Phi} =\left({\mathbf{M}}_0+\Delta \mathbf{M}\right)\boldsymbol{\Phi} \boldsymbol{\Lambda} \coloneq \mathbf{M}\boldsymbol{\Phi } \boldsymbol{\Lambda} $$
(27)

where \( \boldsymbol{\Lambda} =\mathit{\operatorname{diag}}\left({\omega}_1^2,{\omega}_2^2,\dots, {\omega}_l^2\right) \) and Φ = [φ 1, φ 2,  … , φ l ] are the matrices of requested eigenvalues and that of the corresponding eigenvectors for the new design structure.

Consider the shifted generalized eigen-problem of the modified eigen-problem

$$ \left[\left({\mathbf{K}}_0+\Delta \mathbf{K}\right)-{\mu}_{0 s}\left({\mathbf{M}}_0+\Delta \mathbf{M}\right)\right]\boldsymbol{\Phi} \equiv \left[\left({\mathbf{K}}_0-{\mu}_{0 s}{\mathbf{M}}_0\right)+\left(\Delta \mathbf{K}-{\mu}_{0 s}\Delta \mathbf{M}\right)\right]\boldsymbol{\Phi} =\mathbf{M}\boldsymbol{\Phi } \overline{\boldsymbol{\Lambda}} $$
(28)

where \( \overline{\boldsymbol{\Lambda}}=\boldsymbol{\Lambda} -{\mu}_{0 s}\mathbf{I} \). The two eigen-problems in (27) and (28) have the same eigenvectors. Premultiplying (28) by (K 0 − μ 0s M 0)−1 yields

$$ \left[\mathbf{I}+\mathbf{B}\right]\boldsymbol{\Phi} =\mathbf{R} $$
(29)

where

$$ \mathbf{B}={\left({\mathbf{K}}_0-{\mu}_{0 s}{\mathbf{M}}_0\right)}^{-1}\left(\Delta \mathbf{K}-{\mu}_{0 s}\Delta \mathbf{M}\right) $$
(30)
$$ \mathbf{R}={\left({\mathbf{K}}_0-{\mu}_{0 s}{\mathbf{M}}_0\right)}^{-1}\mathbf{M}\boldsymbol{\Phi } \overline{\boldsymbol{\Lambda}} $$
(31)

If the spectral radius ρ(B) of matrix B is less than 1, use of (29) leads to the so-called binomial series expansion

$$ \boldsymbol{\Phi} =\left(\mathbf{I}-\mathbf{B}+{\mathbf{B}}^2-\cdots \right)\ \mathbf{R} $$
(32)

Because R is unknown, replacing Λ with Λ 0 and substituting Φ 0 for Φ in (31) results in

$$ \mathbf{R}\approx {\left({\mathbf{K}}_0-{\mu}_{0 s}{\mathbf{M}}_0\right)}^{-1}\mathbf{M}{\boldsymbol{\Phi}}_{\mathbf{0}}\left({\boldsymbol{\Lambda}}_0-{\mu}_{0 s}\mathbf{I}\right) $$
(33)

Note that multiplication of a basis vector by a scalar does not affect the results (Kirsch et al. 2007), we can drop \( {\boldsymbol{\Lambda}}_0-{\mu}_{0 s}\mathbf{I}=\mathit{\operatorname{diag}}\left({\omega}_{01}^2-{\mu}_{0 s},\dots, {\omega}_{0 l}^2-{\mu}_{0 s}\right) \) and the first basis vectors are given by

$$ {\mathbf{R}}_1={\left({\mathbf{K}}_0-{\mu}_{0 s}{\mathbf{M}}_0\right)}^{-1}\mathbf{M}{\boldsymbol{\Phi}}_{\mathbf{0}} $$
(34)

In summary, for calculating the first l eigenpairs by BCAS method, l × s basis vectors of the subspace R B  = [R 1, R 2,  … , R s ] need to be constructed by the terms of the binomial series in (32)

$$ {\mathbf{R}}_1={\overline{\mathbf{K}}}_0^{-1}{\mathbf{M}\boldsymbol{\Phi}}_0 $$
(35)
$$ {\mathbf{R}}_j=-{\overline{\mathbf{B}}\mathbf{R}}_{j-1}, j=2,\dots, s $$
(36)

where

$$ {\overline{\mathbf{K}}}_0={\mathbf{K}}_0-{\mu}_{0 s}{\mathbf{M}}_0 $$
(37)
$$ \Delta \overline{\mathbf{K}}=\Delta \mathbf{K}-{\mu}_{0 s}\Delta \mathbf{M} $$
(38)
$$ \overline{\mathbf{B}}={\overline{\mathbf{K}}}_0^{-1}\Delta \overline{\mathbf{K}} $$
(39)

The BCAS method can achieve approximate solutions of high quality withs = 2. Based on the information of initial eigenvalues, the shifted frequency μ 0s is chosen as

$$ \left|{\mu}_{0 s}-\frac{\lambda_{01}+{\lambda}_{0 l}}{2}\right|=\underset{1\le j\le m}{ \min}\left|{\mu}_{0 j}-\frac{\lambda_{01}+{\lambda}_{0 l}}{2}\right| $$
(40)

which is the nearest to the center of the l eigenvalues of the initial or “reference” structure.

The reduced eigen-problem is then solved for the first leigenpairs by

$$ \left({\mathbf{R}}_B^T{\mathbf{KR}}_B\right){\boldsymbol{\Theta}}_R=\left({\mathbf{R}}_B^T{\mathbf{MR}}_B\right){\boldsymbol{\Theta}}_R{\boldsymbol{\Lambda}}_R $$
(41)

where Λ R and Θ R are the matrices of the first l eigenvalues and the corresponding eigenvectors of the reduced eigen-problem. Finally, the matrix of eigenvectors and the matrix of eigenvalues for the modified structure can be evaluated by

$$ \boldsymbol{\Phi} ={\mathbf{R}}_B{\boldsymbol{\Theta}}_R,\boldsymbol{\Lambda} ={\boldsymbol{\Lambda}}_R $$
(42)

As the triangular factorization of the shifted stiffness matrix K 0 − μ 0s M 0 has already been given in the “reference” optimization step, the calculation of the subspace basis R B involves only forward and backward substitution. For more details, we refer readers to Ref. (Zheng et al. 2015). Note that, for the BCAS method, all computations are based on matrix-matrix operation and its higher performance can thus be achieved by using the Level-3 BLAS.

However, the approximate reanalysis procedure cannot accommodate extremely large changes in stiffness matrix, hence these should be bounded in some way. This results in the use of an outdated physical model, so that in many cases the approximate solution will converge to a higher value and cannot reach the final optimum. In some certain cases, the approximate solution is not accurate enough and leads to unreliable optimal results, sometime with a better objective value than the optimum results (Amir et al. 2009). In order to efficiently achieve an accurate optimization result, it is necessary to choose the right time to stop a sequence of approximate reanalysis and perform an exact solution. Here, the Modal Assurance Criterion (MAC) (Allemang and Brown 1982) value is adopted to control the approximate optimization procedure.

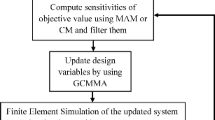
$$ MAC\left({\boldsymbol{\uprho}}_k^A,{\boldsymbol{\uprho}}_p^E\right)=\frac{{\left({\left({\boldsymbol{\uprho}}_k^A\right)}^T\left({\boldsymbol{\uprho}}_p^E\right)\right)}^2}{\left({\left({\boldsymbol{\uprho}}_k^A\right)}^T\left({\boldsymbol{\uprho}}_k^A\right)\right)\left({\left({\boldsymbol{\uprho}}_p^E\right)}^T\left({\boldsymbol{\uprho}}_p^E\right)\right)} $$
(43)

where \( {\boldsymbol{\uprho}}_k^A=\left[{\rho}_{k,1}^A,\dots, {\rho}_{k,{N}_e}^A\right] \), \( {\boldsymbol{\uprho}}_p^E=\left[{\rho}_{p,1}^E,\dots, {\rho}_{p,{N}_e}^E\right] \) are the design variable vector at kthstep and the one corresponding to the previous exact solution, respectively. The MAC value is used to represent the correlation number between the two modal shapes, and its value ranging from 0.7 to 1 can usually be regarded as a good correlation between two design variable vectors (Massa et al. 2011). In this paper, the subspace iteration method with shifting is performed for eigen-problem analysis when the \( MAC\left({\boldsymbol{\uprho}}_k^A,{\boldsymbol{\uprho}}_p^E\right) \) is less than ε ρ  = 0.95. The implementation of the proposed method for solving the optimization problem may be described as following five steps.

Input the boundary condition, material properties, applied loads.

Solving the (1) by MAM: if k = 1 or \( MAC\left({\boldsymbol{\uprho}}_k^A,{\boldsymbol{\uprho}}_p^E\right)\le {\varepsilon}_{\rho} \), perform the subspace iteration with shifting method to solve the eigen-problem; if not, utilize the BCAS method to compute the eigen-problem.

Sensitivity analysis for the objective function.

Update the design variable using GCMMA.

Check convergence: if the convergence criteria are not satisfied, goto step 2; otherwise, perform the postprocessor result.

5 Numerical examples

In this section, we present three examples to illustrate the efficient and accuracy of the proposed method. The subspace iteration method with shifting (SIM) (Bathe 2013) is used to calculate the exact eigenpairs in MAM, where the relative difference of eigenvalues in terms of consecutive iterations is less thanε λ  = 10−8. The filter radius r min = 2.0 is adopted in the numerical examples. The compressed sparse row storage format for matrices is used. All programs are complied by using Intel Fortran Composer XE 2015 with Math Kernel library 11.2, and run on the platform: Intel I5–3450, quad-core CPU with 3.10GHz, 8GB RAM. For the convergence criteria, the following indicator is adopted: the relative difference of the objective function values between two neighboring iterations steps (Kang et al. 2011)

$$ \left\Vert \frac{f_{si}^{k+1}-{f}_{si}^k}{f_{si}^k}\right\Vert <0.0001 $$
(44)

where the optimization step is denoted by superscript k. Meanwhile, we use MAC(ρ E, ρ A) to demonstrate the accuracy of the result, where ρ E and ρ A represent the design variable vectors evaluated by exact method and the proposed approach with BCAS method, respectively.

5.1 Structure 1: 2D cantilever beam

As the first example, the presented structure is a rectangular domain of 1.0m × 0.5m, and its thickness is 0.01. It is clamped at the left side, as shown in Fig. 1. Here, the domain is meshed into 100×50 four-node elements and the total number of DOFs is 10,200. The Young’s module of material is E = 2.0 × 1011Pa, the mass density is ρ = 7.8 × 103 kg/m 3, and Poisson’s ratio is ν = 0.30. Initial values of all pseudo-densities are set to be 0.25. The corresponding first eigenfrequency of the initial structure is 45.05 Hz. The coefficients for the Rayleigh damping are chosen as α = 10−2and β = 10−4.

Fig. 1
figure 1

2D cantilever beam.

Full size image

As shown in Fig. 1, a harmonic force with the amplitude of 10,000 N is vertically applied at the middle node of the right edge, the corresponding frequency intervals are f r  = [0, 50]Hz and f r  = [0, 100]Hz (ω = 2πf r ), respectively. The minimization of dynamic compliance at the loaded point along the force direction is taken as objective function. The first l = 20 modes for the structure are employed in MAM. The optimization seeks the layout of this support structure with a volume 25% of the whole design domain. The iteration histories of the objective function are presented in Fig. 2. The optimized results with exact method and proposed method are shown in Fig. 3 and Fig. 4. From these Figs, it can be found that the results of the proposed method are almost in agreement with the exact solution. The more details of computational results are provided in Tables 1 and 2, the corresponding MAC values for the design variables vector computed by the proposed procedure are 0.9978 and 0.9306, which indicates that, the proposed method can achieve very excellent approximations to the exact results. For the two frequency intervals f r  = [0, 50]Hz and f r  = [0, 100]Hz, the exact method reaches objective values of 0.2270 and 0.5268, and the proposed method reaches 0.2289 (0.8% error) and 0.5246 (0.4% error), respectively. In addition, compared with the exact method, the number of SIM iterations can be reduced significantly and the CPU times for the proposed method are remarkably reduced.

Fig. 2
figure 2

Convergence curve for the objective function of a 2D cantilever beam: the proposed method vs. the exact method. a f r  = [0, 50]Hz. b f r  = [0, 100]Hz

Full size image
Fig. 3
figure 3

Optimized configurations of structure 1 with frequency interval f r  = [0, 50]Hz. a Exact method. b Proposed method

Full size image
Fig. 4
figure 4

Optimized configurations of structure 1 with frequency interval f r  = [0, 100]Hz. a Exact method. b Proposed method

Full size image
Table 1 Results of the 2D cantilever beam under harmonic excitations with multiple frequencies f r  = [0, 50]Hz
Full size table
Table 2 Results of the 2D cantilever beam under harmonic excitations with multiple frequencies f r  = [0, 100]Hz
Full size table

5.2 Structure 2: 2D clamped-clamped beam

Consider a clamped-clamped beam as shown in Fig. 5, the rectangular design domain is a 1.8m × 0.3m rectangular area whose thickness is 0.01 m. The Young’s module of material is E = 2.0 × 1011Pa, Poisson’s ratio ν = 0.30 and structural densityρ = 7.8 × 103 kg/m 3. The design domain is fixed at one end but simply supported at the other. The design domain is discretized with four-node finite elements with a total number of 180×30 elements, and total 11,218 DOFs. In the initial design domain where the all pseudo-densities are uniformly set to be 0.5 and the first eigenfrequency of the initial structure is 46.80 Hz, correspondingly. The coefficients for the Rayleigh damping are chosen as α = 0.01 and β = 10−4.

Fig. 5
figure 5

2D clamped-clamped beam.

Full size image

Here MAM is still implemented with first l = 20 modes in this example. A harmonic force with the amplitude of 10,000 N is applied at middle node of the top edge, and the corresponding frequency interval f r  = [0, 50]Hz is considered here. As the objection function, the dynamic compliance at the loaded point along the force direction is minimized. The volume fraction of solid material is limited to be less than 50%. The final optimization results are shown in Fig. 6 and the iteration curves of the objective function are plotted in Fig. 7. Observing Figs. 6 and 7, it is evident that the approximate result obtained by the proposed method is in agreement with the exact one. The results of the proposed method and the exact method are listed in Table 3. The MAC value for the design vector calculated by the proposed method is 0.99986. The approximate method reaches an objective value of 8.738×10−2, with relative error of 0.03%. Moreover, with a fewer number of SIM iterations in contrast to the exact method, the CPU time of the proposed method is considerable cut down with respect to the one of the exact method.

Fig. 6
figure 6

Optimized configurations of structure 2 with frequency interval f r  = [0, 50]Hz. a Exact method. b Proposed method

Full size image
Fig. 7
figure 7

Convergence curve for the objective function of a 2D clamped-clamped beam: the proposed method vs. the exact method

Full size image
Table 3 Results of the 2D clamped-clamped beam under harmonic excitations with multiple frequencies f r  = [0, 50]Hz
Full size table

5.3 Structure 3: 3D cantilever beam

In this example, we present the solution for the minimum compliance of a 3D cantilever beam to demonstrate accuracy and competence of the proposed method. The cantilever beam has a size of 1.0m × 0.5m × 0.04m. As illustrated in Fig. 8, the beam is fixed on the left side and a harmonic force with the amplitude of 10,000 N is loaded at the middle bottom point of the right side. The domain is meshed into 100 × 50 × 4 cubic elements and the structure has 76,500 DOFs in all. The Young’s module of material is E = 2.0 × 1011Pa, the mass density is ρ = 7.8 × 103 kg/m 3, and Poisson’s ratio is ν = 0.30. Initial values of all pseudo-densities are uniformly set to be 0.30 and the corresponding first eigenfrequency of the initial structure is 8.855 Hz. The coefficients for the Rayleigh damping are chosen as α = 10−2 and β = 10−5.

Fig. 8
figure 8

3D cantilever beam.

Full size image

Here, two frequency intervals are considered, namely f r  = [0, 50]Hz and f r  = [0, 200]Hz, and first l = 15 modes for the structure 3 are employed in MAM for the first frequency interval while l = 20 is used for the last interval. The prescribed volume fraction of solid material is set to 0.3. In Fig. 9, the performance of the proposed method is compared against the one of the exact method. The optimized configurations with exact method and proposed method are shown in Figs. 10 and 11. From Figs. 9 and 11, it can be observed that the proposed method can achieve very good approximation to the exact results. The details of computational results are provided in Tables 4 and 5, the corresponding MAC values for the design variables vector computed by the proposed procedure are 0.9989 and 0.8872, respectively. The exact method reaches objective values of 6.484 × 10−2 and 0.3791 while the proposed method obtains 6.668 × 10−2 (2.8% error) and 0.3859 (1.8% error). From Tables 4 and 5, one could find that the proposed method can achieve very excellent approximations to the exact results. Additionally, compared with the CPU times of exact method, the one of the proposed method are considerably cut down as less number of the SIM iterations. Note that, the BCAS method takes full advantage of Level-3 BLAS for matrix-matrix operation. Therefore, the computational efficiency of the proposed method is greatly improved.

Fig. 9
figure 9

Convergence curve for the objective function of a 3D cantilever beam: the proposed method vs. the exact method. a f r  = [0, 50]Hz. b f r  = [0, 200]Hz

Full size image
Fig. 10
figure 10

Optimized configurations of structure 3 with frequency interval f r  = [0, 50]Hz. a Exact method. b Proposed method

Full size image
Fig. 11
figure 11

Optimized configurations of structure 3 with frequency interval f r  = [0, 200]Hz. a Exact method. b Proposed method

Full size image
Table 4 Results of the 3D cantilever beam under harmonic excitations with multiple frequencies f r  = [0, 50]Hz
Full size table
Table 5 Results of the 3D cantilever beam under harmonic excitations with multiple frequencies f r  = [0, 200]Hz
Full size table

6 Conclusions

An efficient approach for topology optimization was presented. The high computational effort included in solving eigen-problem is decreased by using BCAS method. The reanalysis procedure applied in this paper is based on performing exact solutions of eigen-problem in certain design steps, corresponding to ‘reference’ designs. As a result, in the following series of reanalysis procedures, the factorization of the modified stiffness matrix and those of associated shifted stiffness matrices are not needed. As taking full advantage of Level-3 BLAS for matrix-matrix operations, the proposed approach with BCAS method allows very fast development of approximate solutions of high quality and low computational cost for topology optimization related harmonic response. The numerical examples of finite element models have shown that the proposed optimization procedure with BCAS method is quite effective.