1 Introduction

Layered materials and structures have extensive applications in many areas of engineering. These include the increased use of layered composites in armor systems, aerospace and defensive engineering. Consequently, many researchers analyzed the behaviors of layer composites under different loading conditions while most of them considered the interfaces as flat surfaces perpendicular to the lay-up direction of the layers (Bruck and Gershon 2002; Ootao et al. 2007; Koguhi 2007; Shabana et al. 2006; Pines 2004; Kruft et al. 2008). It is found that severe stresses may induce at the interface between the successive layers due to the properties mismatches. Some studies were accomplished to investigate the effects of modifying the interferences on the induced stresses. Introducing a convex interface/joint design that inspired by the shape and mechanics of trees was among the considered modifications of the interfaces (Xu et al. 2004; Xu and Sengupta 2004). Also, the corner angle effects on the bimaterial corner stresses considering lap and scarf joints were studied (Mohammed and Liechti 2000, 2001). Moreover, Bruck et al. (2004) studied the effects of geometric complexity on the interfacial strength. They found that the complex interface with rectangular interlocking feature and interface with smoother circular feature increase the interfacial strength and reduce the statistical variation. Recently, it is proved that using curved interfaces, which are called nontraditional interfaces, reduces the induced stresses and therefore increases the operational safety (Shabana 2014). Eventually, the behavior of a layer composite depends greatly on the interface profile that can be defined mainly by the interface profile parameter. However, innumerable data are required for the best choice of the interface and structural parameters to attain the optimal performance. Therefore, optimization methods should be applied for more successful and efficient control of the stresses that induce in such structures.

The particle swarm optimization (PSO) is one of the recently used techniques in the literature to modify the structural performance in different applications. The advantages of PSO over other techniques such as genetic algorithm are that it is algorithmically simpler, more robust and generally converges faster (Sunwoo et al. 1991; Omran 2005). For the composite materials applications, Elsawaf et al. (2012a) and Elsawaf et al. (2012b) combined the particle swarm optimization with the simplex method to study the optimum structure design of a composite disk with single and multiple piezoelectric layers and to control the maximum thermal stress induced in the structural layer. Suresh et al. (2007) presented a multi-agent PSO to design an optimal composite box-beam helicopter rotor blade. The continuous geometry parameters (cross-sectional dimensions) and discrete ply angles of the box-beams were considered as design variables while the objectives were to achieve a specified stiffness value and maximum elastic coupling. Kovács et al. (2004) addressed the optimal design of a carbon-fibre-reinforced plastic sandwich-like structure with aluminum webs to optimize the structure for minimum cost and maximum stiffness. Ply arrangement, stresses and maximum deflection were considered as optimization parameters. The optimal lay-up for a rectangular composite wing was achieved in order to maximize the flutter and divergence speeds using different ply orientations (Manan et al. 2010). They used four different biologically inspired optimization methods and they found that the best single result was obtained by using PSO. Using the nature-inspired PSO method, functionally graded materials (FGMs) with generic distributions can be efficiently optimized (Kou et al. 2012). They proposed a feature tree based procedural model, which enables generic and diverse types of material variations, to represent the material heterogeneities. Many explicit functions were incorporated to describe versatile material gradations and the material composition at a given location. Also, Xu et al. (2012) used the PSO combined with analytical model to reduce the thermal residual stresses in FGM coating by designing the thicknesses and compositional distributions of coating layers. For the automotive applications, Metered et al. (2014) recently evaluated the optimum values of the passive suspension system parameters of heavy vehicles using PSO whereas the objective was to minimize the dynamic tyre load generated by vehicle–pavement interaction. They derived the equations of motion and considered the tyre stiffness, suspension stiffness and the damping coefficient of the passive damper as design parameters.

For other applications, Chen and Lin (2008) focused on PSO algorithm to solve the problem of minimizing the printed circuit board assembly time. Simultaneously, optimizing assignment/sequencing problem for multihead surface mounting machine was achieved by minimizing the number of nozzle change operations and pick and place operations. Also, PSO was successfully applied to various fields of power system optimization such as power system stabilizer design (Abido 2002), reactive power and voltage control (Yoshida et al. 2000), and dynamic security border identification (Kassabalidis et al. 2002). Chiu et al. (2009) proposed a compounded PSO clustering approach for the missing value estimation. This was achieved by firstly utilizing the normalization methods to filter outliers and prevent some attributes from dominating the clustering result. Then, the K-means algorithm and reflex mechanism were combined with the standard PSO clustering to quickly converge to a reasonable good solution. Park et al. (2005) presented a new approach to economic dispatch problems with nonsmooth cost functions using PSO.

In this paper, the critical induced thermal stresses in a layered plate are minimized using PSO technique and applying the finite element analysis. The considered composite plate is an isotropic mixture of two components: Nickel (Ni) and Alumina (Al2O3). The interfaces between the layers are considered to be nontraditional and the effect of the interface curvature is studied by considering different shapes of the interface originated from a power law. Different geometrical parameters are optimized so that the critical induced thermal stresses in the structure are minimized. These optimized parameters include the interface profile parameter, the height of the nontraditional interface on the right surface relative to the mid-surface, and the thicknesses of the layers of the plate. In the optimization process, both single-variable and multi-variable optimizations are accomplished. In other words, in certain cases optimization parameters are optimized individually while in other cases the optimization parameters are optimized simultaneously. It is found that the optimized parameters significantly reduce the stresses at the free surface and therefore increase the structural safety and reliability.

2 Problem statement and solution

Modifying the layer composite behaviors, such as the thermal response, is a main objective in order to be used for structures with severe loading conditions. The interfaces between the layers mostly exhibit the maximum weakness in a structure as they exhibit the maximum induced stress. These behaviors are depending mainly on the macroscopic and microscopic geometrical parameters. The microscopic geometrical parameters include the thickness of each layer in the structure, the profile of the interface and the height of the interface on the right surface relative to the mid-surface. The summation of the thicknesses of the layers results in the overall thickness that is a macroscopic geometrical parameter.

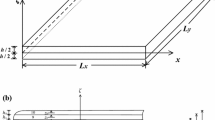
A two-dimensional plane-strain specimen, which represents a cross-sectional cut of the layered structure, is introduced. Figure 1 depicts the considered three-layer plate with both traditional and non-traditional interfaces. The plate width equals 2b whereas its thickness equals h 1 + h 2 + h 3 where h 1, h 2 and h 3 are the thicknesses of the three layers starting from the bottom layer and measured at the mid-surface of the plate. The upper nontraditional interface (Fig. 1b) has a height t on the right surface relative to the mid-surface of the plate. This height can be negative if the interface on the right surface is below its position on the mid-surface. While y-axis is chosen to be orthogonal to the faces of the layers and along their lay-up direction, x-axis is assumed to be orthogonal to the lay-up direction and parallel to the lamina faces. The origin of the coordinate system xy is supposed to lie at the mid-point of the lower face as shown in the figure. The top and bottom layers are made of alumina (Al2O3) and nickel (Ni), respectively, while the intermediate layer is a mixture of 60 % Ni and 40 % Al2O3. Therefore, the ceramic volume fraction satisfies the following relations

$$ {\mathrm{v}}_{\mathrm{c}}=\left\{\begin{array}{l}1\kern2.1em \mathrm{f}\mathrm{o}\mathrm{r}\kern1.5em \mathrm{y}\ge \kern0.5em {\mathrm{h}}_1+{\mathrm{h}}_2\\ {}0.4\kern1.5em \mathrm{f}\mathrm{o}\mathrm{r}\kern1.5em {\mathrm{h}}_1\le \mathrm{y}\le \kern0.5em {\mathrm{h}}_1+{\mathrm{h}}_2\\ {}0\kern2em \mathrm{f}\mathrm{o}\mathrm{r}\kern1.5em \mathrm{y}\le \kern0.5em {\mathrm{h}}_1\end{array}\right. $$
(1)
Fig. 1
figure 1

Layered composite plate, (a) Traditional interfaces (b) Non-traditional interfaces

Full size image

For such cases, the through-thickness variation of the different properties, such as Young’s modulus, Poisson’s ratio and coefficient of thermal expansion, in the three-layer composite system can be written as

$$ \mathrm{P}\left(\mathrm{y}\right)=\left\{\begin{array}{l}{\mathrm{P}}_{\mathrm{c}}\kern6.1em \mathrm{f}\mathrm{o}\mathrm{r}\kern1.5em \mathrm{y}\ge \kern0.5em {\mathrm{h}}_1+{\mathrm{h}}_2\\ {}\mathrm{P}\left({\mathrm{P}}_{\mathrm{c}},{\mathrm{P}}_{\mathrm{m}}\right)\kern3.12em \mathrm{f}\mathrm{o}\mathrm{r}\kern1.5em {\mathrm{h}}_1\le \mathrm{y}\le \kern0.5em {\mathrm{h}}_1+{\mathrm{h}}_2\\ {}{\mathrm{P}}_{\mathrm{m}}\kern5.12em \mathrm{f}\mathrm{o}\mathrm{r}\kern1.5em \mathrm{y}\le \kern0.5em {\mathrm{h}}_1\end{array}\right. $$
(2)

where P c and P m are the properties of the homogeneous ceramic and metal materials, respectively. P(P c , P m ) is the interlayer properties that are evaluated using the microscopic constitutive equations (Shabana 2003).

It is essential to consider the temperature-dependent properties for reliable and accurate prediction of the structure response. Table 1 lists the considered materials properties at different temperatures (Bruck and Gershon 2002). In general, Young modulus decreases while the thermal expansion coefficient increases at elevated temperatures. In the analyses, these properties are assumed to vary linearly with the temperature. Therefore, the material properties of the current composite structure are both position and temperature dependent.

Table 1 Material properties used in the FEM simulations (Bruck and Gershon 2002)
Full size table

In the present analyses, the interfaces between the different layers are assumed to be perfectly bonded at all times and the multilayer system behavior to be elastic–plastic originate from the elastoplasticity of the metal while the ceramic behaves elastically. The plane strain as a geometric approximation of structures is considered. For the finite element mesh, the element used is an 8-node isoparametric element and the numbers of elements along the horizontal and vertical directions are 80 and 70, respectively. Therefore, 2800 elements are used for one half of the model. The element size is refined near the interfaces between the layers and the free edges to accommodate the stress concentration, and the smallest element size equals 0.01 of the thickness of the thinnest layer. For the loading conditions, uniform cooling (no thermal gradient) is assumed while cooling from the fabricated temperature of 1100 K to the room temperature is assumed. Therefore, the temperature difference (T) in the current analysis is considered to be 800 K.

Since the upper interface is critical as it exhibits higher stresses than the lower one (Bruck and Gershon 2002), the geometry of the upper interface is one of the considered optimized parameters for the sake of minimizing the critical induced stresses. The lower interface, on the other hand, is assumed to be a traditional one. The considered profile of the upper interface is following a power law

$$ \mathrm{Y}\left(\mathrm{X}\right)={\mathrm{X}}^{\mathrm{m}} $$
(3)

where Y{=[y − (h 1 + h 2)]/t} denotes the non-dimensional vertical coordinate of the interface relative to the mid-surface; X{=x/b} denotes the non-dimensional horizontal coordinate normalized by half width of the plate; t is the height by which the upper interface is moved on the right surface (X = 1) from its traditional level (relative to the mid-surface); and m is an exponent. When t = 0, the interface is the traditional one that is perpendicular to the lay-up direction of the layers. When t is positive/negative, the ceramic content is decreased/increased relative to its traditional value. Figure 2 shows the interface profiles for various values of the parameter m when t is upward on the right surface of the plate. When m = 1, the interface is a flat surface inclined on the lay-up direction of the layers. For a lower value of the parameter m, the interface profile changes sharply close to the mid-surface of the plate and changes smoothly at the right surface. On the other hand, for higher values of the parameter m, the phenomena of the interface profile are vice versa of those of the lower values.

Fig. 2
figure 2

Interface profiles following the power law

Full size image

However Eq. (3) is valid when t occurs on the right surface, the following relation is to be applied when t occurs on the mid-surface of the plate

$$ \mathrm{Y}\left(\mathrm{X}\right)={\left(1-\mathrm{X}\right)}^{\mathrm{m}} $$
(4)

3 Optimization technique

The main aim of solving an optimization problem of a structure is to minimize the induced stresses and therefore decrease the damage probability. For the considered layer composite structure, it is required to evaluate the optimum values of various parameters to minimize the critical induced thermal stress.

The nonlinear optimization problem which determines the optimum values of the optimized parameters (interface profile parameter m, the height t of the interface, and the thicknesses of the layers) is defined as:

$$ \begin{array}{c}\hfill \mathrm{Find}\ \mathrm{K}=\left({k}_1,\;{k}_2,\;{k}_3,\kern0.24em \dots \right)\hfill \\ {}\hfill \mathrm{T}\mathrm{o}\ \mathrm{minimize}\ {\mathrm{f}}_{\mathrm{obj}}\left(\mathrm{K}\right)={\sigma}_y\hfill \end{array} $$
(5)

where k 1, k 2 and k 3 stand for the design parameters and σ y stands for the critical stress component to be minimized.

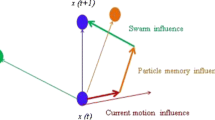
Since there are many local optima in the solution space of the optimization problem (5), PSO technique, which originally contributed by Kennedy and Eberhart (1995) with the modified optimizer introduced by Shi and Eberhart (1998), is applied to get the global optimum. The PSO starts searching the solution by initializing a population of random candidate solutions called particles and then the global optimum solution is obtained by iteratively improving the solutions around the search-space. In the iterative processes, each particle updates its position y (τ)p by tracking the individual best position b (τ)p and the global best position g (τ) selected from all particles positions. In each generation the velocity and position of each particle is updated as follows:

$$ {\mathrm{y}}_{\mathrm{p}}^{\left(\tau +1\right)}={y}_{\mathrm{p}}^{\left(\tau \right)}+{v}_{\mathrm{p}}^{\left(\tau +1\right)}{\mathrm{v}}_{\mathrm{p}}^{\left(\tau +1\right)}=W\times {v}_{\mathrm{p}}^{\left(\tau \right)}+{c}_1\times ran{d}_1\times \left[{b}_{\mathrm{p}}^{\left(\tau \right)}-{y}_{\mathrm{p}}^{\left(\tau \right)}\right]\kern0.5em +{c}_2\times ran{d}_2\times \left[{g}^{\left(\tau \right)}-{y}_{\mathrm{p}}^{\left(\tau \right)}\right] $$
(6)

where v (τ)p is the velocity of the particle p at the generation τ, W is the nonnegative inertia weight that linearly decreases over time, c 1 and c 2 are acceleration coefficients, and rand 1 and rand 2 are random numbers between 0 and 1. Each particle contains a set of variables to be optimized. Searching for the optimum variables is done through a predefined range of each variable. However, during iteration the updated velocity v (τ + 1)p may drive one of the variables in the new position of a particle y (τ + 1)p to fly out of the feasible region (predefined range). In that case, the particle is repositioned to the nearest range’s bound for that variable and the velocity at which is replaced with a random value (Huang and Mohan 2005). The parameters used in this study are listed as follows: c 1 = 2.0 and c 2 = 2.0; W linearly decreases over time from 0.9 to 0.4. Despite the influence of the PSO parameters, the number of particles and the termination criterion of the iterations are crucial to the performance of the PSO algorithm and the quality of the solution. In general, the termination criterion can be classified into two main types. First, the iterations will be terminated when a required solution value is acquired. In the second criterion, the iterative process is terminated when a specific number of iterations is reached. This method generally applied when there is no prior knowledge of the optimum solution. Since in the studied optimization problem given in Eq. ( 5 ) there is no prior knowledge of the optimum solution, the second criterion method is used. Therefore, the particles and the iteration number of improving the solutions should be properly settled on.

4 Results and discussions

The aim of the present study is to provide the designers of layer composites with better choices of the main design parameters in order to create high performance components. This can be achieved by optimizing different geometrical parameters so as to minimize the induced stresses and have safe designed components under different operating conditions. The optimized geometrical parameters include the interface profile parameter, the height of the nontraditional interface on the right surface relative to the mid-surface, and the thicknesses of the layers of the plate. Since the opening mode delamination between two successive layers occurs due to the excessive thermal stress component parallel to the lay-up direction (σ y ), this study concentrates mainly on avoiding this delamination mode.

Some parameters have default values when they are not considered among the optimized parameters. For example, it is considered that all layers of the plate have the same thickness and a layer thickness equals 5 mm if it is not considered among the optimized parameters. Also, the plate width is related to the default layer thickness by b/h 1 = 8. Moreover, the default values of m and t are 1 and 1 mm, respectively. The considered optimization ranges of the interface parameter and the interface height on the right surface are 0 < m ≤ 8 and −5 ≤ t ≤ 5 mm, respectively. Also, the ranges of the intermediate and top layers thicknesses are 0 ≤ h 2 ≤ 5 mm and t ≤ h 3 ≤ 5 mm when t is positive. However, when t is negative these ranges are |t| ≤ h 2 ≤ 5 mm and 0 ≤ h 3 ≤ 5 mm.

The solution convergence and the computational cost in solving an optimization problem using PSO technique depend on two main parameters which are the number of iterations (N i ) and the number of particles (N p ). Therefore, N p and N i should be carefully chosen for the sake of getting accurate results with minimum cost. Figure 3 shows the variation of the opening mode delamination stress (σ y ) with N i for different values of N p while considering both the height of the interface on the right surface and the thickness of the intermediate layer (h 2) as the design parameters. It can be seen for each N p that the stress decreases with N i from a high value till reaching the steady state. When the number of particles is high (N p  = 40), the steady state occurs faster (at lower values of N i ) than the case of low number of particles (N p  = 5). It can be concluded from this figure that it is recommended for N p and N i to be more than or equal 10 and 50, respectively, for the sake of accurate results.

Fig. 3
figure 3

Variation of the minimum stress with the number of particles N p for different number of iterations N i

Full size image

Single and multi-variable optimizations are analyzed. For the single-variable optimization, Fig. 4 shows the variation of σ y with the interface profile parameter m for all particles considering all iterations when t = 1 mm. It can be seen that there are many local minimum of stress whereas the lowest value, which represents the optimum, of the critical stress equals 615 MPa and occurs when m = 8.

Fig. 4
figure 4

Variation of the stress with the interface parameter m when t = 1 mm

Full size image

For linear interface profile (m = 1), the dependence of the induced stress σ y on the height of the interface on the right surface t is shown in Fig. 5. It is clear that the stress is locally minimum at several values of t even when t is negative where the interface on the right surface is below its position on the mid-surface. However, lower stresses are induced when the interface is above its position on the right surface and the global minimum stress equals 472 MPa and occurs when the interface reaches the top right corner of the plate (t = 5 mm).

Fig. 5
figure 5

Variation of the stress with the interface height t when m = 1

Full size image

For the two-variable optimization, Fig. 6 depicts the dependence of σ y on both the interface profile parameter m and the height of the interface on the right surface t. It can be seen that the right half of the figure includes less regions of low stress than the left half. More specifically, the stress behavior within the mid-left region of the figure is more preferable than the right part as it exhibits more points of low stress. Using the obtained numerical results of the stress, it is found that the global minimum of the stress (417 MPa) occurs at values of m and t different from those of the previous single-variable optimizations as the optimum values are m = 5.11 and t = − 4.75 mm.

Fig. 6
figure 6

Variation of the stress with the parameter m and the height t

Full size image

Figures 7 and 8 show the dependence of σ y on two geometrical parameters while the interface profile parameter m is considered as a common parameter in the two figures when t = 1 mm. The effects of the intermediate layer thickness h 2 and the top layer thickness h 3 are added in Figs. 7 and 8, respectively. It can be seen that each of h 2 and h 3 does not seem to have as significant effect as the parameter m does. The upper part of each figure is better than its lower part as it exhibits lower stresses. However, the stress seems to be minimum at the highest value of the parameter m irrespective of the value of either h 2 or h 3 as the difference is small and cannot be detected by the shown colors. Based on the obtained numerical values of the two figures, m = 8 is optimum for the both figures where the global minimum stresses (598 MPa for Fig. 7 and 602 MPa for Fig. 8) occur whereas the corresponding values of h 2 and h 3 are 4.87 and 4.73 mm, respectively.

Fig. 7
figure 7

Variation of the stress with the parameter m and the thickness h 2 when t = 1 mm

Full size image
Fig. 8
figure 8

Variation of the stress with the parameter m and the thickness h 3 when t = 1 mm

Full size image

Figures 9 and 10 depict the effects of the height of the interface on the right surface t on σ y whereas h 2 and h 3 are combined separately with t in Figs. 9 and 10, respectively when m = 1. It can be seen that the main part of each figure has high stress. However, low stress values occur within the most top part of Fig. 9 and top-right corner of Fig. 10. The stress seems to have low values at the highest value of the height t and many values of h 2 as the difference is small and cannot be detected by the shown colors. Therefore, h 2 does not seem to have as significant effect as t does. The numerical results showed that the global minimum stresses (155 MPa for Fig. 9 and 472 MPa for Fig. 10) occur at t = 5 mm whereas the corresponding values of h 2 and h 3 are 7.14 × 10−5  mm and 5 mm, respectively.

Fig. 9
figure 9

Variation of the stress with the height t and the thickness h 2 when m = 1

Full size image
Fig. 10
figure 10

Variation of the stress with the height t and the thickness h 3 when m = 1

Full size image

Figure 11 shows the dependence of σ y on the thicknesses of both the intermediate and top layers h 2 and h 3 when t = 1 mm and m = 1. It can be seen that the effect of h 2 is more dominant than h 3 and the stress decreases with the increase of h 2 . However the stress seems to be minimum at the highest value of h 2 and some high values of h 3 as the difference is small and cannot be detected by the shown colors, it is found that the global minimum stress equals 1200 MPa and occurs at h 2  = 5 mm and h 3  = 4.99 mm.

Fig. 11
figure 11

Variation of the stress with the thicknesses h 2 and h 3 when m = 1 and t = 1 mm

Full size image

For the three-variable optimization, Fig. 12 displays the dependence of σ y on the intermediate layer thickness h 2, height of the interface on the right surface t and the interface parameter m. At the highest position of the interface (t = 5 mm), the stress has many low values when m is less than 4.5 and the thickness of the intermediate layer is less than 2 mm. Looking at the numerical results, it is found that the global minimum stress equals 143 MPa and occurs at h 2 = 5.74 × 10−4  mm, t = 5 mm, and m = 1.14 .

Fig. 12
figure 12

Variation of the stress with the thicknesses h 2 , t, and m

Full size image

It can be concluded from Figs. 7, 8, 9, 10, 11 and 12 that when combining the parameter m or the height t with either thickness h 2 or h 3 the effects of both m and t are beneficial from the stress variation point of view whereas the effect of either h 2 or h 3 is comparatively small. On the other hand, when combining h 2 and h 3 together, the more effective parameter is h 2. When studying the simultaneous effects of h 2, t, and m, as an example of the three-variable optimization, the stress value and the optimum value of each parameter are different from those of the single-variable and two-variable optimizations. Eventually, the minimum stress for the single-variable optimization equals 472 MPa while the corresponding values for the two-variable and three-variable optimizations are 155 and 143 MPa, respectively. Figure 13 depicts the stress variation with the normalized distance (Y 1 = y/h) along the vertical right surface for both single- and three- variable optimizations. It can be seen that the maximum stress is reduced by 69.7 % when using three-variable optimizations instead of single-variable optimizations.

Fig. 13
figure 13

Variation of the stress along the right surface

Full size image

5 Conclusions

Minimizing the induced critical thermal stresses in structures is necessary to enhance the thermal behaviors and therefore the performance of layer composites. Therefore, nonlinear optimizations of layer composites that made of ceramic and metal are achieved using PSO technique, which is a population based optimization technique, combined with the finite element method. Different geometrical parameters are considered as design parameters and optimized to enhance the thermal response of the structure. These optimized parameters include the interface profile parameter m that reflects the interface curvature, the height of the nontraditional interface on the right surface relative to the mid-surface t, and the thicknesses of the different layers of the structure h 1, h 2 and h 3.

For the single-variable optimizations, the optimum values of m and t, where the minimum stress occurs, are their highest values. However the corresponding optimum values are different when combining these two parameters together or with others when applying either the two-variable or three-variable optimizations. Also, for the two-variable optimization, the stress depends on m and t more than the thicknesses of the layers. However, the stress dependency on the intermediate layer thickness is more than its dependency on the top layer thickness. When applying the two-variable and three-variable-optimizations instead of single-variable optimizations, the stress is reduced by 67.2 and 69.7 %, respectively. Eventually, tailoring the geometrical and interface parameters using their optimum values can be used to greatly reduce the induced stress. This leads to increasing the resistance to damage, durability, and reliability of structures made of layer composites.