Optimization of material composition to minimize the thermal stresses induced in FGM plates with temperature-dependent material properties

Abstract

A hybrid genetic algorithm with the complex method is developed for the optimization of the material composition of a multi-layered functionally graded material plate with temperature-dependent material properties in order to minimize the thermal stresses induced in the plate when it is subjected to steady-state thermal loads. In the formulation, the plate is artificially divided into an n _l -layered plate, and a weak-form-based finite layer method is developed to obtain the displacement and stress components induced in the n _l -layered plate using the Reissner mixed variational theorem. Two thermal conditions, namely the specified temperature and heat convection conditions, imposed on the top and bottom surfaces of the plate are considered. The through-thickness distributions of the volume fractions of the constituents are assumed as certain specific/non-specific function distributions, such as power-law, sigmoid, layerwise step and layerwise linear function distributions, and the effective material properties of the plate are estimated using the Mori–Tanaka scheme. Comparisons with regard to the minimization for the peak values of the stress ratios induced in the FGM plates with various optimal material compositions are conducted.

1 Introduction

The concept of functionally graded materials (FGMs) was first proposed by Niino at the National Aerospace Laboratory of Japan in 1984, in which FGMs were used for manufacturing thermal barrier materials (Koizumi 1992, 1993, 1997). Since then, FGMs have gradually replaced the traditional fiber-reinforced composite materials (FRCMs), and have been used to form a variety of beam-, plate- and shell-like structures with advanced industrial applications, especially when these structures are used in more severe high temperature environments.

Numerous articles reported that laminated FRCM structures often produce high residual stresses at the interfaces between adjacent layers, when they were subjected to thermo-mechanical loads. This is mainly due to the abrupt change in the material properties of laminated FRCM when passing through the interfaces, while high residual stresses often cause delamination at the interfaces and transverse cracking occurring in the matrix. In contrast, the material properties of FGM structures gradually and continuously vary through the thickness direction of these, such that the above-mentioned failures of laminated FRCM structures can be overcome. In addition, the material properties of FGM structures along the thickness direction can be designed according to the engineering demands by giving certain specific/non-specific functions of the volume fractions of constituents. Optimization of the material composition of FGM structures in order to enhance their structural performance is thus an important issue.

Tanigawa and Matsumoto (1997) and Kawamura and Tanigawa (1998) presented the optimum material composition to minimize the thermal stresses induced in a single-layered FGM infinite plate and a single-layered FGM circular plate, respectively, subjected to unsteady state thermal loads. For these two FGM plates, one was composed of zirconium oxide and titanium alloy, and the other was alumina and aluminum alloy. The material properties of these plates were considered to obey a power-law distribution varying through the thickness direction according to the volume fractions of the constituents, and the temperature-dependent material properties were taken into account. The effective material properties were estimated using the rule of mixtures (Kerner 1956), and the coupled thermo-elastic analysis of the thermally-loaded plates was based on the classical lamination plate theory. The power of the material law was selected as the design variable, and a nonlinear programming method was used to obtain the optimal value of the power. Unlike the works of Tanigawa and Matsumoto (1997) and Kawamura and Tanigawa (1998), which assumed a specific distribution function of material composition through the thickness direction of the FGM plate, Ootao et al. (1998, 2000) reexamined the above issue by using a step-formed approach. In their work, the FGM plate was artificially divided into a multilayered isotropic plate, a layerwise step function distribution of the volume fractions of constituents was assumed and undetermined, and a genetic algorithm (GA) (Gen and Cheng 1997) was used for the optimization tool in Ootao et al. (1998), while a neural network algorithm (Hagan et al. 1996; Zurada 1995) was used in Ootao et al. (2000). This step-wise approach was extended by Na and Kim (2009, 2010) to the optimal design of material composition of a single-layered FGM panel by considering the reduction of the thermal residual stress and the enhancement of the critical thermal loads of the panel. Vel and Pelletier (2007) and Goupee and Vel (2007) presented a multi-objective optimization problem for seeking the optimal material composition of a single-layered FGM shell/plate to minimize the mass and peak hoop stress induced in either a metal-ceramic or a metal–metal two-phase composite plate, when it was subjected to steady state thermal loads. The volume fractions of the constituent material phases distributed through the thickness direction were assumed as a layerwise Hermite cubic polynomial function (HCPF), and the effective material properties were estimated using the Mori–Tanaka (Mori and Tanaka 1973) and self-consistent (Hill 1965) schemes. In conjunction with the first-order shear deformation theory and differential quadrature (DQ) method, Tornabene and Ceruti (2013) carried out a mixed static and dynamic optimization of four-parameter FGM doubly curved shells and plates. In their work, three optimization approaches, namely the particle swarm optimization algorithm (PSOA), Monte Carlo algorithm and GA, were used, and the material properties were assumed to obey a power-law distribution through the thickness direction of the shell/plate. Based on Reddy’s refined higher-order shear deformation theory (HSDT) (Reddy 1984; Reddy and Phan 1985), Ashjari and Khoshravan (2014) developed a single-objective optimization of the material distribution of simply-supported FGM plates subjected to mechanical loads, in which a layerwise HCPF interpolation was used to construct the through-thickness distributions of the volume fractions of constituents. The effective material properties were estimated using the rule of mixtures, and the real-coded GA and PSOA were used to minimize the weight of the FGM plate with flexibility and stress constraints.

In addition to the above-mentioned applications, GA has also been extended to other analyses of beams, plates and shells. Maletta and Pagnotta (2004) combined GA and the finite element method to identify the elastic constants of composite laminates using the vibration test data. Roy and Chakraborty (2009) developed a GA-based linear quadratic regulator (LQR) for the optimal vibration control design of smart fiber reinforced polymer composite shell structures. The LQR was also used for active vibration control of thin axially functionally graded beams by Bruant and Proslier (2016). Liew et al. (2004) developed a GA to design the optimal shape control of FGM plates with surface-bonded piezoelectric patches and under a temperature gradient. Based on an HSDT combined with a GA, Zhang et al. (2016a) studied the optimal shape control of functionally graded carbon nanotube-reinforced composite (CNTRC) plates with surface-bonded actuators and sensors. Zhang et al. (2016b) also presented the optimization problems for the critical load parameters of a single-ply CNTRC skew plate on the basis of the HSDT, in which the optimal orientation angles of CNTs were searched. Some review articles with regard to the application of GAs to various physical problems were carried out, such as the heat transfer problems (Gosselin et al. 2009) and the stiffness maximization problems of laminated composite plates (Potgieter and Stander 1998).

In this article, we aim at developing a hybrid GA with the complex method (Box 1965) for the optimization of material composition for simply-supported, single-layered and sandwiched FGM plates subjected to steady-state thermal loads in order to minimize the thermal stresses induced in the plates. As we mentioned above, GA has conventionally been used for the optimization of the material composition of FGM structures in order to enhance their structural performance and reduce the residual stresses induced in these. Even though GA has proved to be an effective approach for locating the region in which the global optimum exists, it converges slowly to the optimal solution in the explored region. A hybrid GA with the complex method is thus developed for the current issue, in which the GA is used to perform global exploration among many designs (a so-called population in GA), while the complex method is used to perform the local exploitation around a design (a so-called chromosome in GA), of which the global optimal solutions existing in the neighborhood, such that the convergence rate to obtain the global optimal solutions can be more effective than as usual.

We also extend the Reissner mixed variational theorem (RMVT)-based (Reissner 1984, 1986) finite layer methods (FLMs) (Wu and Li 2010; Wu and Liu 2016; Wu and Ding 2017) to the coupled thermo-mechanical analysis of simply-supported, single-layered and sandwiched FGM plates, which are involved in the current optimization analysis, in which the material properties of the FGM plate are considered to be temperature- and thickness-dependent. In the RMVT-based FLMs, the FGM plate is artificially divided as an n _l -layered plate, the displacement and transverse stress components are regarded as the primary variables, and are expanded as the double Fourier series functions and Lagrange polynomials in the in-plane domain and the thickness direction, respectively. A heat conduction analysis of the FGM plate with either the specified temperature or the heat convection conditions on the top and bottom surfaces is carried out using the modified Pagano method (Wu and Huang 2009; Wu and Lu 2009; Wu et al. 2008). The through-thickness distributions of the volume fractions of constituents are assumed as the specific function distributions, such as the power-law and sigmoid ones, and the non-specific function distributions, such as the layerwise step (also called the step-formed) and layerwise linear ones. The effective material properties of the FGM plate are estimated using the Mori–Tanaka scheme. The accuracies and convergence rates of the RMVT-based FLMs with various orders used for expansions of the primary field variables in the thickness direction for the coupled thermo-mechanical analysis of the thermally-loaded plate are assessed by comparing their solutions with the exact 3D ones available in the literature. Comparisons regarding the minimization for the peak values of the stress ratios induced in the FGM plates with various optimal material compositions are also undertaken.

2 RMVT-based FLMs for the thermal stress analysis of FGM plates

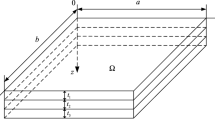
In this section, we extend the RMVT-based FLMs to the thermal residual stress analysis of a simply-supported, FGM plate subjected to thermal loads, as shown in Fig. 1a, in which the material properties of the plate are considered to be dependent upon the temperature in the environment. The in-plane dimensions and thickness of the plate are L _x  × L _y and h, respectively. In the formulation, the plate is artificially divided into n _l layers with a small thickness for each layer, as compared with each of the in-plane dimensions. A global Cartesian coordinate system (i.e., x, y and $\zeta$ coordinates) is placed on the mid-plane of the plate, and a set of local thickness coordinates $z_{m} \,(m = 1,\,2,\,3, \ldots ,\,n_{l} )$, is placed at the mid-plane of each individual layer, as shown in Fig. 1b. The thicknesses of each individual layer and the plate are $h_{m} \,(m = 1,\,2, \ldots ,\,n_{l} )$ and h, respectively, while $h = \sum\nolimits_{m = 1}^{{n_{l} }} {h_{m} }$. The relationship between the global and local thickness coordinates in the mth-layer is $\zeta = \bar{\zeta }_{m} + z_{m}$, in which $\bar{\zeta }_{m} = (\zeta_{m} + \zeta_{m - 1} )/2$, and $\zeta_{m} \;\;{\text{and}}\;\;\zeta_{m - 1}$ are the global thickness coordinates measured from the mid-plane of the plate to the top and bottom surfaces of the m th-layer, respectively.

Fig. 1

a The configuration and coordinates of an FGM plate; b the local thickness coordinate and the thickness for each layer of a ten-layered FGM plate

2.1 Material models

The FGM plate is made of a two-phase composite material, the material properties of which are considered to be thickness-dependent according to the volume fractions of constituents through the thickness coordinate by assuming the specific function distributions, such as the power-law and sigmoid ones, and the non-specific function distributions, such as the layerwise step and layerwise linear ones. The effective material properties of the FGM plate are estimated using the Mori–Tanaka scheme (Mori and Tanaka 1973), and are given as follows:

$$B(\zeta ) = \frac{{V_{c} (\zeta )\,(B_{c} - B_{m} )}}{{\left[ {1 + (1 - V_{c} (\zeta ))\frac{{B_{c} - B_{m} }}{{B_{m} + (4/3)\,G_{m} }}} \right]}} + B_{m} ,$$

(1a)

$$G(\zeta ) = \frac{{V_{c} (\zeta )\,(G_{c} - G_{m} )}}{{\left[ {1 + (1 - V_{c} (\zeta ))\frac{{G_{c} - G_{m} }}{{G_{m} + f_{m} }}} \right]}} + G_{m} ,$$

(1b)

$$\alpha (\zeta ) = \frac{{B_{c} \,\left( {\alpha_{c} - \alpha_{m} } \right)}}{{\left[ {1 - \frac{{B\left( \zeta \right) - B_{c} }}{{B\left( \zeta \right) - B_{m} }}} \right]\,B\left( \zeta \right)}} + \alpha_{m} ,$$

(1c)

$$\lambda (\zeta ) = \frac{{V_{c} (\zeta )\,(\lambda_{c} - \lambda_{m} )}}{{\left[ {1 + (1 - V_{c} (\zeta ))\frac{{\left( {\lambda_{c} - \lambda_{m} } \right)}}{{3\,\lambda_{m} }}} \right]}} + \lambda_{m} ,$$

(1d)

$$V_{m} \left( \zeta \right) = 1 - V_{c} \left( \zeta \right)$$

(1e)

where $f_{m} = G_{m} \,\frac{{9B_{m} + 8G_{m} }}{{6\,(B_{m} + 2G_{m} )}}$, and the subscripts c and m are defined as the material properties of ceramic (the particulate-phase) and metal (the matrix-phase) materials, respectively. $V_{c} \left( \zeta \right)$ and $V_{m} \left( \zeta \right)$ denote the volume fractions of the particulate- and matrix-phase materials. $B\left( \zeta \right),\,\,G\left( \zeta \right),\,\,\alpha \left( \zeta \right)\;\;{\text{and}}\;\;\lambda \left( \zeta \right)$ are the bulk modulus, shear modulus, thermal expansion coefficient and thermal conductivity coefficient of the plate. $B_{c} ,G_{c} ,\alpha_{c} ,\lambda_{c}$ and $B_{m} ,G_{m} ,\alpha_{m} ,\lambda_{m}$ are those material properties of the particulate and matrix phases, respectively. The relationship between the bulk and shear moduli, as well as Young’s modulus (E) and Poisson’s ratio ($\upsilon$) are $B = E/[3(1 - 2\upsilon )]$ and $G = E/[2(1 + \upsilon )]$.

$V_{c} \left( \zeta \right)$ is assumed to be four different functions distributed through the thickness direction of the plate, and is given by

• (a) The power-law function distribution,

  $$V_{c} \left( \zeta \right) = V_{c}^{ - } + \left( {V_{c}^{ + } - V_{c}^{ - } } \right)\,\left\{ {\,\left[ {\zeta + \left( {h/2} \right)} \right]/h} \right\}^{{\,\kappa_{p} }} \quad {\text{when}}\quad \zeta_{0} < \zeta < \zeta_{{n_{l} }} \,\,({\text{i}}.{\text{e}}.,\,\, - h/2 < \zeta < h/2),$$

  (2a)

  where $\kappa_{p}$ denotes the material-property gradient index of the power-law model. $V_{c}^{ + } \;\;{\text{and}}\;\;V_{c}^{ - }$ are the volume fractions of the particulate-phase material at the top and bottom surfaces of the plate, such that $V_{c} = V_{c}^{ + }$, when $\zeta = h/2$, and $V_{c} = V_{c}^{ - }$, when $\zeta = - h/2$.

• (b) The sigmoid function distribution,

  $$V_{c} \left( \zeta \right) = \left\{ {\begin{array}{*{20}l} {V_{c}^{ - } + \left[ {\left( {V_{c}^{ + } - V_{c}^{ - } } \right)/2} \right]\left[ {\left( {2\zeta + h} \right)/h} \right]^{{\kappa_{s} }} } \hfill & { - h/2 \le \zeta \le 0,} \hfill \\ {V_{c}^{ + } - \left[ {\left( {V_{c}^{ + } - V_{c}^{ - } } \right)/2} \right]\left[ {\left( {h - 2\zeta } \right)/h} \right]^{{\kappa_{s} }} } \hfill & {0 \le \zeta \le h/2,} \hfill \\ \end{array} } \right.$$

  (2b)

  where $\kappa_{s}$ denotes the material-property gradient index of the sigmoid model.

• (c) The layerwise step function distribution,

  $$V_{c} \left( \zeta \right) = V_{c}^{(m)} \left[ {H\left( {\zeta - \zeta_{m - 1} } \right) - H\left( {\zeta - \zeta_{m} } \right)} \right]\quad {\text{when}}\quad \zeta_{m - 1} < \zeta < \zeta_{m} \quad {\text{and}}\quad m = 1 - n_{l} ,$$

  (2c)

  where $V_{c}^{(m)}$ denotes the volume fraction of the mth-layer, which is taken as a constant, and $H\left( \zeta \right)$ is the Heaviside step function. In this model, the authors set $V_{c}^{(1)} = V_{c}^{ - }$ and $V_{c}^{{(n_{l} )}} = V_{c}^{ + }$ for the comparison purposes.

• (d) The layerwise linear function distribution,

  $$V_{c} \left( \zeta \right) = V_{c}^{(m - 1)} \left[ {(\zeta_{m} - \zeta )/h_{m} } \right] + V_{c}^{(m)} \left[ {(\zeta - \zeta_{m - 1} )/h_{m} } \right]\quad {\text{when}}\quad \zeta_{m - 1} < \zeta < \zeta_{m} \quad {\text{and}}\quad m = 1 - n_{l} ,$$

  (2d)

  where $V_{c}^{(m - 1)} \left( \zeta \right)$ and $V_{c}^{(m)} \left( \zeta \right)$ stand for the volume fractions at the interfaces between the (m − 1)th and mth layers, as well as the mth and (m + 1)th layers, respectively, and $V_{c}^{(0)} \;\;{\text{and}}\;\;V_{c}^{{(n_{l} )}}$ are the volume fractions of particulate-phase material on the bottom and top surfaces of the FGM plate, such that $V_{c}^{(0)} = V_{c}^{ - }$ and $V_{c}^{{(n_{l} )}} = V_{c}^{ + }$.

2.2 Heat conduction analysis

In the optimization scheme, the heat conduction analysis of the FGM plate subjected to steady-state thermal loads is first carried out according to the predefined through-thickness distribution of volume fractions of constituents, and the temperature distribution of the plate domain thus determined is then used to identity the thermal stresses and deformations induced in the plate. The material properties of the FGM plate are considered to be dependent upon the thickness coordinate and temperature. The modified Pagano method is used for the heat conduction analysis of the plate, and the solution process is briefly described as follows.

The steady state heat conduction equation of the plate without heat generation is given as

$$P_{x,x} + P_{y,y} + P_{\zeta ,\zeta } = 0,$$

(3)

where $P_{k} \left( {k = x,y,\zeta } \right)$ denote the heat fluxes in the $x,y\;\;{\text{and}}\;\;\zeta$ directions.

According to Fourier’s law, the relations between the heat flux and temperature change are

$$P_{k} = - \lambda_{k} T_{,k} ,$$

(4)

where T is the temperature change measured from room temperature, which is $\hat{T}_{0} = 300\,{\text{K}}$. In addition, $\hat{T}$ is defined as the current temperature variable, such that $T = \hat{T} - 300$.

The state space equation related to the heat conduction analysis of the plate is thus given as

$$\left[ {\begin{array}{*{20}l} {T_{,\zeta } } \hfill \\ {P_{\zeta ,\zeta } } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & { - \lambda_{\zeta }^{ - 1} } \hfill \\ {\left( {\lambda_{x} \partial_{xx} + \lambda_{y} \partial_{yy} } \right)} \hfill & 0 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} T \hfill \\ {P_{\zeta } } \hfill \\ \end{array} } \right]$$

(5)

Two different thermal conditions imposed on the top and bottom surfaces of the plate are considered as follows:

• (a) The specified temperature conditions

The temperature changes on the top and bottom surfaces of the plate are given as

$$\begin{array}{*{20}l} {T = \bar{T}^{ - } } \hfill & {{\text{at}}\quad \zeta = - h/2} \hfill \\ \end{array}$$

(6a)

$$\begin{array}{*{20}l} {T = \bar{T}^{ + } } \hfill & {{\text{at}}\quad \zeta = h/2} \hfill \\ \end{array}$$

(6b)

• (b) The heat convection conditions

The thermal conditions on the top and bottom surfaces are given as

$$\begin{array}{*{20}l} { - T_{,\zeta } + \lambda_{a} T = \lambda_{a} \bar{T}^{ - } } \hfill & {{\text{at}}\quad \zeta = - h/2} \hfill \\ \end{array}$$

(7a)

$$\begin{array}{*{20}l} {T_{,\zeta } + \lambda_{b} T = \lambda_{b} \bar{T}^{ + } } \hfill & {{\text{at}}\quad \zeta = h/2} \hfill \\ \end{array}$$

(7b)

where $\lambda_{a}$ and $\lambda_{b}$ denote the surface heat transfer coefficients at the bottom and top surfaces of the plate, respectively. $\bar{T}^{ - }$ and $\bar{T}^{ + }$ are the temperature changes applied at the bottom and top surfaces of the plate.

The temperature changes prescribed on the top and bottom surfaces are expanded as the double Fourier series as $\bar{T}^{ \pm } = \sum\nolimits_{{\hat{m} = 1}}^{\infty } {\sum\nolimits_{{\hat{n} = 1}}^{\infty } {\bar{T}_{{\hat{m}\hat{n}}}^{ \pm } \sin \tilde{m}\,x\;\sin \tilde{n}\,y} }$, in which $\tilde{m} = \hat{m}\,\pi /L_{x}$, $\tilde{n} = \hat{n}\,\pi /L_{y}$ and $\hat{m}\;\,{\text{and}}\;\,\hat{n}$ are the half-wave numbers, the values of which are positive integers. In addition, the thermal conditions at the edges are $T = 0\,{\text{K}}$.

The thermal variables are also expressed as the double Fourier series in the in-plane domain to exactly satisfy the edge conditions, as follows:

$$T\left( {x,y,\zeta } \right) = \sum\limits_{{\hat{m} = 1}}^{\infty } {\sum\limits_{{\hat{n} = 1}}^{\infty } {T_{{\hat{m}\hat{n}}} \left( \zeta \right)\,\,\sin \tilde{m}x\;\sin \tilde{n}y} } ,$$

(8)

$$P_{\zeta } \left( {x,\;y,\;\zeta } \right) = \sum\limits_{{\hat{m} = 1}}^{\infty } {\sum\limits_{{\hat{n} = 1}}^{\infty } {P_{{\zeta \hat{m}\hat{n}}} \left( \zeta \right)\,\,\sin \tilde{m}x\;\sin \tilde{n}y} } ,$$

(9)

where the symbols of double summations will be omitted in the later work of this paper for brevity.

Substituting Eqs. (8) and (9) in Eq. (5) yields

$$\left[ {\begin{array}{*{20}l} {T_{{\hat{m}\hat{n}}} ,_{\zeta } } \hfill \\ {P_{{\zeta \hat{m}\hat{n}}} ,_{\zeta } } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & { - \lambda_{\zeta }^{ - 1} } \hfill \\ { - \left( {\lambda_{x} \tilde{m}^{2} + \lambda_{y} \,\tilde{n}^{2} } \right)} \hfill & 0 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {T_{{\hat{m}\hat{n}}} } \hfill \\ {P_{{\zeta \hat{m}\hat{n}}} } \hfill \\ \end{array} } \right]$$

(10)

Equation (10) represents a system of two simultaneously first-order differential equations in terms of two variables (i.e., $T_{{\hat{m}\hat{n}}} \;\;{\text{and}}\;\;P_{{\zeta \hat{m}\hat{n}}}$) and with temperature- and thickness-dependent coefficients. A modified Pagano method (Wu and Huang 2009) combined with a successive approximation method (Soldatos and Hadjigeorgiou 1990) and an iteration process is used to obtain the through-thickness distributions of the temperature changes, when the temperature-dependent material properties are considered. The solution process can be found in Wu and Huang (2009), and thus is omitted here for brevity.

2.3 RMVT-based FLMs

In this section, we extend the RMVT-based FLMs to the 3D coupled analysis of simply supported, single-layered FGM plates subjected to thermal loads, which are determined from the above-mentioned heat conduction analysis.

2.3.1 The generalized kinematic and kinetic assumptions

In the formulation of RMVT-based FLMs, the FGM plate is artificially divided into an n _l -layered FGM plate with equal thickness for each layer. The primary variables, namely the elastic displacement, transverse shear stress and transverse normal stress components of a typical layer of the plate, of which the domains are in $0 \le x \le L_{x}$, $0 \le y \le L_{y}$ and $\zeta_{m - 1} \le \zeta \le \zeta_{m}$ (i.e., $- h_{m} /2 \le z_{m} \le h_{m} /2$), are thus given by

$$\bar{f}^{(m)} \left( {x,y,z_{m} } \right) = \sum\limits_{i = 1}^{{n_{e} + 1}} {\left[ {\psi_{i}^{(m)} \left( {z_{m} } \right)} \right]\left[ {f^{(m)} \left( {x,y} \right)} \right]_{i} } ,$$

(11)

where $f^{(m)} = u^{(m)} ,v^{(m)} ,w^{(m)} ,\tau_{x\zeta }^{(m)} ,\tau_{y\zeta }^{(m)} \;\;{\text{and}}\;\;\sigma_{\zeta }^{(m)}$, in which $\left( {u^{(m)} } \right)_{i}$, $\left( {v^{(m)} } \right)_{i}$ and $\left( {w^{(m)} } \right)_{i}$ are the elastic displacement components at the ith-nodal plane of the mth-layer of the plate, while $\left( {\tau_{x\zeta }^{(m)} } \right)_{i}$, $\left( {\tau_{y\zeta }^{(m)} } \right)_{i}$ and $\left( {\sigma_{\zeta }^{(m)} } \right)_{i}$ are the transverse shear and normal stress components. $\psi_{i}^{(m)}$ (i = 1, 2, … and (n _e  + 1)) are the corresponding shape functions, and n _e is the related orders used for expansions of each primary variable through the thickness direction of each individual layer.

For an orthotropic elastic material, the linear constitutive equations are given by

$$\left\{ {\begin{array}{*{20}l} {\sigma_{\,x}^{(m)} } \hfill \\ {\sigma_{\,y}^{(m)} } \hfill \\ {\sigma_{\,\zeta }^{(m)} } \hfill \\ {\tau_{\,y\zeta }^{(m)} } \hfill \\ {\tau_{x\,\zeta }^{(m)} } \hfill \\ {\tau_{xy}^{(m)} } \hfill \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {c_{11}^{(m)} } \hfill & {c_{12}^{(m)} } \hfill & {c_{13}^{(m)} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {c_{12}^{(m)} } \hfill & {c_{22}^{(m)} } \hfill & {c_{23}^{(m)} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {c_{13}^{(m)} } \hfill & {c_{23}^{(m)} } \hfill & {c_{33}^{(m)} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {c_{44}^{(m)} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {c_{55}^{(m)} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {c_{66}^{(m)} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\varepsilon_{\,x}^{(m)} } \hfill \\ {\varepsilon_{\,y}^{(m)} } \hfill \\ {\varepsilon_{\,\zeta }^{(m)} } \hfill \\ {\gamma_{\,y\zeta }^{(m)} } \hfill \\ {\gamma_{\,x\zeta }^{(m)} } \hfill \\ {\gamma_{\,xy}^{(m)} } \hfill \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}l} {c_{\alpha 1}^{(m)} } \hfill \\ {c_{\alpha 2}^{(m)} } \hfill \\ {c_{\alpha 3}^{(m)} } \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right]T^{(m)} ,$$

(12)

where $T^{(m)}$ denotes the temperature change of the mth-layer; $\sigma_{x}^{(m)} ,\sigma_{y}^{(m)} , \ldots ,\;\;{\text{and}}\;\;\tau_{xy}^{(m)}$ are the stress components, and $\varepsilon_{x}^{(m)} ,\varepsilon_{y}^{(m)} , \ldots ,\;\;{\text{and}}\;\;\gamma_{xy}^{(m)}$ are the strain components; the stress–temperature coefficients ($c_{\alpha i}^{(m)}$) are defined as $c_{\alpha i}^{(m)} = c_{1i}^{(m)} \alpha_{x}^{(m)} + c_{2i}^{(m)} \alpha_{y}^{(m)} + c_{3i}^{(m)} \alpha_{\zeta }^{(m)} \quad (i = 1 - 3)$; $c_{ij}^{(m)}$ are the elastic coefficients, which are variable through the thickness coordinate in the n _l -layered plate, while they are constants in the homogeneous one.

2.3.2 Reissner’s mixed variational theorem

Reissner’s mixed variational theorem is used to derive the equilibrium equations of the layer elements constituting the plate, and the corresponding energy functional of the plate can be written as follows:

$$\begin{aligned} \Pi_{R} = & \sum\limits_{m = 1}^{{n_{l} }} {\int_{{ - h_{m} /2}}^{{h_{m} /2}} {\iint_{\varOmega } {\left[ {\sigma_{x}^{(m)} \varepsilon_{x}^{(m)} + \sigma_{y}^{(m)} \varepsilon_{y}^{(m)} + \sigma_{\zeta }^{(m)} \varepsilon_{\zeta }^{(m)} + \tau_{x\zeta }^{(m)} \gamma_{x\zeta }^{(m)} + \tau_{y\zeta }^{(m)} \gamma_{y\zeta }^{(m)} + \tau_{xy}^{(m)} \gamma_{\,xy}^{(m)} } \right.}} } \left. { - B\left( {\sigma_{ij}^{(m)} } \right)} \right]dx\,dy\,dz_{m} \\ & \quad - \sum\limits_{m = 1}^{{n_{l} }} {\int_{{ - h_{m} /2}}^{{h_{m} /2}} {\int_{{\varGamma_{\sigma } }} {\left( {\bar{t}_{x}^{(m)} u_{x}^{(m)} + \bar{t}_{y}^{(m)} u_{y}^{(m)} + \bar{t}_{\zeta }^{(m)} u_{\zeta }^{(m)} } \right)} } } \,d\varGamma \,dz_{m} \\ & \quad - \sum\limits_{m = 1}^{{n_{l} }} {\int_{{ - h_{m} /2}}^{{h_{m} /2}} {\int_{{\varGamma_{u} }} {\left[ {(u_{x}^{(m)} - \bar{u}_{x}^{(m)} )t_{x}^{(m)} + (u_{y}^{(m)} - \bar{u}_{y}^{(m)} )t_{y}^{(m)} + (u_{\zeta }^{(m)} - \bar{u}_{\zeta }^{(m)} )t_{\zeta }^{(m)} } \right]} } } \,d\varGamma \,dz_{m} , \\ \end{aligned}$$

(13)

where $\varOmega$ denotes the plate domain on the $x - y$ plane, and $\varGamma_{\sigma } \;\;{\text{and}}\;\;\varGamma_{u}$ denote the portions of the edge boundary, in which the surface traction and elastic displacement components are prescribed, respectively (i.e., $t_{i} = \bar{t}_{i}$ and $u_{i} = \bar{u}_{i}$, in which i = x, y and $\zeta$); $B(\sigma_{ij} )$ is the complementary energy density function.

By means of the generalized kinematic and kinetic assumptions, which are given in Eq. (11), the first-order variation of the Reissner energy functional can be expressed in the following form of

$$\begin{aligned} \delta \,\Pi_{R} & = \sum\limits_{m = 1}^{{n_{l} }} {\int_{{ - h_{m} /2}}^{{h_{m} /2}} {\iint_{\varOmega } {\left\{ {\left( {\delta {\varvec{\varepsilon}}_{p}^{(m)} } \right)^{T} {\varvec{\sigma}}_{p}^{(m)} + \left( {\delta {\varvec{\varepsilon}}_{s}^{(m)} } \right)^{T} {\varvec{\sigma}}_{s}^{(m)} + \delta \varepsilon_{\zeta }^{(m)} \sigma_{\zeta }^{(m)} + \left( {\delta {\varvec{\sigma}}_{s}^{(m)} } \right)^{T} \left( {{\varvec{\varepsilon}}_{\varvec{s}}^{(m)} - {\varvec{S}}^{(m)} {\boldsymbol{\sigma}}_{s}^{(m)} } \right)} \right.}} } \\ & \quad + \delta \sigma_{\zeta }^{(m)} \left. {\left[ {\varepsilon_{\zeta }^{(m)} - \bar{\eta }^{(m)} \sigma_{\zeta }^{(m)} + \left( {{\boldsymbol{Q}}_{a}^{(m)} } \right)^{T} {\varvec{\varepsilon}}_{p}^{(m)} - a_{\alpha }^{(m)} T^{(m)} } \right]} \right\}\,dx\,dy\,dz_{m} \\ & \quad - \sum\limits_{m = 1}^{{n_{l} }} {\int_{{ - h_{m} /2}}^{{h_{m} /2}} {\int_{{\varGamma_{\sigma } }} {\left( {\bar{t}_{x}^{(m)} \delta u_{x}^{(m)} + \bar{t}_{y}^{(m)} \delta u_{y}^{(m)} + \bar{t}_{\zeta }^{(m)} \delta u_{\zeta }^{(m)} } \right)} } \,} d\varGamma \,dz_{m} \\ & \quad - \sum\limits_{m = 1}^{{n_{l} }} {\int_{{ - h_{m} /2}}^{{h_{m} /2}} {\int_{{\varGamma_{u} }} {\left[ {(u_{x}^{(m)} - \bar{u}_{x}^{(m)} )\delta t_{x}^{(m)} + (u_{y}^{(m)} - \bar{u}_{y}^{(m)} )\delta t_{y}^{(m)} + (u_{\zeta }^{(m)} - \bar{u}_{\zeta }^{(m)} )\delta t_{\zeta }^{(m)} } \right]} } } \,d\varGamma \,dz_{m} , \\ \end{aligned}$$

(14)

where the superscript, T, denotes the transposition of the matrices or vectors, and

$$\user2{\boldsymbol{\varepsilon}}_{p}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\varepsilon _{x}^{{(m)}} } & {\varepsilon _{y}^{{(m)}} } & {\gamma _{{xy}}^{{(m)}} } \\ \end{array} } \right]^{T} = {\mathbf{B}}_{1}^{{(m)}} \,{\mathbf{u}}^{{(m)}} ,\quad \user2{\varepsilon }_{s}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\gamma _{{x\zeta }}^{{(m)}} } & {\;\gamma _{{y\zeta }}^{{(m)}} } \\ \end{array} } \right]^{T} = {\mathbf{B}}_{3}^{{(m)}} \,{\mathbf{u}}^{{(m)}} + {\mathbf{B}}_{4}^{{(m)}} \,{\mathbf{w}}^{{(m)}},$$

$${\boldsymbol{\varepsilon}} _{\zeta }^{{(m)}} = {\mathbf{B}}_{6}^{{(m)}} \,{\mathbf{w}}^{{(m)}} ,\quad \user2{\sigma }_{p}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\sigma _{x}^{{(m)}} } & {\sigma _{y}^{{(m)}} } & {\tau _{{xy}}^{{(m)}} } \\ \end{array} } \right]^{T} = {\mathbf{Q}}_{p}^{{(m)}} \,{\mathbf{B}}_{1}^{{(m)}} \,{\mathbf{u}}^{{(m)}} + {\mathbf{Q}}_{{\,a}}^{{(m)}} \,{\mathbf{B}}_{2}^{{(m)}} \,\user2{\sigma }^{{(m)}} - {\mathbf{Q}}_{{\,a}}^{{(m)}} \,T^{{(m)}},$$

$$\user2{\sigma }_{s}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\tau _{{x\zeta }}^{{(m)}} } & {\;\tau _{{y\zeta }}^{{(m)}} } \\ \end{array} } \right]^{T} = {\mathbf{B}}_{5}^{{(m)}} \,\user2{\tau }^{{(m)}} ,\quad \sigma _{\zeta }^{{(m)}} = {\mathbf{B}}_{2}^{{(m)}} \,\user2{\sigma }^{{(m)}},$$

$${\mathbf{u}}^{{(m)}} = \left[ {\begin{array}{*{20}c} {u_{i}^{{(m)}} } \\ {v_{i}^{{(m)}} } \\ \end{array} } \right]_{{i = 1,\,2, \cdots ,n_{e} + 1}} ,\quad {\mathbf{w}}^{{(m)}} = \left[ {w_{i}^{{(m)}} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}} ,\quad \user2{\tau }^{{(m)}} = \left[ {\begin{array}{*{20}c} {\left( {\tau _{{13}}^{{(m)}} } \right)_{i} } \\ {\left( {\tau _{{23}}^{{(m)}} } \right)_{i} } \\ \end{array} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}} ,\quad \user2{\sigma }^{{(m)}} = \left[ {\left( {\sigma _{3}^{{(m)}} } \right)_{i} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}},$$

$${\mathbf{S}}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\left( {1/c_{{55}}^{{(m)}} } \right)} & 0 \\ 0 & {\left( {1/c_{{44}}^{{(m)}} } \right)} \\ \end{array} } \right],\quad {\mathbf{Q}}_{p}^{{(m)}} = \left[ {\begin{array}{*{20}c} {Q_{{11}}^{{(m)}} } & {Q_{{12}}^{{(m)}} } & 0 \\ {Q_{{12}}^{{(m)}} } & {Q_{{22}}^{{(m)}} } & 0 \\ 0 & 0 & {Q_{{66}}^{{(m)}} } \\ \end{array} } \right],\quad {\mathbf{Q}}_{a}^{{(m)}} = \left[ {\begin{array}{*{20}c} {a_{1}^{{(m)}} } \\ {a_{2}^{{(m)}} } \\ 0 \\ \end{array} } \right],\quad {\mathbf{Q}}_{\alpha }^{{(m)}} = \left[ {\begin{array}{*{20}c} {Q_{{\alpha 1}}^{{(m)}} } \\ {Q_{{\alpha 2}}^{{(m)}} } \\ 0 \\ \end{array} } \right],$$

$${\mathbf{B}}_{1}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\left( {\psi _{e}^{{(m)}} } \right)_{i} \partial _{x} } & 0 \\ 0 & {\left( {\psi _{e}^{{(m)}} } \right)_{i} \partial _{y} } \\ {\left( {\psi _{e}^{{(m)}} } \right)_{i} \partial _{y} } & {\left( {\psi _{e}^{{(m)}} } \right)_{i} \partial _{x} } \\ \end{array} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}} ,\quad {\mathbf{B}}_{2}^{{(m)}} = \left[ {\left( {\psi _{e}^{{(m)}} } \right)_{i} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}} ,\quad {\mathbf{B}}_{3}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\left( {D\psi _{e}^{{(m)}} } \right)_{i} } & 0 \\ 0 & {\left( {D\psi _{e}^{{(m)}} } \right)_{i} } \\ \end{array} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}},$$

$${\mathbf{B}}_{4}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\left( {\psi _{e}^{{(m)}} } \right)_{i} \,\partial _{x} } \\ {\left( {\psi _{e}^{{(m)}} } \right)_{i} \,\partial _{y} } \\ \end{array} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}} ,\quad {\mathbf{B}}_{5}^{{(m)}} = \left[ {\begin{array}{*{20}c} {\left( {\psi _{e}^{{(m)}} } \right)_{i} } & 0 \\ 0 & {\left( {\psi _{e}^{{(m)}} } \right)_{i} } \\ \end{array} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}} ,\quad {\mathbf{B}}_{6}^{{(m)}} = \left[ {\left( {D\psi _{e}^{{(m)}} } \right)_{i} } \right]_{{i = 1,\,2, \cdots ,\,n_{e} + 1}},$$

$$Q_{{\,ij}}^{{(m)}} = c_{{\,ij}}^{{(m)}} - a_{{\,j}}^{{(m)}} \,c_{{\,i3}}^{{(m)}} ~\quad \left( {i,j = 1{\text{ and }}2} \right),\quad Q_{{\,66}}^{{(m)}} = c_{{\,66}}^{{(m)}} ,\quad Q_{{\alpha k}}^{{(m)}} = c_{{\alpha k}}^{{(m)}} - a_{\alpha }^{{(m)}} \,c_{{\,k3}}^{{(m)}} \quad ~\left( {k = 1{\text{ and }}2} \right);$$

$$a_{i}^{{(m)}} = c_{{i3}}^{{(m)}} /c_{{33}}^{{(m)}} ,{\text{ in which }}i~ = ~1,2{\text{ and }}\alpha ;\;\bar{\eta }^{{(m)}} = 1/c_{{33}}^{{(m)}}.$$

2.3.3 System equations and boundary conditions

The loading conditions on the top and bottom surfaces are specified, as follows:

$$\begin{array}{*{20}l} {\tau_{x\zeta } = \tau_{y\zeta } = \sigma_{\zeta } = 0} \hfill & {{\text{on}}\quad \zeta = \pm \,0.5h} \hfill \\ \end{array}$$

(15a)

and

$$\begin{array}{*{20}l} {T = \bar{T}^{ \pm } \left( {x,y} \right)} \hfill & {{\text{on}}\quad \zeta = \pm \,0.5h} \hfill \\ \end{array}$$

(15b)

The edge boundary conditions of each individual layer are considered as fully simple supports with free temperature changes, and the following quantities are satisfied.

$$\begin{array}{*{20}l} {u_{y}^{(m)} = u_{\zeta }^{(m)} = \sigma_{x}^{(m)} = T^{(m)} = 0} \hfill & {{\text{at}}\quad x = 0,\,x = L_{x} \,\,{\text{and}}\,\,m = 1,2, \ldots ,n_{l} ,} \hfill \\ \end{array}$$

(16a)

$$\begin{array}{*{20}l} {u_{x}^{(m)} = u_{\zeta }^{(m)} = \sigma_{y}^{(m)} = T^{(m)} = 0} \hfill & {{\text{at}}\quad y = 0,\,y = L_{y} \,\,{\text{and}}\,\,m = 1,2, \ldots ,n_{l} .} \hfill \\ \end{array}$$

(16b)

The primary field variables of each individual layer are expanded as the following forms of a double Fourier series, such that the boundary conditions of the simply supported edges are exactly satisfied for each set of fixed values of $\left( {\hat{m},\;\,\,\hat{n}} \right)$, and they are given as

$$\left( {\begin{array}{*{20}l} {u_{x}^{(m)} ,} \hfill & {\tau_{x\zeta }^{(m)} } \hfill \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {u_{{\hat{m}\hat{n}}}^{(m)} ,} \hfill & {\tau_{{13\hat{m}\hat{n}}}^{(m)} } \hfill \\ \end{array} } \right)\cos \tilde{m}\,x\;\,\sin \tilde{n}\,y,$$

(17)

$$\left( {u_{y}^{(m)} ,\;\tau_{y\zeta }^{(m)} } \right) = \left( {v_{{\hat{m}\hat{n}}}^{(m)} ,\;\tau_{{23\hat{m}\hat{n}}}^{(m)} } \right)\,\sin \tilde{m}\,x\;\,\cos \tilde{n}\,y,$$

(18)

$$\left( {u_{\zeta }^{(m)} ,\;\sigma_{\zeta }^{(m)} ,\;D_{\zeta }^{(m)} ,\;\varPhi^{(m)} } \right) = \left( {w_{{\hat{m}\hat{n}}}^{(m)} ,\;\sigma_{{3\hat{m}\hat{n}}}^{(m)} ,\;D_{{3\hat{m}\hat{n}}}^{(m)} ,\;\varphi_{{\,\hat{m}\hat{n}}}^{(m)} } \right)\,\sin \tilde{m}\,x\;\,\sin \tilde{n}\,y.$$

(19)

By substituting Eqs. (17)–(19) in the weak form [i.e. Eq. (14)], the following system equations of the plate are obtained:

$$\sum\limits_{m = 1}^{{n_{l} }} {\left[ {\begin{array}{*{20}l} {{\mathbf{K}}_{{{\text{I}}\;\,\,{\text{I}}}}^{(m)} } \hfill & {\mathbf{0}} \hfill & {{\mathbf{K}}_{{{\text{I }}\;\,{\text{III}}}}^{(m)} } \hfill & {{\mathbf{K}}_{{{\text{I}}\;\;\,{\text{IV}}}}^{(m)} } \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{K}}_{{{\text{II}}\;\;\,{\text{III}}}}^{(m)} } \hfill & {{\mathbf{K}}_{{{\text{II}}\;\,\,{\text{IV}}}}^{(m)} } \hfill \\ {{\mathbf{K}}_{{{\text{III}}\;\,\,{\text{I}}}}^{(m)} } \hfill & {{\mathbf{K}}_{{{\text{III}}\;\,\;{\text{II}}}}^{(m)} } \hfill & {{\mathbf{K}}_{{{\text{III}}\;\;\,{\text{III}}}}^{(m)} } \hfill & {\mathbf{0}} \hfill \\ {{\mathbf{K}}_{{{\text{IV}}\;\;\,{\text{I}}}}^{(m)} } \hfill & {{\mathbf{K}}_{{{\text{IV}}\;\,\;{\text{II}}}}^{(m)} } \hfill & {\mathbf{0}} \hfill & {{\mathbf{K}}_{{{\text{IV}}\;\;{\text{IV}}}}^{(m)} } \hfill \\ \end{array} } \right]} \left[ {\begin{array}{*{20}l} {{\tilde{\mathbf{u}}}^{(m)} } \hfill \\ {{\tilde{\mathbf{w}}}^{(m)} } \hfill \\ {\tilde{\varvec{\tau }}^{(m)} } \hfill \\ {{\tilde{\boldsymbol{\sigma}}}^{(m)} } \hfill \\ \end{array} } \right] = \sum\limits_{m = 1}^{{n_{l} }} {\left[ {\begin{array}{*{20}l} {{\mathbf{F}}_{\text{I}}^{(m)} } \hfill \\ {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill \\ {{\mathbf{F}}_{\text{IV}}^{(m)} } \hfill \\ \end{array} } \right]} ,$$

(20)

where

$$\begin{aligned}&{\mathbf{K}}_{i\;\;j}^{(m)} = \left( {{\mathbf{K}}_{j\;\,i}^{(m)} } \right)^{T}\, (i,j = {\text{I,}}\,{\text{II,}}\,{\text{III,}}\,{\text{IV,}}\;{\text{V,}}\;{\text{VI}}); \quad {\mathbf{K}}_{{{\text{I}}\;\,{\text{I}}}}^{(m)} = \int_{{ - h_{m} /2}}^{{h_{m} /2}} {\,\left( {{\tilde{\mathbf{B}}}_{1}^{(m)} } \right)^{T} \,{\mathbf{Q}}_{p}^{(m)} \,{\tilde{\mathbf{B}}}_{1}^{(m)} \,dz_{m} },\\ &{\mathbf{K}}_{{{\text{I}}\;\,{\text{III}}}}^{(m)} = \int_{{ - h_{m} /2}}^{{h_{m} /2}} {\,\left( {{\mathbf{B}}_{3}^{(m)} } \right)^{T} \,{\mathbf{B}}_{5}^{(m)} \,dz_{m} }, \quad {\mathbf{K}}_{{{\text{I}}\;\,{\text{IV}}}}^{(m)} = \int_{{ - h_{m} /2}}^{{h_{m} /2}} {\,\left( {{\tilde{\mathbf{B}}}_{1}^{(m)} } \right)^{T} \,{\mathbf{Q}}_{a}^{(m)} \,{\mathbf{B}}_{2}^{(m)} \,dz_{m} },\quad {\mathbf{K}}_{{{\text{II}}\;\,{\text{III}}}}^{(m)} = \int_{{ - h_{m} /2}}^{{h_{m} /2}} {\,\left( {{\tilde{\mathbf{B}}}_{4}^{(m)} } \right)^{T} \,{\mathbf{B}}_{5}^{(m)} \,dz_{m} },\\ &{\mathbf{K}}_{{{\text{II}}\;\,{\text{IV}}}}^{(m)} = \int_{{ - h_{m} /2}}^{{h_{m} /2}} {\,\left( {{\mathbf{B}}_{6}^{(m)} } \right)^{T} \,{\mathbf{B}}_{2}^{(m)} \,dz_{m} }, \quad {\mathbf{K}}_{{{\text{III}}\;\,{\text{III}}}}^{(m)} = \int_{{ - h_{m} /2}}^{{h_{m} /2}} {\,\left( {{\mathbf{B}}_{5}^{(m)} } \right)^{T} \,{\mathbf{S}}^{(m)} \,{\mathbf{B}}_{5}^{(m)} \,dz_{m} },\\ &{\mathbf{K}}_{{{\text{IV}}\;\,{\text{IV}}}}^{(m)} = - \int_{{ - h_{m} /2}}^{{h_{m} /2}} {\,\bar{\eta }^{(m)} \,\left( {{\mathbf{B}}_{2}^{(m)} } \right)^{T} \,{\mathbf{B}}_{2}^{(m)} \,dz_{m} }, \\ &{\mathbf{F}}_{\text{I}}^{(m)} = \left[ {\begin{array}{*{20}c} {\int_{{ - h_{m} /2}}^{{h_{m} /2}} { - \tilde{m}\,\left( {\psi_{e}^{(m)} } \right)_{i} \,Q_{\alpha 1}^{(m)} \,T_{{\hat{m}\hat{n}}}^{(m)} \,dz_{m} } } \\ {\int_{{ - h_{m} /2}}^{{h_{m} /2}} { - \tilde{n}\,\left( {\psi_{e}^{(m)} } \right)_{i} \,Q_{\alpha 2}^{(m)} \,T_{{\hat{m}\hat{n}}}^{(m)} \,dz_{m} } } \\ \end{array} } \right]_{{i = 1,\,2, \ldots ,\,n_{e} + 1}},\quad {\mathbf{F}}_{\text{IV}}^{(m)} = \left[ {\int_{{ - h_{m} /2}}^{{h_{m} /2}} {\left( {\psi_{e}^{(m)} } \right)_{i} \,a_{\alpha }^{(m)} \,T_{{\hat{m}\hat{n}}}^{(m)} \,dz_{m} } } \right]_{{i = 1,\,2, \ldots ,\,n_{e} + 1}},\\ &{\tilde{\mathbf{B}}}_{1}^{(m)} = \left[ {\begin{array}{*{20}l} { - \tilde{m}\,\left( {\psi_{e}^{(m)} } \right)_{i} } \hfill & 0 \hfill \\ 0 \hfill & { - \tilde{n}\,\left( {\psi_{e}^{(m)} } \right)_{i} } \hfill \\ {\tilde{n}\,\left( {\psi_{e}^{(m)} } \right)_{i} } \hfill & {\,\,\tilde{m}\,\left( {\psi_{e}^{(m)} } \right)_{i} } \hfill \\ \end{array} } \right]_{{i = 1,\,2, \ldots ,\,n_{e} + 1}}, \quad {\tilde{\mathbf{B}}}_{4}^{(m)} = \left[ {\begin{array}{*{20}c} {\tilde{m}\,\left( {\psi_{e}^{(m)} } \right)_{i} } \\ {\tilde{n}\,\left( {\psi_{e}^{(m)} } \right)_{i} } \\ \end{array} } \right]_{{i = 1,\,2, \ldots ,\,n_{e} + 1}}, \quad {\tilde{\mathbf{u}}}^{(m)} = \left[ {\begin{array}{*{20}l} {\left( {u_{{\hat{m}\hat{n}}}^{(m)} } \right)_{i} } \hfill \\ {\left( {v_{{\hat{m}\hat{n}}}^{(m)} } \right)_{i} } \hfill \\ \end{array} } \right]_{{i = 1,\,2, \ldots ,\,n_{e} + 1}}, \\ &{\tilde{\mathbf{w}}}^{(m)} = \left[ {\left( {w_{{\hat{m}\hat{n}}}^{(m)} } \right)_{i} } \right]_{{i = 1,\,2, \ldots ,\,n_{e} + 1}}, &\tilde{\varvec{\tau }}^{(m)} = \left[ {\begin{array}{*{20}c} {\left( {\tau_{{13\hat{m}\hat{n}}}^{(m)} } \right)_{i} } \\ {\left( {\tau_{{23\hat{m}\hat{n}}}^{(m)} } \right)_{i} } \\ \end{array} } \right]_{{i = 1,\,2,\, \ldots ,\,n_{e} + 1}}, \quad \tilde{\varvec{\sigma }}^{(m)} = \left[ {\left( {\sigma_{{3\hat{m}\hat{n}}}^{(m)} } \right)_{i} } \right]_{{i = 1,\,2, \ldots ,\,n_{e} + 1}}. \end{aligned}$$

The global stiffness matrices and forcing vector for the thermally-loaded plate can be assembled using Eq. (20), and the primary variables induced at each nodal surfaces of the individual layer can then be obtained by solving these resulting system equations. Subsequently, the in-surface stress components at the nodal surfaces can be obtained using the determined primary field variables, and these are given by

$$\left( {\sigma_{x}^{(m)} ,\;\;\sigma_{y}^{(m)} } \right) = \left( {\sigma_{{1\hat{m}\hat{n}}}^{(m)} ,\;\;\sigma_{{2\hat{m}\hat{n}}}^{(m)} } \right)\,\sin \tilde{m}\,x\;\,\sin \tilde{n}\,y,$$

(21)

$$\tau_{xy}^{(m)} = \tau_{{12\hat{m}\hat{n}}}^{(m)} \;\cos \tilde{m}\,x\;\,\cos \tilde{n}\,y,$$

(22)

where $\left[ {\begin{array}{*{20}c} {\sigma_{{1\hat{m}\hat{n}}}^{(m)} } & {\sigma_{{2\hat{m}\hat{n}}}^{(m)} } & {\tau_{{12\hat{m}\hat{n}}}^{(m)} } \\ \end{array} } \right]^{T} = {\mathbf{Q}}_{p}^{(m)} {\tilde{\mathbf{B}}}_{1}^{(m)} {\tilde{\mathbf{u}}}^{(m)} + {\mathbf{Q}}_{a}^{(m)} {\mathbf{B}}_{2}^{(m)} \tilde{\varvec{\sigma }}^{(m)} - {\mathbf{Q}}_{\alpha }^{(m)} T_{{\hat{m}\hat{n}}}^{(m)}$.

3 Optimization problem

3.1 Statement of the optimization problem

In this work, the optimization of the material composition to minimize the in-plane thermal stresses induced in a thermally-loaded FGM plate is analyzed, and the stress ratio $f_{\sigma }$ is defined as follows:

$$f_{\sigma } \left( \zeta \right) = \left\{ {\begin{array}{*{20}l} {\sigma_{x} \left( \zeta \right)/Y_{t} \left( \zeta \right)} \hfill & {{\text{when}}\quad \sigma_{x} \left( \zeta \right) \ge 0,} \hfill \\ {\left| {\sigma_{x} \left( \zeta \right)} \right|/Y_{c} \left( \zeta \right)} \hfill & {{\text{when}}\quad \sigma_{x} \left( \zeta \right) \le 0,} \hfill \\ \end{array} } \right.$$

(23)

in which $Y_{t}$ and $Y_{c}$ denote the yielding stresses of the composite materials in tension and compression, respectively.

The maximum value of the stress ratio $f_{\sigma } \left( \zeta \right)$ for a typical set of design variables is defined as $f_{\sigma \hbox{max} }$, and a fitness value is thus defined as $1/f_{\sigma \hbox{max} }$ used for sorting process in GA. Four different through-thickness distributions of volume fractions of constituents (i.e., the power-law, sigmoid, layerwise step and layerwise linear function distributions) and two different thermal conditions (i.e., the specified temperature and heat conduction conditions) on the top and bottom surfaces are considered. The minimization of the maximum value of the stress ratio induced in the FGM plate can be accomplished when the prescribed temperature changes are applied on the top and bottom surfaces.

3.2 A hybrid GA with the complex algorithm

A hybrid GA with a local search method, the complex method, is developed for the current optimization problem, in which GA is used as a global search method to explore the optimal design variables in the whole solution space, so that the corresponding peak values of the stress ratios induced in the plate is minimized. To speed up the optimization process of the GA, the authors used the complex method to fine-tune the optimal solution generated by GA. The flow charts of the hybrid GA and the complex method are shown in Figs. 2 and 3.

Fig. 2

The flow chart of a hybrid GA

Fig. 3

The flow chart of the complex method

The GA processes used to accomplish this work are described as follows:

• (a) Initial population The first population consists of n _p designs, which is created by repeating a random generator n _p times, and n _p is taken to be 400 in this work. In each design, a n _g -digit number representing a design variable is randomly generated, which is also called a gene, and a particular combination of these genes arranged in the order of layers is formed as a chromosome, which means there are (n _g  × n _d ) locuses in a chromosome, in which n _d denotes the number of design variables.

• (b) Fitness value As mentioned above, the peak values of the stress ratio ($f_{\sigma max}$) induced in the FGM plate subjected to steady-state thermal loads is defined as the objective function. The value of $1/f_{\sigma max}$ is thus defined as the fitness value, and is used for the sorting process in GA.

• (c) Selection A ranking selection suggested by Grefenstette and Baker (1989) is adopted. The chromosomes are sorted according to their fitness values, such that each chromosome is assigned as a rank, with the best chromosome having the rank n _p , while the worst one the rank 1. The selection probability is linearly assigned to the ranks, and given as follows:

$$P_{s} \left( {{\text{chromosome}}\;j} \right) = \frac{1}{{n_{p} }}\left[ {\eta^{ - } + \frac{{\left( {\eta^{ + } - \eta^{ - } } \right)}}{{\left( {n_{p} - 1} \right)}}\left( {j - 1} \right)} \right]\quad j = 1 - n_{p} ,$$

(24)

in which $\eta^{ + } + \eta^{ - } = 2$ and $\eta^{ - } \ge 0$. In this work, we let $\eta^{ + } = 2$ and $\eta^{ - } = 0$, such that the worst chromosome is eliminated in the next generation.

According to Eq. (24), n _p chromosomes can be reproduced from the current population into the mating pool for the consequent evolution processes.

• (d) Crossover Every two chromosomes are randomly selected from the mating pool to decide whether to conduct the uniform crossover operator on the basis of a given crossover probability P _c , which is taken to be P _c  = 0.6 in this work. A mask pattern with (n _g × n _d ) locuses is used to randomly generate either “0” or “1” digits in each locus. The crossover process between each selected pair of chromosomes is achieved by exchanging the characters in the locuses of these two chromosomes when the corresponding digit in the mask pattern is the digit “1”, and otherwise they remain unchanged.

• (e) Mutation Mutation occurs in each locus of each chromosome in a population when the randomly generated number between 0 and 1 for each locus is greater than the given probability of mutation (P _m ), which is taken to be P _m  = 0.01 in this work.

• (f) Elitist strategy Two chromosomes with the best fitness values are defined as the elites, and they are preserved and copied completely unchanged into the next population by replacing the worst two chromosomes in the current population.

In this article, the complex method is used for a local search to find the minimization of a function of $f({\mathbf{X}}) = f_{\sigma \hbox{max} }$ in terms of n _d design variables and with (n _d  + 1) test points (or chromosomes in GA), in which ${\mathbf{X}} \in R^{{n_{d} }}$. The relevant processes are described as follows:

• (a) Ordering An initial complex consists of n _k feasible points (i.e., n _k chromosomes), in which $n_{k} \ge \left( {n_{d} + 1} \right)$. In this analysis, n _k is taken to be $n_{k} = 2n_{d}$, which are selected from the first 2n _d high fitness values of the chromosomes in the final population. The feasible points are sorted according to their fitness values, and the vertex ${\mathbf{X}}_{h}$ represents a set of design variables with the largest fitness value

• (b) Centroid The centroid of all feasible points (${\mathbf{X}}_{0}$) except ${\mathbf{X}}_{h}$ is calculated by averaging the coordinates in the form of

  $${\mathbf{X}}_{0} = \frac{1}{{\left( {n_{k} - 1} \right)}}\sum\limits_{\begin{subarray}{l} k = 0 \\ k \ne h \end{subarray} }^{{n_{k} }} {{\mathbf{X}}_{k} } .$$

  (25)

• (c) Reflection The reflection point ${\mathbf{X}}_{r}$ is calculated as ${\mathbf{X}}_{r} = {\mathbf{X}}_{0} + \alpha \,\,\left( {{\mathbf{X}}_{0} - {\mathbf{X}}_{h} } \right),$ where $\alpha \ge 1$, while $\alpha$ is taken to be $\alpha = 1$ in this analysis.

• (d) Feasibility study If ${\mathbf{X}}_{r}$ is feasible and $f\left( {{\mathbf{X}}_{r} } \right)\, < \, f\left( {{\mathbf{X}}_{h} } \right)$, the worst point ${\mathbf{X}}_{h}$ is replaced by ${\mathbf{X}}_{r}$, and the complex is modified. If $f\left( {{\mathbf{X}}_{r} } \right)\, \ge \, f\left( {{\mathbf{X}}_{h} } \right)$, the value of $\alpha$ is halved and a new reflection point found. This procedure of finding a new ${\mathbf{X}}_{r}$ with a reduced $\alpha$ is repeated until the relation $f\left( {{\mathbf{X}}_{r} } \right)\, < \, f\left( {{\mathbf{X}}_{h} } \right)$ is satisfied. However, if ${\mathbf{X}}_{r}$, which satisfies $f\left( {{\mathbf{X}}_{r} } \right) \, < \, f\left( {{\mathbf{X}}_{h} } \right)$, cannot be found even if the value of $\alpha$ became a very small number ($\varepsilon$), say $\varepsilon$ = 10⁻⁶, the point is aborted. The reflection process is then restarted by using the point ${\mathbf{X}}_{p}$, which has the second-highest fitness value, instead of ${\mathbf{X}}_{h}$.

• (e) Stopping criteria The algorithm is stopped when the fitness values of the vertices are close enough or the number of the iteration steps is large enough. In this analysis the stopping criteria is given as

$$\left| {\frac{{f\left( {{\mathbf{X}}_{h} } \right) - f\left( {{\mathbf{X}}_{l} } \right)}}{{f\left( {{\mathbf{X}}_{h} } \right)}}} \right| < 10^{ - 5} ,$$

(26)

where X _l is the point with the lowest function value.

It is noted that in the GA there are three parameters to be determined, which are the population size n _p , the crossover probability P _c and the mutation probability P _m , and the selected parameters will substantially affect the performance of the GA. Taking a greater value of n _p will expand the searching range, such that it will ensure to have an efficient GA not converging to a local optimal solution or stucking in its neighbourhood, while it is also time-consuming. Taking a greater value of P _c or P _m will lead to a poor performance of the GA, because it will produce many designs far away the mating designs, while taking a less value of P _c or P _m will result in the searching process stagnant, and finding the reasonable values of P _c and P _m is thus the key to the success of the GA. A guidance for the reasonable values of these parameters has been followed in a general case (De Jong 1975, Goldberg 1989), which are n _p  = 30–200, P _c  = 0.5–1.0 and P _m  = 0.001–0.05, even though these values might be sensitive with the physical problems considered. After repeatedly testing of the GA and adjustments of the values of these parameters, the authors finally selected n _p  = 400, P _c  = 0.6 and P _m  = 0.01 in this work to ensure the optimal solutions found are the global optimal ones.

4 Illustrative examples

In the formulation a notation ${\text{LM}}_{{n_{e} }}$ ($n_{e} = 1,\;\,2\;\,{\text{and}}\;\,3$) is defined to represent various RMVT-based FLMs, in which the in- and out-of-plane displacement, as well as transverse shear and normal stress components are expanded as the $n_{e}$-order Lagrange polynomials in the thickness coordinate of each layer in the following examples.

4.1 Coupled thermo-mechanical analysis of single-layered FGM plates

For comparison purposes, the exact 3D solutions, as obtained by Vel and Batra (2002) using the power series method and Kulikov and Plotnikova (2015) using the sampling surface (SaS) method for the coupled thermo-elastic analysis of a simply-supported, single-layered FGM plate, are used to validate the accuracy and convergence of the current RMVT-based FLMs, in which the specified temperature conditions are applied on the top and bottom surfaces of the plate. The plate is composed of the metal (Al) and ceramic (SiC), and its material properties obey the power-law distribution along the thickness direction according to the volume fractions of the constituents.

The material properties of the Al and SiC are given as follows:

$${\text{For Al (metal)}},\,\,\,E_{m} = 70\;{\text{GPa,}}\,\upsilon_{m} = 0.3 ,\,\alpha_{m} = 23.4 \times 10^{ - 6} /{\text{K,}}\,\lambda_{m} = 233\,{\text{W}}/{\text{m}}\,{\text{K}};$$

(27a-d)

$${\text{For SiC (ceramic)}},\,\,\,E_{c} = 427\;{\text{GPa,}}\,\upsilon_{c} = 0.17 ,\,\alpha_{c} = 4.3\times 10^{ - 6} /{\text{K,}}\,\lambda_{c} = 65\,{\text{W}}/{\text{m}}\,{\text{K}};$$

(28a-d)

where the subscripts m and c denote the metal (matrix-phase) and ceramic (particulate-phase) materials.

The volume fractions of the SiC (ceramic) and Al (metal) materials are given as Eqs. (2a) and (1e), in which $V_{c}^{ + } = 0.5,\;\,V_{c}^{ - } = 0\,\;{\text{and}}\;\,\kappa_{p} = 2$.

The temperature changes applied on the top and bottom surfaces of the plate are given as

$$\bar{T}^{ + } = \bar{T}_{0}^{ + } \,\sin \left( {\pi x/L_{x} } \right)\;\sin \left( {\pi y/L_{y} } \right),$$

(29a)

$$\bar{T}^{ - } = \bar{T}_{0}^{ - } \,\sin \left( {\pi x/L_{x} } \right)\;\sin \left( {\pi y/L_{y} } \right).$$

(29b)

A set of dimensionless variables is given as

$$\begin{aligned} \bar{T} = T\left( {0.5L_{x} ,\;\,0.5L_{y} ,\;\,\zeta } \right)/\left( {\Delta \bar{T}_{0} } \right),\,\bar{p}_{\zeta } = - p_{\zeta } \left( {0.5L_{x} ,\;\,0.5L_{y} ,\;\,\zeta } \right)\,h/\,\left( {\lambda_{m} \,\Delta \bar{T}_{0} } \right), \hfill \\ \left\lfloor {\bar{u}_{x} \;\;\bar{u}_{y} } \right\rfloor = \left\lfloor {u_{x} \left( {0,\;\,0.5L_{y} ,\;\,\zeta } \right)\;\;\;\,u_{y} \left( {0.5L_{x} ,\;\,0,\;\,\zeta } \right)} \right\rfloor \left\lfloor {10/\left( {\alpha_{m} \,\Delta \bar{T}_{0} \,L_{x} } \right)} \right\rfloor ,\,\bar{u}_{\zeta } = 100\;h\;u_{\zeta } \left( {0.5L_{x} ,\;\,0.5L_{y} ,\;\,\zeta } \right)/\left( {\alpha_{m} \,\Delta \bar{T}_{0} \,L_{x}^{2} } \right), \hfill \\ \left[ {\bar{\sigma }_{x} \;\;\,\bar{\sigma }_{y} \;\,\bar{\tau }_{xy} } \right] = \left[ {\sigma_{x} \left( {0.5L_{x} ,\;\,0.5L_{y} ,\;\,\zeta } \right)\;\;\,\sigma_{y} \left( {0.5L_{x} ,\;\,0.5L_{y} ,\;\,\zeta } \right)\,\;\tau_{xy} \left( {0,\;\,0,\;\,\zeta } \right)} \right]\,\left[ {10/\left( {\alpha_{m} \,\Delta \bar{T}_{0} \,E_{m} } \right)} \right], \hfill \\ \left\lfloor {\bar{\tau }_{x\zeta } \;\;\bar{\tau }_{y\zeta } } \right\rfloor = \left\lfloor {\tau_{x\zeta } \left( {0,\;\,0.5L_{y} ,\;\,\zeta } \right)\;\;\;\,\tau_{y\zeta } \left( {0.5L_{x} ,\;\,0,\;\,\zeta } \right)} \right\rfloor \left\lfloor {100\,L_{x} /\left( {\alpha_{m} \,\Delta \bar{T}_{0} \,E_{m} \,h} \right)} \right\rfloor , \hfill \\ \bar{\sigma }_{\zeta } = 100\;L_{x}^{2} \;\sigma_{\zeta } \left( {0.5L_{x} ,\;\,0.5L_{y} ,\;\,\zeta } \right)/\left( {\alpha_{m} \,\Delta \bar{T}_{0} \,E_{m} \,h^{2} } \right)\;\;{\text{and}}\;\;\Delta \bar{T}_{0} = \bar{T}_{0}^{ + } - \bar{T}_{0}^{ - } . \hfill \\ \end{aligned}$$

(30a-h)

Tables 1 and 2 show various RMVT-based FLM solutions of elastic and thermal field variables, induced in the simply-supported, single-layered FGM plate with the specified temperature and heat convection conditions applied on the top and bottom surfaces of the plate, respectively, in which $L_{x} = L_{y}$ and $L_{x} /h = 5\;\,{\text{and}}\;\,10$. It can be seen in Table 1 that the convergent solutions of LM₁, LM₂ and LM₃ are obtained at n _l  = 64, 32 and 16, respectively, for a thick FGM plate (L _x /h = 5), and the relative errors between these convergent solutions and the 3D solutions obtained by Vel and Batra (2002) and Kulikov and Plotnikova (2015) are less than 0.2% in the cases of the specified temperature conditions. Table 2 shows the RMVT-based FLM solutions of various elastic and thermal field variables of the FGM plate in the cases of heat convection surface conditions. The results also show that the convergence rates of the results in these cases are fast, with that of a moderately thick FGM plate ((L _x /h = 10) being faster than that of a thick FGM plate (L _x /h = 5) on the basis of the same order of the FLMs. In addition, the convergence rates of the FLMs were ${\text{LM}}_{3} > {\text{LM}}_{2} > {\text{LM}}_{1}$, in which the symbol “>” means having a faster convergence rate. The ${\text{LM}}_{3}$ method is thus used for the optimization of material composition of single-layered FGM plates in the next section.

Table 1 Results of convergence and accuracy studies for the displacement and stress components induced in a single-layered FGM plate with the specified temperature conditions on the top and bottom surfaces of the plate

Table 2 Results of convergence and accuracy studies for the displacement and stress components induced in a single-layered FGM plate with the heat convection conditions on the top and bottom surfaces of the plate

4.2 Optimization of material composition for asymmetrically single-layered FGM plates

In this section, the authors carry out the optimization of material composition to minimize the peak values of the stress ratios induced in a simply-supported, asymmetrically single-layered FGM plate subjected to the specified temperature and heat convection conditions on the top and bottom surfaces, and with thickness- and temperature-dependent material properties using the above-developed hybrid GA with the complex method. The temperature changes on the top and bottom surfaces are given as $\bar{T}^{ + } = \bar{T}_{0}^{ + } \,\sin \,\left( {\pi x/L_{x} } \right)\;\sin \,\left( {\pi y/L_{y} } \right)$ and $\bar{T}^{ - } = \bar{T}_{0}^{ - } \,\sin \,\left( {\pi x/L_{x} } \right)\;\sin \,\left( {\pi y/L_{y} } \right)$, in which $\bar{T}_{0}^{ + } = 500\,{\text{K}}$ and $\bar{T}_{0}^{ - } = 0\,{\text{K}}$, and $h\;\lambda_{a} = 0.1$ and $h\;\lambda_{b} = 0.1$ are used for the cases of the heat convection conditions. The FGM plate is considered as a two-phase composite one consisting of the metal (titanium alloy, Ti–6Al–4V) and ceramic (zirconium oxide, ZrO₂) materials. The ZrO₂ is the particulate phase, and Ti–6Al–4V the matrix phase. The volume fractions of the particulate phase on the top and bottom surfaces of the plate are taken as $V_{c}^{ + } = 1$ and $V_{c}^{ - } = 0$, and these are assumed to vary along the thickness direction of the plate with the specific function distributions, such as the power-law (Eq. 2a) and sigmoid (Eq. 2b) ones, and the non-specific function distributions, such as the layerwise step (Eq. 2c) and layerwise linear (Eq. 2d) ones. The effective material properties of the plate are estimated using the Mori–Tanaka micromechanics scheme, given in Eqs. (1a)–(1d). The explicit formulas for determinations of the temperature-dependent material properties of the metal (Ti–6Al–4V) and ceramic (ZrO₂) are given in Ootao et al. (2000) and listed as follows:

For the material Ti–6Al–4V,

$$\begin{aligned} E = 122.7 - 0.0565\,T\,\;{\text{GPa,}} \hfill \\ \upsilon = 0.2888 + 32.0\times 10^{ - 6} T, \hfill \\ \alpha = 7.43\times 10^{ - 6} + 5.56\times 10^{ - 9} T - 2.69\times 10^{ - 12} T^{2} \;\; 1/{\text{K}}\quad {\text{when}}\quad 300\,{\text{K}} \le \,\;T \le 1100\,{\text{K}}, \hfill \\ \alpha = 10.291\times 10^{ - 6} \;\; 1/{\text{K}}\quad {\text{when}}\quad 1100\,{\text{K}} \le \,\;T \le 1300\,{\text{K}}, \hfill \\ \lambda = 1.1 + 0.017\,T\;\;\,{\text{W}}/{\text{m}}\,{\text{K}}, \hfill \\ Y_{t} = Y_{c} = 1252.0 - 0.8486\,T\,\;{\text{MPa}}; \hfill \\ \end{aligned}$$

(31a-f)

For the material ZrO₂,

$$\begin{aligned} E = 132.2 - 50.3\times 10^{ - 3} T - 8.1\times 10^{ - 6} T^{2} \;\;{\text{GPa,}} \hfill \\ \upsilon = 0.333, \hfill \\ \alpha = 13.3\times 10^{ - 6} - 18.9\times 10^{ - 9} T + 12.7\times 10^{ - 12} T^{2} \;\; 1/{\text{K}}, \hfill \\ \lambda = 1.71 + 0.21\times 10^{ - 3} T + 0.116\times 10^{ - 6} T^{2} \;\;\,{\text{W}}/{\text{m}}\,{\text{K}}, \hfill \\ Y_{t} = 148.1 + 1.184\times 10^{ - 3} \,T - 31.4\times 10^{ - 6} \,T^{2} \,\;{\text{MPa}}, \hfill \\ Y_{c} = \left( {3136.0/146.0} \right)\,Y_{t} . \hfill \\ \end{aligned}$$

(32a-f)

The geometric parameters of the plate are considered as $L_{x} = L_{y}$ and $L_{x} /h = 10$ in the following analysis, and the temperature distributions of the assorted material properties of the Ti–6Al–4V and ZrO₂ from the room temperature ($\hat{T} = 300\,{\text{K}}$) to $\hat{T} = 1100\,{\text{K}}$ are shown in Fig. 4.

Fig. 4

Variations of the material properties with the temperature, a Ti–6Al–4V, b ZrO2

Figures 5a and 6a show the optimal material compositions of the asymmetrically single-layered FGM plate with the specified temperature and heat convection surface conditions, respectively, and using the power-law and sigmoid material models. The corresponding through-thickness distributions of the in-plane stress ($\sigma_{x}$) and stress ratio ($f_{\sigma }$) induced in the plate are shown in Figs. 5b, c and 6b, c. The material-property gradient indexes $\kappa_{p} \;\,{\text{and}}\;\,\kappa_{s}$ for these two material models are selected as the design variables. $\kappa_{p} \;{\text{and}}\;\,\kappa_{s}$ are represented as a set of four decimal digits, and the ranges of $\kappa_{p} \;\,{\text{and}}\;\,\kappa_{s}$ are thus limited to 00.00 ≤ ($\kappa_{p} \;\,{\text{or}}\;\,\kappa_{s}$) ≤ 100.00. By means of the current hybrid GA with the complex method, the maximum stress ratios ($f_{\sigma \hbox{max} }$) induced in the plate composed of the optimal material compositions for the power-law and sigmoid material models are given in Table 3.

Fig. 5

Optimal results for the asymmetrically single-layered FGM plate with the specified temperature surface conditions and using the power-law and sigmoid material models, a the through-thickness distributions of the volume fractions of the particulate-phase material, b the through-thickness distributions of the in-plane stress, c the through-thickness distributions of the stress ratio

Fig. 6

Optimal results for the asymmetrically single-layered FGM plate with the heat convection surface conditions and using the power-law and sigmoid material models, a the through-thickness distributions of the volume fractions of the particulate-phase material, b the through-thickness distributions of the in-plane stress, c the through-thickness distributions of the stress ratio

Table 3 Maximum stress ratios induced in the asymmetrically single-layered FGM plates composed of the optimal material compositions for different material models and surface conditions

It can be seen in Figs. 5b, c, 6b, c and Table 3 that in the cases of specified temperature conditions the optimal results for the through-thickness distributions of the stress ratios induced in the plate with the power-law model are significantly less than those induced in the plate with the sigmoid model, even though their maximum values and the through-thickness distributions of the in-plane stress are close to each other, while in the cases of the heat conduction surface conditions, the improvement of the optimal results for the stress ratios induced in the plate with the power-law model is minor as compared with those induced in the plate with the sigmoid material model.

Figures 7a and 8a show the optimal material composition of the asymmetrically single-layered plate with the specified temperature and heat convection surface conditions, respectively, in which the layerwise step and layerwise linear material models are used. In the layerwise step material model, the volume fractions from 2nd-layer to (n _l −1)th-layer (i.e., $V_{c}^{(m)} ,\quad {\text{in}}\;\,{\text{which}}\;\,m = 2 - \left( {n_{l} - 1} \right)$ and n _l  = 10) are selected as the design variables subject to $V_{c}^{(1)} = 0$ and $V_{c}^{{(n_{l} )}} = 1;$ while in the layerwise linear material model, the volume fractions at the interfaces between adjacent layers (i.e., $V_{c}^{(m)} ,\quad {\text{in}}\;\,{\text{which}}\;\,m = 1 - \left( {n_{l} - 1} \right)$ and n _l  = 10) are selected as the design variables subject to $V_{c}^{(0)} = 0\;\,{\text{and}}\;\,V_{c}^{{(n_{l} )}} = 1$. The corresponding optimal results for the through-thickness distributions of the in-plane stresses and stress ratios induced in the plate with the specified temperature and heat convection conditions are shown in Figs. 7b, c and 8b, c, respectively, as well as the corresponding maximum stress ratios ($f_{\sigma \hbox{max} }$) of the plate composed of the optimal material compositions for the layerwise step and layerwise linear material models are also given in Table 3. The results show the optimal results for the through-thickness distributions of the in-plane stresses obtained using the layerwise step and layerwise linear material models are close to each other. The through-thickness distribution of the in-plane stress induced in the plate with the optimal material composition of the layerwise linear material model gradually and continuously vary through the thickness direction of the plate, while the in-plane stress induced in the plate with the optimal material composition of the layerwise step material model is discontinuous at the interfaces between adjacent layers due to the material properties suddenly changing at those places. The layerwise linear material model is thus superior to the layerwise step one for the optimization of material composition of FGM plates.

Fig. 7

Optimal results for the asymmetrically single-layered FGM plate with the specified temperature surface conditions and using the material model of layerwise step and linear functions, a the through-thickness distributions of the volume fractions of the particulate-phase material, b the through-thickness distributions of the in-plane stress, c the through-thickness distributions of the stress ratio

Fig. 8

Optimal results for the asymmetrically single-layered FGM plate with the heat convection surface conditions and using the material model of layerwise step and linear functions, a the through-thickness distributions of the volume fractions of the particulate-phase material, b the through-thickness distributions of the in-plane stress, c the through-thickness distributions of the stress ratio

4.3 Optimization of material composition for symmetrically sandwiched FGM plates

In this section, the authors study the optimization of material composition to minimize the peak values of the stress ratios induced in a simply-supported, symmetrically sandwiched FGM plate subjected to the specified temperature conditions on the top and bottom surfaces, and with thickness- and temperature-dependent material properties using the current GA. The prescribed temperature changes on the top and bottom surfaces are the same as those used in Sect. 4.2, in which $\bar{T}_{0}^{ + } = 500\,{\text{K}}$ and $\bar{T}_{0}^{ - } = 0\,{\text{K}}$. The symmetrically sandwiched FGM plate is composed of the homogeneous ceramic face sheets and the symmetrical FGM core, and the core is made of a two-phase composite material consisting of the metal (titanium alloy, Ti–6Al–4V) and ceramic (zirconium oxide, ZrO₂) materials, the material properties of which are the same as those used in the Sect. 4.2. The volume fractions of the particulate phase of the core ($\left[ {V_{c} \left( \zeta \right)} \right]_{\text{core}}$) are symmetric with respect to its mid-surface, and these on the top surface and mid-surface the core are taken as $V_{c} \left( {\zeta = h_{c} /2} \right) = 1$ and $V_{c} \left( {\zeta = 0} \right) = 0$, respectively, as well as these of the face sheets are $\left[ {V_{c} \left( \zeta \right)} \right]_{{{\text{face}}\;{\text{sheets}}}} = 1\quad {\text{when}}\;\, - h/2 \le \zeta \le - h_{c} /2$ and $h_{c} /2 \le \zeta \le h/2$, in which $h_{c}$ denotes the thickness of the core. The values of $V_{c}$ of the upper half layer of the core are assumed to vary along the thickness direction of the core with a variety of material models, such as the power-law, sigmoid, layerwise step and layerwise linear ones, as well as they are given as follows:

• (a) The power-law function distribution,

$$V_{c} \left( \zeta \right) = V_{c}^{0} + \left( {V_{c}^{ + } - V_{c}^{0} } \right)\,\left[ {\zeta /\left( {h_{c} /2} \right)} \right]^{{\,\kappa_{p} }} \quad {\text{when}}\quad 0 < \zeta < \zeta_{{n_{l} }} \,\,\,({\text{i}}.{\text{e}}.,\,\,0 < \zeta < h_{c} /2),$$

(33a)

where $V_{c}^{ + }$ and $V_{c}^{0} \,$ denote the volume fractions of the particulate-phase material at the top and mid-surface of the core, and in this work $V_{c} = V_{c}^{ + } = 1$, when $\zeta = h_{c} /2$, and $V_{c} = V_{c}^{0} = 0$, when $\zeta = 0$. The value of $n_{l}$ is defined as the total number of divided layers in the upper half layer of the core in this case, and $n_{l}$ = 10.

• (b) The sigmoid function distribution,

$$V_{c} \left( \zeta \right) = \left\{ {\begin{array}{*{20}l} {V_{c}^{0} + \left[ {\left( {V_{c}^{ + } - V_{c}^{0} } \right)/2} \right]\;\left( {4\zeta /h_{c} } \right)^{{\kappa_{s} }} } \hfill & {0 \le \zeta \le h_{c} /4,} \hfill \\ {V_{c}^{ + } - \left[ {\left( {V_{c}^{ + } - V_{c}^{ - } } \right)/2} \right]\,\left[ {\left( {h_{c} - 2\zeta } \right)/\left( {h_{c} /2} \right)} \right]^{{\kappa_{s} }} } \hfill & {h_{c} /4 \le \zeta \le h_{c} /2,} \hfill \\ \end{array} } \right.$$

(33b)

• (c) The layerwise step function distribution,

$$V_{c} \left( \zeta \right) = V_{c}^{(m)} \,\left[ {H\left( {\zeta - \zeta_{m - 1} } \right) - H\left( {\zeta - \zeta_{m} } \right)} \right]\quad {\text{when}}\quad \zeta_{m - 1} < \zeta < \zeta_{m} \quad {\text{and}}\quad m = 1 - n_{l} ,$$

(33c)

where $V_{c}^{(1)} = V_{c}^{0}$ and $V_{c}^{{(n_{l} )}} = V_{c}^{ + }$, as well as the values of $V_{c}^{(m)} \quad \left( {m = 2,\;\,3, \ldots ,\;\,\left( {n_{l} - 1} \right)} \right)$ are to be determined.

• (d) The layerwise linear function distribution,

$$V_{c} \left( \zeta \right) = V_{c}^{(m - 1)} \,\left[ {(\zeta_{m} - \zeta )/h_{m} } \right] + V_{c}^{(m)} \,\left[ {(\zeta - \zeta_{m - 1} )/h_{m} } \right]\quad {\text{when}}\quad \zeta_{m - 1} < \zeta < \zeta_{m} \quad {\text{and}}\quad m = 1 - n_{l} ,$$

(33d)

where $V_{c}^{(m - 1)} \left( \zeta \right)$ and $V_{c}^{(m)} \left( \zeta \right)$ stand for the volume fractions at the interfaces between the (m−1)th and mth layers, as well as the mth and (m + 1)th layers, respectively, and $V_{c}^{(0)} \;\,{\text{and}}\;\,V_{c}^{{(n_{l} )}}$ are the volume fractions of particulate-phase material on the mid-surface and top surfaces of the FGM core, such that $V_{c}^{(0)} = V_{c}^{0}$ and $V_{c}^{{(n_{l} )}} = V_{c}^{ + }$, as well as the values of $V_{c}^{(m)} \quad \left( {m = 1,\;\,2,\; \ldots ,\;\,\left( {n_{l} - 1} \right)} \right)$ are to be determined.

Figures 9a and 10a show the optimal material composition of the symmetrically sandwiched FGM plate with the specified temperature surface conditions, in which the material models of specific function distributions (i.e., power-law and sigmoid function ones) and non-specific function distributions (i.e., the piecewise step and piecewise linear ones) are used, respectively, as well as $h_c = 0.8\,h$. The corresponding optimal results for the through-thickness distributions of the in-plane stresses and the stress ratios induced in the plate with various material models are shown in Figs. 9b, c and 10b, c, and the corresponding maximum stress ratios ($f_{\sigma \hbox{max} }$) induced in the plate are given in Table 4.

Fig. 9

Optimal results for the symmetrically sandwiched FGM plate with the specified temperature surface conditions and using the power-law and sigmoid material models, a the through-thickness distributions of the volume fractions of the particulate-phase material, b the through-thickness distributions of the in-plane stress, c the through-thickness distributions of the stress ratio

Fig. 10

Optimal results for the symmetrically sandwiched FGM plate with the specified temperature surface conditions and using the material model of layerwise step and linear functions, a the through-thickness distributions of the volume fractions of the particulate-phase material, b the through-thickness distributions of the in-plane stress, c the through-thickness distributions of the stress ratio

Table 4 Maximum stress ratios induced in the symmetrically sandwiched FGM plates composed of the optimal material compositions for different material models

It can be seen in Fig. 9b, c and Table 4 that the deviation between the results of optimal stresses induced in the plate with the power-law model and the sigmoid material model is minor, even though the maximum stress ratio obtained using the power-law model is less than that obtained using the sigmoid model.

Again, the results of Fig. 10b, c and Table 4 show the optimal results for the through-thickness distributions of the in-plane stresses and stress ratios induced in the plate using the layerwise step and layerwise linear material models are close to each other. The maximum stress ratios obtained using the layerwise step and layerwise linear material models are slightly less than that obtained using the power-law one, while these are much less than that obtained using the sigmoid one.

It can be concluded that the maximum stress ratios induced in the FGM plates with the optimal material composition of the material model of non-specific functions, such as layerwise step or layerwise linear ones, are always less than those values obtained using the material models of specific functions, such as power-law or sigmoid ones. The through-thickness distribution of the in-plane stress induced in the plate obtained using the layerwise linear material model gradually and continuously vary through the thickness direction of the plate, while the in-plane stress induced in the plate obtained using the layerwise step material model is discontinuous at the interfaces between adjacent layers due to the material properties suddenly changing at those places. Thus, using the layerwise linear material model for the current issue produces more satisfactory results, as compared with those obtained using other material models, such as the power-law, sigmoid and layerwise step ones, and thus this approach is recommended.

5 Concluding remarks

In this article, the authors develop a hybrid GA with the complex method for the optimization of the material composition of a simply-supported, asymmetrically single-layered FGM plate and a symmetrically sandwiched FGM one with four material models, such as the power-law, sigmoid, layerwise step and layerwise linear ones, and two thermal surface conditions, such as the specified temperature and heat convection ones. A unified weak-form formulation of various RMVT-based FLMs is developed for the coupled thermo-elastic analysis of simply-supported, multi-layered FGM plates. The layerwise linear material model is recommended, because the through-thickness distribution of the in-plane stress induced in the FGM plate gradually and continuously varied through the thickness direction of the FGM plate, and the corresponding maximum stress ratios induced in the FGM plate are always less than those obtained using the power-law and sigmoid material models.

The current hybrid GA with the complex method is developed and coded by the authors, and this can be extended to examine constrained multi-objective optimization problems in the continued work. As noted above, in this work a layerwise linear material model is recommended for the current optimization problem. It is thus be expected that a lower value of the maximum stress ratio and a more smooth stress distribution along the thickness coordinate of the FGM plate might be obtained when using certain layerwise higher-order function material models, which also becomes a potential issue in the continued work.