1 Introduction

Recently, distributed adaptive networks have received considerable attention owing to their wide range of applications in the fields of environmental monitoring and spectrum sensing [3, 6, 9,10,11, 18, 21]. The distributed estimation algorithms are important for distributed adaptive networks. To this end, the diffusion least-mean-square (DLMS) algorithm has been widely studied because of its simplicity and easy implementation [4, 13,14,15, 29]. Adaptive filtering algorithms based on the mean-square error (MSE) criterion may suffer from severely degraded convergence performance, or even divergence problems when the measurement noise contains impulsive interference [5, 7, 8, 22, 25]. Similarly, distributed estimation algorithms based on the MSE criterion may also suffer from degraded performance when the network suffers from thunder or large pulse electromagnetic interference.

By combining the sign function and the DLMS algorithm, a diffusion sign-error (DSE-LMS) algorithm was developed to ameliorate the robustness against impulsive interference [16]. Similar to other conventional algorithms, although the DSE-LMS algorithm has low computational complexity and is robust against impulsive noise, the application of the sign operation degrades its performance (fast convergence rate and low steady-state error). The contradiction between the fast convergence rate and low steady-state mean-square deviation (MSD) can be solved by using a variable step-size scheme.

Inspired by earlier work [12], a robust variable step-size diffusion sign-error (RVSSDSE-LMS) algorithm is developed herein. As the step size is derived by minimizing the intermediate noiseless posterior error, the proposed algorithm has a fast convergence rate and good tracking capability. Then, the mean-square performance and computational complexity are analyzed. The simulation results demonstrate that the proposed algorithm achieves a fast convergence rate, low steady-state error, and good tracking capability in impulsive noise environments. Owing to the advantages of distributed networks and the variable step-size scheme, the proposed algorithm can be applied to adaptive echo cancellation, active noise control, etc.

2 Diffusion Sign-Error Algorithm

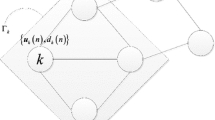
As shown in Fig. 1, each node k obtains an observed output signal dk(i) and a regression vector uk(i) at time i in the distributed network. The distributed algorithms are used to estimate the unknown M × 1 weight vector wo; the linear model can be expressed as:

$$ d_{k} \left( i \right) = \varvec{u}_{k}^{T} \left( i \right)\varvec{w}_{o} + v_{k} \left( i \right) $$
(1)

where uk(i) = [uk(i),uk(i − 1),…,uk(i − M+1)]T, vk(i) is the background noise with variance \( \sigma_{v,k}^{2} \) at agent k.

Fig. 1
figure 1

Distributed network topology

Full size image

Each node k has a set Γk, which includes itself and the nodes that connect with node k. In the set, each node can exchange information with its neighboring nodes. The weight update formula of the DSE-LMS algorithm can be rewritten as [16]:

$$ \varvec{\varphi }_{k} \left( i \right) = \varvec{w}_{k} \left( {i - 1} \right) + \mu_{k} \varvec{u}_{k} \left( i \right){\text{sign}}\left( {e_{k} \left( i \right)} \right) $$
(2)

and

$$ \varvec{w}_{k} \left( i \right) = \sum\nolimits_{{l \in \varGamma_{k} }} {a_{l,k} \varvec{\varphi }_{l} \left( i \right)} $$
(3)

where \( \varvec{\varphi }_{k} \left( i \right) \) is the intermediate weight estimate for wo at agent k and μk is the fixed step-size at agent k. al,k is the combination weight, which satisfies \( \sum\nolimits_{{l \in \varGamma_{k} }} {a_{l,k} } = 1 \);\( a_{l,k} = 0 \) if \( l \notin \varGamma_{k} \). The error signal at agent k is defined as follows:

$$ e_{k} \left( i \right) = d_{k} \left( i \right) - \varvec{u}_{k}^{T} \left( i \right)\varvec{w}_{k} \left( {i - 1} \right) $$
(4)

3 Proposed Algorithm

The variable step-size is generally influenced by the error signal that should be minimized as soon as possible [17]. To solve the conflict between the fast convergence rate and the low steady-state error, a variable step-size of the adaptation step is proposed by minimizing the noiseless intermediate posterior error as follows.

Defining the noiseless intermediate priori error and posterior error, respectively,

$$ e_{a,k} \left( i \right) = \varvec{u}_{k}^{T} \left( i \right)\left( {\varvec{w}_{o} - \varvec{w}_{k} \left( {i - 1} \right)} \right) $$
(5)
$$ e_{p,k} \left( i \right) = \varvec{u}_{k}^{T} \left( i \right)\left( {\varvec{w}_{o} - \varvec{\varphi }_{k} \left( i \right)} \right). $$
(6)

Applying Eqs. (5) and (6) in (2) yields

$$ e_{p,k} \left( i \right) = e_{a,k} \left( i \right) - \mu_{k} \varvec{u}_{k}^{T} \left( i \right)\varvec{u}_{k} \left( i \right){\text{sign}}\left( {e_{k} \left( i \right)} \right). $$
(7)

Then, the proposed variable step-size is derived by solving the following minimization problem:

$$ \mathop {\hbox{min} }\limits_{{\mu_{k} \left( n \right)}} \left\| {e_{p,k} \left( i \right)} \right\|_{1} = \left\| {e_{a,k} \left( i \right) - \mu_{k} \left( i \right)\varvec{u}_{k}^{T} \left( i \right)\varvec{u}_{k} \left( i \right){\text{sign}}\left( {e_{k} \left( i \right)} \right)} \right\|_{1} . $$
(8)

Since the optimization problem is irrelevant to the measurement noise, the step-size constraint [12] can be neglected. As can be seen from Eq. (8), the optimal step-size cannot be obtained by taking its deviation because the equation is the l1-norm with respect to μk. The optimal solution can be obtained by making Eq. (8) equal to 0, and the optimal step-size is derived as:

$$ \mu_{k} \left( i \right) = \frac{{e_{a,k} \left( i \right)}}{{\varvec{u}_{k}^{T} \left( i \right)\varvec{u}_{k} \left( i \right){\text{sign}}\left( {e_{k} \left( i \right)} \right)}}. $$
(9)

\( e_{a,k} \left( i \right) \) can be obtained by using the shrinkage denoising method [1, 2, 17, 19, 30]:

$$ e_{a,k} \left( i \right) = {\text{sign}}\left( {e_{k} \left( i \right)} \right)\hbox{max} \left( {\left| {e_{k} \left( i \right)} \right| - t,0} \right). $$
(10)

However, when the measurement noise vk(i) contains impulsive noise, the estimation results of the shrinkage method cause bias. In order to maintain the accuracy of the estimation method, the selection of threshold parameter t is [20, 27]:

$$ t = \left\{ {\begin{array}{*{20}l} {\frac{{e_{k}^{2} \left( i \right)}}{{\gamma \theta_{k} \left( i \right) + \left| {e_{k} \left( i \right)} \right|}}} \hfill & {\left| {e_{k} \left( i \right)} \right| > \xi \theta_{k} \left( i \right)} \hfill \\ {\sqrt {\sigma_{v,k}^{2} } } \hfill & {\text{else}} \hfill \\ \end{array} } \right. $$
(11)

where \( \theta_{k} \left( i \right) \) is selected as \( \theta_{k} \left( i \right) = \sigma_{e,k} \left( i \right) \); ξ is a positive value. \( \sigma_{e,k} \left( i \right) \) is calculated by:

$$ \sigma_{e,k}^{2} \left( i \right) = \lambda \sigma_{e,k}^{2} \left( {i - 1} \right) + \left( {1 - \lambda } \right){\text{median}}\left( {\varvec{Q}_{k} \left( i \right)} \right) $$

and

$$ \varvec{Q}_{k} \left( i \right) = \left[ {e_{k}^{2} \left( i \right),e_{k}^{2} \left( {i - 1} \right), \ldots ,e_{k}^{2} \left( {i - L + 1} \right)} \right]^{T} $$

where L is the extent of the estimation window.

As can be seen from (9), since \( e_{a,k} \left( i \right){ = }e_{k} \left( i \right) - \nu_{k} \left( i \right) \), the optimal step-size is influenced by the error signal and the noise signal at each node. As the noiseless intermediate posterior error is large in the transient state, \( e_{k} \left( i \right) > > \nu_{k} \left( i \right) \), μk tends to be large. When the proposed algorithm begins to converge to the steady state, \( e_{k} \left( i \right) \approx \nu_{k} \left( i \right) \) and \( e_{a,k} \left( i \right) \approx 0 \), thus making μk(i) close to 0. In addition, when the system suddenly changes, \( e_{a,k} \left( i \right) \) immediately becomes large, and the proposed algorithm achieves good tracking capability. As a result, the step size can be controlled optimally.

The proposed algorithm is summarized in Table 1.

Table 1 RVSSDSE-LMS algorithm
Full size table

4 Performance Analysis

4.1 Convergence Analysis

Taking the mean-square expectation on both sides of Eq. (7), the following is obtained:

$$ E\left( {\left\| {e_{p,k} \left( i \right)} \right\|^{2} } \right) = E\left( {\left\| {e_{a,k} \left( i \right)} \right\|^{2} } \right) - 2\mu_{k} E\left( {\left\| {\varvec{u}_{k} \left( i \right)} \right\|^{2} e_{a,k} \left( i \right){\text{sign}}\left( {e_{k} \left( i \right)} \right)} \right) + \mu_{k}^{2} E\left( {\left\| {\varvec{u}_{k} \left( i \right)} \right\|^{4} } \right). $$
(12)

Assuming that the noise-free prior error signal ea,k(i) is a zero-mean Gaussian process for a long filter [23, 24, 26], and using the Price theorem [28] in the second part of Eq. (12) will yield

$$ E\left( {\left\| {\varvec{u}_{k} \left( i \right)} \right\|^{2} e_{a,k} \left( i \right){\text{sign}}\left( {e_{k} \left( i \right)} \right)} \right) = \sqrt {\frac{2}{\pi }} \frac{{E\left( {\left\| {\varvec{u}_{k} \left( i \right)} \right\|^{2} } \right)\sqrt {\sigma_{a,k}^{2} \left( i \right)} }}{{\sqrt {\sigma_{e,k}^{2} \left( i \right)} }}. $$
(13)

Substituting Eq. (13) into Eq. (12) yields

$$ E\left( {\left\| {e_{p,k} \left( i \right)} \right\|^{2} } \right) = E\left( {\left\| {e_{a,k} \left( i \right)} \right\|^{2} } \right) - 2\mu_{k} \sqrt {\frac{2}{\pi }} \frac{{E\left( {\left\| {\varvec{u}_{k} \left( i \right)} \right\|^{2} } \right)\sqrt {\sigma_{a,k}^{2} \left( i \right)} }}{{\sqrt {\sigma_{e,k}^{2} \left( i \right)} }} +\,\mu_{k}^{2} E\left( {\left\| {\varvec{u}_{k} \left( i \right)} \right\|^{4} } \right). $$
(14)

To obtain maximum gradient attenuation, the following equation should satisfy:

$$ E\left( {\left\| {e_{p,k} \left( i \right)} \right\|^{2} } \right) - E\left( {\left\| {e_{a,k} \left( i \right)} \right\|^{2} } \right) \le 0 $$
(15)

That is

$$ \mu_{k}^{{}} E\left( {\left\| {\varvec{u}_{k} \left( i \right)} \right\|^{2} } \right) - 2\sqrt {\frac{2}{\pi }} \frac{{\sqrt {\sigma_{a,k}^{2} \left( i \right)} }}{{\sqrt {\sigma_{e,k}^{2} \left( i \right)} }} \le 0 $$
(16)

Therefore, the bound of step size is given as follows:

$$ 0 < \mu_{k}^{{}} \le 2\sqrt {\frac{2}{\pi }} \frac{{\sqrt {\sigma_{a,k}^{2} \left( i \right)} }}{{E\left( {\left\| {\varvec{u}_{k} \left( i \right)} \right\|^{2} } \right)\sqrt {\sigma_{e,k}^{2} \left( i \right)} }}. $$
(17)

4.2 Computational Complexity

Table 2 compares the computational complexity of the DLMS, DSE-LMS, and the proposed algorithms in terms of additions, multiplications, and comparisons. The length of the filter is M and τk is the number of neighbors at node k. Owing to the computation of the optimal step-size, the proposed algorithm only requires 2 M + 1 more multiplications, 1 more addition, and τk more comparisons than the DSE-LMS algorithm. In other words, the proposed algorithm has a significant performance improvement than the DSE-LMS algorithm at the cost of litter computational complexity.

Table 2 Summary of the computational complexity
Full size table

5 Simulation Results

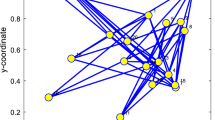
The performance of the proposed variable step-size algorithm is tested in system identification. The unknown parameter vector is randomly generated with length M. A network with N = 20 nodes is shown in Fig. 2. The network MSD is defined as \( NMSD\left( i \right) = \left( {1/N} \right)\mathop \sum \limits_{k = 1}^{N} \varvec{w}_{o} - \varvec{w}_{k} \left( i \right)^{2} \). The NMSD curves are obtained by the overall average of 50 independent trials. The uniform weighting rule is used for combination weights. The variance of the background Gaussian noise \( \varepsilon_{k} \left( n \right) \) is assumed to be known. The impulsive noise \( \vartheta_{k} \left( i \right) = b\left( i \right) \in \left( i \right) \) with the incidence of p is added to the output, and the variance is \( \sigma_{\varepsilon ,k}^{2} = \kappa \sigma_{\varepsilon ,k}^{2} \). The measurement noise vk(i) = \( \varepsilon_{k} \left( i \right) \) + \( \vartheta_{k} \left( i \right) \). The variances of the input signal and Gaussian noise \( \varepsilon_{k} \left( i \right) \) are depicted in Fig. 3.

Fig. 2
figure 2

Topology of the simulated diffusion adaptive network consisting of 20 agents

Full size image
Fig. 3
figure 3

Powers of the input vectors and background Gaussian noises at each agent

Full size image

In the first experiment, the performance of the proposed algorithm and other cited algorithms is compared, as shown in Figs. 4 and 5. Figure 3 shows the variances of the input signal and background Gaussian noise at node k. Figures 4 and 5 show the comparison of the network MSD of the proposed algorithm and the DLMS algorithm with the step size μ = 0.003; the two step-sizes of the DSE-LMS algorithm are 0.001 and 0.002. The forgetting factor of the proposed algorithm is chosen as \( \alpha = 1 - {1 \mathord{\left/ {\vphantom {1 {KM}}} \right. \kern-0pt} {KM}} \) with K = 3. The length of the unknown parameter vector M = 64 and L is chosen as 5. ξ is chosen as 1.53. The amplitudes of impulsive noise are 100 and 1000. To verify the robustness against impulsive noise, impulsive noise with p = 0.1 and p = 0.01 is added at all agents.

Fig. 4
figure 4

NMSD curves of the proposed algorithm compared with DLMS and DSE-LMS algorithms for \( \kappa { = }100 \). ap = 0.01, bp = 0.1

Full size image
Fig. 5
figure 5

NMSD curves of the proposed algorithm compared with DLMS and DSE-LMS algorithms for \( \kappa { = }1000 \). ap = 0.01, bp = 0.1

Full size image

As the proposed robust variable step-size algorithm is derived by minimizing the intermediate noiseless posterior error, it possesses a large step-size and a small step-size at the transient stage and the steady-state stage, respectively, as shown in Figs. 4 and 5. Thus, the proposed algorithm has a fast initial convergence rate and reduced steady-state NMSD compared to the DSE-LMS algorithm in impulsive noise environments.

Figure 6 shows the comparison of the tracking performance of the proposed algorithm and the conventional DLMS and DSE-LMS algorithms in the scenario of a sudden environment, where the coefficients of the impulse response transform during the iterations. The simulation conditions are the same as shown in Fig. 4. The entries of the impulse response are abruptly multiplied by –1 at iteration 1500. As shown in Fig. 6, when the system undergoes change, the intermediate posterior error becomes large and the step size at each agent becomes large to maintain the tracking capability of the proposed algorithm. Thus, the proposed RVSSDSE-LMS algorithm has good tracking capability.

Fig. 6
figure 6

NMSD curves of the proposed algorithm compared with DLMS and DSE-LMS algorithms for \( \kappa { = }1000 \). ap = 0.01, bp = 0.1

Full size image

6 Conclusion

This study has proposed an RVSSDSE-LMS algorithm to improve the performance of the DSE-LMS algorithm for distributed estimation over adaptive networks. The robust variable step-size is achieved by minimizing the l1-norm of the noiseless intermediate posterior error. The proposed RVSSDSE-LMS algorithm uses the optimal step-size mechanism to solve the conflict between the fast convergence rate and low steady-state MSD. Simultaneously, the proposed algorithm can maintain tracking capability when the system mutates. The simulation results show that the RVSSDSE-LMS algorithm outperforms the DSE-LMS and DLMS algorithms in terms of both steady-state error and convergence rate in system identification.