1 Introduction

Memristor was first envisioned and named by Chua in 1971 [6]. Its physical implementation was successfully built by a research team from Hewlett–Packard laboratory in 2008 [23]. According to the research result, it is generally known that the memristor’s resistance (memristance) depends on the magnitude and polarity of the voltage applied over time. That is to say, when a sinusoidal, or any bipolar periodic signal that assumes both positive and negative values, is applied to the memristor, it exhibits a hysteresis loop in the \(u-i\) plane, which is pinched at the origin. This pinched hysteresis loop is considered as a fingerprint of the memristor.

This passive electronic device has generated unprecedented worldwide interest because of its potential applications in the next generation computers and powerful brain-like “neural” computers. In the brain-like neuromorphic circuits, memristor is used to fabricate artificial neural networks to implement synaptic weights between neurons. It can work in a way that is similar to human brains and it prompts more and more researchers to replace resistors in conventional neural networks by memristors, and thus the memristive neural networks can be constructed.

From the viewpoint of circuit theory, the integration of memristor greatly enriches the dynamic behaviors of traditional neural networks and provides a new perspective on the design of powerful neural networks. As reported in [8], the number of EP in a n-neuron memristive system is up to \(2^{2n^2+n}\), which implies that the memristive system can perform more information capacity than others.

Very recently, lots of interesting works on the memristive neural networks have been raised in [1, 12, 21, 26]. For example, in [12], it can be seen that memristive neural networks can perform a number of applications, such as logical operations, image processing operations, complex behaviors, higher brain functions and RSA algorithm. Thus, it is meaningful to investigate the dynamic behaviors of the memristive neural networks.

Among the rich dynamic behaviors, stabilization control can be reviewed as one of the hot-button topics due to its successful utilization in many different science and engineering fields [7, 14, 19, 20, 27, 28, 31,32,33], in which, the finite-time stability analysis of memristive system with Markovian jump parameters was performed in [14], via periodically intermittent control strategy the exponential stabilization for the fuzzy memristive system was reported in [32], besides, Wei et al. [28] discussed the dynamic behaviors of complex-valued memristive neural networks. However, in the aforementioned results, the connection weights and the active functions take values in the field of real or complex numbers.

For high-dimensional neural networks, complex-valued neural networks are known as an effective solution for tasks requiring two-dimensional input vectors, while quaternion neural networks are able to learn the local relations that exist within its components through Hamilton product. Due to the capability to code multidimensional data in real world, an increasing number of studies have been conducted for the quaternion neural networks.

Quaternion was proposed in [9] for the first time and performed a number of meaningful applications from various areas, such as attitude control, quantum mechanics as well as computer graphics [4, 5, 18]. These measurements can be represented as vectors in space \(\mathbb {R}^3\) and \(\mathbb {R}^4\). However, vector algebra is not a division algebra and suffers from mathematical deficiencies when modeling orientation and rotation. In this case, the quaternion domain \(\mathbb {H}\) offers a convenient and unified way to process 3-D and 4-D signals [11, 17, 25]. Therefore, quaternion neural networks are supposed to give further investigation for their broad applications [3, 15, 16, 22, 24].

Motivated by the above observations, this paper aims to develop a rather complete set of properties to study the stabilization control of quaternion-valued memristive neural networks, which is an interesting and challenging topic in the memristive system. The main contributions of this paper are highlighted as: (i) the quaternion algebra is brought into the memristive neural networks, i.e., the states, connection weights take values in quaternion field, which can be seen as an extension of the existing works on real-valued neural networks; (ii) a partial order is proposed in this paper, which can be employed to determine the “magnitude” of two different quaternion-valued; thus, the closed convex hull derived by two different quaternion connections can be derived correspondingly.

This paper is organized as follows. We present the model of a memristive system with states, connection weights as well as active functions expressed by quaternion in Sect. 2. The existence of the EP and its stability analysis are provided in the third section. Section 4 illustrates through simulation results that a memristive system satisfying the given properties is indeed stable. The conclusion is given in the last section.

2 Preliminaries

2.1 Quaternion Algebra

A real quaternion can be given by:

$$\begin{aligned} h=h^{ R }+ h^{ I } i +h^{ J } j +h^{ K } k, \end{aligned}$$
(1)

which implies that a quaternion involving a real part and three imaginary parts i, j, k, and i, j, k are subjected to the Hamilton rule.

Define \(\mathbb {Q}\triangleq \{h^{R}+ h^{I} i +h^{J} j +h^{K} k | h^{R}, h^{I}, h^{J},h^{K}\in \mathbb {R}\}\) and denote the conjugate of h by

$$\begin{aligned} \bar{h}=h^{ R }- h^{ I } i -h^{ J } j -h^{ K } k. \end{aligned}$$

The modulus of \(h\in \mathbb {Q}\) is defined as:

$$\begin{aligned} |h|=\sqrt{h\bar{h}}=\sqrt{(h^{ R })^2+(h^{ I })^2 +(h^{ J })^2 + (h^{ K })^2 }. \end{aligned}$$

Besides, for \(h=(h_1, h_2, \dots , h_n)^T \), let \(|h|=(|h_1|, |h_2|, \dots , |h_n|)^T \) be the modulus of h and \(\Vert h\Vert _1=\sum _{p=1}^n |h_p| \) be the norm of h.

2.2 Model Description

A simple mathematical model of a quaternion-valued memristive system can be described by:

$$\begin{aligned} \dot{x}_p(t) = -d_px_p(t)+\sum _{q=1}^{n} a_{pq} (x_p(t)) f_q(x_q(t)) +\sum _{q=1}^{n} b_{pq} ( x_p(t ) )f_q(x_q(t-\varsigma (t) )) + J_p, \end{aligned}$$
(2)

for \( p=1,2,\dots ,n\), where \(x_p(t) \in \mathbb {Q}\) represents the neuron state, \( d_{ p} >0\) is the self-feedback connection real weight, \( a_{pq}(x_p(t)) \), \( b_{pq}( x_p(t )) \in \mathbb {Q}\) is the feedback connection weight and \( J_p \in \mathbb {R}\) signifies the external input. Moreover, \(\varsigma (t) \) stands for the transmission delay subjected to \(0 \le \varsigma (t)\le \varsigma \), \(\dot{\varsigma }(t)\le \varrho <1\) and \( f_p(x_p(t)) \) is the activation function satisfying \((A_1)\).

\((A_1)\): For \(q=1,2,\dots ,n\), the activation functions are subjected to

$$\begin{aligned} |f_q ( x_1 )-f_q ( x_2) | \le m_q | x_1-x_2 |, \ \ \ |f_q ( x ) | \le \mathcal {F}_q , \end{aligned}$$

where \(m_q, \mathcal {F}_q > 0\).

In this paper, the quaternion connection weights are assumed to own the following properties.

\((A_2)\): \(a_{pq}(x_p(t))\), \(b_{pq}(x_p(t))\) are subjected by:

$$\begin{aligned} \begin{aligned}&a_{pq}(x_p(t)) =\left\{ \begin{array}{ll} a_{pq}^{\intercal }=a_{1pq}^R + a_{1pq}^I i+ a_{1pq}^J j+ a_{1pq}^K k, &{}\quad |x_p(t)|\le \digamma _p, \\ a_{pq}^{\intercal \intercal }=a_{2pq}^R + a_{2pq}^I i+ a_{2pq}^J j+ a_{2pq}^K k, &{}\quad |x_p(t)|> \digamma _p, \end{array} \right. \\&b_{pq}(x_p(t)) =\left\{ \begin{array}{ll} b_{pq}^{\intercal }=b_{1pq}^R + b_{1pq}^I i+ b_{1pq}^J j+ b_{1pq}^K k, &{}\quad |x_p(t)|\le \digamma _p, \\ b_{pq}^{\intercal \intercal }=b_{2pq}^R + b_{2pq}^I i+ b_{2pq}^J j+ b_{2pq}^K k, &{}\quad |x_p(t)|> \digamma _p, \end{array} \right. \end{aligned} \end{aligned}$$

where \(\digamma _p>0\) is the switching jump.

Definition 2.1

(Generalized Inequalities [13]) For any cone \(N \subseteq \mathbb {R}^n\), the partial ordering relation in \(\mathbb {R}^n\) is defined as:

(I).

$$\begin{aligned} x \preceq y \Leftrightarrow y-x \in N; \end{aligned}$$

(II).

$$\begin{aligned} x \prec y \Leftrightarrow y-x \in \text {int}\ N, \end{aligned}$$

where \(\text {int} N\) is the interior of N.

Remark 2.1

As one knows, the complex value can be seen as a two-dimensional vector; thus, the generalized inequalities can be employed to compare the “magnitude” of two complex values, i.e., if N stands for the first (or fourth) quadrant of the complex plane, then any complex value on its “right” side is greater than it, and the complex number in the “upper right” of a complex value is strictly greater than it.

For example, for two different complex values \(x_1=a_1+b_1 i\), \(x_2=a_2+b_2 i\), yields, \(x_2-x_1=a_2-a_1+(b_2-b_1) i\). Now, two cases are proposed in the following lines: (i) \((a_2-a_1)\cdot (b_2-b_1)\ge 0\), (ii) \((a_2-a_1)\cdot (b_2-b_1)<0\). For the case (i), if \(a_2-a_1>0\), \(b_2-b_1>0\), then \(x_1 \prec x_2\); if \(a_2-a_1= 0\), \(b_2-b_1>0\), or \(a_2-a_1>0\), \(b_2-b_1=0\), then \(x_1 \preceq x_2\); if \(a_2-a_1<0\), \(b_2-b_1<0\), then \(x_1 \succ x_2\); For the case (ii), if \(a_2-a_1>0\), \(b_2-b_1<0\), then \(x_1 \prec x_2\); if \(a_2-a_1<0\), \(b_2-b_1>0\), then \(x_1 \succ x_2\).

For two different quaternions \(x_1=a_1+b_1 i +c_1 j +d_1 k=(a_1+b_1 i)+ (c_1+d_1 i)j\triangleq x_{11} + x_{12} j\), \(x_2=a_2+b_2 i+c_2 j +d_2 k=(a_2+b_2 i)+ (c_2+d_2 i)j\triangleq x_{21} + x_{22} j\), the first step is to compare two pairs of two-dimensional vectors \(x_{11}\) and \(x_{21}\), \(x_{12}\) and \(x_{22}\), respectively. If \(x_{11} \prec (\succ ) x_{21}\) and \(x_{12} \prec (\succ ) x_{22}\), then \(x_1\prec (\succ ) x_2\); if \(x_{11} \preceq x_{21}\), \(x_{12} \prec x_{22}\), or \(x_{11} \prec x_{21}\), \(x_{12} \preceq x_{22}\), then one has \(x_1\preceq x_2\); if \(x_{11} \preceq (\succeq ) x_{21}\), \(x_{12} \succ (\prec ) x_{22}\), then \(x_1\preceq (\succeq ) x_2\); if \(x_{11} \prec (\succ ) x_{21}\), \(x_{12} \succeq (\preceq ) x_{22}\), then \(x_1\preceq (\succeq ) x_2\).

According to the above analysis, system (2) can be written as:

$$\begin{aligned} \begin{aligned} \dot{x}_p(t)&\in - d_p x_p(t)+\sum _{q=1}^{n} co[a_{pq}^-, a_{pq}^+ ]f_q(x_{q}(t))\\&\quad +\sum _{q=1}^{n} co [b_{pq}^-, b_{pq}^+ ]f_q(x_{q}(t-\varsigma (t))) +J_p , \end{aligned} \end{aligned}$$
(3)

where \(\tilde{a}_{pq}=\max \{ | a_{pq}^{\intercal }|, |a_{pq}^{\intercal \intercal }| \}\), \(a_{pq}^-=\min \{a_{pq}^{\intercal }, a_{pq}^{\intercal \intercal }\}\), \(a_{pq}^+=\max \{a_{pq}^{\intercal }, a_{pq}^{\intercal \intercal }\}\), \(\tilde{b}_{pq}=\max \{ | b_{pq}^{\intercal }|, |b_{pq}^{\intercal \intercal }| \}\), \(b_{pq}^-=\min \{b_{pq}^{\intercal }, b_{pq}^{\intercal \intercal }\}\), \(b_{pq}^+=\max \{b_{pq}^{\intercal }, b_{pq}^{\intercal \intercal }\}\), \(\mid a_{pq}^{\intercal }\mid =\mid a_{1pq}^R\mid + \mid a_{1pq}^I \mid i+ \mid a_{1pq}^J\mid j+ \mid a_{1pq}^K \mid k\). Besides, \(\mid a_{pq}^{\intercal \intercal }\mid \), \(\mid b_{pq}^{\intercal }\mid \), \(\mid b_{pq}^{\intercal \intercal }\mid \) share the same definition.

Recall that the differential inclusion means that there exist \(a^{*}_{pq}(t) \in co [a_{pq}^-, a_{pq}^+] \), \(b^{*}_{pq}(t) \in co [b_{pq}^-, b_{pq}^+] \) such that

$$\begin{aligned} \dot{ x}_p(t)&= - d_p x_p(t)+\sum _{q=1}^{n}a^{*}_{pq}(t) f_q(x_{q}(t))\nonumber \\&\quad +\sum _{q=1}^{n}b^{*}_{pq}(t) f_q(x_{q}(t-\varsigma (t))) +J_p, \ \ p=1,\dots , n. \end{aligned}$$
(4)

Before moving on, a preliminary result is given below.

Lemma 2.1

([2]) Let \(\Theta \) be a compact convex subset of a Banach space \(\mathcal {X}\). If the set-valued map \(\varphi : \Theta \rightarrow G(\Theta )\) is an upper semi-continuous convex compact map, then \(\varphi \) has a fixed point in \(\Theta \), i.e., there exists \(x\in \Theta \) such that \(x\in \varphi (x)\).

Lemma 2.2

([24]) Let x, \(y\in \mathbb {Q}\), \(\varepsilon >0\) be a constant, then it holds that

$$\begin{aligned} yx +\bar{x}\bar{y} \le \varepsilon \bar{x} x +\frac{1}{\varepsilon } y\bar{y}. \end{aligned}$$

Lemma 2.3

([10]) Suppose that function x(t) is nonnegative when \(t\in (-d, \infty )\) and satisfies the following inequality:

$$\begin{aligned} \dot{x}(t)\le -a x(t)+b x(t-d(t))+c, \ \ \ t\ge 0, \end{aligned}$$

where a, b, c are positive constants with \(a> b\) and \(0\le d(t)\le d\). Then,

$$\begin{aligned} x(t)\le \max _{-d\le \theta \le 0} x(\theta ) e^{-r t}+\frac{ c}{r}, \end{aligned}$$

where r is the positive solution of the following equation

$$\begin{aligned} a-b e^{-r d}-r=0. \end{aligned}$$

Definition 2.2

The EP of \(\breve{x}_p\) of (2) is said to be globally exponentially stable (GES), if there exist constants \(\gamma >0\) and \(\pi >0\) such that

$$\begin{aligned} \Vert x (t)- \breve{x} \Vert _1 \le \gamma e^{- \pi t} \sup _{-\varsigma \le s \le 0} \Vert \zeta (s)- \breve{x }\Vert _1, \ \ t\ge 0, \end{aligned}$$

where \(\zeta (s)\) is the initial value.

3 Main Results

We are now ready to derive the conditions to ensure the existence and uniqueness of the EP for system (2). Subsequently, its stability analysis is also provided.

3.1 Existence of the EP

Theorem 3.1

Suppose that \((A_1)\) holds, then the memristive system (2) has at least one EP.

Proof

Let \(x =(x_1 , \dots , x_n )^T\in \mathcal { X}\), where \(\mathcal { X}\) means a Banach space endowed with the norm \(\Vert x \Vert _1=\sum _{p=1}^n |x_p |\). Thus, the existence of EP for (2) is equivalent to

$$\begin{aligned} x_p (t)\in \frac{1}{d_p} \sum _{q=1}^{n} [a_{pq}^{- }, a_{pq}^{+} ] f_q (x_q(t)) +\frac{1}{d_p} \sum _{q=1}^{n} [b_{pq}^{- }, b_{pq}^{+} ] f_q (x_q(t-\varsigma (t))) +\frac{J_p }{d_p}. \end{aligned}$$
(5)

Construct a compact convex subset of \(\mathcal { X}\) as \(\Theta =\{x =(x_1, \dots , x_n )^T\in \mathcal { X}: \Vert x \Vert _1\le \delta \}\) with

$$\begin{aligned} \delta =\sum _{p=1}^n \left| \frac{J_p }{d_p}\right| +\sum _{p=1}^n\sum _{q=1}^n \frac{ \tilde{a}_{pq} M_q }{d_p} +\sum _{p=1}^n\sum _{q=1}^n \frac{ \tilde{b}_{pq} M_q }{d_p}. \end{aligned}$$

Let \(\psi : \mathcal { X}\rightarrow G(\mathcal { X})\) with \(\psi (x)=(\psi _1 (x),\dots , \psi _n (x))^T\), and

$$\begin{aligned} \psi _p (x)= \frac{1}{d_p} \sum _{q=1}^{n} [a_{pq}^{- }, a_{pq}^{+} ] f_q (x_q(t)) +\frac{1}{d_p} \sum _{q=1}^{n} [b_{pq}^{- }, b_{pq}^{+ } ] f_q (x_q(t-\varsigma (t))) +\frac{J_p }{d_p} , \end{aligned}$$

which implies that \(\psi (x)\) is an upper semi-continuous set-valued map with nonempty compact convex values, i.e., \(\psi \) maps \(\Theta \) into \(G(\Theta )\), or for every fixed \(a^{*}_{pq}(t) \in [a_{pq}^-, a_{pq}^+] \), \(b^{*}_{pq}(t) \in [b_{pq}^-, b_{pq}^+] \), such that:

$$\begin{aligned} \eta _p = \frac{1}{d_p}\sum _{q=1}^{n} a_{pq}^{*}(t) f_q R(x_q(t)) + \frac{1}{d_p}\sum _{q=1}^{n} b_{pq}^{*}(t) f_q^R(x_q(t-\varsigma (t))) + \frac{J_p }{d_p}\in \psi _p (x), \end{aligned}$$
(6)

where \(\eta =(\eta _1, \dots , \eta _n )^T\in \psi (x)\). Considering the expression appearing in \((A_1)\), one has:

$$\begin{aligned} \sum _{p=1}^{n} | \eta _p |&\le \sum _{p=1}^n \left| \frac{J_p }{d_p}\right| +\sum _{p=1}^n\sum _{q=1}^n \frac{ \tilde{a}_{pq} M_q }{d_p} +\frac{ \tilde{b}_{pq} M_q }{d_p} =\delta , \end{aligned}$$
(7)

which implies that

$$\begin{aligned} \Vert \eta \Vert _1=\sum _{p=1}^{n} | \eta _p | \le \delta , \ \ x\in \Theta . \end{aligned}$$

Then, for any \( x\in \Theta \), \(\eta \in \psi (x)\), one can conclude that \(\eta \in \Theta \). Then, according to Lemma 2.1, one can conclude that \( \psi : \Theta \rightarrow G(\Theta )\) has at least one fixed point \(\breve{x} =(\breve{x}_1, \dots , \breve{x}_n )^T\in \Theta \) ensuring \(\breve{x} \in \psi (\breve{x} )\). Thus, there exists at least one EP of (2). This completes the proof. \(\square \)

3.2 Stabilization Control of the EP

Suppose the EP of (2) is \(\breve{x}_p =\breve{x}_p^{ R }+ \breve{x}_p^{ I }i + \breve{x}_p^{J }j + \breve{x}_p^{K }k\). Then, shifting the above EP to the origin by \(y_p(t)=x_p(t)-\breve{x}_p \) gives that

$$\begin{aligned} \dot{y}_p (t)= & {} -d_p y_p(t) +\sum _{q=1}^{n}(a^{*}_{pq}(t) f_q(x_{q}(t))- \breve{a}^{*}_{pq} f_q(\breve{x}_{q} ) )\nonumber \\&+\sum _{q=1}^{n} ( b^{*}_{pq}(t) f_q(x_{q}(t-\varsigma (t)))- \breve{b}^{*}_{pq} f_q(\breve{x}_{q} ) ). \end{aligned}$$
(8)

To derive the main conclusions, by adding the appropriate controller to the right hand of (8), the corresponding controlled memristive system can be given by:

$$\begin{aligned} \begin{aligned} \dot{y}_p (t)&= -d_p y_p(t) +\sum _{q=1}^{n}(a^{*}_{pq}(t) f_q(x_{q}(t))- \breve{a}^{*}_{pq} f_q(\breve{x}_{q} ) )\\&\quad +\sum _{q=1}^{n} ( b^{*}_{pq}(t) f_q(x_{q}(t-\varsigma (t)))\\&\quad - \breve{b}^{*}_{pq} f_q(\breve{x}_{q} ) )+u_p(t)\\&= -d_p y_p(t) +\sum _{q=1}^{n} a^{*}_{pq}(t) ( f_q(x_{q}(t))-f_q(\breve{x}_{q} ))+\sum _{q=1}^{n} (a^{*}_{pq}(t)- \breve{a}^{*}_{pq} )f_q(\breve{x}_{q} )\\&\quad +\sum _{q=1}^{n} b^{*}_{pq}(t) ( f_q(x_{q}(t-\varsigma (t)))- f_q(\breve{x}_{q} ) )\\&\quad + \sum _{q=1}^{n} ( b^{*}_{pq}(t)- \breve{b}^{*}_{pq} ) f_q(\breve{x}_{q} ) +u_p(t) \\&\le -d_p y_p(t) +\sum _{q=1}^{n} a^{*}_{pq}(t) ( f_q(x_{q}(t))-f_q(\breve{x}_{q} ))+\sum _{q=1}^{n} (a^{+}_{pq} - a^{-}_{pq} )\mathcal {F}_q \\&\quad +\sum _{q=1}^{n} b^{*}_{pq}(t) ( f_q(x_{q}(t-\varsigma (t)))- f_q(\breve{x}_{q} ) ) + \sum _{q=1}^{n} (b^{+}_{pq} - b^{-}_{pq} )\mathcal {F}_q +u_p(t), \end{aligned} \end{aligned}$$
(9)

where \(u_p(t)\) is the controller to be designed.

Theorem 3.2

Suppose that the assumptions (\(A_1\))–(\(A_2\)) hold, if there exist two constants \(\varrho _1>0\), \(\varrho _2>0\), such that

$$\begin{aligned} \varrho _2 \max _p m_p^2 < (1-\varrho ) \end{aligned}$$

is true, then the trivial solution of the controlled memristive system (9) is stable under the following controller:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} u_p(t)= -\vartheta _p(t)y_p(t)-\nu _p, \\ \dot{\vartheta }_p(t)= \eta _p \bar{y}_p(t)y_p(t), \end{array}\right. \end{aligned} \end{aligned}$$
(10)

where \(\vartheta _p(t)\in \mathbb {R}^n\), \(\eta _p\) is an arbitrary positive constant and

$$\begin{aligned} \nu _p \succ \sum _{q=1}^{n} (a^{+}_{pq} - a^{-}_{pq} )\mathcal {F}_q+ \sum _{q=1}^{n} (b^{+}_{pq} - b^{-}_{pq} )\mathcal {F}_q. \end{aligned}$$

Proof

The auxiliary function is formatted as:

$$\begin{aligned} \begin{aligned} V(t ) = \sum _{p=1}^n \bar{y}_p (t)y_p (t)+ \int _{t-\varsigma (t)}^t \bar{y}_p (s)y_p (s) \mathrm{d}s+ \sum _{p=1}^n \frac{1}{ \eta _p}(\vartheta _p(t)-M_p)^2, \end{aligned} \end{aligned}$$
(11)

where

$$\begin{aligned} 2 M_p \ge -2 d_p+1 + \varrho _1 m_p^2 + \frac{1}{\varrho _1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} + \frac{1}{\varrho _2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq}. \end{aligned}$$

Before moving on, a new tight estimation can be derived:

$$\begin{aligned} \begin{aligned} \dot{y}_p (t)&\le -d_p y_p(t) +\sum _{q=1}^{n} a^{*}_{pq}(t) ( f_q(x_{q}(t))-f_q(\breve{x}_{q} ))+\sum _{q=1}^{n} (a^{+}_{pq} - a^{-}_{pq} )\mathcal {F}_q \\&\quad +\sum _{q=1}^{n} b^{*}_{pq}(t) ( f_q(x_{q}(t-\varsigma (t)))- f_q(\breve{x}_{q} ) )\\&\quad + \sum _{q=1}^{n} (b^{+}_{pq} - b^{-}_{pq} )\mathcal {F}_q -\vartheta _p(t)y_p(t)-\nu _p\\&\le -d_p y_p(t) +\sum _{q=1}^{n} a^{*}_{pq}(t) ( f_q(x_{q}(t))-f_q(\breve{x}_{q} ))\\&\quad +\sum _{q=1}^{n} b^{*}_{pq}(t) ( f_q(x_{q}(t-\varsigma (t)))- f_q(\breve{x}_{q} ) )\\&\quad -\vartheta _p(t)y_p(t). \end{aligned} \end{aligned}$$
(12)

Then, evaluating the time derivative of V(t) along the solutions of (12) gives:

$$\begin{aligned} \dot{V} (t )&= \sum _{p=1}^n \dot{\bar{y}}_p (t) y_p (t)+ \sum _{p=1}^n \bar{y}_p (t) \dot{y}_p (t) + \sum _{p=1}^n \bar{y}_p (t) y_p (t)\nonumber \\&\quad -(1-\dot{\varsigma }(t))\sum _{p=1}^n \bar{y}_p (t-\varsigma (t)) y_p (t-\varsigma (t)) \nonumber \\&\quad + \sum _{p=1}^n \frac{2}{ \eta _p}(\vartheta _p(t)-M_p) \dot{\vartheta }_p(t) \nonumber \\&\le \sum _{p=1}^n \left( -d_p \bar{y}_p(t) +\sum _{q=1}^{n}( \bar{f}_q(x_{q}(t))-\bar{f}_q(\breve{x}_{q} ))\bar{a}^{*}_{pq} (t)\right. \nonumber \\&\left. \quad +\sum _{q=1}^{n}( \bar{f}_q(x_{q}(t-\varsigma (t)))-\bar{f}_q(\breve{x}_{q} ))\bar{b}^{*}_{pq} (t) \right. \nonumber \\&\left. \quad -\vartheta _p(t)\bar{y}_p(t) \right) y_p(t) + \sum _{p=1}^n \bar{y}_p(t) \left( -d_p y_p(t)\right. \nonumber \\&\left. \quad +\sum _{q=1}^{n} a^{*}_{pq}(t) ( f_q(x_{q}(t))-f_q(\breve{x}_{q} )) \right. \nonumber \\&\left. \quad +\sum _{q=1}^{n} b^{*}_{pq}(t) ( f_q(x_{q}(t-\varsigma (t)))- f_q(\breve{x}_{q} ) ) -\vartheta _p(t)y_p(t) \right) \nonumber \\&\quad +2 \sum _{p=1}^n \vartheta _p(t)\bar{y}_p(t)y_p(t)\nonumber \\&\quad - 2\sum _{p=1}^n M_p \bar{y}_p(t)y_p(t)+ \sum _{p=1}^n \bar{y}_p (t) y_p (t)\nonumber \\&\quad -(1-\varrho )\sum _{p=1}^n \bar{y}_p (t-\varsigma (t)) y_p (t-\varsigma (t)). \end{aligned}$$
(13)

It follows from Lemma 2.2, there exist two constants \(\varrho _1\), \(\varrho _2>0\) such that

$$\begin{aligned} \begin{aligned}&( \bar{f}_q(x_{q}(t))-\bar{f}_q(\breve{x}_{q} ))\bar{a}^{*}_{pq} (t) y_p(t) +\bar{y}_p(t) a^{*}_{pq}(t) ( f_q(x_{q}(t))-f_q(\breve{x}_{q} ))\\&\quad \le \varrho _1 ( \bar{f}_q(x_{q}(t))-\bar{f}_q(\breve{x}_{q} )) ( f_q(x_{q}(t))-f_q(\breve{x}_{q} )) + \frac{1}{\varrho _1 } \bar{y}_p(t) a^{*}_{pq}(t) \bar{a}^{*}_{pq} (t) y_p(t)\\&\quad \le \varrho _1 m_q^2 \bar{ y}_{q}(t) y_{q}(t) + \frac{1}{\varrho _1 } \bar{y}_p(t) \tilde{a}_{pq} \bar{\tilde{a}}_{pq} y_p(t),\\&( \bar{f}_q(x_{q}(t-\varsigma (t)))-\bar{f}_q(\breve{x}_{q} ))\bar{b}^{*}_{pq} (t) y_p(t) +\bar{y}_p(t) b^{*}_{pq}(t) ( f_q(x_{q}(t-\varsigma (t)))-f_q(\breve{x}_{q} ))\\&\quad \le \varrho _2 m_q^2 \bar{ y}_{q}(t-\varsigma (t)) y_{q}(t-\varsigma (t)) + \frac{1}{\varrho _2 } \bar{y}_p(t) \tilde{b}_{pq} \bar{\tilde{b}}_{pq} y_p(t). \end{aligned} \end{aligned}$$
(14)

Thus, together with (12)–(14) and the parameters defined above, a new tight estimation can be derived:

$$\begin{aligned} \begin{aligned} \dot{V}(t )&\le - \sum _{p=1}^{n} \left( 2 d_p-1 - \varrho _1 m_p^2 - \frac{1}{\varrho _1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} - \frac{1}{\varrho _2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq} + 2 M_p \right) \bar{y}_p(t) y_p(t) \\&\quad + ( \varrho _2 \max _p m_p^2-(1-\varrho ) ) \sum _{p=1}^{n} \bar{ y}_{p}(t-\varsigma (t)) y_{p}(t-\varsigma (t))\\&< 0. \end{aligned} \end{aligned}$$
(15)

Based on the above discussions, we can conclude that the stabilization control for system (2) can be realized via the suggested controller (10). The proof is thus completed. \(\square \)

Remark 3.1

The proof of Theorem 3.2 can be explained by LaSalles invariant principle. LaSalles invariant principle is an extension of Lyapunov function, and what is different from the Lyapunov method is the function of V(t) does not require to be positive definite.

Remark 3.2

According to the conclusions derived in Theorem 3.2, an estimation described by the partial order is presented, which gives a new method to compare the “magnitude” of two different quaternions.

Theorem 3.3

Under the assumption \((A_1)\)–\((A_2)\), the trivial solution of (9) is globally exponentially stable based on the following controller:

$$\begin{aligned} u_p(t)= -k_p y_p (t), \end{aligned}$$
(16)

where

$$\begin{aligned} 2k_p\ge -2 d_p + \tilde{\varrho }_1 m_p^2 + \frac{1}{\tilde{\varrho }_1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} + \frac{1}{\tilde{\varrho }_2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq}. \end{aligned}$$

Besides, the control gains are given by

$$\begin{aligned} \begin{aligned}&\gamma _1=\min _p \left( 2 d_p+2 k_p - \tilde{\varrho }_1 m_p^2 - \frac{1}{\tilde{\varrho }_1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} - \frac{1}{\tilde{\varrho }_2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq} \right) , \\&\gamma _2=\tilde{\varrho }_2 \max _p m_p^2, \ \ \ \gamma _1> \gamma _2>0. \end{aligned} \end{aligned}$$

Proof

The structure of the suggested function is formulated as:

$$\begin{aligned} \begin{aligned} V(t )= \sum _{p=1}^n \bar{y}_p (t) y_p (t). \end{aligned} \end{aligned}$$
(17)

Then, repeating the proof of Theorem 3.2 yields,

$$\begin{aligned} \dot{V} (t )&= \sum _{p=1}^n \dot{\bar{y}}_p (t) y_p (t)+ \sum _{p=1}^n \bar{y}_p (t) \dot{y}_p (t) \nonumber \\&\le \sum _{p=1}^n \left( -d_p \bar{y}_p(t) +\sum _{q=1}^{n}( \bar{f}_q(x_{q}(t))-\bar{f}_q(\breve{x}_{q} ))\bar{a}^{*}_{pq} (t)\right. \nonumber \\&\left. \quad +\sum _{q=1}^{n}( \bar{f}_q(x_{q}(t-\varsigma (t)))-\bar{f}_q(\breve{x}_{q} ))\bar{b}^{*}_{pq} (t)\right. \nonumber \\&\left. \quad -k_p \bar{y}_p(t) \right) y_p(t) + \sum _{p=1}^n \bar{y}_p(t) \left( -d_p y_p(t) +\sum _{q=1}^{n} a^{*}_{pq}(t) ( f_q(x_{q}(t))-f_q(\breve{x}_{q} )) \right. \nonumber \\&\left. \quad +\sum _{q=1}^{n} b^{*}_{pq}(t) ( f_q(x_{q}(t-\varsigma (t)))- f_q(\breve{x}_{q} ) ) -k_p y_p(t) \right) \nonumber \\&\le - \sum _{p=1}^{n} \left( 2 d_p+2 k_p - \tilde{\varrho }_1 m_p^2 - \frac{1}{\tilde{\varrho }_1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} - \frac{1}{\tilde{\varrho }_2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq} \right) \bar{y}_p(t) y_p(t)\nonumber \\&\quad + \tilde{\varrho }_2 \sum _{p=1}^{n}m_p^2 \bar{ y}_{p}(t-\varsigma (t)) y_{p}(t-\varsigma (t)) \nonumber \\&\le - \gamma _1 V(t) + \gamma _2 V(t-\varsigma (t)), \end{aligned}$$
(18)

where \(\tilde{\varrho }_1\), \(\tilde{\varrho }_2\) are two constants.

In view of Lemma 2.3, we have

$$\begin{aligned} V (t ) \le \max _{-\varsigma \le \theta \le 0} V(\theta ) e^{-r t}, \end{aligned}$$
(19)

where r is the solution of the following equation:

$$\begin{aligned} \gamma _1 -\gamma _2 e^{-r \varrho }-r=0. \end{aligned}$$

According to the definition of V(t), one has:

$$\begin{aligned} \Vert x(t)-\breve{x}\Vert _1 \le \max _{-\varsigma \le \theta \le 0} \Vert \zeta (\theta )-\breve{x}\Vert _1 e^{-r t}. \end{aligned}$$
(20)

By Definition 2.2, one can conclude that the trivial solution system (9) is globally exponentially stable. This completes the proof. \(\square \)

Corollary 3.1

For two given assumptions \((A_1)\)–\((A_2)\), the trivial solution of (9) is globally asymptotically stable under the following controller:

$$\begin{aligned} u_p(t)= -k_p y_p (t), \end{aligned}$$
(21)

where

$$\begin{aligned} \begin{aligned}&2k_p> -2 d_p + \sigma _1 m_p^2 + \frac{1}{\sigma _1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} + \frac{1}{\sigma _2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq},\\&\sigma _2 \max _p m_p^2 < (1-\varrho ), \end{aligned} \end{aligned}$$

in which \(\sigma _1\), \(\sigma _2\) are two constants.

Proof

Consider a functional defined by:

$$\begin{aligned} V(t )= \sum _{p=1}^n \bar{y}_p (t) y_p (t) + \int _{t-\varsigma (t)}^t\bar{y}_p (s) y_p (s) . \end{aligned}$$
(22)

Then, calculating the time derivative of V(t) along with (12) gives:

$$\begin{aligned} \begin{aligned} \dot{V}(t )&\le - \sum _{p=1}^{n} \left( 2 d_p-1 - \sigma _1 m_p^2 - \frac{1}{\sigma _1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} - \frac{1}{\sigma _2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq} \right) \bar{y}_p(t) y_p(t) \\&\quad + ( \sigma _2 \max _p m_p^2-(1-\varrho ) ) \sum _{p=1}^{n} \bar{ y}_{p}(t-\varsigma (t)) y_{p}(t-\varsigma (t))< 0. \end{aligned} \end{aligned}$$
(23)

Hence, we can conclude that the trivial solution of (9) is globally asymptotically stable. The proof is thus completed. \(\square \)

Remark 3.3

To derive the main conclusions of this paper, two different control strategies are proposed, i.e., adaptive controller and feedback controller, from which one can easily find that the control gain in the adaptive controller can be adjusted according to system parameters, which is very different with the feedback controller.

4 Numerical Example

This section is devoted to verifying the effectiveness of the obtained theoretical results, which can further highlight the conclusions furnished by the proposed methodology.

Example 1

Consider the following two-dimensional memristive neural networks:

$$\begin{aligned}&a_{11}(x_1(t)) =\left\{ \begin{array}{ll} 0.6 + 1.2 i+ 0.6 j+ 0.57 k, &{}\quad |x_1(t)|\le 0, \\ 0.8 + 1.1i+ 0.7 j+ 0.3 k, &{}\quad |x_1(t)|> 0, \end{array} \right. \\&a_{12}(x_1(t)) =\left\{ \begin{array}{ll} -0.2 -0.2 i-0.12 j-0.13 k, &{}\quad |x_1(t)|\le 0, \\ -0.1 -0.1 i-0.2 j-0.1 k, &{}\quad |x_1(t)|> 0, \end{array} \right. \\&a_{21}(x_2(t)) =\left\{ \begin{array}{ll} -0.2-0.2 i-1.1 j-0.7 k, &{}\quad |x_2(t)|\le 0, \\ -0.1-0.9 i-1 j-0.6 k, &{}\quad |x_2(t)|> 0, \end{array} \right. \\&a_{22}(x_2(t)) =\left\{ \begin{array}{ll} 0.5 +1.2 i+1.2 j+0.19 k, &{}\quad |x_2(t)|\le 0, \\ 0.8+ 1.1 i+ 1.23 j+0.1 k, &{}\quad |x_2(t)|> 0, \end{array} \right. \\&b_{11}(x_1(t)) =\left\{ \begin{array}{ll} -1.5-0.35 i-0.5 j-0.5 k, &{}\quad |x_1(t)|\le 0, \\ -1.5 -0.5 i-0.45 j-0.25 k, &{}\quad |x_1(t)|> 0, \end{array} \right. \\&b_{12}(x_1(t)) =\left\{ \begin{array}{ll} - 0.11-0.1 i-0.1 j-0.1 k, &{}\quad |x_1(t)|\le 0, \\ -0.1-0.1 i-0.2 j-0.6 k, &{}\quad |x_1(t)|> 0, \end{array} \right. \\&b_{21}(x_2(t)) =\left\{ \begin{array}{ll} -0.3-0.28 i-0.2 j-0.28 k, &{}\quad |x_2(t)|\le 0, \\ -0.28-0.2 i-0.28 j-0.28 k, &{}\quad |x_2(t)|> 0, \end{array} \right. \\&b_{22}(x_2(t)) =\left\{ \begin{array}{ll} -0.25-1 i-1.5 j-0.9 k, &{}\quad |x_2(t)|\le 0, \\ -0.5-0.7 i-1.5 j-0.7 k, &{}\quad |x_2(t)|> 0. \end{array} \right. \end{aligned}$$

Furthermore, \(d_1\), \(d_2\) are chosen as \(d_1=d_2=2\), the activation functions are described by \(f(s)=0.1\tanh (s)\). It can be easily verified that the activation functions satisfying the condition derived in (\(A_1\)) with \(\mathcal {F}_1=\mathcal {F}_2=0.1\).

Based on the above parameters, a straightforward calculation from Theorem 3.2 gives:

$$\begin{aligned} \begin{aligned} \nu _1&\succ \sum _{q=1}^{2} (a^{+}_{1q} - a^{-}_{1q} )\mathcal {F}_q+ \sum _{q=1}^{2} (b^{+}_{1q} - b^{-}_{1q} )\mathcal {F}_q\\&= 0.031+ 0.015i-0.013j-0.099k,\\ \nu _2&\succ \sum _{q=1}^{2} (a^{+}_{2q} - a^{-}_{2q} )\mathcal {F}_q+ \sum _{q=1}^{2} (b^{+}_{2q} - b^{-}_{2q} )\mathcal {F}_q\\&= 0.067-0.102i+0.005j-0.001k. \end{aligned} \end{aligned}$$

Thus, under the adaptive controller (10), one can choose \(\nu _1=\nu _2=0.07+0.02i+0.02j+0.01k\). Hence, the conditions in Theorem 3.2 are corrected. Then, the trivial solution of the memristive system (9) can be stabilized by the adaptive controller (10).

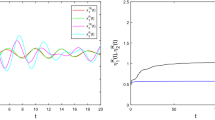
In the numerical simulations, the delay is taken as \(\varsigma (t)=0.5+0.2\sin (2 t)\). Besides, set \(\eta _1=\eta _2=0.5\). The state response with the above conditions is shown in Fig. 1, from which one can see that the states tend to be zero with respect to t, and the control parameters \(\vartheta (t)\) turn out to be constants eventually. The above numerical simulations are in accordance with our main results.

Fig. 1
figure 1

Time evolutions of the states \(\tilde{y}_p (t)\) and trajectories of control parameters \(\vartheta _p(t)\), \(p=1,2\)

Full size image

Remark 4.1

By using the continuous linear state-feedback control method, Wu and Zeng [30] investigated the exponential stabilization of the delayed memristive neural networks. Based on the Lyapunov–Krasovskii functional method and free weighting matrix technique, Wen et al. [29] also studied the exponential stabilization problem of memristive neural networks. By comparison, we can find the above mentioned works are derived based on the LMIs. However, in this paper, the main conclusions are proposed in the form of algebraic inequality, which is very easy to verify.

Besides, the aforementioned memristive system does not involve quaternion connection weights and active functions. For the high-dimensional neural networks, complex-valued neural networks are known as an effective solution for tasks requiring two-dimensional input vectors, while quaternion neural networks are able to learn the local relations that exist within its components through the Hamilton product, which is much more practical to tackle with the multidimensional data in real world. Thus, the conclusions derived in this paper are more general.

Example 2

The highlight of this example is to expound the effectiveness of the technical analysis given in Theorem 3.3 by considering the system expressed in (3) with coefficients given below:

$$\begin{aligned}&a_{11}(x_1(t))=\left\{ \begin{array}{ll} 1.8+1.9 i+1.7 j+1.9 k, &{}\quad |x_1(t)|\le 0, \\ 1.7-1.2 i+1.67 j +k, &{}\quad |x_1(t)|> 0, \end{array}\right. \\&a_{12}(x_1(t))=\left\{ \begin{array}{ll} -0.1-0.1 i-0.09 j-0.11 k, &{}\quad |x_1(t)|\le 0, \\ -0. 2+0.1 i-0.17 j -0.2 k, &{}\quad |x_1(t)|> 0, \end{array}\right. \\&a_{21}(x_2(t))=\left\{ \begin{array}{ll} -2.7-3.7 i -3.4 j-1.7 k, &{}\quad |x_2(t)|\le 0, \\ -2.3-3. 2 i-3.5 j -1.3 k, &{}\quad |x_2(t)|> 0, \end{array}\right. \\&a_{22}(x_2(t))=\left\{ \begin{array}{ll} 3.8+3.9i+2.7 j+ 3.7 k, &{}\quad |x_2(t)|\le 0, \\ 3+3.2 i+2.9 j +3.1 k, &{}\quad |x_2(t)|> 0, \end{array}\right. \\&b_{11}(x_1(t))=\left\{ \begin{array}{ll} -1.5 -1.7 i-1.5 j-1.5 k, &{}\quad |x_1(t)|\le 0, \\ -1.3 -1.34 i -1.3 j - 1.1 k, &{}\quad |x_1(t)|> 0, \end{array}\right. \\&b_{12}(x_1(t))=\left\{ \begin{array}{ll} -0.1- 0.2 i- 0.1 j-0.12 k, &{}\quad |x_1(t)|\le 0, \\ 0.1+0.09 i+0.1 j +0.1 k, &{}\quad |x_1(t)|> 0, \end{array}\right. \\&b_{21}(x_2(t))=\left\{ \begin{array}{ll} -0.3 -0.32 i-0.28 j+ 0. 3 k, &{}\quad |x_2(t)|\le 0, \\ 0.2 +0.22 i+0.18 j +0.1 k, &{}\quad |x_2(t)|> 0, \end{array}\right. \\&b_{22}(x_2(t))=\left\{ \begin{array}{ll} -2-2.2 i- 1.9 j-2.2 k, &{}\quad |x_2(t)|\le 0, \\ -2.5-2.4 i-2.9 j -2.1 k, &{}\quad |x_2(t)|> 0. \end{array}\right. \end{aligned}$$

Besides, \(d_1=d_2=2\), the delays are selected as \(\varsigma (t)=0.5+0.1 \sin ( t)\), the active functions are \(f_q(x_q(t))=0.1 \tanh (x_q(t))\), which comply with the restrictions appeared in \((A_1)\) with \(m_q = 0.1 \), \(\mathcal {F}_q =0.1\), \(q=1,2\).

Fig. 2
figure 2

Time evolutions of the states y(t) without any controller

Full size image

Besides, set \(\tilde{\varrho }_1=\tilde{\varrho }_2=5\), then, a direct consequence of the above parameters and the developed conditions in Theorem 3.3 gives:

$$\begin{aligned} \begin{aligned} 2k_1&\ge -2 d_1 + \tilde{\varrho }_1 m_1^2 + \frac{1}{\tilde{\varrho }_1 } \sum _{q=1}^{2} \tilde{a}_{1q} \bar{\tilde{a}}_{1q} + \frac{1}{\tilde{\varrho }_2 } \sum _{q=1}^{2} \tilde{b}_{1q} \bar{\tilde{b}}_{1q} = 0.67,\\ 2k_2&\ge -2 d_p + \tilde{\varrho }_1 m_p^2 + \frac{1}{\tilde{\varrho }_1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} + \frac{1}{\tilde{\varrho }_2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq}=14.57. \end{aligned} \end{aligned}$$

Thus, one can choose \(k_1=2\), \(k_2=7.5\) and design the control gains as

$$\begin{aligned} \begin{aligned}&\gamma _1=\min _p \left( 2 d_p+2 k_p - \tilde{\varrho }_1 m_p^2 - \frac{1}{\tilde{\varrho }_1 } \sum _{q=1}^{n} \tilde{a}_{pq} \bar{\tilde{a}}_{pq} - \frac{1}{\tilde{\varrho }_2 } \sum _{q=1}^{n} \tilde{b}_{pq} \bar{\tilde{b}}_{pq} \right) =0.43, \\&\gamma _2=\tilde{\varrho }_2 \max _p m_p^2=0.05, \end{aligned} \end{aligned}$$

which implies \(\gamma _1> \gamma _2>0\).

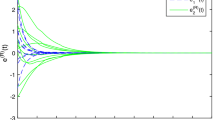
Now, all the conditions derived in Theorem 3.3 are satisfied. The stability of the trivial solution to the controlled system (8) with the designed controller (16) can be shown by the simulation results illustrated in Figs. 2 and 3. The state trajectories of (8) without controller are plotted in Fig. 2, while Fig. 3 exhibits the transient behaviors with the control strategy. As a result, one can see that the control technique performs as expected.

Fig. 3
figure 3

Time evolutions of the states y(t) with the proposed controller (16)

Full size image

5 Conclusion

This paper studies a novel memristor system with the states, connection weights as well as active functions taking values in quaternion field. Based on the theory of set-valued mapping, differential inclusion and vector ordering approach, a comprehensive set of results to ensure the existence of the EP and its stability analysis are developed. What should be pointed is that a partial order is proposed in this paper, which makes the closed convex hull derived by two different quaternion-valued connections meaningful. The analysis motivated by this study suggests some new and interesting dynamical phenomena. In the end, the validity of the proposed methodology is tested by numerical examples.